| Issue |
A&A
Volume 533, September 2011
|
|
|---|---|---|
| Article Number | A42 | |
| Number of page(s) | 10 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201015572 | |
| Published online | 24 August 2011 | |
Dust-driven mass loss from carbon stars as a function of stellar parameters
II. Effects of grain size on wind properties
1
DARK Cosmology Centre, Niels Bohr Institute, University of Copenhagen, Juliane Maries Vej 30, 2100, Copenhagen Ø, Denmark
e-mail: mattsson@dark-cosmology.dk
2
Dept. Physics and Astronomy, Div. of Astronomy and Space Physics, Uppsala University, Box 516, 751 20 Uppsala, Sweden
Received: 11 August 2010
Accepted: 6 July 2011
Context. It is well established that the winds of carbon-rich AGB stars (carbon stars) can be driven by radiation pressure on grains of amorphous carbon and collisional transfer of momentum to the gas. This has been demonstrated convincingly by different numerical wind models that include time-dependent dust formation. To simplify the treatment of dust opacities, radiative cross sections are usually computed using the assumption that the dust grains are small compared to wavelengths around the stellar flux maximum. Considering the typical grain sizes that result from these models, however, the applicability of this small-particle limit (SPL) seems questionable.
Aims. We explore grain size effects on wind properties of carbon stars, using a generalized description of radiative cross sections valid for particles of arbitrary sizes. The purpose of the study is to investigate under which circumstances the SPL may give acceptable results, and to quantify the possible errors that may occur when the SPL does not hold.
Methods. The time-dependent description of grain growth in our detailed radiation-hydrodynamical models gives information about dust particle radii in every layer at every instant of time. Theses grain radii are used for computing opacities and determining the radiative acceleration of the dust-gas mixture. From the large number of models presented in the first paper of this series (based on SPL dust opacities) we selected two samples, i.e., a group of models with strong, well-developed outflows that are probably representative of the majority of wind-forming models, and another group, close to thresholds in stellar parameter space for dust-driven winds, which are referred to as critical cases.
Results. We show that in the critical cases the effect of the generalized description of dust opacities can be significant, resulting in more intense mass loss and higher wind velocities compared to models using SPL opacities. For well-developed winds, however, grain size effects on mass-loss rates and wind velocities are found to be small. Both groups of models tend towards lower degrees of dust condensation compared to corresponding SPL models, owing to a self-regulating feedback between grain growth and radiative acceleration. Consequently, the “dust-loss rates” are lower in the models with the generalized treatment of grain opacities.
Conclusions. We conclude that our previous results on mass-loss rates obtained with SPL opacities are reliable within a wide region of stellar parameter space, except for critical cases close to thresholds of dust-driven outflows where SPL models will tend to underestimate the mass-loss rates and wind velocities.
Key words: stars: AGB and post-AGB / stars: atmospheres / stars: carbon / stars: circumstellar matter / stars: evolution / stars: mass-loss
© ESO, 2011
1. Introduction
Winds of carbon stars are usually considered to be dust-driven winds. Stellar photons, incident on dust particles, will lead to a radiative acceleration of the grains away from the star, and, subsequently, momentum will be transferred to the surrounding gas by gas–grain collisions. Pulsation-induced atmospheric shock waves contribute significantly to this process by intermittently creating cool, dense layers of gas well above the photosphere where dust grains can form and grow efficiently.
Pioneering work on the modelling of AGB star winds was done by Wood (1979), focusing on the effects of shock waves, and later by Bowen (1988), introducing a parameterized opacity to describe the dynamical effects of dust formation in the circumstellar envelope. These early wind models where followed by studies of carbon stars including time-dependent (non-equilibrium) grain growth (e.g., Fleischer et al. 1992; Höfner & Dorfi 1997; Winters et al. 2000) which, despite being based on grey radiative transfer, allowed to describe basic properties of heavily dust-enshrouded carbon stars. In order to obtain reasonably realistic results for objects with less optically thick envelopes, however, it is necessary to combine frequency-dependent radiative transfer (including gas and dust opacities) with time-dependent hydrodynamics and non-equilibrium dust formation (cf. Höfner et al. 2003).
At a point where models of carbon stars are becoming quantitatively comparable to observations as diverse as high-resolution IR spectra (e.g., Nowotny et al. 2010) and spectro-interferometric measurements (e.g., Sacuto et al. 2011), it is necessary to scrutinize a number of underlying physical assumptions and approximations. In particular, this concerns the detailed treatment of dust opacities that are at the core of the wind mechanism and also have a direct influence on observable properties. A common feature of most detailed dust-driven wind models in the literature (including the first paper in this series by Mattsson et al. 2010) is that dust opacities are computed under the assumption that the grain sizes are small compared to the relevant wavelengths (defined by the stellar flux distribution), using the small-particle limit (SPL) of the Mie theory. In this limit, dust opacities are fully determined by the amount of condensed material, irrespective of grain sizes, which greatly simplifies the modelling because an explicit knowledge of the actual grain size distribution in each layer is not required. However, it has been shown that grains may grow to sizes where the use of the SPL is questionable (e.g., Gail & Sedlmayr 1987; Winters et al. 1994, 1997; Mattsson et al. 2010).
The ongoing debate on the mass-loss mechanism of M-type AGB stars has recently put the effects of grain size in these objects into focus. Using detailed non-grey models, Woitke (2006) demonstrated that silicate grains have to be virtually Fe-free in the wind acceleration zone, which leads to insufficient radiative pressure caused by absorption. Models by Höfner (2008) suggest scattering as a possible solution: if conditions in the extended atmosphere allow these grains to grow into the size range of about 0.1–1 μm, scattering becomes dominant over absorption by several orders of magnitude, opening up the possibility of stellar winds driven by scattering on virtually Fe-free silicate grains.
 |
Fig. 1 Relevant dust opacity for radiation pressure (combining effects of absorption and scattering, see Sect. 2) as function of grain radius and wavelength, computed from refractive index data for amorphous carbon by Rouleau & Martin (1991). The black contour shows the region where the flux-weighted monochromatic opacity exceeds the critical opacity, that is required in order for the radiation pressure to balance gravity (see Eqs. (12) and (11), respectively), assuming a Planckian flux distribution with Teff = 2700 K and that 30% of the carbon not bound in CO condense into carbon dust. |
In carbon stars, on the other hand, the effects of grain size are expected to be less dramatic owing to the high absorption cross sections of amorphous carbon grains. As shown in Fig. 1, a wide range of particle sizes can contribute to driving winds, which is different from Fe-free silicates, where small particles are too transparent (cf. Fig. 1 in Höfner 2008). For carbon grains with radii of about 0.1–1 μm, however, the SPL of the Mie theory may severely underestimate the radiative pressure, with possible consequences for the wind properties. The extensive model grid presented by Mattsson et al. (2010, hereafter Paper I) shows that carbon grains in this size range may be quite common, in particular for conditions that allow for efficient grain growth (high C abundance, low effective temperatures, slow winds), indicating a potential inconsistency with the underlying assumption of SPL opacities.
The main objective of this paper is to establish when the small particle approximation can be applied, and to quantify the possible errors that may occur in mass-loss rates, wind velocities, or dust-to-gas ratios in cases where the dust particles grow beyond this regime. For that purpose, we have implemented a generalized description of dust opacities in our models, using actual mean grain sizes and corresponding radiative cross sections that are valid beyond the SPL (see Sect. 2). From the model grid in Paper I (based on the SPL) we select a subgroup of models that show large grains and/or slow winds, and which we therefore can expect to be noticeably affected by the assumptions about dust opacities. Re-computing these models with the newly implemented, generalized treatment of grain opacities gives estimates of the errors introduced by using the small particle limit. It should be noted, however, that the extreme cases discussed here are not necessarily representative of the majority of the wind models in Paper I, but that they rather highlight grain size as a potentially critical property, and presumably give an upper limit of the errors.
2. Modelling method
The results discussed in this paper are based on dynamic atmosphere and wind models that combine non-equilibrium dust formation and frequency-dependent radiative transfer (taking both molecular and dust opacities into account). The effects of stellar pulsation are simulated by a variable inner boundary (“piston” with accompanying luminosity variation) below the stellar photosphere. The general modelling method has been described in detail by Höfner et al. (2003) and Mattsson et al. (2007a, 2010).
The new models presented here include a description of dust opacities that is applicable to grains of arbitrary size, in contrast to our earlier carbon star models, which used a simple limit- case of the Mie theory – valid for particles much smaller than the relevant wavelengths only – irrespective of the actual emerging particle sizes. The more general method of computing radiative cross sections can affect both the radiative energy transfer (temperature structure) and the radiative pressure on dust grains, and, consequently, the acceleration of the wind, if dust particles grow beyond sizes where the SPL holds. Below, we discuss the newly implemented description of dust opacities in detail.
2.1. Dust opacities: dependence on grain size
A crucial quantity in the following discussion is the radiation pressure efficiency factor Qrp, defined as the ratio of the corresponding radiative cross-section, Crp, to the geometric cross-section of a grain, i.e., 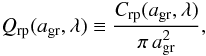 (1)assuming spherical grains with radii agr. The cross section determining radiative pressure is a combination of absorption and scattering cross-sections (Cabs and Csca, respectively),
(1)assuming spherical grains with radii agr. The cross section determining radiative pressure is a combination of absorption and scattering cross-sections (Cabs and Csca, respectively), 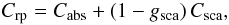 (2)with gsca denoting the mean cosine of the scattering angle, where gsca = 1 corresponds to pure forward scattering (see, e.g., Kruegel 2003). These quantities can be derived from refractive index data of relevant grain materials using the Mie theory. With the definitions given above, the opacity that determines the radiative pressure on an ensemble of dust grains embedded in a gas – with ρ denoting the mass density of the gas-grain mixture – can be expressed as
(2)with gsca denoting the mean cosine of the scattering angle, where gsca = 1 corresponds to pure forward scattering (see, e.g., Kruegel 2003). These quantities can be derived from refractive index data of relevant grain materials using the Mie theory. With the definitions given above, the opacity that determines the radiative pressure on an ensemble of dust grains embedded in a gas – with ρ denoting the mass density of the gas-grain mixture – can be expressed as 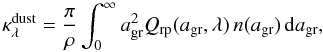 (3)where n(agr) dagr is the number density of grains in the size interval dagr around agr. By defining
(3)where n(agr) dagr is the number density of grains in the size interval dagr around agr. By defining 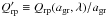 and its grain-size average
and its grain-size average 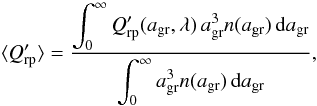 (4)the opacity can be reformulated (without loss of generality) as
(4)the opacity can be reformulated (without loss of generality) as 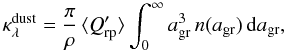 (5)which is a more suitable form for the following discussion.
(5)which is a more suitable form for the following discussion.
In our models the dust particles at distance r from the stellar center, at time t, are described in terms of moments Ki(r,t) of the grain size distribution function n(agr,r,t),  (6)It follows from this definition that K0 is proportional to the total number density of grains (the integral of the size distribution function over all grain sizes), while K1, K2, and K3 are related to the average radius, geometric cross-section and volume of the grains, respectively. The equations determining the evolution of the moments Ki(r,t) (including nucleation, grain growth, and evaporation; cf. Gail & Sedlmayr 1988; Gauger et al. 1990) are described in detail in previous papers (see Höfner et al. 2003, and references therein).
(6)It follows from this definition that K0 is proportional to the total number density of grains (the integral of the size distribution function over all grain sizes), while K1, K2, and K3 are related to the average radius, geometric cross-section and volume of the grains, respectively. The equations determining the evolution of the moments Ki(r,t) (including nucleation, grain growth, and evaporation; cf. Gail & Sedlmayr 1988; Gauger et al. 1990) are described in detail in previous papers (see Höfner et al. 2003, and references therein).
Regarding the computation of dust opacities, the integrals over grain size in Eq. (5) and in the denominator of Eq. (4) are given by the moment K3, while, in general, the time-dependent local grain size distribution in each layer of the model has to be known to evaluate the remaining integral in Eq. (4), involving 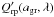 .
.
2.2. The small-particle approximation and its limitations
In the limit case of particles that are much smaller than the relevant photon wavelengths, i.e., 2πagr ≪ λ, however, the problem of computing dust opacities becomes much simpler. According to the Mie theory (see, e.g., Bohren & Huffman 1983), the absorption and scattering efficiencies for small grains behave like Qabs ∝ agr and 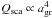 . In this limit, absorption dominates over scattering, implying that Qrp ≈ Qabs, and, consequently, that
. In this limit, absorption dominates over scattering, implying that Qrp ≈ Qabs, and, consequently, that 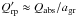 becomes independent of the grain size, making the integration in Eq. (4) trivial. Therefore, provided that 2πagr ≪ λ holds for all relevant wavelengths, the opacity can be reformulated as
becomes independent of the grain size, making the integration in Eq. (4) trivial. Therefore, provided that 2πagr ≪ λ holds for all relevant wavelengths, the opacity can be reformulated as  (7)This expression only depends on the total amount of material condensed into dust (given by K3). Consequently, explicit knowledge of the grain size distribution is not required, which greatly simplifies the modelling. Therefore, many models in the literature, including those presented in Paper I, have used the SPL to describe dust opacities.
(7)This expression only depends on the total amount of material condensed into dust (given by K3). Consequently, explicit knowledge of the grain size distribution is not required, which greatly simplifies the modelling. Therefore, many models in the literature, including those presented in Paper I, have used the SPL to describe dust opacities.
In view of the resulting mean grain sizes for the model grid presented in Paper I, however, it is necessary to investigate the possible effects of size-dependent grain opacities beyond the small particle limit on mass-loss properties of C-type AGB stars. A comparison of Fig. 2 (showing a histogram of typical grain sizes in Paper I) with Fig. 3 (showing the deviations from small particle cross sections as a function of grain size) demonstrates that typical grain sizes are in a range where the small-particle approximation may lead to a considerable underestimation of the radiative pressure.
2.3. Dust opacities beyond the small-particle limit
In principle, the size distribution function n(agr,r,t) can be reconstructed from the moments Ki(r,t), allowing for a general treatment of dust opacities (Eqs. (5) and (4)), but this involves a considerable computational effort, well beyond the scope of this paper. Instead, we test the influence of size-dependent dust opacities on AGB winds with several descriptions that
-
do not require explicit knowledge of the size distribution;
-
are based on the actual moments Ki(r,t); and
-
are not restricted to the small particle limit.
All these descriptions are in the general form of Eq. (5), which means that they are dependent on the total amount of material actually condensed into grains in each layer at a given instant (integral over grain size, proportional to K3), 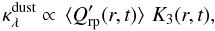 (8)but they use different approximations for
(8)but they use different approximations for 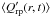 . A common feature of the new models discussed here is that the size-average of
. A common feature of the new models discussed here is that the size-average of 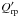 (as defined in Eq. (4)) is approximated by the value of
(as defined in Eq. (4)) is approximated by the value of 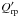 for an average grain size,
for an average grain size,  , in each layer, i.e.,
, in each layer, i.e., 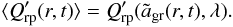 (9)More precisely, we consider the following cases:
(9)More precisely, we consider the following cases:
-
(A)
Models where a fixed grain radius
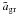 is used when computing
is used when computing 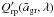 while dust formation (determining K3) is modelled as usual. We study three cases, where
while dust formation (determining K3) is modelled as usual. We study three cases, where 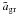 is taken to be either deep in the SPL (10-7 cm), or “optimised” such as to obtain maximum Qrp around the stellar flux maximum (3.55 × 10-5 cm), or very large (10-3 cm). In the “optimised” case, Qrp is about four times higher compared to the SPL at 1 μm (see Fig. 3). Models with a fixed grain radius are considered mainly for reference.
is taken to be either deep in the SPL (10-7 cm), or “optimised” such as to obtain maximum Qrp around the stellar flux maximum (3.55 × 10-5 cm), or very large (10-3 cm). In the “optimised” case, Qrp is about four times higher compared to the SPL at 1 μm (see Fig. 3). Models with a fixed grain radius are considered mainly for reference. -
(B)
Models where
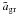 is a mean grain radius derived from the moments Ki(r,t) (with i = 1,2,3), i.e.,
is a mean grain radius derived from the moments Ki(r,t) (with i = 1,2,3), i.e., 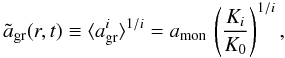 (10)where amon is the monomer radius of the grain material. Which of the three cases gives the best approximation of the true
(10)where amon is the monomer radius of the grain material. Which of the three cases gives the best approximation of the true 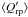 (defined in Eq. (4)) is impossible to say without prior knowledge of the properties of n(agr). Hence, we tested all three cases. The different mean radii
(defined in Eq. (4)) is impossible to say without prior knowledge of the properties of n(agr). Hence, we tested all three cases. The different mean radii 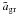 will be referred to as K1, K2 or K3 mean, respectively. From a physical point of view, the K1 mean is simply the mean grain radius resulting from the size distribution as such, while the K2 and K3 means represent grain radii corresponding to the mean grain surface and the mean grain volume, respectively.
will be referred to as K1, K2 or K3 mean, respectively. From a physical point of view, the K1 mean is simply the mean grain radius resulting from the size distribution as such, while the K2 and K3 means represent grain radii corresponding to the mean grain surface and the mean grain volume, respectively.
In all cases the quantity 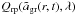 was calculated using the Mie theory for spherical particles of arbitrary size (using the programme BHMIE from Bohren & Huffman 1983, modified by Draine, www.astro.princeton.edu/draine/scattering.html) and refractive index data for amorphous carbon dust taken from Rouleau & Martin (1991)1.
was calculated using the Mie theory for spherical particles of arbitrary size (using the programme BHMIE from Bohren & Huffman 1983, modified by Draine, www.astro.princeton.edu/draine/scattering.html) and refractive index data for amorphous carbon dust taken from Rouleau & Martin (1991)1.
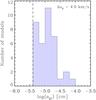 |
Fig. 2 Histogram of resulting mean grain sizes (derived from moment K1 at the outer model boundary; see Eq. (10) and text) for wind-forming models taken from Paper I, with M ⋆ = 1 M⊙ and Δup = 4 km s-1, spanning a range of stellar luminosities, effective temperatures and carbon abundances (see Table 2 in Paper I). The vertical dashed line marks a grain radius of 4 × 10-6 cm where deviations in the opacity from the small-particle limit (SPL) may exceed 10% at wavelength λ = 1 μm (see Fig. 3). |
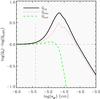 |
Fig. 3 Radiative pressure efficiency factor Qrp and its components Qabs and Qsca, relative to the corresponding small-particle limit (SPL) values QSPL, as functions of grain radius at λ = 1 μm (i.e., near the stellar flux maximum). Data are given for amorphous carbon dust, taken from Rouleau & Martin (1991) and the Q’s are calculated using the Mie theory for spherical particles (programme BHMIE from Bohren & Huffman 1983, modified by Draine, www.astro.princeton.edu/draine/scattering.html). The vertical dashed line marks a grain radius of 4 × 10-6 cm where deviations in the opacity from the SPL may exceed 10% at wavelength λ = 1 μm. |
Input parameters (L ⋆ , Teff, log(C–O), P) and the resulting mean mass-loss rate, mean velocity at the outer boundary and mean degree of dust condensation at the outer boundary, for a subset of models with M ⋆ = 1 M⊙ and Δup = 4.0 km s-1 and the SPL used in the dust opacities.
For completeness sake, we also mention here that the size dependence of the opacity relevant for determining the grain temperature, i.e. 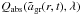 , is treated in a similar way as the radiative pressure.
, is treated in a similar way as the radiative pressure.
3. Definitions and selection of models
An average grain radius less than 4 × 10-6 cm is referred to throughout as “small” regarding radiative cross-sections. This value corresponds to the lower limit of the size range where the actual Qrp (at wavelength λ = 1 μm) may deviate by more than 10% from the value given by the small particle limit (cf. Fig. 3). Below we will also refer to dust opacities as being of type A or type B:, i.e., those with a fixed grain size (type A; for testing) and those using varying characteristic grain sizes based on mean values computed at each time step and spatial grid point throughout the simulation (type B; see Sect. 2 for details).
We present re-computations of two groups of models selected from Paper I, using the modified version of our code (see Sect. 2). The first group of models (numbers 1–12 in Table 1), referred to as “critical cases” in the following, we expect to be significantly affected by including grain-size effects. By “critical” we mean that the flux-mean dust opacity is comparable to the critical opacity, 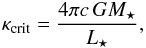 (11)which corresponds to a ratio of unity for (outwards-directed) radiative and (inwards-directed) gravitational acceleration for stellar luminosity L ⋆ and stellar mass M ⋆ (c and G denote the speed of light and the constant of gravity, respectively). In other words, critical cases are defined by a situation where radiation pressure on dust is close to the value required for balancing gravity. In practice this corresponds to models with slow winds in which the dust grains have time to grow larger than usual, and models near some mass-loss threshold in stellar parameter space for which a slight increase/decrease of Qrp could enable or prevent wind formation.
(11)which corresponds to a ratio of unity for (outwards-directed) radiative and (inwards-directed) gravitational acceleration for stellar luminosity L ⋆ and stellar mass M ⋆ (c and G denote the speed of light and the constant of gravity, respectively). In other words, critical cases are defined by a situation where radiation pressure on dust is close to the value required for balancing gravity. In practice this corresponds to models with slow winds in which the dust grains have time to grow larger than usual, and models near some mass-loss threshold in stellar parameter space for which a slight increase/decrease of Qrp could enable or prevent wind formation.
In addition, a “control group” consisting of 12 models with strong, well-developed outflows that also show relatively large average grain sizes (models 13–24 in Table 1) was selected and recomputed for comparison. These models are producing big dust grains according to the definition above (see Fig. 2), but the effects of grain-size dependent opacities may not be that significant, because the momentum transfer efficiency (from radiation to dust and gas) in these cases is near the theoretical maximum, i.e., the single-scattering limit, which corresponds to the mass-loss rate, Ṁ ~ L ⋆ uout/c, where L ⋆ is the luminosity, uout is the flow speed over the outer boundary and c is the speed of light. The optical depth of the wind is high and the wind speed cannot be much affected by an increase of the radiative pressure efficiency factor Qrp.
4. Results and discussion
4.1. Basic tests and constraints
To test the modified code, we have tried to replicate the results from Paper I by adopting a small fixed grain radius agr = 10-7 cm, when calculating 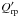 , which should be well within the small particle regime. The average mass-loss rates, wind speeds and mean degrees of dust condensation that we obtained are indeed almost exactly the same as in Paper I, which indicates that the modified code is working properly.
, which should be well within the small particle regime. The average mass-loss rates, wind speeds and mean degrees of dust condensation that we obtained are indeed almost exactly the same as in Paper I, which indicates that the modified code is working properly.
In the opposite limit, i.e., when the particles are much larger than the wavelengths under consideration, Qrp approaches a constant value (see, e.g., Fig. 11 in Paper I), and, consequently, 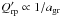 . From Eq. (5) it can therefore be deduced that for a fixed total amount of dust material per volume (represented by the integral over grain size),
. From Eq. (5) it can therefore be deduced that for a fixed total amount of dust material per volume (represented by the integral over grain size), 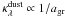 for 2πagr ≫ λ. Because the total amount of grain material per volume is limited by the availability (abundances) of the constituting chemical elements, there is a limiting maximum grain-size where the flux-mean opacity necessarily drops below the critical opacity κcrit and radiative pressure alone cannot overcome gravity.
for 2πagr ≫ λ. Because the total amount of grain material per volume is limited by the availability (abundances) of the constituting chemical elements, there is a limiting maximum grain-size where the flux-mean opacity necessarily drops below the critical opacity κcrit and radiative pressure alone cannot overcome gravity.
Figure 1 illustrates the dependence of the dust opacity on both grain size and wavelength, and shows an estimate of which grain sizes will be relevant for driving winds. The colour scale represents the quantity 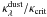 and the black contour marks the region where the monochromatic flux-weighted opacity
and the black contour marks the region where the monochromatic flux-weighted opacity 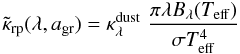 (12)exceeds the critical opacity κcrit, assuming a Planckian flux distribution Bλ with Teff = 2700 K and that 30% of the carbon not bound into CO is condensed into grains (with a free carbon abundance εC − εO = 3.3 × 10-4, M∗ = 1 M⊙, L∗ = 7000 L⊙ and σ denoting the Stefan-Boltzmann constant). An upper limit in grain sizes relevant for driving a wind is clearly apparent from this plot. Adopting a large fixed grain radius (agr = 10-3 cm) should therefore prevent the formation of dust-driven outflows, which is confirmed by our detailed models.
(12)exceeds the critical opacity κcrit, assuming a Planckian flux distribution Bλ with Teff = 2700 K and that 30% of the carbon not bound into CO is condensed into grains (with a free carbon abundance εC − εO = 3.3 × 10-4, M∗ = 1 M⊙, L∗ = 7000 L⊙ and σ denoting the Stefan-Boltzmann constant). An upper limit in grain sizes relevant for driving a wind is clearly apparent from this plot. Adopting a large fixed grain radius (agr = 10-3 cm) should therefore prevent the formation of dust-driven outflows, which is confirmed by our detailed models.
4.2. Recomputed models with optimized type A opacities
By “optimizing” the grain radius used in the opacities for maximum Qrp, we obtain much faster winds and higher mass-loss rates for the critical cases (Models 1–12) compared to using the SPL (see Tables 1 and 2 and Fig. 4, left column). Four out of five cases where SPL models have no resultant wind do indeed have a considerable outflow when using an optimized Qrp. which is roughly a factor of five higher compared to the SPL value.
The actual average grain radius derived from the moment equations for dust formation, i.e., ⟨ agr ⟩ = amon K1/K0, is smaller for models with maximized type A dust opacities compared to SPL models (see Fig. 4). This is a consequence of dust grains having less time to grow; the flow is generally faster and therefore the grains pass through the dust formation zone in a shorter time. In general the mean degrees of dust condensation ⟨ fc ⟩ are lower, which makes the “dust-loss rates” several times lower.
The “control group” of models (13–24) with strong, well-developed dust-driven outflows (when using the SPL) are, as expected, not much affected by maximizing the dust opacity, as far as mass-loss rate and wind velocity are concerned. Those are also models that presumably are quite representative of the majority of wind-producing models in Paper I.
4.3. Recomputed models with type B opacities
In reality, not all grains can obtain the same radii, and especially not the radius that would maximize Qrp. The models with type B dust opacities take into account that Qrp changes in time and space owing to variations of the grain-size distribution, by using a value of 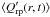 based on different moments of the grain-size distribution (cf. Sect. 2). For the critical-case models, this results in much faster wind speeds and more intense mass loss compared to using the SPL (see Fig. 4). The “control group” of models with strong winds are again much less affected in these respects.
based on different moments of the grain-size distribution (cf. Sect. 2). For the critical-case models, this results in much faster wind speeds and more intense mass loss compared to using the SPL (see Fig. 4). The “control group” of models with strong winds are again much less affected in these respects.
The results are generally quite similar to those of the models with maximized type A opacities, which suggests that the average grain size tends to be such that Qrp is actually close to maximized in the relevant part of the spectrum. The average grain radii are in many cases larger than according to type A models, but still smaller than the grain radii inferred from the K1 moment of the corresponding SPL models in Paper I. The fact that the grain radii tend to be smaller when using the generalized description of dust opacities does not mean that we are approaching the small-particle region again (where the SPL holds exactly), but reflects the effects of self-regulation in the wind mechanism. When dust grains grow beyond the SPL regime, the radiative acceleration becomes more efficient and they are then likely to move away from the dust formation zone faster, which means that they cannot continue to grow. If the momentum transfer from the radiation field to the dust-gas mixture is not sufficient to sustain an outflow, the dust grains may on the other hand continue to grow, which means that small particles (experiencing too little radiation pressure) may grow until they reach optimal size.
The mean degree of dust condensation ⟨ fc ⟩ is typically much lower for critical-case models with type B opacities than for the corresponding SPL models of Paper I, but slightly larger than for models with type A opacities (see Fig. 4). There is one critical K3 mean model (Model 5) that stands out from the rest and shows a ⟨ fc ⟩ value that is several times higher than for the corresponding models with maximized type A opacities, or when 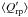 is computed with the K1 and K2 mean grain radii (again, see Fig. 4). The reason is that this particular model shows no net outflow, which means that grain growth is not stopped by falling densities as would be the case in a wind.
is computed with the K1 and K2 mean grain radii (again, see Fig. 4). The reason is that this particular model shows no net outflow, which means that grain growth is not stopped by falling densities as would be the case in a wind.
 |
Fig. 4 From top to bottom: mass-loss rates, wind speeds, mean degrees of dust condensation, dust-to-gas ratios and mean grain radii for models with type A opacities (“optimized Qrp”, first column) and type B opacities (using actual grain sizes based on the moments K1, K2 and K3; Cols. 2–4, respectively) vs. the corresponding quantities in SPL models. The dashed lines show the case of equal values. |
 |
Fig. 5 Mass-loss rates (left panel), wind speeds (middle panel) and mean degree of dust condensation near a “threshold” as function of luminosity. All other stellar parameters are kept the same (M ⋆ = 1 M⊙, Teff = 2600 K, log (C − O) = 8.80). |
4.4. Thresholds for dust-driven winds
In Paper I we argued that for a realistic description of mass loss it is also crucial to know in which parts of stellar parameter space dust-driven mass loss cannot be sustained. Thresholds for dust-driven outflows originate from the simple fact that there exists a critical radiative-to-gravitational acceleration ratio and thus critical values of stellar parameters and element abundances for which the flux-mean opacity equals κcrit (Dominik et al. 1990; Mattson et al. 2007b). In Fig. 5 a threshold in luminosity is shown as an example. The transition regions in parameter space from windless models to strong outflows are not adequately covered with the grid spacing chosen in Paper I. To better resolve the transition region and to quantify the effect of grain-size dependent opacities on the threshold, we have computed a number of additional models close to the expected mass-loss threshold taking smaller steps in log (L ⋆ ) while keeping all other parameters constant. It is evident from the selected models that if the dust grains have the most favorable size (in terms of achieving the highest possible opacity, i.e., using optimized type A opacities), it will be easier to sustain an outflow near a threshold. It is also clear that the wind speed near a mass-loss threshold is significantly affected if the typical grain size is in the optimal range. In Fig. 5 the wind speed is increased by approximately a factor of two relative to the corresponding SPL models. The mass-loss rate differs most at the lowest luminosity, log (L ⋆ /L⊙) = 3.55, in which case grain-size effects mean the difference between no outflow and a sustained dust-driven wind. At the upper end of the tested luminosities, i.e. log (L ⋆ /L⊙) = 3.85, the mass-loss rate is about 50% higher than in the SPL case, while it is almost unaffected for the intermediate values of L ⋆ . The mean degree of dust condensation fc is roughly a factor of two lower compared to the SPL models, like in the critical case models with optimized type A opacities discussed above.
5. Conclusions
In the first paper of this series we presented a large grid of frequency-dependent dynamic models for atmospheres and winds of C-type AGB stars, with the main purpose of providing a more realistic description of dust-driven mass loss as input for stellar evolution models. One of the underlying assumptions of the models, i.e., that dust opacities can be described with the small-particle limit (SPL) of the Mie theory, however, turned out to be questionable with typical emerging grain sizes in a range where the SPL may severely underestimate the actual grain opacities.
Introducing a generalized description of radiative cross sections valid for arbitrary particle radii, we have explored grain size effects on the wind properties of carbon stars. The time-dependent description of grain growth used in our models readily gives particle radii corresponding to various means of the grain size distribution in every layer at every instant of time. To keep the computational effort at a level that will allow the construction of large model grids, we have used descriptions of the dust opacities based on these local mean grain radii.
From the large number of models presented in Paper I we selected two samples, i.e., a group of models with strong, well-developed outflows and another group close to thresholds for dust-driven winds in stellar parameters space, referred to as “critical cases”. For the first group, which is presumably representative of most wind-forming models in Paper I, the effects of grain size on mass-loss rates and wind velocities are small, whereas the critical models show more intense mass loss and (in some cases significantly) higher wind velocities when using the new, generalized description of dust opacities. Models in both groups tend towards lower dust-to-gas ratios, illustrating a self-regulating feedback between grain growth and the increased opacity (and, consequently, higher radiative acceleration) per dust mass. Therefore, in general, the “dust-loss rates” can be expected to be lower than in Paper I.
Extrapolating from the samples investigated here, it seems that the mass-loss rates given in Paper I are reliable, within the limits of current theoretical and observational uncertainties, except for models close to thresholds for dust-driven outflows in stellar parameter space where mass loss is probably underestimated.
Given the results presented here, a full implementation of grain-size-dependent opacities seems to be important as future work. Furthermore, the actual sizes of dust grains may be of great importance for theoretical spectra of dynamic atmosphere models of carbon stars, which we plan to study in the near future.
Note that for all the descriptions of 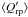 listed above the SPL of the Mie theory is recovered if the assumed or actual grain sizes (in type A or type B opacities, respectively) are much smaller than the relevant wavelengths (defined by the stellar flux distribution), i.e. 2πagr ≪ λ. In particular, opacities of type A with
listed above the SPL of the Mie theory is recovered if the assumed or actual grain sizes (in type A or type B opacities, respectively) are much smaller than the relevant wavelengths (defined by the stellar flux distribution), i.e. 2πagr ≪ λ. In particular, opacities of type A with 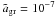 cm should be directly comparable with Paper I.
cm should be directly comparable with Paper I.
Acknowledgments
We thank B. Gustafsson for his comments on the original manuscript draft. Both authors acknowledge support form the Swedish Research Council (Vetenskapsrådet). The Dark Cosmology Centre is funded by the Danish National Research Foundation
References
- Bohren, C. F., & Huffman, D. 1983, Absorption and scattering of light by small particles (New York: John Wiley) [Google Scholar]
- Bowen, G. H. 1988, ApJ„ 329, 299 [Google Scholar]
- Dominik, C., Gail, H.-P., Sedlmayr, E., & Winters, J.M. 1990, A&A, 240, 365 [NASA ADS] [Google Scholar]
- Feast, M. W., Glass, I. S., Whitelock, P. A., & Catchpole, R. M. 1989, MNRAS, 241, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Fleischer, A. J., Gauger, A., & Sedlmayr, E. 1992, A&A, 266, 321 [NASA ADS] [Google Scholar]
- Gail, H.-P., & Sedlmayr, E. 1987, A&A, 171, 197 [NASA ADS] [Google Scholar]
- Gail, H.-P., & Sedlmayr, E. 1988, A&A, 206, 153 [NASA ADS] [Google Scholar]
- Gauger, A., Gail, H.-P., & Sedlmayr, E. 1990, A&A, 235, 345 [NASA ADS] [Google Scholar]
- Höfner, S. 2008, A&A, 491, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Höfner, S., & Dorfi, E. A. 1997, A&A, 319, 648 [NASA ADS] [Google Scholar]
- Höfner, S., Gautschy-Loidl, R., Aringer, B., & Jørgensen, U. G. 2003, A&A, 399, 589 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krügel, E. 2003, The Physics of Interstellar Dust (IoP Series in Astronomy and Astrophysics), ed. E. Kruegel (Bristol: Institute of Physics) [Google Scholar]
- Mattsson, L., Höfner, S., & Herwig, F. 2007a, A&A, 470, 339 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mattsson, L., Wahlin, R., & Höfner, S. 2007b, IAUS, 241, 37 [NASA ADS] [Google Scholar]
- Mattsson, L., Wahlin, R., & Höfner, S. 2010, A&A, 509, A14 (Paper I) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nowotny, W., Höfner, S., & Aringer, B. 2010, A&A, 514, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sacuto, S., Aringer, B., Hron, J., et al. 2011, A&A, 525, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rouleau, F., & Martin, P. G. 1991, ApJ, 377, 526 [NASA ADS] [CrossRef] [Google Scholar]
- Winters, J. M., Dominik, C., & Sedlmayr, E. 1994, A&A, 288, 255 [NASA ADS] [Google Scholar]
- Winters, J. M., Fleischer, A. J., Le Bertre, T., & Sedlmayr, E. 1997, A&A, 326, 305 [NASA ADS] [Google Scholar]
- Winters, J. M., Le Bertre, T., Jeong, K. S., Helling, C., & Sedlmayr, E. 2000, A&A, 361, 641 [NASA ADS] [Google Scholar]
- Woitke, P. 2006, A&A, 460, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wood, P. 1979, ApJ, 227, 220 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Input parameters (L ⋆ , Teff, log(C–O), P) and the resulting mean mass-loss rate, mean velocity at the outer boundary and mean degree of dust condensation at the outer boundary, for a subset of models with M ⋆ = 1 M⊙ and Δup = 4.0 km s-1 and the SPL used in the dust opacities.
All Figures
 |
Fig. 1 Relevant dust opacity for radiation pressure (combining effects of absorption and scattering, see Sect. 2) as function of grain radius and wavelength, computed from refractive index data for amorphous carbon by Rouleau & Martin (1991). The black contour shows the region where the flux-weighted monochromatic opacity exceeds the critical opacity, that is required in order for the radiation pressure to balance gravity (see Eqs. (12) and (11), respectively), assuming a Planckian flux distribution with Teff = 2700 K and that 30% of the carbon not bound in CO condense into carbon dust. |
| In the text | |
 |
Fig. 2 Histogram of resulting mean grain sizes (derived from moment K1 at the outer model boundary; see Eq. (10) and text) for wind-forming models taken from Paper I, with M ⋆ = 1 M⊙ and Δup = 4 km s-1, spanning a range of stellar luminosities, effective temperatures and carbon abundances (see Table 2 in Paper I). The vertical dashed line marks a grain radius of 4 × 10-6 cm where deviations in the opacity from the small-particle limit (SPL) may exceed 10% at wavelength λ = 1 μm (see Fig. 3). |
| In the text | |
 |
Fig. 3 Radiative pressure efficiency factor Qrp and its components Qabs and Qsca, relative to the corresponding small-particle limit (SPL) values QSPL, as functions of grain radius at λ = 1 μm (i.e., near the stellar flux maximum). Data are given for amorphous carbon dust, taken from Rouleau & Martin (1991) and the Q’s are calculated using the Mie theory for spherical particles (programme BHMIE from Bohren & Huffman 1983, modified by Draine, www.astro.princeton.edu/draine/scattering.html). The vertical dashed line marks a grain radius of 4 × 10-6 cm where deviations in the opacity from the SPL may exceed 10% at wavelength λ = 1 μm. |
| In the text | |
 |
Fig. 4 From top to bottom: mass-loss rates, wind speeds, mean degrees of dust condensation, dust-to-gas ratios and mean grain radii for models with type A opacities (“optimized Qrp”, first column) and type B opacities (using actual grain sizes based on the moments K1, K2 and K3; Cols. 2–4, respectively) vs. the corresponding quantities in SPL models. The dashed lines show the case of equal values. |
| In the text | |
 |
Fig. 5 Mass-loss rates (left panel), wind speeds (middle panel) and mean degree of dust condensation near a “threshold” as function of luminosity. All other stellar parameters are kept the same (M ⋆ = 1 M⊙, Teff = 2600 K, log (C − O) = 8.80). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


