| Issue |
A&A
Volume 532, August 2011
|
|
|---|---|---|
| Article Number | A66 | |
| Number of page(s) | 14 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201117144 | |
| Published online | 22 July 2011 | |
Lyman alpha emission from the first galaxies: implications of UV backgrounds and the formation of molecules
1 Kapteyn Astronomical Institute, University of Groningen, PO Box 800, 9700 AV Groningen, The Netherlands
e-mail: latife@astro.rug.nl
2 Leiden Observatory, Leiden University, PO Box 9513, 2300 RA Leiden, The Netherlands
3 ESO Garching, Karl-Schwarzchild-Str.2, 85748 Garching bei Munchen, Germany
4 Physics Department, Technion, Haifa 32000, Israel
Received: 27 April 2011
Accepted: 17 June 2011
The Lyman alpha line is a robust tracer of high redshift galaxies. We present estimates of Lyman alpha emission from a protogalactic halo illuminated by UV background radiation fields with various intensities. For this purpose, we performed cosmological hydrodynamics simulations with the adaptive mesh refinement code FLASH, including a detailed network for primordial chemistry, comprising the formation of primordial molecules, a multi-level model for the hydrogen atom as well as the photo-ionization and photo-dissociation processes in a UV background. We find that the presence of a background radiation field J21 excites the emission of Lyman alpha photons, increasing the Lyman α luminosity up to two orders of magnitude. For a halo of ~ 1010 M⊙, we find that a maximum flux of 5 × 10-15 erg cm-2 s-1 is obtained for J21 × fesc = 0.1, where fesc is the escape fraction of the ionizing radiation. Depending on the environmental conditions, the flux may vary by three orders of magnitude. For J21 × fesc > 0.1 the Lyman alpha luminosity decreases as the atomic hydrogen abundance becomes rather small. The fluxes derived here can be probed using Subaru and the upcoming James Webb Space Telescope. The emission of Lyman alpha photons is extended and comes from the envelope of the halo rather than its core. In the center of the halo, line trapping becomes effective above columns of 1022 cm-2 and suppresses the emission of Lyman alpha. In addition, cooling by primordial molecules may decrease the gas temperature in the central region, which further reduces Lyman α emission. In the central core, H2 is photo-dissociated for a background flux of J21 ≥ 1000. For weaker radiation fields, i.e. J21 < 0.1, H2 and HD cooling are particularly strong in the center of the halo, leading to gas temperatures as low as ~100 K. We also performed a parameter study with different escape fractions of ionizing photons and explored the relative role of ionizing and dissociating radiation. We find that Lyman alpha emission depends more on the strength of the ionizing background. For a constant ionizing background, the Lyman α flux increases at least by an order of magnitude for stronger photodissociation.
Key words: methods: numerical / cosmology: theory / early Universe / galaxies: formation / atomic processes / molecular processes
© ESO, 2011
1. Introduction
The Lyman alpha line is an important probe of the first galaxies as they are potentially strong Lyman alpha emitters. Recently, observations of galaxies have been reported at z > 7 (Bouwens et al. 2011; Bunker et al. 2010; Vanzella et al. 2011). The upcoming James Webb Space Telescope (JWST) will further enhance our ability to detect galaxies at higher redshift by exploring them with higher sensitivity and test our current understanding of early structure formation. The detection of the Lyman alpha line will be a key feature in the observation of galaxies in the early universe.
Numerous Lyman alpha emitters have been detected so far at intermediate redshifts (Lehnert et al. 2010; Steidel et al. 2000; Ouchi et al. 2009; Saito et al. 2008, 2006; Yang et al. 2009; Matsuda et al. 2004). The origin and source of these blobs is still not completely known. The energy sources of these Lyman alpha blobs include photo-ionization by stars or miniquasars (Haiman & Rees 2001; Jimenez & Haiman 2006). Another potential driver of these emitters could be the emission from cold streams and accretion flows (Nilsson et al. 2006; Smith & Jarvis 2007). The accreted gas releases its binding energy in the gravitational potential of the halo, which results in the generation of shocks and the emission of Lyman alpha photons. This scenario has also been supported by theoretical studies and numerical simulations (Haiman et al. 2000; Dijkstra et al. 2006a,b; Yang et al. 2006; Wise et al. 2008; Dijkstra & Loeb 2009; Dekel et al. 2009; Goerdt et al. 2010; Faucher-Giguère et al. 2010; Latif et al. 2011b; Pawlik et al. 2011). Some of the observed Lyman alpha blobs have been associated with massive star forming galaxies (Matsuda et al. 2006).
In our previous study (Latif et al. 2011a), we estimated the emission of Lyman alpha photons from a protogalactic halo in the absence of UV radiation. We found that the emission of Lyman alpha radiation is extended and originates from accretion flows and virial shocks. The situation is however more complicated, due to the presence of ionizing and photodissociating backgrounds, as well as the formation of molecules (Johnson et al. 2007). These are the effects we explore here.
The intense Lyman-Werner background flux can photo-dissociate H2 molecules in atomic cooling halos with virial temperature > 104 K (Machacek et al. 2001; Omukai 2001; Johnson et al. 2007; O’Shea & Norman 2008; Greif et al. 2008; Omukai et al. 2008; Dijkstra et al. 2008; Shang et al. 2010). It is found that the strength of the UV flux below J21 = 103 only delays the collapse and does not quench the formation of H2. Schleicher et al. (2010b) confirmed the previous results and found that for J21 > 103 H2 does not form, but the gas temperature nevertheless declines down to 5000 K due to cooling from higher electronic transitions of hydrogen atom.
The implications of ionizing radiation for the chemistry in the halo are, on the other hand, much more unexplored. During the epoch of reionization, background UV radiation generated by stellar populations will photoionize the intergalactic gas (Gnedin 2000; Schleicher et al. 2008a; Thomas & Zaroubi 2008; Wise & Abel 2008a; Maselli et al. 2009). The recombination following the absorption of stellar photons may further boost the Lyman alpha emission from accretion flows. Furlanetto et al. (2005) found that the photoionizing background can power the Lyman alpha emissivity and can explain the observed Lyman alpha blobs. Our main goal here is to study the impact of background UV on Lyman alpha emission and to see how it influences the spatial emission profile.
Gas ionized by UV radiation cools faster than it recombines, preserving an increased ionization degree. The free electrons act as catalysts in the formation of molecular hydrogen (Saslaw & Zipoy 1967; Galli & Palla 1998; Yoshida et al. 2007). In the absence of dust, H2 formation proceeds via the gas phase, with the dominant formation channel being due to H−: 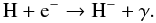 (1)This then leads to H2 formation via the reaction
(1)This then leads to H2 formation via the reaction 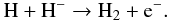 (2)Another prominent coolant in primordial gas is HD. Its dominant formation path is via collisions between H2 molecules and ionized deuterium:
(2)Another prominent coolant in primordial gas is HD. Its dominant formation path is via collisions between H2 molecules and ionized deuterium: 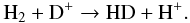 (3)While H2 molecules can cool the gas to a few hundred Kelvin, HD can decrease the temperature even further if it is abundant enough. While the H2 molecule is perfectly symmetric and thus has no permanent dipole moment, the deuterium breaks the symmetry of the molecule, thus creating a small but non-negligible dipole moment. This way, the low energy dipole transitions are no longer forbidden, and the spontaneous emission rates are generally increased.
(3)While H2 molecules can cool the gas to a few hundred Kelvin, HD can decrease the temperature even further if it is abundant enough. While the H2 molecule is perfectly symmetric and thus has no permanent dipole moment, the deuterium breaks the symmetry of the molecule, thus creating a small but non-negligible dipole moment. This way, the low energy dipole transitions are no longer forbidden, and the spontaneous emission rates are generally increased.
In order to investigate the influence of stellar UV radiation on the emissivity of Lyman alpha photons, we have used state-of-the-art high resolution cosmological simulations and include for the first time the detailed chemistry of all relevant processes for primordial gas (i.e., photo-ionization, photo-dissociation, collisional ionization, collisional and radiative recombination and the formation of molecules), treating atomic hydrogen as a multi-level atom and including the effects of line trapping. In this paper, we present a number of simulations with different strengths of background radiation fields and escape fractions of ionizing photons to explore the relative importance of ionizing and photo-dissociating radiation. We follow the collapse of a zero metallicity halo and compute the Lyman α emissivity under different conditions.
This paper is structured as follows. In Sect. 2, we briefly discuss the simulation setup and numerical methods used. In Sect. 3, we give an overview of our chemical model. In Sect. 4, we present the results obtained. Finally, in Sect. 5 we discuss our conclusions.
2. Numerical methodology
To investigate the role of background radiation fields in the emission of Lyman alpha photons from protogalactic halos, we use the code FLASH (Dubey et al. 2009). FLASH is an adaptive mesh, parallel simulations code. It is a module-based Eulerian grid code which can solve a broad range of astrophysics problems. It makes use of the PARAMESH library to handle block structured adaptive grids. It uses the message passing interface (MPI) library to achieve portability and scalability on many different parallel systems. The adaptive mesh technique is used to achieve high dynamic resolution with minimum computational time. We use adaptive mesh refinement (AMR) to add resolution in the regions of interest. We use an unsplit hydro solver with the 3rd order piece-wise parabolic method (PPM) for hydrodynamic calculations (Colella & Woodward 1984). This method is well suited for flows involving shocks and contact discontinuities. A multigrid solver is used to solve for self-gravity (Ricker 2008). The dark matter is simulated based on the particle mesh (PM) method.
We run the COSMICS package developed by Bertschinger (1995) to produce Gaussian random field initial conditions. We make use of constraint realizations implemented in the grafic code (part of the COSMICS package) to select a massive halo. We start our simulation at redshift 100 as determined by COSMICS. Our computational box has a comoving size of 10 Mpc. We use periodic boundary conditions both for hydrodynamics and gravity. We start the simulations with an initial resolution of 5123 grid cells in the central 1 Mpc region and set the rest of the box to a resolution of 1283 grid cells. We initialize 2.6 × 106 particles to compute the evolution of dark matter. For the cosmology, we adopt the ΛCDM model with the WMAP 5-year parameters (Ωm = 0.2581, H0 = 72 km s-1 Mpc-1, Ωb = 0.0441) and a scale-invariant power spectrum with the preferred value of σ8 = 0.8. We select the most massive halo and follow its collapse using the AMR method. We impose 7 additional levels of refinement, which gives 15 levels of refinement in total. This corresponds to a dynamical resolution limit of 75 pc in comoving units. We resolve the Jeans length with a minimum of 20 cells. This should be enough to properly resolve the essential physics, for further details about the significance of resolution criteria see Federrath et al. (2011). This automatically ensures that we also fulfill the Truelove criterion to suppress artificial fragmentation (Truelove et al. 1997).
List of simulations presented in this paper.
3. Chemistry and cooling
Primordial gas is mainly composed of hydrogen and helium. Microphysical processes of these atoms play a vital role in the formation of the first structures. Stars and galaxies are formed in protogalactic halos where collapse is induced due to cooling by hydrogen lines. Lyman alpha line cooling is the dominant process in metal free gas for temperatures down to 8000 K. H2 and HD are the only relevant coolants at temperatures below 104 K (Galli & Palla 1998; Lepp & Shull 1984). Saslaw & Zipoy (1967) were first to realize the importance of molecular hydrogen formation through gas phase reactions. They found that trace amounts of H2 can be formed through gas-phase reactions already at z ~ 300. The rotational and vibrational modes of molecular hydrogen can be excited at low temperatures and cool the gas to a few hundred Kelvin. HD is an important coolant around 100 K and can cool the gas to lower temperatures.
We expect that the metallicity in the IGM may still be close to primordial at high redshift, in particular for isolated halos. For Lyman α emission driven by accretion and infall, adopting a primordial composition thus allows us to capture the dominant effects regulating the emission process. Even for metallicities up to 1% solar, cooling procedes mostly via primordial coolants for the densities in our simulations (Omukai et al. 2005; Jappsen et al. 2007). Depending on the properties of dust grains, they could potentially enhance H2 formation (Cazaux & Spaans 2009). However, we assume here that either the grain-size distribution is such that this effect is not significant, or that the additional H2 formation is suppressed by the photodissociating background. The effects of dust will be explored in more detail in an upcoming paper.
To study the thermal evolution of the gas, it is crucial to model the chemistry of primordial gas in detail. Solving the rate equations self-consistently along with hydrodynamics is a computationally demanding task due to the stiff nature of the reaction network. We devised a chemical network consisting of 36 reactions which involve 23 collisional and 13 radiative processes. The reactions and rate coefficients for these processes and their references are listed in Table 1 of Appendix A. We solve the rate equations of the following 12 species 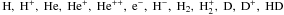 . Our network is based on Anninos et al. (1997); Abel et al. (1997); Schleicher et al. (2008b); Glover & Jappsen (2007), see Appendix A, and includes collisional ionization, radiative recombination, photo-ionization and photo-dissociation rates of all the species. The rate equations for these species are solved using the backward differencing scheme (BDF), see Anninos et al. (1997). The BDF method is not fully implicit but still more accurate and stable than other schemes. We have implemented a comprehensive model for cooling and heating of primordial gas. It comprises collisional excitation cooling, collisional ionization cooling, recombination cooling, Bremsstrahlung cooling, Compton cooling/heating, photo-ionization heating and photo-dissociation heating, as well as a multi-level model for atomic hydrogen line cooling. We also included the cooling due to H2 and HD molecules. The heating/cooling rates are listed in Table 2 of Appendix A. Modeling details of the chemical network are summarized in Appendix A.
. Our network is based on Anninos et al. (1997); Abel et al. (1997); Schleicher et al. (2008b); Glover & Jappsen (2007), see Appendix A, and includes collisional ionization, radiative recombination, photo-ionization and photo-dissociation rates of all the species. The rate equations for these species are solved using the backward differencing scheme (BDF), see Anninos et al. (1997). The BDF method is not fully implicit but still more accurate and stable than other schemes. We have implemented a comprehensive model for cooling and heating of primordial gas. It comprises collisional excitation cooling, collisional ionization cooling, recombination cooling, Bremsstrahlung cooling, Compton cooling/heating, photo-ionization heating and photo-dissociation heating, as well as a multi-level model for atomic hydrogen line cooling. We also included the cooling due to H2 and HD molecules. The heating/cooling rates are listed in Table 2 of Appendix A. Modeling details of the chemical network are summarized in Appendix A.
Another important ingredient of our modeling is the effect of line trapping of Lyman alpha photons. Lyman alpha emission is an efficient cooling process for halos with virial temperatures > 104 K. It is oftenly presumed that gas remains effectively optically thin to Lyman alpha cooling, but large hydrogen column densities produce large optical depths to these lines. At optical depths τ0 > 107, the photon escape time typically becomes longer than gas free fall time. Because of the weak dependence of photon escape time on the gas number density, Tph ∝ n − 1/9, as compared to free fall time, Tff = 1.0/(Gρ)1/2, trapping becomes effective during the process of collapse (Spaans & Silk 2006). A detailed description of our treatment for Lyman alpha trapping and the modeling of the hydrogen line transitions is given in Appendix A.
Schleicher et al. (2010b) found that in the presence of Ly α line trapping, total cooling is compensated as it proceeds through the other transitions of atomic hydrogen. The transition from 2p-1s produces Lyman alpha photons while the transition from 2s-1s produces two continuum photons. These continuum photons are not trapped and cooling proceeds through them, depending on the ambient density. To model all these mechanisms, we have treated atomic hydrogen as multi-level atom by including up to the fifth excited state. We have also considered the electronic transitions from higher levels of hydrogen.
 |
Fig. 1 Density and temperature slices at redshift 5.5. The left-hand panels show density slices through the center of the halo for J21 = 1000, 10, 0.1 from top to bottom and the right-hand panels show the corresponding temperature slices. Velocity vectors are overplotted on the density slices. All plots shown here are for an escape fraction of 1%. |
 |
Fig. 2 Density radial profiles for different background UV fields. The left panel shows density profiles for an escape fraction of 1%. The right panel shows the density profiles for escape fractions of 10% and 50%. |
The radiation produced during the reionization process can have important implications for subsequent structure formation. These photons cannot only photo-heat and ionize the gas but also can photo-dissociate the H2 and HD molecules. The input spectrum is a blackbody with T∗ = 104 K, with the intensity above 13.6 eV reduced by the escape fraction fesc as (Omukai et al. 2008) ![\begin{equation} J_{\nu}^{\rm ex} = J_{21}10^{-21}[B_{\nu}(T_{*})/B_{\nu H}] f(\nu)~ \rm erg~cm^{-2}sr^{-1}s^{-1}Hz^{-1} \label{jrad} \end{equation}](/articles/aa/full_html/2011/08/aa17144-11/aa17144-11-eq55.png) (4)where J21 is the mean intensity of radiation at the Lyman limit, T ∗ is the color temperature of a star. f(ν) is one for non-ionizing photons and equal to fesc for ionizing photons. Bν(T) is the stellar radiation intensity (i.e. black body spectrum),
(4)where J21 is the mean intensity of radiation at the Lyman limit, T ∗ is the color temperature of a star. f(ν) is one for non-ionizing photons and equal to fesc for ionizing photons. Bν(T) is the stellar radiation intensity (i.e. black body spectrum), 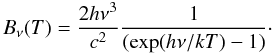 (5)where h is Planck constant, ν is the frequency of radiation, k is Boltzmann constant and T is the radiation temperature. JIH = J21 × fesc represents the ionizing soft UV flux and J21 is the background UV flux below the Lyman limit (i.e. 13.6 eV) in units of 10-21 erg/cm2/s/Hz/sr. While propagating through the intergalactic medium, the photons are attenuated as the optical depth depends on the frequency. In order to approximately account for the effect of self-shielding of gas in the halo, we estimate the optical depth as a function of frequency as
(5)where h is Planck constant, ν is the frequency of radiation, k is Boltzmann constant and T is the radiation temperature. JIH = J21 × fesc represents the ionizing soft UV flux and J21 is the background UV flux below the Lyman limit (i.e. 13.6 eV) in units of 10-21 erg/cm2/s/Hz/sr. While propagating through the intergalactic medium, the photons are attenuated as the optical depth depends on the frequency. In order to approximately account for the effect of self-shielding of gas in the halo, we estimate the optical depth as a function of frequency as 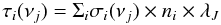 (6)where i denotes the species, j the frequency bin, σ the photo-ionization cross-section of the given species, ni its number density and λJ is the local Jeans length. For a given optical depth, attenuation of the radiation field is calculated as
(6)where i denotes the species, j the frequency bin, σ the photo-ionization cross-section of the given species, ni its number density and λJ is the local Jeans length. For a given optical depth, attenuation of the radiation field is calculated as 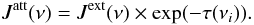 (7)
(7)
 |
Fig. 3 Velocity radial profiles for different background UV fields. The left panel shows the radial velocity profile. Right panel shows the tangential velocity profile of the halo. For the tangential velocity, the average was calculated over the absolute values. So, it is a measure of turbulence rather than rotation. |
 |
Fig. 4 Radial profiles for temperature and species fractions for different background UV fields. The upper left panel of this figure shows the temperature radial profile of the halo. The HII abundance radial profile for the halo is depicted in the upper right panel. H2 abundance is shown in the lower left panel. The HeII radial profile of the halo is depicted in the lower right panel. The escape fraction of ionizing radiation is 1% for all the panels shown. |
 |
Fig. 5 Radial profiles for column density, emissivity, luminosity and flux for various background UV fields. The upper left panel shows the column density radial profile of the halo. The emissivity radial profile for the halo is depicted in the upper right panel, where the dot-dashed line shows the Lyman alpha emissivity and the triple dot-dashed line shows the total emissivity of all the coolants. The lower left panel shows the luminosity radial profile. The flux radial profile of the halo is depicted in the lower right panel. All panels in this figure have an escape fraction of 1% for ionizing photons. |
 |
Fig. 6 Radial profiles for temperature and species fractions for various background UV fields with higher escape fractions of ionizing radiation. The upper left panel of this figure shows the temperature radial profile of the halo. The HII abundance radial profile for the halo is depicted in the upper right panel. H2 abundance is shown in the lower left panel. The HeII radial profile of the halo is depicted in the lower right panel. The legend in each panel shows the values of the escape fraction of ionizing photons and the strength of the background radiation field. |
 |
Fig. 7 Radial profiles for column density, emissivity, luminosity and flux for various background UV fields with higher escape fractions of ionizing radiation. The upper left panel shows the column density radial profile of the halo. The emissivity radial profile for the halo is depicted in the upper right panel, where the dot-dashed line shows the Lyman alpha emissivity while the triple dot-dashed line shows the total emissivity of all the coolants. The lower left panel shows the luminosity radial profile. The radial profile of the enclosed flux from the halo is depicted in the lower right panel. The legend in each panel shows the values of the escape fraction of ionizing photons and the strength of the background radiation field. |
 |
Fig. 8 Cooling rates of H2, HD, as well as H(2p–1s), H(2s–1s) and H(3–2) transitions are plotted against radius in both panels. Left panel is for J21 = 1000 with a 1% escape fraction of ionizing radiation. Right panel is for J21 = 0.1 with an escape fraction of 10%. |
4. Results
We perform nine cosmological simulations with different strengths of the background UV field and escape fractions of ionization radiation as listed in Table 1. We start our simulations at redshift 100. We note that density perturbations decouple from the Hubble flow and begin to collapse through gravitational instabilities. During the non-linear evolution phase gas collapses in the dark matter potentials and gets shock heated. We select a halo of 109 M⊙ at redshift 10 and follow its collapse down to redshift 5.5. At a redshift of about 8, gas becomes photo-ionized as we switch on the ionizing background produced by reionization. The temperature of the gas is raised above 104 K due to photo-ionization heating depending upon the strength of the background flux. Photo-ionized gas recombines and begins to cool and collapse because of recombination cooling. The virialization process continuously transforms the gravitational potential energy into kinetic energy of gas and dark matter. Due to the dissipative nature of the gas, part of the gravitational energy goes into thermal energy and is radiated away. During virialization, the gas becomes turbulent and settles in the center of a halo through cold streams as shown in Fig. 1. The temperature of the gas in filamentary accretion is ~104 K and densities are 10-2 − 1 cm-3. The density radial profiles are shown in Fig. 2. It can be seen from the figure that density varies with distance r like r-2.8. Our simulations reach a maximum density of a few times 105 cm-3. Small fluctuations in the density radial profiles are due to the clumpiness of the medium as the halo is not perfectly symmetric. We show the radial velocity profile for three selected cases in the left panel of Fig. 3. The figure shows that gas is falling into the center of the halo. The variations in the radial velocity profile at the outer radii are due to different accretion rates for various background radiation fields. The gas in the center of the halo becomes stable. The right panel of Fig. 3 shows the tangential velocity radial profile. Variations in tangential velocity are caused by shocks. The total rms velocity hardly depends on the radiation field, as it is mostly due to the virial temperature. We find typical velocities of about ~50 km s-1 as expected from the virial temperature. Virialization shocks also play an important role in the emission of Lyman alpha, for further details see Latif et al. (2011a).
We see that for J21 < 10, the temperature of the gas is ~104 K while for higher intensities (i.e. J21 > 10) it reaches 105 K. The temperature of 105 K is driven by the ionization of helium, which absorbs more energetic photons. Cooling due to helium lines becomes effective at temperatures above 5 × 104 K and keeps the gas temperature at ~105 K. At densities of 1 cm-3, cooling due to radiative recombination becomes very effective and cools the gas down to 104 K. The gas in the surroundings of the halo remains hot (>104 K) as shown in the top left panel of Fig. 4. Similarly, the degree of ionization varies depending upon the impinging radiation intensity, as shown in the upper right panel of Fig. 4. It is small for lower fluxes and large for higher fluxes. We also see that helium remains mostly neutral for lower fluxes and becomes singly ionized for a stronger radiation background. The He+ abundance is shown in the bottom right panel of Fig. 4. At densities > 1 cm-3, the recombination rate becomes high and the gas begins to recombine. Consequently, the degree of ionization declines.
For low background fluxes, a H2 abundance of 10-6 is formed at low densities (i.e. 10-2 cm-3) and a temperature of 104 K, while its formation remains inhibited for higher fluxes at low densities. For a high background radiation field, i.e., J21 ≥ 1000, H2 is photo-dissociated even in the center of the halo. For weaker radiation fields photo-dissociation of molecular hydrogen becomes ineffective and the H2 abundance reaches the universal value (i.e., 10-3). The H2 radial profile for different fluxes is shown in the bottom left panel of Fig. 4. Our results are consistent with previous studies (Shang et al. 2010; Dijkstra et al. 2008; Bromm & Loeb 2003; Johnson et al. 2011). We also computed the column densities for different background fluxes, finding that the column density is higher for low fluxes in the envelope of a halo due to a higher neutral gas fraction. Conversely, the column is low for higher radiation field strengths because of a higher ionization degree. The upper left panel of Fig. 5 shows the column density radial profile.
Based on these results, we computed the emissivity of Lyman alpha photons, finding that it is enhanced in the presence of a background incoming radiation field. It increases with the strength of the radiation field up to 10-22 erg/cm2/s/Hz/sr (i.e., J21 × fesc) and then starts to decline for higher intensity. This decline in emissivity is a consequence of the decreasing abundance of atomic hydrogen. At columns higher than 1022 cm-2, trapping of Lyman alpha becomes effective and consequently the emission of Lyman alpha photons diminishes while cooling still proceeds through higher electronic transitions of hydrogen. For a fixed ionizing background, the emission increases with increasing photo-dissociation flux. The emissivity of Lyman alpha photons as well as the total emissivity is plotted against radius in the upper right panel of Fig. 5. Lyman alpha emission is higher in the envelope of the halo and sharply declines towards the center. This behavior of Lyman alpha emission is due to line trapping of Lyman alpha photons and is consistent with previous studies (Latif et al. 2011a; Schleicher et al. 2010b; Spaans & Silk 2006). In addition to the line trapping, also the cooling by H2 and HD may prevent Lyman alpha emission, as it drives the gas to lower temperatures (i.e. the run J21 = 10). The total emissivity remains roughly constant as cooling is compensated by two-photon continuum processes. Moreover, for higher background radiation field strengths the total emissivity from hydrogen electronic states is higher than for low radiation fields. This is due to a higher molecular hydrogen fraction for low fluxes and a lower H2 fraction for high fluxes through photodissociation. The local variations in emissivity are because of the clumpiness of the medium.
The enclosed Lyman alpha luminosity as a function of radius is shown in the bottom left panel of Fig. 5. The luminosity increases with the strength of the ionizing radiation field up to 0.1 (in units of J21) and then decreases with increasing radiation field strength similar to the emissivity. Luminosity values are of the order of 1043 − 1046 erg s-1 which are comparable to observed Lyman alpha blobs as well as estimates from numerical simulations (Ouchi et al. 2009; Lehnert et al. 2010; Goerdt et al. 2010; Dijkstra et al. 2006a). We also computed the flux. We found that the flux mostly emerges from the envelope of a halo rather than its center and is significantly enhanced in the presence of a background UV field. The total flux varies from 10-18 − 10-15 erg/cm2/s depending upon the ambient radiation field strength. Our results are in agreement with our previous finding that emission of Lyman alpha is extended and emerges from the hot gas in the surroundings of a halo.
Due to large uncertainties in the escape fraction of ionizing radiation (Fernandez & Shull 2011), we have performed a number of simulations to assess the impact of different escape fractions on the emissivity of Lyman alpha photons. We performed simulations with escape fractions of 1%, 10% and 50% for a background radiation field of J21 = 0.01 and 0.1. We found that for a similar value of J21 describing the strength of photodissociation, an increasing escape fraction of ionizing photons enhances the temperature of the gas. Radial profiles of temperature, H+, He+ and H2 abundances are shown in Fig. 6. As expected, the degree of ionization increases for higher escape fraction. The gas is still neutral in the center of the halo but becomes ionized in the surroundings. Column density is shown in the upper right panel of Fig. 7. It is similar to the case with low escape fraction. Differences in the columns is due to different gas ionization fractions. The upper left panel of Fig. 7 shows the emissivity of Lyman alpha photons. It is found that for the same background value of J21, the emissivity is enhanced for higher escape fractions. It reaches a maximum in the envelope of the halo and sharply drops as trapping becomes effective in the center. The total emissivity is again compensated by cooling through higher states of hydrogen atoms. There are some local variations in the emissivity profile due to the density structure, fluctuations in temperature and the ionization degree. We also computed the luminosity and flux for this case and found that the flux is boosted for a higher escape fraction. The radial profiles of luminosity and flux are shown in the bottom panels of Fig. 7. Luminosities and fluxes for all cases are summarized in Table 1.
We also computed the emissivity of various coolants to assess their relative importance for the cooling. We here show three typical cases for background UV fluxes of J21 = 0.01, 0.1 and 1000. Radial profiles of cooling rates from H(2p − 1s), H(2s − 1s) and H(3 − 2) transitions as well as H2 and HD ro-vibrational transitions are shown in Figs. 8 and 9. The left panel of Fig. 8 shows the cooling rates for J21 = 1000. It is found that at radii > 3 × 1020 cm cooling is only coming from electronic transitions of hydrogen. Notable transitions are H(2p–1s), H(2s–1s) and H(3–2). The population of these transitions is regulated by radiative de-excitation and collisional excitation, which makes them efficient coolants. The cooling from H2 and HD remains negligible at these radii. At radii between 3 × 1020 − 1020 cm line trapping of Lyman alpha photons becomes effective and two-photon continuum emission (2s-1s transition) becomes dominant. In the center of the halo ( < 1020 cm) cooling is regulated by trace amounts of molecular hydrogen. The right panel of Fig. 8 shows the cooling rates for J21 = 10. At radii > 1021 cm cooling is dominated by electronic transitions of hydrogen. Molecular hydrogen becomes an effective coolant for radii between 1021 − 1020 cm as cooling from electronic transitions of hydrogen becomes negligible due to lower gas temperatures. In the core of the halo, HD cooling dominates over H2 cooling for J21 ≤ 0.1. It can be seen in Fig. 9 that, similar to previous cases, at radii > 1021 cm the halo is cooled by electronic transitions of hydrogen. Emission from these transitions becomes negligible at lower radii due to lower gas temperatures (<103 K). Again, cooling in the center of the halo is dominated by HD.
5. Discussion and conclusions
We have performed 9 simulations in total to investigate the role of the UV background radiation field in the emission of Lyman alpha photons. We used the adaptive mesh refinement code FLASH to carry out cosmological simulations and coupled it with a chemical network that solves the rate equations of 12 species. Our chemical network includes collisional ionization, radiative recombination, photo-ionization and photo-dissociation processes, the formation of molecules and a multi-level model of atomic hydrogen. We found that the presence of a background flux photo-ionizes the gas and raises the gas temperature to ≥ 104 K. We found that for weak radiation fields (J21 < 100), cooling due to H2 decreases the temperature to at least 1000 K. For J21 < 0.1, cooling by HD is important as well, leading to gas temperatures of ~100 K. We note that the HD cooling function was recently revisited by Coppola et al. (2011). However, they only find differences at high temperatures, where H2 dominates the cooling. The thermal evolution in these cases is remarkably different and provides an environment conducive to star formation in the halos irradiated by weaker radiation fields, while stronger fields may lead to the formation of massive objects.
We noted that the ubiquity of background flux enhances the emission of Lyman alpha photons. We found that the emission of Lyman alpha photons is boosted with ionizing flux up to 10-22 erg/cm2/s/Hz/sr. The emission starts to decrease for higher values of the ionizing flux. This decline in the emissivity of Lyman alpha photons is because of the small abundance of atomic hydrogen in the presence of intense radiation fields. The flux predominantly arises from collisional excitation of atomic hydrogen. We found that the contribution from the recombination is at least few orders of magnitudes smaller.
 |
Fig. 9 Radial profiles of different coolants as mentioned in the legend for a background radiation field of J21 = 0.01 and a 1% escape fraction of ionizing radiation. |
We also noted that the emission of Lyman alpha photons emerges from the envelope of a halo rather than its center. At columns above 1022 cm-2 trapping of Lyman alpha photons becomes effective and consequently the emissivity drops sharply above these columns. Our results are consistent with previous studies (Spaans & Silk 2006; Schleicher et al. 2010b; Latif et al. 2011b). We also computed the flux emanating from the halo. We find that the flux is of the order of 10-17−5 × 10-15 erg/cm2/s for different background UV fluxes. Similar to the emissivity, the flux is extended and comes from the relatively hot gas in the outskirts of a halo. The Lyman alpha wavelength observed at redshift 5.5 will be 0.79 μm. This should be detectable with the upcoming telescope JWST. NIRcam/NIRSpec instruments available on JWST will be well suited for its detections. The mass of our halo is 1010 M⊙ and has an angular size of 0.52 arcsec at redshift 5.5, attainable by JWST. Subaru telescope will also be able to detect this flux using suprime-cam in combination with intermediate-band filters (IA679, IA505) as discussed in the previous studies, see Saito et al. (2006). Our results are in the range of planned surveys in future with Subaru which will make use of next-generation wide-field camera, Hyper Suprime-Cam, and several narrowband filters. We also computed the surface brightness profiles for different background UV fluxes which are shown in Fig. 10. The surface brightness profiles are flat as most of the flux emerges from the envelope of a halo rather than its core. They are comparable to the previously observed values (Saito et al. 2006; Ouchi et al. 2009).
In the presence of large velocity gradients, line trapping of Lyman alpha photons does not remain effective. For τ > 107, only photons far-away in the line wings will be able to escape. Trapping in our case occurs at radii >1020.5 cm, where large velocity gradients are significantly reduced. Scattering of Lyman alpha photons which perform a random walk in frequency and space space will blue shift the frequencies leading to an upper limit on the trapping time ~ tff(Δv/v) (Rees & Ostriker 1977). Although, there are some uncertainties in the diffusion time scale. The issue of trapping has been studied in detail by Spaans & Silk (2006). They found that weak dependence of photon escape time on number density (tesc ∝ n − 1/9) as compared to the free fall time results in tesc/tff ~ n7/18. Consequently, trapping will remain effective.
We found that the critical value of the background UV flux for H2 formation is J21 = 1000, which is in accordance with previous estimates (Omukai 2001; Bromm & Loeb 2003; Wise & Abel 2007; Shang et al. 2010). We also noticed that the HD abundance remains lower than the critical value (i.e.,10-6) for J21 > 0.1. It could be due to little amount of H2 formation and direct photodissociation of HD. Consequently, HD cooling becomes important for lower values of background flux (i.e.,J21 < 0.1). Our results are consistent with the critical value of UV flux for HD derived by Wolcott-Green & Haiman (2011). Collisions produce trace amounts of HD at high densities which is too small to dominate the cooling for higher values of J21. It has been found that HD cooling is mainly controlled by H2 formation rather than direct dissociation. For further details on the role of UV radiation in the formation of HD and its implications for the structure formation see dedicated studies McGreer & Bryan (2008); Wolcott-Green & Haiman (2011). We also performed simulations to take into account the local variations in the background flux, i.e., J21 = 100 and 1000. We found that for these cases, emission of Lyman alpha photons is reduced, even for an escape fraction of even 1%, compared to cases with lower values of J21 = 0.1 and 0.01. However, these are rare occurences, which will only apply in the near vicinity of sources (immediate neighbours). We also studied a few cases for different escape fractions up to 50%, and found that a higher escape fraction of ionizing photons enhances the emissivity of Lyman alpha photons. We also computed the emission in the helium Lyman alpha line and found that it is considerably weaker than HI Ly α, due to the low abundance of ionized helium in the halo. This may, however, be different in the presence of an AGN or HII regions from massive stars. Further discussion on helium lines can be found in Yang et al. (2006) and Haiman et al. (2000).
In our case, ionization predominantly occurs at low densities. Therefore, the contribution of the Lyman alpha recombination emission is a few orders of magnitude lower than the collisionally excited line emission. At radii 1020.5 cm, emission diminishes as Lyman alpha line trapping becomes effective in the center. In the case of radiation sources at high densities, recombination emission could be more important. We have further assumed that the background UV flux is constant in time, although we do not expect significant differences if a more detailed model of the time evolution of the UV flux is adopted. Dijkstra et al. (2004) found that the impact of a radiation background is less at high redshift (z > 10) as compared to z = 3 due to different properties of the halo.
In light of these results, it will be important to obtain a better understanding of the environmental conditions, in particular the strength of the UV background radiation field, for ~1010 M⊙ halos close to the reionization epoch. We are further planning to assess additional uncertainties, in particular those related to the metallicity of the gas.
 |
Fig. 10 Surface brightness radial profiles for different background UV fields. The left panel shows the surface brightness profiles for an escape fraction of 1%. The right panel shows the surface brightness radial profiles for escape fractions of 10% and 50%. |
We have assumed here that the halo is metal free for the reasons mentioned in Sect. 3. Indeed pristine halos may exist down to redshift 6 (Trenti et al. 2009). The presence of small amounts of dust may absorb the Lyman alpha photons and re-emit them as continuum at lower frequencies. This can change the scenario. Nevertheless, if the medium is inhomogeneous, escape of Lyman α becomes possible again (Haiman & Spaans 1999; Neufeld 1991), also see Gould & Weinberg (1996); Hansen & Oh (2006); Shimizu et al. (2011). H2 formation is significantly enhanced even for low dust abundances of 10-5 − 10-4 solar (Cazaux & Spaans 2009). The impact of dust on Lyman alpha emission is an important issue and needs a dedicated study. In an upcoming paper we will explore the influence of dust on the emission of Lyman alpha in detail. The ubiquity of outflows may even enhance the emission of Lyman alpha photons up to 5%, by directly injecting them along the line of sight (Dijkstra & Wyithe 2010) while the presence of turbulence may amplify magnetic fields in these protogalaxies, which may affect subsequent star formation (Schleicher et al. 2010a).
We adopted a background UV flux with a T ∗ = 104 K thermal spectrum, typical for radiation dominated by Pop II stars when z < 6. The H2 abundance is mainly controlled by H − photodissociation for a soft UV spectrum in our simulations. For higher radiation temperatures, it will be governed by H2 photodissociation. This may have a strong impact on the critical J21 values of H2 and HD. If Pop III stars with T ∗ = 105 K dominate the UV background, then the critical value of J21 required for the photo-dissociation of H2 increases by two orders of magnitude as computed by previous studies (Bromm & Loeb 2003; Wise & Abel 2007; Shang et al. 2010). On the other hand, for a T ∗ = 105 K blackbody spectrum, an almost 100 times smaller value for the ionizing UV background suffices to photo-ionize the gas. So, our estimates may vary for a harder spectrum (i.e., 105 K) but we do not expect a big change in the overall conclusions.
Our results include local radiative transfer effects but nonetheless are comparable to complete radiative transfer studies (Dijkstra et al. 2006a,b; Thomas & Zaroubi 2008; Wise & Abel 2008b; Verhamme et al. 2008; Maselli et al. 2009; Hocuk & Spaans 2010; Faucher-Giguère et al. 2010; Zheng et al. 2010, 2011). Lyman alpha radiative transfer strongly depends on the density and velocity profile of a halo due to the resonance nature of the Lyman alpha line and its large scattering cross section. Therefore, we expect some variation in the emergent Lyman alpha flux due to the presence of anisotropies in HI columns along different lines of sight.
We have also ignored the impact of X-rays on the emission of Lyman alpha photons. The presence of X-rays will heat the gas and increase the emissivity of Lyman alpha. Lyman alpha blobs powered by X-ray sources have already been detected (roughly 17% of the observed sources, Geach et al. 2009). Due to complex chemistry involved in the modeling, X-ray sources demand complete radiative transfer simulations to probe their impact on Lyman alpha emission. We intend to pursue this in the future.
Acknowledgments
The FLASH code was in part developed by the DOE-supported Alliance Center for Astrophysical Thermonuclear Flashes (ACS) at the University of Chicago. We thank Robi Banerjee, Christoph Federrath and Seyit Hocuk for discussions on the FLASH code. DRGS acknowledges funding via the European Community Seventh Framework Programme (FP7/2007-2013) under grant agreement No. 229517. Our simulations were carried out on the Gemini machines at the Kapteyn Astronomical Institute, University of Groningen. We thank the anonymous referee for a careful reading of the manuscript and valuable feedback.
References
- Abel, T., Anninos, P., Zhang, Y., & Norman, M. L. 1997, New Astron., 2, 181 [Google Scholar]
- Anninos, P., Zhang, Y., Abel, T., & Norman, M. L. 1997, New Astron., 2, 209 [Google Scholar]
- Bertschinger, E. 1995, [arXiv:astro-ph/9506070] [Google Scholar]
- Bouwens, R. J., Illingworth, G. D., Labbe, I., et al. 2011, Nature, 469, 504 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bromm, V., & Loeb, A. 2003, ApJ, 596, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Bunker, A. J., Wilkins, S., Ellis, R. S., et al. 2010, MNRAS, 409, 855 [NASA ADS] [CrossRef] [Google Scholar]
- Cazaux, S., & Spaans, M. 2009, A&A, 496, 365 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Colella, P., & Woodward, P. R. 1984, J. Comput. Phys., 54, 174 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Coppola, C. M., Lodi, L., & Tennyson, J. 2011, MNRAS, 415, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Dekel, A., Birnboim, Y., Engel, G., et al. 2009, Nature, 457, 451 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Dijkstra, M., & Loeb, A. 2009, MNRAS, 400, 1109 [NASA ADS] [CrossRef] [Google Scholar]
- Dijkstra, M., & Wyithe, J. S. B. 2010, MNRAS, 408, 352 [NASA ADS] [CrossRef] [Google Scholar]
- Dijkstra, M., Haiman, Z., Rees, M. J., & Weinberg, D. H. 2004, ApJ, 601, 666 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Dijkstra, M., Haiman, Z., & Spaans, M. 2006a, ApJ, 649, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Dijkstra, M., Haiman, Z., & Spaans, M. 2006b, ApJ, 649, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Dijkstra, M., Haiman, Z., Mesinger, A., & Wyithe, J. S. B. 2008, MNRAS, 391, 1961 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Bertoldi, F. 1996, ApJ, 468, 269 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dubey, A., Antypas, K., Ganapathy, M. K., et al. 2009, Parallel Computing, 35, 512 [CrossRef] [Google Scholar]
- Faucher-Giguère, C., Kereš, D., Dijkstra, M., Hernquist, L., & Zaldarriaga, M. 2010, ApJ, 725, 633 [NASA ADS] [CrossRef] [Google Scholar]
- Federrath, C., Sur, S., Schleicher, D. R. G., Banerjee, R., & Klessen, R. S. 2011, ApJ, 731, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Fernandez, E. R., & Shull, J. M. 2011, ApJ, 731, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Furlanetto, S. R., Schaye, J., Springel, V., & Hernquist, L. 2005, ApJ, 622, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Galli, D., & Palla, F. 1998, A&A, 335, 403 [NASA ADS] [Google Scholar]
- Geach, J. E., Alexander, D. M., Lehmer, B. D., et al. 2009, ApJ, 700, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Glover, S. C. O., & Jappsen, A. 2007, ApJ, 666, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Glover, S. C. O., & Savin, D. W. 2009, MNRAS, 393, 911 [NASA ADS] [CrossRef] [Google Scholar]
- Gnedin, N. Y. 2000, ApJ, 535, 530 [NASA ADS] [CrossRef] [Google Scholar]
- Goerdt, T., Dekel, A., Sternberg, A., et al. 2010, MNRAS, 407, 613 [Google Scholar]
- Gould, A., & Weinberg, D. H. 1996, ApJ, 468, 462 [NASA ADS] [CrossRef] [Google Scholar]
- Greif, T. H., Johnson, J. L., Klessen, R. S., & Bromm, V. 2008, MNRAS, 387, 1021 [NASA ADS] [CrossRef] [Google Scholar]
- Haiman, Z., & Spaans, M. 1999, ApJ, 518, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Haiman, Z., & Rees, M. J. 2001, ApJ, 556, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Haiman, Z., Spaans, M., & Quataert, E. 2000, ApJ, 537, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Hansen, M., & Oh, S. P. 2006, MNRAS, 367, 979 [NASA ADS] [CrossRef] [Google Scholar]
- Hocuk, S., & Spaans, M. 2010, A&A, 522, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jappsen, A., Glover, S. C. O., Klessen, R. S., & Mac Low, M. 2007, ApJ, 660, 1332 [NASA ADS] [CrossRef] [Google Scholar]
- Jimenez, R., & Haiman, Z. 2006, Nature, 441, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, J. L., Greif, T. H., & Bromm, V. 2007, ApJ, 665, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, J. L., Khochfar, S., Greif, T. H., & Durier, F. 2011, MNRAS, 410, 919 [NASA ADS] [CrossRef] [Google Scholar]
- Latif, M. A., Schleicher, D. R. G., Spaans, M., & Zaroubi, S. 2011a, MNRAS, L217 [Google Scholar]
- Latif, M. A., Zaroubi, S., & Spaans, M. 2011b, MNRAS, 411, 1659 [NASA ADS] [CrossRef] [Google Scholar]
- Lehnert, M. D., Nesvadba, N. P. H., Cuby, J., et al. 2010, Nature, 467, 940 [NASA ADS] [CrossRef] [Google Scholar]
- Lepp, S., & Shull, J. M. 1984, ApJ, 280, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Lipovka, A., Núñez-López, R., & Avila-Reese, V. 2005, MNRAS, 361, 850 [NASA ADS] [CrossRef] [Google Scholar]
- Machacek, M. E., Bryan, G. L., & Abel, T. 2001, ApJ, 548, 509 [NASA ADS] [CrossRef] [Google Scholar]
- Maselli, A., Ciardi, B., & Kanekar, A. 2009, MNRAS, 393, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Matsuda, Y., Yamada, T., Hayashino, T., et al. 2004, AJ, 128, 569 [NASA ADS] [CrossRef] [Google Scholar]
- Matsuda, Y., Yamada, T., Hayashino, T., Yamauchi, R., & Nakamura, Y. 2006, ApJ, 640, L123 [NASA ADS] [CrossRef] [Google Scholar]
- McGreer, I. D., & Bryan, G. L. 2008, ApJ, 685, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Neufeld, D. A. 1991, ApJ, 370, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Nilsson, K. K., Fynbo, J. P. U., Møller, P., Sommer-Larsen, J., & Ledoux, C. 2006, A&A, 452, L23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Omukai, K. 2001, ApJ, 546, 635 [NASA ADS] [CrossRef] [Google Scholar]
- Omukai, K., Tsuribe, T., Schneider, R., & Ferrara, A. 2005, ApJ, 626, 627 [NASA ADS] [CrossRef] [Google Scholar]
- Omukai, K., Schneider, R., & Haiman, Z. 2008, ApJ, 686, 801 [NASA ADS] [CrossRef] [Google Scholar]
- O’Shea, B. W., & Norman, M. L. 2008, ApJ, 673, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Ouchi, M., Ono, Y., Egami, E., et al. 2009, ApJ, 696, 1164 [NASA ADS] [CrossRef] [Google Scholar]
- Pawlik, A. H., Milosavljević, M., & Bromm, V. 2011, ApJ, 731, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Rees, M. J., & Ostriker, J. P. 1977, MNRAS, 179, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Ricker, P. M. 2008, ApJS, 176, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Saito, T., Shimasaku, K., Okamura, S., et al. 2006, ApJ, 648, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Saito, T., Shimasaku, K., Okamura, S., et al. 2008, ApJ, 675, 1076 [NASA ADS] [CrossRef] [Google Scholar]
- Saslaw, W. C., & Zipoy, D. 1967, Nature, 216, 976 [NASA ADS] [CrossRef] [Google Scholar]
- Schleicher, D. R. G., Banerjee, R., & Klessen, R. S. 2008a, Phys. Rev. D, 78, 083005 [NASA ADS] [CrossRef] [Google Scholar]
- Schleicher, D. R. G., Galli, D., Palla, F., et al. 2008b, A&A, 490, 521 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schleicher, D. R. G., Banerjee, R., Sur, S., et al. 2010a, A&A, 522, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schleicher, D. R. G., Spaans, M., & Glover, S. C. O. 2010b, ApJ, 712, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Shang, C., Bryan, G. L., & Haiman, Z. 2010, MNRAS, 402, 1249 [NASA ADS] [CrossRef] [Google Scholar]
- Shimizu, I., Yoshida, N., & Okamoto, T. 2011, MNRAS, submitted [Google Scholar]
- Smith, D. J. B., & Jarvis, M. J. 2007, MNRAS, 378, L49 [NASA ADS] [Google Scholar]
- Spaans, M., & Silk, J. 2006, ApJ, 652, 902 [NASA ADS] [CrossRef] [Google Scholar]
- Steidel, C. C., Adelberger, K. L., Shapley, A. E., et al. 2000, ApJ, 532, 170 [Google Scholar]
- Thomas, R. M., & Zaroubi, S. 2008, MNRAS, 384, 1080 [NASA ADS] [CrossRef] [Google Scholar]
- Trenti, M., Stiavelli, M., & Michael Shull, J. 2009, ApJ, 700, 1672 [NASA ADS] [CrossRef] [Google Scholar]
- Truelove, J. K., Klein, R. I., McKee, C. F., et al. 1997, ApJ, 489, L179 [NASA ADS] [CrossRef] [Google Scholar]
- Vanzella, E., Pentericci, L., Fontana, A., et al. 2011, ApJ, 730, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Verhamme, A., Schaerer, D., Atek, H., & Tapken, C. 2008, A&A, 491, 89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wise, J. H., & Abel, T. 2007, ApJ, 671, 1559 [NASA ADS] [CrossRef] [Google Scholar]
- Wise, J. H., & Abel, T. 2008a, ApJ, 684, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Wise, J. H., & Abel, T. 2008b, ApJ, 685, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Wise, J. H., Turk, M. J., & Abel, T. 2008, ApJ, 682, 745 [NASA ADS] [CrossRef] [Google Scholar]
- Wolcott-Green, J., & Haiman, Z. 2011, MNRAS, 412, 2603 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, Y., Zabludoff, A. I., Davé, R., et al. 2006, ApJ, 640, 539 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, Y., Zabludoff, A., Tremonti, C., Eisenstein, D., & Davé, R. 2009, ApJ, 693, 1579 [NASA ADS] [CrossRef] [Google Scholar]
- Yoshida, N., Oh, S. P., Kitayama, T., & Hernquist, L. 2007, ApJ, 663, 687 [NASA ADS] [CrossRef] [Google Scholar]
- Zheng, Z., Cen, R., Trac, H., & Miralda-Escudé, J. 2010, ApJ, 716, 574 [NASA ADS] [CrossRef] [Google Scholar]
- Zheng, Z., Cen, R., Trac, H., & Miralda-Escudé, J. 2011, ApJ, 726, 38 [NASA ADS] [CrossRef] [Google Scholar]
Appendix
A.1. Chemical model
Collisional and radiative rates.
Heating/cooling rates.
We self-consistently solve the chemical rate equations for our cosmological simulations in an expanding universe. Rate equations are solved for the following species: 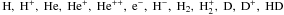 under non-equilibrium ionization/equilibrium conditions. We also treat electronic states of hydrogen, up to 5 levels, as separate species. The rate equations are
under non-equilibrium ionization/equilibrium conditions. We also treat electronic states of hydrogen, up to 5 levels, as separate species. The rate equations are 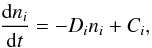 (A.1)where ni is the number density of the ith specie, and Di and Ci are destruction and creation coefficients for the ith specie. Equation (A.1) is solved using the backward differencing scheme (BDF). The solution for Eq. (A.1) is
(A.1)where ni is the number density of the ith specie, and Di and Ci are destruction and creation coefficients for the ith specie. Equation (A.1) is solved using the backward differencing scheme (BDF). The solution for Eq. (A.1) is 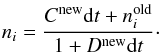 (A.2)Values for
(A.2)Values for 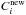 and
and 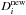 are approximated using species densities from the previous time step and those from the new time step. During each hydrodynamical time step, the chemical time step is computed as
are approximated using species densities from the previous time step and those from the new time step. During each hydrodynamical time step, the chemical time step is computed as 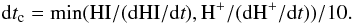 (A.3)For a given chemical time step, species are evolved until the chemical time step becomes equal to the hydrodynamical time step. We take the initial abundances of species from Schleicher et al. (2008b). These are consistent with nucleosynthesis and observational constraints.
(A.3)For a given chemical time step, species are evolved until the chemical time step becomes equal to the hydrodynamical time step. We take the initial abundances of species from Schleicher et al. (2008b). These are consistent with nucleosynthesis and observational constraints.
Strong radiation fluxes can photo-ionize the gas, and for a primordial composition specifically hydrogen and helium. Photo-ionization rates are calculated by solving the following equation (Anninos et al. 1997): 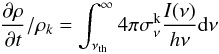 (A.4)where k denotes H, He, He + , I(ν) is the intensity of the radiation field, νth is the threshold energy for each rate for which ionization takes place and
(A.4)where k denotes H, He, He + , I(ν) is the intensity of the radiation field, νth is the threshold energy for each rate for which ionization takes place and 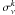 is the frequency dependent photo-ionization rate. In order to compute the photo-heating produced due to ionization of the gas the following equation is solved:
is the frequency dependent photo-ionization rate. In order to compute the photo-heating produced due to ionization of the gas the following equation is solved: 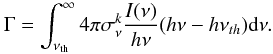 (A.5)Details about H2 and HD chemistry are given in the section below.
(A.5)Details about H2 and HD chemistry are given in the section below.
A.2. H2 and HD chemistry
Neutral hydrogen can capture free electrons, which leads to H2 through the H − route. Another channel for H2 formation is the collision of H atoms with 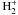 . Similarly, HD can be formed through collisions of H2 molecules with deuterium species. We have included collisional and radiative formation and destruction of H2 and HD in our network. The relevant rates are listed in Table 1. We have also incorporated the photodissociation rates of H − , H2 and
. Similarly, HD can be formed through collisions of H2 molecules with deuterium species. We have included collisional and radiative formation and destruction of H2 and HD in our network. The relevant rates are listed in Table 1. We have also incorporated the photodissociation rates of H − , H2 and 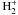 by the background radiation field. Rate equations for H2 and HD species are solved under non-equilibrium conditions, while for the ions H − and
by the background radiation field. Rate equations for H2 and HD species are solved under non-equilibrium conditions, while for the ions H − and 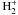 chemical equilibrium is established rapidly. The reactions involving these species occur on short time scale. The photodissociation and photo-ionization rates of these species are calculated by solving Eq. (A.4), where k denotes
chemical equilibrium is established rapidly. The reactions involving these species occur on short time scale. The photodissociation and photo-ionization rates of these species are calculated by solving Eq. (A.4), where k denotes 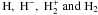 , νth is the threshold energy for photo-dissociation and
, νth is the threshold energy for photo-dissociation and 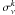 is the frequency dependent photodissociation rate. We also include heating due to photodissociation (for both the Solomon process and direct dissociation) of H2 by absorption of back ground radiation in the Lyman-Werner band. Similarly, we compute the photo-dissociation of HD molecules in the presence of a UV field. We take into account the self-shielding of H2 in the Lyman-Werner band when computing the H2 photodissociation rate. We use the expression given in Eq. (A.6) (Shang et al. 2010). We also include the photodissociation of HD, which is approximately 10% higher than the H2 photodissociation rate for the Solomon process. For direct dissociation they are roughly the same. To compute the H2 column density we use the expression from Shang et al. (2010) as given in Eq. (A.7):
is the frequency dependent photodissociation rate. We also include heating due to photodissociation (for both the Solomon process and direct dissociation) of H2 by absorption of back ground radiation in the Lyman-Werner band. Similarly, we compute the photo-dissociation of HD molecules in the presence of a UV field. We take into account the self-shielding of H2 in the Lyman-Werner band when computing the H2 photodissociation rate. We use the expression given in Eq. (A.6) (Shang et al. 2010). We also include the photodissociation of HD, which is approximately 10% higher than the H2 photodissociation rate for the Solomon process. For direct dissociation they are roughly the same. To compute the H2 column density we use the expression from Shang et al. (2010) as given in Eq. (A.7): ![\appendix \setcounter{section}{1} \begin{equation} f_{\rm sh} = \rm min\left[ 1, \left({{\it N}_{H_{2}} \over {10^{14}~cm^{-2}}}\right)^{-3/4} \right] , \label{rate4} \end{equation}](/articles/aa/full_html/2011/08/aa17144-11/aa17144-11-eq263.png) (A.6)
(A.6)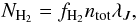 (A.7)where NH2 is the H2 column density, ntot is the total particle density and λJ is the Jeans length. fsh is the self-shielding factor to correct the impinging UV flux (Draine & Bertoldi 1996). This allows us to compute NH2 and fsh from local quantities only. For molecular hydrogen cooling we have used the cooling function of Galli & Palla (1998). We also include heating/cooling rates due to formation and destruction of H2 from Glover & Jappsen (2007). We also include HD photodissociation by a background UV flux in our chemical model. The HD photodissociation rate is adopted from Glover & Jappsen (2007). For HD cooling we have used a fit to the cooling function of Lipovka et al. (2005).
(A.7)where NH2 is the H2 column density, ntot is the total particle density and λJ is the Jeans length. fsh is the self-shielding factor to correct the impinging UV flux (Draine & Bertoldi 1996). This allows us to compute NH2 and fsh from local quantities only. For molecular hydrogen cooling we have used the cooling function of Galli & Palla (1998). We also include heating/cooling rates due to formation and destruction of H2 from Glover & Jappsen (2007). We also include HD photodissociation by a background UV flux in our chemical model. The HD photodissociation rate is adopted from Glover & Jappsen (2007). For HD cooling we have used a fit to the cooling function of Lipovka et al. (2005).
A.3. Lyα trapping
We have modeled the hydrogen atom as a multi-level system with five levels. Our level population model is based on Schleicher et al. (2010b). For the first excited state we distinguish the levels 2s and 2p. Transitions from 2p-1s produce Lyman alpha photons, while transitions from 2s-1s produces the 2-photon continuum. We calculate transition rates from level i to level j using the equation: 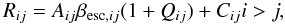 (A.8)
(A.8)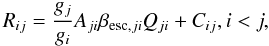 (A.9)where Aij are the radiative decay rates, βesc,ij the escape probabilities of for transition ij and Cij the collisional excitation and de-excitation rates, adopted from Omukai (2001), gi the statistical weight of the ith level and
(A.9)where Aij are the radiative decay rates, βesc,ij the escape probabilities of for transition ij and Cij the collisional excitation and de-excitation rates, adopted from Omukai (2001), gi the statistical weight of the ith level and  , where νij is the frequency of the transition and Jcont,ij is the average intensity of the background radiation field. We take the background radiation field to be a black body temperature 104 K (Glover & Savin 2009). The escape probability for the Ly α photons is given by
, where νij is the frequency of the transition and Jcont,ij is the average intensity of the background radiation field. We take the background radiation field to be a black body temperature 104 K (Glover & Savin 2009). The escape probability for the Ly α photons is given by 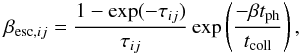 (A.10)where τij is the optical depth at line center of transition ij, tph is the photon diffusion time, tcoll is the collapse time of the gas, and β is a geometrical factor with β = 3 for spherical collapse. Note that tph ≪ tcoll for most transitions. For the Lyman alpha line and other direct transitions to the ground states expressions for optical depth and diffusion time are taken from Spaans & Silk (2006). For Lyman α, tph = L(aτ21)1/3/c, where a is natural-to-thermal line width and the optical depth
(A.10)where τij is the optical depth at line center of transition ij, tph is the photon diffusion time, tcoll is the collapse time of the gas, and β is a geometrical factor with β = 3 for spherical collapse. Note that tph ≪ tcoll for most transitions. For the Lyman alpha line and other direct transitions to the ground states expressions for optical depth and diffusion time are taken from Spaans & Silk (2006). For Lyman α, tph = L(aτ21)1/3/c, where a is natural-to-thermal line width and the optical depth 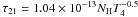 . The cooling function for hydrogen lines is computed from the escape probabilities, level populations and strength of the background radiation field. Further details of all these processes can be found in Omukai (2001) and Schleicher et al. (2010b); Rees & Ostriker (1977); Spaans & Silk (2006); Latif et al. (2011b).
. The cooling function for hydrogen lines is computed from the escape probabilities, level populations and strength of the background radiation field. Further details of all these processes can be found in Omukai (2001) and Schleicher et al. (2010b); Rees & Ostriker (1977); Spaans & Silk (2006); Latif et al. (2011b).
All Tables
All Figures
 |
Fig. 1 Density and temperature slices at redshift 5.5. The left-hand panels show density slices through the center of the halo for J21 = 1000, 10, 0.1 from top to bottom and the right-hand panels show the corresponding temperature slices. Velocity vectors are overplotted on the density slices. All plots shown here are for an escape fraction of 1%. |
| In the text | |
 |
Fig. 2 Density radial profiles for different background UV fields. The left panel shows density profiles for an escape fraction of 1%. The right panel shows the density profiles for escape fractions of 10% and 50%. |
| In the text | |
 |
Fig. 3 Velocity radial profiles for different background UV fields. The left panel shows the radial velocity profile. Right panel shows the tangential velocity profile of the halo. For the tangential velocity, the average was calculated over the absolute values. So, it is a measure of turbulence rather than rotation. |
| In the text | |
 |
Fig. 4 Radial profiles for temperature and species fractions for different background UV fields. The upper left panel of this figure shows the temperature radial profile of the halo. The HII abundance radial profile for the halo is depicted in the upper right panel. H2 abundance is shown in the lower left panel. The HeII radial profile of the halo is depicted in the lower right panel. The escape fraction of ionizing radiation is 1% for all the panels shown. |
| In the text | |
 |
Fig. 5 Radial profiles for column density, emissivity, luminosity and flux for various background UV fields. The upper left panel shows the column density radial profile of the halo. The emissivity radial profile for the halo is depicted in the upper right panel, where the dot-dashed line shows the Lyman alpha emissivity and the triple dot-dashed line shows the total emissivity of all the coolants. The lower left panel shows the luminosity radial profile. The flux radial profile of the halo is depicted in the lower right panel. All panels in this figure have an escape fraction of 1% for ionizing photons. |
| In the text | |
 |
Fig. 6 Radial profiles for temperature and species fractions for various background UV fields with higher escape fractions of ionizing radiation. The upper left panel of this figure shows the temperature radial profile of the halo. The HII abundance radial profile for the halo is depicted in the upper right panel. H2 abundance is shown in the lower left panel. The HeII radial profile of the halo is depicted in the lower right panel. The legend in each panel shows the values of the escape fraction of ionizing photons and the strength of the background radiation field. |
| In the text | |
 |
Fig. 7 Radial profiles for column density, emissivity, luminosity and flux for various background UV fields with higher escape fractions of ionizing radiation. The upper left panel shows the column density radial profile of the halo. The emissivity radial profile for the halo is depicted in the upper right panel, where the dot-dashed line shows the Lyman alpha emissivity while the triple dot-dashed line shows the total emissivity of all the coolants. The lower left panel shows the luminosity radial profile. The radial profile of the enclosed flux from the halo is depicted in the lower right panel. The legend in each panel shows the values of the escape fraction of ionizing photons and the strength of the background radiation field. |
| In the text | |
 |
Fig. 8 Cooling rates of H2, HD, as well as H(2p–1s), H(2s–1s) and H(3–2) transitions are plotted against radius in both panels. Left panel is for J21 = 1000 with a 1% escape fraction of ionizing radiation. Right panel is for J21 = 0.1 with an escape fraction of 10%. |
| In the text | |
 |
Fig. 9 Radial profiles of different coolants as mentioned in the legend for a background radiation field of J21 = 0.01 and a 1% escape fraction of ionizing radiation. |
| In the text | |
 |
Fig. 10 Surface brightness radial profiles for different background UV fields. The left panel shows the surface brightness profiles for an escape fraction of 1%. The right panel shows the surface brightness radial profiles for escape fractions of 10% and 50%. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


