| Issue |
A&A
Volume 532, August 2011
|
|
|---|---|---|
| Article Number | A100 | |
| Number of page(s) | 6 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201117137 | |
| Published online | 01 August 2011 | |
Supernova 2000cb: high-energy version of SN 1987A
1
Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Str. 1, 85741 Garching, Germany
e-mail: utrobin@itep.ru
2
Institute of Theoretical and Experimental Physics, B. Cheremushkinskaya St. 25, 117218 Moscow, Russia
3
Institute of Astronomy of Russian Academy of Sciences, Pyatnitskaya St. 48, 119017 Moscow, Russia
Received: 26 April 2011
Accepted: 6 July 2011
Context. Among type IIP supernovae there are a few events that resemble the well-studied supernova 1987A produced by the blue supergiant in the Large Magellanic Cloud.
Aims. We study a peculiar supernova 2000cb and compare it with the supernova 1987A.
Methods. We carried out hydrodynamic simulations of the supernova in an extended parameter space to describe its light curve and spectroscopic data. The hydrogen Hα and Hβ lines are modeled using a time-dependent approach.
Results. We constructed the hydrodynamic model by fitting the photometric and spectroscopic observations. We infer a presupernova radius of 35 ± 14 R⊙, an ejecta mass of 22.3 ± 1 M⊙, an explosion energy of (4.4 ± 0.3) × 1051 erg, and a radioactive 56Ni mass of 0.083 ± 0.039 M⊙. The estimated progenitor mass on the main sequence lies in the range of 24 − 28 M⊙. The early Hα profile on Day 7 is consistent with the density distribution found from hydrodynamic modeling, while the Hα line on Day 40 indicates an extended 56Ni mixing up to a velocity of 8400 km s-1. We emphasize that the dome-like light curves of both supernova 2000cb and supernova 1987A are entirely powered by radioactive decay. This is unlike normal type IIP supernovae, the plateau of which is dominated by the internal energy deposited after the shock wave propagation through the presupernova. We find signatures of the explosion asymmetry in the photospheric and nebular spectra.
Conclusions. The explosion energy of supernova 2000cb is higher by a factor of three compared to supernova 1987A, which poses a serious problem for explosion mechanisms of type IIP supernovae.
Key words: supernovae: general / supernovae: individual: SN 2000cb
© ESO, 2011
1. Introduction
Type II-plateau supernovae (SNe IIP) represent the most numerous subclass of core-collapse SNe. They are characterized by a ~100 day plateau in the light curve, which is a generic feature of the explosion of a red supergiant (RSG) star (Grassberg et al. 1971; Falk & Arnett 1977). This picture is in line with the theory of stellar evolution that predicts that stars in the range of 9 − 25...30 M⊙ end their life as RSGs (Heger et al. 2003). The RSG nature of type IIP pre-SNe was confirmed by the detection of pre-SNe in archival images (Smartt 2009).
SN 1987A in the Large Magellanic Cloud (LMC), which was identified with the explosion of a blue supergiant (BSG), became a serious challenge for theoreticians. There is still no clear answer to why the pre-SN was a small-radius star. Two major explanations were proposed: (i) the mixing between the He-core and the hydrogen envelope mediated by a fast rotation in combination with the low metallicity (Saio et al. 1988; Weiss et al. 1988; Woosley et al. 1988); (ii) the loss of an extended hydrogen envelope in a close binary system (Hillebrandt & Meyer 1989; Podsiadlowski & Joss 1989). The unresolved issue of the pre-SN origin in the case of SN 1987A is a strong stimulus for studying objects that resemble one another. Pastorello et al. (2005) studied a peculiar SN 1998A, another example of the SN originating in the explosion of a BSG. This SN is very similar photometrically and spectroscopically to SN 1987A, although its explosion energy probably was somewhat higher than that of SN 1987A (Pastorello et al. 2005).
Recently, Kleiser et al. (2011) have analyzed photometric and spectroscopic observations of SN 2000cb and conclude that the SN was related with the explosion of a BSG. In that sense SN 2000cb is another counterpart of SN 1987A. Nevertheless, authors have emphasized differences, particularly, in the light curve shape and in expansion velocities, which were substantially higher in SN 2000cb. Using scaling relations and SN 1987A as a template, Kleiser et al. (2011) have derived the ejecta mass of ~16.5 M⊙ and the explosion energy of ~4 × 1051 erg for SN 2000cb. On the other hand, hydrodynamic modeling has led Kleiser et al. (2011) to the modest estimate of ~1.7 × 1051 erg, comparable to that of SN 1987A. It should be noted, however, that authors did not attain a reasonable fit of the bolometric light curve. The question of reliable SN 2000cb parameters therefore remains open.
Motivated by the importance of the SN 1987A-like events and rather complete observational light curve of SN 2000cb (Kleiser et al. 2011), we revisit the analysis of this SN by employing a standard hydrodynamic model (Utrobin 2004, 2007). A brief description of the hydrodynamic model is presented in Sect. 2. Because the SN parameters cannot be recovered from the photometric data alone, one also needs to use the line profiles in which the mass-velocity distribution is imprinted. By this approach we obtain the basic parameters of the optimal model given in Sect. 3.1, while in Sect. 3.2 we address signatures of the explosion asymmetry in the photospheric and nebular spectra. In Sect. 4 we discuss results and their implications for the explosion mechanism problem, and in Sect. 5 we summarize the conclusions.
Following Kleiser et al. (2011) we adopt a distance to the spiral galaxy IC 1158 of 30 Mpc, a reddening E(B − V) = 0.114 mag, an explosion date of April 21.5 UT (JD 2 451 656), and a recession velocity to the host galaxy of 1918.67 km s-1.
2. Model overview
The hydrodynamic code with one-group radiation transfer (Utrobin 2004, 2007) is used to simulate the SN 2000cb event. The explosion is modeled by placing the supersonic piston close to the outer edge of the 1.6 M⊙ central core, which is removed from the computational mass domain and assumed to collapse to become a neutron star. The hydrodynamic model in spherically-symmetric approximation is determined by the explosion energy (E), the ejecta mass (Menv), the pre-SN radius (R0), and the amount of ejected 56Ni (MNi). The last can be reliably determined at the radioactive tail from the bolometric luminosity or from the flux in broad-band filter by adopting SN 1987A as a template. Parameters E, Menv, and R0 are determined primarily by the plateau luminosity, the plateau duration, and the velocity of the line-absorbing gas at the photospheric epoch. The velocity constraint is usually provided by the absorption minima of weak lines. However, the minima are poorly defined in the case of SN 2000cb which is characterized by broad and blended lines. We therefore rely on the Hα and Hβ line profiles, which are studied with the atmosphere model in the time-dependent approach (Utrobin & Chugai 2005).
The atmosphere model is based on the time-dependent ionization and excitation kinetics of hydrogen and other elements, the time-dependent kinetics of molecular hydrogen, and the time-dependent energy balance for the gas temperature (Utrobin & Chugai 2005). The density distribution, chemical composition, radius of the photosphere, and effective temperature are provided by the hydrodynamic model. The continuum radiation escaping the photosphere is set to be a black body one with the effective temperature and the photospheric brightness corresponding to the one obtained by our models for SN 1987A. The obtained time-dependent structure of the atmosphere is then used to model synthetic spectra at selected epochs. The spectra are simulated by means of the Monte Carlo technique. The Sobolev local escape approximation is assumed for the line radiation transfer dominated by the line absorption. The line emissivity and the Sobolev optical depth are determined by level populations, which in turn are provided with the time-dependent approach. The Thomson scattering on free electrons, Rayleigh scattering on neutral hydrogen, and the relativistic effects are also taken into account. Photons striking the photosphere are assumed to be diffusively reflected back into the atmosphere with the albedo calculated according to Chugai & Utrobin (2000).
It is well established that the evolutionary pre-SN is not the best choice for modeling the SN IIP event (Utrobin & Chugai 2008, 2009). This is also true for SN 2000cb (cf. Kleiser et al. 2011). We, therefore, prefer to search for the appropriate pre-SN model among nonevolutionary hydrostatic RSG configurations that retain major features of the evolutionary models. The essential property of the nonevolutionary model is a smoothed jump in density and chemical composition between the helium core and the hydrogen envelope. The adopted pre-SN model of SN 2000cb is shown in Fig. 1, while the distribution of major constituents is displayed in Fig. 2. As we see below, the ejecta mass of SN 2000cb is slightly higher than SN 1987A. We therefore assume the mass of the unmixed helium-core to be 9 M⊙, which corresponds to the final helium core of a main-sequence star of ≈ 25 M⊙ (Hirschi et al. 2004). It is noteworthy that the result is not sensitive to the helium-core mass, because the mixing effects dominate the variation in the helium-core mass (Utrobin 2007). We adopt the ejected metal core material (mostly oxygen) to be 3 M⊙, which is close to the amount ejected by a 25 M⊙ main-sequence star (Woosley & Weaver 1995). These metals are assumed to be homogeneously mixed in the helium core, and their mixing with the hydrogen envelope follows the mixing of helium (Fig. 2). The 56Ni mixing is another important ingredient of the model, because it markedly affects the light curve shape as well. Moreover, as we will see, the 56Ni mixing can also be effectively probed by the hydrogen line profiles.
 |
Fig. 1 Density distribution as a function of interior mass a) and radius b) for the optimal pre-SN model of SN 2000cb. The central core of 1.6 M⊙ is omitted. |
 |
Fig. 2 The mass fraction of hydrogen (solid line), helium (long dashed line), heavy elements (short dashed line), and radioactive 56Ni (dotted line) in the ejecta of the optimal model. |
3. Results
3.1. Basic parameters
 |
Fig. 3 The density and the 56Ni mass fraction as a function of velocity for the optimal model at t = 50 days (solid lines). Dash-dotted straight lines are the power-law fits of density. The 56Ni distribution is shown for the moderate mixing in the range v ≤ 6800 km s-1 (dotted line) and the strong mixing, v ≤ 8400 km s-1, in the optimal model (solid line). |
The SN 2000cb parameters are found by computing a grid of the hydrodynamical models and the Hα line. The optimal model simultaneously fits the bolometric light curve and the Hα line profile fairly well for the ejecta mass Menv = 22.3 ± 1 M⊙, the explosion energy E = (4.4 ± 0.3) × 1051 erg, the pre-SN radius R0 = 35 ± 14 R⊙, and the 56Ni mass MNi = 0.083 ± 0.039 M⊙. The uncertainties in basic parameters are calculated by assuming a 23% error in the distance and a 5% error in the characteristic duration of the light curve according to Kleiser et al. (2011) and by estimating a 5% error in the photospheric velocity. It is interesting that the pre-SN radius of 35 R⊙ is equal to that of SN 1987A (Utrobin 2005). Remarkably, the amount of 56Ni found from the bolometric light curve coincides with the estimate we obtain using the I magnitude at the radioactive tail and SN 1987A as a template. This means that the empirical bolometric luminosity recovered from the filtered fluxes is reliable.
 |
Fig. 4 The bolometric light curve of the optimal model (thick solid line) overplotted on the empirical bolometric light curve of SN 2000cb recovered from the BVI magnitudes reported by Kleiser et al. (2011) (open circles). Dashed line represents the model with the moderate 56Ni mixing to 6800 km s-1 compared to the one in the optimal model up to 8400 km s-1 (Fig. 3). Dotted line shows the light curve of the model with the 56Ni mixing to 3000 km s-1 observed in SN 1987A. The light curve in the absence of radioactive 56Ni is shown by a thin solid line. |
The density distribution of the freely expanding envelope (Fig. 3) is nearly flat in the velocity range v ≲ 4000 km s-1 and drops in the outer layers with the steepening increasing outward. This behavior can be described by a broken power law with an effective index of − 7.6 and − 10. The density spike in the outermost layers (Fig. 3) is a shell with a mass of ~8 × 10-7 M⊙ formed by the shock breakout (Grassberg et al. 1971; Chevalier 1981). The boundary velocity is ≈ 76 000 km s-1, substantially higher than the boundary velocity of SN 1987A, ≈36 000 km s-1 (Utrobin 2004).
The model bolometric light curve for the case without radioactive 56Ni shows that the initial luminosity peak during the first ten days is produced by the release of the internal energy deposited after the shock wave propagation through the pre-SN (Fig. 4). The peak is substantially broader and more luminous than both the observed and model peaks of SN 1987A, and this reflects the greater explosion energy of SN 2000cb. Remarkably, the major broad maximum of the light curve with a time scale of ~100 days, which resembles a wide dome in shape, is entirely powered by the 56Ni → 56Co → 56Fe decay (Fig. 4), as is the case for SN 1987A. The physics of the dome-like light maximum turns out to be essentially the same as in SNe Ia and SNe Ib/c. The different physics of the light curve on a time scale of 100 days in the normal SNe IIP and the SN 1987A-like events is crucial for understanding the origin of a distinction between these categories of SNe II.
An amount of the 56Ni mixing is probed by the rising part of the light curve after Day 10 (Fig. 4). It is evident that the 56Ni mixing to 3000 km s-1 observed in SN 1987A is inconsistent with the observed light curve, so it indicates stronger mixing. Indeed, the light curves for both versions of the extended (to 6800 km s-1 and 8400 km s-1) 56Ni mixing (Fig. 3) agree well with observations (Fig. 4). A step-like feature of the 56N distribution in the range of 6800 − 8400 km s-1 (Fig. 3), which contains 10-3 M⊙ of 56Ni, is needed to account for the Hα and Hβ absorptions at high velocities on Day 40 (Figs. 5b and d). Remarkably, the strong Hβ absorption on Day 40 is in sharp contrast to the almost undetectable Hβ line in the spectrum of SN 1987A at the same epoch (Hanuschik 1989). This reflects the different situation with the 56Ni mixing in SN 1987A where the radioactive 56Ni is mixed to substantially lower velocity ( ≈ 3000 km s-1).
 |
Fig. 5 The Hα and Hβ lines on Days 7 and 40. The model profiles are calculated for two cases of 56Ni mixing, strong (thick solid line) and moderate (dotted line), and overplotted on the observed profiles (thin solid line). Modeling the Hβ profile includes the Fe II 4924, 5018, 5169 Å and Ba II 4935 Å lines. |
It should be emphasized that the early Hα and Hβ line profiles on Day 7 are not sensitive to the 56Ni distribution at all (Figs. 5a and c), while on Day 40 the absorption is very much sensitive to the 56Ni distribution (Figs. 5b and d). The contributions of the density and 56Ni distributions in the Hα and Hβ absorptions thus turn out to be decoupled. This permits us to use the early Hα absorption to probe the density in the outer layers and the late time Hα absorption to probe an amount of 56Ni mixing in the outer layers. We therefore conclude that the high velocity estimated from the blue absorption wing of the Hα and Hβ profiles on Day 7 can serve as an independent indicator of the small pre-SN radius and the high explosion energy of SN 2000cb.
Generally, hydrogen in the outer layers might be alternatively excited by X-rays from the ejecta/wind interaction. We calculated the X-ray luminosity from the forward and reverse shocks, assuming the mass-loss rate Ṁ = 10-6 M⊙ yr-1 and the wind velocity u = 500 km s-1, i.e., adopting the wind as ten times denser than around SN 1987A (Chevalier & Dwarkadas 1995). Even in this optimistic case, the X-ray luminosity on Day 40 is ~1035 erg s-1, which is able to provide a nonthermal excitation rate of hydrogen not greater than 10-4 of what is produced by 56Ni. We therefore rule out any sizable contribution of the ejecta/wind interaction in the formation of the high-velocity Hα and Hβ absorptions on Day 40.
3.2. Explosion asymmetry
Even though the spherically-symmetric model is consistent with the light curve and the early hydrogen line absorptions, on Day 40 the model overproduces the flux in the red part of the Hα emission component (Fig. 5b). We checked different artificial, spherically-symmetric models and found that they all overproduced the flux in the red part of the Hα emission in the same way. Moreover, the similar model of the Hα line in the normal type IIP SN 1999em on Days 26 and 52 does not show any deficit in the red wing (Utrobin 2007). We therefore suggest that the deficit in the emission in the red part of the Hα emission is related to the asymmetry of the 56Ni distribution; namely, the front side of the envelope presumably contains more 56Ni than does the rear side of the envelope. In this picture, the nonthermal excitation in the rear hemisphere turns out to be lower, and consequently, the Hα emission is weaker than in the front side, which thus explains the observed profile asymmetry.
To check whether the 56Ni asymmetry in SN 2000cb also extends into the deeper layers, as in the case of SN 1987A, we have analyzed the Hα line and the [Ca II] 7292, 7319 Å doublet at the nebular stage, on Day 158. The Hα emissivity reflects the deposition of gamma-ray energy, which is almost local on Day 158 because of the large optical depth of ≈ 6 for gamma-ray absorption. The [Ca II] 7300 Å emission may reflect both the asymmetry of the 56Ni distribution and the distribution of Ca itself. The observed lines (Kleiser et al. 2011), together with the calculated profiles for the spherical model, are shown in Fig. 6. We computed the lines taking the continuum absorption into account, which is predicted by the hydrodynamical model at this stage, and the doublet structure of the [Ca II] 7300 Å line with the finite optical depth of [Ca II] doublet lines.
 |
Fig. 6 The Hα line and the [Ca II] 7300 Å doublet on Day 158. The calculated profiles (thick line) are overplotted on the observed profiles (thin line). At the bottom, residuals between the observed profile and the one computed for the spherically-symmetric model are shown. |
Both the observed Hα and [Ca II] 7300 Å emissions reveal a blueshift with respect to the spherically-symmetric model, which is most apparent in the residuals shown in Fig. 6. The 56Ni asymmetry in the inner layers can be quantified by the blueshift of the mean radial velocity in the range |vr| < 4000 km s-1. For the observed Hα line the flux-weighted shift is −390 km s-1, while for the spherical model profile, the mean shift is −145 km s-1 with the resulting blueshift of −245 km s-1. For the [Ca II] 7300 Å doublet the relative blueshift is −211 km s-1. The found asymmetry is significantly more than the uncertainty in the radial velocity of the SN rest frame related to the host galaxy’s rotation. Indeed, for the inclination angle of IC 1158 i = 62° taken from LEDA and the angle of ~37° between the radius-vector of the SN and the minor axis, the velocity uncertainty of the rest frame turns out to be ± 70 km s-1 assuming the circular velocity of 240 km s-1. We conclude, therefore, that the blueshift of the observed Hα and [Ca II] 7300 Å profiles is real, thus suggesting the predominant ejection of 56Ni in the inner layers within the front hemisphere.
4. Discussion
Our major result is that SN 2000cb was the high-energy explosion of the BSG star. This confirms the general conclusion of Kleiser et al. (2011), who “favor a high-energy explosion of a relatively small radius star, most probably a BSG”. The ejecta mass of 22.3 ± 1 M⊙, combined with the collapsing core of 1.6 M⊙, gives the total pre-SN mass of 23.9 ± 1 M⊙. Adopting the same mass loss by pre-SN of 2.4 ± 1 M⊙ as in type IIP SN 2004et of the comparable pre-SN mass (Utrobin & Chugai 2009), for SN 2000cb we come to the progenitor mass on the main sequence of 26.3 ± 2 M⊙. The error in mass includes the uncertainties in the ejecta mass and the mass loss. This progenitor mass is about the upper limit of the main-sequence stars presumably exploding as SNe IIP (Heger et al. 2003).
Kleiser et al. (2011) have derived two different sets of the ejecta mass and the explosion energy for SN 2000cb. The first one is based upon the analytical scaling relations and the SN 1987A parameters. This approach results in the ejecta mass of ≈ 16.5 M⊙ and the explosion energy of ~4 × 1051 erg. Our ejecta mass is higher by 35%, while the explosion energy is only 10% higher. This should be considered as reasonable agreement. On the other hand, the hydrodynamic modeling of the light curve led Kleiser et al. (2011) to the lower energy of 1.7 × 1051 erg for the ejecta mass of 18 M⊙. It should be noted, however, that these authors did not attain an exact fit of the observational bolometric light curve and did not use the velocity constraints. This means that the hydrodynamical model of Kleiser et al. (2011) cannot be considered optimal, so the comparison with our hydrodynamical model cannot be made in a straightforward way.
Hydrodynamic models of type IIP supernovae.
A summary of the parameters of the best observed SNe IIP, which were derived by a uniform procedure, is compiled in Table 1. The listed parameters are the pre-SN radius, the ejecta mass, the explosion energy, the 56Ni mass, the maximal velocity of 56Ni mixing zone, and the minimal velocity of the hydrogen-rich envelope. All SNe IIP are characterized by a deep mixing of hydrogen, indicated by the low value of 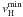 , which is consistent with 2D simulations (Müller et al. 1991; Kifonidis et al. 2003, 2006). In the case of SN 2000cb, the explosion energy is significantly higher, while the 56Ni mixing occurs within the wider mass and velocity ranges than for SN 1987A. The very high degree of the 56Ni mixing is a prominent feature of SN 2000cb that should provide an important observational constraint on the yet poorly known explosion mechanism.
, which is consistent with 2D simulations (Müller et al. 1991; Kifonidis et al. 2003, 2006). In the case of SN 2000cb, the explosion energy is significantly higher, while the 56Ni mixing occurs within the wider mass and velocity ranges than for SN 1987A. The very high degree of the 56Ni mixing is a prominent feature of SN 2000cb that should provide an important observational constraint on the yet poorly known explosion mechanism.
 |
Fig. 7 Explosion energy a) and 56Ni mass b) versus hydrodynamic progenitor mass for seven core-collapse SNe. |
The position of SN 2000cb on the plots of the explosion energy versus the progenitor mass (Fig. 7a) and the total 56Ni mass versus the progenitor mass (Fig. 7b) is consistent with the correlations recovered earlier for the SNe IIP sample studied hydrodynamically in a uniform way (Utrobin et al. 2010). The asymmetry of the 56Ni distribution in SN 2000cb is well established by our analysis of the spectra at the photospheric and nebular stages. The asymmetry of the bulk of radioactive 56Ni is rather moderate in terms of the velocity shift along the line of sight, Δvz ≈ −240 km s-1. We cannot rule out that the actual deprojected asymmetry is stronger. This might be revealed by polarization data that are unfortunately missing. The one-sided ejection of radioactive 56Ni is not unique feature of SN 2000cb, because the line profiles of SN 1987A show evidence that the 56Ni distribution is skewed towards the rear hemisphere (Haas et al. 1990; Chugai 1991). The one-sidedness of the 56Ni ejecta seems to be a common feature for SNe IIP (Chugai 2007) and indicates that the explosion mechanism of both the normal SNe IIP and the SN 1987A-like events seems to be similar.
Two major explosion mechanisms for core-collapse SNe are presently considered as promising: neutrino-driven explosion and magneto-rotational mechanism. Particularly important in this regard is our conclusion about the high value of the explosion energy of SN 2000cb. The neutrino-driven mechanism is currently able to produce the explosion with the energy at best <1051 erg (Scheck et al. 2008), and even a number of 1051 erg seems to be beyond reach of the recent 3D models (Rantsiou et al. 2011). The energetics of the neutrino-driven explosion mechanism is thus at least four times less than what is needed to account for the SN 2000cb phenomenon. This casts serious doubts on the universality of the neutrino-driven mechanism for the SN II explosions. The current situation with the magneto-rotational mechanism is also not very optimistic: the available 2D simulations provide the explosion energy of only ~0.6 × 1051 erg (Ardeljan et al. 2005), by a factor of seven below the energy of SN 2000cb.
On the other hand, hypernovae with the explosion energy of (2−3) × 1052 erg associated with gamma-ray bursts, e.g. SN 1998bw (Iwamoto et al. 1998) and SN 2003dh (Deng et al. 2005), and the type IIP SN2009kf of the similar energy (Utrobin et al. 2010) have already posed a problem for the high-energy explosion mechanism. Presently, we lack firm evidence that a unique explosion mechanism operates in SNe IIP and hypernovae, although the existence of phenomena likewise SN 2000cb and SN 2009kf pushes us towards this line of reasoning.
The BSG configuration of SN 1987A has been partially attributed to the low metallicity of the LMC. The host galaxy of SN 2000cb is the galaxy IC 1158, normal, although slightly subluminous, Sc galaxy with the normal metallicity 12 + log [ O/H] = 8.7 (Anderson et al. 2010). The deprojected galactocentric distance of the SN is ≈ 8 kpc, comparable to that of the Sun. It is unlikely, therefore, that the progenitor of SN 2000cb was a low-metallicity star, although this cannot be completely precluded. Mixing favored by the fast rotation or evolution of the close binary, proposed for SN 1987A, remains viable possibilities for the pre-SN to become a BSG. It is noteworthy that overlapping the mass ranges of SN 2000cb and SN 1987A and of normal SNe IIP indicates that the high stellar mass is unlikely a unique condition that makes the pre-SN into a BSG. Even though high mass of the progenitor favors the BSG structure (Woosley et al. 1997), some additional factor seems to be required to explain the compactness of the pre-SN.
A special remark should be made concerning the attribution of the SN 1987A-like events to SNe IIP. As noted earlier, a dome-like shape of the light curves of SN 1987A and SN 2000cb reflects different physics of the luminosity at the photospheric phase. In the normal SNe IIP the bulk of the radiated energy is an internal energy deposited during the shock wave propagation. This is not true for the SN 1987A-like events because their dome-like light curves are powered by the radioactive decay, while the thermal energy is completely exhausted during the first 10 to 20 days. We propose therefore to distinguish the SN 1987A-like events emphasizing their specific light curve shape by a notation “SN IId” where symbol “d” stands for the “dome”. This would reflect both the apparent observational property and the dominant role of the radioactivity in the light curve shaping.
5. Conclusions
Our goal was to derive the parameters of the peculiar type IIP SN 2000cb from the available observational data by employing hydrodynamical modeling and calculating hydrogen line profiles. We conclude that SN 2000cb was the high-energy explosion of a massive BSG, which was more energetic than SN 1987A by a factor of three. At the same time, these events are close counterparts by their pre-SN structure and by the common physics of their dome-like light curves. SN 2000cb can thus be considered as a high-energy version of SN 1987A.
The progenitor mass, the explosion energy, and the radioactive 56Ni mass of SN 2000cb are consistent with the correlations revealed by the well-observed SNe IIP studied hydrodynamically. This combined with the clear evidence of one-sided 56Ni ejecta, which is rather ubiquitous among SNe IIP, favors a common explosion mechanism for all these SNe. We stress that the high explosion energy of SN 2000cb is far beyond the possibilities of the present-day versions of the neutrino-driven or magneto-rotational mechanism.
Acknowledgments
We thank Io K. W. Kleiser for sending us spectra of SN 2000cb. V.P.U. is grateful to Wolfgang Hillebrandt for the possibility of working at the MPA, and his research has been supported in part by RFBR under grant 10-02-00249-a.
References
- Anderson, J. P., Covarrubias, R. A., James, P. A., Hamuy, M., & Habergham, S. M. 2010, MNRAS, 407, 2660 [NASA ADS] [CrossRef] [Google Scholar]
- Ardeljan, N. V., Bisnovatyi-Kogan, G. S., & Moiseenko, S. G. 2005, MNRAS, 359, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Chevalier, R. A. 1981, Fundam. Cosmic Phys., 7, 1 [NASA ADS] [Google Scholar]
- Chevalier, R. A., & Dwarkadas, V. V. 1995, ApJ, 452, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Chugai, N. N. 1991, SvAL, 17, 400 [NASA ADS] [Google Scholar]
- Chugai, N. N. 2007, in Supernova 1987A: 20 years after. Supernovae and Gamma-ray Bursters, ed. S. Immler, K. Weiler, & R. McCray, AIP Conf. Proc., 937, 357 [Google Scholar]
- Chugai, N. N., & Utrobin, V. P. 2000, A&A, 354, 557 [NASA ADS] [Google Scholar]
- Deng, J., Tominaga, N., Mazzali, P. A., Maeda, K., & Nomoto, K. 2005, ApJ, 624, 898 [NASA ADS] [CrossRef] [Google Scholar]
- Falk, S. W., & Arnett, W. D. 1977, ApJS, 33, 515 [NASA ADS] [CrossRef] [Google Scholar]
- Grassberg, E. K., Imshennik, V. S., & Nadyozhin, D. K. 1971, Ap&SS, 10, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Haas, M. R., Colgan, S. W. J., Erickson, E. F., et al. 1990, ApJ, 360, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Hanuschik, R. W., Thimm, G., & Seidensticker, K. J. 1989, A&A, 220, 153 [NASA ADS] [Google Scholar]
- Heger, A., Fryer, C. L., Woosley, S. E., Langer, N., & Hartmann, D. H. 2003, ApJ, 591, 288 [NASA ADS] [CrossRef] [Google Scholar]
- Hillebrandt, W., & Meyer, F. 1989, A&A, 219, L3 [NASA ADS] [Google Scholar]
- Hirschi, R., Meynet, G., & Maeder, A. 2004, A&A, 425, 649 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Iwamoto, K., Mazzali, P. A., Nomoto, K., et al. 1998, Nature, 395, 672 [NASA ADS] [CrossRef] [Google Scholar]
- Kifonidis, K., Plewa, T., Scheck, L., Janka, H.-Th., & Müller, E. 2003, A&A, 408, 621 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kifonidis, K., Plewa, T., Scheck, L., Janka, H.-Th., & Müller, E. 2006, A&A, 453, 661 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kleiser, Io K. W., Poznanski, D., Kasen, D., et al. 2011, MNRAS, 415, 372 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, E., Fryxell, B., & Arnett, D. 1991, A&A, 251, 505 [NASA ADS] [Google Scholar]
- Pastorello, A., Baron, E., Branch, D., et al. 2005, MNRAS, 360, 950 [NASA ADS] [CrossRef] [Google Scholar]
- Podsiadlowski, Ph., & Joss, P. C. 1989, Nature, 338, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Rantsiou, E., Burrows, A., Nordhaus, J., & Almgren, A. 2011, ApJ, 732, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Saio, H., Nomoto, K., & Kato, M. 1988, Nature, 334, 508 [NASA ADS] [CrossRef] [Google Scholar]
- Scheck, L., Janka, H.-Th., Foglizzo, T., & Kifonidis, K. 2008, A&A, 477, 931 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smartt, S. J. 2009, ARA&A, 47, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Utrobin, V. P. 2004, Astron. Lett., 30, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Utrobin, V. P. 2005, Astron. Lett., 31, 806 [NASA ADS] [CrossRef] [Google Scholar]
- Utrobin, V. P. 2007, A&A, 461, 233 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Utrobin, V. P., & Chugai, N. N. 2005, A&A, 441, 271 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Utrobin, V. P., & Chugai, N. N. 2008, A&A, 491, 507 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Utrobin, V. P., & Chugai, N. N. 2009, A&A, 506, 829 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Utrobin, V. P., Chugai, N. N., & Botticella, M. T. 2010, ApJ, 723, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Weiss, A., Hillebrandt, W., & Truran, J. W. 1988, A&A, 197, L11 [NASA ADS] [Google Scholar]
- Woosley, S. E., & Weaver, T. A. 1995, ApJS, 101, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., Pinto, P. A., & Ensman, L. 1988, ApJ, 324, 466 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., Heger, A., Weaver, T. A., & Langer, N. 1997 [arXiv:astro-ph/9705146] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Density distribution as a function of interior mass a) and radius b) for the optimal pre-SN model of SN 2000cb. The central core of 1.6 M⊙ is omitted. |
| In the text | |
 |
Fig. 2 The mass fraction of hydrogen (solid line), helium (long dashed line), heavy elements (short dashed line), and radioactive 56Ni (dotted line) in the ejecta of the optimal model. |
| In the text | |
 |
Fig. 3 The density and the 56Ni mass fraction as a function of velocity for the optimal model at t = 50 days (solid lines). Dash-dotted straight lines are the power-law fits of density. The 56Ni distribution is shown for the moderate mixing in the range v ≤ 6800 km s-1 (dotted line) and the strong mixing, v ≤ 8400 km s-1, in the optimal model (solid line). |
| In the text | |
 |
Fig. 4 The bolometric light curve of the optimal model (thick solid line) overplotted on the empirical bolometric light curve of SN 2000cb recovered from the BVI magnitudes reported by Kleiser et al. (2011) (open circles). Dashed line represents the model with the moderate 56Ni mixing to 6800 km s-1 compared to the one in the optimal model up to 8400 km s-1 (Fig. 3). Dotted line shows the light curve of the model with the 56Ni mixing to 3000 km s-1 observed in SN 1987A. The light curve in the absence of radioactive 56Ni is shown by a thin solid line. |
| In the text | |
 |
Fig. 5 The Hα and Hβ lines on Days 7 and 40. The model profiles are calculated for two cases of 56Ni mixing, strong (thick solid line) and moderate (dotted line), and overplotted on the observed profiles (thin solid line). Modeling the Hβ profile includes the Fe II 4924, 5018, 5169 Å and Ba II 4935 Å lines. |
| In the text | |
 |
Fig. 6 The Hα line and the [Ca II] 7300 Å doublet on Day 158. The calculated profiles (thick line) are overplotted on the observed profiles (thin line). At the bottom, residuals between the observed profile and the one computed for the spherically-symmetric model are shown. |
| In the text | |
 |
Fig. 7 Explosion energy a) and 56Ni mass b) versus hydrodynamic progenitor mass for seven core-collapse SNe. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


