| Issue |
A&A
Volume 532, August 2011
|
|
|---|---|---|
| Article Number | A52 | |
| Number of page(s) | 8 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201116866 | |
| Published online | 21 July 2011 | |
Spectral line polarization with angle-dependent partial frequency redistribution⋆
III. Single scattering approximation for the Hanle effect
Indian Institute of Astrophysics, Koramangala, Bangalore 560 034, India
e-mail: sampoorna@iiap.res.in
Received: 11 March 2011
Accepted: 6 June 2011
Context. The solar limb observations in spectral lines display evidence of linear polarization, caused by non-magnetic resonance scattering process. This polarization is modified by weak magnetic fields – the process of the Hanle effect. These two processes serve as diagnostic tools for weak solar magnetic field determination. In modeling the polarimetric observations the partial frequency redistribution (PRD) effects in line scattering have to be accounted for. For simplicity, it is common practice to use PRD functions averaged over all scattering angles. For weak fields, it has been established that the use of angle-dependent PRD functions instead of angle-averaged functions is essential.
Aims. We introduce a single scattering approximation to the problem of polarized line radiative transfer in weak magnetic fields with an angle-dependent PRD. This helps us to rapidly compute an approximate solution to the difficult and numerically expensive problem of polarized line formation with angle-dependent PRD.
Methods. We start from the recently developed Stokes vector decomposition technique combined with the Fourier azimuthal expansion for angle-dependent PRD with the Hanle effect. In this decomposition technique, the polarized radiation field (I, Q, U) is decomposed into an infinite set of cylindrically symmetric Fourier coefficients 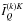 , where K = 0,2, with − K ≤ Q ≤ + K, and k is the order of the Fourier coefficients (k takes values from − ∞ to + ∞). In the single scattering approximation, the effect of the magnetic field on the Stokes I is neglected, so that it can be computed using the standard non-local thermodynamic equilibrium (non-LTE) scalar line transfer equation. In the case of angle-dependent PRD, we further assume that the Stokes I is cylindrically symmetric and given by its dominant term
, where K = 0,2, with − K ≤ Q ≤ + K, and k is the order of the Fourier coefficients (k takes values from − ∞ to + ∞). In the single scattering approximation, the effect of the magnetic field on the Stokes I is neglected, so that it can be computed using the standard non-local thermodynamic equilibrium (non-LTE) scalar line transfer equation. In the case of angle-dependent PRD, we further assume that the Stokes I is cylindrically symmetric and given by its dominant term 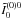 . Keeping only the contribution from
. Keeping only the contribution from 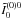 in the source terms for the K = 2 components (which give rise to Stokes Q and U), the value of k is limited to 0, ± 1, ± 2. As a result, the dimensionality of the problem is reduced from infinity to 25 for the K = 2 Fourier coefficients.
in the source terms for the K = 2 components (which give rise to Stokes Q and U), the value of k is limited to 0, ± 1, ± 2. As a result, the dimensionality of the problem is reduced from infinity to 25 for the K = 2 Fourier coefficients.
Results. We show that the single scattered solution provides a reasonable approximation to the emergent polarization computed using the polarized line transfer equation including angle-dependent PRD and the Hanle effect. While the full problem is computationally expensive, the single scattering approximation provides a faster method of solution. The presence of elastic collisions particularly enhances the domain of applicability of this approximation.
Key words: line: formation / polarization / scattering / magnetic fields / methods: numerical / Sun: atmosphere
Appendices A and B are available in electronic form at http://www.aanda.org
© ESO, 2011
1. Introduction
It is now well established that the Hanle effect serves as a diagnostic tool to determine the deterministic or turbulent weak magnetic fields on the Sun (see e.g., Stenflo 1982; Trujillo Bueno et al. 2004). The Hanle effect is a magnetic modification of the Rayleigh scattering spectral line polarization. The scattering polarization signatures in strong resonance lines are particularly sensitive to the frequency redistribution mechanism used in their computation. In the case of Rayleigh scattering, the differences in Q/I computed using angle-averaged and angle-dependent partial frequency redistribution (PRD) functions is between 10% and 30% (Sampoorna et al. 2011, see also Faurobert 1988). In the presence of weak magnetic fields, Nagendra et al. (2002) showed that the Stokes U is very sensitive to the angle-averaging of the redistribution function. However, these authors used a computationally expensive numerical method to solve the polarized line transfer equation including angle-dependent PRD function and the Hanle effect. Our aim here is to present an approximate method based on the concept of the single scattering approximation (see Frisch et al. 2009; Frisch 2010; Anusha et al. 2010; Sampoorna et al. 2011) to solve the above-mentioned problem efficiently.
The problem of angle-dependent PRD is characterized by intricate coupling between angle and frequency variables. This makes the evaluation of scattering integrals, and the solution of polarized transfer equation a challenging problem. A decomposition technique to reduce the non-axisymmetric Stokes transfer equation to cylindrically symmetric one was developed by Frisch (2007), for the case of an angle-averaged PRD with the Hanle effect. This technique was extended by Frisch (2009) to handle angle-dependent PRD with the Hanle effect. Basically the Stokes vector (I,Q,U) is first decomposed into a set of six irreducible components 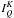 . In the particular case of angle-dependent PRD, these components are also non-axisymmetric. An azimuthal Fourier expansion of the angle-dependent PRD
. In the particular case of angle-dependent PRD, these components are also non-axisymmetric. An azimuthal Fourier expansion of the angle-dependent PRD
functions then allows us to further reduce 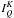 into an infinite set of cylindrically symmetric Fourier coefficients
into an infinite set of cylindrically symmetric Fourier coefficients 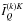 . This method helps us to construct an infinite set of integral equations for the Fourier coefficients of the irreducible source vector components. As shown in Frisch (2010), the problem simplifies when the magnetic field is set to zero or assumed to be turbulent. In this case, the Fourier wavenumber k takes only the values k = 0,1,2, and four components
. This method helps us to construct an infinite set of integral equations for the Fourier coefficients of the irreducible source vector components. As shown in Frisch (2010), the problem simplifies when the magnetic field is set to zero or assumed to be turbulent. In this case, the Fourier wavenumber k takes only the values k = 0,1,2, and four components 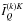 are sufficient to represent the polarized radiation field. As shown in Sampoorna et al. (2011), the polarized radiation field can be calculated by solving a set of integral equations for the corresponding cylindrically symmetric irreducible source vector components. Several numerical methods are described in this reference : two accelerated lambda iteration (ALI) methods, associated with either a core-wing or a frequency-angle by frequency-angle technique, and one scattering expansion method, based on a Neumann series expansion in terms of the mean number of scattering events.
are sufficient to represent the polarized radiation field. As shown in Sampoorna et al. (2011), the polarized radiation field can be calculated by solving a set of integral equations for the corresponding cylindrically symmetric irreducible source vector components. Several numerical methods are described in this reference : two accelerated lambda iteration (ALI) methods, associated with either a core-wing or a frequency-angle by frequency-angle technique, and one scattering expansion method, based on a Neumann series expansion in terms of the mean number of scattering events.
For the Hanle effect with an angle-dependent PRD, the numerical solution is possible only if one truncates the infinite set of integral equations for the Fourier coefficients of the irreducible source vector components. For the type II PRD function (frequency coherent scattering in the atomic rest frame) of Hummer (1962), Domke & Hubeny (1988) showed that, at least five terms in the azimuthal Fourier expansion are needed to get a good agreement with the exact value of the function. This implies that the azimuthal order k takes values 0, ± 1, ± 2, ± 3, and ± 4, for each combination of K and Q of the irreducible source vector. For the Hanle problem, K = 0 and 2, with − K ≤ Q ≤ + K. Hence, we obtain a total of 54 coupled integral equations. Although they can be numerically solved, it is computationally demanding. To simplify this numerically difficult problem, we present an approximate method of solution based on the concept of a single scattering approximation.
In Sect. 2, we briefly recall the decomposition technique presented in Frisch (2009) for the Hanle effect with angle-dependent PRD. In Sect. 3, we derive approximate expressions for the Fourier coefficients of irreducible source vector components applying the single scattering approximation. A generic form for the Hanle scattering redistribution matrix is assumed in Sects. 2 and 3 (see Eq. (4) below). In Sect. 4, we generalize the results of Sects. 2 and 3 to the Hanle scattering redistribution matrix derived by Bommier (1997b, the so-called approximation-II). Section 5 is devoted to the comparison of results computed using the single scattering approximation with those computed using the perturbation method of Nagendra et al. (2002). Conclusions are presented in Sect. 6. Some technical details are given in Appendices A and B.
2. A decomposition method for Hanle effect with angle-dependent PRD
For the sake of clarity, we recall some important equations from Frisch (2009). The polarized transfer equation for the Stokes vector can be written in component form as ![\begin{equation} \mu {\partial I_i \over \partial \tau} = \left[\varphi(x)+r\right] \left[I_i(\tau,x,{\bm\Omega})-S_i(\tau,x,{\bm\Omega})\right], \ \ \ i=0,1,2, \label{rte_stokes_component} \end{equation}](/articles/aa/full_html/2011/08/aa16866-11/aa16866-11-eq24.png) (1)where Ω (θ,χ) is the outgoing ray direction defined with respect to the atmospheric normal and μ = cosθ. The line optical depth τ is defined by dτ = −kl dz, where kl is the frequency–averaged line absorption coefficient, and ϕ(x) is the normalized Voigt function. The frequency x is measured in units of the Doppler width, with x = 0 at the line center. The ratio of continuum to line absorption coefficient is denoted by r. The total source vector is given by
(1)where Ω (θ,χ) is the outgoing ray direction defined with respect to the atmospheric normal and μ = cosθ. The line optical depth τ is defined by dτ = −kl dz, where kl is the frequency–averaged line absorption coefficient, and ϕ(x) is the normalized Voigt function. The frequency x is measured in units of the Doppler width, with x = 0 at the line center. The ratio of continuum to line absorption coefficient is denoted by r. The total source vector is given by 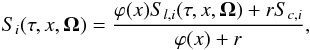 (2)where Sc,i are the components of the unpolarized continuum source vector. We assume that Sc,0 = Bν0, where Bν0 is the Planck function at the line center, and Sc,1 = Sc,2 = 0. The line source vector can be written as
(2)where Sc,i are the components of the unpolarized continuum source vector. We assume that Sc,0 = Bν0, where Bν0 is the Planck function at the line center, and Sc,1 = Sc,2 = 0. The line source vector can be written as 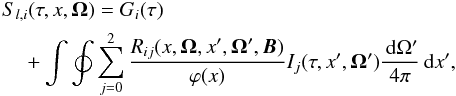 (3)where Ω′ (θ′,χ′) is the direction of the incoming ray defined with respect to the atmospheric normal, and dΩ′ = sinθ′ dθ′ dχ′. For simplicity, we assume that the primary source is unpolarized, namely that only G0(τ) is non-zero, and it is proportional to Bν0. In Sect. 3, we assume a generic form for the elements of the redistribution matrix in the presence of a weak magnetic field B given by
(3)where Ω′ (θ′,χ′) is the direction of the incoming ray defined with respect to the atmospheric normal, and dΩ′ = sinθ′ dθ′ dχ′. For simplicity, we assume that the primary source is unpolarized, namely that only G0(τ) is non-zero, and it is proportional to Bν0. In Sect. 3, we assume a generic form for the elements of the redistribution matrix in the presence of a weak magnetic field B given by 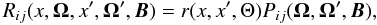 (4)where r(x,x′,Θ) is any redistribution function with proper normalization conditions, such as the type I, II, or III PRD functions of Hummer (1962), and Θ is the angle between the incoming (Ω′) and outgoing (Ω) rays. In terms of the irreducible spherical tensors
(4)where r(x,x′,Θ) is any redistribution function with proper normalization conditions, such as the type I, II, or III PRD functions of Hummer (1962), and Θ is the angle between the incoming (Ω′) and outgoing (Ω) rays. In terms of the irreducible spherical tensors 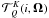 introduced by Landi Degl’Innocenti (1984), the Hanle phase matrix elements can be written as (see Chaps. 5 and 10 of Landi Degl’Innocenti & Landolfi 2004; or Frisch 2007; 2009)
introduced by Landi Degl’Innocenti (1984), the Hanle phase matrix elements can be written as (see Chaps. 5 and 10 of Landi Degl’Innocenti & Landolfi 2004; or Frisch 2007; 2009) 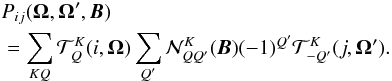 (5)For the coefficients
(5)For the coefficients 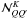 we assume the simple form
we assume the simple form 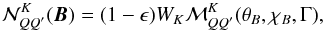 (6)where
(6)where 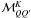 are coefficients that describe the effects of the magnetic field, ϵ the thermalization parameter, WK the depolarizability factors depending on the J-quantum numbers of upper and lower levels, (θB,χB) the polar angles defining the magnetic field orientation with respect to the atmospheric normal, and Γ = 2πνLgu/Aul in standard notation is the Hanle parameter.
are coefficients that describe the effects of the magnetic field, ϵ the thermalization parameter, WK the depolarizability factors depending on the J-quantum numbers of upper and lower levels, (θB,χB) the polar angles defining the magnetic field orientation with respect to the atmospheric normal, and Γ = 2πνLgu/Aul in standard notation is the Hanle parameter.
The Stokes vector and the source vector can each be decomposed into six irreducible components 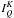 and
and 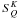 that are non-axisymmetric because of the angle dependence of the PRD function. To describe this angle dependence of the PRD function, we introduce an azimuthal Fourier expansion written as (see Eq. (15) of Frisch 2009)
that are non-axisymmetric because of the angle dependence of the PRD function. To describe this angle dependence of the PRD function, we introduce an azimuthal Fourier expansion written as (see Eq. (15) of Frisch 2009) 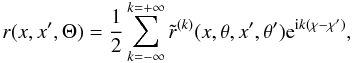 (7)where
(7)where ![\begin{eqnarray} & &\tilde r^{(k)}(x,\theta,x^\prime,\theta^\prime) = (1+\delta_{0k}) {2-\delta_{0k} \over 2\pi} \nonumber \\ \label{tilderq} && \quad \times \int_0^{2\pi} r(x,\theta,x^\prime,\theta^\prime,\chi-\chi^\prime) \cos [k(\chi-\chi^\prime)] \md(\chi-\chi^\prime). \end{eqnarray}](/articles/aa/full_html/2011/08/aa16866-11/aa16866-11-eq61.png) (8)It is easy to verify that
(8)It is easy to verify that 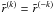 . To describe the azimuthal dependence of the irreducible components
. To describe the azimuthal dependence of the irreducible components 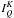 , we introduce the Fourier decomposition
, we introduce the Fourier decomposition 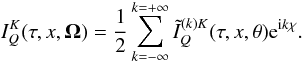 (9)Assuming a similar expansion for the primary source term
(9)Assuming a similar expansion for the primary source term 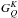 , it is easy to show that
, it is easy to show that 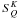 has an azimuthal expansion similar to Eq. (9).
has an azimuthal expansion similar to Eq. (9).
The Fourier coefficients 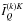 satisfy a non-local thermodynamic equilibrium (hereafter non-LTE) transfer equation
satisfy a non-local thermodynamic equilibrium (hereafter non-LTE) transfer equation ![\begin{equation} \mu {\partial \tilde I^{(k)K}_Q \over \partial \tau} = \left[\varphi(x)+r\right] \left[\tilde I^{(k)K}_Q(\tau,x,{\theta})-\tilde S^{(k)K}_Q(\tau,x,{\theta})\right], \label{rte_afe_ikq} \end{equation}](/articles/aa/full_html/2011/08/aa16866-11/aa16866-11-eq65.png) (10)where the source term is given by Eq. (2) with
(10)where the source term is given by Eq. (2) with 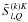 and
and 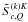 instead of Sl,i and Sc,i. Since the continuum is assumed to be unpolarized,
instead of Sl,i and Sc,i. Since the continuum is assumed to be unpolarized, 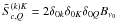 . The Fourier coefficients of the line source vector are given by
. The Fourier coefficients of the line source vector are given by 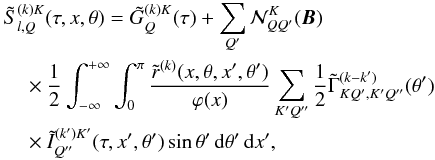 (11)where the primary source term
(11)where the primary source term 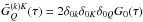 , and k′ = k + Q′ − Q′′. For a given value of k, the values of k′ are clearly restricted to k − 4 ≤ k′ ≤ k + 4. The non-zero azimuthal Fourier coefficients are of the form
, and k′ = k + Q′ − Q′′. For a given value of k, the values of k′ are clearly restricted to k − 4 ≤ k′ ≤ k + 4. The non-zero azimuthal Fourier coefficients are of the form 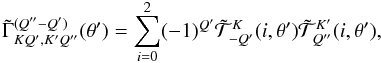 (12)where K and K′ are both even or both odd. The
(12)where K and K′ are both even or both odd. The 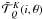 are combinations of trigonometric functions that may be written as
are combinations of trigonometric functions that may be written as 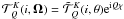 . It is easy to verify that
. It is easy to verify that 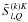 satisfy the following conjugation property
satisfy the following conjugation property ![\begin{equation} \left[\tilde S^{(k)K}_{l,Q}\right]^\ast=(-1)^Q \tilde S^{(-k)K}_{l,-Q}. \label{slkKQ_conjug} \end{equation}](/articles/aa/full_html/2011/08/aa16866-11/aa16866-11-eq79.png) (13)We note that the range of k values extends a priori from − ∞ to + ∞, thereby giving rise to an infinite set of integral equations for
(13)We note that the range of k values extends a priori from − ∞ to + ∞, thereby giving rise to an infinite set of integral equations for 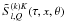 . A solution is possible only if we truncate this infinite set. As already noted in Sect. 1, if we restrict k to k = 0, ± 1, ± 2, ± 3, ± 4, we obtain a set of 54 coupled integral equations. Before going into such a difficult numerical problem, we show in the following section how the problem can be simplified by using a single scattering approximation (see Frisch et al. 2009; Frisch 2010).
. A solution is possible only if we truncate this infinite set. As already noted in Sect. 1, if we restrict k to k = 0, ± 1, ± 2, ± 3, ± 4, we obtain a set of 54 coupled integral equations. Before going into such a difficult numerical problem, we show in the following section how the problem can be simplified by using a single scattering approximation (see Frisch et al. 2009; Frisch 2010).
3. Approximate expressions for the Fourier coefficients 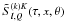
First we make the reasonable assumption that Stokes I is unaffected by the polarization. We can thus describe Stokes I with 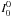 only, neglecting the contributions of the K ≠ 0 terms. For an angle-dependent PRD,
only, neglecting the contributions of the K ≠ 0 terms. For an angle-dependent PRD, 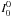 is non-axisymmetric and can be Fourier expanded as in Eq. (9). However, as Stokes I is almost independent of the magnetic field (in the weak field Hanle regime that we consider), we make a further assumption that
is non-axisymmetric and can be Fourier expanded as in Eq. (9). However, as Stokes I is almost independent of the magnetic field (in the weak field Hanle regime that we consider), we make a further assumption that 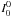 is independent of χ. Hence, only the k = 0 term contributes to
is independent of χ. Hence, only the k = 0 term contributes to 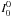 and we can write
and we can write 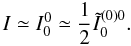 (14)With these approximations, the irreducible component
(14)With these approximations, the irreducible component 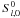 takes a simple form, namely
takes a simple form, namely 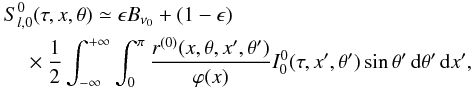 (15)where
(15)where 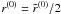 , and the thermalization parameter ϵ = ΓI/(ΓR + ΓI), with ΓR and ΓI being the radiative and inelastic collisional de-excitation rates.
, and the thermalization parameter ϵ = ΓI/(ΓR + ΓI), with ΓR and ΓI being the radiative and inelastic collisional de-excitation rates.
To obtain approximate expressions for the Fourier components 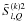 of
of 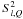 , we apply the single scattering approximation to Eq. (11), namely we keep in the right-hand side of this equation only the contribution from
, we apply the single scattering approximation to Eq. (11), namely we keep in the right-hand side of this equation only the contribution from 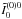 . This amounts to assuming that k′ = K′ = Q′′ = 0. Since k′ = k + Q′ − Q′′, we obtain k = −Q′. Hence, only the components
. This amounts to assuming that k′ = K′ = Q′′ = 0. Since k′ = k + Q′ − Q′′, we obtain k = −Q′. Hence, only the components 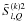 with k = 0, ± 1, ± 2 are non-zero. These 25 Fourier components are given by the following approximate expression
with k = 0, ± 1, ± 2 are non-zero. These 25 Fourier components are given by the following approximate expression 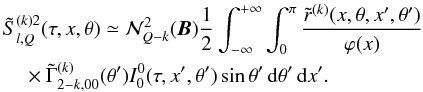 (16)The explicit forms of the azimuthal Fourier coefficients
(16)The explicit forms of the azimuthal Fourier coefficients 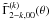 are given in the Appendix A.
are given in the Appendix A.
The irreducible components 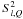 and their Fourier components for k ≠ 0 are complex numbers. We introduce here their real components. Following Frisch (2007, Eqs. (25) and (26)), we define the real components of
and their Fourier components for k ≠ 0 are complex numbers. We introduce here their real components. Following Frisch (2007, Eqs. (25) and (26)), we define the real components of 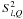 to be
to be ![\begin{equation} S^{{\rm x}2}_{l,Q}={1\over 2} \left[ S^2_{l,Q} + (-1)^Q S^2_{l,-Q}\right], \label{real_sxKlQ} \end{equation}](/articles/aa/full_html/2011/08/aa16866-11/aa16866-11-eq105.png) (17)
(17)![\begin{equation} S^{{\rm y}2}_{l,Q}=-{{\rm i}\over 2} \left[ S^2_{l,Q} - (-1)^Q S^2_{l,-Q}\right]. \label{imag_syKlQ} \end{equation}](/articles/aa/full_html/2011/08/aa16866-11/aa16866-11-eq106.png) (18)For the Fourier components
(18)For the Fourier components 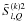 , we use the conjugation property given in Eq. (13) to define their real components as
, we use the conjugation property given in Eq. (13) to define their real components as ![\begin{equation} \tilde S^{{\rm x}(k)2}_{l,Q} = {1\over 2} \left[ \tilde S^{(k)2}_{l,Q} +(-1)^Q\tilde S^{(-k)2}_{l,-Q}\right], \ \ \ Q \ge 0, \label{real_sxkKlQ} \end{equation}](/articles/aa/full_html/2011/08/aa16866-11/aa16866-11-eq107.png) (19)
(19)![\begin{equation} \tilde S^{{\rm y}(k)2}_{l,Q} = -{{\rm i} \over 2} \left[ \tilde S^{(k)2}_{l,Q} -(-1)^Q\tilde S^{(-k)2}_{l,-Q}\right], \ \ \ Q \ge 0. \label{imag_sykKlQ} \end{equation}](/articles/aa/full_html/2011/08/aa16866-11/aa16866-11-eq108.png) (20)For k ≠ 0, using the conjugation property of
(20)For k ≠ 0, using the conjugation property of 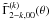 (see Appendix A) and of
(see Appendix A) and of 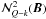 (see Chapter 5 of Landi Degl’Innocenti & Landolfi 2004), we can deduce from Eq. (16) that
(see Chapter 5 of Landi Degl’Innocenti & Landolfi 2004), we can deduce from Eq. (16) that 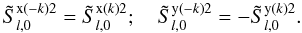 (21)Combining Eqs. (17) and (18) with the azimuthal Fourier expansion of
(21)Combining Eqs. (17) and (18) with the azimuthal Fourier expansion of 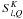 , we obtain
, we obtain 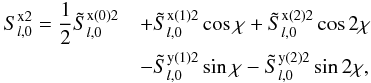 (22)
(22)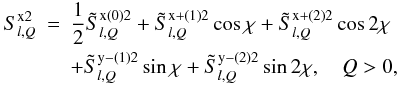 (23)
(23)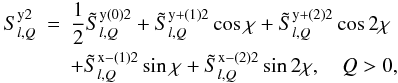 (24)where
(24)where ![\begin{eqnarray} && \tilde S^{{\rm x+}(k)2}_{l,Q}={1\over 2}\left[\tilde S^{{\rm x}(k)2}_{l,Q} +\tilde S^{{\rm x}(-k)2}_{l,Q}\right], \nonumber \\ && \tilde S^{{\rm x-}(k)2}_{l,Q}={1\over 2}\left[\tilde S^{{\rm x}(k)2}_{l,Q} -\tilde S^{{\rm x}(-k)2}_{l,Q}\right],\nonumber \\ && \tilde S^{{\rm y+}(k)2}_{l,Q}={1\over 2}\left[\tilde S^{{\rm y}(k)2}_{l,Q} +\tilde S^{{\rm y}(-k)2}_{l,Q}\right], \nonumber \\ \label{new_real} && \tilde S^{{\rm y-}(k)2}_{l,Q}={1\over 2}\left[\tilde S^{{\rm y}(-k)2}_{l,Q} -\tilde S^{{\rm y}(k)2}_{l,Q}\right], \end{eqnarray}](/articles/aa/full_html/2011/08/aa16866-11/aa16866-11-eq116.png) (25)for k > 0 and Q > 0. There are 25 non-zero real components of
(25)for k > 0 and Q > 0. There are 25 non-zero real components of 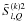 . Explicit expressions are given in Appendix B.
. Explicit expressions are given in Appendix B.
4. The Hanle scattering redistribution matrix
In Sect. 2, the decomposition method is presented with an oversimplified redistribution matrix. Here we show how to extend it to a standard Hanle redistribution matrix that takes into account elastic collisions and that the Hanle effect only operates in the line core.
Using a QED approach, Bommier (1997a,b) derived the Hanle scattering redistribution matrix including the effects of elastic collisions for a two-level atom with unpolarized lower level. For practical applications, she also presents the so-called approximation-II and approximation-III, where the two-dimensional (2D) frequency space (x,x′) is decomposed into several domains, in each domain the frequency redistribution being decoupled from the polarization. The approximation-II uses the angle-dependent PRD functions and approximation-III the corresponding angle-averaged functions. The approximations-II and III of the Hanle redistribution matrix were considered in Nagendra et al. (2002, see also Nagendra et al. 2003), where a perturbation method is used to solve the polarized transfer equations. For approximation-III, a polarized ALI method based on the core-wing approach was later developed by Fluri et al. (2003).
For approximation-III, the domains depend on (x, x′), but for approximation-II they depend in addition on the scattering angle Θ between the incoming and outgoing rays (see Figs. 1 and 2 in Nagendra et al. 2002). Thus, one practical question that arises when applying the decomposition technique developed for angle-dependent PRD presented in Sect. 2 to the case of approximation-II, is how to reduce or remove the (χ − χ′) dependence appearing in the expression of the redistribution matrix given in Eqs. (90) − (98) of Bommier (1997b). Here, to circumvent this problem, we use the angle-averaged domains of approximation-III, together with the angle-dependent redistribution functions of approximation-II. With this simplifying assumption, which as shown in Sect. 5 yields a reasonable solution, it is straightforward to generalize all the equations given in Sects. 2 and 3 to handle the approximation-II of Bommier (1997b). The only difference is that 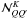 now depends on both x and x′. Therefore in Eqs. (11) and (16),
now depends on both x and x′. Therefore in Eqs. (11) and (16), 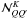 should be inside the frequency integral, and
should be inside the frequency integral, and 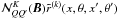 should be replaced by
should be replaced by 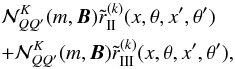 (26)where the index m ( = 1,2,3,4,5) stands for different (x, x′) frequency domains. The domains relevant to the type-III redistribution are represented by m = 1,2,3 and those relevant to the type-II redistribution by m = 4,5. Expressions for the
(26)where the index m ( = 1,2,3,4,5) stands for different (x, x′) frequency domains. The domains relevant to the type-III redistribution are represented by m = 1,2,3 and those relevant to the type-II redistribution by m = 4,5. Expressions for the 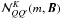 can be found in Bommier (1997b, see also Nagendra et al. 2002; Frisch 2007; Anusha et al. 2011).
can be found in Bommier (1997b, see also Nagendra et al. 2002; Frisch 2007; Anusha et al. 2011).
5. Results and discussions
Here we validate the single scattering approximation presented in Sect. 3, by comparing the solutions computed with this approximation, and those obtained by solving the full radiative transfer equation with an angle-dependent PRD and the Hanle effect. For the latter, we use a perturbation method developed by Nagendra et al. (2002). To obtain the single scattering solution, we first solve the scalar radiative transfer equation with the source term given by Eq. (15), using an ALI method based on the core-wing approach or frequency-angle by frequency-angle approach (see Sampoorna et al. 2011). The scalar intensity 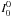 obtained in this way is then used in Eq. (16) or Eqs. (B.1) and (B.2), to compute the single scattered source vector. A formal solution then gives the corresponding single scattered radiation field.
obtained in this way is then used in Eq. (16) or Eqs. (B.1) and (B.2), to compute the single scattered source vector. A formal solution then gives the corresponding single scattered radiation field.
 |
Fig. 1 Comparison of single scattered (dashed lines) and multiple scattered (solid lines) solutions computed with the angle-dependent PRD. A 1D cut-off assumption is used with xc = 3. The model parameters are (a, ϵ, r, ΓE/ΓR) = (10-3, 10-3, 0, 0) and the magnetic field parameters are (Γ, θB, χB) = (1, 30°, 0°). The line of sight is represented by μ = 0.11 and χ = 0°. Panel a) corresponds to T = 1, panel b) to T = 100, and panel c) to T = 104. |
We consider isothermal, self-emitting plane-parallel atmospheres with no incident radiation at the boundaries. These slab models are characterized by (T, a, ϵ, r, ΓE/ΓR), where T is the optical thickness of the slab and ΓE is the elastic collisional rate. The depolarizing collisional rate D(2) is assumed to be 0.5 × ΓE. For all the figures presented in this paper, a = 10-3, ϵ = 10-3, r = 0 (pure line case), and the line of sight is defined by μ = 0.11 and χ = 0°. The magnetic field parameters are taken as Γ = 1, θB = 30°, and χB = 0°.
In Fig. 1, we compare the single scattered solution (dashed lines) with the full radiative transfer solution (hereafter, multiple scattered solution; see solid lines) for T = 1 (panel (a)), 100 (panel (b)), and 104 (panel (c)). For brevity, we only show the Q/I and U/I profiles. The comparison is carried out for the type-II angle-dependent redistribution function of Hummer (1962), i.e., with ΓE/ΓR = 0. We have used a one-dimensional (1D) cut-off assumption, setting the Hanle effect to zero for x > xc with xc = 3. Owing to this abrupt cut-off, spikes or dents are observed around x = 3 (see Fig. 1). Smoother curves can be obtained by using the more realistic 2D domains of Bommier (1997b) (see Fig. 3).
Figure 1 shows that the single scattering approximation can capture the main features of the Q/I and U/I profiles. It is the first time that this approximation has been employed for Stokes U. We can see that it is able to follow the very non-monotonic behavior of U/I. From a quantitative point of view, we observe at line center that the single scattering approximation underestimates the polarization for T = 1 and overestimates it for T = 100 and T = 104. The transition takes place around T = 100. As explained in Frisch et al. (2009) for the case of complete frequency redistribution (CRD), this change in behavior is related to the competition between a limb-darkened outgoing radiation and a limb-brightened incoming one (see also Trujillo Bueno 2001). In the near wings of Q/I, the single scattering approximation strongly underestimates the polarization. We recall that these wings are formed by Rayleigh scattering. For the angle-dependent case, Sampoorna et al. (2011) showed that the exact value of Q/I all along the profile can be obtained by an iterative method incorporating successive scattering orders (see Fig. 5 in this reference). It is likely that this method will also be able to improve the estimation of U/I.
In Fig. 2, we present the single scattered and multiple scattered solutions computed for T = 104, using the more realistic 2D domains of Bommier (1997b). Panel (a) corresponds to the collisionless case and panel (b) to an equal mix of type-II and type-III scattering. We recall that single scattered solutions are calculated with the angle-averaged domains corresponding to approximation-III and the multiple scattered solutions with angle-dependent domains corresponding to approximation-II. Figure 2 shows that this simplifying assumption gives solutions that compare reasonably with the corresponding multiple scattered solutions. The comparison between Figs. 2a and 2b shows that the single scattered solution can become a very good approximation to the multiple scattered solution in the presence of elastic collisions, particularly at the near wing maximum in Q/I profile. For angle-averaged PRD, we also have examples of single scattering solutions providing very accurate approximations (see Fig. 4 of Anusha et al. 2010).
 |
Fig. 2 Comparison of single scattered (dashed lines) and multiple scattered (solid lines) solutions computed with approximation-II of Bommier (1997b). The model parameters are (T, a, ϵ, r) = (104, 10-3, 10-3, 0) and the magnetic field parameters are (Γ, θB, χB) = (1, 30°, 0°). Panel a) corresponds to collisionless case (ΓE/ΓR = 0) and panel b) to an equal mix of type-II and III scattering (ΓE/ΓR = 1). |
The comparison of Fig. 2a with Fig. 1c suggests that U/I is very sensitive to the type of cut-off approximation used. We now discuss this point in more detail. Figure 3 shows the Q/I and U/I profiles computed for the collisionless case, and with three types of frequency domains. The solid lines are computed using a 1D cut-off assumption (xc = 3), and dashed lines with actual 2D domains of Bommier (1997b). The dotted lines are computed using a square domain (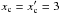 ). Such square domains have been used by Fluri et al. (2003, see their Fig. 2b). Figure 3a shows the single scattered solution, while Fig. 3b shows the multiple scattered solution. Clearly Q/I is insensitive to the type of frequency domains used, while U/I is quite sensitive, particularly in the transition region (3 ≤ x < 5).
). Such square domains have been used by Fluri et al. (2003, see their Fig. 2b). Figure 3a shows the single scattered solution, while Fig. 3b shows the multiple scattered solution. Clearly Q/I is insensitive to the type of frequency domains used, while U/I is quite sensitive, particularly in the transition region (3 ≤ x < 5).
6. Conclusions
The solution of a polarized line transfer equation with an angle-dependent PRD and the Hanle effect is computationally very demanding. To reduce the complexity of the numerical problem, Frisch (2009) developed a decomposition technique for angle-dependent Hanle problem. In this technique, the non-axisymmetric polarized radiation field is decomposed into an infinite set of cylindrically symmetric Fourier coefficients, by applying an azimuthal Fourier expansion of the angle-dependent PRD function. Such a decomposition method allows one to construct an infinite set of integral equations for the Fourier coefficients of the irreducible source vector components, the solution of which is possible only if we truncate this infinite set. Although the truncated integral equations can be numerically solved, this solution is still computationally demanding (at least 54 integral equations need to be solved simultaneously). Therefore, to simplify the problem, here we have presented an approximate method of solution, based on the single scattering approximation. An approximate solution can be obtained by keeping only the contribution of the zeroth order Fourier coefficient, namely, 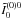 in the source terms for the K = 2 components (see Eq. (16)), which are responsible for the generation of Stokes Q and U. As a result, the number of Fourier coefficients reduces to 25 for K = 2 components. The Stokes I in this approximation is assumed to be cylindrically symmetric and decoupled from Stokes Q and U, so that it is computed through a solution of the scalar non-LTE transfer equation with an angle-dependent PRD function. An ALI method associated with a core-wing technique or frequency-angle by frequency-angle technique is used to solve this scalar transfer problem (see Sampoorna et al. 2011).
in the source terms for the K = 2 components (see Eq. (16)), which are responsible for the generation of Stokes Q and U. As a result, the number of Fourier coefficients reduces to 25 for K = 2 components. The Stokes I in this approximation is assumed to be cylindrically symmetric and decoupled from Stokes Q and U, so that it is computed through a solution of the scalar non-LTE transfer equation with an angle-dependent PRD function. An ALI method associated with a core-wing technique or frequency-angle by frequency-angle technique is used to solve this scalar transfer problem (see Sampoorna et al. 2011).
We have presented the single scattering approximation for a Hanle scattering redistribution matrix with (i) 1D cut-off assumption (see Sect. 3) and (ii) the more realistic frequency domains (see Sect. 4) introduced by Bommier (1997b). We show that the single scattered solution provides a reasonable approximation to the emergent solutions computed by solving the full polarized line transfer equation with angle-dependent PRD and the Hanle effect. To compute the full solution, we use a perturbation method developed by Nagendra et al. (2002). While the perturbation method used by Nagendra et al. (2002) is computationally expensive, the single scattering approximation presented here provides a rapid method of solution. For example, for T = 104 with 41 depth points, seven μ points (eight χ points required only in the case of perturbation method), and 39 frequency points, the perturbation method requires 24 min with 2.7 G Bytes of memory, while single scattered solution can be computed in 20 s with 22 M Bytes of memory, on a Sun Fire V20z Server, 2385 MHz, with a Single-core AMD Opteron processor.
The differences between single scattered and multiple scattered solutions for angle-dependent, as well as angle-averaged PRD are somewhat similar to those for CRD in the line core region. In the case of an angle-dependent and an angle-averaged type-II PRD function, the differences are particularly large at the near wing maximum in Q/I (see Fig. 1c). This difference is reduced in the presence of elastic collisions (see Fig. 2b). Thus, elastic collisions seem to expand the domain of applicability of single scattering approximation. We have also presented the sensitivity of U/I profiles to the choice of different frequency domains (see Fig. 3).
 |
Fig. 3 The effect of three types of frequency domains on Q/I and U/I profiles computed using angle-dependent PRD functions. Solid lines correspond to the 1D cut-off assumption (xc = 3), dotted lines to 2D square domains ( |
The single scattered solution presented in this paper can be improved by including higher orders of scattering. Such a method was presented in Frisch et al. (2009) for the Hanle effect with CRD, and in Sampoorna et al. (2011)
for Rayleigh scattering with angle-dependent PRD, where it was referred to as “scattering expansion method”. It is also possible to construct such a scattering expansion method for the case of Hanle effect with an angle-dependent PRD discussed in this paper. The single scattered solution should be seen as an “approximate solution” to the exact solution, and can be used in many practical applications that do not require highly accurate solution of this rather difficult problem, involving angle-dependent PRD matrices.
Online material
Appendix A: The azimuthal Fourier coefficients 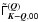
The azimuthal Fourier coefficients 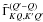 are defined in Eq. (12). It is easy to verify that they satisfy the properties
are defined in Eq. (12). It is easy to verify that they satisfy the properties ![\appendix \setcounter{section}{1} \begin{equation} \left[\tilde \Gamma^{(Q^\prime-Q)}_{KQ,K^\prime Q^\prime} \right]^\ast = \tilde \Gamma^{(Q-Q^\prime)}_{K^\prime Q^\prime,KQ}, \end{equation}](/articles/aa/full_html/2011/08/aa16866-11/aa16866-11-eq162.png) (A.1)
(A.1)![\appendix \setcounter{section}{1} \begin{equation} \tilde \Gamma^{(Q-Q^\prime)}_{K-Q,K^\prime -Q^\prime} = (-1)^{Q+Q^\prime} \left[\tilde \Gamma^{(Q^\prime-Q)}_{KQ,K^\prime Q^\prime}\right]^\ast. \end{equation}](/articles/aa/full_html/2011/08/aa16866-11/aa16866-11-eq163.png) (A.2)In this Appendix, we give only those Fourier coefficients that are of relevance to the problem at hand, namely those corresponding to K′ = Q′ = 0. Owing to the above-mentioned symmetry relations, there are only four independent coefficients, which are given by
(A.2)In this Appendix, we give only those Fourier coefficients that are of relevance to the problem at hand, namely those corresponding to K′ = Q′ = 0. Owing to the above-mentioned symmetry relations, there are only four independent coefficients, which are given by 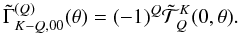 (A.3)If we chose the reference angle γ = 0 (see Landi Degl’Innocenti & Landolfi 2004), then from Eq. (A.6) of Frisch (2010), it is clear that
(A.3)If we chose the reference angle γ = 0 (see Landi Degl’Innocenti & Landolfi 2004), then from Eq. (A.6) of Frisch (2010), it is clear that 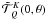 are real and hence that
are real and hence that 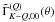 are also real. Using Eq. (A.6) of Frisch (2010) in our Eq. (A.3), we obtain the explicit form for these coefficients
are also real. Using Eq. (A.6) of Frisch (2010) in our Eq. (A.3), we obtain the explicit form for these coefficients 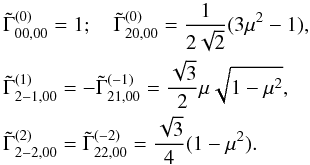 (A.4)
(A.4)
Appendix B: The explicit form of the real components of 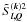
In this Appendix, we list the explicit analytic forms of the 25 non-zero real components of 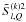 , defined in Eqs. (19), (20), and (25) of the text. For K = 2, we define
, defined in Eqs. (19), (20), and (25) of the text. For K = 2, we define 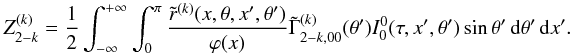 (B.1)We can express all the 25 non-zero real components of
(B.1)We can express all the 25 non-zero real components of 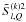 in terms of
in terms of 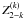 as follows :
as follows : ![\appendix \setcounter{section}{2} \begin{eqnarray} \tilde S^{{\rm x}(0)2}_{l,0}& = & \Re[{\mathcal N}^2_{00}] \, Z^{(0)}_{20}; \qquad\ \ \ \qquad \qquad \quad\ \ \, \tilde S^{{\rm x}(1)2}_{l,0}\ = \ \Re[{\mathcal N}^2_{0-1}] \, Z^{(1)}_{2-1}, \nonumber \\ \tilde S^{{\rm x}(2)2}_{l,0}& = & \Re[{\mathcal N}^2_{0-2}] \, Z^{(2)}_{2-2}; \qquad \qquad \qquad \quad\ \ \, \tilde S^{{\rm y}(1)2}_{l,0}\ =\ \Im[{\mathcal N}^2_{0-1}] \, Z^{(1)}_{2-1}, \nonumber \\ \tilde S^{{\rm y}(2)2}_{l,0} &= & \Im[{\mathcal N}^2_{0-2}] \, Z^{(2)}_{2-2}; \qquad \qquad \qquad \quad\ \ \, \tilde S^{{\rm x}(0)2}_{l,1}\ =\ \Re[{\mathcal N}^2_{10}] \, Z^{(0)}_{20}, \nonumber \\ \tilde S^{{\rm x+}(1)2}_{l,1} &= & {1\over 2} \Re[{\mathcal N}^2_{1-1}-{\mathcal N}^2_{11}] \, Z^{(1)}_{2-1}; \qquad \quad \ \ \tilde S^{{\rm x+}(2)2}_{l,1}\ = \ {1\over 2} \Re[{\mathcal N}^2_{1-2}+{\mathcal N}^2_{12}] \, Z^{(2)}_{2-2}, \nonumber \\ \tilde S^{{\rm y-}(1)2}_{l,1} &= & -{1\over 2} \Im[{\mathcal N}^2_{11}+{\mathcal N}^2_{1-1}] \, Z^{(1)}_{2-1}; \qquad \ \ \, \tilde S^{{\rm y-}(2)2}_{l,1}\ =\ {1\over 2} \Im[{\mathcal N}^2_{12}-{\mathcal N}^2_{1-2}] \, Z^{(2)}_{2-2}, \nonumber \\ \tilde S^{{\rm x}(0)2}_{l,2} &= & \Re[{\mathcal N}^2_{20}] \, Z^{(0)}_{20}; \qquad \qquad \qquad \qquad \, \tilde S^{{\rm x+}(1)2}_{l,2}\ = \ {1\over 2} \Re[{\mathcal N}^2_{2-1}-{\mathcal N}^2_{21}] \, Z^{(1)}_{2-1}, \nonumber \\ \tilde S^{{\rm x+}(2)2}_{l,2} &= & {1\over 2} \Re[{\mathcal N}^2_{2-2}+{\mathcal N}^2_{22}] \, Z^{(2)}_{2-2}; \qquad \quad\ \ \tilde S^{{\rm y-}(1)2}_{l,2}\ =\ -{1\over 2} \Im[{\mathcal N}^2_{21}+{\mathcal N}^2_{2-1}] \, Z^{(1)}_{2-1}, \nonumber \\ \tilde S^{{\rm y-}(2)2}_{l,2}& =& {1\over 2} \Im[{\mathcal N}^2_{22}-{\mathcal N}^2_{2-2}] \, Z^{(2)}_{2-2}; \qquad \quad\ \ \ \,\, \tilde S^{{\rm y}(0)2}_{l,1}\ =\ \Im[{\mathcal N}^2_{10}] \, Z^{(0)}_{20}, \nonumber \\ \tilde S^{{\rm y+}(1)2}_{l,1} &= & {1\over 2} \Im[{\mathcal N}^2_{1-1}-{\mathcal N}^2_{11}] \, Z^{(1)}_{2-1}; \qquad \quad\ \,\, \tilde S^{{\rm y+}(2)2}_{l,1}\ = \ {1\over 2} \Im[{\mathcal N}^2_{1-2}+{\mathcal N}^2_{12}] \, Z^{(2)}_{2-2}, \nonumber \\ \tilde S^{{\rm x-}(1)2}_{l,1}& =& {1\over 2} \Re[{\mathcal N}^2_{1-1}+{\mathcal N}^2_{11}] \, Z^{(1)}_{2-1}; \qquad \quad\ \ \tilde S^{{\rm x-}(2)2}_{l,1}\ =\ {1\over 2} \Re[{\mathcal N}^2_{1-2}-{\mathcal N}^2_{12}] \, Z^{(2)}_{2-2}, \nonumber \\ \tilde S^{{\rm y}(0)2}_{l,2} &= & \Im[{\mathcal N}^2_{20}] \, Z^{(0)}_{20}; \qquad \qquad \qquad \qquad\, \tilde S^{{\rm y+}(1)2}_{l,2}\ = \ {1\over 2} \Im[{\mathcal N}^2_{2-1}-{\mathcal N}^2_{21}] \, Z^{(1)}_{2-1}, \nonumber \\ \tilde S^{{\rm y+}(2)2}_{l,2} &=& {1\over 2} \Im[{\mathcal N}^2_{2-2}+{\mathcal N}^2_{22}] \, Z^{(2)}_{2-2}; \qquad \quad\ \ \tilde S^{{\rm x-}(1)2}_{l,2}\ =\ {1\over 2} \Re[{\mathcal N}^2_{2-1}+{\mathcal N}^2_{21}] \, Z^{(1)}_{2-1}, \nonumber \\ \tilde S^{{\rm x-}(2)2}_{l,2} &= & {1\over 2} \Re[{\mathcal N}^2_{2-2}-{\mathcal N}^2_{22}] \, Z^{(2)}_{2-2}. \label{sxykKQ_approx} \end{eqnarray}](/articles/aa/full_html/2011/08/aa16866-11/aa16866-11-eq175.png) (B.2)The above equations are valid for x < xc in the case of a 1D cut-off assumption. For x > xc, we have to set
(B.2)The above equations are valid for x < xc in the case of a 1D cut-off assumption. For x > xc, we have to set 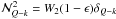 . In the case of approximation-II, the various
. In the case of approximation-II, the various 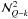 appearing in the above equations should be taken inside the frequency integral appearing in Eq. (B.1), and Eqs. (106)–(113) of Bommier (1997b) have to be used.
appearing in the above equations should be taken inside the frequency integral appearing in Eq. (B.1), and Eqs. (106)–(113) of Bommier (1997b) have to be used.
The various 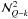 appearing in the above set of equations are given by Eq. (6) in the case of the 1D cut-off assumption and Eqs. (A11)–(A18) of Anusha et al. (in press) in the case of the 2D frequency domains of Bommier (1997b). Below we give the explicit forms of
appearing in the above set of equations are given by Eq. (6) in the case of the 1D cut-off assumption and Eqs. (A11)–(A18) of Anusha et al. (in press) in the case of the 2D frequency domains of Bommier (1997b). Below we give the explicit forms of 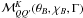 appearing in those equations. We introduce the abbreviations, CB = cosθB, SB = sinθB, c1 = cosχB, s1 = sinχB, c2 = cos2χB, and s2 = sin2χB. In terms of the elements of the
appearing in those equations. We introduce the abbreviations, CB = cosθB, SB = sinθB, c1 = cosχB, s1 = sinχB, c2 = cos2χB, and s2 = sin2χB. In terms of the elements of the 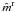 matrix given below (see also Appendix C in Frisch 2007), we have
matrix given below (see also Appendix C in Frisch 2007), we have ![\appendix \setcounter{section}{2} \begin{eqnarray} \Re[{\mathcal M}^2_{00}] = m_{11} &=&1-3S^2_B \Gamma^2 \left[{C^2_B \over 1+\Gamma^2 } + {S^2_B \over 1+4\Gamma^2}\right]; \qquad \qquad \qquad \ \ \Re[{\mathcal M}^2_{1-1}-{\mathcal M}^2_{11}]\ =\ -c^2_1 m_{22}-s^2_1 m_{33}, \nonumber \\ \Re[{\mathcal M}^2_{1-2}+{\mathcal M}^2_{12}]&=&c_1 c_2 m_{24} + s_1 s_2 m_{35} + s_2 c_1 m_{25} + c_2 s_1 m_{34}; \qquad \qquad \qquad \Re[{\mathcal M}^2_{0-1}]\ =\ -c_1 m_{12}-s_1 m_{13}, \nonumber \\ -\Im[{\mathcal M}^2_{11}+{\mathcal M}^2_{1-1}]&=&(c^2_1+s^2_1) m_{23} - c_1 s_1 (m_{22} - m_{33}); \qquad \qquad \qquad \qquad \quad \ \ \Re[{\mathcal M}^2_{0-2}]\ =\ c_2 m_{14}+s_2 m_{15}; \nonumber \\ \Im[{\mathcal M}^2_{12}-{\mathcal M}^2_{1-2}]&=&s_2 c_1 m_{24} - c_2 s_1 m_{35} - c_1 c_2 m_{25} + s_1 s_2 m_{34}; \qquad \qquad \qquad \Im[{\mathcal M}^2_{0-1}]\ =\ s_1 m_{12}-c_1 m_{13}, \nonumber \\ \Re[{\mathcal M}^2_{2-1}-{\mathcal M}^2_{21}]&=&-c_1 c_2 m_{24} - s_1 s_2 m_{35} + s_2 c_1 m_{25} + c_2 s_1 m_{34}; \qquad \qquad \quad \ \Im[{\mathcal M}^2_{0-2}]\ =\ -s_2 m_{14}+c_2 m_{15}, \nonumber \\ \Im[{\mathcal M}^2_{1-2}+{\mathcal M}^2_{12}]&=&s_2 c_1 m_{35} - c_2 s_1 m_{24}+ c_1 c_2 m_{34} - s_1 s_2 m_{25}; \qquad \qquad \qquad \ \ \Re[{\mathcal M}^2_{10}]\ =\ c_1 m_{12}-s_1 m_{13}, \nonumber \\ -\Im[{\mathcal M}^2_{21}+{\mathcal M}^2_{2-1}]&=&s_2 c_1 m_{35} - c_2 s_1 m_{24} - c_1 c_2 m_{34} + s_1 s_2 m_{25}; \qquad \qquad \qquad \ \ \Re[{\mathcal M}^2_{20}]\ =\ c_2 m_{14} - s_2 m_{15}, \nonumber \\ \Im[{\mathcal M}^2_{22}-{\mathcal M}^2_{2-2}]&=&-(c^2_2+s^2_2) m_{45} + c_2 s_2 (m_{44} - m_{55}); \qquad \qquad \qquad \qquad \quad \ \ \Im[{\mathcal M}^2_{10}]\ =\ -s_1 m_{12} - c_1 m_{13}, \nonumber \\ \Im[{\mathcal M}^2_{1-1}-{\mathcal M}^2_{11}]&=&(c^2_1+s^2_1) m_{23} + c_1 s_1 (m_{22}-m_{33}); \qquad \qquad \qquad\ \, \Re[{\mathcal M}^2_{2-2}+{\mathcal M}^2_{22}]\ =\ c^2_2 m_{44} + s^2_2 m_{55}, \nonumber \\ \Re[{\mathcal M}^2_{1-2}-{\mathcal M}^2_{12}]&=&-c_1 c_2 m_{35} - s_1 s_2 m_{24} + s_2 c_1 m_{34} + c_2 s_1 m_{25}; \qquad \Re[{\mathcal M}^2_{1-1}+{\mathcal M}^2_{11}]\ =\ c^2_1 m_{33} + s^2_1 m_{22}, \nonumber \\ \Im[{\mathcal M}^2_{2-1}-{\mathcal M}^2_{21}]&=&s_2 c_1 m_{24} - c_2 s_1 m_{35} + c_1 c_2 m_{25} - s_1 s_2 m_{34}; \qquad \qquad \qquad \ \ \, \Im[{\mathcal M}^2_{20}]\ =\ -s_2 m_{14} - c_2 m_{15}, \nonumber \\ \Im[{\mathcal M}^2_{2-2}+{\mathcal M}^2_{22}]&=&-(c^2_2+s^2_2) m_{45} - c_2 s_2 (m_{44} - m_{55}); \qquad \qquad \qquad \Re[{\mathcal M}^2_{2-2}-{\mathcal M}^2_{22}]\ =\ - c^2_2 m_{55} - s^2_2 m_{44}, \nonumber \\ \Re[{\mathcal M}^2_{2-1}+{\mathcal M}^2_{21}]&=&c_1 c_2 m_{35} + s_1 s_2 m_{24} + s_2 c_1 m_{34} + c_2 s_1 m_{25}, \label{nkqmk} \end{eqnarray}](/articles/aa/full_html/2011/08/aa16866-11/aa16866-11-eq188.png) (B.3)where
(B.3)where ![\appendix \setcounter{section}{2} \begin{eqnarray} m_{12}&=&-\sqrt{{3\over 2}} S_B C_B \Gamma^2 \left[{2C_B^2-1 \over 1+\Gamma^2} + {2 S_B^2 \over 1+4\Gamma^2}\right]; \qquad \qquad \qquad m_{13}\ =\ \sqrt{{3\over 2}} S_B \Gamma \left[{C_B^2 \over 1+\Gamma^2} + { S_B^2 \over 1+4\Gamma^2}\right], \nonumber \\ m_{14}&=&\sqrt{{3\over 2}} S^2_B \Gamma^2 \left[{C_B^2 \over 1+\Gamma^2} - {1+ C_B^2 \over 1+4\Gamma^2}\right]; \qquad \qquad \qquad \qquad \quad m_{15}\ =\ -\sqrt{{3\over 2}} S^2_B C_B \Gamma \left[{1 \over 1+\Gamma^2} - {1 \over 1+4\Gamma^2}\right], \nonumber \\ m_{22}& =& 1 - \Gamma^2 \left[{(1-2C^2_B)^2 \over 1+\Gamma^2} + {4 S^2_B C^2_B \over 1+4 \Gamma^2}\right]; \qquad \qquad \qquad \qquad\ m_{23}\ =\ -C_B \Gamma \left[{1-2C^2_B \over 1+\Gamma^2} - {2 S^2_B \over 1+4 \Gamma^2}\right], \nonumber \\ m_{24}& =& -C_B S_B \Gamma^2 \left[{1-2C^2_B \over 1+\Gamma^2} + {2 (1+C^2_B) \over 1+4 \Gamma^2}\right]; \qquad \qquad \qquad \ \ m_{25} \ =\ S_B \Gamma \left[{1-2C^2_B \over 1+\Gamma^2} + {2 C^2_B \over 1+4 \Gamma^2}\right], \nonumber \\ m_{33}& =& 1 - \Gamma^2 \left[{C^2_B \over 1+\Gamma^2} + {4 S^2_B \over 1+4 \Gamma^2}\right]; \qquad \qquad \qquad \qquad \qquad \ \, m_{34}\ =\ S_B \Gamma \left[{C^2_B \over 1+\Gamma^2} - {1+C^2_B \over 1+4 \Gamma^2}\right], \nonumber \\ m_{35} &=& C_B S_B \Gamma^2 \left[{1 \over 1+\Gamma^2} - {4 \over 1+4 \Gamma^2}\right]; \qquad \qquad \qquad \qquad \quad \ \, m_{44} \ =\ 1- \Gamma^2 \left[{C^2_B S^2_B \over 1+\Gamma^2} + {(1+ C^2_B)^2 \over 1+4 \Gamma^2}\right], \nonumber \\ m_{45} &=& C_B \Gamma \left[{S^2_B \over 1+\Gamma^2} + {1+ C^2_B \over 1+4 \Gamma^2}\right]; \qquad \qquad \qquad \qquad \qquad \quad \ m_{55}\ =\ 1- \Gamma^2 \left[{S^2_B \over 1+\Gamma^2} + {4C^2_B \over 1+4 \Gamma^2}\right]. \label{mbr} \end{eqnarray}](/articles/aa/full_html/2011/08/aa16866-11/aa16866-11-eq189.png) (B.4)
(B.4)
Acknowledgments
I am very grateful to Drs. H. Frisch and K. N. Nagendra for stimulating discussions and critical comments on the manuscript. Thanks are also due to L. S. Anusha for useful comments.
References
- Anusha, L. S., Nagendra, K. N., Stenflo, J. O., et al. 2010, ApJ, 718, 988 [NASA ADS] [CrossRef] [Google Scholar]
- Anusha, L. S., Nagendra, K. N., Bianda, M., et al. 2011, ApJ, 736, in press [Google Scholar]
- Bommier, V. 1997a, A&A, 328, 706 [NASA ADS] [Google Scholar]
- Bommier, V. 1997b, A&A, 328, 726 [NASA ADS] [Google Scholar]
- Domke, H., & Hubeny, I. 1988, ApJ, 334, 527 [NASA ADS] [CrossRef] [Google Scholar]
- Faurobert, M. 1988, A&A, 194, 268 [NASA ADS] [Google Scholar]
- Fluri, D. M., Nagendra, K. N., & Frisch, H. 2003, A&A, 400, 303 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frisch, H. 2007, A&A, 476, 665 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frisch, H. 2009, in Solar Polarization 5, ed. S. V. Berdyugina, K. N. Nagendra, & R. Ramelli (San Francisco: ASP), ASP Conf. Ser., 405, 87 [Google Scholar]
- Frisch, H. 2010, A&A, 522, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frisch, H., Anusha, L. S., Sampoorna, M., & Nagendra, K. N. 2009, A&A, 501, 335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hummer, D. G. 1962, MNRAS, 125, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Landi Degl’Innocenti, E. 1984, Sol. Phys., 91, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Landi Degl’Innocenti, E., & Landolfi, M. 2004, Polarization in Spectral Lines (Dordrecht: Kluwer) [Google Scholar]
- Nagendra, K. N., Frisch, H., & Faurobert, M. 2002, A&A, 395, 305 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nagendra, K. N., Frisch, H., & Fluri, D. M. 2003, in Solar Polarization, ed. J. Trujillo Bueno & J. Sanchez Almeida (San Francisco: ASP), ASP Conf. Ser., 307, 227 [Google Scholar]
- Sampoorna, M., Nagendra, K. N., & Frisch, H. 2011, A&A, 527, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stenflo, J. O. 1982, Sol. Phys., 80, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Trujillo Bueno, J. 2001, in Advanced Solar Polarimetry Theory, Observation, and Instrumentation, ed. M. Sigwarth, ASP Conf. Ser., 236, 161 [Google Scholar]
- Trujillo Bueno, J., Shchukina, N., & Asensio Ramos, A. 2004, Nature, 430, 326 [Google Scholar]
All Figures
 |
Fig. 1 Comparison of single scattered (dashed lines) and multiple scattered (solid lines) solutions computed with the angle-dependent PRD. A 1D cut-off assumption is used with xc = 3. The model parameters are (a, ϵ, r, ΓE/ΓR) = (10-3, 10-3, 0, 0) and the magnetic field parameters are (Γ, θB, χB) = (1, 30°, 0°). The line of sight is represented by μ = 0.11 and χ = 0°. Panel a) corresponds to T = 1, panel b) to T = 100, and panel c) to T = 104. |
| In the text | |
 |
Fig. 2 Comparison of single scattered (dashed lines) and multiple scattered (solid lines) solutions computed with approximation-II of Bommier (1997b). The model parameters are (T, a, ϵ, r) = (104, 10-3, 10-3, 0) and the magnetic field parameters are (Γ, θB, χB) = (1, 30°, 0°). Panel a) corresponds to collisionless case (ΓE/ΓR = 0) and panel b) to an equal mix of type-II and III scattering (ΓE/ΓR = 1). |
| In the text | |
 |
Fig. 3 The effect of three types of frequency domains on Q/I and U/I profiles computed using angle-dependent PRD functions. Solid lines correspond to the 1D cut-off assumption (xc = 3), dotted lines to 2D square domains ( |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


