| Issue |
A&A
Volume 532, August 2011
|
|
|---|---|---|
| Article Number | A52 | |
| Number of page(s) | 8 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201116866 | |
| Published online | 21 July 2011 | |
Online material
Appendix A: The azimuthal Fourier coefficients 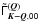
The azimuthal Fourier coefficients 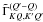 are defined in Eq. (12). It is easy to verify that they satisfy the properties
are defined in Eq. (12). It is easy to verify that they satisfy the properties 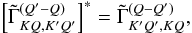 (A.1)
(A.1)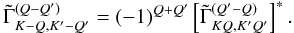 (A.2)In this Appendix, we give only those Fourier coefficients that are of relevance to the problem at hand, namely those corresponding to K′ = Q′ = 0. Owing to the above-mentioned symmetry relations, there are only four independent coefficients, which are given by
(A.2)In this Appendix, we give only those Fourier coefficients that are of relevance to the problem at hand, namely those corresponding to K′ = Q′ = 0. Owing to the above-mentioned symmetry relations, there are only four independent coefficients, which are given by 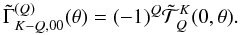 (A.3)If we chose the reference angle γ = 0 (see Landi Degl’Innocenti & Landolfi 2004), then from Eq. (A.6) of Frisch (2010), it is clear that
(A.3)If we chose the reference angle γ = 0 (see Landi Degl’Innocenti & Landolfi 2004), then from Eq. (A.6) of Frisch (2010), it is clear that 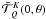 are real and hence that
are real and hence that 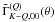 are also real. Using Eq. (A.6) of Frisch (2010) in our Eq. (A.3), we obtain the explicit form for these coefficients
are also real. Using Eq. (A.6) of Frisch (2010) in our Eq. (A.3), we obtain the explicit form for these coefficients 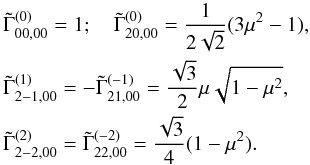 (A.4)
(A.4)
Appendix B: The explicit form of the real components of 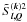
In this Appendix, we list the explicit analytic forms of the 25 non-zero real components of 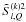 , defined in Eqs. (19), (20), and (25) of the text. For K = 2, we define
, defined in Eqs. (19), (20), and (25) of the text. For K = 2, we define  (B.1)We can express all the 25 non-zero real components of
(B.1)We can express all the 25 non-zero real components of 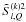 in terms of
in terms of 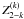 as follows :
as follows : 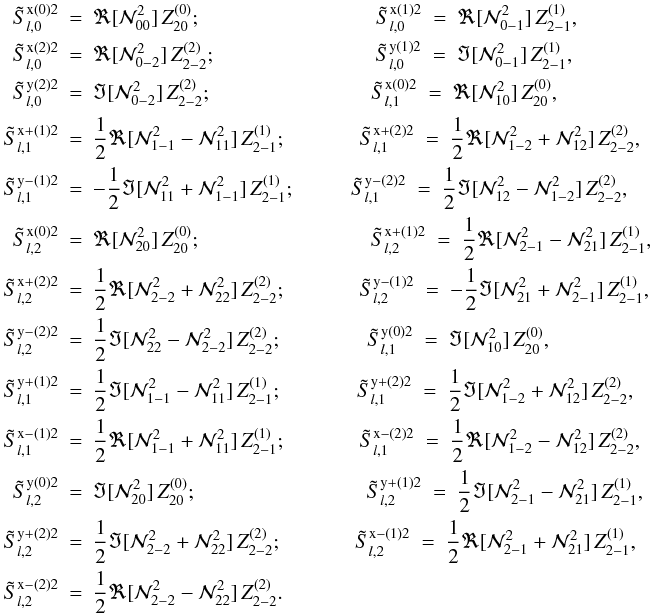 (B.2)The above equations are valid for x < xc in the case of a 1D cut-off assumption. For x > xc, we have to set
(B.2)The above equations are valid for x < xc in the case of a 1D cut-off assumption. For x > xc, we have to set 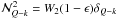 . In the case of approximation-II, the various
. In the case of approximation-II, the various  appearing in the above equations should be taken inside the frequency integral appearing in Eq. (B.1), and Eqs. (106)–(113) of Bommier (1997b) have to be used.
appearing in the above equations should be taken inside the frequency integral appearing in Eq. (B.1), and Eqs. (106)–(113) of Bommier (1997b) have to be used.
The various  appearing in the above set of equations are given by Eq. (6) in the case of the 1D cut-off assumption and Eqs. (A11)–(A18) of Anusha et al. (in press) in the case of the 2D frequency domains of Bommier (1997b). Below we give the explicit forms of
appearing in the above set of equations are given by Eq. (6) in the case of the 1D cut-off assumption and Eqs. (A11)–(A18) of Anusha et al. (in press) in the case of the 2D frequency domains of Bommier (1997b). Below we give the explicit forms of 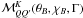 appearing in those equations. We introduce the abbreviations, CB = cosθB, SB = sinθB, c1 = cosχB, s1 = sinχB, c2 = cos2χB, and s2 = sin2χB. In terms of the elements of the
appearing in those equations. We introduce the abbreviations, CB = cosθB, SB = sinθB, c1 = cosχB, s1 = sinχB, c2 = cos2χB, and s2 = sin2χB. In terms of the elements of the 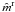 matrix given below (see also Appendix C in Frisch 2007), we have
matrix given below (see also Appendix C in Frisch 2007), we have  (B.3)where
(B.3)where 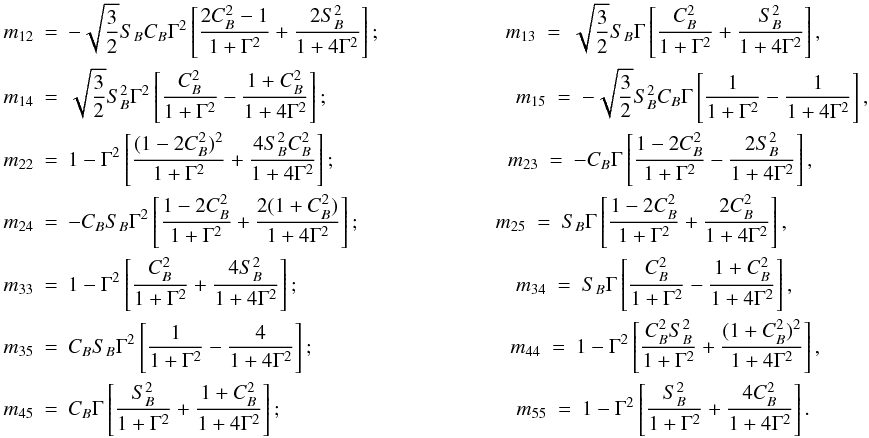 (B.4)
(B.4)
© ESO, 2011
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


