| Issue |
A&A
Volume 532, August 2011
|
|
|---|---|---|
| Article Number | A72 | |
| Number of page(s) | 9 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201116712 | |
| Published online | 25 July 2011 | |
Sparse aperture masking at the VLT⋆
I. Faint companion detection limits for the two debris disk stars HD 92945 and HD 141569
1 LESIA, CNRS/UMR-8109, Observatoire de Paris, UPMC, Université Paris Diderot, 5 place Jules Janssen, 92195 Meudon, France
e-mail: sylvestre.lacour@obspm.fr
2 Sydney Institute for Astronomy, School of Physics, The University of Sydney, NSW 2006, Australia
3 ESO, Karl-Schwarzschild-Strasse 2, 85748 Garching, Germany
4 UJF-Grenoble 1/CNRS-INSU, Institut de planétologie et d’Astrophysique de Grenoble (IPAG) UMR 5274, 38041 Grenoble, France
5 Centro de Astrobiología (INTA-CSIC); LAEFF, PO Box 78, 28691 Villanueva de la Cañada, Spain
Received: 14 February 2011
Accepted: 20 June 2011
Aims. Observational data on companion statistics around young stellar systems is needed to flesh out the formation pathways for extrasolar planets and brown dwarfs. Aperture masking is a new technique that is able to address an important part of this discovery space.
Methods. We observed the two debris disk systems HD 92945 and HD 141569 with sparse aperture masking (SAM), a new mode offered on the NaCo instrument at the VLT. A search for faint companions was performed using a detection strategy based on the analysis of closure phases recovered from interferograms recorded on the Conica camera.
Results. Our results demonstrate that SAM is a very competitive mode in the field of companion detection. We obtained 5σ high-contrast detection limits at λ/D of 2.5 × 10-3 (ΔL′ = 6.5) for HD 92945 and 4.6 × 10-3 (ΔL′ = 5.8) for HD 141569. According to brown dwarf evolutionary models, our data impose an upper mass boundary for any companion for the two stars to, respectively, 18 and 22 Jupiter masses at minimum separations of 1.5 and 7 AU. The detection limits is mostly independent of angular separation, until reaching the diffraction limit of the telescope.
Conclusions. We have placed upper limits on the existence of companions to our target systems that fall close to the planetary mass regime. This demonstrates the potential for SAM mode to contribute to studies of faint companions. We furthermore show that the final dynamic range obtained is directly proportional to the error on the closure phase measurement. At the present performance levels of 0.28 degree closure phase error, SAM is among the most competitive techniques for recovering companions at scales of one to several times the diffraction limit of the telescope. Further improvements to the detection threshold can be expected with more accurate phase calibration.
Key words: instrumentation: high angular resolution / planetary systems / techniques: high angular resolution / stars: individual: HD 92945 / stars: individual: HD 141569
© ESO, 2011
1. Introduction
Since the first imaging of a debris disk around β Pictoris (Smith & Terrile 1984), and the remarkable successes of the radial velocity technique for exoplanet discovery heralded nearly a decade later by a companion to solar-like 51 Pegasi (Mayor & Queloz 1995), the understanding of planetary systems formation and evolution has become one of astronomy’s greatest challenges. Today, at least 22 debris disks have been imaged at optical, infrared, or submillimeter wavelengths. Such disks are thought to be the cradle where planetary systems have recently formed. The observed dust component is not primordial but instead produced by collisions among larger rocky bodies. This makes debris disks obvious places to search for planets, and many show possible indirect signs of their presence, such as dust structures or disk asymmetries.
 |
Fig. 1 Left panel: diffraction pattern observed on star HD 135549. This image is a single frame of 0.4 ms integration time, using the 7-hole pupil mask. Background noise is ≈ 12 ADU, and pic brightness 800 ADU. Right panel: fourier transform of the diffraction pattern. Each peak corresponds to a baseline pair. |
The recent detection and confirmation of a ~9 MJup planet within the disk of β Pic (semi-major axis between 8 and 15 AU) using direct deep imaging validates the link between structures in debris disks and the presence of planets (Lagrange et al. 2009, 2010). Besides this planet, only a couple of planetary-mass objects have been detected around stars with a debris disk. In fact, most debris disks have been imaged around young bright A- or F-type stars, which are either rapid rotators and/or active stars. The search for companions with radial velocity techniques around these stars is therefore extremely difficult. Key breakthroughs have recently been made with high-contrast imaging: a < 3-MJup planetary companion was detected in the outskirts of Fomalhaut’s debris disk (119 AU from the star; Kalas et al. 2008), while four planetary companions of 7, 10, 10, and 10 MJup were imaged at 68, 38, 24, and 14 AU, respectively, from HR 8799 (Marois et al. 2008, 2010). It is not clear whether these objects could have formed through core accretion – and not from gravitational instabilities – the foremost theory of planet formation, although β Pic b is a serious candidate for this formation scenario (Lagrange et al. 2010).
Most companions detected with high-contrast imaging, such as AB Pic b (Chauvin et al. 2005) or 2M1207 b (Chauvin et al. 2004), are believed to be either too far or too massive to have formed through core accretion. An alternate pathway gaining widespread interest is a stellar formation mechanism, i.e., formation during the fragmentation and collapse of a molecular cloud. There are many unanswered questions raised by these models. Do these two processes for forming planets and brown dwarfs/low-mass stars operate exclusively (does one inhibit the other)? Can core accretion from a disk operate when a brown-dwarf companion exists at large separation? In contrast, can disks and planets exist around tight binary systems, composed of the primary star and a very close low-mass star or brown dwarf? How do massive companions impact the dynamic evolution of planets and disks?
To answer these questions, it is necessary to probe the innermost regions of debris disks when searching for substellar companions. For the closest debris disk, direct imaging proved to be a successful technique, as shown for β Pic or Fomalhaut. But most of the young associations (as well as stellar forming regions) lie at more than a hundred parsecs. At such a distance, 10 AU is equivalent to 100 mas, less than twice the diffraction limit of an 8-meter telescope in the near-infrared. This observational domain is not filled by differential imaging techniques, whose inner working angle is typically of few resolution elements. It is neither filled by long baseline interferometry: the field of view of a single mode interferometer is too small, equal to the resolution element of one of its telescopes. The effectiveness of both techniques is reviewed in detail in Absil & Mawet (2010). In terms of angular separation, aperture masking is the missing link in the field of high dynamic observations. It gives a relatively high dynamic range (5 to 7 mag) at a specific angular separation ( ≈ 100 mas) which is of greatest interest for planetary formation.
In this paper, we present three stars observed with an aperture mask at the VLT. In the next section, the instrument is described, along with the observational procedure and data reduction methods. In Sect. 3, we present a clearly resolved detection of the binary star HD 135549 for illustrative and pedagogical purposes. Section 4 reports on the non detection contrast limits obtained with SAM for the two debris disks HD 92945 and HD 141569. We present these limits as a function of flux ratio and infer the mass limit derived from current models.
2. Observation and data reduction
2.1. SAM at NaCo
An aperture mask works by transforming the telescope into a Fizeau interferometer. The point spread function is a complex superposition of fringes at given frequencies. In specific cases, pupil masking can outperform more traditional differential imaging for a number of reasons. First, the masks are designed to have nonredundant array configurations that permit phase deconvolution; slowly moving optical aberrations not corrected by the AO can be accuratly calibrated. Second, the mask primarily rejects baselines with low spatial frequency and passes proportionately far more baselines with higher λ/B resolution than does an orthodox fully filled pupil. Third, high-fidelity recovery of phase information allows “super resolution”, with a marginal loss of dynamic range up to λ/2D. The principal drawback is a loss in throughput so that photon and detector noise can affect the signal-to-noise ratio even where targets are reasonably bright for the AO system to close the loop. In common with all synthesis imaging by interferometry, the effective field-of-view of SAM is determined by the shortest baseline so that the technique is not competitive at separations larger that are greater than several times the formal diffraction limit.
VLT’s SAM mode has grown from earlier seeing-limited experiments on the Keck telescope (Tuthill et al. 2000), and more recently has gained widespread use on adaptive optics equipped telescopes (Tuthill et al. 2006; Lloyd et al. 2006). Commissioning of SAM at NaCo has required important software development from ESO at Paranal. It prompted the development of datacube storage (offered now regularly on NaCo as “cube mode”) and of pupil-tracking observation (the Nasmyth rotator tracks the telescope elevation). SAM is currently under investigation as an additional mode for the VISIR instrument, operating in the mid-infrared. It is under informal study for the SPHERE instrument (Beuzit et al. 2008).
2.2. Observing procedure
Observation log.
Observations were taken in the L prime band (λ = 3.80 ± 0.31 μm) using the “7 holes” mask and the IR wavefront sensor (WFS). The diffraction pattern is plotted in Fig. 1. The physical properties of the mask – as well as the three others – are described in the NaCo manual1. The complete observational sequence for an object typically took two hours. Table 1 contains observing details such as integration times, datacube size, and number of acquisitions.
Each science target is associated to a PSF reference star situated within one degree. A single observing block (OB) is used that encodes replicated observations for both calibrator and target. Rapid star acquisition – which is important for ensuring good calibration – can be augmented by using a simple offset of the telescope without having to preset the telescope and perform a full (instrumental) re-acquisition. In this mode, which has been christened “star hopping”, the adaptive optics loop is opened, while the template orders a dither to bring a different star into the AO field selector. The AO is then closed manually by the operator without incurring the time penalty for re-optimization. Star hopping therefore only works on objects of comparable brightness in the wavefront sensor.
As the observation progresses, the repetition of the template collects eight datacubes of multiple frames (typically a hundred), each at a different dither position on the detector. For these observations, the detector was windowed to 512 × 514 pixels.
A single snapshot observation yields Fourier coverage of 21 spatial frequencies. However, the pupil-tracking mode results in sky rotation on the detector as the parallactic angle changes. This variation with time results sweeps the baselines into circular Fourier tracks and permits rotational aperture synthesis techniques to assist with the filling of the spatial frequency UV-plane plane, as illustrated in Fig. 2.
2.3. Data reduction
 |
Fig. 2 Frequency coverage for targets HD 135549, HD 92945, and HD 141569. |
To the author’s knowledge, two data reduction software libraries are presently available2 to reduce SAM data. One pipeline has been developed by Sydney University, Cornell University, and Caltech from 2004 onwards, based on an earlier pipeline from Berkeley. It has already been used for several papers arising predominantly from Keck aperture masking data (Tuthill et al. 2000). This reduction algorithm is based on fast Fourier transform (FFT). The data presented in this paper have been reduced by the sparse aperture mode pipeline (SAMP) developed at the Observatoire de Paris. This software is similar to that from Sydney university, and numerous tests and cross-checks have produced similar results.
For both pipelines, data reduction follows a similar path:
-
Pre-reduction: the data are (i) flatfielded; (ii) bad-pixel corrected;and (iii) background-subtracted.
-
Complex visibility: complex visibilities are obtained from FFT of the image (Sydney pipeline), or by direct fringe fitting (SAMP)3.
-
Bispectrum: the bispectrum is obtained using multiplication of the complex visibilities corresponding to a triangle of holes in the mask. Bispectrum is averaged over all the frames of each set of eight datacubes. Closure phases are obtained using the argument of the bispectrum.
-
Calibration: closure phases obtained on the calibrator are fitted with a polynomial function, and subtracted from the closure phases on the science object.
-
Detection: the closure phases are fitted with a model of binary star (see Sect. 3). A χ2 map is computed, giving the likelihood of the presence of the companion for any given separation and position angle.
Atmospheric dispersion is not accounted for in our pipeline, but we are aware that in certain conditions (presence of emission lines in the spectrum), it can mimic asymmetry along the elevation axis. Such false detection can be avoided by observation at different parallactic angles.
The effect of fringe blurring due to the large bandwith of L′ filter can technically be accounted for in the fitting process. It would require including a loss of fringe coherence on the edge of the diffraction pattern. However, at this stage, the SAMP pipeline does not include this correction. It is, however, not seen as critical with the seven-hole mask, since the diffraction pattern of the 1.2 m holes are significantly smaller than the coherence length (see Fig. 1). It becomes an acute problem with the small holes of the 18-hole mask, which then justifies using a narrow band filter.
The complex visibilities consist of amplitudes and phases, but for the purposes of binary detection, we typically rely on the phases only (of the bispectrum). This is because of the dependence of absolute visibilities on the adaptive optics correction. They are thus harder to calibrate, and are subject to different biases between the science and the calibrator object. However, by default, the pipelines also process the power spectrum and estimate fringe visibilities. Performance of SAM’s visibility estimation will be the subject of a forthcoming paper.
3. Test case: the HD 135549 binary system
3.1. Principles of faint companion detection with SAM
Aperture masking data yields Fourier phases and amplitudes. They are functionally equivalent to those recovered in long-baseline interferometry, and therefore the same techniques and software can be applied. Image reconstruction is a possibility, but to fulfill the difficult requirements of faint companion detection, direct fitting in the Fourier domain is essential.
Modeling the presence of a two point-like sources in the Fourier domain is trivial. The complex visibility can be written as: ![\begin{equation} V(u,v)=1-r\,\left\{1-\exp \left[{\rm i} 2 \pi (-\alpha u + \delta v)/\lambda\right]\right\} \, , \label{eq} \end{equation}](/articles/aa/full_html/2011/08/aa16712-11/aa16712-11-eq21.png) (1)where u and v are orthogonal spatial frequency vectors (respectively to the east and to the north), α and δ are the right ascension and declination in radians, and r is the flux ratio between the primary and secondary. Figure 3 presents the interferometer fringe phase for a grid of nine models with three different angular separations and three different flux ratios. A direct relationship between the phases and the basic properties of the binary system can be noted. The phases exhibit a sinusoidal curve across the Fourier plane, with the amplitude proportional to the contrast ratio while the period is proportional to the separation. Closure phases are derived from the baseline phases as a simple summation of the three phases corresponding to a closed triangle of holes.
(1)where u and v are orthogonal spatial frequency vectors (respectively to the east and to the north), α and δ are the right ascension and declination in radians, and r is the flux ratio between the primary and secondary. Figure 3 presents the interferometer fringe phase for a grid of nine models with three different angular separations and three different flux ratios. A direct relationship between the phases and the basic properties of the binary system can be noted. The phases exhibit a sinusoidal curve across the Fourier plane, with the amplitude proportional to the contrast ratio while the period is proportional to the separation. Closure phases are derived from the baseline phases as a simple summation of the three phases corresponding to a closed triangle of holes.
 |
Fig. 3 Phase as a function of the spatial frequency. The different plots are models of a binary system with different flux ratio and angular separation. No noise has been added, so the curves represent the perfect case. From top to bottom, the contrast of the primary to secondary decrease. Panels (a)–c)): flux ratio of 1%. Panels (d)–f)): flux ratio of 0.1%. Panels (g)-h)-i)): flux ratio of 0.01%. From left to right, the angular separation gets smaller. Panels (a)-d)-g)): 200 mas. Panels (b)-e)-h)): 100 mas. Panels (c)-f)-i)): 50 mas. In the L′ band, the cut-off frequency of an eight meter telescope is 0.01 mas-1. |
 |
Fig. 4 Theoretical (Monte-Carlo) 1σ detection limits of the 7-hole mask as a function of angular separation and error on closure phases. The ripples on the detection limit curves are not due to uncertainty in the Monte-Carlo simulation, but to the nonhomogeneous coverage of the UV frequency plane. |
Detection as a function of time using individual pairs of source-calibrator files.
Companion searches are performed by fitting the various binary parameters (r, α, and δ) to the measured closure phases, so the detection limit obtained from any given dataset is directly related to the signal-to-noise ratio of the closure phase. A Monte-Carlo simulation was performed to test the theoretical detection limit, as a function of the angular separation and closure phase measurement error bars. The result is presented in Fig. 4. The detection limit is almost constant for any separation larger than λ/D. The Monte-Carlo simulation shows that the dynamic range can be approximated as (as a function of σ(CP) in degrees) 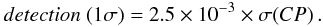 (2)Detections below λ/D can still be significant, but the contrast achieved decreases rapidly with the separation. At half λ/D, limits are worse by a factor of two, while at 0.25 λ/D the degradation in performance is a factor 15. For separations beyond the formal diffraction limit, any fitting process becomes highly model dependent and often strong degeneracies between fitted parameters can appear. A typical example at small separations is the covariance between the flux ratio and separation: it becomes difficult to measure these two parameters independently.
(2)Detections below λ/D can still be significant, but the contrast achieved decreases rapidly with the separation. At half λ/D, limits are worse by a factor of two, while at 0.25 λ/D the degradation in performance is a factor 15. For separations beyond the formal diffraction limit, any fitting process becomes highly model dependent and often strong degeneracies between fitted parameters can appear. A typical example at small separations is the covariance between the flux ratio and separation: it becomes difficult to measure these two parameters independently.
3.2. Detection of the stellar companion to HD 135549
HD 135549 was initially observed for the purpose of a PSF reference star, but it turned out to be a binary system with a contrast ratio around 5% and a separation close to 180 mas. We present the data in this paper for the sake of introducing the technique of detecting faint companions with SAM illustrated by strong, clear systematic signals.
 |
Fig. 5 χ2 surface as a function of α and δ obtained by fixing r to the best-fit value in the model of a binary stated in Eq. (1). A clear minimum indicates the position of the stellar companion. |
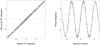 |
Fig. 6 Left panel: measured closure phase as a function of model closure phase assuming the best-fit binary parameters. The rms error between the model and the measurement is 0.28 degrees. Right panel: phase obtained by least square inversion of the closure phase to phase matrix, plotted as a function of the projected baseline (perpendicular to the binary orientation; hence the sinusoidal curve). |
 |
Fig. 7 Closure phase as a function of time for the 10 largest triangles. The triangles are made of the holes a) 1-5-7, b) 1-2-6, c) 1-6-7, d) 4-5-6, e) 1-2-7, f) 1-5-6, g) 4-5-7, h) 1-4-7, i) 2-5-7 and j) 2-5-6; numbered according to the rows of Table 4–19 in the NaCo manual (available online at eso.org). Calibrator data are represented as circles, while binary star data are squares. The dashed line is the polynomial fit of the calibrator, and the solid line is the closure phase predicted by the best fitting binary system model. The same fit quality is obtained on all 35 closure phases. Overall, the average rms error of the fit is 0.28 degrees. |
The free parameters of Eq. (1) are the binary coordinates α and δ, along with the flux ratio r. A map of the reduced χ2 is derived as a function of α and δ (Fig. 5). It indicates the presence of a companion with a strong likelihood at a separation of ≈ 180 mas to the southeast of the star. The best-fit model is compared to the observed data in the two panels of Fig. 6. The lefthand panel shows the observed versus model-predicted closure phase data. The final reduced χ2 is equal to 1.85 while the average residual is 0.28 degree over a total of 35 × 15 = 525 closure phase measurements. According to Eq. (2), this dataset therefore has the capability of a detection limit of 7.5 × 10-4 (1σ detection). The righthand panel shows phases recovered from the closure phases. This is done by inverting the phase to closure phase matrix. The matrix is not fully invertible; for example, tip-tilt is not constrained by the closure phase. Therefore, unknown parameters of the inversion were taken to match the model. The best fit model is over-plotted as a solid line.
The first 15 lines of Table 2 results from the processing of each SCI-CAL acquisition pair separately. An independent model is fitted at each epoch, and the detection can be seen to be rotating in the detector frame (but fixed on the sky). A strong indication that our detection is indeed real lies in the rotation in the detector frame following the parallactic angle evolution. Because the telescope is azimuthal, it is unlikely that a calibration error (including optical aberrations) rotate in such a motion. This validation could not have been made with an equatorial telescope.
The last line of Table 2 gives the best-fitting binary parameters. Separation and dynamic ranges are obtained with high statistical precision. The precision of the closure phase measurement over time is highlighted in Fig. 7, in which each panel depicts a different closure phase. The solid line corresponding to the model can be seen to almost perfectly match the evolution of the closure phase as a function of time.
3.3. On the limitation of the dynamic range
As stated by Eq. (2), the dynamic range is a pure function of the error on the phase. The binary system was observed during good atmospheric conditions (0.7′′ seeing and a coherent time of 8 ms) with a relatively fast frame time of 200 ms. Phases recovered from the interferograms show a median frame-to-frame error of 17 degrees, equivalent to a 180 − nm piston jitter at our observing wavelength. On the other hand, the frame-to-frame closure phase error is only 2.8 degrees. This is a clear indication that most of the 180 − nm rms error is due to the residual of atmospheric perturbation not corrected by the AO system.
Assuming that these residuals were caused by photon noise or readout noise, the remaining 2.8 degrees frame-to-frame error should be uncorrelated. In this case, the final error on a whole acquisition sequence (8 dither of 200 frames) should improve as the square root of the number of frames giving an expected error of 0.07 degrees. For such a scenario, the dynamic range obtained in the final detection should be 1.7 × 10-4 (according to Eq. (2)). Unfortunately, the observed standard deviation for both calibrator and the science target closure phases are significantly larger (0.25 and 0.33 degrees respectively; obtained by comparing different telescope dithers). These larger errors point to an additional systematic term generating biases in the phase closure which do not average out over long data runs. In order to extract the very best contrast ratio in our faint companion detection strategy, these closure phase biases need to be understood and calibrated.
 |
Fig. 8 χ2 as a function of α and δ obtained from the best fit of r in the model of a binary stated in Eq. (1). Left panel: HD 92945. Right panel: HD 141569. The lower limit of the color scale (139) is the number of degree of freedom of the fit. |
Within our present software pipeline, closure phase calibration is performed by subtraction of the PSF reference star closure phases which resulted in an rms closure phase error observed of 0.24 degrees (when comparing different dither positions). Compared to the theoretical limit of the high-frequency noise (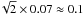 degrees), it is apparent that systematic biases in the closure phase remain the dominant limit to the dynamic range. When fitting the final data with a model of a binary system, the residual error on the closure phases is 0.28 degrees.
degrees), it is apparent that systematic biases in the closure phase remain the dominant limit to the dynamic range. When fitting the final data with a model of a binary system, the residual error on the closure phases is 0.28 degrees.
This statistical analysis shows that the high-frequency noise – assumed to be photon and readout noise – is not limiting the dynamic range. On this specific dataset, one magnitude in contrast ratio could be gained if only it was possible to have a perfect calibration of the closure phase systematics. A higher dynamic range could then be achieve by repetition of the same observation. The reason for these systematics errors is still under debate. Between several possibilities, we can mention i) optical aberrations before the pupil mask; ii) correlated detector read out noise; iii) spatially correlated phase error due to the modal correction of the adaptive optic system. The residuals could be diminished partially by observing several calibrators. But not to a full extent: the noise would average only on the calibrator dataset.
4. The two debris disks HD 92945 and HD 141569
4.1. The targets
4.1.1. HD 92945
HD 92945 (V419 Hya) is a K1.5V star located at 22 pc. (Song et al. 2004) estimated an age of 100 Myr using Ca ii lines. If we suppose HD 92945 to be part of the AB Dor group (López-Santiago et al. 2006), this age agrees with the estimation of ≈50−120 Myr for the whole group (Zuckerman et al. 2004; Luhman et al. 2005). Observations with the Advanced Camera for Surveys (ACS) on the Hubble Space Telescope have revealed it is surrounded by a disk ~30° from edge-on with a 0 7-thick bright ring at 57 AU from the star. The disk has a diffuse component detected between 55 and 170 AU (Golimowski et al. 2007). The inner gap may well be the result of resonances with a stellar or planetary companion (Artymowicz & Lubow 1994).
7-thick bright ring at 57 AU from the star. The disk has a diffuse component detected between 55 and 170 AU (Golimowski et al. 2007). The inner gap may well be the result of resonances with a stellar or planetary companion (Artymowicz & Lubow 1994).
4.1.2. HD 141569
HD 141569 is a 5 ± 3-Myr-old (Merín et al. 2004) pre-main sequence B9.5V star in a triple system. It is located 99-pc away and the central star features an elegant debris disk that was first imaged in the near-infrared (Augereau et al. 1999) and in visible scattered light (Clampin et al. 2003). The two other components of the system form an M2-M4 binary, ~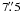 away from the central star. Reche et al. (2009) give an overview of the rich disk structure. It is composed of two annuli with peak luminosity in scattered light at ~200 and ~325 AU from the star. These two rings have azimuthal brightness asymmetries (factors 2 to 3). The outer ring shows a tightly wound spiral structure. The rings are separated by an apparent gap wider than the rings. An extended diffuse emission associated with a faint spiral arm is present in the northeast side of the disk, and is detected to more than 600 AU. Another spiral arm is possibly observed, pointing toward the binary companions. Finally, the disk brightness sharply decreases within 200 AU, suggesting a strong dust depletion in the innermost regions of the disk.
away from the central star. Reche et al. (2009) give an overview of the rich disk structure. It is composed of two annuli with peak luminosity in scattered light at ~200 and ~325 AU from the star. These two rings have azimuthal brightness asymmetries (factors 2 to 3). The outer ring shows a tightly wound spiral structure. The rings are separated by an apparent gap wider than the rings. An extended diffuse emission associated with a faint spiral arm is present in the northeast side of the disk, and is detected to more than 600 AU. Another spiral arm is possibly observed, pointing toward the binary companions. Finally, the disk brightness sharply decreases within 200 AU, suggesting a strong dust depletion in the innermost regions of the disk.
4.2. 5 σ detection limits
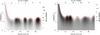 |
Fig. 9 χ2 maps for target HD 92945 (left panel) and HD 141569 (right panel). The solid curves correspond to the isocontours at min(χ2)+1; +4; and +9 (eg. one, two, and three sigmas contours). Multiple minimums are present (false detections). The 5σ detection limits are, averaged over the separation, 2.5 × 10-3 and 4.6 × 10-3 (dashed curve). The right vertical axis was obtained assuming a linear fit of DUSTY evolutionarily models. |
Best-fit detection.
Establishing a high-contrast detection limit follows a different approach than establishing a detection. The most important step is indeed to show that there is no significant detection in our data. A practical approach is to analyze the χ2 maps (Fig. 8). If the minimum value of the χ2 does not significantly differ from the maximum χ2, it means that the binary model does not significantly improve the fit to the data. The χ2 values at best fit are given in Table 3. The detection for the binary system HD 135549 discussed in the previous section is extremely clear with a normalized χ2 of 1.85. This dramatically improves the fit compared to the null hypothesis (no binary χ2/nfreedom = 423). This is not the case for the two debris disk systems. At best fit, the binary model improves the χ2 by a factor of 1.24 for HD 92945 and 1.18 for HD 141569.
Although the χ2 maps indicate a nondetection, robust statistical limits based on these data remain to be derived. To accomplish this, we plot the χ2 in Fig. 9, minimized over position angle, as a function of separation (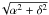 ) and contrast (r). The red solid contours correspond to 1, 2, and 3σ detection limits. Several minima exist in the maps including two 3σ false detection: at 440 mas (contrast 0.16%) and at 160 mas (contrast 0.2%). It is noteworthy to point out that the absence of a companion (equivalent to a binary system with a separation of 0 mas) is within 5 σ of the false detections. This 5σ limit corresponds to the red dashed curves. We define this curve as our 5σ detection limits, hence excluding any detection on the two dataset. This approach is coherent with the generally recognized 5σ criterion to validate a detection.
) and contrast (r). The red solid contours correspond to 1, 2, and 3σ detection limits. Several minima exist in the maps including two 3σ false detection: at 440 mas (contrast 0.16%) and at 160 mas (contrast 0.2%). It is noteworthy to point out that the absence of a companion (equivalent to a binary system with a separation of 0 mas) is within 5 σ of the false detections. This 5σ limit corresponds to the red dashed curves. We define this curve as our 5σ detection limits, hence excluding any detection on the two dataset. This approach is coherent with the generally recognized 5σ criterion to validate a detection.
According to Fig. 9, the average 5σ detection limits of HD 92945 and HD 141569 over the separation range 100−500 mas are respectively 2.5 × 10-3 and 4.6 × 10-3, that is, ΔL′ of 6.5 and 5.8. However, the nondetection limit is not completely uniform over the field of view and can have values that are nearly a factor of two worse. We can observe the detection limit worsening by a factor 2 between λ/D and 0.5 λ/D, with a precipitous drop for still lower spatial separations. These results also confirm the Monte-Carlo simulations (presented in Fig. 4), assuming error bars on the closure phase of 0.2 and 0.4 degrees.
4.3. Jupiter-mass limits
To convert contrast limits into upper bounds for the mass of any possible companion, we must know the absolute magnitude corresponding to the detection limit in each system. We derived the L′ band magnitudes from the K band magnitudes of the calibrators: HD 92933 (K = 5.58 mag) and BD-03 3826 (K = 6.70 mag). We used the temperature reddening from Tokunaga (2000) to convert to L′, and scaled the magnitude with respect to the relative flux observed on both calibrator and science star: HD 92933 is 1.09 ± 0.03 times brighter than HD 92945, and BD-03 3826 is 1.11 ± 0.05 times brighter than HD 141569. As a result, we estimated the L′ magnitude of HD 92945 to be 5.58 mag and HD 141569 to be 6.74 mag. We checked that these values are roughly compatible with the magnitude derived solely by using the isochrones for pre-main sequence stars (Siess et al. 2000) giving 5.6 and 6.3 mag, respectively. Scaling the brightness to derive the absolute magnitude at 10 pc (assuming distances stated in Sect. 4.1), we obtained ML′ = 3.87 mag (HD 92945) and ML′ = 1.76 mag (HD 141569).
Thus, the 5σ upper limits correspond to a nondetection of up to a absolute magnitude of ML′ = 10.4 mag for HD 92945 and ML′ = 7.6 mag for HD 141569. To convert our detection limits to planetary masses limits, we used DUSTY evolutionary models (Chabrier et al. 2000) convolved with the NaCo filters. Towards HD 92945, the models put a limit on the mass of a companion to 18 MJup at a separation of 1.5 AU(λ/D). Towards HD 141569, the models limit the mass of a companion to 22 MJup at 7 AU.
5. Conclusion
We have shown that aperture masking gives detection limits of the order of Δ L′ mag = 6, with an inner working angle close to λ/2D. These results confirm previous detection limits obtained by the same aperture masking technique on the Keck telescope (Kraus et al. 2011; Hinkley et al. 2011) In terms of scientific impact, this observational domain is important because it corresponds to a few astronomical units at a hundred parsec, the distance where the closest formation regions are. The scientific importance of this parameter space is highlighted by T Cha b detected by the same technique (Huélamo et al. 2011).
Simulations of the older debris disk tend to show that a magnitude or two in dynamic range is still needed to observe disk shaping planets. Considering HD 141569, for example, Reche et al. (2009) show that the disk geometry could be best modeled by a flyby star and a planet of a few Jupiter masses. For these kinds of objects, a detection limit of two Jupiter masses would require a precision on the closure phases of 0.01 degree, something only possible if we understand how to precisely account for the systematics errors.
This paper has to be considere along with other direct detection techniques. In the case of HD 92945, Biller et al. (2007) used a spectral differential technique to derive an upper limit of 10.8 mag at 0.5′′ in the H band (5σ). This limit assumes a clear methane signature (a spectral type T8 for the planet) which may not be the case. This assumption is not required for a differential technique using sky rotation: in their Gemini survey, Lafrenière et al. (2007) obtain the same dynamic range (10.8 mag; 5σ) at the slightly larger separation of 0.75′′. Overall, differential imaging techniques often give a dynamic range that is higher than SAM, but with larger inner working angles (typically a few λ/D).
The capacities of future extreme adaptive optics to observe at smaller inner working angle, compared to the ability for aperture masking to probe at higher dynamic range by understanding the systematics, will decide the fate of SAM with respect to faint companion detection.
Acknowledgments
S.L. would like to acknowledge the friendly support of ESO’s staff during observations, including night time support astronomers and telescope operators. A special thanks goes to Dr. J. Girard, the instrument scientist of NaCo. This work received the support of PHASE, the high angular resolution partnership between ONERA, the Observatoire de Paris, CNRS, and University Denis Diderot Paris 7.
References
- Absil, O., & Mawet, D. 2010, A&A Rev., 18, 317 [Google Scholar]
- Artymowicz, P., & Lubow, S. H. 1994, ApJ, 421, 651 [NASA ADS] [CrossRef] [Google Scholar]
- Augereau, J. C., Lagrange, A. M., Mouillet, D., & Ménard, F. 1999, A&A, 350, L51 [NASA ADS] [Google Scholar]
- Beuzit, J.-L., Feldt, M., Dohlen, K., et al. 2008, in SPIE Conf. 7014 [Google Scholar]
- Biller, B. A., Close, L. M., Masciadri, E., et al. 2007, ApJS, 173, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G., Baraffe, I., Allard, F., & Hauschildt, P. 2000, ApJ, 542, 464 [NASA ADS] [CrossRef] [Google Scholar]
- Chauvin, G., Lagrange, A., Dumas, C., et al. 2004, A&A, 425, L29 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Chauvin, G., Lagrange, A., Zuckerman, B., et al. 2005, A&A, 438, L29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Clampin, M., Krist, J. E., Ardila, D. R., et al. 2003, AJ, 126, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Golimowski, D., John Krist, J., Chen, C., et al. 2007, in In the Spirit of Bernard Lyot: The Direct Detection of Planets and Circumstellar Disks in the 21st Century [Google Scholar]
- Hinkley, S., Carpenter, J. M., Ireland, M. J., & Kraus, A. L. 2011, ApJ, 730, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Huélamo, N., Lacour, S., Tuthill, P., et al. 2011, A&A, 528, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kalas, P., Graham, J. R., Chiang, E., et al. 2008, Science, 322, 1345 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kraus, A. L., Ireland, M. J., Martinache, F., & Hillenbrand, L. A. 2011, ApJ, 731, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Lafrenière, D., Doyon, R., Marois, C., et al. 2007, ApJ, 670, 1367 [NASA ADS] [CrossRef] [Google Scholar]
- Lagrange, A., Gratadour, D., Chauvin, G., et al. 2009, A&A, 493, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lagrange, A., Bonnefoy, M., Chauvin, G., et al. 2010, Science, 329, 57 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lloyd, J. P., Martinache, F., Ireland, M. J., et al. 2006, ApJ, 650, L131 [NASA ADS] [CrossRef] [Google Scholar]
- López-Santiago, J., Montes, D., Crespo-Chacón, I., & Fernández-Figueroa, M. J. 2006, ApJ, 643, 1160 [NASA ADS] [CrossRef] [Google Scholar]
- Luhman, K. L., Stauffer, J. R., & Mamajek, E. E. 2005, ApJ, 628, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Marois, C., Macintosh, B., Barman, T., et al. 2008, Science, 322, 1348 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Marois, C., Zuckerman, B., Konopacky, Q. M., Macintosh, B., & Barman, T. 2010, Nature, 468, 1080 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Mayor, M., & Queloz, D. 1995, Nature, 378, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Merín, B., Montesinos, B., Eiroa, C., et al. 2004, A&A, 419, 301 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reche, R., Beust, H., & Augereau, J. 2009, A&A, 493, 661 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Siess, L., Dufour, E., & Forestini, M. 2000, A&A, 358, 593 [NASA ADS] [Google Scholar]
- Smith, B. A., & Terrile, R. J. 1984, Science, 226, 1421 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Song, I., Zuckerman, B., & Bessell, M. S. 2004, ApJ, 614, L125 [NASA ADS] [CrossRef] [Google Scholar]
- Tokunaga, A. T. 2000, Allen’s Astrophysical Quantities, ed.A. N. Cox (Springer-Verlag), 143 [Google Scholar]
- Tuthill, P., Lloyd, J., Ireland, M., et al. 2006, in SPIE Conf. Ser., 6272 [Google Scholar]
- Tuthill, P. G., Monnier, J. D., Danchi, W. C., Wishnow, E. H., & Haniff, C. A. 2000, PASP, 112, 555 [NASA ADS] [CrossRef] [Google Scholar]
- Zuckerman, B., Song, I., & Bessell, M. S. 2004, ApJ, 613, L65 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Detection as a function of time using individual pairs of source-calibrator files.
All Figures
 |
Fig. 1 Left panel: diffraction pattern observed on star HD 135549. This image is a single frame of 0.4 ms integration time, using the 7-hole pupil mask. Background noise is ≈ 12 ADU, and pic brightness 800 ADU. Right panel: fourier transform of the diffraction pattern. Each peak corresponds to a baseline pair. |
| In the text | |
 |
Fig. 2 Frequency coverage for targets HD 135549, HD 92945, and HD 141569. |
| In the text | |
 |
Fig. 3 Phase as a function of the spatial frequency. The different plots are models of a binary system with different flux ratio and angular separation. No noise has been added, so the curves represent the perfect case. From top to bottom, the contrast of the primary to secondary decrease. Panels (a)–c)): flux ratio of 1%. Panels (d)–f)): flux ratio of 0.1%. Panels (g)-h)-i)): flux ratio of 0.01%. From left to right, the angular separation gets smaller. Panels (a)-d)-g)): 200 mas. Panels (b)-e)-h)): 100 mas. Panels (c)-f)-i)): 50 mas. In the L′ band, the cut-off frequency of an eight meter telescope is 0.01 mas-1. |
| In the text | |
 |
Fig. 4 Theoretical (Monte-Carlo) 1σ detection limits of the 7-hole mask as a function of angular separation and error on closure phases. The ripples on the detection limit curves are not due to uncertainty in the Monte-Carlo simulation, but to the nonhomogeneous coverage of the UV frequency plane. |
| In the text | |
 |
Fig. 5 χ2 surface as a function of α and δ obtained by fixing r to the best-fit value in the model of a binary stated in Eq. (1). A clear minimum indicates the position of the stellar companion. |
| In the text | |
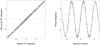 |
Fig. 6 Left panel: measured closure phase as a function of model closure phase assuming the best-fit binary parameters. The rms error between the model and the measurement is 0.28 degrees. Right panel: phase obtained by least square inversion of the closure phase to phase matrix, plotted as a function of the projected baseline (perpendicular to the binary orientation; hence the sinusoidal curve). |
| In the text | |
 |
Fig. 7 Closure phase as a function of time for the 10 largest triangles. The triangles are made of the holes a) 1-5-7, b) 1-2-6, c) 1-6-7, d) 4-5-6, e) 1-2-7, f) 1-5-6, g) 4-5-7, h) 1-4-7, i) 2-5-7 and j) 2-5-6; numbered according to the rows of Table 4–19 in the NaCo manual (available online at eso.org). Calibrator data are represented as circles, while binary star data are squares. The dashed line is the polynomial fit of the calibrator, and the solid line is the closure phase predicted by the best fitting binary system model. The same fit quality is obtained on all 35 closure phases. Overall, the average rms error of the fit is 0.28 degrees. |
| In the text | |
 |
Fig. 8 χ2 as a function of α and δ obtained from the best fit of r in the model of a binary stated in Eq. (1). Left panel: HD 92945. Right panel: HD 141569. The lower limit of the color scale (139) is the number of degree of freedom of the fit. |
| In the text | |
 |
Fig. 9 χ2 maps for target HD 92945 (left panel) and HD 141569 (right panel). The solid curves correspond to the isocontours at min(χ2)+1; +4; and +9 (eg. one, two, and three sigmas contours). Multiple minimums are present (false detections). The 5σ detection limits are, averaged over the separation, 2.5 × 10-3 and 4.6 × 10-3 (dashed curve). The right vertical axis was obtained assuming a linear fit of DUSTY evolutionarily models. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


