| Issue |
A&A
Volume 532, August 2011
|
|
|---|---|---|
| Article Number | A15 | |
| Number of page(s) | 7 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201116661 | |
| Published online | 13 July 2011 | |
Magnetic fields generated by r-modes in accreting quark stars
1
Institut für Theoretische Physik, Ruprecht-Karls-Universität, Philosophenweg 16, 69120 Heidelberg, Germany
e-mail: bonanno@fe.infn.it
2
Dipartimento di Fisica, Universitá di Ferrara and INFN sezione di Ferrara, 44100 Ferrara, Italy
3
Institute for Theoretical Physics, Goethe University, Max-von-Laue-Str. 1, 60438 Frankfurt am Main, Germany
Received: 4 February 2011
Accepted: 29 May 2011
We show that the r-mode instability can generate strong toroidal fields in the core of accreting millisecond quark stars by inducing differential rotation. We follow the spin frequency evolution on a long time-scale, taking into account the magnetic damping rate in the evolution equations of r-modes. The maximum spin frequency of the star is only marginally lower than without the magnetic field. The late-time evolution of the stars that enter the r-mode instability region is instead quite different if the generated magnetic fields are taken into account: they leave the millisecond pulsar region and become radio pulsars.
Key words: X-rays: binaries / gravitational waves / magnetic fields / instabilities / pulsars: general
© ESO, 2011
1. Introduction
Since the first paper in which r-modes in rotating neutron stars were shown to be unstable with respect to the emission of gravitational waves (Andersson 1998), their relevance in Astrophysics was recognized for explaining the observed distribution of the rotation frequency of stars in low-mass-X-ray-binaries (LMXBs) (see Andersson & Kokkotas 2001 for a review). On the other hand, the instability triggered by r-modes is actually damped to some extent by the viscosity of the matter composing the star: the higher the viscosity, the higher the rotation frequency of the star. This opens the possibility of investigating the internal composition of compact stars by studying the viscosity of the different possible high-density phases that can appear in these stellar objects. A number of papers currently deal with the shear and bulk viscosities of nucleonic matter (Sawyer 1989; Haensel & Schaeffer 1992; Haensel et al. 2000, 2001; Benhar & Valli 2007), hyperonic matter (Lindblom & Owen 2002; Haensel et al. 2002; Chatterjee & Bandyopadhyay 2006, 2008; Gusakov & Kantor 2008; Sinha & Bandyopadhyay 2009; Jha et al. 2010), kaon condensed matter (Chatterjee & Bandyopadhyay 2007, 2008), pure quark phases (Madsen 1992, 2000; Alford & Schmitt 2007; Sa’d et al. 2007a,b; Alford et al. 2007; Blaschke & Berdermann 2007; Sa’d 2008; Mannarelli et al. 2008; Jaikumar et al. 2008; Alford et al. 2010), and mixed phases (Drago et al. 2005). Interestingly, by studying the so called “window of instability” of the r-modes, which is determined by the shear and bulk viscosity of the matter, Drago et al. (2008) pointed out that a detection of a sub-millisecond rotating star would indicate a very viscous phase in the star with only quark or hybrid stars as possible candidates.
The temporal evolution of the spin frequency of a star under the effect of an r-modes instability has been studied as well for different types of composition and different physical systems: newly born compact stars and old stars in binaries (Lindblom et al. 1998; Owen et al. 1998; Andersson et al. 2002; Wagoner 2002; Drago et al. 2006, 2008). While neutron stars could be very powerful gravitational wave emitters only during their first months (Owen et al. 1998), hyperonic and quark or hybrid stars could turn into steady gravitational wave sources if present in LMXBs (Andersson et al. 2002; Wagoner 2002; Reisenegger & Bonacic 2003).
R-modes are also responsible for differential rotation in the star, which in turn generates a toroidal magnetic field: besides the viscosity of matter, the production of this magnetic field represents a very efficient damping mechanism for the r-modes. This effect has been proposed and investigated in Rezzolla et al. (2000); Rezzolla et al. (2001b,a) for the case of a newly born neutron star, and it has been recently included in the r-mode equations of the neutron stars in LMXB (Cuofano & Drago 2009, 2010): by calculating the back-reaction of the magnetic field on the r-modes instability, it has been proven that magnetic fields of the order of 1015 G can be produced. Remarkably, this mechanism could be at the origin of the enormous magnetic field of magnetars.
In this paper we follow the scheme developed in Cuofano & Drago (2009, 2010) and extend the calculation to the case of quark stars. In particular, we consider the back-reaction of the magnetic field on r-mode instabilities by inserting the magnetic damping rate into the evolution equations of r-modes. The motivation for this investigation is that the evolution of accreting stars and their internal magnetic field strongly depends on the r-modes instability window which, for quark stars, is qualitatively different from the one of neutron stars. Indeed, owing to the large contribution to the bulk viscosity of the non leptonic weak decays occurring in strange quark matter, the window of instability splits into two windows, a small one at high temperatures (which is actually irrelevant for the evolution) and a big one at low temperatures (Madsen 2000; Drago et al. 2008). Moreover, quark stars do not have a crust (or just a very thin crust) and, as we will discuss, this prevents the trapping of the internal magnetic field developed during the evolution with possible observable signatures.
The paper is organized as follows: in Sect. 2 we introduce the system of equations that provide the temporal evolution of a compact star in a LMXB. In Sect. 3 we show the results of our numerical calculations and finally we present our conclusions in Sect. 4.
2. The temporal evolution model
2.1. R-modes equations
Let us review the derivation of the equations for the evolution of a compact star in presence of the r-modes.
Following the discussion of Wagoner (2002), we begin with the conservation of the angular momentum. The total angular momentum of the star can be decomposed into an equilibrium angular momentum J∗ and a canonical angular momentum Jc, proportional to the r-modes amplitude α: 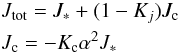 (1)where J ∗ = I ∗ Ω, with Ω the angular velocity and
(1)where J ∗ = I ∗ Ω, with Ω the angular velocity and 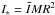 the moment of inertia of a star of mass M and radius R. For a n = 1 polytrope
the moment of inertia of a star of mass M and radius R. For a n = 1 polytrope 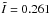 , Kc = 9.4 × 10-2 (see Owen et al. 1998) and Kj is of the order of unity (the results of our calculations are fairly insensitive to the value of Kj).
, Kc = 9.4 × 10-2 (see Owen et al. 1998) and Kj is of the order of unity (the results of our calculations are fairly insensitive to the value of Kj).
The equations for the evolution of a star are based on two simple considerations:
-
the canonical angular momentum, proportional to the r-modesamplitude, increases with the emission of gravitational wavesand decreases because of damping mechanisms (e.g. viscosityand the torque from an internal magnetic field B):
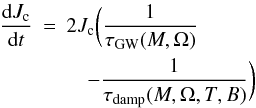 (2)where τGW(M,Ω) and τdamp(M,Ω,T,B) are the gravitational wave emission time-scale and the damping time-scale, respectively, where the latter includes all the mechanisms that muffle the r-modes. Finally, with T we mean the average temperature of the star.
(2)where τGW(M,Ω) and τdamp(M,Ω,T,B) are the gravitational wave emission time-scale and the damping time-scale, respectively, where the latter includes all the mechanisms that muffle the r-modes. Finally, with T we mean the average temperature of the star. -
the total angular momentum takes contributions from the mass accretion and decreases because of the emission of gravitational waves and electromagnetic waves. The electromagnetic wave emission is associated to the presence of an external poloidal magnetic field that is not aligned with the rotation axis. Indicating with τme the braking time-scale due to the external magnetic field, the second equation reads
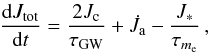 (3)where
(3)where 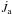 is the variation of the angular momentum caused by the mass accretion. Following Andersson et al. (2002), we assume
is the variation of the angular momentum caused by the mass accretion. Following Andersson et al. (2002), we assume 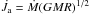 .
.
Combining Eqs. (1) − (3), it is easy to obtain the evolution equations for Ω and for the r-modes amplitude α: ![\begin{eqnarray} \frac{{\rm d}\alpha}{{\rm d}t}&=& \alpha\bigg(\frac{1}{\tau_{\rm GW}}-\frac{1}{\tau_{ \rm damp}}\bigg)\nonumber\\ &&\quad+ K_{\rm c} \alpha^3\bigg[K_j\frac{1}{\tau_{\rm GW}}+(1-K_j)\frac{1}{\tau_{ \rm damp}}\bigg]\nonumber\\ \label{eq4}&&\quad- \frac{\alpha \dot M}{2 \tilde I \Omega}\bigg(\frac{G}{M R^3}\bigg)^{1/2}+\frac{\alpha}{2 \tau_{m_{ \rm e}}} \\ \frac{{\rm d}\Omega}{{\rm d}t}&=& -2 K_{\rm c}\Omega\alpha^3\bigg[K_j\frac{1}{\tau_{\rm GW}}+(1-K_j)\frac{1}{\tau_{ \rm damp}}\bigg]\nonumber\\ \label{eq5} &&\quad- \frac{\dot M\Omega}{M}+\frac{\dot M}{\tilde I}\bigg(\frac{G}{M R^3}\bigg)^{1/2}-\frac{\Omega}{\tau_{m_{ \rm e}}}\cdot \end{eqnarray}](/articles/aa/full_html/2011/08/aa16661-11/aa16661-11-eq25.png) Here we adopt the estimate given in Andersson & Kokkotas (2001) for the gravitational radiation rate from the l = m = 2 current multipole:
Here we adopt the estimate given in Andersson & Kokkotas (2001) for the gravitational radiation rate from the l = m = 2 current multipole: 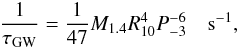 (6)where we used the notation M1.4 = M/1.4 M⊙, R10 = R/10 km and P-3 = P/1 ms.
(6)where we used the notation M1.4 = M/1.4 M⊙, R10 = R/10 km and P-3 = P/1 ms.
Following Cuofano & Drago (2010), the total damping rate is given by the sum of the shear viscosity and bulk viscosity rates plus the damping rate caused by the internal magnetic field: 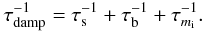 (7)In the above expression the new ingredient is the magnetic damping rate, which generates a back-reaction of the magnetic field on the dynamics of the r-modes. This back-reaction was not considered in previous papers. Notice that the magnetic field can directly modify the r-mode oscillations. This is a further and more complicated back-reaction that we did not include.
(7)In the above expression the new ingredient is the magnetic damping rate, which generates a back-reaction of the magnetic field on the dynamics of the r-modes. This back-reaction was not considered in previous papers. Notice that the magnetic field can directly modify the r-mode oscillations. This is a further and more complicated back-reaction that we did not include.
The estimates of the viscosity damping rates for the case of pure quark matter are given in Andersson et al. (2002). For the shear viscosity it is found: 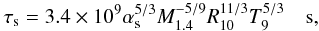 (8)where αs is the strong coupling constant and T9 = T/109 K. For the bulk viscosity, the viscosity coefficient takes the form
(8)where αs is the strong coupling constant and T9 = T/109 K. For the bulk viscosity, the viscosity coefficient takes the form 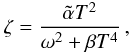 (9)where ω is the frequency of the r-modes in the corotating frame and
(9)where ω is the frequency of the r-modes in the corotating frame and 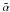 and β are coefficients given in Madsen (1992). Because of this behavior, bulk viscosity is very high at T ~ 109 K and diminishes at lower and higher temperatures. The instability window is then split into a low temperature window (LTW) (at T < 109 K) and an high temperature window (HTW) (T > 109 K). Owing to the fast cooling rate of quark stars, the HTW is crossed very rapidly and does not have a big impact on the evolution of the star. Consequently, we are interested only in the LTW. The bulk viscosity damping time-scale in the low temperature limit (T < 109 K) is given by Andersson et al. (2002):
and β are coefficients given in Madsen (1992). Because of this behavior, bulk viscosity is very high at T ~ 109 K and diminishes at lower and higher temperatures. The instability window is then split into a low temperature window (LTW) (at T < 109 K) and an high temperature window (HTW) (T > 109 K). Owing to the fast cooling rate of quark stars, the HTW is crossed very rapidly and does not have a big impact on the evolution of the star. Consequently, we are interested only in the LTW. The bulk viscosity damping time-scale in the low temperature limit (T < 109 K) is given by Andersson et al. (2002): 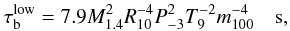 (10)where m100 is the mass of the strange quark in units of 100 MeV. Notice that the value bulk viscosity damping timescale strongly depends on the value of m100.
(10)where m100 is the mass of the strange quark in units of 100 MeV. Notice that the value bulk viscosity damping timescale strongly depends on the value of m100.
The expression of the magnetic damping rate has been derived in Rezzolla et al. (2001b,a), who showed that while the star remains in the instability region, the r-modes generate a differential rotation that can greatly amplify a pre-existing magnetic field. More specifically, if a poloidal magnetic field was originally present, a strong toroidal field is generated inside the star. The energy of the modes is therefore transferred to the magnetic field and the instability is damped.
We assume that the internal stellar magnetic field B is initially based on the solution obtained by Ferraro (Ferraro 1954), which can be written (Cuofano & Drago 2010) ![\begin{eqnarray} &&\mbox{\vec{B}}_{0}^{\rm in}(t=0)=\\ \nonumber && B_{\rm d} \, \left[\left(-3\frac{r^2}{R^2}+5\right) \cos \, \theta \,\mbox{\vec{e}}_r+\left(6\frac{r^2}{R^2}-5\right)\, \sin \, \theta \, \mbox{\vec{e}}_\theta\right], \label{eq1M} \end{eqnarray}](/articles/aa/full_html/2011/08/aa16661-11/aa16661-11-eq45.png) (11)where Bd is the strength of the equatorial magnetic field at the stellar surface.
(11)where Bd is the strength of the equatorial magnetic field at the stellar surface.
To estimate the magnetic field produced by r-modes, we start by writing the l = m = 2 contribution to the perturbation velocity: 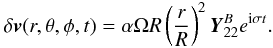 (12)Following Rezzolla et al. (2001b), we obtain the total azimuthal displacement from the onset of the oscillation at t0 up to time t, which reads
(12)Following Rezzolla et al. (2001b), we obtain the total azimuthal displacement from the onset of the oscillation at t0 up to time t, which reads 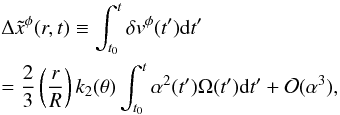 (13)where k2(θ) ≡ (1/2)7(5 ! /π)(sin2θ − 2cos2θ). The relation between the new and the original magnetic field inside the star in the Lagrangian approach reads (Rezzolla et al. 2001b)
(13)where k2(θ) ≡ (1/2)7(5 ! /π)(sin2θ − 2cos2θ). The relation between the new and the original magnetic field inside the star in the Lagrangian approach reads (Rezzolla et al. 2001b) 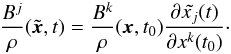 (14)This equation implies that the radial dependence of the initial and final magnetic field is the same. Integrating on time the induction equation in the Eulerian approach we obtain (Rezzolla et al. 2001a)
(14)This equation implies that the radial dependence of the initial and final magnetic field is the same. Integrating on time the induction equation in the Eulerian approach we obtain (Rezzolla et al. 2001a) 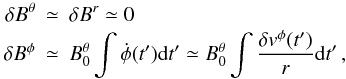 (15)where Bφ is the toroidal component.
(15)where Bφ is the toroidal component.
The expression of the magnetic damping rate reads (Cuofano & Drago 2010) 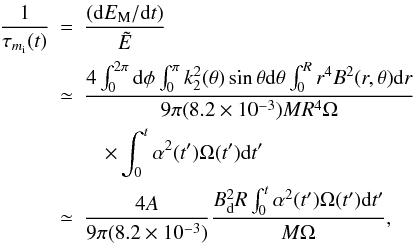 (16)where
(16)where 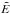 is the energy of the mode, EM is the magnetic energy and A ≈ 0.99. The time integral over the r-mode amplitude α takes contribution from the period during which the star is inside the instability region.
is the energy of the mode, EM is the magnetic energy and A ≈ 0.99. The time integral over the r-mode amplitude α takes contribution from the period during which the star is inside the instability region.
2.2. Temperature evolution
The equations derived above strongly depend on the value of the temperature, therefore we need to compute the thermal evolution of the star as well. For the sake of simplicity, we assume that the temperature is uniform in the star and make use of the estimates derived in Andersson et al. (2002) for quark stars. The heat capacity reads 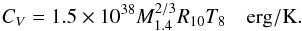 (17)The star essentially cools down by emitting neutrinos through the so-called URCA processes. Taking into account the direct URCA process, which are likely to occur in the core of quark stars, the cooling rate due to emission of neutrinos reads (Andersson et al. 2002)
(17)The star essentially cools down by emitting neutrinos through the so-called URCA processes. Taking into account the direct URCA process, which are likely to occur in the core of quark stars, the cooling rate due to emission of neutrinos reads (Andersson et al. 2002) 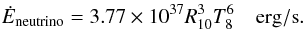 (18)If the star is accreting mass, one has to consider the heating through the accreted material. In particular, for a quark star the heating source comes from the conversion of nucleons into strange matter. Estimating the energy release from this conversion to be around 20 MeV per nucleon (Alcock et al. 1986; Andersson et al. 2002), the heating rate due to the accretion is given by
(18)If the star is accreting mass, one has to consider the heating through the accreted material. In particular, for a quark star the heating source comes from the conversion of nucleons into strange matter. Estimating the energy release from this conversion to be around 20 MeV per nucleon (Alcock et al. 1986; Andersson et al. 2002), the heating rate due to the accretion is given by 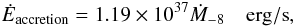 (19)where Ṁ-8 is the accretion rate in units of 10-8 M⊙ per year. The last contribution to the heating of the star comes from the viscosity. Taking into account the contributions of both bulk and shear viscosity, the associated heating rate reads (Owen et al. 1998)
(19)where Ṁ-8 is the accretion rate in units of 10-8 M⊙ per year. The last contribution to the heating of the star comes from the viscosity. Taking into account the contributions of both bulk and shear viscosity, the associated heating rate reads (Owen et al. 1998)  (20)where the expression for τs and τb are given in Eqs. (8) and (10), respectively, and
(20)where the expression for τs and τb are given in Eqs. (8) and (10), respectively, and 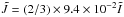 .
.
Finally, the equation for the thermal evolution of the star is given by 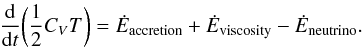 (21)Without r-modes, the temperature is determined by a balance between accretion heating and neutrino cooling:
(21)Without r-modes, the temperature is determined by a balance between accretion heating and neutrino cooling: 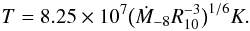 (22)
(22)
3. Results and discussion
By solving Eqs. (4), (5), (16), and (21) it is possible to obtain the temporal evolution of quark stars, taking into account the formation of toroidal magnetic fields through r-mode instability. We show the results for quark stars inside LMXBs only. Equation (15) gives the strength of the new toroidal component created by the winding-up of a pre-existent poloidal field through the differential rotation induced by r-modes. Several questions remain open concerning how the new magnetic fields, produced by the damping of the r-modes, are affected by possible instabilities. In the stably stratified matter of a stellar interior there are two types of instabilities: the Parker (or magnetic buoyancy) and the Tayler instabilities (or pinch-type), both driven by the magnetic field energy in the toroidal field. The condition for the Tayler instability to set in is given by (Spruit 1999, 2002) 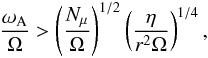 (23)where ωA = B/(4πρ)1/2r is the Alfvén frequency, Nμ ≃ 5 × 104 s-1 is the compositional contribution to the buoyancy frequency, and
(23)where ωA = B/(4πρ)1/2r is the Alfvén frequency, Nμ ≃ 5 × 104 s-1 is the compositional contribution to the buoyancy frequency, and 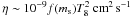 is the magnetic diffusivity that can be obtained from the electrical conductivity σ by using the relation η = 1/(μ0σ) (Haensel 1991). f(ms) takes into account the dependence of the electron fraction on the mass of the strange quark and ranges from 11 to 4 to 2.5 when ms changes from 100 to 200 to 300 MeV. From Eq. (23) we can conclude that in a pure quark star, the Tayler instability sets in for B > Bcr ~ 1012 G. After the development of the Tayler instability, the toroidal component of the field produces a new poloidal component as a result of its decay, which can then be wound up itself, closing the dynamo loop. When the differential rotation stops, the field can evolve into a stable configuration of a mixed poloidal-toroidal twisted-torus shape inside the star with an approximately dipolar field connected to it outside the star (Braithwaite 2006; Braithwaite & Spruit 2004, 2006; Braithwaite & Nordlund 2006). The buoyancy instability occurs for Bcr ≳ 1015 G (Haensel & Zdunik 2006), therefore it is not relevant in our calculations.
is the magnetic diffusivity that can be obtained from the electrical conductivity σ by using the relation η = 1/(μ0σ) (Haensel 1991). f(ms) takes into account the dependence of the electron fraction on the mass of the strange quark and ranges from 11 to 4 to 2.5 when ms changes from 100 to 200 to 300 MeV. From Eq. (23) we can conclude that in a pure quark star, the Tayler instability sets in for B > Bcr ~ 1012 G. After the development of the Tayler instability, the toroidal component of the field produces a new poloidal component as a result of its decay, which can then be wound up itself, closing the dynamo loop. When the differential rotation stops, the field can evolve into a stable configuration of a mixed poloidal-toroidal twisted-torus shape inside the star with an approximately dipolar field connected to it outside the star (Braithwaite 2006; Braithwaite & Spruit 2004, 2006; Braithwaite & Nordlund 2006). The buoyancy instability occurs for Bcr ≳ 1015 G (Haensel & Zdunik 2006), therefore it is not relevant in our calculations.
It is very important that the formation and subsequent stabilization of magnetic fields in the core of compact stars leads to different scenarios depending on the star’s composition. For instance, neutron stars contain a highly conductive crust that acts as a screen for the internal large magnetic field. Conversely, whether quark stars do or do not contain a crust is still controversial. Various types of crusts have been suggested: a tenuous crust made of ions suspended on the electric field associated with the most external layer of a quark star (Alcock et al. 1986); a crust made of a mixed phase of electrons and of quark nuggets (Jaikumar et al. 2006); a crust made of a mixed phase of hadronic and quark matter (Drago & Lavagno 2001). The electric properties of the crust are strongly connected with the electron density, which is suppressed in the core (this was taken into account above while discussing the magnetic diffusivity) and which can be enhanced in the crust, at least in the model where a fraction of hadrons is present in the crust (Drago & Lavagno 2001). Although detailed calculations of the structure of the crust of a quark star are not yet available, we can assume that if a crust does exist, its electric properties interpolate between those of a normal neutron star and those of a bare quark star, the two limiting situations.
 |
Fig. 1 Quark star instability window for three values of the strange quark mass. The dashed lines indicate the evolution of a star in an LMXB during the accretion stage up to the moment in which the star enters the instability window. |
As discussed above, when Tayler instability sets in, a poloidal component with a strength similar to the toroidal one (B ~ 1012 G) is generated. If there is no crust (the case with a crust will be briefly discussed below) this large poloidal component is not screened and diffuses outside the star, preventing the star from additionally accreting mass. Therefore, following this scenario, if a quark star inside an LMXB produces an internal magnetic field larger than the Tayler instability threshold because of the r-mode instability, it should stop accreting mass. Thus this represents, at least in principle, an additional constraint on the highest rotational frequency of the compact stars in LMXBs.
There are many parameters that enter into the equations for the temporal evolution of the frequency of the star. We fix the mass and the radius of the star to be 1.4 M⊙ and 10 km, respectively. A crucial quantity for the bulk viscosity is the mass of the strange quark, for which we will consider the three values ms = 100 − 200 − 300 MeV. The lowest value for ms is basically the current mass of the strange quark as used within MIT bag-like models and the last value is compatible with results of chiral quark models as the NJL model. The astrophysical input parameters concern the mass accretion rate, for which we use the values in the range (10-10−10-8) M⊙ yr-1, and the initial dipolar magnetic field varied in the interval B0 = 108 − 109 G.
Let us begin our discussion with the r-modes instability window shown in Fig. 1. With increasing values of ms, the bulk viscosity increases and therefore the instability region becomes smaller. Also shown by dashed lines are the trajectories of the evolution of a star into an LMXB during the accretion stage and until the star enters the instability window for two extreme values of the mass accretion (10-10 and 10-8 M⊙ yr-1 ).
The evolution is calculated by starting from a configuration below the instability window: an initial value of 100−200 Hz is taken as initial frequency, α is set to zero and the initial temperature is the equilibrium temperature as expressed by Eq. (22). Because of the accretion, the star is spun up until it reaches the instability window and at that point the r-modes instability begins to develop. The bulk viscosity dissipates part of the r-mode energy into heat with a consequent reheating of the star, and the internal magnetic field begins to grow. At the same time, the frequency of the star continues to grow due to the accretion torque, and the amplitude of the r-modes increases. The simultaneous effect of reheating and accretion leads the star to follow the border of the instability window. This is clearly shown in Fig. 2, where the thick lines indicate the paths followed by the star (for different values of the accretion rate) and the dots at which the evolution stops signal the onset of the Tayler instability. The temporal evolution of the r-modes amplitude is shown in Figs. 3 and 4, where we take ms = 100 MeV and ms = 200 MeV, respectively. For both cases the initial dipolar magnetic field has a value of 108 G.
 |
Fig. 2 Instability window and trajectories of the evolution of the frequency and temperature of the star for different values of the mass accretion rate. The short thick lines represent the paths followed by the star after the instability window is touched. The dots indicate the onset of the Tayler instability at which the evolution is stopped. |
 |
Fig. 3 Temporal evolution of α for different values of the mass accretion rate. Here the initial poloidal magnetic field is Bd = 108 G and ms = 100 MeV. |
 |
Fig. 5 Temporal evolution of the internal toroidal magnetic field Bϕ for different values of the mass accretion rate. Here Bd = 108 G and ms = 100 MeV. |
After an initial stage in which α oscillates (the star enters and exits the instability region), α increases steadily. However, the r-mode amplitude remains very small, below the critical value for the development of the nonlinear saturation of the r-mode instability 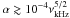 , where νkHz is the spin frequency in units of 1000 Hz (Arras et al. 2003; Bondarescu et al. 2007). Therefore, our calculations are independent of the value of α in the saturation regime. Parallel to the evolution of α we show in Figs. 5 and 6 the temporal evolution of the internal magnetic field. As expected, the value of Bφ follows the same evolution as α. Again, we stopped the evolution as soon as Bφ reaches the threshold for the Tayler instability Bcr ~ 1012 G.
, where νkHz is the spin frequency in units of 1000 Hz (Arras et al. 2003; Bondarescu et al. 2007). Therefore, our calculations are independent of the value of α in the saturation regime. Parallel to the evolution of α we show in Figs. 5 and 6 the temporal evolution of the internal magnetic field. As expected, the value of Bφ follows the same evolution as α. Again, we stopped the evolution as soon as Bφ reaches the threshold for the Tayler instability Bcr ~ 1012 G.
As discussed in Andersson et al. (2002), who did not consider the effect of internal magnetic damping, a quark star inside a LMXB can be spun up up to a maximum frequency, corresponding to the frequency at which the accretion torque balances the spin down torque owing to the emission of gravitational waves. However, taking into account the internal magnetic damping, a quark star without a crust should stop accreting after the onset of Tayler instability is reached. Therefore, an important question is how much the limiting frequency is reduced compared to the case in which the internal magnetic field is not taken into account. To this purpose, we computed the maximum frequencies for both cases, estimating in this way the effect of the internal magnetic field. These frequencies are shown in Fig. 7 as a function of ms and for two values of the initial poloidal magnetic field, Bd = 108 G (dashed line) and Bd = 109 G (dot-dashed line). Notice that the effect of the internal magnetic field is quite small, reducing the maximum rotational frequency only by a few tens Hertz. Moreover, the proven existence of stars in LMXBs rotating at frequencies higher than 600 Hz rules out a value of ms ~ 100 MeV.
 |
Fig. 7 Maximum spin frequencies of quark stars as a function of the mass of the strange quark. The results obtained assuming a initial poloidal magnetic field Bd = 108 G (dashed line) and Bd = 109 G (dot-dashed line) are compared to the result obtained without the internal magnetic field (solid line). |
Finally, we investigate the possible evolutionary scenarios of quark stars beyond the onset of the Tayler instability. Let us first consider a star without a crust: as soon as the Tayler instability sets in, the new magnetic configuration prevents the star from further accreting mass. The new poloidal component, of the same order of magnitude of the toroidal component (~1012 G), will act as a strong braking torque, and the star will lose angular momentum. This evolutionary path is plotted in the plane P–Ṗ in Fig. 8 and is depicted by the green line. It is very interesting to notice that starting from the region of LMXBs, the star evolves into the region of radio pulsars.
On the contrary, a highly conductive crust could screen the internal magnetic field for a very long time. A possible example of such a crust is the one described in Drago & Lavagno (2001) where the most external layer is made of an admixture of hadrons and quarks. In that case the electron fraction (and therefore also the electric conductivity) is high in the crust and decreases towards the core of the star. The evolution of the star depends on the dominant dissipation mechanism associated with the crust. The most relevant one is probably the ambipolar diffusion (see Cuofano & Drago 2009, 2010), whose typical time-scale is 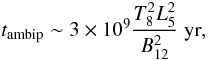 (24)where L5 = L/105 cm is the size of the region embedding the magnetic field. Because of this diffusion mechanism, the internal magnetic field can “quite rapidly” (in a few millions years) diffuse outside the crust, and then the star should stop accreting as well. In the meanwhile, the external magnetic field should spin down the star. In Fig. 8 we indicate with a blue line a sketch of the path followed by the star when there is ambipolar diffusion; in this case the star also evolves into the region of the radio pulsars.
(24)where L5 = L/105 cm is the size of the region embedding the magnetic field. Because of this diffusion mechanism, the internal magnetic field can “quite rapidly” (in a few millions years) diffuse outside the crust, and then the star should stop accreting as well. In the meanwhile, the external magnetic field should spin down the star. In Fig. 8 we indicate with a blue line a sketch of the path followed by the star when there is ambipolar diffusion; in this case the star also evolves into the region of the radio pulsars.
 |
Fig. 8 Trajectories in the plane P–Ṗ of quark stars after the development of the Tayler instability. The green line corresponds to a quark star without a crust; the blue line is obtained if in the crust the main diffusive process is the ambipolar diffusion. The grey area shows the region possibly crossed by the LMXBs during their evolution into radio pulsars. |
It is important that the time spent by the quark star after the Tayler instability and before it reaches the region of the radio pulsars is of the order of a few million years, to be compared with the time spent inside the radio pulsar region, which is of the order of a few hundred million years. Therefore, we can expect that only a few percent of the accreting quark stars that follow the trajectory indicated in Fig. 8 will be detected before they reach the radio pulsar region. In our scenario the trajectories shown in Fig. 8 do not apply to ordinary neutron stars, owing to the presence of a highly conductive crust that acts as a screen for the internal magnetic field generated by r-modes. Therefore, the future observation of objects in the grey area, indicated in Fig. 8, may be a possible confirmation of the existence of quark stars in the pulsar population.
4. Conclusions
We have shown that strong toroidal fields can be generated in the core of an accreting millisecond quark star that enters the r-mode instability window. Tayler instability sets in when the generated toroidal fields exceed the critical value 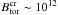 G and a new poloidal component of a similar strength is produced. Our results show that the maximum spin frequency for quark stars does not change significantly when taking into account the internally generated magnetic fields.
G and a new poloidal component of a similar strength is produced. Our results show that the maximum spin frequency for quark stars does not change significantly when taking into account the internally generated magnetic fields.
The scenario after the development of the Tayler instability depends on the presence and the properties of a possible crust. If there is no crust, the generated large poloidal component quickly diffuses outside the core and prevents the further accretion of mass on the star. On the other hand, if there is a highly conductive crust, it could screen the internal magnetic field to some extent. However, taking into account the ambipolar diffusion, which is, in this case, the dominant dissipation mechanism, the star could expel the internal magnetic field in a few millions years, which would then stop the accretion. In both cases the quark star evolves into the region of radio pulsars, as shown in Fig. 8: this represents a new possible scenario for the formation of radio pulsars.
Acknowledgments
L.B. is supported by CompStar a research program of the European Science Foundation. G.P. is supported by the German Research Foundation (DFG) under Grant No. PA1780/2-1. J.S.B. is supported by DFG through the Heidelberg Graduate School of Fundamental Physics.
References
- Alcock, C., Farhi, E., & Olinto, A. 1986, ApJ, 310, 261 [Google Scholar]
- Alford, M. G., & Schmitt, A. 2007, J. Phys. G, 34, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Alford, M. G., Braby, M., Reddy, S., & Schafer, T. 2007, Phys. Rev. C, 75, 055209 [NASA ADS] [CrossRef] [Google Scholar]
- Alford, M. G., Braby, M., & Mahmoodifar, S. 2010, Phys. Rev. C, 81, 025202 [NASA ADS] [CrossRef] [Google Scholar]
- Andersson, N. 1998, ApJ, 502, 708 [NASA ADS] [CrossRef] [Google Scholar]
- Andersson, N., & Kokkotas, K. D. 2001, Int. J. Mod. Phys. D, 10, 381 [NASA ADS] [CrossRef] [Google Scholar]
- Andersson, N., Jones, D. I., & Kokkotas, K. D. 2002, MNRAS, 337, 1224 [NASA ADS] [CrossRef] [Google Scholar]
- Arras, P., et al. 2003, ApJ, 591, 1129 [NASA ADS] [CrossRef] [Google Scholar]
- Benhar, O., & Valli, M. 2007, Phys. Rev. Lett., 99, 232501 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Blaschke, D. B., & Berdermann, J. 2007, AIP Conf. Proc., 964, 290 [NASA ADS] [CrossRef] [Google Scholar]
- Bondarescu, R., Teukolsky, S. A., & Wasserman, I. 2007, Phys. Rev. D, 76, 064019 [NASA ADS] [CrossRef] [Google Scholar]
- Braithwaite, J. 2006, A&A, 449, 451 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Braithwaite, J., & Spruit, H. C. 2004, Nature, 431, 819 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Braithwaite, J., & Nordlund, Å. 2006, A&A, 450, 1077 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Braithwaite, J., & Spruit, H. C. 2006, A&A, 450, 1097 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chatterjee, D., & Bandyopadhyay, D. 2006, Phys. Rev. D, 74, 023003 [NASA ADS] [CrossRef] [Google Scholar]
- Chatterjee, D., & Bandyopadhyay, D. 2007, Phys. Rev. D, 75, 123006 [NASA ADS] [CrossRef] [Google Scholar]
- Chatterjee, D., & Bandyopadhyay, D. 2008, ApJ, 680, 686 [NASA ADS] [CrossRef] [Google Scholar]
- Cuofano, C., & Drago, A. 2009, J. Phys. Conf. Ser., 168, 012008 [NASA ADS] [CrossRef] [Google Scholar]
- Cuofano, C., & Drago, A. 2010, Phys. Rev. D, 82, 084027 [NASA ADS] [CrossRef] [Google Scholar]
- Drago, A., & Lavagno, A. 2001, Phys. Lett. B, 511, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Drago, A., Lavagno, A., & Pagliara, G. 2005, Phys. Rev. D, 71, 103004 [NASA ADS] [CrossRef] [Google Scholar]
- Drago, A., Pagliara, G., & Berezhiani, Z. 2006, A&A, 445, 1053 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Drago, A., Pagliara, G., & Parenti, I. 2008, ApJ, 678, L117 [NASA ADS] [CrossRef] [Google Scholar]
- Ferraro, V. C. A. 1954, ApJ, 119, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Gusakov, M. E., & Kantor, E. M. 2008, Phys. Rev. D, 78, 083006 [NASA ADS] [CrossRef] [Google Scholar]
- Haensel, P. 1991, Nucl. Phys. Proc. Suppl., 24B, 23 [Google Scholar]
- Haensel, P., & Schaeffer, R. 1992, Phys. Rev. D, 45, 4708 [NASA ADS] [CrossRef] [Google Scholar]
- Haensel, P., & Zdunik, J. L. 2006, Nuovo Cim. B, 121, 1349 [NASA ADS] [Google Scholar]
- Haensel, P., Levenfish, K. P., & Yakovlev, D. G. 2000, A&A, 357, 1157 [NASA ADS] [Google Scholar]
- Haensel, P., Levenfish, K. P., & Yakovlev, D. G. 2001, A&A, 327, 130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haensel, P., Levenfish, K. P., & Yakovlev, D. G. 2002, A&A, 381, 1080 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jaikumar, P., Reddy, S., & Steiner, A. W. 2006, Phys. Rev. Lett., 96, 041101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Jaikumar, P., Rupak, G., & Steiner, A. W. 2008, Phys. Rev. D, 78, 123007 [NASA ADS] [CrossRef] [Google Scholar]
- Jha, T. K., Mishra, H., & Sreekanth, V. 2010, Phys. Rev. C, 82, 025803 [NASA ADS] [CrossRef] [Google Scholar]
- Lindblom, L., & Owen, B. J. 2002, Phys. Rev. D, 65, 063006 [NASA ADS] [CrossRef] [Google Scholar]
- Lindblom, L., Owen, B. J., & Morsink, S. M. 1998, Phys. Rev. Lett., 80, 4843 [NASA ADS] [CrossRef] [Google Scholar]
- Madsen, J. 1992, Phys. Rev. D, 46, 3290 [NASA ADS] [CrossRef] [Google Scholar]
- Madsen, J. 2000, Phys. Rev. Lett., 85, 10 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Mannarelli, M., Manuel, C., & Sa’d, B. A. 2008, Phys. Rev. Lett., 101, 241101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Owen, B. J., et al. 1998, Phys. Rev. D, 58, 084020 [NASA ADS] [CrossRef] [Google Scholar]
- Reisenegger, A., & Bonacic, A. A. 2003, Phys. Rev. Lett., 91, 201103 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Rezzolla, L., Lamb, F. K., & Shapiro, S. L. 2000, ApJ, 531, L139 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Rezzolla, L., Lamb, F. K., Markovic, D., & Shapiro, S. L. 2001a, Phys. Rev. D, 64, 104014 [NASA ADS] [CrossRef] [Google Scholar]
- Rezzolla, L., Lamb, F. K., Markovic, D., & Shapiro, S. L. 2001b, Phys. Rev. D, 64, 104013 [NASA ADS] [CrossRef] [Google Scholar]
- Sa’d, B. A. 2008, unpublished [arXiv:0806.3359] [Google Scholar]
- Sa’d, B. A., Shovkovy, I. A., & Rischke, D. H. 2007a, Phys. Rev. D, 75, 065016 [NASA ADS] [CrossRef] [Google Scholar]
- Sa’d, B. A.,Shovkovy, I. A., & Rischke, D. H. 2007b, Phys. Rev. D, 75, 125004 [NASA ADS] [CrossRef] [Google Scholar]
- Sawyer, R. F. 1989, Phys. Rev. D, 39, 3804 [NASA ADS] [CrossRef] [Google Scholar]
- Sinha, M., & Bandyopadhyay, D. 2009, Phys. Rev. D, 79, 123001 [NASA ADS] [CrossRef] [Google Scholar]
- Spruit, H. C. 1999, A&A, 349, 189 [NASA ADS] [Google Scholar]
- Spruit, H. C. 2002, A&A, 381, 923 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wagoner, R. V. 2002, ApJ, 578, L63 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Quark star instability window for three values of the strange quark mass. The dashed lines indicate the evolution of a star in an LMXB during the accretion stage up to the moment in which the star enters the instability window. |
| In the text | |
 |
Fig. 2 Instability window and trajectories of the evolution of the frequency and temperature of the star for different values of the mass accretion rate. The short thick lines represent the paths followed by the star after the instability window is touched. The dots indicate the onset of the Tayler instability at which the evolution is stopped. |
| In the text | |
 |
Fig. 3 Temporal evolution of α for different values of the mass accretion rate. Here the initial poloidal magnetic field is Bd = 108 G and ms = 100 MeV. |
| In the text | |
 |
Fig. 4 As in Fig. 3 with ms = 200 MeV. |
| In the text | |
 |
Fig. 5 Temporal evolution of the internal toroidal magnetic field Bϕ for different values of the mass accretion rate. Here Bd = 108 G and ms = 100 MeV. |
| In the text | |
 |
Fig. 6 As in Fig. 5 with ms = 200 MeV. |
| In the text | |
 |
Fig. 7 Maximum spin frequencies of quark stars as a function of the mass of the strange quark. The results obtained assuming a initial poloidal magnetic field Bd = 108 G (dashed line) and Bd = 109 G (dot-dashed line) are compared to the result obtained without the internal magnetic field (solid line). |
| In the text | |
 |
Fig. 8 Trajectories in the plane P–Ṗ of quark stars after the development of the Tayler instability. The green line corresponds to a quark star without a crust; the blue line is obtained if in the crust the main diffusive process is the ambipolar diffusion. The grey area shows the region possibly crossed by the LMXBs during their evolution into radio pulsars. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


