| Issue |
A&A
Volume 532, August 2011
|
|
|---|---|---|
| Article Number | A111 | |
| Number of page(s) | 11 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201116537 | |
| Published online | 03 August 2011 | |
On acoustic and gravity waves in the solar photosphere and their energy transport
1
Institut für Astrophysik, Friedrich-Hund-Platz 1, 37077 Göttingen, Germany
e-mail: kneer@astro.physik.uni-goettingen.de
2
Kiepenheuer-Institut für Sonnenphysik, Schöneckstr. 6, 79104 Freiburg, Germany
e-mail: nbello@kis.uni-freiburg.de
Received: 18 January 2011
Accepted: 27 June 2011
Aims. We study acoustic and atmospheric gravity waves in the quiet Sun to estimate their energy transport to the chromosphere.
Methods. A two-dimensional time sequence from quiet Sun disc centre was analysed with simultaneous spectroscopic observations in Fe i 5576 Å and Fe i 5434 Å (both with Landé factor g = 0). We calculated response functions of the velocities for the line minimum shifts and atmospheric transmissions of waves for the two lines. For this, NLTE line formation in granular and intergranular model atmospheres from numerical simulations were performed. For the interpretation of the observed waves and for the estimates of energy fluxes, we assumed adiabatic propagation of plane waves in an isothermal model atmosphere. Fourier analyses of intensity and velocity fluctuations were carried out. They yield power, phase, and coherence as functions of frequency ν (from temporal Fourier transforms) and in the kh − ν plane (from three-dimensional transforms). The power spectra, together with the mass densities at velocity formation heights, give then the energy fluxes.
Results. The rms velocities found here in the acoustic and gravity wave domains are lower by a factor ~1.5 as in earlier work. We therefore admit a factor of 2 for an upward correction of the estimated fluxes. For acoustic waves we find: 1) upward propagating waves are present on the Sun with frequencies up to 14−15 mHz (periods U ≈ 70 s); 2) the approximation of plane adiabatic waves in an isothermal atmosphere appears adequate for estimating the energy fluxes; 3) the acoustic energy fluxes are in the same range as found in our earlier work from ground-based, two-dimensional spectroscopy, 1500−3100 W m-2 at an atmospheric height of ~380 km and 1300−2700 W m-2 at 570 km. The energy flux carried by gravity waves is difficult to determine. We find: 1) phase and coherence spectra between continuum and velocity fluctuations show that convective overshoot and gravity waves are superimposed. We account for the convective flows using these coherence spectra. 2) At low frequencies, the vertical wavelength Λz can be short (≪300 km), yielding large corrections for atmospheric transmissions (factors > 100). We thus exclude from the flux estimates waves with |kz| > 20 Mm-1 and with vertical group velocities υgr,z < 0.3 km s-1. They are likely to be strongly reduced in amplitude by radiative damping. 3) With these caveats, the energy fluxes carried by gravity waves are found in the range of 4000 − 8200 W m-2 at 380 km and 700−1400 W m-2 at 570 km. Gravity waves thus also contribute to the energy transport into the chromosphere.
Key words: Sun: photosphere / Sun: chromosphere / Sun: oscillations / techniques: spectroscopic
© ESO, 2011
1. Introduction
The mechanisms of energy transport to the solar chromosphere and corona have been investigated for many decades. The radiative energy losses of the average quiet chromosphere amount to 4600 W m-2 according to Vernazza et al. (1981) up to 14 000 W m-2 given by Anderson & Athay (1989). The models by Vernazza et al. and Anderson & Athay are static. Dynamic models like those by Carlsson & Stein (1995, 1997) do not have the same energy requirements. Thus, the problem of the energy needs of the quiet solar chromosphere is an open issue. For the supply of energy, waves are under intense study. We refer to Stein & Leibacher (1974) and Leibacher & Stein (1981) who review the earlier literature and present physical descriptions of waves in the solar atmosphere. A further review of wave generation, propagation, and dissipation was presented by Stein et al. (2004).
Potential candidates for transport and dissipation of energy in the quiet solar atmosphere, which do not involve magnetic fields, are acoustic waves and internal gravity waves. In previous work, Bello González et al. (2009, henceforth Paper I) and Bello González et al. (2010a, Paper II), we dealt with short-period acoustic waves. See Paper I for a discussion of other work on this topic. We estimated energy fluxes in short-period, acoustic waves of ~3400 W m-2 at a height in the solar atmosphere of ~250 km, and of 1730 − 2100 W m-2 at 450 − 600 km (see also Bello González et al. 2010b). Most recently, from an analysis of high-resolution observations with the two-dimensional (2D) IMaX spectrometer (Martínez Pillet et al. 2011) onboard the balloon-borne SUNRISE telescope (Barthol et al. 2011; Solanki et al. 2010), Bello González et al. (2010c) measured substantial flux in short-period waves, in the frequency range of 5.2−15 mHz, of ~7000 W m-2 at a height of ~200 km.
Atmospheric gravity waves also may play an important role in transporting energy to the chromosphere. They were treated theoretically by, e.g. Souffrin (1966), Stix (1970), and Mihalas & Toomre (1981, 1982) who included radiative damping. Mihalas & Toomre (1982) found a possible energy flux at the base of the chromosphere of 1000 − 10 000 W m-2 from a 10 − 100 times larger initial flux.
Among the observations of gravity waves, we mention the work of Staiger (1987) who found negative phase differences at low frequencies between low and high forming lines. Also Deubner & Fleck (1989) presented clear evidence for the existence of gravity waves. Krijger et al. (2001) analysed TRACE data (Handy et al. 1999). They also saw clear negative phase differences (henceforth phases for brevity) of approximately − 8° between intensity fluctuations in the 1700 Å and 1600 Å passbands of TRACE. Likewise, Rutten & Krijger (2003) used the same TRACE data to find signatures of gravity waves. Recently, Straus et al. (2008) have measured a large energy flux in atmospheric gravity waves, 20 800 W m-2 at a height of 250 km and ~5000 W m-2 at approximately 500 km. From simultaneous observations with Hinode/SOT (Tsuneta et al. 2008) in Mg b2 and SOHO/MDI (Scherrer et al. 1995) in Ni i at 6768 Å, Straus et al. (2009) have confirmed the large energy flux in gravity waves, and obtained ~2000 W m-2 at a height of 720 km. Also in this work, Straus et al. find an acoustic energy flux of 1600 W m-2 at 400 km. These results by Straus et al. (2008, 2009) are outstanding and important, and it is worth undertaking a similar study.
Here, we analyse new observations relevant for estimates of energy fluxes in the quiet solar atmosphere. We determine velocities from 2D time series obtained quasi-simultaneously in the Fe i 5576 Å and 5434 Å lines. We describe the observations and their analysis in Sect. 2. The formation heights of the velocity signals and the transmission of the atmosphere for the measurement of line shifts from waves are presented in Sect. 3. For the interpretation and estimates of energy fluxes, we outline in Sect. 4 the equations of wave propagation in the solar atmosphere. As in Paper II, we assume adiabatic waves in an isothermal atmosphere. In Sect. 5 we present power, phase, and coherence spectra and estimate energy fluxes in acoustic and gravity waves from the velocities measured in the two lines. Section 6 concludes this paper.
2. Observations, data analysis, and rms velocities
2.1. Observations
The observations were obtained on July 16, 2010, from quiet Sun disc centre. We used the Triple Etalon SOlar Spectrometer (TESOS, mounted at the VTT, Tritschler et al. 2002, and references). TESOS can be operated with two F numbers (ratio of diameter of entrance pupil to effective focal length), 1/128 and 1/256 (von der Lühe & Kentischer 2000). We chose F = 1/256, because it gives the higher spatial and spectral resolution (λ/(Δλ) ≈ 300 000). The two Fe i 5576 Å and Fe i 5434 Å lines, both with Landé factors g = 0, were scanned sequentially with exposure times of 50 ms at 36 positions with a step width of 14.56 mÅ for 5576 and at 48 positions with a step width of 14.20 mÅ for 5434. Broadband frames through a filter at 5577 Å with FWHM of 3 Å were taken simultaneously with the narrow-band images. The frames were binned online to a scale of 0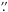 172 per pixel. The total duration of one scan, including both lines, was 21.0 s. Dark and flat field data were recorded as well. The observations were supported by KAOS (Kiepenheuer Adaptive Optics System, von der Lühe et al. 2003). The seeing was good, with Fried parameter r0 between 10 cm and 20 cm for 84 scans (29.4 min) during the early morning and then deteriorated rapidly, such that the solar granulation contrast became low and KAOS lost tracking.
172 per pixel. The total duration of one scan, including both lines, was 21.0 s. Dark and flat field data were recorded as well. The observations were supported by KAOS (Kiepenheuer Adaptive Optics System, von der Lühe et al. 2003). The seeing was good, with Fried parameter r0 between 10 cm and 20 cm for 84 scans (29.4 min) during the early morning and then deteriorated rapidly, such that the solar granulation contrast became low and KAOS lost tracking.
2.2. Data analysis
When scanning a spectral line profile with Fabry-Perot interferometers one obtains intensity fluctuations along the wavelength (Tritschler et al. 2002, their Fig. 6; Bello González & Kneer 2008, Fig. 1). Besides, the narrow-band frames from TESOS with its telecentric mounting exhibit an “orange peel” pattern, and the spectral lines from the scans are locally shifted with respect to the scanning step number and may suffer from asymmetric transmission profiles (Scharmer 2006). These are caused by wavelength shifts of the transmission peaks of the Fabry-Perot etalons, due to (small) local flatness defects of the order of λ/200 (in the visible range) and due to mistuning of the etalons against each other. The data analysis therefore requires special care. We describe it step by step for one spectral line.
-
1.
The broadband and narrow-band frames were dark-correctedand the broadband frames were divided by the correspondingaverage flat field image.
-
2.
The narrow-band flat field scans were (temporally) averaged. The resulting scan was compared with the corresponding line profile from the Fourier transform spectrometer (FTS, Brault & Neckel; quoted by Neckel 1999), which we fitted in position, continuum intensity, and line depression to the profiles observed in each pixel in the flat fields. The intensity fluctuations along wavelength were then obtained by division of the observed profiles by the FTS profiles, normalisation, and high-pass filtering to remove long wavelength fluctuations due to different line widths in observations and FTS profiles. This process also gives the wavelength shifts at each pixel in the field of view (FoV).
-
3.
The flat field scan was divided at each pixel by the corresponding wavelength-dependent intensity fluctuations. The profiles at each pixel were smoothed in wavelength with the Hamming function S = [0.26,0.48,0.26]. Then the wavelength shifts could be removed from the flats by interpolation.
-
4.
Then, at each wavelength position, the flat fields were divided by their average over the FoV, which removes the wavelength-dependent intensity from the flat fields. The resulting frames can be used to correct the science scans.
-
5.
All narrow-band science scans were corrected, pixel by pixel, for the wavelength-dependent intensity fluctuations determined from the flats, then also smoothed in wavelength as the flats, and corrected for the wavelength shifts also determined from the flats.
-
6.
Finally, the frames were divided at each wavelength position by the flats from which the wavelength information had been taken out.
This way, the instrumental effects were eliminated to a large extent from the TESOS data. To perform a low-level image reconstruction, the broadband images from each scan were de-stretched with the average broadband image from this specific scan as reference, using a procedure written by Suetterlin (2002, priv. comm.). The de-stretching parameters were then also applied to the spectroscopic narrow-band frames. Furthermore, the continuum images (averages from the blue and red sides of both lines), were de-stretched with running means over 11 time steps as references, and the de-stretching parameters were again transferred to the line profiles. The resulting FoV amounted to 29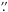 24 × 29
24 × 29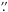 24 (170 × 170 pixels).
24 (170 × 170 pixels).
Then the (relative) continuum intensities were determined from averages over six wavelength positions at either side of the 5434 line and over four positions at either side of 5576. Line minimum intensities and positions were obtained from an interpolation method described in Paper II. The resulting sequences were apodised over 12 pixels in the spatial directions and over six pixels in time. The sequences from the 5576 line were finally shifted by the time difference between the recording of the minima of the 5576 and 5434 lines. For this purpose, the positions of the minima of the line profiles were taken from the averages over the FoV and over time. The 5434 line minimum intensities in this FoV, averaged over time, showed no persistent brightenings that would indicate network magnetic fields.
After subtraction of averages in space and time, the 2D time sequences of continuum intensities, line minimum intensities, and velocities were Fourier-transformed, yielding power, phase, and coherence spectra between two of the various sets. We used the definition by Edmonds & Webb (1972) for the coherence. Since the observations are from quiet Sun disc centre, we may assume azimuthal isotropy and average the spectra azimuthally in the (kx,ky) plane. The Nyquist frequency is νNy = 23.81 mHz and the frequency resolution is Δν = 0.57 mHz, while for the horizontal wavenumber we have khNy = 25.19 Mm-1 and a wavenumber resolution of Δkh = 0.296 Mm-1. To reduce pixelisation in the presentations of the power, phase, and coherence spectra, the data sets were interpolated in the Fourier space by padding the data themselves at the beginning and at the end of the time axis with zero arrays of the same length as the data themselves. This has no effect on the results of flux estimates.
2.3. rms velocities
The rms velocities from the present data are low, lower than those in Papers I and II, and also lower than the values found by other authors. We have here υrms,5576 = 305 m s-1 for 5576, with velocity signals from heights of ~370 km (above τ5 = 1, see the response functions below in Sect. 3.1), and υrms,5434 = 415 m s-1 for 5434, from heights ~560 km. In the data for Paper I the velocity was υrms,5576 = 405 m s-1 from ~250 km, and in Paper II we had υrms,5434 = 510 m s-1 from ~550 km. In the work of other authors we find υrms = 440 m s-1 at 250 km and 500 m s-1 at ~520 km in Canfield & Mehltretter (1973), 500 m s-1 at 250 km and 500 m s-1 at 500 km in Canfield (1976), and ≥ 600 m s-1 at 500 − 600 km in Keil & Canfield (1978). See also the results and discussions in Durrant et al. (1979), Komm et al. (1991), and Hanslmeier et al. (1991). We have applied filters to restrict the velocities either only to the acoustic domain or only to the gravity wave domain. We then obtain for the present data set in 5434, e.g. υrms,ac = 170 m s-1 and υrms,grav = 95 m s-1, while the data for Paper II give υrms,ac = 250 m s-1 and υrms,grav = 135 m s-1.
For a test, we smoothed the 5434 line data from Paper II with a Gaussian with σ ≙ 0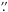 36 (FWHM = 0
36 (FWHM = 0 84!), although the seeing during observation for the present data was good. We obtained υrms,ac = 170 m s-1 and υrms,grav = 90 m s-1, which are similar to the present data. The total rms velocity in the 5434 line, which is dominated by the 5-min oscillations, was reduced somewhat, to 466 m s-1. The rms continuum fluctuations were reduced from 6.3% (of average) to 4.2%, a value similar to the 4.1% obtained from the present data. Possibly, the reduction of velocity amplitudes is also a spectroscopic effect, e.g. asymmetries of the spectrometer transmission varying over the FoV (see Fig. 5 in Scharmer 2006, and the discussion there). At present, we have no means of correcting such effects. The matter needs scrutinisation with especially designed measurements with TESOS.
84!), although the seeing during observation for the present data was good. We obtained υrms,ac = 170 m s-1 and υrms,grav = 90 m s-1, which are similar to the present data. The total rms velocity in the 5434 line, which is dominated by the 5-min oscillations, was reduced somewhat, to 466 m s-1. The rms continuum fluctuations were reduced from 6.3% (of average) to 4.2%, a value similar to the 4.1% obtained from the present data. Possibly, the reduction of velocity amplitudes is also a spectroscopic effect, e.g. asymmetries of the spectrometer transmission varying over the FoV (see Fig. 5 in Scharmer 2006, and the discussion there). At present, we have no means of correcting such effects. The matter needs scrutinisation with especially designed measurements with TESOS.
We have expanded on this point because the energy flux is roughly proportional to 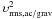 . The present study is based on 2D observations, which were not subject to image reconstruction, while the data for the results in Papers I and II were reconstructed. It was shown in these works and in Bello González et al. (2010c) that the acoustic waves are of small scale. High spatial resolution is obviously needed to find the waves with only small spatial extension, which are likely also the waves with short periods. The energy fluxes from the present data set, to be presented below in Sect. 5, may thus easily be underestimated by a factor of 2 or more.
. The present study is based on 2D observations, which were not subject to image reconstruction, while the data for the results in Papers I and II were reconstructed. It was shown in these works and in Bello González et al. (2010c) that the acoustic waves are of small scale. High spatial resolution is obviously needed to find the waves with only small spatial extension, which are likely also the waves with short periods. The energy fluxes from the present data set, to be presented below in Sect. 5, may thus easily be underestimated by a factor of 2 or more.
3. Response functions and atmospheric transmission
We present below velocity response functions RFυ (in short RF), which give information on the formation heights of the velocity signals. From these one obtains the mass densities ρ for the estimates of the energy fluxes and an assessment of the differences of formation heigths of the lines under study. Furthermore, as repeatedly shown (Bello González et al. 2010c; Papers I and II, and references therein), the extent of the signal forming layers may lead to severe damping of the observable velocities from waves with short wavelength along the line of sight. This effect of atmospheric transmission (Tr) on measurements of energy fluxes was denoted as “underestimated in the past” by Straus et al. (2009). The squares of the Trs are the modulation transfer functions MTFs by which the velocity powers are to be corrected for flux determinations (cf. Eq. (11) below).
For calculating RFs and Trs, we used an intergranular (IGR) and a granular (GR) model atmosphere from the hydrodynamic simulations by Asplund et al. (2000) and the profiles of the two iron lines were calculated in NLTE. The models are from the same IGR and GR and from the same snapshot from the Asplund et al. simulations that have been analysed in detail by Shchukina & Trujillo Bueno (2001). For Fe i 5434, we used the departure coefficients as in Paper II, which had been calculated as in Shchukina & Trujillo Bueno (2001)1.
For Fe i 5576, the NLTE ionisation equilibria of Fe in IGR and GR were taken from Fig. 6 in Shchukina & Trujillo Bueno (2001), which accounts approximately for the difference in line absorption between LTE and NLTE (see Fig. 7 in Shchukina & Trujillo Bueno 2001). For the NLTE line source function of the 5576 line, the ratios of the departure coefficients were obtained from the excitation temperatures given by the dashed curves in Fig. 8 of the same work.
The line profiles from the model atmospheres, which possess an infinite spectral resolution, were convolved with the spectral transmission of the spectrometer (TESOS). The finesses of the three Fabry-Perot etalons were provided by Kentischer (2010, priv. comm.). The effect of spectral broadening from the telecentric mounting, albeit small, was included. The resulting profiles were interpolated to the wavelength steps of the observations and then convolved with the same Hamming smoothing function [0.26, 0.48, 0.26] as the observations.
3.1. Response functions
For the calculation of the RFs, we added a small velocity perturbation to the IGR and GR models while keeping the macroscopic velocities. The method by Eibe et al. (2001) was applied. The resulting velocity RFs are depicted in Fig. 1. In IGR, the maximum of the 5434 RF occurs at a height of approximately 620 km and that of 5576 at 410 km. The mass densities in the IGR model are 5.5 × 10-6 kg m-3 for 5434 and 3.0 × 10-5 kg m-3 for 5576. In GR, the maxima occur for 5434 at 520 km with mass density 1.1 × 10-5 kg m-3 and for 5576 at 350 km with mass density 4.9 × 10-5 kg m-3. The differences in height of signal formation are 210 km in the IGR model and 170 km in the GR model, on average 190 km.
 |
Fig. 1 Velocity response functions RFυ in intergranules (IGRs) and granules (GRs) for Fe i 5434 (solid curves) and Fe i 5576 (dashed) calculated in NLTE from the IGR and GR models of Asplund et al. (2000) and taking the spectral response of the instrument and of the data acquisition and analysis into account. |
3.2. Atmospheric transmission
We note that the relevant quantity of a wave for the Tr calculation is its wavelength Λ along the line of sight. The data for the present study are from disc centre of the Sun. One sees from the dispersion relation, Eq. (2) below, that |kz| becomes large, i.e. the vertical wavelengths become short, in the acoustic domain for large ω and small horizontal wavenumbers kh, and in the gravity wave domain for small ω and large kh.
We calculated Trs of IGR and GR for the two lines for vertical wavenumbers kz = 2π/Λz ranging from 0 to 40 Mm-1. For any frequency ν and horizontal wavenumber kh we determine kz from the dispersion relation, Eq. (2) below. For each kz, linear waves were assumed as υ(z,kz,φ) = υ0(z)·sin(z·kz + φ) with 25 phases φ from 0° to 360°. From the resulting line profiles the maximum and minimum of the Doppler shifts were determined and normalised to those for kz = 0, i.e. for infinite vertical wavelength, yielding Tr(kz). We assumed an exponential increase in the wave amplitudes according to υ0(z) = υ0(z = 0)·exp [z/(2H)], which mimics conservation of energy density ρ(z)·υrms(z)2 = const., with the density scale height H = 107.5 km (see below). This choice gives somewhat larger Trs than assuming constant amplitude with height, thus somewhat smaller correction factors 1/Tr(kz)2 = 1/MTF (cf. Eq. (11) below), for the estimates of fluxes. Figure 2 shows the Trs as functions of kz separately for IGRs and GRs.
 |
Fig. 2 Transmissions as functions of vertical wavenumber kz for Fe i 5434 (solid curves) and Fe i 5576 (dashed) calculated in NLTE from the IGR and GR models of Asplund et al. (2000). |
When estimating the energy fluxes below, we distinguish between IGR and GR for the acoustic waves, but not for the atmospheric gravity waves. The reason is that acoustic waves, on the one hand, mostly possess a vertical group velocity close to the sound speed. The travel time from the base of the photosphere to the formation heights of the lines is only 60 − 80 s, so an allocation of waves to the granular convection is thus possible. The group velocities of gravity waves, on the other hand, vary between few 100 m s-1 to few km s-1 with very different travel times. For gravity waves we use average formation heights of 570 km for 5434 and 380 km for 5576 with average mass densities of 8.3 × 10-6 kg m-3 for the 5434 line and 4.0 × 10-5 kg m-3 for 5576. Likewise, the Trs for IGR and GR are averaged when dealing with gravity waves.
The methods of obtaining the densities at signal formation height from response functions and of correcting the signals applying MTFs have not been well established. The critical issues come from the fact that the solar atmosphere is highly dynamic (e.g. Fleck et al. 2010). It is little known how the flows and temperature fluctuations, excited by the granular convection, influence wave propagation, especially for those with short wavelength of a few 100 km and less. Thus, the concepts of height of formation and MTFs definitely require an assessment. For this, hydrodynamic simulations are needed that include waves. Recently, Leenaarts et al. (2011) have carried out numerical simulations in two spatial dimensions with time-dependent ionisation of hydrogen and self-consistent excitation of acoustic waves, among other features. Calculations of line formation in such dynamic models could then be used to relate such observable quantities as intensity and Doppler-shift fluctuations with those at their formation height and compare them with observed data. Most likely, such radiation transfer simulations will need NLTE calculations for the ionisation equilibria and level populations, possibly time dependent at large atmospheric heights.
4. Wave propagation
Below we use the dispersion relation from the linearised equations of motion to determine the vertical group velocity of acoustic and gravity waves and the inclination of the particle motions with respect to the vertical. The relevant equations can be found, e.g., in Mihalas & Toomre (1981, 1982) and in Bray & Loughhead (1974). See also Paper II. We collect them here for completeness and we show that when following these equations strictly gives the information on the group velocities, and measurements of phases are not needed.
As in Paper II, we adopt the approximation of adiabatic propagation of plane waves in the stratified, solar atmosphere, which we assume is isothermal. Be ω = 2πν the angular frequency and kh and kz the horizontal and vertical components of the wave vector, respectively, with real (ω,kh,kz). In a non-isothermal, non-isotropic atmosphere (kh,kz) are not constant, and become complex numbers with damping (e.g. Mihalas & Toomre 1982). We refer below, in the estimates of energy transport by waves in Sect. 5, to the modelling results about radiative damping in their work.
Under the present assumptions, the acoustic cutoff frequency ωac and the Brunt-Väisälä frequency ωBV are given by 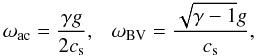 (1)where γ = 5/3 is the ratio of specific heats, g the surface gravity acceleration, and cs the sound velocity for which we take 7 km s-1. With this the acoustic cutoff frequency is ωac = 3.26 × 10-2 s-1 (cutoff period Uac = 193 s), and the Brunt-Väisälä frequency is ωBV = 3.19 × 10-2 s-1. The vertical direction is taken opposite to the vector of the surface gravity. With the above sound speed, the scale height of the density (and pressure) stratification is H =
(1)where γ = 5/3 is the ratio of specific heats, g the surface gravity acceleration, and cs the sound velocity for which we take 7 km s-1. With this the acoustic cutoff frequency is ωac = 3.26 × 10-2 s-1 (cutoff period Uac = 193 s), and the Brunt-Väisälä frequency is ωBV = 3.19 × 10-2 s-1. The vertical direction is taken opposite to the vector of the surface gravity. With the above sound speed, the scale height of the density (and pressure) stratification is H = 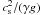 = (ℛT)/(μg) = 107.5 km, with the universal gas constant ℛ and the mean molecular weight μ also assumed to be independent of height.
= (ℛT)/(μg) = 107.5 km, with the universal gas constant ℛ and the mean molecular weight μ also assumed to be independent of height.
The dispersion relation is 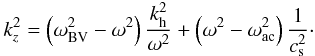 (2)This reduces in an incompressible medium with cs → ∞ and H → ∞, thus
(2)This reduces in an incompressible medium with cs → ∞ and H → ∞, thus 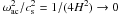 , to
, to 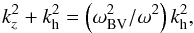 (3)or in this approximation,
(3)or in this approximation, 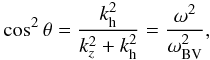 (4)where θ is the angle between the wave vector and the horizontal direction.
(4)where θ is the angle between the wave vector and the horizontal direction.
For 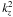 = 0 in Eq. (2), we obtain two limiting curves in the kh − ν plane (with ν = ω/(2π)), dividing this plane into three regimes: (1) acoustic waves with
= 0 in Eq. (2), we obtain two limiting curves in the kh − ν plane (with ν = ω/(2π)), dividing this plane into three regimes: (1) acoustic waves with 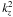 > 0; (2) the regime of evanescent waves with
> 0; (2) the regime of evanescent waves with 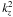 < 0; (3) atmospheric gravity waves with again
< 0; (3) atmospheric gravity waves with again 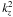 > 0. Figure 3, the “diagnostic” diagram, shows the areas of the various waves (see also below Fig. 5 and following). The above values for cs, ωac, and ωBV were adopted for this figure. Convective signals with finite lifetime may also be present in the gravity wave domain and may extend into the evanescent wave regime.
> 0. Figure 3, the “diagnostic” diagram, shows the areas of the various waves (see also below Fig. 5 and following). The above values for cs, ωac, and ωBV were adopted for this figure. Convective signals with finite lifetime may also be present in the gravity wave domain and may extend into the evanescent wave regime.
 |
Fig. 3 Regimes of acoustic, evanescent, and gravity waves in the kh − ν plane. Dashed and dotted lines: locations of surface gravity waves (fundamental f or p0 mode) and purely horizontal acoustic waves (Lamb waves), respectively. |
The vertical component of the phase velocity becomes ![\begin{eqnarray} \upsilon_{{\rm ph},z} \!=\! {\omega\over k_z} \!=\! \pm\left[\left(\omega_{\rm BV}^2/\omega^2-1\right)\left(k_{\rm h}^2/\omega^2\right)\!-\!\left(\omega_{\rm ac}^2/\omega^2-1\right)/c_{\rm s}^2\right]^{-1/2}, \label{eq5} \end{eqnarray}](/articles/aa/full_html/2011/08/aa16537-11/aa16537-11-eq88.png) (5)where we have used the dispersion relation, Eq. (2). We take ω strictly positive, so the vertical phase velocity carries the sign of kz. In the incompressible limit, the vertical phase velocity reduces to
(5)where we have used the dispersion relation, Eq. (2). We take ω strictly positive, so the vertical phase velocity carries the sign of kz. In the incompressible limit, the vertical phase velocity reduces to 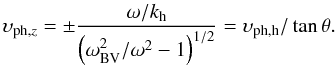 (6)Similarly for the vertical component of the group velocity, one obtains
(6)Similarly for the vertical component of the group velocity, one obtains 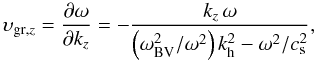 (7)which again reduces in the incompressible limit to
(7)which again reduces in the incompressible limit to 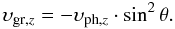 (8)The denominator in Eq. (7) is negative for acoustic waves and positive for gravity waves. Thus, for gravity waves, the vertical group velocity υgr,z takes on the opposite sign of the vertical phase velocity υph,z.
(8)The denominator in Eq. (7) is negative for acoustic waves and positive for gravity waves. Thus, for gravity waves, the vertical group velocity υgr,z takes on the opposite sign of the vertical phase velocity υph,z.
The solution of the wave equations (see Paper II, Eqs. (2) − (5) and (10)) gives the angle ψ between the vertical direction and the direction of the particle motion ![\begin{equation} {\vert\chi\vert^2\over\vert\zeta\vert^2} = \tan^2\psi = {\left[k_z^2+\left({\omega_{\rm ac}/ c_{\rm s}}-{g/ c_{\rm s}^2}\right)^2\right]\cdot k_{\rm h}^2 \over \left({\omega^2/ c_{\rm s}^2}-k_{\rm h}^2\right)^2}\cdot \label{eq9} \end{equation}](/articles/aa/full_html/2011/08/aa16537-11/aa16537-11-eq95.png) (9)Here, χ and ζ denote the horizontal and vertical amplitudes, respectively, of the particle motion. In the incompressible limit one obtains
(9)Here, χ and ζ denote the horizontal and vertical amplitudes, respectively, of the particle motion. In the incompressible limit one obtains 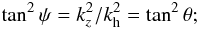 (10)i.e., in this limit, the particles move strictly perpendicularly to the direction of the wave vector.
(10)i.e., in this limit, the particles move strictly perpendicularly to the direction of the wave vector.
The measurements consist of line-of-sight (LOS) velocities from the disc centre of the Sun. The power spectra Pυ(kh,ν) are thus to be corrected for the foreshortening. The total energy fluxes carried by acoustic or atmospheric gravity waves into the vertical direction become 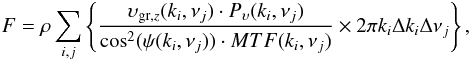 (11)where ρ is the mass density at the formation height of the velocity signal, Δki and Δνj denote the horizontal wavenumber and frequency intervals, respectively, in the kh − ν plane, and MTF is the modulation transfer function (square of the atmospheric transmission, see Sect. 3 above). The summations are taken over pixels in the acoustic wave domain or in the gravity wave domain. The factor 2πki is for azimuthal integration in the kx − ky plane since the power spectra are azimuthal averages.
(11)where ρ is the mass density at the formation height of the velocity signal, Δki and Δνj denote the horizontal wavenumber and frequency intervals, respectively, in the kh − ν plane, and MTF is the modulation transfer function (square of the atmospheric transmission, see Sect. 3 above). The summations are taken over pixels in the acoustic wave domain or in the gravity wave domain. The factor 2πki is for azimuthal integration in the kx − ky plane since the power spectra are azimuthal averages.
5. Results
5.1. Spectra of power, phase, and coherence
5.1.1. Temporal spectra
We begin with one-dimensional (1D) spectra. We calculated at each pixel in the FoV temporal Fourier transforms of the corresponding time sequences and averaged the spectra. The left panel of Fig. 4 shows the temporal power spectra Pυ,5576(ν) and Pυ,5434(ν). The right panel depicts the spectra of phase Zυ,5576−5434(ν) and of coherence Cυ,5576−5434(ν).
 |
Fig. 4 Results of temporal Fourier analysis. Left panel: temporal velocity power spectra Pυ,5576(ν) (dashed) and Pυ,5434(ν) (solid); thin for original power, thick after subtraction of noise level (dotted horizontal lines). Right panel: phases Z (solid) and coherences C (dashed) between the velocities in the 5576 and 5434 lines. |
The power spectrum from the 5576 line reaches the noise level (left panel of Fig. 4) at approximately 16 mHz, and the one from 5434 at approximately 18 mHz. The coherence is high, close to 1.0 in the 2 − 6 mHz band, at periods U of 165 − 500 s, and then decreases towards higher frequencies. The coherence has become very low at 14 − 15 mHz, where the behaviour of phases is random. At phases of 180°, a phase jump to − 180°occurs; i.e., a value of Z > 180° appears at Z − 360°.
The phase around 1.5 mHz is negative, ~ −10°, which is a signature of energy transport by gravity waves upward. Around the same frequency, the coherence shows a dip that indicates a “disturbance” of the gravity wave signal. We come back to this below. The phases are zero for the 5-min oscillations (3.3 mHz) known to be evanescent in the solar atmosphere. Beyond 5 mHz, which is approximately the acoustic cutoff frequency (νac = ωac/(2π)), the phases steadily increase towards higher frequencies. At 10 mHz (period U = 100 s), we measure Δφ ≈ 90°. This gives a phase velocity, from Eq. (5) assuming the horizontal wavenumber kh = 0, of υph,z = 8.19 km s-1 yielding a distance of formation of Δz = υph,z·U·(Δφ/360°) ≈ 205 km. This is close to the average distance of 190 km estimated from the velocity RFs in Fig. 1.
It was noted by Fleck et al. (2010) that high-frequency Doppler signals can be caused by rapid height variations in the velocity RF in a highly dynamic atmosphere with strong velocity gradients. Previous claims of detection of acoustic waves with periods U ≤ 70 s should thus be re-evaluated. In our measurements, the phases (right panel of Fig. 4) show the signature of propagating acoustic waves from 5 mHz up to 14−15 mHz (periods of 67−70 s).
The failure to detect waves with shorter periods (<67−70 s) in the present data does not exclude their existing in the solar atmosphere. In Papers I and II, we had given power and flux spectra in the Fe i 5576 and 5434 lines indicating velocity fluctuations, above noise, with periods down to 50 s and shorter. A proof, by means of phase measurements as in the present study, that these are propagating acoustic waves has not been given. Reardon et al. (2008) find oscillatory power in the chromospheric Ca ii 8542 Å line up to 25 mHz. They suggest that the power at high frequencies in the chromosphere results from turbulence generated from shock oscillations near the cutoff frequency, rather than from direct transmission of high-frequency acoustic waves from the lower atmosphere.
5.1.2. Spectra in the kh–ν plane
We performed 3D Fourier transforms of the data sets and calculated power, phase, and coherence spectra. We may assume isotropy in the x − y plane, so we averaged the spectra azimuthally in the kx − ky plane for analysis in the kh − ν plane with 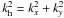 .
.
 |
Fig. 5 Results of Fourier analysis of the velocities measured in the 5576/5434 line pair. Upper left and right: power spectra P of 5576 and 5434 lines, respectively; lower left: phase Z between the two lines with colour bar, levels in degrees; lower right: coherence C with colour bar. See the online version for the colour representation of the phases. |
Figure 5 shows the power, phase, and coherence spectra from the line minimum velocities in the 5576 and 5434 lines. The limiting curves for acoustic and gravity waves are included, except for the power from the 5434 velocities where one can see indications of the modal structure of the 5-min oscillations. The dotted curves in the power spectra indicate the limits of the noise power, which is subtracted for the estimates of energy fluxes below. The noise power, i.e. where the power remains constant with increasing frequency, depends on the horizontal wavenumber. We suggest two reasons for this: 1) especially acoustic waves are travelling predominantly vertically because of upward refraction (Fossum & Carlsson 2006), so the power decreases with increasing horizontal wavenumber kh; 2) the waves have a small horizontal extent, so even purely upward propagating waves leave their signature at non-zero horizontal wavenumbers in the kh − ν plane, albeit with decreasing power towards increasing kh. The decrease in power with increasing kh is reflected in the spectra of Fig. 5.
Coherence C is close to 1 for the 5-min oscillations in the evanescent regime, approximately 0.9 near the acoustic cutoff frequency for small kh, and 0.85 at maximum in the gravity wave regime and decreasing to 0.2 − 0.4 at kh = 10 Mm-1 for gravity waves.
The phases appear random, because of noise, for kh ≥ 13−15 Mm-1 and ν ≥ 14 − 15 mHz. The phase in the f mode and, generally, the phases in the evanescent regime are close to 0°. In the acoustic domain, we find upward propagating waves up to 14 − 15 mHz, as already seen in the temporal phase spectrum of Fig. 4.
In the area of gravity waves, the minimum phase difference is approximately − 40° for kh ≈ 4 Mm-1 and ν ≈ 2.5 mHz. This certainly indicates the presence of atmospheric gravity waves in the velocity field. For 4 Mm-1 and 2.5 mHz we calculate a vertical phase velocity of υph,z = − 2.72 km s-1 from Eq. (5) and from Eq. (7) a vertical group velocity, which enters the energy flux in Eq. (11), of υgr,z = 1.49 km s-1. The phase difference for a height distance Δz = 190 km is obtained as Δφ = 360°·Δz·ν/υph,z ≈ −63°, approximately a factor of 1.5 lower (more negative) than observed. For the same wavenumber and frequency, Straus et al. (2008) find, from numerical hydrodynamic simulations of granular convection and waves, phase differences between heights of 70 km and 250 km, or Δz = 180 km, of Δφ = −20°, and in their measurements −10°. The phase difference Δφ = − 20° yields a vertical phase velocity of υph,z = −8.1 km s-1. In the incompressible limit, the vertical group velocity is obtained from Eqs. (4) and (8) as υgr,z = 6.1 km s-1. A phase difference of − 10° gives υgr,z = 12.2 km s-1. Generally, when wandering through the kh − ν plane and taking the measured phase differences, the vertical group velocities turn out to be substantially higher than those obtained from linear wave theory and also higher than the values of 0.2−1.0 km s-1 given by Mihalas & Toomre (1981, Fig. 8 and Mihalas & Toomre (1982, Fig. 6. A likely reason for the high measured group velocities is discussed shortly.
To learn in more detail which phases are to be expected under the assumptions of linear adiabatic waves, we made an experiment. We let the “waves” observed in the velocities from the 5576 line propagate upward (in the computer) by Δz = 190 km to the formation height of the 5434 line. The equation of propagation is (see Paper II, Eq. (5)) ![\begin{equation} V^\prime_{z,5434} = V_{z,5576}\exp\left[-i\cdot k_z\Delta z + \Delta z/(2H)\right], \label{eq12} \end{equation}](/articles/aa/full_html/2011/08/aa16537-11/aa16537-11-eq128.png) (12)where Vz,5576 is the Fourier transform of the observed velocity field υz,5576(x,y,t) in the 5576 line, and kz is obtained from the dispersion relation.
(12)where Vz,5576 is the Fourier transform of the observed velocity field υz,5576(x,y,t) in the 5576 line, and kz is obtained from the dispersion relation.
 |
Fig. 6 Phase spectrum Z between measured velocities in 5576 and velocities when the former are propagated upward by Δz = 190 km. |
Figure 6 shows the resulting phase spectrum. The noise fluctuations were treated as “waves” and were propagated as well. The phase jumps from +180° to − 180° in the acoustic domain and the many jumps at low frequencies with increasing horizontal wavenumber kh for gravity waves are clearly seen. Comparing this phase spectrum with the one from the observations in Fig. 5, we find good agreement for the evanescent waves and especially for the acoustic waves, up to frequencies of 14 − 15 mHz. We conclude that the assumption of adiabatic linear waves propagating in an isothermal atmosphere is adequate for the purpose of estimating energy fluxes.
 |
Fig. 7 Two examples of phase behaviour of “waves” in the gravity wave domain in bands [4.45 − 5.34 Mm-1; 3.2 − 3.4 mHz]. Dashed and solid: observed waves in 5576 and 5434, respectively; dotted: propagated from 5576 formation height to 5434 formation height according to Eq. (12). |
For gravity waves, the comparison between the phases from the observations and those from the propagation experiment is far from satisfying. We give two examples in Fig. 7 from the FoV where we distilled from small wavenumber and frequency bands of [4.45 − 5.34 Mm-1; 3.2 − 3.4 mHz] the velocity “waves” observed in 5576 and in 5434, and the waves propagated from the 5576 formation level to the 5434 level. Apart from the amplitudes, example a exhibits the behaviour expected for atmospheric gravity waves with upward transport of energy, a phase difference of Δφ = − 48° between the velocities in 5576 and 5434. In example b, little phase difference is measured, if any. Other positions in the FoV even show positive phase differences or differences of 180°.
The power, phase, and coherence spectra in Fig. 5 are noisy at high frequencies and large wavenumbers. Thus, in a next propagation experiment, we included random noise, as well as local random displacements of 2 pixels (~0 34) of the 5576 velocities. With this, the phases also become noisy and the coherences low at high frequencies and large wavenumbers, i.e. at low velocity amplitudes and on small scales. This is still not enough to explain the observed phases in the gravity wave regime. There, apart from some little phase mixing, the phases at small wavenumbers kh < 6−8 Mm-1 remain stable and do not change from those in Fig. 6 (not shown in an additional figure, but see Fig. 9 below).
34) of the 5576 velocities. With this, the phases also become noisy and the coherences low at high frequencies and large wavenumbers, i.e. at low velocity amplitudes and on small scales. This is still not enough to explain the observed phases in the gravity wave regime. There, apart from some little phase mixing, the phases at small wavenumbers kh < 6−8 Mm-1 remain stable and do not change from those in Fig. 6 (not shown in an additional figure, but see Fig. 9 below).
Leaving the effect of magnetic fields aside, we suggest flows from convective overshoot, even at heights of 500−600 km (see e.g. Durrant et al. 1979, their Fig. 8), as the main cause for the disagreement between the phase diagram from observations and the one from the propagation experiment. We show in Fig. 8 the power spectra of the continuum fluctuations and the phase and coherence spectra between continuum data and line minimum velocities for both lines. For the 5576 line, we find phase differences close to zero at small wavenumbers in the gravity wave domain. They gradually increase to ~40° at kh ≈ 12 Mm-1. We speculate that the latter is due to a delay of convective flows into upper layers for small scales. Admittedly however, the convection phenomenon is intricate (e.g., Hirzberger et al. 2001, and references therein). We do not know of recent work based on numerical simulations that explicitly addresses, and explains, the relations between continuum intensities and velocities in high layers and their temporal evolution. For the 5434 line, the picture is even more complex. The phase is negative, ~−30° at low wavenumbers, increases to ~+30° at wavenumbers of approximately 10 Mm-1, and then becomes erratic.
 |
Fig. 8 Results from Fourier analyses of continuum intensity and velocity fluctuations in the 5576 and 5434 lines. Top to bottom: power P in continuum, phase Z between continuum and line minimum velocity fluctuations, coherence C between the two quantities; left column for Fe i 5576, right column for Fe i 5434. |
The coherence between continuum intensity and velocity is high for the 5576 line, C = 0.9 around kh = 4 Mm-1 and ν = 1 mHz. For 5434, the coherence is 0.6 in the same wavenumber/frequency region and decreases towards larger kh and ν.
The continuum-velocity phases and coherences give a hint why, in the gravity wave domain, the phases between the velocities in 5576 and 5434 are so different from the expectation for gravity waves. To simulate the influence of the convective motions proposed here, we performed a further experiment. We subtracted an amount that we attribute to convective motions, from the velocities in the 5576 line, in the Fourier domain, to get V5576 × [1 − C5576(kx,ky,ν)]. Here C5576 denotes the coherence between continuum intensity and line minimum velocity in 5576. These remaining velocities were propagated using Eq. (12) to the level of the 5434 line. The result supposedly mimics the pure gravity waves in 5434. Then we added to this the amount of non-propagated velocities in 5576 due to overshoot motions, i.e. V5576 × C5576(kx,ky,ν). We adopt here zero phase difference of these parts of the signal at the 5576 and 5434 levels, although convective motions may have delays. The important point with this experiment is that the (moduli of) phases of the added signals be much lower than from propagating gravity waves. The simulated signal in 5434 is then V5434,sim = { V5576 × [1 − C5576(kx,ky,ν)] } prop + V5576 × C5576(kx,ky,ν). The subscripts sim and prop denote “simulated” and “propagated”. Finally, noise was included as described above.
The phase and coherence spectra from this experiment are given in Fig. 9. They agree much better with the measurements in Fig. 5 than when neglecting the convective contributions of the flows. Comparison with Fig. 6 demonstrates the expected result that the addition of a signal, which is not propagated in phase from the 5576 forming layer higher up, to the velocities in the 5434 line pulls the phases close to zero, as observed. One must thus be cautious when using measured phases in the gravity wave domain for the determination of phase velocities.
 |
Fig. 9 Phase Z (left panel) and coherence C (right) between line minimum velocities of 5576 and velocities after propagating the former upward by 190 km to 5434 formation height and then adding noise and accounting for coherence with granular convection velocities. See text for details. |
Figure 9 shows a “finger” of negative phases with adjacent phases ~0° at higher frequencies and slightly positive phases at lower frequencies, in the gravity wave domain at wavenumbers 2 − 6 Mm-1 and frequencies of 1 − 2.5 mHz. The finger is the remainder of strongly negative phases and jump to positive phases according to Fig. 6. These are reduced by the addition of motions from the convective overshoot and by the mixing of phases due to noise. Inspection of Fig. 5 also shows this embedded “finger”, but at higher frequencies.
The phase diagrams in Fig. 8 show in addition: 1) for kh ≥ 3 Mm-1, the fundamental f (or p0) mode of the 5-min oscillations exhibits a phase difference of 90° between continuum intensity fluctuations, as proxies for temperature variations, and velocities. This is to be expected from a motion in the evanescent regime with infinite vertical wavelength. But for smaller wavenumbers, the phases tend to lower values. We note that the atmospheric heights of the formation of the continuum fluctuations are not at τ5 = 1, or z = 0 km. The temperature response functions RFT extend over a very wide height range and are low at τ5 = 1, as shown by Kneer et al. (1980) and Pérez Rodríguez & Kneer (2003). They possess contributions from deeper as well as from higher layers. An assessment of a height of formation for a specific atmospheric motion is thus not possible, and interpreting the phase differences in terms of phase velocities is difficult. 2) Remarkably, in the acoustic wave regime, one finds propagating acoustic waves, with increasing phase differences towards increasing frequencies. For 5576, a phase jump from +180° to − 180°occurs at 7.5−8 mHz. For 5434 the jump is at lower frequencies, 6 − 6.5 mHz, which is to be expected since the velocity signals from this line are formed higher than those from 5576. 3) At low wavenumbers and low frequencies near the limiting curve separating the gravity and evanescent wave regimes, the phases become negative, of the order − 60°... −100° in the 5434 line; i.e., the upward velocities come earlier than the intensity increases in continuum.
5.2. Energy fluxes
We now use Eq. (11) to estimate the energy fluxes carried by acoustic waves and by atmospheric gravity waves. We had found good agreement in the acoustic wave domain between the measured phase relations in Fig. 5 and those from propagated waves in Fig. 6. This makes us confident that the application of the linear wave theory of Sect. 4 is adequate for the estimates of the fluxes, although the gravity waves will need special care (see below). The summations with Eq. (11) were carried out up to 18 mHz in frequency for the acoustic fluxes, where the power from the 5434 line has approximately reached the noise level (see Fig. 4). The flux estimates are summarised and compared with the results from other works in Table 1. We discussed above, when describing the observations in Sect. 2, that the rms velocities found in the present analysis are low, by a factor ~1.5 lower than in other studies. We argued that therefore the fluxes may be a factor of 2, or more, too low. Thus we include the flux values multiplied by the factor 2 in the right column of Table 1.
Estimates of energy fluxes in acoustic and atmospheric gravity waves Fac/grav.
5.2.1. Energy flux in acoustic waves
In Papers I and II, we found that more velocity power in short-period waves is measured above IGR than above GR (see also Bello González et al. 2010c). For simplicity and as suggested by Fig. 4b of Paper II for waves with periods >100 s, we adopt here 42% of the power occurring above GR. These cover 45% of the FoV. Then 58% occur above IGR covering 55% of the area. The averages in Table 1 are taken with these relative areas. We add that the fluxes between 15 mHz and 18 mHz amount to 90 W m-2 for both lines and to 180 W m-2 when including the factor of 2, at most.
We note that the acoustic energy fluxes measured from the 5576 line are not much larger than those from 5434. We may speculate that there is little energy dissipation between the two formation heights of 380 km and 570 km, especially for waves with periods U > 100 s. But admittedly, one may also attribute this to the difficulty in determining velocities on small scales with the present data set. Within the limits of accuracy achieved here, the acoustic flux values are in the same range as those found in Paper I for Fe i 5576 at 250 km and in Paper II for Fe i 5434 at 560 km. They are much lower than the acoustic energy flux found by Bello González et al. (2010c), albeit at lower heights, ~200 km, but with much better spatial resolution of 0 15 − 0
15 − 0 18. We also note without showing that, for the flux in acoustic waves, the correction for atmospheric transmission amounts to 25 − 30%.
18. We also note without showing that, for the flux in acoustic waves, the correction for atmospheric transmission amounts to 25 − 30%.
The acoustic flux values in Table 1 were from calculating the fluxes above IGRs and GRs separately and then averaging according to the areas and occurrence of power. In addition, we averaged the IGR and GR densities and transmission functions, both 50/50 as for the fluxes in gravity waves, and re-calculated the acoustic fluxes for both lines. The results differ very little, by 10 W m-2 (20 W m-2 employing the factor of 2), from the average values given in Table 1. We thus expect that averaging over many different GRs and IGRs from the dynamic models would lead to very similar values.
As in Papers I and II, we performed temporal (1D) Fourier transforms of the velocities in the 5576 and 5434 lines (see Fig. 4 above) and calculated the energy fluxes assuming purely vertical propagation. This way of determining the flux is often used (e.g., Fossum & Carlsson 2006) for the reason that acoustic waves tend to propagate vertically. Also, the power spectra from the 3D Fourier transforms of the velocities in Fig. 5 exhibit concentration of power towards low wavenumbers. And, as noted in Paper II, even a purely vertical propagating wave with limited horizontal extent shows power at non-zero horizontal wavenumbers. The results from the temporal Fourier analysis yield flux values 20−30% lower than those from the 3D Fourier analysis. We consider this difference to be within the limits of the accuracy for the present data set.
5.2.2. Energy flux in atmospheric gravity waves
We have seen above that convective flows add to the velocities in the gravity wave domain. We need to eliminate them as much as possible for estimating the energy flux carried by gravity waves. We therefore performed further experiments to quantify, in a general manner, the contributions from different atmospheric velocity signals to the measurements by means of the coherences C. Be V = V(kx,ky,ν), one of the observed signals in Fourier space. A related, similar signal is V′′ = α·V + (1 − α)·N·V, where α with 0 ≤ α ≤ 1 expresses the similarity and N = N(kx,ky,ν) are random numbers with zero average and σ = 1. For α = 0, V and V′′ correspond to completely different signals but with similar amplitudes. Calculating the coherences between V and V′′ with varying α we obtained the empirical relation ![\begin{equation} \alpha = 0.9266-\left[0.8585-C/1.173\right]^{1/2}. \label{eq13} \end{equation}](/articles/aa/full_html/2011/08/aa16537-11/aa16537-11-eq151.png) (13)As a measure of the contribution of the convective flows to the line minimum velocities, we use α5576·V5576 for the 5576 line, where α5576 is calculated from Eq. (13) for the 5576 line with the coherence C between continuum intensity fluctuations and line minimum velocities. We proceed similarly for the flux estimates from the 5434 line. These contributions need to be subtracted before calculating the energy fluxes. We note that these corrections for convective flows reduce the energy fluxes by a factor of 3.5 for 5576 and by a factor of 2 for 5434.
(13)As a measure of the contribution of the convective flows to the line minimum velocities, we use α5576·V5576 for the 5576 line, where α5576 is calculated from Eq. (13) for the 5576 line with the coherence C between continuum intensity fluctuations and line minimum velocities. We proceed similarly for the flux estimates from the 5434 line. These contributions need to be subtracted before calculating the energy fluxes. We note that these corrections for convective flows reduce the energy fluxes by a factor of 3.5 for 5576 and by a factor of 2 for 5434.
Equation (11) for the flux calculation contains two correction factors, 1/MTF and 1/cos2ψ, which both can become very large, >100. For low frequencies and large horizontal wavenumbers, |kz| becomes large and the MTFs decrease to zero. Large inclination angles ψ (with respect to vertical) occur at low frequencies when the vertical component of the group velocity υgr,z is small. We reject contributions with large correction factors, for |kz| > 20, when the MTFs dropped below ~0.01 and for vertical group velocities υgr,z < 0.3 km s-1. We note that limiting the contributions to gravity waves with ψ ≤ 80°, i.e. to particle motions not too close to horizontal, leads to almost the same fluxes as limiting to υgr,z ≥ 0.3 km s-1. We then obtain 4190 W m-2 for the 5576 line and 530 W m-2 for 5434 (without the factor of two, cf. Table 1). We consider it unrealistic to measure, above noise, particle motions more inclined than 80° from LOS observations with rms velocities of ~100 m s-1 in the gravity wave domain.
The various reasons for the limitations come from the data themselves and their handling, as well as from physical considerations, as follows.
-
1.
The concept of MTFs is not well established, so the MTFs used here might overdo the correction.
-
2.
It is difficult to disentangle gravity waves and overshoot motions, and the method applied here is not exact.
-
3.
The power spectra contain residual noise, which would be strongly amplified by large corrections.
-
4.
The time to carry energy from the height of generation of gravity waves, ≤ 100 km according to Mihalas & Toomre (1982), to the heights of velocity signal formation in 5576 and 5434 can be very long since the vertical group velocities can be very low, υgr,z ~ 0.1 km s-1. The radiative damping for these waves is expected to be very large. With an average radiative damping time in the photosphere of ~ 200 s (Mihalas & Toomre 1982, Fig. 3), the energy content of a gravity wave with υgr,z = 0.3 km s-1 is expected to be reduced between the heights of 100 km and ≥ 400 km by a factor of ~150 (Mihalas & Toomre 1982, e.g. case D in their Fig. 10).
-
5.
Mihalas & Toomre (1982) show that one would not expect gravity waves with large |kz| carrying much energy to the chromosphere, again because of strong radiative damping of these waves.
We found that even with these limits, |kz| ≤ 20 Mm-1 and υgr,z ≥ 0.3 km s-1, the correction for atmospheric transmission amounts to a factor of 3.4 for the total energy flux in 5576 and a factor of 2 for the flux in 5434. Figure 10 shows from which locations in the kh − ν plane the contributions to the flux estimates in atmospheric gravity waves stem. Most of the flux occurs at low frequencies. The lower right parts in the images are empty because of the above limitations for kz and υgr,z.
 |
Fig. 10 Contributions to the energy fluxes in atmospheric gravity waves in the kh − ν plane, represented on a logarithmic scale. |
Mihalas & Toomre (1982) have shown that the vertical wavelength is increased by radiative damping, while the vertical group velocity is reduced at the same time. We do not account for these effects of damping since it is either small or not important for the present study because the vertical wavelength is large anyway, or it concerns cases that are marginal, i.e. close to the border of the gravity wave regime, and would somewhat reduce the estimated energy fluxes.
With the above precautions, our estimates of flux carried by gravity waves yield 4100−8200 W m-2 at 380 km and 700−1400 W m-2 at 570 km (cf. Table 1). These values are a factor of 2 (and more, using our lower limits) lower than those given by Straus et al. (2008) in their Fig. 3 for the same heights. At 380 km, the gravity wave flux estimated here is a factor of 2.7 larger than the acoustic flux, and a factor 1.9 smaller at 570 km than the acoustic flux. It is thus obvious that gravity waves are not negligible for mechanical energy transport to the chromosphere. Taking the above fluxes at face value, we find that they contribute with a similar amount as the acoustic waves.
Nevertheless, the fluxes in gravity waves are very uncertain for two reasons. 1) We consider our observed rms velocities on the low side of what has been measured in earlier work. Therefore we admit a factor of 2 for an upward correction of fluxes. 2) The correction factors for atmospheric transmission (MTF) are large, especially for low-frequency waves with large horizontal wavenumber. Without such a correction, the flux values are lower by a factor of 2 to 3.4, as noted above. Even a limitation for vertical group velocities υgr,z ≥ 0.3 km s-1 would then be obsolete, and, in the incompressible limit (as in Straus et al. 2008), the estimates would then yield fluxes of 1420 − 2840 W m-2 at 380 km and 345 − 690 W m-2 at 570 km.
We suggest two reasons for the “agreement” within factors of 2 − 4 with the values given by Straus et al. (2008). On the one hand, these authors overestimate the vertical group velocities by not accounting sufficiently for the strong contribution of convective flows to the velocities in the gravity wave domain. On the other hand, Straus et al. (2008) did not correct for the attenuation of the velocity signals by atmospheric transmission.
6. Conclusions
This study has aimed at estimating the energy transport by acoustic and atmospheric gravity waves in the atmosphere of the quiet Sun. We used a time sequence of 2D spectroscopic observations from disc centre. The two Fe i lines 5576 Å and 5434 Å with Landé factors g = 0 were scanned repeatedly and quasi-simultaneously with the triple etalon spectrometer TESOS (Tritschler et al. 2002) of the Vacuum Tower Telescope at Observatorio del Teide, Tenerife. The resulting rms velocities from the line minimum shifts turned out to be a factor ~1.5 lower than in previous studies, in both the acoustic wave domain and the gravity wave domain. We therefore tentatively multiplied the estimated energy fluxes, which are approximately ∝ 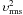 , with a factor of 2 (cf. Table 1 above). We performed 1D (temporal) and 3D Fourier analyses and calculated power, phase, and coherence spectra. They were interpreted, and the fluxes were estimated assuming adiabatic propagation of plane waves in a stratified, isothermal model of the solar atmosphere.
, with a factor of 2 (cf. Table 1 above). We performed 1D (temporal) and 3D Fourier analyses and calculated power, phase, and coherence spectra. They were interpreted, and the fluxes were estimated assuming adiabatic propagation of plane waves in a stratified, isothermal model of the solar atmosphere.
For the acoustic waves we found that above the acoustic cutoff frequency, the phases show upward propagating waves up to frequencies of 14−15 mHz (periods U ≈ 70 s). This does not exclude waves with shorter periods being present in the solar atmosphere. In Papers I and II, we had presented power and flux spectra in the Fe i 5576 and 5434 lines indicating velocity fluctuations, above noise, with periods down to 50 s and shorter. Nonetheless, a proof by means of phase measurements as in the present study is missing that these are propagating acoustic waves.
We peformed a numerical experiment by letting the observed velocities propagate as waves from the 5576 signal forming atmospheric height to that of the 5434 line. A comparison of the resulting phase spectrum (Fig. 6) with the observed phase spectrum (Fig. 5) made us confident that the assumption of linear adiabatic waves in an isothermal atmosphere is accurate enough, within the other uncertainties, to estimate the energy flux carried by acoustic waves.
Within the limits of the above factor of 2, the energy fluxes carried by acoustic waves are similar to those obtained by Bello González et al. (2009, Paper I) and Bello González et al. (2010a, Paper II), and also by Straus et al. (2009): 1530−3060 W m-2 at 380 km and 1330−2660 W m-2 at 570 km.
The study of velocities in the gravity wave domain yielded that atmospheric gravity waves carry energy upward to the chromosphere, which agrees with the finding by Straus et al. (2008, 2009). However, the numerical experiment resulted in very different phase relations from those we measured in the present study and from those measured by Straus et al. (2008, 2009). The reason we suggest for this is that the convective overshoot flows add to the velocities of the gravity waves, up to heights of 400−600 km, and reduce the phase differences expected for gravity waves. The convective and gravity wave velocities are extremely difficult to disentangle. We used the coherences C between continuum intensity fluctuations and velocity fluctuations to estimate the convective velocity contribution (cf. Eq. (13) and text) and subtracted this part from the velocity fields.
Further problems in determining the energy flux in gravity waves arise from the strong corrections for atmospheric transmission of wave signals (or MTF) for waves with large vertical wavenumber |kz| and for waves with very low vertical group velocities. We thus limited the contributions to the energy flux to waves with |kz| ≤ 20 Mm-1 and with υgr,z ≥ 0.3 km s-1. For |kz| > 20 Mm-1, the MTFs become smaller than 0.01 and the correction for foreshortening, 1/cos2ψ in Eq. (11), is of the order of 100 and larger. There are physical justifications for the limitations. Waves with low υgr,z take about a half hour and more to travel from the level of their generation to the line-forming heights and will thus be severely reduced in amplitude by radiative damping. Also, Mihalas & Toomre (1982) conclude from their detailed theoretical study that “gravity waves with large |kz| are unlikely to carry much energy into the chromosphere”.
With these caveats, our flux estimates for atmospheric gravity waves are in the range of 4100−8200 W m-2 at 380 km and 700−1400 W m-2 at 570 km. These values are lower by factors 2 to 4 than those given by Straus et al. (2008) for the same heights.
The assumptions of the linear theory of plane adiabatic waves appears adequate for estimating the acoustic wave flux, and yet the estimate of energy flux carried by gravity waves turns out to be a difficult task. The velocities in the gravity wave regime result from a mixture of waves and convective flows, which are delicate to discriminate. We thus reiterate: we consider it an important further step to guide the interpretation of velocity (and intensity) fluctuations in the solar atmosphere by numerical simulations. It is very likely that the simulations carried out by Straus et al. (2008) allow a better estimate of energy flux to be extracted than from phase differences of velocities determined from shifts of spectral lines. As shown by Mihalas & Toomre (1981), gravity waves manifest themselves in specific phase relations between velocity, temperature, and density fluctuations at identical positions in the atmosphere. Three-dimensional simulations can reveal the production, propagation, and damping/dissipation of gravity and acoustic waves in the solar atmosphere. Such dynamical modelling of the solar atmosphere will also give the opportunity to validate, or refute, or improve, the concept of modulation transfer functions. It was used for the correction of observable signals by, e.g., Straus et al. (2009), in the present study, and in our pevious works. Admittedly, hydrodynamic simulations of waves in the solar atmosphere and calculations of line radiation in dynamic atmospheres, necessarily in NLTE for lines formed at high layers, are difficult tasks, but worth the effort.
Acknowledgments
We acknowledge financial support by the Deutsche Forschungsgemeinschaft through grant Kn 152/32-1 for F.K. and through grant Schm 1168/9 for N.B.G. The Vacuum Tower Telescope is operated by the
Kiepenheuer-Institut für Sonnenphysik, Freiburg, at the Spanish Observatorio del Teide of the Instituto de Astrofísica de Canarias.
References
- Anderson, L. S., & Athay, R. G. 1989, ApJ, 346, 1010 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Nordlund, Å., Trampedach, R., Allen de Prieto, C. A., & Stein, R. F. 2000, A&A, 359, 729 [NASA ADS] [Google Scholar]
- Barthol, P., Gandorfer, A. M., Schüssler, M., et al. 2011, Sol. Phys., 268, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Bello González, N., & Kneer, F. 2008, A&A, 480, 265 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bello González, N., Flores Soriano, M., Kneer, F., & Okunev, O. 2009, A&A, 508, 941 (Paper I) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bello González, N., Flores Soriano, M., Kneer, F., Okunev, O., & Shchukina, N. 2010a, A&A, 522, A31 (Paper II) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bello González, N., Flores Soriano, M., Kneer, F., & Okunev, O. 2010b, in Proc. 25th NSO Workshop, ed. A. Tritschler, K. Reardon, & H. Uitenbroek, Mem. Soc. Astron. Ital., 81, 757 [Google Scholar]
- Bello González, N., Franz, M., Martínez Pillet, V., et al. 2010c, ApJ, 723, L134 [NASA ADS] [CrossRef] [Google Scholar]
- Bray, R. J., & Loughhead, R. E. 1974, The Solar Chromosphere (New York: John Wiley and Sons, Inc.) [Google Scholar]
- Canfield, R. C. 1976, Sol. Phys., 50, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Canfield, R. C., & Mehltretter, J. P. 1973, Sol. Phys., 33, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Carlsson, M., & Stein, R. F. 1995, ApJ, 440, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Carlsson, M., & Stein, R. F. 1997, ApJ, 481, 500 [Google Scholar]
- Deubner, F.-L., & Fleck, B. 1989, A&A, 213, 423 [NASA ADS] [Google Scholar]
- Durrant, C. J., Mattig, W., Nesis, A., Reiss, G., & Schmidt, W. 1979, Sol. Phys., 61, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Edmonds, F. J., Jr., & Webb, C. J. 1972, Sol. Phys., 22, 276 [NASA ADS] [CrossRef] [Google Scholar]
- Eibe, M. T., Mein, P., Roudier, Th., & Faurobert, M. 2001, A&A, 371, 1128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fleck, B., Straus, T., Carlsson, M., et al. 2010, in Proc. 25th NSO Workshop, ed. A. Tritschler, K. Reardon, & H. Uitenbroek, Mem. Soc. Astron. Ital., 81, 777 [Google Scholar]
- Fossum, A., & Carlsson, M. 2006, ApJ, 646, 579 [NASA ADS] [CrossRef] [Google Scholar]
- Handy, B. N., Acton, L. W., Krankelborg, C. C., et al. 1999, Sol. Phys., 187, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Hanslmeier, A., Mattig, W., & Nesis, A. 1991, A&A, 244, 521 [NASA ADS] [Google Scholar]
- Hirzberger, J., Koschinsky, M., Kneer, F., & Ritter, C. 2001, A&A, 367, 1011 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Keil, S. L., & Canfield, R. C. 1978, A&A, 70, 169 [NASA ADS] [Google Scholar]
- Kneer, F., Mattig, W., Nesis, A., & Werner, W. 1980, Sol. Phys., 68, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Komm, R., Mattig, W., & Nesis, A. 1991, A&A, 243, 251 [NASA ADS] [Google Scholar]
- Krijger, J. M., Rutten, R. J., Lites, B. W., et al. 2001, A&A, 379, 1052 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leenaarts, J., Carlsson, M., Hansteen, V., & Gudiksen, B. V. 2011, A&A, 530, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leibacher, J. W., & Stein, R. F. 1981, in the Sun as a Star, ed. S. Jordan, NASA SP-450, 263 [Google Scholar]
- Martínez Pillet, V., del Toro Iniesta, J. C., Álvarez-Herrero, A., et al. 2011, Sol. Phys., 268, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Mihalas, B. W., & Toomre, J. 1981, ApJ, 249, 349 [NASA ADS] [CrossRef] [Google Scholar]
- Mihalas, B. W., & Toomre, J. 1982, ApJ, 263, 386 [NASA ADS] [CrossRef] [Google Scholar]
- Neckel, H. 1999, Sol. Phys., 184, 421 [NASA ADS] [CrossRef] [Google Scholar]
- Pérez Rodríguez, E., & Kneer, F. 2002, A&A, 395, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reardon, K. P., Lepreti, F., Carbone, V., & Vecchio, A. 2008, ApJ, 683, L207 [NASA ADS] [CrossRef] [Google Scholar]
- Rutten, R. J., & Krijger, J. M. 2003, A&A, 407, 735 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scharmer, G. B. 2006, A&A, 447, 1111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scherrer, P. H., Bogart, R. S., Bush, R. I., et al. 1995, Sol. Phys., 162, 129 [Google Scholar]
- Shchukina, N., & Trujillo Bueno, J. 2001, ApJ, 550, 970 [NASA ADS] [CrossRef] [Google Scholar]
- Solanki, S. K., Barthol, P., Danilovic, S., et al. 2010, ApJ, 723, L127 [NASA ADS] [CrossRef] [Google Scholar]
- Souffrin, P. 1966, Ann. Astroph., 29, 55 [NASA ADS] [Google Scholar]
- Staiger, J. 1987, A&A, 175, 263 [NASA ADS] [Google Scholar]
- Stein, R. F., & Leibacher, J. 1974, ARA&A, 12, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Stein, R. F., Bogdan, T. J., Carlsson, M., et al. 2004, in SOHO 13 – Waves, Oscillations and Small-Scale Transient Events in the Solar Atmosphere: A Joint View from SOHO and TRACE, ed. H. Lacoste, ESA SP-457, 93 [Google Scholar]
- Stix, M. 1970, A&A, 4, 189 [NASA ADS] [Google Scholar]
- Straus, T., Fleck, B., Jefferies, S. M., et al. 2008, ApJ, 681, L125 [Google Scholar]
- Straus, T., Fleck, B., Jefferies, S. M., et al. 2009, in The 2nd HINODE Science Meeting, ed. B. Lites, M. Cheung, T. Magara, J. Mariska, & K. Reeves, ASP Conf. Ser., 415, 95 [Google Scholar]
- Tritschler, A., Schmidt, W., Langhans, K., & Kentischer, T. 2002, Sol. Phys., 211, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Tsuneta, S., Ichimoto, K., Katsukawa, Y., et al. 2008, Sol. Phys., 249, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Vernazza, J. E., Avrett, E. H., & Loeser, R. 1981, ApJS, 45, 635 [NASA ADS] [CrossRef] [Google Scholar]
- von der Lühe, O., & Kentischer, T. J. 2000, A&AS, 146, 499 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- von der Lühe, O., Soltau, D., Berkefeld, T., & Schelenz, T. 2003, SPIE, 4853, 187 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Velocity response functions RFυ in intergranules (IGRs) and granules (GRs) for Fe i 5434 (solid curves) and Fe i 5576 (dashed) calculated in NLTE from the IGR and GR models of Asplund et al. (2000) and taking the spectral response of the instrument and of the data acquisition and analysis into account. |
| In the text | |
 |
Fig. 2 Transmissions as functions of vertical wavenumber kz for Fe i 5434 (solid curves) and Fe i 5576 (dashed) calculated in NLTE from the IGR and GR models of Asplund et al. (2000). |
| In the text | |
 |
Fig. 3 Regimes of acoustic, evanescent, and gravity waves in the kh − ν plane. Dashed and dotted lines: locations of surface gravity waves (fundamental f or p0 mode) and purely horizontal acoustic waves (Lamb waves), respectively. |
| In the text | |
 |
Fig. 4 Results of temporal Fourier analysis. Left panel: temporal velocity power spectra Pυ,5576(ν) (dashed) and Pυ,5434(ν) (solid); thin for original power, thick after subtraction of noise level (dotted horizontal lines). Right panel: phases Z (solid) and coherences C (dashed) between the velocities in the 5576 and 5434 lines. |
| In the text | |
 |
Fig. 5 Results of Fourier analysis of the velocities measured in the 5576/5434 line pair. Upper left and right: power spectra P of 5576 and 5434 lines, respectively; lower left: phase Z between the two lines with colour bar, levels in degrees; lower right: coherence C with colour bar. See the online version for the colour representation of the phases. |
| In the text | |
 |
Fig. 6 Phase spectrum Z between measured velocities in 5576 and velocities when the former are propagated upward by Δz = 190 km. |
| In the text | |
 |
Fig. 7 Two examples of phase behaviour of “waves” in the gravity wave domain in bands [4.45 − 5.34 Mm-1; 3.2 − 3.4 mHz]. Dashed and solid: observed waves in 5576 and 5434, respectively; dotted: propagated from 5576 formation height to 5434 formation height according to Eq. (12). |
| In the text | |
 |
Fig. 8 Results from Fourier analyses of continuum intensity and velocity fluctuations in the 5576 and 5434 lines. Top to bottom: power P in continuum, phase Z between continuum and line minimum velocity fluctuations, coherence C between the two quantities; left column for Fe i 5576, right column for Fe i 5434. |
| In the text | |
 |
Fig. 9 Phase Z (left panel) and coherence C (right) between line minimum velocities of 5576 and velocities after propagating the former upward by 190 km to 5434 formation height and then adding noise and accounting for coherence with granular convection velocities. See text for details. |
| In the text | |
 |
Fig. 10 Contributions to the energy fluxes in atmospheric gravity waves in the kh − ν plane, represented on a logarithmic scale. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


