| Issue |
A&A
Volume 532, August 2011
|
|
|---|---|---|
| Article Number | A30 | |
| Number of page(s) | 17 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201016242 | |
| Published online | 18 July 2011 | |
Nonaxisymmetric instabilities of neutron star with toroidal magnetic fields
1
Yukawa Institute for Theoretical Physics, Kyoto University,
Kyoto
606-8502,
Japan
e-mail: kiuchi@yukawa.kyoto-u.ac.jp
2
Astronomical Institute, Tohoku University,
Sendai
980-8578,
Japan
Received:
1
December
2010
Accepted:
23
April
2011
Context.
Aims. Super magnetized neutron stars of ~1015 G, magnetars, and magnetized protoneutron stars born after the magnetically-driven supernovae are likely to have very strong toroidal magnetic fields.
Methods. Long-term, three-dimensional general relativistic magnetohydrodynamic simulations were performed to prepare isentropic neutron stars with toroidal magnetic fields in equilibrium as initial conditions. To explore the effects of rotations on the stability, simulations were done for both nonrotating and rigidly rotating models.
Results. We find the emergence of the Parker and/or Tayler instabilities in both the nonrotating and rotating models. For both nonrotating and rotating models, the Parker instability is the primary instability predicted by the local linear perturbation analysis. The interchange instability also appears in the rotating models. It is found that the Parker instability cannot be suppressed even if the stars rotate rapidly. This finding does not agree with the perturbation analysis, because rigidly and rapidly rotating stars are marginally stable; therefore, in the presence of stellar pulsations that deform the rotational profile, unstable regions develop with a negative gradient of the angular momentum profile. After the onset of the instabilities, a turbulence is excited. In contrast to the axisymmetric case, the magnetic fields never reach a state of equilibrium after the the turbulence develops.
Conclusions. Isentropic neutron stars with strong toroidal magnetic fields are always likely to be unstable against the Parker instability. Turbulent motion is induced and maintained for a long time. This conclusion is different for axisymmetric simulations and suggests that three-dimensional simulation is indispensable for exploring the formation of magnetars or the prominent activities of magnetars such as giant flares.
Key words: stars: neutron / instabilities / magnetohydrodynamics / stars: magnetars
© ESO, 2011
1. Introduction
There is a lot of observational evidence of neutron stars with strong magnetic fields. Observed spin periods and their time derivatives in conjunction with the assumption of a magnetic dipole radiation give us a magnetic field strength as B ∝ (PṖ)1/2 where P and Ṗ are the spin period and its derivative. For radio pulsars, of which more than 1800 are known today (Manchester et al. 2005), the inferred value of the magnetic field strength is in the range 1011−1014 G. For a smaller population of older millisecond pulsars, the typical magnetic field strength is B ~ 108−109 G. For anomalous X-ray pulsars (AXPs) and soft gamma repeaters (SGRs), super strong magnetic fields of 1014−1015 G are again inferred from the measured values of P and Ṗ (Woods & Thompson 2004). Various observed properties of AXPs and SGRs, such as the giant flares from the three SGRs and bursts are often explained by a super strong magnetic field (Thompson & Duncan 1995, 1996, 2001) rather than by rotation, because their spin down luminosities are much lower than the observed luminosity. In addition, temporary detections of spectral lines during SGR/AXP bursts have been reported in several systems (Gavriil et al. 2002; Ibrahim et al. 2003; Rea et al. 2003). If we assume that they are associated with proton cyclotron lines, the magnetic field strength is estimated to give B ~ 1015 G.
For about a dozen accreting X-ray pulsars in binary systems, electron cyclotron line features have been detected, suggesting that B ~ 1012−1013 G according to the formula for the electron cyclotron energy, Ece = ħB/(mec) = 11.58(B/1012 G) keV (Orlandini & Fiume 2001). For many other X-ray pulsars with no detectable electron cyclotron line features, typical magnetic fields are B ~ 1012 G if one assumes that spin up due to accretion of matter is balanced by magnetic braking (Bildsten et al. 1997).
From a theoretical point of view, these strongly magnetized objects deserve detailed study,
because their magnetic fields sometimes exceed the quantum critical field strength,
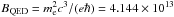 G, at which gyration
radius of the electron pc/(eB) is
shorter than the de Broglie wavelength ħ/p. Above this
limit, magnetic fields affect the properties of atoms, molecules, condensed matters (Lai 2001), propagation of photons, radiative processes,
equation of states, and thermal conductivity in crusts (see Harding & Lai 2006 and references therein). The origin of such extremely
large magnetic fields has been a major concern since their discovery. Specifically, there
are two hypotheses for its origin. In one scenario, the magnetic fields are assumed to be
generated in a rapidly rotating protoneutron star formed after stellar core collapse of a
massive star (Thompson & Duncan 1993), and in
the other it is assumed to be descended from the main sequence stars; i.e., the strong
magnetic field is assumed to be a fossil of a strongly magnetized main sequence star (Wickramasinghe & Ferrario 2005). For exploring
the magnetar formation, there are plenty of magnetohydrodynamic simulations for supernova
core collapse both in Newtonian gravity (Yamada &
Sawai 2004; Kotake et al. 2004; Obergaulinger et al. 2006; Scheidegger et al. 2008; Takiwaki et al.
2009; Burrows et al. 2007) and in general
relativity (Shibata et al. 2006; Cerda-Duran et al. 2007). For these works, the
simulations were performed in axisymmetric spacetime. In most of these simulations, it was
found that toroidal magnetic fields are dominantly enhanced in the protoneutron stars after
the core bounce by the magnetic winding mechanism, and eventually, the protoneutron star
settles to a quasi-equilibrium state. However, it has been well known that purely toroidal
fields in equilibria are often unstable because of the interchange, Tayler, and Parker
instabilities (Acheson 1978; Goossens 1980; Parker 1955, 1966; Tayler
1973). The stability analyses have suggested that nonaxisymmetric modes would play an
essential role for these instabilities and that rapid rotation could suppress these
instabilities (Acheson 1978)1.
G, at which gyration
radius of the electron pc/(eB) is
shorter than the de Broglie wavelength ħ/p. Above this
limit, magnetic fields affect the properties of atoms, molecules, condensed matters (Lai 2001), propagation of photons, radiative processes,
equation of states, and thermal conductivity in crusts (see Harding & Lai 2006 and references therein). The origin of such extremely
large magnetic fields has been a major concern since their discovery. Specifically, there
are two hypotheses for its origin. In one scenario, the magnetic fields are assumed to be
generated in a rapidly rotating protoneutron star formed after stellar core collapse of a
massive star (Thompson & Duncan 1993), and in
the other it is assumed to be descended from the main sequence stars; i.e., the strong
magnetic field is assumed to be a fossil of a strongly magnetized main sequence star (Wickramasinghe & Ferrario 2005). For exploring
the magnetar formation, there are plenty of magnetohydrodynamic simulations for supernova
core collapse both in Newtonian gravity (Yamada &
Sawai 2004; Kotake et al. 2004; Obergaulinger et al. 2006; Scheidegger et al. 2008; Takiwaki et al.
2009; Burrows et al. 2007) and in general
relativity (Shibata et al. 2006; Cerda-Duran et al. 2007). For these works, the
simulations were performed in axisymmetric spacetime. In most of these simulations, it was
found that toroidal magnetic fields are dominantly enhanced in the protoneutron stars after
the core bounce by the magnetic winding mechanism, and eventually, the protoneutron star
settles to a quasi-equilibrium state. However, it has been well known that purely toroidal
fields in equilibria are often unstable because of the interchange, Tayler, and Parker
instabilities (Acheson 1978; Goossens 1980; Parker 1955, 1966; Tayler
1973). The stability analyses have suggested that nonaxisymmetric modes would play an
essential role for these instabilities and that rapid rotation could suppress these
instabilities (Acheson 1978)1.
Motivated by this situation, we studied the axisymmetric instability of neutron stars with toroidal magnetic fields in the previous work (Kiuchi et al. 2008). In that work, magnetized neutron stars in equilibria are prepared as initial conditions by varying its profile and strength and by changing the angular velocity (Kiuchi & Yoshida 2008). Performing the general relativistic magnetohydrodynamic (GRMHD) simulations, we found that slowly rotating neutron stars with the toroidal fields are unstable if they posses magnetic fields whose profile is proportional to the power of cylindrical radius ϖ as B(ϕ) ∝ ϖ2k − 1 with k ≥ 2. The growth timescale is similar to the Alfvén timescale, and its instability type is the interchange instability in the absence of stellar rotation. Only for the case k = 1, slowly rotating neutron stars are stable against the axisymmetric perturbation, so we concluded that the configuration with k = 1 will be the attractor for the unstable neutron stars. We also found that rapid rotation, with which the rotational kinetic energy is much greater than the magnetic energy, suppresses the onset of the interchange instability and stabilizes the neutron stars. These results qualitatively and semi-quantitatively agree with the local linear analysis.
In the magnetorotational explosion scenarios, the magnetic energy is composed primarily of the toroidal field and is at most as high as the rotational kinetic energy. This indicates that the axisymmetric interchange instability would not play an important role in the protoneutron star. However, it is still possible that the neutron star becomes unstable against the Parker and Tayler instabilities, which grow in a nonaxisymmetric way. Stability of magnetars is also an important question along this line (Braithwaite & Nordlund 2005; Braithwaite & Spruit 2004). The rotational effect is negligible for the magnetar. Thus, the toroidal field profile should be similar to that of k = 1 to avoid any onset of the axisymmetric interchange instability. However, such a configuration may still be unstable if the Parker and/or Tayler instabilities are taken into account.
This situation motivated us to extend our previous work (Kiuchi et al. 2008) by exploring the nonaxisymmetric instabilities of neutron stars with toroidal magnetic fields. Following our previous work, we prepared equilibrium neutron stars with purely toroidal magnetic fields as initial conditions. This time, we performed three-dimensional GRMHD simulations by varying the field strength and/or rotation velocity. As mentioned above, the three-dimensional simulation is requested for exploring the Parker and Tayler instabilities.
This paper is organized as follows. In Sect. 2, we briefly review the formulation and numerical methods employed in our numerical-relativity simulation. The set up of numerical simulation and initial models for our GRMHD simulations are described in Sect. 3. In Sect. 4, we present the results of a local linear perturbation analysis as a forecast of the numerical-simulation results. Section 5 is devoted to presenting these results. A summary and discussion are given in Sect. 6.
Throughout this paper, we adopt the geometrical units in which
c = G = 1 with c the speed of light and
G the gravitational constant. Cartesian coordinates are denoted by
xk = (x,y,z). The
coordinates are oriented so that the rotation axis is along the
z-direction. We define the coordinate radius
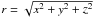 ,
cylindrical radius
,
cylindrical radius 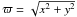 ,
and azimuthal angle
ϕ = tan-1(y/x).
Coordinate time is denoted by t. Greek indices
μ,ν,... denote spacetime components, and small latin
indices i,j,... denote spatial components.
,
and azimuthal angle
ϕ = tan-1(y/x).
Coordinate time is denoted by t. Greek indices
μ,ν,... denote spacetime components, and small latin
indices i,j,... denote spatial components.
2. Formulation and method
The stability of magnetized neutron stars were studied by three-dimensional GRMHD simulation assuming that the ideal MHD condition holds. In this paper we focus on the Parker and/or Tayler instabilities. We upgraded our axisymmetric GRMHD numerical code in Shibata & Sekiguchi (2005) and Kiuchi et al. (2008) to one for three dimensions.
The formulation and the numerical scheme for solving Einstein’s equation are essentially
the same as in Shibata & Nakamura (1995). For
solving Einstein’s evolution equation, we used the original version of the
Baumgarte-Shapiro-Shibata-Nakamura formulation (Shibata
& Nakamura 1995; Baumgarte & Shapiro
1999). We evolved the inverse square of the conformal factor
W ≡ exp(−2φ) with
φ = ln(γ)/12, the trace part of the
extrinsic curvature, K, the conformal three-metric,
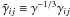 , the tracefree
extrinsic curvature,
, the tracefree
extrinsic curvature, 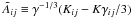 , and a three-auxiliary variable,
, and a three-auxiliary variable,
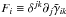 .
Here, γij is the three-metric,
Kij the extrinsic curvature,
γ ≡ det(γij), and
K ≡ Kijγij.
We evolve W, not the conformal factor as in Kiuchi et al. (2009), because our code is designed to simulate black hole
spacetimes with the moving puncture method (Baker et al.
2006; Campanelli et al. 2006; Brugmann et al. 2008). For the conditions of the lapse,
α, and the shift vector, βi,
we adopt a dynamical gauge condition in the following forms (Shibata 2003),
.
Here, γij is the three-metric,
Kij the extrinsic curvature,
γ ≡ det(γij), and
K ≡ Kijγij.
We evolve W, not the conformal factor as in Kiuchi et al. (2009), because our code is designed to simulate black hole
spacetimes with the moving puncture method (Baker et al.
2006; Campanelli et al. 2006; Brugmann et al. 2008). For the conditions of the lapse,
α, and the shift vector, βi,
we adopt a dynamical gauge condition in the following forms (Shibata 2003), 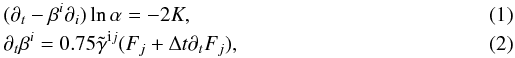 where
Δt denotes the time step in the numerical simulations, and the second
term on the righthand side of (1) is
introduced for stabilizing the numerical computations. The finite-differencing schemes for
solving Einstein’s equation is essentially the same as those in Kiuchi et al. (2009). We use the fourth-order finite-differencing scheme
in the spatial direction and a fourth-order Runge-Kutta scheme in the time integration,
where the advection terms such as
βi∂iW
are evaluated by a fourth-order uncentered difference scheme, as proposed, e.g., in Brugmann et al. (2008).
where
Δt denotes the time step in the numerical simulations, and the second
term on the righthand side of (1) is
introduced for stabilizing the numerical computations. The finite-differencing schemes for
solving Einstein’s equation is essentially the same as those in Kiuchi et al. (2009). We use the fourth-order finite-differencing scheme
in the spatial direction and a fourth-order Runge-Kutta scheme in the time integration,
where the advection terms such as
βi∂iW
are evaluated by a fourth-order uncentered difference scheme, as proposed, e.g., in Brugmann et al. (2008).
List of characteristic quantities for neutron stars with toroidal magnetic fields.
A conservative shock-capturing scheme was employed to integrate the GRMHD equations. Specifically we used a high-resolution central scheme (Kurganov & Tadmor 2000; Lucas-Serrano et al. 2004) with the third-order piece-wise parabolic interpolation and with a steep min-mod limiter in which the limiter parameter b is set to be 2.5 (see Appendix A of Shibata 2003).
Magnetized neutron stars in equilibrium, employed as the initial condition, were computed
to give the polytropic equation of state (Kiuchi &
Yoshida 2008), 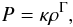 (3)where
P, ρ, κ, and Γ are the pressure,
rest-mass density, polytropic constant, and adiabatic constant, respectively. In this work,
we choose Γ = 2. Because κ is arbitrarily chosen, we adopt the units of
κ = 1 in the following (i.e., the polytropic units of
c = G = κ = 1 are employed). In the numerical simulation, we adopt the
Γ-law equation of state as
(3)where
P, ρ, κ, and Γ are the pressure,
rest-mass density, polytropic constant, and adiabatic constant, respectively. In this work,
we choose Γ = 2. Because κ is arbitrarily chosen, we adopt the units of
κ = 1 in the following (i.e., the polytropic units of
c = G = κ = 1 are employed). In the numerical simulation, we adopt the
Γ-law equation of state as 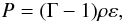 (4)where
ε is the specific internal thermal energy.
(4)where
ε is the specific internal thermal energy.
We monitored the total baryon rest mass Mb,
Arnowitt-Deser-Misner (ADM) mass M, internal energy
Uint, rotational kinetic energy
Trot, total kinetic energy Tkin,
and magnetic energy Hmag, defined by ![\begin{eqnarray} && M_{\rm b} = \int \rho w \sqrt{\gamma} {\rm d}^3x\\ && M = \int {\rm e}^{-\phi}\Big[ \rho h w^2 - P +\frac{1}{16\pi}\{ K_{ij}K^{\it ij}- K^2 - \tilde{R} {\rm e}^{-4\phi} \}\Big]\sqrt{\gamma}{\rm d}^3x\\ \label{eq:int} && U_{\rm int}=\int \rho w \varepsilon \sqrt{\gamma} {\rm d}^3x \\ && T_{\rm rot}=\frac{1}{2}\int \rho h w u_\varphi \Omega \sqrt{\gamma} {\rm d}^3x\\ && T_{\rm kin}=\frac{1}{2}\int \rho h w u_iv^i \sqrt{\gamma}{\rm d}^3x\\ && H_{\rm mag}=\frac{1}{8\pi}\int b^2 w \sqrt{\gamma}{\rm d}^3x \end{eqnarray}](/articles/aa/full_html/2011/08/aa16242-10/aa16242-10-eq81.png) where
where
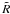 is
the Ricci scalar with respect to
is
the Ricci scalar with respect to 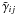 ,
uμ the four velocity of the fluid,
h the specific enthalpy defined by
1 + ε + P/ρ,
w ≡ αut,
vi = ui/ut,
Ω = vϕ, and
b2 = bμbμ.
Here, bμ is the magnetic field observed in the
frame co-moving with the fluid element and M0 denotes the
initial value of the ADM mass. Once each energy component was obtained, we defined the
gravitational potential energy by
,
uμ the four velocity of the fluid,
h the specific enthalpy defined by
1 + ε + P/ρ,
w ≡ αut,
vi = ui/ut,
Ω = vϕ, and
b2 = bμbμ.
Here, bμ is the magnetic field observed in the
frame co-moving with the fluid element and M0 denotes the
initial value of the ADM mass. Once each energy component was obtained, we defined the
gravitational potential energy by 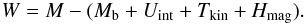 (11)Following
Kiuchi et al. (2008), we define an averaged Alfvén
timescale as
(11)Following
Kiuchi et al. (2008), we define an averaged Alfvén
timescale as 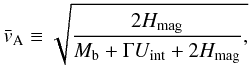 (12)where
we use the relation h = 1 + Γε, which holds in the Γ-law
equation of state. The Alfvén velocity in relativity is given by
(12)where
we use the relation h = 1 + Γε, which holds in the Γ-law
equation of state. The Alfvén velocity in relativity is given by
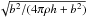 .
Then, we define the averaged Alfvén timescale as
.
Then, we define the averaged Alfvén timescale as
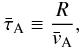 (13)where
R is the equatorial stellar radius. Because the magnetic field
instability grows on the order of the Alfvén timescale (cf. Sect. 4),
(13)where
R is the equatorial stellar radius. Because the magnetic field
instability grows on the order of the Alfvén timescale (cf. Sect. 4), 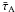 is useful to judge whether or not the instability found in numerical simulation is
associated with a magnetic field effect.
is useful to judge whether or not the instability found in numerical simulation is
associated with a magnetic field effect.
3. Model and numerical setup
3.1. Initial condition
Neutron stars with toroidal magnetic fields in equilibrium, when employed as initial
conditions, are computed by the code described in Kiuchi
& Yoshida (2008). Several key quantities characterizing these magnetized
neutron stars are listed in Table 1. The
instability associated with the presence of toroidal magnetic fields depends on the
profile of the magnetic field as shown by Acheson
(1978), Goossens (1980), Spruit (1999), and Tayler (1973). We assume the toroidal magnetic field profile confined inside the
neutron star is given by 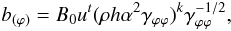 (14)where
k and B0 are constants that determine the
field profile and strength, respectively. The regularity condition of magnetic fields near
the axis of ϖ = 0 requires k ≥ 1. Because of
γϕϕ ∝ ϖ2 for
ϖ → 0, the toroidal magnetic field is proportional to
ϖ2k − 1 near the axis. Previous works
predict that the profile with k ≥ 2 is unstable against axisymmetric
perturbations (Acheson 1978; Goossens 1980; Spruit 1999;
Tayler 1973), and we confirmed this prediction in
the previous paper (Kiuchi et al. 2008). On the
other hand, the profile of k = 1 is stable against axisymmetric
perturbations but may be unstable against nonaxisymmetric ones (see also Lander et al. 2010; Lander & Jones 2011), so in this paper, we focus on the profile of
k = 1.
(14)where
k and B0 are constants that determine the
field profile and strength, respectively. The regularity condition of magnetic fields near
the axis of ϖ = 0 requires k ≥ 1. Because of
γϕϕ ∝ ϖ2 for
ϖ → 0, the toroidal magnetic field is proportional to
ϖ2k − 1 near the axis. Previous works
predict that the profile with k ≥ 2 is unstable against axisymmetric
perturbations (Acheson 1978; Goossens 1980; Spruit 1999;
Tayler 1973), and we confirmed this prediction in
the previous paper (Kiuchi et al. 2008). On the
other hand, the profile of k = 1 is stable against axisymmetric
perturbations but may be unstable against nonaxisymmetric ones (see also Lander et al. 2010; Lander & Jones 2011), so in this paper, we focus on the profile of
k = 1.
Magnetic field strength, B0, is chosen so as to satisfy 8 × 10-3 ≤ H/|W| ≤ 5 × 10-2. These values imply a field strength of 1016−1017 G for a typical neutron star of mass 1.4 M⊙, radius 10 km, and |W| ~ 6 × 1053 erg. These magnetic field strengths are extremely large even for magnetar models and might be less realistic. We give such strong magnetic fields here simply to save the computational costs. The growth timescales of the instabilities caused by the toroidal magnetic field are close to an Alfvén time scale, which is still much longer than the dynamical timescale of the system in the present set up. Thus, a scaling relation should hold for a weaker magnetic field strength. We may apply the scaling relation to derive a generic physical essence from the results obtained in the present set up. Namely, if the magnetic field strength is halved, the growth timescale of the instabilities becomes approximately twice longer, although the qualitative properties of the evolution of the unstable neutron star are essentially the same.
The initial conditions for the nonrotating model is specified if the central density ρc (in the polytropic units) is determined. We choose it to be ρc ≈ 0.22. With this choice, the neutron star has a realistic compactness; e.g., if we assume M ≈ 1.35 M⊙, circumferential radius is R ≈ 11 km (cf. Table 1). The maximum rest mass and gravitational mass of the spherical neutron star for Γ = 2 are 0.1799 and 0.1637, respectively, and the corresponding central density is ≈ 0.318 in our unit.
Simulations were also performed for rotating neutron star models. In this paper, we focus only on rigidly rotating neutron stars with a moderate compactness and ρc is again chosen to be 0.22. For the neutron stars with the Γ = 2 polytrope, the maximum values of Trot/|W| is ~0.09 for M0/Rcir ~ 0.1 (Cook et al. 1994). Local linear stability analysis predicts that rapid rotations will suppress the growth of some of the instabilities associated with the presence of toroidal magnetic fields (Acheson 1978, see also Sect. 4.2). To study whether this is indeed the case, we prepared rapidly rotating models with Trot/|W| ≈ 0.08, and varied the magnetic field strength.
3.2. Grid settings
The simulations were performed on the cell-centered Cartesian, (x,y,z),
grid. Equatorial plane symmetry with respect to z = 0 plane was assumed.
The computational domain of
−L ≤ x ≤ L,
−L ≤ y ≤ L, and
0 ≤ z ≤ L was covered by the grid size
(2N,2N,N) for (x,y,z), where
L and N are constants. Following Kiuchi et al. (2008), we adopted a nonuniform grid as follows. An inner
domain is covered with an uniform grid of spacing Δx and with the grid
size,
(2N0,2N0,N0).
Outside this inner domain, the grid spacing was increased according to the relation,
ξtanh [(i − N0)/Δi] Δx,
where i denotes the ith grid point in each positive
direction, and N0, Δi, and ξ
are constants. Then, the location of ith grid,
xk(i)
(i ≥ 0), for each direction is
![\begin{eqnarray} x^k(i)=\left\{ \begin{array}{ll} (i+1/2)\Delta x & i \leq N_0 \\ (i+1/2)\Delta x + \xi \Delta i \Delta x \log [ \cosh \{(i-N_0)/\Delta i \}] & i > N_0\\ \end{array} \right. \end{eqnarray}](/articles/aa/full_html/2011/08/aa16242-10/aa16242-10-eq140.png) (15)and
xk(−i − 1) = −xk(i),
where
i = 0,1,...N − 1
for xk = x,y, and
z. The chosen parameters of the grid structure for each simulation are
listed in Table 2. To check the validity of our
numerical results, the simulations for models N22H5 and R22H2T8 were performed with three
different grid resolutions. With the highest (lowest) resolution, the coordinate
equatorial radii of neutron stars, LNS, are covered by 130
(80) grid points while the outer boundary location was chosen to be
≃ 8LNS in all the simulations. We confirmed that the modest
resolution in which LNS is covered by 100 grid points is high
enough to draw a resolution-invariant conclusion.
(15)and
xk(−i − 1) = −xk(i),
where
i = 0,1,...N − 1
for xk = x,y, and
z. The chosen parameters of the grid structure for each simulation are
listed in Table 2. To check the validity of our
numerical results, the simulations for models N22H5 and R22H2T8 were performed with three
different grid resolutions. With the highest (lowest) resolution, the coordinate
equatorial radii of neutron stars, LNS, are covered by 130
(80) grid points while the outer boundary location was chosen to be
≃ 8LNS in all the simulations. We confirmed that the modest
resolution in which LNS is covered by 100 grid points is high
enough to draw a resolution-invariant conclusion.
Parameters for the grid structure employed in the numerical simulation.
4. Local linear perturbation analysis
Before showing the results of nonlinear numerical simulations, it is useful to recall the results of linear-stability analysis. By using the local linear perturbation analysis (Acheson 1978), the dispersion relations for the nonrotating and rotating models are derived, and the (local) stability is determined. In the following, the method of the analysis in the Newtonian framework is briefly reviewed.
In the local analysis, a perturbation quantity δQ is assumed to be given
by ![\begin{eqnarray} \delta Q=Q_0 \exp[{\rm i}(l\varpi+m\varphi+nz-\sigma t)], \end{eqnarray}](/articles/aa/full_html/2011/08/aa16242-10/aa16242-10-eq153.png) (16)where
Q0 is a constant, σ the oscillation
frequency, and (l,m,n) the wave number vector. To obtain the local
dispersion relations, we assume that l ≫ 1, n ≫ 1, and
m = O(1), which implies that the perturbations we
consider have very short wavelengths on the meridional plane (for details, cf. Acheson 1978).
(16)where
Q0 is a constant, σ the oscillation
frequency, and (l,m,n) the wave number vector. To obtain the local
dispersion relations, we assume that l ≫ 1, n ≫ 1, and
m = O(1), which implies that the perturbations we
consider have very short wavelengths on the meridional plane (for details, cf. Acheson 1978).
 |
Fig. 1 The growth rate of the instability of a neutron star with toroidal magnetic fields normalized by the maximum growth rate |σmax| (left) and corresponding m mode (right) on the meridian plane for nonrotating Newtonian polytrope with ρ0 = 0.16 and B0 = 0.2. The white colored region and the dotted curve denote the stable region and critical radius, respectively, and rs denotes the stellar radius. |
4.1. Nonrotating case
The dispersion relation for nonrotating models is given, irrespective of the density
profile, by ![\begin{eqnarray} \label{Eq:Disperse} &&\left(1+\frac{l^2}{n^2}\right)\left(1+\frac{v_{\rm A}^2}{c_{\rm s}^2}\right) \sigma^4 \nonumber\\ &&+\left[ v_{\rm A}^2\left(\frac{2}{\varpi}-\frac{\hat{G}}{c_{\rm s}^2}\right)\partial_h \ln\left(\frac{B_{(\varphi)}}{\rho\varpi}\right) -\left(1+\frac{l^2}{n^2}\right)m^2\sigma_{\rm A}^2\left(2+\frac{v_{\rm A}^2}{c_{\rm s}^2}\right) \right]\sigma^2 \nonumber\\ &&+\left(1+\frac{l^2}{n^2}\right)m^4 \sigma_{\rm A}^2 + m^2\sigma_{\rm A}^4 \varpi^2 \left(\frac{\hat{G}}{c_{\rm s}^2}-\frac{2}{\varpi}\right)\partial_h \ln(B_{(\varphi)}\varpi)=0 \end{eqnarray}](/articles/aa/full_html/2011/08/aa16242-10/aa16242-10-eq165.png) (17)where
(17)where
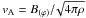 ,
σA = vA/ϖ,
Ĝ = gϖ − (l/n)gz
with gϖ and
gz the gravitational acceleration,
∂h = ∂ϖ − (l/n)∂z,
and cs is the sound speed. For the axisymmetric perturbation,
i.e., m = 0 perturbations, the dispersion relation is reduced to a
quadratic form of σ as
,
σA = vA/ϖ,
Ĝ = gϖ − (l/n)gz
with gϖ and
gz the gravitational acceleration,
∂h = ∂ϖ − (l/n)∂z,
and cs is the sound speed. For the axisymmetric perturbation,
i.e., m = 0 perturbations, the dispersion relation is reduced to a
quadratic form of σ as
![\begin{eqnarray} \left(1+\frac{l^2}{n^2}\right)\left(1+\frac{v_{\rm A}^2}{c_{\rm s}^2}\right)\sigma^2 +\left[ v_{\rm A}^2\left(\frac{2}{\varpi}-\frac{\hat{G}}{c_{\rm s}^2}\right)\partial_h \ln\left(\frac{B_{(\varphi)}}{\rho\varpi}\right) \right]=0. \end{eqnarray}](/articles/aa/full_html/2011/08/aa16242-10/aa16242-10-eq174.png) (18)For
the density profile that is necessary for solving Eq. (17) for a specific model, we prepare the Newtonian spherical polytrope
with Γ = 2 as
(18)For
the density profile that is necessary for solving Eq. (17) for a specific model, we prepare the Newtonian spherical polytrope
with Γ = 2 as 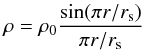 (19)where
ρ0 and rs are the central
density and stellar radius. The spherical density profile is justified by the assumption
of a weak magnetic field; i.e., the magnetic field is too weak to deform the star. In the
Newtonian limit, Eq. (14) becomes
(19)where
ρ0 and rs are the central
density and stellar radius. The spherical density profile is justified by the assumption
of a weak magnetic field; i.e., the magnetic field is too weak to deform the star. In the
Newtonian limit, Eq. (14) becomes
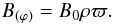 (20)Because
B(ϕ)/ρϖ = const.
in our models (see Eqs. (19) and (20)), we have σ = 0 for
m = 0; i.e., the magnetic field is marginally stable against the
axisymmetric perturbation. Physically, the magnetic field instability caused by the
axisymmetric perturbation is classified as the interchange instability. Our models are
marginally stable against such an instability and we indeed found in the previous study
that they were stable (Kiuchi et al. 2008).
However, the marginally stable profile is not always kept in a stationary state in the
presence of a perturbation. We return to this point in Sect. 5.2.
(20)Because
B(ϕ)/ρϖ = const.
in our models (see Eqs. (19) and (20)), we have σ = 0 for
m = 0; i.e., the magnetic field is marginally stable against the
axisymmetric perturbation. Physically, the magnetic field instability caused by the
axisymmetric perturbation is classified as the interchange instability. Our models are
marginally stable against such an instability and we indeed found in the previous study
that they were stable (Kiuchi et al. 2008).
However, the marginally stable profile is not always kept in a stationary state in the
presence of a perturbation. We return to this point in Sect. 5.2.
For nonaxisymmetric perturbations, we forecast that the Parker (1955; 1966) and the Tayler
(1973) instabilities set in. Following Acheson (1978), we define the critical radius as
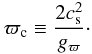 (21)Outside
this critical radius, the magnetic buoyant force exceeds the magnetic hoop stress, whereas
inside it, the magnetic stress is dominant. The Tayler instability could set in near the
axis of ϖ = 0 (Spruit 1999), which
is inside the critical radius. On the other hand, the Parker instability could play a role
in places where the magnetic buoyancy force surpasses the magnetic tension. Thus, we
classify the instability that emerges inside and outside the critical radius as the Tayler
and Parker instabilities, respectively. Analyzing the dispersion relation near the axis of
ϖ = 0, Acheson (1978) and Spruit (1999) concluded that the dominant modes of the
Tayler instability are m = 1 and
l/n ≈ 0 modes, which are associated
with the horizontal motion near the axis of ϖ = 0. However, to clarify
the most relevant unstable modes, we have to determine the growth timescales of the
instability for all the places inside the star. To do this, we calculate the maximum
growth rates of the instability solving the dispersion relation (17) with varying
l/n and m.
(21)Outside
this critical radius, the magnetic buoyant force exceeds the magnetic hoop stress, whereas
inside it, the magnetic stress is dominant. The Tayler instability could set in near the
axis of ϖ = 0 (Spruit 1999), which
is inside the critical radius. On the other hand, the Parker instability could play a role
in places where the magnetic buoyancy force surpasses the magnetic tension. Thus, we
classify the instability that emerges inside and outside the critical radius as the Tayler
and Parker instabilities, respectively. Analyzing the dispersion relation near the axis of
ϖ = 0, Acheson (1978) and Spruit (1999) concluded that the dominant modes of the
Tayler instability are m = 1 and
l/n ≈ 0 modes, which are associated
with the horizontal motion near the axis of ϖ = 0. However, to clarify
the most relevant unstable modes, we have to determine the growth timescales of the
instability for all the places inside the star. To do this, we calculate the maximum
growth rates of the instability solving the dispersion relation (17) with varying
l/n and m.
Figure 1 displays the contours of the growth rate for the model with ρ0 = 0.16 and B0 = 0.2, which give Hmag/|W| = 2.5% and Mb = 0.2 in the polytropic units. These parameters are chosen so as to mimic the initial models shown in Table 1. The most unstable mode at each point is the l/n = 0 mode. This figure shows that the fastest growing mode of the instability is located near the stellar surface and is determined by the Parker instability, because the location is outside the critical radius. The right panel of Fig. 1 shows that instead of the m = 1 mode, a high-order m mode is relevant for this fastest growing mode. The local linear perturbation analysis predicts that the Parker instability primarily emerges near the stellar surface in our nonrotating models.
 |
Fig. 2 The evolution of a) central rest-mass density ρc and b) minimum value of lapse function αmin for nonrotating models N22H1 and N22H5. |
 |
Fig. 3 The evolution of rest-mass density (left) and magnetic energy density (right) on the equator for N22H5. Both of them are plotted on the logarithmic scale. The coordinate time at each slice is shown in each panel. |
 |
Fig. 4 The evolution of the rest-mass density (bottom) and magnetic energy density (top) on a meridian (x-z) plane for N22H5 on the logarithmic scale. The arrows indicate the velocity fields. |
4.2. Rotating case
For the rotating models, the dispersion relation is written as ![\begin{eqnarray} &&\left(1+\frac{l^2}{n^2}\right)\left(1+\frac{v_{\rm A}^2}{c_{\rm s}^2}\right) \omega^4 +\Bigg[v_{\rm A}^2\partial_h \ln\left(\frac{B_{(\varphi)}}{\rho\varpi}\right)\left(\frac{2}{\varpi} -\frac{\hat{G}}{c_{\rm s}^2}\right) \nonumber\\ &&-\left(1+\frac{l^2}{n^2}\right)m^2\sigma_{\rm A}^2 \left(2+\frac{v_{\rm A}^2}{c_{\rm s}^2}\right) -\frac{2\Omega}{\varpi}\partial_h(\Omega \varpi^2)\left(1+\frac{v_{\rm A}^2}{c_{\rm s}^2}\right) \Bigg] \omega^2 \nonumber\\ && -\frac{4\Omega m v_{\rm A}^2}{\varpi}\left(\frac{2}{\varpi}-\frac{\hat{G}}{c_{\rm s}^2}\right) \omega +m^2\sigma_{\rm A}^2 \Bigg[ 2\varpi\Omega\partial_h \Omega+ \left(1+\frac{l^2}{n^2}\right)m^2\sigma_{\rm A}^2 \nonumber\\ \label{Eq:Disperse2}&& - \left(\frac{2}{\varpi}-\frac{\hat{G}}{c_{\rm s}^2}\right) \partial_h \ln(B_{(\varphi)} \varpi) v_{\rm A}^2 \Bigg]=0, \end{eqnarray}](/articles/aa/full_html/2011/08/aa16242-10/aa16242-10-eq189.png) (22)where
ω = σ − mΩ with Ω the angular
velocity. Following Acheson (1978), we focus on a
low-frequency and nonaxisymmetric mode, for which the growth timescale is much longer than
the Alfvén timescale as
(22)where
ω = σ − mΩ with Ω the angular
velocity. Following Acheson (1978), we focus on a
low-frequency and nonaxisymmetric mode, for which the growth timescale is much longer than
the Alfvén timescale as 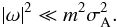 (23)We
also adopt a weak magnetic field approximation in which magnetic energy is assumed to be
everywhere much less than the rotational kinetic energy as
(23)We
also adopt a weak magnetic field approximation in which magnetic energy is assumed to be
everywhere much less than the rotational kinetic energy as 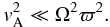 (24)With
these approximations, the bi-quadratic Eq. (22) is reduced to a quadratic equation and its solution is
(24)With
these approximations, the bi-quadratic Eq. (22) is reduced to a quadratic equation and its solution is ![\begin{eqnarray} &&\omega = \left(\frac{\hat{G}}{c_{\rm s}^2}-\frac{2}{\varpi}\right) \frac{mv_{\rm A}^2}{2\Omega\varpi} \pm\frac{mv_{\rm A}}{2\Omega\varpi} \Bigg[ \left(\frac{\hat{G}}{c_{\rm s}^2}-\frac{2}{\varpi}\right)v_{\rm A}^2 \partial_h \ln\left(\frac{B_{(\varphi)}}{\rho\varpi}\right)\nonumber\\ \label{Eq:growth}&&~~~~~~~~~+\Omega^2\varpi \partial_h (\ln\Omega^2) + \frac{m^2v_{\rm A}^2}{\varpi^2}\left(1+\frac{l^2}{n^2}\right) \Bigg]^{1/2}. \end{eqnarray}](/articles/aa/full_html/2011/08/aa16242-10/aa16242-10-eq194.png) (25)This
dispersion relation shows that the instability sets in if either of the following criteria
is satisfied:
(25)This
dispersion relation shows that the instability sets in if either of the following criteria
is satisfied: 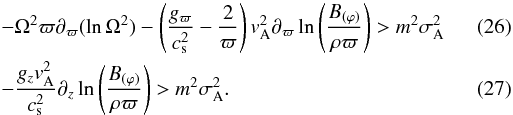 The
inequalities (26) and (27) do not hold for rigidly rotating stars
with the magnetic field profile (20).
However, the angular velocity profile of any star never remains constant in a strict
sense, because the stars in nature usually oscillate around their equilibria, which makes
a gradient in the angular velocity profile. In the presence of negative angular velocity
gradient, the instability criterion (26)
may be satisfied because the first term on the lefthand side of Eq. (26) can be the most dominant one due to the
weakness of the magnetic field as imposed in Eq. (24). For a region in which the Alfvén velocity is much smaller than the
rotational velocity, a small perturbation in the angular velocity is sufficient for
satisfying the inequality (26). We discuss
this issue in Sect. 5.2 in more detail.
The
inequalities (26) and (27) do not hold for rigidly rotating stars
with the magnetic field profile (20).
However, the angular velocity profile of any star never remains constant in a strict
sense, because the stars in nature usually oscillate around their equilibria, which makes
a gradient in the angular velocity profile. In the presence of negative angular velocity
gradient, the instability criterion (26)
may be satisfied because the first term on the lefthand side of Eq. (26) can be the most dominant one due to the
weakness of the magnetic field as imposed in Eq. (24). For a region in which the Alfvén velocity is much smaller than the
rotational velocity, a small perturbation in the angular velocity is sufficient for
satisfying the inequality (26). We discuss
this issue in Sect. 5.2 in more detail.
5. Result
5.1. Nonrotating case
We studied the stability for two nonrotating models listed in Table 1. The simulations were performed for a sufficiently long time, more than ten times the averaged Alfvén timescale or several thousands of units of M0 (cf. Table 1). This is necessary to clarify whether any MHD instability, which grows approximately on an Alfvén timescale, sets in and to determine the final fate after the onset of the instabilities. Figure 2 plots the evolution of the central rest-mass density and the minimum value of the lapse function, which characterize the compactness of the neutron star. For the nonrotating model N22H5, it is observed that the central density (the minimum value of the lapse function) increases (decreases) for t ≲ 200 M0, subsequently decreases (increases) for 200 M0 ≲ t ≲ 600 M0, and then steadily oscillates for t ≳ 600 M0. This suggests that the star contracts first, then expands slightly, and finally settles to another quasi-equilibrium state with oscillations. The final central density is not beyond the marginally stable point, ρc ≈ 0.318. For model N22H1, the qualitative features of the evolution are essentially the same as those of N22H5, but the timescale is different from N22H5 because of the difference in the magnetic field strength. The behavior described above is explained well by the variation in magnetic fields during the evolution as argued below.
Figures 3 and 4
plot the evolution of the rest-mass density and magnetic energy density on the equatorial
plane and on one of meridian (x-z) planes, respectively,
for model N22H5. The panels a−c in these figures show that the magnetic field near the
stellar surface is disturbed by the Parker instability, and then leaks out of the stellar
surface. Because the plasma beta is small, hence the matter inertia is small near the
stellar surface (as shown below), the matter is dragged by the magnetic force and the
stellar surface is consequently distorted. Here, the plasma beta is the ratio of the fluid
pressure to the magnetic pressure,
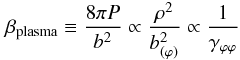 (28)where
we have used Eqs. (3) and (14) assuming Γ = 2 and k = 1.
The minimum value of the plasma beta is initially ≈2 at the stellar surface, and after
the onset of the Parker instability, the leak-out magnetic field loop produces even lower
beta plasma near the stellar surface. As a result, a weak wind expanding outward is
driven. On the other hand, the ingoing magnetic field loop enhances a turbulent motion in
the neutron star. During the transition from the state shown in panel c to d in
Figs. 3 and 4,
the initial magnetic field profile is completely destroyed and turbulent magnetic field is
produced. During the development of the turbulence, the Tayler instability does not appear
to play an important role. However, the region near the axis of ϖ = 0 is
not stable against this instability and thus no mechanism seems to help stabilizing there.
(28)where
we have used Eqs. (3) and (14) assuming Γ = 2 and k = 1.
The minimum value of the plasma beta is initially ≈2 at the stellar surface, and after
the onset of the Parker instability, the leak-out magnetic field loop produces even lower
beta plasma near the stellar surface. As a result, a weak wind expanding outward is
driven. On the other hand, the ingoing magnetic field loop enhances a turbulent motion in
the neutron star. During the transition from the state shown in panel c to d in
Figs. 3 and 4,
the initial magnetic field profile is completely destroyed and turbulent magnetic field is
produced. During the development of the turbulence, the Tayler instability does not appear
to play an important role. However, the region near the axis of ϖ = 0 is
not stable against this instability and thus no mechanism seems to help stabilizing there.
The toroidal magnetic fields that were prepared initially behave like a rubber belt, which fastens the “waist” of neutron stars. The disappearance of the coherent toroidal magnetic fields, therefore, results in the expansion of the star as shown in the panel d of Figs. 3 and 4. After the magnetic field becomes turbulent, the star steadily oscillates around the hypothetical quasi-stationary state. Although the density profile relaxes to a quasi-stationary state, the turbulent motion is maintained. We qualitatively observe the same features for model N22H1, but the growth timescale of the instability is longer than that of N22H5, as mentioned before.
It is interesting to compare the simulation result with the linear analysis. We find the
turbulent field develops in the region that is stable against the perturbation (see the
stable region in Figs. 1 and 4d−f). During the linear growth phase, i.e., Figs. 4a−c, this region is likely to be stable. However,
because the instability destroys the coherent initial magnetic field profile, i.e., the
magnetic field is no longer purely toroidal, the stable region in Fig. 1 is no longer stable after the onset of the instability.
We also point out that the linear analysis in Fig. 1
indicates that the higher m mode is unstable near the stellar surface and
we indeed find such behavior (see Fig. 3b). For
making the mode growth clear, we perform the mode analysis as follows. Because we are
interested in the magnetic field behavior near the surface, we put a ring on the equator
whose radius is nearly equal to the stellar radius. Then, the Fourier components are
defined by 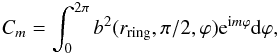 (29)where
rring is the ring radius that is chosen as
4 M0 for model N22H5. Figure 5a plots the evolution of |Cm|
with 1 ≤ m ≤ 10. It is found that all the mode (except for
m = 4 and 8) start growing at
T ≈ 150 M0, which shows that the Parker
instabilities are in operation. For m = 4 and 8,
|Cm| starts growing at
T ≈ 50 M0. This is the artifact from our
choice of the Cartesian coordinate grid.
(29)where
rring is the ring radius that is chosen as
4 M0 for model N22H5. Figure 5a plots the evolution of |Cm|
with 1 ≤ m ≤ 10. It is found that all the mode (except for
m = 4 and 8) start growing at
T ≈ 150 M0, which shows that the Parker
instabilities are in operation. For m = 4 and 8,
|Cm| starts growing at
T ≈ 50 M0. This is the artifact from our
choice of the Cartesian coordinate grid.
 |
Fig. 5 a) Evolution of the Fourier mode for the magnetic energy density for
model N22H5; b) evolution of several energy components for model N22H5;
and c) the same as b) but for model N22H1. All the energy
components are normalized by the rest mass, and the time axes are shown in units of
M0 (bottom) and
|
The nonlinear growth of the Parker instability is reflected in the energy components as shown in Fig. 5. There, the internal energy (7) is separated into the adiabatic part Uad and the heating part Uheat, and they are defined by replacing ε in Eq. (7) to εad ≡ ρΓ−1/(Γ − 1) and to ε − εad, respectively. Figure 5 shows that the ADM mass is approximately conserved, which implies that gravitational waves are not substantially emitted during the evolution of the neutron stars. The magnetic energy gradually decreases, and the kinetic energy increases during t ≲ 500 M0 for model H22M5. This illustrates that the meridional circulation is excited by the instability: Figs. 3 and 4 specifically show that this meridional circular motion is induced by the displacement of the toroidal magnetic field line. In other words, the magnetic field helps for increasing the kinetic energy of the fluid element by liberating the gravitational potential energy. During this procedure, the kinetic energy eventually reaches about ten percent the magnetic energy at t ≈ 200 M0.
For t ≳ 500 M0, the decrease rate of the magnetic energy becomes high, and simultaneously the thermal energy (Uheat) quickly increases. This indicates that the shock heating occurs because of the turbulent motion induced by the distorted magnetic fields. The kinetic energy of the circulation gradually decreases, and the magnetic and thermal energies settle approximately to constant values at a late stage of the evolution. The adiabatic internal energy also settles to a value lower than the initial one at t ≈ 500 M0. This implies that the density distribution changes, as shown in Figs. 3 and 4. As we pointed out above, however, the magnetic field configuration never reaches any equilibrium state, in contrast to the axisymmetric case (Kiuchi et al. 2008).
All the features found in the evolution of the energy components for model N22H1 are essentially the same as for model N22H5 except for the relevant timescale, as found from Figs. 2 and 5. The variation timescales of the various components of the energy for model N22H5 are systematically shorter than those for model N22H1. This is natural because the instability develops approximately in the Alfvén timescale.
As found from Fig. 4, the meridian circulation is
excited by the magnetic field instability. Thus, the growth timescale of the kinetic
energy in the rising phase (t ≲ 200 M0)
should be close to the Alfvén timescale. To check that this is indeed the case, we
evaluated the growth time of the kinetic energy. For this evaluation, the data of
t/M0 ∈ [50,100]
and of
t/M0 ∈ [50,200]
were used for models N22H5 and N22H1, and were fitted by assuming the function form of
∝ et/τk
where τk is the growth time. We find that
τk ≈ 14 M0
and ≈22 M0 for models N22H5 and N22H1, respectively.
Because these values are substantially smaller than the averaged Alfvén timescale given in
Table 1,  is less appropriate for characterizing the growth timescale of the magnetic field
instability. Instead, we find it appropriate to employ the Alfvén timescale in the
vicinity of the stellar surface because both the linear analysis and our simulations
indicate that the instability primarily grows there. The Alfvén timescale
τA estimated at
r/rs = 0.95 is
60 M0 for model N22H5 and
120 M0 for model N22H1. Furthermore, the linear analysis
suggests that the mode of m ~ O(10) is very unstable,
and we find this feature in our simulations as discussed above. Because the growth rate is
proportional to m as we see in Eq. (17), the growth timescale should be given by
τA/m,
~6 M0 for model N22H5 and
12 M0 for model N22H1, which agrees with
τk within a factor of two. In any case, the
growth timescale of the instability is approximately proportional to the Alfvén timescale
normalized by m. Therefore, we can conclude that the primary instability
is the Parker instability as expected in the linear analysis.
is less appropriate for characterizing the growth timescale of the magnetic field
instability. Instead, we find it appropriate to employ the Alfvén timescale in the
vicinity of the stellar surface because both the linear analysis and our simulations
indicate that the instability primarily grows there. The Alfvén timescale
τA estimated at
r/rs = 0.95 is
60 M0 for model N22H5 and
120 M0 for model N22H1. Furthermore, the linear analysis
suggests that the mode of m ~ O(10) is very unstable,
and we find this feature in our simulations as discussed above. Because the growth rate is
proportional to m as we see in Eq. (17), the growth timescale should be given by
τA/m,
~6 M0 for model N22H5 and
12 M0 for model N22H1, which agrees with
τk within a factor of two. In any case, the
growth timescale of the instability is approximately proportional to the Alfvén timescale
normalized by m. Therefore, we can conclude that the primary instability
is the Parker instability as expected in the linear analysis.
5.2. Rotating case
We now study the stability for two rigidly rotating models listed in Table 1. Again, long-term simulations are performed as in the nonrotating models. In Fig. 2, the evolution of the central density and the minimum value of the lapse function for models R22H2T8 and R22H08T8 are plotted together. We note again that for both models, the angular velocity is approximately as large as the Kepler limit at the equatorial stellar surface. The central density for model R22H2T8 (R22H08T8) remains approximately constant until t ≈ 800 M0(1000 M0), and then, gradually increases for t ≲ 2000 M0(2400 M0). Eventually, it settles to a new value for t ≳ 2000 M0(2400 M0). The reason that the final central density is higher than the initial one will be described below.
Although the magnetic field strength and central density for the rotating model R22H08T8 are comparable to those for the nonrotating model N22H1, the evolution process in the central region is significantly different. For model R22H08T8, the central density remains approximately constant for a time much longer for model N22H1. This is because the rotation stabilizes the Tayler instability, which may set in for the nonrotating models, as expected in the local linear perturbation analyses (see Sect. 4.2). The Tayler instability is a primary magnetic field instability associated with the toroidal field near the axis of ϖ = 0 for the nonrotating models, but this is not the case for the rapidly rotating models.
However, the instability is not suppressed by the presence of rapid rotation for all the places inside the neutron star, as Fig. 2 illustrates that the central density varies for a longerterm evolution with t ≈ 2000 M0. This result is totally different from the axisymmetric case (Kiuchi et al. 2008), in which the rapid rotation suppresses the onset of the interchange instability. One of the models studied in Kiuchi et al. (2008) has similar model parameters to those of R22H08T8, which is stable for the axisymmetric perturbations. This implies that a nonaxisymmetric instability is excited for the rapidly rotating models this time. To clarify the relevant instability, we generate Figs. 6 and 7, in which the rest-mass density and the magnetic energy density for model R22H2T8 are plotted on the equatorial and meridian planes, respectively. Until t ≈ 200 M0, we observe that the coherent magnetic field and density profiles remain. However, at t ≈ 400 M0, the magnetic field profile near the stellar surface is deformed in the same manner as for the nonrotating models. During the subsequent evolution, the coherent magnetic field structure is totally destroyed, and a turbulent motion is excited. The surface expands because the plasma beta near the surface is below one due to the leak-out of the magnetic field. Because the coherent toroidal magnetic field, which fastens the waist of the neutron star, disappears, the radius of the neutron star increases. All these features are essentially the same as for the nonrotating models.
 |
Fig. 6 The same as Fig. 3, but for a rotating model R22H2T8. The arrows indicate the velocity fields. |
 |
Fig. 8 Snapshots of magnetic pressure a) for model R22H2T8 and b) for mode N22H5, and those of angular velocity profiles c) for model R22H2T8 and d) for model R22H08T8. Both profiles are plotted along the x-axis on the equator. In panel a), the profile along y-axis is also plotted. In panels c) and d), it is seen that the negative gradients of the angular velocity profiles are developed near the stellar surface. |
The evolution of the magnetic field near the rotation axis in the rotating models is
slightly different from the nonrotating models. Figures 8a and b plot the snapshots of the magnetic pressure defined by
b2/8π along the
x and y-axes on the equator for models R22H2T8 and
N22H5, respectively. In the rotating model R22H2T8, the profile near the center does not
drastically change. However, the magnetic pressure increases gradually and systematically,
and the matter near the axis is pinched by the increased magnetic pressure. This increase
proceeds in the axisymmetric way because the profiles along y-axis is
approximately identical to those along x-axis in Fig. 8a. This might seem to be incompatible with our previous
results (Kiuchi et al. 2008). To clarify this
point, we reconsidered the criterion for the axisymmetric perturbation: 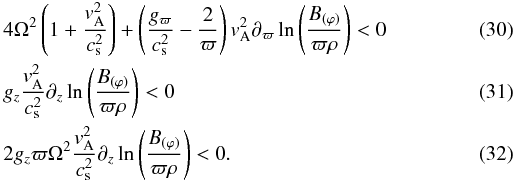 The
axisymmetric instability ignites if any of these inequalities holds. Equations (31) and (32) implies the magnetic field profile given by Eq. (20) is marginally stable. The magnetic field
line strength evolves as
The
axisymmetric instability ignites if any of these inequalities holds. Equations (31) and (32) implies the magnetic field profile given by Eq. (20) is marginally stable. The magnetic field
line strength evolves as 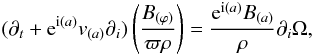 (33)where
ei(a) is a tetrad basis. In axisymmetric simulations, the
field line strength is completely preserved because the poloidal magnetic field, i.e.
B(ϖ) and
B(z), is never generated if the initial
magnetic field is purely toroidal. Then, the inequalities (31) and (32) are never
satisfied during the evolution of the magnetized star. On the other hand, the field line
strength deviates from its initial value in three-dimensional simulations because the
poloidal field is generated by a perturbation induced by a truncation error in general (in
addition to the change of the angular velocity profile as discussed below). As the result,
the inequalities (31) and (32) may hold during the evolution, and the
axisymmetric instability could set in. This is why the magnetic pressure increases and
angular velocity is distorted near the center as seen in Figs. 8a and c. The situation is the same in model R22T08T8. It is interesting
to note that the stellar surface in the rotating model expands whereas the central part
contracts due to the redistribution of the magnetic field profile. In contrast to the
rotating model, the coherent profile of the magnetic fields near the stellar center in the
nonrotating model N22H5 disappears after the onset of the instability, which results in
the systematic expansion of the star as mentioned in the previous section. The nonrotating
models are also marginally stable against the interchange instability, as shown in
Eq. (31). However, these models are
unstable against the nonaxisymmetric mode (see Fig. 1b) and this mode overcomes the interchange mode. It is also interesting to note
that the nonaxisymmetric instability develops at an earlier time than expected from the
central density’s evolution, e.g., at
t ≈ 800 M0(1000 M0)
for R22H2T8 (R22T08T8) (see Fig. 2a). However, the
instability develops before t ~ 600 M0 for
these rotating models as shown in Fig. 9. This also
reflects that the instability, which affects the global structure of the neutron star,
sets in both near the stellar surface and in the central region; namely, the Parker
(interchange) instability plays an important role in the outer (central) region for the
rotating models.
(33)where
ei(a) is a tetrad basis. In axisymmetric simulations, the
field line strength is completely preserved because the poloidal magnetic field, i.e.
B(ϖ) and
B(z), is never generated if the initial
magnetic field is purely toroidal. Then, the inequalities (31) and (32) are never
satisfied during the evolution of the magnetized star. On the other hand, the field line
strength deviates from its initial value in three-dimensional simulations because the
poloidal field is generated by a perturbation induced by a truncation error in general (in
addition to the change of the angular velocity profile as discussed below). As the result,
the inequalities (31) and (32) may hold during the evolution, and the
axisymmetric instability could set in. This is why the magnetic pressure increases and
angular velocity is distorted near the center as seen in Figs. 8a and c. The situation is the same in model R22T08T8. It is interesting
to note that the stellar surface in the rotating model expands whereas the central part
contracts due to the redistribution of the magnetic field profile. In contrast to the
rotating model, the coherent profile of the magnetic fields near the stellar center in the
nonrotating model N22H5 disappears after the onset of the instability, which results in
the systematic expansion of the star as mentioned in the previous section. The nonrotating
models are also marginally stable against the interchange instability, as shown in
Eq. (31). However, these models are
unstable against the nonaxisymmetric mode (see Fig. 1b) and this mode overcomes the interchange mode. It is also interesting to note
that the nonaxisymmetric instability develops at an earlier time than expected from the
central density’s evolution, e.g., at
t ≈ 800 M0(1000 M0)
for R22H2T8 (R22T08T8) (see Fig. 2a). However, the
instability develops before t ~ 600 M0 for
these rotating models as shown in Fig. 9. This also
reflects that the instability, which affects the global structure of the neutron star,
sets in both near the stellar surface and in the central region; namely, the Parker
(interchange) instability plays an important role in the outer (central) region for the
rotating models.
 |
Fig. 9 Time evolution of several energy components for models R22H2T8 a) and for R22H08T8 b). |
The local linear perturbation analysis predicts that our rigidly rotating models are stable against the nonaxisymmetric perturbation as described in Sect. 4.2. Thus, our numerical result does not seem to agree with the linear analysis. However, this is not the case, because our rotating model is close to a marginally stable state and is destabilized by a slight nonlinear perturbation to the rotational velocity. To explain this, we plot the snapshots of the angular velocity in Fig. 8, in which the angular velocity profiles along the x-axis on the equator are plotted for models R22H2T8 and R22H08T8. This shows that the angular velocity deviates slightly from the constant profile, and the negative gradients near the stellar surface, in particular, are developed during the evolution. This time variation comes from the oscillation of the neutron star, which is initially triggered by a perturbation of numerical origin. The initial conditions we gave are in equilibria, but a small numerical error associated with the finite grid resolution induces a perturbation, and then the neutron stars start oscillating around their equilibrium states. Although the perturbation is induced by a numerical error in this case, it is quite natural to expect that any star in nature oscillates, and thus the precisely rigid rotation is not realized. Once the angular velocity profile has the negative gradient, the instability criterion (26) could be satisfied because the first term on the lefthand side has a very high positive value in the rapidly rotating models with weak magnetic fields; i.e., the criterion is satisfied even for a small angular velocity gradient.
The growth process of the instability is reflected well in several energy components. Figure 9 plots their evolution. This shows that the ADM mass, adiabatic internal energy, and rotational kinetic energy remain approximately constant during the evolution. The decrease in the magnetic energy is prominent at t ≈ 1500 M0 for model R22H2T8 and t ≈ 2000 M0 for R22H08T8. The magnetic energy increases only by ~2% during the development of the interchange instability, e.g., for t ≲ 400 M0 for model R22H2T8. The kinetic energy, in which contribution of the rotational kinetic energy is excluded, increases with time. This shows that the meridian motion is developed. We find again that the instability associated with the presence of toroidal magnetic fields cannot be suppressed by the rapid rotation and the magnetic field never reaches an equilibrium state as in the nonrotating models.
It is well known that negative gradient of angular velocity in the presence of magnetic field leads to the MRI (Balbus & Hawley 1991). As discussed above, the negative angular velocity appears in the vicinity of the stellar surface, so we hypothetically estimate the MRI growth rate as σMRI ~ Ωϖ|∂ϖlnΩ|. We fit the angular velocity profile as a function in the radius in Figs. 8c−d and obtain the gradient ∂ϖlnΩ. Putting the value of the gradient, angular velocity, and the stellar radius into the equation, we estimate the growth rate as σMRI M0 ≈ 0.09 (0.1) for model R22H2T8 (R22H08T8). On the other hand, we infer the instability growth rate from the increase in the kinetic energy shown in Fig. 9 with the same strategy for the nonrotating case. The resulting growth rate σ M0 is 0.008 (0.007) for model R22H2T8 (R22H08T8), where we use the data of t/M0 ∈ [0,600] in both the models. Therefore, the growth rates do not match. However, Eqs. (17) and (25) tell us that the growth rates of the interchange and Parker instability depend on the magnetic field strength. We therefore conclude that the instability we find in the rotating model is not the MRI.
 |
Fig. 10 The results of convergence tests for model N22H5; a) the central density; b) the minimum value of lapse function; c) the ADM mass normalized by its initial value; d) the internal energy; e) the magnetic energy; f) the kinetic energy; and g) the normalized Hamiltonian constraint. |
Before closing this section, we show that the convergence is achieved in our numerical
results with an accuracy high enough to draw a quantitatively reliable conclusion.
Figures 10 and 11 plot the evolution of (a) the central density; (b) the minimum value of the
lapse function; (c) the ADM mass; (d) the internal energy; (e) the magnetic energy; (f)
the kinetic energy; and (g) the Hamiltonian constraint violation for models N22H5 and
R22H2T8. The Hamiltonian constraint violation is defined by
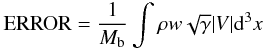 (34)with
(34)with
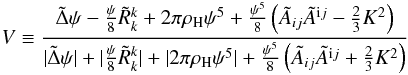 (35)where
(35)where
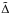 is the Laplacian associated with
is the Laplacian associated with 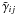 ,
ψ is the conformal factor, and
ρH = (ρh + b2/4π)w2 − (P + b2/8π) − (αbt)2/4π.
In all the panels, we plot the results of three different grid resolutions. In Figs. 10a, b, d, and e, we find a transition time at
t ~ 500 M0 depends slightly on the grid
resolution, but on the whole, the results appear to converge. The ADM mass, which is
approximately conserved in the present situation, is conserved within 99.8 % accuracy (see
Fig. 10c), and the error in the Hamiltonian
constraint violation is in an acceptable level (less than ~1% error; see Fig. 10g). In the panel e, we observe that the convergence is
lost for t ≳ 1000 M0. This is likely to be
caused by the turbulent field developing both outside and inside the star as shown in
Figs. 3f and 4f. To handle such a region and/or turbulent field, we would need a more
sophisticated numerical scheme.
,
ψ is the conformal factor, and
ρH = (ρh + b2/4π)w2 − (P + b2/8π) − (αbt)2/4π.
In all the panels, we plot the results of three different grid resolutions. In Figs. 10a, b, d, and e, we find a transition time at
t ~ 500 M0 depends slightly on the grid
resolution, but on the whole, the results appear to converge. The ADM mass, which is
approximately conserved in the present situation, is conserved within 99.8 % accuracy (see
Fig. 10c), and the error in the Hamiltonian
constraint violation is in an acceptable level (less than ~1% error; see Fig. 10g). In the panel e, we observe that the convergence is
lost for t ≳ 1000 M0. This is likely to be
caused by the turbulent field developing both outside and inside the star as shown in
Figs. 3f and 4f. To handle such a region and/or turbulent field, we would need a more
sophisticated numerical scheme.
From these figures, we conclude that all the qualitative features of the magnetic field instability found in this work are independent of the grid resolution. In the rotating model R22H2T8, we find essentially the same features as the convergence study in the nonrotating model N22H5.
6. Summary and discussion
We explored the nonaxisymmetric instability of neutron stars with purely toroidal magnetic fields. Preparing the nonrotating and rotating neutron stars in equilibrium as the initial conditions, the three-dimensional GRMHD simulations were performed. For the nonrotating models, the local linear perturbation analysis predicts that the Parker instability will be the primary instability, and we confirmed this. Owing to the Parker instability, a turbulent state is developed, and the initially coherent magnetic field profile is totally varied. The magnetic field profile never reaches an equilibrium state, which sharply contrasts with the axisymmetric instability of Kiuchi et al. (2008). The growth timescale of the Parker instability depends on the magnetic field strength, i.e., the Alfvén timescale, and this result also agrees with the local linear perturbation analysis. The present result strongly suggests that three-dimensional treatment is crucial for clarifying the instability of a neutron star with toroidal magnetic fields. In other words, any assumption of the spacetime symmetry (e.g., axisymmetric symmetry) could prevent reaching the correct conclusion.
We also explored the instability of rigidly and rapidly rotating neutron stars. The linear analyses have suggested that rapid rotation could play a role as a stabilizing agent. We confirm that the rapid rotation stabilizes the Tayler instability, which may occur near the axis of ϖ = 0 in the nonrotating case. However, the interchange instability could play a minor role because the neutron stars are marginally stable against it. We note that the interchange mode never develops in the axisymmetric simulations due to the symmetry imposed. We also find that the Parker instability that is relevant near the stellar surface may not be stabilized by the rapid rotation. This is because, by means of a perturbative oscillation, neutron stars may have a region in which the gradient in the angular velocity profile is negative (∂Ω/∂ϖ < 0). This negative gradient can induce the Parker instability when the neutron star shows rapid rotation and weak magnetic fields. As in the nonrotating model, a turbulent state is subsequently developed in the outer region of the neutron star. This result also sends a message that the three-dimensional simulation is essential for investigating a magnetic field instability.
As mentioned in Introduction, a large number of core-collapse supernova simulations based on the magnetorotational mechanism have shown that toroidal magnetic fields are amplified in the protoneutron stars via the winding mechanism. In the assumption of axial symmetry, these fields may be in quasi-equilibrium after the saturation is reached. However, this could disagree with the result of the linear perturbation analysis; i.e., the neutron stars with purely toroidal magnetic fields are often unstable. The present study indeed suggests that such neutron stars are unstable, so that the assumptions of axial symmetry and rapid rotation, which are imposed for most of the magnetohydrodynamical supernova simulations, would be inappropriate. (Note that in axial symmetry, the rapid rotation stabilizes neutron stars with toroidal magnetic fields, as illustrated in Kiuchi et al. 2008.) In a nonaxisymmetric simulation, we may find that a protoneutron star with strongly toroidal magnetic fields is unstable and that a turbulent motion inside it is excited. Magnetohydrodynamic simulations have to be performed in three spatial dimensions.
The stability of more generic magnetic field configurations, i.e., mixed poloidal-toroidal fields, is quite important because such fields would be realized in general. Recently, Braithwaite & Nordlund (2005), Braithwaite & Spruit (2004), and Duez et al. (2010) studied the stability of Newtonian stars with such fields, and report that the mixed field may play an important role in stabilization. They show that the equilibrium profile is maintained on several Alfvén timescales. We plan to study this issue with the weak magnetic field solution obtained by Ioka & Sasaki (2004) in the general relativistic framework.
Recently, Lander et al. (2010) and Lander & Jones (2011) have studied the instability associated with the presence of toroidal magnetic fields by solving the linearized Newtonian MHD equations with their time-domain code. They show that the Tayler instability characterized by the azimuthal mode number m = 1 primarily occurs near the axis of ϖ = 0 and that no pronounced Parker instability sets in near the surface of the star . Similar results were obtained by Duez et al. (2010) with Newtonian resistive MHD simulations. These results seem to be incompatible with our present results. The reason for this discrepancy seems to be that Lander et al. (2010) and Lander & Jones (2011) restrict their studies to low-order azimuthal modes (m ≤ 6), and Duez et al. (2010) employ some kinds of (artificial) viscosity and resistivity for the evolution to remove numerical instability caused by a short-wavelength oscillation. We note that Lander et al. (2010) and Lander & Jones (2011) also use artificial viscosity to stabilize their computations. This suggests that short-wavelength modes might be suppressed in their simulations. As can be seen from Figs. 1 and 3, the Parker instability found in this study is characterized by a high-order azimuthal mode number, which implies that the unstable modes of the Parker instability near the surface have a short wavelength. In Duez et al. (2010), they use a stably stratified model with the polytrope index n = 3 and forecast the instability as we did in Fig. 1. They find the primarily instability is not the Parker instability, but the Tayler instability in their model. This is probably because the restoring force due to the entropy gradient near the surface stabilizes the magnetic buoyant force.
Finally, we end by commenting on a possible potential effect for stabilizing the magnetic field instabilities that are not taken into account in our present work. In a stably stratified region of the star, the buoyant force inhibits the interchange, Parker, and Tayler instabilities from growing (Acheson 1978). For the cold neutron star, the composition gradient induced by chemical inhomogeneities can stably stratify the neutron star matter and supports the gravity mode (g-mode) oscillations. Finn (1987) considered crustal g-modes due to the composition discontinuities in the outer envelopes, whose typical oscillation period is about 5 ms for a canonical neutron star model. Reisenegger & Goldreich (1992) studied the effect of g-modes associated with buoyancy induced by protoneuron composition gradients in the core, whose typical oscillation period is about 2 ms for a canonical neutron star model. If the growth timescale of the Parker instability found in our study is longer than these periods of the g-modes, it is possible that the buoyant forces inside the neutron star suppress the growth of the Parker instability. In the present study, we find that a typical growth timescale of the Parker instability is about 20 M0, which gives a typical growth timescale of 0.1 ms for a canonical neutron star model with a strong magnetic field of 1016 G. For the present models, therefore, it seems that the buoyancy inside the neutron star could not suppress the onset of the Parker instability. However, for a weaker magnetic field strength ≈1015 G, the Parker instability could be suppressed by the buoyancy because a typical growth timescale of the Parker instability becomes 1 ms. To derive a definite answer to this problem, regardless of whether the buoyancy can stabilize the Parker instability inside the neutron star, we have to know the local growth rate of the Parker instability. Unfortunately, in our simulations, it is difficult to estimate it in the vicinity of the stellar surface because the local magnetic structure highly depends on the numerical resolution. To investigate this point more precisely, we have to take the chemical inhomogeneities into account and this implies that it is necessary to implement equations of state that depend on the chemical compositions and to obtain the evolution of the chemical compositions. This is beyond the scope of this paper.
Besides the instabilities listed here, magnetorotational instability (MRI) (Balbus & Hawley 1991) could play an important role in enhancing the magnetic field strength and in modifying the magnetic field profile (Obergaulinger et al. 2006; Shibata et al. 2006). However, any accurate MHD simulation in which the fastest growing mode of MRI is resolved has not been performed yet.
Acknowledgments
K.K. thanks to Y. Sekiguchi and K. Kyutoku for a fruitful discussion. Numerical computations were performed on XT4 at the Center for Computational Astrophysics in NAOJ and on NEC-SX8 at YITP at Kyoto University. This research was supported by Grant-in-Aids for Young Scientists (B) 22740178, for Scientific Research (21340051), and for Scientific Research on Innovative Area (20105004) of Japanese MEXT.
References
- Acheson, D. J. 1978, Phil. Trans. Roy. Soc. Lond. A, 289, 459 [CrossRef] [Google Scholar]
- Baker, J. G., Centrella, J., Choi, D.-I., Koppitz, M., & van Meter, J. 2006, Phys. Rev. Lett. 96, 111102 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Balbus, S. A., & Hawley, J. F. 1991, ApJ, 376, 214 [NASA ADS] [CrossRef] [Google Scholar]
- Baumgarte, T. W., & Shapiro, S. L. 1999, Phys. Rev. D, 59, 024007 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Bildsten, L., Chakrabarty, D., Chiu, J., et al. 1997, ApJS, 113, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Braithwaite, J., & Nordlund, A. 2005, A&A, 450, 1077 [Google Scholar]
- Braithwaite, J., & Spruit, H. C. 2004, Nature, 431, 819 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Burrows, A., Dessart, L., Livne, E., Ott, C. D., & Murphy, J. 2007, ApJ., 664, 416 [NASA ADS] [CrossRef] [Google Scholar]
- Brugmann, B., Gonzalez, J. A., Hannam, M. 2008, Phys. Rev. D, 77, 024027 [NASA ADS] [CrossRef] [Google Scholar]
- Campanelli, M., Lousto, C. O., Marronetti, P., & Zlochower, Y. 2006, Phys. Rev. Lett., 96, 111101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Cook, G. B., Shapiro, S. L., & Teukolsky, S. A. 1994, ApJ, 422, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Duez, V., Braithwaite, J., & Mathis, S. 2010, ApJ, 724, L34 [NASA ADS] [CrossRef] [Google Scholar]
- Finn, L. S. 1987, MNRAS, 227, 265 [NASA ADS] [Google Scholar]
- Goossens, M. 1980, Geo. Astro. Fluid. Dyn., 15, 123 [Google Scholar]
- Gavriil, F. P., Kaspi, V. M., & Woods, P. M. 2002, Nature, 419, 142 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Harding, A. K., & Lai, D. 2006, Rept. Prog. Phys., 69, 2631 [Google Scholar]
- Ibrahim, A. I., Swank, J. H., & Parke, W. 2003, ApJ, 584, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Ioka, K., & Sasaki, M. 2004, ApJ, 600, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Kotake, K., Sawai, H., Yamada, S., & Sato, K. 2004, ApJ, 608, 391 [NASA ADS] [CrossRef] [Google Scholar]
- Kiuchi, K., & Yoshida, S. 2008, Phys. Rev. D, 78, 044045 [NASA ADS] [CrossRef] [Google Scholar]
- Kiuchi, K., Shibata, M., & Yoshida, S. 2008, Phys. Rev. D, 78, 024029 [NASA ADS] [CrossRef] [Google Scholar]
- Kiuchi, K., Sekiguchi, Y., Shibata, M., & Taniguchi, K. 2009, Phys. Rev. D, 80, 064037 [NASA ADS] [CrossRef] [Google Scholar]
- Kurganov, A., & Tadmor, E. 2000, J. Comput. Phys., 160, 214 [Google Scholar]
- Lai, D. 2001, Rev. Mod. Phys., 73, 629 [NASA ADS] [CrossRef] [Google Scholar]
- Lander, S. K., & Jones, D. I. 2011, MNRAS, 412, 1394 [NASA ADS] [CrossRef] [Google Scholar]
- Lander, S. K., Jones, D. I., & Passamonti, A. 2010, MNRAS, 405, 318 [NASA ADS] [Google Scholar]
- Lucas-Serrano, A., Font, J. A., Ibánez, J. M., & Martí, J. M. 2004, A&A, 428, 703 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Manchester, R. N., Hobbs, G. B., Teoh, A., & Hobbs, M. 2005, AJ, 129, 1993; see http://www.atnf.csiro.au/research/pulsar/psrcat/ for the latest number of pulsars [NASA ADS] [CrossRef] [Google Scholar]
- Obergaulinger, M., Aloy, M. A., & Müller 2006, A&A, 450, 1107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Orlandini, M., & Fiume, D. D. 2001, AIP Conf. Proc., 599, 283, [NASA ADS] [CrossRef] [Google Scholar]
- Cerda-Duran, P., Font, J. A., & Dimmelmeier, H. 2007, A&A, 474, 169 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Parker, E. N. 1955, ApJ, 121, 49 [Google Scholar]
- Parker, E. N. 1966, ApJ, 145, 811 [NASA ADS] [CrossRef] [Google Scholar]
- Reisenegger, A., & Goldreich, P. 1992, ApJ. 395, 240 [NASA ADS] [CrossRef] [Google Scholar]
- Rea, N., Israel, G. L., Stella, L., et al. 2003, ApJ, 586, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Scheidegger, S., Fischer, T., & Liebendoerfer, M. 2008, A&A, 490, 231 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shibata, M. 2003, Phys. Rev. D, 67, 024033 [NASA ADS] [CrossRef] [Google Scholar]
- Shibata, M., & Nakamura, T. 1995, Phys. Rev. D, 52, 5428 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Shibata, M., & Sekiguchi, Y. I. 2005, Phys. Rev. D, 72, 044014 [NASA ADS] [CrossRef] [Google Scholar]
- Shibata, M., Liu, Y. T., Shapiro, S. L., & Stephens, B. C. 2006, Phys. Rev. D, 74, 104026 [NASA ADS] [CrossRef] [Google Scholar]
- Spruit, H. C. 1999, A&A, 349, 189 [NASA ADS] [Google Scholar]
- Takiwaki, T., Kotake, K., & Sato, K. 2009, ApJ, 691, 1360 [NASA ADS] [CrossRef] [Google Scholar]
- Tayler, R. J. 1973, MNRAS, 161, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Thompson, C., & Duncan, R. C. 1993, ApJ, 408, 194 [NASA ADS] [CrossRef] [Google Scholar]
- Thompson, C., & Duncan, R. C. 1995, MNRAS, 275, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Thompson, C., & Duncan, R. C. 1996, ApJ, 473, 322 [NASA ADS] [CrossRef] [Google Scholar]
- Thompson, C., & Duncan, R. C. 2001, ApJ, 561, 980 [NASA ADS] [CrossRef] [Google Scholar]
- Wickramasinghe, D., & Ferrario, L. 2005, MNRAS, 356, 1576 [NASA ADS] [CrossRef] [Google Scholar]
- Woods, P. M., & Thompson, C. 2006, in Compact stellar X-ray sources, ed. W. Lewin, & M. van der Klis, Cambridge Astrophysics Series (Cambridge, UK: Cambridge University Press), 39, 547 [Google Scholar]
- Yamada, S., & Sawai, H. 2004, ApJ, 608, 907 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
List of characteristic quantities for neutron stars with toroidal magnetic fields.
All Figures
 |
Fig. 1 The growth rate of the instability of a neutron star with toroidal magnetic fields normalized by the maximum growth rate |σmax| (left) and corresponding m mode (right) on the meridian plane for nonrotating Newtonian polytrope with ρ0 = 0.16 and B0 = 0.2. The white colored region and the dotted curve denote the stable region and critical radius, respectively, and rs denotes the stellar radius. |
| In the text | |
 |
Fig. 2 The evolution of a) central rest-mass density ρc and b) minimum value of lapse function αmin for nonrotating models N22H1 and N22H5. |
| In the text | |
 |
Fig. 3 The evolution of rest-mass density (left) and magnetic energy density (right) on the equator for N22H5. Both of them are plotted on the logarithmic scale. The coordinate time at each slice is shown in each panel. |
| In the text | |
 |
Fig. 4 The evolution of the rest-mass density (bottom) and magnetic energy density (top) on a meridian (x-z) plane for N22H5 on the logarithmic scale. The arrows indicate the velocity fields. |
| In the text | |
 |
Fig. 5 a) Evolution of the Fourier mode for the magnetic energy density for
model N22H5; b) evolution of several energy components for model N22H5;
and c) the same as b) but for model N22H1. All the energy
components are normalized by the rest mass, and the time axes are shown in units of
M0 (bottom) and
|
| In the text | |
 |
Fig. 6 The same as Fig. 3, but for a rotating model R22H2T8. The arrows indicate the velocity fields. |
| In the text | |
 |
Fig. 7 The same as Fig. 4, but for a rotating model R22H2T8. |
| In the text | |
 |
Fig. 8 Snapshots of magnetic pressure a) for model R22H2T8 and b) for mode N22H5, and those of angular velocity profiles c) for model R22H2T8 and d) for model R22H08T8. Both profiles are plotted along the x-axis on the equator. In panel a), the profile along y-axis is also plotted. In panels c) and d), it is seen that the negative gradients of the angular velocity profiles are developed near the stellar surface. |
| In the text | |
 |
Fig. 9 Time evolution of several energy components for models R22H2T8 a) and for R22H08T8 b). |
| In the text | |
 |
Fig. 10 The results of convergence tests for model N22H5; a) the central density; b) the minimum value of lapse function; c) the ADM mass normalized by its initial value; d) the internal energy; e) the magnetic energy; f) the kinetic energy; and g) the normalized Hamiltonian constraint. |
| In the text | |
 |
Fig. 11 The same as Fig. 10 but for model R22H2T8. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


