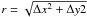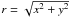| Issue |
A&A
Volume 532, August 2011
|
|
|---|---|---|
| Article Number | A16 | |
| Number of page(s) | 10 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201016053 | |
| Published online | 13 July 2011 | |
Astrometry with the MCAO instrument MAD
An analysis of single-epoch data obtained in the layer-oriented mode⋆
1
Max Planck Institute for Astronomy (MPIA), Königstuhl 17, 69117 Heidelberg, Germany
2
Leiden Observatory, Leiden University, PO Box 9513, 2300 RA Leiden, The Netherlands
e-mail: meyer@strw.leidenuniv.nl
3
INAF Osservatorio Astronomico di Padova, Vicolo dell’Osservatorio, 5, 35122 Padova, Italy
4
INAF Osservatorio Astrofisico di Arcetri, Largo Enrico Fermi, 5, 50125 Firenze, Italy
Received: 3 November 2010
Accepted: 11 May 2011
Context. Current instrument developments at the largest telescopes worldwide involve the installation of multi-conjugated adaptive optics (MCAO) modules. The large field of view and more uniform correction provided by these systems is not only highly beneficial for photometric studies but also for astrometric analysis of, e.g., large dense clusters and exoplanet detection and characterization. The Multi-conjugated Adaptive optics Demonstrator (MAD) is the first such instrument and was temporarily installed and tested at the ESO/VLT in 2007.
Aims. We analyzed the first available MCAO imaging data in the layer-oriented mode obtained with the MAD instrument in terms of astrometric precision and stability.
Methods. We analyzed two globular cluster data sets in terms of achievable astrometric precision. Data were obtained in the layer-oriented correction mode, one in full MCAO correction mode with two layers corrected (NGC 6388) and the other applying ground-layer correction only (47 Tuc). We calculated Strehl maps for each frame in both data sets. Distortion corrections were performed and the astrometric precision was analyzed by calculating mean stellar positions over all frames and by investigating the positional residuals present in each frame after transformation to a master-coordinate frame.
Results. The mean positional precision for stars of brightnesses K = 14−18 mag is ≈ 1.2 mas in the full MCAO correction mode data of the cluster NGC 6388. The precision measured in the GLAO data (47 Tuc) reaches ≈1.0 mas for stars corresponding to 2MASS K magnitudes between 9 and 12. The observations were such that stars in these magnitude ranges correspond to the same detector flux range. The jitter movement used to scan a larger field of view introduced additional distortions in the frames, leading to a degradation of the achievable precision.
Key words: instrumentation: adaptive optics / techniques: image processing / astrometry / methods: observational
© ESO, 2011
1. Introduction
In classical adaptive optics correction, with one reference star, the field of view (FoV) is limited by the effect of anisoplanatism, as only the integrated phase error over the column above the telescope in the direction to the guide star is measured and corrected. Turbulence outside this column, e.g. in the direction of the target, if it cannot be used itself as a guide star, is not mapped and the correction degrades rapidly with growing separation from the guide star. The average wavefront phase error is limited to <1 rad only within the so-called isoplanatic angle, which for typical astronomical sites corresponds to 10′′−20′′ in the Ks-band and only 3′′ in the visible. In the case of a laser guide star as reference source, the phase error is even larger, because of the low focussing altitude and the resulting cone-effect (Tallon & Foy 1990; Yan et al. 2005). Multi conjugated adaptive optics (MCAO; Beckers 1988; Ellerbroek et al. 1994) provides a way of achieving diffraction-limited image quality over larger FoVs of up to 2–4 arcmin, hence overcoming anisoplanatism. Moderate averaged Strehl-ratios, in the range of 10% to 25%, can be achieved, but with a higher uniformity of the point spread function (PSF) over the FoV. This is desired for resolving structures of extended sources, such as galaxies or the cores of star clusters. In MCAO, the three-dimensional structure of the turbulence is reconstructed by means of the information coming from several guide stars, natural or laser. Instead of correcting the turbulence integrated over a single direction, turbulence from different layers is corrected by using several deformable mirrors conjugated to these layers. The maximum achievable performance for the single reference stars is not as good as with classical adaptive optics (AO), because of the turbulence above and below the single corrected layers, but instead the correction is more uniform over a significantly larger FoV. Two layers are typically corrected, the ground layer close to the telescope and a higher layer at around 8–10 km height (depending on the site). Most of the turbulence in the atmosphere is generated in the ground layer. Correcting only this layer (GLAO = ground-layer adaptive optics), one can remove the major contributor to the phase aberrations of the incoming wavefronts (Rigaut 2002). Two different modes are used to combine the signals from the different reference stars, the star oriented (SO) and the layer oriented (LO) modes. In the SO mode, each reference star is observed by one wavefront sensor (WFS) and one detector. The information from the different directions of the guide stars is combined to generate information of the three-dimensional structure of the atmosphere within the mapped FoV. By adopting this approach of turbulence tomography (Tallon & Foy 1990), the influence of a single layer can be computed and corrected with one deformable mirror conjugated to this layer. The first verification of this approach was made in an open loop measurement at the Telescopio Nazionale di Galileo (TNG) (Ragazzoni et al. 2000b). In the layer-oriented approach (Ragazzoni et al. 2000a), each WFS and detector is conjugated to one layer in the atmosphere instead of to a single star. The light of several guide stars is optically co-added to increase the signal-to-noise ratio (SNR) on the detector, such that fainter stars can also be used as guide stars. This increases the sky coverage, the fraction of regions on the sky that can provide a suitable natural asterism, essentially for this approach. In addition the number of wavefront sensors and detectors needed is reduced, reducing the detector read-out noise and the needed computing power compared to the SO approach.
High precision astrometry combined with high angular resolution is essential to many science cases in astronomy. For instance, observations of stars around the supermassive black hole in the center of our own Milky Way (e.g. Trippe et al. 2008; Schödel et al. 2009) and the central regions of globular clusters are only possible with space-based facilities or adaptive-optics-supported observations from the ground. Multi-epoch high-precision proper-motion studies with the Hubble Space Telescope (HST) have made it possible to distinguish cluster members from foreground field stars and to study the internal dynamics and kinematics of several globular clusters and galactic starburst clusters (e.g. King & Anderson 2001; McLaughlin et al. 2006; Rochau et al. 2010). Another field of high precision astrometry is the detection and characterization of extrasolar planets by measuring the astrometric reflex-motion of the star (e.g. Benedict et al. 2002; Bean et al. 2007, FGC/HST; Meyer et al., NACO/VLT, in prep.). This important technique complements the radial velocity method, which is the most efficient detection method. A larger FoV enhances the number of usable reference stars for the measurement of the relative astrometric motion and therefore the achievable precision significantly.
The Multi-conjugated Adaptive optics Demonstrator (MAD) is a prototype instrument for MCAO correction and observation that was installed at the ESO VLT UT3 at the Paranal Observatory in 2007 (Marchetti et al. 2007). MAD was designed to study and test different MCAO systems, both in the lab and on-sky (Hubin et al. 2002; Marchetti et al. 2003; Arcidiacono et al. 2006). MAD employs adaptive optics sensing and correction in the star-oriented and the layer-oriented mode. Two layers are sensed and corrected in the full MCAO mode. The ground layer at the telescope’s pupil and a high layer at 8.5 km altitude.
Future AO instruments will use the MCAO technique, such as the Gemini MCAO System (GeMS) at the Gemini South Observatory on Cerro Pachon, Chile. The Fizeau Interferometer LINC-NIRVANA for the Large Binocular Telescope (LBT) on Mt. Graham in Arizona, will be equipped with four layer-oriented correction units, two for each telescope, which will correct the ground layer and a high layer (e.g. Farinato et al. 2008). One of the science cases for LINC-NIRVANA is the detection and characterization of extrasolar planets.
All the above-mentioned aspects and the uniqueness of the very first MCAO data available encouraged us to analyze this data in terms of astrometric precision and stability. The aim of this present study is to estimate the achievable precision and stability in astrometric measurements obtained with MCAO imaging.
2. Observations and data reduction
The observations analyzed here were conducted with the multi-pyramid wavefront sensor of the MAD instrument in the LO mode (Ragazzoni 1996; Ragazzoni et al. 2000b; Arcidiacono et al. 2008). This sensor has the advantage that it can use up to eight guide stars simultaneously, which can be relatively faint (V < 18) and have an integrated light reaching V = 13. A uniform distribution of these stars is preferable but they can be everywhere in the 2′ × 2′ FoV. A NIR science camera is used for the observations, which is also used in the SO mode, called CAMCAO = CAmera for MCAO. It has a 57′′ × 57′′ FoV but can scan a circular FoV of 2 arcmin diameter. The HgCdTe HAWAII2 IR-detector built by Rockwell has 2048 × 2048 pixels with a pixel scale of 0.028′′/px, a readout noise of 13.8 erms, a full well capacity of 65 000 ADU, and a loss of linearity above 35 000 ADU. Two data sets were analyzed, one in the globular cluster NGC 6388 and the other one in the globular cluster 47 Tuc. Both data sets are test data obtained during the first on-sky test of the LO correction mode with MAD at the VLT.
The goal of the observations was to verify and show the capabilities of MCAO observations in LO mode. The original focus was the photometric analysis, since high precision photometric studies in crowded fields, such as clusters, benefit in particular from the large AO-corrected FoV. We therefore note that the observations analyzed here were not obtained in the context of high precision astrometry. Nevertheless, they represent a unique data set to investigate the possibilities of high precision astrometry with MCAO.
2.1. MCAO – NGC 6388
The data of the globular cluster NGC 6388 were obtained on September 27 2007 using the full MCAO capability of MAD. The observations were made in the Ks band (central wavelength = 2.12 μm) using five guide stars with V = 15.0,15.0,15.6,15.7, and 16.3 mag1, corresponding to an integrated magnitude of 13.67 (Arcidiacono et al. 2008). The guide stars are positioned around the FoV (see Fig. 1, left). The observed field lies at the south-eastern rim of the cluster at RA(J2000)=17:36:22.86, Dec(J2000) = –44:45:35.53. Altogether 30 frames were obtained, the first five in GLAO mode and the last 25 in full MCAO mode. A jitter pattern of five positions was used, which was repeated six times with three slightly different central points, to scan part of the 2′ × 2′ FoV, to help us remove the effects of bad pixel incidents and achieve sky estimation. The first ten frames were obtained with a detector integration time of DIT = 10 s and N = 24 of these DITs (=NDIT) are directly co-added onto one frame, resulting in 240 s total exposure time per frame. In the last twenty frames, the number of exposures was reduced to NDIT = 12, resulting in 120 s of total integration time per frame. In Table 1, the observations are summarized together with performance indicators such as the FWHM of the fitted PSF and the seeing measured by the DIMM monitor. The same data were also analyzed to derive photometry by Moretti et al. (2009).
Summary of the observations of the clusters NGC 6388 and 47 Tuc.
 |
Fig. 1 MAD images of the globular clusters NGC 6388 (left) and 47 Tuc (right). The triangles mark the positions of the AO guide stars relative to the center of the observed FoV. The numbers close to the stars correspond to their HST F606W (visual) magnitude. |
2.2. GLAO – 47 Tuc
The observations of the globular cluster 47 Tuc were obtained on September 22 2007 using only the ground layer adaptive optics approach (Arcidiacono et al. 2008). The center of the cluster (RA(J2000) = 00:24:05.6, Dec(J2000) = –72:04:49.4) was observed with the narrow-band Brγ filter (central wavelength = 2.166 μm) and four guide stars between V = 11.9 mag and V = 12.5 mag, positioned around the field with one guide star in the south-eastern corner of the field (Fig. 1, right side). We analyzed 19 frames with DIT = 2 s and NDIT = 15, corresponding to a total exposure time of 30 s per frame.
 |
Fig. 2 Example Strehl maps for one of the NGC 6388 (left) and 47 Tuc (right) data sets, respectively. |
2.3. Data reduction
Each science frame was flatfield-corrected by using the flatfield image obtained from sky flats taken at the beginning of the night and badpixel-corrected with a badpixel mask obtained from the same flat-field images (Moretti et al. 2009). Sky subtraction was done by median combining all sky and science frames to one single sky frame. This frame was then normalized to the median counts of the science frames before subtraction. In the case of 47 Tuc, no flat-field images were taken in Brγ (central wavelength = 2.166 μm) during the night. Consequently, we used the same flat-field image for correction as for the NGC 6388 data observed in Ks (central wavelength = 2.12 μm). In the case of the NGC 6388 data, jittering was used during the observations and we cut all images to the common FoV after the data reduction. This left a slightly smaller field of the size of 1517 px × 1623 px (42.5′′ × 45.4′′). Only stars that were detected in all frames were used in the following astrometric analysis.
3. Strehl maps
As a check of the AO performance we generated Strehl-maps by calculating the Strehl-ratio for each detected star. After interpolating values for areas where no stars were found, a smooth surface was fitted to the data, leading to a two-dimensional Strehl-map for each frame. In Fig. 2, one example of these maps is shown for each data set.
The Strehl is fairly even over the FoV, mean values being between 10%–23% in the full MCAO case and between 9%–14% in the GLAO case, with a small drop-off to the edges of the field. This shows how uniformly the layer-oriented MCAO approach corrects wavefront distortions. The drop-off to the edges of the FoV can be partly explained by the MCAO and the atmospheric tomography approach. The light coming from the different directions of the guide stars is optically co-added and a correction is computed based on this light distribution. However, the footprints of the columns above the telescope in the direction of the guide stars overlap more in the middle of the field than at the edges in the higher layer. If the control software is not optimized to correct over the whole FoV very evenly, the middle of the field will be corrected better. As the data analyzed here is the first data of MCAO in layer-oriented mode, we are not surprised to see such an effect. A performance evaluation of these data can be found in Arcidiacono et al. (2008). In the case of 47 Tuc, the Strehl is smaller than in the case of the NGC 6388 data. GLAO works as a seeing reduction and Strehl ratios of a few percent are expected. The performance of the ground layer correction was therefore even better than expected, which was most probably because during the ground layer observations the turbulence was particularly concentrated in this layer. MCAO should achieve larger and more uniform Strehl ratios of the order of 20%–30% and diffraction-limited FWHM values. Therefore the MCAO corrections have not yet fully reached expectations. Nevertheless, an even Strehl ratio of ~10% or more over a 1′ × 1′ FoV is already an enhancement compared to the seeing limited and the single guide star case, where the Strehl varies with the separation from the guide star (Roddier 1999; Cresci et al. 2005).
4. Astrometric measurements
4.1. Position measurements
To measure the positions of the stars in the single images of both clusters, we used the program StarFinder (Diolaiti et al. 2000a,b), which is an IDL based code for PSF fitting astrometry and photometry in AO images of stellar fields. The following description accounts for both data sets.
We extracted the PSF for fitting the stars directly from the images, by using in each frame the same 30 stars to create the PSF by averaging these stars after deleting close secondary sources. The selected stars are evenly distributed over the FoV and consist of brighter and fainter ones, with magnitude ranges of K = 11−15.3 in the NGC 6388 data and K = 6.3−12.2 in the 47 Tuc data. We assumed here that the PSF does not vary strongly across the FoV. The analysis and tests we performed on the distributions of the eccentricity and orientation of the PSFs in the full FoV did not show a prominent variation over the field. The eccentricities and the orientations of the PSFs were analyzed by fitting a two-dimensional Moffat function to the individual PSFs with the IDL based non-linear least squares fitting package mpfit2dpeak, provided by Craig Markwardt (Markwardt 2009). Results from e.g. Schödel (2010) and Fritz et al. (2010) show that the PSF variation due to anisoplanatism can add an error to the position measurement of up to 0.1 pixel. These numbers were calculated for a classical AO correction with the S27 camera of the VLT/NACO instrument which has a similar image scale as the MAD detector (27.15 mas/px (NACO) versus 28 mas/px (MAD)), but uses only one AO reference star, located somewhere in the FoV. The data analyzed here are the first ones obtained with multi-conjugated AO correction in the layer-oriented approach. These two circumstances lead to a more uniform PSF over the full FoV, as can also be seen in the even Strehl distribution (see Sect. 3). Another confirmation that this assumption is acceptable can be seen in the case of the 47 Tuc data set. One of the used guide stars lies within the FoV (south-eastern corner, see Fig. 1 right side). Inspection of the eccentricity and orientation of the PSFs shows that the guide star does not differ in either shape or orientation from the other stars. A behavior, such as a change in the PSF that depends on the separation of the stars from the guide star, as in the classic AO correction, cannot be seen.
After deleting false detections, we matched the starlists to identify the stars common to all frames, finding ~130 stars in the NGC 6388 field and ~280 stars in the 47 Tuc field.
4.2. Distortion correction
To investigate the stability of the MCAO and GLAO performance in terms of astrometric precision over time, we first corrected for distortions in the field. During the observations, malfunctioning of the de-rotator occurred because of a software problem, leading to a larger rotational error in several frames. If the AO correction is very stable over time, the relative positions of the stars should be the same after correcting for effects such as the de-rotator problem (Arcidiacono et al. 2010). A misposition of the reference star from the tip of the pyramid-WFS exceeding a few λ/D (where λ is the wavelength and D the telescope diameter) with respect to the theoretical (unrotated) positions, also affects the closed loop performance, generating a correction under-performance. We set up a master-coordinate frame to which the single frame coordinates are later mapped. To create this coordinate frame, we used the best frame, chosen according to the highest mean Strehl ratio in the images, as a first reference frame and mapped all the stellar positions from each individual frame onto this reference frame by calculating the shift and scale in x- and y-direction and the rotation between these frames. The MIDAS2 data reduction software and simple affine transformations were used for the transformations. We did not apply any interpolation directly to the images, but instead worked with the measured coordinates. After correcting for the derived rotation for each frame, as well as for the shift and scale in x and y of each stellar position, a master-coordinate frame was created by averaging the position of each star over all frames. The coordinate frame with averaged positions derived in this way was then used as the master-coordinate frame in the subsequent analysis.
In the following, to complete the necessary distortion correction of each single frame, we analyzed the data using two approaches.
In a first attempt, we corrected only basic distortions, including shift, scale, and rotation. To furthermore explore the full capacity of astrometry with MCAO, we performed a second distortion correction, which included higher order terms.
4.2.1. Basic distortion correction
Once we created the reference frame for each data set, all coordinates from each single frame were then mapped to this master frame, leading to a more reliable calculation of the transformation parameters for the individual frames. One might assume that one can achieve even better transformations between the frames by applying this method iteratively, creating once more a master-coordinate frame. If the distortions in the images, those left over from the AO or systematic ones, were homogeneous over the FoV, the transformations should neither greatly change nor enhance the positions of the master-coordinate frame. But if the distortions are not homogeneous, but depend, for example, on the camera position in the FoV, one would introduce warpings in the master-coordinate frame which one cannot map with a simple combination of shifting, scaling and rotation anymore. We therefore stopped after one iteration.
We then calculated the residual separations between the positions of the stars in the master-coordinate frame and in the individual frames, which were calculated using the obtained transformation parameters, and analyzed them as a measure of astrometric precision.
4.2.2. Separation measurements
To evaluate the astrometric precision and stability of MCAO data, we measured the relative separations between various pairs of stars all over the FoV before and after applying the calculated distortion corrections. For this, we derived a time sequence of the separation over all frames. If only a steady distortion is present in the single frames, then the separations should be stable over time or only scatter within a certain range given by the accuracy of the determination of the position of the stars, which is 0.33 mas for the faintest star used in this analysis. If differential distortions between the single frames are present but these distortions are random, then the scatter in the separations is expected to increase, depending on the strength/amplitude of the differential distortions. A non-perfectly corrected defocus, for example, would change the absolute separation between two stars, but, to first order, not the relative one measured in the individual frames, if this defocus is stable over time. An uncorrected rotation between the frames would change the separation of two stars in the x and y-directions, but not their separation, 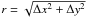 .
.
 |
Fig. 3 Separation between pairs of stars in the NGC 6388 data set plotted against frame number before any distortion correction. The left panel shows the separation in the x-direction, the middle panel in the y-direction, and the right panel the full separation |
Performing this test for several star pairs with short and large separations and with different position angles between the stars before any distortion correction, showed in the case of the NGC 6388 data a recurring pattern in the separation in x,y,r, which is not observable in the 47 Tuc data. Figure 3 shows the separation in x,y, and r over the frame number for five representative pairs of stars in the NGC 6388 data. Looking at the pattern, we find that it repeats itself after five frames for the first ten frames and after ten frames for subsequent frames (where two images were always taken at the same jitter position before moving to the next position), and that this change in separation seems to be correlated with the jitter movement during the observations, which also has a five points pattern with an additional change in the center position. In the case of the MAD instrument the camera itself is moved in the focal plane to execute the jitter pattern. This can lead to vignetting effects for larger jitter offsets and to distortions, which depend on the position of the camera in the FoV. It is unlikely that this pattern is due to problems with the de-rotator because of the uniform repetition of the pattern. This pattern is also not seen in the 47 Tuc data, which was obtained without jitter movements, but experienced the same de-rotator problems.
We performed the same measurements of the same star pairs after applying the calculated distortion correction for shift, scale, and rotation. The strong pattern was found to have disappeared, leaving a more random variation in the separation. In addition, the calculated standard deviation is much smaller, ranging from a factor of ~3 up to a factor of ~19 times smaller. Comparing the single standard deviations shows a smaller scatter among their values than before the distortion correction. All this leads to the conclusion, that the calculated and applied distortions remove a large amount of the separation scatter, but not all of it. The remaining scatter in the separations between the stars in the single frames is still in the range ~1.2−2.8 mas, well above the scatter expected from photon statistics, pointing to uncorrected higher-order distortions.
4.2.3. Basic distortion parameters
The calculated distortion parameters from the basic distortion correction for x-scale, y-scale, and rotation over the frame number, which can be seen as a time-series, are plotted in Fig. 4 for both data sets. Whereas the parameter for the rotation correction looks random, but has a fairly large scatter that reflects the de-rotator problem, the correction parameters for the scale in x and y show a pattern in the case of the NGC 6388 data set (left). This pattern repeats after five (ten) frames, as does the pattern for the separation measurement. As these are the applied correction parameters, they nicely show the existence of the pattern and our ability to correct for this induced scale variation due to the jitter movement. In the 47 Tuc data, there is also some scatter, which can be expected, but no repeating pattern can be seen. In addition, the values are smaller for these ground layer-corrected data, which were obtained without jitter (note the different scaling of the two plots).
 |
Fig. 4 Applied distortion parameters for the basic distortion correction over frame number for the NGC 6388 (left) and 47 Tuc data (right). The panels show from top to bottom the calculated distortion parameters for x scale, y scale, and rotation for each frame. While the rotation parameter is random, the scale parameter of the NGC 6388 data shows a pattern that is not visible in the 47 Tuc data. The vertical lines indicate after which frame the jitter movement of five positions (five or ten frames) was repeated and highlight the introduced pattern. |
4.3. Higher-order distortion correction
We compared the individual frame stellar positions with the reference positions by applying a polynomial fit that also included higher-order transformation terms. To derive the transformation coefficients, we used the IDL routine POLYWARP, which is able to fit a polynomial function of several orders, using a least squares algorithm (see e.g. also Schödel et al. 2009). The polynomial functions used are 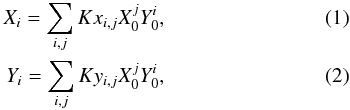 where Xi,Yi are the reference stellar positions, X0,Y0 the stellar positions in the individual frames, and Kxi,j,Kyi,j are the coefficients to be calculated. After performing the fit with orders from i,j ≤ 1 − 10, we decided to perform the final transformation with an order of i,j = 4.
where Xi,Yi are the reference stellar positions, X0,Y0 the stellar positions in the individual frames, and Kxi,j,Kyi,j are the coefficients to be calculated. After performing the fit with orders from i,j ≤ 1 − 10, we decided to perform the final transformation with an order of i,j = 4.
A fit of order four gives an enhancement of 6–10% (NGC 6388) and 14–19% (47 Tuc) of the remaining mean residuals compared to the fit of order 3. Fitting even higher orders is not necessary, as no significant enhancement of the residuals can be seen.
After transformation of the stellar positions in the individual frames to the common reference frame, the residual separations were calculated as in the case of the simpler transformations, (see Sect. 4.2.3).
5. Results
Basic distortion corrections are sufficient for deriving high accuracy photometry (Moretti et al. 2009). However to achieve the highest astrometric precision, a distortion correction including higher orders is necessary. We therefore performed a higher-order distortion correction and present the results below.
5.1. Residual mapping
After calculating the residuals for each frame with respect to the master-coordinate frame, we analyzed the distribution of these residuals over the FoV.
We analyzed contour plots of the residuals by fitting a minimum curvature surface to the data of each frame to look at the spatial distribution of the residuals after the distortion correction The main goal of this test was to check for any strong spatial variation in the residuals over the FoV. No strong spatial variation can be seen, such as for example a strong gradient in one direction. In addition, we analyzed arrow diagrams showing not only the strength, but also the direction of the residuals for each star used to calculate the transformation. We found the orientation of the arrows to be random.
Finally, we calculated the mean residuals over the full FoV for both data sets separately for the x,y, and r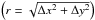 direction for each frame. The mean values are very close to zero (~10-5 − 10-6 pixel), supporting the results from the arrow plots of random orientation, but the mean of the absolute values of the residuals provides a more reliable indicator of the variability present in the data. In the case of an image where the flux is given as flux per pixel, as in any detector image, the ensquared energy is defined as the flux of a PSF within a certain quadratic box with the size of n × n pixel divided by the total flux. The smaller the side length (=diameter) of this box, containing 50% of the total energy, the better the AO correction, moving flux from the wings into the core of the PSF. In Fig. 5, the mean of the absolute values of the residuals over the full FoV in the x and y directions and in the separation r are plotted over the diameter of 50% ensquared energy of the corresponding extracted PSF of each frame and each data set.
direction for each frame. The mean values are very close to zero (~10-5 − 10-6 pixel), supporting the results from the arrow plots of random orientation, but the mean of the absolute values of the residuals provides a more reliable indicator of the variability present in the data. In the case of an image where the flux is given as flux per pixel, as in any detector image, the ensquared energy is defined as the flux of a PSF within a certain quadratic box with the size of n × n pixel divided by the total flux. The smaller the side length (=diameter) of this box, containing 50% of the total energy, the better the AO correction, moving flux from the wings into the core of the PSF. In Fig. 5, the mean of the absolute values of the residuals over the full FoV in the x and y directions and in the separation r are plotted over the diameter of 50% ensquared energy of the corresponding extracted PSF of each frame and each data set.
 |
Fig. 5 Mean of the absolute values of the positional residuals over the diameter of 50% ensquared energy. The upper panels present the NGC 6388 data set and the lower panels the 47 Tuc data set. The plot shows from top to bottom the mean of the absolute values of the residuals to the master frame in the x- and y-directions and the separation |
No correlation of the size of the residuals with the ensquared energy and therefore the performance of the AO system can be seen in the 47 Tuc data set, but there is a small correlation in the NGC 6388 data. What is visible, is that the absolute values of the residuals and their scatter are larger in the case of the NGC 6388 data set than for the 47 Tuc data set, even though the initial observing conditions were better and the measured FWHM values and diameters of 50% ensquared energy are smaller. Compared to a only basic correction of the image distortions (crosses × ), the residuals after a higher order correction (diamonds ◇) are noticeable smaller and do not scatter as much as in the case of the basic distortion correction, showing the superiority of the higher order correction.
The values after the higher order correction give a first impression of how precise the astrometry is in these MAD data. The mean absolute residuals are between 0.020 px and 0.068 px (0.55–1.90 mas) in the x-direction and between 0.028 px and 0.060 px (0.78–1.68 mas) in the y-direction in the MCAO-corrected NGC 6388 data set. For the ground-layer-corrected 47 Tuc data set, the absolute values of the residuals are in the range 0.017–0.034 px (0.47–0.95 mas) and 0.017–0.038 px (0.47–1.07 mas) in the x and y directions, respectively.
With photon statistics alone, the positions should have a smaller range of variation. Taking the positional accuracy calculated from photon statistics for the faintest stars used in this set, the residuals should be within 0.012 px (0.33 mas) and 0.011 px (0.32 mas) in the x and y directions, respectively, in the NGC 6388 case and 0.005 px (0.14 mas) for both, x and y, in the 47 Tuc case. The accuracies Δx,Δy from photon statistics were thereby calculated by 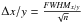 , where FWHMx/y is the full width at half maximum of the fitted PSF in x and y, respectively, and n the number of photons of the fitted star.
, where FWHMx/y is the full width at half maximum of the fitted PSF in x and y, respectively, and n the number of photons of the fitted star.
The basic distortion correction, where we only accounted for shift, scale, and rotation, shows a residual positional scatter that cannot be explained by simple statistical uncertainties. It shows instead that even after a basic distortion correction, there is remaining a positional scatter, which seems to originate in higher order distortions present in the images, as it seems largely independent of the size of the PSF.
The residuals after the higher order corrections show a significant enhancement in the precision, even though the values are still larger than the ones taking only photon statistics into account. However, one has to remember that the latter values only show the lower limit of the possibly reachable positional accuracy. In reality, the uncertainties are likely to be larger, possibly because of AO correction-induced local distortions, which cannot be well described by polynomials and/or errors from the PSF estimation and fit.
In addition, the residuals and scatter were larger when the camera jittered while scanning a bigger FoV. This jitter movement introduced distortions, which can be discerned from the separation measurements and the distortion-correction parameters calculated for scale and rotation, (see Sect. 4.2.3). However the AO correction can also introduce distortions, as it dynamically adapts to atmospheric turbulence changes. With only these two data sets available in the LO correction mode, which are suitable for this analysis, it is not possible at this time to distinguish the different error sources. Although for the 47 Tuc data where no jitter movement was performed, the residuals can be interpreted as the effects of correcting only the ground layer and the AO correction itself.
5.2. Mean positions
As a last step, we calculated the mean position for each star over all corrected frames and its standard deviation as a measure of astrometric precision. In Fig. 6, the achieved astrometric precision is plotted over the K magnitude for each star in the final lists of both data sets (blue × ). The given magnitude represents the estimated 2MASS (Skrutskie et al. 2006) K magnitude of the stars, which provides an indication of the principal relation between precision and intensity. For completeness the total counts are indicated at the upper x-axis of the plots. These values show that we compare stars within the same detected flux range, even though the magnitude ranges differ. This is because for the observations of the cluster 47 Tuc the Brγ narrow-band filter was used instead of the broader Ks-filter and the exposure times were shorter than for the observations of NGC 6388.
As one can see in the plots in Fig. 6 for the NGC 6388 data set (left panels), the fainter stars have less precision in their position than the brighter ones. The mean positional precision of the stars between 14 and 18 mag after the full distortion correction is 0.041 pixels corresponding to 1.143 mas in the x-direction and 0.046 px (1.278 mas) in the y-direction, where x is parallel to the right ascension and y to the declination axes. The median value of the precision in this magnitude range is slightly smaller for x 0.039 px (1.084 mas), and for y 0.042 px (1.179 mas). This is the astrometric precision achievable with the available MAD data in full MCAO mode. Theoretically, as stated above in Sect. 5.1, the faintest stars in this regime should have a precision of about 0.015 px (0.420 mas) assuming only photon statistics. The mean positional precision in the same magnitude range of K = 14–18 mag is then 0.009 px (0.252 mas) in the x- and y-direction. The mean precision from photon statistics was thereby calculated by taking the median of the positional precisions of each star in all individual frames. These estimates for each star are also shown in Fig. 6, plotted as diamonds. The measured precision of the mean position is a factor of 4.6 (x-direction) and 5.1 (y-direction) worse than the one estimated from photon statistics. This is a quite large discrepancy, although one has to take more than simple photon statistics into account when calculating a correct error budget, as for example the error in the PSF estimation used to fit the stellar positions and calculate the uncertainty estimates.
In the GLAO data set of 47 Tuc, the astrometric precision for stars with corresponding 2MASS magnitudes between 9 and 12 mag is 0.034 pixel (0.960 mas) and 0.035 pixel (0.972 mas) in the x- and y directions, respectively. The median value is 0.027 px (0.750 mas) in x and 0.025 px (0.699 mas) in y. Although the fainter stars seem to have slightly larger uncertainties, this correlation is less distinctive than in the MCAO case (NGC 6388). For comparison, the results from the basic distortion correction are also plotted in Fig. 6 as black crosses.
In Table 2, the results described above for the higher-order correction are summarized.
 |
Fig. 6 MAD positional RMS (× ), calculated over all frames as a function of the corresponding 2MASS K-magnitude for both the higher order correction (blue) and the basic distortion correction (black). The left panels show the data of the NGC 6388 cluster, which was observed with the full MCAO mode for the x- and y-direction, and the right panels show the data of the 47 Tuc cluster, observed with ground layer correction. For comparison, the position precision calculated from photon statistics as the median of all frames is also shown (◇). |
Comparing the results for the ground-layer correction with those of the MCAO correction shows that there is a higher precision in the GLAO data. One would expect it the other way round as the initial observing conditions and the average Strehl are better in the MCAO data and the MCAO correction is expected to correct the wavefront distortions more accurately. In addition, the FWHM and the diameter of 50% ensquared energy are smaller in the MCAO data. One of the main differences in the two data sets is the jitter movement. As already shown, this movement introduces distortions.
In a first attempt, we corrected only for shift, scale, and rotation, but the precision achieved afterwards is worse than expected, indicating distortions of higher order. Correcting both the NGC 6388 and the 47 Tuc data sets also for higher order distortions leads to a higher precision in both in addition to a still better correction in the pure ground-layer correction mode (which was also observed without jitter movements).
Summary of the expected and achieved astrometric precisions after a distortion correction including higher orders.
6. Conclusions
We have analyzed the first multi-conjugated adaptive optics data available in the layer oriented approach with respect to astrometric performance. The data were taken with the MCAO demonstrator MAD at the VLT. Two sets of data of globular clusters, observed in two different approaches were analyzed: the globular cluster 47 Tucanae with ground-layer correction only and the globular cluster NGC 6388 in full two-layer MCAO correction.
As a performance measure, we calculated Strehl maps for each frame. The Strehl is fairly uniform over the FoV with a small degradation toward the edges of the FoV and average values between 11% and 23% in the MCAO data and between 9% and 14% in the GLAO data. The lower Strehl in the 47 Tuc data set may partly be explained by only the distortions due to the ground layer having been corrected, although the initial atmospheric conditions were also worse.
After extensive PSF tests, we analyzed the data with the StarFinder code. We created a master frame with positions of isolated stars in the field and calculated in a first attempt distortion parameters for shift and scale in x- and y-direction and a rotation for each frame to this master frame. Separation measurements between stars before and after the distortion correction showed that these corrections indeed reduce the scatter in the separations measured over all frames (Sect. 4.2.2). However, they also highlighted a residual scatter, which is probably due to higher order distortions. A pattern visible in the separation measurements (Fig. 3), as well as in the applied distortion parameters (Fig. 4), is thought to be due to the jitter movement of the camera during the observations. This movement introduced additional distortions which could only be corrected partly, with this distortion correction. To exploit the full capacity of astrometry with MCAO, we performed a fourth order polynomial distortion correction, including also higher order terms.
The mean precision of the positions of the stars, calculated by the scatter in the mean position of the stars over all frames, is 0.041 pixel (1.143 mas) and 0.046 pixel (1.278 mas), for the x- and y-direction, respectively, in the corresponding 2MASS K magnitude range from 14 to 18 mag in the NGC 6388 data set (MCAO). In the 47 Tuc data set (GLAO), the mean precision is 0.034 pixel (0.9602 mas) and 0.035 pixel (0.972 mas) for comparable K magnitudes between 9 and 12.
These results show impressively the capacity of high precision astrometry over a large FoV observed with MCAO.
An astrometric analysis of the core of 47 Tuc was also performed by McLaughlin et al. (2006), who used several epochs of data from the Hubble Space Telescope (HST). They derived positional precisions in the single epoch data, for stars in the same area as the FoV analyzed here, taken with the High Resolution Camera (HRC) of the Advanced Camera for Surveys (ACS) for most stars in the range of 0.01–0.05 pixel. With a plate-scale of 0.027 arcsec/pixel, this corresponds to 0.27–1.35 mas. The errors were calculated in the same way as in this work, taking the standard deviation of the positions in all frames as uncertainties. Detailed distortion corrections were computed for ACS by Anderson (2002), which were applied to the data in the work of McLaughlin et al.. This shows that the precision derived with MAD is comparable to HST/ACS astrometry and with a good distortion characterization, future instruments could yield even higher astrometric precision.
Although the Strehl-ratio is smaller and the FWHM is larger in the GLAO data of the cluster 47 Tuc, the achieved astrometric precision is higher. In addition the observing conditions were worse during the GLAO observations than in the MCAO observations with a mean seeing of 1.13′′ and 0.46′′, respectively. All this leads to the conclusion that the degradation of the astrometric precision in the MCAO data set is mainly due to the jitter movement during the observations, which introduced additional distortions. However, the more complex correction of two layers could have introduced distortions, which we could not correct for. To fully characterize the remaining distortions, one would need to analyse more data, taken under various seeing conditions and observation configurations. As MAD will not be offered again, a fully satisfactory analysis is not possible at this point. Nevertheless, one can interpret the remaining positional uncertainty in the GLAO corrected data, which was obtained without any jitter movement, as distortions remaining from the AO correction and turbulence that has been not compensated for.
All the results presented here are still given in detector coordinates, as we analyzed the data in the context of the adaptive optics correction and instrumentation stability over the full length of the observation. Going to celestial coordinates would involve the correction for effects such as differential aberration and differential refraction to derive the true positions of the stars. As the observed FoV is large, these effects can reach several milliseconds of arc of displacement between stars at different points on the detector (Meyer et al. in prep.). These transformations introduce additional position uncertainties, degrading the astrometric precision further, but need to be performed when comparing data from different epochs, as for example in proper motion studies. The data analyzed here is single epoch data, therefore these corrections did not need to be performed to investigate the stability and possible accuracy of astrometric measurements in MCAO data, as these are effects present in all ground-based imaging data and neither influence nor are influenced by the AO performance.
To make a final comparison between ground-based MCAO and space-based astrometric precision, a multi-epoch study needs to be carried out. As observing time with MAD will not be offered again, this is not possible at the current state and with the available data.
Acknowledgments
The data analyzed here are based on observations collected at the European Southern Observatory, Paranal, Chile, as part of the MAD Guaranteed Time Observations. We would like to thank the anonymous referee for the useful comments and suggestions to this paper.
References
- Anderson, J. 2002, in The HST Calibration Workshop: Hubble after the Installation of the ACS and the NICMOS Cooling System, ed. S. Arribas, A. Koekemoer, & B. Whitmore, 13 [Google Scholar]
- Arcidiacono, C., Lombini, M., Diolaiti, E., Farinato, J., & Ragazzoni, R. 2006, SPIE Conf. Ser., 6272, 627227 [NASA ADS] [Google Scholar]
- Arcidiacono, C., Lombini, M., Ragazzoni, R., et al. 2008, in SPIE Conf. Ser. 7015 [Google Scholar]
- Arcidiacono, C., Lombini, M., Moretti, A., et al. 2010, in SPIE Conf. Ser., 7736 [Google Scholar]
- Bean, J. L., McArthur, B. E., Benedict, G. F., et al. 2007, AJ, 134, 749 [Google Scholar]
- Beckers, J. 1988, in Very Large Telescopes and their Instrumentation, ESO Conference and Workshop Proceedings, Garching, March 21–24, ed. M.-H. Ulrich, 693 [Google Scholar]
- Benedict, G. F., McArthur, B. E., Forveille, T., et al. 2002, ApJ, 581, L115 [NASA ADS] [CrossRef] [Google Scholar]
- Cresci, G., Davies, R. I., Baker, A. J., & Lehnert, M. D. 2005, A&A, 438, 757 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Diolaiti, E., Bendinelli, O., Bonaccini, D., Close, L., Currie, D., & Parmeggiani, G. 2000a, 147, 335 [Google Scholar]
- Diolaiti, E., Bendinelli, O., Bonaccini, D., et al. 2000b, in SPIE Conf. 4007, ed. P. L. Wizinowich, 879 [Google Scholar]
- Ellerbroek, B. L., van Loan, C., Pitsianis, N. P., & Plemmons, R. J. 1994, in SPIE Conf. Ser., 2201, ed. M. A. Ealey, & F. Merkle, 935 [Google Scholar]
- Farinato, J., Ragazzoni, R., Arcidiacono, C., et al. 2008, in SPIE Conf. Ser., 7015 [Google Scholar]
- Fritz, T., Gillessen, S., Trippe, S., et al. 2010, MNRAS, 401, 1177 [NASA ADS] [CrossRef] [Google Scholar]
- Hubin, N., Marchetti, E., Fedrigo, E., et al. 2002, in European Southern Observatory Astrophysics Symposia, 58, ed. E. Vernet, R. Ragazzoni, S. Esposito, & N. Hubin, 27 [Google Scholar]
- King, I. R., & Anderson, J. 2001, in Dynamics of Star Clusters and the Milky Way, ed. S. Deiters, B. Fuchs, A. Just, R. Spurzem, & R. Wielen, ASP Conf. Ser., 228, 19 [Google Scholar]
- Marchetti, E., Hubin, N. N., Fedrigo, E., et al. 2003, in SPIE Conf. Ser. 4839, ed. P. L. Wizinowich, & D. Bonaccini, 317 [Google Scholar]
- Marchetti, E., Brast, R., Delabre, B., et al. 2007, The Messenger, 129, 8 [NASA ADS] [Google Scholar]
- Markwardt, C. B. 2009, in ASP Conf. Ser. 411, ed. D. A. Bohlender, D. Durand, & P. Dowler, 251 [Google Scholar]
- McLaughlin, D. E., Anderson, J., Meylan, G., et al. 2006, ApJS, 166, 249 [Google Scholar]
- Moretti, A., Piotto, G., Arcidiacono, C., et al. 2009, A&A, 493, 539 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ragazzoni, R. 1996, J. Mod. Opt., 43, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Ragazzoni, R., Farinato, J., & Marchetti, E. 2000a, in SPIE Conf. 4007, ed. P. L. Wizinowich, 1076 [Google Scholar]
- Ragazzoni, R., Marchetti, E., & Valente, G. 2000b, Nature, 403, 54 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Rigaut, F. 2002, in Beyond conventional adaptive optics: a conference devoted to the development of adaptive optics for extremely large telescopes, Proceedings of the Topical Meeting held May 7–10, 2001, Venice, Italy, ed. E. Vernet, R. Ragazzoni, S. Esposito, & N. Hubin, Garching, Germany: European Southern Observatory, 2002 ESO Conference and Workshop Proc., 58, 11 [Google Scholar]
- Rochau, B., Brandner, W., Stolte, A., et al. 2010, ApJ, 716, L90 [NASA ADS] [CrossRef] [Google Scholar]
- Roddier, F. 1999, Adaptive Optics in Astronomy (Cambridge University Press) [Google Scholar]
- Schödel, R. 2010, A&A, 509, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schödel, R., Merritt, D., & Eckart, A. 2009, A&A, 502, 91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Tallon, M., & Foy, R. 1990, A&A, 235, 549 [NASA ADS] [Google Scholar]
- Trippe, S., Gillessen, S., Gerhard, O. E., et al. 2008, A&A, 492, 419 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yan, H., Wu, H., Li, S., & Chen, S. 2005, in SPIE Conf. Ser. 5903, ed. R. K. Tyson, & M. Lloyd-Hart, 260 [Google Scholar]
All Tables
Summary of the expected and achieved astrometric precisions after a distortion correction including higher orders.
All Figures
 |
Fig. 1 MAD images of the globular clusters NGC 6388 (left) and 47 Tuc (right). The triangles mark the positions of the AO guide stars relative to the center of the observed FoV. The numbers close to the stars correspond to their HST F606W (visual) magnitude. |
| In the text | |
 |
Fig. 2 Example Strehl maps for one of the NGC 6388 (left) and 47 Tuc (right) data sets, respectively. |
| In the text | |
 |
Fig. 3 Separation between pairs of stars in the NGC 6388 data set plotted against frame number before any distortion correction. The left panel shows the separation in the x-direction, the middle panel in the y-direction, and the right panel the full separation |
| In the text | |
 |
Fig. 4 Applied distortion parameters for the basic distortion correction over frame number for the NGC 6388 (left) and 47 Tuc data (right). The panels show from top to bottom the calculated distortion parameters for x scale, y scale, and rotation for each frame. While the rotation parameter is random, the scale parameter of the NGC 6388 data shows a pattern that is not visible in the 47 Tuc data. The vertical lines indicate after which frame the jitter movement of five positions (five or ten frames) was repeated and highlight the introduced pattern. |
| In the text | |
 |
Fig. 5 Mean of the absolute values of the positional residuals over the diameter of 50% ensquared energy. The upper panels present the NGC 6388 data set and the lower panels the 47 Tuc data set. The plot shows from top to bottom the mean of the absolute values of the residuals to the master frame in the x- and y-directions and the separation |
| In the text | |
 |
Fig. 6 MAD positional RMS (× ), calculated over all frames as a function of the corresponding 2MASS K-magnitude for both the higher order correction (blue) and the basic distortion correction (black). The left panels show the data of the NGC 6388 cluster, which was observed with the full MCAO mode for the x- and y-direction, and the right panels show the data of the 47 Tuc cluster, observed with ground layer correction. For comparison, the position precision calculated from photon statistics as the median of all frames is also shown (◇). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.