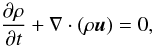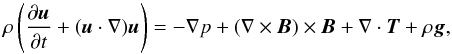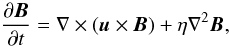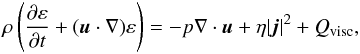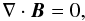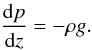| Issue |
A&A
Volume 531, July 2011
|
|
|---|---|---|
| Article Number | A108 | |
| Number of page(s) | 7 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201117099 | |
| Published online | 22 June 2011 | |
Flux emergence within mature solar active regions
Niels Bohr Institute,
Juliane Maries Vej 30,
2100
Copenhagen,
Denmark
e-mail: mactag@nbi.dk
Received: 18 April 2011
Accepted: 20 May 2011
Aims. Recent insterest in flux emergence within mature active regions has led to several observational studies. Our aim is to model such a scenario and investigate the evolution of the system.
Methods. We solve the 3D MHD equations numerically with a Lagrangian-remap scheme. The mature active region is modelled, in the initial condition, with a potential field. The smaller emerging region is a twisted flux tube and is placed between the two polarities of the mature region. The polarities of the new flux are aligned the same way as those of the mature region. The new flux emerges closer to the main negative polarity than the main positive polarity. To investigate the effects of reconnection, the distribution of the parallel electric field is calculated throughout the simulation. The topology of the magnetic field is then studied in regions of interest indicated by the electric field distribution.
Results. The expansion of the new negative polarity is restricted due to the curvature of the overlying field and also because it is of the same sign. Reconnection is found to be strongest at low heights (below the corona) and along the outer side of the new positive polarity and its magnetic tongue. The effect of reconnection, in combination with the pressure between the two flux systems, is to resist the expansion of the new flux. The system then relaxes. Large-scale eruptions, such as CMEs, are not expected from the setup considered. At the new negative polarity, the high magnetic pressure can generate strong parallel electric fields which may lead to localized reconnection. The results of the model are in qualitative agreement with observations.
Key words: magnetohydrodynamics (MHD) / magnetic fields / magnetic reconnection / Sun: atmosphere / methods: numerical
© ESO, 2011
1. Introduction
Solar atmospheric activity is driven by the emergence of magnetic flux from within the Sun’s interior. The concentrations of strong magnetic field that appear on the surface occur in charateristic time-dependent configurations, known as active regions. Such regions can vary in complexity but are generally bipolar, with two fairly distinct areas of opposite polarity (Schrijver & Zwaan 2000). Large active regions can exist for periods from a few days to over a month. Mature active regions become less dynamic with time compared to their initial evolution during emergence. New magnetic flux can, however, emerge within mature active regions and there have been recent observational studies of this. Zuccarello et al. (2008) investigate, via an observational campaign using several different instruments, the emergence of new flux within a mature active region that leads to a flare. The new flux emerges between the two main polarities of the mature region. The axis of the new bipole is at a small angle relative to that of the mature region. Also, the polarities of the new flux are aligned the same way as the larger region, i.e. the negative (positive) polarity of the new flux is on the same side as the negative (positive) polarity of the older region. They find an arch filament system in the chromosphere and that a C-class flare is produced in the low atmosphere (below the corona). They suggest the observed flare can be explained by limited reconnection between the new and old flux systems, which are close to being parallel. Harra et al. (2010) observe a similar event and investigate the outflows produced from the region. In this example, new flux emerges within the positive polarity region, which is dispersed and not compact. Again, the polarities of the new bipole are aligned with those of the mature region. As it expands, strong outflows are observed from the positive polarity of the mature region. Later, as the new flux emerges and expands, outflows are found at the other polarity of the older region. As in Zuccarello et al. (2008), they find C-class flares.
In recent years, simulations have investigated the interaction of emerging regions with overlying coronal magnetic fields. A review of these works is given in Hood et al. (2011). Galsgaard et al. (2007) model a twisted flux tube emerging into a horizontal coronal field. By changing the orientation of the two flux systems, the character of the reconnection changes. When they are almost anti-parallel, high-velocity outflows extend from the reconnection region. This behaviour is not found when the fields are almost parallel. Zuccarello et al. (2008) use this result to argue that limited reconnection is responsible for the C-class flare that they observe, as mentioned above. Other theoretical studies that include overlying fields have tended to focus on the anti-parallel case (e.g. MacTaggart & Hood 2009) since this produces the most dynamic behaviour. To date, there have been few simulations which explicitly include a magnetic field, in the initial condition, that models the geometry of a pre-existing active region. MacTaggart & Hood (2010) model emergence into an overlying arcade. This arcade, however, only represents part of the pre-existing active region.
To investigate the type of scenario presented in Zuccarello et al. (2008) and Harra et al. (2010), we shall model dynamic flux emergence into an overlying bipolar magnetic field that represents the mature active region. Our study will concentrate on a setup that resembles the observations of Zucarrello more than those of Harra et al. (2010), i.e. the new flux will be placed between the the two main polarities of the mature active region rather than inside one of them. The outline of the paper is as follows: Sect. 2 describes the model setup and the initial conditions used in the simulations. In Sect. 3 we examine the dynamics of the emerging flux into the overlying field. Section 4 contains a discussion on how the features of the model relate to the observations. A summary and conclusions complete the paper in Sect. 5.
2. Model setup
In this section we describe the numerical setup and the initial atmosphere and magnetic field configurations.
2.1. Main equations
The 3D compressible and resistive magnetohydrodynamic (MHD) equations are solved using a Lagrangian remap scheme (Arber et al. 2001). In dimensionless form, these are
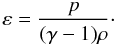 The basic variables are the density ρ, the pressure p, the magnetic field vector B and the velocity vector u. |j| is the magnitude of current density and g is gravity (uniform in the z-direction). γ (= 5/3) is the ratio of specific heats and η is the uniform resistivity. The variables are made dimensionless against photospheric values, namely: pressure, pph = 1.4 × 104 Pa; density, ρph = 3 × 10-4 kg m-3 and scale height Hph = 170 km. The other units used in the simulations are: temperature, Tph = pph/(Rρph) = 5.6 × 103 K; speed, uph = (pph/ρph)1/2 = 6.8 km s-1; time, tph = Hph/uph = 25 s; and magnetic field Bph = (2μ0pph)1/2 = 1.3 × 103 G. We take η = 10-4. For the given resolution, this value of η is the largest for which the results are indistinguishable from those relying solely on numerical resistivity. It is important, however, to explicitly include resistivity for the purpose of ensuring a correct energy balance. The viscosity tensor and viscous contribution to the energy equation are, respectively,
The basic variables are the density ρ, the pressure p, the magnetic field vector B and the velocity vector u. |j| is the magnitude of current density and g is gravity (uniform in the z-direction). γ (= 5/3) is the ratio of specific heats and η is the uniform resistivity. The variables are made dimensionless against photospheric values, namely: pressure, pph = 1.4 × 104 Pa; density, ρph = 3 × 10-4 kg m-3 and scale height Hph = 170 km. The other units used in the simulations are: temperature, Tph = pph/(Rρph) = 5.6 × 103 K; speed, uph = (pph/ρph)1/2 = 6.8 km s-1; time, tph = Hph/uph = 25 s; and magnetic field Bph = (2μ0pph)1/2 = 1.3 × 103 G. We take η = 10-4. For the given resolution, this value of η is the largest for which the results are indistinguishable from those relying solely on numerical resistivity. It is important, however, to explicitly include resistivity for the purpose of ensuring a correct energy balance. The viscosity tensor and viscous contribution to the energy equation are, respectively,
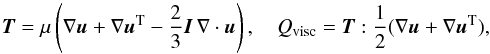 where μ is the viscosity and I is the identity tensor. We use the fluid viscosity as an aid to stability and take μ = 10-4.
where μ is the viscosity and I is the identity tensor. We use the fluid viscosity as an aid to stability and take μ = 10-4.
The equations are solved on a uniform Cartesian grid (x,y,z) of (256,256,256) for the (nondimensionalized) region −120 ≤ x ≤ 120, −120 ≤ y ≤ 120 and −20 ≤ z ≤ 100. The boundary conditions are periodic on the side walls of the computational box and the top and bottom boundaries are closed. Damping layers are included on all sides of the computational domain to reduce the reflection of waves.
Due to computational contsraints (e.g. adequate resolution, memory availability, etc.) the region that we simulate is smaller than the actual regions on the Sun. The length of our region is, approximately, 0.4 that of the region in Harra et al. (2010) and 0.5 that of the region in Zuccarello et al. (2008). It has become common practice in theoretical flux emergence to simulate smaller regions. The results from these studies, assuming no explicit scaling is required (e.g. a critical wavelength for an instability), can be applied to larger regions. This has proved to be a successful approach in gaining deeper insight into active region dynamics (Hood et al. 2011).
2.2. Initial atmosphere
In complex 3D simulations, it is beneficial to have an initial condition that is as close to an equilibrium as is practically possible in order to correctly identify physical processes and not confuse them with the effects of a non-equilibrium initial condition. The initial stratification of the atmosphere is similar to that used in previous flux emergence studies (e.g. Fan 2001; Murray et al. 2006). The solar interior (z ≤ 0) is taken to be marginally stable to convection since in this study we are focussing on the emerging field. The photosphere/chromosphere lies in the region 0 ≤ z ≤ 10, the transition region in 10 ≤ z ≤ 20 and the corona in z ≥ 20. The (non-dimensionalized) temperature is specified as
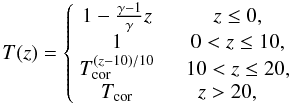 where Tcor = 150 is the coronal temperature. The other state variables, pressure and density, are found by solving the hydrostatic equation
where Tcor = 150 is the coronal temperature. The other state variables, pressure and density, are found by solving the hydrostatic equation
2.3. Initial magnetic field
2.3.1. Equilibrium field (old flux system)
To model a mature active region we use a potential field. From observations, the time scale for dynamic activity in these regions is much greater than that for new emerging flux. Hence, a mature active region can be modelled as a static equilibrium in the initial condition. The potential field can be expressed in terms of a Green function (e.g. Petrie & Neukirch 2000) 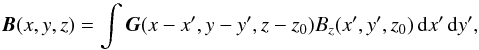 (1)where z0 is the base of the computational domain (in the solar interior) and the Green function is defined by
(1)where z0 is the base of the computational domain (in the solar interior) and the Green function is defined by
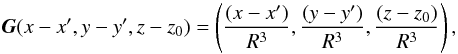 where R2 = (x − x′)2 + (y − y′)2 + (z − z0)2. To produce the two main polarities of the mature active region, two sources are placed below z0. This gives
where R2 = (x − x′)2 + (y − y′)2 + (z − z0)2. To produce the two main polarities of the mature active region, two sources are placed below z0. This gives
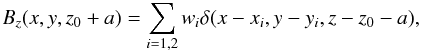 (2)where a is small and negative and wi are the weights for the two polarities. Inserting Eq. (2) into (1) and integrating, gives the expression for the decayed active region magnetic field
(2)where a is small and negative and wi are the weights for the two polarities. Inserting Eq. (2) into (1) and integrating, gives the expression for the decayed active region magnetic field
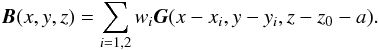 In this paper, we take the values w1 = −150, w2 = 150 and a = −1. The stronger the magnitude of the source, the stronger and more vertical the field of the main polarities. The positions of the main polarities are chosen to be at a small angle to the y-axis. The reason for this is to reflect the observation from Zuccarello et al. (2008) that the relative inclination between the new and old flux systems is at a small angle. In the simulations, the new emerging flux is placed along the y-axis.
In this paper, we take the values w1 = −150, w2 = 150 and a = −1. The stronger the magnitude of the source, the stronger and more vertical the field of the main polarities. The positions of the main polarities are chosen to be at a small angle to the y-axis. The reason for this is to reflect the observation from Zuccarello et al. (2008) that the relative inclination between the new and old flux systems is at a small angle. In the simulations, the new emerging flux is placed along the y-axis.
The initial atmosphere and equilibrium field are tested to discover if any oscillations develop and grow, rendering the initial condition unstable. This is not the case, however, and the initial equilibrium is stable. Figure 1 shows the initial equilibrium field for the old flux system.
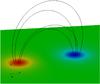 |
Fig. 1 The equilibrium magnetic field of the old active region. A magnetogram (Bz) at the base of the photosphere z = 0 shows the main polarities of this region (blue is negative and red is positive). Some field lines are traced from the negative polarity. The axis connecting the centres of the two polarities is at 11° to the y-axis. |
2.3.2. Magnetic flux rope (new flux system)
For the new emerging flux system we use a twisted flux tube placed in the solar interior along the y-axis with its centre at (x0,z0). In cylindrical coordinates, the magnetic field of the flux rope, B = (Br,Bθ,By) is defined by 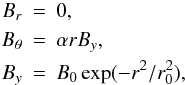 where α is the twist, B0 is the axial field strength, r2 = (x − x0)2 + (z − z0)2 and r0 is the radius of the tube. The pressure difference within the tube, relative to the background hydrostatic pressure, is
where α is the twist, B0 is the axial field strength, r2 = (x − x0)2 + (z − z0)2 and r0 is the radius of the tube. The pressure difference within the tube, relative to the background hydrostatic pressure, is
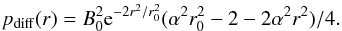 Assuming isotropic thermal conduction in the solar interior is significantly large, the plasma would quickly equalize the temperature inside and outside the flux tube. Hence the density within the tube must be lower than the surrounding background density. To encourage an Ω-loop to form and rise upwards, the density deficit is multiplied by exp(−(y − y0)2/λ2), where y0 is the position of the Ω-loop and λ is a scale parameter. This flux tube model has been used in several previous flux emergence studies (e.g. Fan 2001; Murray et al. 2006; MacTaggart & Hood 2010). A fuller decription can be found in Hood et al. (2011).
Assuming isotropic thermal conduction in the solar interior is significantly large, the plasma would quickly equalize the temperature inside and outside the flux tube. Hence the density within the tube must be lower than the surrounding background density. To encourage an Ω-loop to form and rise upwards, the density deficit is multiplied by exp(−(y − y0)2/λ2), where y0 is the position of the Ω-loop and λ is a scale parameter. This flux tube model has been used in several previous flux emergence studies (e.g. Fan 2001; Murray et al. 2006; MacTaggart & Hood 2010). A fuller decription can be found in Hood et al. (2011).
3. Dynamical evolution
In this section, we shall describe the evolution of emergence within a mature region by focussing on a particular experiment. Each subsection will focus on a particular feature, though all the features are connected.
3.1. Pressures and expansion
The parameters used in this paper are: x0 = 0, y0 = 12, z0 = −8, B0 = 8, a = 2 and α = 0.25. The angle between the axis, connecting the centres of the polarities of the mature region, and the y-axis (and, hence, the axis of the flux rope) is 11°. The coordinates of the centres of the sources are (x1,y1) = (−7.63,39.265) for the main negative source and (x2,y2) = (7.67,−39.265) for the main positive source. The position of the buoyant part of the flux rope is chosen so that when the new bipole emerges, it will be closer the mature region’s negative polarity, as in the observation of Zuccarello et al. (2008).
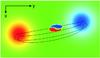 |
Fig. 2 The new flux emerging into the mature region at t = 58. Some field lines of the mature region are shown in black. A field line from the emerging flux is shown in grey. The angle between the axes of the two flux systems is 11°. The magnetogram (at z = 0) displays the shape of the emerging flux – leading polarities with trailing tongues. |
In the simulation, the new flux reaches the base of the photosphere (z = 0) at approximately t = 40. At this time, the magnetic field emerges in a North-South direction before changing to East-West, as shown in Fig. 2. This is common to all buoyant cylindrical flux rope simulations (Hood et al. 2011) and is a direct consequence of the twisted magnetic field. Due to the geometry of the mature region, the expansion of the polarities of the new flux region is asymmetric. The negative (positive) polarity of the new region moves towards the negative (positive) polarity of the old region. Since the new flux emerges closer to the large negative polarity, the new negative polarity has to expand into a more curved field than the new positive polarity. This results in an imbalance of pressure on both sides of the new bipole and allows the new positive polarity to expand more easily than the negative. Figure 3 shows the total pressure, pT = p + |B|2/2, on (x,z) = (0,0) for three different times. At t = 45 (solid line) there is an initial increase in pT just after the emergence of the new flux. Later at t = 65 (dashed line), the pressure profile is no longer symmetric. The total presure on the right (negative polarity) is greater than that on the left (positive polarity). This pressure imbalance is caused by the fact that the new negative polarity experiences greater resistance due to the curvature of the field it pushes into and the fact that that field is of the same sign as the negative polarity. The field encountered by the positive polarity is more horizontal and offers less resistance. At t = 85, a similar profile exists but with a reduction in the total pressure.
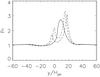 |
Fig. 3 The total pressure along (x,z) = (0,0). Key: t = 45 (solid), t = 65 (dash), t = 85 (dot-dash). |
The magnetic field of the mature region also has an effect on the upward expansion of the new emerging flux. By t = 159, the top of the emerging flux tube field reaches z ≈ 30. This, of course, is a much smaller height than would be attained if the flux rope was expanding into a field-free atmosphere. Murray et al. (2006) find that for a much weaker field strength (B0 = 2) the emerged field reaches z = 30 at t ≈ 70 when there is no overlying field. A description of the pressures between the two flux systems, however, is not enough to fully describe the evolution of the system. For a more complete picture, one must consider the reconnection between the two systems.
3.2. Parallel electric fields and reconnection
Figure 2 shows the new emerging bipole between the two larger polarities of the mature region at t = 58. Some field lines of the mature region are traced in black. A field line of the new bipole is traced in grey. From the view of Fig. 2, there seems to be only a small angle between the field of the new and old flux systems, suggesting that reconnection plays only a small role in the evolution of the system. This, however, is misleading since it is, essentially, a 2D interpretation of a 3D problem. The Ω-shaped emerging flux rope is constantly surrounded by the magnetic field of the mature active region. Hence, there is always a range of different angles that give rise to varying degrees of reconnection. To study the relationship between reconnection and the complex evolving geometry of the system, we shall investigate the distributions of regions of strong parallel electric field.
In resistive MHD, the electric field comes from Ohm’s law
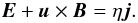 Taking the dot product of this with B/|B| gives the parallel electric field
Taking the dot product of this with B/|B| gives the parallel electric field
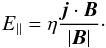 Regions of strong |E∥| are associated with regions of strong reconnection (Schindler 2008). There exist methods to construct magnetic skeletons that describe the topology of magnetic fields from MHD simulations (e.g. Haynes & Parnell 2010). In this study, however, it is sufficient to investigate the distribution of strong |E∥| within the computational domain and how this correlates with the evolving geometry and topology of the magnetic field. By “strong |E∥|” we mean any value greater than some threshold, E0. We choose E0 = 1.4 × 10-5, which, in dimensionless units, is a high value for |E∥| in the simulation. This choice will allow us to identify possible regions of strong reconnection. We can then study the how the changing geometry of the system is affected by these regions.
Regions of strong |E∥| are associated with regions of strong reconnection (Schindler 2008). There exist methods to construct magnetic skeletons that describe the topology of magnetic fields from MHD simulations (e.g. Haynes & Parnell 2010). In this study, however, it is sufficient to investigate the distribution of strong |E∥| within the computational domain and how this correlates with the evolving geometry and topology of the magnetic field. By “strong |E∥|” we mean any value greater than some threshold, E0. We choose E0 = 1.4 × 10-5, which, in dimensionless units, is a high value for |E∥| in the simulation. This choice will allow us to identify possible regions of strong reconnection. We can then study the how the changing geometry of the system is affected by these regions.
 |
Fig. 4 The probability density function (PDF) of |E∥| > E0 as a function of horizontal position for the height z = 4. The data used in the PDF’s construction are from t ∈ [40,165] . The axes are transposed for an easier comparison with the magnetograms. |
Figure 4 shows the probability density function, or PDF, (Silverman 1986) of |E∥| > E0 as a function of horizontal position at the height z = 4 (mid-photosphere). The PDF takes account of the time period from t = 40, when the flux tube appears at the base of the photosphere, to t = 165, the end of the simulation. However, values of |E∥| > E0 do not appear at z = 4 until t = 56. As this plot displays the probability density of |E∥| > E0 for many time steps, one must consider how the new flux expands into the mature active region in order to interpret it correctly.
The emerging flux tube first reaches the plane of z = 4 at t = 56. The centre of the bipole is located at, approximately, (x,y) = (0,7), which is different from the original centre of the buoyant part of the tube, (x,y) = (0,12). This is because, as described earlier, the lateral expansion of the positive polarity is greater than that of the negative. Starting from this position on the PDF, we shall first consider the distribution below this. The development of this part of the density estimate occurs first due to the faster expansion of the positive polarity.
Below y = 7, there is a clear bias in the density of |E∥| > E0 towards one side of the expanding flux tube. This coressponds to the positive polarity and its extended tongue (Luoni et al. 2011). This is the region surrounding the lower part of the new bipole in Fig. 2. As the tube spreads left, the pattern of the probability density become more complicated and multiple peaks begin to form at y ≈ −8.
Moving right from (x,y) = (0,7), the extent of the PDF is much less due to the restricted expansion of the flux tube’s negative polarity. As with the lower left part of the PDF, there is a strong concentration of the probability density for x > 0, corresponding to the tongue of the positive polarity. Towards the end of the simulation, however, at t ∈ [156,165] , there is an increasing number of |E∥| > E0 in the region x ∈ [−10,0] , y ∈ [10,20] . Naively, one would not expect strong reconnection here since this is where the negative polarity of the emerging flux tube interacts with the negative polarity of the mature region. The fact that there is possible reconnection here is a manifestation of the 3D nature of the problem – a complex geometry enabling multiple reconnection regions.
 |
Fig. 5 The probability density function (PDF) of |E∥| > E0 as a function of horizontal position for the height z = 9. The data used in the PDF’s construction are from t ∈ [40,165] . The axes are transposed for an easier comparison with the magnetograms. |
To study the distribution of regions of strong |E∥| higher in the atmosphere, we shall now consider the PDF of |E∥| > E0 in the plane z = 9, which is at the top of the chromosphere and just below the transition region. Figure 5 shows the PDF at z = 9. The values of |E∥| > E0 that contribute to this PDF occur within two time periods. Two distinct regions appear within these time periods and these are labelled in Fig. 5. Region 1, the area below y ≈ 10, develops during t ∈ [66,76] . The main part of this region corresponds to the positive polarity of the emerging flux tube expanding into the overlying field. There is also, however, a small peak at y ≈ 8 that is not associated with the positive polarity of the emerging flux tube. Region 2 corresponds to values of |E∥| > E0 that appear during t ∈ [151,165] and are in a position directly over the negative polarity of the new flux.
At z = 15 (mid transition region) there are some values of |E∥| > E0 that appear at times t = 70,80. These occur in the region corresponding to the tongue of the emerging flux tube’s positive polarity. For brevity, the PDF is not shown.
Higher up in the corona, at z = 22, we perform the same investigation as for the other heights. The result, however, is that |E∥| < E0 for the entire time of the simulation. This result does not mean that there is no reconnection in the corona. It does suggest, however, that reconnection in this region is less significant than in lower layers.
The PDFs suggest a general picture for the development of reconnection throughout the evolution of the system. As the emerging flux tube expands into the overlying field of the mature region, the contact region between the positive polarity, and its associated tongue, of the new flux with the old flux generates a high density of |E∥| > E0. This implies strong reconnection in this region. In the lowest layer considered, z = 4, this occurs throughout the entire simulation. Slightly higher at z = 9, the probability density caused by this expansion only appears during a short time interval. Higher still, at z = 15, the time interval is even shorter. In the corona, no signature is picked up at all. Later in the simulation, at both z = 4 and z = 9, there is a new prominent region of |E∥| > E0 at the negative polarity of the emerging flux tube. This and other complex regions of |E∥| > E0 in the PDFs reflect the 3D nature of the setup. To investigate how reconnection affects the evolution of the system, we must now consider the geometry and topology of the magnetic field in the regions of strong |E∥| highlighted by the PDFs. Figure 6 shows field line connections between the flux rope and the overlying field at t = 93.
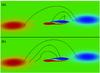 |
Fig. 6 Magnetic field connections at t = 93. a) Shows how, after reconnection, the positive polarity of the new flux now connects to main negative polarity. b) Shows the case for the opposite polarities. |
The top field line in Fig. 6a is part of the original mature active region field that connects the two main polarities. The lowest field line in Fig. 6a belongs to the emerging flux tube and has not reconnected with the overlying field. The squashed shape of the field line at the negative polarity of the tube is due to the build up of pressure there, as described earlier. The middle field line in Fig. 6a shows the effects of reconnection, with magnetic field from near the centre of the tube’s positive polarity now connecting with the main negative polarity. This reconnection occurs in the region of the tube’s positive polarity tongue and is highlighted by the PDFs as the most likely region for strong reconnection.
Figure 6b shows more field lines, but this time with connections to the main positive polarity. As in (a), the top field line, that reaches the corona, is not reconnected. The two lower field lines shown are reconnected, however. Magnetic field from near the centre of the tube’s negative polarity connect to the mature region’s positive polarity. This reconnection occurs at the outer edge of the tube’s positive polarity.
The effect of this reconnection is to resist the growth of the emerging flux tube that expands due to the magetic buoyancy instability. Since the positive polarity of the flux tube now connects to the stationary negative polarity of the mature region, and vice-versa, there is an increased tension force that pulls on the horizontally expanding polarities of the flux tube for reconnected field lines that are shorter than the original field lines that have expanded because of the magnetic buoyancy instability. This, combined with the pressure exerted on the expanding flux by the mature region, helps to slow the expansion down.
In Fig. 5, there is peak in the PDF corresponding to times near the end of the simulation. This peak, labelled region 2, corresponds to a position directly over the negative polarity of the emerging flux tube. One may ask, why is there a peak of |E∥| > E0 over the flux tube’s negative polarity, at z = 9 and not at its positive polarity? The reason lies in the pressure imbalance discussed earlier. At the negative polarity of the flux tube, field lines tend to become more squashed due to the resistance experienced during expansion. This leads to regions of high |E∥|, where the current density and magnetic field vectors become aligned. Although clearly highlighted in the PDF at z = 9, the signature can also be found at lower heights. Figure 7 shows how the magnetic pressure (pm = |B|2/2) and E∥ vary along (x,z) = (0,4) at t = 161. As in Fig. 3, the pressure at the negative polarity is greater than that at the positive polarity. The peaks in E∥ correspond to the peaks in pressure.
 |
Fig. 7 The magnetic pressure and E∥ taken along (x,z) = (0,4) at t = 161. The peaks in magnetic pressure correspond to those in E∥. Only one peak is detected in the PDFs since the other is below (in magnitude) the cutoff E0. Key: pm (solid), E∥ (dash). |
Unlike the reconection highlighted in Fig. 6, analysis of the magnetic field lines in this region yields no obvious changes in topology. If reconnection is occuring in this localized region, it may take the form of slippage between the field lines (e.g. Hornig & Priest 2003). This may also be sign of magnetic diffusion on a larger scale.
3.2.1. Velocity profiles and relaxation
The effects of pressure and reconnection, described in the previous sections, lead to the relaxation of the system. Figure 8 shows the profiles of uy at (x,z) = (0,9) for times t = 70,100,130,160. At t = 70, there is an asymmetric profile with a larger magnitude of uy corresponding to the positive polarity of the new flux tube. This is because, as described earlier, its initial expansion encounters less resistance than that of the negative polarity. At the later times of t = 100,130, however, the strong expansion speed of the positive polarity is reduced due to the restraining effects of reconnected field lines from this polarity connecting to the mature region’s negative polarity (see Fig. 6a) and the pressure between the two flux systems. At the late time of t = 160, the expansion speeds have greatly reduced and the system relaxes.
 |
Fig. 8 Horizontal expansion speeds along (x,z) = (0,9). Key: t = 70 (solid), t = 100 (dash), t = 130 (dot-dash), t = 160 (double dot-dash). |
 |
Fig. 9 Shear profiles along (y,z) = (7,0). Key: t = 70 (solid), t = 160 (dash). |
One feature that has appeared in simulations of twisted flux tube emergence is the ability of an emerged tube to produce an atmospheric flux rope whose axis is different from that of the original tube. Depending of the configuration of the overlying field, these flux ropes can erupt (Hood et al. 2011). One of the key ingredients for the production of atmospheric flux ropes is a shear flow driven by the Lorentz force along the polarity inversion line of the emerging region. In the simulation of this paper, however, the reconnection, descibed previously, acts to restrain such shear flows. Figure 9 displays the shear profiles at (y,z) = (7,0) for times t = 70,160. By the end of the simulation, the shear flows are almost completely diminished. The result of this is that atmospheric flux ropes, as produced in other flux emergence configurations, are not expected in this setup.
4. Comparison to observations
In this section we discuss how some of the results from the simulation relate to those from the observations of Zuccarello et al. (2008).
Apart from the parameter choices for the model, there are two main assumptions concerning the magnetic fields. The first is that the mature region can be modelled using a static magnetic field (at least in the initial condition). The second is that we model the new flux using a twisted flux tube. The first point is justified from both a modelling and an observational perspective. For modelling, as stated earlier, it is beneficial to have an initial equilibrium so that the key factors in the evolution of the system can be isolated and not confused with effects generated by a non-equilibrium initial condition. From an observational perpective, mature regions are much less dynamic than new ones, so treating them as static in the initial condition is a good approximation. For the second point, the approach we have taken is justified, with respect to the observations, since only a weak twist is used and the flux tube produces magnetorams similar to what is observed. Zuccarello et al. (2008) state that they cannot see any clear evidence of twist in the new emerging region based on arches found in Hα images not crossing. This is subject to interpretation and we feel that the case of no twist is unlikely to occur on the Sun. Also, previous simulations (Murray et al. 2006) have shown that flux tubes with little or no twist struggle to emerge. We believe our weakly-twisted flux tube model is a good approximation to the new emerging flux. To test the effects of the twist, he have performed an experiment with even weaker twist, α = 0.15. The results from this are very similar to those of this paper. Hence we are satisfied that our model is justified.
One important feature of the model is that it predicts the correct position of flaring. Brightenings, shown in TRACE images in Zuccarello et al. (2008), occupy an almost linear ribbon close to the footpoints of the new flux. This corresponds to the model prediction of the strongest reconnection being located along the tongue of the positive polarity of the emerging tube. The tongue is a manifestation of the azimuthal magnetic field component, which even a small amount of twist can provide. The observed C-class flare is found to occur in the low atmosphere, i.e. below the corona. The model implies this result, with the strongest reconnection taking place below the corona.
The effect of the “flare” reconnection in the model is to resist the expansion of the new flux. This diminishes the shear flows along the polarity inversion line of the new flux and, by extension, the probability of a large-scale, CME-type, eruption. This ties in with the observations, where a C-class flare is the strongest “eruption”.
5. Summary and conclusions
In this paper, we have modelled the emergence of a twisted flux tube into a mature active region. In the initial condition, the mature region is a potential magnetic field. The flux tube emerges between the two main polarities of the mature region, with the positive (negative) polarity of the new flux being closest to the positive (negative) polarity of the mature region. The axes of the two flux systems are placed, initially, at a small angle of 11°.
When the flux tube emerges into the overlying magnetic field, its negative polarity experiences greater resistance to expansion than its positive polarity. Since the emerging Ω-loop is placed closer to the main negative polarity, the curvature of the overlying field at the flux tube’s negative polarity, combined with the fields being the same sign, results in a greater pressure. The overlying field at the tube’s positive polarity is more horizontal and offers less resistance to expansion.
Analysis of regions of large |E∥| indicate the locations of strong reconnection. These regions correspond to the edge of the new positive polarity and associated tongue, and the new negative polarity. 3D reconnection occurs at the positive polarity and tongue and results in magnetic field lines from the new positive (negative) polarity connecting to the main negative (positive) polarity. Over the new negative polarity, the increased pressure
results in a greater squashing of field lines here, resulting in a strong localized |E∥|. Although no obvious change of topology can be detected, reconnection may occur locally through the slippage of field lines. The regions of strong |E∥| occur in the low atmosphere, i.e. below the corona. This and the locations of reconnection described above are in qualitative agreement with observations, by Zuccarello et al. (2008), of a similar region.
Due to the changes in connectivity described above, the horizontal expansion of the new polarities is resisted by the field lines connecting to the main polarities. This, combined with the resistance involved with expanding into the overlying field, results in the system relaxing. A common feature of twisted flux tube emergence is the production of atmospheric flux ropes that can erupt. This, however, does not occur in the model due to the effects of reconnection that diminish the neccessary shear flows. Hence, large-scale eruptions, like CMEs, would not be expected from this setup.
The results of this study hold primarily for emergence within a mature region with two concentrated polarities. Often, however, bipolar regions contain one polarity that is much more diffuse than the other. The results of this study may hold for emergence within such a region if the new flux is too weak to deform the polarities appreciably. If it is strong enough, however, it could push though the diffuse polarity and produce a different reconnection pattern.
There are several possible extensions to the model. Two obvious choices are a parameter study and the inclusion of extra physics, such as turbulent convection. Another, and perhaps more interesting, way to proceed would be to be to pursue the case, described above, of modelling the mature region with one dispersed polarity. This could also include studying emergence within the diffuse polarity, as in Harra et al. (2010).
Acknowledgments
The author acknowledges financial support from the European Commission through the SOLAIRE Network (MTRN-CT-2006-035484). The author would also like to thank Klaus Galsgaard, Francesca Zuccarello and the International Space Science Institute (ISSI) for an invitation to the ISSI Flux Emergence Workshop. Computer time was provided by the Danish Center for Scientific Computing.
References
- Arber, T. D., Longbottom, A. W., Gerrard, C. L., & Milne, A. M. 2001, J. Comp. Phys., 171, 151 [Google Scholar]
- Fan, Y. 2001, ApJ, 554, L111 [NASA ADS] [CrossRef] [Google Scholar]
- Fan, Y. 2009, ApJ, 697, 1529 [NASA ADS] [CrossRef] [Google Scholar]
- Galsgaard, K., Archontis, V., Moreno-Insertis, F., & Hood, A. W. 2007, ApJ, 666, 516 [NASA ADS] [CrossRef] [Google Scholar]
- Harra, L. K., Magara, T., Hara, H., et al. 2010, Sol. Phys., 263, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Haynes, A. L., & Parnell, C. E. 2010, Phys. Plasmas, 17, 092903 [Google Scholar]
- Hood, A. W., Archontis, V., & MacTaggart, D. 2011, Sol. Phys., in press [arXiv:1103.3685] [Google Scholar]
- Hornig, G., & Priest, E. R. 2003, Phys. Plasmas, 7, 2712 [NASA ADS] [CrossRef] [Google Scholar]
- Luoni, M. L., Mandrini, C. H., Démoulin, P., & van Driel-Gesztelyi, L. 2011, Sol. Phys., in press, DOI: 10.1007/s11207-011-9731-8 [Google Scholar]
- MacTaggart, D., & Hood, A. W. 2009, A&A, 508, 445 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- MacTaggart, D., & Hood, A. W. 2010, ApJ, 716, L219 [NASA ADS] [CrossRef] [Google Scholar]
- Murray, M. J., Hood, A. W., Moreno-Insertis, F., Galsgaard, K., & Archontis, V. 2006, A&A, 460, 909 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petrie, G. J. D., & Neukirch, T. 2000, A&A, 356, 735 [NASA ADS] [Google Scholar]
- Schindler, K. 2008, Physics of Space Plasma Activity (Cambridge University Press) [Google Scholar]
- Schrijver, C. J., & Zwaan, C. 2000, Solar and Stellar Magnetic Activity (Cambridge University Press) [Google Scholar]
- Silverman, B. W. 1986, Density Estimation for Statistical and Data Analysis (Chapman and Hall) [Google Scholar]
- Zuccarello, F., Battiato, V., Contarino, L., et al. 2008, A&A, 488, 1117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Figures
 |
Fig. 1 The equilibrium magnetic field of the old active region. A magnetogram (Bz) at the base of the photosphere z = 0 shows the main polarities of this region (blue is negative and red is positive). Some field lines are traced from the negative polarity. The axis connecting the centres of the two polarities is at 11° to the y-axis. |
| In the text | |
 |
Fig. 2 The new flux emerging into the mature region at t = 58. Some field lines of the mature region are shown in black. A field line from the emerging flux is shown in grey. The angle between the axes of the two flux systems is 11°. The magnetogram (at z = 0) displays the shape of the emerging flux – leading polarities with trailing tongues. |
| In the text | |
 |
Fig. 3 The total pressure along (x,z) = (0,0). Key: t = 45 (solid), t = 65 (dash), t = 85 (dot-dash). |
| In the text | |
 |
Fig. 4 The probability density function (PDF) of |E∥| > E0 as a function of horizontal position for the height z = 4. The data used in the PDF’s construction are from t ∈ [40,165] . The axes are transposed for an easier comparison with the magnetograms. |
| In the text | |
 |
Fig. 5 The probability density function (PDF) of |E∥| > E0 as a function of horizontal position for the height z = 9. The data used in the PDF’s construction are from t ∈ [40,165] . The axes are transposed for an easier comparison with the magnetograms. |
| In the text | |
 |
Fig. 6 Magnetic field connections at t = 93. a) Shows how, after reconnection, the positive polarity of the new flux now connects to main negative polarity. b) Shows the case for the opposite polarities. |
| In the text | |
 |
Fig. 7 The magnetic pressure and E∥ taken along (x,z) = (0,4) at t = 161. The peaks in magnetic pressure correspond to those in E∥. Only one peak is detected in the PDFs since the other is below (in magnitude) the cutoff E0. Key: pm (solid), E∥ (dash). |
| In the text | |
 |
Fig. 8 Horizontal expansion speeds along (x,z) = (0,9). Key: t = 70 (solid), t = 100 (dash), t = 130 (dot-dash), t = 160 (double dot-dash). |
| In the text | |
 |
Fig. 9 Shear profiles along (y,z) = (7,0). Key: t = 70 (solid), t = 160 (dash). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.