| Issue |
A&A
Volume 531, July 2011
|
|
|---|---|---|
| Article Number | A53 | |
| Number of page(s) | 8 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201116750 | |
| Published online | 10 June 2011 | |
Damped large amplitude transverse oscillations in an EUV solar prominence, triggered by large-scale transient coronal waves
1
Centre for Fusion, Space and Astrophysics, Department of PhysicsUniversity of Warwick, Coventry, CV4 7AL, UK
e-mail: J.M.Harris@warwick.ac.uk
2
Central Astronomical Observatory of the Russian Academy of Sciences at Pulkovo, 196140 St. Petersburg, Russia
Received: 18 February 2011
Accepted: 5 May 2011
Aims. We investigate two successive trains of large amplitude transverse oscillations in an arched EUV prominence, observed with SoHO/EIT on the north-east solar limb on 30 July 2005. The oscillatory trains are triggered by two large scale coronal waves, associated with an X-class and a C-class flare occurring in the same remote active region.
Methods. The oscillations are tracked within rectangular slits parallel to the solar limb at different heights, which are taken to move with the apparent height profile of the prominence to account for solar rotation. Time series for the two prominence arch legs are extracted using Gaussian fitting on the 195 Å absorption features, and fitted to a damped cosine curve to determine the oscillatory parameters.
Results. Differing energies of the two triggering flares and associated waves are found to agree with the velocity amplitudes, of 50.6 ± 3.2 and 15.9 ± 8.0 km s-1 at the apex, for the first and second oscillatory trains respectively, as estimated in the transverse direction. The period of oscillation is similar for both trains, with an average of 99 ± 11 min, indicating a characteristic frequency as predicted by magnetohydrodynamics. Increasing velocity amplitude with height during the first oscillatory train, and in-phase starting motions of the two legs regardless of height, for each train, demonstrate that the prominence exhibits a global kink mode to a first approximation. However, discrepancies between the oscillatory characteristics of the two legs and an apparent dependence of period upon height, suggest that the prominence actually oscillates as a collection of separate but interacting threads. Damping times of around two to three cycles are observed. Combining our results with those of previously analysed loop oscillations, we find an approximately linear dependence of damping time upon period for kink oscillations, supporting resonant absorption as the damping mechanism despite limitations in testing this theory.
Key words: Sun: filaments, prominences / Sun: oscillations / Sun: corona / magnetohydrodynamics (MHD)
© ESO, 2011
1. Introduction
Solar prominences or filaments, seen on the solar limb or disk, are cool and dense clouds of plasma embedded in the corona, composed of small-scale ever-changing threads or fibrils (e.g. Berger et al. 2010). The prominence material is in near equilibrium, supported against gravity by the magnetic field (Kippenhahn & Schlüter 1957; Kuperus & Raadu 1974). Oscillations of prominences are of particular interest, and have been observed as line-of-sight (LOS) Doppler velocity oscillations in Hα spectral lines since the 1930’s (Dyson 1930). The oscillations are categorised as either large amplitude oscillations, where the entire prominence oscillates with a velocity amplitude of the order of tens of km s-1 and periods ranging from around 6 to 150 min, or small amplitude oscillations which are localised to part of the prominence, and have velocity amplitudes of around 2–3 km s-1 and typical periods of 10 to 80 min. While small amplitude oscillations are very common (see Oliver & Ballester 2002), large amplitude oscillations are less widely reported and there are relatively few observational analyses (see the review by Tripathi et al. 2009, their Table 1).
In recent years, large amplitude oscillations have been observed not only using Hα (Jing et al. 2003), but also other wavelengths such as EUV (Isobe & Tripathi 2006), microwave (Isobe et al. 2007) and He 10830 Å (Gilbert et al. 2008), enabling the plane-of-sky (POS) velocity to be determined. It is therefore possible to combine the LOS and POS information in order to find the total velocity amplitude, as shown by Isobe & Tripathi (2006). In addition, using space-based instruments, data are available over far longer durations, thus allowing for the detection of oscillations with the longest periods (Foullon et al. 2004, 2009) and increasing the chances of capturing large amplitude events.
Large amplitude oscillations in prominences may occur either as a longitudinal motion of the prominence material along its axis (e.g. Jing et al. 2003), or as a transverse displacement of the prominence axis in either the horizontal (e.g. Isobe & Tripathi 2006) or vertical (e.g. Okamoto et al. 2004) direction with respect to the solar surface. An early observational investigation of large amplitude oscillations by Ramsey & Smith (1966) included four separate oscillatory trains in the same filament with apparently similar periods (of about 15 min), suggesting that the filament has a characteristic frequency independent of the trigger mechanism, which has since been confirmed for small amplitude oscillations (Bashkirtsev & Mashnich 1984). This led to the development of early theoretical models to predict these frequencies, and the emergence of prominence seismology, i.e. the use of oscillatory characteristics to diagnose physical parameters such as the magnetic field within the prominence. For example, Hyder (1966) treats the prominence as a damped harmonic oscillator with magnetic tension as the restoring force, and obtains a radial magnetic field of 2–30 Gauss based on the observations of Ramsey & Smith (1966). Modern theories, such as Joarder & Roberts (1993), rely on magnetohydrodynamics (MHD) in which such characteristic frequencies are inherent, with longitudinal and transverse oscillations corresponding to the slow and the fast kink magnetoacoustic modes respectively.
Due to the rarity of reported large amplitude oscillations in prominences, few measurements have been made of the damping time, i.e. the time taken for the amplitude of an oscillation to be reduced by a factor of e. Damping times of between two and four cycles have been measured for longitudinal oscillations (Jing et al. 2003, 2006; Vršnak et al. 2007), while for transverse oscillations the damping time has not been quantified, although Gilbert et al. (2008) reports a duration of around six cycles for a vertical oscillation. Damping times of two to three cycles are typical for both kink mode loop oscillations (e.g. Nakariakov et al. 1999; Aschwanden et al. 2002) and small amplitude prominence oscillations (e.g. Molowny-Horas et al. 1999; Terradas et al. 2002), and the damping theories in these fields are more developed.
Damping mechanisms for kink oscillations in loops have been extensively studied, with both resonant absorption in the Alfvén continuum (Ionson 1978; Hollweg & Yang 1988) and phase mixing (Heyvaerts & Priest 1983) agreeing well with observed damping times. Resonant absorption has also been investigated in the context of small amplitude prominence oscillations by Arregui et al. (2008b) and again agrees with observations. Various additional mechanisms, such as ion-neutral collisions (Forteza et al. 2007) and resonant absorption in the slow continuum (Soler et al. 2009), have been considered for prominence oscillations, but found to be less significant for fast waves with typically observed parameters (see Oliver 2009, for a review).
There is not yet a definitive answer regarding the damping mechanism at work, although the dependence of the damping time, τ, on the period, P, is different for each theory. For example Ofman & Aschwanden (2002) obtain the scaling law τ ∝ P for resonant absorption, whereas for phase mixing they find τ ∝ P4/3. Ofman & Aschwanden (2002) suggest that by comparing observational values of the period and damping times of loop oscillations to these scaling laws, the damping mechanism can be determined. However, the indices in the two power laws are quite similar and the data points from different observations too widely scattered to differentiate between them. It is therefore important to increase the number of measured events, as well as extend the range of observed periods and damping times, to increase the statistical confidence of the fitted scaling laws.
Large amplitude prominence oscillations can be triggered by Moreton waves (e.g. Gilbert et al. 2008), large-scale coronal waves (Okamoto et al. 2004), or by nearby sub-flares (e.g. Jing et al. 2003) and jets (Isobe & Tripathi 2006). Moreton waves have speeds of around 1000 km s-1 and were first seen by Moreton (1960) using chromospheric filtergrams. They are generated by flares and thought to be the chromospheric signatures of dome-shaped MHD wavefronts (Uchida 1968). Large-scale coronal waves have velocities up to around 400 km s-1, and were first observed using the Extreme-ultraviolet Imaging Telescope (EIT; Delaboudinière et al. 1995) onboard the Solar and Heliospheric Observatory (SoHO) by Moses et al. (1997) and Thompson et al. (1998). Both Moreton and coronal waves are often associated with flares, coronal mass ejections (CMEs) and type II radio bursts (e.g. Veronig et al. 2010). The transient coronal waves were initially considered to be coronal counterparts of the Moreton wave; however differences in the properties of the two wave types and the fact that they are not always observed together suggests that this may not be the case. Alternative interpretations (see review by Wills-Davey & Attrill 2009) include a signature of the restructuring magnetic field following a CME (Delannée & Aulanier 1999).
Here we investigate two successive trains of damped large amplitude transverse oscillations in an EUV prominence, observed on the north-east limb. The oscillatory trains are triggered by large scale coronal waves associated with two flares, which occurred about 11 h apart in the same remote active region. We use 195 Å images from SoHO/EIT to compare oscillatory properties spatially, in the two legs of the prominence, at different heights, and between the two successively excited oscillatory trains. The paper is structured as follows: in Sect. 2 we introduce the event, the data used, and we compare the two large scale coronal waves; in Sect. 3 we first correct the effect of solar rotation before analysing the oscillations, assuming they are purely horizontal with no vertical component; finally, in Sect. 4 we discuss the results and their significance for shedding light on the effects of differing triggers, and for testing damping theories.
2. Event overview
Figure 1a shows a 195 Å intensity image of the Sun from SoHO/EIT on 30 July 2005. The arched solar prominence is seen on the NE limb, at 36° latitude 27° Carrington longitude (Carrington rotation 2032), along with active region NOAA 10792, 470 Mm to the southwest. The prominence axis is oriented from southwest to northeast as shown in Fig. 1b, an Hα image from the Big Bear Solar Observatory (BBSO; Denker et al. 1999), in which the corresponding filament is seen on the disk of the Sun four days later, with AR 10792 now at the disk centre.
 |
Fig. 1 a) EIT 195 Å intensity image showing the prominence and AR 10792. b) Hα intensity image from BBSO, with the corresponding filament and AR 10792 now on the disk of the Sun. |
On 30 July 2005, two large flares, both originating in AR 10792, are detected by the Reuven Ramaty High Energy Solar Spectroscopic Imager (RHESSI; Lin et al. 2002). The two flares are also observed by the Geostationary Operational Environmental Satellite (GOES)-12 (Hanser & Sellers 1996); the first is an X1.3 GOES class flare peaking at 06:35 UT (start 06:17, end 07:01). A type II radio burst with a speed of 1801 km s-1 occurring from 06:26 to 06:47 UT is reported by San Vito Solar Observatory (NOAA solar event lists), which indicates the generation of a shock wave associated with this flare. The second flare is reported by GOES as peaking at 17:07 UT (start 16:39, end 17:37), and is a C8.9 GOES class flare with no related radio burst. Each flare is followed by a large scale coronal wave triggering a train of oscillations in the prominence.
In Fig. 2, we attempt to compare the two coronal waves. The upper panel shows the evolution of the second coronal wave, seen over four 195 Å intensity images from SoHO/EIT with around 10 min between frames, in running difference images (Thompson et al. 1999). Unfortunately the first coronal wave is seen in only one frame, as no 195 Å images are available for much of the duration of the X1.3 class flare, therefore the data is insufficient for a detailed comparison of the two waves. However, equivalent difference images for the two coronal waves, shown in the lower panel, are generated using the difference between the image 27 min (first wave) or 28 min (second wave) after the onset of the flare and the image before the flare. This shows that the intensity depletion is much larger following the first coronal wave, suggesting a higher amplitude. In addition, the absence of a shock in the case of the second coronal wave indicates a slower wave speed than that of the first. We would like to find out whether this difference is reflected in the characteristics of the prominence oscillations.
 |
Fig. 2 Difference images of 195 Å EIT data showing the large scale coronal waves. Upper panel: running difference images of the second wave only, produced using the difference between consecutive images. Lower panel: images are constructed as the difference between the image 27 min (first wave) or 28 min (second wave) after the onset of the flare and the image before the flare. |
The prominence is observed in absorption in the 195 Å intensity images with an average cadence of 12 min; 304 Å images, showing the prominence in emission, are also available but with a 6 h cadence. The oscillatory behaviour starts at around 06:45 UT following the first flare and continues over approximately 18 h. From visual inspection of the data movie, both oscillatory trains have periods of around 100 min, and the displacements of the prominence caused by the oscillations are in the horizontal direction with respect to the solar surface.
3. Analysis of the oscillations
3.1. The effect of solar rotation
During the oscillatory phase, the prominence rotates over the solar limb and so its apparent height above the limb, as observed from SoHO, varies with the rotation of the Sun. Therefore, it is necessary to determine the apparent height profile in order to account for its effect in the subsequent analysis. This height profile can be modelled using a cosine curve (Foullon & Verwichte 2006): 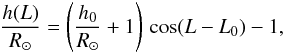 (1)where h/R⊙ is the apparent height above the limb and h0/R⊙ the actual height above the solar surface, measured as a fraction of the solar radius, while L is the Carrington longitude of the limb which varies with time, and L0 the Carrington longitude of the prominence. Determining the parameters h0/R⊙ and L0 therefore allows the apparent height at any time to be calculated.
(1)where h/R⊙ is the apparent height above the limb and h0/R⊙ the actual height above the solar surface, measured as a fraction of the solar radius, while L is the Carrington longitude of the limb which varies with time, and L0 the Carrington longitude of the prominence. Determining the parameters h0/R⊙ and L0 therefore allows the apparent height at any time to be calculated.
 |
Fig. 3 a) Ratio of 304 Å intensity over 195 Å intensity EIT images, the white box indicates the ROI used in c). b) 195 Å EIT image of the prominence on the limb, white boxes indicate two ROIs at 82.3 Mm and 42.1 Mm above the solar surface. c) The maximum 304/195 Å intensity ratio versus height above the solar surface over Carrington longitude, white diamonds indicate the apparent height of the prominence at each time-step, while the white line is Eq. (1) with h0/R⊙ = 0.170 and L0 = 27.5°. |
Figure 3a shows the ratio of the 304 Å intensity over the 195 Å intensity images from EIT, giving an enhanced contrast between the prominence material and the background to facilitate prominence detection, as first pointed out by Foullon & Verwichte (2006). Using the 304/195 Å image ratio and considering a region of interest (ROI) encompassing the prominence, a time-distance plot is produced giving the maximum intensity versus height above the limb over Carrington longitude (Fig. 3c). Large spikes are identified as 3σ above the median value of the surrounding data points and replaced by this median value. The observed apparent height of the prominence at each time-step, corresponding to a given Carrington longitude at the limb, is identified using edge detection, i.e. the largest negative intensity gradient shown with diamonds in Fig. 3c. The best fit to the apparent height data using Eq. (1) gives the parameter values h0/R⊙ = 0.170 ± 0.008 and L0 = 27.5 ± 1.1° (Carrington rotation 2032).
3.2. 195 Å image series
Since the oscillations are assumed to be purely horizontal, eight ROIs defined as rectangular slits, 3 pixels wide and running parallel to the solar limb at different heights, are considered as indicated in Fig. 3b. The height above the limb varies with time, for each slit, according to Eq. (1) and using L0 = 27.5° as found previously. This corrects for solar rotation by moving the slits together with the prominence, thus ensuring that the same prominence material remains in each ROI throughout the duration of the oscillations.
For each moving ROI in 195 Å images, the intensity is averaged across the width of the slit and a time-distance image showing average intensity versus horizontal distance over time, such as Fig. 4a, is produced. Two main absorption features are seen, one corresponding to the NE leg and the other to the SW leg of the prominence (the corresponding filament axis is oriented from SW to NE). The approximate positions of the two legs are identified by eye in each time-distance plot. Then for each time-step the two locations along the slit are determined more precisely using the following automated procedure.
 |
Fig. 4 a) Average 195 Å intensity as a function of horizontal distance and time for the ROI at 76.6 Mm, white diamonds joined by a solid line give the location(s) of the prominence as identified by Gaussian fitting with error bars shown for every second data point, positions at 11:24 and 18:00 UT are in red bold. b) and c) Inverted intensity profiles as a function of horizontal distance, black diamonds joined by a dotted line show the measured intensities, the blue dashed line is the second order polynomial fit to the background, the red dash-dotted lines are Gaussian peaks indicating the prominence location(s), while the solid black line combines these to give the overall fit. |
As per the previous section, large spikes are identified and removed from the intensity profiles, which are then inverted so that the absorption features appear as peaks in the profiles. In most cases both prominence legs are visible, and the intensity data is fitted to two Gaussian peaks with a second order polynomial background, as shown in Fig. 4b at 11:24 UT after the first flare, where the by-eye estimate is used as an initial estimate of the peak centroid. The horizontal location of the prominence leg is then given by the Gaussian centroid, while the standard deviation of the Gaussian curve provides the error on the location (using the width of the Gaussian rather than the error from the fit allows us to account for possible non-Gaussian profiles). Towards the prominence apex, the two legs are often too close to be distinguished, in this case the fitting is performed for only one Gaussian peak as seen in Fig. 4c at 18:00 UT after the second flare.
3.3. Time series analysis
Each of the time series, obtained from Gaussian fitting on the 195 Å absorption features, is divided into two sections starting at 06:44:38 and 17:07:42 UT, corresponding to the first and second oscillatory trains respectively, so that these can be analysed separately. The time series, x(t), are then fitted to a damped cosine curve corresponding to the POS displacement, ξ(t), with a linear trend, x0(t) = a0 + a1t, to account for any long term horizontal motion of the prominence over the time of the oscillations: 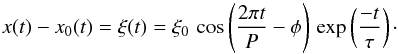 (2)Initial estimates for the parameters used in the fit are calculated as follows: the coefficients of the linear trend, a0 and a1, are obtained from a linear fit of the time series smoothed over 1.5 h; the period, P, is the highest peak from a periodogram (Scargle 1982) of the de-trended time series; the damping time τ, phase φ, and initial displacement amplitude ξ0, are estimated based on the times and displacements of the first two maxima in the de-trended time series. This first fit to Eq. (2) provides an improved estimate of the oscillation parameters, as well as the trend coefficients.
(2)Initial estimates for the parameters used in the fit are calculated as follows: the coefficients of the linear trend, a0 and a1, are obtained from a linear fit of the time series smoothed over 1.5 h; the period, P, is the highest peak from a periodogram (Scargle 1982) of the de-trended time series; the damping time τ, phase φ, and initial displacement amplitude ξ0, are estimated based on the times and displacements of the first two maxima in the de-trended time series. This first fit to Eq. (2) provides an improved estimate of the oscillation parameters, as well as the trend coefficients.
 |
Fig. 5 Examples of fitting to a damped cosine curve. The POS displacements are shown as black diamonds with error bars joined by a dotted line, while the blue line indicates the best fit to Eq. (2) using the mean parameters from a randomisation technique. Upper panels (a), b)): prominence apex at 82.3 Mm. Middle panels (c), d)): NE leg at 65.1. Lower panels (e), f)): SW leg at 65.1 Mm. Left panels (a), c), e)): first oscillatory train. Right panels (b), d), f)): second oscillatory train. |
In order to obtain the errors on the oscillation parameters, a randomisation technique is used, as per Van Doorsselaere et al. (2007) and Verwichte et al. (2009). Gaussian noise, with a standard deviation equal to the displacement uncertainty obtained in Sect. 3.2, is added to each point in the time series. This randomised time series is fitted to Eq. (2), using the parameter values from the first fit as an initial estimate, with the linear trend now fixed. The process is repeated 500 times, producing a distribution of values for each parameter. The oscillation parameters are then taken to be the mean values of the distributions, while their uncertainties are given by the standard deviations. The results are listed in Table 1.
The POS displacement time series fit well to Eq. (2) within the error bars, as shown in Fig. 5 for two ROIs at the prominence apex (panels a, b) and legs (panels c–f), with periods of around 100 min. However in several cases, particularly during the second oscillatory train which has higher relative errors in ξ, the damping time cannot be determined since the standard deviation in the distribution of values for τ is larger than its mean value (e.g. panels d, f).
In Fig. 5, the amplitudes are seen to be higher during the first train of oscillations (left panels), than in the case of the second oscillatory train (right panels). Damping times are varied, with the first oscillatory train consisting of up to six cycles of oscillation (e.g. panels a, e) before the onset of the second flare, while the second set of oscillations can be traced for up to four cycles (e.g. panel f) before its amplitude reduces to below the level of the uncertainties. It can also be seen that the oscillations in the two legs (middle and lower panels) start approximately in phase, but then move gradually out of phase due to slightly differing periods.
Oscillation parameters.
The time differential of ξ(t) gives the velocity in the POS, v(t), with an initial velocity, v0, which is calculated using: 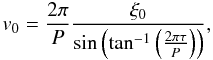 (3)while the uncertainty in v0 is determined from the errors in ξ0 and P, since the dependance on τ via the sine term is small.
(3)while the uncertainty in v0 is determined from the errors in ξ0 and P, since the dependance on τ via the sine term is small.
If we now assume that the oscillations are transverse with respect to the prominence axis, then the initial velocity in the transverse direction, vT, can be calculated based on the angle, θ, between the prominence axis and the north-south line using vT = v0/cos θ. Assuming that the corresponding filament orientation is unchanged when it is seen on the disk four days later on 3 August, we estimate θ = 35 ± 2° from the Hα image in Fig. 1b.
The deduced parameters, v0 and vT, are also given in Table 1. Figure 6 shows the parameters vT, P and φ versus actual height above the solar surface, and the correlation between τ and P, for both legs and oscillatory trains. In Fig. 6b, we find that the majority of the periods range between 90 and 110 min, and generally appear to increase slightly with height. In the SW leg (dashed lines) the periods are generally similar during both oscillatory trains, and during the first oscillatory train (shown in black) are typically 10% longer than those in the NE leg (solid lines). Damping times generally increase with period, as shown in Fig. 6d, although there are exceptions in which longer or shorter damping times are exhibited.
As previously noted, the initial amplitudes, ξ0, v0 and vT, are clearly higher for the first oscillatory train than the second. An increase with height during the first train is also found, up to vT = 50.6 ± 3.2 km s-1 at the prominence apex, while this dependence is not seen for the second oscillatory train. Note that ξ0 exhibits nearly identical behaviour to v0 and vT. In Fig. 6c we confirm that for each of the oscillatory trains, the oscillations between the two legs start in phase at the majority of the measured heights.
 |
Fig. 6 Oscillatory parameters of the EUV prominence, showing a) initial transverse velocity amplitude, b) period and c) initial phase, versus actual height above the solar surface; d) damping time versus period. The first oscillatory train is shown in black, and the second in red. The NE leg is indicated by triangles joined with a solid line, and the SW leg by diamonds joined with a dashed line. |
4. Discussion and conclusions
Figure 6a shows that the initial velocity amplitude at the prominence apex for the first oscillatory train, displayed in black, is over three times that of the second, in red, suggesting that the kinetic energy is a factor of ten higher. This is to be expected due to the difference in flaring energy between the two events, the initial GOES X1.3 class flare having 14.6 times the energy of the later GOES C8.9 class flare. The energy difference is also evident from the qualitative comparison of the two large-scale coronal waves (Sect. 2), since the first appears to have a larger amplitude and higher wave speed than the second.
Despite the different strengths of the triggers, we find that the period of oscillation is similar during both trains, with a global average of 99 ± 11 min. Figure 6b shows that while there are some discrepancies between the periods of the two oscillatory trains, these mainly occur where uncertainties are large (see also Table 1). This suggests a characteristic frequency, dependent on the properties of the prominence rather than the triggering mechanism, which has previously been observed for large amplitude prominence oscillations (e.g. Ramsey & Smith 1966) and is indicative of an MHD mode.
During the first oscillatory train, the velocity amplitudes (shown in black in Fig. 6a) are seen to increase with height, which corresponds to the fundamental oscillatory mode where the prominence oscillates as a whole with its footpoints fixed. This interpretation is confirmed by the phase measurements in Fig. 6c, as the oscillations start approximately in phase between the two legs and regardless of height. This type of collective oscillation is indicative of a global kink mode. The dependence of velocity amplitude on height is not evident during the second oscillatory train, and while this seems to suggest that the footpoints of the prominence are no longer anchored, it is also possible that the higher relative uncertainties in the case of the second train may be concealing its true behaviour.
And yet, there are indications that the prominence oscillates as a collection of separate but interacting filamentary threads, rather than as a solid body. Firstly, in Fig. 6b the period appears to increase slightly with height, with periods around 10–15% shorter at 42 Mm than at 82 Mm. This dependence may suggest that the oscillation periods of separate threads are affected by a combination of factors all varying with height, such as the internal and external densities and magnetic field strengths, and the angle of the prominence axis relative to the solar surface. Secondly, periods in the NE leg (triangles with a solid line) are typically around 10% shorter than those in the SW leg (diamonds with a dashed line). Thirdly, during the first oscillatory train a clear discrepancy is found between the velocity amplitudes of the two prominence legs (displayed in black in Fig. 6a), with the velocities of the SW leg being around 10–15 km s-1 less than those of the NE leg; although this difference is not apparent for the second oscillatory train. Likewise, similar non-collective behaviour is observed in hot loops (e.g. Aschwanden et al. 1999).
 |
Fig. 7 Damping time against period for the first oscillatory train as well as a collection of coronal loop kink oscillations. The black solid line is the fit to τ = cPα with α = 0.9 ± 0.1 and c = 1.6 ± 0.2, where the parameter uncertainties are indicated by dashed black lines. |
We can consider, to a first approximation, that the prominence is subject to a damped kink mode of oscillation. Kink modes in coronal loops also exhibit collective transverse oscillations of the entire structure, albeit with different plasma parameters, and the same damping mechanisms are expected to apply. In the case of resonant absorption (Ruderman & Roberts 2002), the damping time is given by 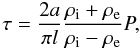 (4)where P is the period of the oscillation, ρi and ρe are the internal and external densities respectively, a is the loop width and l the width of the inhomogeneous layer. By assuming that ρi ≫ ρe so that (ρi + ρe)/(ρi − ρe) ≈ 1, and a/l is approximately constant, Ofman & Aschwanden (2002) obtain the scaling law τ ∝ P, whereas for phase mixing they find τ ∝ P4/3. But using varying realistic parameter values for different loops, multiple scaling laws can be reproduced for a single damping mechanism (Arregui et al. 2008a), suggesting that these assumptions may not be valid when applied to multiple events.
(4)where P is the period of the oscillation, ρi and ρe are the internal and external densities respectively, a is the loop width and l the width of the inhomogeneous layer. By assuming that ρi ≫ ρe so that (ρi + ρe)/(ρi − ρe) ≈ 1, and a/l is approximately constant, Ofman & Aschwanden (2002) obtain the scaling law τ ∝ P, whereas for phase mixing they find τ ∝ P4/3. But using varying realistic parameter values for different loops, multiple scaling laws can be reproduced for a single damping mechanism (Arregui et al. 2008a), suggesting that these assumptions may not be valid when applied to multiple events.
For the large amplitude prominence oscillations on 30 July 2005, we find damping times of around 2–3 cycles in most cases, similar to the typical damping of loop oscillations, and these generally increase with period as predicted for both resonant absorption and phase mixing. The collection of measurements from this prominence alone, in Fig. 6d, shows a tendency towards a linear trend. It addition, it may be possible to learn more by comparing the damping times and periods from other similar events. In Fig. 7, we combine our results, the weighted mean period and damping time (over those heights at which both are available) for each prominence leg during each oscillatory train, with those of previously analysed kink mode coronal loop oscillations. We obtain the best fit to τ = cPα, where the power law index α = 0.9 ± 0.1 and the constant c = 1.6 ± 0.2. This empirically determined scaling indicates the linear dependence of the damping time upon the period of kink oscillations, thus supporting the resonant absorption model.
The wide scattering of data points in Fig. 7 can be considered a result of the expected variation in density contrast and layer thickness over the numerous events. Ideally, such parameters should be taken into account, but the values of ρi, ρe and a can only be measured with limited accuracy, while l cannot generally be determined. Nevertheless, by including a prominence oscillation event with periods of approximately 100 min, compared with up to 40 min (Verwichte et al. 2010) but typically around 3–10 min for loop oscillations, the range of periods and damping times now covers two orders of magnitude. As such, it is expected that the influence of varying density contrast and layer thickness on the scaling is diminished. In the future, since the density contrast is much larger in prominences than coronal loops, the effect of this variation could be further reduced by the analysis of additional large amplitude transverse prominence oscillations.
To sum up briefly, the main features of this analysis are as follows: (a) the correspondence in kinetic energy between flare, large scale coronal wave and prominence oscillation; (b) a collective transverse oscillation, to a first approximation, that is indicative of a global kink mode; (c) evidence of non-collective behaviour, attributed to the filamentary and non-homogeneous structure of the prominence; (d) the range of periods and damping times for kink oscillations covering two orders of magnitude; (e) linear dependence between damping times and periods, consistent with a resonant absorption mechanism.
Acknowledgments
J.H. would like to acknowledge the support of a UK Science and Technology Facilities Council (STFC) Ph.D. studentship, and C.F. acknowledges financial support from the STFC on the CFSA Rolling Grant. EIT data are courtesy of the SoHO/EIT consortium, where SoHO is a project of international cooperation between ESA and NASA. BBSO (New Jersey Institute of Technology, NJIT) Hα data were obtained from the Virtual Solar Observatory (VSO) Catalogue, provided by the National Solar Observatory (NSO) and Stanford University. We acknowledge the use of information from the Solar Event Lists, provided by the National Oceanic and Astmospheric Administration (NOAA) Space Weather Prediction Center.
References
- Arregui, I., Ballester, J. L., & Goossens, M. 2008a, ApJ, 676, L77 [NASA ADS] [CrossRef] [Google Scholar]
- Arregui, I., Terradas, J., Oliver, R., & Ballester, J. L. 2008b, ApJ, 682, L141 [NASA ADS] [CrossRef] [Google Scholar]
- Aschwanden, M. J., Fletcher, L., Schrijver, C. J., & Alexander, D. 1999, ApJ, 520, 880 [NASA ADS] [CrossRef] [Google Scholar]
- Aschwanden, M. J., de Pontieu, B., Schrijver, C. J., & Title, A. M. 2002, Sol. Phys., 206, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Bashkirtsev, V. S., & Mashnich, G. P. 1984, Sol. Phys., 91, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Berger, T. E., Slater, G., Hurlburt, N., et al. 2010, ApJ, 716, 1288 [NASA ADS] [CrossRef] [Google Scholar]
- Delaboudinière, J., Artzner, G. E., Brunaud, J., et al. 1995, Sol. Phys., 162, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Delannée, C., & Aulanier, G. 1999, Sol. Phys., 190, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Denker, C., Johannesson, A., Marquette, W., et al. 1999, Sol. Phys., 184, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Dyson, F. 1930, MNRAS, 91, 239 [Google Scholar]
- Forteza, P., Oliver, R., Ballester, J. L., & Khodachenko, M. L. 2007, A&A, 461, 731 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Foullon, C., & Verwichte, E. 2006, Sol. Phys., 234, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Foullon, C., Verwichte, E., & Nakariakov, V. M. 2004, A&A, 427, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Foullon, C., Verwichte, E., & Nakariakov, V. M. 2009, ApJ, 700, 1658 [NASA ADS] [CrossRef] [Google Scholar]
- Gilbert, H. R., Daou, A. G., Young, D., Tripathi, D., & Alexander, D. 2008, ApJ, 685, 629 [NASA ADS] [CrossRef] [Google Scholar]
- Hanser, F. A., & Sellers, F. B. 1996, in GOES-8 and Beyond, ed. E. R. Washwell, Proc. SPIE, 2812, 344 [Google Scholar]
- Heyvaerts, J., & Priest, E. R. 1983, A&A, 117, 220 [NASA ADS] [Google Scholar]
- Hollweg, J. V., & Yang, G. 1988, J. Geophys. Res., 93, 5423 [NASA ADS] [CrossRef] [Google Scholar]
- Hori, K., Ichimoto, K., & Sakurai, T. 2007, in New Sol. Phys. with Solar-B Mission, ed. K. Shibata, S. Nagata, & T. Sakurai, ASP Conf. Ser., 369, 213 [Google Scholar]
- Hyder, C. L. 1966, ZAp, 63, 78 [Google Scholar]
- Ionson, J. A. 1978, ApJ, 226, 650 [NASA ADS] [CrossRef] [Google Scholar]
- Isobe, H., & Tripathi, D. 2006, A&A, 449, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Isobe, H., Tripathi, D., Asai, A., & Jain, R. 2007, Sol. Phys., 246, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Jing, J., Lee, J., Spirock, T. J., et al. 2003, ApJ, 584, L103 [NASA ADS] [CrossRef] [Google Scholar]
- Jing, J., Lee, J., Spirock, T. J., & Wang, H. 2006, Sol. Phys., 236, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Joarder, P. S., & Roberts, B. 1993, A&A, 277, 225 [NASA ADS] [Google Scholar]
- Kippenhahn, R., & Schlüter, A. 1957, ZAp, 43, 36 [NASA ADS] [Google Scholar]
- Kuperus, M., & Raadu, M. A. 1974, A&A, 31, 189 [NASA ADS] [Google Scholar]
- Lin, R. P., Dennis, B. R., Hurford, G. J., et al. 2002, Sol. Phys., 210, 3 [Google Scholar]
- Molowny-Horas, R., Wiehr, E., Balthasar, H., Oliver, R., & Ballester, J. L. 1999, in JOSO Annu. Rep., 1998, 126 [Google Scholar]
- Moreton, G. E. 1960, AJ, 65, 494 [Google Scholar]
- Moses, D., Clette, F., Delaboudinière, J., et al. 1997, Sol. Phys., 175, 571 [NASA ADS] [CrossRef] [Google Scholar]
- Nakariakov, V. M., Ofman, L., Deluca, E. E., Roberts, B., & Davila, J. M. 1999, Science, 285, 862 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ofman, L., & Aschwanden, M. J. 2002, ApJ, 576, L153 [NASA ADS] [CrossRef] [Google Scholar]
- Okamoto, T. J., Nakai, H., Keiyama, A., et al. 2004, ApJ, 608, 1124 [NASA ADS] [CrossRef] [Google Scholar]
- Oliver, R. 2009, Space Sci. Rev., 149, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Oliver, R., & Ballester, J. L. 2002, Sol. Phys., 206, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Ramsey, H. E., & Smith, S. F. 1966, AJ, 71, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Ruderman, M. S., & Roberts, B. 2002, ApJ, 577, 475 [NASA ADS] [CrossRef] [Google Scholar]
- Scargle, J. D. 1982, ApJ, 263, 835 [NASA ADS] [CrossRef] [Google Scholar]
- Soler, R., Oliver, R., Ballester, J. L., & Goossens, M. 2009, ApJ, 695, L166 [NASA ADS] [CrossRef] [Google Scholar]
- Terradas, J., Molowny-Horas, R., Wiehr, E., et al. 2002, A&A, 393, 637 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thompson, B. J., Plunkett, S. P., Gurman, J. B., et al. 1998, Geophys. Res. Lett., 25, 2465 [Google Scholar]
- Thompson, B. J., Gurman, J. B., Neupert, W. M., et al. 1999, ApJ, 517, L151 [NASA ADS] [CrossRef] [Google Scholar]
- Tripathi, D., Isobe, H., & Jain, R. 2009, Space Sci. Rev., 149, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Uchida, Y. 1968, Sol. Phys., 4, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Van Doorsselaere, T., Nakariakov, V. M., & Verwichte, E. 2007, A&A, 473, 959 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Van Doorsselaere, T., Birtill, D. C. C., & Evans, G. R. 2009, A&A, 508, 1485 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Veronig, A. M., Muhr, N., Kienreich, I. W., Temmer, M., & Vršnak, B. 2010, ApJ, 716, L57 [Google Scholar]
- Verwichte, E., Nakariakov, V. M., Ofman, L., & Deluca, E. E. 2004, Sol. Phys., 223, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Verwichte, E., Aschwanden, M. J., Van Doorsselaere, T., Foullon, C., & Nakariakov, V. M. 2009, ApJ, 698, 397 [NASA ADS] [CrossRef] [Google Scholar]
- Verwichte, E., Foullon, C., & Van Doorsselaere, T. 2010, ApJ, 717, 458 [NASA ADS] [CrossRef] [Google Scholar]
- Vršnak, B., Veronig, A. M., Thalmann, J. K., & Žic, T. 2007, A&A, 471, 295 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, T. J., & Solanki, S. K. 2004, A&A, 421, L33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wills-Davey, M. J., & Attrill, G. D. R. 2009, Space Sci. Rev., 149, 325 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 a) EIT 195 Å intensity image showing the prominence and AR 10792. b) Hα intensity image from BBSO, with the corresponding filament and AR 10792 now on the disk of the Sun. |
| In the text | |
 |
Fig. 2 Difference images of 195 Å EIT data showing the large scale coronal waves. Upper panel: running difference images of the second wave only, produced using the difference between consecutive images. Lower panel: images are constructed as the difference between the image 27 min (first wave) or 28 min (second wave) after the onset of the flare and the image before the flare. |
| In the text | |
 |
Fig. 3 a) Ratio of 304 Å intensity over 195 Å intensity EIT images, the white box indicates the ROI used in c). b) 195 Å EIT image of the prominence on the limb, white boxes indicate two ROIs at 82.3 Mm and 42.1 Mm above the solar surface. c) The maximum 304/195 Å intensity ratio versus height above the solar surface over Carrington longitude, white diamonds indicate the apparent height of the prominence at each time-step, while the white line is Eq. (1) with h0/R⊙ = 0.170 and L0 = 27.5°. |
| In the text | |
 |
Fig. 4 a) Average 195 Å intensity as a function of horizontal distance and time for the ROI at 76.6 Mm, white diamonds joined by a solid line give the location(s) of the prominence as identified by Gaussian fitting with error bars shown for every second data point, positions at 11:24 and 18:00 UT are in red bold. b) and c) Inverted intensity profiles as a function of horizontal distance, black diamonds joined by a dotted line show the measured intensities, the blue dashed line is the second order polynomial fit to the background, the red dash-dotted lines are Gaussian peaks indicating the prominence location(s), while the solid black line combines these to give the overall fit. |
| In the text | |
 |
Fig. 5 Examples of fitting to a damped cosine curve. The POS displacements are shown as black diamonds with error bars joined by a dotted line, while the blue line indicates the best fit to Eq. (2) using the mean parameters from a randomisation technique. Upper panels (a), b)): prominence apex at 82.3 Mm. Middle panels (c), d)): NE leg at 65.1. Lower panels (e), f)): SW leg at 65.1 Mm. Left panels (a), c), e)): first oscillatory train. Right panels (b), d), f)): second oscillatory train. |
| In the text | |
 |
Fig. 6 Oscillatory parameters of the EUV prominence, showing a) initial transverse velocity amplitude, b) period and c) initial phase, versus actual height above the solar surface; d) damping time versus period. The first oscillatory train is shown in black, and the second in red. The NE leg is indicated by triangles joined with a solid line, and the SW leg by diamonds joined with a dashed line. |
| In the text | |
 |
Fig. 7 Damping time against period for the first oscillatory train as well as a collection of coronal loop kink oscillations. The black solid line is the fit to τ = cPα with α = 0.9 ± 0.1 and c = 1.6 ± 0.2, where the parameter uncertainties are indicated by dashed black lines. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


