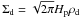| Issue |
A&A
Volume 531, July 2011
|
|
|---|---|---|
| Article Number | A101 | |
| Number of page(s) | 5 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201116629 | |
| Published online | 21 June 2011 | |
Accretion through the inner hole of transitional disks: what happens to the dust?
1
Sterrenkundig Instituut “Anton Pannekoek”, Science Park 904,
1098 XH
Amsterdam,
The Netherlands
e-mail: dominik@uva.nl
2
Afdeling Sterrenkunde, Radboud Universiteit
Nijmegen, Postbus
9010, 6500 GL
Nijmegen, The
Netherlands
3
Institut für Theoretische Astrophysik, Zentrum für Astronomie der
Universität Heidelberg, Albert-Ueberle-Str. 2, 69120
Heidelberg,
Germany
e-mail: dullemond@uni-heidelberg.de
4
Max Planck Institut für Astronomie, Königstuhl 17, 69117
Heidelberg,
Germany
Received: 2 February 2011
Accepted: 11 May 2011
We study the effect of radiation pressure on the dust in the inner rim of transitional disks with large inner holes. In particular, we evaluate whether radiation pressure can be responsible for keeping the inner holes dust-free, while allowing gas accretion to proceed. This has been proposed in a paper by Chiang & Murray-Clay (2007, Nature Phys., 3, 604) who explain the formation of these holes as an inside-out evacuation due to X-ray-triggered accretion of the innermost layer of the disk rim outside of the hole. We show that radiation pressure is clearly incapable of stopping dust from flowing into the hole because of dust pile-up and optical depth effects, and also because of viscous mixing. Other mechanisms need to be found to explain the persistence of the opacity hole in the presence of accretion, and we speculate on possible solutions.
Key words: accretion, accretion disks / circumstellar matter / stars: pre-main sequence / infrared: stars / planets and satellites: formation
© ESO, 2011
1. Introduction
In recent years our understanding of the structure of the dusty disks around young stars has increased considerably with the enormous data volumes of such disks from space-based infrared telescopes (ISO, Spitzer Space Telescope), ground-based infrared interferometry, and millimeter wave observations. One interesting issue that emerged is that a certain fraction of these protoplanetary disks appear to have large inner holes. To be more precise, these objects have inner disks that are nearly dust-free out to several AU, much farther out than the dust sublimation radius. Such disks are frequently termed “transitional disks”, expressing the idea that these disks are in the process of becoming debris disks.
Several ideas for the origin of these holes are being discussed. One idea is that photoevaporation might have drilled a hole in the inner disk (Hollenbach & Gorti 2005; Alexander et al. 2006; Clarke 2007; Ercolano et al. 2008). Another explanation is the presence of planetary systems inside the “gap” (e.g. Alexander & Armitage 2009).
Surprisingly, several transitional disks still show signs of accretion (e.g. Fang et al. 2009; Sicilia-Aguilar et al. 2010), indicating that some gas is streaming through these opacity holes without the usual dust content. Chiang & Murray-Clay (2007, henceforth CM07) propose a mechanism by which the ionizing effect of X-rays from the star causes an inside-out evacuation of the disk. In this scenario, radiation pressure on dust grains plays a crucial role in holding back the dust while allowing the gas to flow in. CM07 make a detailed analysis of the conditions needed to activate the magneto-rotational instability (MRI) necessary for accretion. In their model, the disk is largely viscously inactive because of insufficient ionization. Only directly at the inner rim of the disk, X-rays at energies of about 3 keV from the central star lead to sufficient ionization in a thin layer with column density ~5 × 1023 cm-2. As this layer viscously spreads inward and is being accreted by the star, new layers get exposed to the ionizing radiation. In this way, the disks gets evacuated from the inside out, leading to a steadily growing inner hole. CM07 find accretion rates that range from 10-11 to 10-8 M⊙/yr. If the dust was dragged along with the gas, and if the accretion onto the star occurs in a continuous way through a disk, then there will be no opacity hole. CM07 propose that radiation pressure on dust grains is the mechanism to keep the inner disk free of dust. While CM07 consider the possibility that some dust leaks into the inner hole, there is no mechanism to eventually remove it again from the hole.
Here we revisit this issue of holding back the dust by radiation pressure. Our main concern is the optical depth effect, which limits the total amount of dust that can be affected directly by radiation from the central star. As the accretion layer proceeds into the disk, dust will accumulate and eventually collectively overcome the radiation pressure.
2. Model
Let us consider a radial column of gas and dust in the inner disk rim, exposed to radiation from the star. Radiation pressure acts only on dust grains in the inner few optical mean free paths (τ ⋆ ≲ few), with the radiation force decreasing with increasing optical depth. Ignoring other effects, the innermost grains would therefore quickly catch up with particles at higher optical depth, creating an infinitely thin sheet of dust. Particle diffusion (either thermal or turbulent) will act to keep the thickness of this sheet finite. Furthermore, it will also transport the effect of radiation pressure to the dust deeper in the disk, thereby allowing a larger amount of dust to be affected. The radiation pressure will thus act as an outward moving “snow plow”, piling up more and more dust.
As the dust particles are pushed outward through the gas, they will feel a friction force. The total friction force on the pile will increase as the pile builds up. On the other hand, the radiation pressure is fixed. All particles in the pile will have to share this given amount of radiation pressure. The dust pile will therefore gradually slow down. Even a very small inward pointing accretion flow will eventually stop the snow plow and then drag the dust pile inward with the gas.
2.1. Analytical estimates
2.1.1. When does a pile-up take place at all
The radiation force of the unattenuated stellar luminosity L ⋆ acting on a single grain with radius a in the rim surface located at a distance r0 from the star is given by 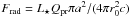 where Qpr is the momentum absorption efficiency of the grain and c is the speed of light. For the analytical and numerical estimates below, we take Qpr = 2, to simulate the most favorable condition for holding grains back with radiation pressure. At the same time, the gas is streaming slowly toward the star, with the accretion velocity vacc. In the Epstein regime and for subsonic dust drift, we can write the friction force per grain as Ffric = 4vaccvthρπa2/3 (e.g. Schaaf 1963) where ρ is the gas density and
where Qpr is the momentum absorption efficiency of the grain and c is the speed of light. For the analytical and numerical estimates below, we take Qpr = 2, to simulate the most favorable condition for holding grains back with radiation pressure. At the same time, the gas is streaming slowly toward the star, with the accretion velocity vacc. In the Epstein regime and for subsonic dust drift, we can write the friction force per grain as Ffric = 4vaccvthρπa2/3 (e.g. Schaaf 1963) where ρ is the gas density and 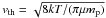 is the thermal velocity of gas particles with mass μmp at a temperature T. mp is the proton mass, and we take μ = 2.3 for molecular gas.
is the thermal velocity of gas particles with mass μmp at a temperature T. mp is the proton mass, and we take μ = 2.3 for molecular gas.
The first question we need to answer is whether there will be any pile-up at all. This is the case if the radiation force onto a single grain exceeds the friction force onto that same grain. The criterion for this is 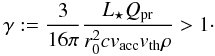 (1)If γ < 1, the dust will accrete with the gas onto the star without delay; i.e., the space velocity of the dust grains will never point away from the star. If γ > 1, on the other hand, the accretion of dust will be delayed until a large enough pile has accumulated.
(1)If γ < 1, the dust will accrete with the gas onto the star without delay; i.e., the space velocity of the dust grains will never point away from the star. If γ > 1, on the other hand, the accretion of dust will be delayed until a large enough pile has accumulated.
2.1.2. Speed of the snow plow relative to the gas
For the moment we will assume that the gas in the outer disk is not moving at all, and that the radiation pressure is simply driving the snow plow a distance s into the disk, starting at a position r0. The speed of the column piled up by radiation pressure can be calculated by equating the radiation force onto a column with 1 cm2 inner surface 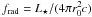 , with the inward-directed collective friction force ffric of all the grains in the pile while the pile is moving relative to the gas with a velocity vdr. The latter force is ffric = σpilevdrvthρ/(ξa), where σpileis the column mass density of dust in the pile and ξ is the specific density of the grains which we take to be 2 g/cm2. Solving for the drift velocity we find
, with the inward-directed collective friction force ffric of all the grains in the pile while the pile is moving relative to the gas with a velocity vdr. The latter force is ffric = σpilevdrvthρ/(ξa), where σpileis the column mass density of dust in the pile and ξ is the specific density of the grains which we take to be 2 g/cm2. Solving for the drift velocity we find 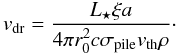 (2)
(2)
2.1.3. Time-dependent solution and total mass supported by radiation pressure
For simplicity we assume that the gas density ρ and the dust-to-gas ratio fdg are constant prior to buildup of the pile. We define a variable s that measures the distance from the rim into the disk, so that we can write the position of the dust pile as rpile(t) = r0 + s(t). Then the dust mass in the pile can be expressed easily as σpile(s) = ρfdgs. The drift velocity at location s into the disk is then 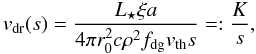 (3)where K: = L ⋆ ξa/(
(3)where K: = L ⋆ ξa/(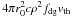 ). As we can see, the velocity of the pile becomes lower and lower as it collects more dust to be pushed forward. We can integrate (3)to find the distance traveled by the pile to be
). As we can see, the velocity of the pile becomes lower and lower as it collects more dust to be pushed forward. We can integrate (3)to find the distance traveled by the pile to be 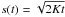 .
.
Now we introduce a constant inward gas motion with velocity vacc. The position of the pile now becomes rpile(t) = r0 + s(t) − vacct, while s(t) remains unchanged. The snowplow comes to a halt at 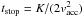 and rstop = r0 + K/vacc − vacctstop. After that, continued mass loading will turn around the motion of the pile and move it, embedded into the accretion flow, into the inner hole and toward the star. The total column at the turn-around point is given by
and rstop = r0 + K/vacc − vacctstop. After that, continued mass loading will turn around the motion of the pile and move it, embedded into the accretion flow, into the inner hole and toward the star. The total column at the turn-around point is given by 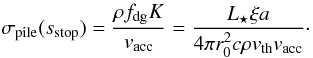 (4)
(4)
Some numerical estimates for observed transitional disks.
2.1.4. Width of the peak from diffusion
We can also estimate the width ΔR of the dust pile as it is produced by the interplay between accretion and viscosity. The diffusion time across ΔR is given by tdiff = ΔR2/D, and the accretion time across the same distance is tacc = ΔR/vacc. Equating these timescales, and using D = ν/Sc where D is the diffusion coefficient, ν is the viscosity (molecular or turbulent) and Sc is the Schmidt number, we find ΔR = ν/(Sc vacc). Please see below for more details on the Schmidt number we use for our calculations.
2.2. Numerical values
Table 1 shows numerical values for the quantities derived above. To derive these values we have relied on standard accretion theory (e.g. Hartmann 2009) and used the following relations: vacc = 3ν/(2r), Σ = Ṁ/(2πRvacc), and ρ = Σ/(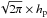 ) with the pressure scale height hp: = cs/ΩK.
) with the pressure scale height hp: = cs/ΩK.
The table shows γ, σpile, rstop, and tstop for the three stars in CM07 and also for HD 100546, a Herbig star that also shows a large gap even though is does have some hot dust close to the star (Benisty et al. 2010). We have included this star because of its higher luminosity, which is helpful for illustrating the pile-up effect. The value of γ shows that the radiation force on individual grains does not greatly exceed the friction force created by the accretion flow – something one would have expected to achieve significant pile-up. Consequently, the total column of dust piled up before the turn-around point is only of the order of 1 × 10-5 g cm-2, and the location where this happens is no more than a few times 10-4 AU, very close indeed to the original starting point of the rim. The pile-up happens on a time scale between 1 and 40 years. So even starting with a clean inner disk, dust will start to flow into the gap after that time.
The higher luminosity of the Herbig star HD 100546 does have a slightly stronger effect, but it will be not any more noticeable than in the case of T Tauri stars.
3. Numerical model
3.1. Model description
The calculations so far are based on a number of simplifying assumptions to make the problem analytically tractable. We also constructed a numerical model to study the radial dust motion in this situation. Instead of solving the complete coupled set of equations involving both the dust and the gas motion, our goal is less ambitious. We want to see whether the radiation pressure can counter the dust pile-up enough to keep the inner hole dust-free. Therefore, we study the reduced problem of radial 1-D dust motion with radiation pressure in a disk with a given inward gas motion.
The model is built in the following way. We start by setting up the gas density ρg(r) at the disk midplane as a function of the radial coordinate r. The gas density is computed semi-selfconsistently by specifying the accretion rate Ṁ in the disk, the turbulence parameter for accretion αa and the flaring angle ϕ for stellar irradiation. Using the flaring angle, the midplane disk temperature is estimated as (Chiang & Goldreich 1997): Tmid(r) = ϕ1/4(r∗/r)1/2T∗, where R∗ is the stellar radius and T∗ is the stellar effective temperature. We assume that no viscous heating takes place (valid for low accretion rates and large inner holes) and that the full 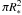 stellar surface is “visible” at any point on the disk surface. From the resulting temperature we can now compute the isothermal sound speed
stellar surface is “visible” at any point on the disk surface. From the resulting temperature we can now compute the isothermal sound speed 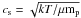 , where k is the Boltzmann constant and μ ≃ 2.3 is the mean molecular weight of the gas and mp is the proton mass. The accretion viscosity coefficient is now given as
, where k is the Boltzmann constant and μ ≃ 2.3 is the mean molecular weight of the gas and mp is the proton mass. The accretion viscosity coefficient is now given as 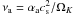 , where
, where 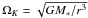 with M∗ the stellar mass. Finally, with Ṁ = 3πΣgνa (valid for r ≫ R∗) the gas surface density Σg can be computed for given value of the accretion rate Ṁ. For more details on standard accretion disk theory, we refer to the book by Hartmann (2009). We do included neither the effect of the dust motion nor of changing dust-to-gas ratios, in our estimation of the gas disk structure.
with M∗ the stellar mass. Finally, with Ṁ = 3πΣgνa (valid for r ≫ R∗) the gas surface density Σg can be computed for given value of the accretion rate Ṁ. For more details on standard accretion disk theory, we refer to the book by Hartmann (2009). We do included neither the effect of the dust motion nor of changing dust-to-gas ratios, in our estimation of the gas disk structure.
We then insert the dust into this model. We assume that the dust grains are small enough that they do not settle much, so that the increase in midplane dust density due to settling is negligible. We focus solely on the radial motion of the dust. At each time step we start with a very simple radiative transfer calculation: we follow the radiation of the star as it moves along the disk equatorial plane outward, i.e. we integrate the equation 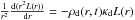 , where ρd(r,t) is the dust density as a function of spatial position r and time t. κd is the Planck-mean dust opacity, computed with the stellar temperature as reference temperature. For simplicity we assume that κd is independent of r, i.e. we neglect the changes in stellar spectrum as it is extincted in the disk. In fact, we do not solve for the frequency-dependent luminosity Lν(r,t), but instead for the frequency-integrated one L(r,t). This exerts a radiation pressure force on the dust grains, in units of dyne/gram-of-dust, of fr(r,t) = κdL(r,t)/(4πcr2). The dust has friction with the gas and we compute the dust velocity by assuming that radiative and friction forces are in equilibrium, i.e. that the dust drifts relative to the accreting gas at its equilibrium drift velocity.
, where ρd(r,t) is the dust density as a function of spatial position r and time t. κd is the Planck-mean dust opacity, computed with the stellar temperature as reference temperature. For simplicity we assume that κd is independent of r, i.e. we neglect the changes in stellar spectrum as it is extincted in the disk. In fact, we do not solve for the frequency-dependent luminosity Lν(r,t), but instead for the frequency-integrated one L(r,t). This exerts a radiation pressure force on the dust grains, in units of dyne/gram-of-dust, of fr(r,t) = κdL(r,t)/(4πcr2). The dust has friction with the gas and we compute the dust velocity by assuming that radiative and friction forces are in equilibrium, i.e. that the dust drifts relative to the accreting gas at its equilibrium drift velocity.
In addition to this systematic dust motion, there is also random motion due to the gas turbulence. While turbulence may be extremely weak in a dead zone, we shall see that even the slightest turbulence will profoundly affect the structure of the dust pile-up region. The turbulent “diffusion” of dust is due to the same turbulence that is believed to be responsible for the accretion process (the turbulent “viscosity” νa, see above). The turbulent diffusion constant Dt is therefore of the same order of magnitude as νa. Exactly what the ratio Da/νa is is not perfectly understood yet (Johansen & Klahr 2005). If viscosity is due to turbulent gas motions, this ratio should be not far from unity. However, it may also be that large scale magnetic fields could remove angular momentum from the disk without inducing much turbulent mixing (Combet & Ferreira 2008). Here we parametrize it as the Schmidt number: Dt = νt/Sc. We treat Sc as a free tuning parameter.
 |
Fig. 1 Results of the numerical model for the source HD 100546 for the case Sc = 1, i.e. Dt = νt and αt = 0.035. Top panel: surface density of dust as a function of radius (horizontal axis) and time (vertical axis). The color is the dust density in normalized units. The contour levels of the diagram are steps of 100.2, i.e. five contours are one factor of 10. The level in the bottom-right corner is the initial value of the dust surface density, 2.3 × 10-3 g/cm2. The bottom panel is the same, but now plotted as different curves for different times, with the vertical axis being the dust surface density. The model actually calculates the density of the dust ρd, but for the plotting we converted it to surface density |
 |
Fig. 2 As Fig. 1, but now for Sc = 103, i.e. Dt = 0.001 νt. Time differences between curves is 300 years this time. |
The dust motion now follows from the continuity equation: 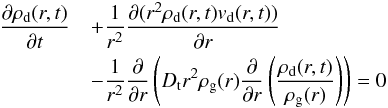 (5)which we solve using implicit integration (“backward Euler”).
(5)which we solve using implicit integration (“backward Euler”).
As an initial condition for the dust we set ρd to 0.01ρg for r ≥ r0 and ρd = 0 for r < r0, where r0 is the initial dust inner rim radius, given in Table 1. We take the dust grains to be a = 0.1 μm in radius, consisting of material with a density of ξ = 3 g cm-3. For simplicity we take a simple geometric opacity of κ = 3/(ξa), which is twice the geometric cross section. As boundary condition at the inner edge of the computational domain we take a simple outflow condition, while at the outer edge of the domain we set ρd = 0.01ρg as a boundary condition.
3.2. Model results
We performed the numerical equivalent models for all sources listed in Table 1. One of the most striking results, found in all models, is that if we take Sc = 1, i.e. Dt = νt, then any outward movement of the dust induced by the radiative pressure is completely overwhelmed by the enormously strong turbulent diffusive mixing. So even for cases where the radiative force would easily push out the grains if no turbulent mixing would occur (Sc → ∞), the grains are washed inward as a result of strong mixing. An example of this is shown in Fig. 1. In this example the time scale for mixing dust toward the inner edge of the computational domain at 9.5 AU is about 10 years only. The overall solution quickly becomes dominated by the outer boundary condition (best seen in the bottom panel), rendering it meaningless at that point.
Why is particle mixing so dominant, almost independent of αt? This can be seen in the following way: if, we take strong/weak turbulence, e.g. α = 0.1 / α = 10-6, then, for a given accretion rate Ṁ, the gas surface density becomes low/high (by virtue of Ṁ = 3πΣνt). So for a given radiation pressure force on the grains, the drift speed is high/low, but also the turbulent mixing as well as the inward gas velocity become high/low. Working out the numbers for the accretion rates given in Table 1, in all cases the turbulent diffusion wins over radiation pressure. The conclusion is that with Sc ≃ 1, the radiation pressure is entirely unable to prevent the dust from drifting inward toward the star.
However, as discussed earlier, if angular momentum transport is not primarily caused by turbulence, much larger Schmidt numbers are allowed. We choose Sc = 103, but keep the αt the same as before. Then we find that for some cases, notably HD 100546, the radiation pressure is strong enough to push the dust outward against both the accretion flow of the gas and the action of turbulent diffusion. For other cases the gas drag of the inward gas motion is still too strong, such as for DM Tau. The results for HD 100546 and DM Tau are shown in Figs. 2, 3.
For HD 100546 one can see that the radiation pressure pushes the grains that are in plain sight of the star outward. But the absorption of the radiation (the same process that transfers radiative momentum to the grains) also shields the dust grains at larger optical depth from stellar light. These dust grains therefore still flow inward with the gas. What happens is, as one can see in the figure, that the dust piles up in a rim of high dust density. According to our model, if one takes an even higher Schmidt number this dust pile-up rim becomes geometrically thinner. However, the total mass in this rim (and thus its optical depth) is only dependent on the amount of dust that has been swept up. The radiation force acts only on the innermost layer of this dust pile-up rim, i.e. the layer of radial optical depth unity. But the diffusion, even if ever so weak, will distributed the momentum that is received by these inner dust grains to the entire mass of dust in the pile-up rim. One also clearly sees that the dust pile-up rim first moves outward, but then slows down as more and more of the radiation momentum has to be divided over an ever increasing mass of dust in the pile-up rim. This dilution of the radiation force means that the outward motion of the rim stalls, and eventually the dust gets dragged inward with the gas flow.
For DM Tau we see that, even with a high Schmidt number, a pile-up never really happens, because the gas drag by the inward moving gas is simply too strong. One sees a nearly instant inward motion taking place, as expected based on the γ value in Table 1 being lower than unity.
 |
Fig. 3 As Fig. 2, but now for the source DM Tau. Time interval between curves is 200 years. The contour levels of the top panel are steps of 100.2, i.e. five contours are one factor of 10. The level in the bottom-right corner is the initial value of the dust surface density, 1 × 10-2 g/cm2. |
4. Discussion and conclusions
In summary, we find strong arguments that radiation pressure alone is wholly insufficient to keep the inner hole of a transitional disk dust-free while low-level accretion is continuing. Both dust pile-up and viscous mixing are easily able to overcome the radiation pressure quickly and refill the inner hole with dust on a level similar to normal dust-to-gas ratios. These processes pose a problem for the inside-out evacuation scenario for transitional disk in its original form. While we do think the MRI activation discussed by Chiang & Murray-Clay (2007) may be responsible for launching a low-level accretion from the inner rim, mechanisms other than radiative forces have to be invoked to keep dust from flowing into the inner holes, or at least from contributing to the opacity in these holes.
An additional force to hold back dust that has been discussed in the literature is photophoresis (Krauss & Wurm 2005), which is a strong force caused by the temperature difference between the illuminated and dark sides of a dust grain. This force may have an effect for larger grains (cm-sizes), but it is irrelevant for the sub-micron-sized grains considered here (see Fig. 1 from Krauss & Wurm 2005).
One possible solution is that the dust has grown to such large sizes in these regions that the dust continuum optical depth drops below unity (Tanaka et al. 2005). A way to achieve this could be efficient dust growth in the pile-up produced by radiation pressure. In fact, the jump in gas surface density will foster faster and more efficient dust settling, further enhancing the dust density. Greatly increased coagulation rates might be the result. Large grains produced in this way could even enter the gap without being visible, and without being an obstacle to the ionizing radiation needed to drive the inside-out evacuation of the disk. However, a much more detailed model of this scenario is required before any conclusions can be drawn.
A second possibility is that the inner hole has been made by a planet orbiting close to the disk rim, and that a pressure bump created by the planet-disk interaction traps particles in the disk rim (Rice et al. 2006). However, Ward (2009) has questioned the effectiveness of this mechanism.
A third possibility would be that torques exerted by one or more planets located in the inner disk hole in the system transport matter so quickly to the star, that the average optical depth in the inner disk remains small even though dust is contained in the accreting matter (Zhu et al. 2011; Perez-Becker & Chiang 2011).
Our model contains a number of simplifications, for example the use of geometrical cross sections for the dust grains. We also did not account for the optical depth of the gas inward of the dust rim. The gas is expected to have much lower optical depth than the dust, but at high enough accretion rates even the gas can become optically thick to stellar radiation (Muzerolle et al. 2004). This effect is rather weak at the low accretion rates we are concerned with (according to Muzerolle et al. it plays virtually no role at Ṁ ≃ 10-9 M⊙/yr), and therefore it is not problematic that we ignore it. As with other assumptions in this paper, we have always made choices that would make it easier to hold back the grains by radiation pressure. The conclusion that dust grains cannot be held back by radiation pressure is therefore a firm one.
Acknowledgments
We would like to thank the anonymous referee and E. Chiang for comments on the first version of this manuscript. C.P.D. acknowledges financial support from the Max Planck Gesellschaft under the SNWG program. C.D. would like to thank the Dutch Top Research School NOVA (network 2) for financial support and the Leids Kerkhoven-Bosscha Fonds for travel support.
References
- Alexander, R. D., & Armitage, P. J. 2009, ApJ, 704, 989 [NASA ADS] [CrossRef] [Google Scholar]
- Alexander, R. D., Clarke, C. J., & Pringle, J. E. 2006, MNRAS, 369, 216 [NASA ADS] [CrossRef] [Google Scholar]
- Benisty, M., Tatulli, E., Ménard, F., & Swain, M. R. 2010, A&A, 511, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Calvet, N., D’Alessio, P., Hartmann, L., et al. 2002, ApJ, 568, 1008 [NASA ADS] [CrossRef] [Google Scholar]
- Chiang, E. I., & Goldreich, P. 1997, ApJ, 490, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Chiang, E., & Murray-Clay, R. 2007, Nat. Phys., 3, 604 [NASA ADS] [CrossRef] [Google Scholar]
- Clarke, C. J. 2007, MNRAS, 376, 1350 [NASA ADS] [CrossRef] [Google Scholar]
- Combet, C., & Ferreira, J. 2008, A&A, 479, 481 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dominik, C., Dullemond, C. P., Waters, L. B. F. M., & Walch, S. 2003, A&A, 398, 607 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ercolano, B., Drake, J. J., Raymond, J. C., & Clarke, C. C. 2008, ApJ, 688, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Fang, M., van Boekel, R., Wang, W., et al. 2009, A&A, 504, 461 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hartmann, L. 2009, Accretion Processes in Star Formation. 2nd edn. (Cambridge University Press) [Google Scholar]
- Hollenbach, D., & Gorti, U. 2005, in Protostars and Planets V, 8433 [Google Scholar]
- Johansen, A., & Klahr, H. 2005, ApJ, 634, 1353 [NASA ADS] [CrossRef] [Google Scholar]
- Krauss, O., & Wurm, G. 2005, ApJ, 630, 1088 [NASA ADS] [CrossRef] [Google Scholar]
- Muzerolle, J., D’Alessio, P., Calvet, N., & Hartmann, L. 2004, ApJ, 617, 406 [NASA ADS] [CrossRef] [Google Scholar]
- Perez-Becker, D., & Chiang, E. 2011, ApJ, 727, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Ricci, L., Testi, L., Natta, A., et al. 2010, A&A, 512, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rice, W. K. M., Armitage, P. J., Wood, K., & Lodato, G. 2006, MNRAS, 373, 1619 [NASA ADS] [CrossRef] [Google Scholar]
- Schaaf, S. A. 1963, Handbuch der Physik, vol. VIII/2 (Berlin, Göttingen, Heidelberg: Springer Verlag), 591 [Google Scholar]
- Sicilia-Aguilar, A., Henning, T., & Hartmann, L. W. 2010, ApJ, 710, 597 [NASA ADS] [CrossRef] [Google Scholar]
- Tanaka, H., Himeno, Y., & Ida, S. 2005, ApJ, 625, 414 [NASA ADS] [CrossRef] [Google Scholar]
- Ward, W. R. 2009, in Lunar and Planetary Institute Science Conference Abstracts, 40, 1477 [Google Scholar]
- Zhu, Z., Nelson, R. P., Hartmann, L., Espaillat, C., & Calvet, N. 2011, ApJ, 729, 47 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Results of the numerical model for the source HD 100546 for the case Sc = 1, i.e. Dt = νt and αt = 0.035. Top panel: surface density of dust as a function of radius (horizontal axis) and time (vertical axis). The color is the dust density in normalized units. The contour levels of the diagram are steps of 100.2, i.e. five contours are one factor of 10. The level in the bottom-right corner is the initial value of the dust surface density, 2.3 × 10-3 g/cm2. The bottom panel is the same, but now plotted as different curves for different times, with the vertical axis being the dust surface density. The model actually calculates the density of the dust ρd, but for the plotting we converted it to surface density |
| In the text | |
 |
Fig. 2 As Fig. 1, but now for Sc = 103, i.e. Dt = 0.001 νt. Time differences between curves is 300 years this time. |
| In the text | |
 |
Fig. 3 As Fig. 2, but now for the source DM Tau. Time interval between curves is 200 years. The contour levels of the top panel are steps of 100.2, i.e. five contours are one factor of 10. The level in the bottom-right corner is the initial value of the dust surface density, 1 × 10-2 g/cm2. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.