| Issue |
A&A
Volume 531, July 2011
|
|
|---|---|---|
| Article Number | A54 | |
| Number of page(s) | 6 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201116577 | |
| Published online | 10 June 2011 | |
Evolution of the dust coma in comet 67P/Churyumov-Gerasimenko before the 2009 perihelion⋆
1 INAF – Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, 50125 Firenze, Italy
e-mail: tozzi@arcetri.astro.it
2 Max-Planck Institut für Sonnensystemforschung, 37191 Katlenburg-Lindau, Germany
3 Instituto de Astrofísica de Canarias, vía Láctea s/n, 38200 La Laguna, Tenerife, Spain
4 Departamento de Astrofísica, Universidad de La Laguna, 38205 La Laguna, Tenerife, Spain
5 University of Maryland, College Park, MD 20742-2421, USA
6 ESA Research and Scientific Support Department, ESTEC, 2200 AG Noordwijk, The Netherland
Received: 25 January 2011
Accepted: 1 May 2011
Context. Comet 67P/Churyumov-Gerasimenko is the main target of ESA’s Rosetta mission and will be encountered in May 2014. Because the spacecraft will orbit the comet nucleus before and after release of the lander Philae, it is necessary to know the conditions in the coma.
Aims. We study the dust environment, including the dust production rate and its variations along the comet’s pre-perihelion orbit.
Methods. The comet was observed during its approach to the Sun on four epochs between early-June 2008 and mid-January 2009 over a large range of heliocentric distances that will be covered by the mission in 2014.
Results. An anomalous enhancement of the coma dust density was measured toward the comet nucleus. The scale length of this enhancement increased with decreasing heliocentric distance of the comet. We interpret this as a result of an unusually slow expansion of the dust coma. Assuming a spherically symmetric coma, we derive the average amount of dust as well as its ejection velocity. The latter increases exponentially with decreasing heliocentric distance (rh), ranging from about 1 m/s at 3 AU to about 25–35 m/s at 1.4 AU. Based on these results we describe the dust environment at those nucleocentric distances at which the spacecraft will presumably be in orbit.
Key words: comets: general / comets: individual: 67P/Churyumov-Gerasimenko
© ESO, 2011
1. Introduction
In May 2014 ESA’s Rosetta spacecraft, an orbiter and lander mission to a comet, will encounter its target, comet 67P/Churyumov-Gerasimenko (hereafter 67P), at a heliocentric distance rh of about 4 AU. It will go in orbit around the nucleus in September 2014, when the comet is at rh = 3.4 AU and begin global observations and mapping of the nucleus (Glassmeier et al. 2007) . At rh ≈ 3 AU, the lander Philae will land on the surface and perform the first-ever in-situ analysis of comet nucleus material. The orbiter will be monitoring the evolution of the nucleus and the coma along the comet’s pre- and post-perihelion orbit for more than one year while approaching the nucleus as close as a few km above the surface.
When approaching the Sun, at distances from about 5 to 2 AU, cometary nuclei usually switch on the activity and produce a gas and dust coma that changes because of secular and short-term effects, e.g., solar heating and rotation of the nucleus. Consequently, an increase of the production rate and expansion speed of the dust is expected as a result of the increased heating of sublimating ices from the nucleus. Unfortunately, not much is published on the coma status and the dust environment of comets at large distances, because comets are very faint when far from the Sun, and require observations with large telescopes, for which observing time is difficult to receive. This applies particularly to the short-period comets of the Jupiter-family, of which the Rosetta target comet 67P is a member. At large rh the Afρ index (A’Hearn et al. 1984) is a questionable measure for the dust production rate because the conditions for radially constant Afρ profiles (homogeneous, isotropic, and constant outflow of the dust) are not fulfilled. It can be suspected that the expansion velocities of the dust in the coma are low, resulting in very long travel times (weeks to months) for the grains through the coma, particularly for the larger grains. This may lead to a pile-up of grains in the coma, reflecting the changing dust production of the nucleus over a range of solar distances.
Apart from the scientific interest in obtaining a better knowledge of the dust coma environment and evolution of 67P along the pre-perihelion orbit, this knowledge is required for the safety and the operations planning of the Rosetta mission. After the Rosetta launch delay in 2003, 67P was selected as the new target of the mission, replacing the original target 46P/Wirtanen, which was much better characterized by Earth-based observations. At the time of its selection 67P had just passed its perihelion. Thus, most observations existing to date were obtained during the subsequent post-perihelion phase (Schulz et al. 2004; Weiler et al. 2004), whereas only a few observations exist of the pre-perihelion phase (Schleicher 2006; Lamy et al. 2006, 2007, 2008), except from those obtained by amateur astronomers (http://cara.uai.it, http://www.aerith.net), (Kidger 2003, 2004).
The 2009 return of the comet was the first and last opportunity to measure the pre-perihelion dust environment of 67P before Rosetta will have arrived at the comet.
Here, we report the results of our dust coma analysis of 67P using observations obtained during the per-perihelion phase 2008–2009 between rh ≈ 3 to 1.4 AU. Our observations are complementary to those reported by Tubiana et al. (2008, 2010), obtained at larger heliocentric distances and those by Lara et al. (2010), obtained during the post-perihelion phase.
2. Observations
Comet 67P was observed at four epochs (see Table 1) during the inbound phase before it reached its perihelion in Feb 2009. During the first three epochs the observations were obtained at the 8.2 m Very Large Telescope (VLT) of the European Southern Observatory in Chile using the FORS2 focal reducer instrument (see http://www.eso.org/sci/facilities/paranal/instruments). The last run, when the comet was in the northern hemisphere, was performed with the Telescopio Nazionale Galileo, TNG, at La Palma with the camera-spectrograph DOLORES (see http://www.tng.iac.es/instruments/). During each run a series of images was acquired with broadband filters (VRI bands) and sometimes narrower band filters, taken a few days apart to check the comet short term variability. Differential tracking of the telescope at the cometary velocity was applied for all 67P images. Because the comet was in front of star-rich regions and because it had a relatively fast proper motion, each run consisted of several (5–9) exposures to reduce the star contribution by median averaging of the images during data processing. At the VLT the observations were performed in service mode and the flux calibration relies on the zero point estimations (Zp) provided by the observatory for each photometric night. The observations at the TNG were taken in visitor mode and a series of photometric standards were obtained for calibration purposes.
Summary log for the observations of comet 67P.
3. Data reduction
All images were processed using standard CCD reduction procedures (bias and flat field correction). Then a first-order constant sky level, measured in image regions away from the comet’s photo-center, was subtracted. After combining all filter frames of a single night (aligned to the comet and median-averaged), possible sky residuals were checked in the resulting frame and subtracted using the ΣAf function (see below). Finally, the images of each night were calibrated in Af, i.e. the albedo multiplied by the filling factor of the dust in the coma (A’Hearn et al. 1984; Tozzi et al. 2007). To allow a comparison of the results obtained at different phase angles, the calibrated images were re-calibrated for the phase equal to 0° using the multiplicative phase correction coefficient (last column of Table 1) given by Schleicher et al. (1998) and recently refined in Schleicher (2010, priv. comm.). The observation series taken over a few days apart were searched for the presence of possible short-term variability. Because no day-to-day variability was found, all images obtained with the same filter during each epoch were median-averaged, which further reduced the contribution of the background stars and increased the signal-to-noise ratio of the cometary coma flux.
These final images in the VRI filters allowed us to assess the dust distribution in the coma of 67P. The gas contamination in the broad band filters was negligible for all four epochs, as was verified in spectra and measurements through an interference filter with the passband centered in regions without any gas emission (central λ = 8340 Å, Δλ = 480 Å). No or negligible gas emission was present in this relatively wide passband, which was verified a posteriori by the spectra as well.
4. Data analysis
The final resulting images were initially analyzed using the ΣAf(ρ) function. ΣAf(ρ) is proportional to the average column density of the solid component at the projected nucleocentric distance ρ. It is equal to 2πρAf(ρ) and is measured in cm. As shown in Tozzi et al. (2007), ΣAf(ρ) is constant with the projected nuclear distance ρ for a comet with a dust outflow of constant velocity and production rate, and if sublimation or fragmentation of the grains are excluded. Only the solar radiation pressure introduces a small linear dependence, but usually only at large distances from the nucleus, definitely larger than our field of view (FOV). Unfortunately, despite all efforts, our final images suffered from remnant flux contamination of the numerous background stars so much that the stars were not completely erased even after using the median average. However, it was always possible to check and verify the radial profile of the ΣAf function up to about 105 km from the nucleus. Figure 1, left panel, gives an example of a measured ΣAf profile. Clearly, it is not constant with radial distance ρ from the nucleus and shows a fast decrease as ρ increases, until it reaches a constant value at about 20 000 km. The Afρ function, shown in the right panel of the same figure, also strongly depends on ρ and clearly cannot be used as a proxy of the dust production rate.
 |
Fig. 1 Left: measured R filter ΣAf in function of the projected nucleocentric distance ρ for observations at rh ≈ 2.3 AU together with the model functions. Crosses represent the measurements, the solid line shows the total model function, the dashed line gives the part related to Nc+Nl and the dotted line that of Ns. The “bumps” (for instance, that at about 32 000 km) are caused by the remnant flux from background stars, easily identifiable by eye in the images. Note that the profile was modeled up to 105 km, but here a smaller part is shown. Right: measured Afρ function for the same date and filter. This shows that the Afρ strongly depends on ρ and consequently it cannot be used as proxy of the dust production. |
Fit parameters of the ΣAf profiles.
The profiles were reproduced with a trial and error procedure by integrating along the line of sight of a spherical symmetric coma with an “optical density distribution” of the dust as ![\hbox{$ \Nd = [\Nc + \Nl {\rm e}^{-(\frac{d}{\Ll})}+\Ns {\rm e}^{-(\frac{d}{\Ls})}]/d^2$}](/articles/aa/full_html/2011/07/aa16577-11/aa16577-11-eq37.png) where d is the (non-projected) nucleocentric distance in km. This function has a constant term Nc that represents the constant optical density and two exponential terms with Ns and Nl that describe a short-scalelength and a long-scalelength optical density increase, respectively. The d2 term represents the spatial density attenuation caused by the geometric expansion of the dust in the coma, Ll and Ls are the relative scalelengths of the long and short-scalelength variations in N(d). Nc, Nl, and Ns describe the “optical density distribution”, i.e. the albedo multiplied by the light scattering area of the grains in a cubic centimeter. They are measured in cm-1 (area over volume, cm2/cm3). Of course, it is necessary to consider the albedo and size distribution of the grains to derive the corresponding spatial density of the dust (number of grains per cubic centimeter).
where d is the (non-projected) nucleocentric distance in km. This function has a constant term Nc that represents the constant optical density and two exponential terms with Ns and Nl that describe a short-scalelength and a long-scalelength optical density increase, respectively. The d2 term represents the spatial density attenuation caused by the geometric expansion of the dust in the coma, Ll and Ls are the relative scalelengths of the long and short-scalelength variations in N(d). Nc, Nl, and Ns describe the “optical density distribution”, i.e. the albedo multiplied by the light scattering area of the grains in a cubic centimeter. They are measured in cm-1 (area over volume, cm2/cm3). Of course, it is necessary to consider the albedo and size distribution of the grains to derive the corresponding spatial density of the dust (number of grains per cubic centimeter).
For comparison with the data, N(d) is integrated along the line of sight. Figure 1 provides an example of the computed profile as a function of the projected nucleocentric distance (ρ) using the adopted model function N(d). The measured radial profiles and the above defined model agree very well. The only differences are within the “bumps” caused by the background stars. The best values of the model parameters Nc, Nl, Ns, and Ll and Ls together with the observing geometry and filters are listed in Table 2 for the four observing epochs. The errors indicated in the table mainly refer to the dominating systematic errors. Nc is most affected by the errors caused by contaminating flux from background stars. Our checks of the ΣAf profiles up to more than 105 km, identifying the star contribution visually, indicate an uncertainty of Nc not greater than a factor two. The Ns estimate is also affected by the systematic errors because Ls is on the order of the seeing, in particular for the observations taken during the first epoch. Hence, for that epoch, Ls should just be considered as an upper limit and, consequently, Ns as a lower limit. The parameters less affected by the systematic errors are Nl and Ll, because Ll is always much larger than the seeing and the intensity of this component is high enough so that the contribution of possible background stars is negligible. By varying these parameters in the adopted function for N(d), we estimate that the uncertainties are better than or on the order of 25% for Nl and Ll.
The last three columns of Table 2 are the optical cross sections (SA), measured as the integral of N(d), of three components: constant (SAc), long-scalelength (SAl) and short-scalelength (SAs). They represent the total area covered by the particles of each component multiplied by the particle albedo. At first order, SA is independent of the seeing and gives “real” value (not just upper or lower limits) also for the short-scalelength component. For the constant component, we arbitrarily computed its optical cross section assuming a limit for the nuclear distance of 5 × 104 km, because in principle it extends to infinity. The results show that while SA of the constant component does not change much with rh, the SA values of the other two components change a lot (by factors up to 20–40). We conclude that the two exponential components were replenished by fresh grains produced as the comet approached the Sun. However, we cannot exclude a small replenishment of fresh grains also in the constant component, because the grain ejection velocity should increase with decreasing rh.
It is important to note that the flux contribution from the nucleus was not negligible when the comet was at rh ≈ 3 AU. With the radius rc = 2.0 km and the geometric albedo in the R filter A = 0.054 (Lamy et al. 2006, 2007; Kelley et al. 2009), the optical cross section (SA) of the nucleus at 0° phase angle is equal to 0.68 km2. Taking into account the factor 4 due to the different definition of albedo (A’Hearn et al. 1984), the optical cross section of the nucleus corresponds to 2.7 km2, which is a large part of the measured SAs = 3.9 km2 of the short-scalelength cross section in our R filter. For the other epochs, the contribution of the nucleus is always negligible.
In the past, such anomalous enhancements were observed in other comets and interpreted by the presence of organic grains that sublimated in the coma with a certain lifetime τ while moving away from the nucleus (Tozzi et al. 2004, 2007). If this is the case, the lifetime (and the scalelength) should decrease when the comet approaches the Sun. Our results for 67P show an increase of Ll with the comet approaching the Sun, which excludes grain sublimation or any other photolytic process as responsible for the enhancement.
 |
Fig. 2 Measured Ll for V (star) and R (square) filters as a function of the heliocentric distance. The lines show the best fit assuming the function described in the text. The solid line represents the V and the dotted line the R filter. |
 |
Fig. 3 Computed grain ejection velocity as function of the heliocentric distance for observations in V (solid line) and in R (dotted line). |
Figure 2 gives the scalelength Ll as a function of the heliocentric distance rh. The scalelength values are well fitted by the function function Ll = 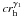 with the best fit given for c = (195 000 ± 29 000) km and γ1 = (− 3.93 ± 0.20) in V and c = (120 000 ± 18 000) km and γ1 = (− 3.20 ± 0.19) in R.
with the best fit given for c = (195 000 ± 29 000) km and γ1 = (− 3.93 ± 0.20) in V and c = (120 000 ± 18 000) km and γ1 = (− 3.20 ± 0.19) in R.
If we assume that this long-scalelength component was caused by fresh dust produced in a spherically symmetric coma during the approach of the comet to the Sun, the coma was expanding with a velocity given by 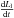 , which is equal to
, which is equal to 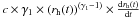 . Because in this part of the orbit the heliocentric distance varies linearly with time as rh = rh0 + v0Tp with Tp = days to perihelion, rh0 = 1.011 AU and v0 = −7.18 × 10-3 AU/day, the time variation of the scalelength is
. Because in this part of the orbit the heliocentric distance varies linearly with time as rh = rh0 + v0Tp with Tp = days to perihelion, rh0 = 1.011 AU and v0 = −7.18 × 10-3 AU/day, the time variation of the scalelength is 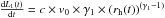 . This is the expansion velocity of the grains that are at nucleocentric distance equal to Ll. It is known that the grains are accelerated by gas drag only in the inner part of the coma, i.e. within few radii of the comet nucleus (see e.g. Combi et al. 1997) and that they move with almost constant velocity beyond that limit. They are affected only by solar radiation pressure, efficient at large scales, and by the gravity of the comet, efficient only very close to the nucleus. This means that roughly speaking, the grains expand in the coma with a widely distributed, but unchanging velocity. Hence, the grains at nucleocentric distance Ll were ejected some time before (ΔT) with the velocity
. This is the expansion velocity of the grains that are at nucleocentric distance equal to Ll. It is known that the grains are accelerated by gas drag only in the inner part of the coma, i.e. within few radii of the comet nucleus (see e.g. Combi et al. 1997) and that they move with almost constant velocity beyond that limit. They are affected only by solar radiation pressure, efficient at large scales, and by the gravity of the comet, efficient only very close to the nucleus. This means that roughly speaking, the grains expand in the coma with a widely distributed, but unchanging velocity. Hence, the grains at nucleocentric distance Ll were ejected some time before (ΔT) with the velocity 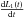 . To compute ΔT, we only need to divide Ll by
. To compute ΔT, we only need to divide Ll by 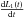 . This gives
. This gives 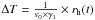 , i.e. the time necessary to reach Ll is linearly dependent on rh. For example, for observations in the R filter, ΔT is about 87 days at rh = 2 AU. The value of
, i.e. the time necessary to reach Ll is linearly dependent on rh. For example, for observations in the R filter, ΔT is about 87 days at rh = 2 AU. The value of 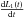 for the same rh and filter is about 150 km/day or 1.73 m/s, i.e. the expansion velocity is quite low. Because the grains are expanding almost freely (see above), the expansion velocity at a certain time T1 is equal to the ejection velocity at time T1 − ΔT. By solving the equations numerically, we get the ejection velocities as functions of the heliocentric distance, as shown in Fig. 3. They are equal to
for the same rh and filter is about 150 km/day or 1.73 m/s, i.e. the expansion velocity is quite low. Because the grains are expanding almost freely (see above), the expansion velocity at a certain time T1 is equal to the ejection velocity at time T1 − ΔT. By solving the equations numerically, we get the ejection velocities as functions of the heliocentric distance, as shown in Fig. 3. They are equal to 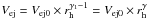 , with Vej0 = 195 ± 21 and 100 ± 11 m/s in V and R, respectively.
, with Vej0 = 195 ± 21 and 100 ± 11 m/s in V and R, respectively.
This formula is similar to the ejection velocity assumed in models, i.e. 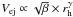 , with β = the ratio of the radiation pressure over solar gravity forces (see e.g. Fulle et al. 2010). We derive γ = –(4.93 ± 0.20) and –(4.20 ± 0.20) in V and R, respectively, which is quite different from the assumed values: –0.5 (Ishiguro 2008; Kelley et al. 2008, 2009) or –3 (Agarwal et al. 2010). The ratio of β, of the particles observed in V with respect to those observed in R is about 3.8 ± 1.2, a fairly high value that is difficult to explain.
, with β = the ratio of the radiation pressure over solar gravity forces (see e.g. Fulle et al. 2010). We derive γ = –(4.93 ± 0.20) and –(4.20 ± 0.20) in V and R, respectively, which is quite different from the assumed values: –0.5 (Ishiguro 2008; Kelley et al. 2008, 2009) or –3 (Agarwal et al. 2010). The ratio of β, of the particles observed in V with respect to those observed in R is about 3.8 ± 1.2, a fairly high value that is difficult to explain.
It is important to note that all results about the grain ejection velocity assume isotropic outflow of the dust. If the comet showed an asymmetric emission (e.g., a jet) in the direction of the observer, this would have changed the results, leading to a higher ejection velocity. However, this would mean that the jet direction and intensity had to remain unchanged for about four days during each epoch, because even the images taken several days apart during each epoch did not show any change in flux. Such a stable jet could only be produced if the spin axis of the nucleus were pointing exactly into the observer’s direction, which could be the case only for one of the three epochs if at all, but certainly not for all three epochs.
5. Discussion
5.1. Other observations
It is important to note that during the post-perihelion phase comet 67P displayed a completely different behavior from what we found in the per-perihelion images. The ΣAf profiles did not show any anomalous enhancement toward the nucleus. For example, the profiles obtained from HST observations (see Lamy et al. 2006) and downloaded from the HST archive, show only the signature of the nucleus itself at ρ close to zero, but are otherwise “flat” up to ρ = 4 × 104 km, the FOV of the images. A similar behavior is also found in other post-perihelion measurements, which demonstrates that the slope parameters of log (I) vs. log (ρ) are equal to about –1 (Lara et al. 2005; Schleicher 2006). Obviously, after perihelion the comet had already developed an extended coma with the conditions necessary for a reliable determination of Afρ (see above).
5.2. Grain size
As shown above, for heliocentric distances greater than ≈2 AU, the dust expansion velocities in the coma of 67P were about two orders of magnitude smaller than those usually claimed for cometary comae (see Crifo & Rodionov 1997; Foster & Green 2007, and references therein). This may be an indication that the grains in 67P were big. Agarwal et al. (2007, 2010) computed that velocities on the order of 30–50 m/s at rh = 1.3 AU correspond to grain radii ranging from about 10 μm to 1 mm (depending on the emission scenario) assuming spherical grains with a density equal to 1 g/cm3. Because it is likely that the grains are fluffy and nonspherical (and the density is much lower than than assumed), their size can be much larger. Hadamcik et al. (2010) have also reported an anomalous slope log (I) vs. log (ρ) (close to –1.5) in the inner coma (ρ between 2000 and 8500 km) in December 2008, which they interpreted as being caused by the presence of large particles. The presence of large and fluffy particles is also consistent with polarization measurements performed in March 2009. Hadamcik et al. (2010) note that the high polarization (6%) observed near the nucleus is typical for small, sub-micron particles (cf. comet Hale-Bopp in Hadamcik & Levasseur-Regourd 2003). This contradiction can be resolved by suggesting large, but porous particles (Hadamcik et al. 2010). Note that several authors (Fulle et al. 2004, 2010; Moreno et al. 2004; Kelley et al. 2008; Ishiguro 2008) suggested the presence of grains in the cm-range based on the observations of a trail, the tail and necklines in 67P.
5.3. Grains density in the coma
For regions with d ≪ Ls ≪ Ll, which are relevant for the Rosetta spacecraft during its close approach or when orbiting the nucleus of 67P, the mean optical density distribution of the dust at a nucleocentric distance d is simply equal to N(d) = (Nc + Nl + Ns)/d2 = N0/d2, where N0 represents the optical density distribution at d = 1 km. For example, at 1.93 AU from the Sun, we find N0 = 4.1 × 10-8 cm-1 (see the R filter results in Table 2). Assuming the power-law size distribution 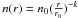 , equal for the three components of N(d), the optical density is equal to
, equal for the three components of N(d), the optical density is equal to ![\hbox{$\Nd = \int{ \frac{\pi r^2 A n_0 }{d^2} \frac{r^{-k}}{r_{0}^{-k}} {\rm d}r} = \frac{\pi A n_0 }{d^2 r_{0}^{-k}} \int{ r^{2-k} {\rm d}r} = \frac{\pi A n_0 }{d^2 r_{0}^{-k} (3-k)} [{r_{x}^{3-k}-{r_{m}^{3-k}}}]$}](/articles/aa/full_html/2011/07/aa16577-11/aa16577-11-eq79.png) with A = the grain albedo, and the integral extended from the minimum (rm) to the maximum (rx) radius of the grains assumed to be spherical. The local density mass owing to the dust is
with A = the grain albedo, and the integral extended from the minimum (rm) to the maximum (rx) radius of the grains assumed to be spherical. The local density mass owing to the dust is ![\hbox{$M(d) = \int{ \frac{4 \pi r^3 \sigma n_0 }{3 d^2} \frac{r^{-k}}{r_0^{-k}} {\rm d}r} = \frac{4 \pi \sigma n_0 }{3 d^2 r_0^{-k}} \int{ r^{3-k} {\rm d}r} = \frac{4 \pi \sigma n_0 }{3 d^2 r_0^{-k} (4-k)} [{r_x^{4-k}-{r_m^{4-k}}}]$}](/articles/aa/full_html/2011/07/aa16577-11/aa16577-11-eq83.png) with σ being the average density of the grains. The ratio
with σ being the average density of the grains. The ratio 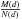 is then independent on d and is equal to
is then independent on d and is equal to ![\hbox{$ \frac{4}{3} \frac{\sigma}{A} \frac{3-k}{4-k} \frac{[{r_x^{4-k}-{r_m^{4-k}}}]}{[{r_{x}^{3-k}-{r_{m}^{3-k}}}]}$}](/articles/aa/full_html/2011/07/aa16577-11/aa16577-11-eq86.png) . Assuming rx ≫ rm and k < 3, as big grains dominate, we have
. Assuming rx ≫ rm and k < 3, as big grains dominate, we have 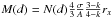 . Consequently, for the given physical parameters of the grains (albedo and density), the ratio
. Consequently, for the given physical parameters of the grains (albedo and density), the ratio 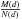 depends on the size of the biggest grains in the dust size distribution, rx and, weakly, on k. With a grain density σ = 0.2 g/cm3, an albedo A = 0.04, and k = 2 the mass density is M(d) = 3.3N(d)rx. For example, for rh ≈ 2 AU, at 10 km from the nucleus, the optical density is 4.1 × 10-10 cm-1. Assuming a maximum grain size of 1 mm, the mass density would be 1.4 × 10-10 g/cm3. Hence, during one orbit revolution at this distance each square meter of the Rosetta spacecraft would intercept a total mass of only 8.6 g. If the maximum grain radius is 5 cm, the mass density would be 6.5 × 10-9 g/cm3 and the mass intercepted would be 430 g, a non-negligible amount, considering that the maximum cross section of the spacecraft is 17 m2.
depends on the size of the biggest grains in the dust size distribution, rx and, weakly, on k. With a grain density σ = 0.2 g/cm3, an albedo A = 0.04, and k = 2 the mass density is M(d) = 3.3N(d)rx. For example, for rh ≈ 2 AU, at 10 km from the nucleus, the optical density is 4.1 × 10-10 cm-1. Assuming a maximum grain size of 1 mm, the mass density would be 1.4 × 10-10 g/cm3. Hence, during one orbit revolution at this distance each square meter of the Rosetta spacecraft would intercept a total mass of only 8.6 g. If the maximum grain radius is 5 cm, the mass density would be 6.5 × 10-9 g/cm3 and the mass intercepted would be 430 g, a non-negligible amount, considering that the maximum cross section of the spacecraft is 17 m2.
It is important to note that the main contribution to the density of the coma in regions close to the nucleus is produced by the short scalelength component, which is sometimes affected by the seeing of the observations. In this case Ns may be a lower limit. However, for the considered example at rh ≈ 2 AU this component is not strongly affected, because its scalelength corresponds to about 1.3″, which is longer than the seeing of the observational nights.
6. Conclusions
The anomalous enhancement of the dust density of the coma of 67P toward the nucleus measured in 2008 and 2009 can be explained by a very slowly expanding dust cloud, with velocities on the order of 1 m/s at rh = 3 AU. The slow dust expansion velocity supports a scenario where at large per-perihelion heliocentric distance the coma of 67P was dominated by large grains, with dimensions greater than 10 μm–1 mm, if they are spherical with a density equal to 1 g/cm3, or much larger, if they are fluffy aggregates. By modeling the radial coma flux profiles with a spherically symmetric coma, the optical density distribution of the dust was quantified as a function of the nucleocentric distance d. The ejection velocity was derived as a function of the heliocentric distance, rh. The model also allowed us to derive the mass density of the dust as a function of d assuming a grain size distribution in which big grains dominate the coma.
References
- Agarwal, J., Müller, M., & Grün, E. 2007, SSR, 128, 79 [Google Scholar]
- Agarwal, J., Müller, M., & Grün, E. 2010, Icarus, 207, 992 [NASA ADS] [CrossRef] [Google Scholar]
- A’Hearn, M. F., Schleicher, D. G., Feldman, P. D., Millis, R. L., & Thompson, D. T. 1984, AJ, 89, 579 [NASA ADS] [CrossRef] [Google Scholar]
- Combi, M. R., Kabin, K., Dezeeuw, D. L., Gombosi, T. I., & Powell, K. G. 1997, Earth Moon and Planets, 79, 275 [Google Scholar]
- Crifo, J. F., & Rodionov, A. V. 1997, Icarus, 127, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Davidsson, B. J. R., & Gutiérrez, P. J. 2005, Icarus, 176, 453 [NASA ADS] [CrossRef] [Google Scholar]
- Foster, M. J., & Green, S. F. 2007, MNRAS, 377, 1064 [NASA ADS] [CrossRef] [Google Scholar]
- Fulle, M., Barbieri, C., Cremonese, G., et al. 2004, A&A, 422, 357 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fulle, M., Colangeli, L., Agarwal, J., et al. 2010, A&A, 522, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Glassmeier, K.-H., Boehnhardt, H., Koschny, D., Kührt, E., & Richter, I. 2007, SSR, 128, 1 [NASA ADS] [Google Scholar]
- Hadamcik, E., & Levasseur-Regourd, A. C. 2003, A&A, 403, 757 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hadamcik, E., Sen, A. K., Levasseur-Regourd, A. C., Gupta, R., & Lasue, J. 2010, A&A, 517, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ishiguro, M. 2008, Icarus, 193, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Kelley, M. S., Reach, W. T., & Lien, D. J. 2008, Icarus, 193, 572 [NASA ADS] [CrossRef] [Google Scholar]
- Kelley, M. S., Wooden, D. H., Tubiana, C., et al. 2009, AJ, 137, 4633 [NASA ADS] [CrossRef] [Google Scholar]
- Kidger, M. R. 2003, A&A, 408, 767 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kidger, M. R. 2004, A&A, 420, 389 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lamy, P. L., Toth, I., Weaver, H. A., et al. 2006, A&A, 458, 669 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lamy, P. L., Toth, I., Davidsson, B. J. R., et al. 2007, SSRv, 128, 23 [NASA ADS] [Google Scholar]
- Lamy, P. L., Toth, I., Groussin, O., et al. 2008, A&A, 489, 777 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lara, L. M., de Léon, J., Licandro, J., & Gutiérrez, P. J. 2005, EMP, 97, 165 [Google Scholar]
- Lara, L. M., Lin, Z.-Y., Rodrigo, R., & IP, W.-H. 2011, A&A, 525, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Levasseur-Regourd, A. C., Hadamcik, E., Sen, A. K., Gupta, R., & Lasue, J. 2010, IAU Symp. Proc. Ser., 263, 259 [NASA ADS] [Google Scholar]
- Moreno, F., Lara, L. M., Muñoz, O., López-Moreno, J. J., & Molina, A. 2004, ApJ, 613, 1263 [NASA ADS] [CrossRef] [Google Scholar]
- Schleicher, D. G. 2006, Icarus, 181, 442 [CrossRef] [Google Scholar]
- Schleicher, D. G., Millis, R. L., & Birch, P. V. 1998, Icarus, 132, 397 [NASA ADS] [CrossRef] [Google Scholar]
- Schulz, R., Stüwe, J. A., & Boehnhardt, H. 2004, A&A, 422, L19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tozzi, G. P., Lara, L. M., Kolokolova, L., et al. 2004, A&A, 424, 325 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tozzi, G. P., Boehnhardt, H., Kolokolova, L., et al. 2007, A&A, 476, 979 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tubiana, C., Barrera, L., Drahus, M., & Boehnhardt, H. 2008, A&A, 490, 377 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tubiana, C., Boehnhardt, H., Agarwal, C., et al. 2011, A&A, 527, 113 [Google Scholar]
- Weiler, M., Rauer, H., & Helbert, J. 2004, A&A, 414, 749 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Left: measured R filter ΣAf in function of the projected nucleocentric distance ρ for observations at rh ≈ 2.3 AU together with the model functions. Crosses represent the measurements, the solid line shows the total model function, the dashed line gives the part related to Nc+Nl and the dotted line that of Ns. The “bumps” (for instance, that at about 32 000 km) are caused by the remnant flux from background stars, easily identifiable by eye in the images. Note that the profile was modeled up to 105 km, but here a smaller part is shown. Right: measured Afρ function for the same date and filter. This shows that the Afρ strongly depends on ρ and consequently it cannot be used as proxy of the dust production. |
| In the text | |
 |
Fig. 2 Measured Ll for V (star) and R (square) filters as a function of the heliocentric distance. The lines show the best fit assuming the function described in the text. The solid line represents the V and the dotted line the R filter. |
| In the text | |
 |
Fig. 3 Computed grain ejection velocity as function of the heliocentric distance for observations in V (solid line) and in R (dotted line). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


