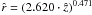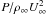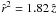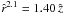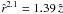| Issue |
A&A
Volume 531, July 2011
|
|
|---|---|---|
| Article Number | A13 | |
| Number of page(s) | 11 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/200912436 | |
| Published online | 31 May 2011 | |
Astrophysical bow shocks: an analytical solution for the hypersonic blunt body problem in the intergalactic medium
Zentrum für Astronomie und Astrophysik, Technische Universität Berlin, Hardenbergstr. 36, 10623 Berlin, Germany
e-mail: schulreich@astro.physik.tu-berlin.de
Received: 6 May 2009
Accepted: 4 April 2011
Aims. Bow shock waves are a common feature of groups and clusters of galaxies since they are generated as a result of supersonic motion of galaxies through the intergalactic medium. The goal of this work is to present an analytical solution technique for such astrophysical hypersonic blunt body problems.
Methods. A method, developed by Schneider (1968, JFM, 31, 397) in the context of aeronautics, allows calculation of the galaxy’s shape as long as the shape of the bow shock wave is known (so-called inverse method). In contrast to other analytical models, the solution is valid in the whole flow region (from the stagnation point up to the bow shock wings) and in particular takes into account velocity gradients along the streamlines. We compare our analytical results with two-dimensional hydrodynamical simulations carried out with an extended version of the VH-1 hydrocode which is based on the piecewise parabolic method with a Lagrangian remap.
Results. It is shown that the applied method accurately predicts the galaxy’s shape and the fluid variables in the post-shock flow, thus saving a tremendous amount of computing time for future interpretations of similar objects. We also find that the method can be applied to arbitrary angles between the direction of the incoming flow and the axis of symmetry of the body. We emphasize that it is general enough to be applied to other astrophysical bow shocks, such as those on stellar and galactic scales.
Key words: shock waves / hydrodynamics / intergalactic medium / galaxies: evolution
© ESO, 2011
1. Introduction
Astrophysical bow shocks are ubiquitous in the Universe and can be observed on all scales, from the Earth’s bow shock through the heliospheric (driven by the moving solar wind) and on to corresponding stellar wind bow shocks. On even larger scales, we see bow shocks of galaxies in the intergalactic medium (IGM) in groups and clusters, and possibly even in mergers of galaxy clusters (Markevitch et al. 2002). The main ingredients of the feature are a compressible medium and a body moving through it supersonically. This was already investigated decades ago in aeronautical engineering in the context of supersonic aircrafts, and is commonly known as the supersonic blunt body problem. However in astronomy, with the exception of a few papers, analytical solutions have been scarce. For example, the paper of Cantó & Raga (1998) considers the supersonic motion of a spherical body and treats the post-shock flow in a thin-shell approximation, which unfortunately restricts the applicability of the method to more realistic problems. The purpose of this paper is to introduce a more general analytical method, which allows calculating the stand-off distance of the shock and the complete post-shock flow. To demonstrate this, the analytic solutions will be compared to numerical two-dimensional simulations. It will be shown that the method even works reasonably well in the case of low Mach number shocks. As an important example of great astrophysical relevance, we analyse the bow shock of a galaxy moving supersonically through the IGM and show that the associated soft X-ray emission can be modelled fairly well.
About half of the galaxies in the Universe are found in groups and clusters, which are large complexes of galaxies held together by the mutual gravitational attraction of their members, intergalactic gas, and, above all, dark matter. With the advent of imaging telescopes in X-ray astronomy, it became evident that galaxy clusters are intensive sources of X-ray radiation owing to the hot plasma located between the galaxies and trapped in the group’s/cluster’s potential well. Because of their low relative speeds, galaxies in groups and poor clusters affect each other and the surrounding IGM gravitationally stronger than the faster-moving cluster galaxies, leading to a variety of fascinating interaction or even merging processes. Galaxies dashing at super- or hypersonic velocities through the IGM produce wakes of gravitationally focused gas, lose mass due to ram pressure, thereby injecting metals into their gaseous environment. Finally, leading bow shock waves are generated ahead of the galaxies that change the state of the gas irreversibly and thus play an important role in the galaxies’ structure and subsequent evolution (Stevens et al. 1999).
Trinchieri et al. (2003, 2005) have studied the complex X-ray emission of the compact galaxy group Stephan’s Quintet (SQ) quite recently using Chandra and XMM-Newton observations. The prominent shock situated in the galaxy system has been resolved with Chandra into a narrow north-south, somewhat clumpy structure between NGC 7318ab and NGC 7319, which is more sharply bounded on the west side (probably due to a contact surface stabilized by a magnetic field that is indicated by radio continuum emission) and embedded in a more extended diffuse emission, which presumably represents preexisting IGM heated up by previous collisions (presumably NGC 7320c was involved). In the simplest scenario, as Trinchieri et al. (2003, 2005) report, the shock results from the high-velocity collision of the gas-rich spiral galaxy NGC 7318b with previously stripped H i gas in SQ. For an upstream H i temperature of 100 K (and number density of about 6.5 × 10-3 cm-3), the velocity of the intruding galaxy is highly hypersonic (~1400 km s-1), resulting in an upstream Mach number in the galaxy’s rest frame of M∞ ≃ 930. The gas inside the bow shock is then heated up to an (observed) energy of 0.5 keV. To explain these low post-shock temperature, the authors suggest an oblique shock scenario with a shock inclination angle β of about 30°. Oblique shocks are a general feature of bow shocks, which are ultimately responsible for the observed IGM structures. The analytic calculation of general bow shocks, however, is fairly complicated. Previous attempts bear severe restrictions, like the spherical shape of the body and the thin-shell approximation of the model by Cantó & Raga (1998). On the other hand, bow shocks are ubiquitous phenomena in the intergalactic and interstellar medium (ISM), and an analytic description like the one given in the present paper is therefore most desirable.
The paper is organized as follows. In Sect. 2 the analytic solution for the blunt body problem is presented. In Sect. 3, this method is applied to Stephan’s Quintet, and the results are also compared to numerical two-dimensional simulations. Section 4 closes the paper with our conclusions.
2. Solution for the hypersonic blunt body problem
A body moving supersonically through a gaseous medium will generate a shock wave, which is generally detached and curved. It appears to be planar at the body’s nose and becomes progressively more oblique sideways, until it decays into a sonic wave at large distances. As a result, this single shock wave represents all possible oblique shock solutions for the given Mach number M∞ with the wave angle ranging from β = π/2 to β = α, where α = arcsin(1/M) is the so-called Mach angle, i.e. the angle forming the cone to which small disturbances in a supersonic flow are confined. The blunt body shock layer, the volume between the body and the shock, is a mixed subsonic-supersonic flow, where the subsonic and supersonic regions are divided by sonic lines, i.e. the loci of points at which the downstream Mach number is unity. Behind the normal, and nearly normal portions of the shock wave, the flow is subsonic, whereas behind the more oblique portions of the shock wave the flow is supersonic. It is precisely this hybrid nature of the flow that makes the blunt body problem extremely challenging mathematically, since the governing highly nonlinear partial differential equations of hydrodynamics are of elliptic type in the subsonic region and of hyperbolic type in the supersonic region (Anderson 2006).
The analysis developed by Schneider (1968) allows a very elegant treatment of the inviscid hypersonic blunt body problem. It is an inverse method, which means that the shock wave shape is assumed, and both the body shape, which supports the assumed shock, and the flow field between shock and body (i.e. the shock layer) are calculated. The fundamental advantage of this method over the ones by other authors is its uniform validity in the whole flow field (from the stagnation region up to large distances from the projectile nose). Until now this method has been adopted in aerospace engineering, in particular for solving the reentry problem of space probes, space shuttles, etc., in planetary or terrestrial atmosphere. However, to the best of our knowledge, this paper demonstrates its first application to an astrophysical problem.
 |
Fig. 1 Shock-oriented coordinate system of boundary-layer type, where z and r are Cartesian coordinates for plane flow, x and y are the distances along the shock surface and normal to it, with u and v as the corresponding velocity components, U∞ is the free-stream velocity, and ψ is the stream function. Flow quantities immediately behind the shock in the point N are denoted by a hat (^), and in the point S by an asterisk (∗) (adapted from Schneider 1968). |
We consider the plane or axisymmetric flow around a body and introduce a shock-oriented curvilinear coordinate system of boundary-layer type, where x is the distance along the shock surface in the plane formed by the shock normal and the direction of the uniform fluid flow, and y is the distance normal to the shock surface (Fig. 1). The corresponding velocity components are denoted by u and v, and z and r are the Cartesian coordinates for plane flow or the cylindrical coordinates for axisymmetric flow. The z-axis may be parallel to the direction of the incident flow. We emphasize that this is only assumed for convenience, but is no general restriction (see Sect. 4). It can be deduced from Fig. 1 that  where
where 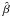 is the shock inclination angle in the point
is the shock inclination angle in the point 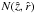 , with the shock-normal through Q intersecting the shock surface. Moreover, S is the point where the streamline through Q crosses the shock wave. The flow quantities immediately behind the shock in the point N are denoted by a hat ( ), and in the point S by an asterisk (∗ ). Undisturbed flow quantities far upstream are denoted by the subscript ∞.
, with the shock-normal through Q intersecting the shock surface. Moreover, S is the point where the streamline through Q crosses the shock wave. The flow quantities immediately behind the shock in the point N are denoted by a hat ( ), and in the point S by an asterisk (∗ ). Undisturbed flow quantities far upstream are denoted by the subscript ∞.
Since the functions ẑ(x) and 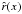 are known for a given shock shape, Eqs. (1) and (2) may be used to calculate the coordinates z and r of a point Q from its coordinates x and y. The curvature of the shock contour in the point N is denoted by
are known for a given shock shape, Eqs. (1) and (2) may be used to calculate the coordinates z and r of a point Q from its coordinates x and y. The curvature of the shock contour in the point N is denoted by 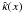 , defined as positive when the surface is concave on the side of positive y (cf. Fig. 1). The curvature of any of the other surfaces of constant y is
, defined as positive when the surface is concave on the side of positive y (cf. Fig. 1). The curvature of any of the other surfaces of constant y is 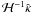 , where
, where 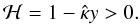 (3)The metric for this coordinate system is (cf. Hayes & Probstein 1966)
(3)The metric for this coordinate system is (cf. Hayes & Probstein 1966) 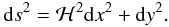 (4)Thus, the governing hydrodynamical steady-state equations for mass, momentum, and energy become
(4)Thus, the governing hydrodynamical steady-state equations for mass, momentum, and energy become 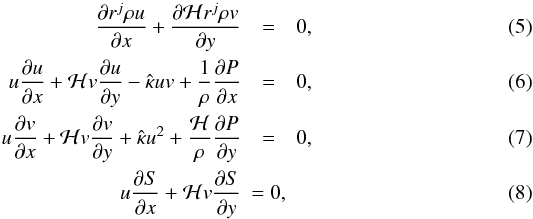 where ρ is the fluid density, P the fluid pressure, S the entropy, r(x,y) the distance from the axis. The parameter j is 0 or 1 for plane or axisymmetric flow, respectively. We used the entropy equation in place of the energy equation. We now want to make a von Mises transformation such that the independent variables (x,y) are replaced by
where ρ is the fluid density, P the fluid pressure, S the entropy, r(x,y) the distance from the axis. The parameter j is 0 or 1 for plane or axisymmetric flow, respectively. We used the entropy equation in place of the energy equation. We now want to make a von Mises transformation such that the independent variables (x,y) are replaced by 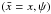 , where ψ is a stream function defined in terms of its partial derivatives
, where ψ is a stream function defined in terms of its partial derivatives  The stream function is constant along a streamline and represents the mass flow between the streamline ψ = const. and the surface of the projectile, per unit depth for plane flows, and per unit azimuthal angle (in radians) for axisymmetric flows; i.e., ψ satisfies the continuity equation. In the point N, the stream function thus is simply
The stream function is constant along a streamline and represents the mass flow between the streamline ψ = const. and the surface of the projectile, per unit depth for plane flows, and per unit azimuthal angle (in radians) for axisymmetric flows; i.e., ψ satisfies the continuity equation. In the point N, the stream function thus is simply 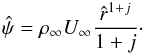 (11)In contrast, ψ is connected with the coordinate r ∗ of the point S by
(11)In contrast, ψ is connected with the coordinate r ∗ of the point S by 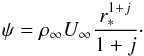 (12)In the new coordinate system with the variable y eliminated, the equations of energy, entropy, and momentum conservation read as
(12)In the new coordinate system with the variable y eliminated, the equations of energy, entropy, and momentum conservation read as 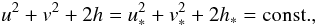 (13)
(13)
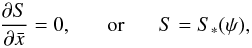 (14)
(14)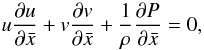 (15)
(15)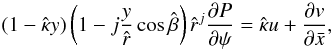 (16)where h is the specific enthalpy.
(16)where h is the specific enthalpy.
The variable y is a dependent variable after the von Mises transformation, and it obeys the equations 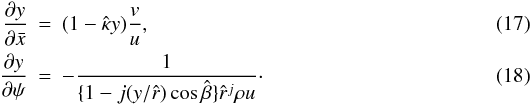 At this point it is useful to introduce the Landau symbol
At this point it is useful to introduce the Landau symbol  , which describes an asymptotic upper bound for the magnitude of a function in terms of another, usually simpler function; e.g.,
, which describes an asymptotic upper bound for the magnitude of a function in terms of another, usually simpler function; e.g., 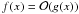 means that |f(x)| is not very large in comparison with |g(x)|. The flow quantities immediately behind the shock may be obtained from the Rankine-Hugoniot jump conditions in terms of the inverse compression ratio across the shock
means that |f(x)| is not very large in comparison with |g(x)|. The flow quantities immediately behind the shock may be obtained from the Rankine-Hugoniot jump conditions in terms of the inverse compression ratio across the shock  . They are
. They are 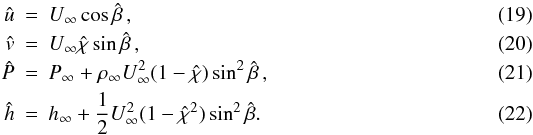 These equations maintain their validity if the hats are replaced by asterisks. The pressure within the shock layer is given by the Newton-Busemann pressure law (see e.g. Hayes & Probstein 1966), a simplified form of the momentum Eq. (16), which reads as
These equations maintain their validity if the hats are replaced by asterisks. The pressure within the shock layer is given by the Newton-Busemann pressure law (see e.g. Hayes & Probstein 1966), a simplified form of the momentum Eq. (16), which reads as 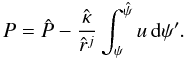 (23)The following method is based on two main assumptions. First, it is assumed that the inverse compression ratio across the shock is very small; i.e.,
(23)The following method is based on two main assumptions. First, it is assumed that the inverse compression ratio across the shock is very small; i.e., 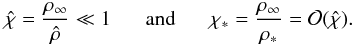 (24)Second, the pressure at the point Q of the disturbed flow field should not be much smaller than the pressure immediately behind the shock in the intersection point of the shock surface with its normal through the point Q; i.e.,
(24)Second, the pressure at the point Q of the disturbed flow field should not be much smaller than the pressure immediately behind the shock in the intersection point of the shock surface with its normal through the point Q; i.e., 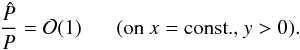 (25)We follow Schneider (1968) to express the pressure in an arbitrary point Q approximately by (see Appendix)
(25)We follow Schneider (1968) to express the pressure in an arbitrary point Q approximately by (see Appendix) ![\begin{equation} P=\hat{P}-\frac{\hat{\kappa}}{\hat{r}^j}\int_\psi^{\hat{\psi}}\{u_*^2+2[h_*-h(\hat{P},S_*)]\}^{1/2}{\rm d}\psi'. \label{eq:newbuseneu} \end{equation}](/articles/aa/full_html/2011/07/aa12436-09/aa12436-09-eq63.png) (26)It may be noted that all quantities on the equation’s right-hand side are given by the boundary conditions at the shock or by the equation of state. Terms coming from the excluded portions of the flow field – namely the stagnation region, as well as the region near the stagnation region where u ≪ û – are of the order of
(26)It may be noted that all quantities on the equation’s right-hand side are given by the boundary conditions at the shock or by the equation of state. Terms coming from the excluded portions of the flow field – namely the stagnation region, as well as the region near the stagnation region where u ≪ û – are of the order of 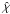 and therefore contribute only negligibly to the integral in Eq. (26). Consequently, the whole gas-dynamic state is known in the streamline coordinate system (
and therefore contribute only negligibly to the integral in Eq. (26). Consequently, the whole gas-dynamic state is known in the streamline coordinate system ( ) by evaluating S = S ∗ (ψ) and P from Eq. (26).
) by evaluating S = S ∗ (ψ) and P from Eq. (26).
The actual location of the body in space can be determined by solving the differential Eq. (18) via separation of variables giving the distance from the shock surface y as a function of  and ψ;
and ψ; 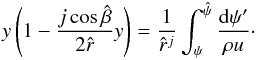 (27)Neglecting errors of
(27)Neglecting errors of 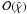 we may replace the velocity component in x-direction by
we may replace the velocity component in x-direction by ![\begin{equation} u^2=u_*^2+2[h_*-h(P,S_*)]+\dots, \end{equation}](/articles/aa/full_html/2011/07/aa12436-09/aa12436-09-eq71.png) (28)which follows from the energy Eq. (13). The integral in Eq. (27) is then
(28)which follows from the energy Eq. (13). The integral in Eq. (27) is then ![\begin{equation} Y=\int_\psi^{\hat{\psi}}\frac{{\rm d}\psi'}{\rho(P,S_*)\,\{u_*^2+2[h_*-h(P,S_*)]\}^{1/2}}\cdot \label{eq:ypsilon} \end{equation}](/articles/aa/full_html/2011/07/aa12436-09/aa12436-09-eq72.png) (29)Solving the quadratic equation in y on the left-hand side of Eq. (27), we have to distinguish between plane (j = 0) and axisymmetric (j = 1) flows. Thus we have
(29)Solving the quadratic equation in y on the left-hand side of Eq. (27), we have to distinguish between plane (j = 0) and axisymmetric (j = 1) flows. Thus we have ![\begin{eqnarray} &&\text{for} \hspace{0.2cm} j=0:\hspace{0.2cm} y=Y\,;\\ &&\text{for} \hspace{0.2cm} j=1:\hspace{0.2cm} y=\frac{\hat{r}}{\cos\hat{\beta}}\left[1-\left(1-\frac{2Y\cos\hat{\beta}}{\hat{r}^2}\right)^ {1/2}\right]\cdot \end{eqnarray}](/articles/aa/full_html/2011/07/aa12436-09/aa12436-09-eq75.png) To finally give these results in the convenient coordinates x and y, the transformations (1) and (2) have to be carried out.
To finally give these results in the convenient coordinates x and y, the transformations (1) and (2) have to be carried out.
In the astrophysical context, the case of a perfect gas with constant specific heats is of great interest. The inverse compression ratio is then given by (see e.g. Landau & Lifshitz 1987) 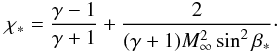 (32)We point out that an analogous relation is valid for
(32)We point out that an analogous relation is valid for 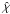 , if all asterisks in Eq. (32) are replaced by hats.
, if all asterisks in Eq. (32) are replaced by hats.
Using the shock conditions (19)–(22), together with Eq. (32), the two integrals (26) and (29), which have to be evaluated, become ![\begin{eqnarray} P &=&\hat{P}-\frac{U_\infty\hat{\kappa}}{\hat{r}^j}\int_\psi^{\hat{\psi}}\limits \Bigg\{ \cos^2\beta_*+ \left[\frac{2}{(\gamma-1)M_ \infty^2}+\sin^2\beta_* \right] \notag\\ &&\times\, \left[ 1- \left(\frac{\sin^2\hat{\beta}}{\sin^2\beta_*} \right)^{\frac{\gamma-1}{\gamma}} \right]\Bigg\}^{1/2}{\rm d} \psi', \label{eq:perfectpressure} \end{eqnarray}](/articles/aa/full_html/2011/07/aa12436-09/aa12436-09-eq77.png) (33)
(33)![\begin{eqnarray} Y&=&\frac{1}{\rho_\infty U_\infty}\int_\psi^{\hat{\psi}}\limits \chi_* (\hat{P}\sin^2\beta_*/P\sin^2\hat{\beta})^{1/\gamma} \notag\\ &&\times\,\Bigg\{\cos^2\beta_*+\left[\frac{2}{(\gamma-1)M_\infty^2}+\sin^2\beta_*\right]\notag\\ &&\times\,\left[1-\left(\frac{P\sin^2\hat{\beta}}{\hat{P}\sin^2\beta_*}\right)^{\frac{\gamma-1}{\gamma}}\right]\Bigg\}^{-1/2} {\rm d} \psi'. \label{eq:perfectY} \end{eqnarray}](/articles/aa/full_html/2011/07/aa12436-09/aa12436-09-eq78.png) (34)The curvature of a curve in space can be calculated by the well-known formula
(34)The curvature of a curve in space can be calculated by the well-known formula ![\begin{equation} \kappa=\frac{\left|\frac{{\rm d}^2r}{{\rm d}z^2}\right|}{\left[1+\left(\frac{{\rm d}r}{{\rm d}z}\right)^2\right]^{3/2}}\cdot \end{equation}](/articles/aa/full_html/2011/07/aa12436-09/aa12436-09-eq79.png) (35)In addition, the following simple relations for the the shock inclination angle turn out to be quite useful:
(35)In addition, the following simple relations for the the shock inclination angle turn out to be quite useful:  The density for a perfect gas is represented by the quantity
The density for a perfect gas is represented by the quantity 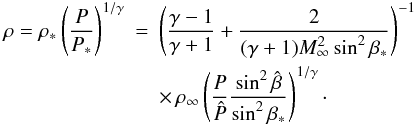 (39)For simplicity we introduce dimensionless units; e.g. the normalized stream function then is Ψ = ψ/ρ∞U∞Lj + 1, where L is a characteristic length.
(39)For simplicity we introduce dimensionless units; e.g. the normalized stream function then is Ψ = ψ/ρ∞U∞Lj + 1, where L is a characteristic length.
On the surface of the body we need ψ = 0, so the pressure on the body surface Pb(x), as well as the shock layer thickness Δ(x), can be obtained by replacing the lower limits in Eqs. (33) and (34) by zero:
![\begin{eqnarray} \frac{P_{\rm b}}{\rho_\infty U_\infty^2}&=&\frac{1}{\gamma M_\infty^2}+(1-\hat{\chi})\sin^2\hat{\beta}\notag\\ &&-\,\frac{\hat{\kappa}}{\hat{r}^j}\int_0^{\hat{\Psi}}\limits \Bigg\{ \cos^2\beta_*+\left[\frac{2}{(\gamma-1)M_\infty^2}+\sin^2\beta_* \right] \notag\\ &&\times\,\left[ 1- \left(\frac{\sin^2\hat{\beta}}{\sin^2\beta_*} \right)^{\frac{\gamma-1}{\gamma}} \right]\Bigg\}^{1/2}{\rm d}\Psi, \label{eq:int1} \end{eqnarray}](/articles/aa/full_html/2011/07/aa12436-09/aa12436-09-eq87.png) (40)where the relation
(40)where the relation 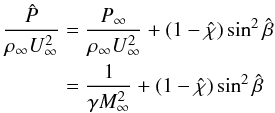 (41)has been used. Furthermore, we get
(41)has been used. Furthermore, we get ![\begin{eqnarray} \text{for} \hspace{0.2cm}j=0&&:\hspace{0.1cm} \Delta=Y\bigg|_{\psi=0},\label{eq:delta1}\\ \text{for} \hspace{0.2cm}j=1&&:\hspace{0.1cm} \Delta=\frac{\hat{r}}{\cos\hat{\beta}}\left[1-\left(1-\frac{2Y|_{\psi=0}\cos\hat{\beta}}{\hat {r}^2}\right)^{1/2}\right],\label{eq:delta2} \end{eqnarray}](/articles/aa/full_html/2011/07/aa12436-09/aa12436-09-eq89.png) with
with ![\begin{eqnarray} Y\bigg|_{\psi=0}&=&\int_0^{\hat{\Psi}}\limits\chi_* (\hat{P}\sin^2\beta_*/P\sin^2\hat{\beta})^{1/\gamma} \\ &&\times\,\Bigg\{\cos^2\beta_*+\left[\frac{2}{(\gamma-1)M_\infty^2}+\sin^2\beta_*\right] \\ &&\times\, \left[1-\left(\frac{P\sin^2\hat{\beta}}{\hat{P}\sin^2\beta_*}\right)^{\frac{\gamma-1}{\gamma}}\right]\Bigg\}^{-1/2}{\rm d}\Psi. \label{eq:int2} \end{eqnarray}](/articles/aa/full_html/2011/07/aa12436-09/aa12436-09-eq90.png) As soon as the bow shock wave is parametrized, the gas-dynamical quantities can be computed by evaluating two integrals (namely Eqs. (40) and (42) or (43) and (46), together with the boundary values (14) and (19)–(22)).
As soon as the bow shock wave is parametrized, the gas-dynamical quantities can be computed by evaluating two integrals (namely Eqs. (40) and (42) or (43) and (46), together with the boundary values (14) and (19)–(22)).
3. Results
3.1. Validation
The applicability of the analytical model for an astrophysical context is tested by simulating the bow shock wave induced by the interaction of an uniform hypersonic flow with the solid unit sphere. For the sake of simplicity we have chosen M∞ ≡ U∞ = 500, which is ensured by setting ρ∞ ≡ γ = 5/3 and P∞ = 1. A simulation snapshot overlaid by the analytical solution is depicted in Fig. 2. At the stage shown here, the simulation was evolved long enough (t = 0.2) so that the bow shock wave has already become stationary for some time. The modulus of the percentage error of the stagnation distance prediction is ~6.2%, and the modulus of the maximum percentage error of the obstacle estimation is ~11.6%. These errors may arise from two sources; first, the analytical method is based on the assumption that the density ratio χ across the shock is very small. Since we consider here a perfect monoatomic gas with γ = 5/3, an error that can reach the 25% is introduced (cf. Eq. (32)). However, for the astrophysically more relevant case of a cooling strong shock, the compression ratio of four only represents a lower limit. Thus, when the cooling time proceeds, relation (24) becomes progressively more precise. Second, the hypersonic gas flow around a sphere features a complex wake that contains inter alia a second shock wave as a result of overexpansion with following compression. This explains especially the increasing deviation of the analytical solution from the numerical result at (or in the vicinity of) the sphere’s equator (Schneider, priv. comm.).
3.2. Application to observations
To model the scenario in SQ, where a large-scale bow shock wave is believed to be formed by the gas-rich spiral galaxy NGC 7318b as it plunges through 100 K H I gas (Trinchieri et al. 2003), the upstream Mach number has chosen to be M∞ = 930. We assumed a plane (j = 0) supersonic flow of perfect monoatomic gas (γ = 5/3) and parametrized the bow shock time-dependently (e.g. by 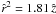 for t = 130 Myr after the start of the interaction). Results are plotted in Figs. 3 and 4.
for t = 130 Myr after the start of the interaction). Results are plotted in Figs. 3 and 4.
 |
Fig. 2 Comparison between the numerical and analytical solution of a bow shock wave generated by a hypersonic flow (M∞ = 500) hitting the solid unit sphere. A perfect monoatomic gas is assumed (γ = 5/3). The analytical body prediction is represented by the thin solid line. The bow shock wave (thick solid line) is parametrized by |
 |
Fig. 3 Upper panel. Shape of the SQ galaxy NGC 7318b (thin line) and the bow shock (thick line) at t = 130 Myr (j = 0, |
The standoff distance of the shock from the nose of the projectile (in this case from the leading edge of the galaxy NGC 7318b of SQ) can be immediately determined to be Δ0 ≃ 2.3 × 1022 cm (≃7.4 kpc). In Fig. 4 analytically derived maps of several fluid variables for the galaxy-IGM interaction process in SQ are shown, namely pressure P (upper left panel), density ρ (upper right panel), temperature T (lower left panel), and the approximate Mach number (since we have ignored v in the derivation, which is the velocity component in y-direction) u/cs ≃ M (lower right panel), where cs is the local downstream velocity of sound. Since values of ẑ that are too low lead to a singularity in the (numerical) integration, the plane and near plane post-shock region are missing. We have written a Fortran program based on the presented method that allows the hypersonic blunt body problem to be solved for the flow quantities in the whole post-shock flow field. Required input variables are the parametrized bow shock 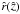 , the flow geometry factor j, the upstream Mach number M∞, and the adiabatic index of the gas γ. Furthermore, upstream density, length scale, and the velocity of the obstacle (or flow, respectively) have to be known to allow an easy comparison to observational data. This tool is available online1.
, the flow geometry factor j, the upstream Mach number M∞, and the adiabatic index of the gas γ. Furthermore, upstream density, length scale, and the velocity of the obstacle (or flow, respectively) have to be known to allow an easy comparison to observational data. This tool is available online1.
To test our analytical results we performed several two-dimensional numerical hydrodynamical simulations. We used the VH-1 hydrocode as a basis, which was written by the Numerical Astrophysics Group at the Virginia Institute for Theoretical Astrophysics (Blondin et al. 1990). The code is based on a third-order accurate extension of the grid-based Godunov scheme, namely a Lagrangian-remap version of the piecewise parabolic method (PPMLR), and features thus good shock capturing. Optically thin radiative cooling via operator splitting has been included. Each numerical simulation has been carried out on an uniform 2400 × 1200 Cartesian grid, with a computational domain of 4.8 × 1023 cm by 2.4 × 1023 cm (~156 × 78 kpc). This results in a grid resolution of Δx = Δy = 2 × 1020 cm (~65 pc). Runs with other grid sizes showed that the output does not depend on resolution. The only difference is that small-scale instabilities and fragmentations of stripped material cannot be resolved on coarser grids. “Outflow” boundary conditions have been used along the top, the bottom, and on the right of the grid, while the left boundary is “inflow”. The galaxy itself was modelled by a simple stratified gaseous ellipse. Each computation begins with the galaxy placed face-on at rest in an uniform supersonic stream of intergalactic gas, corresponding to the situation of the galaxy rushing through the IGM at constant speed.
Figure 5 gives an impression of our simulations. In this example, we tried to reconstruct the conditions that presumably occur in SQ. The ISM of the intruding galaxy NGC 7318b (whose semi-axes have been taken from the NED2) consists in our simple model of three equidistant layers, which are in pressure equilibrium; namely, an H i core (ρcore = 6.2 × 10-24 g cm-3, Tcore = 100 K), a Lockman layer (ρLock = 1.0 × 10-25 g cm-3, TLock = 6000 K), and a Reynolds layer (ρRey = 6.9 × 10-26 g cm-3, TRey = 8000 K). The IGM (ρIGM = 6.7 × 10-27 g cm -3, TIGM = 100 K) flows from left to right at a constant hypersonic speed (M∞ = 930). Solar metallicity is assumed in all the considered media. In Fig. 5 the colour-coded log temperature map (in K) with the superimposed velocity field is visualized at the times 60, 130, and 200 Myr after the start of the simulation. Owing to the reasonably good numerical resolution of the simulation the presented snapshots allow tracking of a multitude of hydrodynamical effects (such as a prominent bow shock wave, Kelvin-Helmholtz instabilities, Rayleigh-Taylor instabilities, gas compression in the course of radiative cooling, a turbulent Karman wake, etc.) that lead to a subsequent evolution of the galaxy’s ISM. Please note that more sophisticated magnetohydrodynamic simulations with an underlying galaxy dark matter halo (which are beyond the scope of this paper) would be required to study a possible reduction or even suppression of fluid dynamical instabilities. However, at high Mach numbers, as they occur in the considered galaxy-IGM interactions, the velocity potential (kinetic energy density) 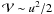 (with u ~ 1400 km s-1) is at least five times higher than the gravitational potential (including dark matter) Φ ~ GM/Rmin (with M ~ 2 × 1045 g, and a minimum distance from the galaxy’s centre of Rmin ~ 7 × 1022 cm). Thus, the bow shock, as well as the shock layer, are unlikely to be influenced significantly by gravity in general and dark matter in particular.
(with u ~ 1400 km s-1) is at least five times higher than the gravitational potential (including dark matter) Φ ~ GM/Rmin (with M ~ 2 × 1045 g, and a minimum distance from the galaxy’s centre of Rmin ~ 7 × 1022 cm). Thus, the bow shock, as well as the shock layer, are unlikely to be influenced significantly by gravity in general and dark matter in particular.
 |
Fig. 4 Analytically derived colour-coded maps of several flow quantities, namely log pressure P in dyn cm-2 (upper left panel), log density ρ in g cm-3 (upper right panel), log temperature T in K (lower left panel), and the velocity ratio u/cs ≃ M (lower right panel) for the SQ galaxy NGC 7318b at the time t = 130 Myr (j = 0, |
The calculated post-shock temperature at the intersection between the galaxy’s axis of symmetry and the tip of the bow shock is about 2.7 × 107 K (kB T ≃ 2.33 keV). In contrast, at the bow shock wings, where the shock inclination angle reaches approximately 30°, the downstream temperature has dropped to about 6.3 × 106 K (kB T ≃ 0.54 keV). Despite the simple assumptions, this value is in remarkably good agreement with the observational data since Trinchieri et al. (2003) measured in SQ a post-shock gas temperature of 0.5 keV.
3.3. Comparison of the analytical with the numerical model
In Figs. 6 and 7 our analytical results are superimposed on the numerically derived maps. In the lower panels the percentage errors are given. We used a shock tracer that scans the computational domain for entropy jumps in order to parametrize the numerically calculated bow shocks. In addition to numerical models of the galaxy-IGM interaction in SQ, we also studied the galaxy group around IC 1262. Chandra and XMM-Newton observations have uncovered an extended cool X-ray ridge at the centre of this group (Trinchieri et al. 2007). The authors speculate that this peculiar structure may have been created by efficient ram pressure stripping of the bright spiral member IC 1263 as it had passed through the group’s dense core (ρIGM = 8.0 × 10-27 g cm-3, TIGM = 2.0 × 107 K) at a relative velocity of ~1000 km s-1 (translating to a Mach number of about 5). Then, gas supersonically streaming behind the bow shock wave may have heated up the stripped ISM to the observed X-ray temperatures. A result of our numerical and analytical computation of this interaction is shown in the lower right panel of Fig. 6.
It is no surprise that the errors grow with increasing distance from the stagnation point and time, since instabilities, which cannot be predicted analytically, begin to grow owing to the increasing influence of shear flows. Moreover, it must be noted that mainly the dense and cold ISM phases of the galaxies (blue to light green regions in Figs. 6 and 7) drive the bow shock waves. Therefore these regions are the ones enclosed by the analytical solution. Bearing these aspects in mind, the agreement is quite good for all considered scenarios (even for the lower Mach number case). Furthermore, the analytically derived fluid variable maps (Fig. 4) are in good agreement with the numerical calculations (compare the shock layer temperature gradient shown in the lower left panel of Fig. 4 with the upper right panel of Fig. 6). The modulus of the percentage error of the log temperature immediately behind and in the vicinity of the bow shock wave lies below 1%. Also the detachment distances are determined quite satisfactorily and the modulus of the percentage error ranges from ~5.9% to ~38.5%. A more detailed discussion of the flow and comparison to new detailed X-ray data of SQ and the group around IC 1262 is the subject of a forthcoming paper.
Finally, it should be noted that the astrophysical possibility of this analytical method is hardly restricted to galaxy-IGM interaction alone; on the contrary, any scenario, such as bow shocks around subclusters, gas bullets, jets (Herbig-Haro objects) or individual stars can be covered with it as well.
 |
Fig. 5 Colour-coded log temperature map (in K) overlaid with the velocity field of the SQ simulation at the times a) t = 60 Myr, b)t = 130 Myr, and c) t = 200 Myr. The vectors drawn show the direction and magnitude of the velocity field. |
4. Conclusion
This paper presented an analytical solution technique for the inviscid hypersonic blunt body problem and applied it for the first time to the interaction between galaxies and the IGM. The method follows an inverse approach, which means that the shape of the bow shock has to be parametrized to be consistent with the galaxy shape. Such an inverse approach has no substantial disadvantage in the view of the fact that at high impact velocities the shape of the bow shock becomes similar to the shape of the body. For lower Mach numbers we find that the problem can be solved iteratively. First, we assumed the geometric form of the bow shock, then analytically derived the shape of the galaxy, and compared it to the relevant parameters (e.g. axes ratio, dimensions). In the next step, the bow shock curve was changed, and the body shape recalculated until convergence was obtained. In all cases we tested, this was achieved fairly rapidly. The solution, which is valid in the whole flow field, and in particular takes velocity gradients into account along streamlines, is based on two main assumptions; first, the density ratio across the shock has to be large, and, second, the pressure at a point Q (Fig. 1) of the disturbed flow field must not to be very small in comparison to the pressure immediately behind the shock in the intersection point of the shock surface with its normal through Q. In our derivation, heat conduction, viscosity, as well as terms of the order of χ (density ratio) are neglected. It should be stressed that it is not required that the shock layer, which is the area between the bow shock wave and the projectile, has to be thin. The presented treatment thus surpasses in sophistication methods like the analytic solution for the thin-shell problem of a hypersonic wind interacting with a rigid sphere by Cantó & Raga (1998) and allows astrophysical problems that involve bow shocks generated by a hypersonic flow to be tackled more realistically.
 |
Fig. 6 Comparison of numerically (here log temperature in K is colour-coded) and analytically derived results. The thin line represents the outer envelope of the galaxy, whereas the thick line represents the bow shock. Upper left. Model of the interaction between NGC 7318b and the IGM in SQ at the time t = 60 Myr (j = 0, |
 |
Fig. 7 Like Fig. 6. Upper left. Model of the interaction between NGC 7318b and the IGM in SQ at the time t = 200 Myr (j = 0, |
For a symmetrically assumed galaxy at a zero angle of attack, the stagnation streamline and the stagnation point are along the centreline. The stagnation streamline crosses the bow shock at precisely the normal shock point (β = π/2) and hence the entropy of the stagnation streamline in the shock layer is maximal (Hayes & Probstein 1966). However, we found that the galaxy need not necessarily be axially symmetric oriented with respect to the flow direction. Then the stagnation streamline does not pass through the normal portion of the shock wave so it does not coincide with the maximum entropy streamline that always intersects the shock at right angles. For all possible (two-dimensional) galaxy inclination angles, however, these two streamlines lie quite close to each other. Consequently, the presented method is applicable if the z-axis of the coordinate system is parallel to the velocity vector of the galaxy and if it goes through the stagnation streamline. The galaxy’s bow shock halves above and below the z-axis then have to be evaluated separately.
Our analytical investigation of galaxy-IGM interactions are in good agreement with results of the two-dimensional numerical simulations carried out with the (pure) hydrodynamics code VH-1, which is PPMLR-based and therefore ideally suited to analysing shocks. As long as the initially made assumptions are not violated by Mach numbers that are too low, accurate predictions of the fluid quantities in the post-shock flow field, as well as the shock’s stand-off distance, are possible. The high potential of the present analytical approximation suggests an application to many other astrophysical problems that involve bow shocks.
Acknowledgments
It is a pleasure to thank Wilhelm Schneider for helpful discussions and Ian R. Stevens for providing essential parts of the used radiative cooling algorithm. Use of VH-1, developed by the numerical astrophysics group at the University of Virginia (http://wonka.physics.ncsu.edu/pub/VH-1), is hereby acknowledged. We also thank the anonymous referee for his/her constructive suggestions which helped to improve the paper. The calculations were performed on the computers of the Institute for Astronomy, University of Vienna (Austria).
References
- Anderson, J. D. 2006, Hypersonic and High-Temperature Gas Dynamics, 2nd edn. (Virginia: AIAA Education Series) [Google Scholar]
- Blondin, J. M., Kallman, T. R., Fryxell, B. A., & Taam, R. E. 1990, ApJ, 356, 591 [NASA ADS] [CrossRef] [Google Scholar]
- Cantó, J., & Raga, A. 1998, MNRAS, 297, 383 [NASA ADS] [CrossRef] [Google Scholar]
- Hayes, W. D., & Probstein, R. F. 1966, Hypersonic Inviscid Flow (New York: Academic Press) [Google Scholar]
- Landau, L. D., & Lifshitz, E. M. 1987, Fluid Mechanics, 2nd edn. (Oxford: Elsevier Butterworth-Heinemann) [Google Scholar]
- Markevitch, M., Gonzalez, A. H., David, L., et al. 2002, ApJ, 567, 27 [Google Scholar]
- Schneider, W. 1968, JFM, 31, 397 (Corrigendum: 1968, JFM, 32, 829) [Google Scholar]
- Stevens, I. R., Acreman, D. M., & Ponman, T. J. 1999, MNRAS, 310, 663 [NASA ADS] [CrossRef] [Google Scholar]
- Trinchieri, G., Sulentic, J., Breitschwerdt, D., & Pietsch, W. 2003, A&A, 401, 173 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Trinchieri, G., Sulentic, J., Pietsch, W., & Breitschwerdt, D. 2005, A&A, 444, 697 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Trinchieri, G., Breitschwerdt, D., Pietsch, W., Sulentic, J., & Wolter, A. 2007, A&A, 463, 153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Derivation of the pressure in the shock layer
The derivation of Eq. (26) in the main text is presented here in detail. The momentum Eq. (15) can be rewritten as 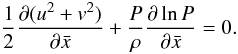 (A.1)From Eqs. (19) and (20) we can estimate the ratio of the velocity components
(A.1)From Eqs. (19) and (20) we can estimate the ratio of the velocity components 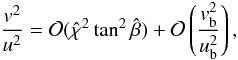 (A.2)where ub and vb are the velocity components at the surface of the body. Because the entropy increases with increasing shock inclination angle β, it is valid to write
(A.2)where ub and vb are the velocity components at the surface of the body. Because the entropy increases with increasing shock inclination angle β, it is valid to write  . Applying approximation (25), we have
. Applying approximation (25), we have  for the enthalpy. Moreover, it turns out that
for the enthalpy. Moreover, it turns out that 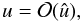 (A.3)where the energy Eq. (13) has been used. In contrast, since the velocity increases along a streamline with decreasing pressure, it holds that
(A.3)where the energy Eq. (13) has been used. In contrast, since the velocity increases along a streamline with decreasing pressure, it holds that 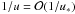 . On the other hand, we can infer from the Rankine-Hugoniot jump conditions (19)–(22) that
. On the other hand, we can infer from the Rankine-Hugoniot jump conditions (19)–(22) that 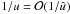 . This is true everywhere in the shock layer except the region, where cosβ ∗ is very small compared to
. This is true everywhere in the shock layer except the region, where cosβ ∗ is very small compared to 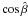 , i.e. where
, i.e. where 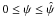 . To include this region we have to write
. To include this region we have to write ![\appendix \setcounter{section}{1} \begin{equation} \frac{1}{u}=\mathcal{O}\left(\frac{1}{u_{\rm b}+[\hat{u}-u_{\rm b}]\psi/\hat{\psi}}\right)\cdot \label{eq:1overu} \end{equation}](/articles/aa/full_html/2011/07/aa12436-09/aa12436-09-eq163.png) (A.4)An analogous relation can be found for the density, if h and P in
(A.4)An analogous relation can be found for the density, if h and P in 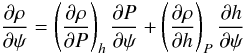 (A.5)are replaced by means of Eqs. (13) and (16). As long as the thermodynamic functions h and P retain their order of magnitude, the thermodynamic functions (∂ρ/∂P)h and (∂ρ/∂h)P for a gas also do not change their orders of magnitude. The formal integration of the momentum Eq. (16) with the boundary condition
(A.5)are replaced by means of Eqs. (13) and (16). As long as the thermodynamic functions h and P retain their order of magnitude, the thermodynamic functions (∂ρ/∂P)h and (∂ρ/∂h)P for a gas also do not change their orders of magnitude. The formal integration of the momentum Eq. (16) with the boundary condition 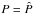 at
at 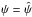 yields
yields ![\appendix \setcounter{section}{1} \begin{equation} \begin{split} \hat{r}^j(\hat{P}-P)&\left[ 1 +\mathcal{O}\left( \left[ \hat{\kappa}+j\frac{\cos\hat{\beta}}{\hat{r}}\right]\frac{1}{\hat{\psi}-\psi} \int_\psi^{\hat{\psi}}y\, {\rm d}\psi'\right)\right]=\\ &\qquad\qquad\quad\hat{\kappa}\int_\psi^{\hat{\psi}}u\,{\rm d}\psi'+\int_\psi^{\hat{\psi}}\frac{\partial v}{\partial \bar{x}}\,{\rm d}\psi'. \label{eq:momsol} \end{split} \end{equation}](/articles/aa/full_html/2011/07/aa12436-09/aa12436-09-eq171.png) (A.6)Furthermore keeping in mind that v is of the order of u everywhere apart from the stagnation region, we see from Eq. (A.5), together with (A.6), that the order of magnitude of ∂ρ/∂ψ does not depend on the stream function ψ, except maybe in the region near the projectile surface, where u can be much smaller than û. Consequently, we obtain
(A.6)Furthermore keeping in mind that v is of the order of u everywhere apart from the stagnation region, we see from Eq. (A.5), together with (A.6), that the order of magnitude of ∂ρ/∂ψ does not depend on the stream function ψ, except maybe in the region near the projectile surface, where u can be much smaller than û. Consequently, we obtain ![\appendix \setcounter{section}{1} \begin{equation} \frac{1}{\rho}=\mathcal{O}\left(\frac{1}{\rho_{\rm b}+[\hat{\rho}-\rho_{\rm b}]\psi/\hat{\psi}}\right)\cdot \label{eq:1overrho} \end{equation}](/articles/aa/full_html/2011/07/aa12436-09/aa12436-09-eq177.png) (A.7)With the aid of our results (A.4), (A.7), and (11), Eq. (18) yields
(A.7)With the aid of our results (A.4), (A.7), and (11), Eq. (18) yields ![\appendix \setcounter{section}{1} \begin{equation} y=\mathcal{O}\left(\frac{\hat{\chi}\hat{r}}{\cos \hat{\beta}}\frac{1}{u_{\rm b}/\hat{u}-\rho_{\rm b}/\hat{\rho}} \ln\frac{u_{\rm b}/ \hat{u}+[1-u_{\rm b}/\hat{u}]\psi/\hat{\psi}}{\rho_{\rm b}/\hat {\rho}+[1-\rho_{\rm b}/\hat{\rho}]\psi/\hat{\psi}}\right)\cdot \label{eq:appsol} \end{equation}](/articles/aa/full_html/2011/07/aa12436-09/aa12436-09-eq178.png) (A.8)Finally, combining Eqs. (17) and (A.8) gives
(A.8)Finally, combining Eqs. (17) and (A.8) gives 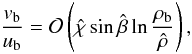 (A.9)which can be combined with Eqs. (21) and (25) to become
(A.9)which can be combined with Eqs. (21) and (25) to become ![\appendix \setcounter{section}{1} \begin{equation} \frac{v_{\rm b}}{u_{\rm b}}=\mathcal{O}\left(\hat{\chi}\left[\frac{P_{\rm b}}{\rho_\infty U_\infty^2}\right]^{1/2}\ln\frac{\rho_{\rm b}}{\hat{\rho}}\right)\cdot \label{eq:vb/ub} \end{equation}](/articles/aa/full_html/2011/07/aa12436-09/aa12436-09-eq180.png) (A.10)The entropy remains constant on streamlines in the post-shock region. It is thus useful to introduce the effective isentropic exponent
(A.10)The entropy remains constant on streamlines in the post-shock region. It is thus useful to introduce the effective isentropic exponent 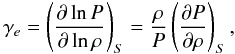 (A.11)which is not smaller than 1 for any gas. Consequently, the change in relative pressure along a streamline is not smaller than the change of relative density, i.e.,
(A.11)which is not smaller than 1 for any gas. Consequently, the change in relative pressure along a streamline is not smaller than the change of relative density, i.e., 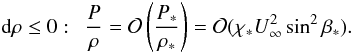 (A.12)On the other hand, the (dimensionless) quantity
(A.12)On the other hand, the (dimensionless) quantity 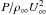 cannot be very large for dρ > 0, so for both dρ ≤ 0 and dρ > 0, we have
cannot be very large for dρ > 0, so for both dρ ≤ 0 and dρ > 0, we have 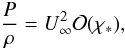 (A.13)which also holds on the body streamline. Thus Eq. (A.10) becomes
(A.13)which also holds on the body streamline. Thus Eq. (A.10) becomes ![\appendix \setcounter{section}{1} \begin{equation} \frac{v_{\rm b}}{u_{\rm b}}=\mathcal{O}\left(\left[\hat{\chi}\chi_* \frac{\rho_{\rm b}}{\hat{\rho}}\right]^{1/2}\ln\frac{\rho_{\rm b}} {\hat{\rho}}\right), \end{equation}](/articles/aa/full_html/2011/07/aa12436-09/aa12436-09-eq187.png) (A.14)which can be simplified by using the assumption (24) and that
(A.14)which can be simplified by using the assumption (24) and that 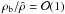
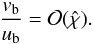 (A.15)If we now temporarily exclude the stagnation region (defined by
(A.15)If we now temporarily exclude the stagnation region (defined by 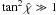 ) from our consideration, Eqs. (A.2) and (A.15) suggest neglecting v2 in comparison with u2 in the momentum Eq. (A.1). Taking the isentropy of the flow on streamlines into account, integration of Eq. (A.1) yields
) from our consideration, Eqs. (A.2) and (A.15) suggest neglecting v2 in comparison with u2 in the momentum Eq. (A.1). Taking the isentropy of the flow on streamlines into account, integration of Eq. (A.1) yields 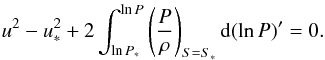 (A.16)If we once again exclude the stagnation region, as well as the region characterized by u ≪ û, the first term of Eq. (A.16) can be rewritten by using
(A.16)If we once again exclude the stagnation region, as well as the region characterized by u ≪ û, the first term of Eq. (A.16) can be rewritten by using 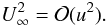 (A.17)With the aid of Eq. (A.13) the integral in Eq. (A.16) can be evaluated:
(A.17)With the aid of Eq. (A.13) the integral in Eq. (A.16) can be evaluated: 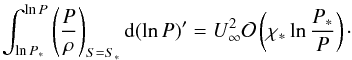 (A.18)Since the gas may expand substantially on the stagnation streamlines, the term ln(P ∗ /P) can become very large. For further analysis it is advantageous to split the integral in Eq. (A.16) into two parts:
(A.18)Since the gas may expand substantially on the stagnation streamlines, the term ln(P ∗ /P) can become very large. For further analysis it is advantageous to split the integral in Eq. (A.16) into two parts: 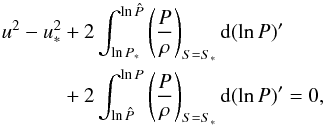 (A.19)where the second integral can be evaluated by using the assumption (25) together with Eq. (A.13):
(A.19)where the second integral can be evaluated by using the assumption (25) together with Eq. (A.13): 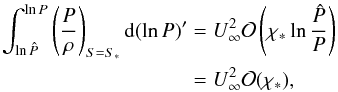 (A.20)
and thus turns out to be negligible. Equation (A.19) then simplifies to
(A.20)
and thus turns out to be negligible. Equation (A.19) then simplifies to 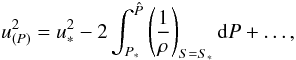 (A.21)or, equivalently,
(A.21)or, equivalently, ![\appendix \setcounter{section}{1} \begin{equation} u^2_{(P)}=u_*^2+2[h_*-h(\hat{P},S_*)]+\dots, \label{eq:unewbuse} \end{equation}](/articles/aa/full_html/2011/07/aa12436-09/aa12436-09-eq201.png) (A.22)where the well-known relation for the enthalpy dh = dP/ρ (for dS = 0) has been used so that h = h(P,S) is an equation of state of the gas. The subscript (P) implies that this approximation is used only to calculate the pressure P. Finally, by inserting Eq. (A.22), the Newton-Busemann pressure law can be rewritten to yield the important result
(A.22)where the well-known relation for the enthalpy dh = dP/ρ (for dS = 0) has been used so that h = h(P,S) is an equation of state of the gas. The subscript (P) implies that this approximation is used only to calculate the pressure P. Finally, by inserting Eq. (A.22), the Newton-Busemann pressure law can be rewritten to yield the important result ![\appendix \setcounter{section}{1} \begin{eqnarray*} P=\hat{P}-\frac{\hat{\kappa}}{\hat{r}^j}\int_{\psi}^{\hat{\psi}}\{u_*^2+2[h_*-h(\hat{P},S_*)]\}^{1/2}{\rm d}\psi', \end{eqnarray*}](/articles/aa/full_html/2011/07/aa12436-09/aa12436-09-eq206.png) (26)used in Sect. 2.
(26)used in Sect. 2.
All Figures
 |
Fig. 1 Shock-oriented coordinate system of boundary-layer type, where z and r are Cartesian coordinates for plane flow, x and y are the distances along the shock surface and normal to it, with u and v as the corresponding velocity components, U∞ is the free-stream velocity, and ψ is the stream function. Flow quantities immediately behind the shock in the point N are denoted by a hat (^), and in the point S by an asterisk (∗) (adapted from Schneider 1968). |
| In the text | |
 |
Fig. 2 Comparison between the numerical and analytical solution of a bow shock wave generated by a hypersonic flow (M∞ = 500) hitting the solid unit sphere. A perfect monoatomic gas is assumed (γ = 5/3). The analytical body prediction is represented by the thin solid line. The bow shock wave (thick solid line) is parametrized by |
| In the text | |
 |
Fig. 3 Upper panel. Shape of the SQ galaxy NGC 7318b (thin line) and the bow shock (thick line) at t = 130 Myr (j = 0, |
| In the text | |
 |
Fig. 4 Analytically derived colour-coded maps of several flow quantities, namely log pressure P in dyn cm-2 (upper left panel), log density ρ in g cm-3 (upper right panel), log temperature T in K (lower left panel), and the velocity ratio u/cs ≃ M (lower right panel) for the SQ galaxy NGC 7318b at the time t = 130 Myr (j = 0, |
| In the text | |
 |
Fig. 5 Colour-coded log temperature map (in K) overlaid with the velocity field of the SQ simulation at the times a) t = 60 Myr, b)t = 130 Myr, and c) t = 200 Myr. The vectors drawn show the direction and magnitude of the velocity field. |
| In the text | |
 |
Fig. 6 Comparison of numerically (here log temperature in K is colour-coded) and analytically derived results. The thin line represents the outer envelope of the galaxy, whereas the thick line represents the bow shock. Upper left. Model of the interaction between NGC 7318b and the IGM in SQ at the time t = 60 Myr (j = 0, |
| In the text | |
 |
Fig. 7 Like Fig. 6. Upper left. Model of the interaction between NGC 7318b and the IGM in SQ at the time t = 200 Myr (j = 0, |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.