| Issue |
A&A
Volume 530, June 2011
|
|
|---|---|---|
| Article Number | A146 | |
| Number of page(s) | 13 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201116739 | |
| Published online | 26 May 2011 | |
Spectral and photometric analysis of the eclipsing binary ϵ Aurigae prior to and during the 2009–2011 eclipse⋆,⋆⋆
1 Astronomical Institute of the Charles University, Faculty of Mathematics and Physics, V Holešovičkách 2, 180 00 Praha 8, Czech Republic
e-mail: pavel.chadima@gmail.com
2
Eureka Scientific, Inc., 2452 Delmer Street, Suite 100, Oakland, CA 94602-3017, USA
3
Department of Astronomy & Physics, Saint Mary’s University, Halifax, NS B3H 3C3, Canada
4
Department of Physics and Astronomy, University of Denver, 2112 East Wesley Avenue, Denver, Colorado 80208, USA
5
Department of Physics and Astronomy, University of Victoria, PO Box 3055 STN CSC, Victoria, B.C., V8W 3P6, Canada
6
Hvar Observatory, Faculty of Geodesy, Kačićeva 26, 10000 Zagreb, Croatia
7
Astronomical Institute of the Academy of Sciences, 251 65 Ondřejov, Czech Republic
8
Hopkins Phoenix Observatory, 7812 West Clayton Drive, Phoenix, Arizona 85033, USA
9
Castanet Tolosan Observatory, 6 place Clémence Isaure, 31320 Castanet Tolosan, France
Received: 17 February 2011
Accepted: 5 April 2011
A series of 353 red electronic spectra (from three observatories, mostly from 6300 to 6700 )A obtained between 1994 and 2010, and of 171 UBV photometric observations (from two observatories) of the 2010 eclipse, were analyzed in an effort to better understand ϵ Aur, the well-known, but still enigmatic eclipsing binary with the longest known orbital period (~27 yrs). The main results follow. (1) We attempted to recover a spectrum of the companion by disentangling the observed spectra of the ϵ Aurbinary failed, but we were able to disentangle the spectrum of telluric lines and obtain a mean spectrum of the F-type primary star. The latter was then compared to a grid of synthetic spectra for a number of plausible values of Teff and log g, but a reasonably good match was not found. However, we conclude that the observed spectrum is that of a low gravity star. (2) We examined changes in the complex Hα line profiles over the past 16 years, with particular emphasis on the 2009–2011 eclipse period, by subtracting a mean out-of-eclipse Hα profile (appropriately shifted in radial velocity) from the observed spectra. We find that the dark disk around the unseen companion has an extended “atmosphere” that manifests itself via blueshifted and redshifted Hα “shell” absorptions seen projected against the F star. Significantly, the Hα shell line first appeared three years before first contact of the optical eclipse when the system was not far past maximum separation. (3) Analyses of radial velocities and central intensities of several strong, unblended spectral lines, as well as UBV photometry, demonstrated that these observables showed apparent multiperiodic variability during eclipse. The dominant period of 6621 was common to all the observables, but with different phase shifts between these variables. This result strongly supports our earlier suggestion that the photometric variability seen during eclipse is intrinsic to the F star, and therefore, the idea of a central brightening due to a hole in the disk should be abandoned. Although variability on similar timescales is also seen in the spectrum and in photometry out of eclipse, we were unable to find a coherent periodicity in these data. Nevertheless, theseresults appear to rule out regular stellar pulsations as the cause of this variability.
Key words: stars: variables: general / binaries : eclipsing / stars: individual:ϵAurigae
Based on spectra obtained at the Dominion Astrophysical Observatory, Ondřejov Observatory and Castanet-Tolosan Observatory and on UBV photometry gathered at the Hvar Observatory and Hopkins Phoenix Observatory.
Tables 1 and 2 are only available at the CDS via anonymous ftp to cdarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/530/A146
© ESO, 2011
1. Introduction
Epsilon Aurigae (7 Aur, HD 31964, HR 1605) is a bright star in the constellation of Auriga (V ~ 3m.0, RA 05h01m58s, Dec +43°49′24′′). It is a single-line eclipsing binary with the longest known orbital period of 27.1 years (98903) (Ludendorff 1903; Chadima et al. 2010). Even more notable than the orbital period is the long duration of the eclipse of almost two years, which in combination with the large binary separation means that an eclipsing object must be huge. Analyzing the primary eclipse, Huang (1965) concluded that the eclipsing object was a cool opaque disk. No secondary eclipse has ever been observed. An object in the center of the disk is invisible, and various hypotheses about its true nature had been put forward, since there is no easy way to derive the individual masses and radii. It is therefore conceivable that ϵ Aurbelongs to those relatively rare binaries (like β Lyr) for which the brighter component in the optical spectral region can be the less massive of the two. To avoid confusion, throughout this paper we use the terms primary and secondary to denote the visible F-type star and the unseen object (presumably hidden in the cool disk), respectively.
Two main models of the system have been considered, often referred to as the high-mass, and the low-mass model (Guinan & DeWarf 2002, and references therein).
The high-mass model was proposed in a remarkable study by Kuiper et al. (1937) and consists of an F0Ia primary of ~36 M⊙ and a 1200–1400 K cool secondary hidden in the opaque disk, with a mass of ~24.5 M⊙. They also estimated the radii of 190 and 2690 R⊙. The separation of the binary components is then ~35 AU. They pointed out that the observed flat-bottomed eclipse can only be understood if the cool eclipsing body is an extended gaseous shell. The model was later developed by Carroll et al. (1991) who considered the F0Ia primary of ~15 M⊙ and the secondary hidden in the opaque disk, with a mass of ~13.7 M⊙. The separation of the binary components in their model is ~27.6 AU. The disk surrounding the secondary is considered to have a protoplanetary origin.
The low-mass model assumes a bloated post-AGB object and a secondary hidden in an optically thick disk, which is assumed to originate from recent accretion of matter flowing from the F primary to secondary. This model was first formulated by Eggleton & Pringle (1985) who suggested the masses of 1.3 M⊙ for the F star and 5 M⊙ for the secondary. Along with Lissauer & Backman (1984), they could not rule out the possibility that the object hidden in the disk is itself a binary, thus making ϵ Aura triple system.
Although these two models are very different ones, there were no firm observational constraints to prefer one over the other. Very regrettably, the distances that follow from the Hipparcos parallax (362–2273 pc; Perryman & ESA 1997) or from the revised reduction (355–4167 pc; van Leeuwen 2007a,b) are so imprecise that they are consistent with both models. Hoard et al. (2010) assembled new Spitzer Space Telescope IRAC observations of ϵ Aur, and after combining them with archival ultraviolet (UV) to mid-infrared data, they obtained a spectral energy distribution (SED) from ~0.1 μm to 100 μm. They argue that this SED can be reproduced by a three-component model consisting of a 2.2 ± 0.9 M⊙ F type post-AGB star (the primary) and a 5.9 ± 0.8 M⊙ B5V star (the secondary) surrounded by a geometrically thick but partly transparent disk of gas and dust with an effective temperature of 550 K. However, we note that the far-UV spectrum of ϵ Aurobserved by the FUSE satellite is an emission line spectrum, probably produced by scattering of continuum photons from a hot star embedded in the occulting disk of the secondary (Bennett et al. 2005; Ake 2006). Future models of the spectral energy distribution should take this into account.
Some additional support for the high-mass model comes from the recent work of Sadakane et al. (2010), who performed an LTE abundance analysis of ϵ Aurusing ATLAS models and applying NLTE corrections. Sadakane et al. (2010) compared ϵ Aurto the reference star HD 81471, an A7 Iab supergiant. They find that both stars have comparable Teff and log g, but that ϵ Aurhad higher microturbulent velocity. Overall abundances of the elements Mg, Si, S, Ca, and TI, and of Sc, Cr, and Fe are comparable and close to solar in both stars. The s-process elements Y, Zr, and Ba are slightly more abundant (by +0.25 dex) in ϵ Aurthan in HD 81471, but Sr is anomalously low in both stars. Carbon and oxygen are underabundant, and N and Na overabundant, in both stars. This abundance pattern is typical of late-type supergiants and is quite different from that of post-AGB stars. In particular, for the four examined post-AGB stars, Sadakane et al. (2010) find enhanced carbon abundances, with [C/Fe] > [N/Fe] for these stars (in contrast to the situation for ϵ Aurand HD 81471). They conclude that the observed abundances of ϵ Aurare normal for high-mass supergiant stars.
 |
Fig. 1 Sample spectrum of ϵ Aurfrom OND, showing the strong, unblended lines of Si ii and Fe ii for which the radial velocity, central intensity, and equivalent width were measured. |
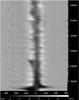 |
Fig. 2 Evolution of the Hα profile from 1994 to present. The x-axis shows heliocentric velocities (in km s-1) and the y-axis shows observation dates (HJD-2 400 000). The intensity scale is shown below. The spectra were linearly interpolated onto a regular time grid to produce this image. The black dashes along the right axis show the actual observation dates. |
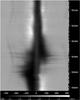 |
Fig. 3 Evolution of the Hα profile during the 2009–2011 eclipse. The x-axis shows heliocentric velocities (in km s-1) and the y-axis shows observation dates (HJD-2 400 000). The intensity scale is shown below. The spectra were linearly interpolated onto a regular time grid to produce this image. The black dashes along the right axis show the actual observation dates. |
It would be impractical to summarize all of the published studies of ϵ Aur. We restrict ourselves to those relevant to the findings presented in this paper. Several investigators, starting with Kuiper et al. (1937), have noticed the presence of a “shell” spectrum during the eclipse, which manifests itself by the presence of additional absorption lines, obviously originating in the optically thin outer atmosphere of the disk. This shell spectrum can be used to analyze of the properties of the disk around the secondary. Hinkle & Simon (1987) observed CO shell lines, which are absent in the spectrum of the primary, and Lambert & Sawyer (1986) found that the K I lines at 7664 and 7699 Å strengthen noticeably at the beginning and during the eclipse. Measuring their radial velocity (RV) and assuming a Keplerian disk, they estimated probable masses of the components of ϵ Auras less than 3 M⊙, and 3 − 6 M⊙, for the primary and secondary, respectively, and argued in favor of the low-mass model. They also observed cyclic line-profile variations on a timescale of about two months and noticed that two known pulsating F-G Ia supergiants, HR 8752 and ρ Cas, have much longer periods of about 1 year. They speculated that, if the two-month variations are indeed caused by photospheric pulsations of the primary, this may lend additional support to the conclusion that its mass is low. Saito et al. (1987) analyzed several shell lines and attempted to derive some properties of the disk. Since the shell lines were blended with the lines of the primary, they corrected the eclipse spectra, dividing them by one reference spectrum taken out-of-eclipse. We note, however, that since the ϵ Aurspectra are intrinsically variable, it may not be optimal to use only one, accidentally chosen reference spectrum for such a correction. Indeed, Ferluga & Mangiacapra (1991) used several out-of-eclipse spectra to derive an “average” reference spectrum, which they used for the reconstruction of 15 pure shell spectra. They then measured the physical quantities characterizing the properties of a number of shell lines originating in the disk. Backman et al. (1985) analyzed hydrogen Brackett lines during the 1982–1984 eclipse. They concluded that the emission and absorption velocities of the Bα and Bγ lines have a time dependence more like what is expected for the primary than the secondary, but with a large uncertainty.
Readers are also referred to a review paper by Guinan & DeWarf (2002) where detailed pieces of information about this mysterious system, as well as important references, can be found.
Recently, a long and extensive series of archival radial velocity beginning in 1899, and photometric observations of eclipses since 1848, have been compiled and analyzed independently by two groups. The results were the new, more precise ephemerides and orbital solutions of Stefanik et al. (2010) and Chadima et al. (2010). These are clearly superior to the previous spectroscopic orbital solution of Wright (1970) since they are based on much longer observational periods and incorporate more accurate RV measurements. Moreover, they simultaneously use photometric measurements to derive a more accurate orbital period and mideclipse epoch. The ephemeris of Stefanik et al. (2010) is 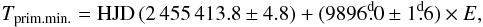 (1)and it redicts the current mideclipse somewhere between July 31 and August 10, 2010. Chadima et al. (2010) derived the ephemeris
(1)and it redicts the current mideclipse somewhere between July 31 and August 10, 2010. Chadima et al. (2010) derived the ephemeris 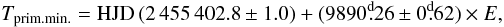 (2)which predicts the current mideclipse to occur on July 24–26, 2010. This orbital solution is used in this paper. Furthermore, Chadima et al. (2010) argue that the brightening observed during the middle of the 1982–1984 eclipse was not due to a central hole in the disk, but was a continuation of the intrinsic F star variations observed out of eclipse.
(2)which predicts the current mideclipse to occur on July 24–26, 2010. This orbital solution is used in this paper. Furthermore, Chadima et al. (2010) argue that the brightening observed during the middle of the 1982–1984 eclipse was not due to a central hole in the disk, but was a continuation of the intrinsic F star variations observed out of eclipse.
The current eclipse began August 2009 and is predicted to end in May 2011. Naturally, this rare event has attracted the attention of many astronomers in an attempt to better understand the nature of this still mysterious system. To this end, the present collaborative effort has obtained a diverse variety of observations using the best available instruments and observational techniques and modern analysis methods. An outstanding example of such work is the recent study by Kloppenborg et al. (2010) in which the 2D image of ϵ Aurwas reconstructed from CHARA multi-aperture, multi-baseline interferometry. Preliminary results obtained during the current eclipse show an image of the primary star being partly eclipsed by a disk-like companion, thereby providing direct confirmation of the Huang (1965) model. Assuming a mass of 5.9 M⊙ (Hoard et al. 2010) for the B star hidden in the disk, they estimated the mass of the F star as 3.6 ± 0.7 M⊙.
Leadbeater & Stencel (2010) report a step-wise increase in the line strength of the K I line at 7699 Å during the current eclipse, which seems to support an earlier suggestion by Ferluga (1990) that the disk has a multiring structure. These and other recent findings about ϵ Aurhave been summarized by Stencel (2010).
The present study is organized as follows. The observational material and its reduction and measurement are presented in Sect. 2. Our attempts at disentangling the ϵ Aurspectra and the comparison of disentangled spectra of the primary with the synthetic spectra are discussed in Sect. 3. Analyses and possible interpretation of the complex and highly variable Hα line profiles are given in Sect. 4. An analysis of the measured radial velocities and central intensities of several spectral lines and UBV photometry is presented in Sect. 5.
2. Observational material, reduction, and measurements
2.1. Spectroscopy
This study is based on the following three series of electronic spectra covering the spectral region around the Hα line.
-
1.
105 CCD spectra with a linear dispersion of10 A mm-1 and atwo-pixel resolution of 21 700 were secured inthe Coudé focus of the 1.22-m reflector at the DominionAstronomical Observatory (DAO) in Canada between 1994 and2010 by SY and PDB. These observations cover the wavelengthrange 6200–6750 .A
-
2.
201 CCD spectra having a linear dispersion of 17 A mm-1 and resolution of 12600 were obtained in the Coudé focus of the 2.0-m reflector of the Ondřejov Observatory (OND) in the Czech Republic in 2006–2010 by PH, PŠ, MŠ, MW, PC, VV, and several additional observers (credited in Acknowledgements). These observations cover the wavelength range 6260 − 6760 .A
-
3.
47 CCD spectra with resolution of 11 000 were obtained with a 0.28-m Celestron 11 telescope at the Castanet-Tolosan Observatory in France (CTO hereafter) by CB during 2009 − 2010.
Initial reductions of the DAO and OND spectra were carried by S.Y. and M.Š., respectively, both in IRAF. The initial reductions of the CTO spectra were carried out by CB in Reshel V1.11. Rectification and all radial velocity, central intensity (CI), and equivalent width (EW) measurements of selected lines in these spectra were carried out by PC in SPEFO (Horn et al. 1996; Škoda 1996). The latest JK 2.63 version of the program SPEFO, developed by the late Mr. J. Krpata, was used. All measurements are presented in detail, together with heliocentric Julian dates (HJDs) of mid-exposures in Table 1 (at the CDS).
A representative Ondřejov red spectrum is displayed in Fig. 1. Quantitative measurements were carried out for several of the stronger, unblended spectral lines: two Si II lines at 6347.109 Å and 6371.371 Å, two Fe II lines at 6416.919 Å and 6432.680 Å, and the Hα line at 6562.817 Å, for which the emission wings were also measured. The RV measurements in SPEFO are based on sliding the direct and reverse line profile on the computer screen until the best coincidence of both profiles is achieved. The zero point of the RV scale was determined individually for each spectrum via measurements of selected telluric lines (Horn et al. 1996).
The behavior of the Hα profile is illustrated well by the 2D images of the line profile over time, shown in Fig. 2 for the entire 1994 to 2011 period, and in Fig. 3 in detail for the 2009–2011 eclipse. Note the high degree of variability of the Hα profile. The velocity scale for these spectra is heliocentric, and one can see the annual sinusoidal variations of several nearby telluric water vapor lines in Fig. 3. A detailed analysis in the Hα variations is presented in Sect. 4.
2.2. Photometry
Here, we use the following two series of photoelectric UBV observations from the phases of the current total eclipse.
-
1.
105 differential observations relative to λ Aur (HD 34411) in a period HJD 55 213 − 55 468 were obtained by HB, DS, PH, MW, and PC with a photoelectric photometer and an uncooled EMI 9789QB tube at the Hvar Observatory (Croatia) 0.65-m Cassegrain reflector. Observations in all three filters consisted of from 7 to 10-s integrations followed by 5-s integrations on the sky. The check star HR 1644 (HD 32655) was observed as frequently as the variable and typically three to five such individual differential observations were obtained for each night of observations. All these observations were reduced and transformed to the standard UBV system with the help of non-linear transformations using the reduction program HEC22 (Harmanec et al. 1994; Harmanec & Horn 1998). The latest release #17 of the program HEC22 was used. This version allows modeling the varying extinction that occurs during the course of each night’s observations. The standard UBV magnitudes of the comparison star λ Aur
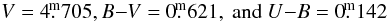 were derived from numerous all-sky observations at Hvar and were added to the magnitude differences var-comp and check-comp to obtain final differential UBV magnitudes of ϵ Aurand HR 1644. All Hvar observations of both stars were tabulated with the HJDs in Table 2 (at the CDS).
were derived from numerous all-sky observations at Hvar and were added to the magnitude differences var-comp and check-comp to obtain final differential UBV magnitudes of ϵ Aurand HR 1644. All Hvar observations of both stars were tabulated with the HJDs in Table 2 (at the CDS). -
2.
66 differential observations, also obtained relative to λ Aur in a period HJD 55 200–55 539 were secured by JH at the Hopkins Phoenix Observatory, USA. His home-built photometer uses a 1P21 photomultiplier tube operated at –950 V and is attached to a Celestron C-8 telescope mounted on a Meade LX-90 mount. Dead time for the detector is determined using an aperture mask. The mask contains irregularly spaced holes that reduce the aperture by 80%. Stars that are close to each other and near the zenith are measured as quickly as possible to reduce the effects of extinction. A bright star and a faint star are measured without, with, and without the aperture mask placed in the light path. Their resulting counts are averaged and used to compute the dead time coefficient of the instrument. Observations are conducted in the standard CVCVCVC format (C = comparison, V = variable). Each observation is composed of three 10-s integrations in each of the three UBV filters, followed by one 10-s integration on the sky, again in UBV . The following values of the comparison star, slightly different from the Hvar values, were adopted:
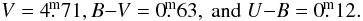 These data1 are on the instrumental UBV system of the instrument.
These data1 are on the instrumental UBV system of the instrument.
 |
Fig. 4 Comparison of the mean, out-of-eclipse spectrum of ϵ Aurwith some ATLAS synthetic spectra. The best-fitting synthetic spectrum has the parameters: Teff = 8000 K, log g = 1.0 [cgs] log Z/X = –0.3, v(rot) = 5.0 km s-1. Two other synthetic spectra are shown, one with higher gravity and one with lower metallicity. |
3. Disentangling and modeling the ϵ Aurspectra
Having at our disposal several hundred ϵ Aurspectra, which span an interval of 17 years, i.e. more than a half of the orbital period, we attempted to disentangle them in the hope of detecting a faint spectrum of the “unseen” secondary, possibly lost in the much more prominent spectrum of the primary. Note, for instance, that if the true mass ratio of the system was not too far from one, the lines of both components would remain blended in all orbital phases since the semi-amplitudes of their RV curves would both be only ~15 km s-1. For the purposes of disentangling spectra, we only used observations obtained prior to the predicted beginning of the current eclipse. This left us with 208 spectra (99 DAO and 109 OND spectrograms). We mainly used the interval 6333 − 6540 Å and also several shorter subintervals (e.g. an interval of 6344 − 6374 Å, containing both Si ii lines). We made no attempt to disentangle Hα, considering its complicated shape, obvious V/R changes of its emission wings, and the possibility that it need not be associated with either the primary or secondary component.
We used the program KOREL, developed by Hadrava (1995, 1997, 2004) and made publicly available by the author. It uses a spectral disentangling technique in the Fourier domain and simplex method of minimalization of the sum of residuals and discrete spectra from various orbital phases, which are rescaled to a linear RV scale. From these data, the spectra of the individual binary or multiple components are derived, as well as, if required, the orbital elements of the binary or multiple system. No assumption is made about the shape of the line profiles; the only requirement inherent to the method is that the component profiles can only vary in their strength and not in their shape. The run of KOREL is controlled by a parameter file with the initial orbital parameters of the system and initial simplex steps. Any of the orbital parameters can either be held fixed or be converged.
We selected only a short wavelength interval 6529−6539 Å containing virtually no stellar lines but only a number of stronger telluric lines, then fixed the orbit of the Earth around the Sun projected into the direction to ϵ Aur, and let the program derive the relative strength of the telluric spectrum for each spectrogram used. Then we fixed these strengths and also all elements of the orbital solution derived by Chadima et al. (2010). We instructed the program to proceed step by step, first allowing for the determination of variable line strengths for both binary components only and finally also allowing for convergence of the epoch of periastron, which is the most uncertain parameter in the adopted orbital solution.
To see whether the resulting sum of squares of residuals χ2 is sensitive to the mass ratio q used (thus indicating the definite presence of a secondary line spectrum), we carried out a number of KOREL solutions for different values of q. Such a mapping has been successfully applied in several other cases – see, for instance, Harmanec et al. (2010).
We applied this mapping to the whole selected wavelength interval, as well as to several sub-intervals but the expected, roughly parabolic dependence of χ2 on the mass ratio has ever been found. We must conclude that, at least for the spectral resolution we had at our disposal, no lines of the secondary spectrum were detected.
After obtaining this null result, we decided to use KOREL only for disentangling the telluric spectrum and recovering the mean out-of-eclipse spectrum of the F-type primary. Using the mean stellar spectrum minimizes the effect of transient, intrinsic variations.
We used a catalog of model atmospheres ATLAS for our calculation of synthetic spectra. We calculated a grid of the synthetic spectra of “classical” F stars based on Kurucz’ ATLAS9 model atmospheres for various temperatures, gravities, and metallicities. In particular, the grid was derived for Teff = 7500−8500 K, log g = 1.0−5.0 [cgs], and metallicities log Z/X from − 0.3 to +3.0. All synthetic spectra were convolved to rotation velocities of the primary in an interval v(rot) = 5.0−25.0 km s-1. Synthetic spectra for higher metallicities and lower gravities were not modeled because the ATLAS catalog does not contain model atmospheres for those parameters owing convergence problems.
The best match between the disentangled and synthetic spectrum (in the sense of the lowest value of χ2) was obtained for a synthetic spectrum with the following characteristics: Teff = 8000 K, log g = 1.0[cgs], log Z/X = −0.3, v(rot) = 5.0 km s-1. Our results are in fair agreement with the spectral analysis by Sadakane et al. (2010). In Fig. 4, the disentangled spectrum is compared with several synthetic spectra, and it is clear that even the model for log g = 1.0 does not describe the observed spectrum properly; that is to say, the two Si ii lines (on the left side of the plot) and two Fe ii lines (on the right side of the plot) should be more prominent than they are for the best synthetic spectrum with log g = 1.0.
To check on the result, we investigated the variation in χ2 as a function of the input quantities, which characterize each model. We also inspected the plots of individual spectra. The conclusion from this exercise is that the synthetic spectra are almost insensitive to the value of the projected rotational velocity for the values used, at least in comparison to other characteristics. This implies that the “optimal” value of the projected rotational velocity should not be given too much weight, even more so because a satisfactory fit between the disantangled and model spectra was not found. The dependence on Teff is almost negligible for the range of investigated values and the spectral lines used. There is, however, a very strong dependence on the gravity and metallicity. In Fig. 4, there are a few synthetic spectra for lower metallicity and higher gravity. It is seen that one could probably reproduce the Si ii and the Fe ii lines by increasing the metallicity and further decreasing log g. Regrettably, we do not have a suitable model atmosphere available to confirm this conjecture.
However, the best-fitting synthetic spectrum already provides a good fit to the weaker lines from 6375–5415 Å, even though it fails to adequately describe the stronger Si ii and Fe ii lines. This behavior illustrates the limitations of the ATLAS model atmospheres used here, because they are plane-parallel LTE models. Both of these assumptions are probably significantly violated in low-gravity, highly evolved stars (regardless of whether the F star is of low or high mass). Therefore, these ATLAS models should be considered as providing only qualitative constraints on the stellar parameters (Teff, log g, abundance). For quantitative work, non-LTE (NLTE) models, and probably spherically symmetric models also, are needed.
4. Analysis of the Hα profile during the 2009–2011 eclipse
The profile of the Hα line of ϵ Aurobserved outside the eclipses consists of a central absorption surrounded by a double emission peaks, which might originate in the extended envelope of the primary (Cha et al. 1994). The whole Hα profile and, especially, its emission wings are very variable, which is sometimes explained by the rotation and physical changes in the envelope around the primary. This variability causes problems in the interpretation of the Hα profile even out of eclipse.
To investigate the assumption that the Hα emission originates in a vicinity of the primary, we calculated orbital solutions for the Si ii lines and the Hα emission wings using RV measurements on the DAO out-of-eclipse spectra. We used the FOTEL program (Hadrava 2004) with input parameters from the solution of Chadima et al. (2010) and only allowed a convergency of the periastron epoch T and the velocity semi-amplitude K1. Results are summarized in Table 3.
In Fig. 5, the orbital solution found from the Si ii lines alone and the solution from the wings of Hα are compared with the solution of Chadima et al. (2010). It is seen that the Hα emission roughly follows the orbital motion of the Si ii lines, i.e., the primary, and therefore must be associated with this component. We infer that a small difference between both solutions is mainly caused by an insufficient interval covered by data used for both orbital solutions (when compared with the orbital period of the ϵ Aur).
To verify that the Hα emission originates near the primary, we selected two rather symmetric Hα profiles from substantially different orbital phases and overplotted them on a heliocentric wavelength scale in Fig. 6. One can see that the whole Hα profile, including the double emission wings, undergoes the RV shift corresponding to the motion of the F star in orbit. This behavior provides strong evidence that the Hα emission is associated with the F-type primary.
 |
Fig. 5 Orbital solutions derived only from the Si ii lines and from the emission wings of Hα are compared to the full Chadima et al. (2010) solution. |
 |
Fig. 6 Comparison of two symmetric Hα profiles from different orbital phases. The orbital phases and the radial velocities of the primary at those phases are labeled. |
 |
Fig. 7 Variation of the Hα core central intensity in the DAO and OND spectra. |
Orbital solutions for T, K1, v0 from fits to the Si ii lines and Hα wings.
During eclipse, Hα undergoes prominent line profile changes. Figure 7 shows a remarkable fact: the CI of the Hα absorption core steadily decreases with the approaching eclipse. An important finding is that this decrease started about three years before the beginning of the optical eclipse, thus confirming the behavior first reported by Kuiper et al. (1937). The Hα EW increased during the same time period. The RV of the central absorption core increased significantly during the first half of the eclipse, but after mideclipse, then suddenly reverted back to negative values. The Hα emission peaks disappear during eclipse. For the current eclipse, the red emission peak had disappeared by HJD 2 455 259 and the blue peak had vanished by HJD 2 455 329. The red emission peak subsequently reappeared after HJD 2 455 524.
From a study of the Hα line profile during the last eclipse (Barsony et al. 1986), we expect the evolution of the Hα profile in the second half of the current eclipse to follow the sequence of events described above in reverse. The observations should show a gradual increase in the Hα absorption core CI, accompanied by a decrease in its EW, and a gradual return of the absorption core RV to the out-of-eclipse values. It is expected that both emission peaks will reappear in reverse order to what was seen in the first half of the eclipse.
Based on the results of previous studies of the shell spectrum (discussed in Sect. 1), we adopted the Kuiper et al. (1937) interpretation of the Hα behavior. We assume that (apart from any intrinsic line profile changes, as seen for other lines) changes in the Hα profile during eclipse are due to additional absorption of the primary’s light by the outer, optically thin atmosphere of the companion’s occulting disk. In other words, we suppose that, since the companion’s disk does not contribute any radiation in the optical region near Hα, the uneclipsed part of the primary star produces a similar Hα profile to the whole stellar disk out of eclipse. However, the region producing the Hα emission may be extended, in which case much of the emission may not be eclipsed during the stellar eclipse, thereby also resulting in a similar eclipse emission profile to the one out of eclipse. We interpret the disappearance of the out-of-eclipse Hα emission during eclipse (Fig. 2) as the result of strong shell absorption at the corresponding wavelength. In this scenario, the intrinsic emission is still present, but is strongly absorbed by material in the occulting disk during eclipse. This disk absorption reflects the velocity field in the rotating disk, which is why its RV increases in the first half of the eclipse. This naturally leads to an apparent disappearance of the red emission peak. As the eclipse goes on, the shell absorption from the other edge of the disk, rotating in the direction towards the observer, becomes dominant and the observed RV of the deepest absorption quickly shifts to negative (i.e., blueshifted) values, thus leading to an apparent disappearance of the blue emission peak. Near the center of the eclipse, both edges of the rotating disk atmosphere are projected against the primary and one should simultaneously see a blueshifted and a redshifted absorption. If the disk were axially symmetric, one should see two absorption cores of the same CI with opposite RVs with respect to the instantaneous RV of the secondary.
 |
Fig. 8 Evolution of the observed Hα profile near mideclipse. |
 |
Fig. 9 Evolution of the corrected Hα profile, with the mean out-of-eclipse profile subtracted, near mideclipse. |
To test and explore our hypothesis, we once again used KOREL to obtain a mean Hα profile, free of telluric lines and intrinsic variations, using only the spectra observed out of eclipse. This mean Hα profile was then shifted to the primary’s RV, using the Chadima et al. (2010) orbital solution, and subtracted from the observed OND spectra. Since the shell absorption should have the out-of-eclipse Hα as its continuum, we finally renormalized the subtracted spectra to a continuum value of unity. In Fig. 8, we show observed Hα line profiles at five epochs near the date of mideclipse. The complex Hα line profiles shown here are similar to those reported by other observers during the current ϵ Aurobserving campaign. In Fig. 9, we show the mean, out-of-eclipse profile and the same five profiles as in Fig. 8, but with the mean, out-of-eclipse profile subtracted from them. The result of the subtraction supports our hypothesis and the validity of our procedure. This is because the subtracted spectra show simple, double-absorption core profiles consistent with what is expected from the occulting disk model. Furthermore, these Hα absorption profiles evolve during the course of the eclipse in a manner consistent with what is expected from the occulting disk model, in contrast to the complex observed Hα profiles of Fig. 8. The red absorption core is much deeper on the earliest spectrum, when most of the light from the primary is absorbed by a receding part of the rotating disk. Furthermore, the ratio of the central intensities of the red/blue absorption cores gradually decreases through unity near mideclipse. At mideclipse (the third spectrum in both figures), the two absorption cores are almost symmetric (after subtraction of the mean, out-of-eclipse profile).
Similar profile changes should also be seen for the Hβ line. We checked 30 available OND spectra covering the Hβ region, observed between 2007 and 2010. Regrettably, we have no out-of-eclipse Hβ spectra and cannot repeat the procedure carried out for Hα. We therefore only present a selection of five original spectra in Fig. 10. It is seen that their CI is decreasing and the absorption core is shifting redward as the mideclipse approaches. During and after the mideclipse, the absorption core quickly becomes blueshifted. This indicates that the evolution of the Hβ profile near the current mideclipse is indeed similar to that of the Hα profile.
 |
Fig. 10 Time evolution of the original Hβ profile during the 2009–2011 eclipse. |
We measured the RVs and CIs of both Hα cores after the subtraction of the mean, out-of-eclipse profile, as well as the EWs of the entire double absorption profile. All these quantities are plotted in Fig. 11. It is seen that the CI decreases and the EW increases with the approach of mideclipse. These changes become more prominent closer to mideclipse as the light from the primary goes through denser parts of the occulting disk, resulting in stronger disk absorption. The RV increases as the line-of-sight absorption through the occulting disk gradually moves closer to the disk’s axis of rotation (and to correspondingly higher orbital velocities). The blue core, with its RVs in the opposite sense, first appears 74 days before the mideclipse2, and it deepens quickly, while the the red core reaches its maximum strength and gradually weakens thereafter. The red core finally disappears 49 days after mideclipse, at about the time when the blue core attains its maximum strength (i.e., minimum CI). The interval when the both cores are visible is therefore 123 days. This is in a good agreement with the estimated time needed for the center of the companion’s occulting disk to transit the disk of the F star. It is also seen that, while the EW of the entire Hα absorption line profile reaches its maximum several days prior to mideclipse, the red and blue absorption cores do not attain equal CI until several days after mideclipse. One possible explanation of this finding is that the center of the disk is not perfectly axially symmetric and that there is a denser region in the receding part of it and a more rarified region in its approaching part. It is important to continue these Hα observations for the second half of the current eclipse to confirm the occulting disk model proposed here.
 |
Fig. 11 Changes of RV (top), CI (middle), and EW (bottom) of the two absorption cores of Hα during eclipse, after subtraction of the mean, out-of-eclipse Hα profile. The first vertical line denotes the beginning of the current photometric eclipse, the second one indicates the date of mideclipse. |
We emphasize that the RVs in Fig. 11 should be corrected for orbital motion before any analysis. But since the “shell” absorption cores originate in the disk around the secondary, their RV measurements should be corrected for an orbital velocity of the secondary, not the primary. Nevertheless, uncertainties in present estimates for the mass ratio are too high, thereby keeping this correction from being inconvincing. However, it was proven that any reasonable value of the mass radio does not change the resulting RVs so much that it would affect our conclusions presented in this section. However, some inconsistencies remain with the occulting disk scenario.
-
1.
The average between the first (HJD 2 455 329) and the last (HJD 2 455 452) corrected spectrum for which both cores are visible is HJD 2 455 391, which disagrees with the predictedtimes of the mideclipse of either HJD 2 455 413.8 ± 4.8 (Stefanik et al. 2010) or HJD 2 455 402.8 ± 1.0 (Chadima et al. 2010).
-
2.
The RVs of the blue core are gradually decreasing during last few observations, while their increase is expected.
-
3.
The last few CIs of the blue core (of the subtracted spectra) are slightly negative, which is, of course, physically impossible.
All of these inconsistencies can be explained if we realize that the out-of-eclipse Hα profile is highly variable, and it is undoubtedly also variable during the eclipse, thereby affecting the observed eclipse profiles. Since we corrected all Hα profiles by subtracting the mean profile, any intrinsic line variations will still affect the individual profiles3. Moreover, the measured quantities in the absorption profiles could also be partly affected by relatively strong telluric lines at 6560.555 Å and 6564.206 Å.
Our hypothesis and results discussed above are potentially good for determining the physical properties of the disk (i.e., its density and velocity structure), which could help in understanding its nature. But for a precise analysis of this kind, one should model the light of the primary going through the various model disks and compare the results with the observed Hα profiles. This task is beyond the scope of this, rather qualitative, analysis.
 |
Fig. 12 Critical Roche lobes for the high and low-mass models are shown to scale, with the lines of sight to Earth shown for the beginning of spectroscopic and photometric eclipse. |
4.1. Sightlines at the onset of spectroscopic and photometric eclipse
As already noted at the beginning of this section, the CI of the Hα absorption core starts to decrease at least three years before the predicted beginning of primary eclipse. This observational result can be used to constrain the structure of the system. We refer to the period when Hα absorption cores deepen below their out-of-eclipse mean value as “spectroscopic eclipse”. From Fig. 7, we estimate that spectroscopic eclipse began around HJD 2 454 000. The Chadima et al. (2010) orbital solution implies that the angle between the sightline at the start of spectroscopic eclipse and the mideclipse sightline is ~85°. JH determined that the 2009 photometric eclipse began on HJD 2 455 056 when the sightline angle was only ~20° relative to the mideclipse line of sight.
In Fig. 12, we show the critical Roche lobes for the high- and low-mass models presented in Sect. 1, and the sightlines at the onset of spectroscopic and photometric eclipse. It is evident that the additional Hα absorption at the start of spectroscopic eclipse cannot be caused by material near the secondary because the binary orientation is close to maximum separation at that time. Therefore there must be some circumbinary material responsible for this additional absorption, suggestive of the Struve (1956) model. However, from our observations, it is seen that this envelope is not homogenous, as proposed by Struve (1956).
The line of sight at the onset of photometric eclipse intersects both critical Roche lobes around the secondary. However, in the case of the high-mass model, the disk around the secondary would almost extend to the critical Roche lobe.
 |
Fig. 13 Dramatic Hα profile variation: the sudden appearance of a deep, blueshifted absorption core, as observed at the DAO during 2005–2006. |
4.2. A remarkable out-of-eclipse Hα profile variation in 2005–2006
An unusual and prominent change in the Hα line profile was observed during 2005–2006, long before the onset of spectroscopic eclipse. The blue emission wing disappeared and was replaced by a deep, blueshifted absorption core (Fig. 13, also Fig. 2). Initially, the first spectrum (in Apr 2005) has a “standard” Hα profile, while the second and the third spectra observed later that year show the gradual appearance of the blueshifted absorption core. By Mar 2007, the final spectrum of this series shows a return to the standard Hα profile, but now with an increase in EW due to the onset of spectroscopic eclipse. Our observational coverage of this period is not sampled well enough to permit a reliable estimate of the timescale of the event. However, considering the first and the last spectrum for which a deviation from the standard Hα profile was seen, we estimate that the event lasted from August 2005 to March 2006. A similar behavior of the Hα profile was also observed and reported by Schanne (2007). However, a similar profile variation is not observed for other spectral lines.
The unusual change in the Hα profile was most probably caused by additional strong absorption from gaseous material with at an RV of about –40 km s-1 relative to the primary. This absorption feature indicates the presence of either a transient outflow of material from the primary star or of some localized circumstellar matter producing an “eclipse” of the primary.
5. A period analysis of the spectroscopic quantities and UBV photometry during the 2009–2011 eclipse
The profiles of the selected spectral lines, measured by us, are all variable on much shorter timescales than for the binary orbital period. To find out whether this variability is irregular or (multi)periodic, we carried out period analyses for individual observables, using two different computer programs. The first program was the HEC27 4, a code developed by P. Harmanec and based on phase dispersion minimalization (Stellingwerf 1978). The second program, PERIOD04, developed by P. Lenz and M. Breger (Lenz & Breger 2005), uses Fourier analysis methods; i.e., the time series of observational data is fitted using a sum of cosine functions.
Initially, we analyzed the periodic behavior of the Hα profile out of eclipse. For analysis of the Hα absorption profile RVs and CIs, we selected the 84 DAO observations prior to HJD 2 454 913. Later observations were excluded because these were affected by the peculiar line profile behavior discussed in Sect. 4.2 and, subsequently, by the onset of spectroscopic eclipse discussed in Sect. 4.1. All out-of-eclipse measurements were included for analyzing of the emission wings: the RVs, the CIs of the red and the blue emission, the emission-peak ratio V/R, and the emission strength (V + R)/2 where V is the peak intensity of the blue wing and R is the peak intensity of the red wing. Both the HEC27 and PERIOD04 analyses found no evidence of periodic behavior in any of the observables analyzed, a result in accordance with that of Cha et al. (1994). We conclude that the physical changes in the circumstellar matter responsible for the Hα emission are not periodic.
Next, we analyzed the behavior of the RVs and the CIs of the two measured Fe ii and Si ii lines. Since we assumed that the eclipse could affect these lines and since we did not have enough observations during the eclipse, we initially analyzed only the out-of-eclipse data. We used both methods but we also did not find any periodic behavior in the changes of these lines.
Periods found during the 2009–2011 ϵ Aureclipse.
After collecting sufficient observations of the current (2009 − 2011) eclipse, we repeated the periodic analyses just for the eclipse period, motivated by indications of periodic behavior during eclipse. We used the PERIOD04 code for this analysis, and we found that all the observables could be reasonably modeled by two sinusoids, except for the RVs of the Si ii lines, which needed three harmonic functions to adequately describe their variations. It is interesting to note that the main period of ~66 days was common to all the analyzed observables. In contrast, the secondary period differed among the observables. However, subsets of the observables shared common secondary periods: all the RVs had the same secondary periods, as did each of the Fe ii line CIs, and each of the Si ii line CIs (Table 4). As a final exercise, we tried to extrapolate these periods to the out-of-eclipse observations (which have much sparser time coverage), but this failed to accurately describe the observed variability. There is evidence that the photometric variability of ϵ Auris quite coherent at some times, but this coherence is lost on longer timescales. This “unpredictable” behavior is presumably due to some intrinsic variability of the F-type primary star.
 |
Fig. 14 RVs of the Fe ii lines (upper panel), the CIs of the 6416.919 Å Fe ii line (middle panel) and the B photometric filter (lower panel) fitted with two sinusoids. In each case the dominant period is 66.21 days, while the secondary period differs among the three cases. |
We decided to investigate whether similar periodic behavior could also be found in the photometric data at our disposal. A correction of the photometry for the eclipse light curve cannot be carried out reliably since there is no accurate model light curve so far. Using an improper model could result in the detection of spurious periodicities. Therefore we only used the photometric observations only from the eclipse period after the second photometric contact. The third contact had not yet occurred at the time of writing. We further assumed that the only brightness variations of ϵ Aurin the UBV passbands were due to the intrinsic variability of the only partially eclipsed F star (Kloppenborg et al. 2010), i.e., we assumed the eclipse imposed no further photometric variability during this period. With these assumptions, we only needed to shift the two datasets of UBV photometry to a common zero point. We computed average values for both datasets in all three passbands and subtracted them from the observed values. Analysis of these data by PERIOD04 revealed that the observations in all filters can also be described by two harmonic functions with both periods nearly identical for all filters. The main period was again ~66 days.
There are small differences in the main and secondary periods found by this analysis, but these can be interpreted as a consequence of fitting data with finite noise on a finite time interval. Considering that the differences in all periods imply phase differences of only a few percent of a cycle at worst, we simply averaged the individual periods and their respective phase shifts. These mean quantities were subsequently held fixedm, while the fit to the observational data was repeated in order to determine their amplitudes. The resulting periods and phase shifts (with respect to the phase of the main RV period) are summarized in Table 4.
The main period was found to be 66.21 days, and it is common to all analyzed quantities, which proves that it is real. There is a phase shift of 0.808 between the RVs and the CIs and 0.323 between the RVs and the UBV photometry. The secondary periods differ among the various observables, but as already mentioned, related observables share common secondary periods, which also suggests these periods are probably real. Figure 14 illustrates the final period fit for the RVs of the Fe ii lines, for the CIs of the 6416.919 Å Fe ii line, and for the B photometric passband.
6. Conclusions
Our spectroscopic and photometric analysis of the ϵ Aurled to the following conclusions as listed below. Since this study does not include observations from the end of the current eclipse and from post-eclipse phases, we intend to update this analysis once these phases have been covered by data from our ongoing observations.
-
1.
We attempted to disentangle the ϵ Aurspectra andrecover the spectra of both components, taking the unknownmass ratio q = M1/M2 as a free parameter, but this effort was unsuccessful. We conclude that there is no secondary spectrum hidden in the prominent primary spectrum. However, it is possible that a secondary spectrum could remain hidden if the ϵ Aurcompanion was itself a binary system.
-
2.
We derived a mean out-of-eclipse spectrum of the primary and compared it with a grid of synthetic spectra for “classical” F stars, using plane-parallel, LTE ATLAS model atmospheres. These analyses indicated that the F star is a low-gravity object, but a good spectral match was not found. However, this analysis should be repeated using more appropriate NLTE, spherically symmetric model atmospheres.
-
3.
We interpreted the complex behavior of the Hα line during eclipse as arising from additional absorption in an extended “atmosphere” around the companion’s disk. We subtracted the mean out-of-eclipse Hα line profile from the profiles observed during eclipse and obtained symmetric two-component absorption profiles. The behavior of these line profiles during the course of the eclipse agreed qualitatively with what is expected from the model presented by Huang (1965). This observational result, when combined with modeling of synthetic spectra for various eclipse phases, should serve to constrain the density and velocity structure of the companion’s disk.
-
4.
A systematic decrease in the central intensity of the Hα line (“spectroscopic eclipse”) began ~3 years before photometric first contact, owing additional circumstellar absorption. At the onset of spectroscopic eclipse, the line of sight to the F star lies far (at an angle of ~85°) from the mideclipse sightline. This implies that circumstellar material associated with the secondary must extend well beyond the occulting disk responsible for the photometric eclipses. In contrast, the sightline at the start of photometric eclipse (first contact) lies only ~20° away from the mideclipse line of sight.
-
5.
We searched for periodic behavior in the variable, out-of-eclipse Hα line, but did not find any periodicity. This implies that the distribution of circumstellar material around the primary (which may be a source of the Hα emission) is complex.
-
6.
During eclipse, both the Si ii and the Fe ii lines we examined showed periodic variations in their radial velocities and central intensities. The UBV photometry showed a similar periodicity. Attempts to extrapolate this periodic solution to the out-of-eclipse observations failed. The main period of the eclipse variability was found to be the same (66.21 days) for the radial velocity, central intensity, and photometric variations. However, these observables did not vary in phase, but exhibited different phase shifts among the variables. The lack of a periodic solution to the out-of-eclipse data appears to rule out regular stellar pulsations as the cause of this variability. The interpretation of the out-of-eclipse variability remains uncertain.
Available from: http://www.hpsoft.com/EAUr09/Data/UBVRIData.html
Note that Cha et al. (1994) made an unsuccessful attempt to find periodic behavior in the Hα profile; see also the first paragraph of Sect. 5.
The program with brief instructions how to use it is available at http://astro.troja.mff.cuni.cz/ftp/hec/HEC27.
Acknowledgments
We would like to thank our colleagues who obtained a few Ondřejov spectra used in this study: Drs. A. Kawka, D. Korčáková, P. Mayer, and P. Zasche, and students B. Kučerová and J. Polster. We acknowledge the use of the public version of the program KOREL written by Dr. P. Hadrava. We profited from the bibliography maintained by the NASA/ADS system and the CDS in Strasbourg. The Czech authors were supported by the grants 205/06/0304, 205/08/H005, 205/09/P476, and P209/10/0715 of the Czech Science Foundation and also from the research programs AV0Z10030501 and MSM0021620860. The University of Denver participants are grateful for support under US NSF grant 10-16678 and the bequest of William Hershel Womble in support of astronomy at the University of Denver.
References
- Ake, T. B. 2006, in Astrophysics in the Far Ultraviolet: Five Years of Discovery with FUSE, ed. G. Sonneborn, H. W. Moos, & B.-G. Andersson (San Francisco: ASP), ASP Conf. Ser., 348, 156 [Google Scholar]
- Backman, D. E., Simon, T., & Hinkle, K. H. 1985, PASP, 97, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Barsony, M., Mould, J. R., & Lutz, B. L. 1986, PASP, 98, 637 [NASA ADS] [CrossRef] [Google Scholar]
- Bennett, P. D., Ake, T. B., & Harper, G. M. 2005, BAAS, 37, 495 [NASA ADS] [Google Scholar]
- Carroll, S. M., Guinan, E. F., McCook, G. P., & Donahue, R. A. 1991, ApJ, 367, 278 [NASA ADS] [CrossRef] [Google Scholar]
- Cha, G., Tan, H., Xu, J., & Li, Y. 1994, A&A, 284, 874 [NASA ADS] [Google Scholar]
- Chadima, P., Harmanec, P., Yang, S., et al. 2010, Inform. Bull. Variable Stars, 5937, 1 [Google Scholar]
- Eggleton, P. P., & Pringle, J. E. 1985, ApJ, 288, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Ferluga, S. 1990, A&A, 238, 270 [NASA ADS] [Google Scholar]
- Ferluga, S., & Mangiacapra, D. 1991, A&A, 243, 230 [NASA ADS] [Google Scholar]
- Guinan, E. F., & DeWarf, L. E. 2002, in Exotic Stars as Challenges to Evolution, ed. C. A. Tout, & W. van Hamme (San Francisco: ASP), ASP Conf. Ser., 279, 121 [Google Scholar]
- Hadrava, P. 1995, A&AS, 114, 393 [NASA ADS] [Google Scholar]
- Hadrava, P. 1997, A&AS, 122, 581 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hadrava, P. 2004, Publ. Astron. Inst. Acad. Sci. Czech Rep., 92, 15 [Google Scholar]
- Harmanec, P., & Horn, J. 1998, J. Astron. Data, 4, 5 [Google Scholar]
- Harmanec, P., Horn, J., & Juza, K. 1994, A&AS, 104, 121 [NASA ADS] [Google Scholar]
- Harmanec, P., Aerts, C., Prša, A., Verhoelst, T., & Kolenberg, K. 2010, A&A, 520, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hinkle, K. H., & Simon, T. 1987, ApJ, 315, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Hoard, D. W., Howell, S. B., & Stencel, R. E. 2010, ApJ, 714, 549 [Google Scholar]
- Horn, J., Kubát, J., Harmanec, P., et al. 1996, A&A, 309, 521 [NASA ADS] [Google Scholar]
- Huang, S. 1965, ApJ, 141, 976 [NASA ADS] [CrossRef] [Google Scholar]
- Kloppenborg, B., Stencel, R., Monnier, J. D., et al. 2010, Nature, 464, 870 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kuiper, G. P., Struve, O., & Strömgren, B. 1937, ApJ, 86, 570 [NASA ADS] [CrossRef] [Google Scholar]
- Lambert, D. L., & Sawyer, S. R. 1986, PASP, 98, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Leadbeater, R., & Stencel, R. 2010 [arXiv: 1003.3617] [Google Scholar]
- Lenz, P., & Breger, M. 2005, Commun. Asteroseismol., 146, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Lissauer, J. J., & Backman, D. E. 1984, ApJ, 286, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Ludendorff, H. 1903, Astron. Nachr., 164, 81 [Google Scholar]
- Perryman, M. A. C., & ESA 1997, The HIPPARCOS and TYCHO catalogues, ESA SP Ser., 1200 (Noordwijk, Netherlands: ESA Publications Division) [Google Scholar]
- Sadakane, K., Kambe, E., Sato, B., Honda, S., & Hashimoto, O. 2010, Publ. Astron. Soc. Japan, 62, 1381 [Google Scholar]
- Saito, M., Kawabata, S., Saijo, K., & Sato, H. 1987, PASJ, 39, 135 [NASA ADS] [Google Scholar]
- Schanne, L. 2007, Inform. Bull. Variable Stars, 5747, 1 [NASA ADS] [Google Scholar]
- Škoda, P. 1996, in Astronomical Data Analysis Software and Systems V, ed. G. H. Jacoby, & J. Barnes (San Francisco: ASP), ASP Conf. Ser., 101, 187 [Google Scholar]
- Stefanik, R. P., Torres, G., Lovegrove, J., et al. 2010, AJ, 139, 1254 [NASA ADS] [CrossRef] [Google Scholar]
- Stellingwerf, R. F. 1978, ApJ, 224, 953 [NASA ADS] [CrossRef] [Google Scholar]
- Stencel, R. E. 2010, Soc. Astron. Sci. Ann. Symp., 29, 7 [NASA ADS] [Google Scholar]
- Struve, O. 1956, PASP, 68, 27 [NASA ADS] [CrossRef] [Google Scholar]
- van Leeuwen, F. 2007a, in Astrophys. Space Sci. Lib., ed. F. van Leeuwen (Berlin: Springer), 350 [Google Scholar]
- van Leeuwen, F. 2007b, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wright, K. O. 1970, Vist. Astron., 12, 147 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Sample spectrum of ϵ Aurfrom OND, showing the strong, unblended lines of Si ii and Fe ii for which the radial velocity, central intensity, and equivalent width were measured. |
| In the text | |
 |
Fig. 2 Evolution of the Hα profile from 1994 to present. The x-axis shows heliocentric velocities (in km s-1) and the y-axis shows observation dates (HJD-2 400 000). The intensity scale is shown below. The spectra were linearly interpolated onto a regular time grid to produce this image. The black dashes along the right axis show the actual observation dates. |
| In the text | |
 |
Fig. 3 Evolution of the Hα profile during the 2009–2011 eclipse. The x-axis shows heliocentric velocities (in km s-1) and the y-axis shows observation dates (HJD-2 400 000). The intensity scale is shown below. The spectra were linearly interpolated onto a regular time grid to produce this image. The black dashes along the right axis show the actual observation dates. |
| In the text | |
 |
Fig. 4 Comparison of the mean, out-of-eclipse spectrum of ϵ Aurwith some ATLAS synthetic spectra. The best-fitting synthetic spectrum has the parameters: Teff = 8000 K, log g = 1.0 [cgs] log Z/X = –0.3, v(rot) = 5.0 km s-1. Two other synthetic spectra are shown, one with higher gravity and one with lower metallicity. |
| In the text | |
 |
Fig. 5 Orbital solutions derived only from the Si ii lines and from the emission wings of Hα are compared to the full Chadima et al. (2010) solution. |
| In the text | |
 |
Fig. 6 Comparison of two symmetric Hα profiles from different orbital phases. The orbital phases and the radial velocities of the primary at those phases are labeled. |
| In the text | |
 |
Fig. 7 Variation of the Hα core central intensity in the DAO and OND spectra. |
| In the text | |
 |
Fig. 8 Evolution of the observed Hα profile near mideclipse. |
| In the text | |
 |
Fig. 9 Evolution of the corrected Hα profile, with the mean out-of-eclipse profile subtracted, near mideclipse. |
| In the text | |
 |
Fig. 10 Time evolution of the original Hβ profile during the 2009–2011 eclipse. |
| In the text | |
 |
Fig. 11 Changes of RV (top), CI (middle), and EW (bottom) of the two absorption cores of Hα during eclipse, after subtraction of the mean, out-of-eclipse Hα profile. The first vertical line denotes the beginning of the current photometric eclipse, the second one indicates the date of mideclipse. |
| In the text | |
 |
Fig. 12 Critical Roche lobes for the high and low-mass models are shown to scale, with the lines of sight to Earth shown for the beginning of spectroscopic and photometric eclipse. |
| In the text | |
 |
Fig. 13 Dramatic Hα profile variation: the sudden appearance of a deep, blueshifted absorption core, as observed at the DAO during 2005–2006. |
| In the text | |
 |
Fig. 14 RVs of the Fe ii lines (upper panel), the CIs of the 6416.919 Å Fe ii line (middle panel) and the B photometric filter (lower panel) fitted with two sinusoids. In each case the dominant period is 66.21 days, while the secondary period differs among the three cases. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


