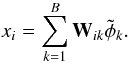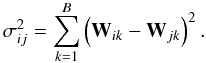| Issue |
A&A
Volume 530, June 2011
|
|
|---|---|---|
| Article Number | A121 | |
| Number of page(s) | 17 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201016222 | |
| Published online | 24 May 2011 | |
Optimized fringe sensors for the VLTI next generation instruments
1
UJF-Grenoble 1/CNRS-INSU, Institut de Planétologie et d’Astrophysique de Grenoble (IPAG), UMR 5274, Grenoble, France
e-mail: nicolas.blind@obs.ujf-grenoble.fr
2
Institut d’Astrophysique et de Géophysique de Liège (IAGL), University of Liège, 4000 Sart Tilman, Belgium
3
European Southern Observatory, Casilla 19001, Santiago 19, Chile
Received: 29 November 2010
Accepted: 30 March 2011
Context. With the arrival of the next generation of ground-based imaging interferometers combining from four to possibly six telescopes simultaneously, there is also a strong need for a new generation of fringe trackers able to cophase these arrays. These instruments have to be very sensitive and to provide robust operations in quickly varying observational conditions.
Aims. We aim at defining the optimal characteristics of fringe sensor concepts operating with four or six telescopes. The current detector limitations lead us to consider solutions based on co-axial pairwise combination schemes.
Methods. We independently study several aspects of the fringe sensing process: 1) how to measure the phase and the group delay, and 2) how to combine the telescopes to ensure a precise and robust fringe tracking in real conditions. Thanks to analytical developments and numerical simulations, we define the optimal fringe-sensor concepts and compute the expected performance of the four-telescope one with our dedicated end-to-end simulation tool sim2GFT.
Results. We first show that measuring the phase and the group delay by obtaining the data in several steps (i.e. by temporally modulating the optical path difference) is extremely sensitive to atmospheric turbulence and therefore conclude that it is better to obtain the fringe position with a set of data obtained simultaneously. Subsequently, we show that among all co-axial pairwise schemes, moderately redundant concepts increase the sensitivity as well as the robustness in various atmospheric or observing conditions. Merging all these results, end-to-end simulations show that our four-telescope fringe sensor concept is able to track fringes at least 90% of the time up to limiting magnitudes of 7.5 and 9.5 for the 1.8- and 8.2-meter VLTI telescopes respectively.
Key words: techniques: high angular resolution / techniques: interferometric / instrumentation: high angular resolution / instrumentation: interferometers / methods: analytical / methods: numerical
© ESO, 2011
1. Introduction
The sensitivity of ground-based interferometers is highly limited by the atmospheric turbulence and in particular by the random optical path difference (OPD) between the telescopes, the so-called piston. By making the fringes randomly move on the detector, the piston blurs the interferometric signal and prevents integration times longer than the coherence time of the atmosphere τ0 (typically a few 10 ms in the near infrared). To reach their ultimate performance and increase their number of potential targets, interferometers need fringe trackers, i.e., instruments dedicated to measuring and compensating in real-time the random piston. By keeping the fringes locked with a precision better than λ/10, they ensure a fringe visibility loss lower than 20% with integration times of a few seconds. Up to now, fringe trackers had to cophase arrays up to three telescopes by combining two baselines (e.g., the FINITO fringe tracker at VLTI, Gai et al. 2003; Le Bouquin et al. 2009). The new generation of interferometric instruments, such as MIRC at CHARA (Monnier et al. 2004), MROI (Jurgenson et al. 2008) or GRAVITY (Gillessen et al. 2010), MATISSE (Lopez et al. 2008) and VSI (Malbet et al. 2008) at the VLTI, requires to cophase arrays of four and possibly six telescopes, raising new fringe tracking challenges. This paper aims at defining the optimal concept of a fringe sensor for these arrays.
This study is focused on solutions based on co-axial pairwise combination of the light beams, as currently used in existing and planned fringe-trackers such as FINITO, CHAMP, and GRAVITY. The reason is that fringe sensing is generally carried out in the detector-noise limited regime and that multi-axial combinations require a larger number of pixels than pairwise co-axial combination. Additionally, we consider only the concepts providing measurements of both the phase delay (phase of the interferometric fringes) and the group delay (position of the white-light fringe). Indeed, the group delay resolves the 2π ambiguity on the phase and is mandatory to ensure an efficient and robust fringe tracking.
To define the optimal four- and six-telescope fringe sensor concepts based on the co-axial pairwise combination, we study three independent points. In Sect. 2 we study the phase estimator. We compare two different implementations of the ABCD fringe coding depending on whether the ABCD samples are obtained simultaneously or sequentially. In Sect. 3 we study the two possible ways to measure the group delay, either by temporally modulating the OPD or by spectrally dispersing the fringes. In Sect. 4 we compare the efficiency of beam combination schemes with various degrees of redundancy (that is, forming all possible baselines of the array or not). We show that the result is a tradeoff between precision and operational robustness. Finally in Sect. 5 we merge the results of the three previous sections to define the optimal concept in the four-telescope case. We perform a detailed estimate of its performance in the VLTI environnement.
 |
Fig. 1 ABCD estimator. Left: conceptual representation of the four phase states sampling the fringes. Right: the measured phase states functions of the time for static (top) and temporally modulated (bottom) ABCD. The total integration time is t0. |
2. Phase estimation
Measuring the phase is essential for a fringe tracker to stabilize the fringes and to cophase the array within a fraction of wavelength. In this section, we therefore consider that we are in a cophasing/phase tracking regime in which the group delay is known. We compare the precision of two different implementations of a phase estimator depending on whether the required measurements are simultaneous or not. The simplest and most efficient way to measure the fringe phase is the so-called ABCD estimator (Shao et al. 1988). It consists in sampling four points in quadrature in the same fringe (see Fig. 1, left), so that the real and imaginary parts of the coherent signal are extracted 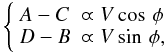 (1)where V and φ are the fringe visibility and phase respectively, the cotangent of the latter being then estimated by
(1)where V and φ are the fringe visibility and phase respectively, the cotangent of the latter being then estimated by 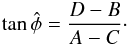 (2)Considering a total integration time t0 to obtain a phase estimation, there are two possible ways to perform the ABCD measurements (Fig. 1, right):
(2)Considering a total integration time t0 to obtain a phase estimation, there are two possible ways to perform the ABCD measurements (Fig. 1, right):
-
Temporal ABCD: it consists in temporally modulating the OPDas for FINITO at VLTI (Gaiet al. 2004), CHAMP at CHARA(Berger et al. 2006), or the KeckInterferometer fringe tracker (Colavitaet al. 2010). We will consider in thefollowing an implementation using a sampling of both outputs ofa beam-splitter (in phase opposition) simultaneously. Thisallows the recording of two phase states Aand C (in phase opposition) fromt = 0 to t0/2, and the B and D phase states by adding a temporal π/2 phase and recording between t = t0/2 and t0. This way one can generate an ABCD fringe coding (see Fig. 1, right and bottom). There is consequently a t0/2 time delay between the (A, C) and (B, D) samples. Other possible implementations (for instance at the Keck Interferometer fringe tracker) consider a continuous modulation over one fringe and only use one of the two interferometric outputs to measure the phase. Providing an exhaustive comparison between possible temporal algorithms is out of the scope of this paper but it might lead to select a different implementation.
-
Static ABCD: with this method we simultaneously measure the four phase states from t = 0 to t0. This method is implemented in the PRIMA FSU at the VLTI (Sahlmann et al. 2009) and is expected to be used on future instruments such as GRAVITY. In this case, there is no time delay between the ABCD samples.
In both cases the same signal-to-noise ratio (SNR) is achieved since the same number of photons is collected. The static ABCD requires twice as many measurements simultaneously, so that the output flux is divided by 2, but each pixel integrates the signal twice as long. However, the temporal and static ABCDs are not fully equivalent in real conditions because of atmospheric and/or instrumental disturbances. We now compare them by taking these effects into account.
2.1. Phase measurement errors
When considering piston or photometric disturbances, the phase quadratic error 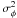 decomposes into the sum of two terms
decomposes into the sum of two terms 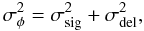 (3)the first one is the noise caused by the interferometric signal detection σsig, which includes detector and photon noises (Shao et al. 1988). The second one, the so-called delay noise σdel, is caused by external disturbances (piston or photometric variations) that combine with a delay between the ABCD measurements. By definition, the temporal ABCD is affected by this noise, but not the static ABCD, since the four measurements are simultaneous. Because this noise is an additionnal term, independent of the source brightness, we can already anticipate that it limits the phase measurements precision at high flux.
(3)the first one is the noise caused by the interferometric signal detection σsig, which includes detector and photon noises (Shao et al. 1988). The second one, the so-called delay noise σdel, is caused by external disturbances (piston or photometric variations) that combine with a delay between the ABCD measurements. By definition, the temporal ABCD is affected by this noise, but not the static ABCD, since the four measurements are simultaneous. Because this noise is an additionnal term, independent of the source brightness, we can already anticipate that it limits the phase measurements precision at high flux.
2.1.1. Detection noise
While integrating the signal, the fringes move slightly because of the atmospheric piston. Their contrast is attenuated by a factor exp(σ2(φp,t1)/2), where φp is the piston phase and σ2(φp,t1) its variance for an integration time t1. The integration time per phase state is twice as large in the static case compared with the temporal case (see Fig. 1, right), implying a more significant contrast loss. Combining this effect with the expression of the detection noise for an ABCD estimator derived from Shao et al. (1988), we obtain 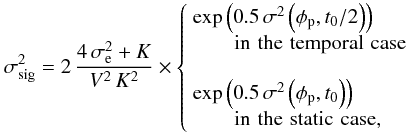 (4)where σe is the read-out noise in electrons per pixel, V is the fringe contrast and K is the number of photo-events for a total integration time t0. The left term corresponds to the sum of the detector and photon noises respectively.
(4)where σe is the read-out noise in electrons per pixel, V is the fringe contrast and K is the number of photo-events for a total integration time t0. The left term corresponds to the sum of the detector and photon noises respectively.
2.1.2. Delay noise
Delay noise is the consequence of piston and photometric variations between the (A, C) and (B, D) measurements, and therefore only affects the temporal method. These disturbances can be induced by the atmosphere (piston and scintillation) or by the instruments (vibrations). Because atmospheric piston and scintillation are independent (Fried 1966), we can separate the delay noise into two terms that are owing to to the piston and the scintillation respectively 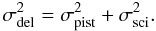 (5)To compute these noises we assume that the disturbances are constant while integrating the (A, C) signal, and that they suddenly change while integrating (B, D).
(5)To compute these noises we assume that the disturbances are constant while integrating the (A, C) signal, and that they suddenly change while integrating (B, D).
Piston noise
– Because of the piston variation between the (A, C) and (B, D) measurements, the phase difference between them is not π/2, as it should be. Taking the point in the middle of the interval t0 as the reference, the measured signal is therefore ![\begin{equation} \left\{ \begin{array}{ll} A-C &\varpropto V\,\cos\left(\phi + \phi_{\rm p}\left(t - t_0/4\right)\right) \\[1.5mm] D-B &\varpropto V\,\sin\left(\phi + \phi_{\rm p}\left(t + t_0/4\right)\right), \end{array} \right. \end{equation}](/articles/aa/full_html/2011/06/aa16222-10/aa16222-10-eq26.png) (6)the comparison with the ideal signal in Eq. (1) shows that the estimated phase
(6)the comparison with the ideal signal in Eq. (1) shows that the estimated phase 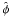 is biased if φp has varied between measurements. When we take into account the piston statistics, this bias results in the following piston noise of variance
is biased if φp has varied between measurements. When we take into account the piston statistics, this bias results in the following piston noise of variance 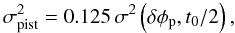 (7)where σ2(δφp,t0/2) is the variance of the difference of piston separated by t0/2. Details of the computation can be found in Appendix A.
(7)where σ2(δφp,t0/2) is the variance of the difference of piston separated by t0/2. Details of the computation can be found in Appendix A.
Scintillation noise
– The fringe visibility depends on the flux imbalance between the two beams I1 and I2 of the interferometer. These unequal fluxes reduce the fringe visibility by a factor 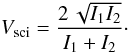 (8)Because of scintillation, I1 and I2, and therefore Vsci, change between the (A, C) and (B, D) measurements. Still considering the middle of the interval t0 as the reference, the measured signal is
(8)Because of scintillation, I1 and I2, and therefore Vsci, change between the (A, C) and (B, D) measurements. Still considering the middle of the interval t0 as the reference, the measured signal is 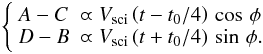 (9)By comparing this equation to the ideal signal (Eq. (1)), we see that a single phase estimation is biased if Vsci varies, that is if I1 and/or I2 vary. Assuming the beams I1 and I2 to be independent and of same statistics, the scintillation noise is
(9)By comparing this equation to the ideal signal (Eq. (1)), we see that a single phase estimation is biased if Vsci varies, that is if I1 and/or I2 vary. Assuming the beams I1 and I2 to be independent and of same statistics, the scintillation noise is 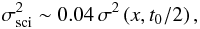 (10)where x = (I1(t + t0/4) − I1(t − t0/4))/I1(t) is the relative flux variation between the (A, C) and (B, D) exposures, ⟨ x ⟩ its mean and σ2(x,t0/2) its variance during a time t0/2. Note that to compute this noise, we consider the extreme case of a mean unbalance between the interferometric inputs equal to 10. Details of the calculations can be found in Appendix A.
(10)where x = (I1(t + t0/4) − I1(t − t0/4))/I1(t) is the relative flux variation between the (A, C) and (B, D) exposures, ⟨ x ⟩ its mean and σ2(x,t0/2) its variance during a time t0/2. Note that to compute this noise, we consider the extreme case of a mean unbalance between the interferometric inputs equal to 10. Details of the calculations can be found in Appendix A.
Typical seeing and atmospheric coherence time τ0 for the different observing conditions considered.
2.2. Performance comparison
To put quantitative numbers to the previous results, we used data provided by ESO collected at the Paranal Observatory in 2008. The FITS files contain the photometric flux and the fringe phase as measured by the FINITO fringe-tracker in the H-band. Data were collected at a frequency of 1 kHz for ATs and 2 kHz for UTs, and for various atmospheric conditions (see Table 1). We computed the variance of the difference of piston and photometries separated by t0/2, for different values of t0. We finally inserted the results in Eqs. (7) and (10) to evaluate piston and scintillation noises in atmospheric conditions ranging from Excellent to Bad (see Table 2). We note that whatever the conditions and the integration time, σpist is always at least twice as large as σsci: when measuring the phase, the piston is therefore far more harmful than the relative variations of flux – this is all the more true when we consider an extremely unfavorable case for scintillation noise, as explained in the previous section.
 |
Fig. 2 Relative errors σφ/λ of temporal (dash) and static (solid) ABCD phase estimators in the H-band as a function of the number of detected photo-events K. Black, blue, magenta, and red curves represent Excellent, Good, Medium and Bad conditions respectively as defined in Table 1. The plots are made for the ATs for an integration time of 2 ms for the specific ABCD implementation considered here. Note that for the static ABCD, the black, blue, and magenta curves are superimposed because of close performances. |
We now compute the phase error σφ in realistic conditions for the temporal and static ABCD methods. Figure 2 represents the phase error relative to the wavelength (i.e. σφ/λ) in the H-band with both methods. It clearly shows that the static ABCD outperforms the temporal one in almost all regimes. It is only in the photon-poor regime and in bad conditions that modulating the fringes is a little more efficient, that is, when the fringe contrast attenuation on the static ABCD becomes important. Yet, regarding the large phase error (σφ > λ/10, see Table 2), phase tracking would be very poor – if possible at all – in such conditions.
 |
Fig. 3 Top: example of polychromatic fringes (solid line) with longitudinal dispersion, modulated by the coherence envelope (dashed lines). Bottom: corresponding phase and group delay measurements (in blue and red respectively) presented in microns. |
In the photon-rich regime, the plateau for the temporal method is caused by the delay noise. For the 1.8-m Auxiliary Telescopes (ATs) at the VLTI, it has an almost null impact on phase tracking in good conditions (σφ < λ/35) even for integration times as long as 8 ms. In bad conditions with integration times longer than 2 ms there could be some limitations (σφ > λ/20) depending on the actual implementation of the temporal ABCD.
Observations with the 8-m Unit Telescopes (UTs) show a higher piston noise, partly owing to instrumental vibrations (Di Lieto et al. 2008): in good conditions, the noise level is similar to that of ATs in bad conditions. Passing from good to bad conditions, the integration time has to be divided by 2 to maintain the performance in a photon-rich regime. In particular, in bad conditions and t0 > 4 ms, the noise level is higher than λ/10 whatever the source, and phase tracking can be almost impossible with a temporally modulated ABCD. This probably explains the difficulty of the FINITO fringe-tracker to close the loop on the UTs for faint objects.
In conclusion, with a temporal phase estimator, the fringe tracking capabilities are compromised in bad atmospheric conditions and on faint sources that require long integration times. Therefore, from a performance point of view, a static method should be preferred because of its lower sensitivity to disturbances.
3. Group delay estimation methods
The group delay (GD) is a measurement complementary to the phase and is mandatory to ensure an efficient fringe tracking. Indeed, a phase estimator only determines the fringe position modulo 2π. The GD lifts this ambiguity (see Fig. 3). It allows one to find and recover the position of maximum contrast, which provides the highest SNR. This is of particular interest when the fringe-tracking is unstable and/or when unseen fringe jumps occur regularly. Moreover, monitoring both the GD and the phase allows one to determine the amount of dispersion induced by atmospheric water vapor (Meisner & Le Poole 2003). This is done routinely at the Keck Interferometer for cophasing in the N-band while measuring the phase and group delay in the K-band (Colavita 2010).
I(λ) and V(λ) being the flux and the complex visibility of the interferometric signal, the coherence envelope is linked to the complex coherent flux I(λ)V(λ) through a Fourier transform 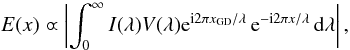 (11)where x is the OPD. Consequently, it is possible to estimate the group delay with two different methods:
(11)where x is the OPD. Consequently, it is possible to estimate the group delay with two different methods:
-
the temporal method estimates the GD by measuring theenvelope amplitude (in other words, the fringecontrast) E(x) at several points around its maximum by modulating the OPD. BEcause the phase needs to be measured at the same time to ensure fringe tracking, the OPD is modulated near the envelope center to keep a high SNR. This method is currently used in FINITO and CHAMP;
-
the spectral method uses the Fourier relation between the coherent spectrum I(λ)V(λ) and the coherence envelope E(x). The coherence envelope is recovered by measuring the coherent spectrum over few spectral channels. This method has been successfully implemented at PTI (Colavita et al. 1999), and more recently in PRIMA (Sahlmann et al. 2009) and in the KI fringe tracker (Colavita et al. 2010).
We could not obtain a realistic analytical description of these group delay estimators. Therefore we decided to compare them with Monte-Carlo simulations, taking into account atmospheric disturbances.
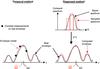 |
Fig. 4 Conceptual representation of the signal processing for group delay estimation. Temporal method (left): an envelope model is fitted on the three envelope amplitude measurements to determine the group delay. Dispersed method (right): from the spectral sampling of the complex coherent signal, an approximated envelope is computed with a Fourier transform operation. The envelope position is determined by fitting an envelope model. |
3.1. Description of the simulations
We aim to compare both methods fairly, so that
-
we use the same fringe coding, i.e. a static ABCDbecause of its lower sensitivity to disturbances (see the previoussection);
-
the signal is integrated during the same amount of time so that each method collects the same amount of photons and is prone to the same disturbances;
-
in both cases, the group delay is estimated in the same way by fitting an envelope model to the processed data. This allows a comparison of the intrinsic quality of the data for both methods. There are obviously many other ways to estimate xGD from a set of data, but we assume that this is a second order problem. Indeed, Pedretti et al. (2004) compared three different algorithms to estimate the group delay with a temporal method and noted only little differences in the performance, even with an algorithm as sophisticated as the one proposed by Wilson et al. (2004).
These choices made, temporal and dispersed methods can also be optimized to improve their performances. Below we describe the characteristics of each method.
3.1.1. Temporally modulated interferogram
Simulations have shown that the temporal estimator is strongly affected by atmospheric and instrumental disturbances. Their effect is all the more minimized than the envelope is more quickly scanned. Our study shows that the optimal way to proceed is to successively measure the fringe contrast in three different points over a five-fringe range (OPD equal to − 2.5λ, 0 and 2.5λ near the envelope maximum). This result agrees with the CHAMP choice (Berger et al. 2006). Once the three contrasts are measured, they are fitted with an envelope model to determine the group delay. A schematic overview of this method is displayed in Fig. 4, left.
The input fluxes have to be monitored to compensate in real time for the photometric/contrast variations that occur between the three measurements. For the sake of simplicity, we consider these photometric estimations to be noise-free. The simulated performance for the temporal method will thus be optimistic.
3.1.2. Spectrally dispersed interferogram
Thanks to the ABCD measurements, we can compute the chromatic complex visibility I(λ)V(λ) on each spectral channel. An approximated coherence envelope is then computed by taking their discrete Fourier transform (Colavita et al. 1999). It is possible to disperse the fringes over three channels to optimize the sensitivity, but we decided to use five channels to enhance the spectral sampling and thus the robustness of the estimator (see Sect. 3.2). For each exposure, a set of dispersed ABCD data is obtained, which enables a new GD estimation.
For a fair comparison between the temporal and the spectral method, they are both fed with the same disturbances and number of photons: therefore we make three GD estimations with the dispersed estimator, introducing disturbances between each estimation, and finally average them.
 |
Fig. 5 Response of the dispersed and temporal group delay estimators (solid and dashed lines respectively) to an OPD ramp xGD in the H-band. The ideal response is represented by the large gray line. In all cases, the coherence envelope has a sinc shape. Top: the envelope model is a sinc function. Bottom: the envelope model is a parabola. Figures on the right are a zoom on the central part of the left-hand side figures. The DR limits are represented with blue arrows on the top-left plot in the ideal case for both estimators. |
3.2. Linearity and dynamic range
A reliable estimation of the group delay is of prime importance since it ensures the measurements to be made in the highest SNR area. We study two quantities in this section, the linearity and the dynamic range, by looking at the response  of both methods to a given OPD ramp xGD. We define the linearity η as the local slope of
of both methods to a given OPD ramp xGD. We define the linearity η as the local slope of 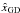 versus xGD
versus xGD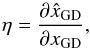 (12)a perfectly linear estimator is one where η = 1. Otherwise the estimator is biased and the envelope is not perfectly stabilized.
(12)a perfectly linear estimator is one where η = 1. Otherwise the estimator is biased and the envelope is not perfectly stabilized.
The group delay is extremely important for the fringe tracking robustness, that is the ability of the estimator to keep the fringes locked in the highest SNR area, in particular after a strong piston stroke (≥ 15 μm). In practice, there are limits outside which the group delay estimation is highly biased and makes the fringe tracker diverge from its operating point. The interval between these limits corresponds to the so-called dynamic range (DR), which is used here to characterize the robustness of the estimators. In practice, the limits of the DR are reached when the slope of 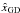 versus xGD changes sign (in other words, when η becomes negative) or when we observe a strong wrapping effect.
versus xGD changes sign (in other words, when η becomes negative) or when we observe a strong wrapping effect.
In the following paragraphs, we simulate noise-free ideal interferograms in the H-band with a sinc-shaped coherence envelope. We fit the results with two different envelope models (a parabola and a sinc function) to study its impact on the GD estimation. The results of this study are presented in Fig. 5.
3.2.1. Temporally modulated interferogram
In the temporal method, the envelope model is critical to ensure a good linearity. Using the most appropriate sinc model with ideal interferograms (Fig. 5, top, dashed line), the linearity is excellent (η = 1), but the DR is limited to 10 fringes (± 8 μm), i.e., to the width of the central lobe. Outside this range the GD estimation is totally non-linear but never crosses the y-axis: the fringe-tracking loop should not diverge but it should recover the envelope center with difficulty, or even could risk to lock the fringes far away from the envelope center.
Using a wrong envelope model (e.g., a parabola; see Fig. 5, bottom, dashed line) leads to a relative bias higher than 10% (η ~ 0.9) whatever the OPD within the dynamic range. Increasing the number of samples or the scan length does not improve the results, which emphasizes that the problem arises from the wrong envelope model. Because of the number of chromatic variables (particularly the longitudinal dispersion), which continually vary during a night and slightly modify the envelope shape, the envelope model cannot be perfect and the temporal estimator will therefore be consistently nonlinear by a few percents. Interestingly, the DR is still equal to the width of the main lobe1 and seems weakly affected by the model quality.
3.2.2. Spectrally dispersed interferogram
On the contrary, the dispersed method is not affected by the envelope model (see Fig. 5, solid lines): because we sample the complex coherent spectrum, we can directly compute a realistic coherence envelope and the fitting model has therefore a weak influence. Dispersing fringes on five spectral channels in the H-band, the linearity is excellent (η ~ 1) over an OPD range of ± 20 μm. Beyond these points a sharp wrapping effect is observed (Fig. 5, left), which marks the DR limits: the discrete sampling of the spectrum induces aliasing effects on the computed envelope (obtained from a discrete Fourier transform of the complex coherent signal, see Eq. (11)), so that outside the DR the GD is estimated on a replica of the true envelope. In practice, if the GD is measured after such a wrap, the fringe tracker will correct the OPD in the wrong direction and finally lock the fringes on a point even more distant from the envelope center than previously. However, because we chose to use five spectral channels, the DR (± 20 μm) is larger than the strongest piston fluctuations which are typically observed on a few milliseconds (~15 μm). Working in the K-band increases the dynamic range up to ± 40 μm, which almost cancels these problems. It is actually possible to infer an expression for the DR with dispersed fringes. Let us assume a spectral band with an effective wavelength λ0 and a width Δλ, and that the fringes are dispersed over Nλ channels. The dynamic range is then ideally (see Appendix B) 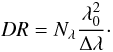 (13)The larger the number of spectral channels, the lower the aliasing and therefore the larger the DR. This relation excellently agrees with the simulation results.
(13)The larger the number of spectral channels, the lower the aliasing and therefore the larger the DR. This relation excellently agrees with the simulation results.
 |
Fig. 6 Relative errors σGD/λ of temporal (dash) and dispersed (solid) GD estimators in different atmospheric conditions. Black, blue, magenta, and red curves represent Excellent, Good, Medium, and Bad conditions respectively as defined in Table 1. The plots are made for the ATs, for a total integration time of 3 ms, constituted of three single exposures of 1 ms. |
When longitudinal dispersion is taken into account, the linearity and DR are slightly reduced because the undersampling of the coherent spectrum leads to a less precise envelope computation. Refining the spectral sampling with more channels improves both linearity and DR, as shown by the simulations.
In conclusion, spectrally dispersing the fringes appears to be the most robust method to measure the group delay. It provides an estimator with
-
a good linearity without the need of a good envelope model,because it inherently computes a realistic envelope;
-
a large DR allowing robust operations and quick recovery of the fringes over an OPD range larger than typical piston variations.
3.3. Group delay measurements precision
We now compare the precision of the GD estimators as a function of the incoming flux and of the disturbances strength. The simulations consist of computing noisy interferograms in the H-band, introducing detector and photon noises as well as piston and photometric disturbances, which are taken from actual FINITO data. For each simulation, we estimate a noisy GD 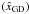 . Its statistics over several thousands of iterations gives the statistical error σGD for both estimators.
. Its statistics over several thousands of iterations gives the statistical error σGD for both estimators.
The results for ATs and an integration time of 1 ms are presented in Fig. 6. It shows the relative error σGD/λ on the group delay measurements as a function of the number of photo-events for various atmospheric conditions. The limitation of the temporal estimator is obvious, with a plateau caused by atmospheric disturbances (piston mainly), which acts like an independent, additional noise at high flux, increasing when atmospheric conditions get worse. The dispersed estimator on the other hand appears to be weakly sensitive to these disturbances. Although we used a favorable hypothesis for the temporal method (the required photometric monitoring is considered noise-free), there is no regime in which this concept is better than the dispersed one. For UTs, the results are similar but with stronger limitations: it appears that the statistical error of the temporal estimator never goes below λ/4 with an integration time as low as 1 ms, whatever the conditions.
Additionally, all the simulations show the same dependency of the statistical error of both GD estimators with respect to the incoming flux K and the visibility V2 Interestingly, we find the same kind of dependency than for the phase (Eq. (4)) in the equivalent regimes.
Interestingly, we find the same kind of dependency than for the phase (Eq. (4)) in the equivalent regimes.
In conclusion, temporally modulating the OPD to estimate the group delay is not as good as the spectrally dispersed fringe method, both in terms of robustness and precision. This is in line with the conclusion of Sect. 2, which showed the sensitivity of temporal fringe coding to external disturbances. We therefore strongly conclude that a static fringe coding scheme dispersed across a few spectral channels should be used to measure the fringe phase and group delay.
4. Optimal co-axial pairwise combination schemes
Theoretically, it is possible to cophase an array of N telescopes by measuring only N − 1 baselines. However because of the noisy measurements and of the varying observing conditions during a night, some baselines can deliver information of poor quality, so that it is beneficial to have some redundancy with additional baselines. It is then possible to retrieve the phase on a baseline in several different ways, ensuring a better fringe tracking stability. The drawback is that when the number of measured baselines increases, each one is less sensitive because the flux of the telescopes is divided between more baselines. The sensitivity of the fringe sensor then depends on a competition between the information redundancy and the sensitivity of the individual baselines. The aim of this section is to determine the most efficient schemes with respect to their intrinsic performance and operationnal advantages.
Several on-going projects will work with four (GRAVITY, MATISSE) to six (VSI, MIRC) telescopes. Therefore we focus on these two cases, assuming that all telescopes are identical. We consider the following schemes, which are illustrated in Fig. 7:
-
the open schemes are made up of the minimal number of baselines,that is N − 1, and are noted NTO. In this case the interferometric outputs are intrisically imbalanced in flux to have baselines with equivalent performance. For instance, in the 4TO case, we do not distribute 50% of the intensity of the telescope 2 onto baselines {12} and {23}, but ~40% and ~60% respectively (see Appendix C.2.2 for the details of this optimization);
-
in the redundant schemes, the flux of each telescope is equally divided between the same number R of baselines. When R = 2 the schemes are more precisely called circular. The nomenclature to designate them below is NTR, on occasion with an additionnal letter when there are several possibilities for the same value of R.
 |
Fig. 7 Various conceptual schemes studied for the 4T and 6T cases (top and bottom respectively) with the associated nomenclature. As explained in Sect. 4.1, we did not study schemes with intrinsically imbalanced photometric inputs other than the open ones, because of lower performance. |
4.1. Study of the combination schemes
We decided to compare the various schemes on the base of three considerations: their intrinsic performances, their ability to provide the individual beam photometries without dedicated outputs, and their robustness to unpredictable and rapidly varying observing conditions.
4.1.1. Performance study
The principle of our analysis is similar to the one that led to the GRAVITY fringe tracker by Houairi et al. (2008). It consists in computing the vector of the optimal optical path estimators x used to drive the delay lines from the noisy and possibly redundant phase information φ. These quantities are linked by the interaction matrix M, which is known 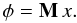 (16)With redundant schemes, the system is overdetermined so that we use a χ2 minimization procedure to compute the control matrix W and then x
(16)With redundant schemes, the system is overdetermined so that we use a χ2 minimization procedure to compute the control matrix W and then x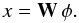 (17)Because φ is noisy, we have to take into account the error on the measurement when computing W to reduce the impact of the noisiest baselines and prevent the solution from diverging. The quantity of interest is finally the error σij on the corrected differential pistons calculated for each baseline { ij } with respect to a reference noise σ0, which corresponds to the error of a simple two-telescope interferometer. The expression of σ0 is derived from Shao et al. (1988) or, in a more general form, from Tatulli et al. (2010). It depends on the considered noise regime, so that the detector and photon noise regimes can be independently studied
(17)Because φ is noisy, we have to take into account the error on the measurement when computing W to reduce the impact of the noisiest baselines and prevent the solution from diverging. The quantity of interest is finally the error σij on the corrected differential pistons calculated for each baseline { ij } with respect to a reference noise σ0, which corresponds to the error of a simple two-telescope interferometer. The expression of σ0 is derived from Shao et al. (1988) or, in a more general form, from Tatulli et al. (2010). It depends on the considered noise regime, so that the detector and photon noise regimes can be independently studied ![\begin{eqnarray} &&\sigma_0^{\rm det} = \displaystyle\frac{A}{K \, V}\\[1.5mm] &&\sigma_0^{\rm phot} = \displaystyle\frac{B}{\sqrt{K} \, V}, \end{eqnarray}](/articles/aa/full_html/2011/06/aa16222-10/aa16222-10-eq99.png) where A and B are proportionality factors depending only on the fringe coding, so that this study is independent of the phase and the group delay estimators used. Results for the different schemes are therefore perfectly comparable within the same regime. Note that the above expressions also agree with our previous results concerning the group delay (Eqs. (14) and (15)).
where A and B are proportionality factors depending only on the fringe coding, so that this study is independent of the phase and the group delay estimators used. Results for the different schemes are therefore perfectly comparable within the same regime. Note that the above expressions also agree with our previous results concerning the group delay (Eqs. (14) and (15)).
To analyse the behaviour of the different schemes in realistic conditions, we consider the following three cases:
-
Ideal case: all baselines are strictly equivalent in terms of flux andvisibility.
-
Resolved-source case: one baseline of the array is highly resolving the source (cases e.g. of an asymmetric source or of a very long baseline). To study this case, we set the fringe visibility to 0.1 on one particular baseline, and to 1 on the others.
-
Low-flux case: the flux of one telescope is set to one tenth of the others to simulate a quick variations of flux (e.g. scintillation) or a technical problem.
The results for these three cases are presented in Tables 3 to 5, showing the relative error ϵij = σij/σ0 on the corrected piston for the various baselines { ij } .
Results of the performance study in the ideal case, where all baselines are equivalent and noted { ij } .
Results of the performance study when the baseline { 12 } resolves the source.
Results of the performance study in the flux drop-out case.
In the ideal case (Table 3), the redundancy slightly degrades the performance in the detector noise regime (because the signal is coded on a larger number of pixels) but does not impact the performance in the photon noise regime. The differences are at maximum of the order of 30% between the various schemes. Open and circular schemes provide a similar performance. However, in the open schemes, the flux is not divided equally between the various baselines to reach an optimal SNR (see Appendix C.2.2). Although the baselines at both ends of the array receive roughly 40% more photons than the others, they are affected by a photometric imbalance, leading to a fringe contrast loss of roughly 10% (i.e. an SNR loss around 20%): this points to a suboptimal use of the input photons. On the other hand, the schemes with more baselines benefit from some redundancy. This explains why open schemes are slightly less sensitive in the photon noise regime than redudant – and balanced – ones. A similar conclusion concerning open schemes was already reached by Houairi et al. (2008) in the 4T case.
If a baseline resolves the target (Table 4), the benefit of redundancy clearly appears. Indeed, whereas the measurement error on the resolving baseline strongly increases with open schemes, the performance degradations are well contained with the redundant ones. There is still a significant improvement between R = 2 and 3, but only limited differences between more redundant schemes.
When a telescope has a reduced flux (Table 5), the overall results do not significantly vary between the various schemes. Having a minimal redundancy (R = 2) appears optimal in the detector noise regime, because more baselines induce a larger overall read-out noise. In the photon noise regime, redundant schemes have very close performances and are slightly more efficient than the open ones. Hence, circular scheme should be favoured with respect to open ones and the use of more redundant schemes is not essential from the performance point of view.
Taking into account the relatively close performance between the redundant concepts and regarding their instrumental complexity (number of baselines to be coded, optical transmission, etc.), schemes with R = 2 or 3 should be favoured.
4.1.2. Extracting the photometry
The knowledge of the photometry is theoretically not mandatory to measure the fringe phase. However, a real-time photometric monitoring is very useful during operation: it provides an additional diagnosis in case for flux-related issues and it allows the image quality to be optimized in all beams simultaneously (otherwise the only way to optimize the flux of each telescope is to optimize them sequentially). Moreover, the knowledge of the photometries allow the fringe visibility to be computed in real-time, revealing possible technical issues (or even astrophysical “problems” such as unknown binaries).
Some of the schemes that we study allow the instantaneous photometry to be extracted on each pupil without the need of dedicated photometric outputs. We found that in the context of pairwise combinations, the photometry can be recovered from the fringe signal itself for every pupil that is part of a closed (sub-)array constituted of an odd number of pupils. Otherwise, the system linking the fringe signals to the photometries is degenerated. Thus, the 4T2, 6T2 and 6T3A schemes cannot extract the photometry since they only contain rings of four and/or six telescopes, whereas the 4T3 and 6T3B can, since there are triangular sub-arrays. This is summarized in Table 6. For arrays with an odd number of telescopes, circular schemes (R = 2) always allow the photometry to be directly estimated.
Ability of the combination schemes to provide the input photometries without dedicated outputs.
4.1.3. Robustness
When observing unknown asymmetrical sources, such as well resolved binary stars, unpredictable baselines can exhibit very low visibilities, changing with a time scale of less than one hour (see Fig. 8 for an example). The fringe position may then become impossible to measure on some baselines, leading to a possible discontinuity in the array cophasing. The case of a resolved source previously studied (see Table 4) is an example of such a situation: when one baseline highly resolves the source, the comparison between the open schemes and the redundant ones clearly shows the benefit of having additional baselines. If we now assume that two baselines fully resolve the source, the schemes with R ≥ 3 provide better performances than the open and circular schemes, and so on. In general, redundancy allows bootstrapping to be performed and therefore the tracking stability to be increased along an observation night, so that schemes with a high number of baselines are favoured.
 |
Fig. 8 Predicted fringe contrast when observing a binary star with equal fluxes and a separation of about 10 mas with the four UTs and a fringe sensor working in the H-band. The left panel shows the (u,v) tracks overlaid on the fringe contrast from the model. The right panel shows the fringe contrast versus time for 4 h for each baseline. The figures were made with the aspro public software from JMMC. |
4.2. Choice of the combination schemes
The various schemes studied here provide similar performances in an ideal situation. When considering more realistic conditions, the benefit of the redundancy clearly appears by improving the tracking robustness in various observing conditions. Additionally, among all the schemes, some provide the input fluxes in real time without the need of dedicated outputs, which is extremely useful for the state machine. We conclude that the best compromises between robustness and sensitivity are the 4T3 and 6T3B schemes. Because of their similar performance and their easier practical implementation, we also consider that the circular schemes 4T2 and 6T2 are suitable, if monitoring the photometric fluxes is not required. In the 4T case, these conclusions agree with the results of Houairi et al. (2008) for the dedicated fringe tracker of GRAVITY. The results in the 6T case are also in agreement with the choices made for CHAMP (Berger et al. 2006) at the CHARA array with a 6T2 configuration, even though we favour a scheme with more baselines for robustness purposes.
Although we study only two cases (four and six pupils), it appears to be the trend that in the context of pairwise combinations with an even number of telescopes, an optimal fringe sensor should measure either N or 3N/2 baselines (R = 2 or 3 respectively) depending on the need for photometries. With an odd number of telescopes, circular schemes should be optimal thanks to their capability to monitor the photometry directly.
5. Estimated performance of the chosen concepts
Now that the optimal fringe sensing concepts have been identified, we study their on-sky performance within the VLTI infrastructure. To this aim, we developed a dedicated software simulation tool called Sim2GFT (2GFT standing for the “2nd Generation Fringe Tracker” of the VLTI). This simulator, consisting of a set of IDL routines, aims at performing realistic simulations of future observations with the 2GFT fringe sensor and evaluating its performance in terms of residual piston jitter after closed-loop control. In the remainder of this section, we assume that single-mode fibers are used to filter the input wavefronts, following Tatulli et al. (2010).
5.1. The Sim2GFT simulator
Sim2GFT is largely based on the GENIEsim software (Absil et al. 2006), and therefore follows the same architecture and philosophy. The simulations are taking into account all major contributors to the final performance, from the atmosphere and the telescopes down to the fringe sensor and delay lines. The signal-to-noise ratio on the phase measurement in the fringe sensor is mainly driven by the amount of coherent and incoherent photons (including the atmospheric and instrumental thermal emission), and by the way they are distributed on the detector. To estimate the amount of coherent and incoherent photons properly, all VLTI and 2GFT subsystems are described by their influence on the intensity, piston, and wavefront quality of the light beams collected by each telescope. The estimated instrumental visibility within the fringe sensor takes into account the visibility loss due to piston jitter, atmospheric refraction, intensity mismatch between the beams due to atmospheric turbulence (scintillation), and longitudinal dispersion in the delay lines. For the piston jitter, a semi-empirical law based on on-sky FINITO data is used to include both the effect of atmospheric piston and vibration-induced piston. Another key element in the simulation is the coupling of the light beams into single-mode fibers, which we estimate by separating the contribution of tip-tilt (through the overlap integral between an offset Airy pattern and the fiber mode) and higher order aberrations (through the estimated Strehl ratio – without tip-tilt – that acts as a multiplicative factor).
The operation of 2GFT is closely related to the detector read-out scheme. Assuming a HAWAII-2RG focal plane array, we consider that the ABCD outputs of all baselines are spread on a single detector line, and that the spectral dispersion is performed on five contiguous detector lines. The detector is read line by line, with a read-out time that depends on the particular arrangement of the ABCD outputs on the lines (it amounts to 201 μs for our design). Deriving a reliable estimation of the phase and group delay requires the five spectral channels to be used3. However, it must be noted that the phase and group delay estimations can be updated each time a new detector line is read, although it will be partly redundant with the previous estimation – this corresponds to the sliding-window estimation already in use at the Keck fringe tracker (Colavita et al. 2010).
The closed-loop behaviour of the fringe tracker is simulated by feeding back the fringe sensor phase delay measurements to the VLTI delay lines, using a simple PID as a controller. Group delay measurements are not explicitly used in our simulations, although in practice they will be used to make sure that fringe tracking is performed on the appropriate (white-light) fringe. The closed-loop simulation relies on a frequency-domain description of the input disturbance (by its power spectral density) and of the subsystems (by their transfer function). The repetition frequency of the loop and the controller gain are optimized as a function of the input photon flux and atmospheric piston to produce the smallest possible piston residual at the output of the closed loop. To ensure a stable fringe tracking, we require the sensing noise to be lower than 100 nm rms for 90% of the measurements on any individual baseline, which would correspond to an SNR > 4 on the fringes in the K-band for 90% of the measurements.
In the following sections, we describe the estimated performance for fringe sensing and fringe tracking of the 4T3 redundant concept with ABCD encoding on five spectral channels over the K-band (from 1.9 to 2.4 μm). The estimations are based on an expected K-band transmission of 3% for the whole VLTI/2GFT instrument.
 |
Fig. 9 Fringe sensing noise plotted at percentile 0.9 (i.e., the noise is actually lower than the plotted curves for 90% of the occurrences) as a function of the target’s K magnitude (or of the stellar flux in photons per second at the entrance of 2GFT) in the 4T3-ABCD case, assuming a K0 III target and using the A0-G1-K0-I1 quadruplet of ATs at the VLTI. The fringe-tracking loop is operated at its maximum frequency as long as the fringe sensing noise per baseline remains < 100 nm rms for 90% of the measurements on any individual baseline. The closed-loop repetition frequency is reduced to maintain this level of performance otherwise (this happens for K > 5 in the present case, as also shown in Fig. 10), until this level cannot be reached any more (beyond K = 7.5 in the present case). Note that the increase in sensing noise for bright targets is caused by the resolved stellar photosphere, which reduces the available coherent flux. |
5.2. Fringe sensing performance
End-to-end simulations of VLTI/2GFT have been performed using the 1.8-m Auxiliary Telescopes (ATs) for a K0 III star located at various distances ranging from about 10 pc to 2 kpc, in standard atmospheric conditions: seeing ε = 0.85′′, coherence time τ0 = 3 ms, outer scale ℒout = 25 m, and sky temperature Tsky = 285 K. The target star is assumed to be located close to zenith. For each magnitude, the closed-loop repetition frequency was chosen to be as high as possible within hardware limitations (< 4 kHz), while keeping the average fringe sensing noise lower than 100 nm rms on all measured baselines.
Figure 9 illustrates the sensing noise per baseline as a function of stellar magnitude (black diamonds). The respective contributions of photon noise and detector noise are represented by dotted and dashed lines. On the bright-side end of the plot, photon noise dominates the noise budget. The increase in photon noise from K = 1.5 to K = −2 is because the star is (strongly) resolved, which reduces the available coherent flux. Detector noise becomes higher than photon noise around K = 3, and the fringe sensing noise reaches its allowed limit (<100 nm rms for 90% of the measurements) around K = 5. For fainter magnitudes, Sim2GFT ensures that the fringe sensing noise remains at the same level by reducing the closed-loop repetition frequency (i.e., increasing the integration time on the fringe sensing detector). This is possible only until magnitude K = 7.5 in the present case, where a phase sensing noise of 100 nm per baseline cannot be reached any more for any integration time, because of the strong fringe blurring that appears at long DITs. The points plotted in the figure at K > 7.5 do not comply with our requirements any more, and have been computed for the repetition frequency that minimizes the fringe sensing noise (~33 Hz in the considered cases).
Also represented in Fig. 9 is the fringe sensing noise per telescope, which results from the optimized estimation of individual telescope pistons from all measured baselines, as explained in Sect. 4.1. The fringe sensing noise per telescope is significantly lower than the measurement noise on each individual baseline because the estimation of the former is based on the information collected by multiple baselines.
 |
Fig. 10 Left: closed-loop repetition time and time delay in the loop as a function of target K magnitude. For stars fainter than K = 6, the loop repetition time is increased (i.e., its frequency decreased) to ensure a sufficient SNR on the detected fringes in each individual measurement (until the specified SNR cannot be reached any more whatever the integration time). Right: noise residuals at the output of the closed loop, for the three main contributors: fringe sensing (FSU), delay line (DL) and atmospheric noises. |
The same kind of performance study was carried out for the Unit Telescopes, showing a similar general behaviour as for ATs. The only differences are
-
the magnitude where stable closed-loop fringe tracking becomesimpossible, which is now around K = 9.5;
-
the decrease in the coupling efficiency for stars fainter than V = 10, which is owing to the reduced performance of the MACAO adaptive optics system.
The latter effect, which is almost nonexistent for ATs (equipped with STRAP for tip-tilt control), speeds up the drop of closed-loop performance at faint magnitudes. The maximum loop repetition frequency (~4 kHz) can actually be maintained until K ≃ 8.5 for UTs. The presence of telescope vibrations for UTs is taken into account in a semi-empirical way in our simulations through an estimation of the visibility loss caused by vibration-induced piston jitter, so that the SNR in the fringe sensing process is estimated in a realistic way. However, let us note that telescope vibrations are expected to strongly affect the residual piston jitter at the output of the closed loop (an effect not simulated in Sim2GFT), so that the results presented in right-hand side plot of Fig. 10 (for ATs) would be significantly degraded for UTs.
5.3. Fringe tracking performance
Figure 10 shows the characteristic times of the closed loop and the noise residuals at the output of the fringe tracking loop. The left-hand side plot shows that for magnitudes brighter than K = 5, the loop can be operated at its maximum repetition frequency (3.6 kHz in this case). For fainter targets, the repetition time is gradually increased to keep a sufficient SNR on each individual fringe measurement. The sudden increase in repetition time around K = 6 is caused by a modification in the loop behaviour: for bright stars, only one spectral channel is read for each repetition time and the information at other wavelengths is taken from previous repetition times, while for fainter stars all spectral channels are read during each repetition time (the main goal of this being to keep the time delay4 in the loop reasonably short even at low repetition frequencies). The time delay is longer than the repetition time in the bright target case, because only one spectral channel is read per repetition time, while the phase estimation uses the phase information from all five spectral channels.
The left-hand side plot of Fig. 10 can be used to derive a limiting magnitude for the chosen fringe sensing concept. One just needs to define a repetition time threshold above which fringe tracking becomes inefficient. Here, we assume a maximum allowed repetition time of 10 ms (i.e., minimum frequency of 100 Hz)5, which gives a limiting magnitude of K = 7.5 on the ATs. In the case of UTs, the limiting magnitude amounts to K = 9.5. In both cases, this coincidentally corresponds to the magnitude where maintaining a phase measurement error below 100 nm is not possible, which indicates that a DIT of 10 ms is actually a sound choice to define limiting magnitudes in closed-loop fringe tracking operation. Note that a limiting magnitude of K = 7.5 in closed-loop fringe tracking with 90% locking ratio under standard atmospheric conditions corresponds quite well to what has been demonstrated on-sky with the PRIMA fringe sensor unit on the ATs (Sahlmann et al. 2009).
The right-hand side of Fig. 10 shows the noise residuals at the output of the fringe-tracking loop, computed per telescope. Note that the fringe sensing noise residual at the output of the loop is much smaller than the actual fringe sensing noise (evaluated at the detection level), due to closed-loop filtering. Also note that the fringe sensing noise is always much lower than the atmospheric noise under typical atmospheric conditions, a behaviour directly related to the constraint imposed on the phase sensing noise per baseline in each repetition time (<100 nm rms for 90% of the measurements). For these reasons, the fringe sensing noise does not significantly affect the residual noise level at the output of the fringe tracking loop. The influence of the fringe sensor on the residual piston noise comes rather from its intrinsic sensitivity, which determines the maximum repetition frequency that can be reached for a given coherent flux.
We also performed simulations in various atmospheric conditions, ranging from bad (seeing ϵ0 = 1.1′′ and coherence time τ0 = 2 ms) to excellent (ϵ0 = 0.5′′ and τ0 = 10 ms). The influence of atmospheric conditions on the fringe tracking performance is mainly twofold: on one hand it determines the input atmospheric noise that needs to be corrected, and on the other hand it affects the amount of available coherent photons because it determines the injection efficiency into single-mode fibres. Our simulations have shown that the limiting magnitude increases by about 2 mag between bad and excellent conditions. For instance, if one defines the limiting magnitude at 100 Hz, it varies between K = 6.2 and K = 8.5 depending on the conditions. These limiting magnitudes do not mean, however, that fringes cannot be detected at fainter magnitudes. We estimate that the ultimate limit for fringe detection (fringes detected for 50% of the measurements at an SNR of 4, using a DIT of 25 ms) should be around K = 9.5 for ATs used in good atmospheric conditions.
6. Conclusions and perspectives
We determined the optimal four- and six-telescopes fringe tracker concepts. We showed that for realistic atmospheric conditions, the measurements of the various phase states (e.g., ABCD) that are needed to derive the fringe phase should better be done simultaneously to limit the influence of external disturbances (piston, scintillation, vibrations, etc.) on the measurement precision. Furthermore, spectrally dispersing the fringes allows the group delay to be evaluated with one set of contemporaneous data, which (like for the phase measurement) minimizes the influence of disturbances. We also showed that this method is more robust to longitudinal dispersion effects. Therefore, we concluded that the optimal way to measure the fringe position (phase and group delay) is to perform a static ABCD fringe coding, dispersed over about five spectral channels.
We also demonstrated that the co-axial pairwise combination schemes with a moderate redundancy provide the best compromise between sensitivity and robust operations. They are less sensitive to varying observing conditions, and some schemes also allow the photometries to be directly extracted from the fringe signal, which is useful for the state machine. We finally favored the 4T3 and 6T3B schemes for four- and six-telescope operations respectively.
Merging these results, we simulated the expected performance of the four-telescope concept. For an efficient fringe-tracking, with fringes locked at least 90% of the time, we expect limiting magnitudes of 7.5 and 9.5 at K band with ATs and UTs respectively. These performances are close to those of single baseline fringe trackers currently in operation. Another important result is that the fringe tracker ultimate performances are not limited by the fringe sensing measurement errors, but rather by the time delay between the measurement of the piston and its correction by the delay lines.
Finally, in the coming years, a new generation of infrared detectors should be available. By providing very high acquisition frequencies and an extremely low read-out noise at the limit of photon-counting, multi-axial schemes should be reconsidered as a possible solution for fringe-tracking, because they would not be limited by the large amount of pixels needed to encode the interferometric signal.
Simulations show that the DR can be increased with a higher number of contrast samples and a higher scan length. But in real operations it also increases the influence of atmospheric disturbances, which is not suitable for precision purposes (see Sect. 3.3).
The time delay of the loop is defined as the amount of time between the middle of the overall integration time used for a phase estimation (i.e., including the contribution of all spectral channels), and the moment when the detector read-out sequence is completed for the considered spectral channel.
For an integration time of 10 ms on the fringe sensor, the estimated loss of visibility caused by piston jitter in standard atmospheric conditions is only 5% for ATs, while it amounts to 28% for UTs (an effect mainly caused by vibrations). Operating at lower frequencies would become impractical in the case of UTs, but could be considered in the case of ATs (especially in good atmospheric conditions).
Acknowledgments
The authors are grateful to the referee, whose careful and thorough review of the text and theoretical formalism helped them improve the papers clarity and quality considerably.
References
- Absil, O., Di Folco, E., Mérand, A., et al. 2006, A&A, 452, 237 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berger, D. H., Monnier, J. D., Millan-Gabet, R., et al. 2006, in Proc. SPIE, 6268 [Google Scholar]
- Colavita, M. M. 2010, PASP, 122, 712 [NASA ADS] [CrossRef] [Google Scholar]
- Colavita, M. M., Wallace, J. K., Hines, B. E., et al. 1999, ApJ, 510, 505 [NASA ADS] [CrossRef] [Google Scholar]
- Colavita, M. M., Booth, A. J., Garcia-Gathright, J. I., et al. 2010, PASP, 122, 795 [NASA ADS] [CrossRef] [Google Scholar]
- Di Lieto, N., Haguenauer, P., Sahlmann, J., & Vasisht, G. 2008, in Proc. SPIE, 7013 [Google Scholar]
- Fried, D. L. 1966, J. Opt. Soc. Am. (1917–1983), 56, 1372 [CrossRef] [Google Scholar]
- Gai, M., Corcione, L., Lattanzi, M. G., et al. 2003, Mem. Soc. Astron. Ital., 74, 472 [Google Scholar]
- Gai, M., Menardi, S., Cesare, S., et al. 2004, in Proc. SPIE, ed. W. A. Traub, 5491, 528 [Google Scholar]
- Gillessen, S., Eisenhauer, F., Perrin, G., et al. 2010, in Proc. SPIE, 7734 [Google Scholar]
- Houairi, K., Cassaing, F., Perrin, G., et al. 2008, in Proc. SPIE, 7013 [Google Scholar]
- Jurgenson, C. A., Santoro, F. G., Baron, F., et al. 2008, in Proc. SPIE, 7013 [Google Scholar]
- Le Bouquin, J.-B., Abuter, R., Haguenauer, P., et al. 2009, A&A, 493, 747 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lopez, B., Antonelli, P., Wolf, S., et al. 2008, in Proc. SPIE, 7013 [Google Scholar]
- Malbet, F., Buscher, D., Weigelt, G., et al. 2008, in Proc. SPIE, 7013 [Google Scholar]
- Meisner, J. A., & Le Poole, R. S. 2003, in Proc. SPIE, ed. W. A. Traub, 4838, 609 [Google Scholar]
- Monnier, J. D., Berger, J., Millan-Gabet, R., & ten Brummelaar, T. A. 2004, in Proc. SPIE, ed. W. A. Traub, 5491, 1370 [Google Scholar]
- Papoulis, A. 1984, Probability, Random Variables and Stochastic Processes (McGraw-Hill) [Google Scholar]
- Pedretti, E., Thureau, N. D., Wilson, E., et al. 2004, in Proc. SPIE, ed. W. A. Traub, 5491, 540 [Google Scholar]
- Sahlmann, J., Ménardi, S., Abuter, R., et al. 2009, A&A, 507, 1739 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shao, M., Colavita, M. M., Hines, B. E., Staelin, D. H., & Hutter, D. J. 1988, A&A, 193, 357 [NASA ADS] [Google Scholar]
- Tatulli, E., Blind, N., Berger, J. P., Chelli, A., & Malbet, F. 2010, A&A, 524, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wilson, E., Pedretti, E., Bregman, J., Mah, R. W., & Traub, W. A. 2004, in Proc. SPIE, ed. W. A. Traub, 5491, 1507 [Google Scholar]
Appendix A: Phase error: detection and delay noise expressions
Considering an ABCD fringe coding (Colavita et al. 1999), the phase is extracted as follows. First we have the four ABCD measurements in quadrature 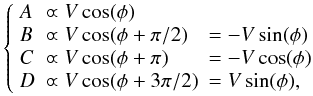 (A.1)where V and φ are the fringe contrast and phase respectively. We extract the real and imaginary part of the complex fringe signal
(A.1)where V and φ are the fringe contrast and phase respectively. We extract the real and imaginary part of the complex fringe signal 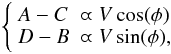 (A.2)and finally we estimate the phase through its cotangent
(A.2)and finally we estimate the phase through its cotangent 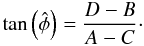 (A.3)We are interested here in the statistical error on the phase measurement, which depends on three sources of noises: detector noise, photon noise, and delay noises. Because these noises are statistically independent, the variance on the phase measurement
(A.3)We are interested here in the statistical error on the phase measurement, which depends on three sources of noises: detector noise, photon noise, and delay noises. Because these noises are statistically independent, the variance on the phase measurement  is simply the quadratic sum of these three noises
is simply the quadratic sum of these three noises  (A.4)
(A.4)
A.1. Detection noises
The detector and photon noises terms (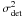 and
and 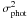 respectively) are derived from Shao et al. (1988) for the ABCD fringe coding, and for the sake of simplicity we put them together into the so-called signal detection noise
respectively) are derived from Shao et al. (1988) for the ABCD fringe coding, and for the sake of simplicity we put them together into the so-called signal detection noise 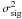
![\appendix \setcounter{section}{1} \begin{eqnarray} &&\sigma_{\rm sig}^2 = \sigma_{\rm det}^2 + \sigma_{\rm phot}^2 \\[1.5mm] &&\sigma^2_{\rm det} = 2\,\displaystyle\frac{4\,\sigma_{\rm e}^2} {V^2 \, K^2} \\[1.5mm] &&\sigma^2_{\rm phot} = 2\,\displaystyle\frac{K} {V^2 \, K^2} , \end{eqnarray}](/articles/aa/full_html/2011/06/aa16222-10/aa16222-10-eq169.png) where K is the number of photo-events collected during the exposure and
where K is the number of photo-events collected during the exposure and 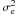 is the detector read-out noise.
is the detector read-out noise.
A.2. Delay noise
The delay noise is caused by the delay between the various measurements needed to estimate the phase and therefore only concerns a temporal phase estimator. Because of instrumental or atmospheric disturbances (e.g. fluctuation of the differential piston or scintillation), the phase estimation can be highly biased. Since Fried (1966) has shown that atmospheric piston and scintillation are uncorrelated, we can study both effects independently 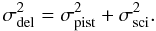 (A.8)
(A.8)
Piston noise calculated with different sets of data on VLTI telescopes in H-band.
A.2.1. Piston noise: σpist
We note here φp(t) the piston term introduced by the atmosphere at a moment t and consider that each (A, C) and (B, D)
measurement lasts half the total integration time t0. Taking the point in the middle of the interval t0 as the reference, the interferometric signal writes ![\appendix \setcounter{section}{1} \begin{eqnarray} && A - C \varpropto V\,\cos \left(\phi+\phi_{\rm p}\left(t - t_0/4\right)\right) \\[1.5mm] && D -B \varpropto V\,\sin \left(\phi+\phi_{\rm p}\left(t + t_0/4\right)\right) . \end{eqnarray}](/articles/aa/full_html/2011/06/aa16222-10/aa16222-10-eq179.png) We note δφp = φp(t + t0/4) − φp(t − t0/4) the piston fluctuation between both measurements
We note δφp = φp(t + t0/4) − φp(t − t0/4) the piston fluctuation between both measurements ![\appendix \setcounter{section}{1} \begin{eqnarray} && A - C \varpropto V\,\cos \left(\phi-\dphi_{\rm p}/2\right) \\[1.5mm] && D - B \varpropto V\,\sin \left(\phi +\dphi_{\rm p}/2\right) , \end{eqnarray}](/articles/aa/full_html/2011/06/aa16222-10/aa16222-10-eq181.png) δφp being unknown, the phase estimator
δφp being unknown, the phase estimator 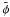 is
is 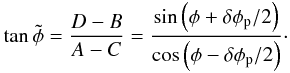 (A.13)As soon as δφp is non null, the phase measurement is biased. If we consider the statistic variations of the piston, this bias can be considered as an additional noise. We now calculate the standard deviation of this phase measurement linked to the piston variations between txo exposures separated by a time t0/2. The standard deviation of the piston for this time will be noted σ(δφp,t0/2). Assuming that the piston variations are small (σ(δφp,t0/2) ≪ 1 rad) and using the second-order expansion formula of Papoulis (1984), the measured phase variance writes as
(A.13)As soon as δφp is non null, the phase measurement is biased. If we consider the statistic variations of the piston, this bias can be considered as an additional noise. We now calculate the standard deviation of this phase measurement linked to the piston variations between txo exposures separated by a time t0/2. The standard deviation of the piston for this time will be noted σ(δφp,t0/2). Assuming that the piston variations are small (σ(δφp,t0/2) ≪ 1 rad) and using the second-order expansion formula of Papoulis (1984), the measured phase variance writes as 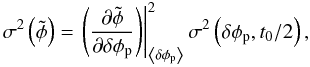 (A.14)where ⟨ δφp ⟩ is the mean piston variation during t0/2. One shows then that
(A.14)where ⟨ δφp ⟩ is the mean piston variation during t0/2. One shows then that 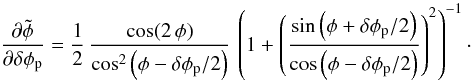 (A.15)Assuming that ⟨ δφp ⟩ = 0, we obtain the scintillation noise
(A.15)Assuming that ⟨ δφp ⟩ = 0, we obtain the scintillation noise 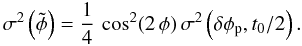 (A.16)This result depends on the mean phase position. Assuming that φ is uniformly distributed over [0,2π] , one finally obtains
(A.16)This result depends on the mean phase position. Assuming that φ is uniformly distributed over [0,2π] , one finally obtains 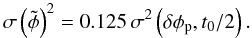 (A.17)This deviation is evaluated here by means of VLTI/FINITO data, and the results are presented in Table A.1 for typical integration times from 2 to 8 ms for ATs and from 1 to 4 ms for UTs.
(A.17)This deviation is evaluated here by means of VLTI/FINITO data, and the results are presented in Table A.1 for typical integration times from 2 to 8 ms for ATs and from 1 to 4 ms for UTs.
A.2.2. Scintillation noise: σsci
The influence of scintillation (i.e., photometric variations) between (A, C) and (B, D) measurements is to induce fringe contrast fluctuations, which can bias the phase measurement. This effect will be studied in the same manner as in the previous section. Considering an ideal interferogram, the real and imaginary parts of the coherent signal write ![\appendix \setcounter{section}{1} \begin{eqnarray} &&A-C \varpropto V_{\rm sci}\left(t-t_0/4\right) \, \cos \phi \\[1.5mm] &&D-B \varpropto V_{\rm sci}\left(t+t_0/4\right) \, \sin \phi , \end{eqnarray}](/articles/aa/full_html/2011/06/aa16222-10/aa16222-10-eq196.png) where Vsci is the contrast attenuation term due to the photometric imbalance between the two beams I1 and I2
where Vsci is the contrast attenuation term due to the photometric imbalance between the two beams I1 and I2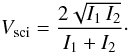 (A.20)Noting the flux variation δi = Ii(t + t0/4) − Ii(t − t0/4), the phase estimator writes
(A.20)Noting the flux variation δi = Ii(t + t0/4) − Ii(t − t0/4), the phase estimator writes 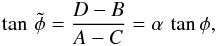 (A.21)where
(A.21)where 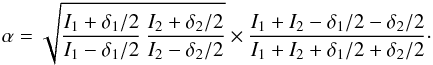 (A.22)Simplifying the first and second terms by I1I2 and I1 + I2 respectively
(A.22)Simplifying the first and second terms by I1I2 and I1 + I2 respectively 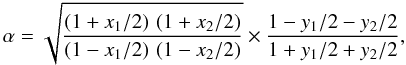 (A.23)with
(A.23)with ![\appendix \setcounter{section}{1} \begin{eqnarray} x_i &=& \delta_i/I_i\\[1.5mm] y_i &=& \delta_i/\left(I_1+I_2\right). \end{eqnarray}](/articles/aa/full_html/2011/06/aa16222-10/aa16222-10-eq207.png)
Photometric noise written with respect to the wavelength in the H-band, for three different integration times.
If the flux varies between both quadratures, α ≠ 1 and the phase estimation is biased. If we consider the statistic variations of the both photometries, this bias can be considered as an additional noise. We therefore calculate the measured photometric variance functions of the variance of the relative photometries σ2(xi,t0/2) between two exposures distant of t0/2. We assume that the two pupils are sufficiently distant to be considered as uncorrelated, which is the case if the baseline is longer than the atmospheric outer scale (typically 20 m). Because the atmosphere follows the same statistics on both, it implies ⟨ x1 ⟩ = ⟨ x2 ⟩ = ⟨ x ⟩ and σ(x1,t0/2) = σ(x2,t0/2) = σ(x,t0/2) ![\appendix \setcounter{section}{1} \begin{eqnarray} \sigma^2\left(\tilde{\phi}\right) &=& \left. \left(\frac{\partial \tilde{\phi}}{\partial x_1} \right) \right|^2_{\langle x_1 \rangle, \langle x_2 \rangle}\sigma^2\left(x_1, t_0/2\right) + \left. \left(\frac{\partial \tilde{\phi}}{\partial x_2} \right) \right|^2_{\left\langle x_1 \right\rangle, \left\langle x_2 \right\rangle}\sigma^2\left(x_2, t_0/2\right) \nonumber \\[1.5mm] &=& 2 \left. \left(\frac{\partial \tilde{\phi}}{\partial x_i} \right) \right|^2_{\left\langle x_1 \right\rangle, \left\langle x_2 \right\rangle}\sigma^2\left(x, t_0/2\right) , \end{eqnarray}](/articles/aa/full_html/2011/06/aa16222-10/aa16222-10-eq212.png) (A.26)with
(A.26)with 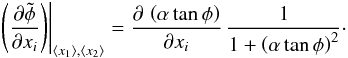 (A.27)To obtain an analytical expression of this quantity, we assume the flux variaitons to be small: δi ≪ Ii. We do a first-order expansion of α and only conserve the terms of the first order
(A.27)To obtain an analytical expression of this quantity, we assume the flux variaitons to be small: δi ≪ Ii. We do a first-order expansion of α and only conserve the terms of the first order ![\appendix \setcounter{section}{1} \begin{eqnarray} \alpha &\sim & \left(1 + x_1/4\right)^2\,\left(1 + x_2/4\right)^2\,\left(1 - y_1/2 - y_2/2\right)^2 \\[1.5mm] &\sim & \left(1 + x_1/2\right)\,\left(1 + x_2/2\right)\,\left(1 - y_1 - y_2\right) \\[1.5mm] &\sim &\left(1 + x_1/2 + x_2/2\right)\left(1 - y_1 - y_2\right) \\[1.5mm] &\sim & 1 + x_1/2 + x_2/2 - y_1 - y_2 . \end{eqnarray}](/articles/aa/full_html/2011/06/aa16222-10/aa16222-10-eq216.png) We expand the latter expression to simplify it
We expand the latter expression to simplify it ![\appendix \setcounter{section}{1} \begin{eqnarray} \alpha &\sim & 1 + \frac{\delta_1}{2 I_1} + \frac{\delta_2}{2 I_2} - \frac{\delta_1 + \delta_2}{I_1 + I_2}\\[1.5mm] &\sim & 1 + \frac{\delta_1 I_2^2 + \delta_2 I_1^2 - \left(\delta_1 + \delta_2\right)I_1 I_2}{2\left(I_1 + I_2\right)I_1 I_2}\\[1.5mm] &\sim & 1 + \frac{I_2 - I_1}{I_2 + I_1}\,\frac{\delta_1 I_2 - \delta_2 I_1}{2 I_1 I_2} \end{eqnarray}](/articles/aa/full_html/2011/06/aa16222-10/aa16222-10-eq217.png) and finally:
and finally: 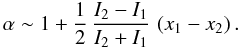 (A.35)Therefore, considering α ~ 1 in the second term of the expression (A.27)
(A.35)Therefore, considering α ~ 1 in the second term of the expression (A.27) 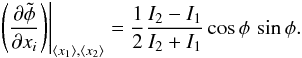 (A.36)Noting that
(A.36)Noting that 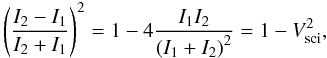 (A.37)we finally show that the variance of the phase measurement due to the photometric noise is
(A.37)we finally show that the variance of the phase measurement due to the photometric noise is 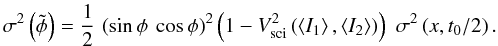 (A.38)Note that the result depends on the mean value of the scintillating visibility Vsci. Hence, a perfectly balanced system should present a null photometric noise. This is an unrealistic effect because of our symetric modelling of the photometric variation with a step. In practice, the quick variations of photometries (i.e. during the integration) induce a noise even for a perfectly symetric combiner. To obtain a more realistic value, we can consider a (worst) case with a mean imbalance between fluxes of a factor of 10, so that Vsci ~ 0.57 and
(A.38)Note that the result depends on the mean value of the scintillating visibility Vsci. Hence, a perfectly balanced system should present a null photometric noise. This is an unrealistic effect because of our symetric modelling of the photometric variation with a step. In practice, the quick variations of photometries (i.e. during the integration) induce a noise even for a perfectly symetric combiner. To obtain a more realistic value, we can consider a (worst) case with a mean imbalance between fluxes of a factor of 10, so that Vsci ~ 0.57 and 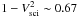 .
.
If we finally average this result over every realisation of φ (still assuming its statistics to be uniform between 0 and 2π) 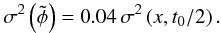 (A.39)Similarly to the piston noise, we present in Table A.2 the results obtained from ESO data on ATs and UTs for different integration times.
(A.39)Similarly to the piston noise, we present in Table A.2 the results obtained from ESO data on ATs and UTs for different integration times.
Appendix B: Theoretical dynamic range for the group delay estimation with dispersed fringes
We analyse here the case of a dispersed estimator for the group delay, similar to what is implemented on PRIMA, PTI or KI. We remind that the coherence envelope E(x) corresponds to the Fourier transform modulus of the coherent signal 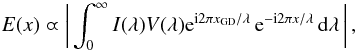 (B.1)where x is the OPD, xGD the position of the envelope centre, and I(λ) and V(λ) the source intensity and visibility, both depending on the wavelength λ. We consider a spectral band centred around λ0 and of width Δλ, so that the coherence length Lc of the wide-band interferogram is
(B.1)where x is the OPD, xGD the position of the envelope centre, and I(λ) and V(λ) the source intensity and visibility, both depending on the wavelength λ. We consider a spectral band centred around λ0 and of width Δλ, so that the coherence length Lc of the wide-band interferogram is 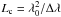 . The fringes are dispersed over Nλ spectral channels of equal width δλ = Δλ/Nλ. In terms of wavenumber, the wide- and narrow-band widths write Δσ = 1/Lc and δσ = Δσ/Nλ.
. The fringes are dispersed over Nλ spectral channels of equal width δλ = Δλ/Nλ. In terms of wavenumber, the wide- and narrow-band widths write Δσ = 1/Lc and δσ = Δσ/Nλ.
For sake of simplicity we consider here an ideal case, that is the all considered quantities are achromatic, in particular the source flux I and visibility V do not depend on the wavelength. We assume we dispose of a fringe coding (ABCD for instance) allowing the complex fringe signal Zk to be computed in each channel k, this latter being defined as 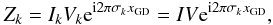 (B.2)where σk = 1/λk is the effective wavenumber on each spectral channel. The discrete Fourier transform of this coherent signal is then
(B.2)where σk = 1/λk is the effective wavenumber on each spectral channel. The discrete Fourier transform of this coherent signal is then ![\appendix \setcounter{section}{2} \begin{eqnarray} \mathcal{F}(x) &=& \sum_{k=1}^{N_{\lambda}} Z_k \, {\rm e}^{-{\rm i} \, 2\pi \sigma_k x} \nonumber \\[1.5mm] &=& \sum_{k=1}^{N_{\lambda}} I\,V\, {\rm e}^{-{\rm i} \, 2\pi \sigma_k \left(x-x_{\rm GD}\right)} , \end{eqnarray}](/articles/aa/full_html/2011/06/aa16222-10/aa16222-10-eq249.png) (B.3)and we finally compute the squared coherence envelope
(B.3)and we finally compute the squared coherence envelope ![\appendix \setcounter{section}{2} \begin{eqnarray} E^2(x) &\varpropto& \left|\mathcal{F}(x)\right|^2 \\[2mm] & = &\mathcal{F}(x) \, \mathcal{F}^*(x) \\[1.5mm] & = & I^2\,V^2\, \sum_{k=1}^{N_{\lambda}} \sum_{l=1}^{N_{\lambda}} {\rm e}^{-{\rm i} \, 2\pi \left(\sigma_k - \sigma_l\right) \left(x-x_{\rm GD}\right)} , \end{eqnarray}](/articles/aa/full_html/2011/06/aa16222-10/aa16222-10-eq250.png) where ℱ∗ is the complex conjugate of ℱ. Because each spectral channel has the same width, σk − σl = δσ (k − l) and we finally derive
where ℱ∗ is the complex conjugate of ℱ. Because each spectral channel has the same width, σk − σl = δσ (k − l) and we finally derive 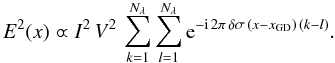 (B.7)The group delay is obtained when this quantity is maximum, that is, when all the phasors in the double summation are in phase. In the present simple case, it is obvious that this happens when x = xGD, which leads to
(B.7)The group delay is obtained when this quantity is maximum, that is, when all the phasors in the double summation are in phase. In the present simple case, it is obvious that this happens when x = xGD, which leads to 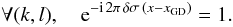 (B.8)And solving this equation finally gives
(B.8)And solving this equation finally gives ![\appendix \setcounter{section}{2} \begin{equation} x = x_{\rm GD} \quad [1/\delta \sigma] , \end{equation}](/articles/aa/full_html/2011/06/aa16222-10/aa16222-10-eq257.png) (B.9)where [ ] is the modulo symbol. In other words, by dispersing the fringes, we find the group delay with an ambiguity equal to 1/δσ. From the definition of δσ, it finally corresponds to an ambiguity (or a dynamic range) equal to
(B.9)where [ ] is the modulo symbol. In other words, by dispersing the fringes, we find the group delay with an ambiguity equal to 1/δσ. From the definition of δσ, it finally corresponds to an ambiguity (or a dynamic range) equal to 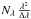 .
.
Appendix C: Noise propagation on pairwise combination schemes
The study conducted in Sect. 4 aims at comparing various co-axial pairwise combination schemes looking at the phase and group delay measurement precision in various configurations. This study is based on analytical descriptions of measurement noises. We here describe various points which were necessary for this study but which are not essential for the comprehension of the results.
C.1. Reference noise
Thanks to Shao et al. (1988), Tatulli et al. (2010) and our study (Eqs. (14) and (15)), we know the analytical expression of the phase and group delay noises in detector- and photon-noise regimes, and for co-axial pairwise combinations. They express as ![\appendix \setcounter{section}{3} \begin{eqnarray} \label{eq:refdet} \sigma_0^{\rm det} &=& \displaystyle\frac{A}{K V} \\[1.5mm] \label{eq:refphot} \sigma_0^{\rm phot} &=& \displaystyle\frac{B}{\sqrt{K} V}, \end{eqnarray}](/articles/aa/full_html/2011/06/aa16222-10/aa16222-10-eq262.png) K and V being the number of photo-events and the fringe visibility. A and B are proportionality factors depending on the fringe coding, which have no influence in the following. These expressions correspond to the noise for a two-telescope (one baseline) instrument and are considered as noise references in the following.
K and V being the number of photo-events and the fringe visibility. A and B are proportionality factors depending on the fringe coding, which have no influence in the following. These expressions correspond to the noise for a two-telescope (one baseline) instrument and are considered as noise references in the following.
C.2. Individual baseline noise
When we consider an interferometric array with more than two telescopes, the flux of each telescope is distributed between several different baselines, increasing the noise on each baselines. We consider two cases here: the open and redundant schemes.
C.2.1. Redundant schemes
The most simple cases are the redundant schemes in which the flux of each pupil is divided between the same number R of baselines. Compared to a two-telescope instrument, the total flux K on each baseline is divided by R, so that the measurement noise is ![\appendix \setcounter{section}{3} \begin{eqnarray} \sigma^{\rm det} &=& \displaystyle A \frac{R}{K V} \nonumber \\[1.5mm] &=& R\,\sigma_0^{\rm det} \label{eq:refdet2} \\[1.5mm] \sigma^{\rm phot} &=& \displaystyle B \frac{\sqrt{R}}{\sqrt{K} V} \nonumber \\[1.5mm] &=& \sqrt{R}\, \sigma_0^{\rm phot} \label{eq:refphot2} . \end{eqnarray}](/articles/aa/full_html/2011/06/aa16222-10/aa16222-10-eq268.png) We are therefore able to compare the different schemes on detector and photon noise regimes on the base of a reference noise.
We are therefore able to compare the different schemes on detector and photon noise regimes on the base of a reference noise.
C.2.2. Open schemes
The open schemes use the minimal number of baselines enabling the array to be cophased, that is, N − 1 baselines. In this case the array is not symmetric, so that splitting the flux of intermediate pupils into equal parts (i.e., taking 50% of their flux for each baseline) implies unequal performances for the different baselines. In this study we give the open schemes intrinsically equivalent baselines, that is, with the same SNR on the fringe position measurements. To do so, we have to consider intrinsically imbalanced photometric inputs for each baseline and we evaluate the optimal fraction of the flux to inject in the different baselines.
Considering two identical telescopes i and j, we combine their light by taking a fraction δi and δj of the incoming fluxes on each telescope respectively. In this case, the total flux available at the baseline is 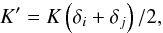 (C.5)and the fringe contrast V is possibly reduced because of the photometric imbalance
(C.5)and the fringe contrast V is possibly reduced because of the photometric imbalance  (C.6)Now considering the noise expressions in Eqs. (C.1) and (C.2), we can easily write the measurement noises in this case, still as a function of our reference noises
(C.6)Now considering the noise expressions in Eqs. (C.1) and (C.2), we can easily write the measurement noises in this case, still as a function of our reference noises ![\appendix \setcounter{section}{3} \begin{eqnarray} \label{eq:asymdet} &&\sigma_{ij}^{\rm det} = \displaystyle\frac{1}{\sqrt{\delta_i \delta_j}} \, \sigma_0^{\rm det} \\[1.5mm] \label{eq:asymphot} &&\sigma_{ij}^{\rm phot} = \displaystyle\sqrt{\frac{\delta_i+\delta_j}{2 \delta_i \delta_j}} \, \sigma_0^{\rm phot} . \end{eqnarray}](/articles/aa/full_html/2011/06/aa16222-10/aa16222-10-eq277.png) The open schemes with four and six telescopes are presented in Fig. C.1 with the associated nomenclature in term of splitting ratio δi. We determine in the following their values.
The open schemes with four and six telescopes are presented in Fig. C.1 with the associated nomenclature in term of splitting ratio δi. We determine in the following their values.
 |
Fig. C.1 Open schemes considered in the four and six telescopes cases. The nomenclature for the flux split ratio δi are represented in the figures. |
4TO case.
For symmetry reasons we consider δ1 = δ4 = 1 and δ2 = δ3 = δ, and therefore the measurement errors on the three baselines write ![\appendix \setcounter{section}{3} \begin{eqnarray*} \sigma_{12}^{\rm det} &=& \sigma_{34}^{\rm det} = \frac{1}{\sqrt{\delta}}\sigma_{0}^{\rm det} \quad\ \ \ \ \sigma_{12}^{\rm phot} = \sigma_{34}^{\rm phot} = \sqrt{\frac{1+\delta}{2\delta}} \sigma_{0}^{\rm phot}\\[1.5mm] \sigma_{23}^{\rm det} &=& \frac{1}{1-\delta} \sigma_{0}^{\rm det} \qquad \qquad \sigma_{23}^{\rm phot} = \frac{1}{\sqrt{1-\delta}} \sigma_{0}^{\rm phot} . \end{eqnarray*}](/articles/aa/full_html/2011/06/aa16222-10/aa16222-10-eq281.png) Our goal is to have equivalent baselines, i.e., we want σij to be equal on the three baselines. Solving this system in detector and photon noise regimes leads to
Our goal is to have equivalent baselines, i.e., we want σij to be equal on the three baselines. Solving this system in detector and photon noise regimes leads to ![\appendix \setcounter{section}{3} \begin{eqnarray*} \delta^{\rm det}\ &=& 0.38 \quad\quad\ \ \ \, \delta^{\rm phot} = 0.42 \\[1.5mm] \sigma_{ij}^{\rm det} &=& 1.62 \sigma_{0}^{\rm det} \quad\, \sigma_{ij}^{\rm phot} = 1.31 \sigma_{0}^{\rm phot} . \end{eqnarray*}](/articles/aa/full_html/2011/06/aa16222-10/aa16222-10-eq283.png)
6TO case.
For symmetry reasons we have δ1 = δ6 = 1, δ2 = δ5 and δ3 = δ4. The measurement errors on the five baselines write ![\appendix \setcounter{section}{3} \begin{eqnarray*} &&\sigma_{12}^{\rm det} = \sigma_{56}^{\rm det}= \frac{1}{\sqrt{\delta_2}} \sigma_{0}^{\rm det}\\[1.5mm] &&\sigma_{12}^{\rm phot} = \sigma_{56}^{\rm phot}= \sqrt{\frac{1+\delta_2}{2\delta_2}} \sigma_{0}^{\rm phot}\\[1.5mm] &&\sigma_{23}^{\rm det} = \sigma_{45}^{\rm det} = \frac{1}{\sqrt{\left(1-\delta_2\right)\left(1-\delta_3\right)}} \sigma_{0}^{\rm det}\\[1.5mm] &&\sigma_{23}^{\rm phot} = \sigma_{45}^{\rm phot}= \sqrt{\frac{2-\delta_2-\delta_3}{2\left(1-\delta_2\right)\left(1-\delta_3\right)}} \sigma_{0}^{\rm phot}\\[1.5mm] &&\sigma_{34}^{\rm det} = \frac{1}{\delta_3} \sigma_{0}^{\rm det}\\ &&\sigma_{34}^{\rm phot} = \frac{1}{\sqrt{\delta_3}} \sigma_{0}^{\rm phot}. \end{eqnarray*}](/articles/aa/full_html/2011/06/aa16222-10/aa16222-10-eq287.png) In the same way as previously, we estimate the optimal value of the different δi
In the same way as previously, we estimate the optimal value of the different δi![\appendix \setcounter{section}{3} \begin{eqnarray*} &&\delta_{2}^{\rm det} = 0.31 \qquad\qquad \delta_{2}^{\rm phot} = 0.37 \\[1.5mm] &&\delta_{3}^{\rm det} = 0.55 \qquad \qquad \delta_{3}^{\rm phot} = 0.54 \\[1.5mm] &&\sigma_{ij}^{\rm det} = 1.81 \sigma_{0}^{\rm det} \qquad \, \sigma_{ij}^{\rm phot} = 1.36 \sigma_{0}^{\rm phot}. \end{eqnarray*}](/articles/aa/full_html/2011/06/aa16222-10/aa16222-10-eq288.png) For the 4TO and 6TO cases we note the different values of δi are close in detector and photon noise regimes, so that these schemes are practically possible. In both regimes we consider the same values: δ = 0.40 in the 4T case; δ2 = 0.34 and δ3 = 0.54 in the 6T case.
For the 4TO and 6TO cases we note the different values of δi are close in detector and photon noise regimes, so that these schemes are practically possible. In both regimes we consider the same values: δ = 0.40 in the 4T case; δ2 = 0.34 and δ3 = 0.54 in the 6T case.
C.3. Estimating the individual fringe position and final measurement noise
We have to estimate N − 1 differential pistons to cophase the interferometric array. In practice we measure B differential pistons (noted 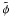 ), with B > N − 1 for redundant schemes, and B = N − 1 for the open ones. Noting x the vector of the N − 1 optical path estimators used to drive the delay lines, the equation system linking
), with B > N − 1 for redundant schemes, and B = N − 1 for the open ones. Noting x the vector of the N − 1 optical path estimators used to drive the delay lines, the equation system linking 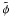 and x is
and x is 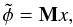 (C.9)where M is the so-called interaction matrix, which is known. We now need to inverse this system by computing the control matrix W:
(C.9)where M is the so-called interaction matrix, which is known. We now need to inverse this system by computing the control matrix W: 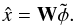 (C.10)For the redundant schemes, M is rectangular and we compute W on the base of a singular value decomposition of M. We therefore solve the system in the sens of a least-squares minimization, i.e., we minimize the quantity
(C.10)For the redundant schemes, M is rectangular and we compute W on the base of a singular value decomposition of M. We therefore solve the system in the sens of a least-squares minimization, i.e., we minimize the quantity
However, the measurements 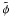 are noisy and we have to weight them to minimize the influence of the noisiest baselines. Considering that the measurements have Gaussian statistics and are statistically independent, the χ2 writes
are noisy and we have to weight them to minimize the influence of the noisiest baselines. Considering that the measurements have Gaussian statistics and are statistically independent, the χ2 writes
where σ is the vector of the error on the measurement 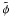 , given by Eqs. (C.3) and (C.4) depending on the noise regime. We modify in consequence the differential phase vector
, given by Eqs. (C.3) and (C.4) depending on the noise regime. We modify in consequence the differential phase vector 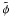 and the interaction matrix M as follow
and the interaction matrix M as follow
C.4. Statistical error on the estimated differential pistons
To compare the various schemes, we are interested in the error on the differential piston xij = xi − xj, which corresponds to the error on the correction applied to the delay lines
Given the definition of 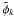 (Eq. (C.14)), the statistical error on these terms is
(Eq. (C.14)), the statistical error on these terms is 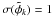 . We finally obtain the quadratic error
. We finally obtain the quadratic error 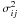 on the corrected differential piston
on the corrected differential piston
All Tables
Typical seeing and atmospheric coherence time τ0 for the different observing conditions considered.
Results of the performance study in the ideal case, where all baselines are equivalent and noted { ij } .
Ability of the combination schemes to provide the input photometries without dedicated outputs.
Piston noise calculated with different sets of data on VLTI telescopes in H-band.
Photometric noise written with respect to the wavelength in the H-band, for three different integration times.
All Figures
 |
Fig. 1 ABCD estimator. Left: conceptual representation of the four phase states sampling the fringes. Right: the measured phase states functions of the time for static (top) and temporally modulated (bottom) ABCD. The total integration time is t0. |
| In the text | |
 |
Fig. 2 Relative errors σφ/λ of temporal (dash) and static (solid) ABCD phase estimators in the H-band as a function of the number of detected photo-events K. Black, blue, magenta, and red curves represent Excellent, Good, Medium and Bad conditions respectively as defined in Table 1. The plots are made for the ATs for an integration time of 2 ms for the specific ABCD implementation considered here. Note that for the static ABCD, the black, blue, and magenta curves are superimposed because of close performances. |
| In the text | |
 |
Fig. 3 Top: example of polychromatic fringes (solid line) with longitudinal dispersion, modulated by the coherence envelope (dashed lines). Bottom: corresponding phase and group delay measurements (in blue and red respectively) presented in microns. |
| In the text | |
 |
Fig. 4 Conceptual representation of the signal processing for group delay estimation. Temporal method (left): an envelope model is fitted on the three envelope amplitude measurements to determine the group delay. Dispersed method (right): from the spectral sampling of the complex coherent signal, an approximated envelope is computed with a Fourier transform operation. The envelope position is determined by fitting an envelope model. |
| In the text | |
 |
Fig. 5 Response of the dispersed and temporal group delay estimators (solid and dashed lines respectively) to an OPD ramp xGD in the H-band. The ideal response is represented by the large gray line. In all cases, the coherence envelope has a sinc shape. Top: the envelope model is a sinc function. Bottom: the envelope model is a parabola. Figures on the right are a zoom on the central part of the left-hand side figures. The DR limits are represented with blue arrows on the top-left plot in the ideal case for both estimators. |
| In the text | |
 |
Fig. 6 Relative errors σGD/λ of temporal (dash) and dispersed (solid) GD estimators in different atmospheric conditions. Black, blue, magenta, and red curves represent Excellent, Good, Medium, and Bad conditions respectively as defined in Table 1. The plots are made for the ATs, for a total integration time of 3 ms, constituted of three single exposures of 1 ms. |
| In the text | |
 |
Fig. 7 Various conceptual schemes studied for the 4T and 6T cases (top and bottom respectively) with the associated nomenclature. As explained in Sect. 4.1, we did not study schemes with intrinsically imbalanced photometric inputs other than the open ones, because of lower performance. |
| In the text | |
 |
Fig. 8 Predicted fringe contrast when observing a binary star with equal fluxes and a separation of about 10 mas with the four UTs and a fringe sensor working in the H-band. The left panel shows the (u,v) tracks overlaid on the fringe contrast from the model. The right panel shows the fringe contrast versus time for 4 h for each baseline. The figures were made with the aspro public software from JMMC. |
| In the text | |
 |
Fig. 9 Fringe sensing noise plotted at percentile 0.9 (i.e., the noise is actually lower than the plotted curves for 90% of the occurrences) as a function of the target’s K magnitude (or of the stellar flux in photons per second at the entrance of 2GFT) in the 4T3-ABCD case, assuming a K0 III target and using the A0-G1-K0-I1 quadruplet of ATs at the VLTI. The fringe-tracking loop is operated at its maximum frequency as long as the fringe sensing noise per baseline remains < 100 nm rms for 90% of the measurements on any individual baseline. The closed-loop repetition frequency is reduced to maintain this level of performance otherwise (this happens for K > 5 in the present case, as also shown in Fig. 10), until this level cannot be reached any more (beyond K = 7.5 in the present case). Note that the increase in sensing noise for bright targets is caused by the resolved stellar photosphere, which reduces the available coherent flux. |
| In the text | |
 |
Fig. 10 Left: closed-loop repetition time and time delay in the loop as a function of target K magnitude. For stars fainter than K = 6, the loop repetition time is increased (i.e., its frequency decreased) to ensure a sufficient SNR on the detected fringes in each individual measurement (until the specified SNR cannot be reached any more whatever the integration time). Right: noise residuals at the output of the closed loop, for the three main contributors: fringe sensing (FSU), delay line (DL) and atmospheric noises. |
| In the text | |
 |
Fig. C.1 Open schemes considered in the four and six telescopes cases. The nomenclature for the flux split ratio δi are represented in the figures. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



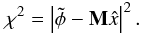
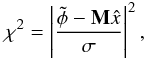
![\appendix \setcounter{section}{3} \begin{eqnarray} && {\bf M}_{ij} \rightarrow {\bf M}_{ij} / \sigma_i, \quad j \in [1, N-1], i \in [1, B] \\[1.5mm] && \tilde{\phi}_i \rightarrow \tilde{\phi}_i / \sigma_i \label{def_phi_modif} . \end{eqnarray}](/articles/aa/full_html/2011/06/aa16222-10/aa16222-10-eq304.png)