EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 530 (June 2011) A&A, 530 (2011) A98 Full HTML
Free Access
Issue
A&A
Volume 530, June 2011
Article Number A98
Number of page(s) 10
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/201016191
Published online 18 May 2011

© ESO, 2011

1. Introduction

The spectra of the hot X-ray emitting interstellar medium (ISM) of elliptical galaxies carry valuable information about the composition of both the stellar and the type Ia supernova (SNIa) ejecta in the late phases of galactic evolution. Chandra and XMM measurements (e.g. Buote 2002; Xu et al. 2002; Gastaldello & Molendi 2002; Buote et al. 2003; Kim & Fabbiano 2004; Humphrey & Buote 2006; Tawara et al. 2008; Ji et al. 2009; Loewenstein & Davis 2010) agree that X-ray bright elliptical galaxies exhibit  [Fe/H]  ~ 0−0.3 dex, namely typically solar or twice. Overall, one can estimate that the contribution of SNIa to the metal enrichment of the hot ISM is quite important, being probably more than 60% (e.g. Humphrey & Buote 2006). This Fe abundance is similar to the average abundance of the stars in the same galaxies, as inferred from absorption lines in optical stellar spectra (Humphrey & Buote 2006), whose observed stellar pattern (e.g. Graves et al. 2007) is well reproduced by the most recent monolithic formation models (e.g. Pipino et al. 2009a).

However, since the theoretical studies by Loewenstein & Mathews (1991; see also Renzini et al. 1993; Pipino et al. 2005), all monolithic collapse+galactic wind models agree in predicting quite high abundances, a factor of two-to-three higher than the observational measurements. Such a high abundance is a clear consequence of the simple assumptions made in the models, where all the iron produced by SNIa after the star formation and wind phases, immediately mixes with the ISM. We refer to this as the theoretical Fe discrepancy. Therefore, either some modifications to the simple galactic wind scheme are required or a completely different galaxy formation scenario should be adopted. The possible physical mechanisms invoked to solve the discrepancy between the predicted Fe abundances and the observed ones (see also Renzini et al. 1993; Arimoto et al. 1997, for earlier studies), can be roughly grouped into several classes: differential ejection of Fe; iron hidden in a colder phase (warm gas or dust); a significant dilution from freshly accreted gas with primordial abundances; and modifications to the SNIa rate. Therefore, some other physical processes must be added to the basic wind model. For instance,the simulations of Tang & Wang (2010) show that the hot and low-density SNIa bubbles move outward faster than the surrounding medium. This differential motion reduces the [Fe/H] by more than 0.2 dex with respect to the case in which the Fe is immediately mixed with the ambient gas. Moreover, because of the high temperature and low density inside the bubbles, the contribution of this Fe-rich gas to the total X-ray emission is negligible, hence the “emission weighted” abundance that we infer from observations mirrors the metallicity of the dense (and relatively less Fe-enriched) shells swept by the SNIa remnants.

Mathews & Brighenti (2003) suggested that a sizable fraction of metals never enters into the hot phase because of dust-assisted cooling. The problem with the cooling scenario is that the observed lines at  ~106 K strongly constrain the amount of metals that can cool (e.g. Peterson et al. 2003; Xu et al. 2002). However, warm ISM is observed in ellipticals and its metallicity is nearly solar (e.g. Athey & Bregman 2009), hence consistent with the measurements in both stars and the hot ISM. According to Brighenti & Mathews (2005), Fe-rich ejecta may cool faster than the ambient medium because of its large radiative emissivity.

Finally, several authors (e.g. Renzini et al. 1993; Arimoto et al. 1997; Brighenti & Matthews 2005; Loewenstein & Davis 2010) assume that the actual SNIa rate in ellipticals is at most one quarter of the observationally derived one, but no study has provided a clear verification of this. A natural consequence of this assumption is that the [Fe/H] is lower. In principle, elliptical galaxies have slightly different star formation histories, hence slightly different SNIa rates. Those with a higher average SNIa rate in the recent past may have undergone a galactic wind until later times and perhaps have not yet accreted enough gas mass to be detectable in the X-rays. Some recent studies have suggested that the present-day SNIa rate correlates with the color of the galaxy (Mannucci et al. 2005). In addition, different progenitor systems produce different SNIa rates. Even if the total number of SNIa that exploded were identical to the present-day SNIa rate, the distribution in time of the SNIa events would change. This affects the fraction of Fe ejected in the wind as opposed to the Fe trapped in the hot ISM.

As far as the abundance ratios are concerned, observations (e.g. Humphrey & Buote 2006; Ji et al. 2009; Loewenstein & Davis 2010) generally agree that [Si/Fe] is between solar and super-solar,  [Mg/Fe]  ~ 0 and that the O is depleted with respect to Mg. While a general consensus appears to emerge after comparing Chandra and XMM data, a caveat is that different abundance patterns may be inferred even from data acquired by different instruments onboard the same telescope, the largest variations being for the O abundance (Ji et al. 2009). According to Loewenstein & Davis (2010),who also measure a strongly super-solar [Ca/Fe], neither a single model  nor a single set of SNIa yields can reproduce the entire abundance pattern observed in NGC 4472. Moreover, the theoretical Fe discrepancy also affects the [element/Fe] ratios, in the sense that the predictions exhibit – in general – lower abundance ratios than the observations, unless a lower than observed effective SNIa rate is adopted. Unfortunately, most previous models developed to address the theoretical Fe discrepancy do not track the evolution of species other than Fe, therefore they cannot be rigorously compared with the ISM abundance pattern. In addition, we recall that most galactic wind models designed to reproduce the hot ISM do not study the formation of the galaxy, nor make predictions about the stellar abundances. In many cases, the simulation begins after the galaxy has already assembled.

In our previous work, we examined the effects of a mild dilution by pristine gas (Pipino et al. 2005), or dust (Calura et al. 2008), to show that the predicted [Fe/H] can be reduced to in turn diminish the disagreement between theory and observation. Here, we revisit the study using of updated dust prescriptions and compare the predicted element ratios [X/Fe] with the observed ones. The present work is designed to constrain some of the above-mentioned theoretical solution put forth to address the theoretical Fe discrepancy. At the same time, we aim to explain the [α/Fe] ratios by means of a self-consistent chemical evolution model that reproduces the properties of the stellar populations in elliptical galaxies. To do so we use the latest theoretical nucleosynthetic yields, incorporate the dust in the model, and explore different SNIa progenitor scenarios.

The basic features of our chemical evolution scheme as well as the model set-up are summarized in Sect. 2. The results are presented and discussed in Sects. 3 and 4. Conclusions are drawn in Sect. 6.

The adopted solar abundances are those of Grevesse & Sauval (1998).

2. The chemical evolution model for elliptical galaxies

2.1. The chemical evolution model

We use the model presented in Pipino et al. (2005 – see also Calura et al. 2008, and Pipino et al. 2011, for the formulation of dust evolution). The galaxy evolves as an open box in which the initial gas mass, with primordial chemical composition, rapidly collapses, on a timescale τ, into the potential well of a dark matter halo.

The rapid collapse triggers an intense and rapid star-formation process, which can be considered as a starburst lasting until the occurrence of a galactic wind, which is powered by the thermal energy injected by stellar winds and SN explosions. At that time (tgw, hereafter), the thermal energy equals the binding energy of gas. After tgw, the galaxies evolve passively. In the particular model that we present, tgw = 1.2 Gyr. The wind stops at tstop = 11 Gyr.

The equation of chemical evolution for the element i takes the form (1)where Gi(t) is the fractional mass of the element i at the time t in the ISM, Xi(t) is defined as the abundance by mass of the element i, and by definition  ∑ iXi = 1.

The first term of Eq. (1) gives the rate at which the element i is removed from the ISM by the star formation process. The variable ψ is the star formation rate calculated according to the law 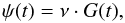(2)where G(t) is the fractional mass of gas and ν is a constant representing the star formation efficiency.

The second term is the rate at which each element is restored into the ISM by single stars with masses in the range ML − MBm, where ML is the minimum mass contributing, at a given time t, to chemical enrichment (the minimum is 0.8   M⊙) and MBm is the minimum binary mass allowed for binary systems leading to SNIa. The initial mass function (IMF) has the Salpeter (1955) form φ(m) ∝ m − (1 + 1.35), and is normalized to unity in the mass interval 0.1−40   M⊙. In particular, Qmi(t − τm) = Qmi   X(t − τm), where Qmi is a matrix that calculates for any star of a given mass m the amount of the newly processed and already present element i, that is returned to the ISM. The quantity τm is the lifetime of a star of mass m (Padovani & Matteucci 1993).

The third term represents the enrichment by SN Ia. In the following, we assume the single degenerate (SD) scenario for our fiducial model: a C − O white dwarf plus a red giant (Whelan & Iben 1973). Following Greggio Renzini (1983) and Matteucci Greggio (1986), the SNIa rate is 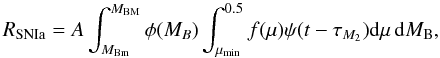(3)where MB is the total mass of the binary system, MBm = 3   M⊙ and MBM = 16   M⊙ are the minimum and maximum masses allowed for the adopted progenitor systems, respectively, and μ = M2/MB is the mass fraction of the secondary, which is assumed to follow the distribution law 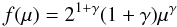(4)and \verbatimmathformule{!/gamma=2}.Finally, μmin is the minimum mass fraction contributing to the SNIa rate at the time t, and is given by: 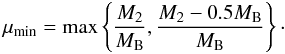(5)The predicted Type Ia SN explosion rate is constrained to reproduce the present day observed value (Mannucci et al. 2008), by fixing the parameter A in Eq. (1). In particular, A represents the fraction of binary systems in the IMF which are capable of producing SNIa explosions. The fiducial model assumes that A = 0.09. We also present a model where we force a sudden transition from A = 0.09 to A < 0.09 after a suitable time (> tgw), to model a lower effective SNIa rate in the late evolutionary phases, than the fiducial case.

We also present a model that considers the double degenerate (DD) wide scenario (see Greggio 2005; and Valiante et al. 2009, for details). We note that when this scenario is constrained to reproduce the present day SNIa rate, the total number of SNIa (hence the total mass of synthesized Fe) is lower than that in the fiducial case by a factor of four. This happens because in the DD scenario an additional further delay is introduced by the timescale of the merging of the two white dwarfs with respect to the SD scenario. In practice, many more systems did not have time to explode in a Hubble time. In addition, we tested the empirical progenitor model by Mannucci et al. (2005; see also Matteucci et al. 2006). Given the diversity of the SNIa light curves, one cannot exclude that different progenitors and explosion characteristics coexist.

The fourth termgives the contribution of either single stars (including SNII) or binaries that do not lead to SNIa in the mass range MBm − MBM. The fifth term represents the enrichment by stars more massive than MBM. The initial galactic gas-infall phase enters the equation via the sixth term, for which adopt the formula 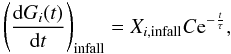(6)where Xi,infall describes the chemical composition of the accreted gas, assumed to be primordial and C is a constant obtained by integrating the infall law over time. Finally, τ is the infall timescale.

The last two terms account for the mass ejection during the galactic wind and possible late-time accretion of the surrounding pristine gas.

The predictions have been averaged over 30 kpc. This choice is consistent with the inner region probed in Loewenstein & Davis (2010) with Suzaku for NGC 4472, which is the galaxy that we use as the prototypical observational case, although the model was not specifically tailored for this galaxy. We note that for this galaxy no particular ISM abundance gradients are reported (Loewenstein & Davis 2010), but for the [Mg/Fe] that roughly decreases by half in the outer regions. Therefore we do not expect unaccounted-for gradients to affect our specific comparison. The study of metallicity gradients in the hot ISM will be the topic of future work.

2.2. Stellar yields

The yields used in this paper are as follows:

  • 1.

    For single low and intermediate mass stars (0.8 ≤ M/M⊙ ≤ 8), we used the yieldsof van den Hoek & Groenewegen (1997) as a function ofmetallicity.

  • 2.

    For SNIa, we adopt either the W7 or the WDD1 models from standard 1D simulations (Iwamoto et al. 1999), as well as the newer C-DDT model from a 2D explosion simulation (Maeda et al. 2010). In particular, the model with deflagration-to-detonation transition (DDT) seem to reproduce the layered structure of the ejecta (Maeda et al. 2010, and references therein) more accurately than the standard deflagration model W7. We also considered a case in which we adopt the empirical yields of François et al. (2004). These yields are a revised version of the Woosley & Weaver (1995, for SNII) and Iwamoto et al. (1999, for SNIa) calculations adjusted to reproduce the chemical abundances in the Milky Way. In our particular case, in which we focus on the late-time chemical evolution, we simply applied the changes to the SNIa yields. According to François et al. (2004), the Mg production in SNIa must increase by a factor of five relative to standard yields, whereas the O and Fe production should not change (models labelled as W7,5xMg hereafter).

  • 3.

    For SNeII, we use the yields of Kobayashi et al. (2006) for the solar composition in the fiducial case (K002, hereafter). We also ran a model with the Kobayashi et al. (2006) Z = 0.001 yields (K0001, hereafter).

Table 1

Model set-up and average stellar abundance ratios.

2.3. Dust model

We refer the reader to Calura et al. (2008) and Pipino et al. (2011) for details of the chemical evolution model with dust, which is constrained by both low- and high-redshift observables. Here we recall the main assumptions. Only the main refractory elements, C, O, Mg, Si, S, Ca, Fe, deplete into dust, and we assume that stars can produce two different types of grains: i) silicate dust, composed by O, Mg, Si, S, Ca and Fe, and ii) carbon dust, composed by C. Following Dwek (1998), we consider that the dust producers are low and intermediate mass stars, type Ia SNe and type II SNe.

The dust destruction is assumed to occur in SN shocks. Following McKee (1989), the SN shock term adopts different destruction efficiencies before and after the galactic wind.

We assume that dust accretion occurs only during the starburst epoch in dense molecular clouds, where volatile elements can condensate onto pre-existing grain cores, producing a volatile component called the mantle (Dwek 1998). Therefore, after the galactic wind occurs and star formation stops, only dust production from long-living stars remains.

2.4. The models

A comprehensive list of all the models is presented in Table 1. In the same table, we show the predicted average stellar abundance ratios (see Pipino et al. 2006, 2008, for their definitions and related discussion). The reader should note that once the yields and the SNIa progenitors are specified, the abundances in the stars do not change. We therefore report them only once for each “class” of models, irrespective of the t > tgw evolution. The predicted abundance and abundance ratios agree very well with the data of Graves et al. (2007). In particular, in models of the classes “1” and “4” – which basically correspond to the models presented in Pipino & Matteucci (2004) and Pipino et al. (2009a) – the [Fe/H] is found to be mildly super-solar, the Mg (as well as the α elements as a whole) is enhanced, while the Ca tracks more closely Fe rather than other α elements, since it is produced by SNIa in a non-negligible way (see Pipino et al. 2009a). Model 5a has very few SNIa at t < tgw, hence a very high α-enhancement, even higher than the observations. Models of the classes “2” and “3” are in between these two extremes and in broad agreement with observations (e.g. Graves et al. 2007). Model 2 predictions are also those that most closely match the observationally inferred stellar Fe and Mg abundances (Thomas et al. 2005; Humphrey & Buote 2006) for the specific case of NGC 4472. Unfortunately, we cannot derive the O, Si, and Ni abundances in integrated stellar spectra, therefore the models are unconstrained in this respect. We predict that the stellar  [O/Mg]  =  + 0.1 dex. This is naturally expected from the specific choice of the Kobayashi et al. yields. The effect of a change in the SNIa progenitor is at the 0.02 dex level. The SNIa rate versus time is shown in Fig. 1. In particular, we show the rate predicted by models 1a (solid), 4a (dashed), 4c (dot-dashed) and 5a (dot-dot-dashed), respectively. The rate predicted by model 1a is exactly the same for all the other models grouped under the categories 1, 2, and 3. Model 5a exhibits a slower late time decrease in the SNIa with respect to the fiducial case. The shaded area indicates the observed range in clusters and lower density environments (“field”) by Mannucci et al. (2008). The horizontal lines mark an older estimate of the present day rate (Cappellaro et al. 1999), which has been used in many previous works and a rate that is one sixth of the Cappellaro et al. value, as an example of an effective1 SNIa rate adopted by other authors (e.g. Loewenstein & Davis 2010).

Before discussing the metal abundances, we note that these models predict a final ISM mass comparable to the observed one. Pipino et al. (2005) selected the models by requiring that they reproduced the gas/star mass ratio and the LX at the corresponding mass in agreement with observations (and the large observational spread). The models presented in the submitted paper basically differ from those of Pipino et al. (2005) only for the nucleosynthesis, hence we expect the features other than the abundances and abundance ratios to be preserved. The current model predicts no outflow in the final Gyr of evolution, and a final gas mass of  ~ 2 × 109   M⊙. Although the model was not tailored to any specific galaxy, it is useful to compare this value to the reported ISM masses for NGC 4472, which range from Mgas(< 13   kpc) ~ 109   M⊙ (Athey 2003, Chandra data) to Mgas(< 30   kpc) ~ 5 × 109 (Irwin & Sarazin 1996, with older ROSAT data).

3. The Fe abundance in the ISM

In studying the chemical composition of the ISM, we first analyze the iron abundance, which is the most accurately determined of all the metals.

The natural predictions of a monolithic collapse + galactic wind model for the Fe abundance are shown in Fig. 2 (solid lines).The model predictions are qualitatively compared to observations in Fig. 2. In particular, the typical range of observed values (shaded areas, cf. Introduction) are given for reference. The predicted high abundance is a clear consequence of the simplest possible model, where all the iron produced after the cessation of the wind is retained by the galaxies, whereas most of the H present during the star forming phase has been ejected and only a minor fraction is restored by the dying stars (<1.5−2 M⊙). The Fe pollution of the gas is dominated by SNIa ejecta.

thumbnail Fig. 1

SNIa rate (in SNuB) versus time predicted by models 1a (solid), 4a (dashed), 4c (dot-dashed), and 5a (dot-dot-dashed), respectively. The shaded areas give the observed range in clusters and lower density environments by Mannucci et al. (2008), respectively. The horizontal lines mark the present day rate by Cappellaro et al. (1999), that has been used by many previous works and a rate that is one sixth of the Cappellaro et al. value, as adopted by Loewenstein & Davis (2010).

At z ~ 0, these models predict a very high (>0.5 dex) [Fe/H], as expected from the continuous Fe production by SNIa. This is at variance with observations (shaded areas in Fig. 2). However, as opposed to previous models where the predicted Fe abundances were offset from the observed values by a factor of three or more, the latest model predictions are only within a factor of two of the observations. One reason is that updated versions of the SNIa W7 model produce  ~0.6   M⊙ of Fe instead of the classically assumed mass of  ~0.74   M⊙. This difference by itself accounts for a 0.1 dex decrease in the predicted [Fe/H]. In addition, models with different durations of the wind and its mass-loading, will have slightly different final values of [Fe/H] in the gas.

The [Fe/H] in the hot ISM can also be used as an age indicator, because of its strong evolution with time (Fig. 2). Values of [Fe/H]  > 1 are typical of ejecta that do not mix with the ambient medium, and also the likely composition of the wind in its intermediate to late phases, namely when most of the pristine H in the galaxy left over after the star formation process has already been expelled. At very late times, when the hot medium has built-up, the Fe abundance decreases because of both the dilution by dying low-mass stars and the decline in the SNIa rate. Therefore, galaxies with similar stellar mass but different [Fe/H] and LX (which roughly track the hot gas mass) may just be at different stages of the halo build-up.

We note that the observed SNIa present-day explosion rate is shown to have little dependence on the galactic mass (e.g. Mannucci et al. 2008), hence on the luminosity in the optical bands. Therefore, one can naively expect a mild (if any) correlation between the Fe abundance in the hot ISM and the galaxy mass. That is, while the stellar abundances obey a very tight galactic mass-metallicity relationship (e.g. O’Connel 1976), this is not true as far as the hot gas abundances are concerned. This is indeed what is observed by Humphrey & Buote (2006) and predicted by wind models (Pipino et al. 2005).

3.1. Solutions to the theoretical Fe discrepancy in wind models

As discussed in the Introduction, the physical mechanisms often invoked to solve the discrepancy between the predicted (theoretical) Fe abundances and the observed one (see also Renzini et al. 1993; Arimoto et al. 1997), can be roughly grouped into several classes: the differential ejection of Fe hidden in a colder phase (warm gas or dust); a significant dilution by freshly accreted gas with primordial abundances; and the modifications to the SNIa rate (the SNIa progenitor/explosion scenario).

We do not attempt to test all the proposed scenarios, some of which can be safely discussed only by means of hydrodynamical models. Here, we focus on some of them. Nonetheless, we believe that the result will be rather general. In particular, we focus on models with dust (marked with d in Table 1), models with SNIa nucleosynthesis differing from the standard W7 explosion (model 1c and categories 2, 3 in Table 1), and models with modified SNIa rates (categories 4, 5 in Table 1). This third set of models mimics either differential ejection (or cooling) of SNIa ejecta (4) or a different progenitor scenario (5).

thumbnail Fig. 2

Lines: predicted [Fe/H] in the ISM versus time. Shaded region: range of typical observed values from the literature (errors not included). Upper panel: Model 1a (fiducial, solid), Model 1ad (fiducial+dust, dashed). Middle panel: Model 1a (fiducial, solid), Model 2a (WDD1 SNIa, dashed), Model 3a (C-DTT SNIa, dot-dashed). Lower panel: Model 1a (fiducial, solid) compared to Models 4a (dashed), Model 4b (dotted), and Model 5a (dot-dashed) with various SNIa rates.

Pipino (2011; see also Calura et al. 2008) predicted the evolution of the Fe abundance in the hot phase of a giant elliptical galaxy with dust. They assumed that no sputtering2 from the hot ISM occurs and that as much as 80% of SNIa ejecta may condense into dust. While this model may not be realistic, it predicts that the dust mass at z ~ 0 is comparable to the upper limit set by the most recent observations (e.g. Temi et al. 2004). Models with lower dust production by SNIa and/or stronger grain destruction do not meet this requirement. In the case of the maximal production of dust (and minimal destruction), the predicted [Fe/H] in the gas at z ~ 0 can decrease by a factor of three with respect to the standard predictions of galactic wind models, hence reconciling the model with observations. In the less extreme and more realistic case presented here (Model 1ad, dashed line in the upper panel of Fig. 2), dust lowers the predicted [Fe/H] by  ~ 0.1 dex. This is not enough to solve the theoretical Fe discrepancy, although it is likely that the combined effect of dust and the other processes discussed in this section can solve the problem.

In the middle panel of Fig. 2, we show that adopting the SNIa yields of the Maeda et al. (2010) 2D explosion models (Model 3a, dot-dashed line) would reduce the predicted [Fe/H] by 0.1 dex. This change alone is small, but coupled with the dust would suffice to reconcile model predictions with observations. No significant differences from to the fiducial case are found when the WDD1 yields from Iwamoto et al. (1999) are adopted.

Finally, we examine different possibilities grouped under the broad cases 4 and 5 (Fig. 2, lower panel). As we have seen in Sect. 2 (Fig. 1), different progenitors correspond to different SNIa rates. We first tested the empirical SNIa rate proposed by Mannucci et al. (2006). In this case, the total number of SNIa that ever exploded and the present-day SNIa rate are very close to our fiducial model 1a (Matteucci et al. 2006).This happens because the t > 3 Gyr evolution in the predicted SNIa rates are very similar (cf. Fig. 7 in Matteucci et al. 2006; Figs. 3 − 5 in Valiante et al. 2009). However, the distribution in time of the SNIa event changes in a way that affects the fraction of Fe ejected in the wind as opposed to the Fe trapped in the hot ISM. The net effect is a slight decrease in the average SNIa rate in the recent past (t > 6 Gyr) that leads to a reduction in the [Fe/H] abundance by  < 0.1 dex. Therefore, we do not discuss it further. To ensure that the models agree with observations, a more significant (a factor of 6 − 9) reduction in the SNIa rate is required (e.g. Loewenstein & Mathews 1991; Renzini et al. 1993; Loewenstein & Davis 2010). However, these solutions deserve more careful modelling by means of chemical evolution simulations and comparison with the latest observations. We achieved this by reducing the constant A in Eq. (3) by a factor of nine. The group 4 of models differ only in the time at which the transition from A = 0.09 to A = 0.01 occurs. A very early occurrence (at t = tGW, model 4a) is not the best solution, because the model is then unable to maintain a wind. Therefore, even if the total number of SNIa is less, their ejecta accumulate in the hot ISM for a longer time. Model 4c is far more successfull. A similar result can be achieved by adopting a completely different SNIa scenario (DD, model 5a, dotted line in the lower panel of Fig. 2), at the expense of a much lower [Fe/H] during the star forming phase. While all previous models reproduce the [Mg/Fe] ratio observed in the stars of present-day ellipticals, model 5a exceeds the observed value because of the strongly suppressed production of Fe during the star forming phase. This model is also unable to maintain a wind for a long time.

We interpret these results indicating that the effective SNIa rate after the wind should be lower than assumed. However, a change caused by the nature of SNIa progenitors is not necessarily the more accurate physical explanation. Either differential winds or a differential (faster) cooling of SNIa ejecta are possible solutions.

The fiducial model predicts that the [Fe/H] in the ISM is a factor of 2 − 3 higher than the average Fe abundance in stars (cf. Table 1). Here we recall that during the star forming phase, the abundance of a given element in the gas is similar to that in the stellar population that formed most recently and certainly higher than the average abundance of that element in the stars. During the galactic wind phase, most of the gas (hence metals) is instead ejected from the galaxy and pollute the intracluster/intergalactic medium (ICM/IGM). The ISM during later phases is then heavily polluted by SNe Ia. Therefore, there is no reason to expect the Fe abundance in the hot ISM to be similar to that in the stars. However, this is what is observed (e.g. Humphrey & Buote 2006). The models (1, 2, 3, and 4), which we introduced to address the theoretical Fe discrepancy, reduce the [Fe/H] ratio in the ISM with time without changing the average abundance in stars, hence reconciling the models with the observations. Model 5a, on the other hand, strongly affects the average stellar Fe abundance, thus does not work in the right direction. Here we note that the Fe abundance inferred from stellar absorption lines depends on the adopted synthetic simple stellar population3 and it is sometimes confused with the average metallicity ([Z/H]) in stars. Finally, the average abundances derived from the Lick indices, while robust in relative sense (i.e. when comparing two galaxies), may be affected by systematic uncertainties. This implies that the comparison between the ratios in the stars and those in the gas is similarly uncertain.

thumbnail Fig. 3

[α/Fe] abundance ratios versus time. The shaded areas represent the observed values and the 99.6% uncertainties in NGC 4472 from Loewenstein & Davis (2010). Results for [Mg/Fe]. Upper row: fiducial model 1a (solid) compared to model 1afd (dashed). Middle row: fiducial model 1a (solid) compared to models 1c (dotted), 2a (dashed), 3a (dot-dashed), respectively. Lower row: fiducial model 1a (solid) compared to models 4a (dot-dashed) and 4c (dashed), respectively. Results for [O/Mg], [Ca/Fe] and [Si/Fe]. Models are coded as in the [Mg/Fe] column except for the model 1afd and in the upper panel that is replaced by models 1ad.The [Fe/H] evolution from Fig. 2 is also reported for comparison to the specific Fe abundance measured in NGC 4472.

We conclude that models with either a realistic dust treatment or a variation in the yields alone, disagree with the observations, but their combined effect is likely to solve the theoretical Fe discrepancy. However, a change in the effective SNIa rate has a larger impact that is even greater than that of a sudden dilution with pristine gas. In passing, we note that a change in the IMF would not affect the conclusions of this section, if the SNIa rate of such a model is tied to the observational present-day value.

4. Abundance ratios in the ISM

After examining the temporal evolution of the [Fe/H] in the ISM of our models and understanding how the theoretical Fe discrepancy can be resolved, we can have a look at the consequences of these assumptions on the ISM abundance pattern.

Figure 3 shows the temporal evolution predictions of the [α/Fe] ratios for our fiducial model 1a (solid lines). The shaded areas represent the observed range of values in NGC 4472 from Loewenstein & Davis (2010).For simplicity, we use the values obtained with Suzaku, whereas the scatter represents the 99.6% confidence levels4.The [Fe/H] evolution from Fig. 2 is also reported for comparison to the specific Fe abundance measured in NGC 4472. We consider the observations for this single galaxy as a proxy for the typical pattern (see also Kim & Fabbiano 2004; Humphrey & Buote 2006; Ji et al. 2009). We note that when the instrument-to-instrument and galaxy-to-galaxy differences are taken into account the observed range increases. We can clearly see that thehigher than observed Fe abundance predicted by model 1a corresponds to low [α/Fe] ratios, at variance with observations.Models 1afd, 3a and 4c, instead, predict the Fe abundances that are less than 0.1 dex away from the observed range in the specific case of NGC 4472. This discrepancy may stem from the model not being explicitly tailored to reproduce this galaxy properties and there might be small differences between the observed and predicted total gas (and H) content that may compensate for this. Abundance ratios, instead, do not have this problem.Here we recall that, when SNIa ejecta dominate, Si and Ca are expected to be more enhanced than Mg and O, because the former elements are produced in a non-negligible way by SNIa. In contrast, Mg and O are produced during the hydrostatic burning in massive stars, thus their abundances should evolve in lock-step. Model 1a indeed predicts that  [Mg/O]  ~ 0, whereas observations imply that  [Mg/O]  ~ 0.3, namely that the O should be under-produced (or the Mg over-produced) by a factor of two. Therefore we are interested in solutions to the theoretical Fe discrepancy put forward in Sect. 3.1 that lead to specific changes in the predicted abundance ratios and could mitigate the disagreement with observations. A simple dilution of pristine gas, instead, would not affect the abundance ratios.

The top row of Fig. 3 compares the results of the models with dust with the fiducial case. For the dust, we note that Fe and O have different condensation temperatures, Fe being a “refractory” element, hence is more easily prone to dust depletion than O. In contrast, Mg has nearly the same condensation temperature as Fe (Lodders et al. 2003). Therefore, if dust is involved – with the canonical prescriptions by Pipino et al. (2011) – the predicted [O/Fe] ratio in the gas increases (model 1ad), hence improving the agreement with observations. In contrast, the increase (dashed lines in the top row) in the [O/Mg] worsen the departure from observations. At the same time, the predicted [Mg/Fe] ratio remains basically the same, hence remains below the observed value. A preferential condensation of Fe with respect to Mg seems to be suggested also by high-redshift observations of Lyman Break Galaxies (Pipino et al. 2011), but currently no theoretical model for the dust formation can explain this. In addition, Ca and Si have condensation temperatures similar to Fe. For Si, the same indication of a differential dust depletion is inferred in high-redshift objects (Vladilo 2002; Calura et al. 2003; Pipino et al. 2011). However, if Fe preferentially condensed (model 1afd, dot-dot-dashed line), the theoretical predictions would lead to the [Mg/Fe] and [O/Fe] ratios in the hot ISM to increase in lock step. Therefore we would still predict  [Mg/O]  ~ 0, at variance with observations5. This means that the dust alone cannot solve both the Fe discrepancy and the abundance pattern simultaneously.

We now focus on the middle row of Fig. 3, namely on the effects of SNIa nucleosynthesis. Model 1c predictions (namely the case with 5xMg in SNIa yields – dotted lines) represent an improvement to the fiducial case. The predicted [Mg/Fe] remains below the observed value, and the prediction does not gain more than 0.1 dex by adding Fe-only dust (model 2cfd, not shown), although the predicted [O/Mg] ratio is in marginal agreement with the observations. These changes of course do not affect the predictions for [Ca/Fe] and [Si/Fe].

Both the lower Fe production and the increase in the Mg yield for the C-DDT SNIa models ensure that model 3a (dot-dashed lines) is very close to reproduce [Mg/Fe], [O/Mg], and [Si/Fe] simultaneously.We stress that, albeit the agreement still being only at a 3σ level, it may become smaller when the systematic uncertainties (instrument-to-instrument) variations are taken into account. Similarly, taking into account metallicity-dependent yields and/or a higher cutoff for the IMF will improve the agreement (see discussion below). In practice, the yields from Maeda et al. (2010) go in the direction suggested by the empirical yields of François et al. (2004). When this choice for the SNIa yield is coupled to, e.g., only Fe dust and to some dilution, it may reproduce a larger set of observables. Unfortunately, the predictions for [Ca/Fe] do not improve with respect to the fiducial case, hence differing from the observation by  ~0.5 dex. When adopting the WDD1 SNIa yields (model 2a, dashed line), the predictions for the [Ca/Fe] ratio are in good agreement with observations. The [Si/Fe] ratio is recovered, whereas predictions for the [Mg/Fe] and the [O/Mg] ratios basically coincide with those of the fiducial model. As noted by Loewenstein & Davis (2010), the SNIa yields that most closely the Ca abundance fail to reproduce the Ni one (Fig. 4) and vice-versa. Our results agree with those of Loewenstein & Davis (2010). Similar claims have also been made by other authors (e.g. Finoguenov et al. 2002), but their quantitative conclusions are less certain, being based on a direct comparison to the stellar yields, without taking into account recycling. We therefore do not attempt a direct comparison.Furthermore, we note that, while Mg, Si and O have been measured by various authors, the Ca abundance provides a weaker constraint. Therefore, the above attempt to find a model that also fits the [Ca/Fe] ratio should be regarded as just an exercise, until more robust observational estimates become available for a larger number of galaxies. Similar results apply to the predictions for [Ne/Fe], which are not shown here.

We briefly mention that the [α/Fe] ratio in SNII ejecta increases with decreasing metallicity (Kobayashi et al. 2006). As a consequence, if we used the model 3b instead of 3a we would increase each [α/Fe] ratio by  ~0.2 dex at most6, with the largest effect for [Ca/Fe]. Only a fraction of the stars will be formed at such low metallicities. Therefore, the true effect of the metallicity dependent yields by Kobayashi et al. (2006) will probably be  ~0.1 dex.It is worth noting that the [α/Fe] ratios in SNII ejecta increase with stellar mass (cf. Fig. 2 in Kobayashi et al. 2006). If we were to extrapolate this trend and adopt 70 M⊙ as the upper mass limit for the IMF in the models, the predicted [O, Mg/Fe] ratios in the hot ISM might increase by  ~0.1 dex, but [Fe/H] would remain unaffected. We avoid this choice in our fiducial models in order not to introduce the additional uncertainty linked to the extrapolation of behaviors that are (in some cases) far from linear. Developments in this sense would require a more extended grid of SNII yields. Nonetheless, a higher mass limit in the IMF would help to improve the agreement between the most promising models and the observations as far as [O/Fe] and [Mg/Fe] are concerned. This choice would not change, instead, the predicted [O/Mg] ratio, since in the Kobayashi et al. (2006) calculations, their yields exhibit a similar increase with the progenitor mass. However, stars suffer from mass loss that increases with increasing metallicity7. The higher the mass loss, the smaller the He and C cores and, hence, the O production. Therefore, when the effect of the mass loss is accounted for, the predicted [O/Mg] ratio in the gas decreases with metallicity during the star forming phase. This effect has been observed, and explained by means of mass loss in massive stars, in the most metal rich-stars of the Milky Way disc (McWilliam et al. 2008) as well as in the Galactic bulge (Cescutti et al. 2009). If this finding were true, we may expect that some of the gas locked in low-mass metal-rich stars is indeed O-depleted. When these stars expel their envelopes in the planetary nebula phase, they may slightly lower the O/Mg ratio in the ISM.

thumbnail Fig. 4

[Ni/Fe] abundance ratio versus time. The shaded areas represent the observed range of values and the 99% uncertainty. Fiducial model 1a (solid) compared to models 1c (dotted), 2a (dashed), 3a (dot-dashed), respectively.

Finally, we discuss the effects of changing either the SNIa explosion rate or their progenitors (lower panel in Fig. 3). As expected, a suppression of the SNIa rate can easily bring several [α/Fe] ratios closely into agreement with the observations. Nonetheless, these models cannot explain the observed [O/Mg] ratio, nor provide a reasonable fit in the case of [Ca/Fe]. However, the major problem with this scenario is explaining the observed SNIa rate.

5. Discussion

In general, the observed abundance ratios exhibit a pattern in which some of them (Ca, Si) are solar to over-solar, and others solar (Mg), whereas the O is depleted with respect to Fe. This is at variance with what happens in the stars (cf. Table 1), where Mg (and probably O) is enhanced, whereas Ca/Fe is solar, in conflict with the behavior of the [Fe/H] in the ISM, which tracks the average Fe abundance in the stars. Such a clear “asymmetry” (Renzini et al. 1993) between α-enhanced stars, and Fe-enhanced hot ISM is well understood in terms of SNeII, which dominate the early phases in the evolution when the stars are formed, and SNIa which dominate the late time ISM abundance pattern. However, the situation is not so clear-cut and not all the α-elements have the same degree of enhancement (depletion) in the stars (hot ISM). The yields for each given element, as well as the recycling by low-mass single stars do play a role in shaping the abundance pattern. Matteucci & Chiappini (2005), Loewenstein & Davis (2010) stressed that to reproduce the abundance ratios of many elements it is important to ensure that an α-enhanced gas is ejected (recycled) by single low-mass stars. That is, the abundance ratios cannot be interpreted by comparing them directly to the predicted SNIa/SNII yield ratio pattern. This is true even if they involve α-elements, namely elements that one naively expects to be produced on the same (negligible) timescale.

Therefore, we argue that the use of abundance ratios provides new insight into the chemical evolution of elliptical galaxies. Either some dilution/differential ejection or Fe-only dust models help in achieving closer agreement with observables once a suitable modification to the SNIa yield relative to the standard W7 model is adopted. The 2D explosion model C-DDT is the most suitable candidate for reproducing both the ISM [Fe/H] and the [α/Fe] ratios in the specific case of NGC 4472.For this specific galaxy, the average stellar [Fe/H] and [Mg/Fe] ratios are  −0.01(± 0.2) dex and 0.26(± 0.03) dex, respectively (Humphrey & Buote 2006; Thomas et al. 2005), hence all models 1, 2, 3, and 4 are consistent to within 1σ as far as the Fe abundance is concerned. These models are consistent with the observationally inferred stellar [Mg/Fe] ratio to within 2σ8, the closest match being given by model 2. As already discussed, model 5 is at odds with the stellar abundance pattern. An interesting follow-up study would be to (re-)derive the stellar abundances for a more extended set of elements by using newer stellar models (e.g. Graves & Schiavon 2008; Thomas et al. 2010) in a sample of galaxies that have homogeneous X-ray observations, in the spirit of Humphrey & Buote (2006).

Finally, we mention alternative scenarios that are not explored here. Hierarchical models (e.g. Kawata & Gibson 2003; Bekki 1998; Cox et al. 2006), in general, do not give satisfactory answers for the opposite reason, namely they predict a too low Fe abundance in the ISM. We note that some of these models are based on simulations in which equal mass disks merge and that have well-known difficulties in explaining the chemical properties of the stars in elliptical galaxies (Ostriker 1980; Thomas 1999, Pipino & Matteucci 2006; Pipino et al. 2009b). Other models incorporate a galaxy formation process that is more similar to the monolithic one (e.g. Kawata & Gibson 2003), although they are characterized by strongly under-solar  [α/Fe]  ratios.

A larger contribution from SNeII may be invoked to explain the observed abundance pattern. This can be easily done by invoking a flatter (e.g. x = 0.95) IMF than the Salpeter one. In this particular case, the [O/Mg] ratio will not change, hence a fix to the SNIa nucleosynthesis will still be required. Moreover, for a given set of SNIa progenitors and the requirement that the model still reproduces the present-day SNIa rate, the predicted [Fe/H] will still be higher than the observed one. Finally, if a flat IMF is maintained for the entire galactic evolution, the larger amount of metals promptly released by SNeII, will cause the stars of the galaxies to be too metal-rich at variance with observations (Pipino & Matteucci 2004) and will not help in reproducing the observed trend of the stellar [Mg/Fe] with galactic mass (Nagashima et al. 2005). If the flat IMF is confined only to the very early phases in which the so-called Pop III (metal-free) stars formed, this regime is so short in time that very few stars are created, compared to the total, therefore their impact should be minimal (e.g. Matteucci & Pipino 2005).

6. Conclusions

The galactic wind models well reproduce the abundance pattern in stars of elliptical galaxies, whereas they predict too much Fe to be released in the hot ISM by SNIa. Several solutions have been put forward, which basically tell us that what happens after the galactic wind phase is a rather complicated mixture of processes that, perhaps, cannot be entirely explained with 1D symmetrical simulations such as chemical evolution models. We have reviewed several solutions proposed to explain the Fe abundance and the abundance ratios pattern in the hot ISM of elliptical galaxies. We have created a comprehensive grid of models to test these solutions using a full chemical evolution scheme.

For the Fe abundance, we can conclude that in models with either a realistic treatment of the dust or a variation in the yields alone, the disagreement with the observations is strongly reduced. Their combined effect solves the theoretical Fe discrepancy. However, a change in the effective SNIa rate (after the wind) has a greater impact, even larger than that of a sudden dilution with pristine gas. A change caused by the nature of SNIa progenitors is not necessarily the most accurate physical explanation. Either differential winds or a differential (faster) cooling of SNIa ejecta mimicking a reduction in the effective SNIa rate can provide more robust physical explanations. We note that a change in the IMF would not affect the conclusions, if the SNIa rate of such a model were tied to the observational present-day value. However, these models alone cannot explain the observed abundance ratios and the differences between the single α elements.

We consider the 2D explosion model C-DDT as the most promising candidate for reproducing the [Fe/H] and the [α/Fe] ratios observed in both stars and ISM. Only the observed values of Ca cannot be explained,although it should be measured in both a larger number of galaxies and with a smaller uncertainty before reaching firm conclusions. Therefore, we are more optimistic than Loewenstein & Davis (2010), who note that there does not seem to be any combination of nucleosynthetic yields from both SNII and SNIa that produces the observed abundance pattern in the hot ISM. We propose that improvements in the SNIa explosion calculations may offer a final solution in the near future. The Fe-only dust may help in achieving a closer agreement with the observables. Unfortunately, we cannot derive the O, Si, and Ni abundances in integrated stellar spectra, thus some suggested solutions remain unconstrained.

1

Namely the value that most accurately reproduces the Fe abundance as opposed to the true observed SNIa rate.

2

According to Itoh (1989), the density and temperature of the hot ISM in ellipticals are such that the lifetime of a Fe dust grain can be as short as  ~106−7   yr. Therefore, Arimoto et al. (1997) argued that it is unlikely to store a large amount of Fe in dust. This argument is consistent with the relatively low mass of dust that could be observed in lanes and clouds. Recent observations, however, claim that the dust mass in ellipticals could be as high as  ~106−7   M⊙, (e.g. Temi et al. 2004).

3

For instance, in the widely used models by Thomas et al. (2003) [Fe/H] is not an independent quantity, but is derived after the total metallicity and α-enhancement are measured; see the discussion in Pipino et al. (2006).

4

We interpreted the 90% observational uncertainties from the first row of Table 1 in Loewenstein & Davis (2010) as typical  ~1.6σ errors . We then evaluated the errors for the abundance ratios with the standard formulae. We then show the so-calculated 3σ (99.6% regions) error in the plots.

5

Assuming that the high [Mg/O] ratio in the ISM is not an instrumental artifact. Otherwise many more models would fit the observed abundance pattern.

6

The reader should recall that the material produced by SNII is locked-up in low-mass long-living stars and then ejected into the ISM where it mixes with SNIa ejecta.

7

In the gas out of which the star formed.

8

With the additional caveat that the stellar value values are robust only in a relative sense.

Acknowledgments

We warmly thank the referee M. Loewenstein for comments that improved the quality of the paper. Useful comments by D.-W. Kim, C. Kobayashi are gratefully acknowledged. A.P. received support from Italian Space Agency through contract ASI-INAF I/016/07/0. F.M. acknowledges financial support from PRIN2007 MIUR (Italian Ministry of Scientific Research) project Prot. No. 2007JJC53X-001.

References

  1. Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 [Google Scholar]
  2. Arimoto, N., & Yoshii, Y. 1987, AA, 173, 23 [Google Scholar]
  3. Arimoto, N., Matsushita, K., Ishimaru, Y., Ohashi, T., & Renzini, A. 1997, ApJ, 477, 128 [NASA ADS] [CrossRef] [Google Scholar]
  4. Athey, A. E. 2003, Thesis (Ph.D.), University of Michigan, Source DAI-B 64/06, 2713 [Google Scholar]
  5. Athey, A. E., & Bregman, J. N. 2009, ApJ, 696, 681 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bekki, K. 1998, ApJ, 504, 50 [NASA ADS] [CrossRef] [Google Scholar]
  7. Bekki, K., Shioya, Y. 1999, ApJ, 513, 108 [NASA ADS] [CrossRef] [Google Scholar]
  8. Brighenti, F., & Mathews, W. G. 2005, ApJ, 630, 864 [NASA ADS] [CrossRef] [Google Scholar]
  9. Buote, D. A. 1999, MNRAS, 309, 685 [NASA ADS] [CrossRef] [Google Scholar]
  10. Buote, D. A. 2002, ApJ, 574, L135 [NASA ADS] [CrossRef] [Google Scholar]
  11. Buote, D. A., Lewis, A. D., Brighenti, F., & Mathews, W. G. 2003, ApJ, 595, 151 [NASA ADS] [CrossRef] [Google Scholar]
  12. Calura, F., Matteucci, F., & Vladilo, G. 2003, MNRAS, 340, 59 [NASA ADS] [CrossRef] [Google Scholar]
  13. Calura, F., Pipino, A., & Matteucci, F. 2008, A&A, 479, 669 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Cappellaro, E., Evans, R., & Turatto, M. 1999, A&A, 351, 459 [NASA ADS] [Google Scholar]
  15. Cescutti, G., Matteucci, F., McWilliam, A., & Chiappini, C. 2009, A&A, 505, 605 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Ciotti, L., D’Ercole, A., Pellegrini, S., & Renzini, A. 1991, ApJ, 376, 380 [NASA ADS] [CrossRef] [Google Scholar]
  17. Cox, T. J., Di Matteo, T., Hernquist, L., et al. 2006, ApJ, 643, 692 [NASA ADS] [CrossRef] [Google Scholar]
  18. David, L. P., Forman, W., & Jones, C. 1991, ApJ, 376, 380 [NASA ADS] [CrossRef] [Google Scholar]
  19. Faber, S. M., Worthey, G., & Gonzalez, J. J. 1992, in IAU Symp., ed. B. Barbuy, & A. Renzini, 149, 255 [Google Scholar]
  20. Finoguenov, A., & Jones, C. 2001, ApJ, 547, L107 [NASA ADS] [CrossRef] [Google Scholar]
  21. Finoguenov, A., Matsushita, K., Bohringer, H., Ikebe, Y., & Arnaud, M. 2002, A&A, 381, 21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. François, P., Matteucci, F., Cayrel, R., et al. 2004, A&A, 421, 613 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Fujita, Y., Fukumoto, J., & Okoshi, K. 1996, ApJ, 470, 762 [NASA ADS] [CrossRef] [Google Scholar]
  24. Fujita, Y., Fukumoto, J., & Okoshi, K. 1997, ApJ, 488, 585 [NASA ADS] [CrossRef] [Google Scholar]
  25. Gastaldello, F., & Molendi, S. 2002, ApJ, 572, 160 [NASA ADS] [CrossRef] [Google Scholar]
  26. Graves, G. J., & Schiavon, R. 2008, ApJS, 177, 446 [NASA ADS] [CrossRef] [Google Scholar]
  27. Graves, G. J., Faber, S. M., Schiavon, R. P., & Yan, R. 2007, ApJ, 671, 243 [NASA ADS] [CrossRef] [Google Scholar]
  28. Greggio, L. 2005, A&A, 441, 1055 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Greggio, L., & Renzini, A. 1983, AA, 118, 217 [Google Scholar]
  30. Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [NASA ADS] [CrossRef] [Google Scholar]
  31. Hayashi, K., Fukazawa, Y., Tozuka, M., et al. 2009, PASJ, 61, 1185 [NASA ADS] [Google Scholar]
  32. Humphrey, P. J., & Buote, D. A. 2006, ApJ, 639, 136 [NASA ADS] [CrossRef] [Google Scholar]
  33. Irwin, J. A., & Sarazin, C. L. 1996, ApJ, 471, 683 [NASA ADS] [CrossRef] [Google Scholar]
  34. Iwamoto, K., Barchwitx, F., Nomoto, K., et al. 1999, ApJS, 125, 439 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  35. Ji, J., Irwin, J. A., Athey, A., et al. 2009, ApJ, 696, 2252 [NASA ADS] [CrossRef] [Google Scholar]
  36. Kawata, D., & Gibson, B. K. 2003, MNRAS, 340, 908 [Google Scholar]
  37. Kim, D.-W., & Fabbiano, G. 2004, ApJ, 613, 933 [NASA ADS] [CrossRef] [Google Scholar]
  38. Kobayashi, C., Arimoto, N. 1999, ApJ, 527, 573 [NASA ADS] [CrossRef] [Google Scholar]
  39. Kobayashi, C., Umeda, H., Nomoto, K., Tominaga, N., & Ohkubo, T. 2006, ApJ, 653, 1145 [NASA ADS] [CrossRef] [Google Scholar]
  40. Lodders, K. 2003, ApJ, 591, 1220 [NASA ADS] [CrossRef] [Google Scholar]
  41. Loewenstein, M. 2001, ApJ, 557, L573 [NASA ADS] [CrossRef] [Google Scholar]
  42. Loewenstein, M., & Mathews W. G., 1987, Proceedings of the Eighth Santa Cruz Summer Workshop in Astronomy and Astrophysics, Santa Cruz, CA (New York: Springer-Verlag), 96 [Google Scholar]
  43. Loewenstein, M., & Davis, D. S. 2010, ApJ, 716, 384 [NASA ADS] [CrossRef] [Google Scholar]
  44. Loewenstein, M., & Mathews, W. G. 1991, ApJ, 373, 445 [NASA ADS] [CrossRef] [Google Scholar]
  45. Mannucci, F., Della Valle, M., Panagia, N., et al. 2005, A&A, 433, 807 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Mannucci, F., Della Valle, M., & Panagia, N. 2006, MNRAS, 370, 773 [NASA ADS] [CrossRef] [Google Scholar]
  47. Mannucci, F., Maoz, D., Sharon, K., et al. 2008, MNRAS, 383, 1121 [Google Scholar]
  48. Mathews, W. G., & Brighenti, F. 2003, ARA&A, 41, 191 [NASA ADS] [CrossRef] [Google Scholar]
  49. Matsushita, K., Makishima, K., et al. 1998, ApJ, 499, L13 [NASA ADS] [CrossRef] [Google Scholar]
  50. Matsushita, K., Ohashi, T., & Makishima, K. 2000, PASJ, 52, 685 [NASA ADS] [Google Scholar]
  51. Matteucci, F., & Greggio, L. 1986, AA, 154, 279 [Google Scholar]
  52. Matteucci, F., & Chiappini, C. 2005, PASA, 22, 49 [NASA ADS] [CrossRef] [Google Scholar]
  53. Matteucci, F., Panagia, N., Pipino, A., et al. 2006, MNRAS, 372, 265 [NASA ADS] [CrossRef] [Google Scholar]
  54. McWilliam, A., Matteucci, F., Ballero, S., et al. 2008, AJ, 136, 367 [NASA ADS] [CrossRef] [Google Scholar]
  55. Maeda, K., Röpke, F. K., Fink, M., et al. 2010, ApJ, 712, 624 [NASA ADS] [CrossRef] [Google Scholar]
  56. Nagashima, M., Lacey, C. G., Okamoto, T., et al. 2005, MNRAS, 363, L31 [NASA ADS] [CrossRef] [Google Scholar]
  57. Nomoto, K., Hashimoto, M., Tsujimoto, T., et al. 1997, Nucl. Phys. A, A621, 467 [NASA ADS] [CrossRef] [Google Scholar]
  58. O’Connel, R. W. 1976, ApJ, 206, 370 [NASA ADS] [CrossRef] [Google Scholar]
  59. Ostriker, J. 1980, ComAp, 8, 177 [Google Scholar]
  60. Padovani, P., & Matteucci, F. 1993, ApJ, 416, 26 [NASA ADS] [CrossRef] [Google Scholar]
  61. Peterson, J. R., Kahn, S. M., Paerels, F. B., et al. 2003, ApJ, 590, 207 [NASA ADS] [CrossRef] [Google Scholar]
  62. Pipino, A. 2010, HiA, 15, 281 [NASA ADS] [Google Scholar]
  63. Pipino, A., & Matteucci, F. 2004, MNRAS, 347, 968 (PM04) [NASA ADS] [CrossRef] [Google Scholar]
  64. Pipino, A., & Matteucci, F. 2006, MNRAS, 365, 1114 [NASA ADS] [CrossRef] [Google Scholar]
  65. Pipino, A., Kawata, D., Gibson, B. K., & Matteucci, F. 2005, A&A, 434, 553 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  66. Pipino, A., Matteucci, F., & Chiappini, C. 2006, ApJ, 638, 739 [NASA ADS] [CrossRef] [Google Scholar]
  67. Pipino, A., D’Ercole, A., & Matteucci, F. 2008, A&A, 484, 679 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  68. Pipino, A., Chiappini, C., Graves, G., & Matteucci, F. 2009a, MNRAS, 396, 1151 [NASA ADS] [CrossRef] [Google Scholar]
  69. Pipino, A., Devriendt, J. E. G., Thomas, D., Silk, J., & Kaviraj, S. 2009b, A&A, 505, 1075 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  70. Pipino, A., Fan, X. L., Matteucci, F., et al. 2011, A&A, 525, 61 [Google Scholar]
  71. Renzini, A., Ciotti, L., D’Ercole, A., & Pellegrini, S. 1993, ApJ, 416, L49 [NASA ADS] [CrossRef] [Google Scholar]
  72. Sakelliou, I., Peterson, J. R., Tamura, T., Paerels, F. B. S., & Kaastra, J. S. 2002, A&A, 391, 903 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  73. Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
  74. Sanchez-Blazquez, P., Gorgas, J., & Cardiel, N. 2006, A&A, 457, 823 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  75. Tamura, T., Bleeker, J. A. M., Kaastra, J. S., Ferrigno, C., & Molendi, S. 2001, A&A, 379, 107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  76. Tang, S., & Wang, Q. D. 2010, MNRAS, 408, 1011 [NASA ADS] [CrossRef] [Google Scholar]
  77. Tawara, Y., Matsumoto, C., Tozuka, M., et al. 2008, PASJ, 60S, 307 [NASA ADS] [Google Scholar]
  78. Temi, P., Brighenti, F., Mathews, W. G., & Bregman, J. D. 2004, ApJS, 151, 237 [NASA ADS] [CrossRef] [Google Scholar]
  79. Thielemann, F. K., Nomoto, K., & Hashimoto, M. 1996, ApJ, 460, 408 [NASA ADS] [CrossRef] [Google Scholar]
  80. Thomas, D. 1999, MNRAS, 306, 655 [NASA ADS] [CrossRef] [Google Scholar]
  81. Thomas, D., Maraston, C., & Bender, R. 2003, MNRAS, 339, 897 [NASA ADS] [CrossRef] [Google Scholar]
  82. Thomas, D., Maraston, C., Bender, R., & Mendes de Oliveira, C. 2005, APJ, 621, 673 [CrossRef] [Google Scholar]
  83. Thomas, D., Maraston, C., & Johansson, J. 2011, MNRAS, 412, 2183 [NASA ADS] [CrossRef] [Google Scholar]
  84. Valiante, R., Matteucci, F., Recchi, S., & Calura, F. 2009, NewA, 14, 638 [Google Scholar]
  85. van den Hoek, L. B., & Groenewegen, M. A. T. 1997, AAS, 123, 305 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  86. Vladilo, G. 2002, A&A, 391, 407 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  87. Whelan, J., & Iben, I. Jr. 1973, ApJ, 186, 1007 [NASA ADS] [CrossRef] [Google Scholar]
  88. Woosley, S. E., Weaver, T. A. 1995, ApJS, 101, 181 [NASA ADS] [CrossRef] [Google Scholar]
  89. Xu, H., Kahn, S. M., Peterson, J. R., et al. 2002, ApJ, 579, 600 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Model set-up and average stellar abundance ratios.

In the text

All Figures

thumbnail Fig. 1

SNIa rate (in SNuB) versus time predicted by models 1a (solid), 4a (dashed), 4c (dot-dashed), and 5a (dot-dot-dashed), respectively. The shaded areas give the observed range in clusters and lower density environments by Mannucci et al. (2008), respectively. The horizontal lines mark the present day rate by Cappellaro et al. (1999), that has been used by many previous works and a rate that is one sixth of the Cappellaro et al. value, as adopted by Loewenstein & Davis (2010).
In the text
thumbnail Fig. 2

Lines: predicted [Fe/H] in the ISM versus time. Shaded region: range of typical observed values from the literature (errors not included). Upper panel: Model 1a (fiducial, solid), Model 1ad (fiducial+dust, dashed). Middle panel: Model 1a (fiducial, solid), Model 2a (WDD1 SNIa, dashed), Model 3a (C-DTT SNIa, dot-dashed). Lower panel: Model 1a (fiducial, solid) compared to Models 4a (dashed), Model 4b (dotted), and Model 5a (dot-dashed) with various SNIa rates.

In the text
thumbnail Fig. 3

[α/Fe] abundance ratios versus time. The shaded areas represent the observed values and the 99.6% uncertainties in NGC 4472 from Loewenstein & Davis (2010). Results for [Mg/Fe]. Upper row: fiducial model 1a (solid) compared to model 1afd (dashed). Middle row: fiducial model 1a (solid) compared to models 1c (dotted), 2a (dashed), 3a (dot-dashed), respectively. Lower row: fiducial model 1a (solid) compared to models 4a (dot-dashed) and 4c (dashed), respectively. Results for [O/Mg], [Ca/Fe] and [Si/Fe]. Models are coded as in the [Mg/Fe] column except for the model 1afd and in the upper panel that is replaced by models 1ad.The [Fe/H] evolution from Fig. 2 is also reported for comparison to the specific Fe abundance measured in NGC 4472.
In the text
thumbnail Fig. 4

[Ni/Fe] abundance ratio versus time. The shaded areas represent the observed range of values and the 99% uncertainty. Fiducial model 1a (solid) compared to models 1c (dotted), 2a (dashed), 3a (dot-dashed), respectively.

In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.