| Issue |
A&A
Volume 530, June 2011
|
|
|---|---|---|
| Article Number | A41 | |
| Number of page(s) | 17 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201016179 | |
| Published online | 05 May 2011 | |
Evolution of inclined planets in three-dimensional radiative discs
Institut für Astronomie & Astrophysik, Universität
Tübingen,
Auf der Morgenstelle 10,
72076
Tübingen,
Germany
e-mail: bertram.bitsch@uni-tuebingen.de
Received:
22
November
2010
Accepted:
4
April
2011
Context. While planets in the solar system only have a low inclination with respect to the ecliptic there is mounting evidence that in extrasolar systems the inclination can be very high, at least for close-in planets. One process to alter the inclination of a planet is through planet-disc interactions. Recent simulations considering radiative transport have shown that the evolution of migration and eccentricity can strongly depend on the thermodynamic state of the disc. So far, this process has only been studied for a few selected planet masses using isothermal discs.
Aims. We extend previous studies to investigate the planet-disc interactions of fixed and moving planets on inclined and eccentric orbits. We also analyse the effect of the disc’s thermodynamic properties on the orbital evolution of embedded planets in detail.
Methods. The protoplanetary disc is modelled as a viscous gas where the internally produced dissipation is transported by radiation. To solve the equations we use an explicit three-dimensional (3D) hydrodynamical code NIRVANA that includes full tensor viscosity, as well as implicit radiation transport in the flux-limited diffusion approximation. To speed up the simulations we apply the FARGO-algorithm in a 3D context.
Results. For locally isothermal discs, we confirm previous results and find inclination damping and inward migration for planetary cores. For low inclinations (i ≲ 2H/r), the damping is exponential, while it follows di/dt ∝ i-2 for larger i. For radiative discs, the planetary migration is very limited, as long as their inclination exceeds a certain threshold. If the inclination is damped below this threshold, planetary cores with a mass up to ≈33 MEarth start to migrate outwards, while larger cores migrate inwards right from the start. The inclination is damped for all analysed planet masses.
Conclusions. In a viscous disc an initial inclination of embedded planets will be damped for all planet masses. This damping occurs on timescales that are shorter than the migration time. If the inclination lies beneath a certain threshold, the outward migration in radiative discs is not handicapped. However, only planets with a mass up to ≈33 MEarth are prone to this outward migration. Outward migration is strongest for circular and non-inclined orbits.
Key words: accretion, accretion disks / planets and satellites: formation / hydrodynamics / planet-disk interactions / radiative transfer
© ESO, 2011
1. Introduction
Planets in our solar system do not all move in the same plane, but are inclined with respect to the ecliptic. The inclinations are in general small. The highest inclined planet is Mercury (i = 7.01°), and only some of the dwarf planets are inclined much higher (e.g. Pluto at i = 17°, or Eris at i = 44.2°). This low inclination with respect to the ecliptic is typically taken as an indication that planets form within a flattened protoplanetary disc. The observed high i for smaller objects are then a result of gravitational scattering processes in the early solar system evolution. Recently, it has been discovered that a relatively large number of transiting close-in planets in extrasolar systems can be inclined significantly with respect to the stellar rotation axis (see e.g. Triaud et al. 2010). This discovery makes it necessary to take inclination into consideration in both numerical simulations and theoretical considerations of planet-disc interaction.
Starting from early work (Goldreich & Tremaine 1980; Papaloizou & Lin 1984; Ward 1986), the effect a protoplanetary disc has on the migration of the planets has been analysed intensively after the discovery of hot Jupiters close to the star (for a review see Papaloizou et al. 2007). Numerical simulations of planet-disc interactions are a valuable tool for a better understanding. Two-dimensional (2D) studies have been performed for example by Bryden et al. (1999); D’Angelo et al. (2002) and later fully three-dimensional (3D) simulations (D’Angelo et al. 2003; Bate et al. 2003) followed. All these simulations only considered isothermal discs. However, recent studies (starting with the work of Paardekooper & Mellema 2006) have shown that including radiation transport in planet-disc interaction studies resulted in a slowed down or even reversed migration (Baruteau & Masset 2008; Paardekooper & Papaloizou 2008; Paardekooper & Mellema 2008; Kley & Crida 2008; Ayliffe & Bate 2010). All authors agree that the inclusion of radiative transfer is important and that it strongly affects the migration properties of low mass planets (type-I-migration) in discs, even though there are differences in the magnitude of the effect. It also affects whether it actually leads to reversal of migration or only to a slow down.
Recently, we have analysed the disc’s influence on the orbital eccentricity (Bitsch & Kley 2010) for planets of different masses in fully radiative discs. We showed that planet-disc interaction leads quite generally (for all planet masses) to a damping of planetary eccentricity on shorter timescales than the migration timescale. Additionally, planets on eccentric orbits embedded in fully radiative discs only migrate outwards, when the eccentricity is damped to a nearly circular orbit. Clearly, eccentricity destroys the very sensitive corotation torques near the planet, which results in inward migration until the orbit is circularised again.
The effect of disc-planet interaction on inclination has not yet been studied in any wide extent, owing to the heavy computational requirements. Tanaka & Ward (2004) analysed the influence of the disc on the inclination of low mass planets in linear studies. They find an exponential damping for any non-vanishing inclination, but their results are only formally valid for i ≪ H/r. Numerical simulations of inclined planets with higher inclinations than H/r (inclination in radians) have shown that exponential damping may be valid up to i ≈ 2H/r. For planets on higher initial inclined orbits, the damping rate deviates from being exponential, and it can be fitted best with a di/dt ∝ i-2 function (Cresswell et al. 2007). Only low mass planets with a mass of about 20−30 earth masses were considered in these studies. The influence on an inclined Jupiter type planet has been considered by Marzari & Nelson (2009). They find that highly inclined and eccentric planets with Jovian masses lose their inclination and eccentricity very fast (on a timescale of order of 103 years), when entering the disc again. Since a highly inclined planet is only disturbed in a small way by the accretion disc (and vice versa), such a planet is only able to open a gap in the disc, when the inclination drops to i < 10.0°. Terquem & Ajmia (2010) considered inclination evolution utilising a Kozai-type of effect for planets on high inclined and eccentric orbits in the presence of the disc.
In the present work we will extend the work on inclined planets and analyse the effect of planet-disc interaction on embedded planets of all masses. In fully three-dimensional hydrodynamical simulations we will consider isothermal as well as fully radiative discs and study the change in inclination of an embedded planet.
In Sect. 2 we give a short overview of our code and numerical methods. In Sect. 3 we measure the change of inclination and semi-major axis for 20 MEarth planets on fixed circular inclined orbits and then let these planets evolve their orbits in the disc due to the torque acting on the planet form the disc in Sect. 4. In Sect. 5 we study the influence of the planetary mass on the evolution of planets on inclined orbits. In Sect. 6 we follow the evolution of 20 MEarth planets on eccentric and inclined orbits. In Sects. 3 to 6 we also point out the differences between the isothermal and fully radiative simulations. Finally we summarise and conclude in Sect. 7.
2. Physical modelling
The protoplanetary disc is modelled as a 3D, non-self-gravitating gas whose motion is described by the Navier-Stokes equations. We treat the disc as a viscous medium, where the dissipative effects can then be described via the standard viscous stress-tensor approach (e.g. Mihalas & Weibel Mihalas 1984). We also assume that the heating of the disc occurs solely through internal viscous dissipation and ignore the influence of additional energy sources (e.g. irradiation form the central star). This internally produced energy is then radiatively diffused through the disc and eventually emitted from its surface. For this process we use the flux-limited diffusion approximation (FLD, Levermore & Pomraning 1981), which allows us to treat the transition from optically thick to thin regions as an approximation. A more detailed description of the modelling and the numerical methodology is provided in our previous papers (Kley et al. 2009) and (Bitsch & Kley 2010). Compared to our previous papers, we now extend the simulations by including planets with different masses on inclined orbits.
2.1. General setup
An important issue in modelling planetary dynamics in discs is the gravitational potential of the planet since this has to be artificially smoothed to avoid singularities.
While in two dimensions a potential smoothing takes care of the otherwise neglected
vertical extension of the disc, in three dimensional simulations the most accurate
potential should be used. As the planetary radius is much smaller than a typical grid
cell, and the planet is treated as a point mass, a smoothing of the potential is required
to ensure numerical stability. In Kley et al.
(2009) we have discussed two alternative prescriptions for the planetary
potential. The first is the classic ϵ-potential 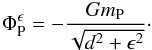 (1)Here
mP is the planetary mass, and
d = |r − rP|
denotes the distance of the disc element to the planet. This potential has the advantage
that it leads to very stable evolutions when the parameter ϵ (stated in
units of the Hill radius) is not too small, i.e. is a significant fraction of the
Roche-lobe size. The disadvantage is that for smaller ϵ, which would
yield a higher accuracy at larger d, the potential becomes very deep at
the planetary position. Additionally, due to the long range nature, the potential differs
from the exact one even for medium to larger distances d from the planet.
(1)Here
mP is the planetary mass, and
d = |r − rP|
denotes the distance of the disc element to the planet. This potential has the advantage
that it leads to very stable evolutions when the parameter ϵ (stated in
units of the Hill radius) is not too small, i.e. is a significant fraction of the
Roche-lobe size. The disadvantage is that for smaller ϵ, which would
yield a higher accuracy at larger d, the potential becomes very deep at
the planetary position. Additionally, due to the long range nature, the potential differs
from the exact one even for medium to larger distances d from the planet.
To resolve these problems at small and large d simultaneously, we have
suggested the following cubic-potential (Klahr & Kley 2006; Kley et al.
2009) ![\begin{equation} \Phi_{\rm P}^{\rm cub} = \left\{ \begin{array}{cc} - \frac{m_{\rm P} G}{d} \, \left[ \left(\frac{d}{r_{\rm sm}}\right)^4 - 2 \left(\frac{d}{r_{\rm sm}}\right)^3 + 2 \frac{d}{r_{\rm sm}} \right] \quad & \mbox{for} \quad d \leq r_{\rm sm} \\[4pt] - \frac{m_{\rm P} G}{d} \quad & \mbox{for} \quad d > r_{\rm sm}. \end{array} \right. \label{eq:cubic} \end{equation}](/articles/aa/full_html/2011/06/aa16179-10/aa16179-10-eq20.png) (2)Here,
rsm is the smoothing length of the potential in units of the
Hill radius. The construction of the planetary potential is in such a way that for
distances larger than rsm the potential matches the correct
1/r potential. Inside this radius
(d < rsm) it is smoothed by a cubic
polynomial. This potential has the advantage of exactness outside the specified
distance rsm, while being finite inside. The
parameter rsm is equal to 0.5 in all our simulations, unless
stated otherwise. The value of the smoothing length of the planetary
potential rsm was discussed in great detail in Kley et al. (2009), where we compared different
smoothing lengths and potential types, resulting in our choice of
rsm = 0.5. In this work we use the cubic-form for the
planetary potential for all fully radiative simulations and for the isothermal simulations
with planets on fixed orbits. We note that for ϵ = 0.25 the depth of the
ϵ-potential at the position of the planet, d = 0,
is identical to the cubic-potential with rsm = 0.5. However,
the difference reaches a maximum of about 20% at d = 0.25, is 10% at
d = 0.5, and slowly diminishes for larger d.
(2)Here,
rsm is the smoothing length of the potential in units of the
Hill radius. The construction of the planetary potential is in such a way that for
distances larger than rsm the potential matches the correct
1/r potential. Inside this radius
(d < rsm) it is smoothed by a cubic
polynomial. This potential has the advantage of exactness outside the specified
distance rsm, while being finite inside. The
parameter rsm is equal to 0.5 in all our simulations, unless
stated otherwise. The value of the smoothing length of the planetary
potential rsm was discussed in great detail in Kley et al. (2009), where we compared different
smoothing lengths and potential types, resulting in our choice of
rsm = 0.5. In this work we use the cubic-form for the
planetary potential for all fully radiative simulations and for the isothermal simulations
with planets on fixed orbits. We note that for ϵ = 0.25 the depth of the
ϵ-potential at the position of the planet, d = 0,
is identical to the cubic-potential with rsm = 0.5. However,
the difference reaches a maximum of about 20% at d = 0.25, is 10% at
d = 0.5, and slowly diminishes for larger d.
Our simulations for moving planets in isothermal discs have shown that in this case the rsm = 0.5 cubic potential yields unstable evolutions. This is due to the relatively steep centre which leads to a significant density enhancement for isothermal discs. Hence, we used in this case directly the much smoother ϵ-potential with ϵ = 0.8 instead, which has been used before in a similar context (Cresswell et al. 2007), without having explored other choices here.
The gravitational torques and forces acting on the planet are calculated by integrating
over the whole disc, where we apply a tapering function to exclude the inner parts of the
Hill sphere of the planet. Specifically, we use the smooth (Fermi-type) function
![\begin{equation} f_b (d)=\left[\exp\left(-\frac{d/R_{\rm H}-b}{b/10}\right)+1\right]^{-1} \label{eq:fermi} \end{equation}](/articles/aa/full_html/2011/06/aa16179-10/aa16179-10-eq32.png) (3)which
increases from 0 at the planet location (d = 0) to 1 outside
d ≥ RH with a midpoint
fb = 1/2 at
d = bRH, i.e. the
quantity b denotes the torque-cutoff radius in units of the Hill
radius. This torque-cutoff is necessary to avoid large, probably noisy contributions from
the inner parts of the Roche lobe and to disregard material that is possibly
gravitationally bound to the planet (Crida et al.
2009). Here we assume (as in our previous paper) a transition radius of
b = 0.8 Hill radii, as a change in b did not influence
the results significantly (Kley et al. 2009).
(3)which
increases from 0 at the planet location (d = 0) to 1 outside
d ≥ RH with a midpoint
fb = 1/2 at
d = bRH, i.e. the
quantity b denotes the torque-cutoff radius in units of the Hill
radius. This torque-cutoff is necessary to avoid large, probably noisy contributions from
the inner parts of the Roche lobe and to disregard material that is possibly
gravitationally bound to the planet (Crida et al.
2009). Here we assume (as in our previous paper) a transition radius of
b = 0.8 Hill radii, as a change in b did not influence
the results significantly (Kley et al. 2009).
2.2. Initial setup
The three-dimensional (r,θ,φ) computational domain consists of a
complete annulus of the protoplanetary disc centred on the star, extending from
rmin = 0.4 to rmax = 2.5 in
units of r0 = aJup = 5.2 AU.
In the vertical direction the annulus extends 7° below and above the disc’s midplane,
meaning 83° < θ < 97°. Here θ denotes the
polar angle of our spherical polar coordinate system measured from the polar axis. The
central star has one solar mass
M∗ = M⊙, and the total disc
mass inside [rmin,rmax] is
Mdisc = 0.01 M⊙. For the
isothermal simulations we assume an aspect ratio of
H/r = 0.037 for the disc, in very close agreement
with the fully radiative models of our previous studies. For the radiative
models H/r is calculated self-consistently from the
equilibrium structure given by the viscous internal heating and radiative diffusion. The
isothermal models are initialised with constant temperatures on cylinders with a profile
T(s) ∝ s-1 with
s = rsinθ. This yields a constant
ratio of the disc’s vertical height H to the radius s.
The initial vertical density stratification is approximately given by a Gaussian:
![\begin{equation} \rho(r,\theta)= \rho_0 (r) \, \exp \left[ - \frac{(\pi/2 - \theta)^2 \, r^2}{2 H^2} \right]\cdot \end{equation}](/articles/aa/full_html/2011/06/aa16179-10/aa16179-10-eq53.png) (4)Here, the density in the
midplane is
ρ0(r) ∝ r-1.5
which leads to a Σ(r) ∝ r−1/2 profile
of the vertically integrated surface density. In the radial and
θ-direction we set the initial velocities to zero, while for the
azimuthal component the initial velocity uφ
is given by the equilibrium of gravity, centrifugal acceleration and the radial pressure
gradient. This corresponds to the equilibrium configuration for a purely isothermal disc.
(4)Here, the density in the
midplane is
ρ0(r) ∝ r-1.5
which leads to a Σ(r) ∝ r−1/2 profile
of the vertically integrated surface density. In the radial and
θ-direction we set the initial velocities to zero, while for the
azimuthal component the initial velocity uφ
is given by the equilibrium of gravity, centrifugal acceleration and the radial pressure
gradient. This corresponds to the equilibrium configuration for a purely isothermal disc.
For our fully radiative model we first run a 2D axisymmetric model (starting from the given isothermal equilibrium) to obtain a new self-consistent equilibrium where viscous heating balances radiative transport/cooling from the surfaces. After reaching that equilibrium, we extend this model to a full 3D simulation, by expanding the grid into φ-direction. The resulting disc for this model has H/r ≈ 0.037 so we choose that value for our isothermal runs.
2.3. Numerical setup
Our coordinate system rotates at the initial orbital frequency of the planet (at r = r0). We use an equidistant grid in r,θ,φ with a resolution of (Nr,Nθ,Nφ) = (266,64,768) active cells for our simulations. At rmin and rmax we use damping boundary conditions for all three velocity components to minimise disturbances (wave reflections) at these boundaries. The velocities are relaxed towards their initial state on a timescale of approximately the local orbital period. The angular velocity is relaxed towards the Keplerian values, while the radial velocities at the inner and outer boundaries vanish. Reflecting boundary conditions are applied for the density and temperature in the radial directions. We apply periodic boundary conditions for all variables in the azimuthal direction. In the vertical direction we set outflow boundary conditions for θmin = 83° and θmax = 97° (the surfaces of the disc). We use the finite volume code NIRVANA (Ziegler & Yorke 1997) with implicit radiative transport in the flux-limited diffusion approximation and the FARGO (Masset 2000) extension as described in Kley et al. (2009).
2.4. Simulation setup
In the first part of our model sequence we consider the orbital evolution of a planet with a fixed mass (20 MEarth) on inclined orbits using different initial inclinations. For comparison we consider isothermal and fully radiative models. Using radiative discs here is a direct extension of a previous study under purely isothermal disc conditions using the same planet mass (Cresswell et al. 2007). We distinguish two different approaches for these 20 MEarth models: first, a model sequence where the planet stays on a fixed inclined orbit and secondly where the planet is free to move inside the computational domain under the action of the planet-disc gravitational forces. For the second models we insert the planet in the disc and let it move immediately, but using a time-dependent mass growth of the planet (through the planetary potential) with a typical switch on time of 10 planetary orbits. For the first set of models the 20 MEarth planet is inserted at the nominal mass in the disc at the start of the simulation. Initially the planet starts at a distance r = aJup = 5.2 AU from the central star. For the fully radiative simulations we set the ambient temperature to a fixed value of 10 K at the disc surface (at θmin and θmax), which ensures that all the internally generated energy is liberated freely at the disc’s surface. This low temperature boundary condition works very well at optically thin boundaries and does not effect the inner parts of the optically thick disc (Kley & Lin 1999; Kley et al. 2009). In the second part of the project we consider sequences of models for a variety of planet masses. We note that a 20 MEarth planet has in our simulations, using our standard resolution, a Roche radius of about 3.3 grid cells. In the last part we limit ourselves to a 20 MEarth planet and simulate the evolution of planets with an initial eccentricity and inclination. For all isothermal simulations, which allow the planet to move freely inside the disc, we use the ϵ-potential. Only for isothermal simulations of planets on fixed inclined orbits, the cubic potential is used. Additionally, the cubic potential is used for all fully radiative simulations as well.
3. Models with an embedded planet on fixed circular inclined orbits
In this section we consider planets on fixed circular and inclined orbits embedded in either isothermal or fully radiative discs. From the disc forces acting on the planet on the fixed orbit we calculate its change of inclination and its migration rate. In this section all simulations use the cubic potential, featuring MPlanet = 20 MEarth, and a semi-major axis of a = 1.0. Our simulations only cover up to 7° above and below the equatorial plane, as the disc gets very thin for these regions. However, we investigate the motion of planets for higher inclinations (for fixed planets up to 15°). The results are not influenced by our limited vertical extent of our computational grid, as the density is very low in the upper layers of the disc.
3.1. Change of inclination
To determine the change of orbital elements for planets on fixed inclined orbits, we
follow Burns (1976). If a small disturbing
force dF (given per unit mass) due to the disc is acting
on the planet, the planet changes its orbit. This small disturbing
force dF may change the planetary orbit in size
(semi-major axis a), eccentricity e and
inclination i. The inclination i gives the angle
between the orbital plane and some arbitrary fixed plane, which is in our case the
equatorial (θ = 90°) plane, which corresponds to the midplane of the
disc. Only forces lying in the orbit plane can change the orbits size and shape, while
these forces can not change the orientation of the orbital plane. In Burns (1976) the specific disturbing force is written as 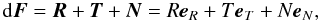 (5)where the
e’s represent an orthogonal unit vector triad. The
perturbing force can be split in these components: R is
radially outwards along r, T
is transverse to the radial vector in the orbit plane (positive in the direction of motion
of the planet), and N is normal to the orbit planet in the
direction R × T.
(5)where the
e’s represent an orthogonal unit vector triad. The
perturbing force can be split in these components: R is
radially outwards along r, T
is transverse to the radial vector in the orbit plane (positive in the direction of motion
of the planet), and N is normal to the orbit planet in the
direction R × T.
Burns (1976) finds for the change of inclination
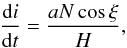 (6)where the numerator
is the component of the torque which rotates the specific angular momentum
H = r × ṙ
about the line of nodes (and which thereby moves the orbit plane). The specific angular
momentum H is defined as
(6)where the numerator
is the component of the torque which rotates the specific angular momentum
H = r × ṙ
about the line of nodes (and which thereby moves the orbit plane). The specific angular
momentum H is defined as
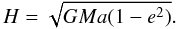 (7)The angle
ξ is related to the true anomaly f in the following
way f = ξ − ω, with ω
being the argument of periapsis. ξ describes the angle between the line
of nodes and the planet on its orbit around the star. For our case of circular orbits the
argument of periapsis ω is zero.
(7)The angle
ξ is related to the true anomaly f in the following
way f = ξ − ω, with ω
being the argument of periapsis. ξ describes the angle between the line
of nodes and the planet on its orbit around the star. For our case of circular orbits the
argument of periapsis ω is zero.
In the simulations the planet’s inclination spans from i = 0.5° to i = 15.0°, in the isothermal as well as in the fully radiative regime. In Fig. 1 we display the rate of change of inclination for planets on fixed inclined orbits in the isothermal and fully radiative scheme, after we average di/dt over 2 planetary orbits, after 150 orbits. As the angle ξ changes after every time step, one needs to average the quantity of di/dt over the time of a planetary orbit to determine an exact value for the change of inclination of the planetary orbit. For both thermodynamic systems the change in inclination is nearly identical and always negative, meaning that moving planets with a non zero inclination lose their initial inclination at a rate according to the current inclination. At i = 4.0° the loss of inclination is at it’s maximum and is reduced for higher and lower inclinations. For high inclined planets (i > 6.0°) this loss is di/dt ∝ i-2, as indicated by the short-dashed fit in black in Fig. 1, and for lower inclined planets (i < 4.0°) the inclination is damped with an exponential decay as indicated by the linear fits in light blue and purple in Fig. 1. This is identical to the behaviour found in Cresswell et al. (2007) and is also confirmed by our simulations of moving planets below.
 |
Fig. 1 Calculated rate of change of the inclination (di/dt) for inclined 20 MEarth planets on fixed circular orbits. Results for the isothermal (red) and fully radiative simulations (dark blue) are shown. Overlayed are in light blue and purple fits for the exponential decay of inclination for small inclinations and in black for the decay di/dt ∝ i-2 for larger inclinations. |
From our measured di/dt for planets on fixed orbits,
we can calculate the inclination damping timescale τinc
according to 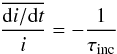 (8)with
i being the inclination of the planet. In the exponential,
small i regime we obtain for the isothermal simulations
τinc = 27 orbits and for the fully radiative simulations
τinc = 20 orbits. Below we compare this to the linear
results of Tanaka & Ward (2004) and moving
planets.
(8)with
i being the inclination of the planet. In the exponential,
small i regime we obtain for the isothermal simulations
τinc = 27 orbits and for the fully radiative simulations
τinc = 20 orbits. Below we compare this to the linear
results of Tanaka & Ward (2004) and moving
planets.
3.2. Change of semi-major axis
The power on the planet determines the change in semi-major axis of the planet, while the torque represents a change in both eccentricity and semi-major axis (Bitsch & Kley 2010). For circular orbits torque and power are identical. For that reason we display and refer only to the torque acting on the planet, instead of mentioning the power as well. A positive torque indicates outward migration, while a negative torque represents inward migration.
In Fig. 2 we display the torque acting on the planet for both thermodynamic systems. The torque is positive for the fully radiative disc and negative for the isothermal disc. In the fully radiative scheme the torque has its maximum at i = 0.0° with a massive loss towards higher inclinations until about i ≈ 4.5°, when the torque is about zero. For even higher inclinations the torque remains at about zero level. In the isothermal case the torque is negative and nearly constant for all inclinations, but with an increase towards higher inclinations.
 |
Fig. 2 Torque acting on a 20 MEarth planet on a fixed inclined circular orbit in dependency of the inclination and thermodynamics of the disc. Torque and power are the same for planets on circular orbits. The torque has been averaged over 20 orbits, taken from t = 180 to t = 200 orbits for the isothermal (solid red line) and from t = 120 to t = 140 for the fully radiative simulation (dashed blue line). |
As for circular orbits the torque determines the change of semi-major axis for our
embedded planets, we expect a positive migration rate for planets in a fully radiative
disc and a negative migration rate for planets in an isothermal disc. To determine a
migration rate for planets on fixed orbits, we follow Burns
(1976) again: ![\begin{equation} \frac{{\rm d}a}{{\rm d}t} = \frac{2}{(G M_*)^{1/2}} a^{3/2} (1-e^2)^{-1/2} \left[ R \, e \sin f + T (1+e \sin f)\right], \end{equation}](/articles/aa/full_html/2011/06/aa16179-10/aa16179-10-eq112.png) (9)where
a is the semi-major axis, e the eccentricity,
f = ξ − ω the true anomaly
and R and T are radial and tangential directions of
the disturbing force, see Eq. (5). Please
note that only forces lying in the orbit plane can change the orbit size, and that for
circular orbits the specific total torque on the planet is simply given by
Γtot = aT, with Ḣ = Γtot.
(9)where
a is the semi-major axis, e the eccentricity,
f = ξ − ω the true anomaly
and R and T are radial and tangential directions of
the disturbing force, see Eq. (5). Please
note that only forces lying in the orbit plane can change the orbit size, and that for
circular orbits the specific total torque on the planet is simply given by
Γtot = aT, with Ḣ = Γtot.
The rate of migration is displayed in Fig. 3. In the fully radiative scheme the planet experiences a positive migration rate (outward migration) for all inclinations smaller than i ≤ 4.5°, but with a strong increase towards lower inclinations (about a factor of 10 for the difference between i = 4.0° and i = 1.5°). For inclinations lower than i ≈ 1.5° the migration rate stays approximately constant. Planets with an inclination of 4.5° and higher seem to be stalled and migrate neither inwards nor outwards. The effects responsible for outward migration seem to be only valid in the small inclined case.
In the isothermal case the migration rate is nearly constant and negative with a slight increase towards higher inclinations, suggesting that an inclined planet will move inwards in the isothermal regime for low inclined planets. Higher inclined planets will move inwards only at a very small rate compared to their low inclined counterparts. For large i the change of semi-major axis approaches zero, as the planet’s orbit is high above the dense regions of the disc, which are capable of influencing the planet’s orbit.
 |
Fig. 3 Calculated rate of change of the semi-major axis (ȧ/a) for inclined 20 MEarth planets on fixed, circular orbits. For inclinations lower than i ≤ 4.5° we observe a positive migration rate, which suggest that low inclinations do not stop outward migration, while we observe a negative migration rate for the isothermal case. |
From these results we conclude that a planet with a non-zero initial inclination will lose this inclination in time. This inclination loss has in principal no effect on the trend of migration, so a planet in a fully radiative disc will migrate outwards, while a planet in an isothermal disc will migrate inwards. In one of the next chapters we will observe moving planets with a non-zero inclination, which will do exactly that.
 |
Fig. 4 Torque density acting on a planet on a fixed inclined orbit in dependency of the inclination of the planet embedded in an isothermal H/r = 0.037 disc (top) and a fully radiative disc (bottom). The snapshots are taken at t = 90 orbits for the isothermal simulations and at t = 150 orbits for the fully radiative simulations. At this time planet-disc interactions are in equilibrium and the planet is at its lowest point in orbit (lower culmination). |
3.3. Torque analysis
To understand the behaviour of the total torque in more detail we now analyse the
space-time variation of the torque of the planet. For that purpose we introduce the radial
torque density Γ(r), which is defined in such a way that the total
torque Γtot acting on the planet is given by
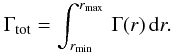 (10)The radial torque
density has been a very useful tool to investigate the origin of the torques in our
previous work on planets on fixed circular orbits. Even though the planet may be on an
inclined orbit, this does not alter our definition of the radial torque
density Γ(r) which is calculated in any case with respect to the
orbital plane of the planet. In Fig. 4 we
display Γ(r) for a selection of our planets in the isothermal and fully
radiative regime.
(10)The radial torque
density has been a very useful tool to investigate the origin of the torques in our
previous work on planets on fixed circular orbits. Even though the planet may be on an
inclined orbit, this does not alter our definition of the radial torque
density Γ(r) which is calculated in any case with respect to the
orbital plane of the planet. In Fig. 4 we
display Γ(r) for a selection of our planets in the isothermal and fully
radiative regime.
 |
Fig. 5 Torque density acting on a 20 MEarth planet on a fixed inclined orbit with i = 2.0° in a fully radiative disc at different phases within its orbit. Integer (half integer) values of the indicated time refer to the upper (lower) culmination. At the intermediate quarterly orbit times the planet moves through the nodal line. |
In the isothermal case the Γ(r)-function follows the same trend for all displayed inclinations. The only difference is near the planet, around the r = 1.0 region. The torque of the low inclined planets declines constantly, while the higher inclined planets (2.0 ≤ i ≤ 4.0) form a little spike in the Γ(r) distribution, which disappears for even higher inclinations again. For higher inclinations the Lindblad-Torques become less and less pronounced, as can be seen in Fig. 4 (top panel). Please keep in mind that for the inclined planets the torque density changes during one orbit, as can be seen from the change in the total torque acting on the planet (top panel in Fig. 6). This is also illustrated in Fig. 5 for the planet with i = 2.0°. It can been seen that for symmetry reasons Γ(r) is identical at upper and lower culmination, and at the crossings of the nodal line, respectively.
 |
Fig. 6 In the top panel we display the evolution of the torque acting on planets in a fully radiative disc on fixed circular, inclined orbits in time. In the bottom panel the normal component of the disturbing force dF, Ncosξ as to be used Eq. (6), is displayed in dependency of time. |
In Fig. 6 the torque acting on planets (please note that for circular orbits torque and power are identical) with different inclinations on fixed circular orbits (top) and the normal component of the disturbing force dF (bottom) for fully radiative discs is displayed. The torque acting on the planets oscillates with time, making two oscillations every orbit. The planet starts at the highest point in orbit (upper culmination) and evolves to the lowest point in orbit (lower culmination) in the time of half an orbit. Then the planet moves to the upper culmination again and reaches it at the end of the orbit. The planets with a lower inclination (i < 4.0°) have clearly a positive average torque, while for the planets with higher inclinations positive and negative contributions approximately cancel out such that the average total torque is very small (see Fig. 2). Higher inclinations also trigger higher amplitudes in the torque distributions. These amplitudes in the torque distribution suggest oscillations in the evolution of the semi-major axis of the planet (to a small degree), which are visible when the planet is allowed to move freely inside the disc (see Figs. 12, 13 and 15).
In the lower panel in Fig. 6 the normal component of the disturbing force Ncosξ is displayed. Ncosξ oscillates also twice in every orbit, as the torque, but it is slightly shifted with respect to the torque. Negative values indicate a reduction of inclination, while a positive force indicates an increase of inclination. The oscillations in Ncosξ indicate oscillations in the inclination, when the planet is allowed to move freely in the disc. Indeed, in case the planet moves inside the disc, these oscillations in the inclination become visible at the beginning of the simulations (see Figs. 11, 13 and 14 below). On average the normal component of the disturbing force Ncosξ is negative, which indicates inclination damping for all simulated inclinations, see Fig. 1.
For simulations in the isothermal regime, the results are nearly identical, with only one exception: the overall torque is negative, which results in inward migration. The normal component of the disturbing force, Ncosξ, is also very similar compared to the results in the fully radiative regime. We therefore forgo to discuss the isothermal results in detail at this point.
To illustrate the dynamical impact of the planet on the disc, we display the surface density of planets with i = 1.0° and i = 4.0° in Fig. 7.
 |
Fig. 7 Surface density for 20 MEarth planets on fixed circular inclined orbits embedded in an isothermal H/r = 0.037 disc with i = 1.0° (top) and i = 4.0° (bottom). The planet is at its lowest point in orbit (lower culmination) at the time of the snapshot. |
The surface density of the i = 1.0° planet is very similar to that of a non inclined planet (not displayed here, but compared to bottom picture of Fig. 8 in Kley et al. 2009), and the torque density Γ(r) is nearly identical. The surface density also shows no disturbances for the i = 1.0° planet, so that we only observe the Lindblad Torques in the isothermal case, see Fig. 4. However, the surface density of the higher inclined planet (i = 4.0°) shows density disturbances near the planet. For the i = 1.0° we also observe a higher density in the planets surroundings and a stronger pronounced spiral wave compared to higher inclined planets. The less pronounced spiral wave for the higher inclined planets leads to a smaller Lindblad Torque for these planets compared to the low inclined planets, which can be seen clearly in Fig. 4.
 |
Fig. 8 Density (in g/cm3) of a r − θ-slice through the isothermal H/r = 0.037 disc with embedded 20 MEarth planets on fixed circular inclined orbits with i = 1.0° (top) and i = 4.0° (bottom). The planet is at its lowest point in orbit (lower culmination) at the time of the snapshot. |
In Fig. 8 the density of a r − θ slice through the planets in the isothermal H/r = 0.037 disc is display. The planets are at their lowest point in orbit when the snapshot was taken. On the one hand, the i = 1.0° planet (top) has accumulated more mass in its vicinity as the i = 4.0° planet (bottom), as the density in the middle of the disc is higher and thus it is easier to accumulate mass. On the other hand, the higher inclined planet seems to disturb the density structure of the disc stronger than the lower inclined planet. This distortion in the density distribution in the r − θ plane reflects in the distorted surface density structure, displayed in the bottom picture of Fig. 7.
In the fully radiative case, the torque density (Fig. 4) shows the well discussed spike in the torque distribution at r = 0.984 (see Kley et al. 2009). This spike is more pronounced for lower inclinations (i ≤ 2.0°) and is reduced for the higher inclinations. This reduction for the torque density at r = 0.984 causes the total torque to decrease for higher inclinations, see Fig. 2. For higher inclinations the Lindblad Torques are also reduced compared to the lower inclined planets.
 |
Fig. 9 Surface density for 20 MEarth planets on fixed circular inclined orbits embedded in a fully radiative disc with i = 1.0° (top) and i = 4.0° (bottom). The planet is at its lowest point in orbit (lower culmination) at the time of the snapshot. |
In Fig. 9 the surface density of 20 MEarth planets in a fully radiative disc with i = 1.0° and i = 4.0° are displayed. The overall surface density distribution of the i = 1.0° planet is nearly identical with the surface density distribution of a non inclined planet (see Fig. 12 in Kley et al. 2009), which is also supported by the identical torque density distributions. The surface density for the higher inclined planet (i = 4.0°) on the other hand shows some differences. The density ahead of the planet (r < 1.0 and φ > 180°) is reduced and the density behind the planet (r > 1.0 and φ < 180°) is increased compared to the density distribution of the low inclined (i = 1.0°) planet. This loss and gain of density results directly in a reduced spike (at r = 0.984) in the torque density (Fig. 4), which reduces the total torque. The density inside the planet’s Roche lobe is also reduced in the high inclined case, as the planet can not accumulate as much mass as a lower inclined planet. This feature was also visible in the isothermal case, but keep in mind that the planet in the isothermal case accumulates more mass than in the fully radiative disc. Also the density in the spiral waves is reduced in the high inclined case, which results in lower Lindblad Torques compared to the low inclined case, see Fig. 4.
 |
Fig. 10 Density (in g/cm3) of a r − θ-slice through the fully radiative disc with embedded 20 MEarth planets on fixed circular inclined orbits with i = 1.0° (top) and i = 4.0° (bottom). The planet is at its lowest point in orbit (lower culmination) at the time of the snapshot. |
In Fig. 10 the density through the fully radiative disc (a r − θ slice) at the planets location for i = 1.0° and i = 4.0° is displayed. Clearly the higher inclined planet accumulated less mass than the lower inclined planet, as the density in the surroundings of the high inclined planet is reduced compared to the discs midplane. Also the higher inclined planet seems to disturb the disc’s density more than the lower inclined planet, which results in small fluctuations in the surface density, see Fig. 9. The little fluctuations in the surface density are less compared to the isothermal case, as the radiative transport/cooling smoothes the density in the disc and the planet does not accumulate as much mass as in the isothermal case, which disturbs the density structure as well.
In the r − θ slices of the disc, the difference in the mass accumulation of the planet in the isothermal and fully radiative regime is very obvious. This effect is caused by the thermodynamics of the disc, as the isothermal disc is unable to heat and cool, the planet can accumulate more mass as in the fully radiative regime. Nevertheless, only in the fully radiative regime the calculated change of semi-major axis predicts outward migration for planets on fixed orbits with i0 ≤ 4.5°.
4. Moving planets on initially inclined orbits
In the previous section we calculated the change of inclination and semi-major axis for 20 MEarth planets on fixed inclined orbits in the isothermal and fully radiative regime. The results stated that the planets will lose their inclination in time and will migrate inwards in the isothermal and outwards in the fully radiative scheme (for i0 ≤ 4.5°). We now want to confirm these results by allowing the planets to move freely inside the disc. For the following simulations we use our standard resolution, with a 20 MEarth planet embedded at r = 1.0 with different inclinations i. The discs thickness is H/r = 0.037. In the first 10 orbits of the planetary evolution the mass of the planet will rise until it reaches its desired mass of 20 MEarth after 10 planetary orbits. This way the disc will not be disturbed as much as by putting a planet with its full mass inside the disc at once. By monitoring inclination and semi-major axis at the same time for a given planet, we can easily observe what influence the inclination has on the migration of the planet. The planets embedded in the isothermal disc are modelled with the ϵ-potential, using rsm = 0.8, while the planets embedded in the fully radiative disc are modelled using the cubic potential with rsm = 0.5.
4.1. Isothermal disc
Our disc only extends 7° above and below the discs midplane, so when simulating a planet with a higher inclination than that, it is not fully embedded in the disc any more. As the disc’s material is concentrated mainly in the middle of the disc, the material high above or below the disc’s midplane will only have a small effect on the planet anyway. Test calculations with an extended θ region of the disc (10° above and below the discs midplane) and an i0 = 8.0° 20 MEarth planet have shown that we do not need such a high extension above and below the disc. The aspect ratio for the disc is H/r = 0.037 in the isothermal case, as this aspect ratio corresponds to the aspect ratio of the fully radiative disc.
In Fig. 11 the evolution of inclination of a 20 MEarth planet in an isothermal H/r = 0.037 disc is displayed. After the planets have reached their final mass after 10 orbits, the inclination begins to drop immediately. Up to i = 4.0° the planet’s loss of inclination is increasing, while for even higher inclinations the damping of inclination is slowed down again (see Fig. 1). High inclined planets will first lose inclination at a quite slow rate, but as their inclination is damped the damping rate increases until the inclination reaches ≈4.0° and will slow down after that until the planets inclination is damped to zero. This results confirms our results for planets on fixed orbits.
 |
Fig. 11 Time evolution of inclination for 20 MEarth planets with individual starting inclinations ranging from i = 1.0° to i = 8.0° in an isothermal H/r = 0.037 disc. The damping of inclination follows the trend of the calculated change of inclination for planets on fixed orbits, see Fig. 1. The black dotted lines indicate our manual fitting with τinc = 23 and in the i0 = 8.0° case an additional fit provides for a di/dt ∝ i-2 fit. |
When the planet remains in the main body of the disc for
i < H/r
(i in radians), the damping of inclination is
exponential: di/dt ∝ − i.
By following Tanaka & Ward (2004) the
linear damping rate for a small planet mass and a small inclination can be obtained:
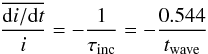 (11)with
the characteristic time
(11)with
the characteristic time 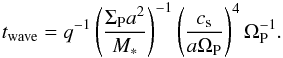 (12)In Table 1 we display τinc for the
isothermal and fully radiative simulations. We compare the linear estimate according to
Eqs. (11) and (12) with our full non-linear results from the
fixed and moving planet simulations.
(12)In Table 1 we display τinc for the
isothermal and fully radiative simulations. We compare the linear estimate according to
Eqs. (11) and (12) with our full non-linear results from the
fixed and moving planet simulations.
Exponential damping rate τinc (in orbits), obtained from our isothermal and fully radiative simulations for three studied cases of planets in discs compared with the linear rate, as given by Tanaka & Ward (2004).
For our isothermal H/r = 0.037 simulations we estimate a linear damping time scale of τinc = 14.2 orbits, which is about a third smaller than our obtained result τinc = 23 for planets on moving orbits (see fits in Fig. 11). The difference between our actual fit and the linear value can be caused by the relatively small aspect ratio of the disc (H/r = 0.037), because the linear theory is formally valid only for embedded planets with H ≫ RHill. Below, we present additional result for an H/r = 0.05 disc and find indeed better agreement of linear and fully non-linear results. However, our obtained τinc = 23 for moving planets is very close to the predicted damping time scale of τinc = 27 for planets on fixed orbits, demonstrating the consistency of our results.
The exponential damping law should be only valid up to i ≈ H/r, but Cresswell et al. (2007) stated that it is valid up to i ≈ 2H/r, which in fact reflects our findings. The higher inclined planets do not lose inclination with an exponential rate at the beginning of the simulations, but with di/dt ∝ i-2. This is also indicated through the black dotted line in Fig. 11 for the i0 = 8.0° planet. As the planets lose their inclination, the damping becomes exponential again (at about i ≈ 3.0°).
In Fig. 12 the evolution of the semi-major axis in an isothermal H/r = 0.037 disc is displayed. After a few orbits the semi-major axis decreases for all planets. During time the semi-major axis shrinks more and more, as you would expect from low mass planets in an isothermal disc. In the beginning the planets with i0 = 8.0° and i0 = 6.0° have a slower inward migration rate than the other planets, but as the inclination is damped in time, the inward migration settles for the same rate for all planets, although it takes about 80 orbits for the i0 = 8.0° planet. The initial higher inclination just delays the inward migration for a few planetary orbits, as could be expected from our results for planets on fixed orbits, see Fig. 3.
The observed migration rate for all planets is constant after the inclination has been damped. The black dashed line in Fig. 12 indicates a linear fit for the evolution of the semi-major axis with ȧ = −3.45 × 10-4/orbit. This decrease of semi-major axis from planets on moving orbits is within 15% of the result for planets on fixed orbits in Fig. 3. The slight difference may be just due to the different setup, stationary versus moving and cubic versus epsilon potential. Additionally, the fit in Fig. 12 is for a later evolutionary time, where the planet has already lost a few percent of its semi-major axis.
 |
Fig. 12 Time evolution of semi-major axis for 20 MEarth planets with individual starting inclinations ranging from i = 1.0° to i = 8.0° in an isothermal H/r = 0.037 disc. The dashed black line indicates a fit to the results with a slope of −3.45 × 10-4/orbit. The change of semi-major axis follows the trend of the change determined for planets on fixed orbits, see Fig. 3. |
In our past simulations we found a dependence of the migration rate/torques due to the aspect ratio of the disc (Kley et al. 2009; Bitsch & Kley 2010). It is now logical to assume that the aspect ratio of a disc will change the damping of inclination for inclined planets as well. In Fig. 13 we display the evolution of the semi-major axis (top) and inclination (bottom) of planets embedded in an isothermal H/r = 0.05 disc.
The inward migration of the planets in the H/r = 0.05 disc is slower compared to planets embedded in a H/r = 0.037 disc, which is in agreement with Tanaka et al. (2002). The inclination damping is slower in the H/r = 0.05 disc by a factor of 2 to 3. Nevertheless, the final outcome is the same, an initially high inclination reduces the inward migration in the beginning, but as inclination is damped, the inward migration settles for the same rate for all the inclinations (but with different rates for different aspect ratios).
The theoretical, linear damping of inclination obtained by following Tanaka & Ward (2004) is τinc = 47.25 orbits (Eq. (12)), which is slightly smaller than our fitted value of τinc = 53 orbits (Fig. 13, bottom). The numerically obtained ratio of the migration rates (53/23 ≈ 2.3) differs from the theoretical linear ratio of (0.05/0.037)4 ≈ 3.3. As the colder disc makes linear theory less applicable in these circumstances, we can infer that the results obtained for the larger H/r = 0.05 disc are more accurate. The numerical exponential decay in the simulations with moving planets matches our estimated rate for planets on fixed orbits quite well. The higher pressure inside the disc seems to have a smoothing effect on the damping, resulting in more accurate results for discs with higher aspect ratio.
For the moving planets, the measured migration rate (da/dt) for the H/r = 0.037 disc is approximately larger by a factor of (0.05/0.037)2 compared to the H/r = 0.05 disc (see dashed black line fit in Fig. 13, top), which is to be expected in the linear case.
 |
Fig. 13 Time evolution of the semi-major axis (top) and inclination (bottom) of a 20 MEarth planet in an isothermal H/r = 0.05 disc. The planets initial inclinations reach from i0 = 1.0° to i0 = 8.0°. The dashed black line in the top panel indicates a linear fit to the results with a slope of −2 × 10-4/orbit. The black dotted lines in the evolution of inclination (bottom) indicate our manual fitting with τinc = 53. |
In an isothermal disc, inclined planets lose inclination and semi-major axis immediately after they are released in the disc, as predicted by our calculations of the change of inclination and semi-major axis for planets on fixed orbits. The migration rate is the same for all initial inclinations, a higher inclination just delays the inward migration for a few orbits.
4.2. Fully radiative disc
In the fully radiative regime we simulate planets to an inclination up to i = 8.0°. As always we use a 2D model in r − θ direction in the radiative equilibrium for the starting configuration of our 3D fully radiative disc. This procedure is described in more detail in (Kley et al. 2009). As in the isothermal case, the planet needs 10 planetary orbits to reach its full mass.
In Fig. 14 the change of inclination for moving planets in a fully radiative disc is displayed. The inclinations range from i0 = 1.0° to i0 = 8.0°. The planets inclination reduces as soon as the planet is released in the disc according to the rate found in Fig. 1. After about 160 orbits the inclination of all planets has reached zero, so that the planet is now orbiting in the equatorial plane.
 |
Fig. 14 Time evolution of inclination for 20 MEarth planets with individual starting inclinations ranging from i = 1.0° to i = 4.0° in a fully radiative disc. The damping of inclination follows the trend of change of inclination for planets on fixed orbits, see Fig. 1. The black dotted lines indicate our manual fitting with τinc = 26.5 for planets with i0 = 2.0°, 4.0°, 6.0° and i0 = 8.0°, which seems very good in the beginning/middle phase of the inclination damping. In the i0 = 8.0° case an additional fit provides for a di/dt ∝ i-2 fit in the beginning of the evolution. |
The estimated linear value for the damping of inclination in the radiative disc is τinc = 27.76 orbits (Eq. (12)), which lies within about a few percent of our fitted value of τinc = 26.5 orbits for moving planets. The difference with the calculated damping timescale τinc = 20 orbits for planets on fixed orbits is slightly larger in this case (see Table 1). But one should keep in mind as well that the exponential fit is valid for very low inclinations in the isothermal case as well, while it is only valid down to ≈0.5° in the fully radiative scheme.
On the other hand, the decay of inclination for initially high inclined planets fits even a little better than in the isothermal case, and the trend of an di/dt ∝ i-2 decay is clearly visible.
In Fig. 15 the evolution of the semi-major axis of planets with initial inclination is displayed. After the planets have reached their final mass at 10 planetary orbits, the initially lower inclined (i up to 4.0°) planets start to migrate outwards as expected from Fig. 3. The migration rates for planets on fixed orbits also matches nicely with the determined migration rate of 1.35 × 10-3/orbit for planets on moving orbits. The two higher inclined planets first stay on their initial orbit before they start their outward migration. It seems that the planet has to lose a certain amount of inclination before it can start to migrate outwards. This result is in agreement with our observations for planets on fixed inclined orbits. A higher inclination weakens the torque responsible for outward migration and if the inclination is too high, the outward migration stops.
The planets seem to migrate outwards at nearly the same speed for all initial inclinations up to 4.0°. But before the planets start to migrate outwards their initial inclination is damped by about 25% for all initial inclinations, which explains the similar migration speed for these planets, see Fig. 3.
 |
Fig. 15 Time evolution of semi-major axis for 20 MEarth planets with individual starting inclinations ranging from i = 1.0° to i = 8.0° in a fully radiative disc. The change of semi-major axis follows the trend of change for planets on fixed orbits, see Fig. 3. The dashed black line in the top panel indicates a linear fit to the results with a slope of 1.35 × 10-3/orbit. |
Low inclinations seem to have only little effect on the migration of planets in the fully radiative scheme, but if the inclination of the planet is so high that its orbit is at some times high above the midplane of the disc, the disc becomes so thin that outward migration is not possible any more.
5. Planets with different masses
Small inclinations seem to have no big effect on migration for a 20 MEarth planet on a circular orbit in the isothermal or fully radiative scheme. The planet’s inclination is reduced in both thermodynamic systems and it migrates inwards in the isothermal and outwards in the fully radiative scheme. In our previous work we found that planets up to ≈33 MEarth migrate outwards in a fully radiative disc (Kley et al. 2009). Planets with higher planetary masses migrate inwards, and considering our previous results it is unlikely that inclination changes this. Nevertheless we here present simulations of planets with masses ranging from 20 up to 100 MEarth in an isothermal H/r = 0.037 disc and in a fully radiative disc. We only present results for moving planets with our usual tool for increasing the planetary mass to its designated mass during the first 10 orbits.
For all simulations we limit ourselves to the cases of i0 = 1.0° and i0 = 4.0° for all planetary masses, in the isothermal H/r = 0.037 disc as well as in the fully radiative disc. Additionally, we display Jovian mass planets with inclinations up to 15° in the isothermal case. For the isothermal case, we again use the ϵ-potential with a smoothing length of rsm = 0.8, as it turned out to be more stable in the isothermal case than the cubic potential, while we use the cubic rsm = 0.5 potential for the fully radiative simulations.
In all simulations displayed in this section the planet is inserted in the disc and starts to move immediately. This means that a massive planet will open a gap in time in the initially unperturbed disc. If the planet were allowed to open a gap before it starts to move in the disc, the evolution of the planet, especially the evolution of inclination, would be slower since an open gap slows down migration and inclination damping.
5.1. Isothermal disc
In Fig. 16 the evolution of inclination for planets with i0 = 1.0° (top) and i0 = 4.0° (bottom) for different planetary masses in an isothermal H/r = 0.037 disc is displayed. The inclination drops immediately after the planet reaches its destined mass at nearly the same rate for all planetary masses in both cases, for the i0 = 1.0° and i0 = 4.0° case. It seems that a higher planetary mass results in a slightly faster damping rate for the inclination. However, when the inclination reaches about 20% of the initial inclination, the 80 and 100 MEarth planets stop their fast inclination damping for a few orbits. After about 150 orbits the inclination of all planets is damped to zero, even for the initially more highly inclined planets.
 |
Fig. 16 Time evolution of the inclination for planets with i0 = 1.0° (top) and i0 = 4.0° (bottom) for different planetary masses in an isothermal H/r = 0.037 disc. |
In Fig. 17 we display the surface densities for planets with different masses for the i0 = 1.0° (top) and i0 = 4.0° (bottom) cases after 60 planetary orbits. The two surface density profiles are very similar, although the planets have a different starting inclination i0 and a different inclination at the time of the snapshot. As the inclination of the i0 = 4.0° and i0 = 1.0° planets evolves very similar (in the trend), it seems not surprising that the surface densities reflect this behaviour. On the other hand, the surface density profiles after 60 orbits do not give a clear hint to explain the slowed down inclination damping for the high mass planets when they reach ≈20% of the initial inclination. As expected, higher mass planets clear deeper and wider gaps inside the disc.
 |
Fig. 17 Surface density for planets on initial inclined, circular orbits with i0 = 1.0° (top) and i0 = 4.0° (bottom) after 60 planetary orbits. |
The measured damping time scale τinc for planets with different planetary masses is displayed in Fig. 18. Starting from the smallest planet in our calculations, the 20 MEarth, the damping time scale reduces until the planets mass is 40 MEarth. For higher mass planets the damping time scale increases again. The increase for the 80 and 100 MEarth planets should be handled with care, as the measurement for these planets is quite difficult due to the bump in the evolution of inclination. If we do not include these two planets in our thoughts, we can safely conclude, that the inclination damping increases with the planetary mass. The inclination of a more massive planet will be damped faster than the inclination of a smaller planet, even more so for radiative discs.
 |
Fig. 18 Measured inclination damping time scale τinc for planets with different planetary masses in the isothermal and fully radiative regime. |
In Fig. 19 the evolution of the semi-major axis for the above mentioned planets is displayed. Interestingly it seems that the evolution of the semi-major axis does not depend on the inclination for circular orbits. All planets with equal masses follow the same evolution independent of the initial inclination. For the 20 MEarth planet we found that the migration rate in the isothermal case does not depend much on the inclination of the planet, see Fig. 3. For higher mass planets this feature seems to be true as well. Of course, the planets migrate inwards at a speed dependent on the planetary mass. A higher planetary mass results in a more rapid inward migration of the planet, as it is predicted by linear theory (Tanaka et al. 2002), although the theory formally applies only for an unperturbed disc. Our discs, however, show clear signs of perturbation in the surface density profile (Fig. 17).
 |
Fig. 19 Time evolution of the semi-major axis for planets with i0 = 1.0° (top) and i0 = 4.0° (bottom) for different planetary masses in an isothermal H/r = 0.037 disc. |
In Fig. 20 the evolution the inclination for planets with a Jovian mass (and for an additional planet with 20 MEarth) in isothermal discs with different aspect ratios is displayed. The damping of inclination follows the predicted trend that the inclination of planets embedded in discs with smaller aspect ratio (H/r = 0.037) is damped faster than the inclination of planets embedded in discs with higher aspect ratio (H/r = 0.05), which was the result for smaller mass planets in our previous isothermal simulations as well. Marzari & Nelson (2009) stated that inclination damping of higher mass planets (e.g. Jovian mass) is considerably faster than for low mass planets (e.g. 20 MEarth). Figure 20 shows clearly the same result for high inclinations (i0 = 15.0), as the 20 MEarth planet loses inclination at a much slower rate.
However, for low inclinations (i < 4.0°) the damping of inclination for Jovian mass planets is considerably slower than for low mass planets. The damping time scales obtained by fitting our simulations are considerably higher for Jovian mass planets in isothermal discs, in the H/r = 0.037 disc τinc,Jup = 120 > 23 = τinc,20ME as well as in the H/r = 0.05 disc τinc,Jup = 145 > 53 = τinc,20ME. The i0 = 10.0° planet with 20 MEarth reflects this behaviour very well. First the damping of inclination is slower than for a Jovian mass planet, then the damping of inclination increases and the planet ends up in the midplane of the disc. The damping of inclination strongly depends on the interactions between disc and planet. As the Jovian mass planet opens a gap in the disc during the time of its evolution, the interactions between planet and disc are reduced, when the gap is opened. Therefore the damping of inclination of a Jovian mass planet is slowed down compared to a 20 MEarth planet, when the inclination is already damped to about i ≈ 4.0° after the planet has evolved for about 120 orbits. After the gap has opened, only little mass remains adjacent to the planet to provide continuing damping. In the beginning of the simulations the gap has not opened yet and inclination damping is faster.
Overall, the damping of inclination starting from high inclinations (i0 = 15°) is faster for planets with a Jovian mass compared to small mass planets (20 MEarth) as the damping time of inclination at high inclinations is much slower for low mass planets, which overcompensates the faster damping at low inclinations. This is in agreement with the statement of Marzari & Nelson (2009).
 |
Fig. 20 Time evolution of inclination for Jovian mass planets in isothermal H/r = 0.037 and H/r = 0.05 discs. The evolution of a 20 MEarth planet in an isothermal H/r = 0.037 disc is added for the inclination plot. The black dotted lines indicate a fit with τinc = 120 for a Jovian mass planet in an H/r = 0.037 disc and a fit with τinc = 145 for a Jovian mass planet in a H/r = 0.05 disc. |
Inclination seems to have no visible effect on the migration of planets inside an isothermal disc, as long as the planet’s orbit is circular. Eccentric orbits, on the other hand, tend to change the migration rate of the planet. Later on, we also investigate planets on inclined and eccentric orbits at the same time.
5.2. Fully radiative disc
In Fig. 21 the evolution of inclination for planets with i0 = 1.0° (top) and i0 = 4.0° (bottom) for different planetary masses in a fully radiative disc is displayed. The inclination is damped for all planetary masses, but a higher planetary mass favours a faster damping of inclination for both starting inclinations. After about 150 orbits the inclination of all planets with both individual starting inclinations is damped to approximately zero. The damping rate of the inclination is about the same for the fully radiative and the isothermal H/r = 0.037 disc.
 |
Fig. 21 Time evolution of the inclination for planets with i0 = 1.0° (top) and i0 = 4.0° (bottom) for different planetary masses in a fully radiative disc. |
In Fig. 18 the measured damping time scale τinc is displayed for isothermal and fully radiative simulations. In the fully radiative case, the damping time scale is reduced for increasing planetary masses. If the planet reaches a certain mass (about 80 MEarth), the damping time scale is not reduced any more. As the planets start to open gaps in the disc, the damping of inclination is not further accelerated. It seems that gap opening planets do not only migrate inwards at the same speed, independent of the planets mass, but also damp their inclination at the same speed.
In Fig. 22 the evolution of the semi-major axis for planets with i0 = 1.0° (top) and i0 = 4.0° (bottom) for different planetary masses in a fully radiative disc is displayed. As expected from our previous simulations (Kley et al. 2009) only planets with a planetary mass of MP ≤ 33 MEarth migrate outwards, while heavier objects migrate inwards. The 35 and 40 MEarth planets seem to migrate inwards just a little bit, before their migration is nearly stopped. The higher mass planets (50, 80 and 100 MEarth) migrate inwards at nearly the same speed as the planets inside the isothermal H/r = 0.037 disc. These observations are independent of the planets inclination.
The outward migrating low mass planets travel outwards at a slightly faster speed in the i0 = 1.0° case compared to the i = 4.0° simulations. This can be expected, as the calculated migration rate for 20 MEarth planets on fixed orbits is about a factor of 5 to 8 higher in the low inclined case. The higher migration rate for the lower inclined planets results in a faster outward migration. Finding the observed difference in the semi-major axis being so small after about 150 orbits is a result of inclination damping. As the inclination is damped, the migration rate increases significantly until the inclination is ≈2.0°, which takes only a few orbits starting from i0 = 4.0°. In this little time frame, the planet is not able to migrate a large distance, so we only observe a small difference in the evolution of the semi major axis.
 |
Fig. 22 Time evolution of the semi-major axis for planets with i0 = 1.0° (top) and i0 = 4.0° (bottom) for different planetary masses in a fully radiative disc. |
6. Inclined and eccentric planets
Inclination did not change the direction of migration for planets on circular orbits. Eccentricity on the other hand stopped the outward migration of low mass planets in fully radiative discs, as long as the eccentricity of the planet is higher than e = 0.02 (Bitsch & Kley 2010). However, planets with lower eccentricity migrate outwards in the fully radiative scheme. If an inclined planet surrounds a star on an eccentric orbit, in what way will these two properties of the orbit influence each other? To find an answer, simulations of a low mass planet (20 MEarth) on an inclined and eccentric orbit in an isothermal H/r = 0.037 and in a fully radiative disc are computed.
6.1. Isothermal disc
Our recent work with planets on eccentric orbits has shown that for isothermal simulations with moving planets on eccentric orbits the cubic potential (for the planetary potential) should be replaced by the ϵ-potential. In the following, isothermal simulations of planets on eccentric and inclined orbits we use the ϵ-potential with a smoothing length of rsm = 0.8.
In this work we limit ourselves to planets with an initial eccentricity of e0 = 0.1, e0 = 0.2 and e0 = 0.4 and with an initial inclination of i0 = 2.0° and i0 = 4.0°. In Fig. 23 the evolution of the semi-major axis (top), the eccentricity (middle) and inclination (bottom) for planets in an isothermal H/r = 0.037 disc is displayed.
 |
Fig. 23 Time evolution of semi-major axis (top), eccentricity (middle) and inclination (bottom) for planets (20 MEarth) with different eccentricity and inclination in an isothermal H/r = 0.037 disc. |
The planets migrate inwards (loss of semi-major axis) as expected for low-mass planets in an isothermal disc. For planets with an initial inclination of i0 = 4.0°, the planets migrate inwards at a slower rate compared to the lower inclined cases. A lower initial eccentricity results in a faster inward migration in the beginning of the simulation for all inclinations. This faster inward migration seems to be in a direct correlation with the planet’s eccentricity (Bitsch & Kley 2010). When the planets eccentricity reaches about e ≈ 0.1, the planet undergoes a short rapid inward migration and a more rapid loss of eccentricity, compared to the loss of eccentricity at different eccentricities. As soon as the e0 = 0.2 planet’s eccentricity is damped to about e ≈ 0.1, the planet undergoes a rapid inward migration leading to nearly the same evolution of semi-major axis as the e0 = 0.1 planet from this time on, again for both inclinations. Interestingly, a lower starting inclination results in a faster inward migration, when the planets have an initial eccentricity, compared to planets on circular orbits, where the inclination seems to have no effect on the migration. A higher initial inclination (i = 4.0°) seems to result in the opposite: a slower inward migration of the planet. We have observed a similar effect for eccentricities: planets with a lower initial eccentricity seem to migrate inwards at a slower rate compared to their highly eccentric counterparts (Bitsch & Kley 2010).
The initial eccentricity is damped for all these simulations with only two small differences. Planets with an initially higher eccentricity need a longer time to be damped to zero and planets with the same eccentricity but a higher inclination also need a longer time to damp their eccentricity. As the eccentricity is damped to lower values, at e ≈ 0.1 we observe a more rapid loss of eccentricity compared to the loss of eccentricity at other times. At this point the planet loses about 50% of its (actual) eccentricity in the time of a few orbits. At this point in time we also observe a faster inward migration of the planet. This dependency of a rapid drop of eccentricity and a resulting decrease of semi-major axis in the isothermal regime is in agreement with the results found in Cresswell et al. (2007) and Bitsch & Kley (2010)
The evolution of the inclination for the low eccentric planet (e0 = 0.1) follows nearly the evolution of a planet on circular orbit. The damping time is in fact marginally longer for the eccentric case, but besides this effect there is no difference. For the e0 = 0.2 case the inclination starts to oscillate slightly in the beginning of the simulation until it is damped to about i ≈ 3.0° or i ≈ 1.5°. Then the inclination follows approximately the damping rate of a planet on a circular orbit (see Fig. 11) until it is damped to about zero. The high eccentric case (e0 = 0.4) shows even more and stronger oscillations in the inclination. In the beginning the planets inclination is pumped up to about ≈5.0°, which is 25% more than the starting inclination. In time, the amplitude of the oscillations becomes smaller and the frequency higher while the overall inclination dissipates in time. These oscillations are observed in Cresswell et al. (2007) as well. The time until the inclination reaches zero is about 4 times as large as in the zero eccentricity case.
By comparing the migration rate of the inclined and eccentric planet with only an eccentric planet (migrating in midplane with a zero inclination), we observe nearly the same migration rate for both planets. Due to these results, it seems that inclination does not influence the migration in an isothermal disc at all.
6.2. Fully radiative disc
For the fully radiative simulations we rely on our cubic rsm = 0.5 potential again. For comparison, the starting eccentricity and inclination for the fully radiative simulations match those of the isothermal simulations. In Fig. 24 the evolution of the semi-major axis (top), the eccentricity (middle) and inclination (bottom) for planets in a fully radiative disc are displayed.
 |
Fig. 24 Time evolution of semi-major axis (top), eccentricity (middle) and inclination (bottom) for planets (20 MEarth) with different eccentricity and inclination in a fully radiative disc. |
In the beginning of the simulations all planets migrate inwards in the same way as in the isothermal simulations, but in contrast to the isothermal simulations the planets reverse their inward migration and migrate outwards after about ≈100 orbits in the low eccentric case (e0 ≤ 0.2). The high eccentric case (e0 = 0.4) takes a much longer time to reverse its inward migration. A higher initial eccentricity results in a later outward migration of the planet. The evolution of the semi-major axis contains at some point a quite fast loss of semi-major axis for the initial low eccentric planets. This loss of semi-major axis correlates to the eccentricity. As soon as the eccentricity is damped to ≈0.1, the fast loss of the semi-major axis sets in. The inclination of the planet seems to play no significant role in the migration process of these simulations, as for the e0 = 0.1 case the higher inclined planet (i0 = 4.0°) migrates outward first, while for the e0 = 0.2 case the lower inclined planet (i0 = 2.0°) migrates outward first.
The initial eccentricity is damped for all planets, but for planets with the same starting eccentricity, the time needed to damp the eccentricity is longer for the higher inclined planets, see the middle of Fig. 24. As the eccentricity is damped to ≈0.1, it is damped with an exponential decay, which seems to result in a faster loss of semi-major axis at the same time in the evolution of the planet. The damping for the initial low eccentric planets (e ≤ 0.2) takes about 120 planetary orbits, while a higher initial eccentricity (e0 = 0.4) takes about three times longer.
The inclination damping follows in principle the evolution of inclination of the isothermal simulations. As soon as the planet is released in the disc, the inclination is damped as long as the eccentricity is very low (e0 = 0.1). Higher eccentricities seem to affect the inclination in such a way that the inclination begins to oscillate. This oscillation is already visible in the e0 = 0.2 case, but becomes much stronger for even higher eccentricities. The oscillations begin to dissipate as soon as the planets eccentricity is damped to about e ≤ 0.1. During time these oscillations lose amplitude and gain frequency (as we can see from the e0 = 0.4 simulation). A higher eccentricity seems to cause a higher and more frequent oscillation of the inclination. These oscillations have been observed in Cresswell et al. (2007) as well.
7. Summary and conclusions
We performed full 3D radiation hydrodynamical simulations of accretion discs with embedded planets of different masses on inclined orbits. In a first sequence of simulations we have analysed in detail the dynamics of a planet with a given mass of 20 MEarth for the isothermal as well as the fully radiative case. For planets on fixed orbits we calculate the expected change of inclination and semi-major axis of an inclined planet on a circular orbit embedded in the disc, which we confirm subsequently through simulations of moving planets. For the isothermal (H/r = 0.037 and H/r = 0.05) as well as for the fully radiative simulations the inclination is damped in time. The damping time scale in isothermal discs depends on the disc’s thickness (H/r), as the inclination is damped faster for discs with lower aspect ratio than in discs with higher aspect ratio. A smaller H/r also results in a faster inward migration compared to a higher H/r. Our simulation results agree in this respect with Tanaka et al. (2002).
For planets on inclined orbits we confirm the outward migration. Our results for planets on fixed orbits agree very well with the simulations of planets moving inside the disc. We find that outward migration interestingly occurs over a relatively large range of inclination, up to about (i = 4.5°), with a faster outward migration for lower inclined planets. For higher inclined planets the migration seems to be stalled in general. In our simulations, the damping of inclination is slower in the fully radiative disc (τinc = 26.5) compared to the isothermal disc having the same scale height (τinc = 23), a difference that may be attributed to the different sound speeds, isothermal versus adiabatic.
As recent studies showed, planets in a fully radiative disc only migrate outwards if they do not exceed a certain critical mass (Kley et al. 2009), beyond which gap formation sets it. This outward migration does crucially depended on the shape of the orbit of the planet in the disc, as discussed in Bitsch & Kley (2010); Kley et al. (2009). Here, we extended those studies to inclined planets and found that planets on circular and inclined orbits migrate inwards in the isothermal case, and migrate outwards (if the planetary mass is low enough and the inclination of the planet is below the threshold of i ≈ 4.5°) in the fully radiative case. For higher mass planets, our previous results have been confirmed in the expected way. Planets with a mass up to ≈33 MEarth migrate outwards and planets with higher masses migrate inwards in the fully radiative scheme. In the isothermal case, planets migrate inwards as predicted by linear theory (Tanaka et al. 2002). When evolving planets with higher planetary masses, the simulations started from unperturbed discs, which changes the damping rate of inclination compared to planets starting in perturbed discs (by the presence of the embedded planet). This was also stated for inclined high mass planets in isothermal discs by Marzari & Nelson (2009). After the inclination is damped in time, the direction of migration only depends on the thermodynamics of the disc and on the planetary mass.
For eccentric and inclined low mass planets we observe a quite different behaviour. Eccentricity seems to slow down the inward migration of planets in the isothermal regime and prevents outward migration in the fully radiative scheme (for low mass planets which would normally migrate outwards). Since eccentricity is damped with time, this leads to slightly faster inward migration in the isothermal regime and to a reverse of the migration direction in the fully radiative scheme. The origin of this outward migration is created by the delicate density structure near the planet, which is destroyed by even a very low amount of eccentricity (Bitsch & Kley 2010). A high initial eccentricity gives rise to oscillations in the inclination, which become weaker and more frequent in time, as the eccentricity is damped. These oscillations seem to be responsible for a slower damping of inclination compared to low eccentric planets.
The results by Marzari & Nelson (2009) for Jovian mass planets indicated that inclination and eccentricity is damped in a very short time compared to low mass planets. We can confirm their results for inclination damping in discs with two different aspect ratios, however this is only true for the damping of high inclinations. For low inclinations (i ≤ 10°) the damping of inclination for low mass planets is faster than for high mass planets. However, when considering the total time needed to damp the inclination of a planet starting from i0 = 15.0°, the damping is much faster for high mass planets, which confirms the results by Marzari & Nelson (2009). A Jovian mass planet with high inclination evolves more rapidly as its interactions with the disc is stronger if no gap has opened yet.
Our results indicate that the inclination as well as the eccentricity of single planets are damped by the disc. At the end of our simulations the planets end up in midplane, meaning they have no remaining inclination. While this is in agreement with the very flat solar system, it seems to be in contradiction to the observed highly inclined exoplanets (Triaud et al. 2010). However, it is known that higher eccentricities as well as inclinations can be produced via planet-planet interaction. For a pair of planets embedded in discs convergent migration processes can excite eccentricity to high values depending on the damping action of the disc (Crida et al. 2008). Stronger scattering events can be induced in case of a multiple planet system still embedded in the disc (Marzari et al. 2010). During the subsequent longterm evolution these initially excited system may then evolve into configurations with very high eccentricity as well as inclination (Chatterjee et al. 2008; Matsumura et al. 2010). Thus, the combination of initial planet-disc interaction with subsequent scattering processes and tidal interaction with the central star is one pathway towards the observed strongly tilted systems (Winn et al. 2010). On the other hand, systems such as Kepler-9 (Holman et al. 2010) seem to show clear evidence for continued migration towards the star.
Acknowledgments
B. Bitsch has been sponsored through the German D-grid initiative. W. Kley acknowledges the support through the German Research Foundation (DFG) through grant KL 650/11 within the Collaborative Research Group FOR 759: The formation of Planets: The Critical First Growth Phase. The calculations were performed on systems of the Computer centre of the University of Tübingen (ZDV) and systems operated by the ZDV on behalf of bwGRiD, the grid of the Baden Württemberg state. Finally, we gratefully acknowledge the helpful and constructive comments of an anonymous referee.
References
- Ayliffe, B. A., & Bate, M. R. 2010, MNRAS, 408, 876 [NASA ADS] [CrossRef] [Google Scholar]
- Baruteau, C., & Masset, F. 2008, ApJ, 672, 1054 [NASA ADS] [CrossRef] [Google Scholar]
- Bate, M. R., Lubow, S. H., Ogilvie, G. I., & Miller, K. A. 2003, MNRAS, 341, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Bitsch, B., & Kley, W. 2010, A&A, 523, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bryden, G., Chen, X., Lin, D. N. C., Nelson, R. P., & Papaloizou, J. C. B. 1999, ApJ, 514, 344 [NASA ADS] [CrossRef] [Google Scholar]
- Burns, J. A. 1976, Am. J. Phys., 44, 944 [NASA ADS] [CrossRef] [Google Scholar]
- Chatterjee, S., Ford, E. B., Matsumura, S., & Rasio, F. A. 2008, ApJ, 686, 580 [NASA ADS] [CrossRef] [Google Scholar]
- Cresswell, P., Dirksen, G., Kley, W., & Nelson, R. P. 2007, A&A, 473, 329 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Crida, A., Sándor, Z., & Kley, W. 2008, A&A, 483, 325 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Crida, A., Baruteau, C., Kley, W., & Masset, F. 2009, A&A, 502, 679 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- D’Angelo, G., Henning, T., & Kley, W. 2002, A&A, 385, 647 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- D’Angelo, G., Kley, W., & Henning, T. 2003, ApJ, 586, 540 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P., & Tremaine, S. 1980, ApJ, 241, 425 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Holman, M. J., Fabrycky, D. C., Ragozzine, D., et al. 2010, Science, 330, 51 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Klahr, H., & Kley, W. 2006, A&A, 445, 747 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kley, W., & Crida, A. 2008, A&A, 487, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kley, W., & Lin, D. N. C. 1999, ApJ, 518, 833 [NASA ADS] [CrossRef] [Google Scholar]
- Kley, W., Bitsch, B., & Klahr, H. 2009, A&A, 506, 971 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Levermore, C. D., & Pomraning, G. C. 1981, ApJ, 248, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Marzari, F., & Nelson, A. F. 2009, ApJ, 705, 1575 [NASA ADS] [CrossRef] [Google Scholar]
- Marzari, F., Baruteau, C., & Scholl, H. 2010, A&A, 514, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Masset, F. 2000, A&AS, 141, 165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matsumura, S., Thommes, E. W., Chatterjee, S., & Rasio, F. A. 2010, ApJ, 714, 194 [NASA ADS] [CrossRef] [Google Scholar]
- Mihalas, D., & Weibel Mihalas, B. 1984, Foundations of radiation hydrodynamics (New York: Oxford University Press) [Google Scholar]
- Paardekooper, S.-J., & Mellema, G. 2006, A&A, 459, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paardekooper, S.-J., & Mellema, G. 2008, A&A, 478, 245 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paardekooper, S.-J., & Papaloizou, J. C. B. 2008, A&A, 485, 877 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Papaloizou, J., & Lin, D. N. C. 1984, ApJ, 285, 818 [NASA ADS] [CrossRef] [Google Scholar]
- Papaloizou, J. C. B., Nelson, R. P., Kley, W., Masset, F. S., & Artymowicz, P. 2007, in Protostars and Planets V, ed. B. Reipurth, D. Jewitt, & K. Keil, 655 [Google Scholar]
- Tanaka, H., & Ward, W. R. 2004, ApJ, 602, 388 [NASA ADS] [CrossRef] [Google Scholar]
- Tanaka, H., Takeuchi, T., & Ward, W. R. 2002, ApJ, 565, 1257 [NASA ADS] [CrossRef] [Google Scholar]
- Terquem, C., & Ajmia, A. 2010, MNRAS, 404, 409 [NASA ADS] [Google Scholar]
- Triaud, A. H. M. J., Collier Cameron, A., Queloz, D., et al. 2010, A&A, 524, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ward, W. R. 1986, Icarus, 67, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Winn, J. N., Fabrycky, D., Albrecht, S., & Johnson, J. A. 2010, ApJ, 718, L145 [NASA ADS] [CrossRef] [Google Scholar]
- Ziegler, U., & Yorke, H. 1997, Comput. Phys. Commun., 101, 54 [Google Scholar]
All Tables
Exponential damping rate τinc (in orbits), obtained from our isothermal and fully radiative simulations for three studied cases of planets in discs compared with the linear rate, as given by Tanaka & Ward (2004).
All Figures
 |
Fig. 1 Calculated rate of change of the inclination (di/dt) for inclined 20 MEarth planets on fixed circular orbits. Results for the isothermal (red) and fully radiative simulations (dark blue) are shown. Overlayed are in light blue and purple fits for the exponential decay of inclination for small inclinations and in black for the decay di/dt ∝ i-2 for larger inclinations. |
| In the text | |
 |
Fig. 2 Torque acting on a 20 MEarth planet on a fixed inclined circular orbit in dependency of the inclination and thermodynamics of the disc. Torque and power are the same for planets on circular orbits. The torque has been averaged over 20 orbits, taken from t = 180 to t = 200 orbits for the isothermal (solid red line) and from t = 120 to t = 140 for the fully radiative simulation (dashed blue line). |
| In the text | |
 |
Fig. 3 Calculated rate of change of the semi-major axis (ȧ/a) for inclined 20 MEarth planets on fixed, circular orbits. For inclinations lower than i ≤ 4.5° we observe a positive migration rate, which suggest that low inclinations do not stop outward migration, while we observe a negative migration rate for the isothermal case. |
| In the text | |
 |
Fig. 4 Torque density acting on a planet on a fixed inclined orbit in dependency of the inclination of the planet embedded in an isothermal H/r = 0.037 disc (top) and a fully radiative disc (bottom). The snapshots are taken at t = 90 orbits for the isothermal simulations and at t = 150 orbits for the fully radiative simulations. At this time planet-disc interactions are in equilibrium and the planet is at its lowest point in orbit (lower culmination). |
| In the text | |
 |
Fig. 5 Torque density acting on a 20 MEarth planet on a fixed inclined orbit with i = 2.0° in a fully radiative disc at different phases within its orbit. Integer (half integer) values of the indicated time refer to the upper (lower) culmination. At the intermediate quarterly orbit times the planet moves through the nodal line. |
| In the text | |
 |
Fig. 6 In the top panel we display the evolution of the torque acting on planets in a fully radiative disc on fixed circular, inclined orbits in time. In the bottom panel the normal component of the disturbing force dF, Ncosξ as to be used Eq. (6), is displayed in dependency of time. |
| In the text | |
 |
Fig. 7 Surface density for 20 MEarth planets on fixed circular inclined orbits embedded in an isothermal H/r = 0.037 disc with i = 1.0° (top) and i = 4.0° (bottom). The planet is at its lowest point in orbit (lower culmination) at the time of the snapshot. |
| In the text | |
 |
Fig. 8 Density (in g/cm3) of a r − θ-slice through the isothermal H/r = 0.037 disc with embedded 20 MEarth planets on fixed circular inclined orbits with i = 1.0° (top) and i = 4.0° (bottom). The planet is at its lowest point in orbit (lower culmination) at the time of the snapshot. |
| In the text | |
 |
Fig. 9 Surface density for 20 MEarth planets on fixed circular inclined orbits embedded in a fully radiative disc with i = 1.0° (top) and i = 4.0° (bottom). The planet is at its lowest point in orbit (lower culmination) at the time of the snapshot. |
| In the text | |
 |
Fig. 10 Density (in g/cm3) of a r − θ-slice through the fully radiative disc with embedded 20 MEarth planets on fixed circular inclined orbits with i = 1.0° (top) and i = 4.0° (bottom). The planet is at its lowest point in orbit (lower culmination) at the time of the snapshot. |
| In the text | |
 |
Fig. 11 Time evolution of inclination for 20 MEarth planets with individual starting inclinations ranging from i = 1.0° to i = 8.0° in an isothermal H/r = 0.037 disc. The damping of inclination follows the trend of the calculated change of inclination for planets on fixed orbits, see Fig. 1. The black dotted lines indicate our manual fitting with τinc = 23 and in the i0 = 8.0° case an additional fit provides for a di/dt ∝ i-2 fit. |
| In the text | |
 |
Fig. 12 Time evolution of semi-major axis for 20 MEarth planets with individual starting inclinations ranging from i = 1.0° to i = 8.0° in an isothermal H/r = 0.037 disc. The dashed black line indicates a fit to the results with a slope of −3.45 × 10-4/orbit. The change of semi-major axis follows the trend of the change determined for planets on fixed orbits, see Fig. 3. |
| In the text | |
 |
Fig. 13 Time evolution of the semi-major axis (top) and inclination (bottom) of a 20 MEarth planet in an isothermal H/r = 0.05 disc. The planets initial inclinations reach from i0 = 1.0° to i0 = 8.0°. The dashed black line in the top panel indicates a linear fit to the results with a slope of −2 × 10-4/orbit. The black dotted lines in the evolution of inclination (bottom) indicate our manual fitting with τinc = 53. |
| In the text | |
 |
Fig. 14 Time evolution of inclination for 20 MEarth planets with individual starting inclinations ranging from i = 1.0° to i = 4.0° in a fully radiative disc. The damping of inclination follows the trend of change of inclination for planets on fixed orbits, see Fig. 1. The black dotted lines indicate our manual fitting with τinc = 26.5 for planets with i0 = 2.0°, 4.0°, 6.0° and i0 = 8.0°, which seems very good in the beginning/middle phase of the inclination damping. In the i0 = 8.0° case an additional fit provides for a di/dt ∝ i-2 fit in the beginning of the evolution. |
| In the text | |
 |
Fig. 15 Time evolution of semi-major axis for 20 MEarth planets with individual starting inclinations ranging from i = 1.0° to i = 8.0° in a fully radiative disc. The change of semi-major axis follows the trend of change for planets on fixed orbits, see Fig. 3. The dashed black line in the top panel indicates a linear fit to the results with a slope of 1.35 × 10-3/orbit. |
| In the text | |
 |
Fig. 16 Time evolution of the inclination for planets with i0 = 1.0° (top) and i0 = 4.0° (bottom) for different planetary masses in an isothermal H/r = 0.037 disc. |
| In the text | |
 |
Fig. 17 Surface density for planets on initial inclined, circular orbits with i0 = 1.0° (top) and i0 = 4.0° (bottom) after 60 planetary orbits. |
| In the text | |
 |
Fig. 18 Measured inclination damping time scale τinc for planets with different planetary masses in the isothermal and fully radiative regime. |
| In the text | |
 |
Fig. 19 Time evolution of the semi-major axis for planets with i0 = 1.0° (top) and i0 = 4.0° (bottom) for different planetary masses in an isothermal H/r = 0.037 disc. |
| In the text | |
 |
Fig. 20 Time evolution of inclination for Jovian mass planets in isothermal H/r = 0.037 and H/r = 0.05 discs. The evolution of a 20 MEarth planet in an isothermal H/r = 0.037 disc is added for the inclination plot. The black dotted lines indicate a fit with τinc = 120 for a Jovian mass planet in an H/r = 0.037 disc and a fit with τinc = 145 for a Jovian mass planet in a H/r = 0.05 disc. |
| In the text | |
 |
Fig. 21 Time evolution of the inclination for planets with i0 = 1.0° (top) and i0 = 4.0° (bottom) for different planetary masses in a fully radiative disc. |
| In the text | |
 |
Fig. 22 Time evolution of the semi-major axis for planets with i0 = 1.0° (top) and i0 = 4.0° (bottom) for different planetary masses in a fully radiative disc. |
| In the text | |
 |
Fig. 23 Time evolution of semi-major axis (top), eccentricity (middle) and inclination (bottom) for planets (20 MEarth) with different eccentricity and inclination in an isothermal H/r = 0.037 disc. |
| In the text | |
 |
Fig. 24 Time evolution of semi-major axis (top), eccentricity (middle) and inclination (bottom) for planets (20 MEarth) with different eccentricity and inclination in a fully radiative disc. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


