EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 529 (May 2011) A&A, 529 (2011) A140 Full HTML
Free Access
Issue
A&A
Volume 529, May 2011
Article Number A140
Number of page(s) 5
Section Astrophysical processes
DOI https://doi.org/10.1051/0004-6361/201116740
Published online 20 April 2011

© ESO, 2011

1. Introduction

The existence of HeH+ in astrophysical environments has been extensively discussed in several papers. Roberge & Dalgarno (1982) surmised that HeH+ is produced in planetary nebulae and in dense molecular clouds under the presence of X-ray and extreme UV ionization sources. Liu et al. (1997) investigated the possible detection of HeH+ in NGC 7027, a very high electron density nebular object, via its j = 1–0 strong rotational line at 149.14 μm, concluding that its identification is complicated by the accidental near-coincidence of that transition frequency with the 149.09 and 149.39 μm lines of CH.

In the past few years, the presence of HeH+ in low temperature and low density helium-rich white dwarfs has been investigated. Harris et al. (2004) demonstrated that this molecule is the dominant positive ion in these objects and strongly affects their opacity. Engel et al. (2005), finally, showed that it might also be possible to detect HeH+ in cool helium stars such as those studied by Saio et al. (2000).

The discovery of the very metal-poor stars (Christlieb et al. 2002; Frebel et al. 2005) strengthened the quest for Population III stars. It then follows that to study the evolution of primordial molecules formed during the post-recombination era is a fundamental step in gaining a clearer understanding of “how and when” these stars were formed.

Since we wish to establish the role of the main molecular species (LiH, LiH+, HeH+, H2, HD+, HD) during the gravitational collapse that led to the first episode of star formation, we need, as is well-known, to obtain opacity data. It is also just as important to know the elementary mechanisms that lead to the formation and destruction of these molecules and the corresponding rates that were present at the conditions of the astrophysical environment. In other words, we have to know as much as possible about the chemical history of all the above species.

An extensive analysis of the lithium chemistry was reported in Bovino et al. (2011), while an analogously accurate study of the reactions involving helium-based molecular species, and in particular the HeH+ molecular cation reaction with H, remains missing. The latter is indeed considered to be the first molecule to appear in the Universe (Lepp et al. 2002): in an environment dominated by a low-density regime where three-body collisions are unlikely to occur, the radiative association is thus the main path to forming that molecule. Hydrogen and helium, which are the most abundant species that would have existed at the early universe epoch, can therefore combine to form HeH+ by means of the familiar reaction 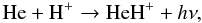He+H+→HeH++hν,\begin{equation} {\rm He} + {\rm H}^+ \rightarrow {\rm HeH}^+ + h\nu, \end{equation}(1)for which the rate coefficient has been obtained from Zygelman et al. (1998) and fitted by Stancil et al. (1998). 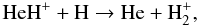The main destruction path for the HeH+ molecules formed is the reaction with H HeH++H→He+H2+,\begin{equation} {\rm HeH}^+ + {\rm H} \rightarrow {\rm He} + {\rm H}_2^+, \end{equation}(2)which however has never been studied with sufficient accuracy from a theoretical point of view. Crossed-beam experimental data for energies higher than 0.2 eV were presented by Rutherford & Vroom (1973), fitted by Linder et al. (1995) and then included in the early universe model calculations of Schleicher et al. (2008), but no direct calculations have been available thus far.

In this paper, we therefore report an accurate analysis, from ab initio data, that deals with the above reaction. We present new quantum calculations for process (2) over a broad range of collision energies. The corresponding rate coefficient was obtained from the calculated reactive cross-sections and is presented in the following sections, where the newly computed abundance of HeH+ is also reported. Finally, we additionally compare it with the known behavior of LiH+ cations under the same environmental conditions and can therefore draw some conclusions about their relative roles during the early universe chemical evolution.

2. The quantum reactive calculations

The elementary reactions indicated in either direction by process (2) have been studied both experimentally (Rutherford & Vroom 1973; Karpas et al. 1979; Tang et al. 2005) and theoretically (Aquilanti et al. 2000; Palmieri et al. 2000; Xu et al. 2008; Ramachandran et al. 2009), because of its peculiar resonant features detected experimentally. Several potential energy surfaces (PES’s) have been obtained and employed, using quasi-classical trajectories, close coupling (time-independent and time-dependent) methods to study the inverse of the reaction (2).

The polar cation of the present study, HeH+, has a large dipole moment (1.66 Debye) and has about 11 vibrational levels (Zygelman et al. 1998). For this reason it is therefore considered of great importance in the early universe as possible coolant during the post-recombination era. As suggested by Dubrovich (1994), molecules with large dipole moments could interact with the cosmic microwave background radiation (CMB) inducing both spatial and spectral distorsions (Maoli et al. 1994). The interaction with the CMB is therefore crucial to determine the evolution and abundance of primordial molecules. The study of the HeH+ chemical evolution, therefore, strongly depends on the accuracy of the main reaction rate coefficients which lead to its destruction or formation. Formation mechanisms for HeH+ have already been extensively investigated (Zygelman et al. 1998) while we wish here to focus on its destruction mechanisms, and in particular on the direct exothermic (0.748 eV) reaction (2). In our calculations we employ one of the latest of the available, calculated PES (Ramachandran et al. 2009). Since it is also known that, under early universe conditions molecules are most likely to be in their roto-vibrational ground state (ν = 0, j = 0), we have further decided to study reaction (2) starting from this level of the target cationic molecule.

The exact quantum study of reactions involving an ionic system is usually rather difficult due to the presence of a long range “tail” in the interaction which therefore requires the use of a large basis set to generate numerically converged cross sections and rates. The use of an accurate computational method which is less costly in terms of resources is therefore mandatory. Tacconi et al. (2011) presented a novel computational implementation of the negative imaginary potential (NIP) scheme proposed earlier by Baer et al. (1990) and which we use here the present study. We begin by solving the Schrödinger equation in a body-fixed (BF) frame of reference, in the presence of an additional NIP. Hence, we write the Hamiltonian of the triatomic system in the BF frame, within the coupled states (CS) (McGuire 1976) approximation 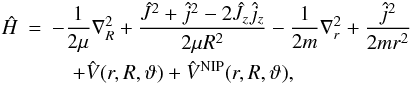Ĥ=−12μ∇R2+Ĵ2+ĵ2−2Ĵzĵz2μR2−12m∇r2+ĵ22mr2 +V̂(r,R,ϑ)+V̂NIP(r,R,ϑ),\begin{eqnarray} \nonumber \hat{H} &=& -\frac{1}{2\mu}\nabla_R^2 + \frac{\hat{J}^2+\hat{j}^2-2\hat{J}_z\hat{j}_z}{2\mu R^2} - \frac{1}{2m}\nabla_r^2 + \frac{\hat{j}^2}{2mr^2} \\ &&\quad+\hat{V}(r, R, \vartheta) + \hat{V}^{\rm NIP}(r, R, \vartheta), \end{eqnarray}(3)where R, r, and ϑ are the Jacobi coordinates, and μ and m are the reduced masses of the triatomic complex and diatomic molecule, respectively. In addition, J and Ω are the total angular momentum and its projection on the relative axis, while j is the diatomic rotational angular momentum. 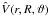\hbox{$\hat{V}(r, R, \vartheta)$} is the interaction potential and 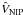\hbox{$\hat{V}_{\rm NIP}$} has the functional form given in Bovino et al. (2010b). The CS approximation provides the exact dynamics when the target rotational angular momentum j is chosen to be equal to 0 (MgGuire 1976). Thus, it is equivalent to the full coupled-channel (CC) formulation. Because of the flux-absorbing effect coming from the NIP, the resulting S-matrix is now non-unitary and its default to unitarity yields here the (state-to-all) reaction probability, as discussed in Tacconi et al. (2011). 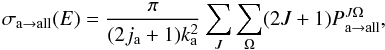From the reaction probability, one can in turn obtain the reactive cross-section σa→all(E)=π(2ja+1)ka2∑J∑Ω(2J+1)Pa→allJΩ,\begin{equation} \sigma_{{\rm a}\rightarrow {\rm all}}(E) = \frac{\pi}{(2j_{\rm a} + 1) k_{\rm a}^2}\sum_J\sum_{\Omega}(2J + 1) P^{J\Omega}_{{\rm a}\rightarrow {\rm all}}, \end{equation}(4)while the rate coefficients are computed by averaging the appropriate reactive cross-sections over a Boltzmann distribution of velocities for the incoming atom. 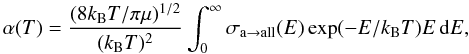α(T)=(8kBT/πμ)1/2(kBT)2∫0∞σa→all(E)exp(−E/kBT)E dE,\begin{equation} \alpha(T) = \frac{(8k_{\rm B}T/\pi\mu)^{1/2}}{(k_{\rm B}T)^2} \int_0^\infty\sigma_{{\rm a}\rightarrow {\rm all}}(E)\exp(-E/k_{\rm B}T)E\,{\rm d}E, \end{equation}(5)where T is the gas temperature, kB is the Boltzmann constant, and μ is the reduced mass of the system. In the following section, we present the effects of the accurate rates computed above on the final chemical evolution.

3. The chemical network and the evolutionary modelling

The evolution of the pregalactic gas is usually considered within the framework of a Friedmann cosmological model and the primordial abundances of the main gas components are taken from the standard big bang nucleosynthesis results (Smith et al. 1993). The numerical values of the cosmological parameters used in the calculation are obtained from WMAP5 data (Komatsu et al. 2009) and are listed in Table 1 (for details, see Coppola et al. 2011).

The abundance of HeH+ is obtained by solving a set of differential coupled rate equations of the form 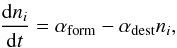dnidt=αform−αdestni,\begin{equation} \frac{{\rm d}n_i}{{\rm d}t} = \alpha_{\rm form} -\alpha_{\rm dest}n_i, \label{evol} \end{equation}(6)where αform and αdest are formation and destruction rates for the reactant species i with number density ni, which in general depend on the number densities of the other species and on the radiation field. The rate coefficients involved in the helium chemistry network are the same as those reported in Galli & Palla (1998, hereafter GP98), with the exception of the destruction reaction (2), which indeed now comes from the present quantum calculations. The additional equations governing the temperature and redshift evolutions were reported in several earlier papers (see e.g. GP98; Bovino et al. 2011), thus are not discussed here.

Table 1

Cosmological model parameters.

4. Results and comparisons

As outlined in the Introduction, our understanding of the early universe evolution depends strongly on our knowledge of the elementary processes involving atomic and molecular species that are assumed to be present at that time. At the molecular level, therefore the observables that one needs to obtain are the various cross-sections related to their mechanisms of occurrence. In the present work, we accurately calculated the cross-sections for the reaction of HeH+ (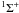Σ+1\hbox{$^1\Sigma^+$}) with H(1S) using quantum dynamics and ab initio data providing the interaction forces.

In the following, we report and discuss our results and compare the new HeH+ abundances produced by the new quantum reaction data with those obtained for another molecular ion present in the chemical network, LiH+ (Bovino et al. 2011).

4.1. The reaction cross-sections

A set of three-hundred coupled equations describing reaction (2) were solved using our in-house code (Tacconi et al. 2011). A direct product of a Colbert-Miller (Colbert & Miller 1992) discrete variable representation (DVR) of 100 points ranging from 0.5 a0 to 12 a0 for the reagent ion vibrational coordinate and a rotational basis of 40 spherical harmonics has been employed to describe the reactive complex. The solution matrix has been propagated up to 50 a0 and the convergence was checked as a function of the propagator step-size, yielding a final convergence of cross-section values within about 1%.

The calculations were carried out over a wide range of energies, from 10-4 to 1.0 eV, and for total angular momentum values (J) ranging from 10 to 90 for the highest energy. The NIP parameters were tested following the Baer criteria (Baer et al. 1990): the NIP stability has been reached for rmin = 2.75   a0, rmax = 5.75   a0, and the NIP order n = 2 (see Tacconi et al. 2011).

Our computed, J-converged integral cross-sections are presented in Fig. 1. From the figure, the non-Langevin behavior of the cross-sections for this ionic reaction is clear since, instead of independent of E at lower energies, they go through a marked maximum around 10-2 eV. In the same figure, we report the experimental (thick line, from Rutherford et al. 1973) and the extrapolated (dotted line, from Linder et al. 1995) cross-sections that reach collision energy values as low as around 10-2 eV. The agreement between our theoretical results and the experimental findings, both measured and extrapolated, is reassuringly good and confirms the physical reliability of the present NIP method for handling ionic reactions. No measured data are available at the lower collision energies as crossed beam experiments with ionic partners become increasingly difficult for that range. We note, however, that the results of Fig. 1 are very different from those for LiH+ (Bovino et al. 2010a) across the same range of energies. These differences are related to the different microscopic mechanisms of the reaction pathways between the two systems, which we plan to analyse in more detail in future work. Qualitatively, the two systems, although both undergoing no barrier, exothermic reactions, have very different exothermicity values that affect the product separations at low energy.

thumbnail Fig. 1

Computed integral cross-sections as a function of energy. The thick line represents the fitted experimental data from Rutherford & Vroom (1973). The dotted line is obtained from the formula given by Linder et al. (1995) by extrapolating the Rutherford’s data.

4.2. The depletion rates

The new rate coefficients are reported in Table 2 and fitted with the formula

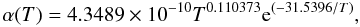α(T)=4.3489×10-10T0.110373e(−31.5396/T),\begin{equation} \alpha (T) = 4.3489\times10^{-10}T^{0.110373} {\rm e}^{(-31.5396/T)}, \end{equation}(7)which is valid for T ≤ 1000 K. The experimental value obtained by Karpas et al. (1979) is also reported for comparison in the same Table. It is again very reassuring to see that the only existing experimental datum at 300 K is indeed very close to our computational value at the same temperature.

To more clearly evaluate the significance of the newly computed cross-sections, we need to view the process (2) within the broader context of the variety of elementary events involved in this molecular cation. To this end, Fig. 2 shows the main processes leading to the formation and the destruction of HeH+. As clearly shown by the figure, the radiative association process (p1) dominates the formation of HeH+ over the entire range of redshifts, while the association involving the He ion (p2) and the other involving the 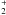H2+\hbox{${\rm H}_2^+$} molecule (p3), have negligible contributions at the lower redshift values, the most important range for the present study.

From the same figure one further realizes that the photodissociation mechanism (d1) is the dominant destruction path of the HeH+ for z ≥ 300, while the chemical path involving the reaction (2), the one that destroys HeH+ (d2) in collision with H, is seen to be the most important process for z ≤ 300. A contribution also comes from the electron-assisted dissociation reaction (d3) that neutralizes the charged partners and dominates over (d2) for z ≤ 10.

thumbnail Fig. 2

Computed production/destruction rates of HeH+ as function of redshift. Solid and dashed curves represent production and destruction processes, respectively.

4.3. A comparison with LiH+

During the so-called dark ages of the universe, we know that the existing molecules interacted both with CMB photons and the present atoms. We do not know, however, wheter these species existed with sufficiently high abundances to produce now detectable signals. Because of its large dipole moment (1.66 Debye) and the high abundances of its atomic components (H and He), HeH+, is certainly one of the prime targets of observations (Persson et al. 2010). This is even more important as our recent ab-initio results (Bovino et al. 2009, 2010a,b, 2011) showed that lithium-containing molecules such as LiH and LiH+, in spite of their significant dipole moments that would favor transitions (5.9 and 0.6 Debye), have very low abundances over the whole range of redshifts studied.

In Fig. 3 we report the calculated rate coefficients for the depletion reaction (2) over a wide range of temperatures (redshifts) together with the earlier calculations for LiH+ depletion (Bovino et al. 2010a). As it is clear from that Figure, the HeH+ + H reaction turns out to be very efficient at the redshifts above 100, with rate values comparable to those of the LiH+ + H destruction reaction given in the same figure (dot-dashed line). However, while the latter remains essentially constant over the whole range of examined redshifts, the efficiency of reaction (2) quickly decreases for z ≤ 100, coming down by about two orders of magnitude by the time unitary redshift values are reached. This behavior therefore favors the HeH+ as a more likely survival candidate vis-á-vis the LiH+ case, thereby providing a good molecular coolant acting during the primordial star formation. In the same figure we also report the experimental rate at 300 K given by Karpas et al. (1979); the rates included in the GP98 model are taken from the experimental data of Rutherford & Vroom (1973). As seen earlier for the cross sections, the experimental rates are in good agreement with our quantum results (see also Table 2).

In Fig. 4 we report the calculated abundances for HeH+ obtained using our new quantum rates discussed above: they are compared with the old ones obtained by GP98 and also with our newest results for LiH+ (Bovino et al. 2011). The scenario emerging from the above calculations indicates that for redshift around z ≃ 20, the molecular HeH+ abundance has now increased by more than one order of magnitude with respect to the earlier calculations. It thus remains a more abundant ionic species than LiH+, hence becoming an interesting molecular candidate for actual detection. As shown by Maoli et al. (1994) (see also Schleicher et al. 2008), the relevant quantity for determining the imprint of molecules on the CMB is the optical depth due to line absorption. In the case of HeH+, the optical depth has a broad peak around a frequency of ~50 GHz, produced by redshifted rotational transitions with j = 4–6 of the ground vibrational level. With the new rate coefficient derived in this work, the maximum value of the optical depth, ~10-7, is about one order of magnitude larger than the value computed earlier by Schleicher et al. (2008), an encouraging result for observational perspectives. 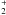The new reaction rate also has an effect on the abundance of H2+\hbox{${\rm H}_2^+$}, which is lower by a factor of ~5 in the range 10 ≲ z ≲ 50 than earlier results. 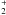However, this reduction has no significant effect on the abundance of H2 because the H2+\hbox{${\rm H}_2^+$} channel of production of H2 is no longer active at these redshifts.

Table 2

Computed rate coefficient for the reaction (2) as a function of T.

thumbnail Fig. 3

Depletion rate coefficients as a function of the temperature. In the upper scale, the redshift is also reported. The experimental rate coefficients of Karpas et al. (1979) and those extrapolated by Schleicher et al. (2008) are also presented. The lithium reactions rate is from Bovino et al. (2010a).

thumbnail Fig. 4

Computed relative abundances of HeH+ in the post-recombination era as function of redshift z: present results (solid curves), results of GP98 (dashed curves). The LiH+ results are from Bovino et al. (2011).

5. Conclusions

We have carried out a new set of ab initio, quantum calculations for the rate coefficient of the reaction (2), which therefore permit us to revise the abundance of HeH+ molecule within the expected conditions operating during the early universe. One of the main results from the present reactive calculations is that the chemical destruction rate of this polar cation depends on temperature dependence in a way is very different from previous data, both experimental and theoretical, especially for temperatures lower than 100 K.

These new results obtained for the HeH+ abundance now indicate that this molecule should be much more likely to have survived at low redshift, since its fractional abundance goes up by more than one order of magnitude from previous estimates, becoming of the order of 10-13. These new findings should be considered the broader context whereby the fractional abundance of LiH+, as calculated by Bovino et al. (2011), turns out to be significant mostly in the low-redshift region of z ≲ 30. Comparing the specific fractional abundances of the two species therefore suggests rather compellingly that the HeH+ ionic molecule, if more abundant than the LiH+, would become more likely to be observed experimentally, even more so than suggested by previous works (GP98; Persson et al. 2010).

We note that, because of its larger dipole moment and greater number of roto-vibrational levels, when compared with LiH+, the molecular cation HeH+ turns out to be the most suitable candidate for experimental observations in different astrophysical environments, a result now supported by the present ensemble of accurate computational studies from quantum, ab initio methods.

Acknowledgments

We thank the CINECA and CASPUR consortia for providing us with the necessary computational facilities and the University of Roma “Sapienza” for partial financial support. We are grateful to Dr. D. De Fazio for providing us with the potential energy surface of Ramachandran et al. (2009). D.G. also thanks F. Palla for discussions on this subject.

References

  1. Aquilanti, V. 2000, Chem. Phys. Lett., 318, 619 [NASA ADS] [CrossRef] [Google Scholar]
  2. Baer, M., Ng C. Y., Neuhauser, D., & Oreg Y. 1990, J. Chem. Soc. Faraday Trans., 86, 1721 [CrossRef] [Google Scholar]
  3. Bovino, S., Wernli, M., & Gianturco, F. A. 2009, ApJ, 699, 383 [NASA ADS] [CrossRef] [Google Scholar]
  4. Bovino, S., Stoecklin, T., & Gianturco, F. A. 2010a, ApJ, 708, 1560 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bovino, S., Tacconi, M., Gianturco, F. A., & Stoecklin T. 2010b, ApJ, 724, 106 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bovino, S., Tacconi, M., Gianturco, F. A., Galli, D., & Palla F. 2011, ApJ, in press [Google Scholar]
  7. Christlieb, N. Bessell, M. S., Beers, T. C., et al. 2002, Nature, 419, 904 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  8. Colbert, D. T., & Miller, W. H. 1992, J. Chem. Phys., 96, 1982 [NASA ADS] [CrossRef] [Google Scholar]
  9. Coppola, C. M., Longo, S., Capitelli, M., Palla, F., & Galli, D. 2011, ApJS, 193, 7 [NASA ADS] [CrossRef] [Google Scholar]
  10. Dubrovich, V. K. 1993, Astron. Lett., 19, 53 [NASA ADS] [Google Scholar]
  11. Engel, E. A., Doss N., Harris G. J., & Tennyson J. 2005, MNRAS, 357, 471 [NASA ADS] [CrossRef] [Google Scholar]
  12. Frebel, A., Aoki, W., Christlieb, N., et al. 2005, Nature, 434, 871 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  13. Galli, D., & Palla, F. 1998, A&A, 335, 403 (GP98) [NASA ADS] [Google Scholar]
  14. Harris, G. J., Lynas-Gray, A. E., Miller, S., & Tennyson, J. 2004, ApJ, 617, L143 [NASA ADS] [CrossRef] [Google Scholar]
  15. Karpas, Z., Anicich, V., & Huntress, Jr. W. T. 1979, J. Chem. Phys., 70, 2877 [NASA ADS] [CrossRef] [Google Scholar]
  16. Komatsu, E., Dunkley, J., Nolta, M. R., et al. 2009, ApJS, 180, 330 [NASA ADS] [CrossRef] [Google Scholar]
  17. Lepp, S., Stancil, P. C., & Dalgarno, A. 2002, J. Phys. B: At. Mol. Opt. Phys., 35, R57 [NASA ADS] [CrossRef] [Google Scholar]
  18. Linder, F., Janev, R. K., & Botero, J. 1995, Atomic and Molecular Porcesses in Fusion Edge Plasmas, ed. R. K. Janev (NY: Plenum Press), 397 [Google Scholar]
  19. Liu, X.-W., Barlow, M. J., Dalgarno, A., et al. 1997, MNRAS, 290, L71 [NASA ADS] [CrossRef] [Google Scholar]
  20. Maoli, R., Melchiorri, F., & Tosti, D. 1994, ApJ, 425, 372 [NASA ADS] [CrossRef] [Google Scholar]
  21. McGuire, P. 1976, Chem. Phys., 13, 81 [NASA ADS] [CrossRef] [Google Scholar]
  22. Palmieri, P., Puzzarini, C., Aquilanti, V., et al. 2000, Mol. Phys., 98, 1835 [NASA ADS] [CrossRef] [Google Scholar]
  23. Persson, C. M., Maoli, R., Encrenaz, P., et al. 2010, A&A, 515, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Ramachandran, C. N., De Fazio, D., Cavalli, S., Tarantelli, F., & Aquilanti, V. 2009, Chem. Phys. Lett., 469, 26 [NASA ADS] [CrossRef] [Google Scholar]
  25. Roberge, W., & Dalgarno, A. 1982, ApJ, 255, 489 [NASA ADS] [CrossRef] [Google Scholar]
  26. Rutherford, J. A., & Vroom, D. A. 1973, J. Chem. Phys., 58, 4076 [NASA ADS] [CrossRef] [Google Scholar]
  27. Saio, H., & Jeffery, C. S. 2000, MNRAS, 313, 671 [NASA ADS] [CrossRef] [Google Scholar]
  28. Schleicher, D. R. G., Galli, D., Palla, F., et al. 2008, A&A, 490, 521 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Smith, M. S., Kawano, L. H., & Malaney, R. A. 1993, ApJS, 85, 219 [NASA ADS] [CrossRef] [Google Scholar]
  30. Stancil, P. C., Lepp, S., & Dalgarno, A. 1998, ApJ, 509, 1 [NASA ADS] [CrossRef] [Google Scholar]
  31. Tacconi, M., Bovino, S., & Gianturco, F. A. 2011, Rendiconti Lincei, in press [Google Scholar]
  32. Tang, X. N., Azhari, A., Fu, C., et al. 2005, J. Chem. Phys., 122, 164301 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  33. Zygelman, B., Stancil, P. C., & Dalgarno, A. 1998, ApJ, 508, 151 [NASA ADS] [CrossRef] [Google Scholar]
  34. Xu, W., Liu, X., Luan, S., Zhang, Q., & Zhang, P. 2008, Chem. Phys. Lett., 464, 92 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Cosmological model parameters.

In the text
Table 2

Computed rate coefficient for the reaction (2) as a function of T.

In the text

All Figures

thumbnail Fig. 1

Computed integral cross-sections as a function of energy. The thick line represents the fitted experimental data from Rutherford & Vroom (1973). The dotted line is obtained from the formula given by Linder et al. (1995) by extrapolating the Rutherford’s data.
In the text
thumbnail Fig. 2

Computed production/destruction rates of HeH+ as function of redshift. Solid and dashed curves represent production and destruction processes, respectively.
In the text
thumbnail Fig. 3

Depletion rate coefficients as a function of the temperature. In the upper scale, the redshift is also reported. The experimental rate coefficients of Karpas et al. (1979) and those extrapolated by Schleicher et al. (2008) are also presented. The lithium reactions rate is from Bovino et al. (2010a).
In the text
thumbnail Fig. 4

Computed relative abundances of HeH+ in the post-recombination era as function of redshift z: present results (solid curves), results of GP98 (dashed curves). The LiH+ results are from Bovino et al. (2011).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.