| Issue |
A&A
Volume 529, May 2011
|
|
|---|---|---|
| Article Number | L3 | |
| Number of page(s) | 6 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201116717 | |
| Published online | 07 April 2011 | |
Letters to the Editor
Probing the dust formation region in IRC +10216 with the high vibrational states of hydrogen cyanide⋆,⋆⋆
1
Centro de Astrobiología, INTA-CSIC, Crta Torrejón km 4, 28850 Torrejón de Ardoz, Madrid, Spain
e-mail: jcernicharo@cab.inta-csic.es
2
LUTH, Observatoire de Paris-Meudon, 5 Place Jules Janssen, 92190 Meudon, France
3
LAOG, Observatoire de Grenoble, UMR 5571-CNRS, Université Joseph Fourier, Grenoble, France
4
Institut de Radioastronomie Millimétrique, 300 rue de la Piscine, 38406 Saint-Martin-d’Hères, France
5
Instituut voor Sterrenkunde, Department of Physics and Astronomy, K.U. Leuven, Celestijnenlaan 200D, 3001 Leuven, Belgium
Received: 14 February 2011
Accepted: 23 March 2011
We report the detection in IRC +10216 of 63 rotational transitions of HCN, most of them with quantum numbers J = 3–2, pertaining to 28 different vibrational states with energies up to 10 700 K (ν1+3ν2+ν3). Some of the transitions were also observed for the rare isotopologue H13CN. The observations were carried out with the IRAM 30-m telescope. The HCN lines with level energies above 5000 K arise within 1.5 stellar radius from the photosphere. Their intensities imply a vibrational temperature of Tvib ≃ 2400 K and a fractional HCN abundance relative to H2, x(HCN) = 5–7 × 10-5. These high-energy levels are mainly populated by photospheric radiation, and their vibrational temperature yields a direct measurement of the stellar photospheric temperature. The lines with energy levels between 2000 and 5000 K yield Tvib ≃ 1300 K and x(HCN) ≃ 0.8–2 × 10-5. They are radiatively excited and arise from a shell extending between 1.5 and 5 stellar radii. Finally, the lines from the low-energy vibrational states (<2000 K) trace a larger region of the envelope (5–28 stellar radii) with Tvib = 400–600 K and x(HCN) = 4–6 × 10-6. They are strongly affected by mid and near-infrared pumping. The line widths increase from 5 km s-1 near the 2400 K photosphere, to 19 km s-1 in the warm 400 K shell. This provides a unique insight into the physical conditions of the gas acceleration and dust formation region.
Key words: astrochemistry / line: identification / molecular processes / stars: AGB and post-AGB / circumstellar matter / stars: individual: IRC +10216
This work was based on observations carried out with the IRAM 30-m telescope. IRAM is supported by INSU/CNRS (France), MPG (Germany) and IGN (Spain).
Table 1 is available in electronic form at http://www.aanda.org
© ESO, 2011
1. Introduction
Hydrogen cyanide (HCN) is one of the most abundant species in the circumstellar envelopes of evolved carbon-rich stars. It has three vibrational modes: ν1 at 3.02 μm, ν2 (bending) at 14.01 μm, and ν3 at 4.77 μm. These fundamental vibrational levels have energies above the ground state E/k = 4764, 1027, and 3017 K, respectively (see González-Alfonso & Cernicharo 1999, for a diagram of the vibrational levels of HCN). The high temperatures and densities prevailing in the innermost regions of circumstellar envelopes and to the strong radiation arising from the central star and the surrounding dust together mean that these levels may be populated by collisions and/or radiation and the HCN emission from them is readily detected with large telescopes in the millimeter, sub-millimeter, and far- and mid-infrared domains (Ziurys & Turner 1986; Guilloteau et al. 1987; Lucas & Cernicharo 1989; Cernicharo et al. 1996, 1999; Fonfría et al. 2008; Shinnaga et al. 2009; Patel et al. 2009).
Maser emission has been observed in carbon-rich stars for several rotational transitions pertaining to highly excited vibrational states of HCN. It is particularly strong towards IRC +10216 and CIT6 (Lucas & Cernicharo 1989; Schilke et al. 2000; Schilke & Menten 2003; Avery et al. 1994; Bieging et al. 2000). Interpretating it is complicated by a wealth of pumping schemes that may affect the HCN levels (Cernicharo et al. 1999). Other lines of vibrationally excited HCN (in the ν1, ν2, and ν3 states, as well as in their overtones and combination states) appear to behave like when they are at thermal equilibrium (Cernicharo et al. 1996), so they can be used to probe the gas physical conditions in the dust formation zone (Fonfría et al. 2008). In this Letter, we present the detection in IRC +10216 at λ = 3 mm and 1 mm of 63 rotational transitions of HCN, which belong to 28 different vibrational states with energies up to 10 700 K above the ground state. Some of these transitions were also detected for H13CN. We derive the vibrational temperatures and HCN abundances between 1 and 28 stellar radii, and make a first direct determination of the photospheric temperature from mm-wave molecular line observations.
 |
Fig. 1 Selected J = 3–2 lines of HCN in various vibrational states (blue labels). The spectra observed with the IRAM 30-m telescope are indicated by black histograms. The line profiles calculated from our model (see text) are plotted in red. The line parameters are given in Table 1. Intensity scale is antenna temperature. Main beam antenna temperatures can be obtained by dividing the TA ∗ scale of the 270 GHz data by a factor of 0.4. Velocity resolution is 2.3 km s-1. |
2. Observations and results
Observations were carried out with the IRAM 30-m telescope in 2004–2009 with the λ = 3 mm SIS receiver and in Dec. 2009–Jan. 2010, using the new broad-band EMIR receiver that covers the 1 mm and 0.8 mm bands. The receivers were used in the single sideband mode, with image rejections ~10 dB at 1 mm and >20 dB at 3 mm. Each receiver was equipped with two channels with linear perpendicular polarizations. The spectrometer was an autocorrelator with a 4 GHz bandwidth and a channel spacing of 2 MHz (2.3 MHz at 260 GHz). The data are part of a spectral survey of IRC +10216 in the 3 mm, 2 mm, and 1 mm atmospheric windows (Cernicharo et al. 2000; Agúndez 2009). During the observations, the local oscillators were shifted in frequency, so that we could check for possible ghost lines from the image sideband. The secondary mirror was wobbled by ± 90′′ at a rate of 0.5 Hz. The pointing and focus of the telescope were checked every ~2 h on the nearby quasar OJ 287. The adopted position of the source is α2000 = 09h47m57.3s, δ2000 = 13°16′43.3′′. The half power beamwidth (HPBW) of telescope at 260 GHz, the frequency of the J = 3–2 lines of HCN, is 9.5′′. The temperature scale was calibrated every five minutes using two absorbers at different temperatures. It is expressed in terms of antenna temperature, 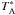 . The atmospheric opacity was obtained from measurements of the sky emissivity using of the ATM code (Cernicharo 1985). On-source integration times were typically 2.5–3 h. The profiles of selected lines are shown in Fig. 1 together with synthetic profiles derived from our model (see Sect. 3). The rest frequencies were computed from the rotational constants and Hamiltonian provided by Maki et al. (1996, 2000) and Zellinger et al. (2003). The last reference gives very accurate constants for the ν1, ν2, ν3, ν1 + ν3, ν1 + ν2, 2ν1, 2ν3, 2ν2, ν1 + 2ν2, and 2ν2 + ν3 and for the perturbed states 4ν2/ν2 + ν3. The constants of Maki et al. were used for all the other vibrational states. Following Maki et al., who used together with the infrared data all pure rotational transitions observed in the laboratory, we estimate uncertainties of 1–2 MHz for the v > 0 J = 3–2 line frequencies, depending on the vibrational level. The Hamiltonian used to compute energy levels for the ℓ-doubling states and for the interacting pair 4ν2/ν2 + ν3 has been described by Maki et al. (1996). The rotational transition frequencies (including ΔJ = 0 transitions) were calculated for 49 vibrational states and checked against laboratory observations when available. In these cases the uncertainties on the predicted frequencies were below 0.1 MHz. Moreover, the J = 7–6 line of several vibrational levels of HCN have been observed by Cernicharo et al. (2010) using these predictions. The observed minus calculated frequencies never exceed 2 MHz. Our frequency calculations have been confirmed by recent laboratory observations of HCN (Pearson et al., priv. comm.).
. The atmospheric opacity was obtained from measurements of the sky emissivity using of the ATM code (Cernicharo 1985). On-source integration times were typically 2.5–3 h. The profiles of selected lines are shown in Fig. 1 together with synthetic profiles derived from our model (see Sect. 3). The rest frequencies were computed from the rotational constants and Hamiltonian provided by Maki et al. (1996, 2000) and Zellinger et al. (2003). The last reference gives very accurate constants for the ν1, ν2, ν3, ν1 + ν3, ν1 + ν2, 2ν1, 2ν3, 2ν2, ν1 + 2ν2, and 2ν2 + ν3 and for the perturbed states 4ν2/ν2 + ν3. The constants of Maki et al. were used for all the other vibrational states. Following Maki et al., who used together with the infrared data all pure rotational transitions observed in the laboratory, we estimate uncertainties of 1–2 MHz for the v > 0 J = 3–2 line frequencies, depending on the vibrational level. The Hamiltonian used to compute energy levels for the ℓ-doubling states and for the interacting pair 4ν2/ν2 + ν3 has been described by Maki et al. (1996). The rotational transition frequencies (including ΔJ = 0 transitions) were calculated for 49 vibrational states and checked against laboratory observations when available. In these cases the uncertainties on the predicted frequencies were below 0.1 MHz. Moreover, the J = 7–6 line of several vibrational levels of HCN have been observed by Cernicharo et al. (2010) using these predictions. The observed minus calculated frequencies never exceed 2 MHz. Our frequency calculations have been confirmed by recent laboratory observations of HCN (Pearson et al., priv. comm.).
Fifthy-eight J = 3–2 lines from HCN and H13CN are identified in our 1 mm spectrum. In addition, several J = 1–0 lines from vibrational levels with ℓ = 0, and several ΔJ = 0 lines arising from the ν2 vibrational level, are detected at 3 mm. The line central velocities and widths were derived from Gaussian fits; the former agree within 3σ (1–1.5 km s-1) with the star velocity (VLSR = −26.5 km s-1). The other line parameters are given in Table 1. Maser emission from the ν2ℓ = −1 J = 2–1 line and apparently normal emission from the 2ν2J = 3–2 lines have been reported previously by Lucas & Cernicharo (1989). The intensities and profile shapes of the latter lines, shown in Fig. 1, are quite similar to those observed 20 years earlier. The strongest J = 3–2 vibrationally excited lines of HCN arise from the ν2, 2ν2, and ν3 states. Detailed modeling of the infrared pumping of these levels has been made by Cernicharo et al. (1999) and González-Alfonso & Cernicharo (1999) to explain the ISO/SWS observations of IRC +10216.
It is striking from Table 1, which lists the J = 1–0 and J = 3–2 lines by order of increasing energies, that the line widths depend on the level energies. Almost all lines pertaining to vibrational states with energies ≥ 5000 K have line widths between 5 and 8 km s-1. Most lines pertaining to states with energies 3000 < Eu/K < 5000 have widths between 8 and 12 km s-1. Finally, all lines from states with Eu/K < 3000 have widths between 13 and 19 km s-1. It is worth noting that all lines from vibrationally excited states have widths <19 km s-1, i.e., much smaller than twice the terminal velocity (Vexp) of the circumstellar envelope (2 × Vexp = 29 km s-1). As a result, the rotational lines pertaining to the vibrationally excited states of HCN must be formed between the stellar photosphere and the end of the dust formation zone, which marks the end of the gas acceleration region (Fonfría et al. 2008).
3. Discussion
The set of J = 3–2 lines, coming from the fundamental, overtone, and combination states of the three vibrational modes of HCN, provides a unique view of the stellar atmosphere and dust formation zone. Some of these lines have already been reported in the literature (Lucas & Cernicharo 1989; Shinnaga et al. 2009; Tenenbaum et al. 2010). However, the lack of rotational frequencies in online catalogs for most vibrational levels has hampered the search for very high excitation lines. Shinnaga et al. (2009) report a line at 265264.8 MHz that they identify with KCl J = 35–34 v = 2. This line is, however, probably the J = 3–2 ℓ = + 2 line of the 2ν2 + ν3 level of HCN (ν = 265 264.1 MHz). Although KCl is observed in IRC +10216 (Cernicharo & Guélin 1987), it is much less abundant than HCN, and no other lines from its excited vibrational states have ever been reported in high-sensitivity surveys (Cernicharo et al. 2000). Three unidentified lines reported by the same authors at 264 665, 265 253, and 265 386 MHz correspond to the 3ν2 + ν3, J = 3–2 ℓ = −1 and the 2ν2 + ν3, ℓ = −2 and ℓ = 0 transitions of HCN. All the other ℓ-doubling components pertaining to those levels are detected in our data (see Table 1), strongly supporting these identifications. Shinnaga et al. (2009) were, nevertheless, able to measure with the e-SMA the size of the emitting region for several vibrationally excited lines with published frequencies (see below). Several U lines reported by Tenenbaum et al. (2010) also correspond to HCN in different vibrational states (see Table 1). These lines have an intensity ≃ 10 times lower than ours, and they correspond to the different beam dilution for a much smaller source than the 30 m telescope HPBW (see below).
From the parameters of Table 1, we have constructed the vibrational temperature diagram shown in Fig. 2. The transitions involving the same rotational levels (e.g. J = 3–2) pertaining to different vibrational states are packed in a relatively small frequency interval and can be observed simultaneously, thanks to the 8 GHz-wide instantaneous bandwidth of the EMIR receiver. This allowed accurate measurement of the line relative intensities over the full range of energies covered by Fig. 2. The data must be fitted by at least three line segments, each of which corresponds to a particular temperature regime and, as we have seen, has a characteristic line width. All lines involving levels with energies > 5000 K are well fitted by a vibrational temperature Tvib = 2400 K. We refer to this region of high Tvib and narrow line widths as zone I. The second segment involves the lines with energy levels between 2000 and 5000 K; it yields Tvib ≃ 1300 K (zone II). Finally, the lines arising from levels ≤ 2000 K, including those from the vibrational ground state, are matched by Tvib = 400 K (zone III). As shown in the next paragraph, this value is an upper limit to the vibrational temperature in zone III, owing to the opacity of the HCN ground state lines. HCN column densities derived from Fig. 2 (assuming a source diameter of 1′′) are 1.5 ± 0.6 × 1017, 2.0 ± 0.9 × 1017, and 1.7 ± 0.5 × 1018 cm-2 for zones I, II, and III, respectively.
 |
Fig. 2 Vibrational temperature diagram derived from the HCN J = 3–2 lines given in Table 1. Upper level population vs. its energy above the ground state. The data is fitted by 3 line segments corresponding to regions with temperatures Tvib ~ 400 K, 1200 K, and 2400 K, respectively. HCN column densities are averaged over a source size of 1′′ diameter. A conservative calibration error of 30% has been applied to all intensities. Values in parentheses correspond to 3σ errors on the derived vibrational temperatures and column densities. Filled triangles correspond to lines with half-power widths Δv < 7 km s-1, filled squares correspond to lines with 7 < Δv < 9 km s-1, empty triangles correspond to lines with 9 < Δv < 12 km s-1, and empty squares to lines with Δv > 12 km s-1. |
In the case of H13CN, only three vibrational states with energies ≤ 3000 K are observed besides the ground state: ν2, 2ν2, and 3ν2. A vibrational temperature diagram based on these three states yields a vibrational temperature of 425 K for H13CN, to be compared with the value derived for the same three states of HCN, 550 K. The HCN/H13CN column density ratio is equal to 19, much more than the intensity ratio of the ground state lines, ≃ 2, but still a factor of 2 lower than the 12C/13C isotopic ratio, ≃ 42 (Kahane et al. 1988, 1992; Cernicharo et al. 1991). As a result, the lines from the lowest vibrationally excited states are less optically thick (τ ≃ 1) than those of the ground state, making it possible to derive meaningful HCN column densities in zone III.
From the intensities TA ∗ observed for each line, it is possible to estimate the dilution factor W and size of the emitting region, assuming the excitation temperature Trot and the opacity τ can be derived from the slopes and column densities on the vibrational diagram of Fig. 2. We use the relation TMB = W Trot (1-e−τ), where TMB = TA∗/0.4 is the observed main-beam averaged line temperature. For the lines with upper levels energies above 5000 K, i.e. originating in zone I, we typically find TMB ≃ 0.08 K. After adopting Trot = Tvib = 2400 K and a line opacity ≃ 1, we derive a diameter of 0.07′′ which decreases to 0.06′′ if the lines are optically very thick. In this zone the source-averaged HCN column density could exceed 1019 cm-2 (see below), and around 30% of the molecules could be in vibrational levels above 5000 K; therefore, even for a vibrational and rotational temperature as high as 2400 K, the opacity of the HCN J = 3–2 lines is still well above unity. Source-averaged HCN column densities below 1017 cm-2 would be needed to have τ(J = 3−2) < 1. The diameter of the star, as derived by interferometric infrared observations and lunar occultations, is ≃ 0.038′′ (Monnier et al. 2000; Ridgway & Keady 1988). So, high-excitation lines of HCN are coming from a compact region with a radius of 1.5 R∗, i.e. from the stellar photosphere and the very high-temperature atmosphere immediately above. The lines in zone I are narrow, and as we have seen, their width is readily explained by a combination of a width of 3–5 km s-1 due to microturbulence, plus a thermal line width (1 km s-1 at 2400 K). This is consistent with our finding that they are formed very close to the photosphere.
Collisional rates are not available for the vibrational levels of HCN. Based on the total collisional rate for the CO2 bending mode we assumed state-to-state collisional rates of a few 10-13–10-14 cm3 s-1 (see, e.g., Ziurys & Turner 1986). Within those assumptions, collisional excitation cannot compete with radiative de-excitation (rates > 1 s-1), unless the densities are as high as 1013 cm-3 (see also Ziurys & Turner 1986), a value that we could expect in the stellar photosphere, but not in the dust formation zone. The high vibrational temperature of 2400 K means that the vibrational states in zone I are mainly pumped by infrared photons. In that case, the vibrational levels will be in radiative equilibrium with the star, and the vibrational temperature observed in zone I measures the stellar photospheric temperature directly (Cernicharo et al. 1999; González-Alfonso & Cernicharo 1999). The latter has been independently derived to be ≃ 2330 K from IR measurements (see Fonfria et al. 2008, and references therein).
Although most high-energy levels are in radiative equilibrium with the star, some may experience peculiar radiative pumping, as may be the case for the interacting pair 4ν2/ν2 + ν3: some rotational levels from 4ν2 are so close in energy to rotational levels of the ν2 + ν3 state that they can be populated efficiently directly from the ground state via this state, thanks to the strong infrared field. This may lead to strong and narrow maser emission (Schilke et al. 2000; Schilke & Menten 2003). Strong masers are not observed in our spectra. Nevertheless, we have observed a very narrow line at 102048.8 MHz that coincides in frequency with the 4ν2J = 2 → ν2 + ν3J = 1 ro-vibrational transition. The masers involving the lower energy ν2 level have to be explained in a different way (Lucas & Cernicharo 1989).
The source diameter of zone II, where level energies are between 2000 K and 5000 K and for which we assume Trot = Tvib = 1300 K, and TMB = 0.4 K is 0.21′′, i.e. a radius of ~5 R∗ for τ ≃ 1 (and 4.4 R∗ for τ > 1). This diameter agrees with what is observed for vibrationally excited SiS by Patel et al. (2009). The lines in zone II are broader (8–13 km s-1), which is consistent with the larger radius at which they are observed. Obviously, the dust starts to form and the gas starts to get accelerated between 1.5 and 5 stellar radii, in agreement with the results of the modeling of the mid-infrared lines of C2H2 and HCN by Fonfría et al. (2008).
Finally, for zone III, where the excited levels have energies close to or below 2000 K, we have Trot = Tvib = 400 K, τ = 1 (as suggested by the HCN/H13CN ratio) and TMB = 5 K. We derive a diameter of 1.1′′, or 29 R∗. This region includes the first two dust formation regions described by Fonfría et al. (2008). This emitting zone is much larger than the one observed by Patel et al. (2009) for SiS. However, it agrees with the value derived by Shinnaga et al. (2009), 23 R∗, for some low vibrational energy levels of HCN. Those authors also find that they have to include another region between 1–15 R∗ which partially coincides with our zones I and II in order to explain their observations.
The line widths observed in zone I (5–8 km s-1) are consistent with a velocity field dominated by thermal broadening ( ≃ 1 km s-1 at 2400 K), plus a turbulent velocity of 3–5 km s-1. Those of zone II (8–13 km s-1) imply an expansion velocity increasing from 0 to 6 km s-1. The expansion velocity reaches 9 km s-1 in zone III. For the expected densities in zones I–III, dust and gas must be tightly coupled, and the vibrational temperatures derived from Fig. 2 must be close to the kinetic temperature of the gas. We have seen that, in zone I, collisional excitation is unlikely to match radiative excitation for populating the HCN vibrationally excited states. Considering the steep decrease in the gas temperature and density with increasing radius (TK changes from 2400 to 1200 K, and density decreases by a factor 25, in 5 stellar radii), a fortiori collisions play a minor role in zones II and III, except if shocks are important. The populations of the vibrationally excited states are thus likely to be controlled by the stellar and hot dust radiations.
Using these results we modeled the HCN emission for the first 49 vibrational states quoted above. We adopted the physical parameters for the star and its envelope derived by Fonfría et al. (2008). We considered the first 28 stellar radii and assumed Trot = Tk = Tvib, with Tvib = Tstar = 2400 K for the region r < 1.5 R∗ (zone I), 1300 K for 1.5 R∗ < r < 5 R∗ (zone II), and 550 K for r > 5 R∗ (zone III). The assumed velocity field is the one derived by Fonfría et al. (2008). The adopted H2 density at r = 1 R∗ is 1010 cm-3. Line strengths were derived from the expressions given by Herzberg (1945), and we used the dipole moment function obtained by DeLeon & Muenter (1984). The emerging brightness temperature was convolved with the HPBW of the IRAM 30-m radio telescope at the frequencies of the J = 3–2 lines ( ≃ 9.5′′). They were converted into antenna temperature to allow direct comparison with the data. The abundance of HCN in each zone has been varied until a good agreement was found (within a factor two) with the observed intensities. We have found abundances in zones I–III of 4–7, 0.8–3, and 4–6 (10-5). The result of the best model is shown as the synthetic profiles in Fig. 1. We find it remarkable that such a simple model predicts most of the observed line intensities within a factor two. This suggests that our assumption of a thermalization of the
rotational levels at three temperatures is a fair approximation. The ν2 = 1 levels are poorly reproduced owing to infrared pumping and maser action throughout a much wider region of the envelope than considered in our model (Lucas & Cernicharo 1989). Asymmetries in the line intensities between ℓ = ± 1 or ± 2 transitions of the same state are evident for ν2, 2ν2, and 3ν2. Similar effects could also explain the poor fit of the ν3 line in Fig. 1. Since the ν3 state is radiatively connected to the ground state the infrared pumping can be efficient over a large region of the inner envelope. The column densities in our models for these zones are 1.5–3.0 × 1019, 1–4 × 1018, and 0.7–1.1 × 1018 cm-2. For comparison purposes, the source-averaged HCN column densities as derived from Fig. 2 and the sizes quoted above are 5.6 × 1019, 4.5 × 1018, and 1.4 × 1018 cm-2 for zones I–III.
The high brightness temperature of the excited HCN lines makes them ideal tools for studying the acceleration region with ALMA down to spatial resolutions of a few R∗. Combining these with previous ISO observations (Cernicharo et al. 1996) and Herschel/HIFI, PACS and SPIRE observations will allow a unique wealth of data to be assembled on the upper atmosphere of an AGB star and lead to investigations of how dust condenses and how the gas gets accelerated – two key questions in stellar astrophysics.
Online material
Line parameters for the observed transitions of HCN and H13CN.
Acknowledgments
We thank the Spanish Ministry of Science and Innovation (MICINN) for funding support through grants AYA2006-14876, AYA2009-07304, and the CONSOLIDER program “ASTROMOL” CSD2009-00038. J.R.G. was supported for this research by a Ramón y Cajal contract. M.A. is supported by a Marie Curie Intra-European Individual Fellowship within the EC FP7 under grant agreement No. 235753. E.D.B. and L.D. acknowledge financial support by the FwO under grant G.0470.07.
References
- Agúndez, M. 2009, Ph.D., Universidad Autónoma de Madrid [Google Scholar]
- Avery, L. W., Bell, M. B., Cunningham, C. T., et al. 1994, ApJ, 426, 737 [NASA ADS] [CrossRef] [Google Scholar]
- Bieging, J. H., Shaked, S., & Gensheimer, P. D. 2000, ApJ, 543, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Cernicharo, J. 1985, ATM a code to compute atmospheric opacity up to 1 THz, IRAM internal report [Google Scholar]
- Cernicharo, J., & Guélin, M. 1987, A&A, 183, L10 [NASA ADS] [Google Scholar]
- Cernicharo, J., Guélin, M., Kahane, C., et al. 1991, A&A, 246, 213 [NASA ADS] [Google Scholar]
- Cernicharo, J., Barlow M., González-Alfonso, E., et al. 1996, A&A, 315, L201 [NASA ADS] [Google Scholar]
- Cernicharo, J., Yamamura, I., González-Alfonso, E., et al. 1999, ApJ, 526, L41 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Cernicharo, J., Guélin, M., & Kahane, C. 2000, A&AS, 142, 181 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cernicharo, J., Waters, L. B. F. M., Decin, L., et al. 2010, A&A, 521, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- DeLeon, R. L., & Muenter, J. S. 1984, J. Chem. Phys., 80, 3992 [NASA ADS] [CrossRef] [Google Scholar]
- Fonfría, J. P., Cernicharo, J., Richter, M. J., & Lacy, J. 2008, ApJ, 673, 445 [NASA ADS] [CrossRef] [Google Scholar]
- González-Alfonso, E., & Cernicharo, J. 1999, in The Universe as Seen by ISO, ed. P. Cox, & M. F. Kessler. ESA-SP, 427, 325 [Google Scholar]
- Guilloteau, S., Omont, A., & Lucas, R. 1987, A&A, 176, L24 [NASA ADS] [Google Scholar]
- Herzberg, G. 1945, Molecular Spectra and Molecular Structure: II Infrared and Raman Specrta of Polyatomic Molecules (New York: D. Van Nostrand Co. Inc.) [Google Scholar]
- Kahane, C., Gómez-González, J., Cernicharo, J., & Guélin, M. 1988, A&A, 190, 167 [NASA ADS] [Google Scholar]
- Kahane, C., Cernicharo, J., Gómez-González, J., & Guélin, M. 1992, A&A, 256, 235 [NASA ADS] [Google Scholar]
- Lucas, R., & Cernicharo, J. 1989, A&A, 218, L20 [NASA ADS] [Google Scholar]
- Lucas, R., Omont, A., & Guilloteau, S. 1988, A&A, 194, 230 [NASA ADS] [Google Scholar]
- Maki, A., Quapp, W., Klee, S., et al. 1996, J. Mol. Spectrosc., 180, 323 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Maki, A., Mellau, G. Ch., Klee, S., et al. 2000, J. Mol. Spectrosc., 202, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Monnier, J. D., Danchi, W. C., Hale, D. S., et al. 2000, ApJ, 543, 861 [Google Scholar]
- Patel, N. A., Young, K. H., Brunken, S., et al. 2009, ApJ, 692, 1205 [NASA ADS] [CrossRef] [Google Scholar]
- Ridgway, S., & Keady, J. J. 1988, ApJ, 326, 843 [NASA ADS] [CrossRef] [Google Scholar]
- Schilke, P., & Menten, K. 2003, ApJ, 583, 446 [NASA ADS] [CrossRef] [Google Scholar]
- Schilke, P., Mehringer, D. M., & Menten, K. 2000, ApJ, 528, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Shinnaga, H., Young, K. H., Tilanus, R. P. J., et al. 2009, ApJ, 698, 1924 [NASA ADS] [CrossRef] [Google Scholar]
- Tenenbaum, E. D., Dodd, J. L., Milam, S. N., et al. 2010, ApJS, 190, 348 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Zellinger, Z., Amano, T., Ahrens, V., et al. 2003, J. Mol. Spectrosc., 220, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Ziurys, L., & Turner, B. E. 1986, ApJ, 300, L19 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Selected J = 3–2 lines of HCN in various vibrational states (blue labels). The spectra observed with the IRAM 30-m telescope are indicated by black histograms. The line profiles calculated from our model (see text) are plotted in red. The line parameters are given in Table 1. Intensity scale is antenna temperature. Main beam antenna temperatures can be obtained by dividing the TA ∗ scale of the 270 GHz data by a factor of 0.4. Velocity resolution is 2.3 km s-1. |
| In the text | |
 |
Fig. 2 Vibrational temperature diagram derived from the HCN J = 3–2 lines given in Table 1. Upper level population vs. its energy above the ground state. The data is fitted by 3 line segments corresponding to regions with temperatures Tvib ~ 400 K, 1200 K, and 2400 K, respectively. HCN column densities are averaged over a source size of 1′′ diameter. A conservative calibration error of 30% has been applied to all intensities. Values in parentheses correspond to 3σ errors on the derived vibrational temperatures and column densities. Filled triangles correspond to lines with half-power widths Δv < 7 km s-1, filled squares correspond to lines with 7 < Δv < 9 km s-1, empty triangles correspond to lines with 9 < Δv < 12 km s-1, and empty squares to lines with Δv > 12 km s-1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


