| Issue |
A&A
Volume 529, May 2011
|
|
|---|---|---|
| Article Number | A131 | |
| Number of page(s) | 11 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201016413 | |
| Published online | 18 April 2011 | |
Simulation of planet detection with the SPHERE integral field spectrograph
1
INAF-Osservatorio Astronomico di Padova, Vicolo dell’Osservatorio 5, 35122 Padova, Italy
e-mail: dino.mesa@oapd.inaf.if
2
UJF-Grenoble 1/CNRS-INSU, Institut de Planétologie et d’Astrophysique de Grenoble (IPAG), UMR 5274, 38041 Grenoble, France
3
LESIA-Observatoire de Meudon, 5 place Jules Janssen, 92195 Meudon, France
4
European Southern Observatory, Karl-Schwarzschild-Strasse 2, 85748 Garching, Germany
5
LAM, UMR 6110, CNRS, Université de Provence, 38 rue Frédéric Joliot-Curie, 13388 Marseille Cedex 13, France
6
Max Planck Institute for Astronomie, Konigsthul 17, Heidelberg, Germany
7
School of Physics, University of Exeter, Stocker Road, Exeter EX4 4QL, UK
Received: 28 December 2010
Accepted: 1 March 2011
Aims. We present simulations of the perfomances of the future SPHERE IFS instrument designed for imaging extrasolar planets in the near infrared (Y, J, and H bands).
Methods. We used the IDL package code for adaptive optics simulation (CAOS) to prepare a series of input point spread functions (PSF). These feed an IDL tool (CSP) that we designed to simulate the datacube resulting from the SPHERE IFS. We performed simulations under different conditions to evaluate the contrast that IFS will be able to reach and to verify the impact of physical propagation within the limits of the near field of the aperture approximation (i.e. Fresnel propagation). We then performed a series of simulations containing planet images to test the capability of our instrument to correctly classify the found objects. To this purpose we developed a separated IDL tool.
Results. We found that using the SPHERE IFS instrument and appropriate analysis techniques, such as multiple spectral differential imaging (MDI), spectral deconvolution (SD), and angular differential imaging (ADI), we should be able to image companion objects down to a luminosity contrast of ~10-7 with respect to the central star in favorable cases. Spectral deconvolution resulted in the most effective method for reducing the speckle noise. We were then able to find most of the simulated planets (more than 90% with the Y-J-mode and more than the 95% with the Y-H-mode) for contrasts down to 3 × 10-7 and separations between 0.3 and 1.0 arcsec. The spectral classification is accurate but seems to be more precise for late T-type spectra than for earlier spectral types. A possible degeneracy between early L-type companion objects and field objects (flat spectra) is highlighted. The spectral classification seems to work better using the Y-H-mode than with the Y-J-mode.
Key words: instrumentation: spectrographs / methods: data analysis / techniques: imaging spectroscopy / planetary systems
© ESO, 2011
1. Introduction
A large number of extrasolar planets have been discovered in the past fifteen years through indirect methods such as radial velocities and transits. Although in the past few years some objects with planetary mass have been imaged around stellar and substellar objects like HR 8799 (Marois et al. 2008), Fomalhaut (Kalas et al. 2008), 2M 1207 (Chauvin et al. 2009), and β Pictoris (Lagrange et al. 2010), imaging of extrasolar planets is still very challenging because of the high planet vs. star luminosity contrast (10-6 for young giant planets and down to 10-8–10-10 for old giant and rocky planets) and the small separation with respect to the central star (few tenths of arcsec for a planet at ~10 AU at some tens of pc).
The next generation of instruments aimed at imaging extrasolar planets will exploit extreme adaptive optics (XAO) systems to correct aberrations up to a high order, providing a high Strehl ratio (SR) and high-efficiency coronagraphs to attenuate the on-axis PSF and reduce its diffraction pattern. The combination of these two devices should be able to reduce the stellar background down to a value of around 10-5 at separations of a few tenths of arcsec. The residual background will be given mainly by the speckle noise generated by the atmosphere and the telescope pupil-phase distortion. To further improve the contrast achievable with these instruments, it will be mandatory to apply differential imaging techniques, such as angular differential imaging (ADI) (Marois et al. 2006), simultaneous spectral differential imaging (S-SDI) (see e.g. Marois et al. 2005), and spectral deconvolution (SD) (see Thatte et al. 2007).
In the next years in particular, three instruments will be able to exploit these techniques to image extrasolar planets. These are the Gemini Planet Imager (GPI) at the Gemini South Telescope (Macintosh et al. 2006), SPHERE at the ESO Very Large Telescope (VLT) (Beuzit et al. 2006), and Project 1640, which is already working at the 5 m Palomar telescope (see Hinkley et al. 2011, and Crepp et al. 2011).
In particular, SPHERE will include three scientific channels: (i) a differential imager and dual band polarimeter called IRDIS that will operate in the near infrared between the band Y and Ks (Dohlen et al. 2008); (ii) a polarimeter called ZIMPOL that will perform differential imaging exploiting the polarized light reflected from the planetary atmosphere in the visual band (Thalmann et al. 2008); (iii) an integral field spectrograph (IFS) that will supply simultaneous images at different wavelengths in the near infrared between the Y and the H bands (Claudi et al. 2008).
Integral field spectrographs also have the potential of providing the spectra of the detected faint companions at close separation, thus allowing much better characterization. IFSs similar to the one designed for SPHERE are also present in GPI and in Project 1640, and are foreseen for future planet imagers like EPICS designed to work for the future E-ELT (Kasper at al. 2010). In this paper we present the results obtained from the simulations we developed to evaluate and to optimize the performances of the SPHERE IFS. In Sect. 2 we give a very short summary of the SPHERE IFS instrument, in Sect. 3 we describe the simulation tools that we used in our work, in Sect. 4 we describe the methods used for the data analysis of the output of our simulations, in Sect. 5 we present the results of the various simulation runs, in Sect. 6 we describe the software that we wrote for the IFS data analysis and the results obtained testing it on the output of our simulations, while in Sect. 7 we report our conclusions.
2. SPHERE IFS description
The SPHERE IFS is designed to work in two different wavelength ranges: (i) 0.95–1.35 μm (Y-J-mode) with a resolution of R = 50 and (ii) 0.95–1.65 μm (Y-H-mode) with a resolution of R = 30. These two ranges and resolutions are achieved through two different dispersers (two Amici prisms – see Oliva 2000). The IFS is composed of several subsystems:
-
the integral field unit (IFU);
-
the collimator optics system;
-
a filter wheel;
-
the disperser optics system;
-
a camera optics system that can be moved to focus spectra on the detector or to produce dithering to reduce noise related to the flat fielding;
-
a 2048 × 2048 Hawaii II detector with pixel of 18 μm housed in a cryostat.
The novel lenslet IFU concept upon which this spectrograph is based (BIGRE, Antichi et al. 2009) allows the entrance slits plane to be made of images of the telescope focal plane and not of images of the telescope pupil, as ordered in the classical TIGER design (Bacon et al. 1995). In this design, each lenslet is an afocal system with two powered surfaces. The thickness of the array is then given by the sum of the focal lengths of the lenslets of the two arrays. The main advantage of the BIGRE configuration over the TIGER one is that it allows a strong reduction of the cross-talk between adjacent lenslets as demostrated by Antichi et al. (2009). The microlens array is composed of 145 × 145 hexagonal lenslets with a pitch of 161.5 μm (corresponding to ~0.012 arcsec). Each lenslet is masked with a circular aperture with a factor of 0.98 to avoid straylight. The full field of view (FOV) of the instrument is a square with a side of 1.77 arcsec. The total length of the whole instrument from the first surface of the IFU to the detector plane is 1061.89 mm. A more detailed description of the whole instrument can be found, e.g., in Claudi et al. (2010).
3. Simulation description
We exploited two software tools for our simulations:
-
the SPHERE package of the CAOS software;
-
the CSP code1.
The CAOS system (Carbillet et al. 2004) is an IDL based software that aims to simulate the behavior of a generic adaptive optic (AO) system from the atmospheric propagation of light to the sensing of the wavefront aberrations and the corrections through a deformable mirror. This is done with a Fraunhofer approach, so that it cannot be used to properly evaluate the impact of Fresnel propagation (see Sect. 5.1). An end-to-end numerical tool has been developed for the simulation of the whole SPHERE instrument within the CAOS environment. It contains detailed instrumental modeling of the Extreme adaptive optics systems, of IRDIS and ZIMPOL (Carbillet et al. 2008). A module simulating the SPHERE IFS has been also developed to properly take both the real and the imaginary parts of the image forming on the lenslet plane into account. In principle, this could allow a complete treatment of the cross-talk among the lenslets when studying the impact of light propagation through the BIGRE. However, the execution of this module turned out to be very time consuming so that it was not possible to use it for a large number of detailed simulations. To overcome this difficulty, we used a shorter code that calculates the impact of the cross-talk between adjacent lenslets (coherent) and adjacent spectra (incoherent) by providing the beam propagation over a sub-sample of 7 hexagonal lenslets. This code is described in detail in Antichi et al. (2009). After running this code we concluded that a value of the cross-talk equal to or less than 10-2 was completely adequate for meeting the objectives of our instrument.
We then decided to use our (IDL oriented) code called CSP to perform all the simulations of light propagation within the IFS, while we decided to use the SPHERE CAOS package to provide real intensities over the IFU entrance focal plane as input for CSP. For this, we performed simulations using the CAOS IRDIS module with 100 atmospheric phase screens at 64 different wavelengths ranging between 0.95 and 1.35 μm (or between 0.95 and 1.65 μm in the Y-H-mode case). There are enough atmospheric screens is large enough to ensure that static speckles dominate noise, as expected in real cases, and to ensure that the PSF has an overall shape representing a realistic stellar halo.
In Fig. 1 we display a monochromatic PSF obtained from the CAOS simulations. Even if the SPHERE package of the CAOS system allows simulating different types of coronagraphs, we preferred to use only a 4-quadrant one for our simulations (Boccaletti et al. 2008). In this way, however, our results are still representative as we were not interested in investigating the performances of all the SPHERE instrument coronagraphs. The choice of making a simulation with only 64 wavelengths was determined because for more wavelengths, the program saturates our computer memory. However, CSP requires 269 PSFs at different wavelengths as input and to obtain them, we performed interpolations starting from the ones resulting from the CAOS simulation2.
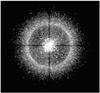 |
Fig. 1 Monochromatic PSF resulting from the CAOS simulation. The bright corona corresponds to the outer working angle of the XAO system. Its radius is roughly 0.5 arcsec at the working wavelength. This image has been obtained using a 4-quadrant coronagraph. The cross structure centered on the center of the image is the signature of this type of coronagraph. |
An early version of the CSP code, described in Berton et al. (2006), has been deeply modified to take variations in the instrument optical design into account. CSP only considers the real part of the image on the lenslet plane and then propagates it through the IFS spectrograph using a Fraunhofer approach, but it can include a treatment of the cross-talk through a parametric approach. The code can be divided into different parts:
-
The image formation part simulates the propagation of the lightthrough the instrument and its main goal is to produce a final imagewith all the spectra. For each spectral step, the exact number ofphotons passing through every microlens is calculated, as well asthe correct position projected on the detector of the center of eachmicroimage. The intermediate images generated by this processare then convolved with a microlens PSF prepared in advance. Allthe monochromatic images are properly shifted to account for thespectral dispersion due to the Amici prisms and are then summedup to create the spectra. Finally the code adds noises to the image:Poisson noise and all the detector noises. An example of the outputof this part of the code is given in Fig. 2.
-
The calibration part performs the same procedure as is described at the previous point using a monochromatic uniform illumination of the IFU (and not a PSF) as input. This part simulates the wavelength calibration lamps and is performed at three different wavelengths. The code, then, reads from the images resulting from these procedures the spectra (having a template that indicates the position of the spectra at the minimum wavelength). Every spectrum is fitted with a Gaussian curve (using the IDL routine GAUSSFIT) and the code finds the center of the Gaussian and its error. Finally, through an appropriate interpolation, the code calculates the shift for each lenslets, using the positions of the previuosly calculated three centers and the theoretical position of the center (well known because we know the wavelength of the calibration lamp). At the end, these results are saved in a wavelength map file where at every pixel of the image is associated a well-defined wavelength.
-
The last part of the simulation procedure is to create of the datacube with the monochromatic images that will be the instrument final output. To this aim we derive a rectangular grid from the original hexagonal pattern of the IFU. This is done by creating a square grid of points at the same distance from each other. For every wavelength, the flux value associated to every point of the grid is calculated by considering the three nearest points at the given wavelength as calculated in the calibration step of the procedure and saved in the wavelength map. The calculation is made with a mean of the fluxes of these three points weighted according to the distance from the grid point considered.
 |
Fig. 2 A small portion of spectra resulting from one of the CSP simulations. |
Where not specified, the simulations were performed assuming a G0 spectral type central star with an absolute magnitude of J = 3.75 and at a distance of 10 pc from the Sun. A total exposure time of 1 h was generally simulated even if, in some cases, longer exposure times were simulated. For these simulations we assumed a readout noise of 10 e−, a dark current of 0.1 e − , and a flat field error of 10-4 (hereinafter detector noise).
4. Data analysis methods
High-performance coronagraphs within an extreme AO system like the one adopted in SPHERE, which gets its sampling frequency equal to 20 cycles/pupil, allows imaging of companion objects down to a contrast of 10-5 within the whole FOV of its IFS (2.5 arcsec diagonal), except for separations smaller than ~0.1 arcsec from the central star. However, to fulfill the goal of the SPHERE instrument to image giant planets around young nearby star, contrasts of ~10-6 − 10-7 are requested. To this aim, speckle noise has to be reduced by a further factor of 10–100. This is done by applying some differential imaging analysis techniques to the final datacube extracted from the IFS data, such as the simultaneous spectral differential imaging (S-SDI) (Marois et al. 2000) and the spectral deconvolution (SD) (Thatte et al. 2007). A natural evolution of the S-SDI technique, using an IFS, has been defined during our work and is described in detail in Sect. 4.1. Another possible technique, normally applied with other analysis techniques, is angular differential imaging (ADI) (Marois et al. 2006).
In this section we briefly present the algorithms we used to implement these methods.
4.1. Multiple differential imaging
As previously said, this techique is an extension to more spectral channels of the previous S-SDI techniques, such as the single differential imaging for two channels and the double differential imaging for three channels (Marois et al. 2000). The final result of the CSP simulation code consists of a datacube composed of 33 (for the Y-J-mode) or 38 (for the Y-H-mode) monochromatic images. On these images we apply the following steps:
-
1.
The images are divided into two groups: planetary images(monochromatic images at wavelengths where the planet signalis potentially present) and reference images (monochromaticimages at wavelengths where the planet signal is very weak orabsent) according to giant-planet atmosphere models.
-
2.
We then distinguish two different cases:
-
Single differences:
-
a reference image is assigned to each planetary image;
-
for each pair, the reference image is spatially scaled (through an interpolation procedure) to the planetary image according to the wavelength ratio between the wavelengths of planetary and reference image;
-
the scaled reference image is subtracted from the planetary one.
-
-
Double differences:
-
two reference images are assigned to each planetaryimage, with the wavelength respectively shorter andlonger than the planetary one. The two reference imagesare chosen in such a way that their wavelengthseparations from the image containing the planet signalare the same;
-
for each group of three images, the reference images are spatially scaled to the planetary image according to the wavelength ratio between the wavelengths of planetary and reference images;
-
the three images are combined according to the double-difference formula defined by Marois et al. (2000).
-
-
-
3.
The procedure at step 2 should eliminate most of the speckle pattern. If the pairs are selected so that the planet image is only present in one of the two images, the planet will not be canceled out.
-
4.
A weighted average of the cleaned differential images provides the best final result suitable for the planet search. We adopted a weight for each single differential image, which is the reciprocal of the wavelength difference between the two (or three) images subtracted to obtain the considered one. In this way we give a greater weight to differences between images with a smaller wavelength separation, where the speckle pattern has a stronger correlation. Since the planetary images are not scaled, the planet position will not shift with wavelength.
There are three critical issues in this procedure:
-
1.
To properly work we have to make an assumption about thespectra of the companion objects that we are looking for.Moreover, this works much better for spectra with largeabsorption bands such as for methane-dominated planets.
-
2.
Each interpolation introduces noise. In our approach, the number of interpolations is effectively reduced to only one per pair (two for each group of three images when using the double differential imaging).
-
3.
Pairing of monochromatic images, and optimal weighting should be given according to the main noise source:
-
if errors are dominated by photon noise, the best procedure isto assign the same weights to all pairs. In this case, pairs shouldbe selected to have similar (or even constant) wavelengthseparations;
-
if errors are dominated by calibration errors (speckle residuals), the best procedure in single differential imaging is to create pairs having the smallest possible wavelength separation, compatible with the gradients present in the planetary spectra. In this case weights should be assigned according to the inverse of the square of wavelength separation;
-
for what concerns double differences, this last approach is limited by the intrinsic width of the emission peaks in the planetary spectrum. Practically, we expect a very small advantage by creating groups of three images with the smallest possible wavelength differences. It should then be more advantageous to have various groups of three images with the same wavelength difference and give the same weight to all of them.
-
4.2. Spectral deconvolution
This method was proposed for the first time in Sparks & Ford (2002) and further developed in Thatte et al. (2007). It exploits that speckles are expected to change regularly with wavelength. Outside a given separation, defined as the bifurcation radius (BR), the speckle spatial excursion over the spectral range is larger than the planet size so that the speckle pattern associated to the star can be reconstructed and eliminated using regions unaffected by the planet image. Differently from the MDI described in the previous section, no assumption about the spectra of the companion objects is needed.
Spectral deconvolution should offer some advantage over the differential imaging approach, at least outside the BR, because it uses the companion spectrum as a whole. The value of the the SPHERE IFS BR is around 0.20 arcsec for the Y-J-mode and about 0.12 arcsec for the Y-H-mode. The procedure we followed is composed of four steps:
-
We scaled single images provided by the CSP data extractionalgorithm to a reference wavelength (in this case we chose thecentral wavelength among those of the 33 or 38 monochromaticimages). Because of this rescaling, the planet will be in differentpositions in every image.
-
We plotted the spectrum for every spaxel of the rescaled datacube (see Fig. 3) and calculated a polynomial fitting function using 1/λ as independent variable. The polynomial degree depends on the distance from the center of the image, in units of the BR. The value of this fitting function is then subtracted from every spectrum. The fit allows the modulation of a given stellar halo speckle brightness with wavelength to be taken into account but its degree is small enough not to fit a potential planetary signal. This should eliminate, or at least reduce, the speckles or diffraction residuals.
-
The subtracted images are then rescaled back to the original scale according to their wavelength, in order to mantain fixed the planet position in all of them.
-
To search for planet signal, the three-dimensional datacube is collapsed to a bi-dimensional image given by the cross-correlation of the spectra in each spaxel with a template planet spectrum. This procedure enhances the signal-to noise of the final image. In general, in our simulations we use a methane-dominated spectrum. However, as we see in Sect. 6, this procedure works well with either a flat or an L-type spectrum, too.
 |
Fig. 3 Example of the simulated spectra on a spaxel rescaled according to the wavelength for SPHERE IFS simulations. The dotted line represents the value of one single pixel on the PSFs used as input for the CSP code. The solid line represents the same thing on the images of the datacube resulting from the CSP simulation (passage of the light through the instrument and correct calibration to create the datacube). The absolute values of these two curve have been normalized to be able to overplot one on the other. |
4.3. Angular differential imaging
In general, we assume that observations are done with the field fixed with respect to the IFU. In this case, the pupil rotates with time on an alt-az telescope, a typical value being 30° over a 1 h exposure time. In this framework3, angular differential imaging (ADI) can be applied to reduce the speckle noise further. Various codes have been written to perform ADI on real images (see Marois et al. 2006). Here, we considered a variant of this method that we defined as azimuthal filtering (“azimuthal”, meaning along arcs at a constant radius). This procedure is composed of the following steps:
-
for each given pixel, we searched for all spaxels that have similarseparation (distance from the center). In our procedure, theannulus width was set at 1 pixel;
-
we plotted the value of the intensity at the selected wavelength for each of these spaxels against the azimuth angle;
-
we drew a fitting line through these points using a cubic spline curve through the averages of these points within arcs of length 4λ/D. After various tests, we chose this value to avoid canceling the planet signal;
-
we subtracted the intensity value on the fitting line from the intensity at the selected wavelength in that spaxel;
-
the procedure was then repeated for all wavelengths;
-
the procedure was iterated over all spaxels.
While this procedure does not completely eliminate the impact of static speckles, it also works well for quasi-static speckles, which are speckles having a lifetime longer than field rotation but shorter than the total exposure time.
5. Simulations results
In this section we review the most important results obtained from our simulations. As said in previous sections, we expect a significant improvement in the contrast using the MDI method compared to a simple S-SDI, when exploiting all of the many monochromatic images provided by an IFS. In particular we expect that the contrast scales with the square root of the number of independent single differences that we can realize when using the whole spectrum. A further improvement can be obtained by correctly coupling the images at different wavelengths. Since the contrast scales with the wavelength separation, we can pair monochromatic images in ascending order of wavelength separation and weight them in descending order according to their wavelength separation.
 |
Fig. 4 Comparison between 5σ contrast obtained with single difference (yellow line), with multiple single differences (red line), and with multiple double differences (green line) from IFS simulations. These results were obtained for a simulation where no detector noise, no cross-talk, and no rotation were considered. |
In Fig. 4 we display these results for a simulation where no detector noise, no cross-talk, and no rotation were considered. In particular, we can see that no further gain is instead obtained using the multiple double-difference method. This is mainly because realistic double differences should be made using a rather large wavelength separation, because of the intrinsic width of the methane bands. In this simulation, as in all the following ones, the jump in the plots around 20λ/D is given by the coronagraph outer working angle effects.
We can further improve the contrast obtained with our instrument by exploiting the rotation of the field with respect to the pupil. As seen in Fig. 5, the improvement is better at large separations, as expected because more noise realizations can be sampled. If quasi-static speckles dominate, the results improve with the square root of the angle (and of the separation), since the planet images sample different noise realizations while rotating around the stellar image. In this case the azimuthal filtering procedure (described above in Sect. 4.3) can be applied.
 |
Fig. 5 Run of the 5σ calibration limit with separation for three cases: (i) no field rotation (red line), rotation by 30° with no azimuthal filtering apllied (yellow line), rotation by 30° with azimuthal filtering applied (green line). |
SD should provide better results than MDI, at least for separations larger than the BR. This is confirmed by the plots displayed in Fig. 6 where we show the run of the 5σ calibration limit for a very bright star. The case shown is for 30° field rotation with azimuthal filtering. In this case we introduced the detector noises using the values indicated at the end of Sect. 3 and a cross-talk total amount of 10-2, too. Results obtained with the spectral deconvolution are slightly better than those obtained using the multiple differential imaging, with difference on the order of 0.2 dex (~0.5 mag). As expected, better results are obtained when the Y-H-mode is considered. In this second case the difference is on the order of 0.3 dex (~0.7–0.8 mag), and the gain is appreciable even at a small separations (0.15 arcsec).
 |
Fig. 6 Run of the 5σ calibration limit with separation for a very bright star. The case shown is for 30° field rotation with azimuthal filtering. Detector noises and a cross-talk with a value of 10-2 were introduced too. Red line is the result obtained with multiple differential imaging while the green is with the spectrum deconvolution method. |
From all these plots we can see that, by using SPHERE IFS and an appropriate combination of the analysis methods described above, we should be able to reach contrasts on the order of 10-7 or even better at large separations from the central star.
5σ calibration limit (30 degree field rotation, azimuthal filtering).
A synthesis of the results from our simulations is presented in Table 1 where we listed the contrasts obtained at different separations from the central star using the two analysis methods for Y-J and Y-H-modes.
5.1. Impact of Fresnel propagation
Out-of-pupil optics could have a strong impact on the performances of any differential technique adopted in high-contrast imaging due to Fresnel propagation, as described by Marois et al. (2006). An optic that is not conjugated to a pupil plane will modify the light distribution in a chromatic way because at this location the beam intensity distribution depends on wavelength through diffraction effects. The closer the optic is to a focal plane, the larger this chromaticity. Even more severe is the fact that this chromaticity is no longer smooth, but cyclic along the spectrum, when the optic is conjugated to a height that is several times the Talbot length defined as 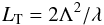 (1)where λ is the light wavelength and Λ the period of a single sinusoidal component of the wavefront across the pupil. For an aberration with a given period, the pupil complex amplitude presenting the electromagnetic field changes from a pure wavefront error to a pure amplitude error over a quarter of the Talbot length. Since the Talbot length is different for different periods, a decorrelation occurs that depends on angular separation. The farther an optic is from the pupil plane (in multiples of Talbot length), the more the decorrelation along spectral domain will be, and speckle correlation will be broken.
(1)where λ is the light wavelength and Λ the period of a single sinusoidal component of the wavefront across the pupil. For an aberration with a given period, the pupil complex amplitude presenting the electromagnetic field changes from a pure wavefront error to a pure amplitude error over a quarter of the Talbot length. Since the Talbot length is different for different periods, a decorrelation occurs that depends on angular separation. The farther an optic is from the pupil plane (in multiples of Talbot length), the more the decorrelation along spectral domain will be, and speckle correlation will be broken.
In the case of SPHERE, the Talbot effect was expected to be strong for those optical components located before the lenslet array, such as the entrance window, the ADC, the derotator and the coronagraphic mask (Yaitskova et al. 2010).
To evaluate the impact of the Fresnel propagation, we cannot use the CAOS package that is based on the Fraunhofer propagation. We then exploited the PROPER code (Krist 2007) to create new PSFs that are then used as input for the CSP code. In Table 2 we list the parameters used to calculate the Fresnel propagation in all the simulations. We report the values of the conjugated distance and the wavefront error (WFE) rms for all the considered optical surfaces.
Most important parameters used for the Fresnel propagation calculation.
To save computing time, we performed all these simulations without considering the effects of the atmosphere (using only 1 atmospheric phase screen). Of course, this is not realistic, because it yields contrasts that are to optimistics. However, the comparison is still meaningful for evaluating the impact of Fresnel propagation itself.
 |
Fig. 8 Plot resulting from a simulation without the Fresnel propagation and without any rotation of the FOV (Y-H-mode). |
From comparison of the plots in Figs. 8 and 9 resulting from simulations that do not include and that do include the Fresnel propagation effects, respectively, one can see that the differences between the two cases are very small, as confirmed by the data reported in Table 3 where the values of the contrast at different separations for simulations performed not considering (second column) and considering (third column) the Fresnel propagation are compared. From the results of these simulations, we can then conclude that the effects of the Fresnel propagation are not too great for our instrument. This is because of the large conjugated distances of the optics (see Table 2) and the not very large pupil size. Fresnel propagation is much more a concern for extremely large telescopes, like E-ELT (see Antichi et al. 2010).
Values of the contrast at different separations for simulations with and without accounting for Fresnel propagation.
6. Data analysis software for companion detection and spectral classification
Through the simulations described in the previous sections, we have demonstrated the capability of the SPHERE IFS instrument to image extrasolar planets down to a contrast of ~10-7 at a separation of a few tenths of arcsec. However, to fully characterize the newly discovered planets (temperature, chemical composition of the atmosphere, etc.), it is important to be able to reconstruct their spectra at a high-fidelity level.
To test this capability, we prepared a pipeline for a data analysis of the calibrated datacube resulting from our simulations. This procedure is composed of five different steps:
-
1.
speckle noise subtraction from the original datacube using thespectral deconvolution algorithm;
-
2.
sum of all the resulting images to create a single multi-wavelength image;
-
3.
search for companion objects on the summed image;
-
4.
extraction of a spectrum for every object found;
-
5.
spectral classification of every object.
The simulation was performed using the same PSFs as in the previous simulations. The FOV is rotated by 30° during the observation and the central star is a G0V star at a distance of 10 pc (this corresponds to a magnitude J = 3.75). Every simulation contains five planets in different positions but at the same separation from the central star (the planets in the same simulation are identical). We perfomed simulations with planets at a separation of 0.3, 0.5 and 1.0 arcsec from the central star. To avoid overlapping of the planets PSFs at the smallest separation, we decided to replace these single simulations with three different ones containing two different planets each (for this reason only for the case at 0.3 arcsec we have six planets for every single case and not five). We then performed different simulations with different luminosity contrasts between the planets and the central star, and adopted values of 10-5, 3 × 10-6, 10-6, and 3 × 10-7. Finally, we performed different simulations with different input spectra: we used a late type T-dwarf spectrum (T7), an early type T-dwarf spectrum (T2), a late type L-dwarf spectrum (L8), and an early type L-dwarf spectrum (L0), taken from the spectra libraries described in Sect. 6.1. To test the capability of our procedure to distinguish between a companion object and a background star, we performed simulations using a flat spectrum (M2) at the low resolution of our instrument as input. Indeed, at this resolution, all the stellar spectra are expected to be flat. Moreover, we did not include any faint background galaxies because they are expected to be spatially resolved as extended objects by our instrument.
While all these spectra come from objects in the solar neighborhood (old objects), our results do not lose generality because, as shown in Sect. 6.2.3, the detectability of the companion objects at a fixed effective temperature is not determined by the gravity effects, which in turn is the main difference between young and older substellar objects.
6.1. Procedure description
In this section we will describe our reduction procedure in more detail. The first two steps are performed using the spectral deconvolution method in the same way as described above in Sect. 4.2. The search for companion objects (third step) is composed of three different steps:
-
for each pixel of the image we compare the flux included in acircle centered on the analyzed pixel and the flux into an externalannulus. The radii values of the circle and of the annulus can bechosen by the user, but for our analysis, we always adopted the val-ues of 1.5, 2, and 4 (pixels). The user can choose the type of statisticto be performed on these regions: a mean or a median. From ourtests we find that the second one was more effective in findingcompanion objects, so we always adopted it for all subsequentanalysis. The procedure finds an object if the value found for theinner circle is greater than for the outer annulus plus the standarddeviation (on the outer annulus) multiplied by a factor that can bechosen by the user and that has to be considered carefully case bycase;
-
if finding more than one object into a radius of 3 pixels, the procedure then retains only the most luminous;
-
finally a two-dimensional Gaussian fit is performed on a small region around the newly discovered object to find its precise position (in 1/1000 of pixel – no evaluation of the error on the position is done in this procedure). We try to minimze the difference between the extracted PSF and the fitting function by performing an iterative procedure to search for the minimum of the difference by changing the parameter of the Gaussian fitting function.
We then extracted the spectrum of the newly found object simply summing the flux of the pixels at a distance less than 1 pixel on every subtracted monochromatic image and subtracting from this value the median from the external annulus. We made the same extraction for two positions at a distance of ± λ/D from the object position along the azimuth (and then at the same separation of the found object) to evaluate the spectral noise. Subtracting the mean of these two spectra from the object spectrum can then improve the final spectral classification that is the last step of our procedure.
To this aim, we compared the output spectra of our simulations with a template spectra grid. We considered T-dwarfs from T0 to T8 and L-dwarfs from L0 to L8, with the spectral type L7 replaced by L7.5, because we could not find such a spectrum in the literature. In addition, we also considered F1V, G0V, K5V, M2V and M8V type star spectra. The data for the T-dwarfs template spectra were taken from Looper et al. (2007) for T0, from Burgasser et al. (2004) for spectra from T1 to T5 and for T8 and from Burgasser et al. (2006) for T6 and T7. The data for the L-dwarfs spectra were taken from Testi et al. (2001). The stellar spectra have been taken from the IRTF online Spectral Library (http://irtfweb.ifa.hawaii.edu/~{}spex/IRTF_ Spectral_ Library/index.html).
The spectral classification was obtained by a cross-correlation (using the IDL routine C_CORRELATE) between the output spectrum of each simulation and the template spectra. The spectral type with the highest cross-correlation coefficient is the one assigned to the simulated planet.
6.2. Results
6.2.1. Companion detection
Number and percentage of found objects (F.O.) and of spurious objects (S.O.) subdivided by the simulation input spectra for the Y-J-mode case.
Number and percentage of found objects (F.O.) and of spurious objects (S.O.) subdivided by different contrasts of the simulated objects for the Y-J-mode case.
In Tables 4 and 6, we display the numbers and the percentages of found objects divided according to the spectral type of the input spectra of the simulations (second and third columns) for the Y-J and the Y-H modes respectively. In the fourth and in the fifth columns of the same tables, we instead report the numbers and the percentages of the spurious objects found with our procedure. It is apparent that we are able to find most of the simulated objects both for the Y-J and the Y-H modes, but the method works better in the second case. Moreover, the number of spurious objects found is much lower for the Y-H-mode case than in the Y-J-mode case. We do stress that almost all the simulated objects that we are not able to find in the final image are for the cases at a separation of 0.3 arcsec where the background noise from the central star is greater. Indeed, it is 100% complete for companions down to a contrast of 3 × 10-7 and separations of 0.5 arcsec, while it is complete at more than 90% for contrasts other than the worst case with a contrast 3 × 10-7 and separation 0.3 arcsec.
To confirm this we report in Tables 5 and 7 the number and the percentage of those found and of the spurious objects as in Tables 4 and 6 but, in this case divided according to the luminosity contrast of the simulated objects. It is apparent from these tables that we are able to find almost all the simulated objects down to a contrast of 10-6, while we lose more than 25% of the simulated objects with a 3 × 10-7 luminosity contrast using the Y-J-mode. On the other hand, we are able to find more than 90% of the objects with a contrast of 3 × 10-7 using the Y-H-mode.
 |
Fig. 10 Histogram with the number of objects (red) and of spurious objects (blue) found for every spectral type in the Y-J-mode case. |
6.2.2. Spectral classification
In Fig. 10 we show the spectral classification of all real objects found, and the spectral classification of the spurious objects. For the real objects, we can see three high peaks corresponding to the M8, T1, and T8 spectral types. The M8 peak is given by the contribution of objects with both an M2 and an L0 input spectrum. The T1 peak is given by the objects with L8 and T2 input spectra. In this case, however, the peak is quite low and the objects classification is more dispersed. Finally, the T8 peak is given by T7 input spectra objects. In general, apart from the case of the L0 spectral type, it seems that our procedure tends to classify the objects with later spectral types rather than the actual ones. We do not have any particular peak in the final distribution for the spurious objects.
A similar histogram, but for the Y-H-mode, is displayed in Fig. 12. Even in this case, we have three peaks in the distribution of the real objects. The first one again corresponds to the M8 spectral type and comes from the contribution of the simulations with M2 and L0 input spectra objects. This means that, as for the Y-J-mode case, these two spectral types seem to originate in a degeneracy. The second peak is around the T4 spectral type and is mainly given by the T2 input spectra simulations, but from the L8 simulations too. The L8 simulations do not give in general a correct identification. Indeed, these objects are recognized alternatively as L2 type or early T type. The last peak is at the T7 spectral type and it is given exclusively by the T7 simulations objects (the T8 detections are given by the simulations with a separation of 0.3 arcsec). In Figs. 11 and 13 we display the same histograms, divided in these cases according to the different luminosity contrasts of the simulated objects indicated with different colors in the figures. From these figures we can see that the overall distribution of the spectral classification is very similar to the global one displayed in Figs. 10 and 12 down to a contrast of 10-6, while they are much more dispersed for the 3 × 10-7 contrast where the spectral classification becomes much less effective.
6.2.3. Effects of the gravity
 |
Fig. 11 Same of Fig. 10 but with the histograms divided for different luminosity contrast. The dashed lines represents the spurious objects. |
To further test the capability of our procedure to distinguish different objects, we performed different simulations using as input the synthetic spectrum of one object with Teff = 800 K and log (g) = 4.0 and of another one with the same temperature and log (g) = 5.5. All the simulations were performed for five different objects (with the same characteristics) at a separation from the central star of 0.5 arcsec and a contrast of 3 × 10-6. Furthermore, we performed simulations both for the Y-J and the Y-H-modes.
For the simulations with the Y-J-mode, all the objects with log (g) = 4.0 were recognized as T8 spectral type (with values of the cross-correlation coefficients around 0.75) while the objects with log (g) = 5.5 were recognized as T7 (4 cases) or T8 (1 case). In this second case, the values of the cross-correlation coefficients are on the order of 0.77.
On the other hand, for the simulations with the Y-H-mode all the objects with log (g) = 4.0 were recognized as T8 spectral type but with higher values of the cross-correlation coefficients (more than 0.93), while all the objects with log (g) = 5.5 were recognized as T6 spectral type (cross-correlation coefficients on the order of 0.92).
In Tables 8 and 9 we report the values of the mean coefficients from the cross-correlation between the output and the input spectra for the Y-J-mode and for the Y-H-mode, respectively. From these results it is apparent that, in the case of the Y-H-mode we are able to correctly classify the objects for the gravity effects, while for the Y-J-mode all the simulated objects are classified as log (g) = 4.0.
Cross-correlation coefficients considering the effects of the gravity with Y-J-mode.
Cross-correlation coefficients considering the effects of the gravity with Y-H-mode.
In conclusion, from our analysis it seems that the Y-H-mode is the best solution for correctly distinguishing between objects with different gravities.
7. Conclusions
We performed detailed simulations of the performances of the SPHERE IFS instrument and considered different data analysis methods that can be exploited to reduce data coming from the instrument. In particular, we exploited the multiple spectral differential imaging (MDI), the spectral deconvolution (SD), and the angular differential imaging (ADI). This latter seems to be especially useful associated with one of the other two methods. It turned out that SD is slightly more effective in reducing the speckle noise than the MDI, and it is less sensitive to the characteristics of the planetary spectrum. From our analysis, however, we can now conclude that, in the best cases, the IFS channel of SPHERE should be able to image companion objects around nearby stars down to a contrast of almost 10-7 at a few tenths of an arcsec.
We then performed detailed simulations to test the possible impact of Fresnel propagation on the final performances of the instrument. This issue created some concerns especially the presence of optics before the lenslet array but, from our simulations made under the same IFS optical setup, a negligible difference results between the achievable constrasts with or without considering the effects of Fresnel propagation.
Because the SD method, as said above, allows better results, we used it to perform a new analysis fn the capability of the instrument to find and to characterize companion objects of the central star.
We then prepared a pipeline with the aim of reducing the datacube resulting from our simulations. To test the effectiveness of this procedure in finding and characterizing planets, we performed a series of simulations with different companion objects’ input spectra, different separations, and different contrasts between the simulated planets and the central star. From these simulations and exploiting the spectral deconvolution method combined with some ADI, we were able to image extrasolar planets down to a luminosity contrast with respect to the central star of 3 × 10-7. In this way we confirmed the results obtained with the previous run of simulations.
We have generally been able to find almost all the simulated objects at the larger separation considered (0.5 and 1.0 arcsec), while the method is less effective at a separation of 0.3 arcsec. However, even in this case, we were able to find more than the 90% of the simulated objects using the Y-J-mode and more than the 95% of the objects using the Y-H-mode.
For the spectral reproducibility of our procedure, we can adopt the following conclusions:
-
The greater the separation from the central star, the larger thepossibility to reconstruct the planets’ spectra with precision(considering planets with the same luminosity contrast).
-
Planets with greater luminosity contrast more easily have a precise spectrum reconstruction.
-
This method allows us to reconstruct and to classify the T type spectra very well while spectral reconstruction and classification seem to be less precise for earlier spectral types. However, even in these cases, the spectral classification generally has a precision of a few spectral types (4 or 5 in the worst cases).
-
Stellar spectra (M and earlier spectral types) are clearly distinguished from T-type spectra while some ambiguity is present for L-type companions. This implies that, in most cases, the characterization of the nature of the detected objects (companion vs. field star) can be obtained from discovery data alone without waiting for common proper motion confirmation. Ambigous cases of L-type companions can be disentangled in several cases from the properties of the object and the parent star (e.g. L-type companion are expected only above a given contrast threshold).
-
The Y-H-mode allows a better spectral classification than for the Y-J-mode.
-
For what concerns the effects of the gravity, they are better disentangled using the Y-H-mode than using the Y-J-mode.
CSP stands for CHEOPS Simulation Program. The code was originally developed in the context of the first feasibility study for a direct imaging planet finder for VLT called CHEOPS (Feldt et al. 2003).
Note, however, that 64 wavelengths are enough to properly sample both the expected spectral extension of speckles over the whole FOV (hypersampling – see Antichi et al. 2009) and each pixel with approximately two sampling per pixel. This should guarantee that interpolation errors are under control.
Acknowledgments
We wish to thank the referee for the constructive comments on the paper. SPHERE is an instrument designed and built by a consortium consisting of LAOG, MPIA, LAM, LESIA, Laboratoire Fizeau, INAF, Observatoire de Geneve, ETH, NOVA, ONERA, and ASTRON in collaboration with ESO.
References
- Antichi, J., Dohlen, K., Gratton, R. G., et al. 2009, ApJ, 695, 1042 [NASA ADS] [CrossRef] [Google Scholar]
- Antichi, J., Verinaud, C., Preis, O., et al. 2010, SPIE, 7736, 109 [NASA ADS] [Google Scholar]
- Bacon, R., Adam, G., Baranne, A., et al. 1995, A&AS, 113, 347 [NASA ADS] [Google Scholar]
- Berton, A., Gratton, R. G., Feldt, M., et al. 2006, PASP, 118, 1144 [NASA ADS] [CrossRef] [Google Scholar]
- Beuzit, J. L., Mouillet, D., Motou, C., et al. 2006, tafp.conf, 353 [Google Scholar]
- Boccaletti, A., Abe, L., Baudrand, J., et al. 2008, SPIE, 7015, 34 [NASA ADS] [Google Scholar]
- Burgasser, A. J., McElwain, M. W., Kirkpatrick, J. D., et al. 2004, AJ, 127, 2856 [NASA ADS] [CrossRef] [Google Scholar]
- Burgasser, A. J., Geballe, T. R., Leggett, S. K., et al. 2006, ApJ, 637, 1067 [NASA ADS] [CrossRef] [Google Scholar]
- Carbillet, M., Verinaud, C., Guarracino, M., et al. 2004, SPIE, 5490, 637 [NASA ADS] [CrossRef] [Google Scholar]
- Carbillet, M., Boccaletti, A., Thalmann, C., et al. 2008, SPIE, 7015, 191 [NASA ADS] [Google Scholar]
- Chauvin, G., Lagrange, A. M., Dumas, C., et al. 2009, A&A, 425, 29 [Google Scholar]
- Claudi, R. U., Turatto, M., Gratton, R. G., et al. 2008, SPIE, 7014, 111 [NASA ADS] [Google Scholar]
- Claudi, R. U., Turatto, M., Giro, E., et al. 2010, SPIE, 7735, 30 [NASA ADS] [Google Scholar]
- Crepp, J. R., Pueyo, L., Brenner, D., et al. 2011, ApJ, 729, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Dohlen, K., Langlois, M., Saisse, M., et al. 2008, SPIE, 7014, 118 [Google Scholar]
- Feldt, M., Hippler, S., Henning, T., et al. 2003, ASPC, 294, 569 [NASA ADS] [Google Scholar]
- Hinkley, S., Oppenheimer, B. R., Zimmerman, N., et al. 2011, PASP, 123, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Kalas, P., Graham, J. R., Chiang, E., et al. 2008, Science, 322, 1345 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kasper, M., Beuzit, J.-L., Verinaud, C., et al. 2010, SPIE, 7735, 81 [NASA ADS] [Google Scholar]
- Krist, J. E. 2007, SPIE, 6675, 23 [Google Scholar]
- Lagrange, A.-M., Bonnefoy, M., Chauvin, G., et al. 2010, Science, 329, 57 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Looper, D. L., Kirkpatrick, J. D., & Burgasser, A. J. 2007, AJ, 134, 1162 [NASA ADS] [CrossRef] [Google Scholar]
- Macintosh, B., Graham, J., Palmer, D., et al. 2006, SPIE, 6272, 18 [NASA ADS] [Google Scholar]
- Marois, C., Doyon, R., Racine, R., et al. 2000, PASP, 112, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Marois, C., Doyon, R., Racine, R., et al. 2005, JRASC, 99, 130 [Google Scholar]
- Marois, C., Phillion, D. W., & Macintosh, D. 2006a, SPIE, 6269, 114 [Google Scholar]
- Marois, C., Lafrenire, D., Doyon, R., et al. 2006b, ApJ, 641, 556 [Google Scholar]
- Marois, C., Macintosh, B., Barman, T., et al. 2008, Science, 322, 1348 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Oliva, E. 2000, MmSAI, 71, 861 [Google Scholar]
- Sparks, W. B., & Ford, H. C. 2002, ApJ, 578, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Testi, L., D’Antona, F., Ghinassi, F., et al. 2001, ApJ, 552, 147 [Google Scholar]
- Thalmann, C., Schmid, H. M., Boccaletti, A., et al. 2008, SPIE, 7014, 112 [NASA ADS] [Google Scholar]
- Thatte, N., Abuter, R., Tecza, M., et al. 2007, MNRAS, 378, 1229 [NASA ADS] [CrossRef] [Google Scholar]
- Yaitskova, N., Dohlen, K., Rabou, P., et al. 2010, SPIE, 7735, 96 [NASA ADS] [Google Scholar]
All Tables
Values of the contrast at different separations for simulations with and without accounting for Fresnel propagation.
Number and percentage of found objects (F.O.) and of spurious objects (S.O.) subdivided by the simulation input spectra for the Y-J-mode case.
Number and percentage of found objects (F.O.) and of spurious objects (S.O.) subdivided by different contrasts of the simulated objects for the Y-J-mode case.
Cross-correlation coefficients considering the effects of the gravity with Y-J-mode.
Cross-correlation coefficients considering the effects of the gravity with Y-H-mode.
All Figures
 |
Fig. 1 Monochromatic PSF resulting from the CAOS simulation. The bright corona corresponds to the outer working angle of the XAO system. Its radius is roughly 0.5 arcsec at the working wavelength. This image has been obtained using a 4-quadrant coronagraph. The cross structure centered on the center of the image is the signature of this type of coronagraph. |
| In the text | |
 |
Fig. 2 A small portion of spectra resulting from one of the CSP simulations. |
| In the text | |
 |
Fig. 3 Example of the simulated spectra on a spaxel rescaled according to the wavelength for SPHERE IFS simulations. The dotted line represents the value of one single pixel on the PSFs used as input for the CSP code. The solid line represents the same thing on the images of the datacube resulting from the CSP simulation (passage of the light through the instrument and correct calibration to create the datacube). The absolute values of these two curve have been normalized to be able to overplot one on the other. |
| In the text | |
 |
Fig. 4 Comparison between 5σ contrast obtained with single difference (yellow line), with multiple single differences (red line), and with multiple double differences (green line) from IFS simulations. These results were obtained for a simulation where no detector noise, no cross-talk, and no rotation were considered. |
| In the text | |
 |
Fig. 5 Run of the 5σ calibration limit with separation for three cases: (i) no field rotation (red line), rotation by 30° with no azimuthal filtering apllied (yellow line), rotation by 30° with azimuthal filtering applied (green line). |
| In the text | |
 |
Fig. 6 Run of the 5σ calibration limit with separation for a very bright star. The case shown is for 30° field rotation with azimuthal filtering. Detector noises and a cross-talk with a value of 10-2 were introduced too. Red line is the result obtained with multiple differential imaging while the green is with the spectrum deconvolution method. |
| In the text | |
 |
Fig. 7 Same as Fig. 6 but for the Y-H-mode. |
| In the text | |
 |
Fig. 8 Plot resulting from a simulation without the Fresnel propagation and without any rotation of the FOV (Y-H-mode). |
| In the text | |
 |
Fig. 9 Same as Fig. 8 but with the Fresnel propagation. |
| In the text | |
 |
Fig. 10 Histogram with the number of objects (red) and of spurious objects (blue) found for every spectral type in the Y-J-mode case. |
| In the text | |
 |
Fig. 11 Same of Fig. 10 but with the histograms divided for different luminosity contrast. The dashed lines represents the spurious objects. |
| In the text | |
 |
Fig. 12 Same as Fig. 10, but for the Y-H-mode case. |
| In the text | |
 |
Fig. 13 Same as Fig. 11, but for the Y-H-mode case. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


