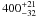| Issue |
A&A
Volume 529, May 2011
|
|
|---|---|---|
| Article Number | L1 | |
| Number of page(s) | 4 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201016219 | |
| Published online | 25 March 2011 | |
Letters to the Editor
First astronomical unit scale image of the GW Orionis triple system
Direct detection of a new stellar companion
1
European Southern Observatory, Alonso de Cordova 3107 Vitacura, Casilla 19001, Santiago de Chile 19, Chile
e-mail: jpberger@eso.org
2
IPAG, CNRS/UMR 5571, Université J. Fourier, BP-53, 38041 Grenoble Cedex, France
3 University of Michigan, 941 Dennison Building, 500 Church Street, Ann Arbor, MI 48109-1090.e, USA
4
California Institute of Technology, 770 S. Wilson Ave. MS 100-22 Pasadena, CA 91125, USA
5
University of St. Andrews, Scotland, UK
6
JPL, California Institute of Technology, M/S 301-355, 4800 Oak Grove Drive, Pasadena, CA 91109, USA
7
INAF-Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, 50125 Firenze, Italy
8
Harvard Smithsonian Center for Astrophysics, 60 Garden Street, Cambridge, MA 02138, USA
9
CEA-DRT-LETI, 17 rue des Martyrs, 38054 Grenoble, France
10
W. M. Keck Observatory, 65-1120 Mamalahoa Hwy, Kamuela, HI 96743, USA
11
University of Massachusetts, Department of Astronomy, Amherst, MA 01003 4610, USA
12
IAS, CNRS/UMR 8617, Université Paris-Sud, 91405 Orsay, France
13
CRAL Observatoire de Lyon 9 avenue Charles André, 69561 Saint Genis Laval, France
Received: 27 November 2010
Accepted: 1 March 2011
Context. Young and close multiple systems are unique laboratories to probe the initial dynamical interactions between forming stellar systems and their dust and gas environment. Their study is a key building block to understanding the high frequency of main-sequence multiple systems. However, the number of detected spectroscopic young multiple systems that allow dynamical studies is limited. GW Orionis is one such system. It is one of the brightest young T Tauri stars and is surrounded by a massive disk.
Aims. Our goal is to probe the GW Orionis multiplicity at angular scales at which we can spatially resolve the orbit.
Methods. We used the IOTA/IONIC3 interferometer to probe the environment of GW Orionis with an astronomical unit resolution in 2003, 2004, and 2005. By measuring squared visibilities and closure phases with a good UV coverage we carry out the first image reconstruction of GW Ori from infrared long-baseline interferometry.
Results.We obtained the first infrared image of a T Tauri multiple system with astronomical unit resolution. We show that GW Orionis is a triple system, resolve for the first time the previously known inner pair (separation ρ ~ 1.4 AU) and reveal a new more distant component (GW Ori C) with a projected separation of ~ 8 AU with direct evidence of motion. Furthermore, the nearly equal (2:1) H-band flux ratio of the inner components suggests that either GW Ori B is undergoing a preferential accretion event that increases its disk luminosity or that the estimate of the masses has to be revisited in favour of a more equal mass-ratio system that is seen at lower inclination.
Conclusions. Accretion disk models of GW Ori will need to be completely reconsidered because of this outer companion C and the unexpected brightness of companion B.
Key words: binaries: general / stars: variables: T Tauri / Herbig Ae/Be / accretion, accretion disks / techniques: interferometric
© ESO, 2011
1. Introduction
Stellar initial masses are controlled by the accretion of gas through disks onto the star in the protostellar phase. For a binary or multiple system this process is more complex because it potentially involves the presence of circumstellar and circumbinary gas reservoirs that control the mass distribution (Bate & Bonnell 1997; Ochi et al. 2005). Understanding the origin of such a distribution therefore requires the observation of multiple systems, the characterisations of their masses, and of the nature of the accretion sources.
Epochs and array configurations of the observations.
GW Orionis is a single-line spectroscopic binary Classical T Tauri Star with an orbital period of 242 days located at ≈ 400 pc (Mathieu et al. 1991)1. The primary star’s mass has been estimated to be 2.5 M⊙ and the secondary’s as 0.5 M⊙ with an expected separation of ~ 1 AU (circular orbit of inclination ≈ 27°). Evidence of a third companion was found based on the analysis of radial velocity residuals (confirmed period of 3850 days; Latham, priv. comm.). The spectral energy distribution (SED) of the unresolved complete system shows a large infrared excess compared with a photosphere from a 5662 K G5 star (Cohen & Kuhi 1979) with a strong 10-microns silicate emission feature. An important near-to-mid-infrared dip in the SED has been interpreted as the signature of a circumbinary (CB) disk, whose inner part is clearing up to 3.3 AU from the star system (Mathieu et al. 1991). Artymowicz & Lubow (1994) have attempted to simulate the interaction of the CB disk with the central system. Photometric time-dimming behaviour led Shevchenko et al. (1998) to conclude that eclipses resulted from material around GW Ori B that covers the central star.
An accurate model of the disk structure is not possible without good knowledge of the stellar components of this system. We present here the first long-baseline interferometer data on GW Ori using the IOTA interferometer and succesfully obtain the first reconstructed image of a T Tauri system with astronomical-unit resolution.
 |
Fig. 1 Squared visibility as a function of the projected baseline (left) and closure phases as a function of UT time for the epochs 2003, 2004, and 2005 (right). The inset shows the corresponding UV coverage. |
Triple system parameters: flux ratio, separation, position angle, associated errors, and reduced χ2 as obtained from the fitting procedure and MIRA reconstruction software.
2. Observations and data reduction
IOTA was a three 45 cm siderostats interferometer, located on Mt. Hopkins Arizona and operated by Smithsonian Astrophysical Observatory (Schloerb et al. 2006). The three telescopes (A,B,C) were movable along two perpendicular axes and could occupy 17 stations offering a way to synthetize a beam with a maximum 35 × 15 m aperture. This corresponds to a resolution of ≈5 × 12 mas in the H-band. Observations took place during period 2003 November – 2005 November. Four array configurations were used to pave the UV plane. The observations were made in the H band using the IONIC3 instrument (Berger et al. 2003). IONIC3 allowed each of the three baselines to be combined separately, which provided six interferograms. Fringe patterns were temporally encoded, detected, and locked with a PICNIC detector array (Pedretti et al. 2004, 2005).
We used the data reduction method described in Monnier et al. (2004) to extract squared visibilities (V2) and closure phases (CP) from the interferograms. Instrumental V2 and CP effects were removed by interspersing each science target acquisition with observations of calibrators with small and known diameters. Table 1 shows a log of our observations. While the calibrators were chosen to match the brightness and spectral type of GW Ori as closely as possible to avoid instrument-induced biases, we estimated that a conservative induced CP systematic error of ≈ 0.5° had to be added quadratically to the statistical error computed from the set of interferograms (Monnier et al. 2006). This additionnal term is essentially dominated by the chromatic response of the beam combiner. Identically, our night-to-night calibration accuracy follow-up led us to adopt a conservative systematic V2 calibration error of σV2 = 0.05 added quadratically to the statistical error on V2. Our calibrated data set resulted in the following statistically independent measurements: 27 V2 and 9 CP in 2003, 111 V2 and 37 CP in 2004 and 6 V2 and 3 CP measurements in 2005. The calibrated data are available from the authors in the OI-FITS format (Pauls et al. 2005).
The calibrated V2 and CP data are presented in Fig. 1. The conclusions that can be drawn from an inspection of these data include: 1) GW Orionis is clearly resolved at most of the spatial scales probed by IOTA; 2) The V2 and CP curves show an oscillation pattern typical of a multiple component system; 3) there is a clear non-zero closure phase signal at all epochs, which hints at non centro-symmetric emission. The contribution of the circumprimary disk’s H-band emission to the V2 curve are most probably negligible because their expected angular size is smaller than the close binary separation, which is already underresolved by our observations. We note that the CB disk inner rim is too far away to contribute significantly to the H-band emission. This inspection combined with the already known binarity of GW Orionis and the evidence of a putative companion to the spectroscopic system (Mathieu et al. 1991 and Latham priv. comm.) has led us to focus our analysis on the search for sources of point-like emission in the data.
3. Modelling and results
3.1. Visibility and closure phase modelling
For the purpose of our fit we temporally binned the data by considering three bins, i.e. 2003 (2003-11-30 to 2003-12-01), 2004 (2004-12-12 to 2004-12-20) and 2005 (2005-11-22). These three epoch bins allowed us to neglect orbital motions within each fit (even for the longest epoch, 2004, the eight days of observations only span 3% of the orbit, and therefore the orbital motion introduces negligible errors). We first fitted simultaneously V2 and CP data with a binary model. To achieve this, we carried-out a χ2 fine grid computation in search for the minimum. We exhaustively searched the parameter space of flux ratios (f), component separations (ρ), and position angles (θ). The resulting fits at all epochs were poor and unacceptable (reduced χ2 > 30), which lead us towards a triple system model as hypothezised by Mathieu et al. (1991). All components were considered to be unresolved and the fine grid covered a range of realistic values. The fitting procedures defined all the above-mentioned parameters with respect to a reference source (A), i.e. not necessarily the primary in the usual sense of it. The fitting procedure revealed that epoch 2005, for which we had the least amount of data, allowed two equally plausible parameters for the tertiary component (C), and both solutions are included. We confirm that the triple model improves the reduced χ2 considerably, finding 0.6, 1.6, and 0.1 for 2003, 2004, and 2005 respectively. The model parameters and associated errors can be found in Table 2. We find that the component flux ratio remains roughly constant for all epochs, which gives confidence in our identification of the components. We adopt the notation that the brightest component is referred to as “A”, the other component in the close pair as “B”, and the new outer component as “C.” We continue our discussion of these results in Sect. 4.
3.2. Image reconstruction
We used the MIRA software (Thiébaut 2008) to independently reconstruct an image out of the V2 and CP data. Only epoch 2004 has sufficient data for such an attempt. This model-independent image (see Fig. 2) is found to support our choice of the triple system discussed in the previous section. Furthermore, even though the procedures are different, the locations of the three components from the image are found to be consistent with the best-model predictions (see Table 2 for a comparison).
 |
Fig. 2 Left: reconstructed image of the 2004 epoch using the MIRA software. Three components are resolved (encircled dots) and identified according to their brightness (A, B and C respectively from brightest to dimmest in H). Blue crosses indicate the positions as obtained from model fitting. Centre: presentation of the data from Table 2. Square point represents the alternative position for epoch 2005. Right: predicted H-band flux ratio as a function of the secondary mass with a primary mass of 3.6 M⊙. Shaded region is the flux-ratio constraint from our observations (epoch 2004). Vertical dashed lines provide the system inclination. Vertical blue lines are the secondary mass estimate corresponding to distance d ≈ 414 ± 7 pc. |
4. Discussion
The system is resolved into three components, the spectroscopic pair (A and B) plus a new outer component (C). The inner pair shows a position reversal from 2003 to 2004 and also 2004 to 2005. This is expected since the orbital period has been measured to be ≈ 242 days – furthermore, our observations happen to coincide with times when the components are approximately in the plane of the sky (circular orbit phases of ~ 0.0, 0.6, 0.0 in 2003, 2004, 2005 respectively). Unfortunately, this timing means that our visual orbit cannot constrain the orbital inclination. On a positive side, this means that our measured separation is close to the actual semi-major axis of the orbit, 1.35 ± 0.10 AU assuming a distance of 400 pc and knowing that the eccentricity of the orbit is ≈ 0 (Mathieu et al. 1991). This corresponds to a system mass of 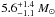 , somewhat higher than the previous estimate of 3.0 M⊙2 (Mathieu et al. 1991).
, somewhat higher than the previous estimate of 3.0 M⊙2 (Mathieu et al. 1991).
Perhaps the most surprising aspect of this inner pair is that the H-band flux ratio is only about a factor of ~ 2. Previous work (e.g., Mathieu et al. 1991) had estimated that the system was composed by two stars of respectively 2.5 M⊙ and 0.5 M⊙ and concluded that the contribution of the secondary to the near-infrared excess was negligible.
To investigate the link between the flux ratios and the masses we used the pre-main-sequence stars theoretical evolutionary models computed by Siess et al. (2000), which were shown to be reliable enough to estimate masses with a 10% to 20% precision (Hillenbrand & White 2004). We considered, as in Mathieu et al. (1991), that the effective temperature of the primary was Teff ≈ 5700 K and the age ≈ 106 yrs. We interpolate from the 106 yrs isochrones that this corresponds to a primary mass of ≈ 3.6 M⊙. The rightmost plot in Fig. 2 shows the expected flux ratio from the Siess et al. (2000) computation as a function of secondary mass. The straight line materializes the observed flux ratio (i.e. 0.57 ± 0.05, 2004). Additionally, we use the mass ratio and mass function determined from radial velocity to compute the requested orbital inclination as in Mathieu et al. (1991).
If we take the most recent and precise determination of the distance by Menten et al. (2007), i.e. 414 ± 7 pc, we can extract from Fig. 2 the following information:
-
Our observation can be explained by a binary system with a massratio close to unity at low inclination and no excess fromcircumstellar emission. Indeed, taking the uppermost distanceestimate of 421 pc the observed flux ratio in the H band can be reproduced by a system seen at low inclination (i ≈ 9°) with a secondary mass of ≈3.1 M⊙, i.e. a mass-ratio of the order of 0.86;
-
With decreasing distance the observed flux ratio requires the addition of H-band excess to the secondary and a slight increase in inclination. For example, if we take the lowest distance boundary of 407 pc, the expected secondary-to-primary ratio is ≈ 0.29, which requires a secondary circumstellar excess of roughly the same value ≈ 0.28. The requested inclination is then ≈11°.
Although this analysis is subject to important uncertainties, including the primary spectral type estimate, we tested that our conclusions hold at a qualitative level, i.e. that the GW Ori inner system is probably seen at a much lower inclination (i.e. ≈ 10°) with more circumsecondary H band emission than previously thought (Mathieu et al. 1991). Reconciling our observation with the observed eclipses by Shevchenko et al. (1998) is a puzzle we cannot solve.
Another important discovery of our work is the existence of source C. We detected C in each epoch and found clear evidence for motion with respect to the inner pair AB. We compared our motion to the preliminary 3850 day orbit recently inferred from long-term radial velocity monitoring (Latham, priv. comm.) but did not find a solution that could simultaneously fit our motions and the spectroscopic orbital elements. If the 20 mas separation of AC is the true semi-major axis, then we would expect an orbital period of ~3600 days, which is quite close to the period seen in the RV residuals. It is far from clear if this hierarchical triple is stable. Additional interferometric monitoring of the inner pair will allow the inclination to be measured directly and the matter will be settled quantitatively in the near future.
5. Conclusion
We have presented the first direct detection of the CTTS GW Orionis as a triple system: both the secondary and tertiary companion are spatially resolved. Our results show that the inner stars have H-band fluxes within a factor of 2 of each other, which suggests that the exact status of the pair should be revisited. The outer companion is clearly detectable, consistent with a roughly 3500 day orbital period, in line with hints from radial velocity residuals. GW Orionis offers a unique laboratory to study the dynamical evolution of a close, young and (perhaps) hierarchical triple system and its interaction with a massive disk and envelope. Rapid progress in determining the full orbital elements of the three components is possible with current interferometers in the coming years.
Distance confirmed by Sandstrom et al. (2007); Menten et al. (2007).
Acknowledgments
This work was supported by ASHRA, PNPS/INSU, and Michelson fellowship program. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France and getCal software from the NASA Exoplanet Science Institute, Caltech. Bibliographic references were provided by the SAO/NASA Astrophysics Data System. IONIC-3 has been developed by LAOG and CEA-LETI, and funded by the CNRS and CNES. We thank Russel White, Lee Hartmann and S. Meimon for useful discussions.
References
- Artymowicz, P., & Lubow, S. H. 1994, ApJ, 421, 651 [NASA ADS] [CrossRef] [Google Scholar]
- Bate, M. R., & Bonnell, I. A. 1997, MNRAS, 285, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Berger, J., Haguenauer, P., Kern, P. Y., et al. 2003, SPIE Conf., 4838, 1099 [NASA ADS] [Google Scholar]
- Cohen, M., & Kuhi, L. V. 1979, ApJS, 41, 743 [NASA ADS] [CrossRef] [Google Scholar]
- Hillenbrand, L. A., & White, R. J. 2004, ApJ, 604, 741 [NASA ADS] [CrossRef] [Google Scholar]
- Mathieu, R. D., Adams, F. C., & Latham, D. W. 1991, AJ, 101, 2184 [NASA ADS] [CrossRef] [Google Scholar]
- Menten, K. M., Reid, M. J., Forbrich, J., & Brunthaler, A. 2007, A&A, 474, 515 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Monnier, J. D., Traub, W. A., Schloerb, F. P., et al. 2004, ApJ, 602, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Monnier, J. D., Berger, J., Millan-Gabet, R., et al. 2006, ApJ, 647, 444 [NASA ADS] [CrossRef] [Google Scholar]
- Ochi, Y., Sugimoto, K., & Hanawa, T. 2005, ApJ, 623, 922 [NASA ADS] [CrossRef] [Google Scholar]
- Pauls, T. A., Young, J. S., Cotton, W. D., & Monnier, J. D. 2005, PASP, 117, 1255 [NASA ADS] [CrossRef] [Google Scholar]
- Pedretti, E., Millan-Gabet, R., Monnier, J. D., et al. 2004, PASP, 116, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Pedretti, E., Traub, W. A., Monnier, J. D., et al. 2005, Appl. Opt. IP, 44, 5173 [NASA ADS] [CrossRef] [Google Scholar]
- Sandstrom, K. M., Peek, J. E. G., Bower, G. C., Bolatto, A. D., & Plambeck, R. L. 2007, ApJ, 667, 1161 [NASA ADS] [CrossRef] [Google Scholar]
- Schloerb, F. P., Berger, J.-P., Carleton, N. P., et al. 2006, SPIE Conf., 6268, 18 [NASA ADS] [Google Scholar]
- Shevchenko, V. S., Grankin, K. N., Mel’Nikov, S. Y., & Lamzin, S. A. 1998, Astron. Lett., 24, 528 [NASA ADS] [Google Scholar]
- Siess, L., Dufour, E., & Forestini, M. 2000, A&A, 358, 593 [NASA ADS] [Google Scholar]
- Thiébaut, E. 2008, in SPIE Conf. Ser., 7013 [Google Scholar]
All Tables
Triple system parameters: flux ratio, separation, position angle, associated errors, and reduced χ2 as obtained from the fitting procedure and MIRA reconstruction software.
All Figures
 |
Fig. 1 Squared visibility as a function of the projected baseline (left) and closure phases as a function of UT time for the epochs 2003, 2004, and 2005 (right). The inset shows the corresponding UV coverage. |
| In the text | |
 |
Fig. 2 Left: reconstructed image of the 2004 epoch using the MIRA software. Three components are resolved (encircled dots) and identified according to their brightness (A, B and C respectively from brightest to dimmest in H). Blue crosses indicate the positions as obtained from model fitting. Centre: presentation of the data from Table 2. Square point represents the alternative position for epoch 2005. Right: predicted H-band flux ratio as a function of the secondary mass with a primary mass of 3.6 M⊙. Shaded region is the flux-ratio constraint from our observations (epoch 2004). Vertical dashed lines provide the system inclination. Vertical blue lines are the secondary mass estimate corresponding to distance d ≈ 414 ± 7 pc. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.