| Issue |
A&A
Volume 529, May 2011
|
|
|---|---|---|
| Article Number | A92 | |
| Number of page(s) | 11 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201015989 | |
| Published online | 08 April 2011 | |
The initial period function of late-type binary stars and its variation
1
Argelander Institute for Astronomy, University of Bonn, Auf dem Hügel 71, 53121 Bonn, Germany
e-mail: pavel@astro.uni-bonn.de
2
European Southern Observatory, Karl-Schwarzschild-Str. 2, 85748 Garching, Germany
e-mail: mpetr@eso.org
Received: 24 October 2010
Accepted: 4 February 2011
The variation in the period distribution function of late-type binaries is studied. It is shown that the Taurus-Auriga pre-main-sequence population and the main-sequence G dwarf sample do not stem from the same parent period distribution with better than 95 per cent confidence probability. The Lupus, Upper Scorpius A, and Taurus-Auriga populations are shown to be compatible with being drawn from the same initial period function (IPF), which is inconsistent with the main-sequence data. Two possible IPF forms are used to find parent distributions to various permutations of the available data, which include Upper Scorpius B (UScB), Chameleon, and Orion Nebula Cluster pre-main-sequence samples. All the pre-main-sequence samples studied here are consistent with the hypothesis that there exists a universal IPF that is modified by binary-star disruption if it forms in an embedded star cluster leading to a general decline of the observed period function with increasing period. The pre-main-sequence data admit a log-normal IPF similar to that arrived at by Duquennoy & Mayor (1991, A&A, 248, 485) for main-sequence stars, provided the binary fraction among pre-main-sequence stars is significantly higher. However, for consistency with proto-stellar data, the possibly universal IPF ought to be flat along the log-P or log-semi-major axis and must be similar to the K1 IPF form derived by means of inverse dynamical population synthesis, which has been shown to lead to the main-sequence period function if most stars form in typical embedded clusters.
Key words: binaries: general / stars: formation / stars: late-type
© ESO, 2011
1. Introduction
The initial distribution of orbital periods of binary-star systems, i.e. the initial period function (IPF), poses an important constraint on star-formation theory as well as being a necessary input for modelling stellar populations. Constraining its form, and its possible variation with star-forming conditions, is thus of fundamental importance. Observations of late spectral-type systems (stellar masses ≲ 2 M⊙) have shown that many young populations have a higher binary proportion than old Galactic-field populations (Mathieu 1994; Zinnecker & Mathieu 2001, for reviews; and more recently Duchêne et al. 2007a,b; Connelley et al. 2008), at least within a certain range of binary star periods. Duchêne (1999) performed a comprehensive comparison of various young stellar groups in terms of their binary properties and concluded that very young star-forming regions are very likely to have a binary excess compared to the field or star clusters. This conclusion is enhanced by the study of proto-stars by Connelley et al. (2008).
However, variations between young populations also appear to be evident, such as when comparing the Taurus-Auriga (Köhler & Leinert 1998) and Orion Trapezium Cluster populations (Prosser et al. 1994; Petr et al. 1998; Petr 1998; Simon et al. 1999) that have a similar age ( ≈ 1 Myr). Connelley et al. (2008) even study the possible variation in the shape of the proto-stellar period function as proto-stars transcend the various stages of their spectral energy distribution evolution. The source of these variations must be understood to unearth any possible systematic variations with the boundary conditions of their birth environment.
In this contribution, we postulate the existence of a universal IPF and test it against observations of binary period distributions for various star-forming regions.
1.1. Binary formation
In this subsection we discuss the theoretical understanding of binary-star formation and of the limitations thereof.
The formation of binary systems remains an essentially unsolved problem theoretically (e.g. Maury et al. 2010). Fisher (2004) shows analytically that isolated turbulent cloud cores can produce a (unknown) fraction of binary systems with the very wide range of orbital periods as observed. However direct cloud collapse calculations are very limited in predicting binary-star properties owing to the severe computational difficulties of treating the magneto-hydrodynamics together with correct radiation transfer and evolving atomic and molecular opacities during collapse. Available results obtained by applying the necessary computational simplifications suggest the preference of a typical period, around1lP ≈ 4, but such a narrow period distribution cannot be transformed to the observed wide range of periods, 0 ≲ lP ≲ 10 (Kroupa & Burkert 2001).
The currently most advanced hydrodynamical simulations were reported by Moeckel & Bate (2010). They allow a turbulent SPH cloud to collapse forming a cluster of 1253 stars and brown dwarfs amounting to 191 M⊙. The cluster has a radius of about 0.05 pc and contains a substantial binary and higher-order multiple stellar population with a large spread in semi-major axis, a, that however peaks at a few AU. After dynamical evolution with or without expulsion of the residual gas, the distribution of orbits remains quite strongly peaked at a few AU with a significant deficit of orbits with a > 10 AU compared to the main-sequence population (their Fig. 11). This state-of-the art computation therewith confirms the above stated issue that it remains a significant challenge for star-formation theory to account for the Gaussian-type distribution of a spanning 10-1 − 104 AU as observed by Duquennoy & Mayor (1991) and Raghavan et al. (2010) for G-dwarfs, by Mayor et al. (1992) for K-dwarfs, and by Fischer & Marcy (1992) for M-dwarfs in the Galactic-field. One essential aspect still missing from these computations is the stellar feedback that starts to heat the cloud as soon as the first proto-stars appear. These heating sources are likely to counter the gravitational collapse such that in reality the extreme densities are not achieved allowing a much larger fraction of wide binaries to survive.
More general theoretical considerations suggest that star formation in dense clusters ought to have a tendency towards a lower binary proportion in warmer molecular clouds (i.e. in cluster-forming cores) because of the reduction in the available phase-space for binary-star formation with increasing temperature (Durisen & Sterzik 1994, hereinafter DS). On the other hand, an enhanced binary proportion for orbital periods lP ≲ 5.6 may be expected in dense clusters owing to the induction of binary formation by means of tidal shear (Horton et al. 2001, hereinafter HBB), thus possibly compensating for the DS effect. The initial period distribution function (IPF) may thus appear similar in dense and sparse clusters, apart from deviations at long periods caused by encounters and the cluster tidal field. A certain fraction of stars form in small-N systems, and the dynamical decay of these is likely to affect the final distribution of lP ≲ 5 binaries (Sterzik & Durisen 1998), giving rise to non-uniform jet activity (Reipurth 2000), but again, quantification of this is next-to-impossible given the neglect of the hydrodynamical component. However, the binary formation channel must vastly dominate over the formation of non-hierarchical higher-order multiples because otherwise even low-density pre-main-sequence stellar populations would have a large fraction of single stars because initially non-hierarchical multiple systems decay on a core-crossing timescale ( ≈ 5 × 104 yr, Goodwin & Kroupa 2005). The low preponderance of high-order multiple proto-stars in observational surveys is noteworthy in this context (Duchêne et al. 2007a).
1.2. On the existence of a universal IPF
This subsection deals with the question whether the existence of a universal IPF can be deduced from observational data.
Assuming binary systems emerge, by whatever process, with a universal IPF consistent with the pre-main-sequence data, and that most stars form in embedded clusters of modest density, Kroupa (1995a, hereinafter K1, 1995b, hereinafter K2) shows that the IPF evolves on a few cluster crossing time scales to the observed Galactic-field, or present-day period function (PDPF). Applying this approach to dense embedded clusters, Kroupa et al. (1999, hereinafter KPM) and Kroupa et al. (2001, hereinafter KAH) find consistency with the observed period function in the Orion Nebula Cluster despite assuming the universal K1 IPF. This suggests that observed variations in the pre-main-sequence-star period function may be attributed to the dynamical history of the respective population, and that there may formally exist a universal parent IPF that emerges from the binary-star formation process and from which the observed pre-main-sequence and main-sequence cases can be generated.
We note that this universal IPF is strictly speaking not observable because of the rapid evolution after binary star birth, but the formal concept of a parent IPF is useful for synthesising binary star populations. This concept is equivalent to that of a universal IMF. Given that the parent distribution of stellar masses that emerges after the proto-stellar phase has been found to be invariant, it is natural to state the Invariant Initial Binary Population Hypothesis (Kroupa 2011). Indeed, given that it is known that the stellar IMF is invariant over a large region of physical star-forming regime, it would be expected that a universal IPF ought also to exist. This is because the mass of a star is the last quantity to be established in the star-formation process, with the binary property of a stellar system being established, essentially, at a prior formation stage. Discarding the notion of a universal IPF, the above star-cluster work at least shows that the dynamical history of a population needs to be taken into account before discussing variations in the period distributions.
There are two general processes driven by fundamentally different physics that evolve an IPF with time. On the one hand, system-internal processes such as the tidal circularisation, star-disk interactions, and decay of small-N proto-systems affect binaries with periods lP ≲ 5. K2 referred to this collectively as a pre-main-sequence eigenevolution of the orbital parameters. Eigenevolution leads to period-eccentricity and period-mass-ratio correlations. On the other hand, binaries with lP ≳ 5 are affected by encounters in embedded clusters (stimulated evolution of the period function). Stimulated evolution does not significantly evolve the eccentricity distribution of a population, but leads to a depletion of the initial period and mass-ratio distribution function for companions with weak binding energy (e.g. K1; K2; Parker et al. 2009).
The aim of this contribution is to quantify the significance of the variation in the observed period distribution of various populations of binary systems in order to allow an improved assessment of a possible underlying parent distribution of orbital periods or equivalently of semi-major axes. In doing so, we test whether there is an invariant IPF and which form this IPF would have. Two IPF forms are studied, namely the K1 IPF (Eq. (4) below), which was previously suggested to unify the pre-main-sequence and main-sequence binary populations, and a log-normal IPF.
The IPF conceived here is a formal initial period distribution function established after the proto-stellar phase has finished. As such, it may not be observable because pre-main-sequence eigenevolution affects the shorter-period binaries on timescales of about 105 yr, while stellar-dynamical and tidal-field influences affect it at longer binary-star orbital periods on the dynamical timescale of the star-forming system. The IPF is therefore as much a theoretical construct as the IMF is, which is also not observable (see the Cluster IMF Theorem, Kroupa 2008). The notion of a formally invariant IPF is very powerful. If this notion were verified to be consistent with observational data, it would be important as a boundary condition for star-formation theory (e.g. Fisher 2004), and also for the generation of theoretical initial stellar populations, such as for N-body experiments of embedded clusters and “classical” binary population synthesis (e.g. de Kool 1996; Johnston 1996), and for dynamical population synthesis (K2; Marks & Kroupa 2011).
1.3. Overview
Section 2 introduces the data sets collected from the literature and used in this contribution for the statistical analysis. Then, in Sect. 3 the significance of the difference between the observed canonical pre-main-sequence and canonical main-sequence period distribution is tested. In the next step of the present analysis (Sect. 4), all data sets are tested for consistency with the K1 IPF and with the log-normal period function of Duquennoy & Mayor (1991, hereinafter DM). All data sets are combined in Sect. 5 to address the question of whether a single parent period function exists of the K1 or the log-normal type, and a revised IPF is constrained using only “matching” pre-main-sequence data in Sect. 6. The conclusions follow in Sect. 7.
2. Data
The observational data sets used here are briefly presented in the subsections below.
In general, the binary star surveys provide for each detected binary system, the observed projected separation, Δ (in AU), which we transform to an estimate of the true semi-major axis, a, via a = Δ/0.95 (Leinert et al. 1993). The values of a are then converted to an orbital period using Kepler’s third law, 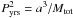 , where Pyrs = P/365.25 is in yr and a in AU, assuming the system mass Mtot = 1.3 M⊙. This transformation is valid only statistically and not on an individual-object basis. A system mass of 1.3 M⊙ is chosen here to reflect the primary being of solar mass with a typical secondary star, which we assume to be of about the average stellar mass. Leinert et al. (1993) used a system mass of 1 M⊙, but this difference amounts to only about 10 per cent in log-mass and is thus of no consequence for the present analysis. In the case of the DM main-sequence sample and the pre-main-sequence binaries with lP < 4 (data by Mathieu 1994; and Richichi et al. 1994), the published lP values are adopted here.
, where Pyrs = P/365.25 is in yr and a in AU, assuming the system mass Mtot = 1.3 M⊙. This transformation is valid only statistically and not on an individual-object basis. A system mass of 1.3 M⊙ is chosen here to reflect the primary being of solar mass with a typical secondary star, which we assume to be of about the average stellar mass. Leinert et al. (1993) used a system mass of 1 M⊙, but this difference amounts to only about 10 per cent in log-mass and is thus of no consequence for the present analysis. In the case of the DM main-sequence sample and the pre-main-sequence binaries with lP < 4 (data by Mathieu 1994; and Richichi et al. 1994), the published lP values are adopted here.
For each observational sample of Nobs,sys systems (each of which may be a binary or a single star), the list of lP values thus obtained is binned into nb bins over the interval lP1 to lP2 covered by the observational survey (obtained from the survey interval in AU, a1 to a2, using Kepler’s third law as above). The so constructed histogram has a bin-width δlPi = (lP2 − lP1)/nb (in most cases equal for all bins except where noted otherwise), and in each bin i of width δlPi there are Nobs,bin(lPi) binaries. The observational estimate of the true period distribution function, expressed as the binary proportion per unit lP interval, is thus obtained from 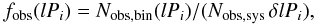 (1)with an associated binomial uncertainty (Petr et al. 1998),
(1)with an associated binomial uncertainty (Petr et al. 1998), ![\begin{equation} e_{\rm obs}(lP_i) = \left( {f_{\rm obs}(lP_i)\,[1 - f_{\rm obs}(lP_i)] \over N_{\rm obs,sys}\,\delta{lP_i} } \right)^{1\over2}\cdot \label{eqn:obsbin} \end{equation}](/articles/aa/full_html/2011/05/aa15989-10/aa15989-10-eq38.png) (2)Binomial uncertainties are used here rather than Poisson uncertainties, Peobs(lPi) = (fobs(lPi)/ [Nobs,sys δlPi ] )1/2, since the typical situation at hand is that of observing Nobs,bin(lPi) successes in Nsys trials, each trial having a probability f(lPi) of success, whereby fobs(lPi) is an estimate of f(lPi). We note that eobs(lPi) < Peobs(lPi).
(2)Binomial uncertainties are used here rather than Poisson uncertainties, Peobs(lPi) = (fobs(lPi)/ [Nobs,sys δlPi ] )1/2, since the typical situation at hand is that of observing Nobs,bin(lPi) successes in Nsys trials, each trial having a probability f(lPi) of success, whereby fobs(lPi) is an estimate of f(lPi). We note that eobs(lPi) < Peobs(lPi).
2.1. Main-sequence data (canonical; can.ms)
The data by Duquennoy & Mayor (1992) is defined as the canonical main-sequence sample because it comprises until recently the largest, and most detailed, multiplicity survey among low-mass main-sequence stars. It mainly consists of G-dwarf stars, but K- and M-dwarf main-sequence binaries have essentially the same period distribution (Fischer & Marcy 1992; Mayor et al. 1992; and Fig. 1 in K1). The characteristics of the DM study that qualify them for the “canonical” main-sequence sample are the large and complete sample of solar-type stars within 22 pc of the Sun, and that all periods are covered. A key finding of the DM study is that the frequency distribution of the binary stars’ orbital periods is unimodal and shows a well-defined log-normal distribution. In this analysis, their published and incompleteness-corrected histogram of lP values, which is based on Nobs,sys = 164, is adopted. The range in period covered in the study is − 1.0 ≤ lP ≤ 10 with δlPi = 1.0, and nb = 11.
A more recent survey of the multiplicity properties of solar-type stars was presented by Raghavan et al. (2010). This survey comprises a sample that is about 2.5 times larger than the DM study and reaches larger distances. In contrast to the DM survey, it is not based on a consistent 13-year spectroscopic survey but uses a compendium of observations from various sources. Raghavan et al. derive a period-distribution that they fit very well using a log-normal form with a peak at log10P = 5.03 and standard deviation of σ(log10P) = 2.28. The DM log-normal distribution peaks at log10P = 4.8 and has a standard deviation of σ(log10P) = 2.3. The Raghavan et al. study leads therefore to very similar results, and for the time being we continue to use the DM survey as the canonical one.
2.2. Pre-main-sequence (PMS) data (canonical, can.pms): Taurus-Auriga
The “canonical” PMS sample, is composed of results obtained from multiple star surveys in the Taurus-Auriga star-forming region.
For short orbital periods, i.e. for lP < 2, binaries detected by the spectroscopic survey of Mathieu (1992, 1994) are considered. Visual binaries in Tau-Aur, with 4.5 ≤ lP ≤ 7.5, were extensively searched and studied by Ghez et al. (1993), Leinert et al. (1993), and Köhler & Leinert (1998), and the data from the latter two publications are included in the “canonical” PMS sample. Slightly shorter period binaries (with 3 ≤ lP ≤ 4) were addressed by Richichi et al. (1994), using lunar occultation measurements. Hence, the “canonical” PMS sample covers a significantly wide range of orbital periods, from lP = 0.5 to lP = 7.5, although not continuously (see lower panel in Fig. 1). All stars included in the “canonical” PMS sample are low-mass stars, similar to the stars included in the “canonical” MS sample. The PMS sample includes classical T Tauri stars and weak-line T Tauri stars that show indistinguishable binary-star period distributions (Köhler & Leinert 1998), and are thus considered as one population in our “canonical” PMS data. Table 1 lists the details for each dataset in terms of, e.g. how many targets, Nobs,sys, have been observed, which are the lower and upper survey limits (expressed in lower and upper semi-major axis), or what distance to the region has been assumed.
Details of binary survey data used in this paper.
In the context of a possible dynamical evolution of the binary stars’ period, it is important to note that the average surface density of young stars in Taurus-Auriga is relatively low (Gomez et al. 1993). Variations or changes in the overall period distribution caused by encounters over the age of the current Taurus-Auriga PMS population, which is ~1 Myr, are expected to be small. Only during the earliest evolutionary phases of the systems, i.e. just after the formation of the stars, is some stimulated dynamical evolution conceivable (Kroupa & Bouvier 2003).
 |
Fig. 1 Testing the likelihood that the observed canonical binary-star period distributions fit the K1 IPF (dashed curve) or the DM PDPF (solid line). The model histograms are shown as dotted and solid lines with expected binomial uncertainties as error-bars (Eqs. (7) and (8)). Solid circles are the G-dwarf main-sequence data in the upper panel and canonical pre-main-sequence data in the lower panel (Sect. 2). The χ2 value and significance probability, |
2.3. Other pre-main-sequence data
Beside Taurus-Aurigae, the orbital period distribution of binary stars surveyed in the star-forming regions of Lupus, Chamaeleon, Upper Scorpius, and the Orion Trapezium Cluster (Table 1) are considered here. By necessity the binary fractions per separation range as published by the respective researchers are adopted such that here no re-analysis of possible contamination is performed as it would go beyond the scope of this contribution.
As for the canonical Tau-Aur PMS data, the surveys comprise low-mass stars with a mixture of weak-line T Tauri and classical T Tauri stars. Although it cannot be completely ruled out that some older ZAMS stars might be included in the samples, the vast majority of the surveyed targets have been confirmed to be of PMS nature (e.g. Covino et al. 1997). Moreover, the orbital period distributions of the samples do not change significantly if the samples are restricted to confirmed PMS stars (e.g. Köhler 2001). None of the surveyed PMS populations in the analysed regions are older than a few Myr. The Orion Trapezium Cluster, with an age of ~1 Myr (Hillenbrand et al. 1997), is likely the youngest region, while Upper Scorpius is the oldest with ~5 Myr (Preibisch et al. 2002). The star-forming regions Chamaeleon and Lupus have ages in-between those of the Orion TC and Upper Scorpius (Chamaeleon: 2 Myr, Luhman 2004; Lupus: ~2−5 Myr, Wichmann et al. 1997; Makarov 2007).
The surveyed regions do have significantly different characteristics with respect to their average stellar densities. Nakajima et al. (1998) analysed the average surface density of companions, which was taken as an indicator of the clustering strength, and found that Lupus is the least clustered region, while the Orion TC is quite strongly clustered. The stellar density in the Orion TC was found to be ~5 × 104 stars/pc3 (McCaughrean & Stauffer 1994). Chamaeleon is considered as a loose stellar aggregate, similar to Lupus, but with a somewhat higher average stellar density (Nakajima et al. 1998). The region Upper Scorpius is part of the Sco-Cen OB association and does not show such a very high stellar density as the Orion TC, although it is very likely that the original configuration of Upper Sco was much denser than today, but that the stars have dispersed with time. The stellar populations in Upper Scorpius are typically divided into Upper Scorpius A (UScA) and Upper Scorpius B (UScB), as these two regions show spatially distinct distributions. Both regions are found at very similar distances (de Zeeuw et al. 1999) and we assume the same overall distance value of 145 pc as adopted in the binary survey paper of Köhler et al. (2000). A notable difference between UScA and UScB is that UScA contains several high-mass (B-type) stars, while no high-mass stars are present in UScB. Interestingly, the observed binary period distributions in UScA and UScB are different, with UScB showing a strong preference for wider binaries, while in UScA mostly binaries with small separations are present (Brandner & Köhler 1998).
It should also be noted that Upper Scorpius and Orion are regions of low-mass and high-mass star formation, while Lupus and Chamaeleon are sites of low-mass star formation only.
A survey of interest in the present context is that by Ratzka et al. (2005) and Simon et al. (1995) of ρ Oph, which has a density in-between that of Taurus-Auriga and the ONC. Köhler et al. (2000) note that UScA and ρ Oph have very similar binary distribution functions. In a future paper we will return to ρ Oph and other clusters such as the Pleiades in a more detailed investigation using N-body computations.
3. Main-sequence versus pre-main-sequence
We estimate the statistical significance of the difference between the observed main-sequence and the pre-main-sequence binary star period distributions by focussing on the “canonical” main-sequence and pre-main-sequence distributions as defined in Sect. 2. The binary proportion per unit log10P interval is given by Eq. (1) 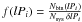 , where Nbin(lPi) is the number of binaries in the ith log-period interval δlPi ( = 1 here), and Nsys is the total number of systems in the survey, whereby each single star and each binary count as a system. To obtain matching data sets, the main-sequence histogram plotted in Fig. 1 of KPM is linearly interpolated to obtain three lPi bins with unit width for lPi = 5.0,6.0,7.0 (i.e. covering the interval 4.5 ≤ lP ≤ 7.5). The resulting data are listed in Table 2.
, where Nbin(lPi) is the number of binaries in the ith log-period interval δlPi ( = 1 here), and Nsys is the total number of systems in the survey, whereby each single star and each binary count as a system. To obtain matching data sets, the main-sequence histogram plotted in Fig. 1 of KPM is linearly interpolated to obtain three lPi bins with unit width for lPi = 5.0,6.0,7.0 (i.e. covering the interval 4.5 ≤ lP ≤ 7.5). The resulting data are listed in Table 2.
Histogram of main-sequence, fms(lPi), and pre-main-sequence, fpms(lPi), binary fractions, and adopted uncertainties.
The well-tried χ2 statistic is applied to test the null hypothesis that both observed distributions stem from the same underlying parent distribution, by calculating 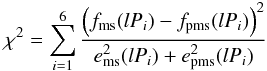 (3)to obtain χ2 = 15.7 with ν = 6 degrees of freedom. Obtaining this large value, or larger, has a significance probability
(3)to obtain χ2 = 15.7 with ν = 6 degrees of freedom. Obtaining this large value, or larger, has a significance probability 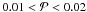 , so that one can be less than 2 per cent confident that the null hypothesis holds true. Excluding the lP < 4 bins where the main-sequence and pre-main-sequence data agree within the uncertainties, and concentrating instead only on the more recent Taurus-Auriga data (Köhler & Leinert 1998), we find that χ2 = 13.2,ν = 3 with
, so that one can be less than 2 per cent confident that the null hypothesis holds true. Excluding the lP < 4 bins where the main-sequence and pre-main-sequence data agree within the uncertainties, and concentrating instead only on the more recent Taurus-Auriga data (Köhler & Leinert 1998), we find that χ2 = 13.2,ν = 3 with 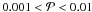 . The null hypothesis can thus be rejected with approximately 99 per cent confidence. It may be concluded that the two observed distributions stem from different parent distributions.
. The null hypothesis can thus be rejected with approximately 99 per cent confidence. It may be concluded that the two observed distributions stem from different parent distributions.
To obtain an additional assessment of the confidence in this result, the Wilcoxon-Signed-Rank (WSR) test (e.g. Bhattacharyya & Johnson 1977) provides a welcome alternative. This is a non-parametric test, making no assumptions about the form of the underlying populations, such as there being a well-defined mean and variance, as opposed to using the χ2 statistic, which makes such assumptions about the underlying distributions. The WSR test assesses the likelihood of observing a certain fraction of the data being asymmetrically distributed about a reference data set. To construct the WSR statistic, the differences fpms(lPi) − fms(lPi) are ordered according to their absolute values. These are ranked, and the ranks associated with the positive differences are added to form the test statistic T + . The statistic is symmetrical, that is, the same result is obtained by considering the negative differences. For the data in Table 2, T + = 21 with n = 6 data points. Obtaining such a large or larger T + has a significance probability 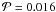 (Table 10 in Bhattacharyya & Johnson 1977). The null hypothesis is thus only supported with a confidence of 1.6 per cent, confirming the above conclusion. Using only the data with lP ≥ 5 gives n = 3 differences, which is too small for this non-parametric test to allow significant conclusions, in contrast to the χ2 test used above, because the latter relies on additional information about the populations.
(Table 10 in Bhattacharyya & Johnson 1977). The null hypothesis is thus only supported with a confidence of 1.6 per cent, confirming the above conclusion. Using only the data with lP ≥ 5 gives n = 3 differences, which is too small for this non-parametric test to allow significant conclusions, in contrast to the χ2 test used above, because the latter relies on additional information about the populations.
The Kolmogorov-Smirnov test cannot be applied here nor later in this paper, because the data sets cover different lP ranges, and fP,ms was estimated by DM after applying incompleteness corrections, that is there exists no list of complete lP values from which a cumulative distribution can be generated.
4. Standard period functions
After establishing with a high level of confidence that the canonical pre-main-sequence and main-sequence period distributions differ significantly, one can proceed to begin inquiring as to how the parent distributions of the two data sets may be described. In the literature, two analytic forms of possible parent distributions for the two data sets have been used.
4.1. Initial period functions (IPFs) and present-day period functions (PDPFs)
For pre-main-sequence binary systems, K1 suggests an IPF, 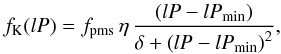 (4)using the canonical pre-main-sequence and main-sequence data as constraints. This does not contradict the results of the previous section since one takes into account through extensive N-body modelling that the main-sequence distribution results from the pre-main-sequence distribution if most stars form in modest (embedded) clusters. K1 found that η = 3.5 and δ = 100 provide good fits to the pre-main-sequence data, and to the main-sequence data after passing through a typical star cluster2 assuming that the overall primordial binary proportion is fpms = 1, and setting the minimum orbital period to 1 d (lPmin = 0). As seen in Fig. 1, we note in particular that fK(lP) is essentially flat for lP ≳ 4.5 (a ≳ 20 AU). With the above parameters Eq. (4) is referred to as the K1 IPF, and IPFs constructed with different values of the parameters are said to be of the K type.
(4)using the canonical pre-main-sequence and main-sequence data as constraints. This does not contradict the results of the previous section since one takes into account through extensive N-body modelling that the main-sequence distribution results from the pre-main-sequence distribution if most stars form in modest (embedded) clusters. K1 found that η = 3.5 and δ = 100 provide good fits to the pre-main-sequence data, and to the main-sequence data after passing through a typical star cluster2 assuming that the overall primordial binary proportion is fpms = 1, and setting the minimum orbital period to 1 d (lPmin = 0). As seen in Fig. 1, we note in particular that fK(lP) is essentially flat for lP ≳ 4.5 (a ≳ 20 AU). With the above parameters Eq. (4) is referred to as the K1 IPF, and IPFs constructed with different values of the parameters are said to be of the K type.
K2 constructed a more elaborate model based on the above K1 IPF, but including eigenevolution for the correct correlation between eccentricity, period, and mass ratio of short-period binaries. This model has lPmin = 1,η = 2.5,δ = 45 and is required to reproduce and predict the period- and mass-ratio-distribution functions and the distribution of orbits in the eccentricity-period diagram for realistic stellar populations. These details are, however, not required in the present treatment and would not lead to different results. A useful feature of Eq. (4) is that it can be easily converted to a period-generating function (Eq. (11b) in K1) ![\begin{equation} lP(X) = lP_{\rm min} + \left[ \delta \left( {\rm e}^{2\,X\over\eta}-1 \right) \right]^{1\over2}, \label{eqn:fpK1gen} \end{equation}](/articles/aa/full_html/2011/05/aa15989-10/aa15989-10-eq102.png) (5)where Xϵ [0,1 ] is a uniform random variate, and with
(5)where Xϵ [0,1 ] is a uniform random variate, and with 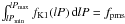 . The maximum allowed log-period, lPmax, follows from Eq. (5) with X = 1. Equation (5) allows the efficient construction of a pre-main-sequence population, as in N-body calculations of the evolution of embedded clusters (e.g. KPM; KAH).
. The maximum allowed log-period, lPmax, follows from Eq. (5) with X = 1. Equation (5) allows the efficient construction of a pre-main-sequence population, as in N-body calculations of the evolution of embedded clusters (e.g. KPM; KAH).
For the PDPF, the Gaussian distribution in lP describes the observed period distribution of local G-dwarfs very well (DM) 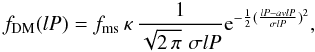 (6)where
(6)where 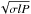 and avlP are, respectively, the variance in lP and the average-lP, and
and avlP are, respectively, the variance in lP and the average-lP, and 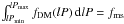 is enforced by adjusting κ, since
is enforced by adjusting κ, since 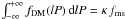 . DM measured an overall binary proportion of fms = 0.58, σlP = 2.3, and avlP = 4.8. This is referred to as the DM PDPF, and period functions constructed according to Eq. (6) but with different values for the parameters are referred to as being of the DM type. A simple period-generating function cannot be written down; we resort instead to the Box-Muller method for generating lPs (e.g. Press et al. 1994).
. DM measured an overall binary proportion of fms = 0.58, σlP = 2.3, and avlP = 4.8. This is referred to as the DM PDPF, and period functions constructed according to Eq. (6) but with different values for the parameters are referred to as being of the DM type. A simple period-generating function cannot be written down; we resort instead to the Box-Muller method for generating lPs (e.g. Press et al. 1994).
4.2. The tests
We test the confidence with which the IPF (the K1-distribution, Eq. (4) with η = 3.5, δ = 100 and fpms = 1) or the PDPF (the DM-distribution, Eq. (6) with σlP = 2.3, avlP = 4.8 and fms = 0.58) can represent each data set of Sect. 2. For each observational sample, the theoretical distributions are converted to matching histograms by generating Nth,sys = 106 periods and binning these into the same lP-bins as in the respective observational sample, obtaining (Eq. (1)) fth(lPi) = fo Nth,bin(lPi)/(Nth,sys δlPi), where fth(lPi) is either of the K (fo = fpms) or the DM (fo = fms) type. Given the size of an observational sample, Nobs,sys, the expected number of binaries in each lP bin is 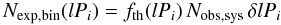 (7)with the associated expected binomial uncertainty
(7)with the associated expected binomial uncertainty ![\begin{equation} e_{\rm N,exp,bin}(lP_i) = \left[ f_{\rm th}(lP_i)\,(1 - f_{\rm th}(lP_i))\, \delta{lP_i}\,N_{\rm obs,sys} \right]^{1\over2}. \label{eqn:thbin} \end{equation}](/articles/aa/full_html/2011/05/aa15989-10/aa15989-10-eq123.png) (8)To quantify the goodness-of-fit, the χ2 statistic for the K or DM distribution becomes
(8)To quantify the goodness-of-fit, the χ2 statistic for the K or DM distribution becomes 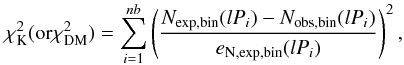 (9)which has nb degrees of freedom since no free parameters are fitted. Terms with Nexp,bin(lPi) = 0 give infinite χ2 since a finite datum is inconsistent with the model, which is treated as having no intrinsic uncertainties. The significance probability,
(9)which has nb degrees of freedom since no free parameters are fitted. Terms with Nexp,bin(lPi) = 0 give infinite χ2 since a finite datum is inconsistent with the model, which is treated as having no intrinsic uncertainties. The significance probability, 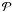 , of obtaining
, of obtaining 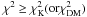 , is evaluated using the incomplete gamma function (Press et al. 1994).
, is evaluated using the incomplete gamma function (Press et al. 1994).
4.3. Results
The above procedure is applied to all the data and the results are shown in Fig. 1. The conclusion with very high confidence (at the 99.5 per cent level or better) is that the canonical main-sequence data are inconsistent with the K1 IPF (upper panel), and that the canonical pre-main-sequence data are inconsistent with the DM PDPF (lower panel). This does not change even if the lP = 9.5 main-sequence value is ignored in the upper panel (giving χ2 = 43 with 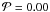 for the K1 IPF). This result is consistent with that of Sect. 2, where it was shown that the canonical main-sequence and pre-main-sequence data differ significantly.
for the K1 IPF). This result is consistent with that of Sect. 2, where it was shown that the canonical main-sequence and pre-main-sequence data differ significantly.
The results of applying this procedure to each of the pre-main-sequence data sets are presented in Fig. 2.
 |
Fig. 2 Similar to Fig. 1 but for all pre-main sequence samples. In all panels, the dotted continuous curves are the model distributions (K1 IPF upper curves, DM PDPF lower curves), whereas the model histograms are shown as solid lines with expected binomial uncertainties as dotted error-bars. Thick histograms are the data (Sect. 2). The χ2 value and probability, |
It is evident that the Taurus-Auriga, Lupus, and UScA populations are consistent with the hypothesis that they be drawn from the K1 IPF. The Cham pre-main-sequence population is marginally consistent with the hypothesis that the parent distribution is the K1 IPF at the 5 per cent confidence level, whereas the full UScB sample is only consistent with the K1 IPF at the 3 per cent confidence level. UScB becomes consistent at the 19 per cent confidence level with the K1 IPF if three of the widest binaries are removed from the sample, assuming these are significantly closer (<90 pc) than the bulk of UScB stars at ~ 145 pc. Their apparent brightness is clearly brighter than expected for their spectral type when placed at 145 pc, and proper motion measurements confirm nearby distances for at least two of the wide binary systems (Perryman et al. 1997; Salim & Gould 2003).
On the other hand, an alternative hypothesis is that the data sets be drawn from the DM PDPF. This hypothesis can be discarded with very high confidence for the Taurus-Auriga, Lupus, and UScB pre-main-sequence populations. It cannot be discarded for the Cham, UScA, and ONC populations. The Cham and UScA populations can, in fact, be drawn from either period function. The higher significance probability for the hypothesis that Cham be drawn from the DM PDPF is however consistent with the hypothesis that Cham started off in a clustered mode with a K1 IPF, the Cham population possibly being an evolved version of the canonical pre-main-sequence population. This is also true for the ONC sample as shown by KPM and KAH.
5. Parent period distribution functions
In Sect. 4.3, the K1 IPF and the DM PDPF were compared with all the available data sets individually.
In this section, data sets are combined and more general solutions for possible parent distributions of the K and DM types (Eqs. (4) and (6) respectively) are sought by scanning the parameter spaces η,δ and σlP,avlP using suitable increments by evaluating Eq. (9) and the associated significance probability 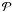 . This procedure is demonstrated in Figs. 3 and 4 by first of all finding all admittable solutions to the canonical data sets. The solutions found in this way agree with the known solutions (the K1 IPF and DM PDPF), and one may have confidence in the algorithm.
. This procedure is demonstrated in Figs. 3 and 4 by first of all finding all admittable solutions to the canonical data sets. The solutions found in this way agree with the known solutions (the K1 IPF and DM PDPF), and one may have confidence in the algorithm.
 |
Fig. 3 Survey of η,δ parameter space for solutions of the K type with fpms = 1 (Eq. (4)) using the canonical pre-main-sequence data. Open circles and small dots delineate models consistent with the data at the 1 and 5 per cent confidence level or better, respectively, whereas the thick solid dot shows a model consistent at the 50 per cent level or better. The K1 IPF is shown as the thick cross. Note that the K1 IPF is not the same as the best solution found here. This is unsurprising because the K1 IPF was derived by constraining the IPF with both the pre-main-sequence and main-sequence period distribution functions. The best solution found here thus lacks one major constraint leading to the K1 IPF, but both are sufficiently close to conclude that the K1 IPF is a good solution to the pre-main-sequence data alone. The straight line shows the asymptotic solution for large δ: fK1(lP) = (η/δ) (lP − lPmin), with η/δ = 0.0339. |
 |
Fig. 4 Survey of σlP,avlP parameter space for solutions of the DM type with fms = 0.58 (Eq. (6)) using the canonical main-sequence data. Open circles and small dots delineate models consistent with the data at the 1 and 5 per cent confidence level or better, respectively, whereas thick solid dots show models consistent at the 50 per cent level or better. The DM PDPF is shown as the thick cross. |
When combining ndat data sets under a common hypothesis, the combined 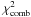 and number of degrees of freedom, nbcomb, are computed as to be
and number of degrees of freedom, nbcomb, are computed as to be 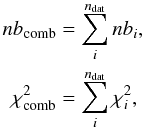 (10)where
(10)where 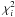 and nbi are the chi-square and number of degrees of freedom of data set i. Possible data sets are i = Lupus, Cham, UScA, UScB, ONC, canonical pre-main-sequence (=can.pms), and canonical main sequence (=can.ms) ] . The significance probability,
and nbi are the chi-square and number of degrees of freedom of data set i. Possible data sets are i = Lupus, Cham, UScA, UScB, ONC, canonical pre-main-sequence (=can.pms), and canonical main sequence (=can.ms) ] . The significance probability, 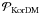 , of obtaining
, of obtaining 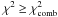 , is evaluated as above (Eq. (9)), and
, is evaluated as above (Eq. (9)), and 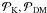 are the resulting combined confidence probabilities when using the K and DM type PFs, respectively, for testing the hypotheses set up in the following. A hypothesis is deemed consistent with the data if
are the resulting combined confidence probabilities when using the K and DM type PFs, respectively, for testing the hypotheses set up in the following. A hypothesis is deemed consistent with the data if 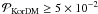 , i.e. if the significance probability is 5 per cent or better.
, i.e. if the significance probability is 5 per cent or better.
The following hypotheses are tested:
-
A PF of the K type is the parent distribution of all combined data sets (ndat = 7). Assuming fpms = 1 and scanning the parameter space, as above, yields no solutions at all in agreement with the data at the 0.001 per cent level or better (
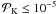 ). Thus, the hypothesis can be discarded at the 99.999 per cent level. Assuming fpms = 0.8 and fms = 0.6 also leads to the rejection of this hypothesis with
). Thus, the hypothesis can be discarded at the 99.999 per cent level. Assuming fpms = 0.8 and fms = 0.6 also leads to the rejection of this hypothesis with 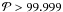 per cent confidence. The general conclusion, stated with a confidence better than 99.999 per cent, is thus that there is no single parent distribution of the K type for all data sets combined.
per cent confidence. The general conclusion, stated with a confidence better than 99.999 per cent, is thus that there is no single parent distribution of the K type for all data sets combined. -
A PF of the DM type is the parent distribution of all combined data sets (ndat = 7). Assuming fms = 0.58,0.8,1.0 and scanning the parameter space, as above, yields no solutions at all in agreement with the data at the 0.001 per cent level or better (
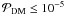 ). Thus, there is no single Gaussian parent distribution of all data sets combined. The hypothesis is rejected with a confidence of higher than 99.999 per cent.
). Thus, there is no single Gaussian parent distribution of all data sets combined. The hypothesis is rejected with a confidence of higher than 99.999 per cent. -
A PF of the K type is the parent distribution of the combined canonical pre-main-sequence and canonical main-sequence data sets (ndat = 2). The relevant confidence is determined from Eq. (10) with [i = can.pms, can.ms]. The result is that there is no solution with a confidence better than
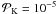 for fpms = 1,0.8,0.6, so that this hypothesis can be discarded with a confidence of higher than 99.999 per cent.
for fpms = 1,0.8,0.6, so that this hypothesis can be discarded with a confidence of higher than 99.999 per cent. -
A PF of the DM type is the parent distribution of the combined canonical pre-main-sequence and canonical main-sequence data sets (ndat = 2). The relevant confidence is determined from Eq. (10) with [i = can.pms, can.ms]. There is no solution with confidence better than
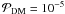 for fms = 0.6. For fms = 0.8, the parameter region σlP = 2.5 ± 0.4,avlP = 5.1 ± 0.2 has
for fms = 0.6. For fms = 0.8, the parameter region σlP = 2.5 ± 0.4,avlP = 5.1 ± 0.2 has 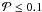 per cent, while for fms = 1.0 the parameter region σlP = 2.6 ± 0.4,avlP = 5.2 ± 0.2 has
per cent, while for fms = 1.0 the parameter region σlP = 2.6 ± 0.4,avlP = 5.2 ± 0.2 has 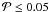 per cent. This hypothesis can thus be discarded with 99.9 per cent confidence.
per cent. This hypothesis can thus be discarded with 99.9 per cent confidence. -
A PF of the K type is the simultaneous parent distribution of the canonical pre-main-sequence data, as well as of the Lupus and UScA pre-main-sequence data sets (ndat = 3). The relevant confidence is determined from Eq. (10) with [i = can.pms, Lupus, UScA]. These are chosen because Fig. 2 indicates that these data sets are similar in that they appear more or less unevolved according to the results of K1 and K2. Scanning η,δ parameter space leads to solutions with
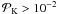 if fpms = 1.0,0.8 (Figs. 5 and 6, respectively), whereas
if fpms = 1.0,0.8 (Figs. 5 and 6, respectively), whereas  if fpms = 0.6. Thus, a simultaneous parent distribution is only possible if the pre-main-sequence binary-star fraction is larger than the main-sequence value of 60 per cent.
if fpms = 0.6. Thus, a simultaneous parent distribution is only possible if the pre-main-sequence binary-star fraction is larger than the main-sequence value of 60 per cent. 
Fig. 5 Testing hypothesis 5 with fpms = 1.0. Survey of η,δ parameter space for solutions of the K type with fpms = 1 (Eq. (4)) for the canonical pre-main-sequence data, together with the Lupus and UScA pre-main-sequence data sets. Open circles and small dots delineate models consistent with the data at the 1 and 5 per cent confidence level, respectively. The K1 IPF is shown as the thick cross, and the straight line is as in Fig. 3. The thick solid dots show models consistent at the 50 per cent level or better.

Fig. 7 Testing hypothesis 6 with fms = 1.0. Survey of σlP,avlP parameter space for solutions of the DM type (Eq. (6)) to the canonical pre-main-sequence data, together with the Lupus and UScA pre-main-sequence data sets. Open circles and small dots delineate models consistent with the data at the 1 and 5 per cent confidence level, respectively. The DM PDPF is shown as the thick cross.
-
A PF of the DM type is the simultaneous parent distribution of the canonical pre-main-sequence data, the Lupus, and UScA pre-main-sequence data sets (ndat = 3). Scanning σlP,avlP parameter space leads to solutions with
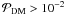 if fms = 1.0 (Fig. 7), whereas
if fms = 1.0 (Fig. 7), whereas 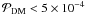 if fms = 0.8 and
if fms = 0.8 and 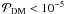 if fms = 0.6. Thus, a simultaneous Gaussian parent distribution is only possible, with a significance probability better than 5 per cent, if the pre-main-sequence binary-star fraction is significantly larger than the main-sequence value of 60 per cent (note that fms in Eq. (6) is here the binary-star fraction required for the combined pre-main-sequence samples).
if fms = 0.6. Thus, a simultaneous Gaussian parent distribution is only possible, with a significance probability better than 5 per cent, if the pre-main-sequence binary-star fraction is significantly larger than the main-sequence value of 60 per cent (note that fms in Eq. (6) is here the binary-star fraction required for the combined pre-main-sequence samples). 
Fig. 8 The revised IPF. In addition to the K1 IPF (thick solid curve), two possible IPF forms are displayed. These are identified as solutions in Figs. 5 and 7, and are shown as the thin solid line (K-type, Eq. (4) with the asymptotic solution δ = 29.52 η;η = 18.7 and fpms = 1.0) and the thick dashed line (DM-type, Eq. (6) with σlP = 2.3,avlP = 5.0,fms = 1.0). The thin dashed line is the DM PDPF. Data points with observational error bars are as indicated in the key. These are used to test hypothesis 5 and 6 giving
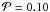 (thin solid curve),
(thin solid curve), 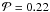 (thick dashed curve) and
(thick dashed curve) and 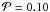 (thick solid curve).
(thick solid curve). -
A PF of the K type is consistent with all pre-main-sequence data (canonical, Lupus, UScA, Cham, UScB, and ONC) (ndat = 6). No parent distribution of the K-type can be found with 0.1 per cent confidence or better. This suggests that these pre-main-sequence data sets may either have different IPFs, or that they stem from the same IPF but were modified, as would be expected for example for the ONC data (KPM, KAH). UScB, however, forms a definite outlier, since it has a significant surplus of binary stars at long periods (Fig. 2), when taking the observational results at face value as we do here for all datasets. After removing possible non-members (cf. Sect. 4.3), a surplus of binary stars at long periods persists although being less significant, which cannot be understood in terms of binary-star disruption in embedded clusters.
-
A PF of the DM type is consistent with all pre-main-sequence data (canonical, Lupus, UScA, Cham, UScB, and ONC) (ndat = 6). No DM-type PF exists with
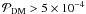 , so that this hypothesis can be rejected with 99.95 per cent confidence.
, so that this hypothesis can be rejected with 99.95 per cent confidence.
6. A revised IPF
In the previous section, the tests of hypotheses 5 and 6 yielded parameter ranges for Eqs. (4) and (6) that are consistent with the combined data at the 5 per cent confidence level or better. These parameter ranges are shown in Figs. 5 and 6 for K-type solutions, and in Fig. 7 for DM-type solutions. The data sets were selected according to which appeared to be the least evolved, using the a priori knowledge gained in K1 and K2.
It is noteworthy that the K-type solutions (η ≈ 2.5 − 3,δ ≈ 40 − 70) are consistent within a 5 % confidence level with the K1 IPF (η = 3.5,δ = 100), thus corroborating the results obtained in K1. This is particularly interesting because here we used data sets including more than one pre-main-sequence population, while in K1 only older Taurus-Auriga data were available but no functional fitting to these data was performed such as here. The K1 IPF was instead obtained using inverse dynamical population synthesis by performing approximate (eye-ball) fits to the pre-main-sequence data, and to the main-sequence data after star-cluster disintegration. The present purely statistical approach confirms the K1 IPF (η ≈ 3.5,δ ≈ 100,fpms ≥ 0.8, with enhanced confidence probability for larger fpms).
A new result obtained here (Fig. 7) is that a log-normal function in orbital period P can also be considered a parent distribution of the same pre-main-sequence data as above. These data are consistent, at the 5 per cent confidence level or better, with being drawn from a parent distribution of the DM-type, if this PF has parameters indistinguishable from those of the DM PDPF (σlP ≈ 2.3,avlP ≈ 5) but with a significantly larger binary proportion, fms = 1.0.
The result is thus that either the K1 IPF (Eq. (4)), a K-type solution with δ ≈ 29.52 η (straight line in Fig. 5), or the Gaussian PF (Eq. (6)) with the above parameters can be parent distributions of pre-main-sequence binary systems with indistinguishable confidence probabilities. This is illustrated in Fig. 8.
7. Conclusions
A fresh look has been taken at the variations evident in the period distribution of binary stars in various stellar populations. The most notable such difference, noted by many authors, lies between the canonical pre-main-sequence population of Taurus-Auriga and the canonical Galactic-field local G-dwarf population. The difference is significant (Sect. 3), but can be understood to result from the stimulated evolution of an initial Taurus-Auriga-type population if most Galactic-field stars originate in modest embedded clusters (K1). That work arrives at a possible initial period function, the K1 IPF (Eq. (4)), which is nearly flat for a ≳ 20 AU.
The variation between pre-main-sequence populations is also studied here, with the result that significant differences are evident, notably between the canonical pre-main-sequence population and the ONC and UScB samples. Stimulated evolution in the dense Orion Nebula Cluster efficiently depletes a K1 IPF to the observed data (KPM, KAH), so that the former difference can be readily accounted for. The latter difference, which results from a significant apparent surplus of long-period binaries in UScB, may indicate that the IPF of the UScB population was very different to that in Taurus-Auriga, as noted by Brandner & Köhler (1998). Noteworthy in this context is that UScA, in which mostly binaries with small separations are present, contains several high-mass (B-type) stars, while no high-mass stars are present in UScB, which appears to contain primarily wider binaries. This is qualitatively consistent with UScA perhaps stemming from denser embedded stellar groups that are already dispersed after dynamical evolution and the expulsion of residual gas by the massive stars. Discarding three of the widest binaries in the UScB data set yields a binary population consistent with the K1 IPF (Sect. 4.3), leaving the ONC as the only pre-main-sequence population that clearly differs from the canonical pre-main-sequence population. In any case, among the data sets used in this paper the UScB data has the lowest number of systems surveyed for binarity, and the region is most likely more affected by containing dispersed mixed populations of stars with different distances and ages than the other data. Hence, the observed orbital-period distribution of binaries in UScB remains to be confirmed.
The (canonical) Taurus-Auriga, Lupus, and UScA populations appear to be the least-evolved and are consistent with being drawn from a common parent IPF if the binary proportion is higher than on the main sequence. The set of possible IPFs is shown in Figs. 5–7, where the K1 IPF is included. Three possible IPFs, all with indistinguishable confidence probabilities, are presented in Fig. 8. While no formal decision can be made based on 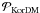 as to which of the three IPFs plotted in Fig. 8 are to be preferred, the a priori knowledge gained in K1 favours the K1 IPF, because (i) it is consistent with the data at the 10 per cent confidence level; (ii) it is the precursor of the Galactic-field PDPF if most stars form in embedded clusters; and (iii) the revised K-type IPF shown as the thin solid line in Fig. 8 leads to a deficit of Galactic-field binaries with lP ≳ 6 (Fig. 8 in K1). Inverse dynamical population synthesis will have to be applied to investigate whether the alternative log-normal IPF (thick dashed line in Fig. 8) can be made consistent with the Galactic-field PDPF for a reasonable library of embedded star clusters. However, by consulting Fig. 1 of Connelley et al. (2008) it becomes readily apparent that a flat distribution function for a ≳ 100 AU provides a more accurate fit than a log-normal function, as is also concluded by those authors and is the case for the K1 IPF. This has since been studied in more detail (Marks et al. 2011) and does suggest that the K1 IPF (Eq. (4)) is a more appropriate description of the data. Parker et al. (2009) come to a similar conclusion and stress that a > 104 AU binaries cannot survive in any clustered environment. They may however form during cluster dissolution (Kouwenhoven et al. 2010).
as to which of the three IPFs plotted in Fig. 8 are to be preferred, the a priori knowledge gained in K1 favours the K1 IPF, because (i) it is consistent with the data at the 10 per cent confidence level; (ii) it is the precursor of the Galactic-field PDPF if most stars form in embedded clusters; and (iii) the revised K-type IPF shown as the thin solid line in Fig. 8 leads to a deficit of Galactic-field binaries with lP ≳ 6 (Fig. 8 in K1). Inverse dynamical population synthesis will have to be applied to investigate whether the alternative log-normal IPF (thick dashed line in Fig. 8) can be made consistent with the Galactic-field PDPF for a reasonable library of embedded star clusters. However, by consulting Fig. 1 of Connelley et al. (2008) it becomes readily apparent that a flat distribution function for a ≳ 100 AU provides a more accurate fit than a log-normal function, as is also concluded by those authors and is the case for the K1 IPF. This has since been studied in more detail (Marks et al. 2011) and does suggest that the K1 IPF (Eq. (4)) is a more appropriate description of the data. Parker et al. (2009) come to a similar conclusion and stress that a > 104 AU binaries cannot survive in any clustered environment. They may however form during cluster dissolution (Kouwenhoven et al. 2010).
We note that the above three pre-main-sequence populations, and in addition the Cham and ONC populations, are all consistent with a monotonically decreasing PF with increasing lP (Figs. 2 and 8). This may suggest that all known pre-main-sequence populations have already suffered some degree of stimulated evolution, and may have begun with the same (universal) IPF. This notion allows reconstruction of the properties of the embedded clusters from which the pre-main-sequence populations might have originated (inverse dynamical population synthesis). Explicit modelling of this evolution has been performed for the ONC (KPM; KAH; Parker et al. 2009) and sparse embedded clusters (K1; K2, Kroupa & Bouvier 2003; Parker et al. 2009).
Thus, at present it cannot be confirmed whether the IPF depends on the star-forming conditions, that is, the presently available data are consistent with an invariant birth or initial binary population.
The typical star cluster is the birth site of most stars in the Galaxy. According to K1, it contains typically 200 binaries in a characteristic radius of about 0.8 pc, while Adams & Myers (2001) find that most stars would originate from compact 10–100 member groups. This estimate can be argued to correspond to the previous one if residual gas loss and subsequent expansion with loss of stars from the modest embedded cluster are taken into account.
References
- Adams, F. C., & Myers, P. C. 2001, ApJ, 553, 744 [NASA ADS] [CrossRef] [Google Scholar]
- Bhattacharyya G. K., & Johnson R. A. 1977, Statistical Concepts and Methods (New York: John Wiley & Sons Publ) [Google Scholar]
- Brandner, W., & Köhler, R. 1998, ApJ, 499, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Connelley, M. S., Reipurth, B., & Tokunaga, A. T. 2008, AJ, 135, 2526 [NASA ADS] [CrossRef] [Google Scholar]
- Covino, E., Alcala, J. M., Allain, S., et al. 1997, A&A, 328, 187 [NASA ADS] [Google Scholar]
- de Kool, M. 1996, NATO ASIC Proc. 477: Evolutionary Processes in Binary Stars, ed. R. A. M. J. Wijers, M. B. Davies, & C. A. Tout, 365 [Google Scholar]
- de Zeuw, P. T., Hoogerwerf, R., de Bruijne, J. H. J., Brown, A. G. A., & Blaauw, A. 1999, AJ, 117, 354 [NASA ADS] [CrossRef] [Google Scholar]
- Duchêne, G. 1999, A&A, 341, 547 [NASA ADS] [Google Scholar]
- Duchêne, G., Bouvier, J., Bontemps, S., André, P., & Motte, F. 2004, A&A, 427, 651 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Duchêne, G., Bontemps, S., Bouvier, J., et al. 2007a, A&A, 476, 229 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Duchêne, G., Delgado-Donate, E., Haisch, K. E., Jr., Loinard, L., & Rodríguez, L. F. 2007b, Protostars and Planets V, 379 [Google Scholar]
- Duquennoy, A., & Mayor, M. 1991, A&A, 248, 485 [NASA ADS] [Google Scholar]
- Durisen, R. H., & Sterzik, M. F. 1994, A&A, 286, 84 (DS) [NASA ADS] [Google Scholar]
- Fisher, R. T. 2004, ApJ, 600, 769 [NASA ADS] [CrossRef] [Google Scholar]
- Fischer, D. A., & Marcy, G. W. 1992, ApJ, 396, 178 [NASA ADS] [CrossRef] [Google Scholar]
- Ghez, A. M., Neugebauer, G., & Matthews, K. 1993, AJ, 106, 2005 [Google Scholar]
- Goodwin, S. P., & Kroupa, P. 2005, A&A, 439, 565 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hillenbrand, L. A. 1997, AJ, 113, 1733 [NASA ADS] [CrossRef] [Google Scholar]
- Horton, A. J., Bate, M. R., & Bonnell, I. A. 2001, MNRAS, 321, 585 (HBB) [NASA ADS] [CrossRef] [Google Scholar]
- Johnston, H. M. 1996, Evolutionary Processes in Binary Stars, ed. R. A. M. J. Wijers, M. B. Davies, & C. A. Tout, NATO ASIC Proc., 477 385 [Google Scholar]
- Köhler, R. 2001, AJ, 122, 3325 [NASA ADS] [CrossRef] [Google Scholar]
- Köhler, R., & Leinert, C. 1998, A&A, 331, 977 [NASA ADS] [Google Scholar]
- Köhler, R., Kunkel, M., Leinert, C., & Zinnecker, H. 2000, A&A, 356, 541 [NASA ADS] [Google Scholar]
- Kouwenhoven, M. B. N., Goodwin, S. P., Parker, R. J., et al. 2010, MNRAS, 404, 1835 [NASA ADS] [Google Scholar]
- Kroupa, P. 1995a, MNRAS, 277, 1491 (K1) [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 1995b, MNRAS, 277, 1507 [NASA ADS] [Google Scholar]
- Kroupa, P. 2001, The Formation of Binary Stars, ed. H. Zinnecker, R. Mathieu, IAU Symp., 200, 199 [Google Scholar]
- Kroupa, P. 2008, The Cambridge N-Body Lectures, Lecture Notes in Physics, 760, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2011, in IAUS 270, Computational Star Formation, ed. J. Alves, B. Elmegreen, J. Girart, & V. Trimble [arXiv:1012.1596] [Google Scholar]
- Kroupa, P., & Bouvier, J. 2003, MNRAS, 346, 343 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P., & Burkert, A. 2001, ApJ, 555, 945 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P., Petr, M. G., & McCaughrean, M. J. 1999, New A, 4, 495 (KPM) [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P., Aarseth, S., & Hurley, J. 2001, MNRAS, 321, 699 (KAH) [NASA ADS] [CrossRef] [Google Scholar]
- Leinert, C., Zinnecker, H., Weitzel, N., et al. 1993, A&A, 278, 129 [NASA ADS] [Google Scholar]
- Luhman, K. L. 2004, ApJ, 602, 816 [NASA ADS] [CrossRef] [Google Scholar]
- Maury, A. J., André, Ph., Hennebelle, P., et al. 2010, A&A, 512, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Makarov, V. V. 2007, ApJ, 658, 480 [NASA ADS] [CrossRef] [Google Scholar]
- Marks, M., & Kroupa, P. 2011, MNRAS, submitted [Google Scholar]
- Marks, M., Kroupa, P., & Oh, S.-K. 2011, MNRAS, submitted [Google Scholar]
- Mathieu, R. D. 1994, ARA&A, 32, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., Duquennoy, A., Halbwachs, J.-L., & Mermilliod, J.-C. 1992, Complementary Approaches to Double and Multiple Star Research, IAU Colloq., 135, 73 [NASA ADS] [Google Scholar]
- McCaughrean, M. J., & Stauffer, J. R. 1994, AJ, 108, 1382 [NASA ADS] [CrossRef] [Google Scholar]
- Moeckel, N., & Bate, M. R. 2010, MNRAS, 404, 721 [NASA ADS] [CrossRef] [Google Scholar]
- Nakajima, Y., Tachihara, K., Hanawa, T., & Nakano, M. 1998, ApJ, 497, 721 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, R. J., Goodwin, S. P., Kroupa, P., & Kouwenhoven, M. B. N. 2009, MNRAS, 397, 1577 [NASA ADS] [CrossRef] [Google Scholar]
- Perryman, M. A. C., Lindegren, L., Kovalevsky, J., et al. 1997, A&A, 323, L49 [NASA ADS] [Google Scholar]
- Petr M. G. 1998, Binary Stars in the Orion Trapezium Cluster: A High angular Resolution Near-Infrared Imaging Study, Ph.D. Thesis, University of Heidelberg [Google Scholar]
- Petr, M. G., Coudé du Foresto, V., Beckwith, S. V. W., Richichi, A., & McCaughrean, M. J. 1998, ApJ, 500, 825 [NASA ADS] [CrossRef] [Google Scholar]
- Preibisch, T., Brown, A. G. A., Bridges, T., Guenther, E., & Zinnecker, H. 2002, AJ, 124, 404 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1994 (Cambridge: University Press), 2nd edition [Google Scholar]
- Prosser, C. F., Stauffer, J. R., Hartmann, L., et al. 1994, ApJ, 421, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Raghavan, D., McAlister, H. A., Henry, T. J., et al. 2010, ApJS, 190, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ratzka, T., Köhler, R., & Leinert, C. 2005, A&A, 437, 611 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reipurth, B. 2000, AJ, 120, 3177 [CrossRef] [Google Scholar]
- Richichi, A., Leinert, C., Jameson, R., & Zinnecker, H. 1994, A&A, 287, 145 [NASA ADS] [Google Scholar]
- Salim, S., & Gould, A. 2003, ApJ, 582, 1011 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, M., Ghez, A. M., Leinert, Ch., et al. 1995, ApJ, 443, 625 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, M., Close, L. M., & Beck, T. L. 1999, AJ, 117, 1375 [NASA ADS] [CrossRef] [Google Scholar]
- Sterzik, M. F., & Durisen, R. H. 1998, A&A, 339, 95 [NASA ADS] [Google Scholar]
- Wichmann, R., Krautter, J., Covino, E., et al. 1997, A&A, 320, 185 [NASA ADS] [Google Scholar]
- Zinnecker, H., & Mathieu, R. 2001, The Formation of Binary Stars, ed. H. Zinnecker, & R. Mathieu, IAU Symp., 200 [Google Scholar]
All Tables
Histogram of main-sequence, fms(lPi), and pre-main-sequence, fpms(lPi), binary fractions, and adopted uncertainties.
All Figures
 |
Fig. 1 Testing the likelihood that the observed canonical binary-star period distributions fit the K1 IPF (dashed curve) or the DM PDPF (solid line). The model histograms are shown as dotted and solid lines with expected binomial uncertainties as error-bars (Eqs. (7) and (8)). Solid circles are the G-dwarf main-sequence data in the upper panel and canonical pre-main-sequence data in the lower panel (Sect. 2). The χ2 value and significance probability, |
| In the text | |
 |
Fig. 2 Similar to Fig. 1 but for all pre-main sequence samples. In all panels, the dotted continuous curves are the model distributions (K1 IPF upper curves, DM PDPF lower curves), whereas the model histograms are shown as solid lines with expected binomial uncertainties as dotted error-bars. Thick histograms are the data (Sect. 2). The χ2 value and probability, |
| In the text | |
 |
Fig. 3 Survey of η,δ parameter space for solutions of the K type with fpms = 1 (Eq. (4)) using the canonical pre-main-sequence data. Open circles and small dots delineate models consistent with the data at the 1 and 5 per cent confidence level or better, respectively, whereas the thick solid dot shows a model consistent at the 50 per cent level or better. The K1 IPF is shown as the thick cross. Note that the K1 IPF is not the same as the best solution found here. This is unsurprising because the K1 IPF was derived by constraining the IPF with both the pre-main-sequence and main-sequence period distribution functions. The best solution found here thus lacks one major constraint leading to the K1 IPF, but both are sufficiently close to conclude that the K1 IPF is a good solution to the pre-main-sequence data alone. The straight line shows the asymptotic solution for large δ: fK1(lP) = (η/δ) (lP − lPmin), with η/δ = 0.0339. |
| In the text | |
 |
Fig. 4 Survey of σlP,avlP parameter space for solutions of the DM type with fms = 0.58 (Eq. (6)) using the canonical main-sequence data. Open circles and small dots delineate models consistent with the data at the 1 and 5 per cent confidence level or better, respectively, whereas thick solid dots show models consistent at the 50 per cent level or better. The DM PDPF is shown as the thick cross. |
| In the text | |
 |
Fig. 5 Testing hypothesis 5 with fpms = 1.0. Survey of η,δ parameter space for solutions of the K type with fpms = 1 (Eq. (4)) for the canonical pre-main-sequence data, together with the Lupus and UScA pre-main-sequence data sets. Open circles and small dots delineate models consistent with the data at the 1 and 5 per cent confidence level, respectively. The K1 IPF is shown as the thick cross, and the straight line is as in Fig. 3. The thick solid dots show models consistent at the 50 per cent level or better. |
| In the text | |
 |
Fig. 6 As Fig. 5. Testing hypothesis 5 with fpms = 0.8. |
| In the text | |
 |
Fig. 7 Testing hypothesis 6 with fms = 1.0. Survey of σlP,avlP parameter space for solutions of the DM type (Eq. (6)) to the canonical pre-main-sequence data, together with the Lupus and UScA pre-main-sequence data sets. Open circles and small dots delineate models consistent with the data at the 1 and 5 per cent confidence level, respectively. The DM PDPF is shown as the thick cross. |
| In the text | |
 |
Fig. 8 The revised IPF. In addition to the K1 IPF (thick solid curve), two possible IPF forms are displayed. These are identified as solutions in Figs. 5 and 7, and are shown as the thin solid line (K-type, Eq. (4) with the asymptotic solution δ = 29.52 η;η = 18.7 and fpms = 1.0) and the thick dashed line (DM-type, Eq. (6) with σlP = 2.3,avlP = 5.0,fms = 1.0). The thin dashed line is the DM PDPF. Data points with observational error bars are as indicated in the key. These are used to test hypothesis 5 and 6 giving |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


