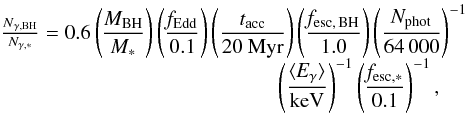| Issue |
A&A
Volume 528, April 2011
|
|
|---|---|---|
| Article Number | A149 | |
| Number of page(s) | 6 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201016357 | |
| Published online | 18 March 2011 | |
Stellar black holes at the dawn of the universe
1
CEA-Saclay IRFU/DSM/Service d’Astrophysique, 91191 Gif-sur-Yvette, France
e-mail: felix.mirabel@cea.fr
2
Instituto de Astronomía y Física del Espacio, cc 67, suc. 28, (C1428) Buenos Aires, Argentina
3
Harvard-Smithsonian Center for Astrophysics, 60 Garden Street, Cambridge, MA 02138, USA
4
Laboratoire APC, 10 rue Alice Domont et Léonie Duquet, 75205 Paris, France
5
Max Planck Institute für Astrophysik, Karl-Schwarzschild-Str. 1, 85741 Garching, Germany
Received: 18 December 2010
Accepted: 27 January 2011
Context. It is well established that between 380 000 and 1 billion years after the Big Bang the Inter Galactic Medium (IGM) underwent a “phase transformation” from cold and fully neutral to warm (≈ 104 K) and ionized. Whether this phase transformation was fully driven and completed by photoionization by young hot stars is a question of topical interest in cosmology.
Aims. We propose here that besides the ultraviolet radiation from massive stars, feedback from accreting black holes in high-mass X-ray binaries (BH-HMXBs) was an additional, important source of heating and reionization of the IGM in regions of low gas density at large distances from star-forming galaxies.
Methods. We use current theoretical models on the formation and evolution of primitive massive stars of low metallicity, and the observations of compact stellar remnants in the near and distant universe, to infer that a significant fraction of the first generations of massive stars end up as BH-HMXBs.
Results. The total number of energetic ionizing photons from an accreting stellar black hole in an HMXB is comparable to the total number of ionizing photons of its progenitor star. However, the X-ray photons emitted by the accreting black hole are capable of producing several secondary ionizations and the ionizing power of the resulting black hole could be greater than that of its progenitor. Feedback by the large populations of BH-HMXBs heats the IGM to temperatures of ≈ 104 K and maintains it ionized on large distance scales.
Conclusions. BH-HMXBs determine the early thermal history of the universe and maintain it as ionized over large volumes of space in regions of low density. This has a direct impact on the properties of the faintest galaxies at high redshifts, the smallest dwarf galaxies in the local universe, and on the existing and future surveys at radio wavelengths of atomic hydrogen in the early universe.
Key words: X-rays: binaries / black hole physics / dark ages, reionization, first stars / cosmology: miscellaneous / intergalactic medium
© ESO, 2011
1. Introduction
The so-called “dark ages” of the universe started ≈ 380 000 years after the Big Bang as matter cooled down and space became filled with neutral hydrogen. This phase of the universe lasted up to about a billion years, when the complex process of reionization of the IGM was completed (Loeb 2010). It is currently believed that most of the reionization was caused by the ultraviolet radiation from massive stars formed in the first generations of galaxies. However, it is uncertain what fraction of ionizing ultraviolet photons could escape from primitive galaxies to produce and maintain the ionization far from galaxies in low density regions of the IGM. Recent observations with the Hubble Space Telescope suggest that the rest-frame ultraviolet radiation from the most distant galaxies detected so far at the heart of the dark ages is not enough to heat and ionize the IGM over large volumes of space. To solve this apparent “photon-starved problem” (Bouwens et al. 2010), it has been suggested by Lehnert et al. (2010) that a fainter population of galaxies below the present detection limit could contribute significantly to the reionization.
X-rays from accreting black holes have a longer mean free path than the ultraviolet photons from massive stars. In this context Madau et al. (2004) and Ricotti & Ostriker (2004) have suggested that a smaller fraction of ionizing photons were provided by primordial black holes of intermediate mass (“miniquasars”, at z > 10) accreting by Bondi-Hoyle from the surrounding gas. However, feedback from Bondi-Hoyle accretion to solitary black holes significantly suppresses both any further inflow (Alvarez et al. 2009; Milosavljevic et al. 2009) and the consequent injection of radiation and high-energy particles to the surrounding medium.
We propose that BH-HMXBs at z ≥ 6, namely, the fossils of massive stars are an important − so far overlooked − agent in the complex process of the reionization of the universe. In the context of the current models on the formation (Krumholz et al. 2009; Turk et al. 2009; Stacy et al. 2010) and collapse (Heger et al. 2003; Meynet & Maeder 2005; Georgy et al. 2009; Linden et al. 2010) of primordial stars, an attractive and realistic alternative to the hypothesis of quasi-radial, Bondi-like accretion on solitary black holes of intermediate mass (“miniquasars”) is accretion on stellar black holes from high-mass stars in binary systems, namely, “microquasars” (Mirabel & Rodríguez 1999). As shown below, the formation rate of BH-HMXBs must have been very large in the young Universe, playing an important role in the thermal history of the IGM, and a complementary role to that of their progenitor stars in the re-ionization process of the IGM over large volumes of space. It is this scenario that we investigate here.
2. Cosmic evolution of BH-HMXBs: a prediction from current theoretical models
Recent hydrodynamic simulations of the formation of the first generations of stars show that a substantial fraction of stars in primordial galaxies form as binaries with typical masses of tens of solar masses (Krumholz et al. 2009; Turk et al. 2009; Stacy et al. 2010). Models of single stars with very low metal content and initial masses of a few tens of solar masses show that they collapse directly with no energetic natal kicks, and end as black holes (Heger et al. 2003; Meynet & Maeder 2005; Georgy et al. 2009).
On the other hand, a recent model of binary evolution of massive stars by Linden et al. (2010) show that the number of HMXBs and ULXs, their time evolution, and orbital period distribution, are strongly metallicity dependent. Linden et al. (2010) find that ULXs formed in a typical starburst of 106 M⊙ with Z = 0.02 Z⊙ outnumber ULXs formed with Z = Z⊙ by a factor of 5, and after 10 Myr by almost three orders of magnitude. Besides, at Z = 0.02 Z⊙, among the ULX population, >95% of the compact objects are black holes formed by direct collapse and therefore after black hole formation it remains gravitationally bound to a companion, donor star. Most of the orbital periods at Z = 0.02 Z⊙ are less than 3 days and accretion is by Roche lobe overflow which creates very luminous and persistent BH-HMXBs. Probably, this trend continues for starbursts with the metallicities (Z ≤ 0.02 Z⊙) of the reionization era.
These models imply that the majority of the first generations of high mass stellar binaries remain gravitationally bound after the formation of black holes. Massive stellar binaries can thus become BH-HMXB microquasars, which are sources of UV photons, X-rays, massive winds, and relativistic jets (Mirabel & Rodríguez 1999). Therefore, in the context of the models of massive stellar evolution and the cosmic evolution of metallicity it is expected that: 1) the fraction of black holes to neutron stars and 2) the fraction of black hole binaries to solitary black holes, should increase with redshift. That is, the rate of formation of bright BH-HMXBs was likely much larger in the early Universe than at present.
3. Formation rate of stellar black holes as a function of metallicity: observations
The cosmic evolution of BH-HMXBs inferred from theoretical models is consistent with the following observational studies of stellar black holes and neutron stars in the near and distant universe:
-
1.
The mass of black holes in HMXBs seems to be adecreasing function of the host galaxy metallicity(Crowther et al. 2010, and references therein). Theblack holes in the binaries M 33 X-7, NGC 300 X-1, and IC10 X-1 are in low-metallicity galaxiesand have masses – determined dynamically – in the range of16 to 30 solar masses, which are higher than themass of any known stellar compact source in the Milky Way andAndromeda galaxies, which have higher metallicities. However,while the model by Linden et al. (2010) supportsthe formation of HMXBs and ULXs in low-metallicity environ-ments, they conclude that it is difficult to create very massive blackholes through common envelope phases, since this tends to stripa high fraction of the primary envelope. Given the low numberstatistics of the known dynamic masses of black holes in HMXBs,it is possible that the relatively high masses of 16 to 30 solar massescome from the selection of the brightest sources, namely, thosethat are at the tip of the iceberg.
-
2.
It is believed that the majority of ultraluminous X-ray sources (ULXs) found in external galaxies are HMXBs that contain black holes accreting at super-Eddington rates (Gladstone et al. 2009). In fact, the occurrence rate per unit galaxy mass of ULXs observed in nearby galaxies is a decreasing function of the galaxy mass – hence of the metallicity – of the host galaxy (Zamperi & Roberts 2009).
-
3.
The space kinematics of Galactic X-ray binaries that contain black holes with more than ten solar masses provides evidence of black hole formation by implosion, with no large kicks due to energetic supernovae (Mirabel & Rodrigues 2003; Mirabel 2010).
-
4.
Observations now support the notion that massive stars with high metal content may end as neutron stars instead of black holes (Meynet & Maeder 2005; Georgy et al. 2009; Linden et al. 2010). Recently formed neutron stars observed as soft gamma ray repeaters and anomalous X-ray pulsars are found in young clusters of large metal content that contain stars with masses of 40–50 solar masses (Figer et al. 2005; Muno et al. 2006).
-
5.
It is believed that the majority of gamma ray bursts of long duration (LGRBs) mark the formation of black holes by the collapse of massive stars. Although a fraction of dark LGRBs may require local extinction columns of Av > 1 mag, the majority of their hosts are faint, irregular galaxies with global limited chemical evolution (Le Floc’h et al. 2003; Fruchter et al. 2006; Han et al. 2010; Levesque et al. 2010). The properties of GRB 090423 at z = 8.1 are similar to those of GRBs observed at low/intermediate redshifts (Salvaterra et al. 2009), suggesting that the mechanisms and progenitors that gave rise to this burst are not too different from those producing GRBs with identified hosts.
-
6.
There is increasing evidence for an enhanced LGRB rate at z > 3 (Daigne et al. 2006; Kistler et al. 2008; Wanderman & Piran 2010; Qin et al. 2010), as expected from the increase in the specific star formation rate (SFR) with decreasing metallicity (Mannucci et al. 2010).
4. Ionizing power of a stellar black hole in an HMXB relative to its progenitor star
In the following we compute the number of ionizing soft X-rays and UV photons from the accretion disk of a BH-HMXB, and then compare its ionization power with that of its progenitor massive star. To this end we assume that the black hole of mass MBH is accreting at a fraction fedd of its Eddington luminosity for a time tacc. Then the ratio of the total number of ionizing photons emitted by the accreting black hole to that emitted by the progenitor star is given by
where Nphot denotes the number of ionizing photons emitted per hydrogen nucleus involved in star formation, ⟨ Eγ ⟩ denotes the mean photon energy of the radiation emitted by the accreting black hole, and fesc,∗ (fesc, BH) denotes the fraction of ionizing photons emitted by the star (accreting black hole) that escape from the galaxy and contribute to the heating and reionization of the IGM.
We have substituted reasonable numbers for each of the parameters: Nphot = 64 000 corresponds to metal-free forming stars with a top-heavy Initial Mass Function (IMF). For a normal stellar population this number would be 16 times lower (Schaerer 2003). The escape fraction of ionizing photons emitted by stars was taken to be fesc,∗ = 0.1, which is consistent with the mean observed escape fraction of ionizing photons from star-forming galaxies (Shapley et al. 2006) at z = 2−3.
HMXBs are expected to inject photons into the IGM at a rate close to Eddington (and possibly super Eddington), and our choice fedd = 0.1 is likely to be conservative (see footnote1). The accretion lasts tacc ≈ 20 Myr, a mean lifetime of donor stars of M∗ = 10−30 M⊙ (Turk et al. 2009; Stacy et al. 2010). The mean photon energy of the radiation emitted by the accreting source depends on the assumed spectral shape, but ⟨ Eγ ⟩ = 1 keV appears – within a factor of a few – of values derived for both the thermal and power-law components of the black hole spectra. Finally, fesc, BH = 1.0 is not well constrained. We took fesc, BH to be larger than fesc,∗ simply because energetic photons can propagate much more easily through HI column densities in the range 1017 − 1020cm-2. For reasonable choices for each of these model parameters, we find that an accreting black hole in a high-mass binary emits a total number of ionizing photons that is comparable to its progenitor star.
However, it should be kept in mind that the ionizing photons emitted by the accreting black hole are more energetic than those from the progenitor star and capable of ionizing more than one hydrogen atom. In a fully neutral medium, the number of secondary ionizations Nsec = 25(Eγ/1 keV), where Eγ is the photon energy (Shull & van Steenberg 1985). Therefore, the ionizing power of the resulting black hole could be greater than that of its progenitor.
5. BH-HMXBs and massive star formation rates in the epoch of reionization
The progenitor star of the black hole should have formed in a molecular cloud, which in turn may have formed more stars, each of which contributed to the total number of ionizing photons emitted by stars. Therefore, in the following we look at the emission of ionizing radiation from a star-forming region as a whole.
Observations of galaxies in the local universe show that their X-ray luminosity in the energy range 2–10 keV correlates strongly with the rate at which they are forming stars (Grim et al. 2003). This local correlation states that the X-ray luminosity (in erg s-1) scales with the SFR in M⊙ yr-1, as L2 − 10 = 7 × 1039 SFR erg s-1. When modeling the impact of X-ray emission from galaxies at very high redshift, the following more general correlation is used (Furlanetto 2006): 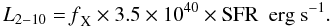 (2)Here, the parameter fX accounts for the likely case that the normalization of the observed correlation depends on redshift. Observations indicate that fX = 0.2 for local galaxies. This important parameter fX depends on several physical processes (all of which are expected to change with redshift). To illustrate this quantitatively, we express the X-ray luminosity of a star-forming galaxy in more fundamental quantities as
(2)Here, the parameter fX accounts for the likely case that the normalization of the observed correlation depends on redshift. Observations indicate that fX = 0.2 for local galaxies. This important parameter fX depends on several physical processes (all of which are expected to change with redshift). To illustrate this quantitatively, we express the X-ray luminosity of a star-forming galaxy in more fundamental quantities as 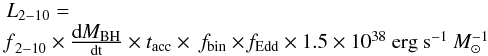 (3)or
(3)or 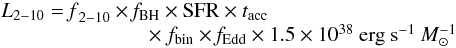 (4)Most of the parameters in this equation were introduced earlier. The fraction f2 − 10 denotes the fraction of the total luminosity that emerges in the 2–10 keV band. For the power law component of the spectra we expect f2 − 10 = 0.1 − 0.5 (equal flux per logarithmic bin of energy or steeper), and we conservatively adopt f2 − 10 = 0.1. We also introduced the parameter fBH, which relates black hole formation rate dMBH/dt to SFR. This fraction can be computed for a given initial IMF under the assumption that every star above some critical mass M∗,crit ends up as black hole. As argued previously, due to mass lost by metallicity-dependent stellar winds even massive stars may end up as neutron stars instead of directly as black holes. However, in the evolution of a close massive binary of low metallicity, due to mass transfer and common envelope phase the primary could lose mass and end its life as a neutron star rather than a black hole, leading to suppression of black hole formation. Linden et al. (priv. comm.) discussed the importance and frequency of such scenario finding that the transition from neutron star to black hole dominated HMXBs is very sharp and metallicity dependent, and that for Z ≤ 0.02 Z⊙ all primary stars with M ≥ 20 M⊙ in HMBs end as black holes in HMXBs. Therefore we assume here that mass transfer in close binaries has little impact on the mass range of stars becoming black holes. For the conservative choices of a Salpeter IMF in the range Mlow = 0.1M⊙, Mup = 100 M⊙, and M∗,crit = 25 M⊙ we find fBH = 0.03. Finally, we expect black holes in binaries to be very efficient accreters, while isolated black holes are not. The parameter fbin denotes the mass fraction of accreting black holes in binaries. The total mass fraction of massive stars in binaries is close to unity, and for simplicity we assume that this total mass fraction is 50%. Since BH-HMXBs are persistent sources of radiation and jets for our model we assume fbin = 0.5.
(4)Most of the parameters in this equation were introduced earlier. The fraction f2 − 10 denotes the fraction of the total luminosity that emerges in the 2–10 keV band. For the power law component of the spectra we expect f2 − 10 = 0.1 − 0.5 (equal flux per logarithmic bin of energy or steeper), and we conservatively adopt f2 − 10 = 0.1. We also introduced the parameter fBH, which relates black hole formation rate dMBH/dt to SFR. This fraction can be computed for a given initial IMF under the assumption that every star above some critical mass M∗,crit ends up as black hole. As argued previously, due to mass lost by metallicity-dependent stellar winds even massive stars may end up as neutron stars instead of directly as black holes. However, in the evolution of a close massive binary of low metallicity, due to mass transfer and common envelope phase the primary could lose mass and end its life as a neutron star rather than a black hole, leading to suppression of black hole formation. Linden et al. (priv. comm.) discussed the importance and frequency of such scenario finding that the transition from neutron star to black hole dominated HMXBs is very sharp and metallicity dependent, and that for Z ≤ 0.02 Z⊙ all primary stars with M ≥ 20 M⊙ in HMBs end as black holes in HMXBs. Therefore we assume here that mass transfer in close binaries has little impact on the mass range of stars becoming black holes. For the conservative choices of a Salpeter IMF in the range Mlow = 0.1M⊙, Mup = 100 M⊙, and M∗,crit = 25 M⊙ we find fBH = 0.03. Finally, we expect black holes in binaries to be very efficient accreters, while isolated black holes are not. The parameter fbin denotes the mass fraction of accreting black holes in binaries. The total mass fraction of massive stars in binaries is close to unity, and for simplicity we assume that this total mass fraction is 50%. Since BH-HMXBs are persistent sources of radiation and jets for our model we assume fbin = 0.5.
Both Eqs. (2) and (4) depend linearly on SFR, and we can express the parameter fX as a combination of physical parameters: 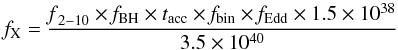 (5)or
(5)or 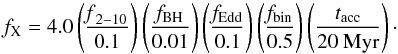 (6)Linden et al. (2010) estimate that at ULX luminosities the number of Z = 0.02 Z⊙ sources should outnumber the Z = Z⊙ HMXBs by a factor of 5. Therefore, in our fiducial conservative model for primordial starbursts fX is at least one order of magnitude higher than the locally observed value (Grim et al. 2003). There are several reasons why we expect fX to be much higher in the young Universe. (1) Microquasars can have spectra that are harder and f2 − 10 could be in some cases as high as f2−10 = 0.5; and (2) fBH is higher in low metallicity environments, i.e., the formation of black holes in metal-enriched environments of galaxies in the local universe is likely to be strongly suppressed compared to more pristine environments. (3) Stars in the young Universe were very likely formed with an IMF that was more top-heavy. This evolution in the IMF alone could boost fBH to much higher values than the fiducial assumed value in Eq. (4). Finaly, the IGM at z = 10 would essentially be transparent to the hard X-ray photons (> 1 keV), and following Dijkstra et al. 2004 we explicitly verified that these models are consistent with the observed unresolved soft X-ray background.
(6)Linden et al. (2010) estimate that at ULX luminosities the number of Z = 0.02 Z⊙ sources should outnumber the Z = Z⊙ HMXBs by a factor of 5. Therefore, in our fiducial conservative model for primordial starbursts fX is at least one order of magnitude higher than the locally observed value (Grim et al. 2003). There are several reasons why we expect fX to be much higher in the young Universe. (1) Microquasars can have spectra that are harder and f2 − 10 could be in some cases as high as f2−10 = 0.5; and (2) fBH is higher in low metallicity environments, i.e., the formation of black holes in metal-enriched environments of galaxies in the local universe is likely to be strongly suppressed compared to more pristine environments. (3) Stars in the young Universe were very likely formed with an IMF that was more top-heavy. This evolution in the IMF alone could boost fBH to much higher values than the fiducial assumed value in Eq. (4). Finaly, the IGM at z = 10 would essentially be transparent to the hard X-ray photons (> 1 keV), and following Dijkstra et al. 2004 we explicitly verified that these models are consistent with the observed unresolved soft X-ray background.
6. Stellar black holes and the thermal history of the IGM
It is an open question how significant may be boosting the X-ray emissivity of star-forming galaxies in the high-redshift Universe for the global ionized fraction (i.e. averaged over the entire volume of the observable Universe). However, it has been shown (Furlanetto 2006) that soft X-rays (Eγ < 2 keV, Pritchard & Furlanetto 2007) and inverse-Compton scattering from relativistic electrons could have profound implications for the amount of heating of the low-density neutral IGM. BH-HMXBs are powerful sources of soft X-rays and relativistic jets, and their heating could in turn affect the overall reionization process indirectly in ways that will need to be investigated further. In Fig. 1 we show that fX (as defined in Eqs. (5) and (6)) is the parameter that determines the thermal history of the IGM. Increasing fX causes the neutral IGM to be heated earlier. As shown in the thermal evolution for fX = 10.0, when the gas temperature approaches 104 K, cooling through collisional excitation of the atomic hydrogen becomes efficient, and further heating is not possible in practice. As discussed in Sect. 8, the formation of low-mass galaxies in the neutral IGM at z = 10 − 20 is suppressed when the gas temperature is as high as 104 K, namely, for fX > 5. For further details on this particular model we refer the reader to Pritchard & Furlanetto (2007).
 |
Fig. 1 Thermal history of the low-density neutral inter galactic medium (IGM) due to heating by accreting stellar black holes in high mass X-ray binaries (BH-HMXBs). This figure shows the gas temperature of the IGM as a function of redshift z for three possible values of fX as defined in Eq. (6): fX = 0.1 (blue dashed line), fX = 1.0 (black dotted line), fX = 10.0 (red solid line)). As discussed in the text, most likely fX > 1. |
7. The 21 cm line of HI during reionization
The precise temperature evolution of the neutral IGM is known to strongly affect the global 21 cm signature expected from neutral HI during the epoch of reionization (Furlanetto et al. 2006). In Fig. 2, we plot the evolution of the brightness temperature (averaged over the entire sky) as a function of redshift following the same prescriptions as in Pritchard & Loeb (2010), again for the same three models with different values of fX. The gas temperature couples to the excitation temperature through collisions, and through scattering of Lyman α photons. When this excitation temperature, also known as the spin temperature, is higher (lower) than the temperature of the cosmic microwave background (CMB), then it is possible to observe hydrogen atoms in emission (absorption) against this CMB. The difference in spin and CMB temperature is referred to as the “brightness” temperature (Furlanetto et al. 2006). Clearly, when the gas is heated earlier, the spin temperature can increase earlier, and hydrogen can be seen in emission earlier in the evolution of the Universe. Increasing fX also reduces the interval in redshift – and therefore – frequency over which hydrogen can be seen in absorption against the CMB (corresponding to negative brightness temperature). Single dipole experiments such as EDGES are currently attempting to measure this signal (Bowman et al. 2008). One of the present challenges in observational astronomy is to directly observe this 21 cm signal from neutral hydrogen in the young Universe (Morales & Wyithe 2010). This can be accomplished with single radio dipole experiments, such as EDGES (Bowman et al. 2008), which are potentially capable of detecting the global 21 cm signal (Pritchard & Loeb 2010) at redshifts z < 30, directly measuring early heating of the IGM.
 |
Fig. 2 Brightness temperature of the hyperfine transition of the ground state of atomic hydrogen (the wavelength of this transition is 21 cm), averaged over the entire sky, as a function of redshift z for the same three different values of fX as in Fig. 1. |
A boosted X-ray emissivity of star forming also affects the fluctuations in the 21 cm background (Pritchard & Furlanetto 2007; Pritchard & Loeb 2008). Detect- ing these fluctuations is one of the prime scientific drivers for the next generations of radio interferometers such as the MWA, LOFAR, and SKA. The fluctuations in the 21 cm background radiation contain the largest amount of cosmological information (Loeb & Zaldarriaga 2004), and are therefore invaluable constraints on cosmological parameters (as well as fundamental physics). However, “astrophysics” introduces additional fluctuations, for example, through temperature fluctuations and through fluctuations in the Lyman α background (Pritchard & Furlanetto 2007; Pritchard & Loeb 2008). Both are sourced (on different scales) by galaxies that themselves provide biased tracers of the underlying density field. To fully exploit the rich data set provided by the 21 cm fluctuations therefore requires a good understanding of the nature of the astrophysical sources illuminating, heating, and ionizing the hydrogen in our Universe. Interestingly, one heats the neutral IGM earlier by boosting fX, which implies that temperature fluctuations are suppressed during the later stages of reionization, which improves the prospects for extracting cosmological information from the 21 cm background (Pritchard & Furlanetto 2007; Pritchard & Loeb 2008).
8. The role of stellar black holes in the formation of dwarf galaxies
The cold dark matter model of the universe provides the framework for significant progress in understanding the large-scale properties and physical principles that govern the large-scale evolution of the universe during the first 400 thousand years. However, it is still poorly understood how the first stars and black holes in galaxies were formed and the way that in less than a billon year these pristine objects re-ionized and re-heated most of the matter in the universe over large volumes of space. The apparent disparity between the number of dwarf galaxies predicted by the cold dark matter model of the universe and the number of small galaxies observed so far in the halo of the Galaxy is a subject of topical interest in cosmology (Loeb 2010). Power et al. (2009) had already pointed out the possible implications of X-ray binaries in primordial globular clusters for the reionization, hence, galaxy formation at high redshifts.
It is believed that the first stars had formed in gas clouds with a virial temperature of a few hundred K due to cooling by molecular hydrogen, H2 (Loeb 2010). But the UV radiation produced by these stars could have easily dissociated H2, making atomic hydrogen (HI) cooling necessary for further star formation. The galaxies that reionized the IGM were therefore likely to have a virial temperature above the H I cooling threshold of 104 K. X-ray, and UV heating by BH-HMXBs of the diffuse IGM during reionization would have resulted in an additional increase in the total minimum galaxy mass Mmin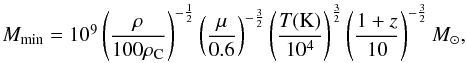 (7)
(7)
where ρC is the critical mass density for a flat Universe, ρ the mass density in the galaxy, μ the mean molecular weight, z the redshift, and T the temperature of the IGM. Once the IGM was heated to a temperature of 104 K, dark matter halos with masses below 109 M⊙ could no longer accrete IGM material because the temperature of the infalling gas increased by an extra order of magnitude as its density increased on its way into these galaxies. In that regime, only gaseous halos with virial temperatures above 105 K could have accreted fresh IGM gas and converted it to stars. The census of dwarf galaxy satellites of the Milky Way requires a related suppression in the abundance of low-mass galaxies relative to low-mass dark matter halos (see Muñoz et al. 2009, and references therein). The thermal history of the IGM therefore has a direct impact on the properties of the faintest galaxies at high redshifts, as well as on the smallest dwarf galaxies in the local universe.
It is interesting to note that black holes of different mass scales play a role in galaxy formation. Feedback from supermassive black holes halt star formation, quenching the unlimited mass growth of massive galaxies (Cattaneo et al. 2009), and we show here that feedback from stellar black holes in HMXBs during the reionization epoch suppress the number of low-mass dwarf galaxies. Therefore, BH-HMXBs in the early universe are an important ingredient in reconciling the apparent disparity between the observed number of dwarf galaxies in the Galactic halo with the number of low-mass galaxies predicted by the cold dark matter model of the universe.
9. Conclusions
The main conclusions of this work are the following:
-
1.
The ratio of black holes to neutron stars and the ratio of black hole binaries to solitary black holes should increase with redshift; that is, the rate of formation of BH-HMXBs was significantly higher in the early Universe than at present.
-
2.
Feedback from one of those BH-HMXBs during its whole lifetime can be more than 1054 erg (orders of magnitude larger than that of the photonic and baryonic energy from a typical core collapse supernova).
-
3.
An accreting black hole in a high-mass binary emits a total number of ionizing photons that is comparable to its progenitor star, but one X-ray photon emitted by an accreting black hole may cause the ionization of several tens of hydrogen atoms in a fully neutral medium.
-
4.
The most important effect of BH-HMXBs in the early universe is the heating of the IGM. Soft X-rays and inverse-Compton scattering from relativistic electrons produced by BH-HMXBs heat the low-density medium over large distances to temperatures of ≈ 104 K, which limits the recombination rate of hydrogen and keeps the IGM ionized.
-
5.
A temperature of the IGM of ≈ 104 K limits the formation of faint galaxies at high redshifts. It constrains the total mass of dwarf galaxies to ≥ 109 M⊙ .
-
6.
BH-HMXBs in the early universe are important ingredients for reconciling the apparent disparity between the observed number of faint dwarf galaxies in the Galactic halo with the number of low-mass galaxies predicted by the cold dark matter model of the universe.
-
7.
An additional effect of metallicity in the formation of BH-HMXBs (Mirabel 2010) is to boost the formation of BH-BH binaries as more likely sources of gravitational waves than NS-NS systems (Belczynski et al. 2010).
To estimate the ionizing power of BH-HMXBs in the early universe we use the observed spectra of the Galactic black hole binary Cygnus X-1, which has a blue supergiant companion, as template for moderate accretion rates. In this system, accretion is persistent and composed mainly by the donor stellar wind. Its X-ray spectrum is characterized by two components: a UV-soft X-ray bump due to thermal emission from the accretion disk with a typical temperature of ≈ 7 eV, and a non-thermal power-law component of hard X-rays that result from Compton up scattering of thermal accretion disk and synchrotron photons by a hot coronal plasma and/or jet. In addition to X-rays, these sources can indeed produce jets and winds of accelerated particles, which in turn may heat and ionize the surrounding medium. On the other hand, for higher accretion rates one can use the ULXs observed in the local universe as templates of BH-HMXBs in the early universe. ULXs often have spectra that resemble the very high (super-soft) state observed in some Galactic black hole binaries (e.g. GRS 1915+105). The majority of ULXs exhibit a complex curvature, which can be modeled by a cool disk component, together with a power law that breaks above 3 keV, probably due to a cool, optically thick corona produced by super-Eddington accretion flows (Gladstone et al. 2009). Examples of steady super-Eddington sources are also SS 433 in the Milky Way, which is blowing the nebula W50 laterally, and the microquasar that is inflating the nebula S26 in the galaxy NGC 7793 (Pakull et al. 2010). SS 433 injects more than 1039 erg s-1 in the interstellar medium and the microquasar in S26 more than 1040 erg s-1. The overall energy injected by these microquasars during their whole lifetime can be more than 1054 erg, which is orders of magnitude more than the photonic and baryonic energy from a typical core collapse supernova.
Acknowledgments
I.F.M. thanks the referee G. Meynet, and A. King, P. Fabbiano, T. Piran, T. Linden and V. Kalogera for useful information and kind comments. This work was supported in part by NSF grant AST-0907890 and NASA grants NNX08AL43G and NNA09DB30A.
References
- Alvarez, M. A., Wise, J. H., & Abel, T. 2009, ApJ, 701, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Belczynski, K., Dominik, M., Bulik, T., et al. 2010, ApJ, 715, L138 [NASA ADS] [CrossRef] [Google Scholar]
- Bouwens, R. J., Illingworth, G. D., Oesch, P. A., et al. 2010, ApJ, 709, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Bowman, J. D., Rogers, A. E. E., & Hewitt, J. N. 2008, ApJ, 676, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Cattaneo, Faber, S. M., Binney, J. A., et al. 2009, Nature, 460, 213 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Crowther, P. A., Barnard, R., Carpano, S., et al. 2010, MNRAS, 403, L1 [Google Scholar]
- Daigne, F., Rossi, E. M., & Mochkovitch, R. 2006, MNRAS, 372, 1034 [NASA ADS] [CrossRef] [Google Scholar]
- Dijkstra, M., Haiman, Z., & Loeb, A. 2004, ApJ, 613, 646 [NASA ADS] [CrossRef] [Google Scholar]
- Figer, D. F., Najarro, F., Geballe, T. R., Blum, R. D., Kudritzki, Rolf, P., et al. 2005, ApJ, 622, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Fruchter, A. S., Levan, A. J., Strolger, L., et al. 2006, Nature, 441, 463 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Furlanetto, S. R. 2006, MNRAS, 371, 867 [NASA ADS] [CrossRef] [Google Scholar]
- Furlanetto, S., Oh, S. P., & Briggs, F. H. 2006, Phys. Rep., 433, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Gladstone, J. C., Roberts, T. P., & Done, C. 2009, MNRAS, 397, 1836 [NASA ADS] [CrossRef] [Google Scholar]
- Gregory, C., Meynet, G., Walder, R., et al. 2009, A&A, 502, 611 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grim, H.-J., Gilfanov, M., & Sunyaev, R. 2003, MNRAS, 339, 793 [NASA ADS] [CrossRef] [Google Scholar]
- Han, X. H., Hammer, F., Liang, Y. C., et al. 2010, A&A, 514, 24 [Google Scholar]
- Heger, A., Fryer, C. L., Woosley, S. E., et al. 2003, ApJ, 591, 288 [NASA ADS] [CrossRef] [Google Scholar]
- Kistler, M. D., Yüksel, H., Beacom, J. F., Stanek, K. Z., et al. 2008, ApJ, 673, L119 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R., Klein, R. I., McKee, C. F., Offner, S. S. R., & Cunningham, A. J. 2009, Science, 323, 754 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Le Floc’h, E., Duc, P.-A., Mirabel, I. F., et al. 2003, A&A, 400, 499 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lehnert, M. D., Nesvadba, N. P. H., Cuby, J.-G., et al. 2010, Nature, 467, 940 [NASA ADS] [CrossRef] [Google Scholar]
- Levesque, E. M. Kewley, L. J., Berger, E., Jabran Zahid, H., et al. 2010, AJ, 140, 1557 [NASA ADS] [CrossRef] [Google Scholar]
- Linden, T., Kalogera, V., Sepinsky, J. F., et al. 2010, ApJ, 725, 1984 [NASA ADS] [CrossRef] [Google Scholar]
- Loeb, A. 2010, in How Did the First Stars and Galaxies Form? (Princeton University Press) [Google Scholar]
- Loeb, A., & Zaldarriaga, M. 2004, Phys. Rev. Lett., 92, 211301-04 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Madau, P., Rees, M. J., Volonteri, M., Haardt, F., Oh, S. P., et al. 2004, ApJ, 604, 484 [NASA ADS] [CrossRef] [Google Scholar]
- Mannucci, F., Cresci, G., Maiolino, R., Marconi, A., Gnerucci, A., et al. 2010, MNRAS, 408, 2115 [NASA ADS] [CrossRef] [Google Scholar]
- Meynet, G., & Maeder, A. 2005, A&A, 429, 581 [Google Scholar]
- Milosavljevic, M., Bromm, V., Couch, S. M., Oh, S. P., et al. 2009, ApJ, 698, 766 [NASA ADS] [CrossRef] [Google Scholar]
- Mirabel, I. F., & Rodrigues, I. 2003, Science, 300, 1119 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Mirabel, I. F., & Rodríguez, L. F. 1999, ARA&A, 37, 409 [NASA ADS] [CrossRef] [Google Scholar]
- Mirabel, I. F. 2010, Proc. IAU Symp. 275, Jets at all Scales. Cambridge University Press, pages 2-8. ed. G. E. Romero, R. A. Sunyaev, T. Belloni [arXiv:1012.4944v1] [Google Scholar]
- Morales, M., & Wyithe, J. S. B. 2010, ARA&A, 48, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Muno, M. P., Clark, J. S., Crowther, P. A., et al. 2006, ApJ, 636, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Muñoz, J. A., Madau, P., Loeb, A., Diemand, J., et al. 2009, MNRAS, 400, 1593 [NASA ADS] [CrossRef] [Google Scholar]
- Pakull, M. W., Soria, R., & Motch, C. 2010, Nature, 466, 209 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Power, C., Wynn, G. A., Combet, C., & Wilkinson, M. 2009, MNRAS, 395, 1146 [NASA ADS] [CrossRef] [Google Scholar]
- Pritchard, J. R., & Furlanetto, S. R. 2007, MNRAS, 376, 1680 [NASA ADS] [CrossRef] [Google Scholar]
- Pritchard, J. R., & Loeb, A. 2008, Phys. Rev. D, 78, 103511 [NASA ADS] [CrossRef] [Google Scholar]
- Pritchard, J. R., & Loeb, A. 2010, Phys. Rev. D, 82, 023006 [NASA ADS] [CrossRef] [Google Scholar]
- Qin, S. F., Liang, E.-W., Lu, R.-J., Wei, J.-Y., Zhang, S.-N., et al. 2010, MNRAS, 406, 558 [NASA ADS] [CrossRef] [Google Scholar]
- Ricotti, M., & Ostriker, J. 2004, MNRAS, 352, 547 [NASA ADS] [CrossRef] [Google Scholar]
- Salvaterra, R., Della Valle, M., Campana, S., et al. 2009, Nature, 461, 1258 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Shapley, A. E., Steidel, C. C., Pettini, M., Adelberger, K. L., Erb, D. K., et al. 2006, ApJ, 651, 688 [NASA ADS] [CrossRef] [Google Scholar]
- Schaerer, D. 2003, A&A, 397, 527 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shull, J.M., & van Steenberg, M. E. 1985, ApJ, 298, 268 [NASA ADS] [CrossRef] [Google Scholar]
- Stacy, A., Greif, T. H., & Bromm, V. 2010, MNRAS, 403, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Turk, M. J., Abel, T., & OShea, B. 2009, Science, 325, 601 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Wanderman, D., & Piran, T. 2010, MNRAS, 406, 1944 [NASA ADS] [Google Scholar]
- Zamperi, L., & Roberts, T. P. 2009, MNRAS, 400, 677 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Thermal history of the low-density neutral inter galactic medium (IGM) due to heating by accreting stellar black holes in high mass X-ray binaries (BH-HMXBs). This figure shows the gas temperature of the IGM as a function of redshift z for three possible values of fX as defined in Eq. (6): fX = 0.1 (blue dashed line), fX = 1.0 (black dotted line), fX = 10.0 (red solid line)). As discussed in the text, most likely fX > 1. |
| In the text | |
 |
Fig. 2 Brightness temperature of the hyperfine transition of the ground state of atomic hydrogen (the wavelength of this transition is 21 cm), averaged over the entire sky, as a function of redshift z for the same three different values of fX as in Fig. 1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.