EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 528 (April 2011) A&A, 528 (2011) A52 Full HTML
Free Access
Issue
A&A
Volume 528, April 2011
Article Number A52
Number of page(s) 6
Section Cosmology (including clusters of galaxies)
DOI https://doi.org/10.1051/0004-6361/201015766
Published online 28 February 2011

© ESO, 2011

1. Introduction

The structure of cluster and galaxy halos predicted by N-body simulations of cold dark matter show several important features, e.g. the universal radial density profile (Navarro et al. 1996, 1997), and the highly non-spherical structure fitted well by a triaxial density profile (Jing & Suto 2002; Law et al. 2009). These features are related to the nature of dark matter as well as to the formation of galaxies and clusters (Kuhlen et al. 2007; Debattista et al. 2008; Bett et al. 2010), which suggest that accurate estimates of the halo properties can provide several constraints on cosmology. In particular, numerical simulations with different assumptions predict halos with different shapes, e.g., simulations with non-interacting cold dark matter predict that halos are triaxial prolate ellipsoids (Allgood et al. 2006). Moreover, if there exists a significant difference between the shape of a galaxy and the shape of its total mass distribution, this would provide additional strong evidence for the existence of dark matter (Suyu & Halkola 2010). In other words, it allows us to test how reliable the light is as a tracer of the matter distribution.

Gravitational lensing provides a powerful tool for studying the mass distribution of clusters of galaxies as well as galaxy halos (see Bartelmann & Schneider 2001; Refregier 2003; Schneider et al. 2006; Munshi et al. 2008, for reviews on weak lensing). This is because gravitational lensing probes the matter distribution regardless of whether it is luminous or dark. The weak lensing technique has been used for cluster mass reconstructions (e.g. Clowe et al. 2006; Bradač et al. 2008), and for the ellipticity of the dark matter distribution (Corless et al. 2009; Deb et al. 2010; Howell & Brainerd 2010). A method to determine galaxy halo ellipticity by stacking galaxies was proposed in Natarajan & Refregier (2000) and has been used to determine the ellipticities of both cluster- or galaxy-size halos (Evans & Bridle 2009; Mandelbaum et al. 2006). A mean ellipticity of 0.46 is found from a sample of 25 clusters using Subaru data (Oguri et al. 2010).

Flexion has been recently studied as the derivative of the shear, and responds to small-scale variations in the gravitational potential (Goldberg & Natarajan 2002; Goldberg & Bacon 2005; Bacon et al. 2006). Different techniques were developed to measure flexion (Irwin & Shmakova 2006; Okura et al. 2007; Massey et al. 2007; Schneider & Er 2008). It was noted that flexion can contribute to studies of the dark matter halos in galaxies and clusters, especially for the detection of mass substructure (Bacon et al. 2010; Er et al. 2010). Flexion has been implemented on small sets of observational data. Okura et al. (2008) performed flexion measurement on data from the Subaru telescope to detect substructure in Abell 1689. Leonard et al. (2007) analyzed images taken by the HST Advanced Camera for Surveys, from which a preliminary galaxy-galaxy flexion signal has been detected. Hawken & Bridle (2009) studied galaxy halo ellipticity using flexion. It is found that the constrains from flexion are comparable to, or even tighter than those from shear. Moreover, since flexion drops off faster than the shear as one goes away from the center of the lens, multiple deflections from the three-dimensional mass distribution between us and distant source galaxies (Howell & Brainerd 2010) may not be significant for flexion.

In this paper, we present a new approach to estimate dark matter halo ellipticity using galaxy-galaxy lensing flexion. The spin-1 flexion, a vector, is decomposed into its two components, the radial and tangential flexion. The tangential-to-radial flexion ratio yields an estimate of dark halo ellipticity. We need to assume that the center of the galaxy or the cluster be known. Whereas for galaxies this may be a lesser problem, the mass centroid of clusters is sometimes difficult to determine. We study the effect of noise coming from an intrinsic flexion. In Sect. 3, we perform a series of numerical tests of our estimate and study how our results are biased by the distribution of background sources, the centroid offsets and intrinsic flexion. We discuss our results in Sect. 4.

2. Basic formalism

The full formalism described here can be found in Bacon et al. (2006); Schneider & Er (2008). Weak lensing shear and flexion are conveniently described using a complex notation. We adopt the thin lens approximation, assuming that the lensing mass distribution is projected onto the lens plane. The dimensionless projected mass density can be written as κ(θ) = Σ(θ)/Σcr, where θ is the angular position, Σ(θ) is the projected mass density, and Σcr is the critical surface mass density.

The first-order image distortion by gravitational lensing is described by the shear γ, which transforms a round source into an elliptical image. The higher-order effect, which is called flexion, is described by two parameters. 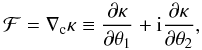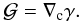The spin-1 flexion is the complex derivative of κℱ=∇cκ≡∂κ∂θ1+i∂κ∂θ2,\begin{equation} {\cal F}= \nabla_{\rm c} \kappa\equiv {\dc \kappa \over \dc\theta_1} + {\rm i}{\dc\kappa \over \dc\theta_2}, \end{equation}(1)and the spin-3 flexion is the complex derivative of γ, 𝒢=∇cγ.\begin{equation} {\cal G}= \nabla_{\rm c} \gamma. \end{equation}(2)

2.1. Radial and tangential flexion

The spin-1 flexion is a vector-like quantity, the gradient of the surface mass density. Therefore, the spin-1 flexion is directed towards the center of the lens in the case of an axi-symmetric mass distribution. However, if the lens deviates from axial symmetry, e.g., due to elliptical halos or mass substructure (Bacon et al. 2010; Hawken & Bridle 2009), the flexion vector will have a different direction.

In galaxy-galaxy lensing, shear can be decomposed into tangential and cross components. Analogously, we decompose the spin-1 flexion into a radial and tangential flexion component. They are defined as ℱR≡ℱT≡\begin{eqnarray} {\cal F}_{\rm R} &\equiv& - \vc{\cal F} \cdot \hat{\vec{r}}; \label{eq:rflexion}\\ {\cal F}_{\rm T} &\equiv& - \vc{\cal F} \cdot \hat{\vec{\phi}}, \label{eq:tflexion} \end{eqnarray}where the spin-1 flexion vector is given by ℱ = (ℱ1,ℱ2) = ∇κ in Cartesian coordinates. 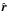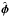rˆ\hbox{$\hat{\vec{r}}$} and φˆ\hbox{$\hat{\vec{\phi}}$} are the unit direction vectors in polar coordinates. For the spin-3 flexion, there is no such a clear intuitive picture of its two components; thus, we only consider the spin-1 flexion in this paper.

As mentioned before, the spin-1 flexion vector is not directed towards the center of an elliptical lens (Fig.1). Therefore, the tangential flexion no longer vanishes and can be used to estimate the ellipticity of the mass distribution.

thumbnail Fig. 1

Spin-1 flexion vector field for an elliptical isothermal density distribution with ϵ = 0.3. ℱ only points towards the center when the background galaxy is located on the major or minor axis of the halo. Note that the length of the vectors are logarithmically scaled, for better visibility.

2.2. Elliptical mass distributions

We now assume that the isodensity contours of the mass distribution are ellipses with ellipticity ϵ, or equivalently, axis ratio (1 − ϵ)/(1 + ϵ), and orientation φ0 of the major axis. In this case, the surface mass density can be written as 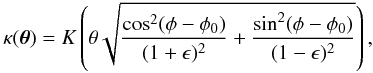κ(θ)=K(θcos2(φ−φ0)(1+ϵ)2+sin2(φ−φ0)(1−ϵ)2),\begin{equation} \kappa(\vc\theta)=K\rund{\theta\sqrt{{\cos^2(\phi-\phi_0)\over (1+\eps)^2} +{\sin^2(\phi-\phi_0)\over (1-\eps)^2}}}, \label{eq:kapp} \end{equation}(5)where the function K(ρ) describes the radial density profile. 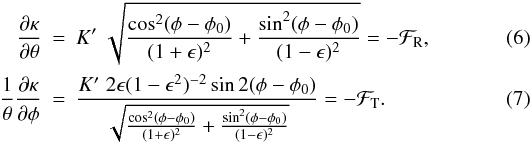The derivatives of κ with respect to radial and azimuthal coordinates are given as ∂κ∂θ=K′cos2(φ−φ0)(1+ϵ)2+sin2(φ−φ0)(1−ϵ)2=−ℱR,1θ∂κ∂φ=K′2ϵ(1−ϵ2)-2sin2(φ−φ0)cos2(φ−φ0)(1+ϵ)2+sin2(φ−φ0)(1−ϵ)2=−ℱT.\begin{eqnarray} {\partial\kappa\over\partial\theta}&=&K'\;\sqrt{{\cos^2(\phi-\phi_0)\over (1+\eps)^2} +{\sin^2(\phi-\phi_0)\over (1-\eps)^2}}=-{\cal F}_{\rm R}, \\ {1\over\theta}{\partial\kappa\over\partial \phi}&=& {K'\;2\eps(1-\eps^2)^{-2}\sin2(\phi-\phi_0)\over \sqrt{{\cos^2(\phi-\phi_0)\over (1+\eps)^2} +{\sin^2(\phi-\phi_0)\over (1-\eps)^2}}}=-{\cal F}_{\rm T}. \end{eqnarray}Both of these derivates have the same radial profile, given by K′. 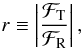We now define the flexion ratio as r≡|ℱTℱR|,\begin{equation} r\equiv \abs{{\cal F}_{\rm T} \over {\cal F}_{\rm R}}, \label{eq:fratio} \end{equation}(8)which is the tangent of the angle between the direction to the mass center and the direction of the flexion vector. 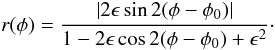For an elliptical mass distribution, this becomes r(φ)=|2ϵsin2(φ−φ0)|1−2ϵcos2(φ−φ0)+ϵ2·\begin{equation} r(\phi)={|2 \epsilon \sin 2(\phi-\phi_0)| \over 1-2\epsilon\cos2(\phi-\phi_0) +\epsilon^2}\cdot \label{eq:ratio-phi} \end{equation}(9)Thus, the flexion ratio r(φ) depends only on the ellipticity ϵ and the orientation φ0 of the mass distribution, not on its radial profile. In particular, it is independent of the lens strength, and thus of the source and lens redshift. In principle, from the measurement of the flexion ratio at two polar positions φ, one can determine both ϵ and φ0, though due to noise, this determination will have large uncertainty. 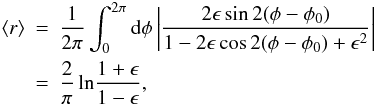Alternatively, one can consider the flexion ratio averaged over all polar angles, ⟨r⟩=12π∫02πdφ|2ϵsin2(φ−φ0)1−2ϵcos2(φ−φ0)+ϵ2|=\begin{eqnarray} \langle r\rangle &=& {1\over 2\pi} \int_0^{2\pi} \d \phi \abs{\frac{2\epsilon\sin 2(\phi-\phi_0)}{1- 2\epsilon \cos 2(\phi-\phi_0) +\epsilon^2}} \nonumber\\ &=&{2\over \pi}\, {\rm ln}{1+ \epsilon \over 1-\epsilon}, \label{eq:rmean} \end{eqnarray}(10)which depends solely on the ellipticity ϵ. Due to its simplicity, this mean flexion ratio can be easily measured from a flexion field in a given aperture.

However, we have to assume to know the center of the lens for calculating the two flexion components. For a galaxy, the center is assumed to be the bright center of galaxy. For clusters, the location of the BCG not necessarily coincides with the mass center. Moreover, ‘intrinsic flexion’ also introduces extra noise (see below).

For a given value of ϵ, the flexion ratio is bounded. One can see from (9) that 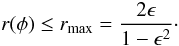r(φ)≤rmax=2ϵ1−ϵ2·\begin{equation} r(\phi) \leq r_{\rm max} = {2\epsilon \over 1-\epsilon^2} \cdot \label{eq:rlimit} \end{equation}(11)Arbitrary large ellipticities, which would allow r to become very large, are implausible and most likely do not exist. We can take limits on ϵ from other observations, e.g., Parker et al. (2007) compared galaxy-galaxy lensing along the major and minor axes, and found that the axis ratio b/a of galaxy halos lies between 0.5 and 0.8 (ϵ ∈  [0.11,0.33]). Moreover, Oguri et al. (2010) analyzed 25 clusters and found  ⟨ 1 − b/a ⟩  = 0.46, corresponding to ϵ = 0.32. Here we use the conservative assumption that ϵ < 0.8, putting an upper bound to the flexion ratio of r < 4.5. We will employ this limit to remove excessively large flexion ratios which are due to noise.

3. Numerical test with NIE toy model

In this section we describe some simulations which we have performed in order to test the behavior of the estimator given in the previous section. For this, we model the surface mass density profile by a non-singular isothermal elliptical profile (NIE), described by 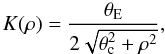K(ρ)=θE2θc2+ρ2,\begin{equation} K(\rho)={\theta_{\rm E}\over2\sqrt{\theta_{\rm c}^2+\rho^2}}, \end{equation}(12)where θE is the Einstein radius, describing the strength of the lens, and θc is the core radius; for θc = 0, this specializes to the singular isothermal elliptical profile (SIE). In our simulations, we take θE = 6′′ and θc = 2′′. Galaxies are randomly distributed within an 1′ × 1′ ‘source plane’ behind the lens. Resulting images are discarded if they are located closer to the halo center than 6′′ (the strong lensing regime) or at distances  |θ|  > 30′′, where the flexion signal will be very small. Moreover, very large flexions cannot be measured (Schneider & Er 2008), thus images with  |ℱ|  > 0.5 are discarded as well.

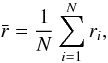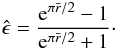The flexion ratio is calculated according to Eq. (8) for each point. A mean flexion ratio is obtained by r̅=1N∑i=1Nri,\begin{equation} \bar r= {1\over N} \sum_{i=1}^N r_i, \label{eq:ratiomean} \end{equation}(13)where N is the number of images for each realization. Then the mass ellipticity is estimated, according to Eq. (10), as ϵ̂=eπr̅/2−1eπr̅/2+1·\begin{equation} \hat \epsilon= \dfrac{{\rm e}^{\pi \bar r /2}-1}{{\rm e}^{\pi \bar r /2}+1} \cdot \label{eq:estimator} \end{equation}(14)

3.1. Noise-free case

Due to the non-linearity, the estimator (14) is expected to be biased. In order to test this, we generated mock data sets with different ϵ = 0.03i, i = 1,2,...20. For each ellipticity, we used 20 realizations, with a density of flexion points of 80   arcmin-2. The filtering described above leads to 63 flexion data for each realization on average.

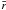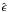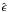For each realization, we calculated \hbox{$\bar r$} from Eq. (13) and estimate ϵ using Eq. (14). In Fig.2, we show \hbox{$\hat\epsilon$} vs. the input value of ϵ. The solid line shows the identity, the plus points are the estimates from the 20 realizations. In fact, the estimates \hbox{$\hat\epsilon$} closely trace the input value. The variance between different realizations becomes larger with increasing ϵ. 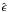The mean over the 20 realizations is shown by the plus points in Fig.3, showing that \hbox{$\hat\epsilon$} very slightly underestimates the input value.

thumbnail Fig. 2

Comparison of the ellipticity estimator (14) with the input ellipticity (solid line). The estimated ellipticity for 20 realizations each for 20 input values of ϵ are shown by pluses, for NIE models with θc = 2′′.

thumbnail Fig. 3

Top panel: comparison of the input ellipticity (solid line) and the estimate (similar as Fig. 2). The plus points show the average estimate for 20 realizations without noise. The other are the result from data with intrinsic noise. All the result are calculated from Eq. (14). The stars are calculated when flexion ratios higher than the upper limit (Eq. (11)) are excluded. Bottom panel: fractional error  |δϵ/ϵ|  of our estimate for the respective cases.

3.2. Intrinsic flexion

Our main source of noise is intrinsic flexion, meaning that the sources can have non-vanishing third-order brightness moments. Depending on the method of flexion measurement, the intrinsic noise may be different (Goldberg & Leonard 2007). Since flexion has the dimension of an inverse length, the intrinsic flexion is also inversely proportional to the image size. Therefore, the distribution of intrinsic flexion depends on the survey and is difficult to obtain from real measurements on current data. Effects of a point spread function (PSF) need to be considered, which is far more difficult for flexion than for shear measurements. In particular, an anisotropic PSF may affect the direction of the flexion vector.

We use a simple model to generate intrinsic noise for our simulated data, by setting ℱobs = ℱ1 + nf1 + i(ℱ2 + nf2). The components of the intrinsic flexion nf1,nf2 are drawn from a Gaussian distribution, with each component being characterized by σℱ1 = σℱ2 = 0.03 arcsec-1. This is slightly larger than the intrinsic scatter found by (Goldberg & Leonard 2007), σa |ℱ|  = 0.03. On the other hand, (Okura et al. 2008) found a larger scatter in their measurement, σℱ = 0.11 arcsec-1. This is however obtained from a massive galaxy cluster, thus may not be suitable for our galaxy-galaxy lensing flexion.

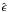In Fig.3 we compare the estimates \hbox{$\hat\epsilon$} with the input values (solid line). The plus points show the mean over 20 realizations without noise (Fig.2), and the dashed line displays estimates with intrinsic noise included. Not surprisingly, our estimates from noisy simulations are larger than the input values (intrinsic noise will cause the estimate to deviate from zero even for a perfectly symmetric mass distribution). This is particularly significant for small ϵ. As an additional test, we reject flexion data which have r > 4.5, and perform our estimate again. The mean result is shown by crosses in Fig.3. 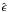One can see that the bias is slightly reduced in this case, in particular for larger ϵ, but still \hbox{$\hat\epsilon$} overestimates the true ellipticity. The amplitude of this bias depends of course on the intrinsic flexion distribution. In Fig.4, we show our estimate as a histogram of 20 noisy realizations for a halo with ϵ = 0.57. The dashed histogram corresponds to rejecting the flexion data with r > 4.5. One can see that the number of overestimates is reduced.

thumbnail Fig. 4

Histogram of the estimated ellipticity for a halo with ϵ = 0.57 from 20 realizations. The solid line is obtained from noise data, the dashed line is the result after excluding the high flexion ratio points.

Another way to estimate the ellipticity of the mass distribution is to fit the flexion ratio with the model (9), with the two free parameters ϵ and φ0. The result for two realizations is presented in Fig.6. The points are calculated from simulated data of an NIE with ϵ = 0.3 (left) and ϵ = 0.6 (right). The dotted lines are the fitting result with Eq. (9) whereas the solid curves show Eq. (9) with the input ellipticity. The fits almost perfectly agree with the input model. 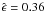For the left panel, the fitting yields ϵ = 0.31 and φ0 = 0.1, whereas \hbox{$\hat\epsilon=0.36$}. 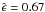In the right panel, ϵ = 0.62 and φ0 = 0.006 from fitting, whereas \hbox{$\hat\epsilon=0.67$}. 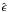In both panels of Fig.6, there are several points with significant deviations from the fitting curves which is the reason for \hbox{$\hat\epsilon$} to be larger than the input value, whereas these points do not strongly affect the fitting result.

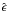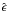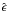Obviously, the fitting method yields a more accurate estimate of the mass ellipticity than the estimator \hbox{$\hat\eps$}, and at the same time also estimates the orientation. It is therefore the preferred method for individual lenses. In contrast, the estimator \hbox{$\hat\eps$} can be applied also to an ensemble of lenses, by superposing their respective flexion values. In this way, \hbox{$\hat\eps$} estimates the weighted mean ellipticity of the ensemble of lenses. Note that in contrast to galaxy-galaxy lensing with the shear method, the individual lenses do not have to be aligned before the averaging; hence, no assumption about the relative orientation of mass and light needs to be made.

thumbnail Fig. 5

Comparison of mean estimator and biweight estimator. The plus point are the result using mean estimate The crosses are the result using biweight center estimate Eq. (15) to calculate  ⟨ r ⟩ .

3.3. Biweight estimator

thumbnail Fig. 6

The flexion ratio r varies with φ. The dashed line is for an SIE halo model. The points are calculated from the simulated data, the dotted line is the fit to the results with Eq. (9). Left is a halo with ϵ = 0.3, and right is ϵ = 0.6.

The assumption that the flexion noise is Gaussian may not be valid, due to the low number density of background galaxies and the flexion measurement. Thus we adopt as an alternative estimator the biweight location estimator, which was studied by Beers et al. 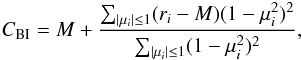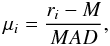(1990) as a possible improvement for non-Gaussian or contaminated normal distributions, CBI=M+∑|μi|≤1(ri−M)(1−μi2)2∑|μi|≤1(1−μi2)2,\begin{equation} C_{\rm BI}=M + {\sum_{|\mu_i|\leq1} (r_i-M)(1-\mu_i^2)^2 \over \sum_{|\mu_i|\leq1}(1-\mu_i^2)^2}, \label{eq:cbi} \end{equation}(15)where M is the sample median and the μi are given by μi=ri−MMAD,\begin{equation} \mu_i={r_i-M \over MAD}, \end{equation}(16)with MAD=median(|ri−M|),\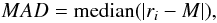begin{equation} MAD= {\rm median} (|r_i-M|), \end{equation}(17)where ri is the flexion ratio of each galaxy image. We perform an additional test for the mean and CBI estimator. 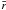In Fig.5, the plus points are the result when we use \hbox{$\bar r$} to calculate  ⟨ r ⟩ , the cross points are the result from using CBI. One can see that the bias is reduced significantly. Moreover, the bias reduction of CBI is independent of halo ellipticity.

3.4. Centroid offset test

Since the ellipticity represents the deviation from symmetry of a mass distribution, a centroid offset will affect the determination of the ellipticity, leading to an additional bias. We simulated this effect, by calculating the radial and tangential flexion components with respect to θ0 + δθ, where θ0 is the true center of the lens, and δθ is the offset. For simplicity, we choose two sets of δθ, one along the major axis, the other along the minor axis of the mass distribution. To isolate this effect, we generate 400 data sets without intrinsic noise, for two NIE with ϵ = 0.3,0.6. The results are shown in Fig.7. A centroid offset indeed biases the estimate of the ellipticity, but the magnitude of this effect is relatively small, as long as the offset is considerably smaller than the Einstein radius of the lens. For the lens with higher ellipticity (bottom panel), an offset along the minor axis has a larger impact on the resulting ellipticity than one along the major axis. We conclude that the effect of misidentifying the lens centroid is of little concern for galaxy lenses, but may be more important for galaxy clusters where the centroid is often ill-defined from observations.

thumbnail Fig. 7

Bias due to the centroid offset. The solid line is our estimate (400 sets of data) without centroid offset. The plus (cross) points are estimate for the centroid offset alone the major (minor) axis of the elliptical halo. The top (bottom) panel is for galaxy halo with ellipticity 0.3 (0.6).

4. Conclusions and outlook

In this paper, we have studied galaxy-galaxy flexion with elliptical mass distributions. We derived the ratio r of radial and tangential flexion and found that it is independent of the radial mass profile of the lens, and of the source and lens redshift. The flexion ratio depends solely on the ellipticity and orientation of the mass distribution. We defined an estimator 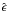\hbox{$\hat\eps$} for the ellipticity in terms of the flexion ratio, and tested its performance with simple simulations. This estimator does not rely on knowing the orientation of the distribution, i.e., assuming that it follows the orientation of the light; hence, it can be used to statistically superpose several lenses and thereby obtain their average ellipticity. The independence of this estimator from an assumed orientation is quite different from methods to constrain lens ellipticities from shear (Brainerd & Wright 2000; Hoekstra et al. 2004), for which the orientation needs to be known. In the appendix we show that an analogous method to that presented here does not work for shear, but is unique to the spin-1 nature of the first flexion.

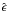For an individual lens with several flexion measurements, the ellipticity and orientation can be derived by fitting the measured flexion ratios with these two parameters. The accuracy of the resulting estimate is substantially better than that of \hbox{$\hat\eps$}.

Our simulations showed that 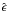\hbox{$\hat\eps$} is biased. A first bias is due to the non-linearity of the relation between estimated ellipticity and mean flexion ratio. The size of this bias depends on the number density of sources for which flexion can be measured, and disappears in the limit of very high source density (or large number of lenses for which the mean ellipticity is explored). Intrinsic flexion causes a more significant bias, in particular for small values of ϵ. A misidentification of the mass centroid is another source of bias; however, if the centroid offset is much smaller than the Einstein radius of the lens, this bias is rather small.

There will be several complications in a real analysis. First, the flexion ℱ can not be directly measured, but only reduced flexion (Schneider & Er 2008). This only requires a small modification, though: if κ is constant on ellipses, so will be ln(1 − κ). Since 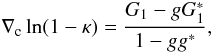∇cln(1−κ)=G1−gG1∗1−gg∗,\begin{equation} \nabla_{\rm c}\ln (1-\kappa)={G_1-g G_1^*\over 1-g g^*}, \label{eq:redflex} \end{equation}(18)where G1 is the spin-1 reduced flexion, 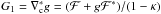G1=∇c∗g=(ℱ+gℱ∗)/(1−κ)\hbox{$G_1=\nabla^*_{\rm c} g=({\cal F}+g {\cal F}^*)/(1-\kappa)$}, and g = γ/(1 − κ) the reduced shear, we can use the phase of (18) instead of the flexion ratio. Furthermore, the impact of intrinsic flexion is uncertain, reflecting our lack of knowledge about its magnitude which is ill-determined from current observations. A further careful study of intrinsic flexion will be of interest before the flexion method is applied to real data.

In addition, as we have shown, a low number density of background sources also introduce bias. Thus a deep survey with more background sources is clearly favoured. Current surveys such as the Hubble Space Telescope (HST), the Canada-France-Hawaii Telescope Legacy Survey (CFHTLS) or Subaru telescope might be able to constrain halo ellipticity using flexion, if the flexion can be measured with sufficient accuracy. The James Webb Space Telescope will almost certainly allow very accurate measurements of the ellipticity of galaxy- and group-sized lenses.

Acknowledgments

We thank Dave Goldberg, Ismael Tereno and the anonymous referee for very useful comments on the manuscript. This project is supported by the Deutsche Forschungsgemeinschaft under the project SCHN 342/7.

References

  1. Allgood, B., Flores, R. A., Primack, J. R., et al. 2006, MNRAS, 367, 1781 [NASA ADS] [CrossRef] [Google Scholar]
  2. Bacon, D. J., Goldberg, D. M., Rowe, B. T. P., & Taylor, A. N. 2006, MNRAS, 365, 414 [NASA ADS] [CrossRef] [Google Scholar]
  3. Bacon, D. J., Amara, A., & Read, J. I. 2010, MNRAS, 1249 [Google Scholar]
  4. Bartelmann, M., & Schneider, P. 2001, Phys. Rep., 340, 291 [NASA ADS] [CrossRef] [Google Scholar]
  5. Beers, T. C., Flynn, K., & Gebhardt, K. 1990, AJ, 100, 32 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bett, P., Eke, V., Frenk, C. S., Jenkins, A., & Okamoto, T. 2010, MNRAS, 404, 1137 [NASA ADS] [Google Scholar]
  7. Bradač, M., Allen, S. W., Treu, T., et al. 2008, ApJ, 687, 959 [NASA ADS] [CrossRef] [Google Scholar]
  8. Brainerd, T. G., & Wright, C. O. 2000, unpublished [arXiv:astro-ph/0006281] [Google Scholar]
  9. Clowe, D., Bradač, M., Gonzalez, A. H., et al. 2006, ApJ, 648, L109 [NASA ADS] [CrossRef] [Google Scholar]
  10. Corless, V. L., King, L. J., & Clowe, D. 2009, MNRAS, 393, 1235 [NASA ADS] [CrossRef] [Google Scholar]
  11. Deb, S., Goldberg, D. M., Heymans, C., & Morandi, A. 2010, ApJ, 721, 124 [NASA ADS] [CrossRef] [Google Scholar]
  12. Debattista, V. P., Moore, B., Quinn, T., et al. 2008, ApJ, 681, 1076 [NASA ADS] [CrossRef] [Google Scholar]
  13. Er, X., Li, G., & Schneider, P. 2011, A&A, submitted [arXiv:1008.3088] [Google Scholar]
  14. Evans, A. K. D., & Bridle, S. 2009, ApJ, 695, 1446 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Goldberg, D. M., & Bacon, D. J. 2005, ApJ, 619, 741 [NASA ADS] [CrossRef] [Google Scholar]
  16. Goldberg, D. M., & Leonard, A. 2007, ApJ, 660, 1003 [NASA ADS] [CrossRef] [Google Scholar]
  17. Goldberg, D. M., & Natarajan, P. 2002, ApJ, 564, 65 [NASA ADS] [CrossRef] [Google Scholar]
  18. Hawken, A. J., & Bridle, S. L. 2009, MNRAS, 400, 1132 [NASA ADS] [CrossRef] [Google Scholar]
  19. Hoekstra, H., Yee, H. K. C., & Gladders, M. D. 2004, ApJ, 606, 67 [NASA ADS] [CrossRef] [Google Scholar]
  20. Howell, P. J., & Brainerd, T. G. 2010, MNRAS, 941 [Google Scholar]
  21. Irwin, J., & Shmakova, M. 2006, ApJ, 645, 17 [NASA ADS] [CrossRef] [Google Scholar]
  22. Jing, Y. P., & Suto, Y. 2002, ApJ, 574, 538 [NASA ADS] [CrossRef] [Google Scholar]
  23. Kormann, R., Schneider, P., & Bartelmann, M. 1994, A&A, 284, 285 [NASA ADS] [Google Scholar]
  24. Kuhlen, M., Diemand, J., & Madau, P. 2007, ApJ, 671, 1135 [NASA ADS] [CrossRef] [Google Scholar]
  25. Law, D. R., Majewski, S. R., & Johnston, K. V. 2009, ApJ, 703, L67 [NASA ADS] [CrossRef] [Google Scholar]
  26. Leonard, A., Goldberg, D. M., Haaga, J. L., & Massey, R. 2007, ApJ, 666, 51 [NASA ADS] [CrossRef] [Google Scholar]
  27. Mandelbaum, R., Hirata, C. M., Broderick, T., Seljak, U., & Brinkmann, J. 2006, MNRAS, 370, 1008 [NASA ADS] [CrossRef] [Google Scholar]
  28. Massey, R., Rowe, B., Refregier, A., Bacon, D. J., & Bergé, J. 2007, MNRAS, 380, 229 [NASA ADS] [CrossRef] [Google Scholar]
  29. Munshi, D., Valageas, P., van Waerbeke, L., & Heavens, A. 2008, Phys. Rep., 462, 67 [NASA ADS] [CrossRef] [Google Scholar]
  30. Natarajan, P., & Refregier, A. 2000, ApJ, 538, L113 [NASA ADS] [CrossRef] [Google Scholar]
  31. Navarro, J. F., Frenk, C. S., & White, S. D. M. 1996, ApJ, 462, 563 [NASA ADS] [CrossRef] [Google Scholar]
  32. Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [NASA ADS] [CrossRef] [Google Scholar]
  33. Oguri, M., Takada, M., Okabe, N., & Smith, G. P. 2010, MNRAS, 405, 2215 [NASA ADS] [Google Scholar]
  34. Okura, Y., Umetsu, K., & Futamase, T. 2007, ApJ, 660, 995 [NASA ADS] [CrossRef] [Google Scholar]
  35. Okura, Y., Umetsu, K., & Futamase, T. 2008, ApJ, 680, 1 [NASA ADS] [CrossRef] [Google Scholar]
  36. Parker, L. C., Hoekstra, H., Hudson, M. J., van Waerbeke, L., & Mellier, Y. 2007, ApJ, 669, 21 [Google Scholar]
  37. Refregier, A. 2003, ARA&A, 41, 645 [NASA ADS] [CrossRef] [Google Scholar]
  38. Schneider, P., & Er, X. 2008, A&A, 485, 363 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Schneider, P., Kochanek, C. S., & Wambsganss, J. 2006, Gravitational Lensing: Strong, Weak and Micro, ed. P. Schneider, C. S. Kochanek, & J. Wambsganss [Google Scholar]
  40. Suyu, S. H., & Halkola, A. 2010, A&A, 524, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

Appendix A: The shear profile in SIE halo

In this appendix, we present the tangential and cross shear profile for an SIE halo model and show that one cannot apply the ratio of cross to tangential shear to estimate the ellipticity of the lens.

To calculate the shear, we calculate the deflection potential using the Poisson equation 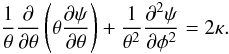1θ∂∂θ(θ∂ψ∂θ)+1θ2∂2ψ∂φ2=2κ.\appendix \setcounter{section}{1} \begin{equation} {1\over \theta}{\dc\over\dc \theta}\rund{\theta {\dc \psi\over \dc \theta}} +{1\over \theta^2}{\dc^2\psi \over\dc \phi^2}=2\kappa. 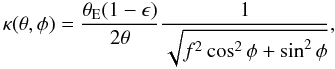\end{equation}(A.1)The convergence can be written in polar coordinates κ(θ,φ)=θE(1−ϵ)2θ1f2cos2φ+sin2φ,\appendix \setcounter{section}{1} \begin{equation} \kappa(\theta,\phi)={\theta_{\rm E}(1-\epsilon)\over 2\theta} \dfrac{1} {\sqrt{f^2\cos^2\phi +\sin^2\phi}}, \label{eq:siepolar} \end{equation}(A.2)where f is the axs ratio. The solution of the Poisson equation can be found in Kormann et al. 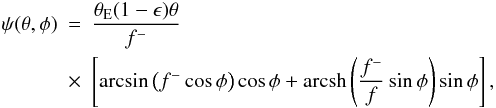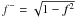(1994), but here we write it in our notation as ψ(θ,φ)=θE(1−ϵ)θf−×[arcsin(f−cosφ)cosφ+arcsh(f−fsinφ)sinφ],\appendix \setcounter{section}{1} \begin{eqnarray} \psi(\theta,\phi) &=& \dfrac{\theta_{\rm E}(1-\epsilon) \theta}{f^-}\\ &\times& \eck{\arcsin \rund{f^-\cos \phi} \cos\phi +{\rm arcsh}\rund{{f^-\over f} \sin\phi}\sin\phi},\nonumber \end{eqnarray}(A.3)where f−=1−f2\appendix \setcounter{section}{1} \hbox{$f^-=\sqrt{1-f^2}$}. Then we rewrite the potential in Cartesian coordinates and calculate the shear by γ1 = (ψ,11 − ψ,22)/2 and γ1 = ψ,12. 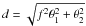We thus obtain the two shear component for the SIE halo, γ1=−θE(1−ϵ)(θ12−θ22)2θ2d;γ2=−θE(1−ϵ)θ1θ2θ2d,\appendix \setcounter{section}{1} \begin{eqnarray} \gamma_1 &=&-\dfrac{\theta_{\rm E} (1-\epsilon)(\theta_1^2-\theta_2^2)} {2\theta^2 d}; \\[5mm] \gamma_2 &=&-\dfrac{ \theta_{\rm E} (1-\epsilon) \theta_1\theta_2} {\theta^2 d}, \end{eqnarray}where d=f2θ12+θ22\appendix \setcounter{section}{1} \hbox{$d=\sqrt{f^2\theta_1^2 +\theta_2^2}$}. According to the definition γt =  −γ1cos2φ − γ2sin2φ, γ ×  = γ1sin2φ − γ2cos2φ, the tangential-to-cross shear for SIE halo reads γt=θE(1−ϵ)2d;γ×=0.\appendix \setcounter{section}{1} \begin{eqnarray} \gamma_{\rm t} &=& {\theta_{\rm E}(1-\epsilon) \over 2 d};\\[5mm] \gamma_{\times} &=& 0. \end{eqnarray}

All Figures

thumbnail Fig. 1

Spin-1 flexion vector field for an elliptical isothermal density distribution with ϵ = 0.3. ℱ only points towards the center when the background galaxy is located on the major or minor axis of the halo. Note that the length of the vectors are logarithmically scaled, for better visibility.
In the text
thumbnail Fig. 2

Comparison of the ellipticity estimator (14) with the input ellipticity (solid line). The estimated ellipticity for 20 realizations each for 20 input values of ϵ are shown by pluses, for NIE models with θc = 2′′.
In the text
thumbnail Fig. 3

Top panel: comparison of the input ellipticity (solid line) and the estimate (similar as Fig. 2). The plus points show the average estimate for 20 realizations without noise. The other are the result from data with intrinsic noise. All the result are calculated from Eq. (14). The stars are calculated when flexion ratios higher than the upper limit (Eq. (11)) are excluded. Bottom panel: fractional error  |δϵ/ϵ|  of our estimate for the respective cases.
In the text
thumbnail Fig. 4

Histogram of the estimated ellipticity for a halo with ϵ = 0.57 from 20 realizations. The solid line is obtained from noise data, the dashed line is the result after excluding the high flexion ratio points.

In the text
thumbnail Fig. 5

Comparison of mean estimator and biweight estimator. The plus point are the result using mean estimate The crosses are the result using biweight center estimate Eq. (15) to calculate  ⟨ r ⟩ .
In the text
thumbnail Fig. 6

The flexion ratio r varies with φ. The dashed line is for an SIE halo model. The points are calculated from the simulated data, the dotted line is the fit to the results with Eq. (9). Left is a halo with ϵ = 0.3, and right is ϵ = 0.6.
In the text
thumbnail Fig. 7

Bias due to the centroid offset. The solid line is our estimate (400 sets of data) without centroid offset. The plus (cross) points are estimate for the centroid offset alone the major (minor) axis of the elliptical halo. The top (bottom) panel is for galaxy halo with ellipticity 0.3 (0.6).

In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.