| Issue |
A&A
Volume 528, April 2011
|
|
|---|---|---|
| Article Number | A6 | |
| Number of page(s) | 15 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201015631 | |
| Published online | 16 February 2011 | |
Convective quenching of stellar pulsations
Laboratoire d’Astrophysique de Toulouse-Tarbes, Université de Toulouse,
CNRS,
14 avenue Edouard Belin,
31400
Toulouse,
France
e-mail: thomas.gastine@ast.obs-mip.fr
Received:
24
August
2010
Accepted:
17
December
2010
Context. We study the convection-pulsation coupling that occurs in cold Cepheids close to the red edge of the classical instability strip. In these stars, the surface convective zone is supposed to stabilise the radial oscillations excited by the κ-mechanism.
Aims. We study the influence of the convective motions on the amplitude and the nonlinear saturation of acoustic modes excited by κ-mechanism. We are interested in determining the physical conditions needed to lead to a quenching of oscillations by convection.
Methods. We compute two-dimensional nonlinear simulations (DNS) of the convection-pulsation coupling, in which the oscillations are sustained by a continuous physical process: the κ-mechanism. Thanks to both a frequential analysis and a projection of the physical fields onto an acoustic subspace, we study how the convective motions affect the unstable radial oscillations.
Results. Depending on the initial physical conditions, two main behaviours are obtained. (i) Either the unstable fundamental acoustic mode has a large amplitude, carries the bulk of the kinetic energy, and shows a nonlinear saturation similar to the purely radiative case; (ii) or the convective motions significantly affect the mode amplitude, which remains very weak. In this second case, convection is quenching the acoustic oscillations. We interpret these discrepancies in terms of the difference in density contrast: larger stratification leads to smaller convective plumes that do not affect the purely radial modes much, while large-scale vortices may quench the oscillations.
Key words: hydrodynamics / convection / instabilities / stars: oscillations / methods: numerical / stars: variables: Cepheids
© ESO, 2011
1. Introduction
The cold Cepheids located near the red edge of the classical instability strip have a large surface convective zone that affects their pulsation properties (e.g. the reviews of Gautschy & Saio 1996; Buchler 2009). The first calculations, done without any convection-pulsation modelling, predicted much cooler red edges than the observed ones. In fact, predicting the red edge location requires a non-adiabatic treatment of this coupling as already stated by Baker & Kippenhahn (1965).
Several time-dependent convection (TDC) models were introduced then to address this coupling (Unno 1967; Gough 1977; Stellingwerf 1982; Kuhfuß 1986; Xiong 1989). More recently, these different models have been largely improved by succeeding in reproducing the correct location of the red edge, despite their disagreements with the physical origin of the mode stabilisation (e.g. Bono et al. 1999; Wuchterl & Feuchtinger 1998; Yecko et al. 1998; Grigahcène et al. 2005; Dupret et al. 2005).
However, these models rely on many free parameters (e.g. the seven dimensionless α coefficients used by Yecko et al. 1998) that are either fitted to the observations or hardly constrained by theoretical values such that they give almost identical results for different parameters sets (see also Kolláth et al. 2002). Despite their own limitations (weak density or pressure contrasts, for instance), 2-D and 3-D direct numerical simulations (DNS) are a good way to investigate the convection-pulsation coupling as the essential nonlinearities are fully taken into account. The purpose of this paper is to present the results of 2-D DNS of the convection-pulsation coupling in which the acoustic oscillations are sustained in a self-consistent way by the κ-mechanism that is responsible for the radial oscillations of Cepheids (Muthsam et al. 2010).
In Gastine & Dintrans (2008a) and Gastine & Dintrans (2008b) (hereafter Papers I
and II), we modelled the κ-mechanism in Cepheids by a simplified approach,
that is, the propagation of acoustic waves in a layer of perfect gas in which the ionisation
region is shaped by a hollow in the radiative conductivity profile. We recall that the
instability of Cepheid variables relies on blocking the emerging radiative flux near the
opacity bumps that are due to the ionisation of light elements like H or He. As the
radiative conductivity is proportional to the inverse of opacity, a conductivity hollow
therefore mimics such an opacity bump. By performing the linear stability of this simplified
model, we precisely determined the physical conditions that are required to obtain unstable
radial modes excited by κ-mechanism in Paper I: (i) the conductivity hollow
must be sufficiently deep; (ii) this hollow must also be located in a precise zone inside
the star, called “the transition region” (Zhevakin
1963; Cox 1980), which defines the limit
where the acoustic mode period Π is close to the local thermal timescale
τtherm as 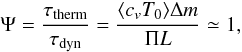 (1)where the
⟨ cvT0 ⟩ Δm
term denotes the amount of internal energy embedded above the ionisation
region and L is the star luminosity (the ratio between the two defining the
thermal time needed for radiating this internal energy towards the surface).
(1)where the
⟨ cvT0 ⟩ Δm
term denotes the amount of internal energy embedded above the ionisation
region and L is the star luminosity (the ratio between the two defining the
thermal time needed for radiating this internal energy towards the surface).
By starting from the most linearly-unstable setups, we performed in Paper II the corresponding nonlinear study by means of direct numerical simulations. Thanks to a powerful method that involves several projections of the computed fields onto suitable subspaces (e.g. Bogdan et al. 1993), both the amplitude and energy of each acoustic mode oscillating in the simulation have been extracted. Their temporal evolutions have then emphasised the strong nonlinear coupling existing between the (unstable) fundamental acoustic mode and the (stable) second overtone. This preferential coupling relies on a 2:1 resonance as the fundamental period is twice the second overtone one (e.g. Simon & Schmidt 1976; Klapp et al. 1985; Buchler & Kovacs 1986). It participates in the nonlinear saturation of the system and is also responsible for the well-known “Hertzsprung progression” observed in the luminosity curves of bump Cepheids (see Paper II for more details).
Following these first two papers devoted to the purely radiative case, we next address here the possible influence of convection onto the acoustic oscillations excited by κ-mechanism. We have first slightly modified the initial physical setup to get a convective zone that overlaps with the hollow in radiative conductivity. We then computed the corresponding 2-D nonlinear simulations and showed that a coupling between the convective motions and pulsations can indeed occur (Sect. 2). Thanks to a frequential analysis (Sect. 3), we next emphasised the qualitative discrepancies between two specific simulations that strongly differ from the role played by convection: in one simulation, the fundamental acoustic mode excited by κ-mechanism seems to not be influenced by the underlying convective motions, while in the other simulation, convection almost cancels it.
To measure the acoustic oscillations in more details in these simulations, we next applied a projection method similar to the one used previously in the purely radiative case. That is, we determined the contribution of acoustic oscillations and convective motions to the energy budget (Sect. 4). The obtained results again show two opposite behaviours: (i) either the amplitude of the linearly-unstable acoustic mode is large and the nonlinear saturation seems similar to what was observed in radiative simulations; (ii) or the amplitude of pulsations remains very weak and strongly modulated, while the bulk of kinetic energy lies in convective motions. In this second case, the convective plumes are quenching the oscillations in a similar way to what is expected to occur close to the red edge of the Cepheid instability strip.
The last part of this study focuses on the physical conditions suitable for quenching the oscillations by convective motions (Sect. 5). We investigate the role of both the convective flux and the density stratification onto the mode amplitude and show that a key parameter for the mode stabilisation could be the density contrast across the whole layer. Indeed, this stratification has an impact on the typical size of the convective plumes, as a weak (strong) stratification leads to large (small) vortices. A clear correlation between the integral scale of convection and the kinetic energy contained in acoustic modes is found, which suggests a screening-like effect of the mode pattern by convective plumes. We finally conclude in Sect. 6 by discussing some interesting outlooks of this work in the direction of time-dependent convection theories.
2. The model
2.1. The convective setup
Our system represents a local zoom around an ionisation region. It is composed of a 2-D
layer
(Lx × Lz)
filled with a monatomic and perfect gas with
γ = cp/cv = 5/3
and
R∗ = cp − cv
the ideal gas constant (cp and
cv being the specific heats). As we are
dealing with local simulations, the vertical gravity
g = −gez
and the kinematic viscosity ν are assumed to be constant. Following
Papers I and II, the ionisation region is represented by a temperature-dependent radiative
conductivity profile that mimics an opacity bump: ![\begin{equation} K(T)=\Kmax\left[1+\Amp\frac{-\pi/2+\arctan(\sigma T^+T^-)}{\pi/2+\arctan(\sigma e^2)}\right], \label{eq:conductivity-profile1} \end{equation}](/articles/aa/full_html/2011/04/aa15631-10/aa15631-10-eq16.png) (2)with
(2)with 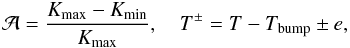 (3)where
Tbump is the position of the hollow in temperature and
σ, e, and
(3)where
Tbump is the position of the hollow in temperature and
σ, e, and 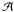 denote its slope, width, and relative amplitude, respectively. We assume both radiative
and hydrostatic equilibria; that is,
denote its slope, width, and relative amplitude, respectively. We assume both radiative
and hydrostatic equilibria; that is, 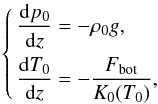 (4)where
Fbot is the imposed bottom flux. Following Papers I and II,
we chose the vertical dimension Lz as the
length scale, i.e.
[x] = Lz, the top
density ρtop and top temperature
Ttop as density and temperature scales, respectively. The
velocity scale is then
(cpTtop)1/2,
while time is given in units of
[t] = Lz/(cpTtop)1/2.
(4)where
Fbot is the imposed bottom flux. Following Papers I and II,
we chose the vertical dimension Lz as the
length scale, i.e.
[x] = Lz, the top
density ρtop and top temperature
Ttop as density and temperature scales, respectively. The
velocity scale is then
(cpTtop)1/2,
while time is given in units of
[t] = Lz/(cpTtop)1/2.
As our aim is to investigate the convection-pulsation coupling, we must ensure that
convection will develop around the conductivity hollow. It means that our model should
satisfy the well-known Schwarzschild’s criterion for the convective instability given by
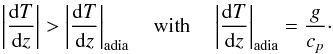 (5)When using Eqs. (4), this defines the following minimum value
for the imposed bottom flux Fbot
(5)When using Eqs. (4), this defines the following minimum value
for the imposed bottom flux Fbot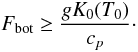 (6)This criterion
thus implies either a decrease in the gravity g or an increase in the
imposed bottom flux Fbot. However, we have shown in Paper I
that one crucial criterion needed to obtain unstable modes excited by
κ-mechanism is that the ratio of a local thermal timescale over the mode
period is approximately
(6)This criterion
thus implies either a decrease in the gravity g or an increase in the
imposed bottom flux Fbot. However, we have shown in Paper I
that one crucial criterion needed to obtain unstable modes excited by
κ-mechanism is that the ratio of a local thermal timescale over the mode
period is approximately 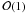 ,
and this is the relation (1) already given
in the Introduction. Because of this timescale criterion, the most favourable setups were
found to require high values in the gravity g to obtain a sufficient
stratification (see Paper I for further details). As a consequence, the only acceptable
way to have a convective zone in our model – while keeping the efficiency of
κ-mechanism – is by not decreasing the gravity g but
rather increasing the bottom flux so as to satisfy Eq. (6).
,
and this is the relation (1) already given
in the Introduction. Because of this timescale criterion, the most favourable setups were
found to require high values in the gravity g to obtain a sufficient
stratification (see Paper I for further details). As a consequence, the only acceptable
way to have a convective zone in our model – while keeping the efficiency of
κ-mechanism – is by not decreasing the gravity g but
rather increasing the bottom flux so as to satisfy Eq. (6).
Figure 1 is a sketch of our convective model. The
need to increase the bottom flux to get a convective zone leads to a numerical difficulty
that was not present in the pure radiative case. Indeed, we can roughly estimate the
typical velocity uconv of a convective element by using a
mixing-length argument of the form 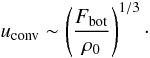 (7)With the typical
values used in the former papers without convection, that is
ρtop ≃ 2.5 × 10-3 and
Fbot ≃ 2 × 10-2, one thus gets
uconv ~ 2 and therefore a Mach number
Ma ≡ u/cs > 1, with
(7)With the typical
values used in the former papers without convection, that is
ρtop ≃ 2.5 × 10-3 and
Fbot ≃ 2 × 10-2, one thus gets
uconv ~ 2 and therefore a Mach number
Ma ≡ u/cs > 1, with
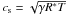 and Ttop = 1. It means that the parameters used in these
radiative setups cannot be generalised to convective simulations as they imply supersonic
flows and shocks.
and Ttop = 1. It means that the parameters used in these
radiative setups cannot be generalised to convective simulations as they imply supersonic
flows and shocks.
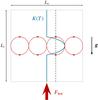 |
Fig. 1 Sketch of our convective model. The blue curve corresponds to the radiative conductivity profile, the dashed line is the Schwarzschild criterion given in Eq. (6), and the large red arrow represents the radiative flux Fbot that is imposed at the bottom. The red rolls correspond to the convective motions that develop in the layer middle. |
To avoid such intricate shocks in the simulation, one should reduce the Mach number of the flow by both increasing the sound speed and decreasing the typical convective velocity. Increasing cs is done by simply doubling the value of the top temperature, that is, Ttop = 2. As Schwarzschild’s criterion (6) imposes a high value for the bottom flux Fbot, we then decrease the convective velocity uconv by increasing the top density to ρtop = 10-2, then a factor 4 compared to the one in the radiative case. We have also doubled the vertical extent of the layer to Lz = 2 to satisfy the timescale criterion (1) while ensuring that the convective zone is deep enough. Finally, concerning the horizontal extent Lx of the layer, the two following constraints remain to be taken into account.
-
1.
If the aspect ratio Lx/Lz is too low, the convective motions are too muchconstrained. Indeed, it is well known that a minimum horizontalwavenumber kx is needed to trigger the convective instability(e.g. Goughet al. 1976). As a consequence,dealing with a low aspect ratio Lx/Lz can lead to a convective pattern thatis too close to the Rayleigh-Bénard one, that is, some largeperiodic rolls along the horizontal direction. To get a small-scaleconvective pattern that is as realistic as possible, one shouldtherefore consider domains with high aspect ratios.
-
2.
Nevertheless, dealing with a large aspect ratio has a strong numerical cost. Indeed, with a sixth-order finite-difference code like the one we are using, the mesh Reynolds number Re = uδx/ν should not be empirically larger than ~5. It means that for a given viscosity ν and spatial resolution, the horizontal extent is limited anyway.
Within these limits, the aspect ratio is kept constant in every simulation discussed in this work, with Lx/Lz = 4 for Lz = 2 (thus Lx = 8).
Concerning the parameters of the conductivity profile, the central temperature
Tbump has been adjusted to satisfy the criterion given in
Eq. (1), which is Ψ = 1 at the location
of the hollow. As in Papers I and II, its relative amplitude
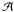 is kept constant with the same value,
is kept constant with the same value, 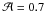 .
At the end, the slope σ and the width e of this profile
are then set up to get profiles that are as similar as possible in the different DNS
computed in this study.
.
At the end, the slope σ and the width e of this profile
are then set up to get profiles that are as similar as possible in the different DNS
computed in this study.
Parameters of the numerical simulations in this work.
Table 1 summarises the properties of the main
numerical simulations performed to study the convection-pulsation coupling. The
penultimate column of this table contains the value of the
frequency ω00 of the fundamental unstable radial mode
excited by κ-mechanism, which lies between 3 and 4 for every DNS computed
in this study. The last column gives the value of the Rayleigh number, which quantifies
the strength of the convective motions. It is given by 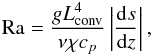 (8)where
Lconv is the width of the convective zone,
χ = K0/ρ0cp
the radiative diffusivity, and s the entropy. Table 1 shows that the Rayleigh numbers of the DNS presented
in this paper are close to 105. This is well above the common critical values
Rac of this number, from which strong convection is known
to develop, e.g. Rac ~ 103 for polytropic
stratifications (Gough et al. 1976).
(8)where
Lconv is the width of the convective zone,
χ = K0/ρ0cp
the radiative diffusivity, and s the entropy. Table 1 shows that the Rayleigh numbers of the DNS presented
in this paper are close to 105. This is well above the common critical values
Rac of this number, from which strong convection is known
to develop, e.g. Rac ~ 103 for polytropic
stratifications (Gough et al. 1976).
2.2. Dimensional values of the physical quantities
The numerical simulations computed in this work are performed in dimensionless units and can thus accommodate a range of physical models. We can nevertheless redimension our units to determine if they are close enough to the realistic values of a typical Cepheid star. We assume that the top of our layer is located under the surface at a temperature of 12 000 K. It thus leads to the temperature scale [T] = 6000 K. For the G8 simulation given in Table 1, we have approximately T ∈ [2.,13.] , meaning that our layer covers a temperature range from 12 000 K to 78 000 K, which encompasses the second Helium ionisation zone. For a 5 M⊙ Cepheid star with parameters close to the ones of δ-Cephei (i.e. R ~ 40 R⊙, L ~ 2000 L⊙ and Teff ≃ 6000 K), such a temperature range represents approximately 10% of the star radius, leading to a length scale [z] = 1.9 × 109 m1. The density that corresponds to the temperature of 12 000 K is approximately 4 × 10-5 kg/m3, giving a density scale [ρ] = 4 × 10-3 kg/m3 for the G8 simulation. In such a star, one has ρbot/ρtop ≃ 170, while our model has a slightly lower density contrast of about ρbot/ρtop ≃ 140.
The timescale that corresponds to the G8 simulation can then be computed with the scaling
d/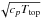 ,
leading to [t] = 1.3 × 105 s. It means that a frequency
ω00 = 3.85 for the fundamental acoustic unstable mode
corresponds in dimensional units to a mode period of 2.5 days. This value is nearly the
same as the period of δ-Cephei, 5.36 days.
,
leading to [t] = 1.3 × 105 s. It means that a frequency
ω00 = 3.85 for the fundamental acoustic unstable mode
corresponds in dimensional units to a mode period of 2.5 days. This value is nearly the
same as the period of δ-Cephei, 5.36 days.
With these scalings, we can also check that the gravity and fluxes of the DNS are consistent with their stellar counterparts. The gravity g = 8 in our units then reads as g = 0.84 m/s2. This value is very close to an estimate of the surface gravity g = GM/R2, that leads to g = 0.8 m/s2 for δ-Cephei. Concerning the fluxes, Fbot = 4.5 × 10-2 then becomes 5.2 × 108 J/s/m2. A good estimate of the real flux is obtained with F = L/4πR2, leading for δ-Cephei to 7.7 × 107 J/s/m2. Our simple model thus overestimates the heat flux but in a rather moderate way with respect to what is usually done in global DNS (e.g. Brandenburg et al. 2000). Such an accuracy in the heat flux is in fact inherent in the study of the κ-mechanism, because the thermal timescale has to be close enough to the dynamical one to fulfil the criterion (1).
We can roughly estimate the kinematic viscosity of δ-Cephei with the following law ν ≃ 1.2 × 10-17T5/2/ρ m2/s (see Chapman 1954), that gives ν = 2.5 × 10-3 m2/s in the layer we focus on. A value νDNS = 2.5 × 10-4 in the DNS becomes νDNS = 6 × 109 m2/s. We have thus overestimated the viscosity by a factor 1012. Such an enormous value is a limitation of every DNS that cannot account for the small scale of convection because of the limited numerical resolution (e.g. Chan & Sofia 1986). As a consequence, the viscosity is overestimated and leads to significantly lower Rayleigh and Reynolds numbers than the real ones.
Table 2 sums up the differences between the stellar parameters of a Cepheid of 5 M⊙ with the dimensional units of our local DNS. We notice that the values of our parameters are self-consistent as we both recover temperature and density variations that are compatible with the real ones, while keeping oscillation period, flux, and gravity close enough to their stellar counterparts.
Comparison between the main physical quantities given in both the dimensionless units of the DNS and the corresponding dimensional values, and their stellar counterparts for a 5 M⊙ Cepheid.
2.3. Numerical methods
As in Papers I and II, the linear stability analysis of the initial setup (4) has been computed thanks to the LSB code
(linear solver builder, Valdettaro et al. 2007).
This spectral solver, based on the iterative Arnoldi-Chebyshev algorithm (Arnoldi 1951), gives both the complex eigenvalues
λ = τ + iω and corresponding
eigenfunctions ψ of a generalised eigenproblem of the form  (9)where the sparse
matrices A and B result from the projection of the
differential operators onto the Gauss-Lobatto grid. We especially focus on the acoustic
modes that are found to be linearly excited by the κ-mechanism, that is,
those of which the real part of the eigenvalue is positive, τ > 0.
Furthermore, this linear stability analysis was computed without
consideration of the convective flux perturbations. This approximation, called
the frozen-in convection, means that only the radiative contribution of
the total flux perturbation is allowed to change during the mode pulsation. We will see
further that this approximation is well-suited in our case, as the computed eigenfunctions
overlap quite well with the vertical profiles extracted from the nonlinear simulation done
with convection.
(9)where the sparse
matrices A and B result from the projection of the
differential operators onto the Gauss-Lobatto grid. We especially focus on the acoustic
modes that are found to be linearly excited by the κ-mechanism, that is,
those of which the real part of the eigenvalue is positive, τ > 0.
Furthermore, this linear stability analysis was computed without
consideration of the convective flux perturbations. This approximation, called
the frozen-in convection, means that only the radiative contribution of
the total flux perturbation is allowed to change during the mode pulsation. We will see
further that this approximation is well-suited in our case, as the computed eigenfunctions
overlap quite well with the vertical profiles extracted from the nonlinear simulation done
with convection.
Concerning the DNS, we used the Pencil Code2 again. This non-conservative code is an high-order finite-difference code (sixth order in space and third order in time) that conserves the physical quantities up to the discretisation errors of the scheme. On multiprocessor clusters, it takes advantage of the MPI libraries (message passing interface) that allow distributing of the computing tasks on several processors having their own memory. This code is fully explicit, except for the radiative diffusion term that is solved implicitly thanks to an alternate direction implicit scheme (hereafter ADI) of our own already discussed in Paper I. However, this new study has needed an improvement of this implicit solver because the convective motions that develop in our simulations require its parallelisation because of
-
1.
the weakness of the mode growth rates τ ~ 10-3 computed from the newsetups that imposes that the simulations be carried out for a muchlonger time than in the purely radiative case;
-
2.
the convection itself that now requires a higher aspect ratio ensuring an efficient development of all additional spatial scales. Higher resolutions are thus compulsory when addressing the convection-pulsation coupling.
In its 2-D version, the Pencil Code has a domain decomposition along the vertical direction such that the first direction of our ADI solver (the horizontal one) fits in this topology. In contrast, the second direction of the solver (the vertical one) is trickier to parallelise as it needs a transposition of the data based on massive communications between processors. Figure 2 displays a sketch explaining how the parallelisation of the ADI solver is done. Once the tridiagonal system is solved in the second direction, one transposes the data once again to keep the original domain decomposition back. With this powerful algorithm, the semi-implicit nonlinear simulations of turbulent convection can then run on massively parallel clusters with the high resolutions induced by high Rayleigh numbers (see Table 1). Typically, our 2-D simulations of the convection-pulsation coupling were performed using a mid resolution of about 512 × 512 (i.e. 512 grid points in each direction).
 |
Fig. 2 Sketch of the parallelisation of the ADI scheme. a) the initial domain decomposition of the Pencil Code for a 2-D domain in the (x, z) plane. The coloured lines denote the data owned by the first processor (blue lines) and by the second one (green lines); b) the domain decomposition after the transposition needed to use the ADI solver. |
2.4. 2-D DNS of the κ-mechanism with convection
 |
Fig. 3 Snapshot of the modulus of the vorticity field |∇ × u| in the G8 a) and in the G8H8 simulations b). |
With the parallel ADI solver for the radiative diffusion implemented in the Pencil Code
(see Fig. 2), we advance the following hydrodynamic
equations in time: 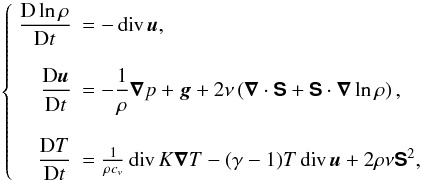 (10)where
ρ, u, and T denote the
density, velocity, and temperature, respectively. The operator
D/Dt = ∂/∂t + u·∇
is the usual total derivative, while S is the (traceless)
rate-of-strain tensor given by
(10)where
ρ, u, and T denote the
density, velocity, and temperature, respectively. The operator
D/Dt = ∂/∂t + u·∇
is the usual total derivative, while S is the (traceless)
rate-of-strain tensor given by 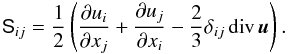 (11)Finally, we impose that
all fields are periodic in the horizontal direction, while stress-free boundary conditions
(i.e. uz = 0 and
dux/dz = 0) are
assumed for the velocity in the vertical one. Concerning the temperature, a perfect
conductor at the bottom (i.e. flux imposed) and a perfect insulator at the top (i.e.
temperature imposed) are applied.
(11)Finally, we impose that
all fields are periodic in the horizontal direction, while stress-free boundary conditions
(i.e. uz = 0 and
dux/dz = 0) are
assumed for the velocity in the vertical one. Concerning the temperature, a perfect
conductor at the bottom (i.e. flux imposed) and a perfect insulator at the top (i.e.
temperature imposed) are applied.
In order to ensure that both the nonlinear saturation and thermal relaxation are achieved, the simulations were performed for very long times, typically t ≳ 3000. With the eigenfrequencies computed from the linear stability analysis, ω00 ≃ 3 − 4 (see Table 1), this corresponds approximately to 1500 oscillation periods of the fundamental unstable acoustic mode.
Figure 3 displays a snapshot of the modulus of the vorticity field (i.e. |∇ × u| ) at a given time for the two simulations emphasised in Table 1, the G8 (Fig. 3a) and G8H8 ones (Fig. 3b). The vorticity field highlights the convective motions that are, as expected by the sketch on Fig. 1, superimposed on the radiative conductivity hollow located approximately in the middle of the layer. Moreover, one notes that the typical size of the convective plumes differs in the two simulations as the eddies have a smaller scale in the G8 simulation than in the G8H8 one. Accordingly, the overshooting of convective elements into the lower stably stratified layer is also more important in the G8H8 case than in the G8 one. It suggests a lower value of the Péclet number in that case as a faster thermalisation of the convective plumes at the interface between the convective/radiative regions is associated with more extensive penetration (Dintrans 2009).
Beyond the qualitative differences seen in the vorticity field, a good way to compare the DNS is to study the temporal evolution of average quantities, such as the vertical mass flux ⟨ ρuz ⟩ , where the brackets ⟨ ··· ⟩ denote an overall average. Indeed, since we are doing simulations where both convective motions and oscillations of acoustic modes are present, it is instructive to use a simple diagnostic that roughly separates their relative contributions. Because the convective plumes have both ascending and descending movements, the average vertical mass flux removes their contribution quite well, so one then gets a good tracer of the amplitude of the acoustic modes only. Figure 4 shows the resulting temporal evolution of ⟨ ρuz ⟩ for the G8 simulation and the G8H8 one. As displayed in the zoom in the bottom left corner, the time evolution shows an oscillating behaviour in both cases due to the radial oscillations of the fundamental (and unstable) acoustic mode excited by κ-mechanism. In the G8 simulation, the amplitude first experiences an exponential growth until reaching the nonlinear saturation regime for time t ~ 1000. The transient duration is well compatible with the growth rate of this mode that is about τ ~ 10-3. At first glance, the temporal evolution of ⟨ ρuz ⟩ in the G8 simulation is similar to what has been observed in the purely radiative simulations of Paper II, that is, a linear growth of the amplitude before a saturation at a well-defined value on a timescale ∝ 1/τ.
In contrast, the dynamics of the G8H8 simulation differ radically as the amplitude remains low compared to the radiative case and is highly modulated in time. As a consequence, no clear nonlinear saturation is observed in this case, and this kind of behaviour has not been found in the purely radiative models. It means that the acoustic oscillations are more influenced by convective motions in the G8H8 simulation than in the G8 one. To further study the physics involved in this coupling, we next perform a frequential analysis of these simulations.
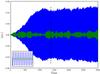 |
Fig. 4 Temporal evolution of the mean vertical mass flux ⟨ ρuz ⟩ for the two simulations G8 (solid blue line) and G8H8 (solid green line). The two vertical dashed black lines define the boundaries of the zoom displayed in the bottom left corner. |
3. Frequential analysis
3.1. Fourier decomposition
An efficient tool for determining the modes that are present in a numerical simulation
consists in taking first a double Fourier transform in space and time of the vertical mass
flux 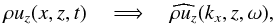 where
kx = (2π/Lx)ℓ
denotes the horizontal wavenumber, with
ℓ = [0,1,2,... ] , while ω is the
frequency. Second, one plots the power spectrum of
where
kx = (2π/Lx)ℓ
denotes the horizontal wavenumber, with
ℓ = [0,1,2,... ] , while ω is the
frequency. Second, one plots the power spectrum of 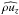 in the plane (z,ω) for each value of ℓ and “shark fin
profiles" emerge about definite frequencies corresponding to eigenmodes (Dintrans & Brandenburg 2004). The last
operation requires an integration over the vertical direction z to get
the final mean spectra for each ℓ of the initial field
ρuz.
in the plane (z,ω) for each value of ℓ and “shark fin
profiles" emerge about definite frequencies corresponding to eigenmodes (Dintrans & Brandenburg 2004). The last
operation requires an integration over the vertical direction z to get
the final mean spectra for each ℓ of the initial field
ρuz.
 |
Fig. 5 Left: temporal power spectrum of the vertical mass flux
|
 |
Fig. 6 Left: temporal power spectrum for the vertical mass flux
|
Figure 5 displays the results of this Fourier
analysis applied to the G8 simulation, with the power spectrum of
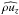 for the first three values of ℓ on the left side, and the corresponding
mean spectra on the right one. Many discrete peaks around given frequencies are clearly
noticed not only in the radial plane ℓ = 0 but also in the nonradial one
ℓ = 1, even if the amplitudes are weaker by an order of magnitude in
this last case. As expected, the fundamental radial acoustic mode
ω00 = 3.85, which is the only one to be unstable linearly,
has the largest amplitude in the ℓ = 0 plane. This signature is seconded
by numerous weaker amplitude peaks, of which the frequency is a multiple of
ω00. In fact, these peaks do no correspond to overtones as
they do not overlap with the theoretical eigenfrequencies sorted out by the linear
stability analysis (see computed overtones in Fig. 5). They instead correspond to harmonics of the fundamental mode, and this is a
signature of the large amplitude of this mode. Indeed, the presence of high-amplitude
harmonics implies that the mode has enough amplitude to generate them through a nonlinear
cascade. To a certain extent, the same behaviour is obtained for the nonradial planes
ℓ = 1 and ℓ = 2, but with a much lower amplitude.
for the first three values of ℓ on the left side, and the corresponding
mean spectra on the right one. Many discrete peaks around given frequencies are clearly
noticed not only in the radial plane ℓ = 0 but also in the nonradial one
ℓ = 1, even if the amplitudes are weaker by an order of magnitude in
this last case. As expected, the fundamental radial acoustic mode
ω00 = 3.85, which is the only one to be unstable linearly,
has the largest amplitude in the ℓ = 0 plane. This signature is seconded
by numerous weaker amplitude peaks, of which the frequency is a multiple of
ω00. In fact, these peaks do no correspond to overtones as
they do not overlap with the theoretical eigenfrequencies sorted out by the linear
stability analysis (see computed overtones in Fig. 5). They instead correspond to harmonics of the fundamental mode, and this is a
signature of the large amplitude of this mode. Indeed, the presence of high-amplitude
harmonics implies that the mode has enough amplitude to generate them through a nonlinear
cascade. To a certain extent, the same behaviour is obtained for the nonradial planes
ℓ = 1 and ℓ = 2, but with a much lower amplitude.
The temporal evolution of the mean vertical mass flux displayed in Fig. 4, which is similar to the ones obtained in the purely radiative case, could indicate a nonlinear saturation of the G8 simulation based on a 2:1 resonance between an unstable driving mode and a linearly stable overtone that acts as a slave mode (see Paper II for further details). But the Fourier analysis in Fig. 5 emphasises that there is no overlap between the frequencies of the DNS and the overtones ones. It means that the coupling between different eigenmodes is not favoured in the G8 simulation and a resonance-like phenomenon is not the physical process responsible for its nonlinear saturation. Furthermore, the presence of numerous large-amplitude harmonics is a hint of mono-mode saturation, such as the one observed for instance with Van der Pol’s oscillators (e.g. Krogdahl 1955; Takeuti & Aikawa 1981; Buchler & Goupil 1984).
The same Fourier analysis applied to the simulation G8H8 gives quite different results compared to the G8 ones (Fig. 6). One first recovers the signature of some acoustic mode in the (z,ω) plane, especially in the radial ℓ = 0 one where the fundamental mode is visible around the frequency ω00 = 3.80. But the disappearance of the harmonics for each value of ℓ means that the corresponding amplitudes of eigenmodes are much lower than in the G8 case. And indeed, the amplitude of the fundamental mode in the Fourier space is weaker by an order of magnitude in the G8H8 simulation.
The differences in amplitude obtained previously in the time series in Fig. 4 are thus confirmed by the results obtained in this Fourier analysis: a high amplitude of the unstable acoustic mode, observed in the G8 simulation, goes with numerous harmonics and significant frequential signatures, while a weaker amplitude of this mode, observed in the G8H8 simulation, is coupled with the disappearance of these harmonics.
3.2. Harmonic analysis
To visualise the structure of an eigenmode oscillating in a direct numerical simulation,
hydrodynamics specialists have developed a diagnostic tool called the “harmonic analysis”.
This method has been, for instance, used to visualise internal wave attractors propagating
in a non separable container (e.g. Hazewinkel et al.
2008; Grisouard et al. 2008). The idea is
to filter out the vertical velocity uz at a
given frequency ω following the relation
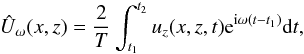 (12)where
t2 = t1 + nT,
with n an integer, and
T = 2π/ω the period. The
obtained 2-D (complex) field Û thus gives the pattern that evolves in
time in simulations like cosωt or sinωt. In Grisouard et al. (2008), the chosen frequency was
imposed by a forcing term of the form
cosωforct such that internal waves
propagating in their simulation were necessarily at this single frequency
ωforc (or its harmonics
2ωforc,3ωforc,... ).
In our case, the filtering frequency is of course given by the acoustic modes excited by
κ-mechanism, and the resulting field
Ûω(x,z) should
correspond to the eigenvectors that are solutions of the linear eigenvalue problem (9). We apply this method to the two simulations
G8 and G8H8 for a filtering frequency equal to the fundamental mode one, then
ω = 3.85 and ω = 3.80 for the G8 and G8H8 simulation,
respectively (see Table 1). The resulting modulus
| Ûω(x,z) | is displayed
in Figs. 7 (G8) and 8 (G8H8).
(12)where
t2 = t1 + nT,
with n an integer, and
T = 2π/ω the period. The
obtained 2-D (complex) field Û thus gives the pattern that evolves in
time in simulations like cosωt or sinωt. In Grisouard et al. (2008), the chosen frequency was
imposed by a forcing term of the form
cosωforct such that internal waves
propagating in their simulation were necessarily at this single frequency
ωforc (or its harmonics
2ωforc,3ωforc,... ).
In our case, the filtering frequency is of course given by the acoustic modes excited by
κ-mechanism, and the resulting field
Ûω(x,z) should
correspond to the eigenvectors that are solutions of the linear eigenvalue problem (9). We apply this method to the two simulations
G8 and G8H8 for a filtering frequency equal to the fundamental mode one, then
ω = 3.85 and ω = 3.80 for the G8 and G8H8 simulation,
respectively (see Table 1). The resulting modulus
| Ûω(x,z) | is displayed
in Figs. 7 (G8) and 8 (G8H8).
 |
Fig. 7 Harmonic analysis of the vertical velocity field uz for the G8 simulation around the eigenfrequency ω00 = 3.85. Top: amplitude of the modulus of the filtered velocity |Ûω00(x,z)| . Bottom: normalised vertical profile of the horizontal average of the filtered velocity |Ûω00| (solid black line) and the corresponding velocity eigenvector computed thanks to the linear stability analysis (dashed blue line). |
 |
Fig. 8 Harmonic analysis of the vertical velocity field uz for the G8H8 simulation around the eigenfrequency ω00 = 3.80. Top: amplitude of the modulus of the filtered velocity |Ûω00(x,z)| . Bottom: normalised vertical profile of the horizontal average of the filtered velocity |Ûω00| (solid black line) and the corresponding eigenvector of the linear stability analysis (dashed blue line). |
For the G8 simulation, the 2-D field
|Ûω00| shows only
variations in the vertical direction and has a quasi-periodic behaviour in the horizontal
one (upper panel in Fig. 7). This corresponds well to
the pattern that we are expecting for a radial acoustic mode. Moreover, the convective
plumes appear merely as very faint hints in the form of several short wiggles. It means
that the vertical motions at the frequency ω00 are dominated
by the acoustic radial mode. A definitive confirmation comes from the comparison between
the theoretical eigenvector and the horizontal average of
|Ûω00| given by
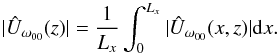 (13)The result is
shown in the bottom panel in Fig. 7. This vertical
profile is then compared to the eigenfunction
uz computed in the linear stability
analysis, and the two lines overlap almost perfectly, meaning that the motions at the
frequency ω00 in the DNS have a vertical structure that
corresponds to the unstable fundamental mode.
(13)The result is
shown in the bottom panel in Fig. 7. This vertical
profile is then compared to the eigenfunction
uz computed in the linear stability
analysis, and the two lines overlap almost perfectly, meaning that the motions at the
frequency ω00 in the DNS have a vertical structure that
corresponds to the unstable fundamental mode.
The same harmonic analysis performed on the G8H8 simulation at the frequency ω00 = 3.80 leads to different results (Fig. 8). The 2-D modulus |Ûω00(x,z)| indeed differs significantly from the previous one as large horizontal variations are observed, and the expected invariance of the radial acoustic mode in that direction is broken (upper panel in Fig. 8). It means that convection now has a strong impact on the mode pattern at this filtering frequency. The convective plumes strongly affect the acoustic oscillations in this DNS, and this is consistent with both the temporal modulation of the vertical mass flux amplitude observed in Fig. 4 and the lower Fourier amplitude of the fundamental mode in Fig. 6. Despite this stronger coupling with convection, we recover the structure of the unstable acoustic mode after averaging | Ûω00 | along the horizontal direction (lower panel in Fig. 8). The agreement between the eigenvector and the vertical profile is rather remarkable but not really surprising, since the average in the horizontal direction leads exactly to the smoothing of the convective perturbations.
The frequential analysis developed in this section (Fourier decomposition in the plane (z, ω) and the harmonic filtering) confirms the discrepancies that were observed in the temporal evolutions of the mean vertical mass flux ⟨ ρuz ⟩ (Fig. 4): the acoustic oscillations are not influenced by convection in the G8 simulation, whereas the convective motions have a strong effect on the modes’ evolution in the G8H8 simulation. We now investigate this effect in more detail by the means of projections onto an acoustic subspace that give the temporal evolution of the kinetic energy embedded in the pulsations.
4. Energy of oscillations
4.1. The projection method
 |
Fig. 9 Comparison between normalised vertical velocity (uz) profiles for the fundamental mode (n = 0,ℓ = 0) according to the harmonic analysis of the DNS (solid black line) and the adiabatic eigenvector (dashed blue line). |
We had already determined the energy contained in the acoustic modes of radiative simulations by projection of the physical fields onto an acoustic subspace (Paper II). This acoustic subspace was built from both normal and adjoint eigenmodes that were themselves solutions of the linear equations for the perturbations. The need to consider the adjoint problem, not only the regular one, was imposed by the non-hermiticity of the oscillation operator. The radiative diffusion was indeed so large close to the surface of the equilibrium models that strong non-adiabatic effects made the regular eigenmodes non-orthogonal (see also Bogdan et al. 1993). However, in the current 2-D simulations with convection, the setup is significantly changed and the radiative diffusivity χ ∝ 1/ρ is lower than in the non-convective case (the top density is multiplied by a factor 4 in the convective setup, see Sect. 2.1). The corresponding non-adiabatic effects at the surface are then weaker, and we use a simpler approach than the one in Paper II. This method, based on the adiabatic eigenvectors, has been validated in Dintrans & Brandenburg (2004) by measuring the wave field generated by the oscillations of an entropy bubble in an isothermal atmosphere.
To use this approximation, we must first ensure that the vertical velocity profiles in
our 2-D DNS are close enough to the adiabatic eigenfunctions of the linear problem for the
perturbations. This is done in Fig. 9 where we
compare the vertical profile obtained in the previous harmonic analysis of the G8
simulation to the adiabatic eigenfunction uz.
The agreement between these two profiles is rather comfortable, indicating that we can
shape our acoustic subspace from the adiabatic eigenvectors with good confidence. This
approach has the main advantage simplifying the computation of the kinetic energy contents
as Lynden-Bell & Ostriker (1967) have
demonstrated that adiabatic eigenvectors are mutually orthogonal for this particular
scalar product 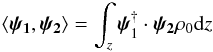 (14)where the symbol †
denotes the Hermitian conjugate. The acoustic subspace is then given by the following
relation
(14)where the symbol †
denotes the Hermitian conjugate. The acoustic subspace is then given by the following
relation 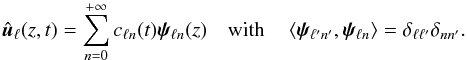 (15)This defines the
projection of the Fourier transform
(15)This defines the
projection of the Fourier transform 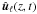 of the velocity onto the
adiabatic eigenvector
ψℓn(z) of
degree ℓ and radial order n. The complex and
time-dependent coefficient
cℓn(t) entering in this
projection is computed from
of the velocity onto the
adiabatic eigenvector
ψℓn(z) of
degree ℓ and radial order n. The complex and
time-dependent coefficient
cℓn(t) entering in this
projection is computed from 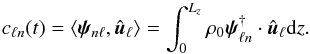 (16)As an example, when a
given eigenmode (ℓ, n) is present in the simulation,
this projection method leads to a projection coefficient that behaves as
cℓn(t) ∝ eiωℓnt,
with ωℓn the mode frequency.
(16)As an example, when a
given eigenmode (ℓ, n) is present in the simulation,
this projection method leads to a projection coefficient that behaves as
cℓn(t) ∝ eiωℓnt,
with ωℓn the mode frequency.
4.2. The kinetic energy content
The Parseval equality written in the Fourier space reads
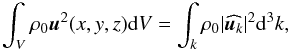 (17)where
(17)where
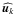 denotes the Fourier transform in space of u. In our case, we
only perform a Fourier transform of the velocity field in the horizontal direction,
therefore
denotes the Fourier transform in space of u. In our case, we
only perform a Fourier transform of the velocity field in the horizontal direction,
therefore 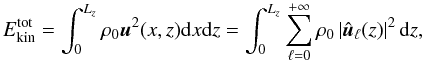 (18)with
kx = (2π/Lx)ℓ
still. With Eqs. (15–18), this leads to
(18)with
kx = (2π/Lx)ℓ
still. With Eqs. (15–18), this leads to 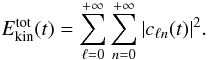 (19)This last
equation means that the kinetic energy content of a single acoustic mode is simply equal
to the square of its amplitude coefficient. In the 2-D simulations with convection, we
have
(19)This last
equation means that the kinetic energy content of a single acoustic mode is simply equal
to the square of its amplitude coefficient. In the 2-D simulations with convection, we
have 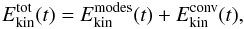 (20)where
(20)where
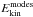 and
and
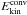 are the
kinetic energy embedded in acoustic modes and convective motions, respectively. In our
setup, the fundamental radial mode (ℓ = 0,n = 0) is the
only one that is excited by κ-mechanism, therefore the acoustic energy is
contained in low-degree and low-order modes (accordingly with the power spectra in
Fig. 5). We can thus restrict the analysis to these
modes only in the summations entering in Eq. (19), leading to
are the
kinetic energy embedded in acoustic modes and convective motions, respectively. In our
setup, the fundamental radial mode (ℓ = 0,n = 0) is the
only one that is excited by κ-mechanism, therefore the acoustic energy is
contained in low-degree and low-order modes (accordingly with the power spectra in
Fig. 5). We can thus restrict the analysis to these
modes only in the summations entering in Eq. (19), leading to 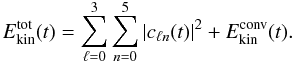 (21)The ratio of the kinetic
energy contained in acoustic modes can then be defined as
(21)The ratio of the kinetic
energy contained in acoustic modes can then be defined as 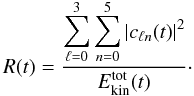 (22)
(22)
 |
Fig. 10 Temporal evolution of the acoustic kinetic energy ratio R(t) for the two simulations G8 (solid blue line) and G8H8 (dashed green line) according to Eq. (22). |
Figure 10 displays the temporal evolution of this ratio R(t) for the two simulations G8 and G8H8. In the G8 simulation, we see that the acoustic energy linearly increases until its nonlinear saturation above time tsat ≳ 103, in a similar way to what has been observed with the mean vertical mass flux in Fig. 4. This timescale tsat is still compatible with the linear growth rate of the fundamental mode, that is, τ ~ 10-3 and tsat ~ 1/τ. Once this saturation is reached, the energy ratio remains high (i.e. ≳ 70%, with the remaining 30% in the convection), and this behaviour is similar to the one observed in purely radiative simulations (see Paper II for further details). In other words, the acoustic oscillations are not affected much by the convective motions in this simulation.
In contrast, the acoustic energy ratio remains very weak in the G8H8 simulation. Indeed, despite some transient increases during which non-trifling values R ≃ 10% are obtained, the average ratio is R ≲ 1 − 5%, and convective motions are responsible for the bulk of the kinetic energy content. In this case, the radial oscillations excited by κ-mechanism are thus quenched by convective plumes. This situation is relevant to the red edge of the classical instability strip, where the unstable acoustic modes are supposed to be damped by the surface convective motions.
4.3. Mean-field analysis
Beyond the temporal evolution of the energy ratio displayed in Fig. 10, it is interesting to precisely locate the zones where kinetic energy is due to acoustic modes and convective motions. Towards this goal, a simple mean-field analysis is a valuable tool for separating the mean-field component of the motion (the acoustic oscillations in our setup) from its fluctuating part (here the convective plumes). Such an approach has been used for instance to check the mixing-length theory of convection thanks to velocity correlations (Chan & Sofia 1987).
In our simulations, we are interested in the mean-field velocity correlations that can
account for the acoustic modes and the convective plumes. We first separate the vertical
velocity field into a mean part and a fluctuating one
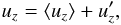 (23)where ⟨ ··· ⟩ is
an horizontal average. We then square this expression and average along the horizontal
direction to get
(23)where ⟨ ··· ⟩ is
an horizontal average. We then square this expression and average along the horizontal
direction to get 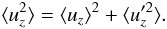 (24)This equation is the
mean square velocity, which can be split between an acoustic contribution and a convective
one, i.e.
(24)This equation is the
mean square velocity, which can be split between an acoustic contribution and a convective
one, i.e. 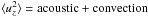 . To separate these
different contributions, we recall that
⟨ uz ⟩ is a good proxy for measuring the
acoustic oscillations, as the vertical convective motions almost vanish after their
averaging in the horizontal direction (ascending and descending plumes are comparable).
The acoustic contribution to Eq. (24) thus
reads as
. To separate these
different contributions, we recall that
⟨ uz ⟩ is a good proxy for measuring the
acoustic oscillations, as the vertical convective motions almost vanish after their
averaging in the horizontal direction (ascending and descending plumes are comparable).
The acoustic contribution to Eq. (24) thus
reads as 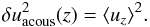 (25)With Eq. (24), we then extract the contribution of the
convective motions to the mean square velocity field as
(25)With Eq. (24), we then extract the contribution of the
convective motions to the mean square velocity field as 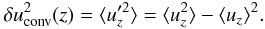 (26)Figure 11 displays the vertical profiles of
(26)Figure 11 displays the vertical profiles of
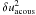 and
and
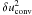 for the simulations
G8 and G8H8. In both simulations, one notes that the maximum of the convective
contribution is approximately located at the layer middle, corresponding to the radiative
conductivity profile displayed in Fig. 1, while the
acoustic part reaches its maximum close to the surface because of the eigenvector shape.
for the simulations
G8 and G8H8. In both simulations, one notes that the maximum of the convective
contribution is approximately located at the layer middle, corresponding to the radiative
conductivity profile displayed in Fig. 1, while the
acoustic part reaches its maximum close to the surface because of the eigenvector shape.
However, the acoustic contribution to the velocity correlation for the G8 simulation is
greater than the convective one, and a profile similar to the velocity eigenfunction is
obtained (see Fig. 9 for instance). In contrast, for
the G8H8 simulation, this acoustic part 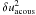 is much
weaker than the one due to convective motions.
is much
weaker than the one due to convective motions.
These trends can easily be linked to what was obtained previously with the projection
formalism (see Fig. 10). Indeed, the vertical
profiles in Fig. 11 can be integrated to get a ratio
between the acoustic oscillations and the (total) mean square velocity
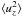 as
as 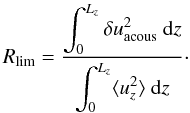 (27)This last equation,
derived from a mean-field analysis, contains the same physical information as in
Eq. (22) because the obtained ratio is
very close to the one computed with the projection method in the saturated regime
(Fig. 10): Rlim ≃ 75%
for the G8 simulation and Rlim ≃ 3% for the G8H8 one. The
second-order correlations
(27)This last equation,
derived from a mean-field analysis, contains the same physical information as in
Eq. (22) because the obtained ratio is
very close to the one computed with the projection method in the saturated regime
(Fig. 10): Rlim ≃ 75%
for the G8 simulation and Rlim ≃ 3% for the G8H8 one. The
second-order correlations  and
and
 are thus another
good tool to separate and locate the different contributions to the flow velocity.
are thus another
good tool to separate and locate the different contributions to the flow velocity.
 |
Fig. 11 Vertical second-order velocity correlations for the simulations G8 (blue lines) and G8H8 (green lines). The acoustic contribution (Eq. (25)) is displayed as solid lines, while the convective one (Eq. (26)) is plotted as dashed lines. |
The amount of energy contained in convective motions and in oscillations has been studied thanks to both the projection formalism already used in purely radiative simulations and to the second-order correlations of velocity. One recovers the main physics underlined in the frequential analysis; that is, the mode amplitude is strong in the G8 simulation and the oscillations clearly dominate the motions in the flow, as opposed to the G8H8 simulation in which convection is dominant.
5. The mode quenching
We are now going to focus on the physical process that leads to the different behaviours obtained in our different DNS. In fact, as presented in Table 1, the main physical parameters of these simulations are very close: for instance, for the G8 and G8H8 simulation, there is mainly a 20% variation in the mean radiative conductivity Kmax. Some of the parameters of the conductivity hollow (e.g. Tbump and σ) also differ since they have been adjusted to satisfy the criterion given in Eq. (1) in each DNS. We can classify the simulations given in Table 1 into three different categories:
-
the first category encompasses the simulations similar to the G8one, in which the amplitude of the unstable acoustic mode isimportant (R ≳ 70%), and that do not seem affected much by convection.This case concerns the simulation G7 of Table 1;
-
the second category, similar to G8H8, contains the DNS, in which the amplitude of the acoustic mode is very weak (R ≲ 10%). In this case, the oscillations are quenched by convective plumes that dominate the flow. This case also concerns the G6 and G6F7 simulations of Table 1;
-
at last, there are intermediate simulations, in which the amplitudes of oscillations and convection are comparable (R ≃ 30−50%). These simulations also show strong temporal modulation of the amplitude of oscillations, i.e., the standard deviation of the ratio of energy is larger than in previous categories. It mainly concerns the simulations G8H9 and G6F5 of Table 1.
5.1. The role of the convective flux
 |
Fig. 12 Mean vertical profiles of radiative ℱrad (solid blue line), turbulent enthalpy ℱconv (dashed green line), kinetic ℱkin (dotted black line), modes ℱmod (dot-dashed magenta line), and total ℱtot (dotted red line) fluxes for the G8 a) and G8H8 b) simulations. All fluxes have been normalised with respect to the bottom value Fbot. |
A first attempt at explaining these different physical behaviours is to compare the heat transport between the various DNS that are summarised in Table 1. In particular, the study of the respective amount of heat carried out by convection and radiation may lead to a natural explanation of the mode quenching observed in the G8H8 simulation, because, from an intuitive point of view, the higher the convective flux, the stronger the quenching.
The vertical heat transport is ensured by the radiative ℱrad, enthalpy
ℱent, and kinetic ℱkin fluxes given by (e.g. Hurlburt et al. 1984) 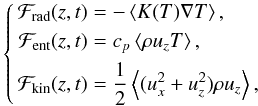 (28)where
the brackets denote a horizontal average. The enthalpy flux ℱent can be
developed in mean and fluctuating components from the following decomposition for the
total
temperature T
(28)where
the brackets denote a horizontal average. The enthalpy flux ℱent can be
developed in mean and fluctuating components from the following decomposition for the
total
temperature T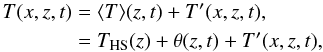 (29)where
THS is the hydrostatic background temperature profile,
θ the temperature eigenfunction of the unstable acoustic mode, and
T′ the turbulent fluctuating temperature around the horizontal average
⟨ T ⟩ . The enthalpy flux then reads as
(29)where
THS is the hydrostatic background temperature profile,
θ the temperature eigenfunction of the unstable acoustic mode, and
T′ the turbulent fluctuating temperature around the horizontal average
⟨ T ⟩ . The enthalpy flux then reads as
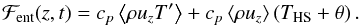 (30)We now average this
last expression in time over a multiple of the mode period to get
(30)We now average this
last expression in time over a multiple of the mode period to get
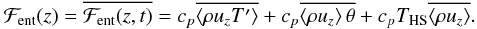 (31)Finally, as there is no
average mass flux over an oscillation period (i.e.
(31)Finally, as there is no
average mass flux over an oscillation period (i.e. 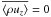 ), the enthalpy flux carried by
both the convection and acoustic oscillations is given by
), the enthalpy flux carried by
both the convection and acoustic oscillations is given by 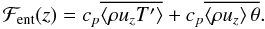 (32)The first term on the
right hand side denotes the turbulent transport of enthalpy usually defined as the
convective flux (e.g. Hurlburt et al. 1984), while
the second one corresponds to enthalpy transported by the acoustic modes. This second
contribution is usually negligible in simulations of compressible convection because of
the weakness of modes that are driven by turbulent fluctuations in pressure (Bogdan et al. 1993). In our case, the modes can be
excited efficiently through the κ-mechanism, so their contribution to the
heat transport should be taken into account. To determine the net contribution of the
acoustic modes to the total flux, we thus separate the usual turbulent enthalpy part
because of the convective plumes (hereafter denoted ℱconv) from the enthalpy
transport due to modes (hereafter ℱmod). By taking the average in time of
Eqs. (28) and using Eq. (32), one finally gets
(32)The first term on the
right hand side denotes the turbulent transport of enthalpy usually defined as the
convective flux (e.g. Hurlburt et al. 1984), while
the second one corresponds to enthalpy transported by the acoustic modes. This second
contribution is usually negligible in simulations of compressible convection because of
the weakness of modes that are driven by turbulent fluctuations in pressure (Bogdan et al. 1993). In our case, the modes can be
excited efficiently through the κ-mechanism, so their contribution to the
heat transport should be taken into account. To determine the net contribution of the
acoustic modes to the total flux, we thus separate the usual turbulent enthalpy part
because of the convective plumes (hereafter denoted ℱconv) from the enthalpy
transport due to modes (hereafter ℱmod). By taking the average in time of
Eqs. (28) and using Eq. (32), one finally gets 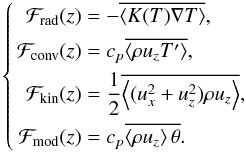 (33)The
vertical profiles of these fluxes (normalised to the imposed bottom value
Fbot) are given in Fig. 12 for the G8 (upper panel) and G8H8 (lower panel) simulations. For both DNS,
the bulk of the total flux is transported by the radiative flux, except in the convective
zone where ℱconv reaches 15% of the total flux for the G8 simulation and 40%
for the G8H8 one. We also notice a larger overshooting in the second DNS, because the
downdrafts penetrating in the radiative zone are stronger (see Fig. 3). As expected, this significant penetration is associated with both a
negative convective flux and a low value for the kinetic flux (~5%). The
convective fluxes in our DNS are nevertheless relatively weak compared to what is expected
to occur in Cepheid stars (see e.g. Yecko et al.
1998). These limited values are a direct issue of the rather moderate Rayleigh
number numerically affordable in this kind of DNS.
(33)The
vertical profiles of these fluxes (normalised to the imposed bottom value
Fbot) are given in Fig. 12 for the G8 (upper panel) and G8H8 (lower panel) simulations. For both DNS,
the bulk of the total flux is transported by the radiative flux, except in the convective
zone where ℱconv reaches 15% of the total flux for the G8 simulation and 40%
for the G8H8 one. We also notice a larger overshooting in the second DNS, because the
downdrafts penetrating in the radiative zone are stronger (see Fig. 3). As expected, this significant penetration is associated with both a
negative convective flux and a low value for the kinetic flux (~5%). The
convective fluxes in our DNS are nevertheless relatively weak compared to what is expected
to occur in Cepheid stars (see e.g. Yecko et al.
1998). These limited values are a direct issue of the rather moderate Rayleigh
number numerically affordable in this kind of DNS.
Concerning ℱmod, one notes that it is hardly as large as the convective flux in the G8 simulation, while it almost vanishes in the G8H8 one. In the G8 simulation where the amplitude of the unstable acoustic mode is the largest, about 10% of the heat flux is carried out by acoustic modes. This quantity is thus another good tracer of the significance of the amplitude of the acoustic modes compared to the convective motions, since ℱmod becomes large when the amplitude of the acoustic oscillations is strong enough.
 |
Fig. 13 Ratio of the kinetic energy in acoustic modes displayed as a function of the maximum of the normalised convective flux ℱconv for the different DNS presented in Table 1. The blue dots correspond to the mean kinetic ratio obtained with the projection method, while the vertical grey bars represent the standard deviation. |
The differences in the amount of heat transported by turbulent convection may be a first hint of the physical origin of the mode quenching observed in our DNS. To confirm this hypothesis, we thus gathered the values of the maximum of the normalised convective flux for all the DNS in Table 1. Figure 13 displays the amount of energy contained in acoustic modes compared to these maximum values. For moderate to stronger convective fluxes, we recover a tight relationship between the fraction of ℱconv and the efficiency of the κ-mechanism; that is, the energy ratios in acoustic modes become lower with increasing convective fluxes. But this correlation disappears in the region of smaller convective fluxes with ℱconv ≲ 20%. Indeed, one observes here that the efficiency of the κ-mechanism is independent of the value of the convective flux, because the modes may be either quenched or excited for similar values of ℱconv.
Figure 13 thus emphasises that the physical origin of the mode quenching does not solely rely on the amount of the convective flux, because the acoustic oscillations are also damped in DNS where the convective transport is inefficient. This result indicates that other underlying physical processes are involved in this mode quenching.
5.2. The role of the stratification
 |
Fig. 14 Mean vertical profiles of density ρ for the G8 simulation (solid blue line) and the G8H8 simulation (dashed green line). |
The differences between the physical parameters of the DNS given in Table 1 seem at a first look negligible. However the
variations of gravity g, flux Fbot, and
radiative conductivity Kmax lead to significantly modified
equilibrium fields, especially concerning the density profile. The mean vertical profile
of density is close to the hydrostatic equilibrium, which reads as 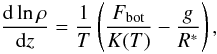 (34)where the radiative
conductivity K(T) is given by Eq. (2). Increasing
β = Fbot/Kmax
or decreasing the gravity g then leads to a weaker derivative of the
density. Figure 14 displays the mean vertical
density profile for the simulations G8 and G8H8. It shows that a 20% change in the
radiative conductivity leads to significantly different density values, especially at the
bottom of the layer where one notes a factor of two between the simulations.
(34)where the radiative
conductivity K(T) is given by Eq. (2). Increasing
β = Fbot/Kmax
or decreasing the gravity g then leads to a weaker derivative of the
density. Figure 14 displays the mean vertical
density profile for the simulations G8 and G8H8. It shows that a 20% change in the
radiative conductivity leads to significantly different density values, especially at the
bottom of the layer where one notes a factor of two between the simulations.
To compare the differences in the density stratification between the simulations of
Table 1, we may use an analytical approximation
of the density scale
Hρ ≡ − (dlnρ/dz)-1
at the middle of the layer. Starting from Eq. (34), one can approximate the temperature profile by
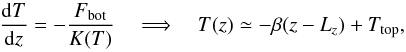 (35)where we suppose
that the mean temperature profile is linear; that is, the conductivity profile is
neglected and assumed to be
K(T) ≃ Kmax. The
hydrostatic equilibrium then reads as
(35)where we suppose
that the mean temperature profile is linear; that is, the conductivity profile is
neglected and assumed to be
K(T) ≃ Kmax. The
hydrostatic equilibrium then reads as
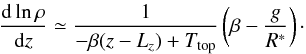 (36)We can then approximate
the density scale Hρ in the middle layer by
(36)We can then approximate
the density scale Hρ in the middle layer by
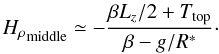 (37)This approximation allows
us to compare the different simulations of Table 1.
The results given in Table 3 emphasises a
correlation between the density profile and the ratio of energy contained in acoustic
modes; that is, the weaker Hρ, the larger
Rlim. In contrast, acoustic modes are quenched by convective
motions if the value of Hρ increases
(simulations G8H8 or G6 for instance).
(37)This approximation allows
us to compare the different simulations of Table 1.
The results given in Table 3 emphasises a
correlation between the density profile and the ratio of energy contained in acoustic
modes; that is, the weaker Hρ, the larger
Rlim. In contrast, acoustic modes are quenched by convective
motions if the value of Hρ increases
(simulations G8H8 or G6 for instance).
 |
Fig. 15 Ratio of the kinetic energy in acoustic modes displayed as a function of the mean density scale ⟨ Hρ ⟩ for the different DNS presented in Table 1. The blue dots correspond to the mean kinetic ratio obtained with the projection method, while the vertical grey bars represent the standard deviation. |
We can also extract the real values of Hρ directly from the DNS field to check that the results obtained in Table 3 are confirmed without the constant radiative conductivity profile approximation done in Eq. (37). Figure 15 displays the ratio R(t) as a function of the mean density scale ⟨ Hρ ⟩ for the different DNS. We recover the correlation between the value of the density scale and the significance of pulsations compared to the convective motions. Likewise, Fig. 15 emphasises the three different behaviours presented before, because one gets the two extrema (high amplitude of modes or mode-quenching by convection) but also “mixed”-simulations with R ≃ 30 − 50% and very large standard deviations, meaning that an important modulation of pulsations occurs.
5.3. Spectrum and integral scale
Figure 15 seems to indicate that the density stratification plays a strong role in the stabilisation of acoustic modes excited by κ-mechanism. According to the mixing length theory (Vitense 1953; Böhm-Vitense 1958), higher values of Hρ mean that the typical size of convective eddies increases. This assumption is also displayed on Fig. 3, where the difference in size between the vortices of the G8 and G8H8 simulations are noticeable. To determine the role played by the different scales of the flow onto the pulsations, we now focus on the power spectra of the different DNS.
 |
Fig. 16 Normalised kinetic energy power spectrum in the middle of the convective zone for the G8 simulation (solid blue line) and the G8H8 simulation (dashed green line). The kinetic energy spectrum E(k) ~ k-3 has been superimposed as a solid black line. |
The power spectrum is obtained with a Fourier transform of the kinetic energy in the
horizontal direction: 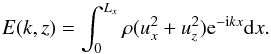 (38)The normalised
power spectrum at the middle of the convective layer (z ≃ 1.2) is then
displayed in Fig. 16 for the two simulations G8 and
G8H8. One notes that the G8 simulation reaches its maximum at a higher value
of kx than G8H8. The energy spectrum is
thus shifted to smaller scales in the G8 simulation than in the G8H8, in which the kinetic
energy is contained in larger scales. It corresponds to what is observed on the vorticity
fields of Fig. 3, where the convective eddies are
larger in the G8H8 simulation than in the G8 one.
(38)The normalised
power spectrum at the middle of the convective layer (z ≃ 1.2) is then
displayed in Fig. 16 for the two simulations G8 and
G8H8. One notes that the G8 simulation reaches its maximum at a higher value
of kx than G8H8. The energy spectrum is
thus shifted to smaller scales in the G8 simulation than in the G8H8, in which the kinetic
energy is contained in larger scales. It corresponds to what is observed on the vorticity
fields of Fig. 3, where the convective eddies are
larger in the G8H8 simulation than in the G8 one.
We can also mention that we recover a scaling law E(k) ~ k-3 in the kinetic energy spectra. This result corresponds to the standard dimensional analysis of the enstrophy cascade in 2-D turbulence (e.g. Lesieur 1997).
From Eq. (38), we can determine the
integral scale, which is the scale associated with the most energetic structures of the
flow: 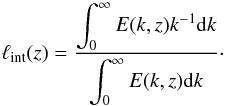 (39)Once again, we
compute the integral scale at the middle of the convective zone for the different DNS of
Table 1. Figure 17 displays the value of
(39)Once again, we
compute the integral scale at the middle of the convective zone for the different DNS of
Table 1. Figure 17 displays the value of 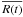 with respect to the integral scale ℓint and illustrates the
same trend as in Fig. 15: the larger the integral
scale, the lower the energy ratio. The integral scale is, in fact, another way to get the
information obtained with the Hρ length
scale, but it relies on the properties of the turbulence of the flow.
with respect to the integral scale ℓint and illustrates the
same trend as in Fig. 15: the larger the integral
scale, the lower the energy ratio. The integral scale is, in fact, another way to get the
information obtained with the Hρ length
scale, but it relies on the properties of the turbulence of the flow.
 |
Fig. 17 Ratio of the kinetic energy in acoustic modes displayed as a function of the integral scale (Eq. (39)) for the different DNS presented in Table 1. The blue dots correspond to the mean kinetic ratio obtained with the projection method, while the vertical gray bars represent the standard deviation. |
The comparison of these length scales in our DNS is a first hint of the physics responsible for the mode quenching. In light of Figs. 15–17, the density stratification seems to have a significant impact on how the oscillations develop in the presence of convection. With the increase in the size of the eddies (increase of ℓint), the acoustic part in the energy budget gradually vanishes.
We may explain this mode quenching by the spatial distribution of the convective plumes: large eddies entail a strong “screening effect” on the acoustic radial mode. One can imagine that the amplitude of such a mode is affected by the motions that are not coherent with its vertical structure: in this case, large eddies with a large amount of energy distributed both in radial and nonradial motions is incoherent with the “main” velocity field owing to the purely radial pulsations. In the less stratified simulations, such as G8H8, the convective plumes are large enough and present an important horizontal filling-factor that leads to a velocity field that is incompatible with the acoustic mode structure.
This screening effect, or such a spatial distribution of the convective plumes , has been already found to be responsible of the modulation and quenching of gravity modes in DNS of the penetrative convection (Dintrans et al. 2005). In our DNS, where oscillations are sustained by a physical process acting continuously, the amplitude of pulsations (and their nonlinear saturation) may thus be ruled by the extent of the screening of large vortices onto the purely radial velocity field.
6. Conclusion
In this paper, we have investigated the convection-pulsation coupling thanks to nonlinear 2-D direct numerical simulations (DNS). Despite their intrinsic limitations (weak pressure contrasts across the computational domain or the need for high viscosities leading to unrealistic values for the Rayleigh number, see e.g. Brandenburg et al. 2000), DNS are without a doubt a usefull way to address this interaction since they fully account for the nonlinearities.
This study follows our former work on the κ-mechanism in purely radiative simulations, where we studied both the instability and its nonlinear saturation (Gastine & Dintrans 2008a,b, Papers I and II, respectively). We then again modelled the ionisation region responsible for the oscillations of classical Cepheids by a hollow in the radiative conductivity profile, and local simulations of a perfect gas layer centred on this ionisation bump were performed. The initial physical setup was, however, slightly modified to get a convective zone superimposed on the hollow in radiative conductivity. Furthermore, some important numerical improvements were developed (mostly the parallelisation of the ADI solver) because considering strong convective motions coupled with acoustic oscillations requires higher spatial resolutions than the ones used in the purely radiative case.
Using this parallel solver, we performed 2-D DNS of the convection-pulsation coupling in which the oscillations are sustained by a continuous physical process based on the κ-mechanism. Convective motions that develop in these simulations lead to various impacts on the acoustic modes.
-
In a first set of DNS, the instability behaves in a similar way towhat is observed in purely radiative simulations: a linear growthand a nonlinear saturation of the acoustic oscillations. The bulk ofkinetic energy is embedded in acoustic motions, whileconvection participates in up to 20% to the energy budget.However, contrary to what was observed inPaper II, the nonlinear saturation does not involveany resonance between modes. The frequential analysisemphasises numerous harmonics of the fundamental acousticmode that are probably indicative of a mono-mode saturation. Inthis case, the convection does not affect the oscillations much.
-
In a second category of DNS, the convective motions have a stronger influence on the acoustic oscillations. There is no clear nonlinear saturation of the κ-instability, while the amplitudes of acoustic modes remain very weak. Moreover, the kinetic energy is almost entirely due to the downward-directed convective eddies. The vanishing of harmonics in the frequential analysis is further evidence of the weakness of the mode amplitudes. In this case, convective plumes are quenching the oscillations, and this physical phenomenon looks like what is expected to occur in the coldest Cepheids close to the red edge of the instability strip. In these stars, the large surface convective zone is indeed suspected to stabilise the global radial oscillations.
The various behaviours obtained in these local simulations of the κ-mechanism with convection were further studied in the last part of this paper, where we gave some ideas to explain the physical conditions that lead to the mode quenching. Both the influence of the amount of heat carried by convection and the density contrast across the layer were investigated. We first showed that, even in the inefficient regime where convection only carries 10 − 15% of the total heat flux, the convective plumes may cancel the radial oscillations, indicating that the strength of convection is not the only parameter that explains the mode quenching. The density contrast seems, on the contrary, to play a strong role in the dynamics of acoustic modes. In fact, weaker stratifications (that is, higher values of the density scale Hρ) correspond to bigger vortices. It means that the scale of the more powerful structure in the flow is larger when the stratification is weaker. In the less stratified simulations, where the acoustic modes appear to be strongly quenched by convection, the convective plumes are indeed larger and that leads to an important horizontal filling factor. In our DNS, the amplitude of radial pulsations (and their nonlinear saturation) may thus be governed by the screening effect of large convective vortices.
The 2-D DNS of the κ-mechanism with convection presented in this paper are a first step in our study of the convection-pulsation coupling occurring in the coldest Cepheid stars with an outer convective zone. They are based on a simplified physical model that keeps the main physics responsible for exciting acoustic modes by the κ-mechanism. The opacity bump is for instance modelled by a hollow in the radiative conductivity profile, whose shape is adjusted to get unstable acoustic modes superimposed on convection. One of the main prospects of this pioneering work is thus to improve this model toward more realistic stellar conditions (e.g. inputs from tabulated opacities or coding of a free-surface boundary condition for the velocity). Such developments are, however, challenging as they will require huge numerical improvements in the Pencil Code.
Another interesting prospect is the comparison between our 2-D DNS and the prescriptions of different time-dependent convection (TDC) models (e.g. Stellingwerf 1982; Kuhfuß 1986; Yecko et al. 1998). In fact, even if our simplified model of the κ-mechanism is far from the realistic stellar parameters, it could be interesting in our simulations to compare the temporal evolution of the convective and kinetic fluxes modulated by acoustic oscillations with their TDC counterparts. We will check the validity of such approaches and give some constraints on the multiple dimensionless α coefficients involved in these 1-D models.
The values were taken in a 5 M⊙ stellar model provided by the Helas network on http://www.astro.up.pt/helas/stars/
Acknowledgments
This work was granted access to the HPC resources of CALMIP under the allocation 2010-P1021. It is also a pleasure to thank Jérôme Ballot for his fruitful help on hydrostatic stellar models.
References
- Arnoldi, W. E. 1951, QApMa, 9, 17 [Google Scholar]
- Baker, N., & Kippenhahn, R. 1965, ApJ, 142, 868 [NASA ADS] [CrossRef] [Google Scholar]
- Bogdan, T. J., Cattaneo, F., & Malagoli, A. 1993, ApJ, 407, 316 [NASA ADS] [CrossRef] [Google Scholar]
- Böhm-Vitense, E. 1958, Z. Astrophys., 46, 108 [Google Scholar]
- Bono, G., Marconi, M., & Stellingwerf, R. F. 1999, ApJS, 122, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Brandenburg, A. & Dobler, W. 2002, CoPhC, 147, 471 [Google Scholar]
- Brandenburg, A., Nordlund, A., & Stein, R. F. 2000, Geophysical & Astrophysical Convection, ed. P. A. Fox, & R. M. Kerr (New York: Gordon and Breach Science Publishers) [Google Scholar]
- Buchler, J. R. 2009, in AIP Conf. Ser. 1170, ed. J. A. Guzik, & P. A. Bradley, 51 [Google Scholar]
- Buchler, J. R., & Goupil, M.-J. 1984, ApJ, 279, 394 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Buchler, J. R., & Kovacs, G. 1986, ApJ, 303, 749 [NASA ADS] [CrossRef] [Google Scholar]
- Chan, K. L., & Sofia, S. 1986, ApJ, 307, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Chan, K. L., & Sofia, S. 1987, Science, 235, 465 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Chapman, S. 1954, ApJ, 120, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Cox, J. P. 1980, Theory of Stellar Pulsation, ed. J. P. Cox [Google Scholar]
- Dintrans, B. 2009, CoAst, 158, 45 [Google Scholar]
- Dintrans, B., & Brandenburg, A. 2004, A&A, 421, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dintrans, B., Brandenburg, A., Nordlund, Å., & Stein, R. F. 2005, A&A, 438, 365 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dupret, M.-A., Grigahcène, A., Garrido, R., Gabriel, M., & Scuflaire, R. 2005, A&A, 435, 927 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gastine, T., & Dintrans, B. 2008a, A&A, 484, 29, Paper I [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gastine, T., & Dintrans, B. 2008b, A&A, 490, 743, Paper II [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gautschy, A., & Saio, H. 1996, ARA&A, 34, 551 [NASA ADS] [CrossRef] [Google Scholar]
- Gough, D. O. 1977, ApJ, 214, 196 [NASA ADS] [CrossRef] [Google Scholar]
- Gough, D. O., Moore, D. R., Spiegel, E. A., & Weiss, N. O. 1976, ApJ, 206, 536 [NASA ADS] [CrossRef] [Google Scholar]
- Grigahcène, A., Dupret, M.-A., Gabriel, M., Garrido, R., & Scuflaire, R. 2005, A&A, 434, 1055 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grisouard, N., Staquet, C., & Pairaud, I. 2008, J. Fluid Mech., 614, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Hazewinkel, J., van Breevoort, P., Dalziel, S. B., & Maas, L. R. M. 2008, J. Fluid Mech., 598, 373 [NASA ADS] [CrossRef] [Google Scholar]
- Hurlburt, N. E., Toomre, J., & Massaguer, J. M. 1984, ApJ, 282, 557 [NASA ADS] [CrossRef] [Google Scholar]
- Klapp, J., Goupil, M. J., & Buchler, J. R. 1985, ApJ, 296, 514 [NASA ADS] [CrossRef] [Google Scholar]
- Kolláth, Z., Buchler, J. R., Szabó, R., & Csubry, Z. 2002, A&A, 385, 932 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krogdahl, W. S. 1955, ApJ, 122, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Kuhfuß, R. 1986, A&A, 160, 116 [NASA ADS] [Google Scholar]
- Lesieur, M. 1997, Turbulence in Fluids (Dordrecht, Boston, London: Kluwer Academic Publishers) [Google Scholar]
- Lynden-Bell, D., & Ostriker, J. P. 1967, MNRAS, 136, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Muthsam, H. J., Kupka, F., Mundprecht, E., et al. 2010, [arXiv:1009.2409] [Google Scholar]
- Simon, N. R., & Schmidt, E. G. 1976, ApJ, 205, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Stellingwerf, R. F. 1982, ApJ, 262, 330 [NASA ADS] [CrossRef] [Google Scholar]
- Takeuti, M., & Aikawa, T. 1981, Sci. Rep. Tohoku Univ. Eighth Ser., 2, 106 [NASA ADS] [Google Scholar]
- Unno, W. 1967, PASJ, 19, 140 [NASA ADS] [Google Scholar]
- Valdettaro, L., Rieutord, M., Braconnier, T., & Fraysse, V. 2007, JCoAM, 205, 382 [NASA ADS] [Google Scholar]
- Vitense, E. 1953, Z. Astrophys., 32, 135 [NASA ADS] [Google Scholar]
- Wuchterl, G., & Feuchtinger, M. U. 1998, A&A, 340, 419 [NASA ADS] [Google Scholar]
- Xiong, D. 1989, A&A, 209, 126 [NASA ADS] [Google Scholar]
- Yecko, P. A., Kolláth, Z., & Buchler, J. R. 1998, A&A, 336, 553 [NASA ADS] [Google Scholar]
- Zhevakin, S. A. 1963, ARA&A, 1, 367 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Comparison between the main physical quantities given in both the dimensionless units of the DNS and the corresponding dimensional values, and their stellar counterparts for a 5 M⊙ Cepheid.
All Figures
 |
Fig. 1 Sketch of our convective model. The blue curve corresponds to the radiative conductivity profile, the dashed line is the Schwarzschild criterion given in Eq. (6), and the large red arrow represents the radiative flux Fbot that is imposed at the bottom. The red rolls correspond to the convective motions that develop in the layer middle. |
| In the text | |
 |
Fig. 2 Sketch of the parallelisation of the ADI scheme. a) the initial domain decomposition of the Pencil Code for a 2-D domain in the (x, z) plane. The coloured lines denote the data owned by the first processor (blue lines) and by the second one (green lines); b) the domain decomposition after the transposition needed to use the ADI solver. |
| In the text | |
 |
Fig. 3 Snapshot of the modulus of the vorticity field |∇ × u| in the G8 a) and in the G8H8 simulations b). |
| In the text | |
 |
Fig. 4 Temporal evolution of the mean vertical mass flux ⟨ ρuz ⟩ for the two simulations G8 (solid blue line) and G8H8 (solid green line). The two vertical dashed black lines define the boundaries of the zoom displayed in the bottom left corner. |
| In the text | |
 |
Fig. 5 Left: temporal power spectrum of the vertical mass flux
|
| In the text | |
 |
Fig. 6 Left: temporal power spectrum for the vertical mass flux
|
| In the text | |
 |
Fig. 7 Harmonic analysis of the vertical velocity field uz for the G8 simulation around the eigenfrequency ω00 = 3.85. Top: amplitude of the modulus of the filtered velocity |Ûω00(x,z)| . Bottom: normalised vertical profile of the horizontal average of the filtered velocity |Ûω00| (solid black line) and the corresponding velocity eigenvector computed thanks to the linear stability analysis (dashed blue line). |
| In the text | |
 |
Fig. 8 Harmonic analysis of the vertical velocity field uz for the G8H8 simulation around the eigenfrequency ω00 = 3.80. Top: amplitude of the modulus of the filtered velocity |Ûω00(x,z)| . Bottom: normalised vertical profile of the horizontal average of the filtered velocity |Ûω00| (solid black line) and the corresponding eigenvector of the linear stability analysis (dashed blue line). |
| In the text | |
 |
Fig. 9 Comparison between normalised vertical velocity (uz) profiles for the fundamental mode (n = 0,ℓ = 0) according to the harmonic analysis of the DNS (solid black line) and the adiabatic eigenvector (dashed blue line). |
| In the text | |
 |
Fig. 10 Temporal evolution of the acoustic kinetic energy ratio R(t) for the two simulations G8 (solid blue line) and G8H8 (dashed green line) according to Eq. (22). |
| In the text | |
 |
Fig. 11 Vertical second-order velocity correlations for the simulations G8 (blue lines) and G8H8 (green lines). The acoustic contribution (Eq. (25)) is displayed as solid lines, while the convective one (Eq. (26)) is plotted as dashed lines. |
| In the text | |
 |
Fig. 12 Mean vertical profiles of radiative ℱrad (solid blue line), turbulent enthalpy ℱconv (dashed green line), kinetic ℱkin (dotted black line), modes ℱmod (dot-dashed magenta line), and total ℱtot (dotted red line) fluxes for the G8 a) and G8H8 b) simulations. All fluxes have been normalised with respect to the bottom value Fbot. |
| In the text | |
 |
Fig. 13 Ratio of the kinetic energy in acoustic modes displayed as a function of the maximum of the normalised convective flux ℱconv for the different DNS presented in Table 1. The blue dots correspond to the mean kinetic ratio obtained with the projection method, while the vertical grey bars represent the standard deviation. |
| In the text | |
 |
Fig. 14 Mean vertical profiles of density ρ for the G8 simulation (solid blue line) and the G8H8 simulation (dashed green line). |
| In the text | |
 |
Fig. 15 Ratio of the kinetic energy in acoustic modes displayed as a function of the mean density scale ⟨ Hρ ⟩ for the different DNS presented in Table 1. The blue dots correspond to the mean kinetic ratio obtained with the projection method, while the vertical grey bars represent the standard deviation. |
| In the text | |
 |
Fig. 16 Normalised kinetic energy power spectrum in the middle of the convective zone for the G8 simulation (solid blue line) and the G8H8 simulation (dashed green line). The kinetic energy spectrum E(k) ~ k-3 has been superimposed as a solid black line. |
| In the text | |
 |
Fig. 17 Ratio of the kinetic energy in acoustic modes displayed as a function of the integral scale (Eq. (39)) for the different DNS presented in Table 1. The blue dots correspond to the mean kinetic ratio obtained with the projection method, while the vertical gray bars represent the standard deviation. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


