| Issue |
A&A
Volume 527, March 2011
|
|
|---|---|---|
| Article Number | A74 | |
| Number of page(s) | 17 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201015383 | |
| Published online | 28 January 2011 | |
A Sino-German λ6 cm polarization survey of the Galactic plane
III. The region from 10° to 60° longitude
1
National Astronomical Observatories,
CAS, Jia-20 Datun Road, Chaoyang
District,
Beijing
100012,
PR China
e-mail: xhsun@nao.cas.cn; hjl@nao.cas.cn; wangchen@nao.cas.cn
2
Max-Planck-Institut für Radioastronomie,
Auf dem Hügel 69,
53121
Bonn,
Germany
e-mail: xhsun@mpifr-bonn.mpg.de; wreich@mpifr-bonn.mpg.de; preich@mpifr-bonn.mpg.de; rwielebinski@mpifr-bonn.mpg.de; pmueller@mpifr-bonn.mpg.de
Received: 13 July 2010
Accepted: 25 November 2010
Aims. We study polarized short-wavelength emission from the inner Galaxy, which is nearly invisible at long wavelengths because of depolarization. We attempt to obtain information on the diffuse continuum emission at short wavelengths to help us to separate Galactic thermal and non-thermal components.
Methods. We conducted a total intensity and polarization survey of the Galactic plane at λ6 cm using the Urumqi 25 m telescope for the Galactic longitude range of 10° ≤ l ≤ 60° and the Galactic latitude range of |b| ≤ 5°. Missing absolute zero levels of Stokes U and Q maps were restored by extrapolating the WMAP five-year K-band polarization data. For total intensities, we recovered missing large-scale components by referring to the Effelsberg λ11 cm survey.
Results. Total intensity and polarization maps are presented with an angular resolution of  and a sensitivity of 1 mK TB and 0.5 mK TB in total and polarized intensity, respectively. The λ6 cm polarized emission in the Galactic plane originates within about 4 kpc distance, which increases for polarized emission out of the plane. The polarization map shows “patches”, “canals”, and “voids” with no correspondence in total intensity. We attribute the patches to turbulent magnetic field cells. Canals are caused by abrupt variation in the polarization angles at the boundaries of patches rather than by foreground Faraday screens. The superimposition of foreground and Faraday screen rotated background emission almost cancels the polarized emission locally, such that polarization voids appear. By modelling the voids, we estimate the Faraday screen’s regular magnetic field along the line-of-sight to be larger than about 8 μG. We separated thermal (free-free) and non-thermal (synchrotron) emission according to their different spectral indices. The spectral index for the synchrotron emission is based on WMAP polarization data. The fraction of thermal emission at λ6 cm is about 60% in the plane.
and a sensitivity of 1 mK TB and 0.5 mK TB in total and polarized intensity, respectively. The λ6 cm polarized emission in the Galactic plane originates within about 4 kpc distance, which increases for polarized emission out of the plane. The polarization map shows “patches”, “canals”, and “voids” with no correspondence in total intensity. We attribute the patches to turbulent magnetic field cells. Canals are caused by abrupt variation in the polarization angles at the boundaries of patches rather than by foreground Faraday screens. The superimposition of foreground and Faraday screen rotated background emission almost cancels the polarized emission locally, such that polarization voids appear. By modelling the voids, we estimate the Faraday screen’s regular magnetic field along the line-of-sight to be larger than about 8 μG. We separated thermal (free-free) and non-thermal (synchrotron) emission according to their different spectral indices. The spectral index for the synchrotron emission is based on WMAP polarization data. The fraction of thermal emission at λ6 cm is about 60% in the plane.
Conclusions. The Sino-German λ6 cm polarization survey of the inner Galaxy provides new insights into the properties of the magnetized interstellar medium for this very complex Galactic region, which is Faraday thin up to about 4 kpc in the Galactic plane. Within this distance polarized patches are identified as intrinsic structures related to turbulent Galactic magnetic fields of spatial scales from 20(d/4 kpc) to 200(d/4 kpc) pc.
Key words: surveys / radio continuum: general / methods: observational / ISM: magnetic fields / polarization
© ESO, 2011
1. Introduction
We have mapped a broad region of the Galactic plane at λ6 cm as part of the Sino-German polarization survey of the Milky Way. In previous papers (Sun et al. 2007, Paper I; Gao et al. 2010, Paper II), we studied the Galactic plane emission in the anti-centre direction of the Milky Way. They included the study of the properties of selected regions showing evidence for strong Faraday rotation. Even in the direction of the anti-centre, Faraday screens have been observed at this relatively high radio frequency implying quite high rotation measures (RMs) and strong regular magnetic fields. In the present paper, we extend this work to a region closer to the Galactic centre, where Faraday effects are expected to be even more considerable.
Since the first detection of diffuse polarized emission from the Milky Way galaxy (Westerhout et al. 1962; Wielebinski et al. 1962), it has become evident that synchrotron emission is highly polarized. Radio polarization observations provide the most important data to study the magnetized warm interstellar medium (WIM), whose properties have not yet been fully understood. The separation of the thermal emission from the dominating non-thermal synchrotron component at low frequencies is also needed to determine the properties of the WIM. The inner Galactic plane is particularly interesting, but requires high-frequency observations to overcome strong depolarization effects. Radio continuum emission originates predominantly in spiral arms, and there are several arms along the line-of-sight towards the inner Galaxy (Hou et al. 2009).
Several total-intensity surveys covering the Galactic plane have already been conducted (see the review by Wielebinski 2005) and are accessible via the “MPIfR Survey Sampler”1. Among these surveys, the Effelsberg λ11 cm survey (Reich et al. 1990a) and λ21 cm survey (Reich et al. 1990b) include the inner Galaxy and have latitude extensions of |b| ≤ 5° and |b| ≤ 4°, respectively. These surveys have high resolution and sensitivity, so that they are well suited to study large-scale diffuse emission. Early high-frequency surveys such as the Parkes λ6 cm survey (Haynes et al. 1978) and the Nobeyama λ3 cm survey (Handa et al. 1987) also cover the inner Galactic plane. However, their latitude extents are |b| ≤ 2° and 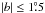 , respectively, too narrow to fully trace the layer of the WIM.
, respectively, too narrow to fully trace the layer of the WIM.
Polarization observations reveal the orientation of magnetic fields after correcting for Faraday rotation along the line-of-sight, which is produced by the magnetized diffuse WIM and magnetized thermal clumps. The clumps are called Faraday screens (Wolleben & Reich 2004). Some H ii regions have been identified as Faraday screens, but often Faraday screens do not have counterparts in total intensity observations at centimetre bands. Faraday rotation also causes depolarization (Sokoloff et al. 1998). The “polarization horizon” was defined by Landecker et al. (2002) as the distance beyond which entire depolarization occurs. In other words, the magnetized WIM is Faraday-thick beyond that distance (Sokoloff et al. 1998). The polarization horizon depends on wavelength and increases towards shorter wavelengths, where Faraday depolarization is less important (Sokoloff et al. 1998).
Previous polarization surveys of the Galactic plane were reviewed by Reich (2006). Some were carried out with single-dish telescopes such as the Effelsberg λ11 cm survey (Junkes et al. 1987; Duncan et al. 1999) and the Parkes λ13 cm survey (Duncan et al. 1997), and others by interferometers such as the Canadian Galactic Plane Survey (CGPS, Taylor et al. 2003; Uyanıker et al. 2003; Landecker et al. 2010) and the Southern Galactic plane survey (SGPS, Gaensler et al. 2001; Haverkorn et al. 2006) both at λ21 cm. Except for the CGPS survey, all the other surveys cover large parts of the inner Galaxy. The polarized emission observed by the Effelsberg telescope at λ11 cm and the Parkes telescope at λ13 cm in the inner Galaxy probably originates in the Sagittarius-Carina arm (Duncan et al. 1999), which implies a polarization horizon of about 1 kpc at Galactic longitudes of about 30°. The polarized emission in the SGPS survey at λ21 cm was claimed to originate in the Crux arm (Gaensler et al. 2001), corresponding to a polarization horizon of about 3.5 kpc at longitudes of about 330°. This is surprising, as the polarization horizon at λ21 cm is expected to be nearer than that at λ11 cm. However, these two surveys have not included polarized large-scale structures, which is crucial for any scientific interpretation of polarized structures resulting from Faraday effects (Reich 2006).
The paper is organized as follows. We briefly describe the observations and data processing in Sect. 2. Survey maps as well as zero-level restorations of U and Q are presented in Sect. 3. Discrete objects and polarized structures are discussed in Sects. 4 and 5, respectively. The separation of thermal and non-thermal emission components is performed in Sect. 6. In Sect. 7, we give a summary. The survey data will be available from the “MPIfR Survey Sampler” and the web-page of the λ6 cm survey at NAOC2 after completion of the project.
2. Observations and data processing
2.1. General
We carried out the Sino-German λ6 cm polarization survey of the Galactic plane by using the Urumqi 25 m telescope of the NAOC. The results of the first small survey section covering 122° ≤ l ≤ 129° and |b| ≤ 5° were published in Paper I. In Paper II, results for the region of 129° ≤ l ≤ 230° were presented. The region 60° ≤ l ≤ 122° will be discussed in a forthcoming paper. In Papers I and II, numerous Faraday screens without total intensity correspondence hosting strong regular magnetic fields were the most outstanding polarization features. In this paper, we present the results for the inner Galaxy in the range of 10° ≤ l ≤ 60° and − 5° ≤ b ≤ 5°, where diffuse emission is the most prominent.
To carry out the survey, the Urumqi telescope was equipped with a λ6 cm receiving system constructed at the MPIfR. The λ6 cm survey has a resolution of  and high sensitivity to match the available lower-frequency surveys from the Effelsberg telescope. The system temperature was about 22 K towards the zenith. The central frequency was 4.8 GHz (or λ = 6.25 cm as used for all calculations throughout the paper), and the original bandwidth was 600 MHz. To avoid the influence of stationary communication satellites, the bandwidth was often reduced to 295 MHz. The corresponding central frequency is then 4.963 GHz. The system gain is TB [K] /S [Jy] = 0.164. More detailed information about the receiving system was presented in Paper I.
and high sensitivity to match the available lower-frequency surveys from the Effelsberg telescope. The system temperature was about 22 K towards the zenith. The central frequency was 4.8 GHz (or λ = 6.25 cm as used for all calculations throughout the paper), and the original bandwidth was 600 MHz. To avoid the influence of stationary communication satellites, the bandwidth was often reduced to 295 MHz. The corresponding central frequency is then 4.963 GHz. The system gain is TB [K] /S [Jy] = 0.164. More detailed information about the receiving system was presented in Paper I.
The Galactic plane was scanned in both the longitude and latitude directions. For the longitude scans, the plane was divided into sections of typical size  . The size varied to include large structures completely and avoid strong sources at the edge areas. For the latitude scans, the plane was divided into sections 2° × 10° in size. Two neighbouring sections were overlapped by
. The size varied to include large structures completely and avoid strong sources at the edge areas. For the latitude scans, the plane was divided into sections 2° × 10° in size. Two neighbouring sections were overlapped by  to ease the later adjustment of intensity levels. The separation of sub-scans was 3′ to assure full sampling. The scanning velocity was 4°/min, thus a section was finished after about 100 min. Therefore, observations did not span too large ranges in azimuth and elevation, and the influence of the varying ground emission was significantly reduced. Observations were always made at night time with clear sky.
to ease the later adjustment of intensity levels. The separation of sub-scans was 3′ to assure full sampling. The scanning velocity was 4°/min, thus a section was finished after about 100 min. Therefore, observations did not span too large ranges in azimuth and elevation, and the influence of the varying ground emission was significantly reduced. Observations were always made at night time with clear sky.
The primary calibrator was 3C 286, which has a flux density of 7.5 Jy, a polarization percentage of 11.3%, and a polarization angle of 33°. Both 3C 48 and 3C 138 served as secondary calibrators. The unpolarized calibrators were 3C 295 and 3C 147. A calibration source was observed before and after each survey section.
The dual-channel receiving system provided left-hand (LHC) and right-hand (RHC) polarization channels, and the correlation of the two channels provided Stokes U and Q. The average of the LHC and RHC channels provided I, assuming no circular polarization. Raw data were recorded on disk. For each individual sub-scan, a linear fit based on the two ends was subtracted, U and Q channels were corrected for phase and parallactic angle, and finally raw maps were calculated. The raw maps of I, U, and Q were stored in nod2-format (Haslam 1974). Additional processing was based on a standard procedure developed for Effelsberg continuum and polarization observations as detailed in Papers I and II. Briefly, spikes were removed, baselines were corrected, and scanning effects were suppressed by the “unsharp masking” method (Sofue & Reich 1979). Each processed map was multiplied by a factor determined from the calibration source data to convert map units into a physical scale. The baselines of longitude scans were adjusted with respect to the level of the latitude scans. Therefore, structures exceeding about 10° in the latitude direction were missing in the original survey maps. Afterwards, maps observed in these orthogonal directions were added in the Fourier domain with the spatial weights defined by the typical scale of the scanning noise (Emerson & Gräve 1988). To eliminate position errors and shifts among the maps, we picked up strong sources and compared them with far more precise source positions from the NVSS survey (Condon et al. 1998) and made corrections if necessary. From the processing, it is clear that the I, U, and Q maps have the latitude ends set to zero. The polarization angle (ψ) and polarized intensity (PI) were calculated as  and
and  (Wardle & Kronberg 1974), where σU, Q is the average rms-noise of U and Q. We note that the polarization angles are relative to the Galactic north and run anti-clockwise.
(Wardle & Kronberg 1974), where σU, Q is the average rms-noise of U and Q. We note that the polarization angles are relative to the Galactic north and run anti-clockwise.
The rms-noise for the surveyed area is about 1 mK TB for I, and 0.5 mK TB for the U, Q, and PI maps, which was measured from nearly “empty” regions without obvious emission features or gradients. The theoretical rms-noise for I, U, and Q maps assuming a perfectly stable receiving system is calculated from the system temperature Tsys, the bandwidth Δν, and the integration time Δt (see Fig. 1) according to  . Four latitude and three longitude coverages were typically observed for each section. With a bandwidth of 295 MHz and an integration time of 0.75 s for each coverage, the theoretical rms-noise is 0.8 mK TB for I and 0.6 mK TB for U and Q. Thus, the measured rms-noise is close to the expectations for a perfect receiving system. The rms-noise varies because of the different bandwidths used and the effective integration time (see Fig. 1). In general, the rms-noise becomes larger towards lower longitude regions, where the diffuse emission is stronger and the typical elevations are lower. The systematic uncertainty in the polarization angle is about 1°, and the calibration scale error is about 5%. Both estimates were inferred from observations of 3C 286.
. Four latitude and three longitude coverages were typically observed for each section. With a bandwidth of 295 MHz and an integration time of 0.75 s for each coverage, the theoretical rms-noise is 0.8 mK TB for I and 0.6 mK TB for U and Q. Thus, the measured rms-noise is close to the expectations for a perfect receiving system. The rms-noise varies because of the different bandwidths used and the effective integration time (see Fig. 1). In general, the rms-noise becomes larger towards lower longitude regions, where the diffuse emission is stronger and the typical elevations are lower. The systematic uncertainty in the polarization angle is about 1°, and the calibration scale error is about 5%. Both estimates were inferred from observations of 3C 286.
 |
Fig. 1 Effective integration time in sec for I, U, and Q from top to bottom. The time was scaled by a factor of 0.5 when the observations were made with a reduced bandwidth of Δν = 295 MHz. |
2.2. Instrumental polarization
Instrumental effects related to the properties of the Urumqi telescope, the λ6 cm feed, and receiving system cause polarization from unpolarized sources. Thus, intrinsically unpolarized H ii regions show polarized intensity, which exhibits a ring-like pattern for compact sources. The radius of the ring is about that of the beam width, and the maximum intensity is measured to be less than 3% of the peak value of total intensity (Sun et al. 2006). Instrumental polarization at this level is not important towards the anti-centre region, where only a few strong sources are located. In the inner Galaxy, however, there are many strong compact H ii regions, which together add up so that their instrumental polarization becomes significant and a proper cleaning is required.
 |
Fig. 2 Example of instrumental polarization cleaning applied to the λ6 cm survey polarized intensity data for the case of the H ii region G30.7−0.1. The upper panel shows the original polarized intensity and the lower panel the cleaned map. The contours start at 50 mK TB and increase in steps of 50 mK TB. |
The cleaning method we applied has already been described in Paper I in some detail. By observing unpolarized calibrators, we obtained maps of total intensity (Ical) and polarization (Ucal and Qcal). Here the polarization is assumed to be caused completely by instrumental impurity, which can be quantitatively represented as the convolution between the total intensity of the calibrator and the instrumental terms (Uinst and Qinst) as Ucal = Ical ⊗ Uinst and Qcal = Ical ⊗ Qinst. We performed a de-convolution in the Fourier domain to derive the instrumental terms. We convolved the survey total intensity maps with the instrumental polarization terms to determine the instrumental polarization, and subtracted these instrumental contributions from the observed polarization maps to obtain the cleaned maps. This method was previously and successfully applied by Sofue et al. (1987).
We used the H ii region RCW 174 ( ,
,  ) as a calibrator, which shows a high signal-to-noise ratio. It was used to clean the survey maps fairly well. In Fig. 2, we show the elimination of the instrumental polarization for the H ii region G30.7 − 0.1. The total intensity of this H ii region is about 11 K TB, and the polarized intensity caused by instrumental effects is about 0.3 K TB, which is reduced to about 0.06 K TB, or about 0.5%, after cleaning.
) as a calibrator, which shows a high signal-to-noise ratio. It was used to clean the survey maps fairly well. In Fig. 2, we show the elimination of the instrumental polarization for the H ii region G30.7 − 0.1. The total intensity of this H ii region is about 11 K TB, and the polarized intensity caused by instrumental effects is about 0.3 K TB, which is reduced to about 0.06 K TB, or about 0.5%, after cleaning.
In general, the residual instrumental polarization is far lower than 1% for the cleaned maps. Sources with total intensities higher than 250 mK TB have a residual polarization at about the 5σ level. Compared to the large fluctuations in the diffuse polarized intensities along the Galactic plane, these residual instrumental effects are usually negligible.
3. Survey results
As described above, the I, U, and Q intensities were set to zero at both latitude edges (b = ± 5°), because of baseline fitting to remove the ground radiation contributions. This implies that the maps have a relative zero-level. For I maps, this is equivalent to an intensity offset, though the observed small-scale structures are not influenced. Thus, the zero-level setting of the total intensity is only crucial when the diffuse emission is quantitatively assessed as we do below when separating thermal and non-thermal emission (see Sect. 6). However, polarized intensities and polarization angles depend on U and Q non-linearly, so their morphology and structures are changed significantly by the missing large-scale emission (e.g. Reich 2006), which is thus essential to recover to ensure a correct physical interpretation.
3.1. Zero-level restoration for U and Q
Unfortunately, no λ6 cm polarization data exist at an absolute zero-level, to which we might refer. The ongoing C-Band All-Sky Survey (CBASS)3 is expected to provide the missing large-scale emission. The CBASS has a resolution of 44′ and a sensitivity of about 0.1 mK, which is very similar to that of the Urumqi λ6 cm polarization survey when smoothed to the same angular resolution. Thus, the CBASS data are well suited for zero-level restoration. However, as shown later, the required absolute zero-level of polarization at λ6 cm must be accurate to about 2 mK to be superior to the zero-level restoration scheme we present in the following.
We developed a calibration scheme for the λ6 cm survey in Paper I, where the correct zero-levels of U and Q were tied to the three-year WMAP K-band (22.8 GHz) data (Page et al. 2007). We now used the more precise five-year WMAP results (Hinshaw et al. 2009). The K-band polarization data include all large-scale structures. We calculated the corresponding polarized intensities at 4.8 GHz including all large-scale components ( ) by
) by  (1)and subsequently for U and Q
(1)and subsequently for U and Q![\begin{equation} \label{abso_uq} \begin{array}{rcl} U\rm ^{4.8\,GHz}_{zero}&=&{PI}\rm^{4.8\,GHz}_{zero} \sin\left(2\psi^{22.8\,GHz}+\mathcal{R}\lambda^2\right),\\[5mm] Q\rm^{4.8\,GHz}_{zero}&=&{PI}\rm^{4.8\,GHz}_{zero} \cos\left(2\psi^{22.8\,GHz}+\mathcal{R}\lambda^2\right), \end{array} \end{equation}](/articles/aa/full_html/2011/03/aa15383-10/aa15383-10-eq55.png) (2)where ψ is the polarization angle, βPI is the spectral index for the polarized intensity (T ∝ νβ with T being the brightness temperature and ν the frequency), and ℛ is the Faraday depth. Assuming the interstellar medium to be a uniform slab, the Faraday depth and RM observed from diffuse polarized emission are related by ℛ = 2RM (Sokoloff et al. 1998). For extragalactic sources and pulsars, the Faraday depth is equivalent to RM.
(2)where ψ is the polarization angle, βPI is the spectral index for the polarized intensity (T ∝ νβ with T being the brightness temperature and ν the frequency), and ℛ is the Faraday depth. Assuming the interstellar medium to be a uniform slab, the Faraday depth and RM observed from diffuse polarized emission are related by ℛ = 2RM (Sokoloff et al. 1998). For extragalactic sources and pulsars, the Faraday depth is equivalent to RM.
As already described in Paper I, we convolved the U and Q maps of both the λ6 cm survey and the WMAP K-band survey to a resolution of 2°, calculated the intensities according to Eqs. (1) and (2), estimated the differences from the observed λ6 cm maps, and finally added these differences to the original U and Qλ6 cm maps. However, towards the inner Galaxy significant depolarization might occur even at λ6 cm. The observed polarized λ6 cm emission originates at shorter distances than that observed at K-band. In this case, the above scheme needs to be modified, otherwise too much polarization will be added. We therefore need to determine the spectral index of the polarized intensity, investigate the polarization horizons at both wavelengths, and check the Faraday depths before applying any zero-level restoration.
3.1.1. Spectral index of polarized intensity
Diffuse polarized emission originates from the Galactic synchrotron radiation, while total intensity is a mixture of synchrotron and free-free emission. Hence, the total intensity spectral index is not that of the synchrotron emission. Polarization observations at low frequencies suffer from significant depolarization, and are thus not suited to determining the synchrotron spectral index. At high frequencies, polarized intensity is usually very weak because of the generally steep spectrum. In the inner Galaxy, polarized emission at both the WMAP K- and Ka-band (33 GHz) (Hinshaw et al. 2009) is fortunately strong enough for this purpose.
 |
Fig. 3 TT-plot between WMAP K-band (22.8 GHz) and Ka-band (33 GHz) for polarized intensities for the region of 40° ≤ l ≤ 60° (upper panel) and 10° ≤ l ≤ 30° (lower panel) within the latitude range of |b| ≤ 5°. |
We performed TT-plots (Turtle et al. 1962) of the polarized intensity between the K- and Ka-bands for every 10° × 10° section of the region 10° < l < 60° and |b| < 5°, and found a trend of steepening spectral index from larger to smaller longitudes. The transition region is between longitudes 30° and 40°. For the same area, Reich & Reich (1988a) reported a spectral steepening in total intensity between 408 MHz and 1420 MHz. We modelled the spectral index as follows. For the region 10° ≤ l ≤ 30° the spectral index is βPI = −3.1, for the region 40° ≤ l ≤ 60° the spectral index is βPI = −2.7 (Fig. 3), and for the transition region the spectral index is a linear interpolation between − 2.7 and − 3.1. We note that the spectral index error for the region 10° ≤ l ≤ 30° is Δβ = 0.1 from the TT-plot, but increased to Δβ = 0.4 for the area 40° ≤ l ≤ 60° because of the lower signal-to-noise ratio there.
At K- and Ka-bands, depolarization is negligible and the polarization from spinning dust can also be neglected (Gold et al. 2011). This means that polarized emission in both bands shows intrinsic synchrotron emission. The spectral index derived from polarization data also applies for the total intensity of the Galactic synchrotron emission component, i.e. βsyn = βPI.
3.1.2. Polarization horizon
To check whether the λ6 cm and K-band surveys observe polarized emission from the same polarization horizon, we performed simulations to show the polarized intensities at these two frequencies versus distances for several directions along the Galactic plane. The simulations were based on the hammurabi code developed by Waelkens et al. (2009) and the new Galactic 3D-emission model developed by Sun et al. (2008) using modifications for high-resolution simulations of selected patches by Sun & Reich (2009), where a Kolmogorov spectrum for the random magnetic fields was included. For each line of sight, the complex polarization  was calculated following Sun et al. (2008) as
was calculated following Sun et al. (2008) as 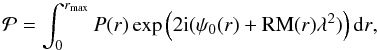 (3)where P(r) is the polarized intensity at r, ψ0(r) is the intrinsic polarization angle, and the integral was conducted from the observer to a specified distance of rmax along the line of sight. The polarized intensity is the absolute value of
(3)where P(r) is the polarized intensity at r, ψ0(r) is the intrinsic polarization angle, and the integral was conducted from the observer to a specified distance of rmax along the line of sight. The polarized intensity is the absolute value of  . The positions were selected to be in the plane and above the plane at latitudes of about 5° and longitudes between 10° and 60°. The simulations have an angular resolution of about 30″. The results are shown in Fig. 4, where the data have been averaged for an area with a radius of
. The positions were selected to be in the plane and above the plane at latitudes of about 5° and longitudes between 10° and 60°. The simulations have an angular resolution of about 30″. The results are shown in Fig. 4, where the data have been averaged for an area with a radius of  centred on the coordinates marked in each panel. As explained by Sun & Reich (2009), the coordinates of the target patches for simulations had to be adapted to the HEALPix (Górski et al. 2005) projection scheme. The polarized intensities at 22.8 GHz were scaled to 4.8 GHz with a spectral index detailed in Sect. 3.1.1 to facilitate the comparison.
centred on the coordinates marked in each panel. As explained by Sun & Reich (2009), the coordinates of the target patches for simulations had to be adapted to the HEALPix (Górski et al. 2005) projection scheme. The polarized intensities at 22.8 GHz were scaled to 4.8 GHz with a spectral index detailed in Sect. 3.1.1 to facilitate the comparison.
 |
Fig. 4 Simulated polarized intensity at λ6 cm (4.8 GHz) and K-band (22.8 GHz) versus distance for various directions as indicated by the Galactic coordinates in each panel. The dotted lines show the polarized intensity at K-band scaled to λ6 cm with a spectral index as modelled in Sect. 3.1.1. The solid lines show PI at λ6 cm. |
Figure 4 shows that at λ6 cm the polarization horizon in the Galactic plane is about 3 kpc for 10° ≤ l ≤ 30° and increases to about 5 kpc for 40° ≤ l ≤ 60°. We adopt 4 kpc as the λ6 cm polarization horizon in our discussion below. Figure 4 also shows that about 20%–30% of the intrinsic Galactic polarized emission is observed in the Galactic plane at λ6 cm. Above the Galactic plane at latitudes of about 5°, only less than about 20% of the polarized emission is missed. At the latitude edges of the λ6 cm survey, the polarized emission traced at both wavelengths originate in volumes that are not significantly different.
3.1.3. Faraday depth
The Faraday depth in a certain direction can be estimated from RMs of extragalactic sources, pulsars, and diffuse emission. The RMs of extragalactic sources contain contributions along the line-of-sight from the Sun to the Galactic outskirts. However, the polarization horizon inferred from the simulations is about 4 kpc at λ6 cm, which is shorter than the path length across the Galaxy. Therefore, RMs of extragalactic sources cannot be used directly. We retrieved RMs of pulsars in the region of 10° < l < 60° and |b| < 5° from the ATNF pulsar catalogue (Manchester et al. 2005). The distances of these pulsars were estimated using the NE2001 Galactic electron density model (Cordes & Lazio 2002). Pulsar RMs versus distances are displayed in Fig. 5. The average Faraday depth at distances up to the λ6 cm polarization horizon of 4 kpc was estimated from the standard deviation of pulsar RMs (excluding one RM outlier of 580 rad m-2) to be about 22 rad m-2. This corresponds to an angle rotation of about 5° at λ6 cm and we conclude that the Faraday depth in Eq. (2) can be neglected.
 |
Fig. 5 Pulsar RM versus distance based on the NE2001 electron density model. For most of the data the RM error bars are too small to be seen. |
Variations in the Faraday depth with longitude cannot be reliably obtained from the small number of pulsar RMs shown in Fig. 5. We simulated U and Q maps at 4.8 GHz and 22.8 GHz using the Galactic 3D-emission models by Sun et al. (2008), derived polarization angle maps at both frequencies, and calculated the RM map. The RMs are found to be within ± 10 rad m-2 from 10° longitude to 50° longitude, which is consistent with the result obtained for pulsar RMs. From l = 50° to l = 57° the RMs can be as large as about 50 rad m-2 corresponding to an angle rotation of about 11°, which in principle should be taken into account. As shown below, the zero-level correction that has to be added to U and Q for this region is less than 1 mK TB, which is about twice the rms-noise. Therefore, we neglect this RM correction.
3.1.4. A modified scheme for U and Q zero-level restoration
Because of the different polarization horizons at λ6 cm and the K-band in the Galactic plane, the scaled difference to the K-band polarized emission cannot be used to perform a correction to the polarization zero-levels. We thus modified the correction scheme of Paper I by referring to the high-latitude regions in the range  , where the λ6 cm and K-band surveys observe polarized emission from nearly the same volume. A similar modification was made in Paper II, where the polarized emission in the plane is very weak.
, where the λ6 cm and K-band surveys observe polarized emission from nearly the same volume. A similar modification was made in Paper II, where the polarized emission in the plane is very weak.
We obtained the differences between the λ6 cm and K-band U and Q maps for the two high-latitude regions. The correction values were calculated by linear interpolation in the direction of latitude and added to the original U and Q data. The U and Q corrections averaged from the difference maps for  are plotted versus longitude in Fig. 6. The values shown in Fig. 6 are the maximal and minimal corrections for U and Q being applied for each latitude scan. For the region of 50° ≤ l ≤ 60°, the average correction is about 0.6 mK TB for U and 0.8 mK TB for Q, which justifies neglecting a Faraday-depth-dependent correction in view of the rms-noise of 0.5 mK TB.
are plotted versus longitude in Fig. 6. The values shown in Fig. 6 are the maximal and minimal corrections for U and Q being applied for each latitude scan. For the region of 50° ≤ l ≤ 60°, the average correction is about 0.6 mK TB for U and 0.8 mK TB for Q, which justifies neglecting a Faraday-depth-dependent correction in view of the rms-noise of 0.5 mK TB.
 |
Fig. 6 Longitude profiles showing U and Q corrections averaged for |
In Fig. 7, we show the pixel distributions of polarized intensities and polarization angles. The distributions with and without adding the large-scale components are quite similar. This result differs significantly from that obtained for the survey regions of the outer Galaxy presented in Papers I and II, where the large-scale corrected polarization angle distribution peaks at 0°.
 |
Fig. 7 Pixel distribution of polarized intensities (top) and polarization angles (bottom) before and after baseline restoration. |
 |
Fig. 8 Maps at λ6 cm for the region 10° ≤ l ≤ 60°. From top to bottomI, U, and Q maps are shown as observed. Overlaid contours on the I map run in steps of 2n × 200 mK TB with n = 0, 1, 2, .... |
3.1.5. Accuracy of the zero-level restoration scheme
The spectral index of polarized intensity has an uncertainty of Δβ = 0.1 for the inner region 10° < l < 30°. This corresponds to a restoration uncertainty of less than 20% or about 2 mK TB for areas where the U and Q values are as high as 10 mK TB (Fig. 6). For the outer region 40° < l < 60°, the spectral index has a large uncertainty of Δβ = 0.4, but the typical added U and Q values are around 1 mK TB (Fig. 6). This again means an uncertainty of about 2 mK TB for the zero-level. In other words, the uncertainty from the applied zero-level restoration for the entire survey region caused by the spectral index uncertainty is up to the 4 × σ level of the observed polarized intensity, but mostly below.
On the basis of the simulations presented in Sect. 3.1.2, the λ6 cm survey could miss up to about 20% of polarized intensity at the latitude edges. This is equivalent to a spectral index uncertainty of about Δβ = 0.1. As already shown above, this does not have a significant influence on the results.
When the CBASS λ6 cm polarization survey becomes available, missing large-scale components of this survey can be added without extrapolation over a wide frequency range. Compared to the present extrapolation method, an improvement will be obtained in case the zero-level in U and Q can be measured with an accuracy better than 2 mK.
3.2. Overview of the survey maps
 |
Fig. 9 Zero-level restored PI maps overlaid by total intensity contours and bars showing B-vectors. The contours run in steps of 2n × 50 mK TB with n = 0, 1, 2, .... The lengths of B-vectors are proportional to PI. Below an intensity cutoff of 2.5 mK TB (5 × rms-noise), no bars are shown. |
The I, U, and Q maps are shown in Fig. 8. The PI maps calculated from the zero-level restored U and Q maps are shown in Figs. 9 and 10. The I maps display strong diffuse emission concentrated along the ridge of the Galactic plane, where a high density of discrete sources such as H ii regions and supernova remnants (SNRs) can be seen. The emission becomes stronger towards lower longitudes. The longitude profile for I averaged within an interval b = ± 2° is compared with that of the Parkes λ6 cm survey (Haynes et al. 1978) in Fig. 11. The total intensity structures agree quite well. The TT-plot yields an intensity ratio of 1.0 ± 0.1 and an arbitrary offset of about 1000 mK (which was added to the Parkes data release). This proves in addition that both λ6 cm surveys are consistent.
Polarized emission shows different structures from those seen in total intensity (Figs. 9 and 10). There is strong polarized emission even far above the plane, which is similar to that seen in the Effelsberg λ11 cm survey maps (Junkes et al. 1987; Duncan et al. 1999). However, the polarized structures revealed by these two surveys do not correspond to each other, because of different base-line settings and polarization horizons. A 10°-region centred at l = 50°, b = 0° has been observed as part of the Toruń λ6 cm survey project (Ryś et al. 2006). The most prominent polarized structures, such as the patch at  ,
, 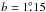 , agree with our λ6 cm polarization survey.
, agree with our λ6 cm polarization survey.
It is evident that the B-vectors do not align well with the Galactic plane, which is either intrinsic or caused by strong Faraday rotation along the line-of-sight.
The most prominent structures are:
-
1.
structures visible in both total and polarized intensities, whichare point sources and SNRs. Particularly bright sources areG34.7 − 0.4 (W 44), G39.7 − 2.0 (W 50), and G54.4 − 0.3 (HC 40). A weak polarized filament is traced from
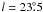 , b = 5° towards lower latitudes. This filament was previously identified as an extension of the North Polar Spur (NPS) by total intensity observations at λ21 cm by Sofue & Reich (1979). For the first time, we are also able to trace this filament in polarization;
, b = 5° towards lower latitudes. This filament was previously identified as an extension of the North Polar Spur (NPS) by total intensity observations at λ21 cm by Sofue & Reich (1979). For the first time, we are also able to trace this filament in polarization; -
2.
polarized patches without corresponding total intensities. The patches span wide scales from tens of arcmin to several degrees. Most of them are seen outside the Galactic plane ridge. More patches are seen at low than high longitudes. These patches are probably produced by turbulent fields as discussed below;
-
3.
narrow depolarization regions commonly called “canals”. They are most pronounced in the region around 11° < l < 15°. These canals are not related to total intensity structures. As demonstrated later, an abrupt polarization angle change by about 0.6π over 3′ can produce these canals;
-
4.
large depolarized regions we call “voids”. Most voids do not correspond to a total intensity minimum or other feature. An example is seen at
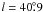 ,
,  . These regions were modelled in Sect. 5.2 by the Faraday screen model already used in Papers I and II.
. These regions were modelled in Sect. 5.2 by the Faraday screen model already used in Papers I and II.
4. Discrete objects
For point-like or compact sources, flux densities were obtained by fitting a two-dimensional elliptical Gaussian. A list of compact sources from the entire survey will be presented in a forthcoming paper. Studies of SNRs located in this area will also be presented in subsequent papers. Other discrete objects such as the NPS extension as well as H ii regions are discussed in this section. Polarized structures with no counterparts in total intensity are analysed in Sect. 5.
4.1. Extended sources in general
Prominent extended sources are found to be either SNRs or H ii regions. Their spectra differ and can be used to identify them. Shell-type SNRs are non-thermal sources with spectral indices close to α ~ −0.5, whereas H ii regions are thermal with nearly flat spectra. The spectra of strong sources can be determined from their integrated flux density at several frequencies. For weak sources, whose flux density cannot be determined very well, we investigated their spectra by TT-plots and fit their slopes. The maps throughout the paper were smoothed to the  required to perform TT-plots. The TT-plot method largely circumvents the influence of background emission differences amongst maps from different surveys. Plerions and pulsar wind nebulae (PWNe) are non-thermal SNRs, but exhibit flat spectra similar to those of H ii regions. However, all types of SNRs are polarized and show X-ray emission, while H ii regions are usually associated with strong infrared sources. The ratio of IRAS 60 μm to radio continuum intensity is usually much larger for H ii regions than for SNRs (e.g. Fürst et al. 1987). We used X-ray images from the ROSAT all-sky survey4 and high-resolution IRAS 60 μm maps (Cao et al. 1997) to distinguish between SNRs and H ii regions.
required to perform TT-plots. The TT-plot method largely circumvents the influence of background emission differences amongst maps from different surveys. Plerions and pulsar wind nebulae (PWNe) are non-thermal SNRs, but exhibit flat spectra similar to those of H ii regions. However, all types of SNRs are polarized and show X-ray emission, while H ii regions are usually associated with strong infrared sources. The ratio of IRAS 60 μm to radio continuum intensity is usually much larger for H ii regions than for SNRs (e.g. Fürst et al. 1987). We used X-ray images from the ROSAT all-sky survey4 and high-resolution IRAS 60 μm maps (Cao et al. 1997) to distinguish between SNRs and H ii regions.
 |
Fig. 11 Total intensity I along Galactic longitude averaged within b = ± 2°. The solid line shows the λ6 cm survey data and the dotted line the Parkes survey (Haynes et al. 1978) data with an offset of about 1000 mK. |
4.2. H ii regions
H ii regions reside predominantly in spiral arms and thus numerous H ii regions are seen in the present survey section as the line-of-sight intersects many spiral arms (Hou et al. 2009). Most of the known H ii regions were catalogued by Paladini et al. (2003) and Hou et al. (2009). They are visible in the I maps. Some emission complexes, such as for example the W 51 complex centred at  ,
, 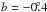 , host many individual H ii regions surrounded by diffuse emission. Such a study is beyond the scope of this paper. The λ6 cm survey reveals some previously unknown large and weak H ii regions as demonstrated by Shi et al. (2008). However, some efforts are required to discover new H ii regions in the current region because of obscuration by strong diffuse emission. We therefore limit our investigation to two objects out of the Galactic plane or longitudes close to l = 60°, where the diffuse emission is weaker.
, host many individual H ii regions surrounded by diffuse emission. Such a study is beyond the scope of this paper. The λ6 cm survey reveals some previously unknown large and weak H ii regions as demonstrated by Shi et al. (2008). However, some efforts are required to discover new H ii regions in the current region because of obscuration by strong diffuse emission. We therefore limit our investigation to two objects out of the Galactic plane or longitudes close to l = 60°, where the diffuse emission is weaker.
We identified two thermal structures in this survey region, which could be new H ii regions. The first one, G12.8 − 3.6, at 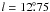 ,
, 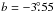 , has a size of about 100′ × 24′ (Fig. 12). Its integrated flux density is difficult to measure because of its complex environment. The spectral index from a TT-plot between the λ6 cm and Effelsberg λ11 cm data is α = 0.15 ± 0.29, which indicates that the source is thermal. The object is at the latitude limit of the Effelsberg λ21 cm survey, which was not used for the analysis. The thermal nature of G12.8 − 3.6 is further corroborated by infrared emission at 60 μm coinciding exactly with the radio emission (Fig. 12). The second source, G56.7 − 0.6, located at
, has a size of about 100′ × 24′ (Fig. 12). Its integrated flux density is difficult to measure because of its complex environment. The spectral index from a TT-plot between the λ6 cm and Effelsberg λ11 cm data is α = 0.15 ± 0.29, which indicates that the source is thermal. The object is at the latitude limit of the Effelsberg λ21 cm survey, which was not used for the analysis. The thermal nature of G12.8 − 3.6 is further corroborated by infrared emission at 60 μm coinciding exactly with the radio emission (Fig. 12). The second source, G56.7 − 0.6, located at  ,
, 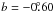 , has an apparent size of about 65′ × 27′ (Fig. 13). The flux densities measured from the λ6 cm survey and Effelsberg λ11 cm and λ21 cm surveys are 1.76 ± 0.09 Jy, 1.32 ± 0.07 Jy, and 1.96 ± 0.11 Jy, respectively, which yields a spectral index of α = 0.08 ± 0.06. Unfortunately, we cannot find exciting stars for both structures from other database.
, has an apparent size of about 65′ × 27′ (Fig. 13). The flux densities measured from the λ6 cm survey and Effelsberg λ11 cm and λ21 cm surveys are 1.76 ± 0.09 Jy, 1.32 ± 0.07 Jy, and 1.96 ± 0.11 Jy, respectively, which yields a spectral index of α = 0.08 ± 0.06. Unfortunately, we cannot find exciting stars for both structures from other database.
 |
Fig. 12 IRAS 60 μm greyscale image showing the H ii region G12.8 − 3.6. Contours display total intensities at λ6 cm starting at 10 mK TB and running in steps of 10 mK TB. |
 |
Fig. 13 λ6 cm total intensity image for the newly identified H ii region G56.7 − 0.6 shown in greyscale and contours, which start at 10 mK TB running further in steps of 10 mK TB. |
Another object G57.7+0.3 was already proposed by Sieber & Seiradakis (1984) to be a H ii region, but was not catalogued by Paladini et al. (2003). We measured flux densities at λ6 cm and in the Effelsberg λ11 cm and λ21 cm surveys to be 2.51 ± 0.13 Jy, 2.33 ± 0.13 Jy, and 2.54 ± 0.20 Jy, respectively. The spectral index is α = 0.00 ± 0.07. Since strong infrared emission is associated, we confirm this source to be a H ii region.
4.3. The southern North Polar Spur extension
The North Polar Spur (NPS) is most probably a local and very old SNR (Salter 1983). Its filamentary shell structure should not be affected when running across the Galactic plane. However, the strong emission from unrelated more distant Galactic plane emission causes so much confusion that it becomes very difficult to trace the NPS in this area. This was already demonstrated by λ21 cm observations by Sofue & Reich (1979). At λ6 cm, confusion is less pronounced, so that the filamentary southern NPS extension can be traced from l = 23°, b = 5° towards a latitude of about  in total intensity. At lower latitudes, it is confused with strong diffuse emission (Fig. 14). The NPS extension can also be traced by its polarization towards a lower latitude of about
in total intensity. At lower latitudes, it is confused with strong diffuse emission (Fig. 14). The NPS extension can also be traced by its polarization towards a lower latitude of about  and eventually to a latitude of about −3°. The average polarized intensity is about 15 mK TB. At about
and eventually to a latitude of about −3°. The average polarized intensity is about 15 mK TB. At about  ,
, 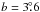 , the NPS divides into two filaments as seen at λ21 cm in total intensity (Sofue & Reich 1979). This is also seen at λ6 cm, where polarization from the two filaments can also be seen. The southern filament is longer and the northern part shorter at λ6 cm in total intensity than at λ21 cm. The southern filament is inclined by about 50° relative to the Galactic plane, while the northern filament is inclined by 30°. The B-vectors are roughly orientated tangential to the northern filament. For the southern filament, the B-vector direction is almost parallel to the Galactic plane for latitudes below about
, the NPS divides into two filaments as seen at λ21 cm in total intensity (Sofue & Reich 1979). This is also seen at λ6 cm, where polarization from the two filaments can also be seen. The southern filament is longer and the northern part shorter at λ6 cm in total intensity than at λ21 cm. The southern filament is inclined by about 50° relative to the Galactic plane, while the northern filament is inclined by 30°. The B-vectors are roughly orientated tangential to the northern filament. For the southern filament, the B-vector direction is almost parallel to the Galactic plane for latitudes below about  .
.
Wolleben (2007) modelled the NPS as two local shells based mainly on DRAO 1.4 GHz all-sky polarization survey data (Wolleben et al. 2006). However, this polarization survey suffers strong depolarization for latitudes below about 30°, which prevents the tracking of the NPS towards low latitudes. This global model does not account for the division of the filamentary shell that is observed. Follow-up observations extending the λ6 cm survey to the higher latitude NPS regions will soon be available hence we postpone any further discussion.
 |
Fig. 14 Polarization image for the southern NPS extension. Contours show total intensities and bars represent B-vectors. Contours start at 5 mK TB and run in steps of 4.5 mK TB. |
5. Polarized structures
5.1. General considerations
The maximum theoretical polarization percentage of synchrotron emission is about 75%. However, random magnetic fields may reduce the polarization percentage significantly. For a ratio of random to regular magnetic fields of 1.5, the intrinsic percentage polarization reduces to about 30% (Sun et al. 2008). We use this value throughout this paper. Two mechanisms may smear out polarized emission: depth depolarization and beam depolarization.
Depth depolarization occurs when polarized synchrotron emission is mixed with thermal gas. Polarized emission originating at different distances along the line-of-sight experiences a different amount of Faraday rotation and thus different polarization angles. Adding polarized emission components along the line-of-sight causes a reduction up to an entire cancellation of polarization. Quantitatively the amount of depolarization p, i.e. the ratio of the observed to intrinsic polarized percentage, can be written as (Sokoloff et al. 1998)  (4)where
(4)where 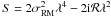 , and σRM is the RM scattering along the line-of-sight. If σRM = 0, Eq. (4) simplifies to p = sin(ℛλ2)/ℛλ2, which is frequently used.
, and σRM is the RM scattering along the line-of-sight. If σRM = 0, Eq. (4) simplifies to p = sin(ℛλ2)/ℛλ2, which is frequently used.
Beam depolarization occurs by means of Faraday rotation in front of the synchrotron-emitting medium. RM variations on scales smaller than the beam width result in a polarization angle difference. By integration across the beam, the observed polarization is reduced. Following Sokoloff et al. (1998) the depolarization factor p can be expressed as 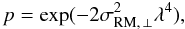 (5)where σRM, ⊥ is the RM variance across the beam. A rough estimate of σRM, ⊥ can be given as (Gaensler et al. 2001)
(5)where σRM, ⊥ is the RM variance across the beam. A rough estimate of σRM, ⊥ can be given as (Gaensler et al. 2001)  (6)where K is a constant, ne is the electron density, b is the strength of the random magnetic field, L is the depth through the Faraday rotating medium, and l is the coherent length of the random magnetic fields. The quantity KnebL is roughly equal to σRM and l is about the spatial scale resolved by the beam for a distance L.
(6)where K is a constant, ne is the electron density, b is the strength of the random magnetic field, L is the depth through the Faraday rotating medium, and l is the coherent length of the random magnetic fields. The quantity KnebL is roughly equal to σRM and l is about the spatial scale resolved by the beam for a distance L.
For this λ6 cm survey section, the polarization horizon in the Galactic plane was estimated to be about 4 kpc based on simulations described by Sun & Reich (2009) (see Fig. 4). At distances larger than 4 kpc, the average pulsar RM is about 200 rad m-2 and the RM variance along the line-of-sight is about 400 rad m-2 (Fig. 5). With these values, a depolarization factor p of about 0.2 is calculated using Eq. (4), which means a quite significant depolarization. The extended H ii region W 35 at  ,
, 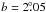 is located at a distance of about 2.9 kpc (Müller et al. 1987) and almost does not modulate polarization, which is consistent with the simulated polarization horizon. Synchrotron emission originates at most in spiral arms, so that we see polarized emission from the Sagittarius and the Scutum arms for the inner region and only from the Sagittarius arm for the outer region (see Fig. 15). For the longitude range of 50° < l < 60°, the line-of-sight is almost tangential to the Sagittarius arm (Fig. 15). It is commonly assumed that the large-scale magnetic fields follow the spiral arms (Han et al. 2006) and thus RM increases. This results in a higher degree of depolarization in this direction.
is located at a distance of about 2.9 kpc (Müller et al. 1987) and almost does not modulate polarization, which is consistent with the simulated polarization horizon. Synchrotron emission originates at most in spiral arms, so that we see polarized emission from the Sagittarius and the Scutum arms for the inner region and only from the Sagittarius arm for the outer region (see Fig. 15). For the longitude range of 50° < l < 60°, the line-of-sight is almost tangential to the Sagittarius arm (Fig. 15). It is commonly assumed that the large-scale magnetic fields follow the spiral arms (Han et al. 2006) and thus RM increases. This results in a higher degree of depolarization in this direction.
 |
Fig. 15 Sketch of the location of Galactic spiral arms taken from the polynomial spiral arm model of Hou et al. (2009). The longitude range of the present survey section is indicated. The dashed circle has a radius of 4 kpc, and indicates the polarization horizon at λ6 cm in the Galactic plane. |
The λ6 cm maps of this survey section show numerous depolarization features such as voids and canals (Figs. 9 and 10). Within the polarization horizon, depth depolarization is not important, because absolute pulsar RMs and their fluctuations are small. If beam depolarization is significant, we calculate that for a depolarization factor of p = 0.1 a RM variance across the beam of about 275 rad m-2 is required (see Eq. (5)). According to Eq. (6),  . Pulsar RMs give σRM ≤ 400 rad m-2, and l/L is about the beam size. This implies that σRM, ⊥ ≈ 6 rad m-2, or p = 1. We conclude that beam depolarization can be largely neglected.
. Pulsar RMs give σRM ≤ 400 rad m-2, and l/L is about the beam size. This implies that σRM, ⊥ ≈ 6 rad m-2, or p = 1. We conclude that beam depolarization can be largely neglected.
Most of the Faraday screens discussed in Papers I and II cause no large depolarization of background emission, but rotate the polarization background position angle. After rotation, the polarized background and foreground emission have different polarization angles compared to their surroundings. The observed sum of both components then shows a decrease in polarized intensity. A simple model was described and extensively used in Papers I and II. The positions were defined as “on” if the line-of-sight passes the Faraday screen and “off” otherwise. In general, the polarized intensity and angle towards “on” and “off” positions can be expressed as  (7)A Faraday screen causes an angle rotation ψs = RMsλ2. The subscripts “fg” and “bg” denote the foreground and background components, respectively. If only data at one frequency are available, the model may be simplified such that ψbg = ψfg = ψoff. For the anti-centre regions as discussed in Papers I and II, the dominating emission originates from the disk field, where the magnetic field is in general parallel to the Galactic plane. This means that ψoff is close to 0°.
(7)A Faraday screen causes an angle rotation ψs = RMsλ2. The subscripts “fg” and “bg” denote the foreground and background components, respectively. If only data at one frequency are available, the model may be simplified such that ψbg = ψfg = ψoff. For the anti-centre regions as discussed in Papers I and II, the dominating emission originates from the disk field, where the magnetic field is in general parallel to the Galactic plane. This means that ψoff is close to 0°.
5.2. Polarized patches
Regions showing strong polarized emission are predominantly “patches”, such as the extended feature centred at  ,
,  . Most of these patches do not have corresponding total intensity emission. The patches show either intrinsic polarization from a region in interstellar space or they are caused by Faraday screen modulation of polarized background emission.
. Most of these patches do not have corresponding total intensity emission. The patches show either intrinsic polarization from a region in interstellar space or they are caused by Faraday screen modulation of polarized background emission.
We consider a Faraday screen origin for the patches in general as being unlikely. In this scenario, the polarization angles of the foreground and background components must differ. Faraday screens have to rotate the polarized background, so that a reduction in the angle difference to the foreground component is obtained. In this case, the polarized emission appears to be stronger than for its surroundings. The survey maps show that the polarized intensity of the patches is in most cases much larger than that of their surroundings. In general, the ratio of PIoff/PIon is estimated to be less than about 0.3. If foreground and background polarized intensities are nearly identical, their angles should satisfy ψs ≈ ψfg − ψbg ≈ 90° (see Eq. (7)) towards all the patches. It is unlikely that this is true over a wide area. If foreground and background intensities differ significantly, a ratio of PIoff/PIon less than 0.3 cannot be caused at all by Faraday screen action. The RMs of the Faraday screens have to be less than 200 rad m-2 as inferred from pulsar RMs (Fig. 5). This results in a maximum angle rotation by a Faraday screen of about 45° at λ6 cm. Moreover, it is generally believed that the magnetic field perpendicular to the plane is much smaller than that parallel to the plane (e.g. Han & Qiao 1994; Han et al. 1999; Sun et al. 2008). Thus, angle differences between the background and foreground approach zero, and the patches are unlikely to be produced by Faraday screens.
Thus we consider the patches to be mainly intrinsically polarized features. Since they have no correspondence in total intensity, they are not caused by polarized objects such as SNRs. We instead consider the patches as diffuse synchrotron emission components originating from turbulent field cells, whose power spectrum follows a power law with a non-zero spectral index. The synchrotron emission observed from various turbulent field cells with different magnetic field orientations is smooth or almost structureless in total intensity. Polarized emission, however, shows irregularities or inhomogeneities depending on the field orientation in the different cells and their correlation. As shown by high angular resolution simulations by Sun & Reich (2009), turbulent magnetic fields with a Kolmogorov-like spectrum produce polarized features without corresponding total intensity. In the anti-centre region, the cosmic-ray electron density is low and the polarized intensities contributed by individual turbulent field cells is also small. Therefore we do not expect to see many polarized patches, which is consistent with the λ6 cm observations presented in Papers I and II. At K-band, the polarization horizon is large everywhere in the Galaxy. Many turbulent cells along the line-of-sight average out all distinct structures and thus individual polarized patches are not expected to be seen in the WMAP maps (Hinshaw et al. 2009), in agreement with the observations.
 |
Fig. 16 U, Q, and PI structure functions for the present λ6 cm survey section. The structure functions calculated for smoothed ( |
We apply structure functions to study the properties of the polarized patches following the approach by Sun & Reich (2009). It is yet unknown how the turbulent magnetic field properties are reflected in structure functions. The structure functions are not influenced by missing large-scale components, so the analysis is based on the original maps. The structure functions for U, Q, and PI at λ6 cm are shown in Fig. 16. For comparison, we retrieved the Effelsberg λ11 cm U and Q data for this survey region, smoothed them to the same angular resolution as the λ6 cm survey, and re-calculated the polarized intensity. The structure function for the smoothed PI at λ11 cm as well as the original with an angular resolution of  are also shown in Fig. 16. All structure functions can be described by a power law. The spectral index is about 0.3 for the
are also shown in Fig. 16. All structure functions can be described by a power law. The spectral index is about 0.3 for the  angular resolution data and 0.1 for the
angular resolution data and 0.1 for the 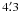 resolution λ11 cm PI data. The spectral index refers to spatial scales between about 20′ and 3°, which in turn correspond to sizes of about 20 pc and 200 pc for the polarized patches when their distance is 4 kpc.
resolution λ11 cm PI data. The spectral index refers to spatial scales between about 20′ and 3°, which in turn correspond to sizes of about 20 pc and 200 pc for the polarized patches when their distance is 4 kpc.
The morphology of patches resulting from turbulent magnetic-field cells should vary with frequency and resolution. The statistical properties such as the slope of the structure function should be independent of frequency. However, the statistics depend on the angular resolution. For low angular resolutions, polarized patches from nearby turbulent field cells dominate, causing the spectrum of the structure function to steepen. The slope of the λ11 cm structure functions on a logarithmic scale changed from about 0.1 to 0.24 after smoothing, which is consistent with the above expectation. The slope of 0.24 for smoothed λ11 cm PI is almost the same, compared to the value 0.3 calculated for the λ6 cm polarization data. This result supports our argument that polarized patches reflect turbulent field cells. The slight discrepancy between our results for λ11 cm and λ6 cm may stem from differences in their polarization horizon and correspondingly different emission volumes. Simulations were made as described in Sect. 3.1.2, which indicate that the polarization horizon at λ11 cm is about 1–3 kpc compared to about 4 kpc at λ6 cm.
5.3. Large polarization voids
We define “voids” as large almost completely depolarized regions without any correspondence in total intensity. Stil & Taylor (2007) reported on regions of about 10° in size, where the density of extragalactic sources from the NVSS is reduced by a factor 2–4. The size of these polarization shadows indicates a local origin for the depolarization of which Stil & Taylor (2007) discussed several possibilities. The voids seen at λ6 cm might be caused by neither depth nor beam depolarization as discussed above. We instead use the Faraday screen model described above to understand the polarization voids.
The void G40.9 − 4.2, located at  ,
,  , has a size of about 55′ × 40′ (Fig. 17). It is almost entirely depolarized towards its centre. To demonstrate the importance of absolute calibration when discussing “voids”, we show the original polarized intensity map and the map with large-scale emission added in Fig. 17. The void G40.9 − 4.2 appears as a polarized emission feature in the original map and turns into a depression when large-scale components are added. Instead of using the spectral index of βPI = −2.7, we also show the large-scale level restored with a spectral index of βPI = −3.1 (lower panel in Fig. 17), which is the lower spectral index limit for this longitude range (see Sect. 3.1.1). As shown in Fig. 17, the “void” shrinks slightly in size, but its morphology remains almost unchanged. This demonstrates that the uncertainties related to the spectral index determination do not have a large influence on the analysis of polarized structures.
, has a size of about 55′ × 40′ (Fig. 17). It is almost entirely depolarized towards its centre. To demonstrate the importance of absolute calibration when discussing “voids”, we show the original polarized intensity map and the map with large-scale emission added in Fig. 17. The void G40.9 − 4.2 appears as a polarized emission feature in the original map and turns into a depression when large-scale components are added. Instead of using the spectral index of βPI = −2.7, we also show the large-scale level restored with a spectral index of βPI = −3.1 (lower panel in Fig. 17), which is the lower spectral index limit for this longitude range (see Sect. 3.1.1). As shown in Fig. 17, the “void” shrinks slightly in size, but its morphology remains almost unchanged. This demonstrates that the uncertainties related to the spectral index determination do not have a large influence on the analysis of polarized structures.
Another outstanding example of a void is G55.3−1.5 located at  ,
,  (Fig. 18). Its size is about 51′ × 22′. The polarized emission drops close to zero towards its centre direction. In this case, the large-scale corrections of U and Q are very close to zero and therefore the maps with and without restoration are almost identical.
(Fig. 18). Its size is about 51′ × 22′. The polarized emission drops close to zero towards its centre direction. In this case, the large-scale corrections of U and Q are very close to zero and therefore the maps with and without restoration are almost identical.
According to the Faraday screen model (Eq. (7)), the foreground and background polarized intensity should be almost equal and the polarization angle rotation by the Faraday screen is ψs = 90° + ψfg − ψbg. The “off” polarization angle should be ψoff = (ψfg + ψbg)/2. For both voids, we measured ψoff ≈ 160°, implying that ψfg + ψbg = 320°. As both ψfg and ψbg are in the range between 0° and 180°, we obtain − 40° ≤ ψfg − ψbg ≤ 40°, and subsequently 50° ≤ ψs ≤ 130°. The RM of the Faraday screens needs to be about 220 rad m-2 to account for ψs = 50°, which is about the RM maximum constrained by pulsar RM in this area (Fig. 5). Larger values could not be entirely ruled out, because there are no pulsar RMs measured in the direction of the voids. For ψs = 50°, the angle difference between the foreground and background emission is about 40°. For a smaller angle difference, the RM of the Faraday screens must be larger.
 |
Fig. 17 Polarized intensity maps for the void G40.9 − 4.2. The upper panel shows the original map, the middle panel shows the map with the zero-level restored with a spectral index of βPI = −2.7 according to the restoration model discussed in Sect. 3.1.1. The lower panel shows the map with the zero-level restored using the lowest possible spectral index of βPI = −3.1 (see Fig. 3). PI is always shown in grey scale, and bars indicate polarization B-vectors. |
 |
Fig. 18 Polarization void G55.3 − 1.5. PI is shown in grey scale, and bars indicate polarization B-vectors. |
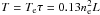 mK. Here the opacity τ was calculated according to the formula by Rohlfs & Wilson (2004), where ne is the electron density in cm-3 and L the size of the Faraday screen in pc. The electron temperature Te was taken to be 8000 K. The non-detection of the Faraday screen in total intensity provides an upper limit to the electron density of about 1.2 cm-3 for G40.9 − 4.2, and 1.4 cm-3 for G55.3 − 1.5, when taking 5 × rms-noise as an upper limit and assuming the depth of the Faraday screen is the mean of the projected major and minor axes. The resulting lower limits for the regular magnetic field strength along the line-of-sight is then about 8 μG for G40.9 − 4.2, and 9 μG for G55.3 − 1.5.
mK. Here the opacity τ was calculated according to the formula by Rohlfs & Wilson (2004), where ne is the electron density in cm-3 and L the size of the Faraday screen in pc. The electron temperature Te was taken to be 8000 K. The non-detection of the Faraday screen in total intensity provides an upper limit to the electron density of about 1.2 cm-3 for G40.9 − 4.2, and 1.4 cm-3 for G55.3 − 1.5, when taking 5 × rms-noise as an upper limit and assuming the depth of the Faraday screen is the mean of the projected major and minor axes. The resulting lower limits for the regular magnetic field strength along the line-of-sight is then about 8 μG for G40.9 − 4.2, and 9 μG for G55.3 − 1.5.
In the above discussions, we assumed uniform emissivity along the line-of-sight. For a local emissivity enhancement (see Sun et al. 2008, for details), the distance to the Faraday screens would be shorter, the size of the Faraday screen smaller, and its regular magnetic field stronger.
5.4. Canals
We see copious filamentary polarization minima in the λ6 cm survey maps, which were named “canals” in previous low-frequency observations (e.g. Haverkorn et al. 2004). The polarized intensity along the canals drops to typically 10%–30% compared to their surroundings. One of the most pronounced canals (see Fig. 9) runs from  ,
,  to
to 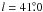 ,
, 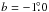 . Another striking one is located at l = 33°,
. Another striking one is located at l = 33°,  (Fig. 9). Many more canals appear towards the lower longitude regions, in particular the region between longitude of 10° and 13° (Fig. 10). The length of the canals varies from tens of arcmin to several degrees. The width of the canals is about 5′ to about 15′, similar to the beam size.
(Fig. 9). Many more canals appear towards the lower longitude regions, in particular the region between longitude of 10° and 13° (Fig. 10). The length of the canals varies from tens of arcmin to several degrees. The width of the canals is about 5′ to about 15′, similar to the beam size.
The depolarization along the canals may be attributed to variations in the polarization angles across the beam size D. We allow the angles to vary linearly by Δψ over a finite region x0, i.e.,  , where | x | ≤ x0/2. The depolarization factor p can then be calculated following Sokoloff et al. (1998) as
, where | x | ≤ x0/2. The depolarization factor p can then be calculated following Sokoloff et al. (1998) as 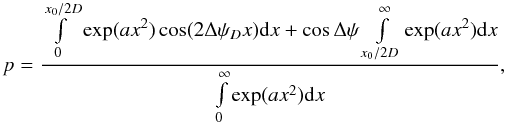 (8)where ΔψD = ΔψD/x0 is the angle increment over the beam D, and a = −4ln2. The results are shown in Fig. 19. The polarization angles around the canals in our maps show sharp variations, where x0 ≈ 3′ meaning that x0/D ≈ 0.3, and 0.5π ≲ Δψ ≲ 0.7π. These parameters correspond to depolarization factors of 0–0.3 in Fig. 19, which are consistent with the observations.
(8)where ΔψD = ΔψD/x0 is the angle increment over the beam D, and a = −4ln2. The results are shown in Fig. 19. The polarization angles around the canals in our maps show sharp variations, where x0 ≈ 3′ meaning that x0/D ≈ 0.3, and 0.5π ≲ Δψ ≲ 0.7π. These parameters correspond to depolarization factors of 0–0.3 in Fig. 19, which are consistent with the observations.
 |
Fig. 19 Depolarization factors for different polarization angle change (Δψ) across the scale x0 and the ratio of x0 to the beam size D. |
Variations in the polarization angles can be either intrinsic or extrinsic (Haverkorn et al. 2004). At λ6 cm an angle change of 90° requires a Faraday depth of about 400 rad m-2, which is not supported by pulsar RMs for this area. Therefore an intrinsic scenario for the origin of the canals is likely, which means that they are caused by rapid variations in the polarization angle across the beam size. Thus, canals delineate boundaries of polarized patches produced by turbulent magnetic field cells whose polarization angles differ. Whenever the angle difference matches the conditions for small depolarization factors displayed in Fig. 19, canals are expected to show up in the polarized intensity maps.
6. Total intensity emission from the Galactic disk: thermal and non-thermal separation
By combining the present λ6 cm survey section with the corresponding Effelsberg λ11 cm and λ21 cm maps, we performed a decomposition of thermal and non-thermal emission components according to their different spectra. For this purpose, all maps were smoothed to 10′.
The observed total intensities T(ν) consist of several components  (9)where Tcmb = 2.728 ± 0.004 K (Fixsen et al. 1996) is the isotropic brightness temperature of the cosmic microwave background radiation. This component was already removed from the λ6 cm data by applying a zero-level setting. The contribution from unresolved extragalactic sources Tegs(ν) is only about several mK at λ6 cm (e.g. Reich & Reich 1988a) and thus can be ignored in view of the much higher Galactic emission in the Galactic plane. As stated before, the λ6 cm maps miss Galactic large-scale emission and Tzero must be corrected by using other data.
(9)where Tcmb = 2.728 ± 0.004 K (Fixsen et al. 1996) is the isotropic brightness temperature of the cosmic microwave background radiation. This component was already removed from the λ6 cm data by applying a zero-level setting. The contribution from unresolved extragalactic sources Tegs(ν) is only about several mK at λ6 cm (e.g. Reich & Reich 1988a) and thus can be ignored in view of the much higher Galactic emission in the Galactic plane. As stated before, the λ6 cm maps miss Galactic large-scale emission and Tzero must be corrected by using other data.
The emission from the Galaxy Tgal(ν) can be written as 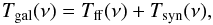 (10)where Tff(ν) ∝ νβff stands for the brightness temperature of free-free emission and Tsyn(ν) ∝ νβsyn for synchrotron emission. For latitudes in the range
(10)where Tff(ν) ∝ νβff stands for the brightness temperature of free-free emission and Tsyn(ν) ∝ νβsyn for synchrotron emission. For latitudes in the range  , it is known that the synchrotron emission clearly dominates the observed total intensity. We tie the zero-level of the λ6 cm data to the Effelsberg λ11 cm survey, which was corrected for missing large-scale emission (see Reich et al. 1990a, for details). The λ11 cm intensities for the area
, it is known that the synchrotron emission clearly dominates the observed total intensity. We tie the zero-level of the λ6 cm data to the Effelsberg λ11 cm survey, which was corrected for missing large-scale emission (see Reich et al. 1990a, for details). The λ11 cm intensities for the area  were extrapolated towards λ6 cm using the spectral index model devised in Sect. 3.1.1. The difference between the extrapolated and the original λ6 cm data were fitted linearly along latitudes and the offsets were added to the observed λ6 cm data. The assumption of a very small thermal emission fraction for the area
were extrapolated towards λ6 cm using the spectral index model devised in Sect. 3.1.1. The difference between the extrapolated and the original λ6 cm data were fitted linearly along latitudes and the offsets were added to the observed λ6 cm data. The assumption of a very small thermal emission fraction for the area  was checked using the WMAP free-free emission template (Gold et al. 2009). By extrapolating the thermal component to λ11 cm, we find that it amounts to 2%–7% of the total intensity. By neglecting this thermal emission, the λ6 cm total intensity was underestimated up to 4 mK TB, which is less than the 5 × σ level for total intensity.
was checked using the WMAP free-free emission template (Gold et al. 2009). By extrapolating the thermal component to λ11 cm, we find that it amounts to 2%–7% of the total intensity. By neglecting this thermal emission, the λ6 cm total intensity was underestimated up to 4 mK TB, which is less than the 5 × σ level for total intensity.
 |
Fig. 20 Decomposed thermal (upper panel) and non-thermal component (lower panel) for the λ6 cm survey between 10° ≤ l ≤ 60° based on the non-thermal spectral index model in Sect. 3.1.1 and βff = −2.1 for optically thin thermal emission. |
For the separation of thermal and non-thermal emission, we follow the method already used by Paladini et al. (2005) and others. The thermal fraction at frequency ν0 is calculated as 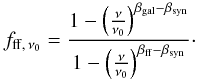 (11)It is assumed that the combination of free-free emission and synchrotron emission results in a power-law, namely Tgal(ν) ∝ νβgal. The λ6 cm data together with the Effelsberg λ11 cm and λ21 cm data were used to derive the spectral index βgal. Good linear relations on logarithmic scales hold for almost all the pixels. The spectral index of free-free emission is fixed as βff = −2.1, because the optical thin condition is in general satisfied in this wavelength range (Paladini et al. 2005). The spectral index of the synchrotron emission is modelled in Sect. 3.1.1 according to the polarized intensities observed at K- and Ka-bands by WMAP. The spectral index towards the inner Galaxy is consistent with that obtained by Reich & Reich (1988a) for the frequency range between 408 MHz and 1420 MHz, which justifies the use of spectral indices derived in Sect. 3.1.1 to the frequency range of 1.4 GHz to 4.8 GHz as well. For reliable results, the three spectral indices have to satisfy βsyn < βgal < βff. If βgal is smaller than the spectral index of synchrotron emission, we consider the entire emission as non-thermal. This situation happens at some spots out of the Galactic plane, where uncertainties in the zero-level setting have the largest influence on the spectral index. If βgal > −2.1, which happens for a few strong sources in the Galactic plane, the emission is attributed entirely to the free-free radiation.
(11)It is assumed that the combination of free-free emission and synchrotron emission results in a power-law, namely Tgal(ν) ∝ νβgal. The λ6 cm data together with the Effelsberg λ11 cm and λ21 cm data were used to derive the spectral index βgal. Good linear relations on logarithmic scales hold for almost all the pixels. The spectral index of free-free emission is fixed as βff = −2.1, because the optical thin condition is in general satisfied in this wavelength range (Paladini et al. 2005). The spectral index of the synchrotron emission is modelled in Sect. 3.1.1 according to the polarized intensities observed at K- and Ka-bands by WMAP. The spectral index towards the inner Galaxy is consistent with that obtained by Reich & Reich (1988a) for the frequency range between 408 MHz and 1420 MHz, which justifies the use of spectral indices derived in Sect. 3.1.1 to the frequency range of 1.4 GHz to 4.8 GHz as well. For reliable results, the three spectral indices have to satisfy βsyn < βgal < βff. If βgal is smaller than the spectral index of synchrotron emission, we consider the entire emission as non-thermal. This situation happens at some spots out of the Galactic plane, where uncertainties in the zero-level setting have the largest influence on the spectral index. If βgal > −2.1, which happens for a few strong sources in the Galactic plane, the emission is attributed entirely to the free-free radiation.
The thermal and non-thermal components separated in this way for the inner Galactic plane are shown in Fig. 20. The Effelsberg λ21 cm survey has latitude limits of b = ± 4°, so we perform the decomposition up to that latitude. It is obvious that the thermal emission component is more confined to the Galactic plane than the non-thermal emission. We note that some SNRs such as W 50 and SNR G53.2 − 2.6 show up as distinct sources in the thermal emission, because their spectral indices are larger than that of the diffuse synchrotron emission. However, these individual objects do not influence our results, which focus on the large-scale diffuse emission.
 |
Fig. 21 Galactic latitude profiles for the averaged thermal emission component at λ6 cm (solid lines), the averaged WMAP free-free emission (dotted line), and the baseline-corrected λ6 cm total intensity (dot-dashed line). |
 |
Fig. 22 Galactic latitude profiles for the averaged thermal emission component at λ6 cm derived with the spectral index βsyn = −2.7 (solid lines) and βsyn = −3.1 (dotted line). |
On average, the thermal fraction is about 60% at the Galactic plane for the longitude range of 10° ≤ l ≤ 60°. The thermal fraction decreases towards higher latitudes and drops to about 10% for latitudes of ± 2°, becoming about zero at latitudes beyond ± 4°. The thermal fraction reaches maximum values of about 78% within the longitude range 20° < l < 30° and latitude range of  . This fraction is similar to the value of 82% reported by Paladini et al. (2005). The corresponding maximum thermal fraction at 1.4 GHz is about 51%. Reich & Reich (1988b) estimated a fraction of about 40% for the longitude range of 15° ≤ l ≤ 50° at that frequency, whereas Paladini et al. (2005) obtained a value of 68%. We ascribe this inconsistency to the different spectral indices used for the synchrotron component, which was βsyn = −2.7 by Paladini et al. (2005), but βsyn = −3.1 for this region in the present study. The spectral index of synchrotron emission we derived from the WMAP K- and Ka-band polarized intensities in Sect. 3.1.1 is quite probably the more reliable substitute for βsyn. The maximum thermal fraction is about 60% in the range of 36° < l < 44° and |b| ≤ 4°, corresponding to about 36% at 1.4 GHz. This is consistent with the result obtained by Alves et al. (2010) based on a recombination line study when taking the uncertainties of this approach into account, as discussed by Alves et al. (2010).
. This fraction is similar to the value of 82% reported by Paladini et al. (2005). The corresponding maximum thermal fraction at 1.4 GHz is about 51%. Reich & Reich (1988b) estimated a fraction of about 40% for the longitude range of 15° ≤ l ≤ 50° at that frequency, whereas Paladini et al. (2005) obtained a value of 68%. We ascribe this inconsistency to the different spectral indices used for the synchrotron component, which was βsyn = −2.7 by Paladini et al. (2005), but βsyn = −3.1 for this region in the present study. The spectral index of synchrotron emission we derived from the WMAP K- and Ka-band polarized intensities in Sect. 3.1.1 is quite probably the more reliable substitute for βsyn. The maximum thermal fraction is about 60% in the range of 36° < l < 44° and |b| ≤ 4°, corresponding to about 36% at 1.4 GHz. This is consistent with the result obtained by Alves et al. (2010) based on a recombination line study when taking the uncertainties of this approach into account, as discussed by Alves et al. (2010).
We compared the thermal emission component derived with the WMAP five-year MEM free-free emission template (Gold et al. 2009). Both maps were smoothed to 2° angular resolution to eliminate the influence of small-scale structures. The profiles averaged for the longitude range of 10° < l < 30° and 40° < l < 60° are shown in Fig. 21. Near the plane within b = ± 2°, the thermal emission we obtained is larger than that from the WMAP template by about 20%. The inconsistency may stem for a small part from the uncertainties in recovering the large-scale emission at λ6 cm. There are, however, large uncertainties in the WMAP template (Gold et al. 2009) towards the Galactic plane. In particular, the influence of anomalous dust emission is unclear and needs further investigation.
Since the spectral index has particularly large uncertainties for the area 40° < l < 60°, we investigated its potential influence on the accuracy to separate thermal and non-thermal components. We used the most negative spectral index possible, βsyn = −3.1, instead of βsyn = −2.7, to calculate the missing large-scale emission to be added and repeated the separation with this spectral index. The difference is quite significant as displayed in Fig. 22. However, using a spectral index of βsyn = −3.1 results in significant thermal emission even at high latitudes. This clearly contradicts the results from WMAP. We conclude that the spectral index must be close to βsyn = −2.7, which we used to perform our separation.
7. Summary
We have presented I, U, Q, and PI maps covering the region 10° ≤ l ≤ 60° and |b| ≤ 5° of the Sino-German λ6 cm survey of the Galactic plane. We have briefly described the observations and data processing, in addition to the restoration process to obtain the correct zero-levels in U and Q using the WMAP five-year K-band data, which needs modification compared to the anti-centre survey sections because of different polarization horizons at λ6 cm and K-band. Combining simulations by Sun & Reich (2009) for the diffuse Galactic emission with RMs from pulsars we argue that the polarization horizon at λ6 cm is about 4 kpc in the Galactic plane, so that the observed polarized emission originates from the Sagittarius or the Scutum arm. At K-band, the polarization horizon exceeds the dimension of the Galaxy. At absolute latitudes of around 5°, however, the differences in polarized emission at both wavelengths is largely reduced and almost the same volume is observed.
There are various structures in the λ6 cm polarized intensity maps that have no counterpart in total intensity. We have analysed the properties of polarized patches and concluded that they are caused by turbulent magnetic-field cells. This demonstrates that polarization measurements have great potential to retrieve the turbulent properties of Galactic magnetic fields. We show that the observed “canals” occur when polarization angles vary by 0.5π–0.7π on scales of about 3′ along the boundaries of polarized patches. Large depolarization “voids” are regions where the polarized intensity drops close to zero. They result from Faraday screens at about half the distance of the polarization horizon. The screens rotate the background polarization such that it cancels foreground polarization of the same intensity. These Faraday screens must host strong regular magnetic fields along the line-of-sight.
This λ6 cm survey section also enables high-frequency studies of known objects and the discovery of weak H ii regions and SNRs. We briefly discussed two newly identified H ii regions G12.8 − 3.6 and G56.7 − 0.6. We were able to trace the NPS extension closer towards the Galactic plane in polarization and total intensity than at longer wavelengths.
We have separated thermal and non-thermal components for this Galactic plane region, where an adjustment of the λ6 cm base-levels for total intensities was made by referring to the Effelsberg λ11 cm survey. For the separation process, we decompose the total intensity according to the spectral index of thermal emission (βff = −2.1) and synchrotron emission. The synchrotron spectral index was deduced from WMAP K- and Ka-band polarization maps. At λ6 cm, the fraction of thermal emission in the plane is about 60% on average.
We have demonstrated that the total intensity and polarized structures revealed in the λ6 cm survey maps provide new and important insights into the magneto-ionic properties of the Galaxy.
Acknowledgments
We like to thank the staff of the Urumqi Observatory for qualified assistance during the installation of the receiving system and the survey observations. In particular we are grateful to Otmar Lochner for the construction of the λ6 cm receiver, installation and commissioning. Maozheng Chen and Jun Ma helped with the installation of the λ6 cm receiving system and maintained it since 2004. We thank Prof. Ernst Fürst for his support of the survey project and critical reading of the manuscript. The MPG and the NAOC supported the construction of the Urumqi λ6 cm receiving system by special funds. The Chinese survey team is supported by the National Natural Science foundation of China (10773016, 10833003, 10821061) and the National Key Basic Research Science Foundation of China (2007CB815403). X.H.S. acknowledges financial support by the MPG and by Prof. Michael Kramer during his stay at MPIfR Bonn. Finally we like to thank the referee for constructive comments, which helped in particular to clarify the calibration procedures used.
References
- Alves, M. I. R., Davies, R. D., Dickinson, C., et al. 2010, MNRAS, 405, 1654 [NASA ADS] [Google Scholar]
- Cao, Y., Terebey, S., Prince, T. A., & Beichman, C. A. 1997, ApJS, 111, 387 [NASA ADS] [CrossRef] [Google Scholar]
- Condon, J. J., Cotton, W. D., Greisen, E. W., et al. 1998, AJ, 115, 1693 [NASA ADS] [CrossRef] [Google Scholar]
- Cordes, J. M., & Lazio, T. J. W. 2002, unpublished [arXiv:0207156] [Google Scholar]
- Duncan, A. R., Haynes, R. F., Jones, K. L., & Stewart, R. T. 1997, MNRAS, 291, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Duncan, A. R., Reich, P., Reich, W., & Fürst, E. 1999, A&A, 350, 447 [NASA ADS] [Google Scholar]
- Emerson, D. T., & Gräve, R. 1988, A&A, 190, 353 [NASA ADS] [Google Scholar]
- Fixsen, D. J., Cheng, E. S., Gales, J. M., et al. 1996, ApJ, 473, 576 [NASA ADS] [CrossRef] [Google Scholar]
- Fürst, E., Reich, W., & Sofue, Y. 1987, A&AS, 71, 63 [NASA ADS] [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
- Gaensler, B. M., Dickey, J. M., McClure-Griffiths, N. M., et al. 2001, ApJ, 549, 959 [NASA ADS] [CrossRef] [Google Scholar]
- Gao, X. Y., Reich, W., Han, J. L., et al. 2010, A&A, 515, A64 (Paper II) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gold, B., Bennett, C. L., Hill, R. S., et al. 2009, ApJS, 180, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Gold, B., Odegard, N., Weiland, J. L., et al. 2011, ApJS, 192, 15 [Google Scholar]
- Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Han, J. L., & Qiao, G. J. 1994, A&A, 288, 759 [NASA ADS] [Google Scholar]
- Han, J. L., Manchester, R. N., & Qiao, G. J. 1999, MNRAS, 306, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Han, J. L., Manchester, R. N., Lyne, A. G., Qiao, G. J., & van Straten, W. 2006, ApJ, 642, 868 [NASA ADS] [CrossRef] [Google Scholar]
- Handa, T., Sofue, Y., Nakai, N., Hirabayashi, H., & Inoue, M. 1987, PASJ, 39, 709 [NASA ADS] [Google Scholar]
- Haslam, C. G. T. 1974, A&AS, 15, 333 [Google Scholar]
- Haverkorn, M., Katgert, P., & de Bruyn, A. G. 2004, A&A, 427, 549 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haverkorn, M., Gaensler, B. M., McClure-Griffiths, N. M., Dickey, J. M., & Green, A. J. 2006, ApJS, 167, 230 [CrossRef] [Google Scholar]
- Haynes, R. F., Caswell, J. L., & Simons, L. W. J. 1978, AuJPAS, 45, 1 [Google Scholar]
- Hinshaw, G., Weiland, J. L., Hill, R. S., et al. 2009, ApJS, 180, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Hou, L. G., Han, J. L., & Shi, W. B. 2009, A&A, 499, 473 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Junkes, N., Fürst, E., & Reich, W. 1987, A&AS, 69, 451 [NASA ADS] [Google Scholar]
- Landecker, T. L., Uyanıker, B., & Kothes, R. 2002, in Astrophysical Polarized Backgrounds, ed. S. Cecchini, S. Cortiglioni, R. Sault, & C. Sbarra, AIP Conf. Ser., 609, 9 [Google Scholar]
- Landecker, T. L., Reich, W., Reid, R. I., et al. 2010, A&A, 520, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Manchester, R. N., Hobbs, G. B., Teoh, A., & Hobbs, M. 2005, AJ, 129, 1993 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, P., Reif, K., & Reich, W. 1987, A&A, 183, 327 [NASA ADS] [Google Scholar]
- Page, L., Hinshaw, G., Komatsu, E., et al. 2007, ApJS, 170, 335 [NASA ADS] [CrossRef] [Google Scholar]
- Paladini, R., Burigana, C., Davies, R. D., et al. 2003, A&A, 397, 213 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paladini, R., De Zotti, G., Davies, R. D., & Giard, M. 2005, MNRAS, 360, 1545 [NASA ADS] [CrossRef] [Google Scholar]
- Reich, W. 2006, in Cosmic Polarization, ed. R. Fabbri (Research signpost), 91 [Google Scholar]
- Reich, P., & Reich, W. 1988a, A&AS, 74, 7 [Google Scholar]
- Reich, P., & Reich, W. 1988b, A&A, 196, 211 [NASA ADS] [Google Scholar]
- Reich, W., Fürst, E., Reich, P., & Reif, K. 1990a, A&AS, 85, 633 [Google Scholar]
- Reich, W., Reich, P., & Fürst, E. 1990b, A&AS, 83, 539 [NASA ADS] [Google Scholar]
- Rohlfs, K., & Wilson, T. L. 2004, Tools of radio astronomy, ed. K. Rohlfs, & T. L. Wilson, 261 [Google Scholar]
- Ryś, S., Chyży, K. T., Kus, A., et al. 2006, Astron. Nachr., 327, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Salter, C. J. 1983, BASI, 11, 1 [Google Scholar]
- Shi, W., Sun, X., Han, J., Gao, X., & Xiao, L. 2008, ChJAA, 8, 575 [Google Scholar]
- Sieber, W., & Seiradakis, J. H. 1984, A&A, 130, 257 [NASA ADS] [Google Scholar]
- Sofue, Y., & Reich, W. 1979, A&AS, 38, 251 [NASA ADS] [Google Scholar]
- Sofue, Y., Reich, W., Inoue, M., & Seiradakis, J. H. 1987, PASJ, 39, 95 [NASA ADS] [Google Scholar]
- Sokoloff, D. D., Bykov, A. A., Shukurov, A., et al. 1998, MNRAS, 299, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Stil, J. M., & Taylor, A. R. 2007, ApJ, 663, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Sun, X. H., & Reich, W. 2009, A&A, 507, 1087 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sun, X. H., Reich, W., Han, J. L., Reich, P., & Wielebinski, R. 2006, A&A, 447, 937 [Google Scholar]
- Sun, X. H., Han, J. L., Reich, W., et al. 2007, A&A, 463, 993 (Paper I) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sun, X. H., Reich, W., Waelkens, A., & Enßlin, T. A. 2008, A&A, 477, 573 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Taylor, A. R., Gibson, S. J., Peracaula, M., et al. 2003, AJ, 125, 3145 [NASA ADS] [CrossRef] [Google Scholar]
- Turtle, A. J., Pugh, J. F., Kenderdine, S., & Pauliny-Toth, I. I. K. 1962, MNRAS, 124, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Uyanıker, B., Landecker, T. L., Gray, A. D., & Kothes, R. 2003, ApJ, 585, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Waelkens, A., Jaffe, T., Reinecke, M., Kitaura, F. S., & Enßlin, T. A. 2009, A&A, 495, 697 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wardle, J. F. C., & Kronberg, P. P. 1974, ApJ, 194, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Westerhout, G., Seeger, C. L., Brouw, W. N., & Tinbergen, J. 1962, Bull. Astron. Inst. Netherlands, 16, 187 [NASA ADS] [Google Scholar]
- Wielebinski, R. 2005, in Cosmic Magnetic Fields, ed. R. Wielebinski, & R. Beck, Lecture Notes in Physics (Berlin: Springer Verlag), 664, 89 [Google Scholar]
- Wielebinski, R., Shakeshaft, J. R., & Pauliny-Toth, I. I. K. 1962, The Observatory, 82, 158 [Google Scholar]
- Wolleben, M. 2007, ApJ, 664, 349 [NASA ADS] [CrossRef] [Google Scholar]
- Wolleben, M., & Reich, W. 2004, A&A, 427, 537 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wolleben, M., Landecker, T. L., Reich, W., & Wielebinski, R. 2006, A&A, 448, 411 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Figures
 |
Fig. 1 Effective integration time in sec for I, U, and Q from top to bottom. The time was scaled by a factor of 0.5 when the observations were made with a reduced bandwidth of Δν = 295 MHz. |
| In the text | |
 |
Fig. 2 Example of instrumental polarization cleaning applied to the λ6 cm survey polarized intensity data for the case of the H ii region G30.7−0.1. The upper panel shows the original polarized intensity and the lower panel the cleaned map. The contours start at 50 mK TB and increase in steps of 50 mK TB. |
| In the text | |
 |
Fig. 3 TT-plot between WMAP K-band (22.8 GHz) and Ka-band (33 GHz) for polarized intensities for the region of 40° ≤ l ≤ 60° (upper panel) and 10° ≤ l ≤ 30° (lower panel) within the latitude range of |b| ≤ 5°. |
| In the text | |
 |
Fig. 4 Simulated polarized intensity at λ6 cm (4.8 GHz) and K-band (22.8 GHz) versus distance for various directions as indicated by the Galactic coordinates in each panel. The dotted lines show the polarized intensity at K-band scaled to λ6 cm with a spectral index as modelled in Sect. 3.1.1. The solid lines show PI at λ6 cm. |
| In the text | |
 |
Fig. 5 Pulsar RM versus distance based on the NE2001 electron density model. For most of the data the RM error bars are too small to be seen. |
| In the text | |
 |
Fig. 6 Longitude profiles showing U and Q corrections averaged for |
| In the text | |
 |
Fig. 7 Pixel distribution of polarized intensities (top) and polarization angles (bottom) before and after baseline restoration. |
| In the text | |
 |
Fig. 8 Maps at λ6 cm for the region 10° ≤ l ≤ 60°. From top to bottomI, U, and Q maps are shown as observed. Overlaid contours on the I map run in steps of 2n × 200 mK TB with n = 0, 1, 2, .... |
| In the text | |
 |
Fig. 9 Zero-level restored PI maps overlaid by total intensity contours and bars showing B-vectors. The contours run in steps of 2n × 50 mK TB with n = 0, 1, 2, .... The lengths of B-vectors are proportional to PI. Below an intensity cutoff of 2.5 mK TB (5 × rms-noise), no bars are shown. |
| In the text | |
 |
Fig. 10 The same as Fig. 9 for the lower longitude regions. |
| In the text | |
 |
Fig. 11 Total intensity I along Galactic longitude averaged within b = ± 2°. The solid line shows the λ6 cm survey data and the dotted line the Parkes survey (Haynes et al. 1978) data with an offset of about 1000 mK. |
| In the text | |
 |
Fig. 12 IRAS 60 μm greyscale image showing the H ii region G12.8 − 3.6. Contours display total intensities at λ6 cm starting at 10 mK TB and running in steps of 10 mK TB. |
| In the text | |
 |
Fig. 13 λ6 cm total intensity image for the newly identified H ii region G56.7 − 0.6 shown in greyscale and contours, which start at 10 mK TB running further in steps of 10 mK TB. |
| In the text | |
 |
Fig. 14 Polarization image for the southern NPS extension. Contours show total intensities and bars represent B-vectors. Contours start at 5 mK TB and run in steps of 4.5 mK TB. |
| In the text | |
 |
Fig. 15 Sketch of the location of Galactic spiral arms taken from the polynomial spiral arm model of Hou et al. (2009). The longitude range of the present survey section is indicated. The dashed circle has a radius of 4 kpc, and indicates the polarization horizon at λ6 cm in the Galactic plane. |
| In the text | |
 |
Fig. 16 U, Q, and PI structure functions for the present λ6 cm survey section. The structure functions calculated for smoothed ( |
| In the text | |
 |
Fig. 17 Polarized intensity maps for the void G40.9 − 4.2. The upper panel shows the original map, the middle panel shows the map with the zero-level restored with a spectral index of βPI = −2.7 according to the restoration model discussed in Sect. 3.1.1. The lower panel shows the map with the zero-level restored using the lowest possible spectral index of βPI = −3.1 (see Fig. 3). PI is always shown in grey scale, and bars indicate polarization B-vectors. |
| In the text | |
 |
Fig. 18 Polarization void G55.3 − 1.5. PI is shown in grey scale, and bars indicate polarization B-vectors. |
| In the text | |
 |
Fig. 19 Depolarization factors for different polarization angle change (Δψ) across the scale x0 and the ratio of x0 to the beam size D. |
| In the text | |
 |
Fig. 20 Decomposed thermal (upper panel) and non-thermal component (lower panel) for the λ6 cm survey between 10° ≤ l ≤ 60° based on the non-thermal spectral index model in Sect. 3.1.1 and βff = −2.1 for optically thin thermal emission. |
| In the text | |
 |
Fig. 21 Galactic latitude profiles for the averaged thermal emission component at λ6 cm (solid lines), the averaged WMAP free-free emission (dotted line), and the baseline-corrected λ6 cm total intensity (dot-dashed line). |
| In the text | |
 |
Fig. 22 Galactic latitude profiles for the averaged thermal emission component at λ6 cm derived with the spectral index βsyn = −2.7 (solid lines) and βsyn = −3.1 (dotted line). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


