| Issue |
A&A
Volume 527, March 2011
|
|
|---|---|---|
| Article Number | A44 | |
| Number of page(s) | 7 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/200912124 | |
| Published online | 24 January 2011 | |
H2, HD, and D2 abundances on ice-covered dust grains in dark clouds
1
LAMAp/LERMA, UMR8112 du CNRS, de l’Observatoire de Paris et de l’Université
de Cergy Pontoise,
5 mail Gay-Lussac,
95000
Cergy Pontoise Cedex,
France
e-mail: jean-louis.lemaire@obspm.fr
2
Univ. Paris-Sud, ISMO, UMR 8214, 91405
Orsay,
France
3
CNRS, UMR 8214, ISMO,
91405
Orsay,
France
4
UPMC Univ. Paris 6, UMR 7092, LPMAA,
75005
Paris,
France
5
CNRS, UMR 7092, LPMAA,
75005
Paris,
France
Received:
20
March
2009
Accepted:
21
December
2010
Aims. We seek to study the abundances of H2, HD, and D2 adsorbed onto ice-covered dust grains in dark molecular clouds in the interstellar medium.
Methods. We use our previously developed detailed model describing temperature-programmed desorption (TPD) experiments of H2 and its isotopologues on water ice. We here extrapolate these model results from laboratory conditions to conditions similar to those found in dark molecular clouds.
Results. By means of our model we are able to infer three important results. (i) The time scale for H2 and isotopologues to accrete onto dust grains is less than 104 yrs. (ii) Due to the higher binding energy of D2 with respect to HD, D2 becomes the most abundant deuterated species on grains by ~50% with respect to HD (a few times 10-5 with respect to H2). (iii) The surface coverage of D2 as a function of temperature shows that at very low temperatures (i.e., less than 10 K), D2 may be two orders of magnitude more abundant than HD. Possible implications for deuteration of water on grain surfaces are discussed when it forms through reactions between OH and H2.
Key words: ISM: molecules / molecular processes / astrochemistry
© ESO, 2011
1. Introduction
In cold dark molecular clouds, the main gas components are molecular hydrogen (H2) and helium, accounting for 90% and 10% of the total number density, respectively. These are the main gas components by ~ four orders of magnitude. When it comes to mass, H2 and He still are the principal components (~74% and ~25%, respectively), but another component is the interstellar dust (~1%). In dark clouds, the temperature is typically ≲10–15 K, the density is ~104–105 cm-3, and it is expected most heavier species will have frozen out onto the dust grain surfaces where they form a thick layer of molecular ice, the principal ice component being water (Gibb et al. 2004).
Most of the theoretical and experimental work on H2 ice surface chemistry has so far focused on H2 formation (through the H + H → H2 surface reaction) in terms of the efficiency and the energy budget (e.g. Govers et al. 1980; Congiu et al. 2009), and the role of the substrate in the formation process has also been studied (Hornekær et al. 2003, 2005). The main reason for this is that it is assumed H2 does not freeze out onto dust grains as the sublimation temperature is ~4 K (Sandford et al. 1993; Buch & Devlin 1994; Dissly et al. 1994). However, the amount of gas phase H2 is so overwhelming that grain-H2 collisions are inevitable at all temperatures found in a cold dark cloud. Moreover, icy grain mantles are believed to be amorphous in nature, and their corrugated surface might have a large surface area. This means that the presence of molecular hydrogen on the surface of icy grain mantles should be considered in detail in the context of surface chemistry.
If non-negligible amounts of H2 are present on the grain surface, the chemistry
could be affected. In particular, any barrier-less reactions involving H2 could
be enhanced on the surface, with the formation of water being one such example. It is
suggested by Tielens et al. (1983) that the following
reaction may take place on dust grain surfaces:
 (1)This reaction has been
studied theoretically alongside several others reaction paths, and is found to be the most
efficient path under cold, dark-cloud conditions (Cuppen
& Herbst 2007). One of the key questions for this route to be active in
such regions is, how much H2 is available on the surface? As a side question, the
deuteration of water may be considered, since the above reaction could also take place with
H2 substituted by HD or D2, which naturally raises the question of
how much HD and D2 is available on the surface.
(1)This reaction has been
studied theoretically alongside several others reaction paths, and is found to be the most
efficient path under cold, dark-cloud conditions (Cuppen
& Herbst 2007). One of the key questions for this route to be active in
such regions is, how much H2 is available on the surface? As a side question, the
deuteration of water may be considered, since the above reaction could also take place with
H2 substituted by HD or D2, which naturally raises the question of
how much HD and D2 is available on the surface.
In this paper, we aim at estimating the grain surface abundances of H2, HD, and D2, by considering molecular hydrogen interactions with the surface of amorphous solid water (ASW). Pure ASW is considered here as a template that mimics the surface of water-dominated icy mantles. To calculate the abundance of H2 and its isotopologues on such a surface under physical conditions relevant to dark clouds, it is necessary to estimate their population distributions over the surface as a function of the surface temperature and gas-phase densities. In the present case, our calculations incorporate the binding energy distributions of H2, HD, and D2 that are fitted to a set of temperature-programmed desorption (TPD) experiments conducted at temperatures of 10–30 K on a porous ASW sample using the experimental set-up FORMOLISM (FORmation of MOLecules in the InterStellar Medium, previously described in, e.g., Amiaud et al. 2006, 2007, 2008). These values are then incorporated into a toy model that allows us to estimate grain surface abundances of H2, HD, and D2.
The article is structured as follows. In Sect. 2 we provide a very short description of the experimental results. In Sect. 3 we present a toy model that allows us to interpret the experimental results and we discuss the validity of this model. Section 4 provides some direct results of this model, that are discussed in an astrophysical context, before giving a closing summary in Sect. 6.
2. Description of desorption
The primary aim of this paper is to obtain the number of hydrogen molecules (and isotopologues) adsorbed onto the interstellar grains. This number is the result of a balance between adsorption and desorption processes.
In the following we present and use results of experiments carried out to study and measure the difference in binding energy of H2 and its isotopologues (i.e., HD and D2) on a sample of pure amorphous solid water (ASW) ice. The main experimental results are only briefly reported here. More details in the TPD experiments will be presented in a forthcoming paper. Here we only report on details important for understanding the results.
The experiments were performed in an ultra-high vacuum chamber where a sample of ASW ice was grown on a copper sample. For these experiments we grew 10 mono-layers (1 ML ≡ 1015 cm-2) of porous ASW ice. Due to the porosity of the ice, the total ice surface is ~3.6 times higher than the surface of the copper sample as evaluated in Amiaud et al. (2006). This ice template is believed to be a good template for our purposes (see Sect. 3.2). We performed a set of TPD experiments. It is a technique in which a programmed temperature ramp induces a controlled heating of the surface, while the desorption kinetics of species initially adsorbed on the surface are monitored with a mass spectrometer. These spectra are then analysed in terms of adsorption energy distribution.
A central question arises: Can the time scales used in experiments be translated to astronomical time scales? The answer is yes, because for the description of the experiments we adopt a model, which assumes thermodynamical equilibrium at any moment (see Sect. 3). Therefore, it is not time dependent.
Classically a molecule has a definite adsorption energy Eads,
and one can write the desorption flux rate (φout) as
 (2)where
A is the number of attempts per second of the molecule to desorb, and
θ the coverage, i.e., the number of molecules adsorbed per
cm2. We note that A is inversely proportional to the root of the
mass of the species such that A(H2) =
A(D
(2)where
A is the number of attempts per second of the molecule to desorb, and
θ the coverage, i.e., the number of molecules adsorbed per
cm2. We note that A is inversely proportional to the root of the
mass of the species such that A(H2) =
A(D .
In the case of an amorphous surface, the adsorption energy is not unique but has to be
replaced by a large distribution of energies depending on the coverage
Eads(θ) (e.g. Govers et al. 1980; Chang et al. 2005; Hornekær et al. 2005; Amiaud et al. 2006; Fillion et al. 2009).
We emphasise that the wide binding energy range of these distributions (originating from the
amorphous nature of the surface) affects the residence time scales of the molecules on the
surface dramatically. Therefore, the amorphous nature of the surface together with small
differences in binding energy distributions between isotopologues are governing the amount
of species that can accumulate on the surface.
.
In the case of an amorphous surface, the adsorption energy is not unique but has to be
replaced by a large distribution of energies depending on the coverage
Eads(θ) (e.g. Govers et al. 1980; Chang et al. 2005; Hornekær et al. 2005; Amiaud et al. 2006; Fillion et al. 2009).
We emphasise that the wide binding energy range of these distributions (originating from the
amorphous nature of the surface) affects the residence time scales of the molecules on the
surface dramatically. Therefore, the amorphous nature of the surface together with small
differences in binding energy distributions between isotopologues are governing the amount
of species that can accumulate on the surface.
 |
Fig. 1 Adsorption energy distributions of H2 on a porous ASW ice with a surface at 10 K for three values of desorbing flux equal to accreting fluxes corresponding to number densities in the gas phase at 10 K of nH2 = 107, 1, 10-6 cm-3 (see text for full description). |
Following Amiaud et al. (2006) we model the
distribution of adsorption sites with a polynomial function: ![\begin{equation} g(E) = a(E_0 - E)^b \hspace{1 cm} \left[ {\rm cm}^{-2}~{\rm meV}^{-1}\right]. \label{eq:e_dis} \end{equation}](/articles/aa/full_html/2011/03/aa12124-09/aa12124-09-eq30.png) (3)The parameters
a, E0, and b are parameters
that are determined from fitting the TPD experiments, where also the pre-exponential factor,
A, was determined (see Eq. (2)). The two parameters a and b are independent
of species, and the best-fit values are
a = 5.86 × 10-4 cm-2 meV-2.6 and
b = 1.6 (without dimension). The fitting of our experimental data to the
model using the χ square method shows a very low sensitivity to the
A value and consequently a slight change in the
E0 value in the 1012–1013 range, as
discussed in Amiaud et al. (2006). As the S/N for
D2 is smaller than for the others isotopes, we have determined 1013
for D2 and calculated the values for HD and H2 in order to be
consistent. The values of A and E0 are given in
Table 1. The difference in the value of
E0 is equal to the difference in zero-point energy, and is
also tabulated in Table 1. Using the parameters given
in Table 1, one can calculate the desorption rates at
a given temperature and given coverage. The problem can be inverted: knowing the desorption
rates and coverage, the population distribution on the surface may be derived. Then in the
astrophysical context we assume a steady state regime in which the accretion rate (or
φin) from the gas phase is counterbalanced by the desorption
rates (or φout) and thereafter constraining the population of
adsorption sites.
(3)The parameters
a, E0, and b are parameters
that are determined from fitting the TPD experiments, where also the pre-exponential factor,
A, was determined (see Eq. (2)). The two parameters a and b are independent
of species, and the best-fit values are
a = 5.86 × 10-4 cm-2 meV-2.6 and
b = 1.6 (without dimension). The fitting of our experimental data to the
model using the χ square method shows a very low sensitivity to the
A value and consequently a slight change in the
E0 value in the 1012–1013 range, as
discussed in Amiaud et al. (2006). As the S/N for
D2 is smaller than for the others isotopes, we have determined 1013
for D2 and calculated the values for HD and H2 in order to be
consistent. The values of A and E0 are given in
Table 1. The difference in the value of
E0 is equal to the difference in zero-point energy, and is
also tabulated in Table 1. Using the parameters given
in Table 1, one can calculate the desorption rates at
a given temperature and given coverage. The problem can be inverted: knowing the desorption
rates and coverage, the population distribution on the surface may be derived. Then in the
astrophysical context we assume a steady state regime in which the accretion rate (or
φin) from the gas phase is counterbalanced by the desorption
rates (or φout) and thereafter constraining the population of
adsorption sites.
In Fig. 1 we show schematically such a set of energy occupations of various desorbing fluxes of H2 at 10 K. The desorbing fluxes are expressed in flux equivalent of nH2 in a dark cloud at 10 K. We see that the denser the cloud is, the more molecules are adsorbed onto the surface, because to compensate for the high incoming flux a greater desorption and therefore a greater coverage is required.
At this point a comparison has to be made with Perets et al. (2007). They performed TPD measurements of ASW ice exposed to atomic D or H beams and to molecular HD or D2 beams. They extract their parameters using a rate-equations-based model that describes desorption of molecular hydrogen when both atomic and molecular hydrogen are adsorbed on the surface. They find single adsorption energies for HD and D2 (resp. 68.7 and 72.0 meV) because they have deliberately chosen a low coverage (~1%). Therefore these two energies correspond to the high energy tail of our distribution in Fig. 1. It is noticeable that the difference in Eads for HD and D2 is in agreement with the results reported here. Nevertheless we want to stress that in this paper we prefer to deal with an energy distribution rather than with unique values of adsorption energies for H2, HD, and D2. This is mandatory for the sake of extrapolation to the dense clouds in the interstellar medium (ISM), as in such cases all the species are in competition on the grains ice mantle.
3. Model description and validity
In this section we first describe our model before discussing its validity in an astrochemical context. We have chosen to construct a model based directly on the experimental conditions and results rather than trying to incorporate the present results into a full astrochemical model.
3.1. Model
We have successfully created a model to describe our experimental results (e.g. Amiaud et al. 2006). This model is designed to reproduce our TPD-experiments and we are going here through some of the details.
We start by noting that the change in number of adsorbed molecules, N,
on the surface is  (4)where
φin is the rate of adsorption and
φout is the rate of desorption.
φin may be written as
(4)where
φin is the rate of adsorption and
φout is the rate of desorption.
φin may be written as
 (5)where
n is the (gas) density,
(5)where
n is the (gas) density, 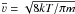 is the mean velocity at a given temperature, T, and S is
the sticking coefficient. We implicitly assume that the gas and surface temperatures are
identical and for this reason we set the sticking coefficient equal to unity. The rate of
desorption is given by
is the mean velocity at a given temperature, T, and S is
the sticking coefficient. We implicitly assume that the gas and surface temperatures are
identical and for this reason we set the sticking coefficient equal to unity. The rate of
desorption is given by  (6)Here
r(Eads,T) is the
desorption rate at a single adsorption site, Eads the
adsorption energy and P the population. Because only one molecule is
allowed per adsorption site, the population distribution is given in the Fermi-Dirac
formalism (Amiaud et al. 2006) by
(6)Here
r(Eads,T) is the
desorption rate at a single adsorption site, Eads the
adsorption energy and P the population. Because only one molecule is
allowed per adsorption site, the population distribution is given in the Fermi-Dirac
formalism (Amiaud et al. 2006) by
 (7)with
μ the Fermi energy or chemical potential.
(7)with
μ the Fermi energy or chemical potential.
With respect to describing the population we closely follow the results of Amiaud (2006) and Amiaud et al. (in prep.). They show
that the coverage of H2 on the ice is
![\begin{eqnarray} P(E_{\rm H_2}, T, \mu_{\rm H_2}) &=& a\left(E_0 - E_{\rm H_2} \right)^{b} \times \left\{ 1+\exp\left(-\frac{E_{\rm H_2}-\mu_{\rm H_2}}{kT} \right) \right. \nonumber\\ & & + \exp\left[-\frac{\left(E_{\rm H_2} - E_{\rm D_2}\right) - \left(\mu_{\rm H_2} - \mu_{\rm D_2}\right)}{kT} \right] \nonumber\\ & & \left. + \exp\left[-\frac{\left(E_{\rm H_2} - E_{\rm HD}\right) - \left(\mu_{\rm H_2} - \mu_{\rm HD}\right)}{kT} \right] \right\}^{-1} \end{eqnarray}](/articles/aa/full_html/2011/03/aa12124-09/aa12124-09-eq52.png) (8)and
similarly for HD and D2. Here, EX
is the energy of species X,
a = 5.86 × 10-4 cm-2 meV-2.6,
b = 1.6 and values for E0 are given in
Table 1. We do not make any assumptions regarding
the chemical potential, μ, but calculate it explicitly for each species
using the closing relation
φin = φout (see below). We now
only consider the steady-state solution to Eq. (4), that is dN/dt = 0 or
φin = φout. This allows us to
determine the number of adsorbed H2, HD, and D2 molecules,
N:
(8)and
similarly for HD and D2. Here, EX
is the energy of species X,
a = 5.86 × 10-4 cm-2 meV-2.6,
b = 1.6 and values for E0 are given in
Table 1. We do not make any assumptions regarding
the chemical potential, μ, but calculate it explicitly for each species
using the closing relation
φin = φout (see below). We now
only consider the steady-state solution to Eq. (4), that is dN/dt = 0 or
φin = φout. This allows us to
determine the number of adsorbed H2, HD, and D2 molecules,
N:  (9)
(9)
3.2. Validity
To use this model in an astrochemical context it is necessary to make a number of assumptions. We go through them here and discuss their validity in detail.
To estimate the gas phase abundance of H2 and its isotopologues we use the model results of Flower et al. (2004). They modeled the gas phase abundance of compounds containing H and their isotopologues in a time-dependent chemical model. Grains were also included in their model, but only play a role in terms of the total charge distribution. It is important to note that the detailed model results of Flower et al. (2004) only are valid in the absence of heavy elements (see Walmsley et al. 2004, for a full discussion). In our model we do not consider others species than H2 and its isotopologues, which is in contrast to the real ISM where more than 150 species have been detected so far.
Also, it is necessary to assume that the ice covering dust grains consists of water only, since all experiments are performed on pure water ice. This is again in contrast to real interstellar ices where it is known that ices are composed of several species, e.g., H2O, CO2, CO and more complex organic species like CH3OH (e.g., Gibb et al. 2004). The primary ice component besides H2O is CO2 with an abundance of ~10–50% with respect to H2O. For our purposes the underlying structure of the ice is not so important as long as the top layer is pure water ice.
Ice morphology and ice template used in the present study are also subject to discussion. The solid icy mantle that covers the grain has an amorphous signature in dense regions (see e.g., Dartois et al. 2002, 2003), but so far the degree of porosity and the thickness is not a direct observational result. The porosity can be very high for an ice grown at 10 K from gas phase (as it is the case in our experiments), but it can easily be reduced by cosmic rays, UV radiation, thermal processing and possibly chemical processing (Palumbo 2006).
We have demonstrated that there are two types of binding energy distributions, one for the compact amorphous ice and one for the porous amorphous ice. But, as we have shown, the energy distribution of adsorption sites is changing dramatically toward porous distribution as soon as a fraction of a layer of porous ice is deposited on top of a compact amorphous ice (Fillion et al. 2009). Therefore it is highly probable that the correct binding energy distribution of H2 on icy dust grains is closer to the porous distribution than the compact one. It is classically assumed that the thickness of water ice on grains is about 100 ML in dense clouds (Schutte 1998). Due to processing, the porosity is certainly reduced in comparison to what can be formed in the laboratory. Therefore the 10 ML porous ice sample used in the laboratory would be equivalent to a thicker ice mantle (<100 ML) under astrophysical conditions. We have studied the effect of the change of the porosity in detail, and it does not affect the present study by much. We believe that the ice used in the experiment is a reasonable mean template for the icy, partly processed mantle.
4. Astrophysical implications
By using the above mentioned model, it is possible to extrapolate from laboratory conditions to conditions in the ISM. The main difference in the two scenarios is the much lower molecular flux which is made up for by the much longer time-scales relevant in dark clouds. We therefore adopt the experimental model as a simple toy model of the adsorption and desorption of H2, HD, and D2 from an ice-covered grain surface. In doing this we are able to deduce three important results. These are:
-
accretion time scales under same assumptions;
-
differences in species abundances on the surface of the grain as a function of density assuming initial gas phase conditions as in Flower et al. (2004) ;
-
surface coverage as a function of grain temperature.
Furthermore, we are able to make certain inductions regarding the formation of water, however, this does not arise from an extrapolation of experimental results. In the following we present these results in more detail.
4.1. Accretion time
We first of all want to examine whether our assumption regarding steady-state is realistic compared to the total life-time of a molecular cloud. Statistical equilibrium is reached when a single molecule has sufficient time to explore several adsorption sites on a grain surface through diffusion. Amiaud et al. (2006) already estimated that the average number of sites a molecule can explore is of the order of 109.
We define the steady-state accretion time-scale as  (10)We show the variation in
Fig. 2 as a function of H2 density at a
temperature of 10 K. As expected, the accretion time drops with increasing density. For
number densities of 104 cm-3 the accretion time scale is
~103 years in the case of H2 and HD whereas it is a few
times 103 years for D2. At very high densities of
107 cm-3 the accretion time scale is from a few tens of years to
~102 years. The ratio of accretion time-scales
τH2:τHD:τD2
is ~1:1.5:37.5 independent of the gas phase density of H2. The
reason for this is that both HD and D2 are more strongly bound to the surface
than H2 and once they are on the surface, they stay there.
(10)We show the variation in
Fig. 2 as a function of H2 density at a
temperature of 10 K. As expected, the accretion time drops with increasing density. For
number densities of 104 cm-3 the accretion time scale is
~103 years in the case of H2 and HD whereas it is a few
times 103 years for D2. At very high densities of
107 cm-3 the accretion time scale is from a few tens of years to
~102 years. The ratio of accretion time-scales
τH2:τHD:τD2
is ~1:1.5:37.5 independent of the gas phase density of H2. The
reason for this is that both HD and D2 are more strongly bound to the surface
than H2 and once they are on the surface, they stay there.
 |
Fig. 2 The accretion time-scale as given in Eq. (10) shown as a function of H2 number density for H2, HD, and D2. |
In the case of cold dark clouds on their way to undergo star formation, a relevant time-scale and measure for the life-time is the free-fall time, τff. For a cloud with a density of 104 cm-3τff is of the order of 105 years. As the density increases to 107 cm-3τff decreases to ~104 years. In both cases the actual lifetime of the cloud is probably longer due to the effects of both ambipolar diffusion and turbulence, two mechanisms that can support a cloud against collapse (e.g., Ballesteros-Paredes et al. 2007), leading to typical cloud lifetimes of ~106 years. Thus, we conclude that our assumption regarding steady-state is valid compared to the total life-time of dark clouds, ~105–106 years. We also note that this result is in agreement with Flower et al. (2004) who find a steady-state time-scale of the order of 105 years, almost independent of number density.
4.2. Surface vs. gas phase abundance
We have calculated the abundance of H2 and its isotopologues on the surface of dust grain as a function of H2 gas phase density at a grain and gas temperature of 10 K. Results are shown in Fig. 3.
 |
Fig. 3 HD (gray) and D2 (black) fractional abundances. The gas phase fractional abundances are with respect to gas phase H2 (g: dashed line) and solid phase fractional abundances are with respect to solid phase H2 (s: full line). Gas phase abundances are from Flower et al. (2004) and the gas and grain surface temperature are both 10 K. |
Because of the higher zero-point energy (2.6 meV higher than HD) D2 is more
tightly bound to the surface and as a result, the abundance of D2 on the grain
surface is ~30 times higher than in the gas phase, when compared to solid and
gas phase H2 respectively. On the other hand, the HD abundance in the gas phase
and on the surface are comparable, with a surface abundance that is a few times lower than
the D2 surface abundance. The absolute abundance of D2 on the
surface is ~10-4 with respect to solid phase H2. The
abundance increases slightly with increasing H2 number density, when this is in
the range of 104–107 cm-3. The absolute abundance of HD
both on the surface and in the gas phase is a few times 10-5 with respect to
solid and gas phase H2 respectively. When examining the absolute abundance of
H2 on the surface we find that it is ~2 × 10-6 with
respect to the gas phase abundance. To derive this result, we first calculated the number
of grains by assuming a grain/gas mass ratio of 0.01, an average grain mass density of
3 g cm-3 and that the radius of all grains is 0.1 μm:
 (11)We then scaled our
experimental fluxes to those of the ISM and from that derived the number of H2
molecules per cm2, which was then converted to total number of H2
molecules per grain. This implies a density on the surface of ~0.18 compared to
H2O. This is consistent with previous results, where, e.g. Dissly et al. (1994) and Buch & Devlin (1994) find that the surface abundance is
~0.05–0.3 for water ice mixed with H2. Thus our results show, that
in cold, dark molecular clouds, the dominant deuterated species on grains is D2
and not HD even though HD may be more abundant in the gas phase by a factor ~5
(Flower et al. 2004). We also find that the total
amount of D on the grain surface (again, at 10 K and 105 cm-3) is of
the order of 10-4 with respect to solid state H2.
(11)We then scaled our
experimental fluxes to those of the ISM and from that derived the number of H2
molecules per cm2, which was then converted to total number of H2
molecules per grain. This implies a density on the surface of ~0.18 compared to
H2O. This is consistent with previous results, where, e.g. Dissly et al. (1994) and Buch & Devlin (1994) find that the surface abundance is
~0.05–0.3 for water ice mixed with H2. Thus our results show, that
in cold, dark molecular clouds, the dominant deuterated species on grains is D2
and not HD even though HD may be more abundant in the gas phase by a factor ~5
(Flower et al. 2004). We also find that the total
amount of D on the grain surface (again, at 10 K and 105 cm-3) is of
the order of 10-4 with respect to solid state H2.
This result is not trivial and deserves a little more attention. The segregation mechanism on the ice is a competition between the three isotopes. For a given site exposed to each of the three isotopes, D2 has the highest probability to stay, followed by HD and H2, as can be inferred from the values of adsorption energies. But the probability for an H2 molecule to stay (meaning that HD and D2 evaporate) is not zero even if it is low. Therefore, as the number of incoming H2 molecules is four orders of magnitude greater than for others isotopes, H2 will succeed in “kicking out” HD quite efficiently because the adsorption energy difference between HD and H2 is very low (see Table 1). On the other hand, D2, even if it is the less abundant, has a higher adsorption energy and therefore can compete efficiently with the higher abundance of H2.
Our model predicts that the abundances of HD and D2 will be higher with
respect to H2 in the solid phase than with their counterparts in gas phase.
However, the absolute H2 abundance on the grain is so small
(~10-6) that the absolute HD and D2 solid state
abundances with respect to gas phase H2 is of the order of 10-10,
that is,  .
.
Lipshtat et al. (2004) have made a theoretical study on the formation of H2, HD, and D2 on grains. They find an enhanced production of HD and D2 versus H2 in the 16–20 K range. This is obtained by considering different adsorption energies for H and D atoms. In this range, we find a very low abundance of deuterated molecular hydrogen adsorbed on grain, but a significant amount of H2 on the grain. This again emphasises the fact that a complete model for molecular hydrogen formation on grains should include the possibility of competition between not only hydrogen atoms and hydrogen molecules but between all the five species (H, D, H2, HD, and D2) together on the grain.
4.3. Surface abundance vs. temperature
We show here the results of a calculation of the abundance as a function of temperature for an initial H2 density of 105 cm-3. This is displayed in Fig. 4 both in units of mono-layers (1 ML = 1015 cm-2) and in units of molecules per grain, where we have calculated this for a “standard” grain with radius 0.1 μm. We see that D2 is more abundant than HD on the surface except at higher temperatures (i.e., >20 K). We also note, that at low temperatures (<6 K) the D2 abundance comes within 3 orders of magnitude to that of H2.
 |
Fig. 4 Top. Surface abundance of H2, HD, and D2 as a function of temperature for a gas density of 105 cm-3 (full lines). We express the surface abundance both in terms of ML but also surface number density for a grain with radius 0.1 μm. For comparison we show the results of Govers et al. (1980) for H2 and HD (dashed lines). Bottom. Fractional abundances of HD and D2 with respect to H2 on the surface. |
We compare our results with the experimental results presented in Govers et al. (1980), noting that these results were obtained on a non-porous surface. To make a direct comparison we multiplied the coverage values presented in Govers et al. by 3.6. This is shown in Fig. 4. This method does not take competition into account, that is, using this method, it is possible to have one full layer of H2 adsorbed on the grain as well as one full layer of HD at the same time. This lack of competition is what leads to the break at 9–10 K. Also, we predict a higher abundance at higher temperatures compared to Govers et al. This is a direct result of the higher binding energy.
If we assume a column density towards a dark cloud of
NH = 1020 cm-2, for example, it is
possible to convert the local surface density on one grain to a total column density of
adsorbed H2, HD, and D2 by estimating the total number of grains
(see Eq. (11)). This may be compared
directly with Fig. 4 to derive a column density of
adsorbed H2 in the case where the local density is
105 cm-3. At a temperature of 10 K, we find that it is
 cm-2,
cm-2,
 cm-2 and
cm-2 and
 cm-2. Thus,
both adsorbed HD and D2 are at present not directly detectable in absorption. A
detection of solid H2 is claimed towards the W5 region (Sandford et al. 1993), however this detection still needs confirmation.
If true, it would imply an H2 column density of
~1018 cm-2, but this should only be seen as a strict
upper limit at present.
cm-2. Thus,
both adsorbed HD and D2 are at present not directly detectable in absorption. A
detection of solid H2 is claimed towards the W5 region (Sandford et al. 1993), however this detection still needs confirmation.
If true, it would imply an H2 column density of
~1018 cm-2, but this should only be seen as a strict
upper limit at present.
5. Case study: water formation
Our model results have so far demonstrated the importance of including the binding energy difference between H2 and its isotopologues. We emphasise that the results shown here should only give an indication of what can be done with elaborate chemical models that take both gas phase and surface reactions into account.
As an example of application of this result is the deuteration of water. The observed
abundance of gas phase deuterated water (HDO) ranges from 10-4 to 10-2
(Parise et al. 2005). This corroborates a scenario
in which water forms on the surface of dust grains through the following surface reaction:
 (12)This reaction was
originally proposed by Tielens et al. (1983), where
it is one among three routes of water formation on dust grains. We only consider this route
as it is the only one involving H2 explicitly and it shows no barrier.
(12)This reaction was
originally proposed by Tielens et al. (1983), where
it is one among three routes of water formation on dust grains. We only consider this route
as it is the only one involving H2 explicitly and it shows no barrier.
 |
Fig. 5 Water formation involving H2, HD and D2 and their branching ratios in the cases where there is complete scrambling in the intermediate H3O molecule and no scrambling (see reaction 12). |
In Fig. 5 we show the possible reactions between H2, HD or D2, and OH along with their branching ratios. The branching ratios are determined by assuming that the probability for forming an O–H bond is equal to that of forming an O–D bond. Furthermore we consider both cases with and without complete scrambling of the intermediate H3O molecule. As an example, we consider the case of OH + HD and assume complete scrambling. The intermediate molecule is H2DO, i.e., 2/3 of the bonds are with H and 1/3 with D. As a result, the probability of forming H2O is 2/3 and it is 1/3 for forming HDO.
Since the reaction is without barrier (Tielens et al.
1983), the likelihood that OH will react with H2, HD, or D2
depends only on their respective surface coverages (illustrated for the case of complete
scrambling only):  where
P(X) is the probability of forming X
and θY is the surface coverage of species
Y. The proportionality constant, k0, is
identical for all three probabilities (Charnley et al.
1997), again the reason being that the reactions are barrier-less.
where
P(X) is the probability of forming X
and θY is the surface coverage of species
Y. The proportionality constant, k0, is
identical for all three probabilities (Charnley et al.
1997), again the reason being that the reactions are barrier-less.
If we use the coverages in Fig. 4 it is possible to plot the relative abundance of HDO and D2O with respect to H2O as a function of temperature. This is shown in Fig. 6 both in the case of complete and no scrambling. If there is no scrambling, D2O is not produced unless OH is deuterated, which we do not take into account. We find that typical values of the fractionation are from 10-5−10-4, implying that this water formation route should contribute with this value to the overall water deuteration. If there is complete scrambling, we find that the abundances of HDO and D2O are within a factor of 2–3 of each other. We emphasise here, that this is a limiting case and we also stress that the fractionation predicted here is only valid for one route of water formation.
 |
Fig. 6 Water fractionation in the case of complete scrambling (full line) and no scrambling (dashed line). The gas phase density of H2 is 105 cm-3 as in Fig. 4. |
Another way of considering water deuteration is the following. At temperatures lower than ~15 K, there will on average always be at least one HD or D2 molecule present on the grain surface. In the interval of ~15–19 K, there will be less than one deuterated molecule present per grain, but more than one H2 molecule. Therefore, at temperatures greater than ~15 K, deuteration of water should not (on average) occur following the above reaction.
Observations of solid phase deuterated water in cold dark clouds places an upper limit of 10-3 with respect to H2 (Parise et al. 2003; Dartois et al. 2003), which is consistent with our results, as long as the water is formed at temperatures greater than ~6 K. It should also be noted, that the above route is not the only one to form water on dust grains (Tielens et al. 1983; Miyauchi et al. 2008; Ioppolo et al. 2008; Dulieu et al. 2010).
6. Summary
In this study, we have used the binding energy distributions valid for H2, HD, and D2 adsorbed on a cold porous ASW in order to estimate their abundances on the surface of icy grains mantles under typical dark cloud conditions. The parameters describing the binding energy distributions were obtained from the simulation of a set of TPDs performed between 10 K and 30 K with H2, HD, and D2 on a porous 10 ML ASW sample. Our calculation is based upon a model describing the simultaneous interaction of the three species in thermal equilibrium with the surface. The model enables us to extrapolate the experimental results to the astrophysical context, assuming a steady state regime between gas phase accretion and thermal desorption. Our calculation confirms the important role played by the wide range of binding energies and by the small differences in zero-point energy found between the isotopologues. In particular, we have demonstrated that the most abundant deuterated species on a grain surface at 10 K typically is D2 and not HD, even though the latter is the more abundant gas phase isotopologue.
We have used this to derive certain “order of magnitude” estimates regarding the accretion time-scales and also the surface abundance of these species as functions of both density and temperature. This we have used to estimate water fractionation on grains, as long as it proceeds following one specific formation route.
The results presented here show that a deep understanding of experiments can provide new insights when modeling the interstellar medium. As an example, the difference in binding energy will be one of the main mechanisms responsible for the abundances of deuterated water molecules observed.
Acknowledgments
We acknowledge the support of the French National PCMI programme funded by the CNRS, as well as the strong financial support from
the ANR (Agence Nationale de la Recherche; contract 07-BLAN-0129), the Conseil Régional d’Ile de France through a SESAME programme (No. E1315 and I-07-597R) and from the Conseil Général du Val d’Oise. We are indebted to H. Cuppen for very fruitful discussions.
References
- Amiaud, L. 2006, Ph.D. Thesis, Université de Cergy-Pontoise, http://tel.archives-ouvertes.fr/tel-00124797/en/ [Google Scholar]
- Amiaud, L., Fillion, J.-H., Baouche, S., et al. 2006, J. Chem. Phys., 124, 094702 [NASA ADS] [CrossRef] [Google Scholar]
- Amiaud, L., Dulieu, F., Fillion, J.-H., Momeni, A., & Lemaire, J. L. 2007, J. Chem. Phys., 127, 144709 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Amiaud, L., Momeni, A., Dulieu, F., et al. 2008, Phys. Rev. Lett., 100, 056101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ballesteros-Paredes, J., Klessen, R. S., Mac Low, M.-M., & Vazquez-Semadeni, E. 2007, in Protostars and Planets V, ed. B. Reipurth, D. Jewitt, & K. Keil, 63 [Google Scholar]
- Buch, V., & Devlin, J. P. 1994, ApJ, 431, L135 [NASA ADS] [CrossRef] [Google Scholar]
- Chang, Q., Cuppen, H., & Herbst, E. 2005, A&A, 434, 599 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Charnley, S. B., Tielens, A. G. G. M., & Rodgers, S. D. 1997, ApJ, 482, L203 [NASA ADS] [CrossRef] [Google Scholar]
- Congiu, E., Matar, E., Kristensen, L. E., Dulieu, F., & Lemaire, J.-L. 2009, MNRAS, 397, 96 [Google Scholar]
- Cuppen, H. M., & Herbst, E. 2007, ApJ, 668, 294 [Google Scholar]
- Dartois, E., d’Hendecourt, L., Thi, W., Pontoppidan, K. M., & van Dishoeck, E. F. 2002, A&A, 394, 1057 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dartois, E., Thi, W.-F., Geballe, T. R., et al. 2003, A&A, 399, 1009 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dissly, R. W., Allen, M., & Anicich, V. G. 1994, ApJ, 435, 685 [NASA ADS] [CrossRef] [Google Scholar]
- Dulieu, F., Amiaud, L., Congiu, E., et al. 2010, A&A, 512, 30 [Google Scholar]
- Fillion, J.-H., Amiaud, L., Congiu, E., et al. 2009, Phys. Chem. Chem. Phys., 11, 4396 [NASA ADS] [CrossRef] [Google Scholar]
- Flower, D. R., Pineau des Forêts, G., & Walmsley, C. M. 2004, A&A, 427, 887 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gibb, E. L., Whittet, D. C. B., Boogert, A. C. A., & Tielens, A. G. G. M. 2004, ApJS, 151, 35 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Govers, T., Mattera, L., & Scoles, G. 1980, J. Chem. Phys., 72, 5446 [NASA ADS] [CrossRef] [Google Scholar]
- Hornekær, L., Baurichter, A., Petrunin, V. V., Field, D., & Luntz, A. C. 2003, Science, 302, 1943 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Hornekær, L., Baurichter, A., Petrunin, V. V., et al. 2005, J. Chem. Phys., 122, 124701 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ioppolo, S., Cuppen, H. M., Romanzin, C., van Dishoeck, E. F., & Linnartz, H. 2008, ApJ, 686, 1474 [NASA ADS] [CrossRef] [Google Scholar]
- Lipshtat, A., Biham, O., & Herbst, E. 2004, MNRAS, 348, 1055 [NASA ADS] [CrossRef] [Google Scholar]
- Miyauchi, N., Hidaka, H., Chigai, T., et al. 2008, Chem. Phys. Lett., 456, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Palumbo, M. E. 2006, A&A, 453, 903 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Parise, B., Simon, T., Caux, E., et al. 2003, A&A, 410, 897 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Parise, B., Caux, E., Castets, A., et al. 2005, A&A, 431, 547 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perets, H.B., Lederhandler, A., Biham, O., et al. 2007, A&A, 661, 163 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sandford, S. A., Allamandola, L. J., & Geballe, T. R. 1993, Science, 262, 400 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Schutte, W. A. 1998, in Astrophysics and Space Science Library, ed. P. Ehrenfreund, C. Krafft, H. Kochan, & V. Pirronello, 236, 69 [Google Scholar]
- Tielens, A. G. G. M., Hagen, W., & Greenberg, J. M. 1983, J. Phys. Chem., 87, 4220 [Google Scholar]
- Walmsley, C. M., Flower, D. R., & Pineau des Forêts, G. 2004, A&A, 418, 1035 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Adsorption energy distributions of H2 on a porous ASW ice with a surface at 10 K for three values of desorbing flux equal to accreting fluxes corresponding to number densities in the gas phase at 10 K of nH2 = 107, 1, 10-6 cm-3 (see text for full description). |
| In the text | |
 |
Fig. 2 The accretion time-scale as given in Eq. (10) shown as a function of H2 number density for H2, HD, and D2. |
| In the text | |
 |
Fig. 3 HD (gray) and D2 (black) fractional abundances. The gas phase fractional abundances are with respect to gas phase H2 (g: dashed line) and solid phase fractional abundances are with respect to solid phase H2 (s: full line). Gas phase abundances are from Flower et al. (2004) and the gas and grain surface temperature are both 10 K. |
| In the text | |
 |
Fig. 4 Top. Surface abundance of H2, HD, and D2 as a function of temperature for a gas density of 105 cm-3 (full lines). We express the surface abundance both in terms of ML but also surface number density for a grain with radius 0.1 μm. For comparison we show the results of Govers et al. (1980) for H2 and HD (dashed lines). Bottom. Fractional abundances of HD and D2 with respect to H2 on the surface. |
| In the text | |
 |
Fig. 5 Water formation involving H2, HD and D2 and their branching ratios in the cases where there is complete scrambling in the intermediate H3O molecule and no scrambling (see reaction 12). |
| In the text | |
 |
Fig. 6 Water fractionation in the case of complete scrambling (full line) and no scrambling (dashed line). The gas phase density of H2 is 105 cm-3 as in Fig. 4. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


