| Issue |
A&A
Volume 526, February 2011
|
|
|---|---|---|
| Article Number | A52 | |
| Number of page(s) | 17 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201015741 | |
| Published online | 21 December 2010 | |
Polycyclic aromatic hydrocarbon processing by cosmic rays
1
Sterrewacht Leiden, Leiden University,
PO Box 9513,
2300 RA
Leiden,
The Netherlands
e-mail: elisabetta.micelotta@nasa.gov
2
Institut d’Astrophysique Spatiale, Université Paris Sud and CNRS
(UMR 8617), 91405
Orsay,
France
3
CRESST and NASA Goddard Space Flight Center,
Greenbelt,
MD
20771,
USA
4
Universities Space Research Association,
10211 Wincopin Circle, Suite
500
Columbia, MD
21044,
USA
5
NASA Ames Research Center, MS 245-3, Moffett Field, CA
94035,
USA
Received:
11
September
2010
Accepted:
22
October
2010
Context. Cosmic rays are present in almost all phases of the ISM. Polycyclic aromatic hydrocarbons (PAHs) and cosmic rays represent an abundant and ubiquitous component of the interstellar medium. However, the interaction between them has never before been fully investigated.
Aims. To study the effects of cosmic ray ion (H, He, CNO and Fe-Co-Ni) and electron bombardment of PAHs in galactic and extragalactic environments.
Methods. We calculate the nuclear and electronic interactions for collisions between PAHs and cosmic ray ions and electrons with energies between 5 MeV/nucleon and 10 GeV, above the threshold for carbon atom loss, in normal galaxies, starburst galaxies and cooling flow galaxy clusters.
Results. The timescale for PAH destruction by cosmic ray ions depends on the electronic excitation energy E0 and on the amount of energy available for dissociation. Small PAHs are destroyed faster, with He and the CNO group being the more effective projectiles. For electron collisions, the lifetime is independent of the PAH size and varies with the threshold energy T0.
Conclusions. Cosmic rays process the PAHs in diffuse clouds, where the destruction due to interstellar shocks is less efficient. In the hot gas filling galactic halos, outflows of starburst galaxies and intra-cluster medium, PAH destruction is dominated by collisions with thermal ions and electrons, but this mechanism is ineffective if the molecules are in denser cloudlets and isolated from the hot gas. Cosmic rays can access the denser clouds and together with X-rays will set the lifetime of those protected PAHs. This limits the use of PAHs as a “dye” for tracing the presence of cold entrained material.
Key words: dust, extinction / cosmic rays / galaxies: halos / galaxies: starburst / ISM: jets and outflows / intergalactic medium
© ESO, 2010
1. Introduction
A remarkable characteristic of the IR emission features is that they dominate the mid-IR spectrum of almost all objects associated with dust and gas and illuminated by UV photons, ranging from H ii regions to ultraluminous infrared galaxies (see Tielens 2008, for a recent review). At present, these feature are (almost) universally attributed to the IR fluorescence of far-ultraviolet (FUV)-pumped polycyclic aromatic hydrocarbon (PAH) molecules containing 50–100 carbon atoms (Tielens 2008). PAHs have recently been detected in association with shocked hot gas, but it is difficult to establish a clear connection between the two. Tappe et al. (2006) detected spectral features in the emission of the supernova remnant N132D in the Large Magellanic Cloud, which they attribute to emission by large PAHs. Reach et al. (2006) have identified four supernova remnant with IR colors maybe indicating PAH emission, and Andersen et al. (2007) investigated the presence of PAHs in a subset of galactic supernova remnants in the GLIMPSE survey. PAHs have also been observed interwoven with the X-ray emission arising from the bipolar outflow of the starburst galaxy M 82 (Armus et al. 2007) and in the high-latitude coronal gas of the edge-on galaxies NGC 5907, NGC 5529 and NGC 891 (Irwin & Madden 2006; Irwin et al. 2007; Whaley et al. 2009).
Unfortunately the lack of theoretical studies on PAH processing in shocked regions combined with the difficulty in disentangling the PAH features intrinsic to the shocked region with those arising from the surrounding material makes the interpretation of such observations rather complicated. In our previous works (Micelotta et al. 2010a,b, hereafter MJTa and MJTb) we studied the survival of aromatic molecules in interstellar shocks with velocities between 50 and 200 km s-1 and in a hot post-shock gas, such as the Herbig- Haro jets in the Orion and Vela star forming regions (Podio et al. 2006), in the local interstellar cloud (Slavin 2008) and in the outflow of the starburst galaxy M 82 (Engelbracht et al. 2006). We found that interstellar PAHs (NC = 50) do not survive in shocks with velocities greater than 100 km s-1 and larger PAHs (NC = 200) are destroyed for shocks with velocities ≥125 km s-1. Even where destruction is not complete, the PAH structure is likely to be severely denatured by the loss of an important fraction (20−40%) of the carbon atoms. The typical PAH lifetimes are of the order of a few ×108 yr for the Galaxy. In a tenuous hot gas (nH ≈ 0.01 cm-3, T ≈ 107 K), typical of the coronal gas in galactic outflows, PAHs are principally destroyed by electron collisions, with lifetimes measured in thousands of years, i.e. orders of magnitude shorter than the typical lifetime of such objects.
Cosmic rays (CRs) are an important component of the ISM, contributing considerably to its energy density (::tag lxir empty(formule)id=493 content=!/simeq2 eV cm-3, Tielens 2005; Padovani et al. 2009). CRs consist mainly of relativistic protons, α-particles (~10%), and heavier ions and electrons (~1%). The spectrum (intensity as a function of the energy) of the ionic CR component measured near the Earth spans from ~100 MeV to ~1020 eV, and decreases steeply with energy. The spectrum of the electronic component is even steeper and ranges from ~600 MeV to 103 GeV (Ip & Axford 1985; Gaisser & Stanev 2006).
The lowest-energy CRs in the ISM, with energy between 5 MeV and few GeV, are excluded from the heliosphere or severely slowed down by the solar wind. Hence, they cannot be directly observed even with far-ranging spacecraft (Shapiro 1996) and their spectra have to be evaluated theoretically (Shapiro 1991).
CRs with energy up the few 1015 eV (the “knee” observed in the spectrum: Drury 1994) are thought to be produced in the Galaxy, mainly by supernova shocks in the disk. Because of their charge, CRs are tied to the galactic magnetic field and are confined to a spheroidal volume with radius of ~20 kpc and half-thickness of ~1–15 kpc (Ginzburg 1988; Shibata et al. 2007), with a small but finite escape probability. The magnetic field randomizes the trajectories of CRs as they propagate through the Galaxy, so their distribution is almost isotropic except close to the sources.
From the point of view of PAH destruction, CRs have then two interesting characteristics: first, for energies up to 10 GeV they can efficiently transfer energy to the PAH, with possible consequent destruction (see Sects. 2 and 3); second, they permeate almost homogeneously the ISM and can penetrate into regions such as dense clouds which are otherwise not much affected by high temperature ions and electrons (MJTb).
The aim of this work is to quantify the destructive potential of CRs and to compare it with other mechanisms (interstellar shocks, collisions within a hot gas, X-ray and FUV absorption), in galactic and extragalactic environment.
The paper is organized as follows: Sects. 2 and 3 describe the treatment of high energy ion and electron interactions with PAHs, Sect. 4 presents the CR spectra adopted for our study and Sect. 5 illustrates the calculation of the collision rate between PAHs and CRs. We present our results on PAH destruction and lifetime in Sect. 6 and discuss the astrophysical implications in Sect. 7, summarizing our conclusions in Sect. 8.
2. High energy ion interactions with solids
2.1. Collisions with high energy ions
To describe the effects of high-energy ion collisions with PAH molecules we adopt a similar approach to that used in our previous work (MJTa and MJTb), based on the theory of ion interaction in solids. Ions colliding with a PAH will excite the molecule and the excitation can lead to fragmentation or, alternatively, the excess energy can be radiated away. A calculation of the fragmentation process thus consists of two steps: 1) the calculation of the excitation energy after collision, 2) the probability of dissociation of an excited PAH. The former is discussed here. The latter is described in Sect. 2.2.
Energetic ions can interact with a solid through two simultaneous processes (Lindhard et al. 1963): the nuclear stopping or elastic energy loss, where the energy is directly transferred from the projectile ion to a target nucleus via a binary elastic collision, and the electronic stopping or inelastic energy loss, consisting of the energy loss to the electron plasma of the medium. For high energies characteristic of CRs (above ~1 MeV/nucleon) we only need to be concerned by electronic stopping, which can be well described by the Bethe–Bloch equation (see e.g. Ziegler 1999, and references therein).
The Bethe-Bloch equation was derived considering the electromagnetic interaction of an energetic particle with the electron plasma of a solid. A PAH molecule is not a solid but its large number of delocalized electrons can be treated as an electron gas (see MJTb and references therein). It is therefore appropriate to consider the energy loss to such an electron plasma in terms of the Bethe-Bloch electronic stopping power, S (energy loss per unit length). When S is known, a specific procedure has to be applied to calculate the effective amount of energy transferred into a single molecule, taking into account the finite geometry of the PAH (see Sect. 3).
The stopping of high velocity ions in matter has been a subject of interest for more than a century, starting with the work of Marie Curie in 1898–1899 (Curie 1900). For a theoretical review on the topic, we refer the reader to Ziegler (1999) and references therein. In the following, we summarize the basic methods and equations for evaluating the stopping power of high energy ions and we illustrate the modifications introduced into the theory in order to treat the interaction with PAH molecules.
For high energy light ions (H, He and Li above 1 MeV/nucleon), the fundamental relation
describing the stopping power, S, in solids is the relativistic
Bethe-Bloch equation, commonly expressed as ![\begin{eqnarray} \label{S1_eq} S & = & \frac{\kappa Z_2}{\beta^2}\,Z_1^2\,L(\beta) \\ & = & \frac{\kappa Z_2}{\beta^2}\,Z_1^2\,\left[L_0(\beta)+Z_1L_1(\beta)+ Z_1^2L_2(\beta) ...\right] \end{eqnarray}](/articles/aa/full_html/2011/02/aa15741-10/aa15741-10-eq18.png) where
where
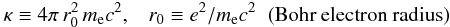 (3)me
is the electron mass, Z1 and Z2
are the projectile and target atomic numbers respectively and
β = v/c is the relative projectile
velocity. The term L(β) is defined as the stopping
number, and its expansion in Eq. (2) contains all the corrections to the basic
ion-electron energy loss process.
(3)me
is the electron mass, Z1 and Z2
are the projectile and target atomic numbers respectively and
β = v/c is the relative projectile
velocity. The term L(β) is defined as the stopping
number, and its expansion in Eq. (2) contains all the corrections to the basic
ion-electron energy loss process.
The first term L0 includes the fundamental Bethe-Bloch
relation (Bethe 1930, 1932; Bloch 1933a,b) for the stopping of high-energy ions, together with the two
corrective terms C/Z2 and
δ/2 introduced by Fano
(1963)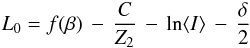 (4)where
(4)where
![\begin{eqnarray} \label{f_eq} f(\beta) \equiv \ln\,\left[\frac{2\,m_{\rm e}c^2\,\beta^2}{1\,-\,\beta^2}\right]\,-\,\beta^2 \end{eqnarray}](/articles/aa/full_html/2011/02/aa15741-10/aa15741-10-eq29.png) (5)C/Z2
is the shell correction and takes into account the fact that as soon as
the projectile loses energy into the target, its velocity decreases from relativistic
values, thus the Bethe-Bloch theory requirement of having particles with velocity far
greater than the velocity of the bound electron is no longer satisfied. In this case, a
detailed accounting of the projectile’s interaction with each electronic orbital is
required. The shell correction is important for protons in the energy range of 1–100 MeV,
with a maximum contribution of about 10%.
(5)C/Z2
is the shell correction and takes into account the fact that as soon as
the projectile loses energy into the target, its velocity decreases from relativistic
values, thus the Bethe-Bloch theory requirement of having particles with velocity far
greater than the velocity of the bound electron is no longer satisfied. In this case, a
detailed accounting of the projectile’s interaction with each electronic orbital is
required. The shell correction is important for protons in the energy range of 1–100 MeV,
with a maximum contribution of about 10%.
ln ⟨ I ⟩ , which is part of the original Bethe-Bloch relativistic stopping formula, represents the mean ionization, and corrects for the fact that the energy levels of the target electrons are quantized and not continuous.
δ/2 represents the density effect and provides the correction to the reduction of the stopping power due to polarization effects in the target. The dielectric polarization of the target material reduces the particle electromagnetic field from its free-space values, resulting in a variation of the energy loss. The density effect becomes important only for particles with kinetic energies exceeding their rest mass (938 MeV for proton).
The term Z1 L1 takes into account the Barkas effect. This is due to the target electrons, which respond to the approaching particles slightly changing their orbits before the energy loss interaction can occur.
The term 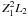 is the Bloch
correction and provides the transition between the two approaches used to evaluate the
energy loss of high-energy particles to target electrons: the classical Bohr
impact–parameter approach (Bohr 1913, 1915), and the quantum-mechanical Bethe momentum
transfer approach (Bethe 1930, 1932).
is the Bloch
correction and provides the transition between the two approaches used to evaluate the
energy loss of high-energy particles to target electrons: the classical Bohr
impact–parameter approach (Bohr 1913, 1915), and the quantum-mechanical Bethe momentum
transfer approach (Bethe 1930, 1932).
Both the Barkas and Bloch corrections are usually quite small and contribute less than few percent to the stopping at energies from 1 MeV/nucleon to 104 MeV.
The term L0 can be evaluated as a function of the energy of
the incoming ion using the following definition (Ziegler
1999): ![\begin{eqnarray} \label{beta2Ion_eq} \beta^2 \equiv \left(\frac{v}{c}\right)^2\;=\;1\,-\,\frac{1} {\left[1\,+\,E(\rm{GeV})\,/\,0.931494\;\it{M}_{\rm 1} (\rm{amu})\right]^2}. \end{eqnarray}](/articles/aa/full_html/2011/02/aa15741-10/aa15741-10-eq34.png) (6)Using
Eq. (4), we can rewrite the expression
for the stopping power (Eq. (2)) in the following way
(6)Using
Eq. (4), we can rewrite the expression
for the stopping power (Eq. (2)) in the following way ![\begin{eqnarray} \label{stoppingTotal_eq} S &=& \frac{\kappa\,Z_2}{\beta^2}\,Z_1^2\,\Bigg\lbrace\,\left[f(\beta)\,-\,\frac{C}{Z_2}\,-\, \ln \langle I \rangle\,-\,\frac{\delta}{2}\right]\nonumber \\ && +Z_1\,L_1(\,\rm {Barkas}\,)\,+\,\it{Z}_{\rm 1}^{\rm 2}L_2(\,\rm {Bloch}\,)\Bigg\rbrace . \end{eqnarray}](/articles/aa/full_html/2011/02/aa15741-10/aa15741-10-eq35.png) (7)For
the stopping power in units of eV/(1015 atoms/cm2) the prefactor
constant has the value κ = 5.099 × 10-4, while for the
stopping units of eV/Å the above prefactor has to be multiplied by
N/1023, where N is the atomic density of
the target (atoms/cm3). In our calculation we adopt the values for amorphous
carbon (Z2 = 6, M2 = 12,
N = 1.1296 × 1023 atoms/cm3), which yields
κ = 5.7508 × 10-4.
(7)For
the stopping power in units of eV/(1015 atoms/cm2) the prefactor
constant has the value κ = 5.099 × 10-4, while for the
stopping units of eV/Å the above prefactor has to be multiplied by
N/1023, where N is the atomic density of
the target (atoms/cm3). In our calculation we adopt the values for amorphous
carbon (Z2 = 6, M2 = 12,
N = 1.1296 × 1023 atoms/cm3), which yields
κ = 5.7508 × 10-4.
An empirical expression for the Barkas correction term is available (Ziegler 1999), whereas the Bloch correction can be evaluated using the Bichsel parametrisation (Bichsel 1990). Bonderup (1967) estimates that ⟨ I ⟩ = 11.4 Z2 (eV), but this is not always in agreement with experimental data and unfortunately there are no simple algorithms for the shell correction and density effect. As a consequence, no simple analytical expressions for the stopping power are available.
The SRIM program (Ziegler et al. 1985) calculates accurate stopping powers from Eq. (7) using different methods to evaluate the corrective terms. The shell correction C/Z2 is the average of the values obtained from the Local Density Approximation theory (LDA) and Hydrogenic Wave Function (HWF) approach (Ziegler 1999). The first is an ab initio calculation based on realistic solid state charge distributions, while the second uses parameterized functions based on experimental stopping data. For the density correction δ/2, the values tabulated in ICRU (1984) are used, while the term ln ⟨ I ⟩ is derived by adjusting the theoretical value obtained from the LDA theory (e.g. Lindhard & Scharff 1952) in order to fit the sum ln ⟨ I ⟩ + C/Z2 evaluated empirically from experimental stopping data.
As already mentioned, Eq. (7) is valid for
light ions, H, He and Li. The stopping power for ions with
Z1 > 3 is usually calculated using the heavy-ion
scaling rule, as reported for example by Katz et al.
(1972)![\begin{eqnarray} \label{heavy_eq} S(Z_1,\,\beta) = S(p,\,\beta)[Z_1^*/Z_{\rm p}^*]^2 \end{eqnarray}](/articles/aa/full_html/2011/02/aa15741-10/aa15741-10-eq47.png) (8)where
S(p, β) is the stopping power of a
proton at the same speed as the ion of atomic number Z1
(Eq. (7)),
(8)where
S(p, β) is the stopping power of a
proton at the same speed as the ion of atomic number Z1
(Eq. (7)),
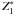 and
and
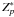 are the
effective charge numbers of ion Z1 and of a proton
respectively, with the expression given by Barkas (see e.g. Henriksen et al. 1970).
are the
effective charge numbers of ion Z1 and of a proton
respectively, with the expression given by Barkas (see e.g. Henriksen et al. 1970). ![\begin{eqnarray} \label{zeff_eq} Z_1^* = Z_1\,\left[1\,-\,\exp\left(-125\,\beta\,Z_1^{-2/3}\right)\right]. \end{eqnarray}](/articles/aa/full_html/2011/02/aa15741-10/aa15741-10-eq51.png) (9)To
verify the effective importance of the corrective terms to the Bethe-Bloch equation in our
specific case of interest (H, He, C and Fe impacting on carbon), we compared the output
from SRIM with the stopping power calculated from the following approximate equation
(9)To
verify the effective importance of the corrective terms to the Bethe-Bloch equation in our
specific case of interest (H, He, C and Fe impacting on carbon), we compared the output
from SRIM with the stopping power calculated from the following approximate equation
![\begin{eqnarray} \label{stoppingApprox_eq} S = \frac{\kappa\,Z_2}{\beta^2}\,Z_1^2\,\left[f(\beta)\,-\, \ln \langle I \rangle\right] \end{eqnarray}](/articles/aa/full_html/2011/02/aa15741-10/aa15741-10-eq52.png) (10)where
we adopt the carbon mean ionization energy calculated by SRIM1 using the method described above, ⟨ I ⟩ = 79.1 eV. For the
heavier ions C and Fe we use the proton stopping power from Eq. (10) into Eq. (8).
(10)where
we adopt the carbon mean ionization energy calculated by SRIM1 using the method described above, ⟨ I ⟩ = 79.1 eV. For the
heavier ions C and Fe we use the proton stopping power from Eq. (10) into Eq. (8).
We find a maximum discrepancy between the two curves of ~10%, very small with respect to the other astrophysical uncertainties and indicating that our approximate equation is adequate to describe the energy loss. In this specific case, not only the Barkas and Bloch corrections, but also the shell correction and the density effect play a marginal role. Figure 1 shows the comparison between the “accurate” SRIM curve and the approximate one for H and Fe, our lightest and heaviest projectiles respectively.
Using Eqs. (8) and (10) we can then calculate the electronic stopping power dE/dx of energetic ions and from this the energy loss to the PAH molecule (Sect. 3). Since the stopping power is a decreasing function of the ion energy and increases quadratically with Z1, the major contribution to the energy loss will come from the less energetic particles for a given ion, and from the heavier species for a given velocity (Fig. 1).
 |
Fig. 1 Stopping power of hydrogen and iron impacting on carbon, as a function of the energy per nucleon of the ion. The lower validity limit of the Bethe-Bloch equation is 1 MeV/nucleon. We compare the output from the SRIM code, which computes all corrections, and our approximate equation which includes only the mean ionization correction. |
2.2. Ion energy loss and dissociation probability
To calculate the energy transferred to a PAH during collisions with high energy ions we adopt the configuration shown in Fig. 2 (see also MJTb).
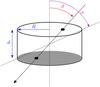 |
Fig. 2 Coordinate system adopted to calculate the energy transferred to a PAH via electronic excitation by ion collisions. The molecule is modeled as a disk with radius R and thickness d. The trajectory of the incoming particle is identified by the angle ϑ, while the angle α corresponds to the diagonal of the disk. |
The molecule is modeled as a thick disk with radius R given by the usual
expression for the radius of a PAH: 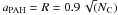 Å,
where NC is the number of carbon atoms in the molecule
(Omont 1986). For a 50 C-atom PAH,
R = 6.36 Å. The thickness of the disk,
d ~ 4.31 Å is the thickness of the electron density assumed for
the PAH (see MJTb).
Å,
where NC is the number of carbon atoms in the molecule
(Omont 1986). For a 50 C-atom PAH,
R = 6.36 Å. The thickness of the disk,
d ~ 4.31 Å is the thickness of the electron density assumed for
the PAH (see MJTb).
The path l, through the PAH, along which the incoming ion loses its
energy is defined by the impact angle ϑ and by the dimensions of the
molecule. Inspection of Fig. 2 shows that, if
|tan(ϑ)| < tan(α),
l(ϑ) = d/|cosϑ| ,
otherwise
l(ϑ) = 2R/|sinϑ| .
The rigorous method to calculate the energy loss along
l(ϑ) takes into account the progressive slowing down
of the projectile in traversing the target. This is explained in Sect. 3 of MJTb.
Nevertheless, in the present case we consider high energy particles for which the energy
loss along the path l is small compared to the initial energy (cf.
Fig. 1). In other words, the energy of the incoming
ion remains almost constant during the interaction, thus the amount of energy lost after
travelling the distance l(ϑ) can be simplified to
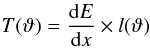 (11)where
dE/dx = S(ϑ) is
the stopping power (energy lost per unit length) from Eqs. (10) and/or (8), and
dE is the amount of energy lost after travelling the distance
dx. The difference between the results from the two methods is of the
order of few percent, which fully justifies the use of approximation in Eq. (11).
(11)where
dE/dx = S(ϑ) is
the stopping power (energy lost per unit length) from Eqs. (10) and/or (8), and
dE is the amount of energy lost after travelling the distance
dx. The difference between the results from the two methods is of the
order of few percent, which fully justifies the use of approximation in Eq. (11).
The ion collision will leave the molecule electronically excited. Internal conversion
and/or intersystem crossing will transfer this excitation (largely) to the vibrational
manifold. De-excitation can occur through two competing decay channels: emission of
infrared photons and dissociation and loss of a C2 fragment. The latter is the
process that we are interested in because it leads to PAH fragmentation. The emission of a
C2 fragment is suggested by experiments on fullerene C60 which
have shown that the ejection of C2 groups is one of the preferred fragmentation
channel. Moreover, the loss of acetylene groups C2H2 has been
observed in small PAHs. In fact, in a PAH molecule, a side group
C2Hn (with n = 0, 1, 2) is
easier to remove because only two single bonds have to be broken, while the ejection of a
single external C-atom requires one single and one double bond to be broken, and for an
inner C-atom from the skeleton three bonds needs to be broken. To quantify the PAH
destruction due to ion collisions we need to determine the probability of dissociation,
P, rather than IR emission. For the detailed calculation and a
discussion of the dissociation probability, we refer the reader to Sect. 4.1 in MJTb. For
the sake of clarity, the basic equations are reproduced here. The total dissociation
probability is calculated by combining the rates for fragmentation
(k0exp [−E0/k Tav] )
and IR decay (kIR/(nmax + 1))
into the following expression ![\begin{eqnarray} \label{totalProb2_eq} P = \frac{k_{\rm 0}\,\exp \left[-E_{\rm 0}/k\,T_{\rm av} \right]} {\left[k_{\rm IR}/(n_{\rm max}+1)\right]\:+\:k_{\rm 0}\, \exp \left[-E_{\rm 0}/k\,T_{\rm av} \right]} \end{eqnarray}](/articles/aa/full_html/2011/02/aa15741-10/aa15741-10-eq78.png) (12)where
k0 and E0 are the Arrhenius
pre-exponential factor and energy describing the fragmentation process respectively,
kIR and nmax are the IR photon
emission rate and number of IR photons (MJTb), and k is the Boltzmann
constant. The temperature Tav is chosen as the geometrical
mean between two specific effective temperatures of the PAH
(12)where
k0 and E0 are the Arrhenius
pre-exponential factor and energy describing the fragmentation process respectively,
kIR and nmax are the IR photon
emission rate and number of IR photons (MJTb), and k is the Boltzmann
constant. The temperature Tav is chosen as the geometrical
mean between two specific effective temperatures of the PAH 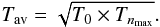 (13)In
the microcanonical description of a PAH, the temperature, T, describing
the excitation (for fragmentation purposes) is related to the internal energy,
E′, by
(13)In
the microcanonical description of a PAH, the temperature, T, describing
the excitation (for fragmentation purposes) is related to the internal energy,
E′, by 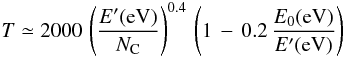 (14)where
E0 is the binding energy of the fragment (Tielens 2005). The temperatures
T0 and
Tnmax in Eq. (13) are the temperatures when the internal
energy equals the initial transferred energy (E′ = E)
and when the internal energy equals the energy after emission of
nmax photons
(E′ = E − nmax × Δε)
with Δε being the average energy of the emitted IR photon. For the number
of photons, nmax, required to be emitted to have the
probability per step drop by an order of magnitude, we adopt 10, the average photon energy
is set equal to 0.16 eV, corresponding to a typical CC mode, and the pre–exponential is
set equal to 1.4 × 1016 s-1 (MJTb). For the photon emission rate
we adopt the typical value kIR = 100 photons s-1
(Jochims et al. 1994).
(14)where
E0 is the binding energy of the fragment (Tielens 2005). The temperatures
T0 and
Tnmax in Eq. (13) are the temperatures when the internal
energy equals the initial transferred energy (E′ = E)
and when the internal energy equals the energy after emission of
nmax photons
(E′ = E − nmax × Δε)
with Δε being the average energy of the emitted IR photon. For the number
of photons, nmax, required to be emitted to have the
probability per step drop by an order of magnitude, we adopt 10, the average photon energy
is set equal to 0.16 eV, corresponding to a typical CC mode, and the pre–exponential is
set equal to 1.4 × 1016 s-1 (MJTb). For the photon emission rate
we adopt the typical value kIR = 100 photons s-1
(Jochims et al. 1994).
From the above equations one can see that P depends on the binding energy of the fragment, E0, on the PAH size, NC, and on the energy transferred, T, which in turns depends on the initial energy of the projectile. For a fixed value of the transferred energy, the dissociation probability decreases for increasing E0 and NC because either more energy is required in the bond that has to be broken or because the energy is spread over more vibrational modes and hence the internal excitation temperature is lower. On the other hand, the more energy that is deposited in the PAH, the higher is the dissociation probability.
The fragment binding energy E0, which is a crucial parameter in the evaluation of the dissociation probability is, unfortunately, presently not well constrained. As in our previous work (MJTb) we investigated the impact on the PAH destruction process for E0 = 3.65, 5.6 and 4.58 eV, the latter value is consistent with extrapolations to interstellar conditions and is our reference value.
As mentioned at the end of Sect. 2.1, the stopping power increases with the atomic number of the projectile and decreases with its energy. Thus, for a given pathlength, the energy transferred, and therefore the dissociation probability, will be higher for low energy heavy particles.
3. Collisions with high energy electrons
To model the interaction of high-energy electrons with PAH molecules, we refer to the formalism used to describe the irradiation effects in solid materials, in particular carbon nanostructures (Banhart 1999). In the collisions of high-energy (relativistic) electrons with nuclei, the screening effect of the surrounding electrons is negligible. The electron-nucleus interaction can thus be treated in terms of a binary collision using a simple Coulomb potential, applying the appropriate relativistic corrections (e.g. Reimer & Braun 1989; Banhart 1999).
If the energy transferred to the nucleus exceeds the displacement energy Td, i.e. the minimum energy required to produce a vacancy– interstitial pair which does not spontaneously recombine, the atom will be knocked out. If its energy is above the threshold value for further displacements, it can remove other atoms in its environment generating a collision cascade.
In this description the “bulk” nature of the target enters only after the first interaction, when projectile and displaced atom propagate into the solid. Therefore, if we limit ourselves to the first interaction only, this approach can be applied to electron-PAH collisions and allows us to take into account the “molecular” nature of our target. In fact, this is the same binary collision approach used to describe the nuclear interaction (elastic energy loss) in collisions between PAHs and relatively low energy ions in interstellar shocks (MJTa).
A PAH is a planar molecule with tens to hundreds of carbon atom. In this case the target
nucleus is a single carbon in the PAH. If the energy transferred exceeds a threshold value
the target nucleus will be ejected from the molecule. The displacement energy then has to be
replaced by the threshold energy T0, which represents the
minimum energy to be transferred in order to knock-out a carbon atom from a PAH. The
interaction between a high energy CR electron and a PAH occurs between the impinging
electron and one single target carbon atom in the molecule. The energy is transferred from
the projectile electron to a target carbon atom through a binary collision. Thus, each
electron collision implies the loss of one single carbon atom, in contrast to ion collisions
where each interaction causes the ejection of a C2 fragment from the PAH
molecule. The scattering geometry is shown in Fig. 3.
After the collision, the target nucleus is knocked out and recoils at an angle Θ with
respect of the initial direction of motion of the projectile electron. The
energy T transferred to the nucleus depends on the scattering angle
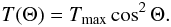 (15)The
term Tmax is the maximum transferable energy, corresponding to a
head-on collision (Θ = 0), and is given by the following equation (Simmons 1965)
(15)The
term Tmax is the maximum transferable energy, corresponding to a
head-on collision (Θ = 0), and is given by the following equation (Simmons 1965) 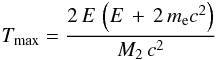 (16)where
E is the electron kinetic energy, me is the
electron mass and M2 is the target atomic mass.
(16)where
E is the electron kinetic energy, me is the
electron mass and M2 is the target atomic mass.
 |
Fig. 3 Scattering geometry for the elastic collision of an electron (mass me, impact parameter p, initial velocity v) on a massive particle (mass M2, initial velocity zero). After the impact, the target particle is knocked out and recoils at an angle Θ with respect of the initial direction of motion of the projectile electron. |
The total displacement/removal cross section, σ, i.e. the cross section
for collisions able to transfer more than the threshold
energy T0, is defined as the integral over the solid angle of
the differential cross section dσ/dΩ, which provides the probability for
atomic recoil into the solid angle dΩ 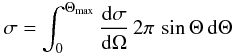 (17)where
Θ = 0 corresponds to the transfer of Tmax and
Θ = Θmax is the recoil angle corresponding to the transfer of the minimun
energy T0. The calculation of the total cross
section σ for atom displacement/removal would require the analytical
treatment of the Mott scattering of a relativistic electron by a nucleus (Mott 1929, 1932).
The corresponding equations have to be solved numerically, but McKinley & Feshbach (1948) found an analytical approximation
which provides reliable values of σ for light target elements such as
carbon (under the assumption of an isotropic displacement/threshold energy). We adopt the
formulation of the analytical expression reported by Banhart
(1999)
(17)where
Θ = 0 corresponds to the transfer of Tmax and
Θ = Θmax is the recoil angle corresponding to the transfer of the minimun
energy T0. The calculation of the total cross
section σ for atom displacement/removal would require the analytical
treatment of the Mott scattering of a relativistic electron by a nucleus (Mott 1929, 1932).
The corresponding equations have to be solved numerically, but McKinley & Feshbach (1948) found an analytical approximation
which provides reliable values of σ for light target elements such as
carbon (under the assumption of an isotropic displacement/threshold energy). We adopt the
formulation of the analytical expression reported by Banhart
(1999)![\begin{eqnarray} \label{sigmaElectron_eq} \sigma &=& \frac{4\,Z_2^2\,E_{\rm R}^2}{m_{\rm e}^2\,c^4}\;\left(\frac{T_{\rm max}}{T_{\rm 0}}\right)\, \pi\,a_{\rm 0}^2\;\left(\frac{1\,-\,\beta^2}{\beta^4}\right)\; \left\{1\,+\,2\,\pi\,\alpha\,\beta\,\,\left(\frac{T_{\rm 0}}{T_{\rm max}}\right)^{1/2}\right. \nonumber \\ &&\left. -\,\frac{T_{\rm 0}}{T_{\rm max}}\;\left[1\,+\,2\,\pi\,\alpha\,\beta\,+\, \left(\beta^2\,+\,\pi\,\alpha\,\beta \right)\,\ln\,\left(\frac{T_{\rm max}}{T_{\rm 0}}\right)\,\right]\,\right\} \end{eqnarray}](/articles/aa/full_html/2011/02/aa15741-10/aa15741-10-eq114.png) (18)where
Z2 is the atomic number of the displaced atom (in our case,
carbon), ER is the Rydberg energy (13.6 eV),
mec2 is the electron rest mass
(0.511 MeV), a0 is the Bohr radius of the hydrogen atom
(5.3 × 10-11 m),
β = v/c, v being the
velocity of the incident electron, and
α = Z2/137, where 1/137 is the fine structure
constant.
(18)where
Z2 is the atomic number of the displaced atom (in our case,
carbon), ER is the Rydberg energy (13.6 eV),
mec2 is the electron rest mass
(0.511 MeV), a0 is the Bohr radius of the hydrogen atom
(5.3 × 10-11 m),
β = v/c, v being the
velocity of the incident electron, and
α = Z2/137, where 1/137 is the fine structure
constant.
The term T0 is the minimum energy which has to be transferred into the PAH in order to remove a carbon atom and represents the analog of the displacement energy Td in a solid. For an extended discussion about the determination of the threshold energy T0 we refer the reader to MJTb (Sect. 2.2.1). We recall here that the value of T0 is, unfortunately, not well established, because there are no experimental determinations on PAHs and the theoretical evaluation is uncertain. We decided to explore possible values: 4.5 and 7.5 eV, close to the energy of the single and double C-bond respectively and 15 eV, compatible with the expected threshold for a single walled nanotube. We adopt 7.5 eV as our reference value, consistent with all the experimental data.
To calculate β as a function of the kinetic energy of the incident
electron, it is important to remember that we are considering relativistic particles, thus
the appropriate expression for the kinetic energy is the following: 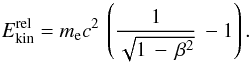 (19)From
Eq. (19) we then
derive β
(19)From
Eq. (19) we then
derive β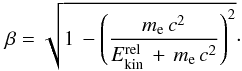 (20)The
displacement cross section σ calculated from Eqs. (18) and (20), is shown in Fig. 4 as a
function of the electron kinetic energy, for three different values
of T0. Above threshold the cross section increases with
electron energy and decreases again at higher energies because of relativistic effects,
reaching the constant value given by the following asymptotic expression
(20)The
displacement cross section σ calculated from Eqs. (18) and (20), is shown in Fig. 4 as a
function of the electron kinetic energy, for three different values
of T0. Above threshold the cross section increases with
electron energy and decreases again at higher energies because of relativistic effects,
reaching the constant value given by the following asymptotic expression 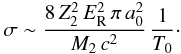 (21)As
expected σ decreases for increasing values of the threshold energy. Around
the peak the change of T0 from 4.5 to 15 eV introduces a
variation in the cross section of a factor of about 9, which reduces to 3.4 – the
ratio 15/4.5, cf. Eq. (21) – for electron
energies above ~2 MeV.
(21)As
expected σ decreases for increasing values of the threshold energy. Around
the peak the change of T0 from 4.5 to 15 eV introduces a
variation in the cross section of a factor of about 9, which reduces to 3.4 – the
ratio 15/4.5, cf. Eq. (21) – for electron
energies above ~2 MeV.
 |
Fig. 4 High energy electron cross section for carbon atom removal, calculated for three values of the threshold energy T0. |
4. The CR spectrum
The stopping power of ions with energy above ~1 MeV/nucleon decreases with increasing energy (cf. Sect. 2.1). This implies that the CRs responsible for the major energy transfer to a PAH, and subsequent damage, are the lower-energy ones (below 1 GeV/nucleon). Unfortunately this part of the CR spectrum is not accessible from the Earth because of the phenomenon called solar modulation (Shapiro 1991). CRs entering the heliosphere see their intensity reduced by the effect of the solar wind, especially at low energies and when the solar cycle is at its maximum. The solar magnetic field is frozen within the plasma of the solar wind and drawn out with it into a spiral structure. CRs encountering the solar wind are then convected outward. Moreover when such charged particles interact with the expanding magnetic field, they are adiabatically decelerated. Hence, the CRs observed at a given energy were originally much more energetic.
Because of the solar modulation, the interstellar CR spectrum at low energies needs to be evaluated theoretically by solving the transport equation for particles in the ISM, assuming an appropriate CR spectrum at the sources and taking into account all possible mechanisms able to modify the intensity of the CRs during their propagation (energy losses, fragmentation etc. Shapiro 1991). The Pioneer and Voyager spacecraft have probed the heliosphere out to beyond 60 AU, greatly improving the understanding of the spectra of protons and heavier nuclei with energies above ~100 MeV and the effects of solar modulation, although limited information is available on CR nuclei below ~100 MeV (Webber 1998). To describe the propagation and escape of Galactic CRs (at energies below a few ×1015 eV), a widely used approach is the leaky-box model, which assumes that the particles are confined to the Galaxy, with frequent visits to the disk boundaries where they have a small probability of leaking out (Ip & Axford 1985; Simpson & Garcia-Munoz 1988; Indriolo et al. 2009).
Following Webber & Yushak (1983) and Bringa et al. (2007) the CR intensity
I(E) as a function of the total energy per ion,
E, is then given by 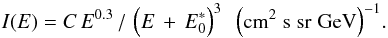 (22)The
constant C can be determined by matching Eq. (22) with the high-energy CR spectrum measured on the Earth (see below).
The scaling factor
(22)The
constant C can be determined by matching Eq. (22) with the high-energy CR spectrum measured on the Earth (see below).
The scaling factor 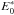 sets the level
of low-energy CRs (Webber & Yushak 1983),
which is mainly determined by ionization loss and Coulomb collisions (Ip & Axford 1985). At higher energies (above
~1 GeV/nucleon) diffusive losses dominate.
sets the level
of low-energy CRs (Webber & Yushak 1983),
which is mainly determined by ionization loss and Coulomb collisions (Ip & Axford 1985). At higher energies (above
~1 GeV/nucleon) diffusive losses dominate.
The interstellar CR spectrum can be constrained by molecular observations. CR protons
ionize atomic and molecular hydrogen and this ionization drives interstellar chemistry
through ion-molecule reactions. Analysis of molecular observations in diffuse clouds result
in an average primary ionization rate of 4 × 10-16 s-1
(H-nuclei)-1 (Indriolo et al. 2009, and
references therein). The CR ionization rate follows from a convolution of the CR spectrum,
Eq. (22), with the hydrogen ionization
cross section (Bringa et al. 2007). The scaling
factor 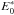 can be
calculated then from
can be
calculated then from 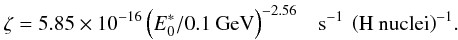 (23)Again,
because of the steep decrease of the ionization cross section with energy, the CR ionization
rate is most sensitive to the low energy CR flux. For hydrogen this results in
(23)Again,
because of the steep decrease of the ionization cross section with energy, the CR ionization
rate is most sensitive to the low energy CR flux. For hydrogen this results in
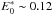 GeV. For heavier particles we
adopt the same scaling rule as Bringa et al. (2007):
GeV. For heavier particles we
adopt the same scaling rule as Bringa et al. (2007):
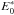 (ion) =
(ion) = 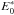 (H) × M1 GeV particle-1,
where M1 is the mass of the particle in amu.
(H) × M1 GeV particle-1,
where M1 is the mass of the particle in amu.
To calculate the constant C, we matched Eq. (22) with the high-energy spectrum detected on Earth. For the high energy
data, which are not influenced by the solar modulation, we adopt the expression from Wiebel-Sooth et al. (1998)![\begin{eqnarray} \label{ionHighSpectrum_eq} I(E) = I_0\,\left[E\,(\rm{GeV}) / (1000\,GeV)\right]^{-\gamma} \;\;\;\rm{\left(cm^2\;s\;sr\;GeV\right)^{-1}} \end{eqnarray}](/articles/aa/full_html/2011/02/aa15741-10/aa15741-10-eq133.png) (24)where
I0 and γ depend on the CR ion.
(24)where
I0 and γ depend on the CR ion.
In this study we consider the most abundant CR components: H, He, the group C, N, O and the group Fe, Co, Ni. The latter are in fact often detected as a group because of the experimental difficulty in distinguishing between particles with similar mass. The spectra were calculated using the method described above, with the high-energy parameters I0 and γ from Wiebel-Sooth et al. (1998). The matching between the low and high energy regimes is at E = 1 TeV. A list of the parameters required for the calculation is reported in Table 1, and the resulting CR spectra are shown in Fig. 5. For the lowest energy of the interstellar CR spectrum, we choose the value of 5 MeV/nucleon, consistent with the limit of ~1 MeV/nucleon adopted by Ip & Axford (1985) for their calculation of the CRs spectrum, and which corresponds to the lower limit of the energy range where ionization loss rapidly diminishes the propagation of CRs in the ISM.
CR ion spectra parameters.
The same approach as that used for heavy particles (ions) can be applied to CR electrons.
In this case solar modulation also alters the spectrum of the electrons entering the solar
cavity. The interstellar spectrum at low energies has to be calculated solving the transport
equation for electrons in the ISM, taking into account the energy loss processes relevant
for electrons, i.e. bremsstrahlung, synchrotron and inverse Compton. The low energy spectrum
then has to be connected to the measured high-energy spectrum, which is not affected by the
modulation. We adopt the expression from Cummings
(1973), calculated in the framework of the leaky-box model (see also Ip & Axford 1985; Moskalenko & Strong 1998) ![\begin{eqnarray} \label{elec_eq} I(E) = A\,\left[E(\rm{GeV})\times10^3\right]^{-\gamma}\;\;\; \rm{\left(cm^2\;s\;sr \;GeV \right)^{-1}} \end{eqnarray}](/articles/aa/full_html/2011/02/aa15741-10/aa15741-10-eq140.png) (25)where
E is in GeV and
(25)where
E is in GeV and
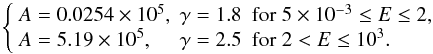 The
calculated spectrum is shown in Fig. 5. For the lowest
energy, we again adopt a value of 5 MeV, coherent with the range of influence of
bremsstrahlung, the dominant energy loss mechanism for electrons with energies less than a
few hundreds of MeV.
The
calculated spectrum is shown in Fig. 5. For the lowest
energy, we again adopt a value of 5 MeV, coherent with the range of influence of
bremsstrahlung, the dominant energy loss mechanism for electrons with energies less than a
few hundreds of MeV.
It is important to underline the fact that the method used to calculate the interstellar CR spectrum at low energies, i.e. solving the transport equation for particles adopting appropriate parameters in order to match the measurements, does not provide an unique solution. It has been shown that different sets of parameters for the transport model result in a set of different spectral shapes all consistent with the CR intensity measured at higher energies (see e.g. Mewaldt et al. 2004). Strong constraints on the low-energy CR spectrum have been provided by the interstellar ionization rate (e.g. Indriolo et al. 2009; Padovani et al. 2009, and references therein), which allowed to exclude some models, for instance the the W98 model (Webber 1998) for protons and the C00 model (Moskalenko et al. 2002) for electrons. Despite such improvement, the ambiguity on the low-energy region of the CR spectrum has not been completely solved yet. This uncertainty does not affect the conclusions of our present work, but it is important to keep it in mind.
 |
Fig. 5 Interstellar CR spectrum of H, He, CNO, Fe-Co-Ni and electrons as a function of the particle energy. |
5. Collision rate and C-atom ejection rate
To calculate the collision rate between PAHs and CR ions and electrons, with energy fluxes described by Eqs. (22) and (25) respectively, we follow the procedure illustrated below.
For ion collisions, where the energy is transferred to the whole PAH via electronic
excitation, we first need to calculate the term Σ(E), which takes into
account all possible ion trajectories through the PAH, with their corresponding transferred
energies and dissociation probabilities. Adopting the configuration shown in Fig. 2 we have 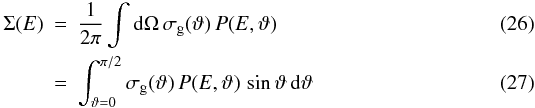 with
Ω = sinϑ dϑ dϕ,
with ϕ running from 0 to 2π and ϑ
from 0 to π/2. The geometrical cross section seen by an incident particle
with direction defined by the angle ϑ is given by
with
Ω = sinϑ dϑ dϕ,
with ϕ running from 0 to 2π and ϑ
from 0 to π/2. The geometrical cross section seen by an incident particle
with direction defined by the angle ϑ is given by 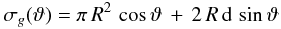 (28)which
reduces to
σg = π R2
for ϑ = 0 (face-on impact) and to
σg = 2 R d for
ϑ = π/2 (edge-on impact). The term
P(E,ϑ) represents the total probability for dissociation
upon ion collision, for a particle with energy E and incoming
direction ϑ. The ion collision rate is calculated by convolution of the
term Σ(E) over the CR spectrum
Ii(E)
(28)which
reduces to
σg = π R2
for ϑ = 0 (face-on impact) and to
σg = 2 R d for
ϑ = π/2 (edge-on impact). The term
P(E,ϑ) represents the total probability for dissociation
upon ion collision, for a particle with energy E and incoming
direction ϑ. The ion collision rate is calculated by convolution of the
term Σ(E) over the CR spectrum
Ii(E) 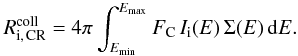 (29)Because
each (electronic) ion interaction leads to the removal of two carbon atoms from the PAH, to
obtain the C-atom ejection rate the collision rate has to be multiplied by a factor of 2:
(29)Because
each (electronic) ion interaction leads to the removal of two carbon atoms from the PAH, to
obtain the C-atom ejection rate the collision rate has to be multiplied by a factor of 2:
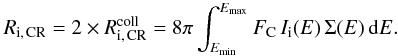 (30)The
factor, FC, takes Coulombian effects into account (see below).
For Emax we adopt a value of 10 GeV, corresponding to the
highest energy for which experimental stopping determinations exist and thus for which
Eq. (7) is valid. Moreover the CR intensity
and stopping power decrease rapidly, so ions with energy above 10 GeV do not contribute
significantly to the integral in Eq. (29).
Concerning the lower integration limit, we perform the calculation for
Emin = 5 MeV/nucleon, the lower limit assumed for the
CR spectra.
(30)The
factor, FC, takes Coulombian effects into account (see below).
For Emax we adopt a value of 10 GeV, corresponding to the
highest energy for which experimental stopping determinations exist and thus for which
Eq. (7) is valid. Moreover the CR intensity
and stopping power decrease rapidly, so ions with energy above 10 GeV do not contribute
significantly to the integral in Eq. (29).
Concerning the lower integration limit, we perform the calculation for
Emin = 5 MeV/nucleon, the lower limit assumed for the
CR spectra.
For interactions with CR electrons, each binary collision results in the ejection of one
single C-atom. Thus the ejection rate coincides with the collision rate, and are both given
by the following relation 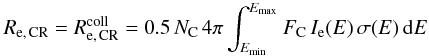 (31)where
the ejection cross section per target atom σ has to be
multiplied by the number of C-atom in the molecule, NC. The
factor 0.5 takes the angle averaged orientation into account (MJTa). As for the CR ions we
assume as integration limits the values Emin = 5 MeV and
Emax 10 GeV. For the electrons, the upper limit is not
constrained by the stopping theory (the expression for the ejection cross section holds for
even higher energies) and is only related to the steepness of the spectrum which results in
a negligible contribution from electrons with energy above 10 GeV (cf. Fig. 5).
(31)where
the ejection cross section per target atom σ has to be
multiplied by the number of C-atom in the molecule, NC. The
factor 0.5 takes the angle averaged orientation into account (MJTa). As for the CR ions we
assume as integration limits the values Emin = 5 MeV and
Emax 10 GeV. For the electrons, the upper limit is not
constrained by the stopping theory (the expression for the ejection cross section holds for
even higher energies) and is only related to the steepness of the spectrum which results in
a negligible contribution from electrons with energy above 10 GeV (cf. Fig. 5).
The Coulombian correction factor FC (MJTb) takes into account the fact that both target and projectiles are charged, and that the collision cross section could be enhanced or diminished depending on the charge of the PAH. Because we are considering high energy ions and electrons, which are unaffected by the Coulombian field, FC is always unity.
6. Results
 |
Fig. 6 PAH survival time against collisions with CR ions, as a function of the fraction f of the transferred energy that goes into vibrational excitation. The lifetime has been calculated for PAHs of different sizes (NC), assuming three values for the binding energy of the ejected fragment, E0. The line style indicates the type of ion: dotted for H, dashed for He, solid for CNO and dot-dot-dashed for Fe-Co-Ni. The line color indicates the value of the fragment binding energy: gray for E0 = 3.65 eV, black for E0 = 4.58 eV and red for E0 = 5.6 eV. |
6.1. PAH lifetime
Collisions with CR ions and electrons will cause a progressive decrease in the number of
carbon atoms in a PAH molecule. For interactions with ions, after a
time t this number is reduced to 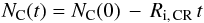 (32)and
the fraction of carbon atoms ejected from this PAH is
(32)and
the fraction of carbon atoms ejected from this PAH is 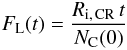 (33)where
Ri, CR is the C-atom ejection rate from Eq. (30). We assume that the PAH is destroyed after
the ejection of 1/3 of the carbon atoms initially present in the molecule. This occurs
after a time τ0 which we adopt as the PAH lifetime against CR
ions bombardment, and is given by
(33)where
Ri, CR is the C-atom ejection rate from Eq. (30). We assume that the PAH is destroyed after
the ejection of 1/3 of the carbon atoms initially present in the molecule. This occurs
after a time τ0 which we adopt as the PAH lifetime against CR
ions bombardment, and is given by 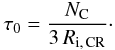 (34)For
electron collisions, the number of carbon atoms in the PAH molecule after a
time t is
(34)For
electron collisions, the number of carbon atoms in the PAH molecule after a
time t is ![\begin{eqnarray} \label{NtELECTRON_eq} N_{\rm C}(t) = N_{\rm C}(0) \exp \left[-t\,/\,\tau'\right] \end{eqnarray}](/articles/aa/full_html/2011/02/aa15741-10/aa15741-10-eq170.png) (35)and
the fraction of carbon atoms ejected from this PAH is
(35)and
the fraction of carbon atoms ejected from this PAH is ![\begin{eqnarray} \label{FlELECTRON_eq} F_{\rm L}(t) = \left(1 - \exp \left[ -t\,/\,\tau' \right] \right) \end{eqnarray}](/articles/aa/full_html/2011/02/aa15741-10/aa15741-10-eq171.png) (36)with
the time constant
τ′ = NC/Re, CR,
where Re, CR is the ejection rate from Eq. (31). The ejection of 1/3 of carbon atoms
originally present in the PAH molecule, after which the PAH is considered destroyed, takes
the time τ0 given by
(36)with
the time constant
τ′ = NC/Re, CR,
where Re, CR is the ejection rate from Eq. (31). The ejection of 1/3 of carbon atoms
originally present in the PAH molecule, after which the PAH is considered destroyed, takes
the time τ0 given by 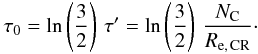 (37)As
for ion collisions, we adopt τ0 as the PAH survival time
against CR electrons. The ejection rate Re, CR scales
linearly with NC, hence the corresponding
lifetime τ0 is independent of PAH size.
(37)As
for ion collisions, we adopt τ0 as the PAH survival time
against CR electrons. The ejection rate Re, CR scales
linearly with NC, hence the corresponding
lifetime τ0 is independent of PAH size.
For collisions with ions, we calculated the lifetime of PAHs of four sizes NC = 50, 100, 200 and 1000 (radius aPAH = 6.36, 9, 12.7, 28.5 Å, nmax = 10, 20, 40 and 200 respectively) bombarded by CR H, He, CNO and Fe-Co-Ni ions, assuming three different values for the electronic binding energy, E0 = 3.65, 4.58 and 5.6 eV (cf. Sect. 4.1 in MJTb). In principle, not all the energy transferred to the PAH will be internally converted into vibrational modes, with consequent relaxation through dissociation (or IR emission). Other processes can occur, for instance the production of Auger electrons which will carry away from the molecule a part of the transferred energy. We don’t know exactly how quantify this energy partitioning and so we introduce a factor f, which represents the fraction of the transferred energy T that goes into vibrational excitation.
The survival time as a function of the factor f is shown in Fig. 6. The PAH lifetime becomes shorter as more energy goes into vibrational excitation (increasing f) and for lower values of E0, because this implies a higher temperature, Tav, and a lower energy to eject a fragment, resulting in a larger dissociation probability (Eq. (12)).
The dissociation probability is more sensitive to E0 when the energy available for dissociation is lower, i.e. light projectile and small f, and when the same amount of energy has to be spread over more bonds (increasing size). This explains why the separation between the time constant curves corresponding to the different values of E0 decreases with increasing available energy and mass of the projectile (from H to Fe-Co-Ni), while it gets bigger for larger PAHs. Big PAHs are more resistent to CR bombardment because for any given transferred energy their dissociation probability is lower.
The lifetime against Fe-Co-Ni bombardment is essentially constant – except for very low available energy and very large molecules (NC = 1000). Its large value, τ0 ~ few 109 yr, results from the fact that, despite the huge amount of energy transferred into the molecule (cf. Fig. 1), the Fe-Co-Ni abundance in CRs is small. This leads to a low collision rate and long lifetime. For hydrogen, the high abundance is not enough to compensate for the small stopping power, which rapidly decreases above 1 MeV/nucleon. As a result the lifetimes are long. Since the energy transferred to the molecule is small, the collision rate and the survival times are sensitive to the adopted parameters: the fraction of the energy transferred available for dissociation f, the fragment binding energy E0 and the PAH size. This variability is shown in Fig. 6. The situation for helium and CNO lies somewhere between the cases for H and Fe-Co-Ni.
The CR electron time constant is independent of the PAH size, and has been calculated for three values of the threshold energy for carbon atom ejection, T0 = 4.5, 7.5 and 15 eV. The results are shown in Fig. 7 and summarized in Table 2. The PAH lifetime is longer for increasing values of T0 because of the diminution in the cross section σ. Given that σ is almost constant for energies above ~2 MeV, for a fixed T0 this part of the spectrum does not contribute to the variation. Because of the small ejection cross section and the steep CR electron spectrum, all the calculated time constants are long (τ0 > 1013 yr).
Time constant τ0 for carbon atom ejection following PAH collisions with CR electrons.
6.2. Discussion of the uncertainties
The first source of uncertainty affecting the study of PAH interaction with high energy particles is the accuracy of the stopping theory used to calculate the energy loss of ions in matter. This is a difficult issue because the current theory, based on the Bethe-Bloch equation and described in Sect. 2.1, is in fact a combination of different theoretical approaches with corrections coming from fits to the experimental data. A better way to pose the problem is by instead asking: “How accurately can stopping powers be calculated?” The comparison between theory and experiments, together with the evaluation of possible variation sources such as structural variations in the targets, provides an accuracy ranging from 5 to 10% (Ziegler 1999).
In our calculation we do not use the complete Bethe-Bloch equation (implemented in the SRIM code with all corrective terms) but the analytical approximation given by Eq. (10). The discrepancy between the stopping power curves from these two formulations is very small, and introduces an uncertainty of at most 10% in our calculation. An additional source of uncertainty comes from the calculation of the energy transferred to the PAH using the approximation in Eq. (11), which assumes a constant stopping power along the distance travelled through the molecule. In this case the difference with the exact calculation is also limited to less than 10%.
Concerning the collisions with high energy ions, the dominant source of uncertainty in the determination of the PAH lifetime is the fragment binding energy E0 (cf. MJTb, Sect. 4.1), which is strongly modulated by other parameters: type of ion, PAH size and fraction of energy available for dissociation, as clearly shown in Fig. 6. To give an example, when E0 goes from 3.65 to 5.6 eV, the time constant for a 50 carbon atoms PAH colliding with helium varies by a factor of ~2 × 107 for f = 0.25 and by a factor of 8 for f = 1. For CNO impacting on a 200 C-atom molecule the change is a factor of 7 and 3 for f = 0.25 and f = 1 respectively. These numbers give an idea of the huge and complex variability induced by the uncertainty in the parameter E0.
 |
Fig. 7 Time constant τ0 for carbon atoms removal due to collisions with CR electrons, as a function of the threshold energy T0. |
In the treatment of PAH collisions with high energy electrons, two sources of uncertainty have to be considered: the analytical approximation to the numerical solution for the ejection cross section (Eq. (18)) and the choice of the threshold energy T0. While the discrepancy between the analytical expression and the numerical solution for σ is only a few percent (McKinley & Feshbach 1948), the variation of T0 from 4.5 to 15 eV implies a variation in the cross section of about a factor of 9 around the peak (electron energy ~0.1 MeV), and a factor of 3 above 2 MeV, where the cross section becomes almost constant. This results in a change of the electron time constant of a factor of ~3.4, consistent with the cross section variation. To summarize, in our study we explored a wide range in values for T0 and E0, and the resulting variation is in some sense the maximum possible.
A final remark concerns the CR spectrum at low energies. As previously mentioned, the major contribution to PAH destruction comes from low-energy CRs, both because the energy transfer is more efficient for low energy projectiles (ions) and the CR intensity decreases with increasing energy (for both ions and electrons). Unfortunately, because of the solar modulation this part of the spectrum is not accessible to measurements from Earth and needs to be evaluated theoretically. The result of this evaluation is not unique, and various spectral shapes of the interstellar CR spectrum have been shown to be consistent with the measured CR intensity (cf. Sect. 4). The spectra we adopt, which of course match the measured high energy spectra, have been calculated using a rigorous physics and taking into account all possible constraints from available measurements, including the stringent requirements from the CR ionization rate. Nevertheless the lack of data in such a crucial CR energy region still represents a source of uncertainty that is important to keep in mind, although it does not have a significant impact at the level of accuracy for our study. For an overview of the current state of the art of the uncertainties in the CR fluxes we refer the reader to Padovani et al. (2009) and references therein.
7. Discussion
7.1. The lifetime of PAHs against CR processing
In Sect. 6.1, we estimated the PAH lifetime against CR bombardment in the neighborhood of the Sun, i.e. considering an interstellar spectrum based on galactic CR measurements near the Earth but corrected for the influence of the Heliosphere (cf. Sect. 4). Figure 8 shows the PAH lifetime against CR bombardment (ions + electrons) as a function of the size of the molecule, NC, for f = 0.5 and 1, assuming our reference values of 7.5 and 4.6 eV for the parameters T0 and E0 respectively. These lifetimes should be compared to the lifetime against shock destruction of PAHs of approximately 150 Myr (MJTa). Depending on the amount of transferred energy available for dissociation (50 or 100%), CRs are calculated to be the dominant destruction agent in the warm ISM for PAHs with less then ~150 and ~280 C-atoms respectively. For larger PAHs, shocks take over. In this assessment, it should be kept in mind that shock processing occurs predominantly in warm intercloud medium of the ISM: shocks faster than 100 km s-1 are very rare in the cloud phase since supernova remnants predominantly expand in the warm or hot intercloud medium and the shock speed in clouds is then down by the square root of the density ratio between these different phases in the ISM (Jones et al. 1994). Shock processing of PAHs in diffuse clouds will then predominantly occur when cloud material exchanges with the warm intercloud medium (where shock timescales are short). The timescale for this exchange is included in the lifetime estimate for shock processing. CRs on the other hand penetrate all phases of the ISM, except perhaps the densest molecular cloud cores, and can process all material that they interact with.
Finally, we note that the PAH survival times against CR electrons (τ0 > 1013 yr) are longer than the Hubble time, implying that CR electron collisions are not important for the processing of interstellar PAHs. We point out the fact that this study does not include the secondary electrons with an energy of about 30 eV produced by primary CR electrons by the initial ionization of H or H2 in diffuse clouds. Such electrons are energetic enough to induce some PAH fragmentation but, although initially abundant, they decay easily.
 |
Fig. 8 PAH survival time against CR bombardment (ions + electrons) as a function of the molecule size (NC). The total lifetime has been calculated for f = 0.5 and 1, where f is the fraction of the transferred energy available for dissociation, and adopting our reference values for the threshold energy for carbon atom ejection, T0 = 7.5 eV and for the fragment binding energy, E0 = 4.6 eV. We remind the reader of the variation in the calculated survival time against CRs, due to the uncertainty on the parameters E0 and T0 (cf. Figs. 6 and 7). The PAH lifetime against shock destruction in the ISM is shown for comparison. |
7.2. PAHs in galactic halos
ISO and Spitzer observations revealed that PAHs are abundant in the halos of normal spiral galaxies (Irwin & Madden 2006; Irwin et al. 2007; Whaley et al. 2009). Here, we will discuss the potential role of CRs in the destruction of these PAHs.
After having estimated the PAH lifetime against CR bombardment in the vicinity of the Sun, the question that needs to be addressed is whether the CR spectrum changes across the galaxy and with the galactic latitude, and how this may affect the PAH lifetime.
7.2.1. The CR spectrum in galactic halos
A powerful tool to probe the presence of CRs in regions distant from the Solar System
has been provided by gamma and radio astronomy. CR protons interact hadronically with
the nuclei of the interstellar medium (mainly protons and α particles)
producing both charged and neutral pions (Fermi
1950; Stecker 1973). Charged pions decay
into secondary leptons, while neutral pions decay into two γ photons:
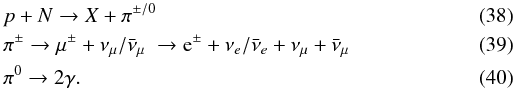 Electrons
loose energy via synchrotron and inverse Compton, producing detectable radio emission,
while γ-rays are directly measurable by gamma-ray telescopes. The
quantity of cosmic-ray protons can then be calculated from their decay products,
moreover, because photons are not affected by magnetic fields, they can provide a direct
indication about the location of their sources (e.g. Ramana Murthy & Wolfendale 1993; Hunter et al. 1997).
Electrons
loose energy via synchrotron and inverse Compton, producing detectable radio emission,
while γ-rays are directly measurable by gamma-ray telescopes. The
quantity of cosmic-ray protons can then be calculated from their decay products,
moreover, because photons are not affected by magnetic fields, they can provide a direct
indication about the location of their sources (e.g. Ramana Murthy & Wolfendale 1993; Hunter et al. 1997).
Different studies (see Shibata et al. 2007, and references therein) have shown that the slope of the energy spectrum is almost independent of the observational site in the Galaxy, but this is not true for the amplitude of the spectrum. In the galactic plane the CR intensity shows a longitudinal gradient (Shibata et al. 2007), with an exponential decrease from the Galactic center toward the periphery with a scale length of 20 kpc. Assuming the galactic parameters from Shibata et al. (2007) we obtain an enhancement at the Galactic center of about a factor 1.5 with respect to the Solar System.
Radio and gamma observations, together with the study of unstable CR nuclei such as 10Be (Hayakawa et al. 1958; Simpson & Garcia-Munoz 1988) have demonstrated that CRs are not confined to the thin disk which contains their sources, as assumed by the leaky-box model (Simpson & Garcia-Munoz 1988), but are able to travel long distances outside the galactic plane. Various models for CR propagation (e.g. Ginzburg et al. 1980; Ginzburg 1988; Berezinskii et al. 1990; Strong & Moskalenko 1998) assume a thin disk (half-thickness hd ~ 100–200 pc) located on the galactic plane, where the sources reside, surrounded by a large diffusive halo with half-thickness hh ~ 1–15 kpc , where CRs spend part of their life.
Using the formalism developed by Shibata & Ito
(2007) the latitudinal gradient of the CR intensity for a given
ion i can be written as 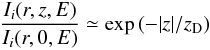 (41)where
r is the radial distance from the center of the galaxy projected on
the galactic plane and z is the latitudinal distance from the Galactic
plane. Equation (41) shows that the CR
intensity attenuates with the scale height zD of the
diffusion coefficient. The latitudinal gradient is calculated assuming the value
zD = 2.5 kpc proposed by e.g. Shibata et al. (2007) and is shown in Fig. 9.
(41)where
r is the radial distance from the center of the galaxy projected on
the galactic plane and z is the latitudinal distance from the Galactic
plane. Equation (41) shows that the CR
intensity attenuates with the scale height zD of the
diffusion coefficient. The latitudinal gradient is calculated assuming the value
zD = 2.5 kpc proposed by e.g. Shibata et al. (2007) and is shown in Fig. 9.
Ultimately, CRs are thought to be accelerated by supernova remnants, tapping some 10% of the SN energy. For other galaxies, we will scale the overall CR density with the star formation rate of the galaxy and we will adapt scale lengths and scale heights appropriate for the Milky Way. Since the CR intensity decreases exponentially outside the galactic plane, we expect the PAH lifetime at higher latitudes to be enhanced by the same factor.
 |
Fig. 9 The latitudinal CR gradient in both Milky Way (MW) and NGC 891, as a function of the vertical distance z from the galactic plane together with the vertical variation of the interstellar radiation field G0 in NGC 891 (courtesy Galliano). The CR intensity I decreases with the scale height zD of the diffusion coefficient. |
7.2.2. The origin and evolution of PAHs in galactic halos
PAH emission has been observed at high latitudes in several normal galaxies with scale heights of 2–3 kpc (Irwin & Madden 2006; Irwin et al. 2007; Whaley et al. 2009). The study of NGC 891, the edge-on twin of the Milky Way, is particularly instructive. While the vertical distribution of the 8 μm PAHs emission is noticeably narrower than that of the cold dust radiating at 450 μm, modeling reveals that this likely reflects the variation of the stellar population from the disk to the halo; e.g., the dominant (FUV) heating sources of the PAHs are located in the disk while the old stellar population, which contributes substantially to the heating of the dust, extends some 3 kpc above the disk (Whaley et al. 2009).
Some of the PAH molecules, as well as the dust, present at high galactic latitudes may originate from mass losing AGB stars in the halo. For the Milky Way, recent optical and infrared surveys (2MASS and DENIS) have revealed the presence of C-rich AGB stars enshrouded in dusty ejecta at distances of 2–6 kpc above the plane (Groenewegen et al. 1997; Mauron 2008). Some 100 such C-stars are known in the halo up to distances of 150 kpc and many of these belong to the tidal stream of the Sgr dwarf galaxy (Mauron & Kendall 2005). There is no complete census of such objects and a mass balance of PAHs and dust in the halo cannot yet be assessed.
More likely, though, most of the PAHs and dust represent signpost of the large scale circulation of matter between the disk and halo. Indeed, the vertical distribution of PAHs is similar to that of the dust – once the differences in heating are accounted for – and to other tracers of this circulation pattern such as the diffuse ionized gas. If PAHs are indeed transported to high latitudes through the action of the galactic fountain, then the acceleration associated with this process must have been very gentle since PAHs are quickly destroyed in shocks faster than 100 km s -1 (MJTa). Likely, PAHs are entrained as cloud(let)s sheared off the chimney walls in the hot gas of the venting supernovae and lifted high above the plane. As shown in MJTb, PAHs are rapidly destroyed in hot gas. Hence, after evaporation of these cloudlets driven by thermal conduction from the hot gas, PAHs will be gone and clouds subsequently condensing through thermal instabilities in the halo will not show up in the PAH emission bands.
Hence, PAHs in the halo may represent a “molecular dye” with which this entrainment aspect of the disk-halo circulation flow can be separated from the evaporation/condensation pattern and followed in detail. The effectiveness of this PAH-dye is modified on the one hand by the diffusion of the FUV photons needed for their excitation from the disk and on the other hand by destruction of PAHs in the harsh environment of the halo. Here, we are concerned with the latter aspect, the lifetime of PAHs at high latitudes above the plane. First, the residence time is of interest. With a total mass of Warm Intercloud material of ~109 M⊙ in the lower (~0.5 kpc) halo and a circulation rate of 5 M⊙/yr between the plane and the halo for the Milky Way, the residence time of PAHs at these latitudes is some 2 × 108 yr. The residence time at the higher latitudes (~2 kpc) we are interested in here will be commensurately larger. At the latitudes where PAHs are observed (~2 kpc), we expect that supernova shock waves, an important destruction agent in the disk of the galaxy, are of little concern. UV photolysis is generally considered to be a main agent for the destruction of small (<50 C-atoms) PAHs, weeding out the less stable (e.g., smallest and/or non-compact) PAHs on a rapid timescale (Tielens 2008). Indeed, the minimum size in the PAH-size-distribution is thought to reflect this process. However, because this process is very sensitive to size, compact PAHs only slightly larger than this minimum size are essential “indestructible”. Thus, we expect that PAHs transported upwards from the plane by the galactic fountain have already been weeded down to the most stable forms and because of the decreased UV flux with latitude (Fig. 9), further UV photolysis will be of little concern. Using the results of this paper, we can estimate the destruction of PAHs by CRs.
Taking the CR distribution in the halo from Sect. 7.2.1 we calculate the CR destruction
timescale. Because of its similarity with the Milky Way, we adopt for NGC 891 the same
diffusion scale height zD = 2.5 kpc. This implies that the
latitudinal gradient from Eq. (41) is
the same for both galaxies. The CR intensity variation in NGC 891 with respect to the
solar neighborhood is given by the following expression 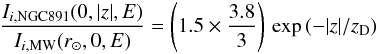 (42)where
1.5 is the CR enhancement factor in the galactic center with respect to the solar
neighborhood and the factor 3.8/3 takes into account the increased cosmic-ray intensity
in NGC 891 due to its higher star formation rate
(3.8 M⊙ yr-1, Popescu et al. 2004) with respect to the Milky Way (::tag lxir
empty(formule)id=3460
content=!/sim3 M⊙ yr-1,Scalo 1986; Prantzos & Silk
1998). At the typical PAH detection scale height
|z| = 3 kpc we obtain a decrease of the CR intensity of a factor
of 0.6. The lifetime against destruction will be then enhanced by a factor of (1/0.6).
(42)where
1.5 is the CR enhancement factor in the galactic center with respect to the solar
neighborhood and the factor 3.8/3 takes into account the increased cosmic-ray intensity
in NGC 891 due to its higher star formation rate
(3.8 M⊙ yr-1, Popescu et al. 2004) with respect to the Milky Way (::tag lxir
empty(formule)id=3460
content=!/sim3 M⊙ yr-1,Scalo 1986; Prantzos & Silk
1998). At the typical PAH detection scale height
|z| = 3 kpc we obtain a decrease of the CR intensity of a factor
of 0.6. The lifetime against destruction will be then enhanced by a factor of (1/0.6).
The total PAH lifetime in the halo of NGC 891 compared with the circulation timescale is shown in Fig. 10. Depending on the amount of energy available for dissociation, the survival time against CRs for PAHs with more than ~100 C – atoms is comparable or longer than the circulation lifetime. PAHs could be good tracers of material entrained in the plane and carried to high latitudes by the galactic fountain as long as this material never loses its “identity” through evaporation into the hot gas followed by recondensation into cloudlets. Of course, as emphasized by Whaley et al. (2009), such a study has to properly evaluate the flux of the pumping of UV photons in order to be of quantitative value. In that case, mid-IR studies can potentially trace this entrainment process and the exchange between cool and hot phases on arcsecond size scales. Nevertheless other factors have to be taken into account, such as the possibility of local PAH production in the halo.
 |
Fig. 10 Total PAH lifetime against CR bombardment in the halo of NGC 891, evaluated at an altitude of 3 kpc from the galactic plane, compared with the circulation timescale between the disk and the halo. The value of the circulation lifetime represents a lower limit, as indicated by the arrow. Otherwise as Fig. 8. |
7.3. PAHs in galactic winds
Starburst galaxies are characterized by very intense star formation, usually concentrated in the nuclear region of the galaxy, which can occur as a single instantaneous burst or as a high star formation activity sustained over a period of time. Since galactic supernovae are considered the most probable acceleration source for CRs with energy below the “knee” (few 1015 eV – see e.g. Drury 1994), we expect that an enhancement of the SFR will result in a corresponding increase of the CR intensity and dust destruction by shocks.
In our previous work (MJTb) we discussed the observation of PAH molecules in the bipolar outflow of the starburst galaxy M 82 (Armus et al. 2007; Galliano et al. 2008). PAHs have been detected far outside the galactic plane at least up to 6 kpc from the disk (Engelbracht et al. 2006), in a region which is spatially correlated with an extended X-ray emission originating from tenuous hot gas (electron density ne = 0.013 cm-3, temperature T = 5.8 × 106 K). Our study has demonstrated that, under these conditions, PAHs are destroyed by collisions with thermal electrons on a timescale of few thousand years. Our conclusion was that the PAH survival is possible only if the molecules are isolated from this hot gas, probably in cooler cloudlets of PDR-type gas entrained in the galactic wind.
In fact supernova-driven galactic-scale winds, often called “superwinds”, are commonly observed in starburst galaxies, including M 82 (see e.g. Strickland & Heckman 2009, and references therein). In addition, theoretical studies (Ipavich 1975; Breitschwerdt et al. 1991, 1993; Zirakashvili et al. 1996; Ptuskin et al. 1997), together with radio (Heesen et al. 2009) and X-ray observations (Everett et al. 2008) suggest the possibility of a CR-driven galactic wind, i.e. the possibility of “bulk” transport of CRs outwards into the halo, in addition to the diffusive transport predicted by CR propagation models (cf. Sect. 7.1).
Assuming also that the M 82 superwind could be partially CR-driven, we can try to evaluate the CR intensity at the high latitudes where PAHs are detected, to assess PAH lifetimes against CR bombardment and compare them with the survival time in hot gas of the outflow. Unfortunately the properties of superwinds at high galactic latitudes are not well constrained. Theoretical studies mainly concern small regions around the nucleus of the galaxy (radii of few hundred pc from the center), where the transport of matter is dominated by advection (Völk 2003; Strickland & Heckman 2009), while in the outer regions diffusion is expected to be dominant (e.g. Zirakashvili & Völk 2006, for the starburst galaxy NGC 253). This is not the case in the Milky Way, where the CR transport is diffusive on a kpc scale and becomes convective only at larger distances (Ptuskin et al. 1997).
On the other hand, the CR propagation in M 82 is not yet totally understood. Star formation, and thus SNRs which re-presents the main CR sources, are concentrated in the small nuclear region from which the galactic superwind originates, we could then expect CRs being advectically transported by the wind out of the galactic plane up to a certain height (~few hundred pc), and diffusing after in the volume occupied by the superwind, which is roughly a cylinder flaring at high z with height of ~12 kpc on the North side and 7.5 kpc on the South side (Lehnert et al. 1999; Stevens et al. 2003). It would also be possible that CRs occupy a spheroidal halo as in the Milky Way, maybe diffusing back to the disk after leaving the wind region.
Because of this lack of information, especially on the confinement volume for the CRs, what we present here is a toy-model based on some simplifying assumptions, but which could be useful to interpret PAH observations in the outflow of M 82. To calculate the CR spectrum in M 82 we adopt the same spectral index as in the Milky Way (γ = 2.7) and we assume that in the starburst nucleus the CR intensity scales with the supernova rate νSN (SN yr-1) which is directly related to the star formation rate in the galaxy. Taking the values νSN(M 82) = 0.11 SN yr-1 (Huang et al. 1994) and νSN(MW) = 0.02 SN yr-1 (Diehl et al. 2006) we obtain IM 82(E)/IMW(E) = νSN(M 82)/νSN(MW) = 0.11/0.02 = 5.5.
Since PAHs are detected at vertical distances which are large compared with the typical height of the convective zone, we neglect this latter and assume pure diffusive CR transport above the galactic plane. We adopt the exponentially-decreasing CR latitudinal gradient from Eq. (41) (Shibata et al. 2007) with zD = hh/3, where hh is the maximum distance that CRs can reach above the plane through diffusion. Since the exact confinement region in M 82 is not known, we just take hh equal to the vertical height of the galactic superwind (12 kpc in the North side, 7.5 in the South side), i.e. we assume that CRs can occupy at least as the same volume than the gas from the outflow.
The PAH lifetime against CR bombardment at the vertical distance |z|
above the starburst nucleus of M 82 is then given by the following expression
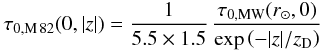 (43)where
5.5 and 1.5 are the two enhancement factor of the CR intensity in M 82 with respect to the
Milky Way (5.5) and in the galactic center with respect to the solar neighborhood (1.5),
which will imply a decrease of the same factor for the PAH lifetime with respect to the
survival time τ0,MW(r⊙,0) in the
vicinity of the Solar System (Fig. 8). On the other
hand the latitudinal gradient will result in a corresponding increase of
τ0,M 82 for increasing | z | , with
scale height zD(North) = 4 kpc and
zD(South) = 2.5 kpc.
(43)where
5.5 and 1.5 are the two enhancement factor of the CR intensity in M 82 with respect to the
Milky Way (5.5) and in the galactic center with respect to the solar neighborhood (1.5),
which will imply a decrease of the same factor for the PAH lifetime with respect to the
survival time τ0,MW(r⊙,0) in the
vicinity of the Solar System (Fig. 8). On the other
hand the latitudinal gradient will result in a corresponding increase of
τ0,M 82 for increasing | z | , with
scale height zD(North) = 4 kpc and
zD(South) = 2.5 kpc.
Let us calculate the PAH lifetime at the maximum distance
|z| = 6 kpc where the molecules have been detected. This is done by
scaling the time constants
τ0,MW(r⊙,0) in Fig. 8 by the factor 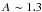 (averaged over the two
hemispheres) and the result is shown in Fig. 11. The
PAH lifetime against CRs is longer than the starburst timescale (tens of Myr), except for
the smallest molecules when f = 1, and for large PAHs
(NC > 150–200) it is comparable or longer than the
circulation lifetime (~200 Myr). In MJTb we showed that in the outflow of M 82
PAH destruction due to X-ray absorption would take place on a timescale of at least
~20 Myr (assuming that each X-ray photon absorption will lead to
fragmentation). This is comparable to or larger than the starburst lifetime. PAHs
dispersed in the hot gas will be rapidly destroyed by collisions with electrons. To
survive they need to be isolated from this hot gas, presumably in a cooler and denser gas
entrained in the superwind. On the other hand CRs and X-rays can penetrate in those
clumps, thus the PAH lifetime there will be determined by the cosmic radiation and/or
X-rays, depending on the PAH size and on the effective value of the survival time against
X-rays (cf. Sect. 6.1 in MJTb).
(averaged over the two
hemispheres) and the result is shown in Fig. 11. The
PAH lifetime against CRs is longer than the starburst timescale (tens of Myr), except for
the smallest molecules when f = 1, and for large PAHs
(NC > 150–200) it is comparable or longer than the
circulation lifetime (~200 Myr). In MJTb we showed that in the outflow of M 82
PAH destruction due to X-ray absorption would take place on a timescale of at least
~20 Myr (assuming that each X-ray photon absorption will lead to
fragmentation). This is comparable to or larger than the starburst lifetime. PAHs
dispersed in the hot gas will be rapidly destroyed by collisions with electrons. To
survive they need to be isolated from this hot gas, presumably in a cooler and denser gas
entrained in the superwind. On the other hand CRs and X-rays can penetrate in those
clumps, thus the PAH lifetime there will be determined by the cosmic radiation and/or
X-rays, depending on the PAH size and on the effective value of the survival time against
X-rays (cf. Sect. 6.1 in MJTb).
 |
Fig. 11 Total PAH lifetime against CR bombardment in the outflow of the starburst galaxy M 82, evaluated at an altitude of 6 kpc from the galactic plane. The PAH survival time is compared with the circulation, starburst and X-rays timescales. The values of the circulation and X-rays timescales represent lower limits, as indicated by the arrows. Otherwise as Fig. 8. |
7.4. PAHs in galaxy clusters
We consider now the PAH processing by CRs in an extragalactic environment, focusing on the specific case of cooling flow galaxy clusters. The measurements of high-energy gamma and neutrino radiation produced by the interaction of CRs (mainly protons) with the intra-cluster medium (ICM) have demonstrated that galaxy cluster are able to confine CRs for cosmological times (Berezinsky et al. 1997). Our choice is thus motivated by the reasonable expectation to find a non-negligible population of CRs in such environments, although the spectral index and amplitude are not well constrained by observations.
Many clusters of galaxies with cooling flows host a central galaxy which often shows nuclear activity. Many papers support the presence of CR protons in the relativistic plasma bubbles produced by Active Galactic Nuclei (AGN), where the energetics are sufficient to inject a significant amount of CRs into the ICM (see Pfrommer & Enßlin 2004, and references therein). The slope of the injected spectrum depends on the fraction of particles released from the plasma. If all the CR content is ejected by the radio plasma, we expect to find a moderately flat spectrum (αinj ≈ 2.5) consistent with the flat spectra of CR electrons indicated by the radio emission from radio galaxies. On the other hand, if only a small fraction of the CR population is able to leave the plasma via diffusion, we expect to find an even flatter spectrum (αinj ≈ 2.2) because the escape probability increases with momentum (Enßlin 2003).
Another possible source of CRs in galaxy clusters is represented by the galactic winds from the central galaxy transporting CRs accelerated within the galaxy itself. Because Supernova Remnants (SNRs) are believed to be the main sources of Galactic CRs (e.g. Ginzburg 1993; Drury 1994), the expected injection spectral index is αinj ≈ 2.4, if no further re-acceleration occurs. Apart from protons, the principal constituents of Galactic CRs are helium, carbon and iron ions.
The CR population in galaxy clusters will then result from the combination of the
above-mentioned sources, with a spectral index αinj which
reflects its composite origin. After injection from the source, CRs start diffusing away
from the central AGN. For the treatment of the transport of CR protons
through the thermal ICM, we refer to the model elaborated by Pfrommer & Enßlin (2004). The CR proton
distribution function is described by a power-law in energy (or momentum) where the
injection spectral index is modified by the diffusion through the intra-cluster gas
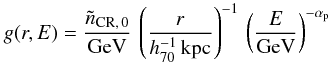 (44)with
αp = αinj + αdiff.
The coefficient αdiff results from the fact that diffusion is
momentum-dependent, and equals ≈1/3 for active diffusive transport of CR protons in a
Kolmogorov-like spectrum of hydro-magnetic turbulence (Kolmogorov 1941). The model assumes the standard ΛCDM cosmology with
H0 = 70 h70 km s-1 Mpc-1,
where h70 indicates the scaling with
H0. The normalization factor
(44)with
αp = αinj + αdiff.
The coefficient αdiff results from the fact that diffusion is
momentum-dependent, and equals ≈1/3 for active diffusive transport of CR protons in a
Kolmogorov-like spectrum of hydro-magnetic turbulence (Kolmogorov 1941). The model assumes the standard ΛCDM cosmology with
H0 = 70 h70 km s-1 Mpc-1,
where h70 indicates the scaling with
H0. The normalization factor
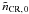 is the crucial parameter required to determine the CR spectrum.
is the crucial parameter required to determine the CR spectrum.
Pfrommer & Enßlin (2004) constrained
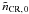 for a sample of nearby cooling flow galaxy clusters with the aid of γ-ray
observations, using the fact that CR protons interact hadronically with the thermal
intra-cluster gas producing both charged and neutral pions (see Sect. 7.2.1). Charged
pions decay into secondary electrons/positrons + neutrinos/antineutrinos, while neutral
pions decay into two γ’s
(π0 → 2γ). The amount of cosmic protons can
then be calculated from their decay products, which are detectable in the
γ-ray and radio bands.
for a sample of nearby cooling flow galaxy clusters with the aid of γ-ray
observations, using the fact that CR protons interact hadronically with the thermal
intra-cluster gas producing both charged and neutral pions (see Sect. 7.2.1). Charged
pions decay into secondary electrons/positrons + neutrinos/antineutrinos, while neutral
pions decay into two γ’s
(π0 → 2γ). The amount of cosmic protons can
then be calculated from their decay products, which are detectable in the
γ-ray and radio bands.
It is important to remember here that the threshold energy for pion production is Eth = 0.78 GeV, implying that only the proton population with energy exceeding the threshold is able to produce pions hadronically, and can then be constrained by γ-ray and radio observations. At lower energies the dominant energy loss mechanism for CR protons is Coulombian diffusion on the electrons in the plasma (electronic excitation), which results in the depopulation of the CR energy distribution with consequent modification of the power-law spectrum (Mannheim & Schlickeiser 1994).
Unfortunately, it is not possible to observationally constrain the low-energy CR population in galaxy clusters, thus following the argument from Nath & Biermann (1994) we decided to extrapolate Eq. (44) down to a minimum energy Emin representing the characteristic energy scale at which the spectrum deviates from a power-low. A similar approach is used by Pfrommer & Enßlin (2004) as well. For the cut-off energy we adopt the value Emin = 50 MeV, consistent with the range ~50–75 MeV found by Nath et al. (2006) in their study of the production of 6Li by CR protons in galaxy clusters. Emin represents the lower energy that an energetic proton has to reach before suffering large Coulombian losses, and can be equivalently expressed in terms of the quantity of matter to be traversed in order to experience the same Coulombian losses.
As previously mentioned, we assume the presence in the cluster CR population of the main
components of the Galactic CRs other than hydrogen: helium, carbon and iron. The
distribution function (44) for the heavier
elements is obtained by simply scaling the proton distribution
function g(r,E) with the abundance with respect to the
hydrogen χi of the corresponding ion
i = H, He, C, Fe 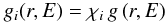 (45)where
E is the total kinetic energy of the CR ion. For the
CR abundances we assume the standard values of the galactic CRs:
χH:χHe:χC:χFe = 1:0.1:10-2:10-3
(Maurin & Taillet 2003). The low-energy
cut-off for the heavier ions has been derived in the same way as for Galactic CRs, i.e.
scaling the proton value
(45)where
E is the total kinetic energy of the CR ion. For the
CR abundances we assume the standard values of the galactic CRs:
χH:χHe:χC:χFe = 1:0.1:10-2:10-3
(Maurin & Taillet 2003). The low-energy
cut-off for the heavier ions has been derived in the same way as for Galactic CRs, i.e.
scaling the proton value 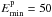 MeV by
the ion atomic mass,
MeV by
the ion atomic mass, 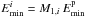 , but different
parametrizations are also possible (Nath &
Biermann 1994).
, but different
parametrizations are also possible (Nath &
Biermann 1994).
The CR intensity I(E) (to which we usually refer as
“spectrum”) is related to the distribution function by the following expression
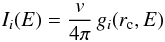 (46)where
v = βc is the velocity of the ion. The distribution
function gi is calculated for a given
distance rc from the center of the cluster. We adopt the
value corresponding to the cooling radius of the cluster, which defines the region where
the majority of the hadronically-generated γ-ray luminosity originate.
(46)where
v = βc is the velocity of the ion. The distribution
function gi is calculated for a given
distance rc from the center of the cluster. We adopt the
value corresponding to the cooling radius of the cluster, which defines the region where
the majority of the hadronically-generated γ-ray luminosity originate.
When the CR intensity is known, we can estimate the total lifetime against CR bombardment, τ0. As an example, we calculate τ0 in two nearby cooling flow clusters from the Pfrommer & Enßlin (2004) sample, A85 and Virgo, whose main properties are listed in Table 3. A85 is one of the farther cluster in the sample, with low electron density ne, large core radius rc and high central temperature T0. Virgo is the closest cluster to us, with quite high electron density, very small core radius and high central temperature.
Pfrommer & Enßlin (2004) calculated
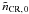 for different values of the proton spectral index αp. We adopt
the value corresponding to
αp = αinj + αdiff = 2.7,
with αdiff ≈ 1/3, because is consistent with the spectrum of
the CR sources (AGN + SNRs) and allows a direct comparison with Galactic CRs.
for different values of the proton spectral index αp. We adopt
the value corresponding to
αp = αinj + αdiff = 2.7,
with αdiff ≈ 1/3, because is consistent with the spectrum of
the CR sources (AGN + SNRs) and allows a direct comparison with Galactic CRs.
Relevant parameters and CR normalization factor
 for the two cooling flow clusters A85 and Virgo from the Pfrommer & Enßlin (2004) sample.
for the two cooling flow clusters A85 and Virgo from the Pfrommer & Enßlin (2004) sample.
The results of our calculation are shown in Fig. 12. In the galactic clusters under examination the cosmic-ray density is enhanced with respect to the solar neighborhood, resulting in lifetimes which are shorter by about 2–3 order of magnitude (cf. Fig. 8). The longer time constants obtained for Virgo are the consequence of its lower CR density with respect to A85.
 |
Fig. 12 Total PAH lifetime against CR bombardment in the cooling flow galaxy clusters A85 and Virgo, compared with the survival time, τHG, in a hot gas. The value adopted for the lowest energy of the CR spectrum, Emin, is 50 MeV/nucleon (see text), otherwise as Fig. 8. |
In our previous work (MJTb) we showed that collisions with thermal electrons and protons represent an efficient destruction mechanism for PAHs immersed in an ionized gas of ~106 K. Since the ICM is a moderately tenuous hot plasma, it would be not surprising to find a quite short lifetime τHG for the PAHs dispersed in the medium, due to such collisions. We calculate the PAH lifetime in the hot intra-cluster medium of A85 and Virgo using Eq. (27) in MJTb and the temperatures and densities listed in Table 3. In both clusters, PAHs embedded in the hot gas are rapidly destroyed on timescales of 1–103 yr. In cold embedded gas, the lifetime of PAHs is set by CRs to be ~106–3 × 108 yr (Virgo) and ~105–3 × 107 yr (A85).
The existence of PAHs in the intra-cluster medium is not yet well constrained observationally. In fact to the best of our knowledge a detection has not been reported, but hopefully future observations will be able to provide more insights. Many of the quantities involved in our calculation are not well constrained, in particular the exact amplitude, shape and composition of the CRs spectrum in the cluster and the value of the parameters E0 and T0. Because the PAH lifetime in galaxy clusters set by CRs is still short, a replenishing mechanism would be required to explain their observation in such environments. We face here another example of the well-known conundrum about the discrepancy between the PAH/dust lifetime and the injection time scale into the interstellar medium (2.5 × 109 yr).
8. Conclusions
We have extensively investigated the stability of PAHs against CR ions (H, He, CNO and Fe-Co-Ni) and electron bombardment in both galactic and extragalactic environments. We consider CR particles with energy between 5 MeV/nucleon and 10 GeV. Collisions can lead to carbon atom ejection, with a consequent disruption and destruction of the molecule. The effects of CRs were then compared with the other destruction mechanisms discussed in our previous works: PAH processing by shocks with velocities between 50 and 200 km s-1 (MJTa) and collisions with thermal ions and electrons in a hot gas (T = 103–108 K, MJTb).
An ionic collision consists of two simultaneous processes which can be treated separately: a binary collision between the projectile ion and a single atom in the target (nuclear interaction) and energy loss to the electron cloud of the molecule (electronic interaction). In the high-energy regime considered here the nuclear stopping is totally negligible, and the energy loss process is dominated by the electronic interaction, well described by the Bethe-Bloch equation. The interaction of PAHs with high-energy electrons can be treated in term of a binary collision between the incident electron and a single nucleus in the target.
The CR spectra we adopt in the solar neighborhood are based on measurement near the Earth but corrected for the influence of the Heliosphere (solar modulation). To estimate the CR variation across the disk and in the galactic halo we adopt specific models based on γ-ray measurements. In external galaxies we scale the overall CR density with the star formation rate of the galaxy, adapting scale lengths and scale heights appropriate for the Milky Way.
We find that the timescale for PAH destruction by CR ions depends on the electronic excitation energy E0 and the amount of energy available for dissociation. Small PAHs are destroyed faster, with He and the CNO group being the more effective projectiles. CRs are able to process PAHs in diffuse clouds, where the destruction due to interstellar shocks is less efficient. For electron collisions, the lifetime is independent of the PAH size and varies with the threshold energy T0. The minimum lifetime is 1.2 × 1013 yr, longer than the Hubble time. Such a long timescale excludes CR electrons as an important agent for PAH destruction.
PAHs have been detected both in the halo of normal galaxies like NGC 891 and in the outflows of starburst galaxies like M 82. Our work shows that in both these environments the lifetime against CR bombarding of large PAHs (NC > 150–200) is comparable to or longer than the circulation timescale between disk and halo and the starburst lifetime (~200 Myr and ~20 Myr respectively). PAHs dispersed in the hot gas filling the galactic halo and the starburst outflow are rapidly destroyed by collisions with thermal ions and electrons, but this mechanism is inefficient if the molecules are isolated from this gas in denser cloudlets. CRs can access the denser clouds and together with X-rays will set the lifetime of those protected PAHs, which can be used as a “dye” for tracing the presence of cold entrained material.
In cooling flow galaxy clusters like A85 and Virgo the cosmic ray intensity is remarkably enhanced with respect to the solar neighborhoods, as a consequence the PAH lifetime is much shorter. Nevertheless, the survival time against CR bombardment is at least two orders of magnitude longer than the PAH lifetime in a hot gas (1–103 yr), implying that the molecules will be rapidly destroyed in the gas phase of the ICM. They could survive if protected in some cold entrained material and in this case the PAH lifetime will be set by CRs. Future observations would hopefully provide more insights about the validity of our predictions.
The major source of uncertainty in the determination of the time scale for PAH processing by CRs resides in the choice of the nuclear threshold energy T0 (for electron collisions) and the fragment binding energy E0 (for ion collisions). Our conclusions are robust despite the large variability in the PAH lifetime induced by the incertitude on the above parameters. Nevertheless this variation emphasizes again the importance of a better determination of these quantities.
We find that thermal ions/electrons in a hot gas are much more effective in destroying PAHs than CRs. This is due to the fact that the stopping power of the thermal ions/electrons under consideration (T ~ 107 K, ne ~ 0.1 cm-3) is high, close to its maximum value, and allows the transfer into the molecule of enough energy to have the dissociation probability close to one (the dissociation probability increases with the transferred energy). Almost any ion/electron is able to destroy a PAH, and the resulting destruction efficiency is very high (cf. MJTa and MJTb).
On the other hand, in the energy range we consider here for CR ions (5 MeV/nucleon-10 GeV), the stopping power, and then the energy transferred into the PAH and the dissociation probability for PAHs, decrease rapidly for increasing energy of the incoming ion. For CR electrons (5 MeV–10 GeV) the cross section for carbon atom removal is almost constant but very small (~6 × 10-23 cm2). For both ions and electrons the CR spectra are decreasing functions of the energy. The combination of these two factors implies that only few CRs are able to destroy PAHs, resulting in a destruction efficiency very low compared to thermal ions/electrons in a hot gas.
Our results show that CRs set a timescale for the destruction of PAHs with less than a ≃100 C-atoms of only 100 Million years in the interstellar medium. Larger PAHs or very, very small dust grains – with NC > 100 atoms – are predominantly processed by interstellar shock waves (rather than CRs) on a very similar timescale (τshock ≃ 150 Myr; MJTa).
PAH molecules are modelled to be efficiently formed as molecular intermediaries or sideproducts of the soot formation process in the stellar ejecta from C-rich objects, in particular C-rich AGB stars (Frenklach & Feigelson 1989; Cherchneff et al. 1992, 2000; Cherchneff 2000; Cau 2002). If we assume that AGB stars are the primary source for PAH replenishment in the ISM, the injection timescale, τformation ≃ 3 × 109 Myr (Jones et al. 1994) is much longer than the lifetime estimated above. Thus, there is a factor of about 50 discrepancy between the injection and destruction timescales for PAHs in the ISM. This parallels the discrepancy between the injection and destruction timescales for interstellar grains (Jones et al. 1994). As for dust grains, the conclusion seems to be inescapable that PAHs must be reformed rather efficiently in the ISM itself.
As suggested by Jones et al. (1996), interstellar PAHs may be the fragmentation products of carbonaceous grain collisions in shocks. Experiments mimicking the effects of grain-grain collisions support the formation of PAHs and fullerenes as well as carbon chains and clusters from Hydrogenated Amorphous Carbon (HAC) grains (Scott et al. 1997). This would replenish the PAH population on a similar timescale (≃100 Myr) as the destruction timescale. With the numbers quoted above, if all of the carbon were injected into the ISM in the form of HAC grains, this scheme would (almost) be in steady state with 5% of the elemental C in the form of PAHs. However, this comes at the expense of the rapid destruction of carbon grains, as seems to be suggested by the work of Serra Díaz-Cano & Jones (2008). So, this would have to be fit into a general model where gaseous carbon accretes and reacts with carbonaceous (e.g., HAC) grains in interstellar clouds (cf., Jones 1990; Jones et al. 1990).
This growth process is then balanced by grain-grain collisions in strong shock waves in the intercloud medium producing PAHs that are then destroyed through CR interaction in the diffuse ISM. While such a model could work numerically, the basic premise – rapid accretion and reaction of gaseous carbon on grains forming predominantly HAC-like layers – has not been demonstrated in the laboratory. Moreover, observationally, depletion studies suggest that carbon does not seem to partake in the rapid exchange between gas and solid phases in the ISM (Tielens 2009). Alternatively, rather than interstellar PAHs resulting from chemical processes in stellar ejecta – either directly or through the shattering of carbon grains – these species may be largely formed from smaller carbon molecules through chemical processes in the ISM.
Theoretical studies show that ion-molecule reactions can form benzene-like species in the dense and warm environments of pre-Planetary Nebulae (such as CRL 618) and in protoplanetary disks around young stars (Herpin & Cernicharo 2000; Woods et al. 2005; Woods & Willacy 2007). However, such special environments are few and far apart and not important in a model for the global presence of PAHs in the ISM. Models predicts that ion-molecule chemistry in cold dense molecular clouds can produce benzene but at peak abundances at early times of 10-9. Likely more relevant are the steady state abundances at long times and those are much less (10-14; McEwan et al. 1999). So, the gas phase formation of PAHs in molecular clouds does not seem a very promising route. Essentially, the basic building block of PAHs (acetylene) is not very abundant and there isn’t much free carbon around to drive the chemistry since most of it is locked up in CO in molecular clouds. In conclusion, the origin of interstellar PAHs is still clouded in quite some intriguing mystery.
Acknowledgments
We would like to thank the referee for careful reading and valuable comments. We are grateful to F. Galliano for providing us with the values of G0 in NGC 891 and to H. Leroux for useful discussions on the physics of radiation damage in carbon materials. E.R.M. thanks G. Lavaux for support and technical assistance and acknowledges financial support by the EARA Training Network (EU grant MEST-CT-2004-504604). Studies of interstellar PAHs at Leiden Observatory are supported by the advanced-ERC grant 246876 on “The role of large Polycyclic Aromatic Hydrocarbon molecules in the Universe”.
References
- Andersen, M., Rho, J., Hewitt, J., & Reach, W. 2007, BAAS, 38 932 [Google Scholar]
- Armus, L., Draine, B., Engelbracht, C., et al. 2007, BAAS, 38, 789 [NASA ADS] [Google Scholar]
- Banhart, F. 1999, Rep. Prog. Phys., 62, 1181 [NASA ADS] [CrossRef] [Google Scholar]
- Berezinskii, V. S., Bulanov, S. V., Dogiel, V. A., & Ptuskin, V. S. 1990, Astrophysics of cosmic rays, ed. V. S. Berezinskii, S. V. Bulanov, V. A. Dogiel, & V. S. Ptuskin [Google Scholar]
- Berezinsky, V. S., Blasi, P., & Ptuskin, V. S. 1997, ApJ, 487, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Bethe, H. 1930, Ann. Phys., 397, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Bethe, H. 1932, Z. Phys., 76, 293 [Google Scholar]
- Bichsel, H. 1990, Phys. Rev. A, 41, 3642 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bloch, F. 1933a, Z. Phys., 81, 363 [Google Scholar]
- Bloch, F. 1933b, Ann. Phys., 408, 285 [CrossRef] [Google Scholar]
- Bohr, N. 1913, Philos. Mag., 25, 10 [Google Scholar]
- Bohr, N. 1915, Philos. Mag., 30, 581 [Google Scholar]
- Bonderup, E. 1967, Mat. Fys. Medd. Dan. Vid. Selsk., 35, 17 [Google Scholar]
- Breitschwerdt, D., McKenzie, J. F., & Voelk, H. J. 1991, A&A, 245, 79 [NASA ADS] [Google Scholar]
- Breitschwerdt, D., McKenzie, J. F., & Voelk, H. J. 1993, A&A, 269, 54 [NASA ADS] [Google Scholar]
- Bringa, E. M., Kucheyev, S. O., Loeffler, M. J., et al. 2007, ApJ, 662, 372 [NASA ADS] [CrossRef] [Google Scholar]
- Cau, P. 2002, A&A, 392, 203 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cherchneff, I. 2000, in The Carbon Star Phenomenon, ed. R. F. Wing, IAU Symp., 177, 331 [Google Scholar]
- Cherchneff, I., Barker, J. R., & Tielens, A. G. G. M. 1992, ApJ, 401, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Cherchneff, I., Le Teuff, Y. H., Williams, P. M., & Tielens, A. G. G. M. 2000, A&A, 357, 572 [NASA ADS] [Google Scholar]
- Cummings, A. C. 1973, Ph.D. Thesis, California institute of technology [Google Scholar]
- Curie, M. 1900, Comptes Rendus, 130, 76 [Google Scholar]
- Diehl, R., Halloin, H., Kretschmer, K., et al. 2006, Nature, 439, 45 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Drury, L. O. 1994, Contemporary Phys., 35, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Ebeling, H., Edge, A. C., Bohringer, H., et al. 1998, MNRAS, 301, 881 [NASA ADS] [CrossRef] [Google Scholar]
- Engelbracht, C. W., Kundurthy, P., Gordon, K. D., et al. 2006, ApJ, 642, L127 [NASA ADS] [CrossRef] [Google Scholar]
- Enßlin, T. A. 2003, A&A, 399, 409 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Everett, J. E., Zweibel, E. G., Benjamin, R. A., et al. 2008, ApJ, 674, 258 [NASA ADS] [CrossRef] [Google Scholar]
- Fano, U. 1963, Ann. Rev. Nucl. Part. Sci., 13, 1 [NASA ADS] [CrossRef] [EDP Sciences] [PubMed] [Google Scholar]
- Fermi, E. 1950, Progress Theor. Phys., 5, 570 [Google Scholar]
- Frenklach, M., & Feigelson, E. D. 1989, ApJ, 341, 372 [NASA ADS] [CrossRef] [Google Scholar]
- Gaisser, T. K., & Stanev, T. 2006, Nucl. Phys. A, 777, 98 [Google Scholar]
- Galliano, F., Madden, S. C., Tielens, A. G. G. M., Peeters, E., & Jones, A. P. 2008, ApJ, 679, 310 [NASA ADS] [CrossRef] [Google Scholar]
- Ginzburg, V. L. 1988, Sov. Phys. Uspekhi, 31, 491 [NASA ADS] [CrossRef] [Google Scholar]
- Ginzburg, V. L. 1993, Phys. Uspekhi, 36, 587 [Google Scholar]
- Ginzburg, V. L., Khazan, I. M., & Ptuskin, V. S. 1980, Ap&SS, 68, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Groenewegen, M. A. T., Oudmaijer, R. D., & Ludwig, H.-G. 1997, MNRAS, 292, 686 [NASA ADS] [CrossRef] [Google Scholar]
- Hayakawa, S., Ito, K., & Terashima, Y. 1958, Progress Theor. Phys. Suppl., 6, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Heesen, V., Beck, R., Krause, M., & Dettmar, R.-J. 2009, A&A, 494, 563 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Henriksen, T., Horan, P. K., & Snipes, W. 1970, Radiat. Res., 43, 1 [CrossRef] [PubMed] [Google Scholar]
- Herpin, F., & Cernicharo, J. 2000, ApJ, 530, L129 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Huang, Z. P., Thuan, T. X., Chevalier, R. A., Condon, J. J., & Yin, Q. F. 1994, ApJ, 424, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, S. D., Bertsch, D. L., Catelli, J. R., et al. 1997, ApJ, 481, 205 [NASA ADS] [CrossRef] [Google Scholar]
- ICRU 1984, H. O. Wyckoff (ICRU Scientific Counsellor), ICRU Report, 37, Intl. Comm. Rad. Units, Bethesda, MD [Google Scholar]
- Indriolo, N., Fields, B. D., & McCall, B. J. 2009, ApJ, 694, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Ip, W.-H., & Axford, W. I. 1985, A&A, 149, 7 [NASA ADS] [Google Scholar]
- Ipavich, F. M. 1975, ApJ, 196, 107 [Google Scholar]
- Irwin, J. A., & Madden, S. C. 2006, A&A, 445, 123 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Irwin, J. A., Kennedy, H., Parkin, T., & Madden, S. 2007, A&A, 474, 461 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jochims, H. W., Ruhl, E., Baumgartel, H., Tobita, S., & Leach, S. 1994, ApJ, 420, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, A. P. 1990, MNRAS, 247, 305 [NASA ADS] [Google Scholar]
- Jones, A. P., Duley, W. W., & Williams, D. A. 1990, QJRAS, 31, 567 [NASA ADS] [Google Scholar]
- Jones, A. P., Tielens, A. G. G. M., Hollenbach, D. J., & McKee, C. F. 1994, ApJ, 433, 797 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, A. P., Tielens, A. G. G. M., & Hollenbach, D. J. 1996, ApJ, 469, 740 [NASA ADS] [CrossRef] [Google Scholar]
- Katz, R., Sharma, S. C., & Homayoonfar, M. 1972, Nuclear Instruments and Methods, 100, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Kolmogorov, A. 1941, Akademiia Nauk SSSR Doklady, 30, 301 [Google Scholar]
- Lehnert, M. D., Heckman, T. M., & Weaver, K. A. 1999, ApJ, 523, 575 [NASA ADS] [CrossRef] [Google Scholar]
- Lindhard, J., & Scharff, M. 1952, Mat. Fys. Medd. Dan. Vid. Selsk., 27, 15 [Google Scholar]
- Lindhard, J., Scharff, M., & Schiott, H. E. 1963, Mat. Fys. Medd. Dan. Vid. Selsk., 33, 14 [Google Scholar]
- Mannheim, K., & Schlickeiser, R. 1994, A&A, 286, 983 [NASA ADS] [Google Scholar]
- Matsushita, K., Belsole, E., Finoguenov, A., & Böhringer, H. 2002, A&A, 386, 77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maurin, D., & Taillet, R. 2003, in Physique et Astrophysique du Rayonnement Cosmique, ed. E. Parizot, A. Marcowitch, V. Tatischeff, G. Pelletier, & P. Salati [Google Scholar]
- Mauron, N. 2008, A&A, 482, 151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mauron, N., & Kendall, T. 2005, in The Three-Dimensional Universe with Gaia, ed. C. Turon, K. S. O’Flaherty, & M. A. C. Perryman, ESA Spec. Publ., 576, 699 [Google Scholar]
- McEwan, M. J., Scott, G. B. I., Adams, N. G., et al. 1999, ApJ, 513, 287 [NASA ADS] [CrossRef] [Google Scholar]
- McKinley, W. A., & Feshbach, H. 1948, Phys. Rev., 74, 1759 [NASA ADS] [CrossRef] [Google Scholar]
- Mewaldt, R. A., Wiedenbeck, M. E., Scott, L. M., et al. 2004, in Physics of the Outer Heliosphere, ed. V. Florinski, N. V. Pogorelov, & G. P. Zank, AIP Conf. Ser., 719, 127 [Google Scholar]
- Micelotta, E. R., Jones, A. P., & Tielens, A. G. G. M. 2010a, (MJTa), A&A, 510, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Micelotta, E. R., Jones, A. P., & Tielens, A. G. G. M. 2010b, (MJTb), A&A, 510, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mohr, J. J., Mathiesen, B., & Evrard, A. E. 1999, ApJ, 517, 627 [NASA ADS] [CrossRef] [Google Scholar]
- Moskalenko, I. V., & Strong, A. W. 1998, ApJ, 493, 694 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moskalenko, I. V., Strong, A. W., Ormes, J. F., & Potgieter, M. S. 2002, ApJ, 565, 280 [Google Scholar]
- Mott, N. F. 1929, Royal Soc. London Proc. Ser. A, 124, 422 [NASA ADS] [CrossRef] [Google Scholar]
- Mott, N. F. 1932, Royal Soc. London Proc. Ser. A, 135, 429 [NASA ADS] [CrossRef] [Google Scholar]
- Nath, B. B., & Biermann, P. L. 1994, MNRAS, 267, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Nath, B. B., Madau, P., & Silk, J. 2006, MNRAS, 366, L35 [NASA ADS] [Google Scholar]
- Oegerle, W. R., & Hill, J. M. 2001, AJ, 122, 2858 [NASA ADS] [CrossRef] [Google Scholar]
- Omont, A. 1986, A&A, 164, 159 [NASA ADS] [Google Scholar]
- Padovani, M., Galli, D., & Glassgold, A. E. 2009, A&A, 501, 619 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pfrommer, C., & Enßlin, T. A. 2004, A&A, 413, 17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Podio, L., Bacciotti, F., Nisini, B., et al. 2006, A&A, 456, 189 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Popescu, C. C., Tuffs, R. J., Kylafis, N. D., & Madore, B. F. 2004, A&A, 414, 45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prantzos, N., & Silk, J. 1998, ApJ, 507, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Ptuskin, V. S., Voelk, H. J., Zirakashvili, V. N., & Breitschwerdt, D. 1997, A&A, 321, 434 [NASA ADS] [Google Scholar]
- Ramana Murthy, P. V., & Wolfendale, A. W. 1993, Gamma-ray Astronomy, ed. P. V. Ramana Murthy, & A. W. Wolfendale [Google Scholar]
- Reach, W. T., Rho, J., Tappe, A., et al. 2006, AJ, 131, 1479 [NASA ADS] [CrossRef] [Google Scholar]
- Reimer, L., & Braun, C. 1989, Appl. Opt., 28, 4718 [NASA ADS] [Google Scholar]
- Scalo, J. M. 1986, Fund. Cosm. Phys., 11, 1 [Google Scholar]
- Scott, A., Duley, W. W., & Pinho, G. P. 1997, ApJ, 489, L193 [NASA ADS] [CrossRef] [Google Scholar]
- SerraDíaz-Cano, L., & Jones, A. P. 2008, A&A, 492, 127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shapiro, M. M. 1991, NATO ASIC Proc., 337, Cosmic Rays, Supernovae and the Interstellar Medium, ed. M. M. Shapiro, R. Silberberg, & J. P. Wefel, 1 [Google Scholar]
- Shapiro, M. M. 1996, Nuovo Cimento C Geophysics Space Physics C, 19, 893 [Google Scholar]
- Shibata, T., & Ito, T. 2007, ApJ, 655, 892 [NASA ADS] [CrossRef] [Google Scholar]
- Shibata, T., Honda, N., & Watanabe, J. 2007, Astropart. Phys., 27, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Simmons, J. H. W. 1965, Radiation Damage in Graphite (Pergamon Press) [Google Scholar]
- Simpson, J. A., & Garcia-Munoz, M. 1988, Space Sci. Rev., 46, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Slavin, J. D. 2008, Space Sci. Rev., 50 [Google Scholar]
- Stecker, F. W. 1973, ApJ, 185, 499 [NASA ADS] [CrossRef] [Google Scholar]
- Stevens, I. R., Read, A. M., & Bravo-Guerrero, J. 2003, MNRAS, 343, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Strickland, D. K., & Heckman, T. M. 2009, ApJ, 697, 2030 [NASA ADS] [CrossRef] [Google Scholar]
- Strong, A. W., & Moskalenko, I. V. 1998, ApJ, 509, 212 [NASA ADS] [CrossRef] [Google Scholar]
- Tappe, A., Rho, J., & Reach, W. T. 2006, ApJ, 653, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Tielens, A. G. G. M. 2005, The Physics and Chemistry of the Interstellar Medium (University of Cambridge Press) [Google Scholar]
- Tielens, A. G. G. M. 2008, ARA&A, 46, 289 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tielens, A. G. G. M. 2009, Origin and Evolution of the Interstellar Medium, ed. H. A. Thronson, M. Stiavelli, & A. Tielens, 271 [Google Scholar]
- Völk, H. J. 2003 [arXiv:astro-ph/0303078v1] [Google Scholar]
- Webber, W. R. 1998, ApJ, 506, 329 [Google Scholar]
- Webber, W. R., & Yushak, S. M. 1983, ApJ, 275, 391 [Google Scholar]
- Whaley, C. H., Irwin, J. A., Madden, S. C., Galliano, F., & Bendo, G. J. 2009, MNRAS, 395, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Wiebel-Sooth, B., Biermann, P. L., & Meyer, H. 1998, A&A, 330, 389 [NASA ADS] [Google Scholar]
- Woods, P. M., & Willacy, K. 2007, ApJ, 655, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Woods, P. M., Nyman, L., Schöier, F. L., et al. 2005, A&A, 429, 977 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Ziegler, J. F. 1999, J. Appl. Phys., 85, 1249 [Google Scholar]
- Ziegler, J. F., Biersack, J. P., & Littmark, U. 1985, The Stopping and Ranges of Ions in Matter, ed. J. F. Ziegler, 1 (Pergamon Press) [Google Scholar]
- Zirakashvili, V. N., Breitschwerdt, D., Ptuskin, V. S., & Voelk, H. J. 1996, A&A, 311, 113 [NASA ADS] [Google Scholar]
- Zirakashvili, V. N., & Völk, H. J. 2006, ApJ, 636, 140 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Time constant τ0 for carbon atom ejection following PAH collisions with CR electrons.
Relevant parameters and CR normalization factor
 for the two cooling flow clusters A85 and Virgo from the Pfrommer & Enßlin (2004) sample.
for the two cooling flow clusters A85 and Virgo from the Pfrommer & Enßlin (2004) sample.
All Figures
 |
Fig. 1 Stopping power of hydrogen and iron impacting on carbon, as a function of the energy per nucleon of the ion. The lower validity limit of the Bethe-Bloch equation is 1 MeV/nucleon. We compare the output from the SRIM code, which computes all corrections, and our approximate equation which includes only the mean ionization correction. |
| In the text | |
 |
Fig. 2 Coordinate system adopted to calculate the energy transferred to a PAH via electronic excitation by ion collisions. The molecule is modeled as a disk with radius R and thickness d. The trajectory of the incoming particle is identified by the angle ϑ, while the angle α corresponds to the diagonal of the disk. |
| In the text | |
 |
Fig. 3 Scattering geometry for the elastic collision of an electron (mass me, impact parameter p, initial velocity v) on a massive particle (mass M2, initial velocity zero). After the impact, the target particle is knocked out and recoils at an angle Θ with respect of the initial direction of motion of the projectile electron. |
| In the text | |
 |
Fig. 4 High energy electron cross section for carbon atom removal, calculated for three values of the threshold energy T0. |
| In the text | |
 |
Fig. 5 Interstellar CR spectrum of H, He, CNO, Fe-Co-Ni and electrons as a function of the particle energy. |
| In the text | |
 |
Fig. 6 PAH survival time against collisions with CR ions, as a function of the fraction f of the transferred energy that goes into vibrational excitation. The lifetime has been calculated for PAHs of different sizes (NC), assuming three values for the binding energy of the ejected fragment, E0. The line style indicates the type of ion: dotted for H, dashed for He, solid for CNO and dot-dot-dashed for Fe-Co-Ni. The line color indicates the value of the fragment binding energy: gray for E0 = 3.65 eV, black for E0 = 4.58 eV and red for E0 = 5.6 eV. |
| In the text | |
 |
Fig. 7 Time constant τ0 for carbon atoms removal due to collisions with CR electrons, as a function of the threshold energy T0. |
| In the text | |
 |
Fig. 8 PAH survival time against CR bombardment (ions + electrons) as a function of the molecule size (NC). The total lifetime has been calculated for f = 0.5 and 1, where f is the fraction of the transferred energy available for dissociation, and adopting our reference values for the threshold energy for carbon atom ejection, T0 = 7.5 eV and for the fragment binding energy, E0 = 4.6 eV. We remind the reader of the variation in the calculated survival time against CRs, due to the uncertainty on the parameters E0 and T0 (cf. Figs. 6 and 7). The PAH lifetime against shock destruction in the ISM is shown for comparison. |
| In the text | |
 |
Fig. 9 The latitudinal CR gradient in both Milky Way (MW) and NGC 891, as a function of the vertical distance z from the galactic plane together with the vertical variation of the interstellar radiation field G0 in NGC 891 (courtesy Galliano). The CR intensity I decreases with the scale height zD of the diffusion coefficient. |
| In the text | |
 |
Fig. 10 Total PAH lifetime against CR bombardment in the halo of NGC 891, evaluated at an altitude of 3 kpc from the galactic plane, compared with the circulation timescale between the disk and the halo. The value of the circulation lifetime represents a lower limit, as indicated by the arrow. Otherwise as Fig. 8. |
| In the text | |
 |
Fig. 11 Total PAH lifetime against CR bombardment in the outflow of the starburst galaxy M 82, evaluated at an altitude of 6 kpc from the galactic plane. The PAH survival time is compared with the circulation, starburst and X-rays timescales. The values of the circulation and X-rays timescales represent lower limits, as indicated by the arrows. Otherwise as Fig. 8. |
| In the text | |
 |
Fig. 12 Total PAH lifetime against CR bombardment in the cooling flow galaxy clusters A85 and Virgo, compared with the survival time, τHG, in a hot gas. The value adopted for the lowest energy of the CR spectrum, Emin, is 50 MeV/nucleon (see text), otherwise as Fig. 8. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


