| Issue |
A&A
Volume 526, February 2011
|
|
|---|---|---|
| Article Number | A138 | |
| Number of page(s) | 6 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201015637 | |
| Published online | 12 January 2011 | |
Alleviating α quenching by solar wind and meridional flows
1
NORDITA, AlbaNova University Center,
Roslagstullsbacken 23,
10691
Stockholm,
Sweden
e-mail: dhruba.mitra@gmail.com
2
School of Mathematics, University of Manchester,
Oxford Road,
Manchester
M13 9PL,
UK
3
Astronomy Unit, School of Mathematical Sciences, Queen Mary
University of London, Mile End
Road, London
E1 4NS,
UK
4
Department of Astronomy, Stockholm University,
10691
Stockholm,
Sweden
Received:
25
August
2010
Accepted:
1
December
2010
Aims. We study the ability of magnetic helicity expulsion to alleviate catastrophic α-quenching in mean field dynamos in two–dimensional spherical wedge domains.
Methods. Motivated by the physical state of the outer regions of the Sun, we consider α2Ω mean field models with a dynamical α quenching. We include two mechanisms which have the potential to facilitate helicity expulsion, namely advection by a mean flow (“solar wind”) and meridional circulation.
Results. We find that a wind alone can prevent catastrophic quenching, with the field saturating at finite amplitude. In certain parameter ranges, the presence of a large-scale meridional circulation can reinforce this alleviation. However, the saturated field strengths are typically below the equipartition field strength. We discuss possible mechanisms that might increase the saturated field.
Key words: Sun: dynamo / magnetohydrodynamics (MHD)
© ESO, 2011
1. Introduction
Mean field dynamo models have provided an important framework for studying the generation
of large-scale astrophysical magnetic fields and their spatio-temporal dynamics. However,
these widely used models have been presented with a serious challenge – namely the so called
catastrophic α quenching (Gruzinov
& Diamond 1994). In the mean field (MF) context this effect, which is a
consequence of the conservation of magnetic helicity (Krause
& Rädler 1980; Zeldovich et al.
1983), manifests itself as the decrease of the α-effect with
increasing magnetic Reynolds number ReM (Vainshtein & Cattaneo 1992; Cattaneo
& Hughes 1996) at finite field strength. In models without magnetic
helicity fluxes, the quenching of α can become severe, with
α decreasing as 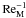 – truly
catastrophic for dynamo action in the Sun, stars and galaxies where the Reynolds numbers are
all very large (>109). This catastrophic quenching is
captured by mean-field models which use dynamical alpha quenching, such as that considered
by Blackman & Brandenburg (2002). This
catastrophic quenching is independent of the details of the dynamo mechanism and is a direct
effect of the conservation of magnetic helicity. See, e.g., Brandenburg & Käpylä (2007) who have demonstrated catastrophic quenching
for non-local alpha effect or Chatterjee et al.
(2011) who have demonstrated the occurrence of catastrophic quenching in
distributed dynamos. It has been suggested that the quenching may be alleviated by the
expulsion of magnetic helicity through open boundaries (Blackman & Field 2000; Kleeorin et al.
2000). At least three different physical mechanisms may help in the expulsion of
small scale magnetic helicity: (a) large scale shear (Vishniac & Cho 2001; Subramanian &
Brandenburg 2004; Brandenburg & Sandin
2004; Moss & Sokoloff 2011); (b)
turbulent diffusion of magnetic helicity (Mitra et al.
2010a); (c) non-zero mean flow out from a boundary of the domain, e.g. a wind. A
number of recent studies have demonstrated the possibility of this alleviation of quenching
for solar (Chatterjee et al. 2010, 2011; Guerrero et al.
2010) and galactic dynamos (e.g. Shukurov et al.
2006).
– truly
catastrophic for dynamo action in the Sun, stars and galaxies where the Reynolds numbers are
all very large (>109). This catastrophic quenching is
captured by mean-field models which use dynamical alpha quenching, such as that considered
by Blackman & Brandenburg (2002). This
catastrophic quenching is independent of the details of the dynamo mechanism and is a direct
effect of the conservation of magnetic helicity. See, e.g., Brandenburg & Käpylä (2007) who have demonstrated catastrophic quenching
for non-local alpha effect or Chatterjee et al.
(2011) who have demonstrated the occurrence of catastrophic quenching in
distributed dynamos. It has been suggested that the quenching may be alleviated by the
expulsion of magnetic helicity through open boundaries (Blackman & Field 2000; Kleeorin et al.
2000). At least three different physical mechanisms may help in the expulsion of
small scale magnetic helicity: (a) large scale shear (Vishniac & Cho 2001; Subramanian &
Brandenburg 2004; Brandenburg & Sandin
2004; Moss & Sokoloff 2011); (b)
turbulent diffusion of magnetic helicity (Mitra et al.
2010a); (c) non-zero mean flow out from a boundary of the domain, e.g. a wind. A
number of recent studies have demonstrated the possibility of this alleviation of quenching
for solar (Chatterjee et al. 2010, 2011; Guerrero et al.
2010) and galactic dynamos (e.g. Shukurov et al.
2006).
In this paper we study the effects of a number of mechanisms which may facilitate the expulsion of magnetic helicity from the dynamo region. Initially we consider the effects of advection by a mean flow in a similar manner to Shukurov et al. (2006); see also the recent study in a one dimensional model by Brandenburg et al. (2009). We envisage that in the Sun the wind could be loaded with magnetic helicity through coronal mass ejections (Blackman & Brandenburg 2003). Another potentially important mechanism is meridional circulation. The presence of such a circulation in the Sun is supported by a number of observations which have found evidence for a near-surface poleward flow of 10–20 ms-1. Even though the corresponding compensating equatorward flow has not yet been detected, it is however assumed it must exist because of mass conservation. Substantial effort has recently gone into the construction of flux transport dynamo models which differ from the usual αΩ dynamos by including an additional advective transport of magnetic flux by meridional circulation. (see e.g. Dikpati & Gilman 2009, for a recent summary). If magnetic flux is advected by meridional circulation, it can be expected that such a circulation will also transport magnetic helicity to the surface layers, which might thus facilitate its subsequent expulsion by the wind. We therefore study the effects of meridional circulation on the quenching.
The structure of the paper is as follows. In Sect. 2 we introduce our model and its various ingredients. Section 3 contains our results, and we give a short summary here. First we consider our model with an imposed wind but no meridional circulation. We show that a strong enough wind that penetrates deeply enough into the convection zone can indeed alleviate quenching. We then make a systematic study of the alleviation of quenching as a function of the two parameters specifying the wind, namely the maximum velocity and the depth down to which the wind penetrates the convection zone. Next we select a particular set of these two parameters such that for large ReM there is no alleviation of quenching. We then introduce a meridional circulation and show that a combination of a wind and circulation is able to limit the quenching in cases where the wind alone cannot. We further study the effect of the characteristic velocity of meridional circulation on quenching. Our conclusions are presented in Sect. 4.
2. The model
We study two-dimensional (axisymmetric) mean field models in a spherical wedge domain, r1 ≤ r ≤ r2, θ1 ≤ θ ≤ π/2, where r,θ,φ are spherical polar coordinates. The choice of this “wedge” shaped domain is motivated by recent Direct Numerical Simulations (DNSs) of forced and convective dynamos in spherical wedges cut from spheres (Mitra et al. 2010b; Käpylä et al. 2010), and the intention to make a similar development of this work.
We consider an α2Ω mean field model with a “dynamical alpha” in
the presence of an additional mean flow 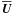 .
In the simplest case, where we consider no wind and no meridional circulation, the mean flow
is in the form of a uniform rotational shear given by
.
In the simplest case, where we consider no wind and no meridional circulation, the mean flow
is in the form of a uniform rotational shear given by
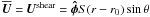 . For the more realistic cases we
use
. For the more realistic cases we
use 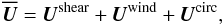 (1)where
Uwind and
Ucirc are respectively the large-scale velocity
of the wind and circulation. The particular forms we use are given in Sects. 2.1 and 2.2 below.
Thus, we integrate
(1)where
Uwind and
Ucirc are respectively the large-scale velocity
of the wind and circulation. The particular forms we use are given in Sects. 2.1 and 2.2 below.
Thus, we integrate 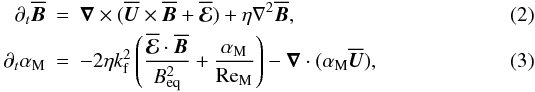 where
where
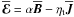 , and
α = αM + αK is
the sum of the magnetic and kinetic α-effects respectively. The magnetic
Reynolds number,
ReM/3 ≡ ηt/η
and Beq is the equipartition field strength. We take
ηt = 1, Beq = 1 and
kf = 100 in our simulations. Here Eq. (2) is the standard induction equation for mean
field models and Eq. (3) describes the
dynamical evolution of α; see Blackman
& Brandenburg (2002). The last term in the right hand side of Eq. (3) models the advective flux of magnetic
helicity.
, and
α = αM + αK is
the sum of the magnetic and kinetic α-effects respectively. The magnetic
Reynolds number,
ReM/3 ≡ ηt/η
and Beq is the equipartition field strength. We take
ηt = 1, Beq = 1 and
kf = 100 in our simulations. Here Eq. (2) is the standard induction equation for mean
field models and Eq. (3) describes the
dynamical evolution of α; see Blackman
& Brandenburg (2002). The last term in the right hand side of Eq. (3) models the advective flux of magnetic
helicity.
We solve Eqs. (2) and (3) using the Pencil Code1 which employs a sixth order centered finite-difference method to evaluate the spatial derivatives and a third order Runge-Kutta scheme for time evolution.
Our aim here is to study the effects of the various mechanisms discussed above in alleviating the catastrophic quenching of the magnetic field as ReM increases.
2.1. The wind and the “corona”
In order to include the effects of the solar wind we must include an outer region in our
model through which the wind flows, by extending the outer boundary beyond the convection
zone to radius
r3 > r2.
We shall refer to the region
r2 ≤ r ≤ r3 as
the “corona”. We take the wind to be strong in the corona and to grow weaker as we go into
the convection zone. This is represented by choosing the following form for
Uwind, ![\begin{eqnarray} label{uwindr}\Uwind_r &=& \frac{1}{2} U_0 \left [ 1+\tanh\left(\frac{r-r_2}{w} \right) \right] , \\\ \label{uwindth} \Uwind_\theta &=& 0, \\ \Uwind_\phi &=& 0, \end{eqnarray}](/articles/aa/full_html/2011/02/aa15637-10/aa15637-10-eq27.png) where
U0 and w are control parameters which
determine the strength of the wind speed and its depth of penetration into the convection
zone respectively. Larger values of w correspond to deeper penetration.
We let the kinematic α-effect to go to zero in the corona by choosing
where
U0 and w are control parameters which
determine the strength of the wind speed and its depth of penetration into the convection
zone respectively. Larger values of w correspond to deeper penetration.
We let the kinematic α-effect to go to zero in the corona by choosing
![\begin{equation} \alpk = -\frac{\alpha_0}{2}\tanh \left( \frac{\theta-\pi/2}{0.05} \right) \left[1 -\tanh\left(\frac{r-r_2}{w_{\alpha}} \right) \right] , \label{ystep_xcutoff} \end{equation}](/articles/aa/full_html/2011/02/aa15637-10/aa15637-10-eq30.png) (7)with
α0 = 16.
(7)with
α0 = 16.
2.2. The meridional circulation
We consider the effects of a meridional circulation, by including a velocity
Ucirc given by ![\begin{eqnarray} \Ucirc_r&=&\vamp g(r)\frac{1}{\sin\theta}\frac{\partial} {\partial\theta}\left(\sin\theta\,\psi\right), \\ \Ucirc_\theta&=&-\vamp g(r)\frac{1}{r}\frac{\partial}{\partial r}(r\psi), \\ \psi&=&\frac{f(r)}{r}\sin^2(\theta-\theta_1)\cot\theta, \\ f(r)&=& (r-r_2)(r-r_1)^2, \\ g(r)&=& \frac{1}{2}\left[1 -\tanh\left(\frac{r-r_2}{w_{\rm circ}} \right) \right], \\ \label{circulation} \Ucirc_{\phi} &=& 0. \end{eqnarray}](/articles/aa/full_html/2011/02/aa15637-10/aa15637-10-eq32.png) Here
vamp is a parameter controlling the magnitude of circulation
speed and wcirc determines the effective depth of penetration
of the circulation into
r > r2. As a
characteristic speed of circulation, vcirc, we take the
maximum absolute magnitude of the θ component of
Ucirc at
r = r2, i.e. at the surface of the Sun.
Helioseismology shows this velocity to be about 10 to 20 metres per second in the Sun. A
typical velocity field is shown in Fig. 1, and the
profile of αK is shown in Fig. 2. In these figures, the parameters are chosen to be
α0 = 16,
wα = 0.2, U0 = 2,
r2 = 1.5, w = 0.3,
vamp = 75, rcirc = 0.98,
wcirc = 0.02.
Here
vamp is a parameter controlling the magnitude of circulation
speed and wcirc determines the effective depth of penetration
of the circulation into
r > r2. As a
characteristic speed of circulation, vcirc, we take the
maximum absolute magnitude of the θ component of
Ucirc at
r = r2, i.e. at the surface of the Sun.
Helioseismology shows this velocity to be about 10 to 20 metres per second in the Sun. A
typical velocity field is shown in Fig. 1, and the
profile of αK is shown in Fig. 2. In these figures, the parameters are chosen to be
α0 = 16,
wα = 0.2, U0 = 2,
r2 = 1.5, w = 0.3,
vamp = 75, rcirc = 0.98,
wcirc = 0.02.
 |
Fig. 1 Plot of the velocity field: the arrows show the meridional circulation and the wind, and the contours show the angular velocity. The solar radius is taken to be unity. Although our domain extends out to 5 solar radii, for clarity only a part of it is shown here. The curve at unit radius denotes the surface of the Sun. |
 |
Fig. 2 The kinetic alpha effect, αK, and wind radial velocity, Ur, as a function of radial coordinate r for three different latitudes, equator (upper curve), mid-latitude (middle curve) and latitude of upper boundary (lower curve). Note that the curves for the radial velocities differ only in r < 1, where the meridional circulation is non-zero. |
2.3. Boundary conditions
For the magnetic field we use perfect conductor boundary conditions both at the base of
the convection zone (at r = r1) and at the
lateral boundary at the higher latitude
(θ = θ1). We assume the magnetic field to
be antisymmetric about the equator
(θ = π/2), and at the outer radial
boundary of the corona (r = r3) we use the
normal field condition. In terms of the magnetic vector potential
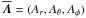 , where
, where
 ,
these conditions become
,
these conditions become 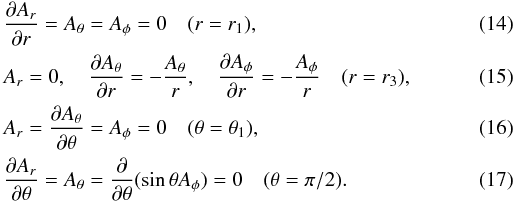 For
αM, on those boundaries where the boundary condition on the
magnetic field is “perfect-conductor” (i.e. at the bottom of the convection zone and at
the higher latitude), we choose
For
αM, on those boundaries where the boundary condition on the
magnetic field is “perfect-conductor” (i.e. at the bottom of the convection zone and at
the higher latitude), we choose 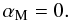 (18)At the other two
boundaries, we recall that since the PDE being solved is of first order in space we only
need to specify one condition, which we have already imposed at the lower boundary. To
calculate the derivative at the outer boundary we therefore just extrapolate the solution
from inside to outside by a second order polynomial extrapolation. This is equivalent to
using second order one sided finite difference at these boundaries.
(18)At the other two
boundaries, we recall that since the PDE being solved is of first order in space we only
need to specify one condition, which we have already imposed at the lower boundary. To
calculate the derivative at the outer boundary we therefore just extrapolate the solution
from inside to outside by a second order polynomial extrapolation. This is equivalent to
using second order one sided finite difference at these boundaries.
As the initial condition for the magnetic field we choose our seed magnetic vector potential from a random Gaussian distribution with no spatial correlation and root-mean-square value of the order of 10-4 times the equipartition field strength. Also, initially we take αM = α − αK = 0.
3. Results
In order to demonstrate that our dynamo is excited, and displays both oscillations and equatorward migration, we first use the velocity field and the kinetic α profile shown in Fig. 1, with ReM = 3 × 102 and solve Eqs. (2) and (3) simultaneously. The resulting space-time diagram for the three components of the magnetic field is shown in Fig. 3. This is a typical example of the “butterfly” diagrams that are obtained with this model.
 |
Fig. 3 Spacetime diagrams for the three components of the magnetic field. These plots are for the set of parameters corresponding to the velocity field and αK shown in Figs. 1 and 2. |
As mentioned above, an important feature of MF dynamos in the absence of wind and
meridional circulation (i.e. when U0 = 0 and
vamp = 0), is that they are severely quenched as
ReM increases. To show this we have plotted in Fig. 4a the time-series of the total magnetic energy
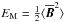 for several values of
ReM. Here, ⟨ ... ⟩ denotes averaging over the domain
r1 ≤ r ≤ r2.
Clearly the total magnetic energy decreases with ReM. Similar quenching, as a
result of the dynamical evolution of the alpha term, has been seen in many different models
of the solar dynamo (see, e.g., Chatterjee et al.
2010, 2011; Guerrero et al. 2010, for some recent examples), and also in models of galactic
dynamos (Shukurov et al. 2006).
for several values of
ReM. Here, ⟨ ... ⟩ denotes averaging over the domain
r1 ≤ r ≤ r2.
Clearly the total magnetic energy decreases with ReM. Similar quenching, as a
result of the dynamical evolution of the alpha term, has been seen in many different models
of the solar dynamo (see, e.g., Chatterjee et al.
2010, 2011; Guerrero et al. 2010, for some recent examples), and also in models of galactic
dynamos (Shukurov et al. 2006).
 |
Fig. 4 a) Time series of EM for U0 = 0 and vamp = 0, i.e. no wind or circulation, for 5 different values of ReM. b) The corresponding plot with U0 = 1, w = 0.3 and vamp = 75. The time-averaged magnetic energy ⟨ EM ⟩ t is calculated by time-averaging these time-series between the two dashed vertical lines. The other parameters used are α0 = 16, wα = 0.2, r2 = 1.5, and w = 0.3. |
To substantiate this further we plot in Fig. 5 the
time-averaged magnetic energy
⟨ EM ⟩ t as a function of
ReM, where the time averaging is done over several diffusion times
(T) in the saturated nonlinear stage (i.e. after the kinematic growth
phase is over). Time averaging is here indicated by the subscript t after
the averaging sign. As can be seen in the absence of wind, i.e. with
U0 = 0, such time-averaged energy falls off approximately as
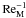 . This gives
a quantitative measure of the quenching. (The point at ReM = 2 × 106
appears anomalous; we believe this is because we have not run the code for long enough to
achieve the final saturated state.)
. This gives
a quantitative measure of the quenching. (The point at ReM = 2 × 106
appears anomalous; we believe this is because we have not run the code for long enough to
achieve the final saturated state.)
To demonstrate the ability of the wind and circulation to act together to alleviate quenching, we have plotted in Fig. 4(b) the time-series of EM for several different values of ReM, in the presence of the wind (with U0 = 1, vamp = 75 and depth parameter w = 0.3). The dependence of the time-averaged magnetic energy ⟨ EM ⟩ t on ReM in this case is also plotted in Fig. 5. Comparing Fig. 4(b) with Fig. 4(a) and also comparing the two lines in Fig. 5 we clearly see that with the parameters chosen the wind in conjunction with the circulation is capable of alleviating quenching. This is one of our principal results. Note that the saturated mean field energy that we observe at large ReM is still rather small, only slightly exceeding 10-4 of the equipartition value.
 |
Fig. 5 The time-averaged magnetic energy as a function of ReM for U0 = 0 (no wind) and U0 = 1 and w = 0.3 and vamp = 75. |
Next we attempt to isolate the role of each parameter in our model. First we make a detailed systematic study of how quenching depends on the two parameters U0 and w of our model, for a fixed value of ReM = 107 and zero circulation, vamp = 0. For each pair of parameters we ran our code for up to 50 diffusion times. In some cases the time series of EM declines as a function of time initially, but at larger times recovers to unquenched values, e.g. U0 = 1 in Fig. 6. In some other cases we observe that the recovery is merely temporary and at large times EM goes to zero. As an example we first show in Fig. 6 the time-series of EM for various values of U0, for a fixed w = 0.3. Clearly, as the wind velocity increases the transport of magnetic helicity out of the domain at first becomes more efficient and we observe less quenching. But this alleviation of quenching must have its limits because for a large enough wind speed the magnetic field itself will be advected out of the domain faster than it is generated, thus killing the dynamo (see, e.g., Shukurov et al. 2006; Brandenburg et al. 1993; Moss et al. 2010). However with penetration factor w = 0.3 we did not find this effect, even when U0 = 100, but with w = 0.5, winds with U0 ≥ 20 kill the dynamo. We deduce that it is necessary to advect large-scale field from a substantial proportion of the dynamo region for the dynamo to be killed by advection.
Then we consider the parameter w which controls the depth of penetration of the wind into the convection zone. The dependence of the time-series of magnetic energy on this parameter is shown in Fig. 7, for ReM = 107 and U0 = 2. We also note that there is a subset of parameters for which the transients are so long that it is difficult to decide whether the asymptotic state is a quenched dynamo or not, within reasonable integration times. In our parameter space, i.e. in the U0 − w plane, the positions of the quenched and unquenched runs are shown in Fig. 8; summarizing the dependence of quenching on these parameters. For all the runs we label as unquenched the butterfly diagram is also restored at large times.
 |
Fig. 6 Time series of EM for 5 different values of U0, namely, U0 = 0.1(∗ ),0.4(◇),1(▵ ), 2(□) and 10(× ) with all other parameters held fixed, in particular ReM = 107, w = 0.3. |
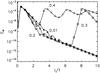 |
Fig. 7 Time series of EM for 5 different values of w, [w = 0.01(∗ ), 0.2(▵ ), 0.3(□), and 0.4(× ).] with all other parameters held fixed, i.e., ReM = 107, U0 = 2 with no circulation. |
 |
Fig. 8 The incidence of quenched and unquenched solutions in the U0 − w plane. The positions of quenched models are denoted by the symbol ∗ , the symbol ◇ identifies unquenched models. The arrow is explained in Sect. 3.1. |
3.1. The effect of circulation
Next we consider the effect of meridional circulation on the quenching. If the wind penetrates inside the convection zone too deeply then we expect that circulation will have either no effect, or just a marginal effect, because the wind by itself will be efficient enough in removing small-scale magnetic helicity from deep within the domain. But if the wind does not penetrate so deeply, circulation may play an important role in dredging magnetic helicity from deep inside the domain to near the surface from where the wind can remove it. To see whether this idea can work, we select one point in the phase diagram in Fig 8, where we obtain the quenched solution marked by the arrow. Then we turn on the meridional circulation. The comparison between the time-series of EM with and without circulation is shown in Fig. 9. It can be seen that the final magnetic energy reached does not depend on the amplitude of circulation if the amplitude of circulation is greater than a critical value. Note that this alleviation of quenching by the circulation only works for those points in the U0 − w parameter space which lie close to the boundary between the quenched and non-quenched states in the phase diagram. For points with very small w, i.e. in cases where the wind penetrates very little into the convection zone, even a very strong circulation cannot remove the quenching.
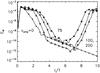 |
Fig. 9 Time series of EM as a function of time for U0 = 2 and w = 0.25 with vamp = 0(+ ),75(∗ ),100(◇),and200(▵ ). |
Another possible mechanism that can transport magnetic helicity from the bulk of the convection zone to its surface is the diffusion of magnetic helicity. This can be described by adding the term κt∇2αM to the right hand side of Eq. (3), where κt is an effective turbulent diffusivity of the magnetic helicity. Numerical simulations have estimated κt ~ 0.3ηt (Mitra et al. 2010a). We have checked that such a diffusive flux of magnetic helicity can alleviate quenching at least as effectively as the meridional circulation, in the presence of the wind.
Finally we note that the alleviation of quenching as described here is independent of some details of the underlying dynamo model. In particular it does not depend on whether we have an α2 dynamo or an α2Ω dynamo. To check this assertion explicitly we also solved the same problem but with Ushear = 0 in Eq. (1). The results are shown in Fig. 10 where we compare the alleviation of quenching for the α2 dynamo (top panel) against the corresponding α2Ω dynamo (bottom panel).
 |
Fig. 10 The behaviour of the time-averaged magnetic energy as a function of magnetic Reynolds number ReM, which shows the alleviation of quenching, with wind speed U0 = 2 and depth parameter w = 0.8 (upper panel). Also shown is the corresponding plot in the absence of a wind, which clearly shows a catastrophic quenching. The lower panel is for a α2Ω dynamo. |
4. Conclusions
We have introduced two observationally motivated effects that may help reduce the catastrophic quenching found in mean field dynamo models. An outward flow from the dynamo region (“wind”) is found to be effective in allowing the quenching to saturate at finite values of the field strength. The wind alone is, however, only effective when it penetrates quite deeply into the convection zone. These effects are modified to some extent by the presence of a meridional circulation which has the ability to transport small scale helicity from deep in the convection zone to near the surface, from where the wind can more effectively remove it. However, the effects of circulation in our model are not dramatic. It is also true that the saturation fields in our model are rather small compared to the equipartition field strength. This was also observed in the model of Shukurov et al. (2006); see also Moss & Sokoloff (2011). One possibility, that we have not explored, is that the neglected inhomogeneity of the solar convection zone may be important.
It is interesting to try to estimate the various parameters of our model in physical units
and to compare them with the solar values. We have taken the solar radius as the unit of
length (7 × 1010 cm). The α effect can be taken to be a measure
of the small scale velocity in the Sun,
α ~ (1/3)|u|,
where 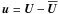 . The
Baker & Temesvary (1966) tables give
estimates for small-scale velocities in the convection zone of the Sun of between
4 × 103–2 × 105 cm s-1, in regions where convection is
efficient. As we have considered the convection zone to be homogeneous we consider
104 cm s-1 to be a reasonable estimate. Then, as
α = 16 in our units the unit of velocity is
~104/(3 × 16) cm s-1 ~ 2 × 103 cm s-1,
and the unit of time, obtained from length and velocity units given above, is
~108 s ≈ 10 yrs. Thus our characteristic cycle period,
T ≈ 1, corresponds to approximately 10 years. Then the maximum wind speed
we have used (U0 = 10) would correspond to
2 × 103 cm s-1. The speed of the meridional circulation at the
surface in our units is vsurf = 0.47 for
vamp = 75. Translated to physical units this becomes
vsurf ≈ 1 m s-1, which is of the same order of
magnitude as the solar meridional velocity. If in the estimates above we use the maximum and
minimum values of the small-scale velocity as given by the Baker and Temesvary tables,
instead of the mean, the maximum surface speed of meridional circulation will be between
0.4 m s-1 and 20 m s-1 . The speed of the solar wind that we have
used is significantly smaller than that of the actual solar wind, but on the other hand the
real solar wind is a highly fluctuating turbulent flow, whereas we have considered a
constant outflow.
. The
Baker & Temesvary (1966) tables give
estimates for small-scale velocities in the convection zone of the Sun of between
4 × 103–2 × 105 cm s-1, in regions where convection is
efficient. As we have considered the convection zone to be homogeneous we consider
104 cm s-1 to be a reasonable estimate. Then, as
α = 16 in our units the unit of velocity is
~104/(3 × 16) cm s-1 ~ 2 × 103 cm s-1,
and the unit of time, obtained from length and velocity units given above, is
~108 s ≈ 10 yrs. Thus our characteristic cycle period,
T ≈ 1, corresponds to approximately 10 years. Then the maximum wind speed
we have used (U0 = 10) would correspond to
2 × 103 cm s-1. The speed of the meridional circulation at the
surface in our units is vsurf = 0.47 for
vamp = 75. Translated to physical units this becomes
vsurf ≈ 1 m s-1, which is of the same order of
magnitude as the solar meridional velocity. If in the estimates above we use the maximum and
minimum values of the small-scale velocity as given by the Baker and Temesvary tables,
instead of the mean, the maximum surface speed of meridional circulation will be between
0.4 m s-1 and 20 m s-1 . The speed of the solar wind that we have
used is significantly smaller than that of the actual solar wind, but on the other hand the
real solar wind is a highly fluctuating turbulent flow, whereas we have considered a
constant outflow.
To summarise, we have presented a very simplified model, in order to explore some basic ideas relevant to the solar dynamo.
We cannot claim to have “solved” the quenching problem, but feel we have identified, and to some extent quantified, mechanisms of potential interest. We appreciate that there are a number of desirable improvements, even in this MF formulation. These include using a more realistic solar-like rotation law, investigation and comparison of the effects of other fluxes of magnetic helicity (e.g. Zhang et al. 2006), the diffusive magnetic helicity flux (Mitra et al. 2010a), the inclusion of compressibility in some form, but most importantly perhaps, using a more realistic model for the solar wind allowing for magnetic helicity loading via coronal mass ejections. Notwithstanding these possible shortcomings, we do feel that our results provide motivation for further investigations in the context of solar and stellar dynamos. Investigations using DNS (e.g. Warnecke & Brandenburg 2010) appear likely to be especially interesting, and we hope to pursue this approach.
Acknowledgments
We thank an anonymous referee for suggesting several improvements to the paper. This work was supported by the the Leverhulme Trust, the European Research Council under the AstroDyn Research Project 227952, and the Swedish Research Council grant 621-2007-4064. Computational resources were granted by QMUL HPC facilities purchased under the SRIF initiative.
References
- Baker, N. H., & Temesvary, S. 1966, Tables of Convective Stellar Envelopes (New York: Institute for Space Studies) [Google Scholar]
- Blackman, E., & Field, G. B. 2000, ApJ, 534, 984 [NASA ADS] [CrossRef] [Google Scholar]
- Blackman, E., & Brandenburg, A. 2002, ApJ, 579, 359 [Google Scholar]
- Blackman, E., & Brandenburg, A. 2003, ApJ, 584, L99 [NASA ADS] [CrossRef] [Google Scholar]
- Brandenburg, A., & Käpylä, P. J. 2007, New. J. Phys., 9, 305 [Google Scholar]
- Brandenburg, A., & Sandin, C. 2004, A&A, 427, 13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brandenburg, A., & Subramanian, K. 2005, Phys. Rep., 417, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Brandenburg, A., Donner, K.-J., Moss, D., et al. 1993, A&A, 271, 36 [NASA ADS] [Google Scholar]
- Brandenburg, A., Candelaresi, S., & Chatterjee, P. 2009, MNRAS, 398, 1414 [NASA ADS] [CrossRef] [Google Scholar]
- Cattaneo, F., & Hughes, D. W. 1996, Phys. Rev. E, 54, 4532 [NASA ADS] [CrossRef] [Google Scholar]
- Chatterjee, P., Brandenburg, A., & Guerrero, G. 2010, Geophys. Astrophys. Fluid Dyn., 104, 591 [NASA ADS] [CrossRef] [Google Scholar]
- Chatterjee, P., Guerrero, G., & Brandenburg, A. 2011, A&A, 525, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dikpati, M., & Gilman, P. A. 2009, Space Sci. Rev., 144, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Gruzinov, A. V., & Diamond, P. H. 1994, Phys. Rev. Lett., 72, 1651 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Guerrero, G., Chatterjee, P., & Brandenburg, A. 2010, MNRAS, 409, 1619 [NASA ADS] [CrossRef] [Google Scholar]
- Kleeorin, N., Moss, D., Rogachevskii, I., & Sokoloff, D. 2000, A&A, 361, L5 [NASA ADS] [Google Scholar]
- Käpylä, P. J., Korpi, M. J., Brandenburg, A., Mitra, D., & Tavakol, R. 2010, Astron. Nachr., 331, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Krause, F., & Rädler, K.-H. 1980, Mean-field Magnetohydrodynamics and Dynamo Theory (Oxford: Pergamon Press) [Google Scholar]
- Mitra, D., Candelaresi, S., Chatterjee, P., Tavakol, R., & Brandenburg, A. 2010a, Astron. Nachr., 331, 130 [Google Scholar]
- Mitra, D., Tavakol, R., Käpylä, P. J., & Brandenburg, A. 2010b, ApJ, 719, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Moss, D., & Sokoloff, D. 2011, Astron. Nachr. 332, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Moss, D., Sokoloff, D., Beck, R., & Krause, M. 2010, A&A, 512, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shukurov, A., Sokoloff, D., Subramanian, K., & Brandenburg, A. 2006, A&A, 448, L33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Subramanian, K., & Brandenburg, A. 2004, Phys. Rev. Lett., 93, 205001 [NASA ADS] [CrossRef] [Google Scholar]
- Vainshtein, S. I., & Cattaneo, J. 1992, ApJ, 393, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Vishniac, E. T., & Cho, J. 2001, ApJ, 550, 752 [NASA ADS] [CrossRef] [Google Scholar]
- Warnecke, J., & Brandenburg, A. 2010, A&A, 523, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zeldovich, Ya. B, Ruzmaikin, A. A., & Sokoloff, D. D. 1983, Magnetic Fields in Astrophysics (New York: Gordon and Breach Science Publishers). [Google Scholar]
- Zhang, H., Sokoloff, I., Rogachevskii, I., et al. 2006, MNRAS, 365, 276 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Plot of the velocity field: the arrows show the meridional circulation and the wind, and the contours show the angular velocity. The solar radius is taken to be unity. Although our domain extends out to 5 solar radii, for clarity only a part of it is shown here. The curve at unit radius denotes the surface of the Sun. |
| In the text | |
 |
Fig. 2 The kinetic alpha effect, αK, and wind radial velocity, Ur, as a function of radial coordinate r for three different latitudes, equator (upper curve), mid-latitude (middle curve) and latitude of upper boundary (lower curve). Note that the curves for the radial velocities differ only in r < 1, where the meridional circulation is non-zero. |
| In the text | |
 |
Fig. 3 Spacetime diagrams for the three components of the magnetic field. These plots are for the set of parameters corresponding to the velocity field and αK shown in Figs. 1 and 2. |
| In the text | |
 |
Fig. 4 a) Time series of EM for U0 = 0 and vamp = 0, i.e. no wind or circulation, for 5 different values of ReM. b) The corresponding plot with U0 = 1, w = 0.3 and vamp = 75. The time-averaged magnetic energy ⟨ EM ⟩ t is calculated by time-averaging these time-series between the two dashed vertical lines. The other parameters used are α0 = 16, wα = 0.2, r2 = 1.5, and w = 0.3. |
| In the text | |
 |
Fig. 5 The time-averaged magnetic energy as a function of ReM for U0 = 0 (no wind) and U0 = 1 and w = 0.3 and vamp = 75. |
| In the text | |
 |
Fig. 6 Time series of EM for 5 different values of U0, namely, U0 = 0.1(∗ ),0.4(◇),1(▵ ), 2(□) and 10(× ) with all other parameters held fixed, in particular ReM = 107, w = 0.3. |
| In the text | |
 |
Fig. 7 Time series of EM for 5 different values of w, [w = 0.01(∗ ), 0.2(▵ ), 0.3(□), and 0.4(× ).] with all other parameters held fixed, i.e., ReM = 107, U0 = 2 with no circulation. |
| In the text | |
 |
Fig. 8 The incidence of quenched and unquenched solutions in the U0 − w plane. The positions of quenched models are denoted by the symbol ∗ , the symbol ◇ identifies unquenched models. The arrow is explained in Sect. 3.1. |
| In the text | |
 |
Fig. 9 Time series of EM as a function of time for U0 = 2 and w = 0.25 with vamp = 0(+ ),75(∗ ),100(◇),and200(▵ ). |
| In the text | |
 |
Fig. 10 The behaviour of the time-averaged magnetic energy as a function of magnetic Reynolds number ReM, which shows the alleviation of quenching, with wind speed U0 = 2 and depth parameter w = 0.8 (upper panel). Also shown is the corresponding plot in the absence of a wind, which clearly shows a catastrophic quenching. The lower panel is for a α2Ω dynamo. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


