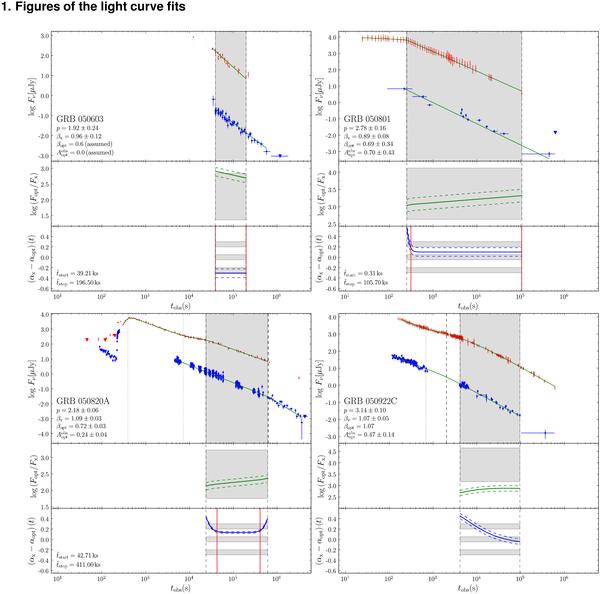
Optical and X-ray afterglow light curves of the 27 bursts that entered our sample. Upper panel: the optical data in the R_c band are shown as dots and the X-ray data at 1.73 keV as bigger dots with an error bar in time. The light-curve fits are over-plotted. Upper limits are shown as downwards-pointing triangles. The grey box is the overlapping time interval of the late-time evolution. Vertical dotted and dashed lines indicate breaks in the optical and X-ray band. Information on the SEDs are shown in the bottom left (see also Table B.1). The given extinction, 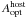, is the observed host-extinction in the R_c band based on the deduced host extinction in the V-band, 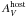. Additionally, we deduced the electron index, p, from β_x. The electron index is either p = 2β if ν_c < ν_x or p = 2β + 1 if ν_c > ν_x (e.g., Zhang & Mészáros 2004). Its error was computed by propagating the uncertainty in β_x. Middle panel: the flux density ratio between the optical and X-ray afterglow is shown as a solid line and its error as a dashed line for the shared time interval of the late-time evolution. The grey box represents the allowed parameter space of the flux density ratio (Table 1). The upper boundary is the expected flux density ratio for ν_c ≤ ν_opt, while the lower one shows the expected ratio for ν_c ≥ ν_x. If the cooling break is in between the optical and the X-ray bands, the expected flux-density ratio lies be in between these boundaries. The expected flux density ratio depends on the electron index. Not all bursts could be corrected for host extinction. The error on the electron index was neither propagated into the error of the expected nor of the observed flux-density ratio. Lower panel: the first logarithmic derivative of the flux-density ratio, 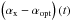, is shown as a solid curve and its error is plotted as a dashed line. For t/t_break ≇ 1, the first logarithmic derivative is identical to the difference in the decay slopes obtained from the light-curve fit (asymptotic values). Usually breaks in the light curves tend to be smooth instead of sharp. Because of this, the first logarithmic derivative deviates from the asymptotic value close to a break depending on the smoothness of the break. Two solid lines are plotted to highlight the time interval when the asymptotic decay slopes were reached within 1σ. The precise values are shown on the left and in Table 3. Within 3σ, the asymptotic difference in the decay slopes agrees either with  +1/4, 0, −1/4 depending on the spectral and dynamical regime and the circumburst density profile. Furthermore, an envelope is drawn around expected values,  +1/4, 0, −1/4, with a width of 0.1 to guide the eye.