| Issue |
A&A
Volume 526, February 2011
|
|
|---|---|---|
| Article Number | A160 | |
| Number of page(s) | 13 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201015530 | |
| Published online | 14 January 2011 | |
Nucleosynthesis-relevant conditions in neutrino-driven supernova outflows
II. The reverse shock in two-dimensional simulations
1
Department of PhysicsUniversity of Basel,
Klingelbergstraße 82,
4056
Basel,
Switzerland
e-mail: a.arcones@unibas.ch
2
Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Straße 1, 85741
Garching,
Germany
Received: 4 August 2010
Accepted: 4 December 2010
After the initiation of the explosion of core-collapse supernovae, neutrinos emitted from the nascent neutron star drive a supersonic baryonic outflow. This neutrino-driven wind interacts with the more slowly moving, earlier supernova ejecta forming a wind termination shock (or reverse shock), which changes the local wind conditions and their evolution. Important nucleosynthesis processes (alpha-process, charged-particle reactions, r-process, and νp-process) occur or might occur in this environment. The nucleosynthesis depends on the long-time evolution of density, temperature, and expansion velocity. Here we present two-dimensional hydrodynamical simulations with an approximate description of neutrino-transport effects, which for the first time follow the post-bounce accretion, onset of the explosion, wind formation, and the wind expansion through the collision with the preceding supernova ejecta. Our results demonstrate that the anisotropic ejecta distribution has a great impact on the position of the reverse shock, the wind profile, and the long-time evolution. This suggests that hydrodynamic instabilities after core bounce and the consequential asymmetries may have important effects on the nucleosynthesis-relevant conditions in the neutrino-heated baryonic mass flow from proto-neutron stars.
Key words: supernovae: general / neutrinos / nuclear reactions, nucleosynthesis, abundances / hydrodynamics
© ESO, 2011
1. Introduction
Supernova outflows are an important astrophysical site for several nucleosynthesis processes. A variety of isotopes seem to be exclusively produced there and contribute to the metal enrichment of the interstellar medium from which old halo stars and later our Solar System have formed. Therefore, the fingerprints of supernova nucleosynthesis are searched for in the old halo stars and are attempted to be extracted from the Solar System abundances (e.g., Sneden et al. 2008). Studying the long-time evolution of core-collapse supernovae is a challenging problem because the explosion mechanism is not yet fully understood (Janka et al. 2007) and because of the high computational demands for simulating such a dynamical environment. CPU time requirements become even more extreme when multidimensional simulations combined with accurate neutrino transport are supposed to follow the supernova ejecta for many seconds. In this paper, we take advantage of a computationally efficient neutrino transport approximation (Scheck et al. 2006) to present the first results of two-dimensional simulations of core-collapse supernovae that track the outflow evolution for up to three seconds.
Simultaneously with the onset of the core-collapse supernova explosion, the proto-neutron star forms and cools by emitting neutrinos (Pons et al. 1999). The latter deposit energy in the layers near the proto-neutron star surface and thus drive a baryonic mass outflow. Because of ongoing neutrino-energy input, the entropy of this wind grows with distance from the neutron star, and the pressure gradient exceeds the gravitational force of the compact remnant. Therefore the neutrino-heated matter is accelerated quickly and even reaches supersonic velocities (Duncan et al. 1986). After first promising results of Woosley et al. (1994), neutrino-driven winds have been investigated intensely as a site where heavy elements could be produced via rapid neutron capture (see Arnould et al. 2007, for a review of r-process sites and physics). However, the conditions for successful r-processing found by Woosley et al. (1994) could neither be confirmed by other simulations at that time (Witti et al. 1994; Takahashi et al. 1994), nor by more recent ones (e.g., Arcones et al. 2007; Fischer et al. 2010). Roberts et al. (2010) explain the numerical problems that artificially produced suitable conditions for the production of heavy n-rich elements (Hoffman et al. 1997) in the simulations of Woosley et al. (1994). Because of the lack of the appropriate conditions in more recent neutrino-driven wind simulations, efforts continue to find possible missing physical ingredients. In Arcones et al. (2007), hereafter Paper I, we studied in detail the evolution of the neutrino-driven wind and its interaction with the earlier supernova ejecta for different stellar progenitors and neutrino luminosities. This interaction results in a wind termination shock (or reverse shock), which changes the evolution of nucleosynthesis-relevant conditions: density, temperature, expansion velocity (see Paper I). However, integrated nucleosynthesis based on those simulations (Arcones & Montes 2010) show that no heavy r-process elements can be produced.
First systematic studies of neutrino-driven winds were based on solving stationary wind equations (see e.g., Qian & Woosley 1996; Otsuki et al. 2000; Thompson et al. 2001). These steady-state models could not consistently account for the reverse shock, which is a hydrodynamical feature found in several simulations (e.g., Janka & Müller 1995; Janka & Müller 1996; Burrows et al. 1995; Buras et al. 2006b; Arcones et al. 2007; Fischer et al. 2010). The impact of the reverse shock on the r-process has been investigated by means of parametric, steady-state models of subsonic “breeze” solutions combined with an outer boundary at constant pressure (Sumiyoshi et al. 2000; Terasawa et al. 2002) or supersonic winds with fixed asymptotic temperature (e.g., Wanajo et al. 2002; Wanajo 2007), or two-stage outflow models where a faster wind phase is followed by a slower expansion phase (Kuroda et al. 2008; Panov & Janka 2009). There are also recent studies (Wanajo et al. 2010; Roberts et al. 2010) of the effect of the reverse shock on the νp-process (Fröhlich et al. 2006; Pruet et al. 2006; Wanajo 2006). A discussion of the implications of the reverse shock on the nucleosynthesis will be given in Sect. 4.
In Paper I, we have analyzed the behaviour of the reverse shock based on spherically symmetric hydrodynamic simulations. We found by analytic means that the position of the reverse shock depends on wind velocity and density, but also on the pressure of the supernova ejecta with which the wind collides. This pressure is strongly related to the explosion energy and progenitor structure. Therefore, the evolution of a mass element that has crossed the reverse shock is more complicated than a simple boundary at constant pressure or temperature. Here we show that multidimensional effects lead to an anisotropic mass and density distribution of the initial supernova ejecta, which has a big impact on the position of the reverse shock. The location of the latter becomes angle dependent. In our two-dimensional (2D) simulations, the neutrino-driven wind boundary is therefore strongly deformed to a non-spherical shape. As a consequence, the properties of the shocked wind medium are strongly dependent on the direction. The results presented here will help to improve the simple extrapolations for the ejecta evolution that are used in nucleosynthesis studies. They will allow to constrain the parameter space of possible wind histories.
The paper is organized as follows. Numerical method and computed models are described in Sect. 2. Our results of two simulations for a chosen stellar progenitor are presented in Sect. 3, where we also compare 2D to 1D results (Sect. 3.2) and analyze the impact of varying the progenitor (Sect. 3.3). A detailed discussion of the assumptions, approximations, and future improvements is included in Sect. 3.4. Finally, the possible nucleosynthesis implications of our results are addressed in Sect. 4 and we summarize our findings in Sect. 5.
2. Two-dimensional simulations
Observations indicate that core-collapse supernova are highly anisotropic. Therefore, multidimensional simulations are more realistic than spherically symmetric ones. However, they are computationally much more expensive. Using the same hydro code as in Paper I, we have performed hydrodynamical simulations of the neutrino-driven wind phase in two dimensions. We follow the evolution of the supernova ejecta for two seconds starting at a few milliseconds after bounce. As in Paper I, our simulations are done with a Newtonian hydrodynamics code, which includes general relativity corrections in the gravitational potential (Marek et al. 2006). It is combined with an efficient neutrino transport approximation (Scheck et al. 2006). In order to improve the performance of our simulations, the central high-density region of the neutron star is excised and its behaviour is prescribed by an inner boundary condition. This allows us also to vary the contraction and final radius of the neutrons star, which are determined by the uncertain high-density equation of state. Neutrino luminosities at the boundary are chosen such that the explosion energy is around 1.5 B. A detailed description of the numerical method, initial models, and boundary treatment can be found in Paper I, Scheck et al. (2006), and Kifonidis et al. (2003).
Here we discuss six different models: two (T10-l1-r1 and T10-l2-r1) are based on a 10.2 M⊙ star (data provided by A. Heger, priv. comm.), three (T15-l2-r1, T15-l1-r1, and T15-l1-r0) on a 15 M⊙ progenitor (s15s7b2, Woosley & Weaver 1995), and one (T25-l5-r4) on a 25 M⊙ progenitor (s25a28, Heger et al. 2001). All progenitors were followed through core collapse by A. Marek and are mapped to our 2D code typically 10 ms after bounce. In all models the subsequent contraction of the neutron star and its cooling behaviour are described as explained by Scheck et al. (2006) and defined by parameters Rf for the final boundary radius and t0 for the contraction timescale (see Table 1). The neutrino luminosity imposed at the lower grid boundary is 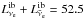 , 38.6, and 30.3 B/s for the models including “l1”, “l2”, and “l5” in the name, respectively. For the model names we follow the same convection as in Paper I. In Table 1, we summarize the values of the input parameters. The initial configuration of the progenitor model is spherically symmetric. Since the code conserves this symmetry, it is necessary to add nonradial perturbations to some quantity to trigger the growth of nonradial hydrodynamic instabilities in regions where the conditions allow for the development of such instabilities. Following Scheck et al. (2006) we apply seed perturbations of the velocity field in our simulations, for which we choose cell-to-cell random variations with a typical amplitude of 0.1%. The resolution of our two-dimensional simulations is around 900 radial grid points and 180 angular bins. The number of radial zones is increased depending on the requirements in the outer layers of the proto-neutron star, where the density gradient is very steep and neutrinos decouple from matter.
, 38.6, and 30.3 B/s for the models including “l1”, “l2”, and “l5” in the name, respectively. For the model names we follow the same convection as in Paper I. In Table 1, we summarize the values of the input parameters. The initial configuration of the progenitor model is spherically symmetric. Since the code conserves this symmetry, it is necessary to add nonradial perturbations to some quantity to trigger the growth of nonradial hydrodynamic instabilities in regions where the conditions allow for the development of such instabilities. Following Scheck et al. (2006) we apply seed perturbations of the velocity field in our simulations, for which we choose cell-to-cell random variations with a typical amplitude of 0.1%. The resolution of our two-dimensional simulations is around 900 radial grid points and 180 angular bins. The number of radial zones is increased depending on the requirements in the outer layers of the proto-neutron star, where the density gradient is very steep and neutrinos decouple from matter.
3. Results
In this section we describe the explosion and ejecta evolution for models T10-l1-r1 and T10-l2-r1, give an analytic explanation of the reverse shock behaviour in Sect. 3.1, and compare to spherically symmetric models (Sect. 3.2) and to the more massive progenitors (Sect. 3.3). The model parameters and overview of the results are presented in Table 1: the proto-neutron star contraction is characterized by its time scale t0 and the final boundary radius Rf. The boundary luminosity (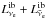 ) is constant during the first second and later decays as t−3/2. The end of the simulation is denoted by the time tend given in seconds after bounce. Mbar is the baryonic mass of the neutron star. The neutron star radius Rns is defined as the location where the density is 1011 g cm-3. ΔEtot is the total energy radiated in neutrinos of all flavors (measured in bethe [B] = 1051 erg), Lνe and
) is constant during the first second and later decays as t−3/2. The end of the simulation is denoted by the time tend given in seconds after bounce. Mbar is the baryonic mass of the neutron star. The neutron star radius Rns is defined as the location where the density is 1011 g cm-3. ΔEtot is the total energy radiated in neutrinos of all flavors (measured in bethe [B] = 1051 erg), Lνe and 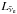 are the luminosities of electron neutrinos and antineutrinos at 500 km, ⟨ ϵνe ⟩ and
are the luminosities of electron neutrinos and antineutrinos at 500 km, ⟨ ϵνe ⟩ and 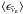 are the corresponding mean energies, Eexp is the explosion energy, texp is the post-bounce time when the explosion sets in (defined as the moment when the energy of expanding postshock matter exceeds 1049 erg).
are the corresponding mean energies, Eexp is the explosion energy, texp is the post-bounce time when the explosion sets in (defined as the moment when the energy of expanding postshock matter exceeds 1049 erg).
Parameters and results at one second after bounce (see text).
The initial distribution is spherically symmetric except for small random seed perturbations. As neutrinos deposit energy behind the shock, a negative entropy gradient establishes. The region between neutron star and shock thus becomes Ledoux-unstable and convective overturn appears. Neutrino-heated, high entropy matter streams upwards, while downflows transport low entropy matter from the shock to the neutron star. The down-flows and rising bubbles evolve quickly on time scales of the order of tens of milliseconds. The mass distribution below the shock becomes highly anisotropic and is dominated by low spherical harmonics modes. In this phase continuous neutrino heating aided by convection leads to an explosion. The evolution after the onset of the explosion is shown in Fig. 1 by the entropy distribution at different times after bounce.
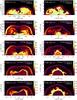 |
Fig. 1 Entropy distribution in models T10-l1-r1 (left column) and T10-l2-r1 (right column) for different times after bounce as indicated in every panel. The figures are plotted such that the polar axis is oriented horizontally with “south” (θ = π) on the left and “north” (θ = 0) on the right. The thin grey line marks the shock radius. In the panel for t = 1500 ms of model T10-l1-r1, the radial lines mark the angular directions at θ = 25 degrees (green line) and 100 degrees (red line), along which radial profiles are shown in Fig. 6. |
After the launch of the explosion a proto-neutron star forms at the center and cools and deleptonizes by emitting neutrinos. During this phase, neutrino-heated matter expands away from the proto-neutron star surface, in what is known as neutrino-driven wind and collides with the previous, more slowly moving ejecta. The interaction of the supersonic wind with the supernova ejecta results in a wind termination shock (reverse shock). At this discontinuity, kinetic energy is transformed into internal energy, which produces an increase of the entropy (see panels of Fig. 1 at t ≥ 500 ms) and the wind is decelerated. At late times the changes become slower, shock and ejecta expand quasi-self-similarly.
The neutrino-driven wind is spherically symmetric because it depends only on the neutrino emission of the proto-neutron star, which is isotropic. However, the distribution of the early ejecta is highly anisotropic. This produces a deformation of the reverse shock and of the shocked wind. The reverse shock radius and the properties of the shocked matter become angle dependent. An example of a two-dimensional feature is the downflow present at θ ≈ π/2 in model T10-l1-r1, which corresponds to the low entropy region visible in the panels for t = 500−2000 ms of Fig. 1. This feature leads to a big deformation of the reverse shock, in contrast to model T10-l2-r1, where the reverse shock stays almost spherically symmetric as no strong, long-lasting downflows have formed. These variations in the evolution and structure of the two models are not an immediate consequence of the different boundary luminosities. In Table 1 one can see that many parameters of both models are very similar. The anisotropy of the ejecta depends on chaotic effects that are triggered by the initial random perturbations (for more details see Scheck et al. 2006).
High-density, low-entropy regions in the ejecta, which are the remainders of former downflows, act like obstacles preventing faster wind expansion in those directions. In the analytic discussion of Paper I, we found that the reverse shock radius (Rrs) depends on the pressure of the more slowly moving early ejecta: 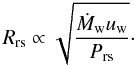 (1)The mass outflow rate (Ṁw) and the velocity (uw) of the wind are the same at all angles because the wind is spherically symmetric. Therefore, the variation of the reverse shock radius with angle is caused by the pressure variations of the anisotropic ejecta (Prs).
(1)The mass outflow rate (Ṁw) and the velocity (uw) of the wind are the same at all angles because the wind is spherically symmetric. Therefore, the variation of the reverse shock radius with angle is caused by the pressure variations of the anisotropic ejecta (Prs).
The aspherical matter distribution in the layer between reverse shock and forward shock leads also to an angle dependence of the entropy jump, which depends on the reverse-shock position and wind velocity (approximately as  , Arcones et al. 2007). Figure 2 shows the radius of the reverse shock (bottom panel) and the entropy, pressure, radial velocity, and temperature of the decelerated wind matter just after the reverse shock as functions of the azimuthal angle for model T10-l1-r1 at t = 1.5 s after bounce. Pressure and reverse shock radius are related as roughly given by Eq. (1). Moreover, the pressure determines also the angle between radial direction and reverse shock (Sect. 3.1). The temperature, which is one of the most relevant quantities for nucleosynthesis, depends mainly on the position of the reverse shock. When the reverse shock is at a smaller radius the shocked matter reaches higher temperatures. The link between these quantities and the geometrical structure of the reverse shock can be explained by analytic means as we show in the next section.
, Arcones et al. 2007). Figure 2 shows the radius of the reverse shock (bottom panel) and the entropy, pressure, radial velocity, and temperature of the decelerated wind matter just after the reverse shock as functions of the azimuthal angle for model T10-l1-r1 at t = 1.5 s after bounce. Pressure and reverse shock radius are related as roughly given by Eq. (1). Moreover, the pressure determines also the angle between radial direction and reverse shock (Sect. 3.1). The temperature, which is one of the most relevant quantities for nucleosynthesis, depends mainly on the position of the reverse shock. When the reverse shock is at a smaller radius the shocked matter reaches higher temperatures. The link between these quantities and the geometrical structure of the reverse shock can be explained by analytic means as we show in the next section.
 |
Fig. 2 Latitudinal variation of the reverse shock radius (bottom) and of the entropy, pressure, radial velocity, and temperature of the wind matter just after passing the reverse shock in model T10-l1-r1 at t = 1.5 s after bounce. |
3.1. Analytic discussion
 |
Fig. 3 Schematic representation of the velocities in a fluid going through an oblique shock (red line). Only the velocity component perpendicular to the shock, u⊥ , is changed when a mass element crosses the shock; the tangential component, u∥ , is conserved. Therefore, the direction of the flow is changed at the shock. |
We use the Rankine-Hugoniot conditions (see Paper I for further discussion) to understand the behaviour of the shocked matter and its angular dependence. The neutrino-driven wind expands in the radial direction with velocity uw, hits the slow-moving, anisotropic ejecta, and a deformed reverse shock results. As shown schematically in Fig. 3, there is an angle φ between reverse shock and radial direction. For spherical explosions this angle is always π/2, since the reverse shock can only be perpendicular to the radius vector. In an oblique shock the velocity can be decomposed into two components: tangential (u∥
) and perpendicular (u⊥
) to the shock. The tangential component of the velocity is continuous through an oblique shock (Landau & Lifshitz 1959). Following the notation introduced in Fig. 3, this implies that: 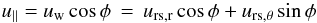 (2)with
(2)with  being the radial and lateral components of the velocity of the shocked matter (urs), respectively.
being the radial and lateral components of the velocity of the shocked matter (urs), respectively.
The perpendicular component of the velocity, u⊥
, is changed according to the Rankine-Hugoniot conditions. The mass conservation condition, including the angle dependence, is: 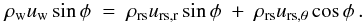 (5)The momentum continuity condition for an oblique shock is:
(5)The momentum continuity condition for an oblique shock is: 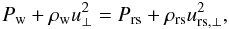 (6)where only the perpendicular components of the velocities enter. We can thus write a relation between the pressure and the angle φ:
(6)where only the perpendicular components of the velocities enter. We can thus write a relation between the pressure and the angle φ: 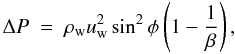 (7)where ΔP = Prs − Pw is the pressure jump at the reverse shock (note that usually Pw ≪ Prs), uw is the radial wind velocity (Fig. 3), and β is:
(7)where ΔP = Prs − Pw is the pressure jump at the reverse shock (note that usually Pw ≪ Prs), uw is the radial wind velocity (Fig. 3), and β is: 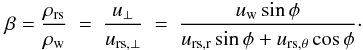 (8)The variation of the pressure jump (and thus of the entropy and temperature increase by the reverse shock) with angle φ can be deduced from Eq. (7). Since β > 1 usually, this equation implies that when φ goes to π/2, i.e., the reverse shock is perpendicular to wind velocity, ΔP and the entropy jump are larger (see middle panel in Fig. 4). As there is (roughly) a pressure balance between Prs and the pressure of the slow-moving early ejecta, which is higher in the downflows, φ tends to be about π/2 in regions where downflows are present. In Fig. 4 the upper panel shows that the density reaches highest values where the downflow is located (θ ≈ 100 degrees). Consistently, the pressure in this region is also large as shown in the middle panel. This leads to straight sections in the reverse shock shape and to the occurrence of kinks between locations of downflows.
(8)The variation of the pressure jump (and thus of the entropy and temperature increase by the reverse shock) with angle φ can be deduced from Eq. (7). Since β > 1 usually, this equation implies that when φ goes to π/2, i.e., the reverse shock is perpendicular to wind velocity, ΔP and the entropy jump are larger (see middle panel in Fig. 4). As there is (roughly) a pressure balance between Prs and the pressure of the slow-moving early ejecta, which is higher in the downflows, φ tends to be about π/2 in regions where downflows are present. In Fig. 4 the upper panel shows that the density reaches highest values where the downflow is located (θ ≈ 100 degrees). Consistently, the pressure in this region is also large as shown in the middle panel. This leads to straight sections in the reverse shock shape and to the occurrence of kinks between locations of downflows.
 |
Fig. 4 Distribution of density, pressure, and absolute value of the velocity in the wind and shocked matter for model T10-l1-r1 at t = 1.5 s after bounce. In the middle panel the radial velocity field is indicated by arrows. |
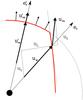 |
Fig. 5 Schematic representation of the velocities in a fluid going through the reverse shock (red line) when a kink leads to the collimation of the outflowing matter. |
The reverse shock in model T10-l1-r1 thus exhibits several kinks (Fig. 4) due to the anisotropic pressure distribution of the ejecta. Figure 5 shows, in a simplified way, the effects of these kinks. An oblique reverse shock is less effective in decelerating the flow (Eq. (8)) because the tangential component of the velocity is conserved through the shock. This leads to higher velocities outside the non-spherical parts of the reverse shock (urs in Fig. 5) compared to spherical regions (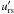 in Fig. 5). This can be seen in the velocity field marked by arrows in the middle panel of Fig. 4. The velocity of the ejecta is not directed radially after the wind has passed an oblique shock. This produces collimated high-velocity outflows starting at the kinks (Fig. 4, bottom panel and Fig. 1). Moreover, the kinks of the reverse shock are associated with minimum values of the pressure and entropy for the shocked material as visible in Fig. 2.
in Fig. 5). This can be seen in the velocity field marked by arrows in the middle panel of Fig. 4. The velocity of the ejecta is not directed radially after the wind has passed an oblique shock. This produces collimated high-velocity outflows starting at the kinks (Fig. 4, bottom panel and Fig. 1). Moreover, the kinks of the reverse shock are associated with minimum values of the pressure and entropy for the shocked material as visible in Fig. 2.
3.2. Two-dimensional versus one-dimensional simulations
Convection enhances neutrino heating, leading to earlier and more energetic explosions in 2D than in 1D, for the same inner-boundary parameters. Earlier explosions imply that the neutron star accretes matter during less time, thus its mass is slightly smaller in 2D (see Table 1). These differences alter the wind and reverse shock properties, making it difficult to contrast exactly one- and two-dimensional simulations. In this section we compare the one-dimensional model M10-l1-r1 (see Paper I) to the two-dimensional model with the same inner boundary parameters: T10-l1-r1. First, we examine the differences between the radial profiles of both models at a given time and later the evolution of relevant quantities.
 |
Fig. 6 Profiles of radial velocity, pressure, density, temperature, and entropy as functions of radius at time 1.5 s after bounce. The one-dimensional model M10-l1-r1 (black lines) is compared to profiles of the two-dimensional model T10-l1-r1 at angles θ = 25 degrees (green lines) and θ = 100 degrees (red lines). |
Figure 6 shows the radial profiles of different quantities at 1.5 s after bounce. The one-dimensional model M10-l1-r1 is displayed by black lines. For the two-dimensional model, T10-l1-r1, the radial profiles differ at all azimuthal angles. Therefore, we chose two angles (see radial lines in panel for t = 1500 ms of Fig. 1): θ = 25 degrees (green line) and θ = 100 degrees (red line), where Rrs adopts extreme values. As in Paper I, the radial profiles show an increase of the entropy in the region where neutrinos deposit energy (r ≲ 20 km) and a constant entropy value in the wind. Matter close to the neutron star absorbs neutrinos and moves outwards. The fast drop of the density and pressure allows the expansion to become supersonic. The wind velocity increases first approximately as u ∝ r and then approaches an asymptotic value (uw). The interaction of the fast wind with the slow-moving earlier ejecta results in a sudden drop of the velocity and a jump of the pressure, density, temperature, and entropy to higher values at the reverse shock. While the wind is still very similar in the one- and two-dimensional simulations, there are significant differences in the conditions of the slow-moving ejecta and therefore in the reverse shock position. The variations in the wind are just a consequence of different neutron star properties due to the evolution towards explosion, which is not the same in one and two dimensions, as explained before. However, the two profiles of model T10-l1-r1 are identical in the wind phase indicating that this region is spherically symmetric. This is expected because the neutrino emission is isotropic and the neutron star stays spherical without rotation. The differences in the profiles appear at the position of the reverse shock, which in 2D depends on the angle and is also different from the 1D case. Notice that for θ = 100 degrees the velocity of the slow-moving ejecta is very small because of the presence of relics of a strong downflow.
 |
Fig. 7 Evolution of reverse shock radius, and of the entropy, pressure, density, and temperature of the shocked neutrino-wind matter for models M10-l1-r1 (black lines) and T10-l1-r1 at θ = 25 degrees (green lines) and θ = 100 degrees (red lines). |
Since the main differences between 1D and 2D originate from the reverse shock radius and are linked to the properties of the supernova ejecta, we show in Fig. 7 the evolution of the quantities of matter that has passed the reverse shock. The evolution in 2D is presented for fixed azimuthal angles θ = 25 degrees (green lines) and 100 degrees (red lines), corresponding to the lines of same colors in Fig. 1. In 2D the reverse shock radius changes significantly between different angles with corresponding variations of the temperature. This has an impact on nucleosynthesis as we will discuss later in Sect. 4. The behaviour of the reverse shock radius follows Eq. (1). The entropy in the two-dimensional simulation is always lower, even when the reverse shock radius is larger than in the one-dimensional case. This is explained by the fact that the reverse shock for the green ray is oblique to the radial direction and the entropy jump is thus reduced (see Sect. 3.1). Moreover, in 2D the neutron-star mass is slightly smaller, which leads to lower entropies in the wind itself (Qian & Woosley 1996).
Note that the wind phase can be studied just by one-dimensional simulations because (without rotation) it stays spherically symmetric. Even simple steady-state wind models Otsuki et al. (2000); Thompson et al. (2001) are sufficient to determine the wind properties, e.g. for discussing the nucleosynthesis in the wind. However, the interaction of the wind with the supernova ejecta is a hydrodynamical problem that requires supernova explosion simulations. Moreover, we have shown here that one-dimensional models are not enough to account for all the possibilities of the long-time evolution of the ejecta.
3.3. Progenitor dependence
The reverse shock depends on the pressure of the more slowly moving earlier ejecta, which is different for different progenitor stars, as shown in Paper I. For similar explosion energies, more massive progenitors have slower ejecta and therefore the ejecta shell possesses a higher pressure so that the reverse shock stays at a smaller radius. We have seen in the previous section that an anisotropic distribution of the pressure in 2D has a big impact on the reverse shock position. It is thus interesting to study the combined effect of the two ingredients: progenitor structure and anisotropic ejecta.
In Fig. 8 the entropy distributions are shown for the rest of the models in Table 1, representing the explosions of 15 M⊙ and 25 M⊙ progenitors. Note that the time is different in every panel because the panels correspond to the moments tend when our simulations were stopped. We can compare models with the same parameters for the proto-neutron star evolution, but different progenitors, e.g., T10-l1-r1 and T15-l1-r1. The evolution of the ejecta in these two models is considerably different, although the boundary conditions are the same. This is even more visible in the case of models T10-l2-r1 and T15-l2-r1. The wind termination shock is almost spherically symmetric in the 10 M⊙ star, while it is highly asymmetric due to the presence of long-lasting downflows in the 15 M⊙ progenitor. The third model for the 15 M⊙ case (Fig. 8, upper panel) also develops a relatively spherical reverse shock. Although there is no unambiguous relation between the evolution of the ejecta and the shape of the reverse shock on the one hand and the boundary conditions or the progenitor structure on the other, more massive progenitor stars like T25-l5-r4 favor long-lasting and more slowly expanding downdrafts because of their denser structure and higher mass infall rates. The same trend can be observed in the cases of lower boundary luminosities (e.g. in T15-l2-r1) and less energetic explosions. For the explosion models of the 10 M⊙ star shown in Fig. 1, the expansion is relatively fast because of the more dilute silicon and oxygen shells, and therefore all downflows are blown away during the first half a second, even when lower luminosities are assumed in the simulations.
However, the ejecta distribution does not only depend on the progenitor and on variations of the boundary conditions that influence the strength of the explosion. Initial random perturbations must be imposed on the progenitor (or post-bounce) model to trigger the growth of instabilities and anisotropies. These develop in a stochastic and chaotic way and thus can lead to significant variations of the ejecta morphology, i.e., of the number and position of downflows and the direction and size of high-entropy bubbles, all of which have an influence on the deformation of the forward and reverse shocks and thus on associated variations of the nucleosynthesis-relevant conditions in the early supernova ejecta and in the neutrino wind.
In spite of that, for roughly similar explosion energy the progenitor structure has a systematic influence –at least in a constrained sense– on the evolution of the supernova shock and of the wind-termination shock: as seen from the comparison of model T10-l1-r1 (Fig. 1, left) with models T15-l1-r0, T15-l1-r1, and T15-l2-r1 (Fig. 8), all of which possess similar explosion energy, both shocks expand significantly more slowly in the case of the more massive progenitor. This trend was already obtained for 1D models in Paper I and is independent of the explosion asymmetries that have developed as a consequence of the (stochastic and chaotic) growth of nonradial instabilities in the shell enclosed by the forward shock and the reverse shock. Such a systematic dependence of the ejecta evolution on the progenitor structure is therefore independent of the dimension and for this reason also of the particular initial seed perturbation by which the ejecta asymmetry was initiated to grow in our 2D models. The reason for this progenitor-dependent variation is the denser structure of the shells around the iron core in more massive progenitor stars as discussed in the second paragraph of this section and in more detail in Paper I.
The multi-dimensional situation, however, allows for an even more extreme effect that is not possible in the 1D case: in progenitors significantly more massive than our 10 M⊙ model (or, alternatively, in the case of very weak explosions), long-lasting accretion by the neutron star can take place and the explosion can become extremely asymmetric such that the neutrino-driven outflow can be confined to narrow angular wedges (see models T15-l2-r1 and T25-l5-r4 in Fig. 8). While neutron-star accretion is still going on, the outflow is then prevented to become supersonic in some directions so that a termination shock can be absent at these angles. It is therefore clear that basic trends defined by progenitor properties (like those mentioned above) are superimposed in the multi-dimensional situation by potentially very large nonradial explosion asymmetries, which cannot be predicted merely on grounds of the progenitor structure and the value of the explosion energy, but can have a high relevance for the nucleosynthetic output of the supernova.
 |
Fig. 8 Entropy distribution for models T15-l1-r0, T15-l1-r1, and T15-l2-r1 of a 15 M⊙ progenitor and model T25-l5-r4 of a 25 M⊙ star at the end of the simulations. |
3.4. Discussion of assumptions, approximations, and future improvements
In the present work our goal was to identify differences between the nucleosynthesis-relevant conditions of the neutrino-driven wind in two dimensions compared to spherical symmetry. We, however, did not intend to cover the topic of multi-dimensional effects in the winds in its full breadth, but concentrated in particular on the interaction of the wind with the more slowly moving, dense ejecta shell behind the supernova shock. This interaction has obviously stronger and more important consequences than a variety of other nonradial perturbations that can make the wind outflow anisotropic at typically much smaller level.
The wind termination (or reverse) shock, which separates the supersonic wind region from the subsonic ejecta shell, exhibits strong non-spherical deformations because of the large-scale inhomogeneities imprinted on the structure of the ejecta by the nonradial hydrodynamic instabilities at the beginning of the explosion. When the reverse shock is located at a sufficiently small radius, it alters the wind conditions at such a high temperature that the nucleosynthesis in the outflow can be strongly affected. Different from the one-dimensional case, where the reverse-shock radius is simply a function of the wind properties (mass-loss rate and expansion velocity) and explosion properties (energy and shock radius) as discussed in Paper I, the location of the reverse shock in the multi-dimensional case also depends on the inhomogeneities that are present in the ejecta shell. Dense relics of long-lasting accretion funnels, for example, propagate more slowly and prevent the reverse shock from rapid expansion.
In order to gain insight into such effects, we followed two-dimensional models for sufficiently long evolution periods with the emphasis on maintaining high spatial resolution from the steeping density gradient at the proto-neutron star surface through the neutrino-wind region, reverse shock, and inhomogeneous ejecta shell, out to the expanding supernova shock. We employed a number of assumptions and approximations which we will critically discuss in the following.
We emphasize that in the present work we want to highlight basic and general aspects of anisotropic wind-ejecta interaction. However, we neither intend to make predictions for particular progenitors nor do we want to give a statistical overview of possible outcomes. Both are not possible in view of our incomplete knowledge of the exact explosion mechanism and the use of two-dimensional models.
3.4.1. Random initial seed perturbations
In order to initiate the growth of nonradial flows in hydrodynamically unstable regions, we perturbed our spherical initial models with random seeds (Sect. 2). Random perturbations are a simple, flexible, and partly tested (see below) procedure to introduce small-amplitude deviations from spherical symmetry in any available progenitor or post-bounce model. Of course, it would be interesting to start with a more realistic assumption based on predictions from self-consistent stellar evolution modeling. However, multi-dimensional simulations were performed only for special evolution stages of selected progenitor stars (e.g., Young et al. 2005; Meakin & Arnett 2006, 2007,and references therein). Therefore, there are no multi-dimensional progenitor data at the onset of the gravitational instability for a range of stellar masses and the fluctuations of quantities in the core at this stage are not well constrained.
Moreover, tests suggest that the exact properties of the initial perturbation pattern are not overly important except in the improbable and special case that a low-mode, global asymmetry is present in the progenitor core. The influence of different random seeds – different amplitudes, different random realizations, and also initial perturbations of different quantities – has been explored (at least to some extent) by Buras et al. (2006a); Scheck et al. (2006). One might suspect that a high-mode, low-amplitude pattern of the initial perturbations may have an influence on the fastest growing mode(s) in the hydrodynamically unstable regions after core bounce as well as on the linear growth timescales of these most unstable mode(s). However, it seems unlikely that any memory of such a high-mode seed pattern is retained once the hydrodynamical instabilities have reached the fully nonlinear regime because the involved growth is characterized by highly chaotic and stochastic interactions of structures on different scales.
Buras et al. (2006a) tested the amplification of random perturbations on the level of 1–2% imposed on the density structure of the progenitor core before collapse. They found that these initial seeds increase by factors of a few in the supersonically infalling layers during the collapse (and are damped in the subsonically falling regions) as predicted by Lai & Goldreich (2000). However, the changes of the model evolution after core bounce turned out to be insignificant compared to the standard case in which they imposed perturbations on the level of 0.1% just after core bounce and thus only shortly before the hydrodynamically unstable conditions develop in the supernova core (see Appendix E in Buras et al. 2006a).
Scheck et al. (2006) investigated the effects of different random seeds imposed on models after core bounce, perturbing different quantities – radial velocity or density – with an amplitude of 0.1 percent. They found that different random realizations (keeping the progenitor star and boundary conditions the same) lead to differences of the convective patterns and thus of the detailed structures of the anisotropies in the dense shell behind the supernova shock. But while the number of long-lasting downflows, their locations, the shock deformation and the angular distribution and volume of buoyant high-entropy bubbles varied, little sensitivity to the initial seeds was seen for the global properties of the supernova explosion, i.e., the explosion timescale and the average shock radius and explosion energy as functions of time. Of course, the transition from a long-lasting, asymmetric accretion phase to the spherical neutrino wind will depend on the size and persistance of the asymmetric accretion funnels that are formed when vigorous, non-radial instabilities stir the ejecta during the early explosion stage.
For the present paper we picked a set of models that provides a kind of representative overview of different possible morphologies (see Figs. 1 and 8) that were also seen in the larger set of calculations by Scheck et al. (2006).
3.4.2. Anisotropic neutrino emission and flavor conversions
We describe the neutrino emission from the dense core of the proto-neutron star by choosing time-dependent (spherically symmetric) luminosities for neutrinos and antineutrinos of all flavors at the inner grid boundary, which is placed significantly below the neutrinosphere.
Naturally, the neutrino flux evolution imposed there has a strong influence on all stages of the evolution of neutrino-driven supernovae: on the shock revival and explosion, on the potentially long-lasting post-explosion accretion, and in particular also on the power and duration of the neutrino-driven wind. The dependence of the dynamical and thermodynamical properties of the neutrino wind (mass-loss rate, entropy, and expansion timescale) on the luminosities and mean energies of the radiated neutrinos was in detail discussed in previous works, in particular by Qian & Woosley (1996) and by Thompson et al. (2001), while the dependence of the wind termination shock on the neutrino-wind properties was the subject of Paper I. Making assumptions about the neutrino fluxes at the inner grid boundary implies that we can only explore possible dynamical scenarios in a parameterized way, but we are unable to determine what exactly happens in a particular progenitor star.
Similarly, the neutrino-flavor evolution necessarily plays a crucial role for setting the neutron-to-proton ratio in the wind. Thus it decides about the nucleosynthesis processes that can take place in this environment. While we think that it is not possible to make reliable predictions of the electron fraction Ye in the wind on the basis of our transport approximations, we are confident that the set of models presented here can still shed light on fundamental aspects of anisotropies that can occur during the dynamical evolution driven by the neutrino heating between the neutron-star surface and the supernova shock.
Asymmetric neutrino emission, e.g. associated with non-spherical accretion or convective activity inside the nascent neutron star, might also play a role for creating anisotropies in the wind ejecta. The most extreme case of asymmetric accretion are long-lasting downflows on one side of the proto-neutron star, while mass loss in the wind is going on in other directions. Such a situation can – at least temporarily – occur in our simulations. Because of the violent impact of the accretion flows on the neutron star surface, associated with rapid motions of the tips of the accretion funnels, strong sonic waves are launched and create non-radial perturbations in the neutrino-heated outflows (Scheck et al. 2006).
These hydrodynamical perturbations of the winds are usually much bigger than any asymmetries caused by anisotropic neutrino emission from the accretion downflows. This is so because the supersonically infalling matter in the downflows has only little time to experience neutrino losses: It reaches sufficiently high temperatures and densities only shortly before it impacts on the neutron-star surface. After deceleration, it quickly spreads sideways around the surface of the neutron star and settles into the hot accretion layer surrounding the accretor. While the anisotropic emission from the accretion flows contributes to the neutrino luminosity only on the level of some percent, most of this anisotropic emission occurs in regions where the optical depth for neutrinos is much lower than unity. The reabsorption of these neutrinos is therefore very improbable and is unable to cause any significant asymmetries in the baryonic wind outflow (typically such asymmetries remain well below one percent). Instead, the wind is driven by neutrino interactions in regions much closer to the neutrinosphere, composed of accreted matter that has experienced efficient mixing upon being dispersed in a turbulent vortex layer. In addition, the strong surface gravity of the neutron star prevents asymmetries in the accretion layer so that this layer acts as the base of a nearly isotropic wind.
A convective region below the neutrinosphere, which is only partly included in our computational volume (its inner part is omitted with the excised neutron-star core), also has little impact on wind anisotropies. Hydrodynamic simulations of the proto-neutron star formation and of the accretion during the first hundreds of milliseconds after bounce (Buras et al. 2006b; Dessart et al. 2006) show that the convective shell is placed at a density well above that of the neutrinosphere. The convective layer is found to be separated from the neutrinospheric region by a stable shell. The proto-neutron star convection in the post-explosion phase (later than one second after bounce) has not been explored by hydrodynamic simulations yet. We suspect – and conclude from the structure of our present models near the inner grid boundary – that this separation between convective layer and neutrinosphere is maintained also during the later stages. Our suspicion is justified by the decreasing optical depth in the vicinity of the neutrinosphere, which allows neutrino transport to become more efficient than energy transport by convection. The convectively stable shell around the convective core of the proto-neutron star precludes convective asymmetries from having an immediate and undamped influence on the driving layer of the wind outflow. Perturbations of the wind induced by convection thus remain small.
Buras et al. (2006b); Dessart et al. (2006) showed that proto-neutron star convection speeds up the lepton number loss (by temporarily decreasing the electron-antineutrino luminosity) and increases the energy transport by higher muon and tau neutrino luminosities. At the same time it leads to reduced mean energies of the radiated neutrinos. While such effects are relevant for detailed modeling of the Kelvin-Helmholtz cooling of the nascent neutron star, they are subsumed by our treatment of the inner grid boundary. We therefore do not expect them to introduce any qualitatively new features into our models beyond what we can and have explored by variations of the boundary condition.
Neutrino-flavor conversions near and above the proto-neutron star surface, in particular due to neutrino-neutrino forward scattering (see Duan et al. 2010, for a recent review) are disregarded in the present work, but may change the luminosity and spectral evolution of the different kinds of neutrinos radiated by the forming neutron star. During the post-bounce accretion phase and the onset of the explosion, when the luminosities and spectra of different neutrino flavors show pronounced differences, such collective neutrino oscillations might have some relevance for the dynamics and for setting the neutron-to-proton ratio and thus the nucleosynthesis conditions in the early supernova ejecta. However, it is more uncertain whether any important effects remain during the Kelvin-Helmholtz cooling of the proto-neutron star after the explosion has been launched. Hydrodynamical calculations of this phase in spherical symmetry, using sophisticated neutrino transport methods (but also ignoring the effects of neutrino flavor oscillations; Hüdepohl et al. 2010; Fischer et al. 2010) predict that after the end of the post-bounce accretion the luminosities and spectra for all kinds of neutrinos become very similar. Given that, flavor conversions will certainly have little influence on the neutrino-energy deposition and therefore on the dynamics of the neutrino-driven wind. Moreover, also their effect on the electron fraction in the neutrino-heated outflow is probably relatively minor. Nevertheless, subtle changes of the neutrino flux spectra due to energy- and direction-dependent oscillation effects cannot be excluded. Since the neutron-to-proton ratio and the element formation in the wind outflow are highly sensitive to details of the electron neutrino and antineutrino luminosities and spectra, a closer investigation of this aspect may be desirable, but is very ambitious in the multi-dimensional context.
3.4.3. General relativity
The approximation of general relativistic gravity used in our simulations has been tested in great detail for its accuracy in different phases of stellar core collapse. Corresponding results were published in several preceding papers. Marek et al. (2006) compared the neutron star structure, stability properties, and oscillation behavior obtained with the effective relativistic potential and fully relativistic calculations of nonrotating and rotating collapsing stellar iron cores. Liebendörfer et al. (2005) compared the dynamics and neutrino emission during the collapse phase, core bounce, and early post-bounce evolution in 1D (see also Marek et al. 2006). Arcones et al. (2007) (Paper I) investigated the structure of the neutrino-driven wind in comparison to steady-state relativistic wind solutions. Hüdepohl et al. (2010) and in particular Müller et al. (2010) explored the Kelvin-Helmholtz cooling evolution of proto-neutron stars and their neutrino emission. In these studies fully relativistic models were contrasted with simulations in which approximated relativistic gravity (plus gravitational redshift in the neutrino transport where applied) were combined with otherwise Newtonian hydrodynamics.
The core-collapse phase, core bounce, shock break-out, and early accretion were found to be in excellent agreement, the neutron-star structure, its binding energy, neutrino emission properties and total energy loss were found to be reproduced in all quantities to better than 10% and in most cases and phases even to percent accuracy, and the neutrino-driven wind profiles turned out to be nicely compatible with steady-state relativistic solutions. Although there can be differences in smaller details, the main effects of general relativity seem to be captured well by our approximative treatment. The reasons for this result are the facts that (1) the effective relativistic potential was constructed to explicitly include the relativistic modifications of the Tolman-Oppenheimer-Volkoff equations compared to Newtonian hydrostatic equilibrium (see Marek et al. 2006); and (2) the fluid velocities in the supernova core hardly ever exceed 10–20% of the speed of light, in which case Newtonian fluid dynamics is still a good approximation.
3.4.4. Neutron star motion
A kicked neutron star will move away from the grid center but will remain the center of the neutrino-driven wind. The neutron star motion may thus lead to a distortion of the wind-ejecta interaction and may change the location of the reverse shock in the wind and thus its influence on the wind properties. Such influence on the detailed evolution of a particular model was indeed seen by Scheck et al. (2006), who performed runs (for fixed progenitor, boundary conditions, and perturbation seeds) without and with applying a Galilei transformation on the flow around a neutron star at the grid center by giving the surrounding fluid a coherent motion with the negative sign of the neutron star kick velocity. This procedure was assumed to capture the main effects of the neutron star movement.
Although such effects can be relevant for determining the detailed evolution and ejecta properties of a particular model star (which was not the goal of this work) they are unlikely to change the basic and general conclusions that we have drawn from our simulations. Since the neutron-star velocity vns is typically small compared to the sound speed and the terminal wind velocity, vns ≪ cs and vns ≪ uw(r ≫ Rns), it is hard to imagine that allowing the neutron star to move (instead of anchoring it at the grid center as in our models) will affect the overall picture that we have obtained for the anisotropic wind-ejecta interaction.
3.4.5. Three-dimensional modeling
Performing simulations in two dimensions imposes the artifical constraint that all structures are axially symmetric. Of course, this naturally raises the question what differences one might expect in three dimensions.
Ignoring the important question whether 2D/3D differences have any influence on the success of the neutrino-heating mechanism for supernova explosions (a very first statement in this context was recently published by Nordhaus et al. 2010), and relying on the viability of this mechanism (which is a fundamental assumption in our study), basic features of the 2D asymmetries observed in our calculations seem to be confirmed by recent 3D simulations: Wongwathanarat et al. (2010) followed the evolution of a small set of 3D models over a similarly long post-bounce period (but with considerably less spatial resolution than used in our 2D calculations). The 3D slice of Fig. 3, right panel, in the latter publication exhibits the same overall behavior and structural features for the neutrino-driven wind phase in 2D and 3D models, namely an essentially spherical wind, an asymmetric wind-termination shock, and an inhomogeneous and strongly anisotropic ejecta shell behind the forward shock. Also in 3D the reverse shock is highly deformed and its effect on the wind properties and nucleosynthesis conditions depends on the outflow direction. We are therefore confident that our main findings for the wind-ejecta interaction are valid not only in the considered 2D situation.
Of course, the present parameterized explosion models, which do not yield any information about the explosion properties (energy, timescale) of a progenitor star, cannot be conclusive on the consequences of these asymmetries for the explosive nucleosynthesis of individual stars, nor does our present knowledge of the explosion mechanism allow for any statements in a statistical sense.
Rotation of the nascent neutron star is an additional degree of freedom, which we ignored in the models of this paper. It will cause a global pole-equator asymmetry of the wind and of the wind-ejecta interaction with potentially interesting implications. This should be studied in future work by systematic variations of the proto-neutron star spin.
4. Nucleosynthesis implications
We have shown the impact of multidimensional effects on the dynamical evolution of the neutrino-driven wind, reverse shock and supernova ejecta. In this section, we want to briefly address the possible implications of our results for the nucleosynthesis processes occurring in supernova outflows: charged-particle reactions, alpha process (Woosley & Hoffman 1992; Witti et al. 1994), νp-process (Fröhlich et al. 2006; Pruet et al. 2006; Wanajo 2006), and occasionally r-process (Arnould et al. 2007, for a review).
Since the works of Cameron (1957) and Burbidge et al. (1957), core-collapse supernova outflows have been the best studied candidate for the production of heavy elements. However, this environment is facing more and more problems to fulfill the requirements (high entropy, low electron fraction and fast expansion) for the production of heavy r-process elements (A > 90). The conditions found to be necessary for a robust and strong r-process (e.g., Hoffman et al. 1997) are not achieved by recent long-time supernova simulations (Paper I, Hüdepohl et al. 2010; Fischer et al. 2010). This is also the case for our 2D simulations, where the wind entropies are too low to get the high neutron-to-seed ratios necessary for the r-process.
Yet galactic chemical evolution models (see e.g., Ishimaru et al. 2004; Qian & Wasserburg 2008) suggest that at least a subset of core-collapse supernovae could be responsible of the origin of half of the heavy r-process elements. Therefore, one may speculate that the r-process could take place in neutrino-driven winds because of some still unknown aspect of physics that might cure the problems revealed by the present hydrodynamical models. In this case the reverse shock could have important consequences (Wanajo et al. 2002). Depending on the temperature at the reverse shock the r-process path is different. When the reverse-shock temperature is low (Trs ≲ 0.5 GK), neutron-capture and beta-decay timescales are similar (Blake & Schramm 1976) and shorter than (γ,n) timescales. This is also known as “cold r-process” (Wanajo 2007; Panov & Janka 2009). In contrast, when the reverse shock is at high temperatures, there is an (n,γ) − (γ,n) equilibrium as in the classical r-process (Kratz et al. 1993; Freiburghaus et al. 1999; Farouqi et al. 2010). The final abundances for these two types of evolution are very different, see e.g., Wanajo et al. (2002); Wanajo (2007); Kuroda et al. (2008); Panov & Janka (2009); Arcones & Martinez-Pinedo (2010). Also the impact of the nuclear physics input varies depending on how matter expands (Arcones & Martinez-Pinedo 2010).
In addition to the r-process, whose astrophysical site is still uncertain, there are other nucleosynthesis processes occurring in supernova outflows. The reverse shock can affect the production of p-nuclei that happens in neutrino-driven winds via charged-particle reactions (Woosley & Hoffman 1992) and the νp-process (Fröhlich et al. 2006; Pruet et al. 2006; Wanajo 2006). This is becoming more important, because the most recent and most sophisticated supernova simulations show that the ejecta are proton-rich for several seconds (Fischer et al. 2010) and even until completion of the proto-neutron star cooling and deleptonization (Hüdepohl et al. 2010). The impact of the reverse shock on these nucleosynthesis processes can show up in two ways. First, the temperature jump leads to an increase of the photo-dissociation rate. When the latter is too high, newly formed nuclei are destroyed. However, when the photo-dissociation rate is moderate, the temperature increase favors the captures of charged particles. The other important effect of the reverse shock is the strong reduction of the expansion velocity with the consequence that the temperature stays constant or decreases only slowly after a mass element has crossed the reverse shock. Depending on the exact value of the temperature, photo-dissociations or charged-particle reactions continue to take place. Moreover, when the expansion becomes slower, the matter stays exposed to high neutrino fluxes for a longer time. This increases the efficiency of the νp-process. However, one should notice that the processes described here are possible only when the reverse-shock radius is sufficiently small, e.g., during the first few seconds after the onset of the explosion, because otherwise the temperature at the reverse shock is already too low to play any role. Recently, Wanajo et al. (2010) suggested a possible significant impact of the reverse shock on the nucleosynthesis under these conditions, in contrast to the small effects reported by Roberts et al. (2010). Therefore, further nucleosynthesis studies should be done, taking into account the reverse-shock behaviour found in Paper I and in particular in the present work, where a huge variability due to multi-dimensional effects was obtained.
5. Conclusions
With a small set of two-dimensional simulations for three progenitor stars of different masses (Table 1) we have demonstrated that the reverse-shock radius and the conditions of the shocked neutrino-driven wind matter in supernova explosions become strongly angle dependent. As we found in Paper I by analytic means, the position of the reverse shock depends on the wind properties (mass outflow rate and velocity) as well as on the pressure of the more slowly moving supernova ejecta. Comparison of the radial profiles of 1D and 2D simulations shows that the neutrino-driven wind is spherically symmetric. This is caused by the isotropic neutrino emission from a neutron star that stays spherical in the absence of rotation. Multi-dimensional simulations including rotation could lead to differences in the wind (Metzger et al. 2007; Wanajo 2006) and thus significant changes in its interaction with the supernova ejecta. Although without rotation the wind develops identically in all directions, a strong angular variation of the reverse shock position can appear because of the anisotropic matter (and thus pressure) distribution in the more slowly moving, early supernova ejecta.
When the radial location of the reverse shock is constrained by the existence of dense downdrafts in the ejecta shell that follows the supernova shock, the angle between the reverse shock and the wind velocity, which goes in the radial direction, can be estimated. We have found an analytic expression that relates this angle to the jump of the pressure at the reverse shock. The presence of the downflow features in the supernova ejecta shell with local density and pressure maxima leads to angular variations of the radius of the reverse shock and thus a deformation of the wind-shell boundary with kinks appearing in the regions where the obliqueness of the shock abruptly changes. The Rankine-Hugoniot conditions imply that oblique shocks are less efficient in decelerating matter. This produces a collimation of the shocked flow in the vicinity of the kinks. Finally, we have proven that basic features of the progenitor dependence seen in Paper I are also present in our two-dimensional simulations, e.g., a slower expansion of the forward and reverse shocks in more massive stars. However, such general aspects are superimposed by an enormous amount of variability of explosions even of the same progenitor and similar explosion energy due to the chaotic growth of nonradial hydrodynamic instabilities from small initial seed perturbations.
In summary, we have found that in the multi-dimensional case the expansion of the wind matter varies with the angular direction because it is influenced by the anisotropic distribution of the earlier ejecta, which evolves chaotically from initial random perturbations. Therefore, we strongly recommend that future nucleosynthesis studies should test the effect of different extrapolations of the evolution of the shock-decelerated ejecta. Our results can be used as guidance for the overall variability that is possible and affects the nucleosynthesis-relevant conditions in multi-dimensional supernova environments.
Acknowledgments
We thank G. Martínez-Pinedo, F. Montes, I. Panov, F.-K. Thielemann, and S. Wanajo for stimulating discussions. We are grateful to S. Woosley and A. Heger for providing us with the progenitor models, to A. Marek for computing the collapse and prompt shock propagation phases with the Vertex-Prometheus neutrino-hydrodynamics code. A. Arcones is supported by the Swiss National Science Foundation. The work of H.-T. Janka and collaboration visits were supported by the Deutsche Forschungsgemeinschaft through the Transregional Collaborative Research Centers SFB/TR 27 “Neutrinos and Beyond” and SFB/TR 7 “Gravitational Wave Astronomy”, and the Cluster of Excellence EXC 153 “Origin and Structure of the Universe” (http://www.universe-cluster.de). The computations were performed on the NEC SX-5/3C and the IBM p690 “Regatta” system of the Rechenzentrum Garching, and on the IBM p690 cluster “Jump” of the John von Neumann Institute for Computing (NIC) in Jülich.
References
- Arcones, A., Janka, H.-T., & Scheck, L. 2007, A&A, 467, 1227 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arcones, A., & Martinez-Pinedo, G. 2010, Phys. Rev. C, submitted [arXiv:1008.3890] [Google Scholar]
- Arcones, A., & Montes, F. 2010, ApJ, submitted [arXiv:1007.1275] [Google Scholar]
- Arnould, M., Goriely, S., & Takahashi, K. 2007, Phys. Repts., 450, 97 [Google Scholar]
- Blake, J. B., & Schramm, D. N. 1976, ApJ, 209, 846 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buras, R., Janka, H.-T., Rampp, M., & Kifonidis, K. 2006a, A&A, 457, 281 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buras, R., Rampp, M., Janka, H.-T., & Kifonidis, K. 2006b, A&A, 447, 1049 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burbidge, E. M., Burbidge, G. R., Fowler, W. A., & Hoyle, F. 1957, Rev. Mod. Phys., 29, 547 [NASA ADS] [CrossRef] [Google Scholar]
- Burrows, A., Hayes, J., & Fryxell, B. A. 1995, ApJ, 450, 830 [NASA ADS] [CrossRef] [Google Scholar]
- Cameron, A. G. W. 1957, Stellar Evolution, Nuclear Astrophysics, and Nucleogenesis, Report CRL-41, Chalk River [Google Scholar]
- Dessart, L., Burrows, A., Livne, E., & Ott, C. D. 2006, ApJ, 645, 534 [NASA ADS] [CrossRef] [Google Scholar]
- Duan, H., Fuller, G. M., & Qian, Y. 2010, Ann. Rev. Nucl. Part. Sci., 60, 569 [Google Scholar]
- Duncan, R. C., Shapiro, S. L., & Wasserman, I. 1986, ApJ, 309, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Farouqi, K., Kratz, K., Pfeiffer, B., et al. 2010, ApJ, 712, 1359 [NASA ADS] [CrossRef] [Google Scholar]
- Fischer, T., Whitehouse, S. C., Mezzacappa, A., Thielemann, F., & Liebendörfer, M. 2010, A&A, 517, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Freiburghaus, C., Rembges, J.-F., Rauscher, T., et al. 1999, ApJ, 516, 381 [NASA ADS] [CrossRef] [Google Scholar]
- Fröhlich, C., Martínez-Pinedo, G., Liebendörfer, M., et al. 2006, Phys. Rev. Lett., 96, 142502 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Heger, A., Woosley, S. E., Martínez-Pinedo, G., & Langanke, K. 2001, ApJ, 560, 307 [Google Scholar]
- Hoffman, R. D., Woosley, S. E., & Qian, Y.-Z. 1997, ApJ, 482, 951 [NASA ADS] [CrossRef] [Google Scholar]
- Hüdepohl, L., Müller, B., Janka, H., Marek, A., & Raffelt, G. G. 2010, Phys. Rev. Lett., 104, 251101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ishimaru, Y., Wanajo, S., Aoki, W., & Ryan, S. G. 2004, ApJ, 600, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Janka, H.-T., & Müller, E. 1995, ApJ, 448, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Janka, H.-T., & Müller, E. 1996, A&A, 306, 167 [NASA ADS] [Google Scholar]
- Janka, H.-T., Langanke, K., Marek, A., Martínez-Pinedo, G., & Müller, B. 2007, Phys. Repts., 442, 38 [Google Scholar]
- Kifonidis, K., Plewa, T., Janka, H.-T., & Müller, E. 2003, A&A, 408, 621 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kratz, K., Bitouzet, J., Thielemann, F., Moeller, P., & Pfeiffer, B. 1993, ApJ, 403, 216 [Google Scholar]
- Kuroda, T., Wanajo, S., & Nomoto, K. 2008, ApJ, 672, 1068 [NASA ADS] [CrossRef] [Google Scholar]
- Lai, D., & Goldreich, P. 2000, ApJ, 535, 402 [NASA ADS] [CrossRef] [Google Scholar]
- Landau, L., & Lifshitz, E. 1959, Course of Theoretical Physics. Fluid mechanics, Vol. 6 (Pergamon) [Google Scholar]
- Liebendörfer, M., Rampp, M., Janka, H.-T., & Mezzacappa, A. 2005, ApJ, 620, 840 [NASA ADS] [CrossRef] [Google Scholar]
- Marek, A., Dimmelmeier, H., Janka, H.-T., Müller, E., & Buras, R. 2006, A&A, 445, 273 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meakin, C. A., & Arnett, D. 2006, ApJ, 637, L53 [CrossRef] [Google Scholar]
- Meakin, C. A., & Arnett, D. 2007, ApJ, 667, 448 [NASA ADS] [CrossRef] [Google Scholar]
- Metzger, B. D., Thompson, T. A., & Quataert, E. 2007, ApJ, 659, 561 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, B., Janka, H., & Dimmelmeier, H. 2010, ApJS, 189, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Nordhaus, J., Burrows, A., Almgren, A., & Bell, J. 2010, ApJ, 720, 694 [NASA ADS] [CrossRef] [Google Scholar]
- Otsuki, K., Tagoshi, H., Kajino, T., & Wanajo, S. 2000, ApJ, 533, 424 [NASA ADS] [CrossRef] [Google Scholar]
- Panov, I. V., & Janka, H.-T. 2009, A&A, 494, 829 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pons, J. A., Reddy, S., Prakash, M., Lattimer, J. M., & Miralles, J. A. 1999, ApJ, 513, 780 [NASA ADS] [CrossRef] [Google Scholar]
- Pruet, J., Hoffman, R. D., Woosley, S. E., Janka, H.-T., & Buras, R. 2006, ApJ, 644, 1028 [Google Scholar]
- Qian, Y., & Wasserburg, G. J. 2008, ApJ, 687, 272 [NASA ADS] [CrossRef] [Google Scholar]
- Qian, Y.-Z., & Woosley, S. E. 1996, ApJ, 471, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Roberts, L. F., Woosley, S. E., & Hoffman, R. D. 2010, ApJ, 722, 954 [NASA ADS] [CrossRef] [Google Scholar]
- Scheck, L., Kifonidis, K., Janka, H.-T., & Müller, E. 2006, A&A, 457, 963 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sneden, C., Cowan, J. J., & Gallino, R. 2008, ARA&A, 46, 241 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sumiyoshi, K., Suzuki, H., Otsuki, K., Terasawa, M., & Yamada, S. 2000, PASJ, 52, 601 [Google Scholar]
- Takahashi, K., Witti, J., & Janka, H.-T. 1994, A&A, 286, 857 [NASA ADS] [Google Scholar]
- Terasawa, M., Sumiyoshi, K., Yamada, S., Suzuki, H., & Kajino, T. 2002, ApJ, 578, L137 [NASA ADS] [CrossRef] [Google Scholar]
- Thompson, T. A., Burrows, A., & Meyer, B. S. 2001, ApJ, 562, 887 [NASA ADS] [CrossRef] [Google Scholar]
- Wanajo, S. 2006, ApJ, 647, 1323 [Google Scholar]
- Wanajo, S. 2006, ApJ, 650, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Wanajo, S. 2007, ApJ, 666, L77 [NASA ADS] [CrossRef] [Google Scholar]
- Wanajo, S., Itoh, N., Ishimaru, Y., Nozawa, S., & Beers, T. C. 2002, ApJ, 577, 853 [NASA ADS] [CrossRef] [Google Scholar]
- Wanajo, S., Janka, H., & Kubono, S. 2010, ApJ, accepted [arXiv:1004.4487] [Google Scholar]
- Witti, J., Janka, H.-T., & Takahashi, K. 1994, A&A, 286, 841 [NASA ADS] [Google Scholar]
- Wongwathanarat, A., Janka, H., & Mueller, E. 2010, ApJ, 725, L106 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., & Hoffman, R. D. 1992, ApJ, 395, 202 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., & Weaver, T. A. 1995, ApJS, 101, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., Wilson, J. R., Mathews, G. J., Hoffman, R. D., & Meyer, B. S. 1994, ApJ, 433, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Young, P. A., Meakin, C., Arnett, D., & Fryer, C. L. 2005, ApJ, 629, L101 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Entropy distribution in models T10-l1-r1 (left column) and T10-l2-r1 (right column) for different times after bounce as indicated in every panel. The figures are plotted such that the polar axis is oriented horizontally with “south” (θ = π) on the left and “north” (θ = 0) on the right. The thin grey line marks the shock radius. In the panel for t = 1500 ms of model T10-l1-r1, the radial lines mark the angular directions at θ = 25 degrees (green line) and 100 degrees (red line), along which radial profiles are shown in Fig. 6. |
| In the text | |
 |
Fig. 2 Latitudinal variation of the reverse shock radius (bottom) and of the entropy, pressure, radial velocity, and temperature of the wind matter just after passing the reverse shock in model T10-l1-r1 at t = 1.5 s after bounce. |
| In the text | |
 |
Fig. 3 Schematic representation of the velocities in a fluid going through an oblique shock (red line). Only the velocity component perpendicular to the shock, u⊥ , is changed when a mass element crosses the shock; the tangential component, u∥ , is conserved. Therefore, the direction of the flow is changed at the shock. |
| In the text | |
 |
Fig. 4 Distribution of density, pressure, and absolute value of the velocity in the wind and shocked matter for model T10-l1-r1 at t = 1.5 s after bounce. In the middle panel the radial velocity field is indicated by arrows. |
| In the text | |
 |
Fig. 5 Schematic representation of the velocities in a fluid going through the reverse shock (red line) when a kink leads to the collimation of the outflowing matter. |
| In the text | |
 |
Fig. 6 Profiles of radial velocity, pressure, density, temperature, and entropy as functions of radius at time 1.5 s after bounce. The one-dimensional model M10-l1-r1 (black lines) is compared to profiles of the two-dimensional model T10-l1-r1 at angles θ = 25 degrees (green lines) and θ = 100 degrees (red lines). |
| In the text | |
 |
Fig. 7 Evolution of reverse shock radius, and of the entropy, pressure, density, and temperature of the shocked neutrino-wind matter for models M10-l1-r1 (black lines) and T10-l1-r1 at θ = 25 degrees (green lines) and θ = 100 degrees (red lines). |
| In the text | |
 |
Fig. 8 Entropy distribution for models T15-l1-r0, T15-l1-r1, and T15-l2-r1 of a 15 M⊙ progenitor and model T25-l5-r4 of a 25 M⊙ star at the end of the simulations. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


