| Issue |
A&A
Volume 526, February 2011
|
|
|---|---|---|
| Article Number | A48 | |
| Number of page(s) | 9 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201015512 | |
| Published online | 20 December 2010 | |
The chemical composition of the Orion star forming region
II. Stars, gas, and dust: the abundance discrepancy conundrum
1
Instituto de Astrofísica de Canarias,
38200
La Laguna, Tenerife,
Spain
e-mail: ssimon@iac.es
2
Departamento de Astrofísica, Universidad de La
Laguna, 38205
La Laguna, Tenerife,
Spain
3
LUTH, Observatoire de Paris, CNRS, Université Paris
Diderot, 5 Place Jules
Janssen, 92190
Meudon,
France
Received: 2 August 2010
Accepted: 8 October 2010
Aims. We re-examine the recombination/collisional emission line (RL/CEL) nebular abundance discrepancy problem in the light of recent high-quality abundance determinations in young stars in the Orion star-forming region.
Methods. We re-evaluate the CEL and RL abundances of several elements in the Orion nebula and estimate the associated uncertainties, taking into account the uncertainties in the ionization correction factors for unseen ions. We estimate the amount of oxygen trapped in dust grains for several scenarios of dust formation. We compare the resulting gas+dust nebular abundances with the stellar abundances of a sample of 13 B-type stars from the Orion star-forming region (Ori OB1), analyzed in Papers I and III of this series.
Results. We find that the oxygen nebular abundance based on recombination lines agrees much better with the stellar abundances than the one derived from the collisionally excited lines. This result calls for further investigation. If the CEL/RL abundance discrepancy were caused by temperature fluctuations in the nebula, as argued by some authors, the same kind of discrepancy should be seen for the other elements, such as C, N and Ne, which is not what we find in the present study. Another problem is that with the RL abundances, the energy balance of the Orion nebula is not well understood. We make some suggestions concerning the next steps to undertake to solve this problem.
Key words: ISM: abundances / HII regions / dust, extinction / stars: abundances / stars: atmospheres
© ESO, 2010
1. Introduction
The knowledge of the chemical composition of stars and of the interstellar matter is the basis of our understanding the chemical evolution of galaxies. In particular, elements such as carbon, nitrogen, and oxygen provide vital clues for the stellar evolution and nucleosynthesis as well as on the history of galaxies (see e.g. proceedings of CNO in the Universe by Charbonnel et al. 2003). H ii regions have for a long time been privileged sites to measure chemical abundances in galaxies because they were easily observable at large distances and because the techniques to analyze their spectra in terms of abundances are simple. However, the last two decades have shown the important potential of stars, now that computers allow the calculation of very elaborate stellar atmosphere models and large telescopes allow one to obtain suitable spectra of individual stars not only in the Milky Way, but also in other galaxies. Indeed, stars are superior to nebulae as abundance indicators in that they are not affected by depletion into dust grains. Another problem with H ii regions is that depending on the methods used to derive abundances, the results are different. When using collisional emission lines (CELs), the derived abundances are systematically smaller than when using recombination lines (RLs) (see García-Rojas & Esteban 2007, and references therein). What is the reason for these discrepancies? And which one of the two abundances (if any) should one believe? After several decades of studies on this, the debate is still not closed. Peimbert (1967) has argued for the presence of temperature fluctuations (of still unknown cause) that bias the nebular abundances derived by CELs downwards. A recent reassessment of this point of view can be found in Peimbert & Peimbert (2009). Stasińska et al. (2007) have examined the hypothesis of inhomogeneous abundances in the interstellar medium (ISM) and concluded that if this were the case, it is the RL abundances which would be severely biased upwards. Ercolano (2009) showed that CEL-RL abundance discrepancies can be obtained in a chemically homogeneous medium if it contains X-ray-ionized dense clumps. However, she finds that the required X-ray flux to accound for the observed abundance discrepancy in the Orion nebula far exceeds the Orion’s known stellar and diffuse X-ray budget.
One way to attack this problem of abundance bias is to confront abundances derived in H ii regions with those derived in B-type stars in the same environment, since both type of objects are expected to share the same chemical composition, reflecting the present-day abundance pattern of the galactic region where they are located. This has been done, for example in the galaxy NGC 300, where oxygen abundances have been derived for blue supergiants as well as for giant H ii regions by Bresolin et al. (2009, 2010). The conclusion of that study was that stars and H ii regions (CELs) give overall the same abundances. However, in view of the existence of important abundance scatter in galaxies (demonstrated for the spiral galaxy M 33 by Rosolowsky & Simon 2008), more accurate tests are needed. In particular, one should compare the abundances of B-type stars with those of the associated H ii region.
In the Milky Way, Przybilla et al. (2008) compared the abundances of a small but representative sample of B-type stars in the solar vicinity with the abundances in the Orion nebula published by Esteban et al. (2004) and with the abundances in the neutral ISM from absorption line measurements. They concluded that taking into account depletion in dust, all sets of abundances are remarkably similar. The abundances from Esteban et al. (2004) were those derived from recombination lines, which would argue in favor of RLs giving the right nebular abundances. An update of the study of Przybilla et al. was however warranted, with a more critical analysis of CEL and RL abundances in the Orion nebula and a more complete stellar data base centered in the Orion star-forming region (Ori OB1), to better adress the RL/CEL abundance discrepancy.
In Simón-Díaz (2010, Paper I), the first of this series of papers, we used the stellar atmosphere code FASTWIND (Puls et al. 2005) to perform a thorough self-consistent spectroscopic analysis with a high-quality set of spectra of 13 early B-type stars from the various subgroups comprising the Orion OB1 association. In this study it was shown that the dispersion of O and Si abundances between stars in the various subgroups found in previous analyses (e.g. Cunha & Lambert 1992, 1994) was a spurious result and the consequence of a bad characterization of the abundance errors propagated from the uncertainties in the stellar parameter determination. This result is confirmed in Nieva & Simón-Díaz (in prep., Paper III) by means of an independent spectroscopic analysis with the Atlas9 code (Kurucz 1993), and recent versions of DETAIL and SURFACE (Giddings 1981; Butler & Giddings 1985). In Paper III we also extend the elements analyzed to C, N, Mg, Ne, and Fe.
In this paper, we focus on the stellar vs. nebular abundance comparison taking into account the effect of depletion onto dust grain in the nebula. The paper is structured as follows: in Sect. 2 we present a brief summary of the abundances in B-type stars in the Orion OB1 association from our recent studies. In Sect. 3 we present a critical analysis of CEL and RL abundances of various elements in the Orion nebula. In Sect. 4 we analyze the depletion of the elements in the dust phase that is occuring in the Orion nebula. In Sect. 5 we draw inferences from the comparison of stellar and nebular abundances in Orion. The main conclusions of this work are summarized in Sect. 6.
2. Abundances in B-type stars
Table 1 summarizes the stellar abundances derived in Papers I and III. Two types of uncertainties are given along with the mean values. The first one refers to the dispersion of abundances obtained for the 13 analyzed stars. The second one (in parentheses) indicates the uncertainties intrinsic to the method of abundance determination in a given star (i.e. accounting for the effect of stellar parameters, microturbulence, and line-by-line abundance dispersion). The derived abundances agree with those computed by Przybilla et al. (2008) for a small sample of B-type stars in the solar vicinity, confirming the homogeneity of present-day abundances in the solar neighborhood as derived by young massive stellar objects already suggested by these authors. While the intrinsic uncertainties are on the order of 0.1 dex, the abundances obtained in the various stars of our sample are remarkably coherent and lead to an unprecedented accuracy of the overall stellar abundance pattern in Orion.
Summary of abundances in B-type stars in Ori OB1.
3. Gas phase abundances in the Orion nebula
Newly computed densities, temperatures, and ionic abundances from optical spectra of the Orion nebula.
RL abundances of O, C, and Ne from the E04 optical spectrum of the Orion nebula.
Newly computed CEL abundances of N, Ne, Ar, S from the E04 optical spectrum of the Orion nebula.
The gas phase abundances in an ionized nebula can be readily obtained from observed intensity ratios of its emission lines through methods that are well-known and described e.g. in Osterbrock & Ferland (2006). After correcting the observed line fluxes for interstellar extinction, determining the temperature and density of the emitting zones with appropriate line ratios, the ionic abundances are obtained directly from emission line ratios. Elemental abundances are then obtained by summing the abundances of the observed ions and accounting for unseen ionic species with ionization correction factors (icfs). The chemical composition determined in this way depends on the quality of the observational data, the adopted dereddening procedure, the temperature, density indicators, and the chosen icfs. The procedures are quite standard, but may deviate in some detail from one author to another. Of course, the results depend on the set of atomic data that are used.
3.1. O
O from CELs.
Oxygen is the element for wich the abundances can be determined most reliably in H ii regions, because both ions that are expected to be present, O+ and O2+, emit strong lines in the optical and, in addition, the temperature and density of the emitting zones can be easily obtained from appropriate line ratios.
There have recently been a number of optical observations of the Orion nebula with high resolution and very good signal-to-noise ratio. To obtain a set of abundances in the Orion nebula that gives a fair account of uncertainties and possible variations from one point to another, we rederived in a consistent way the CEL abundances of oxygen in different positions of the Orion nebula from the reddening-corrected intensities of by Esteban et al. (1998, E98), Esteban et al. (2004, E04), Blagrave (2006, B06), Mesa-Delgado et al. (2009, M09). We included the two slit positions provided by E98, B06, and M09. In the case of E98, both spectra correspond to the nebula, while for B06 and M09, one of them is located in the shock front of one of the Herbig-Haro objects of the Orion nebula. For the abundance analysis, we assumed that the electron density throughout is the one given by the [O ii]3726/3729 line ratio1. We have considered that Hβ and [O iii]5007 are emitted in a zone whose temperature is obtained from the [O iii]4363/5007 line ratio and that lines from [O ii]3727 and [N ii]6584 are emitted in a zone whose temperature is obtained from the [N ii]5755/6584 line ratio. The references for the atomic data used in the calculations are listed in Table 7 in Appendix A. The intensities of the forbidden lines were obtained from a 5-level model atom.
The resulting electron densities, temperatures, and abundances of O+, O2+, and O in units of ϵ(X) = 12 + log X/H are listed in Table 2. The uncertainties (listed as quartiles in the table) were obtained by Monte-Carlo simulations, taking into account observational errors in the dereddened line intensities as listed in the original papers2.
We find that CEL results are remarkably consistent with each other once the same atomic data and procedures are applied to all the spectra, when disregarding the two Herbig-Haro objects (labelled HH in the table). This is because of the exceptional quality of the data reported in the original papers. As for our B stars, the dispersion of the derived CEL oxygen abundances is smaller than the formal errors: excluding the two Herbig-Haro object, the average value of ϵ(O) is 8.51 and the dispersion is 0.02 dex. For convenience, below we will exclusively use the abundances derived from the spectra by E04.
O from RLs.
The method using recombination lines to determine ionic abundances has the advantage of being almost independent of errors in the electron temperature. On the other hand, it relies on very weak lines and requires a certain know-how to choose the best strategy for the different observed multiplets. We therefore adopted the ionic abundances derived in the original paper. Note that the abundances derived by E04 from individual recombination lines of the same ion differ much more than expected from observational errors only. The final adopted abundances are a weighted mean of the sum-values of the most reliable multiplets. The error attributed to the final RL abundances by E04, which we adopt here as well, is also a result of this weighting process.
Esteban et al. (2004) derive RL abundances for both O+ and O2+. But they note that the RL O+ abundance, which is based on a single faint line in a spectral region much affected by sky emission, is not very reliable. We will thus use only their abundance of O2+, and from it derive the RL oxygen abundance using the O2+/O+ obtained from forbidden lines. The result is presented in Table 3.
3.2. N, Ne, S, Ar
N, Ne, S, Ar from CELs.
We use the same procedure as for oxygen to derive the CEL ionic abundances of N+, Ne2+, Ar2+, S+, and S2+ from the E04 spectrum, using the atomic data listed in Table 7. Like for oxygen, the uncertainties in the ionic abundances are determined from Monte-Carlo simulations of the observational errors. The resulting ionic abundances are displayed in Table 4. To obtain the corresponding elemental abundances, we need to use ionization correction factors. Previous studies (E98, E04) used icfs from a variety of sources that are not necessarily consistent and sometimes outdated. To obtain the most reliable set of icfs for our purpose, we constructed a tailored photoionization model of the Orion nebula with the Cloudy code (Ferland et al. 1998). The way we proceeded to obtain the model is described in detail in Appendix B. From this model we derive icfs for N, Ne, S and Ar3. Those and the resulting elemental abundances are listed in Table 4. There are non negligible differences between our total abundances and the ones found by E04 (and García-Rojas & Esteban 2007). They stem essentially from the different icfs adopted in each case. Our values should be more reliable, because they were obtained from a tailored model. Note that some icfs are large, especially that of N+, which we find to be on the order of 10 (E04 attributed a value of about 6). In this case, even with a tailored photoionization model, we cannot be entirely confident in the result we find. Concerning neon, the icf derived from our model implies that Ne/O is not equal to Ne++/O++, which is the classical recipe to derive the neon abundance. Using the spectroscopic data for about 80 zones in the Orion nebula from O’Dell & Harris (2010), we find that Ne++/O++ shows no trend with O++/H over a range of one decade in O++/H. This would rather support the classical icf for Ne over the one we derived from our model. Indeed, model atmospheres become more uncertain at energies above 40 eV, and the nebular constraint provided by our photoionization model is given by the very weak [Ar iv] lines. On the other hand, Rubin et al. (2010) used infrared line intensities measured by the Spitzer Space Telescope to derive 12 + log (Ne/H) = 8.01 ± 0.01 without the need of any icf because both [Ne ii] and [Ne iii] lines are observed. This value is very close to the one we derive with our model icf. In view of this dilemma, we give in Table 5 the values of Ne derived both with our model icf and with the classical icf.
Ne from RLs.
Of the elements N, Ne, S and Ar, reliable abundances from recombination lines exist only for Ne, using the Ne2+ ion. The results are listed in Table 3, again using both the model icf and the classical one.
3.3. C
For carbon there are no CELs in the optical wavelength range, and one has to resort to ultraviolet observations. There are several difficulties with this: the extinction correction is important and may be inaccurate. Collisionally excited ultraviolet lines depend very strongly on the electron temperature, so using temperatures derived from [N ii] or [O iii] lines may lead to substantial errors. Rubin et al. (1993) performed a detailed photoionization modeling to infer the carbon abundance by direct comparison of model results with observational data in several locations of the Orion nebula. They point out however that their model was not able to explain the C iii] 1907,09 and the C ii] 2324-29 lines at the same time. As a result, their carbon abundance is not very accurate. We will use the value ϵ(C) = 8.4 and assign to it an uncertainty of ± 0.25 dex
In the optical, there are several RLs that allow one to determine the abundance of C2+. We use the value determined by E04 and list it in Table 3. To determine the total carbon abundance from RLs, we use the icf derived from our photoionization model, as done for the other elements. The result is listed in Table 3.
Summary of gas-phase abundances in the Orion nebula.
3.4. Fe
There are many forbidden lines of Fe+, Fe2+ and Fe3+ in the optical spectra of the Orion nebula. To make the best use of them, multilevel atoms of over 15 levels have to be considered. Rodríguez & Rubin (2005) performed a detailed analysis of the Fe spectrum in the Orion nebula using the spectrum of E04, and compared the Fe abundance obtained by summing the observed abundances of Fe+, Fe2+ and Fe3+ with the abundance derived using an icf implied by their photoionization model analysis. They found an inconsistency of about a factor 4, implying that one or several of the atomic data involved in the analysis are wrong.
3.5. Mg and Si
Collisionally excited lines of Si and Mg ions are not present in the optical range. Observations are available in the UV: Si iii] 1883,93 and Mg ii 2768. The former have been analyzed by Rubin et al. (1993), together with C iii] 1907,09. These authors find a Si/C ratio of 0.016 with an accuracy of about 30%. The absolute abundance of Si is plagued however with the uncertainty in the C abundance as deduced from UV lines. The abundance of Mg was inferred from a photoionization modeling by Baldwin et al. (1991), but its value is not accurate, because the observed intensity of Mg ii 2768 is very uncertain. In addition, the flux of Mg ii 2768 received at Earth is affected by interstellar absorption.
3.6. Summary of gas phase abundances
In Table 5 we summarize our nebular abundance analysis by giving our adopted values of the gas phase C, N, O, Ne, S, Ar, Mg, Si, and Fe abundances. The error bars now include the uncertainties from the Monte-Carlo analysis and the uncertainties in the icfs, all added in quadrature. The element with the best determination is oxygen. For nitrogen, the large icf introduces an uncertainty difficult to evaluate, but possibly larger than indicated in the table. For neon, the icf derived from our photoionization model leads to an abundance larger by 0.2 than the one obtained using a classical icf. This issue needs to be investigated further. The abundance of carbon from CELs is quite uncertain, as are the abundances of the refractory elements Fe, Si and Mg, each one for different reasons.
Figure 1 compares the abundances of C, N, O, Ne, Mg, Si, and Fe in the Orion nebula obtained using CELs (green boxes) and RLs (red boxes) with the abundances in the B stars of Orion OB1 (cyan boxes). In each case, the height of the boxes represents the uncertainties, indicated in Table 1 (standard deviation from the 13 stars) and Table 5 (Orion nebula).
 |
Fig. 1 Comparison of C, N, O, Ne, Mg, Si, and Fe abundances obtained from B-type stars (cyan), CEL (green), and RL (red). For Ne there are two green and red boxes, respectively, corresponfing to different icfs (see text). The height of the boxes represents the uncertainties, indicated in Tables 1 and 5. Note that for Mg there is no evaluation of the uncertainty. See text for more detail. |
4. Depletion of the elements in the dust phase
Before comparing the nebular abundances with the stellar ones, one has to consider that some of the material in the nebula may be in the form of dust grains, whose total mass and chemical composition cannot be directly accessed. That the abundances of the refractory elements Mg, Si, and Fe in the gas phase of the Orion nebula (Table 5) are lower than those found in the atmospheres of our sample of B stars (Table 1) by at least one order of magnitude clearly indicates that these elements are mostly found in dust grains. We find, by comparing the numbers in those two tables, that ~90% of Mg, ~80–90% of Si, and ~93–98% of Fe are trapped in dust grains. If we knew the chemical composition of dust, we could estimate the degree of depletion of the other elements.
According to Draine (2003), silicates of the type Mg-Fe pyroxenes (MgxFe1−xSiO3) and olivines (Mg2xFe2−2xSiO4) contribute a substantial fraction of the total mass of interstellar dust. These molecules are the main cause for the depletion of Si. In addition, Mg, Fe, and O could be in oxide form (MgO, FeO, Fe2O3, Fe3O4). To estimate the amount of oxygen depletion in the Orion nebula, we investigate all combinations of dust grain compositions presented in Table 6. We implemented and IDL procedure that calculates Odust for each of the combinations. The input parameters of the program are the stellar and nebular Si, Fe, and Mg abundances, plus the nebular gas phase oxygen abundance. Once the total amount of Si, Fe, and Mg available to form dust grains is computed, the program determines the amount of O, Fe, and Mg used to form silicates (the whole amount of Si depleted is used to this aim); then, with the remaining Fe and Mg available, the amount of O used to form Fe and Mg oxides is derived. Finally, the total amount of oxygen in the nebula (gas + dust) is determined for each combination of dust grain composition by adding the amount of oxygen depleted in silicates and oxides to the nebular gas phase abundance.
Dust composition possibilities considered in this study.
 |
Fig. 2 Upper panel: amount of oxygen expected to be in solid form for various dust composition scenarios (see Table 6). Lower panel: comparison of the stellar oxygen abundance (wide cyan rectangle) with the gas+dust oxygen abundance in the nebula for the different dust scenarios. Green rectangles are obtained with CEL gas abundances, red rectangles are obtained with RL gas abundances. See text for an explanation of the considered uncertainties. |
We ran the IDL program 1000 times with random independent values for each of the input abundances4 to derive mean values and uncertainties of the amount of oxygen trapped in dust for each of the dust grain compositions considered. The results are presented in the upper panel of Fig. 2. We find that the oxygen depletion is in the range 125–135 ppM, with corresponding uncertainties of ~10 ppM. This agrees very well with the value of 0.12 dex estimated by Mesa-Delgado et al. (2009).
The total amount of oxygen in the nebula (gas + dust) determined for each combination of dust grain composition is presented in the bottom panel of Fig. 2. Two cases are shown: the green boxes represent the results using CEL abundances, while the red boxes represent the results using RL abundances. We see that the correction for O depletion owing to dust grains does not depend much on the details of the dust composition in the different combinations of dust grains we considered5. For comparison with the total nebular value, the stellar oxygen abundance is given in cyan. The height of the green and red boxes represent the error bars combining the uncertainties in the gas phase abundance determination and in the dust phase abundance. The height of the cyan box represents the dispersion in the oxygen stellar abundances given in Table 1. The verdict from Fig. 2 is clear. Oxygen abundances in the Orion nebula derived from RLs, when corrected for the effects of depletion in dust grains, are very similar to those found in the B stars of the Ori OB1 association. This is not the case for the oxygen CEL abundances, which lead to much lower values. We note that the oxygen CEL abundances would actually be compatible with the stellar abundances if using the intrinsic uncertainties of the analysis of individual stars (see Table 1). But as argued in Sect. 2, the degree of coherence between the abundances obtained for the 13 studied stars indicates that the oxygen abundance of the Ori OB1 cluster is determined with much better accuracy than ~0.10 dex.
Concerning the other elements considered in this study, there are observational arguments that a significant fraction of carbon atoms must be locked in carbon-based dust and in PAHs although the amount of carbon depletion in nebulae is still very poorly known (Draine 2003; Jenkins 2009). To our knowledge, there is no indication that nitrogen could be present in solid form, except perhaps in ices (Hily-Blant et al. 2010), which are not expected to be present in ionized gas. As for neon, which is a noble gas, it is not expected to be incorporated in dust grains, at least not in significant amounts.
5. Discussion
Our study therefore leads us to the conclusion that the oxygen abundances derived in the Orion nebula from CELs are incompatible with the abundances derived in the B stars (once the effects of depletion in dust grains are taken into account), while RL oxygen abundances agree better (although the mean values seem to be somewhat higher that the stellar one).
That RL abundances are more reliable than CEL abundances has been argued in many papers by Peimbert and coworkers (see e.g. Peimbert & Peimbert 2009), including E04. One of the arguments is that the abundance discrepancy factor between RL and CEL abundances can be explained by temperature fluctuations of the same order as the difference between the temperature derived from the [O iii] 4363/5007 line ratio and the one derived from the Balmer jump. In addition, temperature fluctuations of that order in the Orion nebula have been inferred from the spatial variation of Te[O iii] across the nebula (O’Dell et al. 2003; Rubin et al. 2003).
There are, however, a certain number of controversial points to consider.
First, when looking at Fig. 1, we see that the carbon RL abundance is slightly higher than the carbon abundance in the B stars, while we applied no correction for the depletion of carbon in dust grains. If we adopt the Si, Mg, and Fe depletions inferred from this figure, we infer a total dust-to-gas mass ratio in the silicates and oxides of 0.41 ± 0.03%. With the “Orion mixture” considered in Cloudy, this implies a carbon depletion of ~50%. Then the total gas+dust carbon abundance, as derived from RLs, would be higher than the stellar one by about 0.2 dex. Note that the CEL carbon abundance is also higher than in the stars. However, in that case, the error bar is large and the CEL value is not really reliable. The nitrogen CEL abundance is slightly above the stellar one. However, taking into account the large icf (see Table 4) and the larger error bar on stellar N abundances (see Table 1), both values are perhaps compatible. For neon, the RL abundance is somewhat uncertain and does not provide a useful constraint, but the CEL abundance is compatible with the stellar value if taking the model icfs and lower by about 0.2 dex if using the classical icfs. If the oxygen RL/CEL abundance discrepancy is caused by temperature fluctuations, one would expect the CEL abundances for C, N, and Ne to be significantly below the stellar values, and the RL abundances equal to the stellar ones. This is clearly not what occurs for carbon (for neon, the diagnostic depends on what icf is used).
The second problem is related to the energy budget. To show this, we constructed a photoionization model with exactly the same parameters as the model shown in Fig. B.2, except that for C, O, and Ne we take the RL abundances listed in Table 3 (and for N we also assume an RL-like abundance, by adding 0.14 dex to the CEL value). This model is shown in Fig. B.3. As seen in that figure, the value of Te[O iii] returned by the model is below the observed one by 2 sigmas. In order for the model to reproduce the observed Te[O iii] , one would need to consider extra heating, at least in some zones. Then, the computed intensities of the forbidden lines would be signficantly higher than observed. A model with slightly lower input abundances, in which the chemical composition of the nebular gas is exactly the same as found for the stars (but taking depletion into account) gives basically the same result: the nebular model becomes too cool and additional heating would make the mismatch between predicted and observed forbidden line intensities even worse.
Could it be, then, that the solution lies in oxygen-rich condensations, as studied by Stasińska et al. (2007)? This does not seem to be the case, at least in Orion. As found by those authors, oxygen rich condensations would bias the RL abundances upwards, while we found in this paper that the RL abundances are compatible with the stellar ones.
6. Conclusion
The aim of the present paper was to re-examine the RL-CEL nebular abundance discrepancy problem in the light of recent high-quality abundance determinations in young stars. In this study, we focused on one object: the Orion star-forming region. There is no H ii region in the solar neigborhood in which the stellar and gas phase abundances can be derived with better accuracy, and the stars from the Orion OB1 association, which share the same composition as the associated H ii region, have been studied in great detail.
We have re-evaluated the CEL and RL abundances of several elements in the Orion nebula and estimated the associated uncertainties, taking into account the uncertainties in the ionization correction factors for unseen ions. We estimated the amount of oxygen trapped in dust grains for several scenarios for dust formation. We compared the resulting gas+dust nebular abundances with the stellar abundances of a sample of 13 B-type stars from the Orion star-forming region (Ori OB1), analyzed in Papers I and III of this series.
We find that the oxygen nebular abundance based on recombination lines agrees much better with the stellar abundances than that derived from the collisionally excited lines.
However, there remain problems to be solved. First, the abundances of the other elements, C, N, and Ne, although admittedly less accurate, do not deliver such a clear-cut picture. If the RL-CEL abundance discrepancy were caused by temperature fluctuations, as argued by Peimbert & Peimbert (2009), one should observe the same kind of bias in the CEL abundances of the other elements. Hopefully, the consideration of further elements, such as S and Ar, whose abundances will soon be available for the stars of the Orion OB1 association, will bring useful additional constraints. Another problem is that with the RL abundances, the energy balance of the Orion nebula is not well understood. Investigating this problem will require detailed photoionization modeling and an accurate account of all heating and cooling processes taking place in this specific case, as well as the effect of uncertainties in the collision strenghts for the transitions of interest. In parallel to such studies, another avenue to start exploring is the possibility of remaining biases in the stellar abundance determinations, for example because of a slight offset in the description of the ionization of oxygen in the model atmospheres of B-type stars, which unfortunately cannot be checked directly here, since only O ii lines are seen in the studied stars (see Simón-Díaz 2010).
An important step forward would be to repeat the analysis performed in this paper for objects where the RL-CEL discrepancy is larger. The choice of the Orion nebula, while imposed by the quality of relevant observations and data analysis, is indeed not the best one to investigate the RL-CEL nebular abundance discrepancy problem in H ii regions because the discrepancy there is actually quite modest: ≃0.12 dex. With an adequate observing strategy and data handling, it should be possible to investigate the RL-CEL abundance discrepancy in different environments, for example at low metallicities. This is a necessary condition to get a definite handle on this exasperating problem.
Densities given by [Cl iii] or [Ar iv] doublets would, in principle, be more appropriate for the high-excitation zone, but they are much more uncertain in the Orion nebula. Fortunately the abundance analysis is not strongly affected by the density in the expected range of densities. Densities derived from the [S ii]6717/6731 line ratio are slightly lower than those derived from [O ii]3726/3729.
For completeness, we mention that Jenkins (2009) inferred from a detailed study of absorption line measurements in the solar vicinity that a significant proportion of interstellar oxygen should be trapped in ices. This statement, however, does not affect our estimates, since ices are not expected to survive in an ionized nebula, because of the effect of photosputtering (Grigorieva et al. 2007).
This value agrees better with recent determinations of the distance to the Orion nebula (see Menten et al. 2007, and references therein).
Acknowledgments
Financial support from the Spanish Ministerio de Ciencia e Innovación under the project AYA2008-06166-C03-01 is acknowledged. This work has also been partially funded by the Spanish MICINN under the Consolider-Ingenio 2010 Program grant CSD2006-00070: First Science with the GTC (http://www.iac.es/consolider-ingenio-gtc).
References
- Aggarwal, K. M., & Keenan, F. P. 1999, ApJS, 123, 311 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Baldwin, J. A., Ferland, G. J., Martin, P. G., et al. 1991, ApJ, 374, 580 [NASA ADS] [CrossRef] [Google Scholar]
- Blagrave, K. 2006, Ph.D. Thesis [Google Scholar]
- Bresolin, F., Gieren, W., Kudritzki, R.-P., et al. 2009, ApJ, 700, 309 [NASA ADS] [CrossRef] [Google Scholar]
- Bresolin, F., Stasińska, G., Vílchez, J. M., Simon, J. D., & Rosolowsky, E. 2010, MNRAS, 404, 1679 [NASA ADS] [Google Scholar]
- Butler, K., & Giddings, J. R. 1985, in Newsletter of Analysis of Astronomical Spectra, No. 9 (Univ. London) [Google Scholar]
- Charbonnel, C., Schaerer, D., & Meynet, G. 2003, ASP Conf. Ser., 304 [Google Scholar]
- Cunha, K., & Lambert, D. L. 1992, ApJ, 399, 586 [NASA ADS] [CrossRef] [Google Scholar]
- Cunha, K., & Lambert, D. L. 1994, ApJ, 426, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 2003, ARA&A, 41, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Ercolano, B. 2009, MNRAS, 397, L69 [NASA ADS] [Google Scholar]
- Esteban, C., Peimbert, M., Torres-Peimbert, S., & Escalante, V. 1998, MNRAS, 295, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Esteban, C., Peimbert, M., García-Rojas, J., et al. 2004, MNRAS, 355, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Ferland, G. J., Korista, K. T., Verner, D. A., et al. 1998, PASP, 110, 761 [Google Scholar]
- Froese Fischer 2004, http://hf8.vuse.vanderbilt.edu [Google Scholar]
- FroeseFischer, C., & Tachiev, G. 2004, ADNDT, 87, 1 [Google Scholar]
- Galavis, M., Mendoza, C., & Zeippen, C. J. 1995, A&AS, 111, 347 [NASA ADS] [Google Scholar]
- Galavis, M. E., Mendoza, C., & Zeippen, C. J. 1997, A&AS, 123, 159 [Google Scholar]
- Galavis, M. E., Mendoza, C., & Zeippen, C. J. 1998a, A&AS, 131, 499 [Google Scholar]
- Galavis, M. E., Mendoza, C., & Zeippen, C. J. 1998b, A&AS, 133, 245 [Google Scholar]
- García-Rojas, J., & Esteban, C. 2007, ApJ, 670, 457 [NASA ADS] [CrossRef] [Google Scholar]
- Giddings, J. R. 1981, Ph.D. Thesis, University of London [Google Scholar]
- Grigorieva, A., Thébault, P., Artymowicz, P., & Brandeker, A. 2007, A&A, 475, 755 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hillier, D. J., & Miller, D. L. 1998, ApJ, 496, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Hily-Blant, P., Walmsley, M., Pineau Des Forêts, G., & Flower, D. 2010, A&A, 513, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hubeny, I., & Lanz, T. 1995, ApJ, 439, 875 [Google Scholar]
- Hudson, C. E., & Bell, K. L. 2004, MNRAS, 348, 1275 [NASA ADS] [CrossRef] [Google Scholar]
- Jenkins, E. B. 2009, ApJ, 700, 1299 [NASA ADS] [CrossRef] [Google Scholar]
- Keenan, F. P., Aller, L. H., Bell, K. L., et al. 1996, MNRAS, 281, 1073 [NASA ADS] [Google Scholar]
- Kurucz, R. L. 1993, CD-ROM No. 13 (Cambridge, Mass.: SAO) [Google Scholar]
- McLaughlin, B. M., & Bell, K. L. 2000, JPhB, 33, 597 [Google Scholar]
- Mendoza, C. 1983, IAUS, 103, 143 [Google Scholar]
- Mendoza, C., & Zeippen, C. J., 1982a, MNRAS 202, 981 [Google Scholar]
- Mendoza, C., & Zeippen, C. J., 1982b, MNRAS 198, 127 [NASA ADS] [Google Scholar]
- Mendoza, C., Zeippen, C. J., & Storey, P. J. 1999, A&AS, 135, 159 [Google Scholar]
- Menten, K. M., Reid, M. J., Forbrich, J., & Brunthaler, A. 2007, A&A, 474, 515 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mesa-Delgado, A., Esteban, C., & García-Rojas, J. 2008, ApJ, 675, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Mesa-Delgado, A., Esteban, C., García-Rojas, J., et al. 2009, MNRAS, 395, 855 [NASA ADS] [CrossRef] [Google Scholar]
- Astrophysics of gaseous nebulae and active galactic nuclei 2006, 2nd. ed. D. E. Osterbrock, & G. J. Ferland (Sausalito, CA: University Science Books) [Google Scholar]
- O’Dell, C. R., & Harris, J. A. 2010, AJ, 140, 985 [CrossRef] [Google Scholar]
- O’Dell, C. R., Peimbert, M., & Peimbert, A. 2003, AJ, 125, 2590 [NASA ADS] [CrossRef] [Google Scholar]
- Pauldrach, A. W. A., Hoffmann, T. L., & Lennon, M. 2001, A&A, 375, 161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peimbert, M. 1967, ApJ, 150, 825 [NASA ADS] [CrossRef] [Google Scholar]
- Peimbert, M., & Peimbert, A. 2009, Rev. Mex. Astron. Astrofis. Ser. Conf. [arXiv:0912.3781] [Google Scholar]
- Przybilla, N., Nieva, M. F., & Butler, K. 2008, ApJ, 688, L103 [NASA ADS] [CrossRef] [Google Scholar]
- Puls, J., Urbaneja, M. A., Venero, R., et al. 2005, A&A, 435, 669 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ramsbottom, C. A., Bell, K. L., & Keenan, F. P. 1997, MNRAS, 284, 754 [NASA ADS] [Google Scholar]
- Rodríguez, M., & Rubin, R. H. 2005, ApJ, 626, 900 [NASA ADS] [CrossRef] [Google Scholar]
- Rosolowsky, E., & Simon, J. D. 2008, ApJ, 675, 1213 [NASA ADS] [CrossRef] [Google Scholar]
- Rubin, R. H., Dufour, R. J., & Walter, D. K. 1993, ApJ, 413, 242 [NASA ADS] [CrossRef] [Google Scholar]
- Rubin, R. H., Martin, P. G., Dufour, R. J., et al. 2003, MNRAS, 340, 362 [NASA ADS] [CrossRef] [Google Scholar]
- Rubin, R. H., Simpson, J. P., O’Dell, C. R., et al. 2010, MNRAS [arXiv:1008.2736] [Google Scholar]
- Simón-Díaz, S. 2010, A&A, 510, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Simón-Díaz, S., & Stasińska, G. 2008, MNRAS, 389, 1009 [NASA ADS] [CrossRef] [Google Scholar]
- Simón-Díaz, S., Herrero, A., Esteban, C., & Najarro, F. 2006, A&A, 448, 351 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stasińska, G., Tenorio-Tagle, G., Rodríguez, M., & Henney, W. J. 2007, A&A, 471, 193 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stasińska, G., Morisset, C., Tovmassian, G., et al. 2010, A&A, 511, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Storey, P. J., & Zeippen, C. J. 2000, MNRAS, 312, 813 [Google Scholar]
- Tachiev, G., & Froese Fischer, C. 1999, JPhB, 32, 5805 [Google Scholar]
- Tachiev, G. I., & Froese Fischer, C. 2002, A&A, 385, 716 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tayal, S. S., & Gupta, G. P. 1999, ApJ, 526, 544 [NASA ADS] [CrossRef] [Google Scholar]
- Tayal, S. S. 2007, ApJS, 171, 331 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Atomic data for nebular emission line
Appendix B: Photoionization model
To estimate the ionization correction factors as well as possible for the elements whose ionic abundances were derived from the optical spectrum of E04, we constructed a photoionization model reproducing the observed characteristics of this spectrum.
The model was constructed with the photoionization code Cloudy (as last described in Ferland et al. 1998), using version 8.0. We considered an open geometry (as appropriate for the Orion nebula) and taken the “intrinsic line fluxes” and “aperture slit” options. Of the options offered by Cloudy, this one seems the most approriate for the E04 observation.
Because we are here mainly interested in the icfs, we do not try to fit all observed line intensities (we already know that this would not be possible for RLs and CELs simultaneously). On the other hand, we aim at reproducing the line ratios indicative of density ([Ar iv] 4740/4711, [O ii] 3726/3729, and [S ii] 6731/6716) and ionization structure ([O iii] 5007/[O ii] 3727, [S iii] 9069/([S ii] 6731+16) and [Ar iv] 4711+40/[Ar iii] 7135).
We assumed an exponential density law, which is usually considered for the Orion nebula (see e.g. Rubin et al. 1993): N(H) = Nmax exp[(x-xp)/h], with N(H) = Nmax for x > xp. We considered as free parameters h, Nmax, and xp, and fixed the internal radius of the model to be r0 = 0.9xp.
The second important input to the photoionization model is the ionizing radiation field. We considered the stellar parameters derived for θ1 Ori C by Simón-Díaz et al. (2006) and obtained the spectral energy distribution (SED) as predicted by the stellar atmopshere codes WMbasic (Pauldrach et al. 2001), CMFGEN (Hillier & Miller 1998), TLUSTY (Hubeny & Lanz 1995), and FASTWIND (Puls et al. 2005). Figure B.1 compares the four SEDs, also indicating the ionization energies for various of the ions present in the Orion nebula. As commented in Simón-Díaz & Stasińska (2008), there are important discrepancies between the ionizing SEDs predicted by the four stellar atmosphere codes. We considered the four SEDs in our photoionization models, and it turned out that WMbasic gives the best solution for this case (this argument is based on the simultaneous fitting of the ionization degree constraints, corresponding to the ionization of S+, O+, and Ar2+; see also Fig. B.1). We also explored slight changes in the effective temperature, and found that the indicated stellar parameters (Teff = 39 000 K, log g = 4.1) provide the best solution.
In all cases, a total number of hydrogen ionizing photons, Q(H0) = 1048.67 photons s-1 was considered. This value was obtained assuming the same mv magnitude and extinction as in Simón-Díaz et al. (2006), but adopting a distance to the Orion nebula of 400 pc6, instead of the value originally adopted 450 pc.
 |
Fig. B.1 Comparison of the ionizing SEDs for Θ1 Ori C as predicted by various stellar atmosphere models. Stellar parameters: Teff = 39 000, log g = 4.0 (derived by Simón-Díaz et al. 2006, by means of a spectroscopic analysis of the optical spectra using FASTWIND). |
List of nebular line ratios used to compare with the output of the photoionization models and the corresponding observed values (from E04).
Finally, we took grains into account in the computation of all the models, assuming the “Orion type” grain composition considered by Cloudy, scaled by a factor 1.1. This scale factor was included to obtain the same abundance of Si, Mg, and Fe in grains as computed in this paper (see Sect. 4).
 |
Fig. B.2 Results from a photoionization model in which the input abundances are the CEL ones given in Table 5. The numbers to the right of each line ratio indicate the deviation from the observed value in units of κ(O) and the value obtained from the photoionization model (the observed value being given in Table B.1). In the right column are listed the logarithms of the icfs corresponding to this model. |
 |
Fig. B.3 Results from a photoionization model in which the input abundances are the RL ones given in Table 5. The numbers to the right of each line ratio indicate the deviation from the observed value in units of κ(O) and the value obtained from the photoionization model (the observed value being given in Table B.1). In the right column are listed the logarithms of the icfs corresponding to this model. |
To judge the quality of the model, we use the same procedure as Stasińska et al. (2010), plotting for each observable O (i.e. here for each relevant line ratio) the value of 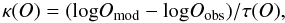 (B.1)where Omod is the value returned by the model, Oobs is the observed value, and τ(O) the accepted tolerance in dex for this observable. For each observable, the value of τ(O) is defined by
(B.1)where Omod is the value returned by the model, Oobs is the observed value, and τ(O) the accepted tolerance in dex for this observable. For each observable, the value of τ(O) is defined by 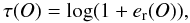 (B.2)where er(O) is the maximum “acceptable” relative error on the observable. A model is satisfactory only if for each of the observables used as constraints, κ(O) is found to be between −1 and + 1. Table B.1 lists the values of the observables used as constraints to fit the model and the corresponding values of er(O) attributed to them (it also lists, for information, some other observables that are not used as constraints, such as line ratios indicative of the electron temperature or of the element abundances).
(B.2)where er(O) is the maximum “acceptable” relative error on the observable. A model is satisfactory only if for each of the observables used as constraints, κ(O) is found to be between −1 and + 1. Table B.1 lists the values of the observables used as constraints to fit the model and the corresponding values of er(O) attributed to them (it also lists, for information, some other observables that are not used as constraints, such as line ratios indicative of the electron temperature or of the element abundances).
Figure B.2 is a graphic representation of one of our best models and of the quality of the fits. In this model (Model B.1) the input abundances are the CEL ones given in Table 5. In the right panel of the figure the icfs are listed corresponding to the model7. We may notice that using the CEL abundances implies a Te[O iii] in the model much higher than observed. This suggests that the input abundances (especially that of oxygen) might be too small. Since we argue in Sect. 5 that the gas phase oxygen abundance seems to be better estimated by RLs than by CELs, one may wonder whether it is correct to fit the ionization state of the nebula with ratios of CELs, as we have done. We believe that this procedure is reasonably correct, unless the discrepancy between RL and CEL abundances is much different in the low ionization and in the high ionization zone.
Figure B.3 shows the results of another model where this time the input abundances of C, O, and Ne are those obtained from the RL lines and the abundance of N is the CEL one increased by 0.14 dex. The aim of this model is to discuss the energy budget problem as presented in Sect. 5.
All Tables
Newly computed densities, temperatures, and ionic abundances from optical spectra of the Orion nebula.
Newly computed CEL abundances of N, Ne, Ar, S from the E04 optical spectrum of the Orion nebula.
List of nebular line ratios used to compare with the output of the photoionization models and the corresponding observed values (from E04).
All Figures
 |
Fig. 1 Comparison of C, N, O, Ne, Mg, Si, and Fe abundances obtained from B-type stars (cyan), CEL (green), and RL (red). For Ne there are two green and red boxes, respectively, corresponfing to different icfs (see text). The height of the boxes represents the uncertainties, indicated in Tables 1 and 5. Note that for Mg there is no evaluation of the uncertainty. See text for more detail. |
| In the text | |
 |
Fig. 2 Upper panel: amount of oxygen expected to be in solid form for various dust composition scenarios (see Table 6). Lower panel: comparison of the stellar oxygen abundance (wide cyan rectangle) with the gas+dust oxygen abundance in the nebula for the different dust scenarios. Green rectangles are obtained with CEL gas abundances, red rectangles are obtained with RL gas abundances. See text for an explanation of the considered uncertainties. |
| In the text | |
 |
Fig. B.1 Comparison of the ionizing SEDs for Θ1 Ori C as predicted by various stellar atmosphere models. Stellar parameters: Teff = 39 000, log g = 4.0 (derived by Simón-Díaz et al. 2006, by means of a spectroscopic analysis of the optical spectra using FASTWIND). |
| In the text | |
 |
Fig. B.2 Results from a photoionization model in which the input abundances are the CEL ones given in Table 5. The numbers to the right of each line ratio indicate the deviation from the observed value in units of κ(O) and the value obtained from the photoionization model (the observed value being given in Table B.1). In the right column are listed the logarithms of the icfs corresponding to this model. |
| In the text | |
 |
Fig. B.3 Results from a photoionization model in which the input abundances are the RL ones given in Table 5. The numbers to the right of each line ratio indicate the deviation from the observed value in units of κ(O) and the value obtained from the photoionization model (the observed value being given in Table B.1). In the right column are listed the logarithms of the icfs corresponding to this model. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


