| Issue |
A&A
Volume 526, February 2011
|
|
|---|---|---|
| Article Number | A95 | |
| Number of page(s) | 9 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201014322 | |
| Published online | 04 January 2011 | |
Timing of the accreting millisecond pulsar IGR J17511-3057
1
INAF/Osservatorio Astronomico di Cagliari, località Poggio dei Pini, strada
54,
09012
Capoterra,
Italy
e-mail: ariggio@oa-cagliari.inaf.it
2
Università di Cagliari, Dipartimento di Fisica,
SP Monserrato-Sestu km 0,7,
09042
Monserrato ( CA), Italy
3
Dipartimento di Scienze Fisiche e Astronomiche, Università di
Palermo, via Archirafi
36, 90123
Palermo,
Italy
4
Osservatorio Astronomico di Roma, Sede di Monteporzio Catone, via
Frascati 33, 00040
Roma,
Italy
Received:
25
February
2010
Accepted:
23
October
2010
Context. Timing analysis of accretion-powered millisecond pulsars (AMPs) is a powerful tool for probing the physics of compact objects. The recently discovered IGR J17511-3057 was the twelfth discovered of the 13 AMPs known. The Rossi XTE satellite provided an extensive coverage of the 25 days-long observation of the source outburst.
Aims. Our goal is to investigate the complex interaction between the neutron star magnetic field and the accretion disk by determining the angular momentum exchange between them. The presence of a millisecond coherent flux modulation allows us to investigate this interaction from the study of pulse arrival times. To separate the neutron star proper spin frequency variations from other effects, a precise set of orbital ephemeris is mandatory.
Methods. Using timing techniques, we analysed the pulse phase delays by fitting differential corrections to the orbital parameters. To remove the effects of pulse phase fluctuations, we applied the timing technique that had been already successfully applied to the case of an another AMP, XTE J1807-294.
Results. We report a precise set of orbital ephemeris. We demonstrate that the companion star is a main-sequence star. We find pulse phase delay fluctuations on the first harmonic with a characteristic amplitude of about 0.05, similar to those also observed for the AMP XTE J1814-338. For the second time, an AMP shows a third harmonic detected during the entire outburst. The first harmonic phase delays exhibit a puzzling behaviour, while the second harmonic phase delays clearly spin-up. The third harmonic also shows a spin-up, although not highly significant (3σ c.l.). The presence of a fourth harmonic is also reported. If we assume that the second harmonic is a good tracer of the spin frequency of the neutron star, we infer a mean spin frequency derivative for this source of 1.65(18) × 10-13 Hz s-1.
Conclusions. To interpret the pulse phase delays of the four harmonics, we apply the disk threading model, but obtain different and incompatible Ṁ estimates for each harmonic. In particular, the phase delays of the first harmonic are heavily affected by phase noise, and consequently, on the basis of these data, it is not possible to derive a reliable estimate of Ṁ. The second harmonic gives a Ṁ consistent with the flux assuming that the source is at a distance of 6.3 kpc. The third harmonic gives a lower Ṁ value, with respect to the first and second harmonic, and this would reduce the distance estimate to 3.6 kpc.
Key words: stars: neutron / stars: magnetic field / pulsars: general / pulsars: individual:IGR J17511-3057 / X-rays: binaries
© ESO, 2011
1. Introduction
Accretion-powered millisecond pulsars (hereafter AMPs) are transient low mass X-ray binaries, that exhibit a coherent modulation of their X-ray fluxes with periods of the order of few milliseconds. In the recycling scenario, AMPs are seen as the progenitors of millisecond radio pulsars (see e.g. van den Heuvel 1984), the accretion process being responsible for the spinning up of the neutron star (hereafter NS) to millisecond periods.
The AMP IGR J17511-3057 was discovered by INTEGRAL on 12 September, 2009 during a Galactic bulge monitoring programme (Baldovin 2009). Although very close to the previously known AMP XTE J1751-305, the source position measured by INTEGRAL implied that it was a newly discovered X-ray source. The observation of a coherent modulation of the X-ray flux in the data from a ToO observation performed by the Rossi X-ray Timing Explorer (hereafter RXTE) with a period of about 4 ms permitted Markwardt et al. (2009b) to classify IGR J17511-3057 as an AMP and confirmed it as a new transient X-ray source. Altamirano et al. (2010) reported the presence of burst oscillations at the NS frequency. An analysis of a Chandra observation by Nowak et al. (2009) gave the best source position with an uncertainty of 0.6′′. IGR J17511-3057 was observed by Swift and the data analysed by Bozzo et al. (2010), which provided a description of the X-ray spectrum. Torres et al. (2009) reported a possible near-infrared counterpart. Considering a ToO XMM-Newton observation, Papitto et al. (2010) obtained a set of orbital parameters and performed a detailed analysis of the X-ray spectrum. Riggio et al. (2009), analysing a RXTE observation, refined these orbital parameters. Miller-Jones et al. (2009) set an upper limit on the radio emission. Surprisingly, another transient X-ray source (XTE J1751-305) went into outburst very near the position of IGR J17511-3057 on 7 October, 2009 (Chenevez et al. 2009); its pulsations were detected by RXTE (Markwardt et al. 2009a) while observing IGR J17511-3057, which faded beneath its detection threshold on 8 October, 2009.
In this paper, we present a detailed timing analysis of the RXTE ToO observation of the source IGR J17511-3057.
2. Observation and data analysis
We analyse an RXTE observation of IGR J17511-3057. In particular, we use data from the PCA (proportional counter array) instrument board on the RXTE satellite (ObsId P94041 and P94042). We used data collected in event packing mode, with time and energy resolutions of 122 μs and 64 energy channels, respectively. We selected data in the energy range 2–25 keV to maximise the signal-to-noise ratio, since above ~20 keV the background is the dominant signal.
 |
Fig. 1 PCU 2 count rate (2–25 keV), subtracted of its background, is reported as a function of time during the outburst. The superimposed model represents the best fit using a piecewise linear function. The abrupt flux increase at the end of the outburst is due to the onset of an outburst from the AMP XTE J1751-305. The dashed vertical lines correspond to the type-I bursts present in the observation, while the continuous vertical lines correspond to the slope change, which depends on the model used to describe the count rate. The filled circles are relative to the ObsId 94041, while the triangles are the XTE J1751-305 observation (ObsId 94042). |
The X-ray flux follows a piecewise linear decay as showed in Fig. 1, with a peak flux of 70 counts s-1 PCU-1. The re-brightening visible in Fig. 1, 24 days after the start of the observation, is due to the AMP XTE J1751-305 in the field of view of RXTE going into outburst. The analysed data cover the time span from 12 September 2009 (MJD 55 086.8) to 22 October 2009 (MJD 55 126.8). We corrected the photon arrival times for the motion of the Earth-spacecraft system with respect to the Solar System barycentre and reported them as barycentric dynamical times at the Solar System barycentre using the faxbary tool (DE-405 solar system ephemeris). We used the Chandra source position reported by Nowak et al. (2009), which is reported in Table 1. The uncertainty in the source position quoted by Nowak et al. (2009) is 0.6′′, at the 1σ confidence level.
2.1. Derivation of the orbital ephemeris
To obtain a first estimate of the mean spin frequency, we produced a power spectrum from
the first data file of the ObsID 94041-01-01-00. This was obtained averaging 53 power
spectra 64-seconds long each and using a bin size of 2-11 s. We found a strong
signal at ~244.81 Hz, in good agreement with the value reported by Markwardt et al. (2009b). We divided the observation
into time intervals of about 400 s each and performed an epoch folding search on each data
interval around the averaged spin period with a period resolution of
4 × 10-9 s. For each time interval, we obtained an estimate of the best
spin period. We excluded all the intervals for which the maximum in the
χ2 curve was not significant (3σ c.l.),
according to the criterion stated by Leahy et al.
(1983). A sinusoidal Doppler modulation of the spin period due to the source
motion in the binary system was evident. We fitted the Doppler frequency shifts with the
formula 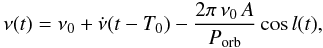 (1)where
ν0 is the spin frequency at the time
T0,
(1)where
ν0 is the spin frequency at the time
T0, 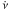 is the spin frequency derivative, A is the ratio of the projected orbit
semi-major axis to the speed of light, and
l(t) = 2π(t − T ⋆ )/Porb,
where T ⋆ is the time of passage through the
ascending node and Porb is the orbital period. With a
reduced χ2 (hereafter
is the spin frequency derivative, A is the ratio of the projected orbit
semi-major axis to the speed of light, and
l(t) = 2π(t − T ⋆ )/Porb,
where T ⋆ is the time of passage through the
ascending node and Porb is the orbital period. With a
reduced χ2 (hereafter
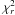 and defined
as χ2/d.o.f.) of 0.59(532.2/898), we obtained a first set of
orbital parameters and a much more reliable estimate of the barycentric spin frequency.
and defined
as χ2/d.o.f.) of 0.59(532.2/898), we obtained a first set of
orbital parameters and a much more reliable estimate of the barycentric spin frequency.
Orbital and spin parameters for IGR J17511-3057.
Using this preliminary orbital solution, we analysed the pulse phase delays to get a more precise estimate of the orbital and spin parameters. We epoch-folded data across time intervals of about 1500 s using 32 phase channels. An example of the folded pulse profile is shown in Fig. 2.
 |
Fig. 2 A folded pulse profile is shown. For clarity, two spin cycles are plotted. The continuous line is the best-fit using first, second, and third harmonics. We also report the single contribution to the profile of the first harmonic (dotted line), second harmonic (dot-dashed line), third harmonic (bi-dot dashed line), and fourth harmonic (dashed line). |
A harmonic decomposition of each pulse profile up to the fourth harmonic was necessary.
To do that we fitted each normalised pulse profile using the expression 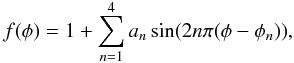 (2)where
a1, a2,
a3, and a4 are the sinusoidal
semi-amplitudes (hereafter fractional amplitudes) of the first, second, third, and fourth
harmonics, respectively, and φ1,
φ2, φ3, and
φ4 their corresponding phases. We rejected the pulse phase
delays for which the following two conditions were not both satisfied: i) the signal is
not detected at least at a 3σ confidence level (Leahy et al. 1983); ii) the best-fit fractional amplitude had to be at
least 3σ from the zero level
(ai/δai ≥ 3).
(2)where
a1, a2,
a3, and a4 are the sinusoidal
semi-amplitudes (hereafter fractional amplitudes) of the first, second, third, and fourth
harmonics, respectively, and φ1,
φ2, φ3, and
φ4 their corresponding phases. We rejected the pulse phase
delays for which the following two conditions were not both satisfied: i) the signal is
not detected at least at a 3σ confidence level (Leahy et al. 1983); ii) the best-fit fractional amplitude had to be at
least 3σ from the zero level
(ai/δai ≥ 3).
We first tried to fit the pulse phase delays with a polynomial to describe the pulse phase delay long-term fluctuations plus the usual formula φorb(t), describing the pulse phase residuals due to differential corrections to the initial orbital parameter estimates (Deeter et al. 1981; see e.g. Riggio et al. 2007)
We attempted to describe the phase fluctuations using a polynomial up to the ninth degree
to fit obtaining a 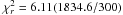 , which is formally
unacceptable.
, which is formally
unacceptable.
Owing to the presence of these phase fluctuations, we decided to apply the timing technique described in Riggio et al. (2007) to separate the orbital modulation from the phase fluctuations, to obtain more accurate estimates of the orbital parameters.
Following Riggio et al. (2007), we define the
pulse phase differences as 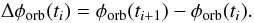 (3)We excluded all the
points for which
ti+1 − ti > Porb
to optimise the filter efficiency (Riggio et al.
2007).
(3)We excluded all the
points for which
ti+1 − ti > Porb
to optimise the filter efficiency (Riggio et al.
2007).
We iterated the process until convergence. In the last iteration (see Fig. 3), 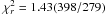 , which represents a far
closer fit than the previous approach. The orbital ephemeris best-fit results are reported
in Table 1, where the errors have been multiplied
by the factor
, which represents a far
closer fit than the previous approach. The orbital ephemeris best-fit results are reported
in Table 1, where the errors have been multiplied
by the factor 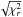 (Bevington & Robinson 2003).
(Bevington & Robinson 2003).
 |
Fig. 3 In the top panel of this figure the pulse phase delays (filled squares) and the corresponding pulse phase delay differences (filled circles) of the data corrected with the orbital ephemeris obtained from the fit to the frequency Doppler shifts are reported. Each pulse phase point is obtained by fitting the folded pulse profile over about 1500 s of data. It is evident that there is no trace of this fluctuation in the pulse phase delay differences, giving a striking confirmation of the goodness of the method. In the bottom panel, we report the residuals (in σ units) with respect to the best fit orbital solution derived from the pulse phase delay differences using the timing technique described in the text. |
The values obtained are in perfect agreement with those reported by Papitto et al. (2009) from an analysis of a XMM-Newton observation and by Riggio et al. (2009) on the basis of RXTE data covering a shorter time interval. The measured uncertainties in the orbital parameters are a factor of two smaller than the best-fit orbital solution previously given by Riggio et al. (2009). We also note that the orbital period we derive here has a relative uncertainty as small as 0.03%.
To fit the pulse phase delays with a physically meaningful torque that takes into account the decreasing X-ray flux (hence Ṁ, where the X-ray flux is a good tracer of the mass accretion rate onto the NS), we need to describe the flux evolution during the outburst, i.e. both the bolometric flux at the peak of the outburst and the shape of the light curve.
To estimate the bolometric flux of the source at the peak of the outburst, we considered
the spectrum collected by the PCA in Standard 2 Mode (129 energy channels recorded at a
time resolution of 16 s) during Obs. 94041-01-01-04, which started on 55 089.283 MJD and
had a total exposure of 10 480 s. We considered only data taken by the PCU2 to avoid
cross-calibration problem between PCUs. We selected only events detected in its top Xenon
layer to maximise the signal-to-noise ratio (Jahoda et al.
2006). The background was modelled using the bright source model, which is
appropriate for sources emitting >40 c s-1 PCU-1. We used
the latest version (11.7) of the PCA response matrix generator, restricting ourselves to
the 3–50 keV band and adding a systematic error of 0.5% to spectral counts1. As observed for other AMPs, the X-ray emission of
IGR J17511-3057 is dominated by power-law-like
emission extending to high (>50 keV) energies. We modelled this using a simple
thermal Comptonisation model (nthcomp, Zdziarski et al.
1996; Życki et al. 1999), fixing the
temperature of the hot electrons to 100 keV. Given the poor coverage of the PCA at low
energies, we also constrained the absorption column to be nH =
1 × 1022 cm-2, as suggested by an
XMM-Newton observation performed during the same outburst (Papitto et al. 2010). A 6.6 keV emission line was also
added to model residuals in the iron range, though this feature is probably due to the
contamination of the Galactic ridge in the field of view of the PCA (Markwardt et al. 2009b). The reduced chi-square of the fit is good
(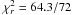 ). The
unabsorbed flux we detect in the 3–50 keV band is
1.14(1) × 10-9 erg cm-2 s-1, which extrapolated
to the 0.5–200 keV band infers a flux there of
~2 × 10-9 erg cm-2 s-1. Under the
hypothesis that emission is isotropic, this corresponds to a bolometric luminosity of
Lx ~ 1.5 × 1037
). The
unabsorbed flux we detect in the 3–50 keV band is
1.14(1) × 10-9 erg cm-2 s-1, which extrapolated
to the 0.5–200 keV band infers a flux there of
~2 × 10-9 erg cm-2 s-1. Under the
hypothesis that emission is isotropic, this corresponds to a bolometric luminosity of
Lx ~ 1.5 × 1037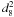 erg s-1,
where d8 is the distance to the source in units of 8 kpc. We
note that an upper limit of 10.6 kpc on the source distance was set by Bozzo et al. (2010), by insisting that the burst peak
luminosity does not exceed the Eddington limit, while Altamirano et al. (2010), from the analysis of the type-I bursts observed by
RXTE and Swift found an upper limit of 6.9 kpc. On
the basis of the spectral analysis of XMM-Newton data, Papitto et al. (2010) also gave a lower limit of
≃7 kpc, which was, however, based on some assumptions. Moreover, as the source is only a
few degrees away from the Galactic centre and its X-ray emission is not heavily absorbed
(nH ~ 1022 cm-2), it is highly probable
that the distance does not exceed 8 kpc. Assuming that
LX = ϵGMṀ/R
with ϵ ≃ 1, we eventually deduce a peak mass accretion rate of the order
of ≃1.5 × 10-9
erg s-1,
where d8 is the distance to the source in units of 8 kpc. We
note that an upper limit of 10.6 kpc on the source distance was set by Bozzo et al. (2010), by insisting that the burst peak
luminosity does not exceed the Eddington limit, while Altamirano et al. (2010), from the analysis of the type-I bursts observed by
RXTE and Swift found an upper limit of 6.9 kpc. On
the basis of the spectral analysis of XMM-Newton data, Papitto et al. (2010) also gave a lower limit of
≃7 kpc, which was, however, based on some assumptions. Moreover, as the source is only a
few degrees away from the Galactic centre and its X-ray emission is not heavily absorbed
(nH ~ 1022 cm-2), it is highly probable
that the distance does not exceed 8 kpc. Assuming that
LX = ϵGMṀ/R
with ϵ ≃ 1, we eventually deduce a peak mass accretion rate of the order
of ≃1.5 × 10-9 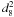 M⊙ yr-1,
which is the estimate we use in the following to compare the dynamical estimates of
Ṁ from the timing analysis.
M⊙ yr-1,
which is the estimate we use in the following to compare the dynamical estimates of
Ṁ from the timing analysis.
To describe the light curve shape, we chose to fit it with a piecewise linear function composed of three segments, as shown in Fig. 1. We fitted only the first 23 days of data since the subsequent data are affected by the concomitant XTE J1751-305 outburst. We modelled each of the three intervals with a function ci(t) = ci(1 − (t − Ti)/τi),Ti ≤ t < Ti+1, where ci is the count rate at t = Ti and τi the linear decay timescale for the ith piece. For the sake of simplicity, we wrote this piecewise function as c0f(t), where c0 is the count rate at the peak. The best-fit result is reported in Fig. 1.
2.2. Timing analysis
The spin frequency evolution in AMPs is thought to be driven by the accretion process. Matter falling from the accretion disk onto the NS transfers its angular momentum to the NS, which is spun-up to millisecond spin periods. However, as was evident from the first attempts (Ghosh et al. 1977), the magnetic field-accretion disk interaction can exert a negative torque onto the NS, spinning it down. This is called the threaded disk model. Owing to the complexity of the problem, the details of the NS magnetosphere-disk interaction are still not well understood. Three examples of AMPs that spin-down while accreting have been reported (Galloway et al. 2002; Burderi et al. 2006; Papitto et al. 2008).
As already observed in another two AMPs (see e.g. Burderi et al. 2007, for SAX J1808.4-3658; and Riggio et al. 2008, for XTE J1807-294), for this source the first harmonic is also dominated by fluctuations and then unusable for our scope. We note that the two AMPs cited above (SAX J1808.4-3658 and XTE J1807-294) display a second harmonic with a more regular behaviour.
An alternative interpretation of the pulse frequency derivatives was given by Hartman et al. (2008), who suggested that the red
timing noise affecting the pulse phase delays can mimic a spin frequency derivative. Patruno et al. (2009) attempted to demonstrate that the
pulse phase delays are correlated with the X-ray flux, rather than the genuine spin
evolution of the source, produced by the motion of the hot-spot related to the flux.
Unfortunately, this correlation is not clear, even in the sign, in all AMPs and differs,
in the same sources (see e.g. SAX J1808.4-3658 and XTE J1807-294), for each harmonic
component, as noted by Patruno et al. (2009). We
tested this hypothesis using the method described in Patruno et al. (2009), adopting a constant spin frequency model to derive the
pulse phase residuals. For the best-fit solution that maximises the linear correlation
between the phase residuals and flux, we obtained 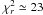 (4625/201 d.o.f.), indicating that, for this source, the pulse phase residuals of the
first harmonic cannot be ascribed to flux variation and/or fluctuations.
(4625/201 d.o.f.), indicating that, for this source, the pulse phase residuals of the
first harmonic cannot be ascribed to flux variation and/or fluctuations.
In the following, we will work under widely accepted hypothesis that the pulse frequency is the NS spin frequency. We analyse the pulse phase delays and apply to them a disk threading model to derive the Ṁ and compare this value with that obtained from the spectral analysis of the same data.
We epoch-folded data across time intervals of about 3.0 ks (one pulse profile per data file) and 32 phase bins. A third harmonic was detected throughout the outburst. A fourth harmonic was also detected in the first 15 days of the outburst. In Figs. 4–7 the first, second, third, and fourth harmonic pulse phase delays are reported, respectively. The fractional amplitudes, as defined in Eq. (2), were corrected to take into account the instrumental background (~11 counts s-1 PCU-1 in the 2–25 keV energy band) and the background due to the presence of the Galactic ridge in the field of view of RXTE (Markwardt et al. 2009b). To estimate this supplementary background, we used the observations of the AMP XTE J1751-305 when both sources went to quiescence, in particular the observations from MJD 55 115.400 to 55 126.745, which represent a total exposure time of 33.7 ks. Owing to the low count rate, we used the faint background model, obtaining a count-rate of ~7 counts s-1 PCU-1 in the same energy band. In Fig. 8, the fractional amplitudes for the four harmonics are reported.
The mean spin frequency reported in Table 1 is obtained by fitting the first harmonic pulse phase delays with a constant spin frequency model. The value obtained in this way for the spin frequency is ν = 244.8339515569(24) Hz. However, the systematic effects due to the uncertainty of 0.6′′ (Nowak et al. 2009) in the source position brings the mean spin frequency error to 7 × 10-8 Hz (see Burderi et al. 2007).
2.2.1. First harmonic
We started fitting the first harmonic pulse phase delays with a constant spin frequency
derivative to estimate the mean spin frequency derivative. From the fit we obtained
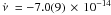 Hz s-1
with a
Hz s-1
with a 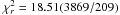 ,
clearly unacceptable.
,
clearly unacceptable.
To improve this result, we used the threaded disk model previously applied to the AMPs
by Rappaport et al. (2004). According to this
model, the net torque acting on an AMP is 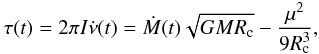 (4)where
I is the NS moment of inertia, Ṁ is the mass
accretion rate, M is the mass of the NS, μ is the
magnetic dipole moment of the NS, and Rc the co-rotation
radius.
(4)where
I is the NS moment of inertia, Ṁ is the mass
accretion rate, M is the mass of the NS, μ is the
magnetic dipole moment of the NS, and Rc the co-rotation
radius.
To apply this model to our data, we required an expression for Ṁ(t). We then assumed that the bolometric luminosity L(t) is a good tracer of Ṁ. For the hypothesis that the spectral variation during the outburst is insignificant, it is possible to assume that L(t) is proportional to the background subtracted count rate. We can then write Ṁ(t) = Ṁmax f(t), where Ṁmax is the maximum accretion rate corresponding to the flux peak and f(t) is the functional form of the count rate previously derived.
An expression for
ν̇
as a function of Ṁ can easily be derived from Eq. (4) to be ![\begin{equation} \label{eq_nudot} \nudot(t) = \!\Biggl[1.427\;\frac{m^{2/3} P^{1/3}_{-3} \dot{M}_{^{\rm max}_{-10}}}{I_{45}} f(t)- \\ 5.232\; \frac{\mu^2_{26}}{mI_{45}P^2_{-3}} \!\Biggr]~ \times 10^{-14} \;\textrm{Hz s}^{-1}, \end{equation}](/articles/aa/full_html/2011/02/aa14322-10/aa14322-10-eq87.png) (5)where
m is the NS mass in units of M⊙,
(5)where
m is the NS mass in units of M⊙,
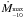 is the maximum mass accretion rate in units of
10-10 M⊙ y-1,
P-3 the spin period in units of 10-3 s, and
I45 the NS moment of inertia in
1045 g cm2. In this work, we adopted the FPS (Friedman
Pandharipande Skyrme, see Friedman &
Pandharipande 1981; Pandharipande &
Ravenhall 1989) equation of state for which, fixing NS mass to be
M = 1.4 M⊙, we obtain a radius of
RNS = 1.14 × 106 cm and a moment of inertia
I = 1.29 × 1045 g cm2.
is the maximum mass accretion rate in units of
10-10 M⊙ y-1,
P-3 the spin period in units of 10-3 s, and
I45 the NS moment of inertia in
1045 g cm2. In this work, we adopted the FPS (Friedman
Pandharipande Skyrme, see Friedman &
Pandharipande 1981; Pandharipande &
Ravenhall 1989) equation of state for which, fixing NS mass to be
M = 1.4 M⊙, we obtain a radius of
RNS = 1.14 × 106 cm and a moment of inertia
I = 1.29 × 1045 g cm2.
The pulse phase delay formula used for the fit is obtained by doubly integrating Eq. (5) with respect to time (see e.g. Burderi et al. 2007).
From the fit of the first harmonic, we obtained a magnetic dipole strength of
μ = 1.64(7) × 1027 G cm3 and
Ṁmax =
5.7(6) × 10-9 M⊙ y-1, with a
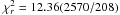 ,
which is still unacceptable. The results are reported in Fig. 4.
,
which is still unacceptable. The results are reported in Fig. 4.
 |
Fig. 4 In the top panel, we show the first harmonic pulse phase delays and the best-fit curves, considering a constant spin frequency derivative (dashed line) and the disk threading model proposed by Rappaport et al. (2004). In the bottom panel, we show the residuals (in σ units) of the first harmonic with respect to the best-fit model given by the threaded disk. |
This large 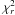 is clearly
due to fluctuations in the pulse phase delays, as it is possible to see in the best-fit
residuals reported in Fig. 4 (bottom panel).As
anticipated, we unsuccessfully tried to interpret it with the model suggested by Patruno et al. (2009). The origin of these
fluctuations remains unexplained.
is clearly
due to fluctuations in the pulse phase delays, as it is possible to see in the best-fit
residuals reported in Fig. 4 (bottom panel).As
anticipated, we unsuccessfully tried to interpret it with the model suggested by Patruno et al. (2009). The origin of these
fluctuations remains unexplained.
2.2.2. Second harmonic
For the second harmonic that is less affected by phase noise (Burderi et al. 2006; Riggio et al.
2008), we repeated the fitting procedure using these phase delays. In the
constant spin frequency derivative case, we obtained
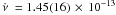 Hz s-1
with a
Hz s-1
with a 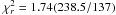 . The best-fit curve is
reported in Fig. 5. We adopted the same disk
threading expression used for the first harmonic to describe the second harmonic. In
this case, we had to assume that μ = 0 since μ and
Ṁmax strongly correlate. In this case, therefore, the
derived value of Ṁmax has to be considered as a lower limit
to the mass accretion rate at the peak of the outburst, since the value of the magnetic
moment higher than zero will give a higher value for Ṁmax.
. The best-fit curve is
reported in Fig. 5. We adopted the same disk
threading expression used for the first harmonic to describe the second harmonic. In
this case, we had to assume that μ = 0 since μ and
Ṁmax strongly correlate. In this case, therefore, the
derived value of Ṁmax has to be considered as a lower limit
to the mass accretion rate at the peak of the outburst, since the value of the magnetic
moment higher than zero will give a higher value for Ṁmax.
 |
Fig. 5 In the top panel of this figure, the second harmonic pulse phase delays are shown. The dashed and the continuous lines are the second harmonic best-fit curves considering a constant spin frequency derivative and the physical model considering the material torque proportional to the flux, respectively. In the bottom panel, the residuals (in σ units) of the second harmonic with respect the constant spin frequency derivative are shown. |
The best-fit results are reported in Table 1. In
this case, the best-fit value of Ṁmax=
0.92(10) × 10-9 M⊙ year-1, with
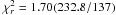 , is in good agreement
with our estimate of the bolometric flux for a source distance of about 6.3(3) kpc.
, is in good agreement
with our estimate of the bolometric flux for a source distance of about 6.3(3) kpc.
2.2.3. Third harmonic
Since in this source, the third harmonic is significantly detected in nearly the whole
outburst we proceeded with the same method used for the first and second harmonic. From
the fit with the constant spin frequency derivative, we obtained
ν = 244.83395151(6) Hz and 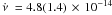 Hz s-1 with a
Hz s-1 with a 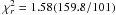 . The best-fit curve is
reported in Fig. 6. We applied the threaded disk
model to describe the third harmonic and, as already done for the second harmonic, we
fixed μ = 0 since μ and
Ṁmax correlate in the fit.
. The best-fit curve is
reported in Fig. 6. We applied the threaded disk
model to describe the third harmonic and, as already done for the second harmonic, we
fixed μ = 0 since μ and
Ṁmax correlate in the fit.
 |
Fig. 6 In the top panel of this figure, we report the third harmonic pulse phase delays and its best-fit curves considering a constant spin frequency derivative (dashed line) and the physical model considering the material torque proportional to the flux (continuous line). In the bottom panel, we show the residuals in units of σ with respect to the constant spin frequency derivative model. |
The obtained best-fit values are Ṁmax=
3.1(9) × 10-10 M⊙ year-1 for
the peak mass accretion rate and ν = 244.83395150(6) Hz with a reduced
χ2 of 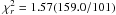 . The third harmonic shows
a spin-up, which is not however highly significant (≳3σ c.l.). The
peak mass accretion rate deduced is quite low compared to the one obtained from the
bolometric flux for a source distance of 6.3(3) kpc. The source distance is about
3.6(5) kpc.
. The third harmonic shows
a spin-up, which is not however highly significant (≳3σ c.l.). The
peak mass accretion rate deduced is quite low compared to the one obtained from the
bolometric flux for a source distance of 6.3(3) kpc. The source distance is about
3.6(5) kpc.
2.2.4. Fourth harmonic
The fourth harmonic is sporadically detected in the first 15 days of the outburst, with
a fractional amplitude of ~1%. From the fit with the constant spin frequency
derivative, we obtained 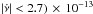 Hz s-1 (2σ c.l.) with a
Hz s-1 (2σ c.l.) with a
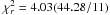 . The best-fit curve is
reported in Fig. 7.
. The best-fit curve is
reported in Fig. 7.
 |
Fig. 7 In the top panel of this figure, the fourth harmonic pulse phase delays and its best-fit curves considering a constant spin frequency derivative (dashed line) and the physical model considering the material torque proportional to the flux (continuous line) are reported. In the bottom panel, we show the residuals in units of σ with respect to the constant spin frequency derivative model. |
The obtained best-fit values are
Ṁmax < 1.6 × 10-9 M⊙
year-1 (2σ c.l.) for the peak mass accretion rate with a
reduced χ2 of 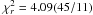 .
.
We note that, as already done in Burderi et al. (2007) and Riggio et al. (2008), we take into account the effect of the source position uncertainty on the obtained values of ν and ν̇ adopting the same method described in Riggio et al. (2008).
 |
Fig. 8 The fractional amplitudes of the four harmonics are reported. Points in correspondence with the type-I bursts are not plotted due to difficulties in estimating the persistent flux. |
In particular, in the case of constant spin frequency derivative the uncertainties are
about Δν = 6.1 × 10-8 Hz in the frequency and
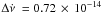 Hz s-1 in the spin frequency derivative, while in the case of the physical
model the uncertainties are about Δν = 6.1 × 10-8 Hz
in the frequency and
ΔṀ = 4.3 × 10-11M⊙
y-1 in the peak accretion rate.
Hz s-1 in the spin frequency derivative, while in the case of the physical
model the uncertainties are about Δν = 6.1 × 10-8 Hz
in the frequency and
ΔṀ = 4.3 × 10-11M⊙
y-1 in the peak accretion rate.
 |
Fig. 9 In the left panel, the phase lags for the first three harmonics are reported. The phase lags are measured with respect to the maxima of each component, as done in Papitto et al. (2010). In the right panel, the fractional amplitude for the three harmonics are reported. |
2.3. Spectral variability of the pulse profile
Emulating Papitto et al. (2010) who analysed the XMM-Newton observation of the same outburst, we analysed the energy dependence of the phase and amplitude of the three harmonic components. To achieve high quality statistics, we epoch-folded data from 55 089.233 MJD to 55 092.5379 MJD, excluding the three data files where a type-I burst was present, with an exposure time of 81 ks and a coverage of 28%. We chose this interval because the pulse phase delays have a quite stable linear trend with an average first harmonic phase scattering of 0.005. We consider only data from PCU2. We also evaluated the contribution to the background from the Galactic bulge, using the data described in the previous section, in the working hypothesis that the changes due to the different observational data and slightly different instrument pointing are small (see Papitto et al. 2010, for a detailed discussion). For these reasons, small systematics might be present and the confidence intervals might be underestimated. The fractional amplitude of the first harmonic (Fig. 9, right panel) increases from 17.5(3)% at 2.5 keV to 26.7(3)% at 6 keV. It remains roughly constant around 23% up to 12 keV, where the fractional amplitude is 25.4(3)%. Above 12 keV, there is a steady decline of the fractional amplitude, although up to the energy band 25–60 keV it is still clearly detectable with a fractional amplitude of 5.2(3)%. The second and third harmonic fractional amplitudes show a behaviour similar to the first harmonic one that increases with energy to a maximum (around 10–20 keV) of 3.7(4)% and 2.2(4)%, respectively. We also observe a decline in the fractional amplitude above 20 keV for these harmonics. Fractional amplitudes as a function of photon energies were not clearly detected for the fourth harmonic, probably because of the long integration time and the smearing caused by the observed fourth harmonic phase fluctuations of ~0.05 (see Fig. 7), which is a considerable fraction of the fourth harmonic period. The first harmonic displays phase lags (reported in Fig. 9, left panel). As described in Papitto et al. (2010), there is a steady decrease in the phase lag up to ~10 keV, where a break is clearly visible. Beyond 10 keV, the pulse phase lag still decreases, but at a lower rate.
 |
Fig. 10 Two type-I burst timing analysis is reported. For each burst in the top panel, the PCU2 count rate of the type-I burst present in this observation, in the middle panel the pulse phase delays and in the bottom panel the fractional amplitude are reported. |
The second harmonic shows a different trend with respect to the first harmonic. It reaches the maximum lag around 10 keV, shows no time lag at 25 keV, but then experiences a sudden jump of ~–450 μs between 25 and 50 keV.
The third harmonic phase lags are roughly constant throughout the energy band. We note that in the energy band 25.7–59.8 keV the phase lags for the second and third harmonic coincide.
2.4. Type-I burst timing
We performed a timing analysis of all the 10 type-I bursts detected in the observation, with the goal of studying the pulse profile evolution during the burst. In Fig. 10, we show the results for the second and fifth type-I bursts, the most finely sampled of the bursts in the RXTE observation. The starting date of these bursts is 55 089.721 MJD (TDB) and 55 094.619 MJD (TDB), and the decay time is 8.0(1) s and 8.5(1) s, respectively. We divided each burst in chunks holding (roughly) the same number of events so that in each folded profile a fractional amplitude of ~20% can be easily detectable. We folded each chunk using 8 phase bins and performed an harmonic decomposition using only the first harmonic. The results of this analysis are reported in Fig. 10. During both bursts, the pulse phase delays remain stable and, with the exception of the very first seconds, locked to the pulse phase delays during the persistent emission (see Fig. 10, mid panel). The fractional amplitude behaviour is even more interesting because it is, within the errors, quite constant during both bursts and locked at the pre-burst value (Fig. 10, bottom panel). A detailed spectral and temporal analysis of all these type-I bursts was reported by Altamirano et al. (2010), although with different techniques.
3. Discussion
Among the AMPs known, IGR J17511-3057 displays several peculiarities. The highest first harmonic fractional amplitude of the source has a peak value (background corrected) at the beginning of the outburst of about 23% that linearly decrease to 17% at the end of the outburst (see Fig. 8), while the highest ever observed fractional amplitude was observed by Patruno et al. (2010) in XTE J1807-294.
The pulse shape is complex, showing, on integration times of 3 ks, a second harmonic, a third harmonic and sporadically a fourth harmonic with fractional amplitudes of 2.5%, 1.6%, and 1%, respectively (see Fig. 8). A third harmonic as strong as the second harmonic could be, following Poutanen & Beloborodov (2006), an indication that both hot spots are visible with the secondary spot only partially visible, since for a single spot the third harmonic should be much smaller than the second harmonic (a2/a3 ≳ 5, Poutanen & Beloborodov 2006), suggesting intermediate values for the inclination angle. In the AMPs, Hartman et al. (2008) reports a sporadically detectable third harmonic in SAX J1808.4-3658, while Patruno et al. (2010) detected sporadically a third and a fourth harmonic in XTE J1807-294.
That in IGR J17511-3057, the third harmonic is visible for nearly all the outburst with a total of 105 detections over 216 folded pulse profiles makes this source peculiar.
Moreover, while the fractional amplitude of the first harmonic clearly shows a steady decrease with the flux, this decrease is less evident in the second and third harmonics, for which the fractional amplitude remains more stable when the X-ray flux decreases (see Fig. 8).
However, the most interesting and puzzling result is the different behaviours of the phase
delays for the four harmonic components. In particular, as for the other AMPs, such as
SAX J1808.4-3658 and XTE J1807-294 (see e.g. Burderi et al.
2007; Hartman et al. 2008, 2009; Riggio et al.
2008; Patruno et al. 2010), the first
harmonic has clear phase fluctuations (see Fig. 4). A
discussion about the results based on the analysis of the first harmonic is strongly
affected by these phase fluctuations. We can only speculate about the nature of these
fluctuations. The amplitude of these fluctuations, ~0.05 in phase units, may
corresponds to hot spot movements of ~18 degrees, already seen in numerical
simulations (see Romanova et al. 2004; Bachetti et al. 2010), although on timescales of fractions
of seconds, while the observed timescales are of a few days. We also tried to interpret
these phase fluctuations with the model suggested by Patruno
et al. (2010). We adopted a constant spin frequency model and a linear relation
between flux and pulse phase residuals. The most closely fitting correlation parameter set
gave a 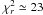 , which is clearly unacceptable. A
model to describe and correctly interpret these fluctuations needs to be developed.
, which is clearly unacceptable. A
model to describe and correctly interpret these fluctuations needs to be developed.
However, under the working hypothesis that some exchange of angular momentum between the NS and the accreting matter has to occur during X-ray outbursts, when the accretion rate is at its maximum, we try to interpret the behaviour of the phase delays of the second and third harmonic, which appear to be less affected by phase fluctuations. That the phase delays derived from the second harmonic appear more stable than those derived from the first harmonic has been observed, for instance, during the 2002 outburst from SAX J1808.4-3658. Burderi et al. (2007) showed that, while the first harmonic phase delays clearly show a phase shift at days 14 from the beginning of the 2002 outburst, a similar phase shift was not present in the phase delays derived from the second harmonic. A similar behaviour was also observed by Riggio et al. (2008) for the AMP XTE J1807-294, which went onto outburst just once in 2003 in the RXTE era. In both these cases, the interpretation of the phase delays derived from the second harmonic in terms of accretion torques provided reasonable spin frequency derivatives (and inferred mass accretion rates onto the NS), although a different interpretation was given for both sources by Hartman et al. (2009); Patruno et al. (2009). These results have naturally to be taken with great caution, since phase fluctuations may still affect phase delays derived from the second (or higher) harmonic.
For IGR J17511-3057, again, the second harmonic shows a more regular behaviour with respect to the first harmonic and suggests a spin-up of the NS (see Fig. 5). From the fit with our simplified torque model, we obtain an Ṁ estimate, fixing μ = 0, of Ṁmax = 0.92(10) × 10-9 M⊙ year-1, which would be compatible with the observed X-ray flux from the source if we placed the source at a distance of 6.3 kpc. This could indirectly suggest that the second harmonic component is a better tracer of the spin frequency evolution, even if a physical model that explains all the phenomenology observed in all the AMPs still needs to be developed. Results obtained on the second harmonic give, as in the case of the AMPs SAX J1808.4-3658 (Burderi et al. 2006; Hartman et al. 2009) and XTE J1807-294 (Riggio et al. 2008), reasonable values for the physical parameters of the system.
However, if we consider the third harmonic we find that it shows a spin-up that is not however highly significant (≳3σ) and smaller than the value inferred for the second harmonic. The lower limit to the accretion rate Ṁmax = 3.1(9) × 10-10 M⊙ year-1 implies a distance of 3.6(5) kpc, at ~5σ based on the value inferred from the second harmonic. This value is not compatible with the second harmonic one. The lack of literature and observations of the third harmonic behaviour in other AMPs does not allow us to compare with other cases, leaving this question open.
A fourth harmonic was detected sporadically during the outburst. We attempted to fit the pulse phase delays with the same models adopted for the other harmonics but the result was inconclusive. We note that the fourth harmonic is affected by phase fluctuations (~0.02) that are comparable to the first harmonic’s fluctuations. It is probable that integrating on long timescales, the large fluctuations make the detection of the fourth harmonic unfeasible.
We performed a high-resolution timing analysis of all the type-I bursts present in this RXTE observation. The results are very similar for all the bursts, and we show bursts 2 and 5 (see Fig. 10) since these are the most finely sampled in the RXTE observation. The first harmonic phase delays appear to rise in correspondence with the rapidly rising phase of the burst, implying that there had been a frequency drift during the first few seconds after the burst onset (Altamirano et al. 2010), and a return to the phase value during the persistent emission during the burst decay, giving some evidence that the burst probably starts not far from the hot spot in the polar cap. The fractional amplitude in each burst instead remains locked (within the errors) with the persistent emission value during all the burst, suggesting surprisingly that the temperature gradient does not vary during the burst. An interpretation of this behaviour is beyond the scope of this work.
From the orbital ephemeris reported in Table 1, the
pulsar mass function is fX =
1.070854(21) × 10-3 M⊙. From this value of
mass function, we can derive a minimum mass for the companion star of
0.14 M⊙, considering an inclination angle of 90° and a NS mass
of 1.4 M⊙. For this minimum mass, the companion star of
IGR J17511-3057 is one of the more massive
companion stars among the AMPs, together with XTE J1807-294 and SAX J1748.9-2021 (Altamirano et al. 2008). Using the relation
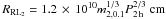 (Paczyński 1971), where m2,0.1 is the
companion mass in 0.1 M⊙ units and
P2 h is the orbital period in two-hour units, we obtain for
the companion’s Roche lobe radius a value of 0.248 R⊙. This
value is larger than expected for a low-mass main sequence star (see Chabrier & Baraffe 2000, 5 Gyr track), for which the corresponding
radius is about 0.15 R⊙. It can be shown that the contact
condition between Roche lobe and companion star pose a firm lower limit to the inclination
of the system of ~20 degrees, corresponding to a companion mass of
~0.45 M⊙. For smaller inclination angles, the
companion star would overfill its Roche lobe. This obviously excludes the companion star
being a white dwarf or an helium-core star, while strongly suggesting that the companion
star is a main sequence star, possibly bloated as a consequence of its evolutionary history
(Podsiadlowski et al. 2002) or slightly evolved
(Tutukov & Iungelson 1987). The nature of
the companion star is discussed thoroughly in Papitto et al.
(2010).
(Paczyński 1971), where m2,0.1 is the
companion mass in 0.1 M⊙ units and
P2 h is the orbital period in two-hour units, we obtain for
the companion’s Roche lobe radius a value of 0.248 R⊙. This
value is larger than expected for a low-mass main sequence star (see Chabrier & Baraffe 2000, 5 Gyr track), for which the corresponding
radius is about 0.15 R⊙. It can be shown that the contact
condition between Roche lobe and companion star pose a firm lower limit to the inclination
of the system of ~20 degrees, corresponding to a companion mass of
~0.45 M⊙. For smaller inclination angles, the
companion star would overfill its Roche lobe. This obviously excludes the companion star
being a white dwarf or an helium-core star, while strongly suggesting that the companion
star is a main sequence star, possibly bloated as a consequence of its evolutionary history
(Podsiadlowski et al. 2002) or slightly evolved
(Tutukov & Iungelson 1987). The nature of
the companion star is discussed thoroughly in Papitto et al.
(2010).
N. Shaposhnikov, K. Jahoda, C. B. Markwardt 2009, http://www.universe.nasa.gov/xrays/programs/rxte/pca/doc/rmf/pcarmf-11.7/
Acknowledgments
We thank the anonymous referee for having help us to greatly improve the paper.
We also thank Sergey B. Popov for several fruitful discussions.
This work is supported by the Italian Space Agency, ASI-INAF I/088/06/0 contract for High Energy Astrophysics.
References
- Altamirano, D., Casella, P., Patruno, A., Wijnands, R., & van der Klis, M. 2008, ApJ, 674, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Altamirano, D., Watts, A., Linares, M., et al. 2010, MNRAS, 409, 1136 [NASA ADS] [CrossRef] [Google Scholar]
- Bachetti, M., Romanova, M. M., Kulkarni, A., Burderi, L., & di Salvo, T. 2010, MNRAS, 403, 1193 [NASA ADS] [CrossRef] [Google Scholar]
- Baldovin, C. 2009, The Astronomer’s Telegram, 2196, 1 [Google Scholar]
- Bevington, P. R., & Robinson, D. K. 2003, Data reduction and error analysis for the physical sciences, 3rd Ed. (McGraw-Hill) [Google Scholar]
- Bozzo, E., Ferrigno, C., Falanga, M., et al. 2010, A&A, 509, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burderi, L., Di Salvo, T., Menna, M. T., Riggio, A., & Papitto, A. 2006, ApJ, 653, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Burderi, L., Di Salvo, T., Lavagetto, G., et al. 2007, ApJ, 657, 961 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G., & Baraffe, I. 2000, ARA&A, 38, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Chenevez, J., Kuulkers, E., Beckmann, V., et al. 2009, The Astronomer’s Telegram, 2235, 1 [NASA ADS] [Google Scholar]
- Deeter, J. E., Pravdo, S. H., & Boynton, P. E. 1981, ApJ, 247, 1003 [NASA ADS] [CrossRef] [Google Scholar]
- Friedman, B., & Pandharipande, V. R. 1981, Nuclear Physics A, 361, 502 [Google Scholar]
- Galloway, D. K., Chakrabarty, D., Morgan, E. H., & Remillard, R. A. 2002, ApJ, 576, L137 [NASA ADS] [CrossRef] [Google Scholar]
- Ghosh, P., Pethick, C. J., & Lamb, F. K. 1977, ApJ, 217, 578 [NASA ADS] [CrossRef] [Google Scholar]
- Hartman, J. M., Patruno, A., Chakrabarty, D., et al. 2008, ApJ, 675, 1468 [NASA ADS] [CrossRef] [Google Scholar]
- Hartman, J. M., Patruno, A., Chakrabarty, D., et al. 2009, ApJ, 702, 1673 [NASA ADS] [CrossRef] [Google Scholar]
- Jahoda, K., Markwardt, C. B., Radeva, Y., et al. 2006, ApJS, 163, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Leahy, D. A., Elsner, R. F., & Weisskopf, M. C. 1983, ApJ, 272, 256 [NASA ADS] [CrossRef] [Google Scholar]
- Markwardt, C. B., Altamirano, D., Strohmayer, T. E., & Swank, J. H. 2009a, The Astronomer’s Telegram, 2237, 1 [NASA ADS] [Google Scholar]
- Markwardt, C. B., Altamirano, D., Swank, J. H., et al. 2009b, The Astronomer’s Telegram, 2197, 1 [Google Scholar]
- Miller-Jones, J. C. A., Russell, D. M., & Migliari, S. 2009, The Astronomer’s Telegram, 2232, 1 [NASA ADS] [Google Scholar]
- Nowak, M. A., Paizis, A., Wilms, J., et al. 2009, The Astronomer’s Telegram, 2215, 1 [Google Scholar]
- Paczyński, B. 1971, ARA&A, 9, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Pandharipande, V. R., & Ravenhall, D. G. 1989, in Nuclear Matter and Heavy Ion Collisions, ed. M. Soyeur, H. Flocard, B. Tamain, & M. Porneuf, NATO ASIB Proc, 205, 103 [Google Scholar]
- Papitto, A., Menna, M. T., Burderi, L., di Salvo, T., & Riggio, A. 2008, MNRAS, 383, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Papitto, A., Riggio, A., Burderi, L., et al. 2009, The Astronomer’s Telegram, 2220, 1 [NASA ADS] [Google Scholar]
- Papitto, A., Riggio, A., di Salvo, T., et al. 2010, MNRAS, 407, 2575 [NASA ADS] [CrossRef] [Google Scholar]
- Patruno, A., Wijnands, R., & van der Klis, M. 2009, ApJ, 698, L60 [NASA ADS] [CrossRef] [Google Scholar]
- Patruno, A., Hartman, J. M., Wijnands, R., Chakrabarty, D., & van der Klis, M. 2010, ApJ, 717, 1253 [NASA ADS] [CrossRef] [Google Scholar]
- Podsiadlowski, P., Rappaport, S., & Pfahl, E. D. 2002, ApJ, 565, 1107 [NASA ADS] [CrossRef] [Google Scholar]
- Poutanen, J., & Beloborodov, A. M. 2006, MNRAS, 373, 836 [NASA ADS] [CrossRef] [Google Scholar]
- Rappaport, S. A., Fregeau, J. M., & Spruit, H. 2004, ApJ, 606, 436 [NASA ADS] [CrossRef] [Google Scholar]
- Riggio, A., di Salvo, T., Burderi, L., et al. 2007, MNRAS, 382, 1751 [NASA ADS] [Google Scholar]
- Riggio, A., Di Salvo, T., Burderi, L., et al. 2008, ApJ, 678, 1273 [NASA ADS] [CrossRef] [Google Scholar]
- Riggio, A., Papitto, A., Burderi, L., et al. 2009, The Astronomer’s Telegram, 2221, 1 [NASA ADS] [Google Scholar]
- Romanova, M. M., Ustyugova, G. V., Koldoba, A. V., & Lovelace, R. V. E. 2004, ApJ, 610, 920 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, M. A. P., Jonker, P. G., Steeghs, D., Simon, J. D., & Gutowski, G. 2009, The Astronomer’s Telegram, 2216, 1 [NASA ADS] [Google Scholar]
- Tutukov, A. V., & Iungelson, L. R. 1987, Ap&SS, 130, 15 [NASA ADS] [CrossRef] [Google Scholar]
- van den Heuvel, E. P. J. 1984, J. Astrophys. Astron., 5, 209 [Google Scholar]
- Zdziarski, A. A., Johnson, W. N., & Magdziarz, P. 1996, MNRAS, 283, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Życki, P. T., Done, C., & Smith, D. A. 1999, MNRAS, 309, 561 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 PCU 2 count rate (2–25 keV), subtracted of its background, is reported as a function of time during the outburst. The superimposed model represents the best fit using a piecewise linear function. The abrupt flux increase at the end of the outburst is due to the onset of an outburst from the AMP XTE J1751-305. The dashed vertical lines correspond to the type-I bursts present in the observation, while the continuous vertical lines correspond to the slope change, which depends on the model used to describe the count rate. The filled circles are relative to the ObsId 94041, while the triangles are the XTE J1751-305 observation (ObsId 94042). |
| In the text | |
 |
Fig. 2 A folded pulse profile is shown. For clarity, two spin cycles are plotted. The continuous line is the best-fit using first, second, and third harmonics. We also report the single contribution to the profile of the first harmonic (dotted line), second harmonic (dot-dashed line), third harmonic (bi-dot dashed line), and fourth harmonic (dashed line). |
| In the text | |
 |
Fig. 3 In the top panel of this figure the pulse phase delays (filled squares) and the corresponding pulse phase delay differences (filled circles) of the data corrected with the orbital ephemeris obtained from the fit to the frequency Doppler shifts are reported. Each pulse phase point is obtained by fitting the folded pulse profile over about 1500 s of data. It is evident that there is no trace of this fluctuation in the pulse phase delay differences, giving a striking confirmation of the goodness of the method. In the bottom panel, we report the residuals (in σ units) with respect to the best fit orbital solution derived from the pulse phase delay differences using the timing technique described in the text. |
| In the text | |
 |
Fig. 4 In the top panel, we show the first harmonic pulse phase delays and the best-fit curves, considering a constant spin frequency derivative (dashed line) and the disk threading model proposed by Rappaport et al. (2004). In the bottom panel, we show the residuals (in σ units) of the first harmonic with respect to the best-fit model given by the threaded disk. |
| In the text | |
 |
Fig. 5 In the top panel of this figure, the second harmonic pulse phase delays are shown. The dashed and the continuous lines are the second harmonic best-fit curves considering a constant spin frequency derivative and the physical model considering the material torque proportional to the flux, respectively. In the bottom panel, the residuals (in σ units) of the second harmonic with respect the constant spin frequency derivative are shown. |
| In the text | |
 |
Fig. 6 In the top panel of this figure, we report the third harmonic pulse phase delays and its best-fit curves considering a constant spin frequency derivative (dashed line) and the physical model considering the material torque proportional to the flux (continuous line). In the bottom panel, we show the residuals in units of σ with respect to the constant spin frequency derivative model. |
| In the text | |
 |
Fig. 7 In the top panel of this figure, the fourth harmonic pulse phase delays and its best-fit curves considering a constant spin frequency derivative (dashed line) and the physical model considering the material torque proportional to the flux (continuous line) are reported. In the bottom panel, we show the residuals in units of σ with respect to the constant spin frequency derivative model. |
| In the text | |
 |
Fig. 8 The fractional amplitudes of the four harmonics are reported. Points in correspondence with the type-I bursts are not plotted due to difficulties in estimating the persistent flux. |
| In the text | |
 |
Fig. 9 In the left panel, the phase lags for the first three harmonics are reported. The phase lags are measured with respect to the maxima of each component, as done in Papitto et al. (2010). In the right panel, the fractional amplitude for the three harmonics are reported. |
| In the text | |
 |
Fig. 10 Two type-I burst timing analysis is reported. For each burst in the top panel, the PCU2 count rate of the type-I burst present in this observation, in the middle panel the pulse phase delays and in the bottom panel the fractional amplitude are reported. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


