EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 526 (February 2011) A&A, 526 (2011) A40 Full HTML
Free Access
Issue
A&A
Volume 526, February 2011
Article Number A40
Number of page(s) 9
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/200913988
Published online 17 December 2010

© ESO, 2010

1. Introduction

One of the fundamental problems of star formation theory is finding an explanation of how the excess angular momentum may be extracted from the accreting gas and dust so that it may continue to travel inwards and eventually accumulate on the newly forming star. With the realisation that observed shocked gas was in fact the result of impacting high velocity jets and outflows ejected from such stars (Bally et al. 2007; Ray et al. 2007), came the proposal that such ejecta could be the underlying vehicle for angular momentum transport. The theoretical foundations have long been laid in which jets are ejected via magneto-centrifugal forces (Pudritz et al. 2007; Shang et al. 2007), but without observational verification. It became clear that high angular resolution observations are required to test the theory, since all such models describe acceleration and collimation on scales of tens of AU.

A significant observational breakthrough has been made in recent years by our team. We have conducted a series of studies revealing for the first time indications that we can observe the jet rotating. This combined endeavour may prove to be the long-awaited observational backing for the magneto-centrifugal theory of star formation. The first study constituted observations of the outflow from Class 0 source HH 212, in three slit positions stepped parallel to the flow direction, and revealed a difference in radial velocity of 2 km s-1 across the flow in the H2 2.12 μm near-infrared (near IR) line at 6″ (2500 AU) from the star (Davis et al. 2000). This was taken as the first observational hint of jet rotation, given the context of a concurrent study of the HH 212 disk which revealed a radial velocity gradient in the same sense (Wiseman et al. 2001). Independantly, other studies examined jets from less embedded Class II sources at optical and near-ultraviolet (near UV) wavelengths, and harnessed the high resolution of the Hubble Space Telescope (HST) in order to observe jets closer to their ejection point. The DG Tau and RW Aur jets, examined with a similar parallel slit configuration, revealed radial velocity gradients of 5−20 km s-1 within 100 AU of the star (Bacciotti et al. 2002; Woitas et al. 2005). Furthermore, these gradients were sustained for  ~100 AU along both lobes of the RW Aur bipolar jet. This sustainability does not favour alternative interpretations such as jet precession or asymmetric shocking. Such positive indications of jet rotation required a survey. We therefore examined several T Tauri systems, to study a series of 8 jet targets including two bipolar jets. This time the slit was placed perpendicular to the flow, which maximises the opportunity of detecting a rotation signature by observing across the full jet width. It also maximises survey efficiency and avoids difficulties introduced by uneven slit illumination (Woitas et al. 2005). Analysis in the optical and near UV consistently produced systematic radial velocities differences of typically 15−25 km s-1 close to the ejection point (Coffey et al. 2004, 2007). These very encouraging statistics led to a pilot study to detect gradients in younger Class I sources, since rotation signatures should be present at all evolutionary stages. Indeed, near IR spectra of HH 26 and HH 72 revealed gradients in their radial velocity profiles transverse to the flow direction at 1000 AU from the star (Chrysostomou et al. 2008).

In response to the positive outcome of this pilot study, we now conduct a wider survey of younger sources to consolidate the results. Three Class 0/I systems were observed in near IR lines, using the high spectral resolution (R  ~ 18 000) available with GNIRS on GEMINI South. Based on previous detections of outflows in the near IR, we choose HH 34 (Davis et al. 2001; Davis et al. 2003), HH 111-H (Davis et al. 2001b), and HH 212 NK1 and SK1 (Davis et al. 2000). The [Fe ii] 1.64 μm emission traces the hot inner parts of the jet while the H2 emission at 2.12 μm traces the warmer outer regions. Analysis of the spatially broad emission, which is resolved under good seeing conditions, takes full advantage of the high spectral resolution setting. Hence, using spectral analysis techniques, we are able to determine whether or not a Doppler gradient is present and in what sense, and thus the magnitude of the implied toroidal velocity.

Table 1

Targets investigated in this paper, all located in Orion at 414 pc (Menten et al. 2007).

2. Sample

2.1. HH 34

The HH 34 jet, first reported by Reipurth (1986), is the name given to the most recent ejection of the highly collimated S-shaped parsec-scale HH 34 flow from a Class I source in Orion, which is located at 414 pc distant (Menten et al. 2007). It has since been well studied via imaging and spectroscopy, but perhaps most impressive are the deep high resolution HST optical images (Reipurth et al. 2002), used to determine morphology, photometry and excitation of the flow, and reveal that the jet abruptly changes direction possibly due to the powerful tidal effects of a companion star. This is in addition to the large scale S-shape of the flow already reported by Bally et al. (1994) and Devine et al. (1997). Periodic time-variable ejection modeling of the jet have successfully reproduced the flow structure and morphology (Raga et al. 1998, 2002a), while Masciadri et al. (2002a) investigate precession of the flow as a deceleration mechanism. More recently, high resolution optical integral field spectroscopy observations (Beck et al. 2007) show agreement with the kinematics and electron density structure predicted by existing internal working surface models, although radial velocity studies show no evidence of a Doppler gradient across the flow but this may be because the effective resolution of 20 km s-1 did not allow a detection. Close to the source, the H2 counter-part to the optical jet emission was first traced by Davis et al. (2001), while the same region was also seen in [Fe ii] 1.64 μm emission (Davis et al. 2003). Further recent near-IR kinematic and diagnostic studies of the jet physics include Podio et al. (2006); Takami et al. (2006); Garcia Lopez et al. (2008); Antoniucci et al. (2008).

2.2. HH 111 - H

The highly collimated HH 111 Class I outflow was first reported by Reipurth (1989). Located in Orion, the HH 111 flow has been studied in detail over the years. Observations of the outflow itself at high resolution include HST optical images (Hartigan et al. 2001; Reipurth et al. 1997b) and spectra (Raga et al. 2002b). As with HH 34, it shows a chain of well aligned knots ending in a bowshock, the H knot being one of the brightest and located at 33″ (13 700 AU) from the source. Originating from a known multiple system, it is remarkable for its stability over parsec scales. It is also a strong H2 emitter (Gredel & Reipurth 1993), and is associated with a powerful CO outflow (Cernicharo et al. 1996). The H2 flow has been examined using echelle spectroscopy (Davis et al. 2001b) which revealed knot H to have a double-peaked profile, interpreted with a simple, geometrical bow shock model. A sister bipolar flow, HH 121 (Gredel & Reipurth 1993, 1994), originates from the same position but is offset in PA by 60° from HH 111. The core of this quadrupolar outflow has also been examined (Rodriguez et al. 2008) with a detection possibly indicating two disks. Models of the ejection history of HH 111 western lobe (Raga et al. 2002b; Masciadri et al. 2002b) show the bow shocks to be the result of an ejection velocity time-variability, while near IR spectral diagnostic studies (Nisini et al. 2002) demonstrate the nature of the shocked gas.

2.3. HH 212 NK1 & SK1

HH 212 is a well-known H2 outflow from a Class 0 source in Orion. Early imaging observations (Zinnecker et al. 1998) clearly show a highly symmetric bipolar flow, with a total length of 240″ (0.5 pc). The H2 knots closest to the source in each lobe (~6″) are named NK1 and SK1. The HH 212 system is also associated with a collimated CO outflow (Lee et al. 2006), and an SiO flow (Codella et al. 2007; Cabrit et al. 2007; Lee et al. 2007, 2008). Near IR diagnostic studies include Caratti o Garatti et al. (2006), which examines physical properties and cooling mechanisms, and Smith et al. (2007), which reveals excitation properties consistent with outward-moving bow shocks close to the plane of the sky.

The first hint that jet rotation is detectable in a young stellar jet actually came with the observations of HH 212 by Davis et al. (2000), based on a difference in the radial velocity across the receding lobe of the H2 flow. This was interpreted as such given the agreement with the sense of a radial velocity gradient across the disk of the same system (Wiseman et al. 2001). Codella et al. (2007) report no sign of jet rotation in the SiO emission near NK1, whereas in the region SK2−SK4 (~10−14″ from source), they find a gradient in a direction contrary to that reported for SK1 by Davis et al. (2000). It is therefore also contrary to that of the disk which has a 5 km s-1 difference between the blue-shifted ammonia gas in the north-east and the red-shifted gas in the south-west (Wiseman et al. 2001). However, Lee et al. (2008) recently conducted a higher resolution rotation study of the HH 212 flow and report matching gradients in the southern and northern lobes of the SiO jet in a sense that also matches that of the disk. They note that the slope of the gradient in the northern lobe (at 800 AU from the disk plane) is smaller than the southern lobe (at 450 AU). Indeed, a very comprehensive H2 study of this system was conducted using GEMINI/Phoenix (Correia et al. 2009), in which the various kinematic possibilities are modeled with the conclusion that the observations cannot be reproduced by jet rotation alone, though jet rotation may be included with other effects such as precession. Furthermore, near IR diagnostic studies (Smith et al. 2007) report a gradient in excitation transverse to the jet axis across in the inner knots, suggesting a transverse source motion rather than precession, possibly related to the jet bending and the transverse gradient in radial velocity. A similar gradient in excitation transverse to the jet axis in the T Tauri star Th 28 was reported by Coffey et al. (2008), which possibly suggests asymmetric shocking.

3. Observations

Observations were conducted, in queue mode, with the GEMINI Near InfraRed Spectrograph (GNIRS) on GEMINI South in mid-October 2006, late December 2006 and early January 2007. Near IR spectra were obtained of four jets from Class 0 and I sources (see Sect. 2) for one slit position at a given distance along the outflow, and orientated perpendicular to the direction of propagation. Observations were made (with position angle measured east of north) of the HH 34 jet at 1″ (400 AU) from the source (PAslit = 77, 257° according to guide star availability on the observation date), and the H knot in the HH 111 jet located at 34″ (14 000 AU) from the source (PAslit = 7°). Observations were also made of one knot in the approaching and receding jet from HH 212, namely NK1 and SK1 respectively, both located at 6″ (2500 AU) from the source (PAslit = 116°).

Using the long slit (49″) and the long-blue camera configuration, in combination with the 110.5 l/mm grating and choosing a 2-pixel slit-width (0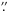\hbox{$\farcs$}10), we achieve a spectral resolving power of R  ~ 17 800. The corresponding velocity resolution is 17 km s-1. Average seeing during the observations varied between 0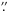\hbox{$\farcs$}5 and 0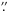\hbox{$\farcs$}8.

thumbnail Fig. 1

Position-velocity diagram of [Fe ii] and H2 emission from the HH 34 approaching jet. Positive distances correspond to south-west. Both are spatially unresolved under the seeing of 0\hbox{$\farcs$}4 and 0\hbox{$\farcs$}6 respectively.

We can use profile fitting to achieve an effective spectral resolution which is beyond the actual resolution of the observations. Given a line profile which is intrinsically Gaussian, fitting allows an effective resolution which improves with climbing signal-to-noise. The one sigma error on the centroid is given by: 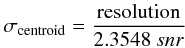σcentroid=resolution2.3548 snr\begin{eqnarray} \sigma_{\rm centroid} = \frac{\rm resolution}{2.3548~snr} \label{centroid} \end{eqnarray}(1)where resolution is either spatial or spectral, depending on the application, and snr is the signal-to-noise ratio (Whelan et al. 2008).

We chose filters G0504 and G0503 respectively, in order to detect the emission of [Fe ii] 1.64 μm and H2 2.12 μm. The standard procedure for observations in the near IR was adopted. Eight integrations of 300 s were made, using the ABBA technique, and then co-added. Two such exposures in each filter were obtained, in order to reach sufficient signal-to-noise in the jet borders. The data were calibrated and reduced according to standard procedures, using the tools within IRAF specifically designed for the reduction of GEMINI data. This included running tasks to correct for non-linearity (nsprepare) and spatial distortions (nsdist). Wavelength calibration was achieved using a dispersion scale derived from arc lines (nswavelength), which straightened and dispersion corrected the exposure (nstransform). All velocities are adjusted to the LSR reference frame (rvcorrect) and further adjustment was made for the LSR velocity of each system, VLSR, Table 1. Additional overheads of standard star observations were not required for a radial velocity analysis, and so data are not flux calibrated.

4. Data analysis

If protostellar jets are accelerated magneto-centrifugally then, with sufficient observing resolution and good signal-to-noise, it should be possible to detect the rotation signature of the flow. For good signal-to-noise, we can expect a typical accuracy in radial velocity of  ~1.5 km s-1. In the case of a rotating jet, the gas on one side of the flow axis is expected to display a higher Doppler shift than on the other side. Therefore, measuring a gradient in the radial velocity profile in the direction perpendicular to that of jet propagation can be interpreted as a signature of jet rotation. In such a case, the magnitude of the radial velocity differences (typically accurate to  ~2 km s-1) between the two sides of the flow axis allows derivation of a toroidal velocity component. Observationally, this requires that the jet axis is identifiable, and that high spatial and spectral velocity resolution is achieved to reveal the velocity profile as a function of distance from the jet axis. Clearly, this study is very demanding, and so obtaining useful observations from the ground is difficult. If the signal-to-noise is sufficiently high, however, we can reach beyond the nominal resolution via profile fitting of jet emission lines.

As expected, the H2 emission was found to be spatially broad, and so is almost always spatially resolved (with the exception of HH 34). Therefore, we could profile fit in the dispersion direction to obtain a jet radial velocity profile transverse to the flow propagation, and thus determine the magnitude and direction of any implied jet toroidal velocity. First, the emission was binned and fitted with a Gaussian in the spatial direction, the peak of which was assumed to denote the jet axis. This was used as a reference point in determining differences in radial velocity between one side of the jet and the other. Each pixel row of the unbinned emission was then fitted with a Gaussian in the spectral direction, and the measured radial velocities at mirrored positions either side of this central position were subtracted. In a couple of cases where the emission profile was not entirely symmetric, cross-correlation was deemed more appropriate. In this way, we find how any differences in Doppler shift vary with distance from the jet axis.

For the [Fe II] emission, the spectral profile clearly traces both a high and low velocity component of jet material. Spatially, however, the emission is more confined to the jet axis and the seeing is never sufficiently clear for emission to be resolved implying the atomic jet width is at least  <0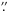\hbox{$\farcs$}6. Thus, in our seeing limited data, we cannot access the Doppler profile across the atomic component of the flow.

5. Results

5.1. HH 34

The HH 34 jet was clearly detected in both [Fe ii] and H2 emission. The observations are taken at only 1″ (400 AU) above the disk-plane. Exposures for a given filter were not co-added, in order to preserve the information obtained in higher seeing conditions. Figure 1 shows the position-velocity plots for one exposure, taken in October. The data contained reflected continuum emission with which the seeing at the time of observation could be measured. Unfortunately, the jet width is unresolved in both lines under the seeing of 0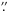\hbox{$\farcs$}4 and 0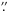\hbox{$\farcs$}6 respectively. The [Fe ii] higher velocity component (HVC) is travelling at −96 (±2) km s-1, consistent with measurements of Davis et al. (2003); Takami et al. (2006) and Garcia Lopez et al. (2008). Meanwhile, the H2 lower velocity component (LVC) is travelling at −15 (±1) km s-1. The H2 exposures show a deceleration from −15 to −10 km s-1 between October and December observations. There is currently no available measure on the sense of disk rotation for this system.

5.2. HH 111 - H

While the HH 111 jet is clearly detected in both [Fe ii] and H2 emission, Fig. 2, the signal-to-noise in H2 was extremely poor in spite of the long integration. There was no reflected continuum emission in either line from which to determine the seeing during observations, and so we rely on the weather report at the time. The [Fe ii] HVC is travelling at −107 (±1) km s-1, while the H2 LVC is travelling at −39 (±2) km s-1, in line with Davis et al. (2001b). Disk observations show that the northern side is blue-shifted with respect to the southern side (Yang et al. 1997; Lee et al. 2009). We therefore could expect to detect positive values of radial velocity differences, Δvrad. Our results are all within error bars about zero, and so we do not detect a clear Doppler gradient. A mere hint of a gradient may be apparent, but these are in the opposite direction (i.e. negative values of differences in radial velocity, Δvrad) to that expected based on the sense of disk rotation measurements. Note that we are examining this jet knot at 33″ from the source and so environmental influences are more likely come into play in significantly disrupting the flow kinematics. Finally, in the position-velocity diagram, we see that a second emission peak in H2 was observed (offset spatially by 0″2). The emission is much fainter and appears to trace an offset HVC in H2, with VLSR measured as −110 (±3) km s-1. A similar faint HVC is sometimes seen in echelle spectra of bow shocks, see e.g. Smith et al. (2003) (on HH 7). In this case, the HVC is attributed to a fast-moving mach disk.

thumbnail Fig. 2

Top: position-velocity plots for the H knot of the HH 111 jet in [Fe ii] and H2 emission, where positive distances correspond roughly to north; bottom: radial velocity profile across the jet in the spatially resolved H2 emission, and a plot of the differences in the Doppler shift, Δvrad, between one side of the jet knot and the other.

thumbnail Fig. 3

Top: position-velocity plots for the approaching lobe of the Class 0 bipolar jet HH 212, NK1 knot, in [Fe ii] and H2 emission, where positive distances correspond to south-east; bottom: radial velocity profile across the jet in the spatially resolved H2 emission, and a plot of the differences in the Doppler shift, Δvrad, between one side of the jet knot and the other. However, caution must be taken in its interpretation given that the emission intensity is asymmetric in the position direction.

5.3. HH 212 - NK1

There is a clear detection in both [Fe ii] and H2 emission in the NK1 knot from the HH 212 outflow of its deeply embedded Class 0 source, Fig. 3. [Fe ii] emission is notably fainter with about a third of the signal-to-noise of H2. The [Fe ii] HVC is travelling at −27 (±1) km s-1, while the H2 LVC is travelling at −8 (±1) km s-1, consistant with Davis et al. (2000) and Correia et al. (2009). The jet width is unresolved in [Fe ii] emission, but resolved in H2, and shows a slight hint of a Doppler gradient. Although nearly all Δvrad data points are within error bars about zero, there is a systematic trend such that the differences in radial velocity are consistently negative rather than randomly scattered about zero. The Doppler analysis suggests that the south-east side of the flow to be redder than the northwest side. However, for NK1, this spatial intensity distribution is asymmetric (as seen in the position-velocity plot), and as also seen in the H2 study by Correia et al. (2009). Recall from Sect. 4 that the emission was binned and fitted with a Gaussian in the spatial direction to determine the jet axis, and that this was used as a reference point in determining differences in radial velocity between one side of the jet and the other. Therefore, the spatial asymmetry introduces inaccuracies in determining the location of the jet axis, and hence the velocity differences across the jet.

5.4. HH 212 - SK1

The receding jet knot SK1 from HH 212 was clearly detected in both [Fe ii] and H2, Fig. 4. Again, the jet width in [Fe ii] emission is unresolved. The H2 LVC is travelling at +6 (±1) km s-1, consistant with Davis et al. (2000). For H2, the values of Δvrad are consistently negative, although again we see a spatial asymmetry in the emission (see position-velocity plot). The direction of the Doppler shift reveals the south-east side of the flow to be redder than the northwest side. This matches the hint of a gradient seen in our NK1 dataset (Sect. 5.3). It also matches the direction of the H2 measurements of Davis et al. (2000) and Correia et al. (2009) and the direction of the Doppler gradient reported for the disk (Wiseman et al. 2001). However, caution must be taken in the interpretation of the H2 gradient for both NK1 and SK1. The emission intensity is asymmetric in the position direction in both lobes, but on opposite sides of the jet axis, as also seen in the H2 study by Correia et al. (2009).

Overall, the results for HH 212 are in agreement with those obtained by Davis et al. (2000) for SK1 with different telescopes and at different epochs (7 years apart). Davis et al. (2000) and Lee et al. (2008) both report a high positive Doppler slope in SK1 with respect to NK1, and we find the same trend. Therefore, these signatures are real and persist over time.

Lastly, note that the [Fe ii] HVC is measured as having a radial velocity of −25 (±1) km s-1. This is highly unusual given that this is the receding jet lobe. To ensure the measurement is correct, we have checked the offsets of the slits in the raw data headers; the LSR velocity correction with respect to the observation dates; the position of the emission line with respect to the OH sky lines in the original raw data images; the wavelength calibration procedure; and the velocity of the H2 line with regard to the literature. No errors were found in the acquisition or calibration of the data, and all other measurements are consistent with previously reported values in the literature. Therefore, this velocity measurement appears to be real but we cannot find an explanation for it based on these data.

thumbnail Fig. 4

Top: position-velocity plots for the approaching lobe of the Class 0 bipolar jet HH 212, SK1 knot, in [Fe ii] and H2 emission, where positive distances correspond to south-east; bottom: radial velocity profile across the jet in the spatially resolved H2 emission, and a plot of the differences in the Doppler shift, Δvrad, between one side of the jet knot and the other. However, caution must be taken in its interpretation given that the emission intensity is asymmetric in the position direction.

5.5. Sources of errors

Difficulty in determining transverse Doppler profiles arises if the slit is unevenly illuminated, e.g. if the target is not well-centered in the slit. Using a slit orientated perpendicular to the jet propagation direction (as in our observations) ensures that uneven slit illumination is a second order effect, and hence the problem of the so-called slit-effect is negligible (Chrysostomou et al. 2008). This was not the case in previous studies using a slit parallel to the flow (i.e. Bacciotti et al. 2002; Woitas et al. 2005), and so the subtraction of the uneven illumination effect added an element of complexity to the data reduction which we have avoided here.

6. Discussion

We have detected gradients in the transverse Doppler-shift profile in resolved H2 jet targets. We now examine whether or not we are justified in interpreting these gradients as a rotation of the flow, and thus whether we can claim to support the magneto-centrifugal mechanism of ejection. We first investigate whether the implied toroidal velocity and angular momentum flux are realistic, in the context of jet and disk rotation measurements reported in the literature. We then examine the statistical foundations for such a claim.

The implied jet toroidal velocity may be calculated from the measured radial velocity differences. The implied toroidal velocity is vφ = (△ vrad/2)/cos   ijet, where ijet is the inclination angle with respect to the plane of the sky, and  △ vrad is the radial velocity difference between two sides of the jet. We see a systematic radial velocity difference of  ~3 km s-1 for the HH 212 jet. The implied toroidal velocity is then  ~1.5 km s-1. This is in line with values derived by Chrysostomou et al. (2008) of 1 to 7 km s-1 measured for two Class I sources examined in H2 emission. These authors demonstrated the velocity signature to be consistent with a simple jet rotation model. The value is also in the same range as those measured in H2 emission for HH 212 SK1 by Davis et al. (2000), in which the authors point out that the expected jet rotation speed based on the disk rotation measurements of Wiseman et al. (2001) is  ~2 km s-1, thus demonstrating that our measurements are consistent with a jet rotation interpretation. It is also clear from the modeling of Correia et al. (2009) that the toroidal velocity may be confused with other kinematic signatures, and so our calculations are broad indications.

Comparing with more evolved Class II T Tauri jets, our toroidal velocity is substantially lower than those measured in optical and near-UV emission close to the launch point, which yielded typically 10 to 20 km s-1 (Bacciotti et al. 2002; Woitas et al. 2005; Coffey et al. 2004, 2007). These results originate from the resolved atomic emission which is more collimated, and so would be expected to yield higher toroidal velocity values with respect to the molecular component. Unfortunately, without resolving the atomic component in our Class 0/I sample, it is not possible to make a direct comparison between the two classes, in order to understand the evolution of angular momentum extraction over the age of the source.

Nevertheless, we attempt to gain a rough estimate. The angular momentum extraction may be approximated as 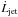\hbox{$\dot L_{\rm jet}$}  ~ rvφṀjet. For the molecular knot HH 212 SK1, Davis et al. (2000) report Ṁjet  ~ 4.2  ×  10-8   M⊙ yr-1. This is in the range of 2 to 5  ×  10-8   M⊙ yr-1 reported for Class I outflows (Antoniucci et al. 2008). We adopt vφ  =  1.5 km s-1 at an average distance from the jet axis of 0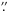\hbox{$\farcs$}4. Although the jet is resolved, we do not see reflected continuum emission which we could use in a PSF deconvolution to determine the true jet radius. These values give 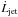\hbox{$\dot L_{\rm jet}$}  ~ 1  ×  10-5   M⊙ yr-1 AU km s-1. This is in line with that for HH 26 of 2  ×  10-5   M⊙ yr-1 AU km s-1 derived at 1−2″ from the disk plane, for a jet radius of 0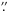\hbox{$\farcs$}44. However, our result implies a specific angular momentum which is 3 times higher than that of the SiO knot SS Lee et al. (2008), which lies closer to the star at 2″. The difference mainly arises from a smaller adopted SiO jet radius of 0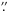\hbox{$\farcs$}1.

Roughly comparing Class 0/I values with those for Class II jets, we take the example of T Tauri systems CW Tau, RW Aur and DG Tau, which have been studied close to the jet footpoint, i.e. 0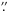\hbox{$\farcs$}5 (70 AU) from the disk-plane. Coffey et al. (2008) report angular momentum fluxes in one lobe from each system as 1, 3 and 13  ×  10-6   M⊙ yr-1 AU km s-1 respectively for the atomic component. We find up to an order of magnitude difference between the angular momentum extraction of Class 0/I versus Class II sources. This is a rough indication of the magnitude of the decrease in angular momentum extraction as the young stars evolve. Indeed, the decrease in mass accretion flux supports this: a comparison between Class II (Gullbring et al. 1998) and Class I (Antoniucci et al. 2008) shows the mass accretion rates for the Class I are between one and two orders of magnitudes larger than those of Class II.

It seems possible that we are observing a jet rotation signature in these data. We must also consider whether it is probable. Does the gradient in the radial velocity profile in the transverse direction represent a rotation of the jet, or could it be a signature of an asymmetric bowshock, precession of the flow, or indeed a combination of effects?

Steady-state MHD jet models imply that the rotation of the flow should persist to large distances, as a necessary outcome of magnetic flux conservation. Nevertheless, an important observational precaution is to examine the flow close to the launch point. In this way, we try to ensure that environmental factors do not significantly disrupt the inherent jet kinematics. This is not always observationally possible due to high opacity close to the star, especially when dealing with younger more embedded flows as is the case here. Hence the need to observe these younger outflows at the position of the brightest knots, which are not necessarily close to the launch region. Given this observational obstacle we must examine the overall context of our results.

Support for a rotation argument lies in important consistency checks. For example, if the jet is rotating as a result of the launch mechanism, we should consistently measure gradients in the jet Doppler profile transverse to the flow direction for many targets. Also, the direction of the implied jet toroidal velocity should match measurements for the direction of the disk rotation within the same system, since the jet is supposedly extracting its angular momentum. Likewise, the implied sense of rotation should be the same in both lobes of a bipolar jet and should persist along the flow.

From our survey, it appears that transverse Doppler gradients may be consistently measured in Class 0/I jets in the near IR H2 emission, as we set out to establish following the initial findings of Chrysostomou et al. (2008). Furthermore, we provide confirmation of a previous detection for HH 212 Davis et al. (2000), thus also demonstrating a persistence of the transverse Doppler gradient over time (from 1999 to 2006). Together with the fact that gradients are also consistently measured in Class II jets in the optical and near UV, we have an encouraging case so far.

Next we consider Doppler gradients of jet and disk. Agreement is compulsory to validate a jet rotation interpretation. For HH 212, we confirm an agreement in sense, as also reported by both Davis et al. (2000) for SK1 and Lee et al. (2008). However, they do not agree with the NK1 results of Davis et al. (2000) or the SiO results of Codella et al. (2007). Furthermore, given the spatial asymmetries we find in this case, our results must be treated with caution. We cannot determine a clear gradient in the jet for HH 111 in order to compare with the disk (Yang et al. 1997; Lee et al. 2009), but the data suggest a gradient which opposes that of the disk. Other cases examined are the T Tauri systems DG  Tau (Bacciotti et al. 2002; Testi et al. 2002), RW Aur (Coffey et al. 2004; Cabrit et al. 2006), CW Tau (Coffey et al. 2007) and HH 30 (Coffey et al. 2007; Pety et al. 2006). Agreement has also been confirmed for DG Tau, in which jet observations were conducted close to the launch point and where the transverse gradient persists for 100 AU. Disconcertingly, RW Aur shows a disagreement in sense. This may be a complex triple system and hence must be further investigated to confirm that no other influences are coming into play. For CW Tau, agreement has been found in preliminary disk results (C. Dougados, priv. comm. ). For HH 30, the jet rotation sense was deemed inconclusive. It has since been revealed that the HH 30 jet is in fact wiggling (Anglada et al. 2007), due to the orbital motion of the binary source (Guilloteau et al. 2008). Lastly, agreement has been recently found in both HH 211 and CB26 (Lee et al. 2007; Launhardt et al. 2009). Overall, of the 8 systems for which both jet and disk gradients are studied at this early stage of our work, four show clear agreement and 1 shows clear disagreement. The statistics are as yet too low to be significant.

Agreement between Doppler gradients in both lobes of a bipolar jet is also compulsory to validate a jet rotation interpretation. We measure an agreement in the gradient between the two lobes of the HH 212 bipolar flow. However, we again sound a note of caution based on the spatial asymmetry and the fact that we observe far from the source. This supports the agreement also found in SiO measurements in the two lobes (Lee et al. 2008), although the same agreement was not found in Davis et al. (2000). Only two other bipolar flows have been examined. They are from the T Tauri systems Th 28 and RW Aur (Coffey et al. 2004), and in both cases agreement was found. Furthermore, in two cases were these bipolar jets have been observed with the slit parallel to the flow, the gradient has persisted along the jet over a distance of 90 AU in the same direction in both lobes. Such a scenario is not likely to arise from a signature of asymmetric shocking, and certainly not from jet precession where the gradient should be opposite in the two lobes. In other words, in the case of precession, for several slits parallel to the jet (mimiking an IFU), the poloidal velocity peak is offset with respect to the central slit in opposite directions for each lobe, and hence the radial velocity profile shows a gradient opposite in direction in each lobe. In this case, also, there is a periodic change in the direction of the gradient as a function of distance along each jet lobe. Such changes are not found in these parallel slit studies.

Although statistics are limited, we are building our way towards a statistical argument to support the fact that we are indeed observing jet rotation. Such information is critical in finally providing observational confirmation for the widely accepted but untested centrifugal MHD wind launching mechanism. Obviously, any evidence which suggests protostellar jets are launched centrifugally would, of course, in turn support the idea that the same mechanism is at work in their larger-scale brethren, i.e. the AGN jets. Indeed, the latest observations indicate jet rotation is also detectable in active galactic nuclei (Young et al. 2007). Together with observations indicating jet rotation in protostellar jets, this provides support for the universality of the theory of magneto-centrifugal ejection.

7. Conclusions

We have conducted a ground-based survey in near IR lines of four jets from Class 0/I sources to search for signatures of jet rotation. These embedded sources make the use of adaptive optics very difficult, due to the absence of a nearby optical guide star. Thus, our results are derived from seeing-limited observations and rely on profile fitting in the spectral direction. 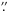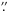For HH 34, we find emission in [Fe ii] and H2 is detected but spatially unresolved with seeing of 0\hbox{$\farcs$}4−0\hbox{$\farcs$}6 across the jet within 1″ of the driving source. For HH 111-H, we find we cannot resolve a clear gradient across the jet, but perhaps glimpse only a hint of one, which is opposite to the direction of the disk. Similarily, in the NK1 knot of the HH 212 bipolar flow, we see a hint of a gradient but this time in the same direction as the disk. Lastly, we detect a gradient of typically 2−5 km s-1 in SK1 knot of HH 212. We find agreement in the sense of the gradient in both HH 212 lobes, as would be expected if the measurements are of jet rotation. The result confirms an earlier detection in SK1 by Davis et al. (2000) and Correia et al. (2009), and also matches the disk rotation sense Wiseman et al. (2001). Furthermore, it demonstrates the persistence of the gradient over a time frame of seven years.

For HH 212, we can estimate a possible implied toroidal velocities of 1.5 km s-1, previously shown to be consistent with a simple jet rotation model (Chrysostomou et al. 2008), and angular momentum flux estimates of 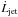\hbox{$\dot L_{\rm jet}$}  ~ 1  ×  10-5   M⊙ yr-1 AU km s-1. A direct comparison cannot be made between Class 0/I and Class II angular momentum extraction, since [Fe ii] is unresolved in our data. We are therefore prevented from determining a clear trend over evolutionary time, although we obtain a rough indication that there may be up to an order of magnitude decrease in angular momentum extraction as the young stars evolve. However, for the HH 212 and HH 111 knots, which were observed very far from the driving source, we must consider that the gradients are less likely to be unaffected by external factors such as asymmetric shocking.

Our analysis illustrates the observational difficulties in conducting this study, as it pushes instrumentation to the limit in its demand for a combination of high spatial and spectral resolution, as well as good sensitivity. Overall, it is clear that in order to safely interpret Doppler gradients as signatures of jet rotation, there is a need for improved statistics via high resolution multi-wavelength jet observations close to the source, and comparison with the associated disk rotation sense.

Acknowledgments

Based on observations at the Gemini Observatory, under Program ID GS-2006B-Q-46, which is operated by the Association of Universities for Research in Astronomy, Inc., under a cooperative agreement with the NSF on behalf of the Gemini partnership: the National Science Foundation (United States), the Science and Technology Facilities Council (United Kingdom), the National Research Council (Canada), CONICYT (Chile), the Australian Research Council (Australia), CNPq (Brazil) and SECYT (Argentina). The present work was supported in part by the European Community’s Marie Curie Actions – Human Resource and Mobility within the JETSET (Jet Simulations, Experiments and Theory) network, under contract MRTN-CT-2004-005592. D.C. wishes to acknowledge funding received from the Irish Research Council for Science, Engineering and Technology (IRCSET).

References

  1. Anglada, G., Estalella, R., Mauersberger, R., et al. 1995, ApJ, 443, 682 [NASA ADS] [CrossRef] [Google Scholar]
  2. Anglada, G., López, R., Estalella, R., et al. 2007, AJ, 133, 2799 [NASA ADS] [CrossRef] [Google Scholar]
  3. Antoniucci, S., Nisini, B., Giannini, T., & Lorenzetti, D. 2008, A&A, 479, 503 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Bailey, J. 1998, MNRAS, 301, 161 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bally, J., & Devine, D. 1994, ApJ, 428, L65 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bally, J., Reipurth, B., & Davis, C. J. 2007, in Protostars & Planets V, ed. B. Reipurth, D. Jewitt, & K. Keil (Tuscon: Univ. Arizona Press), 215 [Google Scholar]
  7. Bacciotti, B., Ray, T. P., Mundt, R., Eislöffel, J., & Solf, J. 2002, ApJ, 576, 222 [NASA ADS] [CrossRef] [Google Scholar]
  8. Beck, T. L., Riera, A., Raga, A. C., & Reipurth, Bo 2007, AJ, 133, 1221 [NASA ADS] [CrossRef] [Google Scholar]
  9. Brannigan, E., Takami, M., Chrysostomou, A., & Bailey, J. 2006, MNRAS, 367, 315 [NASA ADS] [CrossRef] [Google Scholar]
  10. Cabrit, S., Pety, J., Pesenti, N., & Dougados, C. 2006, A&A, 452, 897 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Cabrit, S., Codella, C., Gueth, F., et al. 2007, A&A, 468, L29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Caratti o Garatti, A., Giannini, T., Nisini, B., & Lorenzetti, D. 2006, A&A, 449, 1077 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Cernicharo, J., & Reipurth, B. 1996, ApJ, 460, L57 [NASA ADS] [CrossRef] [Google Scholar]
  14. Chrysostomou, A., Bacciotti, F., Nisini, B., et al. 2008, A&A, 482, 575 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Claussen, M. J., Marvel, K. B., Wootten, A., & Wilking, B. A. 1998, ApJ, 507, L79 [NASA ADS] [CrossRef] [Google Scholar]
  16. Codella, C., Cabrit, S., Gueth, F., et al. 2007, A&A, 462, L53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Coffey, D., Bacciotti, F., Woitas, J., Ray, T. P., & Eislöffel, J. 2004, ApJ, 604, 758 [NASA ADS] [CrossRef] [Google Scholar]
  18. Coffey, D., Bacciotti, F., Ray, T. P., Eislöffel, J., & Woitas, J. 2007, ApJ, 663, 350 [NASA ADS] [CrossRef] [Google Scholar]
  19. Coffey, D., Bacciotti, F., & Podio, L. 2008, ApJ, 689, 1112 [NASA ADS] [CrossRef] [Google Scholar]
  20. Correia, S., Zinnecker, H., Ridgway, S. T., & McCaughrean, M. J. 2009, A&A, 505, 673 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Davis, C. J., Berndsen, A., Smith, M. D., Chrysostomou, A., & Hobson, J. 2000, MNRAS, 314, 241 [NASA ADS] [CrossRef] [Google Scholar]
  22. Davis, C. J., Ray, T. P., Desroches, L., & Aspin, C. 2001, MNRAS, 326, 524 [NASA ADS] [CrossRef] [Google Scholar]
  23. Davis, C. J., Hodapp, K. W., & Desroches, L. 2001b, A&A, 377, 285 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Davis, C. J., Whelan, E., Ray, T. P., & Chrysostomou, A. 2003, A&A, 397, 693 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Davis, C. J., Nisini, B., Takami, M., et al. 2006, ApJ, 639, 969 [NASA ADS] [CrossRef] [Google Scholar]
  26. Devine, D., Bally, J., Reipurth, B., & Heathcote, S. 1997, AJ, 114, 2095 [NASA ADS] [CrossRef] [Google Scholar]
  27. Eislöffel, J., & Mundt, R. 1992, A&A, 263, 292 [NASA ADS] [Google Scholar]
  28. Garcia Lopez, R., Nisini, B., Giannini, T., et al. 2008, A&A, 487, 1019 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Gredel, R., & Reipurth, B. 1993, ApJ, 407, L29 [NASA ADS] [CrossRef] [Google Scholar]
  30. Gredel, R., & Reipurth, B. 1994, A&A, 289, L19 [NASA ADS] [Google Scholar]
  31. Guilloteau, S., Dutrey, A., Pety, J., & Gueth, F. 2008, A&A, 478, L31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Gullbring, E., Hartmann, L., Briceno, C., & Calvet, N. 1998, ApJ, 492, 323 [NASA ADS] [CrossRef] [Google Scholar]
  33. Hartigan, P., Morse, J. A., Reipurth, B., Heathcote, S., & Bally, J. 2001, ApJ, 559, L157 [NASA ADS] [CrossRef] [Google Scholar]
  34. Heathcote, S., & Reipurth, B. 1992, AJ, 104, 2193 [NASA ADS] [CrossRef] [Google Scholar]
  35. Hirth, G., Mundt, R., & Solf, J. 1997, A&AS, 126, 437 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Launhardt, R., Pavlyuchenkov, Y., Gueth, F., et al. 2009, A&A, 494, 147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Lee, C.-F., Ho, P. T. P., Beuther, H., et al. 2006, ApJ, 639, 292 [NASA ADS] [CrossRef] [Google Scholar]
  38. Lee, C., Ho, P. T. P., Palau, A., et al. 2007, ApJ, 670, 1188 [NASA ADS] [CrossRef] [Google Scholar]
  39. Lee, C., Ho, P. T. P., Bourke, T. L., et al. 2008, ApJ, 685, 1026 [NASA ADS] [CrossRef] [Google Scholar]
  40. Lee, C., Mao, Y., & Reipurth, B. 2009, ApJ, 694, 1395 [NASA ADS] [CrossRef] [Google Scholar]
  41. Masciadri, E., de Gouveia Dal Pino, E. M., Raga, A. C., & Noriega-Crespo, A. 2002a, ApJ, 580, 950 [NASA ADS] [CrossRef] [Google Scholar]
  42. Masciadri, E., Velázquez, P. F., Raga, A. C., Cantó, J., & Noriega-Crespo, A. 2002b, ApJ, 573, 260 [NASA ADS] [CrossRef] [Google Scholar]
  43. Menten, K. M., Reid, M. J., Forbrich, J., & Brunthaler, A. 2007, A&A, 474, 515 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Nisini, B., Caratti o Garatti, A., Giannini, T., & Lorenzetti, D. 2002, A&A, 393, 1035 [Google Scholar]
  45. Pesenti, N., Dougados, S., Cabrit, S., et al. 2004, A&A, 416, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Pety, J., Gueth, F., Guilloteau, S., & Dutrey, A. 2006, A&A, 458, 841 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Podio, L., Bacciotti, F., Nisini, B., et al. 2006, A&A, 456, 189 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  48. Pudritz, R. E., Ouyed, R., Fendt, C., & Brandenburg, A. 2007, in Protostars & Planets V, ed. B. Reipurth, D. Jewitt, & K. Keil (Tuscon: Univ. Arizona Press), 277 [Google Scholar]
  49. Raga, A., & Noriega-Crespo, A. 1998, AJ, 116, 2943 [NASA ADS] [CrossRef] [Google Scholar]
  50. Raga, A. C., Velázquez, P. F., Cantó, J., & Masciadri, E. 2002a, A&A, 395, 647 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Raga, A. C., Noriega-Crespo, A., Reipurth, B., et al. 2002b, ApJ, 565, L29 [NASA ADS] [CrossRef] [Google Scholar]
  52. Ray, T. P., Dougados, C., Bacciotti, F., Eislöffel, J., & Chrysostomou, A. 2007, in Protostars & Planets V, ed. B. Reipurth, D. Jewitt, & K. Keil (Tuscon: Univ. Arizona Press), 231 [Google Scholar]
  53. Reipurth, B. 1989, Nature, 340, 42 [NASA ADS] [CrossRef] [Google Scholar]
  54. Reipurth, B. 2000, ApJ, 534, 317 [NASA ADS] [CrossRef] [Google Scholar]
  55. Reipurth, B., Bally, J., Graham, J. A., Lane, A. P., & Zealey, W. J. 1986, A&A, 164, 51 [NASA ADS] [Google Scholar]
  56. Reipurth, B., Raga, A. C., & Heathcote, S. 1992, ApJ, 392, 145 [NASA ADS] [CrossRef] [Google Scholar]
  57. Reipurth, B., Bally, J., & Devine, D. 1997a, AJ, 114, 2708 [NASA ADS] [CrossRef] [Google Scholar]
  58. Reipurth, B., Hartigan, P., Heathcote, S., Morse, J. A., & Bally, J. 1997b, AJ, 114, 757 [NASA ADS] [CrossRef] [Google Scholar]
  59. Reipurth, B., Heathcote, S., Morse, J., Hartigan, P., & Bally, J. 2002, AJ, 123, 362 [NASA ADS] [CrossRef] [Google Scholar]
  60. Rodriguez, L. F., Torrelles, J. M., Anglada, G., & Reipurth, B. 2008, AJ, 136, 1852 [NASA ADS] [CrossRef] [Google Scholar]
  61. Shang, H., Li, Z.-Y., & Hirano, N. 2007, in Protostars & Planets V, ed. B. Reipurth, D. Jewitt, & K. Keil (Tuscon: Univ. Arizona Press), 261 [Google Scholar]
  62. Smith, M. D., Khanzadyan, T., & Davis, C. J. 2003, MNRAS, 339, 524 [NASA ADS] [CrossRef] [Google Scholar]
  63. Smith, M. D., O’Connell, B., & Davis, C. J. 2007, A&A, 466, 565 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  64. Takami, M., Bailey, J., Gledhill, T. M., Chrysostomou, A., & Hough, J. H. 2001, MNRAS, 323, 177 [NASA ADS] [CrossRef] [Google Scholar]
  65. Takami, M., Chrysostomou, A., Ray, T. P., et al. 2006, ApJ, 641, 357 [NASA ADS] [CrossRef] [Google Scholar]
  66. Testi, L., Bacciotti, F., Sargent, A. I., Ray, T. P., & Eislöffel, J. 2002, A&A, 394, 31 [Google Scholar]
  67. Wiseman, J., Wootten, A., Zinnecker, H., & McCaughrean, M. 2001, ApJ, 550, L87 [NASA ADS] [CrossRef] [Google Scholar]
  68. Whelan, E., & Garcia, P. 2008, Jets from Young Stars II, ed. F. Bacciotti, E. T. Whelan, & L. Testi (Berlin: Springer), Lecture Notes in Physics, 742, 123 [Google Scholar]
  69. Whelan, E., Ray, T. P., & Davis, C. J. 2004, A&A, 417, 247 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  70. Woitas, J., Bacciotti, F., Ray, T. P., et al. 2004, A&A, 432, 149 [Google Scholar]
  71. Yang, J., Ohashi, N., Yan, J., et al. 1997, ApJ, 475, 683 [NASA ADS] [CrossRef] [Google Scholar]
  72. Young, S., Axon, D. J., Robinson, A., Hough, J. H., & Smith, J. E. 2007, Nature, 450, 74 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  73. Zinnecker, H., McCaughrean, M. J., & Rayner, J. T. 1998, Nature, 394, 862 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]

All Tables

Table 1

Targets investigated in this paper, all located in Orion at 414 pc (Menten et al. 2007).

In the text

All Figures

thumbnail Fig. 1

Position-velocity diagram of [Fe ii] and H2 emission from the HH 34 approaching jet. Positive distances correspond to south-west. Both are spatially unresolved under the seeing of 0\hbox{$\farcs$}4 and 0\hbox{$\farcs$}6 respectively.
In the text
thumbnail Fig. 2

Top: position-velocity plots for the H knot of the HH 111 jet in [Fe ii] and H2 emission, where positive distances correspond roughly to north; bottom: radial velocity profile across the jet in the spatially resolved H2 emission, and a plot of the differences in the Doppler shift, Δvrad, between one side of the jet knot and the other.
In the text
thumbnail Fig. 3

Top: position-velocity plots for the approaching lobe of the Class 0 bipolar jet HH 212, NK1 knot, in [Fe ii] and H2 emission, where positive distances correspond to south-east; bottom: radial velocity profile across the jet in the spatially resolved H2 emission, and a plot of the differences in the Doppler shift, Δvrad, between one side of the jet knot and the other. However, caution must be taken in its interpretation given that the emission intensity is asymmetric in the position direction.
In the text
thumbnail Fig. 4

Top: position-velocity plots for the approaching lobe of the Class 0 bipolar jet HH 212, SK1 knot, in [Fe ii] and H2 emission, where positive distances correspond to south-east; bottom: radial velocity profile across the jet in the spatially resolved H2 emission, and a plot of the differences in the Doppler shift, Δvrad, between one side of the jet knot and the other. However, caution must be taken in its interpretation given that the emission intensity is asymmetric in the position direction.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.