| Issue |
A&A
Volume 524, December 2010
|
|
|---|---|---|
| Article Number | A38 | |
| Number of page(s) | 11 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201015394 | |
| Published online | 22 November 2010 | |
Parallaxes and physical properties of 11 mid-to-late T dwarfs
1
INAF/Osservatorio Astronomico di Torino, Strada Osservatorio
20,
10025
Pino Torinese,
Italy
e-mail: fmarocco@libero.it, smart@oato.inaf.it
2
Università degli Studi di Torino, Facoltà di Scienze MFN –
Dipartimento di Fisica, via Pietro
Giuria 1, 10126
Torino,
Italy
3
Centre for Astrophysics Research, Science and Technology Research
Institute, University of Hertfordshire, Hatfield
AL10 9AB,
UK
4
Gemini Observatory, Northern Operations Center, 670 N. Aohoku Place,
Hilo, HI
96720,
USA
5 Anglo-Australian Observatory,
PO Box 296, Epping,
NSW1710,
Australia
6
Joint Astronomy Centre,
660 North Aohoku Place,
Hilo, HI
96720,
USA
7
Institute of Astronomy, Madingley Road, Cambridge
CB3 0HA,
UK
8
Instituto de Astrofísica de Canarias, vía Láctea s/n, 38205 La Laguna, Tenerife, Spain
9
Departamento de Astrofísica, Universidad de La Laguna
(ULL), 38205 La
Laguna, Tenerife,
Spain
10
National Astronomical Observatory of Japan,
2-21-1 Osawa,
Mitaka, Tokyo
181-8588,
Japan
Received: 14 July 2010
Accepted: 20 August 2010
Aims. We present parallaxes of 11 mid-to-late T dwarfs observed in the UKIRT Infrared Deep Sky Survey. We use these results to test the reliability of model predictions in magnitude–color space, determine a magnitude-spectral type calibration, and, estimate a bolometric luminosity and effective temperature range for the targets.
Methods. We used observations from the UKIRT WFCAM instrument pipeline processed at the Cambridge Astronomical Survey Unit. The parallaxes and proper motions of the sample were calculated using standard procedures. The bolometric luminosity was estimated using near- and mid-infrared observations with two different methods. The corresponding effective temperature ranges were found adopting a large age-radius range.
Results. We show the models are unable to predict the colors of the latest T dwarfs indicating the incompleteness of model opacities for NH3, CH4 and H2 as the temperature declines. We report the effective temperature ranges obtained.
Key words: stars: low-mass / brown dwarfs / stars: fundamental parameters / stars: distances / astrometry
© ESO, 2010
1. Introduction
Since the first discovery of a T dwarf by Nakajima et al. (1995) understanding the atmospheric processes and the role of chemical composition for such low temperature objects has been very challenging. This remains an important goal, particularly given that we consider these objects to be the link between stars and giant exoplanets, therefore, their properties offer insights into formation and evolution of planetary systems.
Infrared magnitudes and spectral types of the 11 targets.
 |
Fig. 1 Observations for the targets ULAS 0901 (top panel) and 1315 (bottom panel). The highest point is the discovery image. The observational history and distance of these two targets are similar but they differ by a magnitude in apparent brightness. The solution shows the effect of low signal-to-noise observations in the beginning of the parallax sequence. |
One of the fundamental parameters required to determine the physical properties and to constrain theoretical models of celestial objects is distance. Until now, only a few late T dwarfs have known distances: Wolf940B (Harrington & Dahn 1980), HD3651B (Perryman et al. 1997), 2MASS J0415-0935 (Vrba et al. 2004), 2MASS J0939-2448 (Burgasser et al. 2008), ULAS J003402.77-005206.7 (Smart et al. 2010). Thus the theoretical models have been constrained by the earlier T dwarfs. The UKIRT Infrared Deep Sky Survey (Lawrence et al. 2007, hereafter UKIDSS) is revealing large numbers of new T dwarfs (Burningham et al. 2010; Lodieu et al. 2009a,b; Burningham et al. 2008; Pinfield et al. 2008; Chiu et al. 2008; Lodieu et al. 2007; Kendall et al. 2007) and in particular cool T8/T9 dwarfs. An important follow up for the coolest T dwarfs observed in the UKIDSS is the determination of their parallax. As shown in Smart et al. (2010, hereafter SJL10) for ULAS J003402.77-005206.7 using the UKIDSS discovery image it is possible to reduce the time required to determine a preliminary parallax and here we present 10 additional objects.
In this contribution all targets will be referred to by the discovery acronym and right ascension short format hence ULAS J003402.77-005206.7 becomes ULAS 0034, the full-names are given in Table 1. In Sect. 2 we describe the observations and procedures and in Sect. 3 we report the results for the 11 targets. In Sect. 4 we compare these results to current models and in Sect. 5 we calculate Lbol and Teff of the objects in the sample. Finally in Sect. 6 we discuss the results obtained.
2. Observations and reduction procedures
The observations for the parallax determination began in 2007 and the target list of 11 objects was drawn from confirmed T dwarfs observed at that time in the UKIDSS Large Area Survey. In Table 1 we list the objects along with MKO magnitudes (Tokunaga et al. 2002) and near-infrared (hereafter NIR) spectral types. The NIR spectral type classification follows the scheme described in Burgasser et al. (2006a). The only object with an already published parallax was SDSS 0207 which was included because the USNO parallax had a large relative error (~28%, Vrba et al. 2004).
The procedures for observing, image treatment and parallax determination follow those described in SJL10. In that paper the parallax observations of ULAS 0034 maintained the same target position as the discovery image and were aligned using a simple linear transformation. Assuming the astrometric distortion pattern does not change, the use of the discovery image as part of the parallax solution allows a much shorter dedicated observational campaign to obtain a precise parallax. For CFBDS 0059, SDSS 0207, ULAS 0948 and ULAS 2239 this was not possible because the target was very close to a chip edge in the first UKIDSS image. The WFCAM astrometric distortion is significant, so moving the reference frame on the focal plane results in poorer astrometric transformations (i.e. larger residuals in the solutions) and so in this situation those frames that are significantly offset are given lower weight.
Initially all observations were made with the same total exposure time of 400 s. For this exposure, in the case of the anonymous stars in the field of ULAS 0034, the centroiding precision is a constant 20 mas until around J = 18.4 and deteriorates quickly to 60 mas at J = 19.2 (Fig. 2 in SJL10). To ensure that centroiding precision is optimal even in poor observing conditions we have increased the exposure times to 710 s for the faint targets (ULAS 0034, 0948, 1150, 1315, 2239 and CFBDS 0059). The precision of the final solutions for the faint targets reflects the poor quality of some of the earlier 400 s observations.
In Fig. 1 we plot the solution of ULAS 0901 (top panel) and 1315 (bottom panel) which are objects of similar distances and observational history but with magnitudes of 17.90 and 18.86 respectively, e.g. straddling the precision borderline, to show high and low quality solutions.
3. Results
The astrometric parameters derived for the 11 targets are in Table 2. For each one we report: target name, position (J2000), number of reference stars, number of observations used, absolute parallax, proper motion components, tangential velocity, the time span covered by the observations and the relative-to-absolute parallax correction applied.The proper motion of the targets have all been brought to an absolute system using the galaxies in the field.
The relative errors for most of the targets are less than 10%. Observations are continuing and we hope to be able to reduce them to 5% by the end of the campaign. Significant exceptions are ULAS 1150, 1315 and 2239 which are also amongst the faintest objects under study, hence degraded the most by the borderline signal-to-noise in the early observations. In addition, parallax observations of ULAS 2239 were shifted from the discovery image position lowering the weight of the first point.
In Table 3 we compare the astrometric distances obtained here with the estimated ones given in the discovery paper of each object. The estimations were made with different techniques and the reader is referred to the discovery papers (see footnote to Table 1) for further details. The discovery distance range is usually much larger than our measured one and is overestimated for the late-Ts. This comparison underlines the need for measured parallaxes that are model independent.
4. Model fitting
In Figs. 2 and 3 we present four color - absolute magnitude diagrams for a sample of L and T dwarfs with MJ > 12 and MK > 12 respectively. The 11 targets are plotted as filled circles. Parallaxes and magnitudes of the other objects are from two on-line archives:
-
1)
The L/T dwarf archive maintained by S. K. Leggett(http://staff.gemini.edu/~sleggett/2010_phot_tab.txt,hereafter Leggett archive): This archive contains a compendiumof 225 objects with MKOYJHKL′M′ magnitudes and IRAC [3.55],[4.49], [5.73] and [7.87] magnitudes. Where usedthese objects are plotted as filled squares.
-
2)
The M/L/T dwarf archive (www.dwarfarchives.org, hereafter Dwarf archive): This is an on line compendium of all published L/T dwarfs and selected M dwarfs. As of 10/01/2010 there were 752 L & T dwarfs, reporting JHK magnitudes, parallaxes and proper motions. Where used these objects are plotted as filled triangles.
To make Figs. 2 and 3 clearer we omitted the error bars on the literature objects. An indication of the typical uncertainty on these points is given by the black cross above the legend.
All magnitudes are in the MKO system and preferentially taken from the Leggett archive as they are measured directly in that system. The majority of the infrared magnitudes in the Dwarf archive are in the 2MASS system and when needed we use the relations in Stephens & Leggett (2004) to convert to the MKO system.
Colored lines in Figs. 2 and 3 are the model predictions by Burrows et al. (2006, hereafter BSH06) and Allard et al. (2003, 2007, 2009, hereafter BTSettl09). BSH06 tracks covers the temperature range 700–2000 K, with log [g] = 4.5, 5.0, 5.5 and [Fe/H] = – 0.5, 0, +0.5. BTSettl09 covers the range 500–780 K, with log [g] = 4.5, 5.0, 5.25 and [Fe/H] = – 0.2, 0, +0.2. For a given metallicity (indicated in the plots by a given color) log[g] increases from left to right in J−H, while it increases from right to left in J−K.
Model colors and magnitudes were obtained by convolving the theoretical spectra with the UKIDSS filter profiles (Hewett et al. 2006) to calculate fluxes. We interpolate the model spectra with a spline to have the same binning as the filter profiles, apply the selected profile, and integrate to obtain the total flux. The integrated fluxes were then converted into an absolute magnitude using as a zero point a Vega spectrum treated the same way.
The absolute magnitudes plotted in Figs. 2 and 3 require from the models the flux at 10 pc. The BSH06 models supply the flux at the surface of the object and at 10 pc, the latter calculated assuming the radius-log (g)−Teff relation from Burrows et al. (1997). The BTSettl09 models provide only the flux at the surface of the object, to find the flux at 10pc we assume the radii from Baraffe et al. (2003) corresponding to the model log (g) and effective temperature.
In Figs. 2 and 3 we note that the BTSettl09 tracks for high and low metallicity are swapped in the different color spaces. In J-H space tracks for high metallicity are bluer than the low metallicity ones, while in J−K they are redder. This follows the trend suggested by BSH06 tracks for higher temperature, and can be seen also in the models of Saumon & Marley (2008). Due to this swap, the predictions for the T9 dwarfs are incompatible in the two color spaces, i.e. they predict high gravity – low metallicity in J−H and low gravity – high metallicity in J−K. Moreover, the T9s are redder than predicted by the theoretical models, especially in J−K. This failure may be due to an incorrect prediction of the flux emitted in the H and K-band resulting from known opacity deficiencies in modeling the collision-induced absorption of H2 and the wing of the K I doublet resonance, and the lack of an appropriate list of absorption lines of CH4 and NH3 at such low temperatures (Leggett et al. 2010).
The predictions for earlier objects are consistent in the two color spaces, but in Fig. 2 they tend to slightly underestimate the magnitudes of the T6.5-T7s. Further discussion on the models predictions and individual objects is in Sect. 6.
Parallaxes and proper motions of the 11 targets.
In Fig. 4 we present three absolute magnitude – IR spectral type diagrams. The IR spectral type classification follows the scheme described in Geballe et al. (2002) for L dwarfs and the scheme described in Burgasser et al. (2006a) for T dwarfs. The over plotted curves are polynomial fits derived in Liu et al. (2006), with the dotted line representing the polynomial obtained excluding from the fit all the known and possible binaries, while the dashed line is the one obtained excluding only the known binaries. Possible binaries were selected by Liu et al. based on their relatively high Teff compared to objects of similar spectral type in the Golimowski et al. (2004) measurements. One of the possible binaries indicated by Liu et al. (SDSS J1021-0304) was confirmed as a binary by Burgasser et al. (2006b), so now is plotted as a known binary. Following the convention used before, filled circles are the 11 targets and squares are objects from the Leggett archive, while blue objects are known binaries and green objects are possible binaries. The trend for T 8.5 and T9 is an extrapolation of the Liu et al polynomial, since their sample consisted of objects between L0 and T8.
The 11 targets indicate a steeper trend in the sequence beyond T8 than the extrapolation of the Liu et al. polynomial. In Fig. 4 the red lines are our 4-th order polynomials fit to the data including the new objects presented here, but excluding the 14 objects without magnitude naturally in the MKO system. This choice was made as the Stephens & Leggett (2004) transformations from the 2MASS to the MKO system were derived using hotter objects and employing them may introduce systematic errors in the resulting fit of the cooler objects. In Table 4 we list the coefficients and errors of the fit. The difference between the two fits with and without possible binaries is reduced compared to Liu et al., probably because of the smaller statistical weight of the possible binaries in this study (5 over a total sample of 61 objects) with respect to Liu et al. (6 over 43). As the sample of late T dwarfs is still small, identification of possible binaries in this region may be incomplete.
The 1-sigma distance range obtained here compared to those estimated in the discovery papers.
 |
Fig. 2 Color–magnitude diagrams for a sample of L and T dwarfs. The colored lines are theoretical tracks from BSH06 and BTSettl09, for different gravities and metallicities. For each metallicity, the gravity increases from left to right, assuming the values 4.5,5.0,5.5 for BSH06 tracks and 4.5, 5.0, 5.25 for BTSettl09. The 11 targets presented here are plotted as filled circles with their associated error bars, the Dwarf archive objects are plotted as triangles and the Leggett archive objects as squares. All magnitudes in the MKO system. The cross above the legend indicates the typical uncertainty on the literature objects. |
 |
Fig. 3 Same as Fig. 2 but with the color J−K instead of J−H. For each metallicity, the gravity increases from right to left, assuming the values 4.5,5.0,5.5 for BSH06 tracks and 4.5,5.0,5.25 for BTSettl09. |
We also tested polynomials from 3rd to 10th order but after 4th order there was no significant improvement in the sigma of the fit.
 |
Fig. 4 J, H and K-band absolute magnitude as a function of IR spectral type. Labeled objects are those with new parallaxes presented here. Blue squared points are known to be unresolved binaries, while green squared points are possible unresolved binaries. The over plotted lines are polynomial fit by Liu et al. (2006) based on data tabulated by Knapp et al. (2004). The dotted line was obtained excluding all the known and possible binaries, the dashed one excluding only the known binaries. The red lines are our new polynomial fits. |
5. Luminosity and effective temperature
Next we calculate an effective temperature range for our targets. To do this we used the classical Stefan-Boltzmann law: 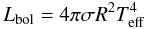 (1)hence to calculate the temperature we need to know the radius and the bolometric luminosity of each object.
(1)hence to calculate the temperature we need to know the radius and the bolometric luminosity of each object.
To determine a radius, we consider the models of Baraffe et al. (2003) we see that the radius of T dwarfs decreases rapidly when the object is very young but after 0.5 Gyr it is very constant. Therefore if we can constrain the age of our objects we can use these models to constrain the radius. In Fig. 5 we report the galactic velocity components (U,V,W) of the 11 targets. The components were calculated from the proper motions in Table 2 assuming a radial velocity range of +80/–80 km s-1. Given this large range in Vrad, the uncertainty in the proper motion becomes negligible, so we ignore it in this calculation. The overplotted box is the locus of very young objects (age < 0.1 Gyr, Zuckerman & Song 2004) while the ellipsoid is the locus of young disk objects (age < 0.5 Gyr, Eggen 1969). Even given this very conservative range in possible radial velocities no objects fall in the boxed area or in the ellipsoid area in all three components. We therefore conclude that all objects are older than 0.5 Gyr. For the 0.5–10 Gyr models from Baraffe et al. (2003) we find the radius has a range of 1.2–0.8 RJup (in a temperature range of 500–2000 K). This is also consistent with the radii predicted by Burrows et al. (1997) models for objects of the same age and temperature.
To calculate the bolometric flux (and hence the luminosity) we combined the available measured spectrum of each object (Burningham et al. 2008; Leggett et al. 2009) flux calibrated using UKIDSS YJHK photometry, with the model spectra. For ULAS 0034 and 1335 we have the spectrum in the near- and mid-infrared (hereafter MIR) region, while for the other objects we only have the NIR portion. To find the bolometric flux we use model spectra to estimate the flux where we do not have observations: at short wavelengths (λ < 1.0 μm), and, for ULAS 0034 and 1335, in the region between the near- and mid-infrared spectrum (2.4 μm < λ < 7.5 μm) or, for the other targets, in the entire portion from 2.4 μm to 15 μm. The flux emitted beyond 15 μm was estimated assuming a Rayleigh-Jeans tail.
The models used are the already mentioned BTSettl09 and the non-equilibrium models by Hubeny & Burrows (2007), covering the temperature range from 700 to 1900 K, for log [g] = 4.5,5.0 and 5.5, assuming values of Kzz = 102, 104 and 106 cm2 s-1 (eddy diffusion coefficient), for different speed of the CO/CH4 reaction (for further details see Hubeny & Burrows 2007; Saumon et al. 2006 and reference therein).
For each object we took the models in a wide range of temperature ( ± 200 K around the temperature predicted by the temperature-type relation given by Stephens et al. 20091), gravity (log [g] from 4.5 to 5.5) and metallicity ([Fe/H] from –0.2 to +0.2) and we scaled them using the available magnitudes (listed in Tables 1 and 5). For each model we took the average scaling factor obtained and we compared it with the range given by the known distance and the radius range adopted (i.e. the square of 0.8 RJup/distance ± 3σ – the square of 1.2 RJup/distance ± 3σ). We discarded the models whose average scaling factor was out of this pseudo-3σ range. We joined each one of the remaining spectra with the measured one and we calculate the resulting bolometric flux, the luminosity and hence the temperature range (corresponding to the radius range). Then we compared the temperature obtained with the one associated with the model employed. We discarded those models whose temperature differed by more than 100 K from the temperature range obtained. Finally we assumed the mean flux given by the remaining models as our final estimation and hence we calculate the luminosity and the temperature range.
The uncertainty in the flux is given by the spread in values plus a 3% uncertainty in the magnitudes used to calibrate the observed spectra and to scale the model ones. The uncertainty in the luminosity and the temperature is the result of the standard propagation of the errors on the flux and the distance, ignoring the uncertainty in the radius, given the wide range adopted.
The results are shown in Table 6. In the first column we indicate the target short name, in the second one its spectral type, in the third the temperature estimated using the temperature-spectral type relation given by Stephens et al. (2009), in the fourth the range of models employed, in the fifth the range of models kept after the first step (so after comparing the scaling factors), in the sixth the range of models kept after the second step (so after comparing the temperatures), in the seventh our assumed bolometric flux, in the eighth the associated luminosity and in the last the temperature range obtained.
We note that the use of MIR magnitudes and spectra increases our ability to constrain the object temperature. For ULAS 0034 and 1335 the bolometric flux is well constrained and the width of the temperature range obtained (150–200 K) is mainly due to the radius. Using the NIR spectrum and photometry only, the uncertainty on the flux increases and the temperature range obtained doubles.
To have an idea of the eventual systematics, we also tested the technique described in Cushing et al. (2008), e.g. to fit the object spectrum using the model spectra. The best fit spectrum was selected as the one that minimize: 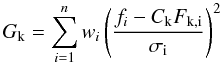 (2)where n is the number of data pixels, fi is the measured flux in the i-th spectral interval, Ck is the scaling factor (R/d)2, Fk,i is the k-th model flux and σi is the error in the measured spectrum. The weight associated to each bin (wi) is the extension of the bin itself (Δλ) as suggested by Cushing et al. The scaling factor can be provided by the fit, however, since we know the distance to the dwarf we consider fixed values of Ck, assuming again the radius range previously indicated. We selected the best fit models for the two extreme configurations, i.e. 0.5 Gyr–1.2 RJup and 10 Gyr–0.8 RJup.
(2)where n is the number of data pixels, fi is the measured flux in the i-th spectral interval, Ck is the scaling factor (R/d)2, Fk,i is the k-th model flux and σi is the error in the measured spectrum. The weight associated to each bin (wi) is the extension of the bin itself (Δλ) as suggested by Cushing et al. The scaling factor can be provided by the fit, however, since we know the distance to the dwarf we consider fixed values of Ck, assuming again the radius range previously indicated. We selected the best fit models for the two extreme configurations, i.e. 0.5 Gyr–1.2 RJup and 10 Gyr–0.8 RJup.
Since we don’t have an associated noise spectrum for ULAS 0827, 0948, 1018, 1150, 1315 and CFBDS 0059 we minimize: 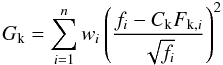 (3)The uncertainty in the extremes takes into account half of the models grid spacing based on fitting (for further details see Cushing et al.), plus an additional percentage on the flux due to the incomplete spectral coverage. This percentage was estimated comparing the measured IRAC magnitudes of ULAS 0034 and 1335 with the model’s predicted ones. The differences between measured and model magnitudes gives an average uncertainty of ~70% on the calculated flux between 2.5 and 7.5 μm. For ULAS 0034 and 1335 in this interval there is ~40% of the total emergent flux, so we obtain a relative error σF,rel = .7 × .4 = .28. This implies an additional uncertainty of ~7% on the temperature. For the other 9 objects, the uncertainty in the temperature was estimated extending the relative sigma calculated for ULAS 0034 and 1335 to the uncovered part of the flux (~60%, that results in an uncertainty σF,rel = .7 × .6 = .42).
(3)The uncertainty in the extremes takes into account half of the models grid spacing based on fitting (for further details see Cushing et al.), plus an additional percentage on the flux due to the incomplete spectral coverage. This percentage was estimated comparing the measured IRAC magnitudes of ULAS 0034 and 1335 with the model’s predicted ones. The differences between measured and model magnitudes gives an average uncertainty of ~70% on the calculated flux between 2.5 and 7.5 μm. For ULAS 0034 and 1335 in this interval there is ~40% of the total emergent flux, so we obtain a relative error σF,rel = .7 × .4 = .28. This implies an additional uncertainty of ~7% on the temperature. For the other 9 objects, the uncertainty in the temperature was estimated extending the relative sigma calculated for ULAS 0034 and 1335 to the uncovered part of the flux (~60%, that results in an uncertainty σF,rel = .7 × .6 = .42).
The choice of the weight function is arbitrary. Different choices can lead to different results, as seen by Cushing et al. (2008) and Stephens et al. (2009). Given this, we prefer the results obtained with the first method described. The values obtained with this spectral technique are summarized in Table 7. They are largely consistent with the ones obtained scaling the model spectra.
Coefficients of the polynomial fit.
 |
Fig. 5 The galactic velocity components U,V and W obtained from the proper motions in Table 2 assuming a Vrad range of +80/–80 km s-1. The triangle indicates the +80 km s-1 extreme, the diamond indicates the –80 km s-1 extreme. The overplotted black box is the locus of young stars (Zuckerman & Song 2004, age < 0.1 Gyr), the ellipsoid is the locus of young disk stars (Eggen 1969, age < 0.5 Gyr). |
We also performed a completely model independent flux calculation for ULAS 0034 and 1335, that have a completely measured spectral energy distribution. We determined the bolometric flux emitted integrating the measured spectrum between 1 and 2.5 μm, then adding the flux emitted between 2.5 and 7.5 μm calculated using the IRAC magnitudes (assuming a constant flux distribution over the passband2), finally we integrated the measured 7.5–15 μm spectrum. The flux emitted beyond 15 μm was estimated assuming a Rayleigh-Jeans tail. The results obtained for ULAS 0034 and 1335 with this approach are consistent with the one obtained with the other techniques described within the uncertainty quoted in Table 6.
6. Discussion
In Fig. 6 we present a Teff-spectral type diagram of the 11 T-dwarfs of the sample, for each of which we plot the temperature range displayed in Table 6. When needed, objects have been offset by ± 0.1 in spectral type, to avoid overlaps. Over plotted for comparison we have the effective temperature – infrared type relation derived by Stephens et al. (2009). All the ranges are consistent with the relation except for ULAS 0948, 0901 and 1315, that are cooler than predicted.
We now discuss individual objects with temperature values or indications of peculiarity in the literature.
6.1. ULAS 0034
There are several estimations of the temperature of this object. In the discovery paper, Warren et al. (2007) estimate a conservative range of 600 ≤ Teff ≤ 700 K using the measured NIR spectrum and the near- and mid-infrared photometry with a grid of solar-abundance BTSettl model, calibrated using the parameters of 2MASS0415, and a linear fit of Teff vs. H-[4.5] color for hotter stars; Delorme et al. (2008) using the NIR spectrum and the same grid described in Warren et al. (2007) determine Teff ≈ 670 K; in Leggett et al. (2009) the published range is 550 ≤ Teff ≤ 600, obtained fitting the measured NIR and MIR spectrum with model spectra by Saumon & Marley (2008); finally, in SJL10 using the parallax reported in this paper and the model fitting in Leggett et al. (2009), using a model radius of 0.11 R⊙ (as implied by the spectral fits constraints on gravity), derive a bolometric luminosity of L/L⊙ = 1.10 ± 0.01 × 10-6, consistent with the temperature range 550–600 K. In this work, using NIR and MIR spectrum, the MKO NIR photometry and the IRAC MIR photometry, we find a luminosity of L/L⊙ = 1.13 ± 0.06 × 10-6, consistent with the value obtained by Leggett et al. (2009). The difference between the temperature range derived here and by Leggett et al. is due to the different technique used: the Leggett et al. spectral fitting result is similar to that derived spectrally here, given in Table 7.
6.2. CFBDS 0059
In the discovery paper (Delorme et al. 2008) of this object they estimate Teff ~ 620 K comparing the spectral indices with a solar metallicity grid of BTSettl model spectra. In Leggett et al. (2009) the technique adopted is the same described in Sect. 6.1, and the range obtained is 550 < Teff < 600. Here we found a range 490 < Teff < 600 consistent with Leggett et al., larger because of the different technique used. Moreover, as noted in Delorme et al. (2008) using the Besançon stellar population model (Robin et al. 2003), the kinematics suggest that the target is a older member of the thin disk (age ~ 4 Gyr) that corresponds, using Baraffe et al. (2003) radii, to a radius R ≈ 0.9 RJup and a Teff ≈ 570 K. As regards its gravity and metallicity, we noted in Sect. 4 that the model predictions are not consistent, so we do not go further in the analysis of these physical properties.
6.3. SDSS 0207
In Vrba et al. (2004) they find a πabs = 34.85 ± 9.87 mas and μtot = 156.3 ± 11.4 mas/yr for SDSS 0207, both consistent with the values found here. The model predictions in Figs. 2 and 3 indicates log [g] = 5.0 and low or solar metallicity while the BSH06 clear tracks indicates a metal-rich nature in J−K.
There are two previous estimates of effective temperature for this object: Golimowski et al. (2004), using the measured spectrum and estimating the bolometric correction using M′ and L′ photometry, find Lbol/L⊙ = 1.51 ± 0.87 × 10-5; Vrba et al. (2004) using the K-band magnitude and the bolometric correction derived by Golimowski et al. and find Lbol/L⊙ = 1.74 ± 1.04 × 10-5. Both these values are consistent with our result.
6.4. ULAS 0901
ULAS 0901 is much cooler than what expected for its type, see Fig. 6. In Fig. 4 the dwarf is fainter than the other T7.5 s of the sample, in particular in MJ and MH. This maybe an indication that ULAS 0901 is half a subclass later, i.e. a T8.
In Lodieu et al. (2007) ULAS 0901 is indicated as a high gravity – solar metallicity object, based on the low K-band flux. The model prediction of the gravity and the metallicity of this object in Figs. 2 and 3 are log [g] = 4.5 and [Fe/H] = + 0.2 (in contrast with this finding) but we must point out the known degeneracy between gravity and metallicity (Knapp et al. 2004). This degeneracy could be the reason for the discrepancy between our result and Lodieu et al.
6.5. ULAS 1018
The model predictions in Figs. 2 and 3 are not consistent for ULAS 1018. In the J−K space it appears as a solar-metallicity low-gravity (log [g] = 4.5) object, while the J−H prediction is low-gravity and low-metallicity ([Fe/H] = – 0.5). The uncertainty in color and magnitude prevent us to draw a firm conclusion on the properties of this object. We mention here that ULAS 1018 is indicated as a metal-poor object by Murray et al. (in prep.) based on its very blue H−K, while in Lodieu et al. (2007), was indicated as a possible metal-rich object, based on the high K-band flux and narrow Y-band flux peak.
The bolometric luminosity and thus the temperature range obtained are consistent with an object of spectral type T5.
6.6. ULAS 1150
This object is a peculiar T6.5, with T7-T6.5 indices in the J and K band (H2O–J = 0.087, CH4−J = 0.302, CH4–K = 0.032, Pinfield et al. 2008), but T3 in the H (H2O–H = 0.455). Pinfield et al. suggest that it could be a low-gravity high-metallicity object, based on the K-band enhancement and the Y-band suppression. In Fig. 2 it assumes an anomalous position, lying on the low-gravity high-metallicity side of the theoretical curves while in Fig. 3 the model predicts a low/solar metallicity. The large errors prevent us from making any comments on its gravity.
IRAC magnitudes of ULAS 0034, SDSS 0207 and ULAS 1335 (Warren et al. 2007; Patten et al. 2006; Burningham et al. 2008) used to scale the model spectra.
Fluxes, luminosities and temperatures of the sample obtained scaling the model spectra using the measured magnitudes, e.g. the first method discussed in Sect. 5.
The bolometric luminosity and thus the temperature range obtained are consistent with an object of spectral type T6.5.
6.7. ULAS 1315
In Fig. 6 it appears significantly cooler than the other T7.5s. In the discovery paper, Pinfield et al. (2008), no particular indication of peculiarity were detected. Looking at Figs. 2 and 3 it is easy to see that ULAS 1315 is particularly faint in MK (it is the bluest in J−K), and the K-band suppression indicates high gravity, as predicted by the models. However the indication of high metallicity in the same plots is in contradiction with this interpretation as a metal-rich object would show an enhancement in the K-band flux. It is fainter than the other T7.5 s also in MJ and MH, this results in an extremely cool temperature, almost 200 K less than what expected. This can indicate that ULAS 1315 is a T8 (the spectral indices H2O-J, CH4-J and CH4-H corresponds to a T8, while H2O-H to a T7, see Pinfield et al. 2008).
6.8. ULAS 1335
Temperatures obtained fitting the observed spectrum, e.g. the second method discussed in Sect. 5.
 |
Fig. 6 Temperature ranges plotted as a function of the spectral type. Uncertainties in each extreme point of the range are in Table 6. The uncertainty in spectral type is half subtype. The over plotted dotted line is the effective temperature-infrared type relation derived by Stephens et al. (2009). |
There are two previous estimations of the temperature of this object: Burningham et al. (2008), using a solar-metallicity BTSettl model grid and a comparison of the H–[4.49] color with theoretical expectations, find Teff ~ 550–600 K; Leggett et al. (2009), using the technique described in Sec. 6.1, find Teff = 500–550 K. The luminosity obtained here (Lbol = 1.09 ± 0.06 × 10-6 L⊙) is formally consistent with both those ranges, given the large uncertainty in the radius, but it is closer to the value obtained in Burningham et al. (2008). As in the case of the other late T dwarfs, ULAS 0034 and CFBDS 0059, the model predictions are contradictory in the different color spaces and we are therefore unable to say anything about the other parameters of this objects.
7. Conclusions
We present the parallax and proper motions of 11 cool T dwarfs taking advantage of the UKIDSS discovery image to shorten the time required for a precise determination. We find that the models do not predict the colors and absolute magnitudes of the coolest T dwarfs, and that, given the observed colors and absolute magnitudes, the models predict contradictory behaviours depending on which color is considered.
We examine two methods for the calculation of Teff, one of which derives the temperature from the luminosity, which is determined using available spectroscopic data complemented with model spectra scaled using measured photometry, and the other of which does a least-squares-like model spectrum fit to the observed spectrum. The second method is very dependent on the data weighting selection and so we prefer the former technique. The two approaches give consistent results however the former gives a larger range in temperature.
The observations of these 11 objects are continuing at a lower frequency of 4 observations per year. At the end of the observing campaign all the objects in the sample will have a time coverage of 4 years, allowing us to obtain a more precise and robust parallax solution. Also, enhanced photometry for ULAS 0901 and ULAS 0948 is expected within the year.
The inclusion of MIR observations increases our ability to determine the object parameters, especially for the temperature. With IRAC photometry and a MIR spectrum the emitted flux is well constrained and the limiting factor becomes the radius, producing a range of ~150 K. Using a NIR spectrum and photometry only, the uncertainty in the flux is on the order of that on the radius, and the temperature range obtained doubles. For the future we hope that the Warm-Spitzer and WISE missions will continue to provide MIR observations for the study of these objects.
Acknowledgments
The authors would like to acknowledge the support of: the Royal Society International Joint Project 2007/R3; the PARSEC International Incoming Fellowship and IPERCOOL International Research Staff Exchange Scheme within the Marie Curie 7th European Community Framework Programme. This research has benefitted from the M, L, and T dwarf compendium housed at dwarfArchives.org and maintained by Chris Gelino, Davy Kirkpatrick, and Adam Burgasser. The United Kingdom Infrared Telescope is operated by the Joint Astronomy Centre on behalf of the Science and Technology Facilities Council of the UK, all of the data used here were obtained as part of the UKIRT Service Programme. S.K.L.’s research is supported by the Gemini Observatory, which is operated by the Association of Universities for Research in Astronomy, Inc., on behalf of the international Gemini partnership of Argentina, Australia, Brazil, Canada, Chile, the United Kingdom, and the United States of America. N.L. acknowledges funding from the Spanish Ministry of Science and Innovation through the Ramón y Cajal fellowship number 08-303-01-02.
References
- Allard, N. F., Allard, F., Hauschildt, P. H., Kielkopf, J. F., & Machin, L. 2003, A&A, 411, L473 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Allard, F., Allard, N. F., Homeier, D., et al. 2007, A&A, 474, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Allard, N. F., Noselidze, I., & Kruk, J. W. 2009, A&A, 506, 993 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baraffe, I., Chabrier, G., Barman, T. S., Allard, F., & Hauschildt, P. H. 2003, A&A, 402, 701 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burgasser, A. J., Geballe, T. R., Leggett, S. K., Kirkpatrick, J. D., & Golimowski, D. A. 2006a, ApJ, 637, 1067 [NASA ADS] [CrossRef] [Google Scholar]
- Burgasser, A. J., Kirkpatrick, J. D., Cruz, K. L., et al. 2006b, ApJS, 166, 585 [NASA ADS] [CrossRef] [Google Scholar]
- Burgasser, A. J., Tinney, C. G., Cushing, M. C., et al. 2008, ApJ, 689, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Burningham, B., Pinfield, D. J., Leggett, S. K., et al. 2008, MNRAS, 391, 320 [NASA ADS] [CrossRef] [Google Scholar]
- Burningham, B., Pinfield, D. J., Lucas, P. W., et al. 2010, MNRAS, 821 [Google Scholar]
- Burrows, A., Marley, M., Hubbard, W. B., et al. 1997, ApJ, 491, 856 [NASA ADS] [CrossRef] [Google Scholar]
- Burrows, A., Sudarsky, D., & Hubeny, I. 2006, ApJ, 640, 1063 [NASA ADS] [CrossRef] [Google Scholar]
- Chiu, K., Liu, M. C., Jiang, L., et al. 2008, MNRAS, 385, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Cushing, M. C., Marley, M. S., Saumon, D., et al. 2008, ApJ, 678, 1372 [NASA ADS] [CrossRef] [Google Scholar]
- Delorme, P., Delfosse, X., Albert, L., et al. 2008, A&A, 482, 961 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eggen, O. J. 1969, PASP, 81, 553 [NASA ADS] [CrossRef] [Google Scholar]
- Geballe, T. R., Knapp, G. R., Leggett, S. K., et al. 2002, ApJ, 564, 466 [NASA ADS] [CrossRef] [Google Scholar]
- Golimowski, D. A., Leggett, S. K., Marley, M. S., et al. 2004, AJ, 127, 3516 [NASA ADS] [CrossRef] [Google Scholar]
- Harrington, R. S., & Dahn, C. C. 1980, AJ, 85, 454 [NASA ADS] [CrossRef] [Google Scholar]
- Hewett, P. C., Warren, S. J., Leggett, S. K., & Hodgkin, S. T. 2006, MNRAS, 367, 454 [NASA ADS] [CrossRef] [Google Scholar]
- Hubeny, I., & Burrows, A. 2007, ApJ, 669, 1248 [NASA ADS] [CrossRef] [Google Scholar]
- Kendall, T. R., Tamura, M., Tinney, C. G., et al. 2007, A&A, 466, 1059 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Knapp, G. R., Leggett, S. K., Fan, X., et al. 2004, AJ, 127, 3553 [NASA ADS] [CrossRef] [Google Scholar]
- Lawrence, A., Warren, S. J., Almaini, O., et al. 2007, MNRAS, 379, 1599 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Leggett, S. K., Cushing, M. C., Saumon, D., et al. 2009, ApJ, 695, 1517 [NASA ADS] [CrossRef] [Google Scholar]
- Leggett, S. K., Burningham, B., Saumon, D., et al. 2010, ApJ, 710, 1627 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, M. C., Leggett, S. K., Golimowski, D. A., et al. 2006, ApJ, 647, 1393 [NASA ADS] [CrossRef] [Google Scholar]
- Lodieu, N., Pinfield, D. J., Leggett, S. K., et al. 2007, MNRAS, 379, 1423 [NASA ADS] [CrossRef] [Google Scholar]
- Lodieu, N., Burningham, B., Hambly, N. C., & Pinfield, D. J. 2009a, MNRAS, 397, 258 [NASA ADS] [CrossRef] [Google Scholar]
- Lodieu, N., Dobbie, P. D., Deacon, N. R., Venemans, B. P., & Durant, M. 2009b, MNRAS, 395, 1631 [NASA ADS] [CrossRef] [Google Scholar]
- Nakajima, T., Oppenheimer, B. R., Kulkarni, S. R., et al. 1995, Nature, 378, 463 [NASA ADS] [CrossRef] [Google Scholar]
- Patten, B. M., Stauffer, J. R., Burrows, A., et al. 2006, ApJ, 651, 502 [NASA ADS] [CrossRef] [Google Scholar]
- Perryman, M. A. C., Lindegren, L., Kovalevsky, J., et al. 1997, A&A, 323, L49 [NASA ADS] [Google Scholar]
- Pinfield, D. J., Burningham, B., Tamura, M., et al. 2008, MNRAS, 390, 304 [NASA ADS] [CrossRef] [Google Scholar]
- Robin, A. C., Reylé, C., Derrière, S., & Picaud, S. 2003, A&A, 409, 523 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Saumon, D., & Marley, M. S. 2008, ApJ, 689, 1327 [NASA ADS] [CrossRef] [Google Scholar]
- Saumon, D., Marley, M. S., Cushing, M. C., et al. 2006, ApJ, 647, 552 [NASA ADS] [CrossRef] [Google Scholar]
- Smart, R. L., Jones, H. R. A., Lattanzi, M. G., et al. 2010, A&A, 511, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stephens, D. C., & Leggett, S. K. 2004, PASP, 116, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Stephens, D. C., Leggett, S. K., Cushing, M. C., et al. 2009, ApJ, 702, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Tokunaga, A. T., Simons, D. A., & Vacca, W. D. 2002, PASP, 114, 180 [NASA ADS] [CrossRef] [Google Scholar]
- Vrba, F. J., Henden, A. A., Luginbuhl, C. B., et al. 2004, AJ, 127, 2948 [NASA ADS] [CrossRef] [Google Scholar]
- Warren, S. J., Mortlock, D. J., Leggett, S. K., et al. 2007, MNRAS, 381, 1400 [NASA ADS] [CrossRef] [Google Scholar]
- Zuckerman, B., & Song, I. 2004, ARA&A, 42, 685 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
All Tables
The 1-sigma distance range obtained here compared to those estimated in the discovery papers.
IRAC magnitudes of ULAS 0034, SDSS 0207 and ULAS 1335 (Warren et al. 2007; Patten et al. 2006; Burningham et al. 2008) used to scale the model spectra.
Fluxes, luminosities and temperatures of the sample obtained scaling the model spectra using the measured magnitudes, e.g. the first method discussed in Sect. 5.
Temperatures obtained fitting the observed spectrum, e.g. the second method discussed in Sect. 5.
All Figures
 |
Fig. 1 Observations for the targets ULAS 0901 (top panel) and 1315 (bottom panel). The highest point is the discovery image. The observational history and distance of these two targets are similar but they differ by a magnitude in apparent brightness. The solution shows the effect of low signal-to-noise observations in the beginning of the parallax sequence. |
| In the text | |
 |
Fig. 2 Color–magnitude diagrams for a sample of L and T dwarfs. The colored lines are theoretical tracks from BSH06 and BTSettl09, for different gravities and metallicities. For each metallicity, the gravity increases from left to right, assuming the values 4.5,5.0,5.5 for BSH06 tracks and 4.5, 5.0, 5.25 for BTSettl09. The 11 targets presented here are plotted as filled circles with their associated error bars, the Dwarf archive objects are plotted as triangles and the Leggett archive objects as squares. All magnitudes in the MKO system. The cross above the legend indicates the typical uncertainty on the literature objects. |
| In the text | |
 |
Fig. 3 Same as Fig. 2 but with the color J−K instead of J−H. For each metallicity, the gravity increases from right to left, assuming the values 4.5,5.0,5.5 for BSH06 tracks and 4.5,5.0,5.25 for BTSettl09. |
| In the text | |
 |
Fig. 4 J, H and K-band absolute magnitude as a function of IR spectral type. Labeled objects are those with new parallaxes presented here. Blue squared points are known to be unresolved binaries, while green squared points are possible unresolved binaries. The over plotted lines are polynomial fit by Liu et al. (2006) based on data tabulated by Knapp et al. (2004). The dotted line was obtained excluding all the known and possible binaries, the dashed one excluding only the known binaries. The red lines are our new polynomial fits. |
| In the text | |
 |
Fig. 5 The galactic velocity components U,V and W obtained from the proper motions in Table 2 assuming a Vrad range of +80/–80 km s-1. The triangle indicates the +80 km s-1 extreme, the diamond indicates the –80 km s-1 extreme. The overplotted black box is the locus of young stars (Zuckerman & Song 2004, age < 0.1 Gyr), the ellipsoid is the locus of young disk stars (Eggen 1969, age < 0.5 Gyr). |
| In the text | |
 |
Fig. 6 Temperature ranges plotted as a function of the spectral type. Uncertainties in each extreme point of the range are in Table 6. The uncertainty in spectral type is half subtype. The over plotted dotted line is the effective temperature-infrared type relation derived by Stephens et al. (2009). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


