| Issue |
A&A
Volume 524, December 2010
|
|
|---|---|---|
| Article Number | A90 | |
| Number of page(s) | 17 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201015331 | |
| Published online | 25 November 2010 | |
Evaluation of image-shift measurement algorithms for solar Shack-Hartmann wavefront sensors
1
Institute for Solar Physics of the Royal Swedish Academy of Sciences,
AlbaNova University Center,
10691
Stockholm,
Sweden
e-mail: mats@astro.su.se
2
Stockholm Observatory, AlbaNova University Center,
10691
Stockholm,
Sweden
Received: 3 July 2010
Accepted: 13 September 2010
Context. Solar Shack–Hartmann wavefront sensors measure differential wavefront tilts as the relative shift between images from different subapertures. There are several methods in use for measuring these shifts.
Aims. We evaluate the inherent accuracy of the methods and the effects of various sources of error, such as noise, bias mismatch, and blurring. We investigate whether Z-tilts or G-tilts are measured.
Methods. We test the algorithms on two kinds of artificial data sets, one corresponding to images with known shifts and one corresponding to seeing with different r0.
Results. Our results show that the best methods for shift measurements are based on the square difference function and the absolute difference function squared, with subpixel accuracy accomplished by use of two-dimensional quadratic interpolation. These methods measure Z-tilts rather than G-tilts.
Key words: atmospheric effects / instrumentation: adaptive optics / site testing
© ESO, 2010
1. Introduction
High-resolution observational astronomy with telescopes operated on the ground relies on methods for combating the effects from turbulence in the Earth’s atmosphere. Turbulence varies with time scales on the order of ms, mixing air that varies in temperature and therefore in refractive index. The wavefronts of the light from astronomical objects, which are flat when they enter the atmosphere, are distorted by the optically active atmosphere, which causes image motion and blurring in the images collected through the telescope. Measurements of the wavefronts allow us to correct for these effects, both in real time and in post processing.
There are several different methods for measuring in real time the variation of the wavefront phase of the light over the telescope pupil. For solar telescopes, the one exclusively used is the Shack-Hartmann (SH; Shack & Platt 1971) wavefront sensor (WFS). This is true for the adaptive optics (AO) systems of present 1-meter class, high-resolution solar telescopes (Rimmele & Radick 1998; Scharmer et al. 2000, 2003; von der Lühe et al. 2003; Rimmele et al. 2004). SH wide-field WFSs are used for characterizing the atmospheric turbulence above existing and future solar telescopes (Waldmann 2007; Waldmann et al. 2008; Scharmer & van Werkhoven 2010).
An SH WFS estimates the wavefront from measurements of the local wavefront tilt in several regions of the pupil called subpupils. The local tilts manifest themselves as image motion in the focal plane associated with each subpupil. For night-time telescopes, this image motion is (comparably) easily measured by tracking the peak of the image of a natural or artificial point source. As no point sources are available on the sun, one instead has to resort to measuring relative image motion by matching solar features in the different subpupil images. This can be done by finding the minimum of the degree of mismatch of the images as a function of image shift. This procedure requires solving two distinct subproblems: 1) computing the mismatch function as a function of image shift in steps of whole pixels and 2) finding the minimum of the mismatch function with subpixel precision. The latter involves interpolation between the whole-pixel grid points. This procedure for solar correlation tracking was apparently pioneered by Smithson & Tarbell (1977) and von der Lühe (1983).
The SH WFSs developed for the AO systems currently in use at different solar telescopes use a variety of shift measurement methods, so do the sensors used for turbulence characterization. This suggests that the choices of methods were based on personal preferences and technological momentum from other applications rather than on a thorough evaluation of the performance of these methods on relevant data.
Several algorithms for measuring the mismatch and performing the interpolation were investigated by Yi & Molowny Horas (1992). However, because the purpose of their work was different from ours (image remapping in post-processing), they used much larger fields of view (FOVs) than is currently practical for real-time solar SH WFS.
As part of a project on characterization of the atmospheric turbulence using SH WFS, Waldmann (2007) and Waldmann et al. (2008) address these problems for setups more similar to ours. The recent MSc thesis of Johansson (2010) has expanded on Waldmann’s work in this area. She implemented a number of different methods for image-shift measurements and tested them on synthetic data relevant to solar SH WFSs. Comparisons with their methods and results will appear throughout this paper.
Correlation algorithms (CAs).
In this paper we investigate, by use of artificial data relevant to present solar SH WFSs, a number of different algorithms for measuring whole-pixel image shifts and interpolating to get subpixel accuracy. The algorithms are defined in Sect. 2. We investigate the inherent accuracy of the algorithms in Sect. 3, by testing them on identical images with known shifts, as well as the influence of noise and variations in intensity level. In Sect. 4 we use the best methods on images formed through artificial seeing and evaluate the performance for different seeing conditions. We discuss our results in Sect. 5.
2. Algorithms
2.1. Correlation algorithms
In Table 1 we define five different correlation algorithms (CAs), which we use to calculate the image mismatch on a grid of integer pixel shifts i,j. The names and acronyms of the CAs are also given in the table. These mismatch values make a matrix c with elements ci,j. A coarse estimate of the image shift, (δx,δy), is then given by the indices corresponding to the grid position with the minimum mismatch value, (imin,jmin). This shift should be sought within a maximum range in order to reduce the number of false matches to other parts of the granulation pattern. The algorithms in Sect. 2.2 are then used to refine this estimate to subpixel accuracy.
Perhaps most straight-forward is the SDF algorithm, in which one calculates the mismatch in a Least Squares (LS) sense.
Subtracting the intensity mean, expanding the square in the SDF algorithm, and retaining only the cross term gives twice the covariance (with negative sign), which is the basis of the following two algorithms. The CFI algorithm calculates the covariance in the image domain. It is the one being used for the Dunn Solar Telescope system (Rimmele & Radick 1998). The correlation coefficient differs from the covariance only by division with the standard deviations of the two images, so methods based on the former (e.g., Waldmann et al. 2008) should give results similar to those of CFI.
The covariance can also be calculated in the Fourier domain, taking advantage of the Fast Fourier Transform (FFT). The CFF algorithm was developed by von der Lühe (1983) for an image stabilization system and is used today in the KAOS AO implementation used at the Vacuum Tower Telescope (von der Lühe et al. 2003). For small images, such as those involved in SH WFS calculations, one can expect errors from wrap-around effects. That is, because of the assumption of periodicity implicit in finite-size Fourier transforms, for large shifts, structures in one image are not matched with structures at the shifted location but with structures shifted in from the opposite side of the image.
Knutsson et al. (2005) derived a method based on the Fourier spectrum of the correlation function (correlation spectrum phase). It is supposed to give results similar to the CFF method but with some accuracy sacrificed for speed. We have not investigated this method.
The CFF method requires apodization of the images, i.e., the multiplication of a window
function that reduces ringing effects from the discontinuities caused by the Fourier
wrap-around. When not explicitly stated otherwise, we use a Hamming window written as
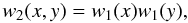 (1)where w1 is the
1-dimensional Hamming window (Enochson & Otnes
1968),
(1)where w1 is the
1-dimensional Hamming window (Enochson & Otnes
1968), 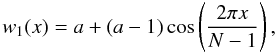 (2)where a = 0.53836 and
N is the linear size of the window. See also Sect. 3.3.5 below.
(2)where a = 0.53836 and
N is the linear size of the window. See also Sect. 3.3.5 below.
The ADF algorithm is fast because it can be calculated very efficiently in CPU instructions available for many architectures, particularly for 8-bit data. Keller et al. (2003) use ADF for the IR AO system of the McMath-Pierce solar telescope. So do Miura et al. (2009) in their recently presented AO system used for the domeless solar telescope at Hida Observatory.
Because the shape of the ADF minimum does not match the assumption of a parabolic shape implicit in the subpixel algorithms, squaring the ADF correlation values leads to an improvement. This adds a completely negligible computational cost to that of ADF, as squaring is done after summing. In fact, because it does not move (imin,jmin), only the at most nine grid points used for subpixel interpolation (see Sect. 2.2) have to be squared. This ADF2 method was developed by G. Scharmer in 1993 for use in the correlation tracker systems of the former Swedish Vacuum Solar Telescope (Shand et al. 1995) and is in use in the AO and tracker systems of the Swedish 1-meter Solar Telescope (SST; Scharmer et al. 2000, 2003).
Smithson & Tarbell (1977) showed that a linear trend in intensity shifts the covariance peak from the correct position. Therefore one should subtract a fitted plane from both g and gref before applying the CAs. However, the granulation data used in our simulations have negligible trends and for the difference based algorithms (ADF, ADF2, and SDF), a consistent bias in the intensity level cancels automatically. We therefore saved computing time in our tests by limiting the pre-processing of the data to only subtracting the mean values, and only when calculating CFI and CFF.
Interpolation algorithms (IA) or subpixel minimum finding algorithms.
2.2. Subpixel interpolation
The methods in Sect. 2.1 are responsible for making a coarsely sampled 2D correlation function with a reasonable shape. The interpolation algorithms (IAs) in this section then have to find the minimum with better accuracy than given by the sampling grid.
November & Simon (1988) found that
interpolation methods should be based on polynomials of degree 2. Methods based on
polynomials of higher degree systematically underestimate the shift for small
displacements, while first degree polynomials give a systematic overestimation. The
algorithms we consider can all be described as fitting a conic section,
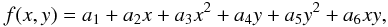 (3)to the 3 × 3-element submatrix s
of c centered on the sample minimum of c with elements
(3)to the 3 × 3-element submatrix s
of c centered on the sample minimum of c with elements
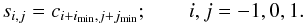 (4)The interpolated shift vector,
(δx,δy), is the position of the minimum of the fitted function,
(xmin,ymin).
The algorithms differ in the number of points used and whether the fitting is done in 2D
or in each dimension separately. The definitions, names, and acronyms of the different
methods are given in Table 2.
(4)The interpolated shift vector,
(δx,δy), is the position of the minimum of the fitted function,
(xmin,ymin).
The algorithms differ in the number of points used and whether the fitting is done in 2D
or in each dimension separately. The definitions, names, and acronyms of the different
methods are given in Table 2.
The 1QI method is based on numerical 1D derivatives using the center row (column) of s (November 1986). It is equivalent to a LS estimate using only the center row (column) of s. It does not use the corner elements of s.
The 1LS algorithm consists of, separately for the x and y directions, fitting a 1D polynomial of degree 2 to all the elements in s. This is equivalent to the procedure of Waldmann (2007), projection of the data onto the axes (i.e., summing the rows (columns)), and doing LS fitting on the result. Waldmann uses Lagrange interpolation but this is mathematically equivalent to a LS fit.
The 2QI algorithm was derived by Yi & Molowny Horas (1992, their Eq. (9)) as an extension of the 1QI algorithm.
The 2LS algorithm is based on expressions for the conic section coefficients derived by Waldmann (2007). Johansson (2010) found that Waldmann’s expression for one of the 2LS coefficients is missing a factor 2. We are using the corrected expression.
Waldmann (2007) compared four different subpixel methods: 1LS, 2LS, and a 2D fit to a Gaussian. He found that the Gaussian fit gave the best results and the polynomial method worked almost as well. Because the Gaussian fit is more computationally heavy, he adopted the latter. Johansson (2010) tested the Gaussian fit and got results comparable to Waldmann’s but much better results for the polynomial fits. Based on Johansson’s results, we have not evaluated Gaussian fits as a method for subpixel interpolation.
Miura et al. (2009) use a method for subpixel interpolation, where they find the centroid of a spot generated by inverting and then clipping the mismatch measured with ADF. This method is not considered here.
 |
Fig.1 Granulation image used for simulation experiments. a) 430.5 nm (G-band) SST diffraction limited granulation image (GI). 2000 × 2000 pixels, image scale 0″̣041/pixel. b) Degraded to resolution of a 9.8 cm subpupil, shifted by a whole number of pixels, and re-sampled to 200 × 200 0″̣41-pixels. |
3. Algorithm accuracy
The goal of this experiment with artificial data is to establish the accuracy of the algorithms themselves, for granulation images (GI), which are identical except for a known shift and detector imperfections such as noise and bias. In reality, the images will be different because the atmospheric turbulence not only shifts the images but also smears them differently. Those effects will be addressed in Sect. 4 below.
3.1. Artificial data
For this experiment, the images should be identical except for a known shift, defined to subpixel precision without introducing errors that are caused by the re-sampling needed for subpixel image shifting. We therefore start with a high-resolution image, degrade the resolution, shift it by a known number of whole high-resolution pixels, and then down-sample it to the SH image scale.
Specifically, we use a 2000 × 2000-pixel, high-quality SST G-band image with an image scale of 0″̣041/pixel, see Fig. 1a. The image was recorded on 25 May 2003 by Mats Carlsson et al. from ITA in Oslo and corrected for atmospheric turbulence effects by use of Multi Frame Blind Deconvolution (Löfdahl 2002). We degraded it to 9.8 cm hexagonal (edge to edge) subpupil resolution at 500 nm. This degraded image was shifted by integer steps from 0 to 20 times the high-resolution pixels, as well as in steps of 10 pixels from 30 to 60. The so degraded and shifted GIs were box-car compressed by a factor 10 to 200 × 200 pixels of size 0″̣41. This procedure gives images with known subpixel shifts, δx and δy, without any re-sampling, except for the compression. Figure 1b shows a sample compressed image.
The data with 0–20 high-resolution pixel shifts were made to test subpixel accuracy, while the 30–60-pixel shifts are for testing linearity with larger shifts.
The diffraction limited resolution, λ / Dsub ≈ 1″ at 500 nm, corresponds to >2 pixels. This means subpixel accuracy corresponds to super-resolution accuracy.
The resulting images had more contrast than the real data from our SH WFS, so some bias was added to change the RMS contrast to ~3% of the mean intensity. The resulting images were stored in two versions, with and without Gaussian noise with a standard deviation of 0.5%1. The digitization noise of a 12-bit camera is insignificant compared to the Gaussian noise but may be significant for an 8-bit camera. We do not include the effects of digitization in our simulations.
3.2. Processing
The 200 × 200-pixel FOV is much larger than the FOV of the SH WFS, which allows the use of many different subfields in order to get better statistics. Centered on each of 17 × 17 grid positions, subimages, g, of size 16 × 16 or 24 × 24 pixels, were defined. The subimages defined in the unshifted reference image, gref, were larger in order to accommodate a shift range limited to ± 8 pixels along each axis direction, except for CFF, which uses two images of equal size. Note also that for CFF, the size of the correlation matrix is limited by the subimage size. For 16 × 16-pixel subfields, this limits the range to ± 6 pixels (in reality to even less).
The different sizes of g, 16 × 16 and 24 × 24 pixels, have two purposes: 1) We want to see how a change in size affects some of the methods and 2) we will compare CFF using 24 × 24 pixels with the other methods using 16 × 16 pixels. If the image geometry on the detector accommodates a 24 × 24-pixel gref, then it can also accommodate 24 × 24-pixel g subfields if no oversize reference image is needed.
We measured the shifts with each combination of CAs in Sect. 2.1 and IAs in Sect. 2.2. We do this with and without noise and with and without multiplying the reference image by 1.01, giving an approximate 1% bias mismatch. The bias mismatch sensitivity is investigated because it is known to be a problem with the ADF and ADF2 methods.
 |
Fig.2 Errors in measured shifts vs. real shifts for four different CFs, zero noise N, and zero bias mismatch B. Mean values and ± 1σ error bars calculated with robust statistics. The dashed line in the CFF panel corresponds to p1 − 1, where p1 is fitted to Eq. (5). |
For each real shift, δxreal (and δyreal, we will simplify the notation by referring to both axis directions with x when possible), we calculate the mean and standard deviation, σ, of the measured shifts, δxmeasured, by use of the outlier-robust statistics based on Tukey’s Biweight as implemented in the IDL Astronomy User’s Library (Landsman 1993).
After removing 4σ outliers, we fit the data to the relationship
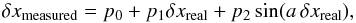 (5)where
a = 2π / 1 pixel, by use of the
robust nonlinear LS curve fitting procedure MPFIT (Moré
1978; Markwardt 2009). The linear
coefficient, p1, of these fits is listed in the tables below.
(5)where
a = 2π / 1 pixel, by use of the
robust nonlinear LS curve fitting procedure MPFIT (Moré
1978; Markwardt 2009). The linear
coefficient, p1, of these fits is listed in the tables below.
3.3. Results
In Fig. 2, the SDF, ADF2, CFI, and CFF CAs are compared for the case of no noise and no bias mismatch, using the 2QI IA and 24 × 24-pixel subfields. The errors are a mix of systematic and random errors. The SDF and ADF2 algorithms give a tighter correlation between the true and measured image shifts than the CFI and CFF algorithms. November & Simon (1988) found similar undulating effect of small errors near whole and half pixel shifts calculated by CFF and larger errors in between. Ballesteros et al. (1996) make a similar observation with ADF.
The ADF and CFF methods produce many outliers, which is the main reason we need the robust statistics mentioned in Sect. 3.2. A very small fraction of these outliers, on the order 10-5 of all cases for CFF, zero for all other CAs, are caused by the correlation matrix minimum falling on an outer row or column. The rest are caused by false minima in the correlation matrix, which happen to be deeper than the real minimum. This can happen occasionally if a secondary minimum is located on or near a grid point, while the real minimum is between grid points. The effect is more severe for ADF because of the more pointy shape of its minimum. For CFF, minima corresponding to large shifts are attenuated by two effects: apodization lowers the intensity away from the center of the subimage and the digital Fourier transform wraps in mismatching structure from the other side of the subimage. This can lead to detection of false minima corresponding to small shifts.
The dashed line in the CFF panel represents the linear part of the fit to Eq. (5); its slope is p1 − 1. The CFF method systematically underestimates large shifts. Comparison between the fitted line and the mean values shows a slight nonlinearity in the CFF method, making the underestimation worse for larger shifts.
The deviation of p1 from unity and the undulations are systematic errors. The former can be calibrated while the latter mix with the random errors represented by the error bars.
 |
Fig.3 Results using The SDF/2QI methods with 24 × 24-pixel subfields. Small shifts, δr ≲ 2 pixels, and different combinations of noise, N, and bias mismatch, B, as indicated in the labels of each tile. Error bars are ± 1σ. The blue line is a fit to Eq. (5). |
Figure 3 illustrates the effects of noise and of
bias mismatch for SDF. Here we limit the plots to 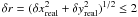 pixels. The blue line corresponds to the fit of Eq. (5). The amplitudes of the undulations,
p2, is ~0.01 pixel. Noise does not appear to change the
undulating errors significantly but it does make the random errors more dominant. Bias
mismatch has a similar effect and overwhelms the differences due to noise. It also appears
to change a minute systematic overestimation of the shifts to an equally small
underestimation.
pixels. The blue line corresponds to the fit of Eq. (5). The amplitudes of the undulations,
p2, is ~0.01 pixel. Noise does not appear to change the
undulating errors significantly but it does make the random errors more dominant. Bias
mismatch has a similar effect and overwhelms the differences due to noise. It also appears
to change a minute systematic overestimation of the shifts to an equally small
underestimation.
3.3.1. Tables
The complete results of these simulations are presented in Tables 3–8.
Simulation results, no bias mismatch, no noise.
Simulation results, no bias mismatch, 0.5% noise.
Simulation results, 1% bias mismatch, no noise.
Simulation results, 1% bias mismatch, 0.5% noise.
While the standard deviations in the plots are for each real shift individually, and therefore do not include the undulations, the standard deviations in the tables are for intervals of real shifts and therefore do include the undulations. The measured shifts might be expected to have near-Gaussian distributions, which is true for ADF2 and SDF and mostly for CFI. ADF often has complicated, multi-peak distributions. All CFF distributions are double-peaked and/or asymmetrical.
We give the results for all shifts, δr, but also separately for small shifts (< 1 pixels and < 2 pixels, resp.), medium shifts (shifts between 3 and 5 pixels in length), and large shifts (>5 pixels). The small shifts are relevant to AO performance in closed loop. The large shift results tell us something about performance in open loop, which is relevant for wavefront sensor calibration, site testing, image restoration, and when trying to close an AO loop.
Simulation results, no bias mismatch, no noise. Flat top window for FFT.
Simulation results, no bias mismatch, 0.5% noise. Flat top window for FFT.
3.3.2. Identical images
In Table 3, we show the performance of the different methods with noise free data.
We begin by noting that in many cases the errors for large shifts are smaller than those for small shifts. This may seem counterintuitive but it is simply a consequence of using only whole pixel shifts for the larger shifts. The IAs have smaller systematic errors on the grid points, see the undulations in Fig. 2.
The ADF CA produces many 4σ outliers. It is not surprising that it gives much worse results than ADF2, because the two CAs by definition share the location of the whole pixel minimum but the ADF minimum does not have the parabolic shape assumed by the IAs.
SDF and ADF2 are clearly better than the CFI and CFF methods. CFF can compete for the very smallest shifts (<1 pixel) if we use 24 × 24 pixels for CFF and 16 × 16 pixels for the other CAs (which is the most fair comparison, since the optics need to accommodate 24 × 24 pixels in order to get the oversize reference image for the non-CFF CAs).
Except for CFF, the errors appear more or less independent of the magnitude of the shifts. CFF deteriorates significantly in three ways at larger shifts: The number of outliers increases, the random error increases, and the shifts are systematically underestimated, as shown by the nonunity slopes. The former two effects can be explained by the assumption of periodicity of the digital Fourier transform. The signal for large shifts is diluted by mismatching granulation shifted in from the opposite end of the FOV.
For SDF and ADF2, the 2D IAs are clearly better than the 1D ones. 2QI is marginally better than 2LS. The best results with SDF and ADF2 are an error RMS of less than 0.02 pixels, corresponding to 0″̣008. Increasing the subfield size from 16 to 24 pixels squared reduces the error by approximately 30%.
3.3.3. Noisy images
Adding 0.5% noise to the images give the results shown in Table 4. The errors grow but the behavior is similar to the zero-noise case.
The best results with SDF and ADF2 16 × 16 are an error RMS of less than 0.03 pixels, corresponding to 0″̣012. CFF with 24 × 24 gives similar results for small shifts. As in the case of zero noise, increasing the subfield size from 16 to 24 pixels squared reduces the error by approximately 30%.
With 24 × 24 pixels, SDF and ADF2 give results similar to the 16 × 16-pixel zero-noise case. Surprisingly, the number of outliers for ADF is significantly reduced by the added noise. But σ increases more than for ADF, so this may be an effect of making the error distribution more Gaussian.
3.3.4. Bias mismatch
Subtracting a fitted plane (or just the mean intensity as in our experiment, see Sect. 2.1) from each subimage removes mismatches in intensity bias for CFI and CFF. We did not do this for the difference based CAs (SDF, ADF, and ADF2), where a consistent bias cancels. However, if there is a bias mismatch between the images this cancellation is not effective. Such bias mismatch could come from, e.g., variations in a thin cloud layer in the case when gref is not from the same exposure as g, or small drifts in the pupil location on the SH, causing variations in the light level from the outermost subpupils.
We re-processed all the data after multiplying the reference image by 1.01, introducing a 1% bias mismatch with the other images. In Tables 5 and 6 we show the results for the difference based CAs. As expected, the CFI and CFF results did not change from the ones in Tables 3 and 4 and they are therefore not repeated.
For small shifts, the SDF and ADF2 results are now worse than for CFF, even when comparing the methods using the same image size. SDF is more robust against bias mismatch than ADF2. There is now no real difference between ADF and ADF2, possibly indicating that the parabolic shape of the ADF2 correlation function is destroyed by the bias mismatch. The SDF error RMS is 0.7 pixels for 16 × 16 and 0.4 pixels for 24 × 24, which makes it the best method for large shifts.
With a bias mismatch, 0.5% noise added to the images does not significantly change the results for the difference based CAs. We conclude that bias mismatch should be removed in pre-processing by subtraction of the intensity mean.
3.3.5. Window function
The CFF method requires apodization, i.e., the multiplication of the subimage (after subtracting the fitted plane) by a window function. The intention is to reduce ringing effects from the discontinuities caused by Fourier wrap-around. For the results above, we used a 2D Hamming window. In Tables 7–8 we show the results when we instead use a window with the center ~50% of the area flat, and a taper only in the pixels outside this area. This is similar to the window used by Waldmann (2007). See Fig. 4 for the two types of window functions.
 |
Fig.4 Window functions, 24 × 24 pixels. Left: Hamming window. Right: Flat-top window. |
The results are mixed. The errors are larger but there are fewer outliers. The results are similar with and without noise. The systematic underestimation is reduced, resulting in slopes closer to unity. Based on these data we cannot say which window is better, they would have to be evaluated specifically for any new situation where one wants to use CFF. The important result for our purposes is that the comparison between SDF and ADF2 vs. CFF does not depend on the window function used.
 |
Fig.5 Sample wavefront and the subpupil pattern of 85 hexagonal microlenses. The circle represents the 98 cm SST pupil and the gaps between adjacent microlenses have been exaggerated for clarity. The geometry is actually such that there is no space between the microlenses. a) The 1003-mode simulated wavefront phase. b) Piecewise plane approximation. c) Local tilts only. |
4. Image shift as a measure of wavefront tilt
For wavefront sensing, the quantities that really need to be measured are the average wavefront gradients at the positions corresponding to the subapertures. One assumes that a shift in image position corresponds perfectly to the average gradient of the wavefront across the subaperture. However, in addition to local gradients, continuous wavefront aberrations across the telescope aperture also result in local wavefront curvature. Is the assumption valid anyway and how good is it for different seeing conditions, as quantified with Fried’s parameter r0?
Using Kolmogorov statistics for different r0 without any assumption of partial correction by an AO system makes the statistics from this experiment relevant to open-loop WFS. I.e., systems for measuring seeing statistics (e.g., Scharmer & van Werkhoven 2010) and the capture phase for AO systems, but not necessarily AO systems in closed loop.
4.1. Artificial data
The setup corresponds to a filled 98-cm pupil (like the SST) with 85 subapertures, each 9.55 cm edge-to-edge. In Fig. 5a we show one sample Kolmogorov wavefront phase. The superimposed pattern shows the geometry of 85 hexagonal microlenses circumscribed by a telescope pupil. Figure 5b demonstrates the local plane approximation implicit in SH wavefront sensing, while Fig. 5c shows just the tilts.
The exact geometry does not matter for the results reported here, since our tests do not involve the step where wavefronts are reconstructed from the shift measurements. However, the geometry discussed is along the lines planned for the next generation SST AO system, and in that respect motivates the particular subaperture size and shape investigated.
We generated 100 wavefront phases, φi, following Kolmogorov statistics. For making each simulated phase screen, the following procedure was used. 1003 random numbers were drawn from a standard normal distribution, scaled with the square root of the atmospheric variances and used as coefficients for atmospheric Karhunen-Lòeve (KL) functions 2–1004. We used KL functions based directly on the theory of Fried (1978), as implemented by Dai (1995). These modes are numbered in order of decreasing atmospheric variance, and the exact range of indices is motivated by KL1 being piston and KL1005 a circular mode, starting a higher radial order. Figure 5a shows a sample wavefront masked with the pattern of the 85 hexagonal microlens geometry.
For all simulations, we used a wavelength of 500 nm and a telescope aperture diameter of Dtel = 98 cm. In order to cover a range of different seeing conditions, we scaled these wavefront phases to different values of Fried’s parameter, r0 ∈ {5,7,10,15,20} cm, by multiplying with (Dtel / r0)5 / 6. Using the same wavefront shapes scaled differently like this, the performance for different values of r0 should be directly comparable.
For each random wavefront, separately scaled to each value of r0, and for each subpupil defined by a microlens, we generated an image by convolving the GI in Fig. 1a with a PSF based on the subpupil and the local wavefront phase.
We want to examine the effect of using different subfield sizes. Increased subfield size can be used in different ways: Either one can change the image scale, so the same amount of granulation fits in the FOV but in better pixel resolution. Or one can keep the original image scale so more granulation fits in the FOV. (Or something in between.) Therefore we make images at three different image scales by box-car compressing them by three different integer factors, 7, 10, and 13. The resulting image scales are 0″̣29/pixel, 0″̣41/pixel, and 0″̣53/pixel.
To summarize: the images we have generated were downgraded to the resolution of the subpupil, shifted by the local wavefront tilt and also somewhat blurred by the local wavefront curvature, the latter in particular for data with small r0. A bias was then added to make the RMS contrast of the granulation pattern approximately 3% of the mean intensity.
4.2. Processing
For each subfield size, noise, and r0, relative shifts and tilts were calculated for 490000 randomly selected pairs of subpupil images. We operate on image pairs corresponding to subpupils from different random wavefronts, so results are not influenced systematically by spatial correlations.
For the shift measurements, we use all the CF methods from Sect. 2 except ADF, applied to the two images in a pair. We use only the 2QI method for subpixel interpolation.
Shift measurements were calculated twice, with and without 1% noise added to the images. We increased the noise level from the 0.5% used in Sect. 3.3.3 to make the effect of noise clearer and thus allow better comparison of different methods. We do not investigate bias mismatch in this experiment. The conclusion from Sect. 3 is that bias mismatch should be compensated for before applying the shift measurement methods.
For comparison with the shift measurements,
δxshift, we fitted Zernike tip and tilt to
each wavefront, within each hexagonal subpupil. The relative wavefront tilt for an image
pair is the difference between the Zernike tilts for the two subpupils in the pair. These
relative tip/tilt coefficients in radians,
αx, are converted to image shift,
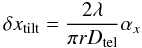 (6)where r is the image scale
in rad/pixel. We calculate the robust statistics of the resulting shifts, remove
4σ outliers, and fit the data to the relationship
(6)where r is the image scale
in rad/pixel. We calculate the robust statistics of the resulting shifts, remove
4σ outliers, and fit the data to the relationship 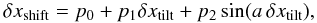 (7)where
a = 2π / 1 pixel. Compare Eq. (5).
(7)where
a = 2π / 1 pixel. Compare Eq. (5).
4.3. Results
Table 9 shows the results from images with image scale 0″̣41/pixel and different subfield sizes, N × N pixels with N = 16, 24, and 36. In seconds of arc, this corresponds to 6″̣56, 9″̣84, and 14″̣76 squared. The results using the additional image scales 0″̣29/pixel and 0″̣53/pixel and a single array size, N = 24, are in Table 10.
In addition to the tabulated results, we calculated the following: The standard deviation
of δxtilt varies linearly with
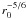 as expected from Kolmogorov statistics:
σtilt = 2.68, 2.02, 1.50, 1.07, 0.84 pixels
as expected from Kolmogorov statistics:
σtilt = 2.68, 2.02, 1.50, 1.07, 0.84 pixels
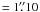 , 0″̣83, 0″̣62, 0″̣44, 0″̣34 for r0 = 5, 7, 10, 15, 20 cm,
resp. Correlation coefficients calculated after removal of outliers are very high: they
round to 1.00 in all cases, except CFF and CFI at N = 16 for which they
are 0.98–0.99.
, 0″̣83, 0″̣62, 0″̣44, 0″̣34 for r0 = 5, 7, 10, 15, 20 cm,
resp. Correlation coefficients calculated after removal of outliers are very high: they
round to 1.00 in all cases, except CFF and CFI at N = 16 for which they
are 0.98–0.99.
Results from seeing simulation.
Results from seeing simulation.
4.3.1. Failures
If the errors were normal distributed, using a 4σ limit for defining outliers should give a failure rate of 0.0063%. With almost 5 × 105 samples we expect the normal distribution to be well realized but the actual failure rates are larger. All CAs show an excess but by far it is the CFF results that suffer from the highest number of outliers, particularly for small subfields and small r0. CFI is also slightly worse than SDF and ADF2.
All failure rates are ≲ 10%. They are >2% for r0 = 5 cm with all methods when using the smallest image scale, 0″̣29/pixel, and for small FOVs and r0 = 5, 7 cm (and CFI r0 = 5 cm, noise, N = 16). Figure 6 illustrates how failure rates sometimes increase with noise, sometimes decrease. With noise, the failure rate decreases with large FOV in arcsec (exception: N = 36 and r0 = 7 cm). The variation is less systematic without noise.
 |
Fig.6 Failure rates in percent for different FOV sizes and CAs. Red: r0 = 20 cm; Green: r0 = 10 cm; Blue: r0 = 7 cm. N × N-pixel subfields. Diamonds (◇): image scale 0″̣41/pixel, varying N = {16,24,36} as labeled in the plots; Down triangles (▿): 0″̣29/pixel, N = 24; Up triangles (▵): 0″̣53/pixel, N = 24. All the above without noise. Crosses (×): corresponding FOVs, with noise. Note different vertical scales. |
4.3.2. Shift errors
We now plot some of the results in pixels rather than seconds of arc so we can compare with the results in Sect. 3.
Figure 7 shows the easiest case: the largest subfields, 36 × 36 pixels, and the best seeing, r0 = 20 cm, resulting in the smallest shifts. The ADF2 results are so similar to the SDF results that we only show the latter of those two methods.
The errors in Fig. 7 are consistent with the ones in Fig. 2. We recognize the undulations but we also see a linear trend, not only for CFF. SDF and CFF: σerr ≈ 0.025 matches undulations plus error bars (CFF because for 20 cm we are dominated by small shifts). CFI: σerr ≈ 0.045 is actually slightly better than in Fig. 2. These results (as opposed to the ones in Fig. 8) are comparable because 20 cm is much larger than the subpupil size so the images are not blurred by local phase curvature. We cannot directly compare the noisy data, because here we have 1% noise, in the earlier experiment we used 0.5%.
Linear fit offsets are small, |p0| ≲ 0.002 pixels for all CAs, except CFI that has |p0| ≲ 0.016 pixels. The undulations fit sines with an amplitude of p2 ≈ 0.01 pixels in almost all cases, consistent with Figs. 2 and 3, where we used identical images with known shifts. The exceptions are cases when both N and r0 are small. In the latter cases the fits to the sine function sometimes give as small amplitudes as p2 ≈ 0.002 pixels or less.
For shifts smaller than 0.2 pixels, the overall overestimation turns into underestimation. For CFF, the slope and the undulations work in the same direction, making the underestimation larger for the smaller shifts.
Figure 8 shows the most demanding test: the smallest subfields, 16 × 16 pixels, and the worst seeing, r0 = 5 cm, resulting in the largest shifts and the images most blurred by local phase curvature. Note much larger dispersion and error in p1 for CFF.
4.3.3. Z-tilts and G-tilts
The wavefront tilt measured over a subpupil is by necessity an approximation because in reality the tilts vary over the subpupil. In the night-time literature, two kinds of tilts are discussed (e.g., Tokovinin 2002). G-tilts correspond to averaging the wavefront Gradient, which is mathematically equivalent to measuring the center of Gravity of the PSF. However, because of noise and asymmetrical PSFs this can never be realized in practice. Windowing and thresholding the PSF gives measurements that are more related to Z-tilts, corresponding to Zernike tip/tilt and the location of the PSF peak. When interpreting the measurements, we need to know what kind of tilts are measured by our methods.
The simulated tilts are implemented as coefficients to the Zernike tip and tilt
polynomials. So if the shifts measure Z-tilts, the expected
p1 is by definition ![\begin{equation} \label{eq:8} E[p_1\mid{\rm Z\mbox{-}tilt}]\equiv1 . \end{equation}](/articles/aa/full_html/2010/16/aa15331-10/aa15331-10-eq120.png) (8)In order to derive the expected
p1 for G-tilts, we use formulas given by Tokovinin (2002). The variance of the differential
image motion can be written as
(8)In order to derive the expected
p1 for G-tilts, we use formulas given by Tokovinin (2002). The variance of the differential
image motion can be written as 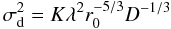 (9)where D is the subpupil
diameter and K is a number that depends on the kind of tilt. The
expected p1 should be equal to the ratio of
σd for G-tilts and Z-tilts, i.e.,
(9)where D is the subpupil
diameter and K is a number that depends on the kind of tilt. The
expected p1 should be equal to the ratio of
σd for G-tilts and Z-tilts, i.e., ![\begin{equation} E[p_1\mid{\rm G{\mbox{-}}tilt}] = \sqrt{K_{\rm G}/K_{\rm Z}} \approx 0.966, \label{eq:7} \end{equation}](/articles/aa/full_html/2010/16/aa15331-10/aa15331-10-eq125.png) (10)where we used
K = KG = 0.340 for G-tilts and
K = KZ = 0.364 for Z-tilts, which is
asymptotically correct for large separations between subpupils. This corresponds to a
3.4% difference in tilt measurements with Z-tilts giving the larger numbers, regardless
of wavelength, seeing conditions, and aperture size. For smaller separations,
E [p1 | G - tilt] is even smaller and
depends somewhat on whether the shifts are longitudinal or transversal (parallel or
orthogonal to the line separating the apertures).
(10)where we used
K = KG = 0.340 for G-tilts and
K = KZ = 0.364 for Z-tilts, which is
asymptotically correct for large separations between subpupils. This corresponds to a
3.4% difference in tilt measurements with Z-tilts giving the larger numbers, regardless
of wavelength, seeing conditions, and aperture size. For smaller separations,
E [p1 | G - tilt] is even smaller and
depends somewhat on whether the shifts are longitudinal or transversal (parallel or
orthogonal to the line separating the apertures).
In our results for all the CAs except CFF, 1.007 ≲ p1 ≲ 1.010. This means they overestimate Z-tilts systematically by ≲ 1% and G-tilts by ≳4.6%. This result appears to be robust with respect to noise, subfield size, image scale, and seeing conditions.
 |
Fig.7 2D histograms of shift measurement errors for simulated seeing. 36 × 36-pixel subfields, 0″̣41/pixel, r0 = 20 cm. Top: no noise; Bottom: 1% noise. Blue line: fit to Eq. (7); Red lines: linear part of fit (dashed: ±1σ). |
 |
Fig.8 2D histograms of shift measurement errors for simulated seeing. 16 × 16-pixel subfields, 0″̣41/pixel, r0 = 5 cm. Top: no noise; Bottom: 1% noise. Blue line: fit to Eq. (7); Red lines: linear part of fit (dashed: ± 1σ). |
The CFF p1 values confirm the underestimation of the image shift found in Sect. 3.2. They depend mostly on the size of the subfield but also to some extent on r0 and noise. CFF p1 improves with larger FOV in arcsec, regardless of number of pixels and r0. For small FOVs, CFF p1 is smaller than the G-tilts slope of 0.966, grows with FOV size to cross G-tilt at ~14″. For the other CAs, p1 is independent of FOV size. CFF slope improved with subfield size. Is it the size in pixels or the size in arcsec that is important? Figure 9 makes it clear that the size in arcsec is the important parameter and that with even larger FOVs we should expect to measure something closer to Z-tilts. We conjecture that the important parameter is the number of 1″ resolution elements that fit within the FOV.
4.3.4. RMS errors
The RMS errors, σerr, are calculated after removing the outliers and after subtracting the linear fit. In spite of having more outliers removed from the calculations, the errors are worse for CFF than for the other methods.
Compared to the noise-free data, adding 1% image noise significantly increases σerr. In many cases it also decreases the number of fails (all cases with N = 24,36, most cases with N = 16). This probably means the noise makes the error distribution more Gaussian.
σerr decreases with increasing r0, indicating that the algorithms perform better in good seeing, as expected. But are the results worse in bad seeing because of local phase curvature (i.e., smearing) or just because the shifts are larger? The relative measure, σerr / σtilt, does not decrease as much with r0 for zero-noise data and actually tends to increase for noisy data. So the latter should not be the major effect.
How do the errors depend on the FOV size in pixels and in seconds of arc? Figure 10 visualizes the following results from the tables. Without noise, the CFI and CFF results improve with N as well as the FOV size in arcsec with constant N (particularly from 6″̣9 to 9″̣8). SDF (and ADF2, the results are so similar that we show only SDF) errors are more or less independent of FOV size, whether in pixels or in arcsec. With 1% noise, however, for all methods, the errors improve only slightly or grow when N is constant and we increase the FOV size in arcsec (particularly from 7″ to 13″). When N is increased from 16 to 24 with almost constant 7″ FOV, there is a significant improvement. There is also significant improvement when N is increased from 24 to 36 (although FOV in arcsec is increased too). So for the RMS error, FOV in pixels is more important than FOV in arc seconds with noisy data.
 |
Fig.9 CFF slopes p1 for different FOV sizes, no noise. Red: r0 = 20 cm; Green: r0 = 10 cm; Blue: r0 = 7 cm. N × N-pixel subfields. Diamonds (◇): image scale 0″̣41/pixel, varying N = {16,24,36} as labeled in the plots; Down triangles (▿): 0″̣29/pixel, N = 24; Up triangles (▵): 0″̣53/pixel, N = 24. All the above without noise. Crosses (×): corresponding FOVs, with noise. The dotted lines correspond to Z-tilt (p1 = 1.0) and G-tilt (p1 = 0.966), respectively (see Eq. (10)). The gray band at the top represents the 1.007 ≲ p1 ≲ 1.010 range of the other CA results. |
 |
Fig.10 Standard deviations of errors. σerr for different FOV sizes and CAs. Red: r0 = 20 cm; Green: r0 = 10 cm; Blue: r0 = 7 cm. N × N-pixel subfields. Diamonds (◇): image scale 0″̣41/pixel, varying N = {16,24,36} as labeled in the plots; Down triangles (▿): 0″̣29/pixel, N = 24; Up triangles (▵): 0″̣53/pixel, N = 24. Symbols below the dotted line correspond to data without noise, above the line with 1% noise. Note different vertical scales. |
5. Discussion and conclusions
We have evaluated five different correlation algorithms and four different interpolation algorithms in two experiments with artificial data. Among these are the algorithms in use for the AO systems installed at the major high-resolution solar telescopes today. The experiment in Sect. 3 examined the inherent performance of the methods with identical images and known shifts, and introduced also the effects of noise and a mismatch in intensity level (bias) between images. We used image contrast and noise levels that resemble the setup at the SST. In Sect. 4, we introduced also local wavefront curvature and different seeing conditions.
Based on the results of both experiments, we recommend SDF and ADF2 (in that order) for calculating the correlation functions. They give significantly smaller random errors and more predictable systematic errors than the competing methods. The SDF results are marginally better so if computational speed is not an issue, use SDF. But ADF2 may, by virtue of speed, be preferable. For subpixel interpolation, 2QI and 2LS perform better than the one-dimensional interpolation algorithms.
It is clear from Sect. 3 that bias mismatch has a strong and negative effect on the performance of the difference based methods. We have not established how much bias mismatch can be tolerated. Our conclusion is that it should be compensated for in pre-processing, before the shift measurement methods are applied. The simulated bias mismatch comes from multiplication with 1.01 but is compensated for by subtraction for CFI and CFF. Based on the fact that the latter methods give identical results with and without the bias mismatch (to the number of digits shown in the table), we conclude that it does not matter whether the mismatch is removed by multiplication or by subtraction.
Waldmann (2007) considers only a single correlation algorithm (CFF) but tries a few different interpolation algorithms: 1LS, 2LS, and a Gaussian fit. He finds a Gaussian fit to give the better results but the almost as good 1LS is less complicated so he uses that. On the other hand, Waldmann et al. (2008) try CFF, CFI (almost: correlation instead of covariance) and ADS, but use only 1LS for interpolation. They find CFF best and ADF worst. Trying all combinations of those methods, Johansson (2010) confirmed that Gaussian and 1LS perform similarly together with CFF. She also found a similar performance for SDF and ADF2 with 1LS and Gaussian, but significantly better performance when interpolated with 2QI and 2LS. Based on this, we did not try a Gaussian fit here because of its greater computational cost.
We have demonstrated that with the recommended methods, we can measure shifts in identical, noise-free 24 × 24-pixel images with an RMS error of 0.012 pixels, corresponding to 0″̣008 in our setup. With realistic image noise RMS of 0.5% the errors increase by 40% to 0.017 pixels. Increasing the noise RMS to 1% gives unacceptably high measurement errors in bad seeing, particularly with small subimages. Increasing the subfield size from 16 to 24 pixels squared reduced the error by approximately 30%.
One method is not necessarily the best choice both for open loop and for closed loop. In open loop, performance for large shifts and predictable systematic errors are important. However, CFF can compete with SDF and ADF2 in closed loop, where wavefronts are already compensated for and the CFF random errors are small. The underestimation of the shifts can be reduced by using a larger FOV and can also be compensated for with a different servo gain. Based on our results, it is difficult to find a reason to ever use the CFI method.
We have found that SDF, ADF2, and CFI measure Z-tilts with a 1% systematic overestimation, rather than G-tilts. For the FOV sizes relevant to solar SH WFS, the CFF method severely underestimates the tilts but it is likely that for larger FOVs, also CFF measures Z-tilts.
Johansson (2010) processed also images together with a reference image that was slightly distorted geometrically (compressed image scale in one direction and expanded in the other) and found that it could significantly affect the results. We have not examined this effect here. A relevant further test involving anisoplanatic effects would require geometrical distortions and differential blurring whose shape and magnitude can be calculated from realistic atmospheric turbulence profiles.
We end by emphasizing that small details in processing may have large effects on the results. Examples from our evaluation include ADF versus ADF2 and the choice of apodization for CFF. As in so many other situations, it is important to keep track of implementation details and other tricks, so they are not lost when upgrading SH software.
This noise level corresponds to photon noise from a CCD with 40 ke− full well. For a WFS set up to be running all day, the noise level would be larger when the sun is at low elevation and the image therefore darker. However, it is likely that the performance is then limited by other effects than noise, such as image warping from anisoplanatism.
Acknowledgments
I acknowledge many discussions with Göran Scharmer, Pit Sütterlin and Tim van Werkhoven. Thomas Berkefeld and Torsten Waldmann helped me understand some details of their work with the VTT adaptive optics system and simulations of wide-field wavefront sensors. I am grateful to George (formerly Guang-ming) Dai for calculating and sharing the radial Karhunen–Lòeve functions used for the atmospheric turbulence simulations. The Swedish 1-m Solar Telescope is operated on the island of La Palma by the Institute for Solar Physics of the Royal Swedish Academy of Sciences in the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofísica de Canarias.
References
- Ballesteros, E., Collados, M., Bonet, J. A., et al. 1996, A&AS, 115, 353 [Google Scholar]
- Dai, G.-M. 1995, J. Opt. Soc. Am. A, 12, 2182 [NASA ADS] [CrossRef] [Google Scholar]
- Enochson, L. D., & Otnes, R. K. 1968, Programming and Analysis for Digital Time Series Data (U.S. Dept. of Defense, Shock and Vibration Info. Center) [Google Scholar]
- Fried, D. L. 1978, J. Opt. Soc. Am., 68, 1651 [NASA ADS] [CrossRef] [Google Scholar]
- Johansson, U. 2010, Masters Thesis, Stockholm University [Google Scholar]
- Keller, C. U., Plymate, C., & Ammons, S. M. 2003, in Innovative Telescopes and Instrumentation for Solar Astrophysics, ed. S. L. Keil, & S. V. Avakyan, Proc. SPIE, 4853, 351 [Google Scholar]
- Knutsson, P. A., Owner-Petersen, M., & Dainty, C. 2005, Opt. Express, 13, 9527 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Landsman, W. B. 1993, in Astronomical Data Analysis Software and Systems II, ed. R. J. Hanisch, R. J. V. Brissenden, & J. Barnes, ASP Conf. Ser., 52, 246, see also http://idlastro.gsfc.nasa.gov [Google Scholar]
- Löfdahl, M. G. 2002, in Image Reconstruction from Incomplete Data II, ed. P. J. Bones, M. A. Fiddy, & R. P. Millane, Proc. SPIE, 4792, 146 [Google Scholar]
- Markwardt, C. B. 2009, in Astronomical Data Analysis Software and Systems XVIII, ed. D. A. Bohlender, D. Durand, & P. Dowler, ASP Conf. Ser., 411, 251, see also http://purl.com/net/mpfit [Google Scholar]
- Miura, N., Noto, Y., Kato, S., et al. 2009, Opt. Rev., 16, 558 [CrossRef] [Google Scholar]
- Moré, J. 1978, in Lecture Notes in Mathematics, Numerical Analysis, ed. G. A. Watson (Springer-Verlag), 630, 105 [Google Scholar]
- November, L. J. 1986, Appl. Opt., 25, 392 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- November, L. J., & Simon, G. W. 1988, ApJ, 333, 427 [Google Scholar]
- Rimmele, T. R., & Radick, R. R. 1998, in Adaptive Optical System Technologies, ed. D. Bonaccini, & R. K. Tyson, Proc. SPIE, 3353, 72 [Google Scholar]
- Rimmele, T. R., Richards, K., Hegwer, S., et al. 2004, in Telescopes and Instrumentation for Solar Astrophysics, ed. S. Fineschi, & M. A. Gummin, Proc. SPIE, 5171, 179 [Google Scholar]
- Scharmer, G. B., Dettori, P., Löfdahl, M. G., & Shand, M. 2003, in Innovative Telescopes and Instrumentation for Solar Astrophysics, ed. S. Keil, & S. Avakyan, Proc. SPIE, 4853, 370 [Google Scholar]
- Scharmer, G. B., Shand, M., Löfdahl, M. G., Dettori, P. M., & Wei, W. 2000, in Adaptive Optical Systems Technologies, ed. P. L. Wizinowich, Proc. SPIE, 4007, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Scharmer, G. B., & van Werkhoven, T. I. M. 2010, A&A, 513, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shack, R., & Platt, B. C. 1971, J. Opt. Soc. Am., 61, 656 [Google Scholar]
- Shand, M.,Wei, W., & Scharmer, G. 1995, in Field Programmable Gate Arrays (FPGAs) for Fast Board Development and Reconfigurable Computing, ed. J. Schewel, Proc. SPIE, 2607, 145 [Google Scholar]
- Smithson, R. C., & Tarbell, T. D. 1977, Correlation tracking study for meter-class solar telescope on space shuttle, Tech. rep., Lockheed Missiles and Space Co. [Google Scholar]
- Tokovinin, A. 2002, PASP, 114, 1156 [NASA ADS] [CrossRef] [Google Scholar]
- von der Lühe, O. 1983, A&A, 119, 85 [NASA ADS] [Google Scholar]
- von der Lühe, O., Soltau, D., Berkefeld, T., & Schelenz, T. 2003, in Innovative Telescopes and Instrumentation for Solar Astrophysics, ed. S. L. Keil, & S. V. Avakyan, Proc. SPIE, 4853, 187 [Google Scholar]
- Waldmann, T. A. 2007, Diploma Thesis, Kiepenheuer Institut für Sonnenphysik [Google Scholar]
- Waldmann, T. A., Berkefeld, T., & von der Lühe, O. 2008, in Adaptive Optics Systems, ed. N. Hubin, C. E. Max, & P. L. Wizinowich, Proc. SPIE, 7015, 70155O [Google Scholar]
- Yi, Z., & Molowny Horas, R. L. 1992, in LEST Technical Report, Proc. LEST Mini-Workshop: Software for Solar Image Processing, ed. Z. Yi, T. Darvann, & R. Molowny Horas, 56 [Google Scholar]
All Tables
All Figures
 |
Fig.1 Granulation image used for simulation experiments. a) 430.5 nm (G-band) SST diffraction limited granulation image (GI). 2000 × 2000 pixels, image scale 0″̣041/pixel. b) Degraded to resolution of a 9.8 cm subpupil, shifted by a whole number of pixels, and re-sampled to 200 × 200 0″̣41-pixels. |
| In the text | |
 |
Fig.2 Errors in measured shifts vs. real shifts for four different CFs, zero noise N, and zero bias mismatch B. Mean values and ± 1σ error bars calculated with robust statistics. The dashed line in the CFF panel corresponds to p1 − 1, where p1 is fitted to Eq. (5). |
| In the text | |
 |
Fig.3 Results using The SDF/2QI methods with 24 × 24-pixel subfields. Small shifts, δr ≲ 2 pixels, and different combinations of noise, N, and bias mismatch, B, as indicated in the labels of each tile. Error bars are ± 1σ. The blue line is a fit to Eq. (5). |
| In the text | |
 |
Fig.4 Window functions, 24 × 24 pixels. Left: Hamming window. Right: Flat-top window. |
| In the text | |
 |
Fig.5 Sample wavefront and the subpupil pattern of 85 hexagonal microlenses. The circle represents the 98 cm SST pupil and the gaps between adjacent microlenses have been exaggerated for clarity. The geometry is actually such that there is no space between the microlenses. a) The 1003-mode simulated wavefront phase. b) Piecewise plane approximation. c) Local tilts only. |
| In the text | |
 |
Fig.6 Failure rates in percent for different FOV sizes and CAs. Red: r0 = 20 cm; Green: r0 = 10 cm; Blue: r0 = 7 cm. N × N-pixel subfields. Diamonds (◇): image scale 0″̣41/pixel, varying N = {16,24,36} as labeled in the plots; Down triangles (▿): 0″̣29/pixel, N = 24; Up triangles (▵): 0″̣53/pixel, N = 24. All the above without noise. Crosses (×): corresponding FOVs, with noise. Note different vertical scales. |
| In the text | |
 |
Fig.7 2D histograms of shift measurement errors for simulated seeing. 36 × 36-pixel subfields, 0″̣41/pixel, r0 = 20 cm. Top: no noise; Bottom: 1% noise. Blue line: fit to Eq. (7); Red lines: linear part of fit (dashed: ±1σ). |
| In the text | |
 |
Fig.8 2D histograms of shift measurement errors for simulated seeing. 16 × 16-pixel subfields, 0″̣41/pixel, r0 = 5 cm. Top: no noise; Bottom: 1% noise. Blue line: fit to Eq. (7); Red lines: linear part of fit (dashed: ± 1σ). |
| In the text | |
 |
Fig.9 CFF slopes p1 for different FOV sizes, no noise. Red: r0 = 20 cm; Green: r0 = 10 cm; Blue: r0 = 7 cm. N × N-pixel subfields. Diamonds (◇): image scale 0″̣41/pixel, varying N = {16,24,36} as labeled in the plots; Down triangles (▿): 0″̣29/pixel, N = 24; Up triangles (▵): 0″̣53/pixel, N = 24. All the above without noise. Crosses (×): corresponding FOVs, with noise. The dotted lines correspond to Z-tilt (p1 = 1.0) and G-tilt (p1 = 0.966), respectively (see Eq. (10)). The gray band at the top represents the 1.007 ≲ p1 ≲ 1.010 range of the other CA results. |
| In the text | |
 |
Fig.10 Standard deviations of errors. σerr for different FOV sizes and CAs. Red: r0 = 20 cm; Green: r0 = 10 cm; Blue: r0 = 7 cm. N × N-pixel subfields. Diamonds (◇): image scale 0″̣41/pixel, varying N = {16,24,36} as labeled in the plots; Down triangles (▿): 0″̣29/pixel, N = 24; Up triangles (▵): 0″̣53/pixel, N = 24. Symbols below the dotted line correspond to data without noise, above the line with 1% noise. Note different vertical scales. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


