| Issue |
A&A
Volume 524, December 2010
|
|
|---|---|---|
| Article Number | A81 | |
| Number of page(s) | 4 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201015234 | |
| Published online | 25 November 2010 | |
Sunyaev-Zel’dovich galaxy clusters number counts: consequences of cluster scaling-law evolution
1
Laboratoire Astrophysique de Toulouse-Tarbes, UMR 5572, Université de
Toulouse,
14 rue Edouard Belin,
31400
Toulouse,
France
e-mail: pierre.delsart@ast.obs-mip.fr; alain.blanchard@ast.obs-mip.fr
2
Instituto de Telecomunicações, Universidade de Aveiro, Campus
Universitario de Aveiro,
3810-183
Aveiro,
Portugal
e-mail: dbarbosa@av.it.pt
Received: 18 June 2010
Accepted: 6 September 2010
Aims. Galaxy cluster surveys based on Sunyaev-Zeldovich effect (SZE) mapping are expected from ongoing experiments. Such surveys are expected to provide a significant amount of information relevant to cosmology from the number counts redshift distribution. We estimate predicted SZE counts and their redshift distribution taking the current cosmological constraints and the X-ray cluster temperature distribution functions into account. Comparison between local and distant cluster temperature distribution functions provides evidence of evolution in the abundance of X-ray clusters that is inconsistent with using standard scaling relations of cluster properties in the framework of the current concordance model. The hypothesis that there is some evolution in the scaling law driven by non-gravitational processes is a natural solution to this problem.
Methods. We performed an MCMC statistical study using COSMOMC and combining current CMB observations from WMAP, the SNIa Hubble diagram, the galaxy power spectrum data from SDSS and X-ray clusters temperature distributions to predict SZE cluster number counts.
Results. Our approach allows a first estimation of expected SZ counts that considers both cosmological constraints as well as data on the temperature distribution function in a consistent way. Models in which SZ gas temperature and X-ray temperature follow the same redshift evolution lead to significantly lower SZE clusters number counts with a distinctive redshift distribution. Ongoing microwave SZE surveys will therefore shed new light on intracluster gas physics and greatly help to identify the role of possible non-gravitational physics in the history of the hot-gas component of x-ray clusters.
Key words: cosmological parameters / X-ray: galaxies: clusters
© ESO, 2010
1. Introduction
Knowledge of the galaxy cluster population has greatly progressed, thanks both to targeted observations and to systematic surveys carried by space X-ray facilities. The hot intracluster gas is also known to interact with the incoming photons of the cosmic microwave background (CMB), leaving a specific frequency imprint known as the thermal Sunyaev-Zeldovich effect (Sunyaev & Zeldovich 1972). This change in the sky brightness of the CMB can be written as a function of frequency and the Compton parameter, y, proportional to the integrated gas pressure along the line-of-sight of the cluster. For an individual cluster, the integrated Compton parameter Y is the value of y integrated over the solid angle subtended by the clusterwhich angular size which is nearly independent of redshift. This turns the SZE effect into a very effective probe of clusters at cosmological distances. Furthermore, SZE selection should be very attractive because the signal depends on an integral of the intracluster gas pressure, independently of its spatial distribution.
The relevance of these SZE cluster surveys for cosmological applications has been outlined in the past (Markevitch et al. 1994; Barbosa et al. 1996), motivating the onset of key science projects for some of the most exciting experiments in the microwave regime. In particular, the Planck Surveyor ESA mission and the South Pole Telescope (Ruhl et al. 2004) (SPT hereafter) are crucial for exploring the SZE number counts and their cosmological significance. With redshifts obtained from the optical and infrared follow-up, such samples can potentially complement other cosmological probes and constrain the matter density parameter ΩM, the amplitude of matter fluctuations measured by the parameter σ8, the dark energy content of the Universe, and its equation of state w (Lima & Hu 2007). Besides these important cosmological inferences, the SZE cluster cartography may also reveal the cluster formation processes out to high redshifts, an aspect that is further explored here.
2. Cluster modelling
Modelling the clusters population and its evolution needs two key ingredients. The first one is an expression of the mass function and its dependence on cosmology. This was first attempted by Press and Schechter in 1974 (Press & Schechter 1974). Since that time, numerical simulations have shown that the mass function follows a simple and nearly universal scaling relation with a dependence actually close to the initial Press and Schechter proposition with its deviations much below the precision level needed for current day applications (Tinker et al. 2008). The second key ingredient is the relation between cluster mass and observable quantities. From scaling arguments (Kaiser 1991), we can relate the temperature measured from X-ray to the mass, 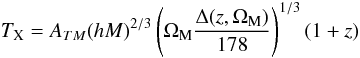 (1)in which Δ(z,ΩM) represents the density contrast (relative to the background density) by which clusters are defined, h is the Hubble parameter, and ATM describes the normalization of the TX − M relation. Hydrodynamical simulations of cluster formation have provided mass-temperature relations that actually follow the above relationship with dispersion of about 20%, while the normalization constant ATM is uncertain depending on the gas physics (Kay et al. 2007). The magnitude of the SZE is controlled by Y, the integrated Compton parameter that depends on the gas mass and the average gas temperature:
(1)in which Δ(z,ΩM) represents the density contrast (relative to the background density) by which clusters are defined, h is the Hubble parameter, and ATM describes the normalization of the TX − M relation. Hydrodynamical simulations of cluster formation have provided mass-temperature relations that actually follow the above relationship with dispersion of about 20%, while the normalization constant ATM is uncertain depending on the gas physics (Kay et al. 2007). The magnitude of the SZE is controlled by Y, the integrated Compton parameter that depends on the gas mass and the average gas temperature: 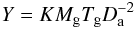 (2)where Da is the angular distance, Mg the total gas mass of the cluster, Tg its (mass-)average temperature, and K a normalization that only depends on physical constants. Because it is independent of the actual spatial distribution of the hot gas, this relation makes the SZE signal an appealing proxy for the total mass. If the gas was isothermal in clusters, one would have Tg = TX. However, it is known that clusters are not isothermal with the temperature declining in outer parts (Vikhlinin et al. 2005) following a scaling law. We can therefore still assume that the gas temperature follows some scaling laws but with a different normalization Tg = ξTX. By using the observed gas fraction in clusters (Sadat et al. 2005), a dark matter mass profile according to numerical simulation of cold dark matter (Navarro et al. 1997), and the observed temperature profile (Vikhlinin et al. 2005), one can estimate ξ ~ 0.6, a value which is quite uncertain, due to the difference in the region probe by X-ray and by SZ (see for instance Kay et al. 2008). Therefore, in the following this number is left as a quantity to be determined from observations. With the above mass-temperature relation, the Y − M relation can be evaluated numerically as
(2)where Da is the angular distance, Mg the total gas mass of the cluster, Tg its (mass-)average temperature, and K a normalization that only depends on physical constants. Because it is independent of the actual spatial distribution of the hot gas, this relation makes the SZE signal an appealing proxy for the total mass. If the gas was isothermal in clusters, one would have Tg = TX. However, it is known that clusters are not isothermal with the temperature declining in outer parts (Vikhlinin et al. 2005) following a scaling law. We can therefore still assume that the gas temperature follows some scaling laws but with a different normalization Tg = ξTX. By using the observed gas fraction in clusters (Sadat et al. 2005), a dark matter mass profile according to numerical simulation of cold dark matter (Navarro et al. 1997), and the observed temperature profile (Vikhlinin et al. 2005), one can estimate ξ ~ 0.6, a value which is quite uncertain, due to the difference in the region probe by X-ray and by SZ (see for instance Kay et al. 2008). Therefore, in the following this number is left as a quantity to be determined from observations. With the above mass-temperature relation, the Y − M relation can be evaluated numerically as 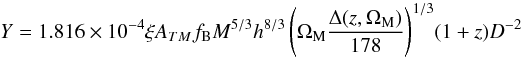 (3)with fB as the baryonic gas fraction, D the dimensionless part of the angular distance, and Y expressed in arcmin2. In this work, we take fB as the universal baryonic fraction corrected for some possible depletion Υ:
(3)with fB as the baryonic gas fraction, D the dimensionless part of the angular distance, and Y expressed in arcmin2. In this work, we take fB as the universal baryonic fraction corrected for some possible depletion Υ: 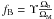 , which acts linearly as ξ. At the virial radius Υ is close to one; accordingly, Υξ was set to 0.6 for all clusters. This factor may vary with temperature, mass, and redshift, but there is no robust indication about that (Ferramacho & Blanchard 2007). For a typical coma-like cluster with about 1015 solar masses, observed at z = 1, and using the standard scaling laws, the typical Compton distortion is Y is of the order of 2.3 × 10-4 arcmin2, corresponding at 143 GHz to a flux decrement with respect to the mean CMB flux of –21 mJy, or a temperature fluctuation of –650 μK, well above both Planck and SPT sensitivity thresholds. Assuming the above relations, we can now compute the SZE source counts, as well as their redshifts distribution, as expected in a Friedmann-Lemaître cosmological model. Theoretical number counts predictions of cosmic objects can be obtained from the mass function describing the formation and evolution of objects over redshift. In this way, cluster counts dN(z) for clusters with intrinsic Y greater than a sensitivity threshold Y0 are described as
, which acts linearly as ξ. At the virial radius Υ is close to one; accordingly, Υξ was set to 0.6 for all clusters. This factor may vary with temperature, mass, and redshift, but there is no robust indication about that (Ferramacho & Blanchard 2007). For a typical coma-like cluster with about 1015 solar masses, observed at z = 1, and using the standard scaling laws, the typical Compton distortion is Y is of the order of 2.3 × 10-4 arcmin2, corresponding at 143 GHz to a flux decrement with respect to the mean CMB flux of –21 mJy, or a temperature fluctuation of –650 μK, well above both Planck and SPT sensitivity thresholds. Assuming the above relations, we can now compute the SZE source counts, as well as their redshifts distribution, as expected in a Friedmann-Lemaître cosmological model. Theoretical number counts predictions of cosmic objects can be obtained from the mass function describing the formation and evolution of objects over redshift. In this way, cluster counts dN(z) for clusters with intrinsic Y greater than a sensitivity threshold Y0 are described as 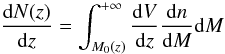 (4)where the mass threshold M0(z) is obtained from Eq. (3); dV is the volume element, accounting for the geometry and expansion rate of the Universe; and
(4)where the mass threshold M0(z) is obtained from Eq. (3); dV is the volume element, accounting for the geometry and expansion rate of the Universe; and 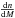 is the cluster mass function, depending on the matter and energy densities of the universe and on the initial power spectrum of mass fluctuations. On the other hand, the very same SZE cluster population is a source of non-Gaussian secondary CMB anisotropies (Cole & Kaiser 1988; Komatsu & Kitayama 1999; Bond et al. 2005; Taburet et al. 2010), which connects the present large-scale structure to the primordial CMB spectrum. This offers a way to pin down the very nature of the astrophysical evolution with the redshift of the cluster Y − M relation.
is the cluster mass function, depending on the matter and energy densities of the universe and on the initial power spectrum of mass fluctuations. On the other hand, the very same SZE cluster population is a source of non-Gaussian secondary CMB anisotropies (Cole & Kaiser 1988; Komatsu & Kitayama 1999; Bond et al. 2005; Taburet et al. 2010), which connects the present large-scale structure to the primordial CMB spectrum. This offers a way to pin down the very nature of the astrophysical evolution with the redshift of the cluster Y − M relation.
3. The X-ray picture
Since cluster masses are hardly measurable directly, it is necessary to use a relation between mass with some other observables, including its dispersion, to derive constraints from the observed temperature distribution function of X-ray clusters (Oukbir & Blanchard 1992). The constraints read as a thin region in the parameter space (ATM, σ8) (Pierpaoli et al. 2003), a known degeneracy between ATM and σ8 that has been clearly identified and quantified. In the present analysis we use the standard Λ-cold dark matter picture (ΛCDM) and Bayesian Monte Carlo Markov chain (MCMC) estimations. We use the COSMOMC parameters estimation package with constraints provided by CMB data from WMAP 7 years (Jarosik et al. 2010), Supernovae SN Ia data from the SDSS compilation sample (Kessler et al. 2009), matter power-spectrum P(k) estimation from SDSS LRG DR7 (Reid et al. 2010), and our estimation of the cluster temperature distribution at different redshifts above 3 keV.
For this, we use the local temperature distribution function of X-ray clusters from a local sample of clusters (redshift below 0.1) with fluxes above 2 × 10-11ergs-1cm-2 in the [0.1–2.4] keV band, galactic latitude |b| > 20 degrees obtained from the cluster X-ray data base BAX and no additional cut. This results in a homogenous and comprehensive flux limited sample comprising 65 clusters. This flux was selected as the lowest possible for which all clusters have their temperature measured, where the latter is mainly the integrated emission weighted temperature. The theoretical temperature distribution function was derived from the mass function with the above mass temperature relation, using the Sheth, Mo, and Tormen mass function (Sheth et al. 2001). We can then constraint the six cosmological parameters of this vanilla model (ΩM, ΩB, τ, h, n, σ8) and the normalization ATM of the mass-temperature relation.
 |
Fig. 1 Cluster temperature-distribution function in the local and distant universe. Triangles are our estimation of the temperature distribution function. The stars represent the estimated temperature distribution function at high redshift from the 400 deg2 sample restricted to the redshift range [0.4–0.6]. The continuous line corresponds to the predicted temperature distribution adjusted to fit CMB, SNIa, LSS, and the local temperature distribution function. The predictions for this model at redshift 0.5 (the lower continuous line) are far in excess of the abundances estimated from observations. For visual comparison, the dashed lines are the corresponding predictions with an evolving mass-temperature relation, Eq. (6), with α = − 1 (not fitted). |
The constraints on the six cosmological parameters are not affected essentially by the addition of the cluster constraint because of the free ATM. As an illustration, we provide the theoretical temperature distribution function computed for the median model (the normalization being ATM = 7.31 keV, Ωm = 0.317, σ8 = 0.842 and h = 0.669, Fig. 1), compared to the observed local abundance of X-ray clusters. Clearly, this model reproduces the local abundance of clusters well. A previous claim that the predicted abundance of X-ray clusters in a standard concordance-cosmological model exceeds the observed abundance at high redshift led us to compute the high redshift (z ~ 0.5) temperature distribution function of clusters in the best concordance model and compare it to the one inferred from the high-redshift subsample of the 400 deg2 survey (Vikhlinin et al. 2009). We find the standard scaling relation vastly overpredicts the derived X-ray cluster distribution function at high redshift. If we allow for some redshift evolution to compare the predicted abundance of X-ray clusters a mass temperature relation, we may rewrite the TX − M relation as 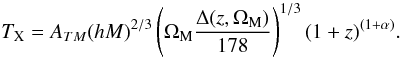 (5)Such a non-standard scaling law has been advocated (Vauclair et al. 2003) with α ~ −1 in order to match the abundance of high redshift X-ray clusters in a concordance cosmology for flux-selected surveys. The predicted temperature distribution function at high redshift with non-standard evolution of the mass-temperature evolution (using a power-law index of α = −1 without further adjustment) is clearly preferred over the non-evolving one. Potential explanations for this evolution are likely to lie in non-gravitational heating of the intracluster gas, possibly tracing sources of cosmic stellar formation or/and additional complex physical processes within clusters, an area that is the subject of intense investigations (Voit 2005; McNamara et al. 2005; Cattaneo & Teyssier 2007; da Silva et al. 2009).
(5)Such a non-standard scaling law has been advocated (Vauclair et al. 2003) with α ~ −1 in order to match the abundance of high redshift X-ray clusters in a concordance cosmology for flux-selected surveys. The predicted temperature distribution function at high redshift with non-standard evolution of the mass-temperature evolution (using a power-law index of α = −1 without further adjustment) is clearly preferred over the non-evolving one. Potential explanations for this evolution are likely to lie in non-gravitational heating of the intracluster gas, possibly tracing sources of cosmic stellar formation or/and additional complex physical processes within clusters, an area that is the subject of intense investigations (Voit 2005; McNamara et al. 2005; Cattaneo & Teyssier 2007; da Silva et al. 2009).
4. The anticipated Sunyaev-Zel’dovich number counts
 |
Fig. 2 Predicted galaxy clusters number counts detected from the Sunyaev-Zeldovich effect, after joint analysis of CMB, SNIa, LSS data and estimated temperature distribution function. Models describing self consistently the low and high redshift temperature distribution functions, needing non-standard evolution of TX − M relation, lead to lower abundance of clusters, showing a deficit in the cluster number increasing with redshift (right). The best model being Ωm = 0.317, σ8 = 0.842, h = 0.669 and ATM = 7.31. |
An early attempt to estimate SZE number counts using the mass function and scaling laws as well as an estimation of their contribution to CMB fluctuations on small scales, has been made by Bartlet and Silk ( 1994). The use of SZE counts as a cosmological probe (Barbosa et al. 1996) was in around the early framework of Planck Surveyor Phase A studies and soon followed by detailed investigations (Aghanim et al. 1997; Holder et al. 2000; Kay et al. 2001; Benson et al. 2002; Diego et al. 2002) that went on to exploit the potential of SZE survey counts as a cosmic probe. Such estimations were usually performed under the assumption of the standard scaling law of the mass-temperature relation.
Since the SZE number counts are by definition the number of galaxy clusters brighter than a certain flux threshold Sν, this reduces to the number of galaxy clusters more massive than a mass threshold M0. depending on the redshift z, from the Y − M relation. The consequence of the dispersion is dealt with by assuming that it can be approximated in practice by a shift in the mass-temperature normalization (Blanchard et al. 2000), which can be included in our fudge factor ξ. To work out a consistent modelling of the clusters population and its evolution in the same picture, another MCMC analysis included the redshift-evolution power-law index α as an additional free parameter and added the high-redshift temperature distribution functions as a complementary observational constraint. For each of these models, we can compute the corresponding SZE source counts as well, as their redshift distribution of the clusters, allowing comparison of the importance of evolution effect to the statistical uncertainty inherent to the set of observations under consideration.
Here, we evaluate expected high-sensitivity flux limits for both Planck and SPT as fiducial numbers. An important source of complexity, and possibly uncertainty in this topic is the accuracy of our knowledge of the experiment selection functions (Melin et al. 2005; Juin et al. 2007). We focus on the theoretical curves, leaving to future works full understanding of the selection functions used to find clusters, which will need comprehensive modelling of the observational and detection processes, including understanding the known complexities of the missions algorithms to identify clusters and measure its fluxes. As fiducial criteria, we adopted three different sensitivity thresholds: Y = 2 × 10-3 (Case 1), corresponding to a secure lower limit for the sensitivity of Planck, Y = 4 × 10-4 (Case 2) for SPT or for an optimistic flux limit for Planck, Y = 4 × 10-5 (Case 3) which could be achieved if the selection function is under control for experiments like SPT (Ruhl et al. 2004) or AMIBA (Ho et al. 2009).
From the above discussion, at the brightest fluxes, source counts should be relatively free from resolution and/or selection effects and show allow some detection of the signature of evolution. Our final predicted counts and the associated uncertainties are shown in Fig. 2: we give the predicted counts falling in the central 68% interval using cosmological models fitted to the local temperature distribution function assuming a standard scaling law for the mass-temperature relation, in the same figure we provide expected counts for self-consistent modelling of the cluster population, allowing evolution in the mass-temperature relation, and including the high-redshift temperature distribution function data as an additional constraint.
It is clear that the integrated source counts show significant differences between the two cases. The possible lack of accurate knowledge of the Y − M normalization and of the selection function is likely to limit the interpretation of SZE integrated counts. However, the redshift distribution is definitively different, with a clear drop in the high-redshift tail after z > 1 when the X-ray motivated evolution is taken into account. Because the SZE effect is sensitive to the actual average temperature of the gas, the observations in SZE will clarify whether the kind of evolution needed for reproducing X-ray number counts affects the overall cluster gas or only the central region from which the X-ray emission comes. This is fairly encouraging as the high-redshift clusters are likely to be point-like in a moderately low-resolution survey as will be provided by Planck, and thus alleviating the complex and possibly unsecured modelling of their spatial distribution for determining the selection function.
5. Conclusion
Current cosmological data and existing surveys of X-ray clusters provide tight constraints, hence accurate predicted SZE number counts. The X-ray data probe an inconsistency between the theoretically expected and the observed high-redshift temperature distribution function under the current vanilla ΛCDM cosmology if the standard scaling of the mass-temperature relation is used. The hypothesis that some evolution in the scaling law driven by non-gravitational processes is a natural solution to this problem. Our MCMC statistical study shows that evolution is required and it will lead to a significant lowering of the anticipated SZE cluster number counts. Indeed, this may explain part of the statistical discrepancies suggested by South Pole Telescope (Lueker et al. 2009) for the presence of an SZE signal anisotropy contribution to CMB fluctuations lower than expected in ΛCDM. This may also result from the geometrical structure of clusters (Taburet et al. 2010). While the X-ray data allowed the highlight of a redshift evolution in the galaxy cluster population, the SZE number counts can potentially provide deeper insight into the actual nature of this evolution by providing information that tests whether gas clusters has undergone a significant amount of non-gravitational heating that affects their global energy budget. This would call for further dedicated investigations of cluster abundance and formation with potential consequences on the design of future experiments.
Acknowledgments
We acknowledge discussions with N. Aghanim, M. Douspis, J. Silk and A. da Silva. DB is supported by the FCT Ciência 2007 programme funded through QREN and COMPETE. D.B. and P.D. were sponsored by FCT project PTDC/CTE-AST/65925/2006. We acknowledge the use of Cosmological MonteCarlo (COSMOMC) software package for statistical analysis. This research has made use of the X-Rays Clusters Database (BAX), operated by the Laboratoire d’Astrophysique de Tarbes-Toulouse (LATT). We acknowledge the use of the Legacy Archive for Microwave Background Data Analysis (LAMBDA). We acknowledge Université Paul Sabatier for the use of the Hyperion cluster.
References
- Aghanim, N., de Luca, A., Bouchet, F. R., Gispert, R., & Puget, J.-L. 1997, A&A, 325, 9 [NASA ADS] [Google Scholar]
- Barbosa, D., Bartlett, J. G., Blanchard, A., & Oukbir, J. 1996, A&A, 314, 13 [NASA ADS] [Google Scholar]
- Bartlett, J. G., & Silk, J. 1994, ApJ, 423, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Benson, A. J., Reichardt, C., & Kamionkowski, M. 2002, MNRAS, 331, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Blanchard, A., Sadat, R., Bartlett, J. G., & LeDour, M. 2000, A&A, 362, 809 [NASA ADS] [Google Scholar]
- Bonamente, M., Joy, M. K., LaRoque, S. J., et al. 2006, ApJ, 647, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Bond, J. R., Contaldi, C. R., Pen, U.-L., et al. 2005, ApJ, 626, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Cattaneo, A., & Teyssier, R. 2007, MNRAS, 376, 1547 [NASA ADS] [CrossRef] [Google Scholar]
- Cole, S., & Kaiser, N. 1988, MNRAS, 233, 637 [NASA ADS] [Google Scholar]
- da Silva, A. C., Catalano, A., Montier, L., et al. 2009, MNRAS, 396, 849 [NASA ADS] [CrossRef] [Google Scholar]
- Diego, J., Martínez-González, E., Sanz, J. L., Benitez, N., & Silk, J. 2002, MNRAS 331, 556 [Google Scholar]
- Ferramacho, L. D., & Blanchard, A. 2007, A&A, 463, 423 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ho, P. T. P., Altamirano, P., Chang, C.-H., et al. 2009, ApJ, 694, 1610 [NASA ADS] [CrossRef] [Google Scholar]
- Holder, G. P., & Carlstrom, J. E. 1999, Microwave Foregrounds, 181, 199 [NASA ADS] [Google Scholar]
- Holder, G. P., Mohr, J. J., Carlstrom, J. E. et al. 2000, ApJ, 544, 629 [NASA ADS] [CrossRef] [Google Scholar]
- Jarosik, N., Bennett, C. L., Dunkley, J., et al. 2010, ApJS, submitted [arXiv:1001.4744] [Google Scholar]
- Juin, J. B., Yvon, D., Refregier, A., & Yèche, C. 2007, A&A, 465, 57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaiser, N. 1991, ApJ, 383, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Kay, S. T., Liddle, A. R., & Thomas, P. A. 2001, MNRAS, 325, 835 [NASA ADS] [CrossRef] [Google Scholar]
- Kay, S. T., da Silva, A. C., Aghanim, N. et al. 2007, MNRAS, 377, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Kay, S. T., Powell, L. C., Liddle, A. R., & Thomas, P. A. 2008, MNRAS, 386, 2110 [NASA ADS] [CrossRef] [Google Scholar]
- Kessler, R., Becker, A. C., Cinabro, D., et al. 2009, ApJS, 185, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Komatsu, E., & Kitayama, T. 1999, ApJ, 526, L1 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lamarre, J.-M., Giard, M., Pointecouteau, E., et al. 1998, ApJ, 507, L5 [Google Scholar]
- Lima, M., & Hu, W. 2007, Phys. Rev. D, 76, 123013 [NASA ADS] [CrossRef] [Google Scholar]
- Lueker, M., Reichardt, C. L., Schaffer, K. K., et al. 2010, ApJ, 719, 1045 [NASA ADS] [CrossRef] [Google Scholar]
- Markevitch, M., Blumenthal, G. R., Forman, W. et al. 1994, ApJ, 426, 1 [NASA ADS] [CrossRef] [Google Scholar]
- McNamara, B. R., Nulsen, P. E. J., Wise, M. W., et al. 2005, Nature, 433, 45 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Melin, J.-B., Bartlett, J. G., & Delabrouille, J. 2005, A&A, 429, 417 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Oukbir, J., & Blanchard, A. 1992, A&A, 262, L21 [NASA ADS] [Google Scholar]
- Pariiskii, Y. N. 1972, AZh, 49, 1322 [NASA ADS] [Google Scholar]
- Pierpaoli, E., Borgani, S., Scott, D., & White, M. 2003, MNRAS, 342, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Consortia Blue Book, 2005 http://www.rssd.esa.int/Planck [Google Scholar]
- Press, W. H., & Schechter, P. 1974, ApJ, 187, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Reid, B. A., Percival, W. J., Eisenstein, D. J., et al. 2010, MNRAS, 404, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Ruhl, J., Ade, P. A. R., Carlstrom, J. E., et al. 2004, Proc. SPIE, 5498, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Sadat, R., Blanchard, A., Vauclair, S. C., et al. 2005, A&A, 437, 31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sheth, R. K., Mo, H. J., & Tormen, G. 2001, MNRAS, 323, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Sunyaev, R. A., & Zeldovich, Y. B. 1972, Comments on Astrophysics and Space Physics, 4, 173 [Google Scholar]
- Taburet, N., Douspis, M., & Aghanim, N. 2010, MNRAS, 404, 1197 [NASA ADS] [Google Scholar]
- Tinker, J., Kravtsov, A. V., Klypin, A., et al. 2008, ApJ, 688, 709 [NASA ADS] [CrossRef] [Google Scholar]
- Vauclair, S. C., Blanchard, A., Sadat, R., et al. 2003, A&A, 412, L37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vikhlinin, A., Markevitch, M., Murray, S. S., et al. 2005, ApJ, 628, 655 [NASA ADS] [CrossRef] [Google Scholar]
- Vikhlinin, A., Burenin, R. A., Ebeling, H., et al. 2009, ApJ, 692, 1033 [NASA ADS] [CrossRef] [Google Scholar]
- Voit, G. M. 2005, Rev. Mod. Phys., 77, 207 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Cluster temperature-distribution function in the local and distant universe. Triangles are our estimation of the temperature distribution function. The stars represent the estimated temperature distribution function at high redshift from the 400 deg2 sample restricted to the redshift range [0.4–0.6]. The continuous line corresponds to the predicted temperature distribution adjusted to fit CMB, SNIa, LSS, and the local temperature distribution function. The predictions for this model at redshift 0.5 (the lower continuous line) are far in excess of the abundances estimated from observations. For visual comparison, the dashed lines are the corresponding predictions with an evolving mass-temperature relation, Eq. (6), with α = − 1 (not fitted). |
| In the text | |
 |
Fig. 2 Predicted galaxy clusters number counts detected from the Sunyaev-Zeldovich effect, after joint analysis of CMB, SNIa, LSS data and estimated temperature distribution function. Models describing self consistently the low and high redshift temperature distribution functions, needing non-standard evolution of TX − M relation, lead to lower abundance of clusters, showing a deficit in the cluster number increasing with redshift (right). The best model being Ωm = 0.317, σ8 = 0.842, h = 0.669 and ATM = 7.31. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


