| Issue |
A&A
Volume 524, December 2010
|
|
|---|---|---|
| Article Number | A75 | |
| Number of page(s) | 11 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201014458 | |
| Published online | 24 November 2010 | |
A population of gamma-ray emitting globular clusters seen with the Fermi Large Area Telescope
1
Space Science Division, Naval Research Laboratory,
Washington, DC
20375,
USA
2
National Research Council Research Associate, National Academy of
Sciences, Washington,
DC
20001,
USA
3
W. W. Hansen Experimental Physics Laboratory, Kavli Institute for
Particle Astrophysics and Cosmology, Department of Physics and SLAC National
Accelerator Laboratory, Stanford University, Stanford, CA
94305,
USA
4
Istituto Nazionale di Fisica Nucleare, Sezione di Pisa,
56127
Pisa,
Italy
5
Laboratoire AIM, CEA-IRFU/CNRS/Université Paris Diderot, Service
d’Astrophysique, CEA Saclay, 91191
Gif sur Yvette,
France
6
Istituto Nazionale di Fisica Nucleare, Sezione di Trieste,
34127
Trieste,
Italy
7
Dipartimento di Fisica, Università di Trieste,
34127
Trieste,
Italy
8
Istituto Nazionale di Fisica Nucleare, Sezione di Padova,
35131
Padova,
Italy
9
Dipartimento di Fisica “G. Galilei”, Università di
Padova, 35131
Padova,
Italy
10
Istituto Nazionale di Fisica Nucleare, Sezione di Perugia,
06123
Perugia,
Italy
11
Dipartimento di Fisica, Università degli Studi di
Perugia, 06123
Perugia,
Italy
12
Centre d’Étude Spatiale des Rayonnements, CNRS/UPS,
BP 44346,
31028
Toulouse Cedex 4,
France
e-mail: jurgen.knodlseder@cesr.fr; natalie.webb@cesr.fr; benoit.pancrazi@cesr.fr
13
Department of Physics, Center for Cosmology and Astro-Particle
Physics, The Ohio State University, Columbus, OH
43210,
USA
14
Dipartimento di Fisica “M. Merlin” dell’Università e del
Politecnico di Bari, 70126
Bari,
Italy
15
Istituto Nazionale di Fisica Nucleare, Sezione di Bari,
70126
Bari,
Italy
16
Laboratoire Leprince-Ringuet, École polytechnique, CNRS/IN2P3,
Palaiseau,
France
17
INAF-Istituto di Astrofisica Spaziale e Fisica Cosmica,
20133
Milano,
Italy
18
George Mason University, Fairfax, VA
22030,
USA
19
Laboratoire de Physique Théorique et Astroparticules, Université
Montpellier 2, CNRS/IN2P3, Montpellier, France
20
Department of Physics, Stockholm University,
AlbaNova, 106 91
Stockholm,
Sweden
21
The Oskar Klein Centre for Cosmoparticle Physics, AlbaNova,
106 91
Stockholm,
Sweden
22 Royal Swedish Academy of Sciences Research Fellow, funded
by a grant from the K. A. Wallenberg Foundation, Swedish
23
NASA Goddard Space Flight Center, Greenbelt, MD
20771,
USA
24
Department of Physics and Department of Astronomy, University of
Maryland, College
Park, MD
20742,
USA
25
CNRS/IN2P3, Centre d’Études Nucléaires Bordeaux Gradignan, UMR
5797, 33175
Gradignan,
France
26
Université de Bordeaux, Centre d’Études Nucléaires Bordeaux
Gradignan, UMR 5797, 33175
Gradignan,
France
27
Dipartimento di Fisica, Università di Udine and Istituto Nazionale
di Fisica Nucleare, Sezione di
Trieste, Gruppo Collegato di Udine, 33100
Udine,
Italy
28
Osservatorio Astronomico di Trieste, Istituto Nazionale di
Astrofisica, 34143
Trieste,
Italy
29
Department of Physical Sciences, Hiroshima
University, Higashi-Hiroshima, Hiroshima
739-8526,
Japan
30 Agenzia Spaziale Italiana (ASI) Science Data Center, 00044
Frascati (Roma), Italy
31
Center for Space Plasma and Aeronomic Research (CSPAR), University
of Alabama in Huntsville, Huntsville, AL
35899,
USA
32
Institució Catalana de Recerca i Estudis Avançats (ICREA),
Barcelona,
Spain
33
Research Institute for Science andEngineering, Waseda University,
3-4-1, Okubo, Shinjuku,
169-8555
Tokyo,
Japan
34
Department of Physics, University of Washington,
Seattle, WA
98195-1560,
USA
35
Istituto Nazionale di Fisica Nucleare, Sezione di Roma “Tor
Vergata”, 00133
Roma,
Italy
36
Department of Physics and Astronomy, University of
Denver, Denver,
CO
80208,
USA
37
Hiroshima Astrophysical Science Center, Hiroshima University,
Higashi-Hiroshima,
739-8526
Hiroshima,
Japan
38
Max-Planck Institut für extraterrestrische Physik,
85748
Garching,
Germany
39
Institut für Astro- und Teilchenphysik and Institut für
Theoretische Physik, Leopold-Franzens-Universität Innsbruck,
6020
Innsbruck,
Austria
40
Santa Cruz Institute for Particle Physics, Department of Physics
and Department of Astronomy and Astrophysics, University of California at Santa
Cruz, Santa Cruz,
CA
95064,
USA
41
NYCB Real-Time Computing Inc., Lattingtown, NY
11560-1025,
USA
42
Department of Chemistry and Physics, Purdue University
Calumet, Hammond,
IN
46323-2094,
USA
43
Institute of Space and Astronautical Science,
JAXA, 3-1-1 Yoshinodai, Sagamihara,
229-8510
Kanagawa,
Japan
45
Institut de Ciencies de l’Espai (IEEC-CSIC),
Campus UAB,
08193
Barcelona,
Spain
46
Consorzio Interuniversitario per la Fisica Spaziale (CIFS),
10133
Torino,
Italy
47
INTEGRAL Science Data Centre, 1290
Versoix,
Switzerland
48
Center for Research and Exploration in Space Science and
Technology (CRESST) and NASA Goddard Space Flight Center, Greenbelt, MD
20771,
USA
49
Department of Physics and Center for Space Sciences and
Technology, University of Maryland Baltimore County, Baltimore, MD
21250,
USA
50
North-West University, Potchefstroom Campus, Potchefstroom
2520, South
Africa
51
Dipartimento di Fisica, Università di Roma “Tor
Vergata”, 00133
Roma,
Italy
52
Department of Physics, Royal Institute of Technology
(KTH), AlbaNova,
106 91
Stockholm,
Sweden
53
School of Pure and Applied Natural Sciences, University of Kalmar,
391 82
Kalmar,
Sweden
54
Max-Planck-Institut für Radioastronomie,
Auf dem Hügel 69,
53121
Bonn,
Germany
Received: 18 March 2010
Accepted: 13 August 2010
Context. Globular clusters with their large populations of millisecond pulsars (MSPs) are believed to be potential emitters of high-energy gamma-ray emission. The observation of this emission provides a powerful tool to assess the millisecond pulsar population of a cluster, is essential for understanding the importance of binary systems for the evolution of globular clusters, and provides complementary insights into magnetospheric emission processes.
Aims. Our goal is to constrain the millisecond pulsar populations in globular clusters from analysis of gamma-ray observations.
Methods. We use 546 days of continuous sky-survey observations obtained with the Large Area Telescope aboard the Fermi Gamma-ray Space Telescope to study the gamma-ray emission towards 13 globular clusters.
Results. Steady point-like high-energy gamma-ray emission has been significantly detected towards 8 globular clusters. Five of them (47 Tucanae, Omega Cen, NGC 6388, Terzan 5, and M 28) show hard spectral power indices (0.7 < Γ < 1.4) and clear evidence for an exponential cut-off in the range 1.0 − 2.6 GeV, which is the characteristic signature of magnetospheric emission from MSPs. Three of them (M 62, NGC 6440 and NGC 6652) also show hard spectral indices (1.0 < Γ < 1.7), however the presence of an exponential cut-off can not be unambiguously established. Three of them (Omega Cen, NGC 6388, NGC 6652) have no known radio or X-ray MSPs yet still exhibit MSP spectral properties. From the observed gamma-ray luminosities, we estimate the total number of MSPs that is expected to be present in these globular clusters. We show that our estimates of the MSP population correlate with the stellar encounter rate and we estimate 2600 − 4700 MSPs in Galactic globular clusters, commensurate with previous estimates.
Conclusions. The observation of high-energy gamma-ray emission from globular clusters thus provides a reliable independent method to assess their millisecond pulsar populations.
Key words: pulsars: general / globular clusters: general / gamma rays: general
© ESO, 2010
1. Introduction
With their typical ages of ~1010 years, globular clusters form the most ancient constituents of our Milky Way Galaxy. These gravitationally bound concentrations of ten thousand to one million stars are surprisingly stable against collapse which implies some source of internal energy that balances gravitation. The potential energy of binary systems is a plausible source of this internal energy, tapped by close stellar encounters that harden the orbits of the systems (Hut et al. 1992). Indeed, globular clusters contain considerably more close binary systems per unit mass than the Galactic disk which eventually show up as rich populations of X-ray binaries (Clark 1975). This scenario is strengthened by the observation that the number of low-mass X-ray binary systems containing neutron stars is directly correlated with the stellar encounter rate (Gendre et al. 2003a). Another consequence of this scenario is the presence of many millisecond pulsars1 (hereafter MSPs, see e.g. Camilo & Rasio 2005; Ransom 2008), also known as “recycled” pulsars, i.e. pulsars that were spun-up to millisecond periods by mass-accretion from a binary companion (Alpar et al. 1992).
Observations with the Large Area Telescope (LAT) onboard the Fermi Gamma-ray Space Telescope have confirmed MSPs as gamma-ray sources (Abdo et al. 2009a,b). The spectral energy distribution of millisecond pulsars is characterised by hard (1.0 ≲ Γ ≲ 2.0) power law spectra with exponential cut-offs in the 1–3 GeV energy range (Abdo et al. 2009b). Recently, Abdo et al. (2009c) presented the first detection of a globular cluster (GC) in the gamma-ray domain. This GC, 47 Tuc, has a spectral energy distribution best described by a photon index of 1.3 ± 0.3 with a cut-off energy of 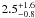 GeV (Abdo et al. 2009c) typical of the other MSPs detected to date (Abdo et al. 2009b). Further, 47 Tuc contains at least 23 MSPs, known from radio and X-ray observations. The lack of variability over days to months is consistent with MSP emission. In addition, folding the data on known ephemerides from the 47 Tuc pulsars reveals no significant detections, thus it appears that the gamma-ray emission is not due to a single MSP but rather attributable to an entire population of MSPs in this globular cluster. Using the observed, average efficiency of converting spin down energy into the observed gamma-ray luminosity, constraints can be placed on the MSP population (Abdo et al. 2009c).
GeV (Abdo et al. 2009c) typical of the other MSPs detected to date (Abdo et al. 2009b). Further, 47 Tuc contains at least 23 MSPs, known from radio and X-ray observations. The lack of variability over days to months is consistent with MSP emission. In addition, folding the data on known ephemerides from the 47 Tuc pulsars reveals no significant detections, thus it appears that the gamma-ray emission is not due to a single MSP but rather attributable to an entire population of MSPs in this globular cluster. Using the observed, average efficiency of converting spin down energy into the observed gamma-ray luminosity, constraints can be placed on the MSP population (Abdo et al. 2009c).
As the number of neutron star X-ray binaries are correlated with encounter rate and MSPs are the progeny of these systems, it would follow that the number of MSPs per globular cluster scales in a similar way. It is difficult to test such a correlation using radio and X-ray observations as the former are affected by dispersion and scattering by the turbulent ionized interstellar medium, in particular for clusters near the Galactic bulge, while the latter are affected by interstellar absorption rendering the detection difficult due to the low count rates observed.
The gamma-ray domain is not affected by interstellar absorption and there is also the added advantage that the gamma-ray beams may be wider than the radio/X-ray beams (e.g. Abdo et al. 2010a), which would permit more MSPs to be detected in the gamma-ray domain than those at lower energies, thus making gamma-ray observations ideal for testing such a correlation.
In this paper we consider gamma-ray sources that are spatially consistent with GCs and that show the spectral characteristics of MSPs, i.e. that have hard power law spectra with exponential cut-offs in the few GeV regime, that are steady, and that are point-like. We analyse Fermi LAT data for 13 globular clusters (see Table 1) and include in our list the 8 globular clusters that have been formally associated with sources in the first year Fermi LAT catalogue (Abdo et al. 2010b, hereafter named 1FGL sources). We add two further globular clusters that lie spatially close to 1FGL sources (Omega Cen and NGC 6624), and include also NGC 6441 due to the high stellar collision rate that is believed to favour the formation of MSPs (Freire et al. 2008), NGC 6752 due to its relative proximity of 4 kpc (D’Amico et al. 2002), and M 15 due to its relatively large population of known MSPs (Anderson 1993).
Globular clusters analysed in this work.
2. Observations
2.1. Data preparation
The data used in this work have been acquired by the LAT telescope aboard the Fermi Gamma-ray Space Telescope during continuous regular sky survey covering the period August 8th 2008–February 12th 2010 (546 days). Events satisfying the standard low-background event selection (“Diffuse” events; Atwood et al. 2009) and coming from zenith angles < 105° (to greatly reduce the contribution by Earth albedo gamma rays) were used. Furthermore, we selected only events where the satellite rocking angle was inferior to 40° for the first 12 months, and inferior to 52° for the remaining period. We further restricted the analysis to photon energies above 200 MeV; below this energy, the effective area in the “Diffuse class” is relatively small and strongly dependent on energy. All analysis was performed using the LAT Science Tools package, which is available from the Fermi Science Support Center, using P6_V3 post-launch instrument response functions (IRFs). These take into account pile-up and accidental coincidence effects in the detector subsystems that were not considered in the definition of the pre-launch IRFs.
2.2. Analysis method
For the analysis of each globular cluster we selected events within squared regions-of-interest (ROIs) that have been aligned in Galactic coordinates. Events have been binned into 25 logarithmically-spaced energy bins covering the range 200 MeV–50 GeV and into spatial pixels of 0.1° × 0.1° in size using a Cartesian projection. The size and location of the ROIs have been chosen to avoid nearby strong sources and the bright diffuse emission from the Galactic plane while maintaining the largest possible coverage of the point-spread function for the globular clusters of interest. The ROI definitions are summarised in Table 2.
Definition of ROIs used for analysis.
The observed events in each of the ROIs have been modelled using components for the gamma-ray and instrumental backgrounds and for known sources in the field. The backgrounds are a combination of extragalactic and Galactic diffuse emissions and some residual instrumental background. The Galactic component has been modelled using the LAT standard diffuse background model gll_iem_v02.fit for which we kept the normalisation as a free parameter. The extragalactic and residual instrumental backgrounds have been combined into a single component which has been taken as being isotropic. The spectrum of this component has been modelled using the tabulated model isotropic_iem_v02.txt and the normalisation has been kept as a free parameter2. In addition to the diffuse components, we included all point sources (except for the source that corresponds to the globular cluster of interest) from the first-year catalogue (Abdo et al. 2010b) that were detected with TS ≥ 25 for a given ROI in the background model. As usual, the Test Statistic TS is defined as twice the difference between the log-likelihood with (ℒ1) and without (ℒ0) the source, i.e. TS = 2(ℒ1 − ℒ0) (TS = 25 corresponds to a detection significance of ~4σ, Abdo et al. 2010b). In general, the spectral distributions of the point sources have been fitted using power law models for which we kept the total flux and the spectral index as free parameters. Only if a point source has been identified as a gamma-ray pulsar, we fitted its spectral distribution using an exponentially cut-off power law for which we kept the normalisation, the spectral index and the cut-off energy as free parameters.
As a first analysis step, we localised the gamma-ray emission by fitting a point source on top of the background model for a grid of test positions using the binned maximum likelihood fitting procedure gtlike. For each ROI, the grid has been centred on the nominal position of the globular cluster3 and was comprised of 20 × 20 positions with a spacing of 3′. We modelled the spectrum of the point source using a simple power law for which we kept the integrated flux and the spectral index as free parameters. The TS values obtained for the point source at the grid positions were then interpolated using a minimum curvature surface method to approximate the TS surface near the globular cluster. This surface was then used to localise TSmax, the position (αJ2000,δJ2000) at which TS is maximised. The 95% confidence region for the true source location was derived from the surface contour that fulfils TSmax − 6.0. For simplicity, we approximated this contour by a circle with radius r95.
As next step, we determined the spatial extent of the gamma-ray emission by replacing the point source in the grid search by 2D Gaussian-shaped intensity profiles and by repeating the search for various Gaussian extents σext. Typically, we performed the grid search for σext = 0.1°, 0.2°, and 0.3°, but eventually we also performed runs for σext = 0.05° and 0.4° to better constrain the source extent. The dependence of TSmax on σext was then determined by adjusting a parabola to the pairs (TSmax,σext) of values, which in all cases gave a satisfactory fit near the maximum. Using this parabola we then determined the maximum TSmax and the corresponding σext as the maximum likelihood estimate of the source extent. All the LAT sources were consistent with being point sources, and we determined the 2σ upper extension limit from the parabola by searching the σext for which the TS decreased by 4 from its maximum value. If the optimum σext was formally >0, we added this (generally small) offset to the upper limit.
Once we established that the gamma-ray source is spatially consistent with the globular cluster and that the source is not extended, we determined the spectral characteristics of the source by fitting a point source at the nominal position of the globular cluster on top of the background model to the data. We again used the binned maximum likelihood fitting procedure gtlike for this purpose. For the spectral model of the source we used an exponentially cut-off power law N(E) = N0E − Γe − E/Ec, with normalisation N0, spectral index Γ, and cut-off energy Ec. We estimated the significance sc of the cut-off by repeating the fit using a simple power law model, and by using 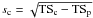 , where TSc and TSp are the TS values obtained using the exponentially cut-off power law and the simple power law, respectively.
, where TSc and TSp are the TS values obtained using the exponentially cut-off power law and the simple power law, respectively.
We determined 68% confidence intervals for all spectral parameters by successively varying each parameter while optimising the others until TS = TSmax − 1.0 is fulfilled. The resulting statistical parameter uncertainties are to first order consistent with the values that we obtained using gtlike, which are estimated from the covariance matrix of the parameters at maximum likelihood. While the latter uncertainties are by definition symmetric about the maximum likelihood parameter values, our method allows for the determination of asymmetric confidence intervals, which are particularily relevant for describing the statistical uncertainty in the measurements of Ec.
In addition to the statistical uncertainties we also estimated systematic uncertainties for all spectral parameters that arise from uncertainties in the precise knowledge of the effective area of the LAT telescope and of its energy dependence. We do this by repeating the gtlike fits using modified instrument response functions that bracket the uncertainties in the effective area. For each parameter we quote as systematic uncertainty the maximum parameter offset that is obtained with respect to the analysis done with the P6_V3 IRF.
We also searched for possible flux variability of the sources associated with the globular cluster by fitting our source model to the data on a monthly basis. For this analysis we fixed the power law spectral indices of all sources and the normalisation of the isotropic diffuse component to the values we obtained for the full dataset. The normalisation of the Galactic diffuse component was kept as a free parameter due to the fact that this component was found to vary significantly, in particular for ROIs that are close to the Galactic plane. From this analysis we obtained lightcurves for all globular clusters that we fitted to a constant flux model using a χ2 minimisation procedure. Since we fit lightcurves for 17 months of data, we have 16 degrees-of-freedom in this minimisation, and the source can be considered as not being constant at the 68% or 95% confidence levels if 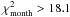 or > 26.3, respectively.
or > 26.3, respectively.
Finally, we derived the spectral energy distributions (SEDs) of the globular clusters by dividing the energy range from 200 MeV to 20 GeV into 8 logarithmically-spaced energy bins, and by fitting the fluxes or normalisations of all model components independently for each bin. For all sources, we assumed simple power law models with a fixed spectral index of Γ = 2.1 within each energy bin. Since the energy bins chosen are relatively narrow, the precise value of the slope has little impact on the resulting spectra. The normalisations of the diffuse components (Galactic diffuse and isotropic backgrounds) are fitted independently for each energy bin, which makes this analysis less sensitive to systematic uncertainties in the spectral energy distribution of these model components.
We also note that we searched for pulsations from MSPs in globular clusters and, to date, no significant pulsations have been reported from any of the pulsars that has been searched. However, we only have accurate ephemerides (derived from times of arrival measured with the Parkes, Nancay, and Jodrell Bank radio telescopes) for 15 globular cluster MSPs, limiting our search to only ~10% of the known globular cluster pulsar population. This illustrates the pressing need for more contemporaneous timing solutions in order to reveal the gamma-ray pulsations from globular cluster MSPs.
 |
Fig. 1 Gaussian kernel smoothed (σ = 0.1°) counts maps of the ROIs for the 8 significant globular cluster candidates. The insets show adaptively smoothed background subtracted counts maps for a 3° × 3° large region around the globular cluster. Circles indicate the nominal locations of the globular clusters. |
2.3. Results
For 11 of the 13 ROIs analysed, a gamma-ray source has been found in the Fermi LAT data that is spatially consistent with a globular cluster. For two ROIs (NGC 6441 and NGC 6624) we were unable to find a convincing gamma-ray counterpart; however, gamma-ray sources were detected close by to both globular clusters. For NGC 6441 we found evidence for a faint gamma-ray source (TS = 29) that we localised at αJ2000 = 17h50.5m and δJ2000 = − 36°52′ with r95 = 7.5′, yet with an offset of 11.7′, the globular cluster is located just outside the 99% error contour. NGC 6624 is close to 1FGL J1823.4 − 3009 (Abdo et al. 2010b) which we detected with TS = 43, and which we localised at αJ2000 = 18h23.5m and δJ2000 = − 30°13′ with r95 = 6.3′. With an offset of 8.6′, NGC 6624 is also located just outside the 99% error contour of the gamma-ray source. Formally, we can not establish an association of NGC 6441 and NGC 6624 with the gamma-ray sources, and hence we excluded both objects from further analysis. Both gamma-ray sources, however, are rather faint, and more data are needed before an association of these sources with globular clusters definitely can be excluded.
Three of the 11 gamma-ray sources that are spatially consistent with a globular cluster have TS < 25 (NGC 6541, NGC 6752, and M 15), hence we cannot claim a significant detection for these cases. NGC 6541 has been associated in the first year catalogue with 1FGL J1807.6 − 4341 (Abdo et al. 2010b), yet with TS = 25.3 this source was just barely above the threshold of TS = 25 used for compilation of the catalogue. In our dedicated analysis we find a lower detection significance of TS = 12.0 for the source, which can be explained by differences in the analysis method and data selection with respect to the catalogue analysis. In particular, the catalogue analysis determined TS using an unbinned maximum likelihood analysis which has recently been recognized to provide larger TS values in several low-latitude fields than the binned analysis
This leaves us with 8 significant globular cluster candidates for which we show smoothed raw and residual counts maps in Fig. 1. For each of these clusters we determined fluxes and spectral parameters using exponentially cut-off power laws. For the 3 non-significant globular clusters we derived formal 2σ upper flux limits by fitting a point source at the nominal cluster position to the data for which we increased the flux, starting from its maximum likelihood value, until the TS decreased by 4 with respect to the maximum. As a spectral model we used an exponentially cut-off power law for which we fixed the spectral index and the cut-off energy to the weighted average values of Γ = 1.4 and Ec = 1.6 GeV that were obtained for the 8 significantly detected globular cluster candidates. We added to these statistical upper limits the systematic uncertainty that has been obtained using the bracketing IRFs (cf. Sect. 2.2) and that accounts for uncertainties in the effective area of the LAT. The fluxes and spectral characteristics as well as the maximum likelihood locations of the gamma-ray sources are summarised in Table 3. Quoted uncertainties are statistical and systematic.
Gamma-ray characteristics of globular clusters.
Table 3 quotes also the variability indicator 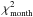 , which is inferior to 26.3 for all globular cluster candidates, indicating that none of the gamma-ray sources exhibit significant time variability. All 8 sources thus match the expected property of globular clusters for being non-variable sources of gamma rays. Table 3 also shows that the 8 significant sources exhibit the expected spectral characteristics of globular clusters: a flat (Γ < 2) power law spectral index with an exponential cut-off in the few GeV domain. For two of the sources (M 62 and NGC 6440), however, the statistical significance of the cut-off is sc < 3σ. More data are clearly needed here before definite conclusions about the reality of the exponential cut-off can be drawn. Finally, we show in Fig. 2 the spectral energy distributions of the 8 significant globular cluster candidates. In the following we comment on the analysis results for each of these globular clusters.
, which is inferior to 26.3 for all globular cluster candidates, indicating that none of the gamma-ray sources exhibit significant time variability. All 8 sources thus match the expected property of globular clusters for being non-variable sources of gamma rays. Table 3 also shows that the 8 significant sources exhibit the expected spectral characteristics of globular clusters: a flat (Γ < 2) power law spectral index with an exponential cut-off in the few GeV domain. For two of the sources (M 62 and NGC 6440), however, the statistical significance of the cut-off is sc < 3σ. More data are clearly needed here before definite conclusions about the reality of the exponential cut-off can be drawn. Finally, we show in Fig. 2 the spectral energy distributions of the 8 significant globular cluster candidates. In the following we comment on the analysis results for each of these globular clusters.
 |
Fig. 2 Spectral energy distributions of the 8 significant globular cluster candidates. Lines indicate the exponentially cut-off power law models that have been fitted to the data using the binned maximum likelihood fitting procedure, and for which the spectral parameters are quoted in Table 3. The dotted part of the lines indicate the extrapolation of the exponentially cut-off power law model towards energies below 200 MeV. |
2.4. Comments on individual clusters
2.4.1. 47 Tucanae
47 Tuc was the first globular cluster to be associated with a gamma-ray source detected by Fermi LAT (Abdo et al. 2009c). The maximum likelihood position of the gamma-ray source is only 1.7′ offset from the cluster core, which is well inside the 95% confidence error radius of 3.3′. The spatial and spectral characteristics that we derive from the present dataset are compatible with those published in our previous work (Abdo et al. 2009c), yet the ~2.8 times longer exposure now allows us to constrain the spectral source parameters considerably better. In particular, the uncertainty on the energy flux of 47 Tuc has been reduced by a factor ~2 to less than 10%, improving the constraint on the total gamma-ray luminosity of the cluster, and hence on the expected population of millisecond pulsars (cf. Sect. 3).
2.4.2. Omega Cen
Omega Cen is one of the globular clusters in our list for which no MSP has so far been detected. Omega Cen is situated near the southern giant radio-lobe of the nearby Cen A radio galaxy which is also an extended source of GeV gamma rays (Abdo et al. 2010c). To account for emission from the radio lobes in our analysis we included a spatial template based on the 22 GHz WMAP microwave map (Hinshaw et al. 2009) in our background model. Formally, the position of the gamma-ray source near Omega Cen (1FGL J1328.2 − 4729) is inconsistent with the location of the globular cluster. It turned out, however, that 1FGL J1328.2 − 4729 is a superposition of two distinct sources that can be separated thanks to their different spectral characteristics. While the first source shows a cut-off in the few GeV domain, the second source is rather hard (Γ = 1.6 ± 0.2), with no cut-off and can be clearly isolated from the first one by selecting only events >10 GeV. This results in a best fitting location of αJ2000 = 13h28.7m and δJ2000 = −47°30′ with a 95% error radius of r95 = 4.0′. Alternatively, we fixed a point source at the location of Omega Cen and fitted the location of the residual counts to αJ2000 = 13h28.8m and δJ2000 = −47°29′ with a 95% error radius of r95 = 3.1′. Both locations are spatially consistent with the radio source SUMSS J132840−472748, which has formally been associated to 1FGL J1328.2−4729 in the Fermi LAT first year catalogue of active galactic nuclei (Abdo et al. 2010d). The gamma-ray source is also consistent with the radio source PMN J1328 − 4728 and the X-ray sources 1WGA J1328.6 − 4727 and 1RXS J132846.7 − 472759, which all are possibly just different designators for the same source detected by other instruments.
We thus include this source in our background model and re-determine the localisation of the source that is only visible below a few GeV. This results in a maximum likelihood position of αJ2000 = 13h26.5m and δJ2000 = −47°29′ with a 95% error radius of r95 = 7.5′. This position is 3.2′ offset from the centre of Omega Cen, and thus the gamma-ray source is spatially fully consistent with the location of the globular cluster.
2.4.3. M 62
M 62 has formally been associated with 1FGL J1701.1−3005 (Abdo et al. 2010b) and also our maximum likelihood position is only 1.6′ offset from the core of the globular cluster, which is thus well within r95 = 4.4′. The gamma-ray source shows only marginal (sc = 2.5) evidence for an exponential cut-off and exhibits the largest formal cut-off energy (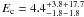 GeV) of all sources. The SED (cf. Fig. 2) shows no clear indication for a distinct cut-off, and if there were not a lack of flux below ~600 MeV, the SED would probably also be compatible with a soft power law. M 62 is located in a region of intense Galactic diffuse emission (angular distance from the Galactic centre <10°; cf. Fig. 1) which makes any proper extraction of spectral parameters difficult. In particular, we recognised that the source spectrum is rather sensitive to the exact choice of the ROI, which is readily explained by systematic uncertainties in the model of Galactic diffuse emission that we used for the analysis. We thus qualify the gamma-ray source associated with M 62 only as possible globular cluster candidate (in contrast to being a plausible candidate), and await the accumulation of more data before drawing any definite conclusions.
GeV) of all sources. The SED (cf. Fig. 2) shows no clear indication for a distinct cut-off, and if there were not a lack of flux below ~600 MeV, the SED would probably also be compatible with a soft power law. M 62 is located in a region of intense Galactic diffuse emission (angular distance from the Galactic centre <10°; cf. Fig. 1) which makes any proper extraction of spectral parameters difficult. In particular, we recognised that the source spectrum is rather sensitive to the exact choice of the ROI, which is readily explained by systematic uncertainties in the model of Galactic diffuse emission that we used for the analysis. We thus qualify the gamma-ray source associated with M 62 only as possible globular cluster candidate (in contrast to being a plausible candidate), and await the accumulation of more data before drawing any definite conclusions.
2.4.4. NGC 6388
NGC 6388 has formally been associated with 1FGL J1735.9−4438 (Abdo et al. 2010b). Our position is consistent with that of 1FGL J1735.9 − 4438 and NGC 6388 is found right on the 95% confidence contour of the gamma-ray source, at an angular separation of 5.7′. The SED shows a clear cut-off at 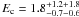 GeV which is typical of the cut-off energies that are observed for MSPs (Abdo et al. 2009b). The Fermi LAT source thus qualifies as a plausible candidate for a globular cluster. We note that no MSP has so far been detected in this GC.
GeV which is typical of the cut-off energies that are observed for MSPs (Abdo et al. 2009b). The Fermi LAT source thus qualifies as a plausible candidate for a globular cluster. We note that no MSP has so far been detected in this GC.
2.4.5. Terzan 5
Terzan 5 has formally been associated with 1FGL J1747.9 − 2448 (Abdo et al. 2010b) and our maximum likelihood position is offset by 2.4′ from the cluster centre, which is inferior to r95 = 2.9′ for this source. 1FGL J1747.9 − 2448 has recently been studied by Kong et al. (2010). Using an exponentially cut-off power law model, they obtained a spectral index of Γ = 1.9 ± 0.2, a cut-off energy of Ec = 3.8 ± 1.2 GeV, and 0.1−10 GeV photon and energy fluxes of 2 × 10-7 ph cm-2 s-1 and 1.2 × 10-10 erg cm-2 s-1, respectively. Our analysis confirms the presence of the exponential cut-off at a significance of 7.1σ, yet with slightly different spectral parameters. In particular, our fluxes are lower by about a factor of 2, and our SED (our Fig. 2) more closely follows an exponentially cut-off model rather than the SED derived by Kong et al. (2010, their Fig. 2). Possibly, the choice of a rather large ROI with a radius of 15° for their analysis introduced some systematic uncertainties due to the inaccurate subtraction of Galactic diffuse emission in this complex region near the Galactic centre. We used a rectangular ROI of 6° × 6° for our analysis which considerably reduces the impact of the Galactic diffuse model on the analysis, and which allows for a more reliable determination of the spectral parameters of the source. The spectral parameters we obtain for Terzan 5 are indeed very close to those observed for 47 Tuc, making the gamma-ray source a very plausible candidate for being a globular cluster.
2.4.6. NGC 6440
NGC 6440 has formally been associated with 1FGL J1748.7 − 2020 (Abdo et al. 2010b), and our fitted position is offset by 1.3′ from the cluster core, well within r95 = 5.2′. The SED, however, shows no convincing evidence for an exponential cut-off, and also the spectral analysis results in only sc = 1.4σ, too small to claim the detection of a cut-off. The spectral analysis may have suffered from the proximity of the Galactic plane and the related uncertainties due to the subtraction of the diffuse emission, as well as the proximity of a bright gamma-ray pulsar (PSR J1741 − 2054, Abdo et al. 2009d). In any case, the gamma-ray source associated with NGC 6440 is a relatively faint source, and more data are required to allow for an accurate spectral characterisation of the emission. Pending the acquisition of these data we thus qualify the source only as a possible candidate for being a globular cluster.
2.4.7. M 28
M 28 has been formally associated with 1FGL J1824.5 − 2449 (Abdo et al. 2010b), and our source position is offset by only 1.6′ from the centre of the cluster, well within the 95% error radius of 8.0′. Figure 1 suggests a somewhat elongated shape for the gamma-ray source that may indicate a superposition of two objects, yet the source is formally consistent with a point source, although with the largest of all upper limits of σext < 15.6′. The SED of M 28 shows a clear exponential cut-off, which is detected at a significance level of 4.3σ, the third largest significance after Terzan 5 and 47 Tuc. The gamma-ray source associated to M 28 thus qualifies as a plausible globular cluster candidate.
Note that Pellizzoni et al. (2009) have reported the detection (at 4.2σ significance) of pulsations from PSR J1824 − 2452A with the AGILE satellite during a 5-day interval in August 2007, while no pulsations have been seen for other periods of comparable duration. PSR J1824 − 2452A is one of the 12 known MSPs in M 28 and ranks among the youngest and most energetic millisecond pulsars that are known (Knight et al. 2006). The >100 MeV flux of (18 ± 5) × 10-8 ph cm-2 s-1 that Pellizzoni et al. (2009) quote for the 5-day period is significantly larger than the flux of (2.6 ± 1.3) × 10-8 ph cm-2 s-1 that we measured from the cluster using our dataset. Searches for pulsations from PSR J1824 − 2452A in the Fermi LAT data have so far not revealed any significant detection. Furthermore, we did not find any evidence for significant flux variations from M 28 on time-scales from 1 week to 1 month. Typical flux measurement uncertainties for 1 week, however, amount to ± 8 × 10-8 ph cm-2 s-1 (1σ), hence flares from M 28 of the duration and amplitude quoted by AGILE formally cannot be excluded by our data.
2.4.8. NGC 6652
NGC 6652 has been formally associated with 1FGL J1835.3 − 3255 (Abdo et al. 2010b), and our source position is offset by 1.7′ from the cluster, well below r95 = 7.5′. The SED does not reveal a convincing exponential cut-off although the spectral analysis suggests sc = 3.2σ, mainly due to the lack of flux below ~ 600 MeV. The gamma-ray source associated with NGC 6652 is a rather faint source, and also here, more data are required to better constrain the SED before definite conclusions should be drawn. Pending the acquisition of these data we thus qualify the source only as a possible candidate for being a globular cluster. Establishing a firm exponential cut-off is particularily interesting in this case since so far no MSP has been detected in NGC 6652.
Isotropic gamma-ray luminosities and expected numbers of MSPs.
3. Discussion
3.1. Omega Cen, NGC 6388 and NGC 6652
Three of the globular clusters for which we detected gamma-ray counterparts, Omega Cen, NGC 6388 and NGC 6652, deserve attention, since so far no MSPs have been detected in these objects. Present pulsar searches in the radio and X-ray domains are severely limited by the instrument sensitivity, and only in a few examples (e.g. 47 Tuc and M 15) has the end of the pulsar luminosity function possibly been reached (Camilo & Rasio 2005). In some cases, this may simply be because pulsars are generally intrinsically weak objects, and globular clusters are often distant. Interstellar scattering, which broadens pulsations because of multipath propagation, can also be a major obstacle, especially for MSPs in clusters at low Galactic latitudes. Furthermore, interstellar absorption hinders detection in the X-ray range, in particular for clusters that are situated near the Galactic plane.
NGC 6388 and NGC 6652 are indeed the most distant objects in our list of globular clusters for which gamma-ray emission is significantly detected (see Table 4). Among the 26 globular clusters in which MSPs have so far been detected4, 6 have distances that are comparable to or larger than those of NGC 6388 and NGC 6652. Four of these clusters (NGC 1851, M 53, M 3, and M 15) show considerably lower dispersion measures than NGC 6388 and NGC 6652, hence radio pulsars are more easily detected in these systems despite their large distances. The two other clusters (NGC 6441 and NGC 6517) have dispersion measures that are comparable to the estimates for NGC 6388 and NGC 6652, yet uncertainties in the dispersion measure estimates (Cordes & Lazio 2002) or selection effects in the radio surveys that are very difficult to quantify (Hessels et al. 2007) may explain why no MSPs have so far been detected in these clusters.
Omega Cen is substantially closer than NGC 6388 and NGC 6652, at a distance that is comparable to that of 47 Tuc (Bono et al. 2008). However, while 47 Tuc is situated at high galactic latitudes with a correspondingly small dispersion measure of ~25 pc cm-3, Omega Cen is closer to the galactic plane and has an estimated dispersion measure of 126 pc cm-3 (Cordes & Lazio 2002), so MSPs searches will be more difficult in Omega Cen compared to 47 Tuc. Omega Cen has been searched for radio pulsars by Edwards et al. (2001) with the Parkes 64 m radio telescope at 660 MHz without success. Current X-ray observations of this cluster with Chandra and XMM-Newton (Haggard et al. 2009; Gendre et al. 2003b) are not deep enough to uniquely identify MSPs. However, Haggard et al. (2009) note that their Chandra observations do not rule out the presence of MSPs, as numerous sources occupy the region of the colour-magnitude diagram (CMD) where MSPs would be expected to lie. They compared their X-ray CMD with that of Grindlay et al. (2001) for 47 Tuc and adjusted for the somewhat larger hydrogen column density to Omega Cen versus 47 Tuc (and slightly different distances and exposure times). Eighteen objects are found in the range of brightness and colour expected for MSPs in Omega Cen. This range of colours is also typical of chromospherically active single stars and binaries, but many or all of these objects may be MSPs. Our estimate is also commensurate with the 28 (with an rms dispersion of 6) MSPs predicted via two body tidal capture (Di Stefano & Rappaport 1992).
3.2. Expected MSP populations
Under the assumption that MSPs share the same characteristics in the various globular clusters that we studied, we may use the observed gamma-ray luminosities to obtain estimates on the total number of MSPs expected to reside in each cluster. Here we closely follow the formalism that has been developed by Abdo et al. (2009c) to estimate the size of the MSP population in 47 Tuc. The total number NMSP of MSPs present in a globular cluster is estimated from the isotropic gamma-ray luminosity of the cluster Lγ, the average spin-down power ⟨ Ė ⟩ of MSPs, and the estimated average spin-down to gamma-ray luminosity conversion efficiency ⟨ ηγ ⟩ using 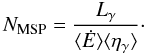 (1)We compute the isotropic gamma-ray luminosity using Lγ = 4πSd2, where S is the observed energy flux and d the distance to the globular cluster. ⟨ Ė ⟩ for the pulsar populations in individual clusters are only poorly known since measurements of Ė are significantly affected by acceleration in the gravitational potential of the globular cluster (Bogdanov et al. 2006). We therefore adopt a value of ⟨ Ė ⟩ = (1.8 ± 0.7) × 1034 erg s-1 for all clusters as a best estimate that has been derived by comparing the log Ṗ distribution of Galactic field MSPs to the acceleration corrected log Ṗ distribution obtained for MSPs in 47 Tuc (Abdo et al. 2009c). This value is close to the value of ⟨ Ė ⟩ = 3.0 × 1034 erg s-1 that is obtained as average for Galactic field MSPs from the ATNF catalogue. Since intrinsically luminuous pulsars are more easily detected, this average is likely biased towards high values. Limiting the average to the local (<1 kpc) Galactic field MSPs in the ATNF catalogue indeed reduces the average value to ⟨ Ė ⟩ = 1.1 × 1034 erg s-1, consistent with our adopted value. Furthermore, we assume ⟨ ηγ ⟩ = 0.08 as derived from observations of nearby MSPs (Abdo et al. 2009c). The results are summarised in Table 4. The statistical and systematic uncertainties in the energy flux have been added in quadrature and we quote the resulting uncertainty from that combination for Lγ and NMSP.
(1)We compute the isotropic gamma-ray luminosity using Lγ = 4πSd2, where S is the observed energy flux and d the distance to the globular cluster. ⟨ Ė ⟩ for the pulsar populations in individual clusters are only poorly known since measurements of Ė are significantly affected by acceleration in the gravitational potential of the globular cluster (Bogdanov et al. 2006). We therefore adopt a value of ⟨ Ė ⟩ = (1.8 ± 0.7) × 1034 erg s-1 for all clusters as a best estimate that has been derived by comparing the log Ṗ distribution of Galactic field MSPs to the acceleration corrected log Ṗ distribution obtained for MSPs in 47 Tuc (Abdo et al. 2009c). This value is close to the value of ⟨ Ė ⟩ = 3.0 × 1034 erg s-1 that is obtained as average for Galactic field MSPs from the ATNF catalogue. Since intrinsically luminuous pulsars are more easily detected, this average is likely biased towards high values. Limiting the average to the local (<1 kpc) Galactic field MSPs in the ATNF catalogue indeed reduces the average value to ⟨ Ė ⟩ = 1.1 × 1034 erg s-1, consistent with our adopted value. Furthermore, we assume ⟨ ηγ ⟩ = 0.08 as derived from observations of nearby MSPs (Abdo et al. 2009c). The results are summarised in Table 4. The statistical and systematic uncertainties in the energy flux have been added in quadrature and we quote the resulting uncertainty from that combination for Lγ and NMSP.
It is encouraging to note that the estimates of MSP populations in the above globular clusters are very similar to theoretical and/or observational constraints made in other wavelengths. In Terzan 5, 33 MSPs are known so far and many more are expected based on the extrapolation of the radio luminosity function (Ransom et al. 2005). Indeed, by comparing the total radio luminosity of Terzan 5 to the radio luminosity function of field pulsars, Fruchter & Goss (2000) estimate the number of pulsars in the cluster to be 60–200, and also Kong et al. (2010) estimate that the number of pulsars in Terzan 5 could be as large as ~200. For NGC 6440, Freire et al. (2008) estimate that it may house as many pulsars as Terzan 5, a prediction that is compatible with our observations. Heinke et al. (2005) estimate that a total of ~25 MSPs exist in 47 Tuc (<60 at 95% confidence), regardless of their radio beaming fraction, based on their deep Chandra X-ray observations of this cluster. This is comparable to the upper limit of 30 MSPs derived by McConnell et al. (2004) from the radio luminosity distribution of pulsars. As noted above, Haggard et al. (2009) and Di Stefano & Rappaport (1992) obtain similar estimates for the number of MSPs in Omega Cen as well. Kulkarni et al. (1990) used radio observations of Galactic globular clusters visible from the northern hemisphere and took into account selection effects in the various radio surveys, and then after estimating the relative efficiency of pulsar production in the individual clusters, produced a census of the cluster population of pulsars. Their estimates are surprisingly close to ours where they deduce 150 MSPs in Terzan 5, 86 in NGC 6440, 18 in M 28, 21 in M 15 but only 5 in NGC 6652, the latter being the only cluster for which they estimate a quantity that is remarkably dissimilar to our work (see Table 4). We recall, however, that we classified NGC 6652 only as a possible globular cluster candidate because of the rather weak evidence for an exponential cut-off in the spectrum. The acquisition of more data is definitely required before any firm conclusions about the number of MSPs in NGC 6652 should be drawn.
3.3. Stellar encounters and the formation of MSPs
It has been shown for globular clusters that the number of neutron star X-ray binaries is correlated with the stellar encounter rate Γe (see Sect. 1 and Gendre et al. 2003a). Since MSPs are believed to be the progeny of these systems, we may expect a similar correlation between our estimated number of MSPs (or equivalently the observed gamma-ray luminosity) and Γe.
To test the link between the formation of MSPs and the stellar encounter rate, we compute the latter using 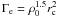 , where ρ0 is the central cluster density, given in units of L⊙ pc-3, and rc is the cluster core radius, given in units of pc. We used the central cluster densities and angular core radii θc quoted in Harris (1996) (February 2003 revision) along with the distance estimates listed in Table 4 using
, where ρ0 is the central cluster density, given in units of L⊙ pc-3, and rc is the cluster core radius, given in units of pc. We used the central cluster densities and angular core radii θc quoted in Harris (1996) (February 2003 revision) along with the distance estimates listed in Table 4 using 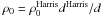 (Djorgovski 1993), and using rc = dtanθc. We then normalised the stellar encounter rates so that Γe = 100 for M 62 (for M 62 we obtain
(Djorgovski 1993), and using rc = dtanθc. We then normalised the stellar encounter rates so that Γe = 100 for M 62 (for M 62 we obtain 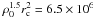 L⊙1.5 pc-2.5).
L⊙1.5 pc-2.5).
 |
Fig. 3 Predicted number of MSPs versus stellar encounter rate Γe. Horizontal error bars indicate the uncertainties in Γe due to the distance uncertainties given in Table 4 and due to uncertainties in θc that we estimated from the spread of values quoted in the recent literature. The data have been fitted by a linear relation NMSP = 0.5 × Γe + 18. |
Figure 3 shows evidence for a linear correlation between the predicted numbers of MSPs and the stellar encounter rates. Taking into account the uncertainties, the correlation is well fitted by NMSP = (0.5 ± 0.2) × Γe + (18 ± 9) (correlation coefficient 0.7). A similar correlation (not shown) is obtained if we plot the isotropic gamma-ray luminosity versus the encounter rate, since NMSP and Lγ are linearly related by Eq. (1). The correlation is well fitted by Lγ = (5.5 ± 1.9) × 1032 × Γe + (2.6 ± 0.7) × 1034 erg s-1.
Using our correlation we predict 2600 − 4700 MSPs that are observable in gamma rays in Galactic globular clusters. Kulkarni et al. (1990) estimate a total of ~10000 pulsars in Galactic globular clusters, subject to uncertainties in pulsar beaming and binarity. It has been suggested that the rare electron-capture accretion induced collapse channel will have a low kick velocity and may thus dominate the final cluster MSP population (Ivanova et al. 2008). However, since binaries dominate the production channels, the extrapolation from the observed sample to the total population based on encounter rate, used for the estimate of the total pulsar population by Kulkarni et al. (1990), should still be relevant. On the low end, Heinke et al. (2005) estimated the Galactic globular cluster pulsar population as 700, essentially from X-ray observations and the stellar encounter rate, the latter being commensurate with the estimate of Wijers & van Paradijs (1991) which was deduced from radio observations. Fruchter & Goss (1990) deduced the total number of MSPs in the Galactic globular system to lie between 500 and 2000, but concluded that the expected number of pulsars in a globular cluster depends only weakly on the stellar collision rate.
It appears that our independent method of determining the number of MSPs in Galactic globular clusters through gamma-ray observations is entirely compatible with earlier estimates.
4. Conclusions
An analysis of Fermi LAT data from 13 globular clusters has revealed 8 significant, point-like and steady gamma-ray sources that are spatially consistent with the locations of the clusters. Five of them (47 Tuc, Omega Cen, NGC 6388, Terzan 5, and M 28) show hard spectral power law indices (0.7 < Γ < 1.4) and clear evidence for an exponential cut-off in the range 1.0 − 2.6 GeV, which is the characteristic signature of magnetospheric emission from MSPs. We thus classify these 5 sources as plausible globular cluster candidates. Three of them (M 62, NGC 6440 and NGC 6652) also show hard spectral indices (1.0 < Γ < 1.7), however the presence of an exponential cut-off cannot unambiguously be established. More data are required before definite conclusions can be drawn; hence we qualify these 3 sources as possible globular cluster candidates.
From the 8 globular clusters that are associated with significant gamma-ray sources, 5 are known to harbour MSPs. In Omega Cen, NGC 6388 and NGC 6652, however, no MSPs have so far been detected, neither by radio nor by X-ray observations. The observation of gamma-ray signatures that are characteristic of MSPs provides strong support that these GCs indeed also harbour important populations of MSPs. In particular, we predict from the observed gamma-ray luminosities that the total MSP populations amount to 10–30 (Omega Cen), 80–300 (NGC 6388), and 30–80 (NGC 6652) in these clusters. Deep radio and X-ray follow-up observations may help to unveil first members of these populations.
Our predicted number of MSPs shows evidence for a positive correlation with the stellar encounter rate in a similar way to their progenitors, the neutron star low mass X-ray binaries. This correlation allows us to deduce the total number of MSPs in Galactic globular clusters (2600–4700) which lies midway between all previous estimates, supporting such a correlation. Such an estimate can be used to derive constraints on the original neutron star X-ray binary population, essential for understanding the importance of binary systems in slowing the inevitable core collapse of globular clusters.
See http://www.naic.edu/~pfreire/GCpsr.html/ for an updated list.
The models can be downloaded from http://fermi.gsfc.nasa.gov/ssc/data/access/lat/BackgroundModels.html
Acknowledgments
The Fermi LAT Collaboration acknowledges generous ongoing support from a number of agencies and institutes that have supported both the development and the operation of the LAT as well as scientific data analysis. These include the National Aeronautics and Space Administration and the Department of Energy in the United States, the Commissariat à l’Énergie Atomique and the Centre National de la Recherche Scientifique/Institut National de Physique Nucléaire et de Physique des Particules in France, the Agenzia Spaziale Italiana and the Istituto Nazionale di Fisica Nucleare in Italy, the Ministry of Education, Culture, Sports, Science and Technology (MEXT), High Energy Accelerator Research Organization (KEK) and Japan Aerospace Exploration Agency (JAXA) in Japan, and the K. A. Wallenberg Foundation, the Swedish Research Council and the Swedish National Space Board in Sweden. Additional support for science analysis during the operations phase is gratefully acknowledged from the Istituto Nazionale di Astrofisica in Italy and the Centre National d’Études Spatiales in France.
References
- Abdo, A. A., Ackermann, M., Atwood, W. B., et al. 2009a, ApJ, 699, 1171 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al., 2009b, Science, 325, 848 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009c, Science, 325, 845 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009d, Science, 325, 840 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010a, ApJS, 187, 460 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010b, ApJS, 188, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010c, Science, 328, 725 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010d, ApJ, 715, 429 [NASA ADS] [CrossRef] [Google Scholar]
- Alpar, M. A., Cheng, A. F., Ruderman, M. A., & Shaham J. 1992, Nature, 300, 728 [Google Scholar]
- Anderson, S. B. 1993, Ph.D. Thesis, California Inst. of Tech., Pasadena [Google Scholar]
- Atwood, W. B., Abdo, A. A., Ackermann, M., et al. 2009, ApJ, 697, 1071 [NASA ADS] [CrossRef] [Google Scholar]
- Beccari, G., Ferraro, F. R., Possenti, A., et al. 2006, ApJ, 131, 2551 [Google Scholar]
- Bogdanov, S., Grindlay, J. E., Heinke, C. O., et al. 2006, ApJ, 646, 1104 [NASA ADS] [CrossRef] [Google Scholar]
- Bono, G., Stetson, P. B., Sanna, N., et al. 2008, ApJ, 686, L87 [NASA ADS] [CrossRef] [Google Scholar]
- Camilo, F., & Rasio, F. A. 2005, ASPC, 328, 147 [Google Scholar]
- Chaboyer, B., Sarajedini, A., & Amandroff, T. E. 2000, AJ, 120, 3102 [NASA ADS] [CrossRef] [Google Scholar]
- Clark, G. W. 1975, ApJ, 199, L143 [NASA ADS] [CrossRef] [Google Scholar]
- Cordes, J. M., & Lazio, T. J. W. 2002, [arXiv:astro-ph/0207156] [Google Scholar]
- D’Amico, N., Possenti, A., Fici, L., et al. 2002, ApJ, 570, 89 [Google Scholar]
- Di Stefano, R., & Rappaport, S. 1992, ApJ, 396, 587 [NASA ADS] [CrossRef] [Google Scholar]
- Djorgovski, S. 1993, ASP Conf. Ser., 50, 373 [Google Scholar]
- Edwards, R. T., van Straten, W., & Bailes, M. 2001, ApJ, 560 365 [NASA ADS] [CrossRef] [Google Scholar]
- Freire, P. C. C., Ransom, S., Bégin, S., et al. 2008, ApJ, 675, 670 [NASA ADS] [CrossRef] [Google Scholar]
- Fruchter, A. S., & Goss, W. M. 1990, ApJ, 365, L63 [NASA ADS] [CrossRef] [Google Scholar]
- Fruchter, A. S., & Goss, W. M. 2000, ApJ, 536, 865 [NASA ADS] [CrossRef] [Google Scholar]
- Gendre, B., Barret, D., & Webb, N. 2003a, A&A, 403, 11 [Google Scholar]
- Gendre, B., Barret, D., & Webb, N. 2003b, A&A, 400, 521 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grindlay, J. E., Heinke, C., Edmonds, P. D., & Murray, S. S. 2001, Science, 292, 2290 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Haggard, D., Cool, A. M., & Davies, M. B. 2009, ApJ, 697, 224 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, W. E. 1996, AJ, 112, 1487 [NASA ADS] [CrossRef] [Google Scholar]
- Heinke, C. O., Grindlay, J. E., Edmonds, et al. 2005, ApJ, 625, 796 [NASA ADS] [CrossRef] [Google Scholar]
- Hessels, J. W. T., Ransom, S. M., Stairs, I. H., Kaspi, V. M., & Freire, P. C. C. 2007, ApJ, 670, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Hinshaw, G., Weiland, J. L., Hill, R. S., et al. 2009, ApJS, 180, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Hut, P., McMillan, S., Goodman, J., et al. 1992, PASP, 104, 981 [NASA ADS] [CrossRef] [Google Scholar]
- Ivanova, N., Heinke, C. O., Rasio, F. A., Belczynski, K., & Fregeau, J. M. 2008, MNRAS, 386, 553 [NASA ADS] [CrossRef] [Google Scholar]
- Kong, A. K. H., Hui, C. Y., & Cheng, K. S. 2010, ApJ, 712, 36 [Google Scholar]
- Knight, H. S., Bailes, M., Manchester, R. N., & Ord, S. M. 2006, ApJ, 653, 580 [NASA ADS] [CrossRef] [Google Scholar]
- Kulkarni, S. R., Narayan, R., & Romani, R. W. 1990, ApJ, 356, 174 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, J.-W., & Carney, B. W. 2006, AJ, 132, 2171 [NASA ADS] [CrossRef] [Google Scholar]
- McConnell, D., Deshpande, A. A., Connors, T., & Ables, J. G. 2004, MNRAS, 348, 1409 [NASA ADS] [CrossRef] [Google Scholar]
- McLaughlin, D. E., Anderson, J., Meylan, G., et al. 2006, ApJS, 166, 249 [Google Scholar]
- Moretti, A., Piotto, G., Arcidiacono, C., et al. 2009, A&A, 493, 539 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nucita, A. A., de Paolis, F., Ingrosso, G., Carpano, S., & Guainazzi, M. 2008, A&A, 478, 763 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ortolani, S., Barbuy, B., & Bica, 1994, A&AS, 108, 653 [Google Scholar]
- Ortolani, S., Barbuy, B., Bica, E., Zoccali, M., & Renzini, A. 2007, A&A, 470, 1043 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pellizzoni, A., Pilia, M., Possenti, A., et al. 2009, ApJ, 695, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Ransom, S. M. 2008, AIPC, 983, 415 [Google Scholar]
- Ransom, S. M., Hessels, J. W. T., Stairs, I. H., et al. 2005, Science, 307, 892 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Rees, R. F., & Cudworth, K. M. 1991, AJ, 102, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Sarajedini, A., Bedin, L. R., Chaboyer, B., et al. 2007, AJ, 133, 1658 [NASA ADS] [CrossRef] [Google Scholar]
- van de Ven, G., van den Bosch, R. C. E., Verolme, E. K., & de Zeeuw, P. T. 2006, A&A, 445, 513 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van den Bosch, R. C. E., de Zeeuw, P. T., Gebhardt, K., Noyola, E., & van de Ven, G. 2006, ApJ, 641, 852 [NASA ADS] [CrossRef] [Google Scholar]
- Wijers, R. A. M. J., & van Paradijs, J. 1991, A&A, 241, L37 [NASA ADS] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Gaussian kernel smoothed (σ = 0.1°) counts maps of the ROIs for the 8 significant globular cluster candidates. The insets show adaptively smoothed background subtracted counts maps for a 3° × 3° large region around the globular cluster. Circles indicate the nominal locations of the globular clusters. |
| In the text | |
 |
Fig. 2 Spectral energy distributions of the 8 significant globular cluster candidates. Lines indicate the exponentially cut-off power law models that have been fitted to the data using the binned maximum likelihood fitting procedure, and for which the spectral parameters are quoted in Table 3. The dotted part of the lines indicate the extrapolation of the exponentially cut-off power law model towards energies below 200 MeV. |
| In the text | |
 |
Fig. 3 Predicted number of MSPs versus stellar encounter rate Γe. Horizontal error bars indicate the uncertainties in Γe due to the distance uncertainties given in Table 4 and due to uncertainties in θc that we estimated from the spread of values quoted in the recent literature. The data have been fitted by a linear relation NMSP = 0.5 × Γe + 18. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


