| Issue |
A&A
Volume 523, November-December 2010
|
|
|---|---|---|
| Article Number | A12 | |
| Number of page(s) | 6 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201015496 | |
| Published online | 10 November 2010 | |
The stellar phase density of the local Universe and its implications for galaxy evolution
School of Physics and Astronomy, University of Nottingham, University Park, Nottingham NG7 2RD UK
e-mail: michael.merrifield@nottingham.ac.uk
Received: 29 July 2010
Accepted: 24 August 2010
This paper introduces the idea that the general mixing inequality obeyed by evolving stellar phase densities may place useful constraints on the possible history of the over-all galaxy population. We construct simple models for the full stellar phase space distributions of galaxies’ disk and spheroidal components, and reproduce the well-known result that the maximum phase density of an elliptical galaxy is too high to be produced collisionlessly from a disk system, although we also show that the inclusion of a bulge component in the disk removes this evolutionary impediment. In order to draw more general conclusions about the evolution of the galaxy population, we use the Millennium Galaxy Catalogue to construct a model of the entire phase density distribution of stars in a representative sample of the local Universe. In such a composite population, we show that the mixing inequality rules out some evolutionary paths that are not prohibited by consideration of the maximum phase density alone, and thus show that the massive ellipticals in this population could not have formed purely from collisionless mergers of a low mass galaxy population like that found in the local Universe. Although the violation of the mixing inequality is in this case quite minor, and hence avoidable with a modest amount of non-collisionless star formation in the merger process, it does confirm the potential of this approach. The future measurement of stellar phase densities at higher redshift will allow this potential to be fully exploited, offering a new way to look at the possible pathways for galaxy evolution, and to learn about the environment of star formation through the way that this phase space becomes populated over time.
Key words: galaxies: structure / galaxies: kinematics and dynamics / galaxies: evolution
© ESO, 2010
1. Introduction
The stars that make up galaxies exist in a six-dimensional phase space of positions and velocities, which offers a large amount of freedom in the possible configurations of stellar populations, and hence the morphologies and dynamics of the galaxies that they combine to form. However, because stars do not move instantaneously from one place to another, and similarly their velocities only change smoothly via finite gravitational accelerations, the evolution of their configuration obeys the simple collisionless Boltzmann equation, 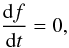 (1)which requires that the phase density f, the number of stars per unit volume in both space and velocity, remains constant around any given star as it travels through space (Binney & Tremaine 2008).
(1)which requires that the phase density f, the number of stars per unit volume in both space and velocity, remains constant around any given star as it travels through space (Binney & Tremaine 2008).
In principle, this equation places a very strong constraint on the manner in which a stellar system’s properties can evolve with time. However, there is one significant complication in that although Eq. (1) guarantees that the number of stars within any region of phase space remains constant, the shape of that region can become grossly distorted over time, wrapping itself around in a serpentine fashion. Just as a confectionery chef lightens the density of toffee by repeatedly pulling it into strands and wrapping them around, thus trapping air between the layers of toffee, so the phase wrapping of a stellar system will create a complex tangle of the original phase density distribution and empty space. In practice, one can only hope to measure the phase space density over a finite region; even in principle, since stars are intrinsically a discretized sampling of phase space density, it may not be possible to resolve the complex phase-wrapped structure. Instead, one measures an average that combines both the phase density from potentially many original locations and the mixed-in empty space, creating a “coarse grained” distribution function that will always tend to be diluted down from the original maximum phase density, and thus does not obey Eq. (1).
However, the tendency of this evolution to always dilute the maximum phase density still places a strong constraint on the possible ways in which a stellar system can evolve, irrespective of the details of its evolution. For example, Carlberg (1986) pointed out that the maximum phase space density in an elliptical galaxy of comparable mass to the Milky Way is significantly higher than that found in a disk of similar mass. It is therefore fundamentally impossible for such a disk system to be converted into an elliptical through collisionless processes since there is no way of generating the high phase density at the centre of the elliptical by mixing the lower phase densities of a disk.
Although intriguing, this seemingly-fundamental challenge to the current paradigm in which ellipticals form from mergers of disk systems has not generally been viewed as a matter of great concern. As pointed out by Lake (1989), the controversial region of high-density phase space represents a tiny fraction of the stellar distribution right at the extreme maximum of phase density, so that a relatively minor change to the properties of the initial disk, such as modestly decreasing its scale-height at large radii, can produce adequate numbers of stars at high phase density to populate this small region. Alternatively, as noted by Hernquist (1993) and as we will also see below, the denser bulge component of a typical disk galaxy can straightforwardly fill this gap. Finally, a small amount of star formation triggered by the transformation process could easily produce the requisite component at high stellar densities, since the gas-dynamic processes of star formation are highly collisional and therefore not subject to this collisionless constraint. So, there are a variety of ways to explain away such a violation of the mixing constraint at this extreme end of the distribution of phase densities, without any fine tuning of the processes, and thus there is no compelling reason to throw out the entire paradigm of merger-driven galaxy evolution on the basis of such an argument.
However, the physics of phase mixing also places limits on possible evolutionary paths followed by stars that do not lie in this extreme region of high-density phase space. The more general criterion was derived by Tremaine et al. (1986), who proved the following theorem. Define the mass of stars within a galaxy that find themselves in regions of phase space where the density is greater than f to be M(f), and the volume in phase space that these stars occupy to be V(f). Since both of these quantities vary monotonically with f, one can construct a function M(V) for the system. For a galaxy to evolve from an initial form Mi(V) to a final state Mf(V), it is a necessary condition that 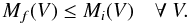 (2)A more recent discussion of this formula and the derivation of an interesting alternative “mixing inequality” can be found in Dehnen (2005).
(2)A more recent discussion of this formula and the derivation of an interesting alternative “mixing inequality” can be found in Dehnen (2005).
In interpreting the inequality of Eq. (2), it is important to recall that M orders the stars from the highest phase densities, fmax, to the lowest, so the smallest values of M(V) occur at the highest phase densities. In this region, we can write M(V) ≈ fmax × V, so the inequality in Eq. (2) reduces directly to the criterion introduced above, that the maximum phase density can only decrease. In principle, though, we now have a much more general constraint at all values of f. However, as Tremaine et al. (1986) noted, the cumulative nature of M(V) means that, for simple stellar distributions, if the criterion is met at small values of V (high phase densities), it will likely be globally met as well. Thus, in studying the evolution of simple single model galaxies, such as the collapse of a uniform spherical distribution to create a credible elliptical galaxy, Tremaine et al. (1986) showed that the primary constraint comes from considering the highest phase density material.
Such simple isolated models of individual galaxies are clearly somewhat unrealistic. Real galaxies typically have at least two stellar components, a disk and a spheroid, which each contribute to create a rather more complex phase density distribution. Further, if we are exploring the role that multiple mergers play in shaping the morphologies of galaxies, we cannot just consider the properties of single galaxies in isolation, but rather must look at the phase density of the entire population. Fortunately, although the above formalism was originally considered in the context of the properties of simple models for individual galaxies, it can equally well be applied to any self-contained set of stellar systems, including the entire population of galaxies, each containing multiple components.
In this paper, we begin to develop the methodology for such an analysis. In Sect. 2, we describe the way in which the phase space density distribution might be reasonably approximated for the components of each galaxy, and re-derive the original Carlberg (1986) result as a test case. In Sect. 3, we calculate an initial estimate for the stellar phase density distribution of the local Universe, and show that application of the general mixing theorem provides some interesting pointers on the possible progenitors of elliptical galaxies. Section 4 discusses how this methodology could be taken further.
2. Stellar phase densities of individual components
In order to analyze a multi-component picture of the phase space of galaxies, we need to construct models for the individual components. Combining these components to derive the global properties of the population is then reasonably straightforward. In principle, within a single galaxy, the populated phase spaces for the different components can overlap: a bulge star could have a similar position and velocity to a disk star. However, the hot nature of the bulge, the rotation of the disk, and the different spatial scales of the components, mean that in practice this overlap is small, so, to a reasonable approximation, M(f) and V(f) can be constructed for a single galaxy by simple summation of the component bulge and disk parts, and these quantities can then be further summed to derive the corresponding functions for the overall population. Of necessity, the ingredients of this model will be somewhat simplified, but, as we will see below, the functions involved stretch over many orders of magnitude, so uncertainties of factors of a few introduced by any approximations should not unduly compromise the results.
2.1. Spheroidal components
The original study by Carlberg (1986) modeled elliptical galaxies as self-gravitating collections of stars following a modified Hubble profile. Although this assumption returns a convenient analytical form for the maximum phase density in such systems, it is somewhat unrealistic in several aspect. First, this profile flattens to a central core, which is not seen in many spheroids: if we are interested in the regions of highest phase density, it is exactly this part of the system that we have to consider most closely. Second, the assumption that the system is self-gravitating neglects the effects of any dark matter halo. This assumption leads to the rather unphysical corollary that the derived maximum phase density is independent of the number of stars in the galaxy, so would attribute the same value to both high and low surface brightness systems.
Here, we adopt a somewhat more observationally-motivated model for spheroidal components. We assume that the projected light of a spheroid can be represented by a de Vaucouleurs law, with effective radius and luminosity derived from the photometry. We then approximate this function using a Dehnen (1993) model with γ = 1.5, thus allowing an analytic formula for stellar density as a function of radius. For the velocity distribution, we assume a Gaussian function with a dispersion σ that does not vary with radius. Ideally, one would use measured kinematics to determine the dispersion, but these data do not exist for the whole population, and such complexity goes beyond the philosophy of this analysis. Instead, we use the dispersion predicted by the structural parameters of each galaxy. We could use the fundamental plane relations to determine an appropriate value for σ, but it was found that in practice this value was rather sensitive to errors in the photometric decompositions of galaxies, which occasionally gave implausible values for scale-lengths and surface brightnesses in bulge components. However, the luminosity of the spheroidal component seems to be more robustly derived in such decompositions, so here we estimate the expected velocity dispersion from this quantity alone via the Faber–Jackson relation, 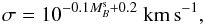 (3)where
(3)where 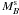 is the absolute magnitude of the spheroidal component in the B-band (Forbes & Ponman 1999).
is the absolute magnitude of the spheroidal component in the B-band (Forbes & Ponman 1999).
With the stellar density and velocity distribution determined at each point in this model for a galaxy’s spheroidal component, we can integrate over the galaxy’s phase space to derive the complete distribution of phase densities, and hence construct M(f) and V(f).
2.2. Disk components
The treatment of disk components is also motivated by the original analysis of Carlberg (1986), who modeled their spatial distribution as an exponential in the radial direction, and a self-gravitating sheet with a constant scale-height in the perpendicular z direction. The constant scale-height then dictates the radial decrease in the z-component of the velocity dispersion, σz. If one further assumes that the other two components of velocity dispersion vary in the same way with radius, forming a Gaussian velocity ellipsoid, the phase density distribution across the disk plane is fully specified. As Carlberg (1986) noted, such a distribution has the rather strange property that the phase density rises with radius in the galaxy, such that the highest values are found in the outer parts of the disk. If this maximum phase density of the disk is to translate into the maximum phase density of an elliptical galaxy during a merger, the galaxy must somehow turn itself inside-out. Although such a scenario seems unlikely, it is always possible for cold outer parts of disks to end up forming late in-falling streamers that sink to the middle of a merger product. Even the metallicity gradients seen in ellipticals and disks, which both tend to decrease with radius, do not present an insurmountable problem given a small amount of star formation in the merger and a relatively metal-rich bulge in the original disk galaxy.
We therefore follow this relatively simple prescription of Carlberg (1986), so that the stellar density is given by 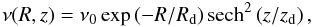 (4)with a radial cut-off at R = 3Rd reflecting that found in most exponential disks (van der Kruit 2001). The exact radius and form for this cut-off turns out not to make much difference to the analysis since the numbers of stars at such large radii is so small. The disk scale-length Rd is obtained from photometric decomposition of the galaxies we are modeling, while for the scale-height zd we follow Mao & Mo (1998) in setting zd = 0.2Rd (Bottema 1993). For the kinematic parameters, we adopt the linear fit between velocity dispersion and B-band disk absolute magnitude,
(4)with a radial cut-off at R = 3Rd reflecting that found in most exponential disks (van der Kruit 2001). The exact radius and form for this cut-off turns out not to make much difference to the analysis since the numbers of stars at such large radii is so small. The disk scale-length Rd is obtained from photometric decomposition of the galaxies we are modeling, while for the scale-height zd we follow Mao & Mo (1998) in setting zd = 0.2Rd (Bottema 1993). For the kinematic parameters, we adopt the linear fit between velocity dispersion and B-band disk absolute magnitude, 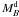 , from Bottema (1993) to obtain
, from Bottema (1993) to obtain 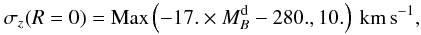 (5)with the limit at small velocity dispersions to ensure that the central dispersion does not end up smaller than the typical dispersion of the cold gas from which stars form. The variation in σz with radius is then set by the requirement of a constant scale-height, which implies that it declines exponential with radius with a scale-length of 2Rd. We further assume, as previous authors have done, that the shape of the velocity ellipsoid does not vary significantly with radius, and set
(5)with the limit at small velocity dispersions to ensure that the central dispersion does not end up smaller than the typical dispersion of the cold gas from which stars form. The variation in σz with radius is then set by the requirement of a constant scale-height, which implies that it declines exponential with radius with a scale-length of 2Rd. We further assume, as previous authors have done, that the shape of the velocity ellipsoid does not vary significantly with radius, and set 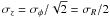 , motivated by the values found in the Solar neighbourhood of the Milky Way, and the epicyclic approximation which fixes the value of σR / σφ for a flat rotation curve (Binney & Tremaine 2008).
, motivated by the values found in the Solar neighbourhood of the Milky Way, and the epicyclic approximation which fixes the value of σR / σφ for a flat rotation curve (Binney & Tremaine 2008).
Once again, with both photometric and kinematic parameters defined, we can integrate across phase space to determine the phase density distribution of any disk component with a specified total luminosity and radial scale-length, and hence derive M(f) and V(f).
 |
Fig. 1 The distribution of stellar mass as a function of phase density, m(f), for model disk and spheroids with a mass of 5 × 1010 M⊙, and for a model of Milky Way-like disk galaxy with both a disk and a bulge component. |
2.3. A simple application
As a simple test of these models, we now seek to reproduce the original result of Carlberg (1986) concerning the maximum phase densities in disks and ellipticals. Figure 1 shows the distribution of phase densities that one obtains for a typical galactic disk which has been approximately matched to the properties of the Milky Way, with an absolute magnitude of 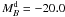 , a disk scale-length of 4 kpc, and a disk mass of 5 × 1010 M⊙ (Binney & Merrifield 1998). The figure also shows the phase density distribution for an identical-mass elliptical galaxy with an effective radius of Re = 10 kpc. This phase space density function has been normalized in the plot such that the area under the curve is proportional to the mass of stars that find themselves at a phase density within the range of integration, so that
, a disk scale-length of 4 kpc, and a disk mass of 5 × 1010 M⊙ (Binney & Merrifield 1998). The figure also shows the phase density distribution for an identical-mass elliptical galaxy with an effective radius of Re = 10 kpc. This phase space density function has been normalized in the plot such that the area under the curve is proportional to the mass of stars that find themselves at a phase density within the range of integration, so that 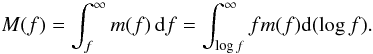 (6)As derived by Carlberg (1986), the maximum phase density found in the elliptical exceeds that of the disk, but, as also noted by Lake (1989), the area under the curves where this excess occurs is really very small, so the conflict is fairly insignificant.
(6)As derived by Carlberg (1986), the maximum phase density found in the elliptical exceeds that of the disk, but, as also noted by Lake (1989), the area under the curves where this excess occurs is really very small, so the conflict is fairly insignificant.
This point is underlined when one considers the more general mixing constraint on M(V) shown in Fig. 2, where it is clear that rearranging only ~ 107 M⊙ of the total 5 × 1010 M⊙, or ~ 0.02% of the stellar mass, at the highest phase densities (and hence smallest values of V) would be sufficient to eliminate the violation of the mixing inequality.
As Figs. 1 and 2 further illustrate, the conflict can also be readily eliminated if one follows the suggestion of Hernquist (1993) and adds to the disk galaxy a bulge component similar to that found in the Milky Way with a velocity dispersion of 110 kms-1, an effective radius of 2.75 kpc, and a mass of 1 × 1010 M⊙ (Binney & Merrifield 1998). Note that although this model is only intended to very approximately reproduce the phase-space properties of the Milky Way’s bulge, the maximum phase-space density that it produces in Fig. 1 agrees well with the value of ~ 10-5 M⊙pc-3(kms-1)-3 inferred by Wyse (1998). The maximum phase density decreases with luminosity in typical spheroidal components (Mao & Mo 1998), so even this relatively small bulge adds in sufficient stars at high phase densities to generate the missing high-density extreme of the elliptical. Thus, there would be no violation of the mixing constraint of Eq. (2) in turning this disk-dominated galaxy into a typical elliptical galaxy through collisionless mixing processes.
 |
Fig. 2 The cumulative mass in stars below any given phase density as a function of the volume of phase space occupied by those stars. The disk, spheroid and Milky Way-like models of Fig. 1 are shown. To evolve collisionlessly from one form to another, a stellar system can only move downward in this plot. |
3. Stellar phase density of the local Universe
Although the above test case is interesting, it does not place any strong limits on the possible general evolutionary paths for galaxies, since for any individual case one could always find potential progenitors with structural parameters such that the mixing constraint is not violated. It is therefore more interesting to consider the properties of the entire population of galaxies, to determine more globally what evolutionary paths the whole population may or may not have followed.
An important first step in this direction was made by Mao & Mo (1998), who explored the phase density as a function of absolute magnitude for a reasonably large sample of disk and elliptical galaxies. They also went beyond considering just the extrema of the phase density distribution by also calculating an average “effective phase density” for these galaxies. Through this analysis, they were able to show that disk- and spheroid-dominated galaxies follow distinct sequences of phase space density as a function of absolute magnitude. However, they did not possess the decompositions of individual galaxies into spheroids and disks that would have allowed them to model multiple components within single systems. Thus, they were not in a position to calculate the full stellar phase space density distribution to ascertain whether, for example, the bulge components of disk galaxies might be sufficient to eliminate any apparent violation of mixing constraints, as was illustrated in Sect. 2.3. In addition, the galaxies they analyzed comprised a somewhat heterogeneous sample, so they did not have access to a statistically complete sample that would have enabled them to determine the stellar phase density of the local Universe in a well-defined volume.
We therefore seek to extend this analysis by considering the data from the Millennium Galaxy Catalogue1 (MGC; Liske et al. 2003). This survey over 37.5 deg2, complete to mB = 24, provides a well-defined and thorough sampling of galaxies in the local Universe, and the availability of colour data offers at least a crude conversion from B-band luminosity to stellar mass (Bell & de Jong 2001), although the connection between these quantities is necessarily indirect due to the effects of varying stellar populations and extinction. Moreover, Allen et al. (2006) have shown that the MGC images of these galaxies are of sufficient quality to be decomposed with some confidence into separate disk and spheroidal components. In carrying out such decompositions, Driver et al. (2007) found that a relatively modest fraction of “pseudo-bulges” are better fitted by a less centrally-concentrated spheroid function than a de Vaucouleurs law, but that a de Vaucouleurs law spheroid plus an exponential disk was a generally reasonable approximation to the observed photometry, allowing us to employ the simple phase-space components adopted in the current analysis.
Estimating the stellar phase density distribution of the local Universe from these data is relatively straightforward. For each of the 10 095 galaxies in the MGC for which the decomposition into exponential disk and de Vaucouleurs spheroid has been made, one calculates the model phase space densities of the two components as in Sect. 2. These components are then converted from luminosity phase densities into mass phase densities using the colour prescription of Bell & de Jong (2001). Finally, the contribution of each galaxy is weighted according to its total absolute magnitude to allow for the different volumes sampled by this survey at different absolute magnitudes, such that each absolute magnitude bin of galaxies in the MGC contributes a signal proportional to the galaxy luminosity function at that magnitude, as derived by Driver et al. (2007).
The results of this analysis are presented in Fig. 3. It is notable that, even with the large data set of the MGC, dividing the sample by luminosity still produces relatively modest numbers of galaxies per bin, which vary significantly in their properties; these variations result in the noise apparent in the greyscale image. However, when the luminosity bins are all combined, this residual sampling noise is dramatically reduced, producing the reliable smooth total stellar phase space density distributions shown in the left-hand panels.
 |
Fig. 3 The phase density of stars in the local Universe as a function of the absolute magnitude of the galaxies that produce them, as derived from the Millennium Galaxy Catalogue. The panels show both the individual disk and spheroid components and the sum of the two. The projection of these plots by integrating over the distribution of galaxy luminosities shows the total stellar phase density of the local Universe. Here, f is expressed in M⊙pc-3(kms-1)-3 and m in pc3(kms-1)3Mpc-3. The dashed and dotted line show, respectively, the mean trend in effective and central phase density for components considered by Mao & Mo (1998). |
Figure 3 also compares these results to the mean trends established by Mao & Mo (1998). For the spheroidal component, there is good agreement between the two analyses on the upper cut-off in phase densities. The effective phase density derived by Mao & Mo (1998) appears somewhat higher than a measure that one would infer from the greyscale, but the logarithmic nature of the plot is somewhat misleading, and it is notable that the value of this effective phase density does lie very close to the mode in the projection of the full distribution.
The disk component reveals a similar phenomenon, with the effective phase density again lying very close to the peak of the distribution. The central phase density of the disk is less informative, since, as noted in Sect. 2.2, it does not represent a maximum value, but rather the minimum value in the plane of the disk. Of course, lower values of phase density can be found away from the plane of the disk, so this local minimum value has little physical significance in the context of the total distribution of phase densities. The difference between the Mao & Mo (1998) disk relation and the observed phase density distribution at bright magnitudes is more interesting, but also has a relatively simple explanation. In their analysis, Mao & Mo (1998) selected disk-dominated systems to derive this relation, so the total absolute magnitude on the abscissa when plotting their data corresponds quite closely to the disk luminosity. However, in the current analysis a random sample of galaxies from the local Universe has been selected, and at such bright magnitudes these systems are frequently spheroid-dominated, with relatively faint but often quite extended disk components. These lower-luminosity disks produce the lower phase density of stars that we see in the disk-component distribution.
The net result of combining these components produces a total stellar phase density distribution in the local Universe that is quite similar to that found in a typical spiral galaxy (see Fig. 1), with a degree of structure that can be attributed to the distinct disk and spheroid components. This similarity is not so surprising really, since consideration of the galaxy luminosity function shows that most of the stellar light comes from galaxies with luminosities around the break in the Schechter function, and at these luminosities a galaxy is typically a spiral system like that modeled in Fig. 1.
More interestingly, though, we can now begin to look systematically at the properties of different sub-classes of galaxies and individual components. As a simple illustration, Fig. 4 shows the average cumulative mass function M(V) derived from the phase space density distribution for the spheroidal components in the local Universe with masses of ~ 5 × 1010 M⊙. Also shown on this figure is the average M(V) curve derived from all the galaxies in the sample with total stellar masses between 1 × 108 M⊙ and 5 × 108 M⊙. The individual galaxy curves that make up this latter average have been normalized by multiplying both M and V by the factor required to generate from them a system containing ~ 5 × 1010 M⊙ of stars. Thus, it represents the M(V) curve of the progenitors of these higher-mass spheroids if the latter systems form from random galaxy mergers of the lower-mass systems. The fact that M(V) for the small galaxies does not lie above the curve for the large spheroids at all values of V means that these functions violate the mixing inequality of Eq. (2), so we can state quite generally that no combination of collisionless merger processes bringing small systems like these together could have produced the final large spheroids.
 |
Fig. 4 The cumulative mass function derived from the Millennium Galaxy Catalogue for spheroids of mass ~ 5 × 1010 M⊙, and for a population of possible progenitor galaxies at masses between 1 × 108 M⊙ and 5 × 108 M⊙. |
In this case, it is interesting to note that the issue does not arise at the highest phase densities (lowest values of V), as the compact spheroidal components of the small galaxies provide more than enough stars at these densities to produce the bigger spheroids. Rather it is at intermediate phase densities where one runs out of spheroid stars, but has yet to tap into the lower phase densities of disk stars, that the deficit arises. As such, this apparent violation of the mixing theorem is somewhat harder to explain away than the original result comparing a single disk to a single spheroid, where the discrepancy occurs just in the extreme tail of the phase density distribution.
Although this violation of the mixing theorem is formally statistically significant – with samples of galaxies of this size, one can re-sample the distribution to get a good handle on the random errors in M(V) – it is nonetheless probably still not a major problem for the fundamental paradigm of hierarchical galaxy formation. As with the single galaxy result, it only involves a rather small fraction of the total mass of the system, and a relatively minor addition of extra mass through star formation could reorder the curves. In addition, presumably today’s large spheroids did not form from progenitors exactly akin to today’s small galaxies, so one might not expect this inequality to be met even if the large spheroids did form purely from collisionless mergers of pre-existing galaxies. Indeed, there is now strong evidence that the structural parameters of even non-star-forming systems have evolved strongly over time (Williams et al. 2010, and references therein). Nonetheless, this example illustrates the potential power in using phase space constraints to study the possible evolutionary paths that galaxies might follow, and where extra stars would have to be added in to allow other paths to be pursued. It also underlines the point that there is more to such analyses than considering just the maximum phase density.
4. Discussion
In this paper, we have introduced a methodology for modeling the full stellar phase space density of any combination of disk and spheroidal stellar systems, including that which makes up the local galaxy population in the Universe. We have also discussed the general inequality that limits the possible ways in which this phase density distribution can evolve. As we have seen, such analyses can make use of more than just the rather non-robust constraint provided by the maximum phase density, and offer a potentially powerful tool for determining the possible paths by which these systems could have evolved.
Of necessity, the phase space model considered here has been rather simple, but the explosion of available data means that over time many of the simplifying assumptions can be eliminated. Large infrared surveys like Two Micron All-Sky Survey offer a more direct window on the stellar mass distribution in galaxies, and its decomposition into disk and bulge components (e.g. Méndez-Abreu et al. 2008). Further, extensive spectroscopic studies of galaxies using integral field units
(e.g. Krajnović et al. 2006) and detailed dynamical modeling of such data (e.g. de Lorenzi et al. 2009) mean that the simple generalized parameterizations of both the photometric and kinematic properties of galaxies can soon be replaced by reasonably direct measurements of the phase-space density distribution on a galaxy-by-galaxy basis.
Another obvious direction in which to extend this analysis is to the more distant Universe. At these greater distances, it is challenging to obtain the necessary high-quality photometric and kinematic observations, but steps are already being taken both to determine the distribution of light within such distant galaxies (e.g. Huertas-Company et al. 2007), and in establishing at least the broad kinematic scaling relations analogous to those used here (e.g. MacArthur et al. 2008). Comparison between the phase density distributions of stars in distant galaxies and that in the local Universe will allow a more direct test as to which evolutionary paths are available to galaxies of different types. It also offers the prospect of a new perspective on the star formation history of the Universe, in that by determining the phase densities of stars that have to be added over time so as to avoid violation of the mixing constraint, we will be able to go beyond the simple numbers game of how many stars form at different epochs to learn about the smaller-scale environments in which these stars must have formed.
The Millennium Galaxy Catalogue consists of imaging data from the Isaac Newton Telescope and spectroscopic data from the Anglo Australian Telescope, the ANU 2.3 m, the ESO New Technology Telescope, the Telescopio Nazionale Galileo and the Gemini North Telescope. The survey has been supported through grants from the Particle Physics and Astronomy Research Council and the Australian Research Council. The data and data products are publicly available from http://www.eso.org/~jliske/mgc/.
References
- Allen, P. D., Driver, S. P., Graham, A. W., et al. 2006, MNRAS, 371, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, E. F., & de Jong, R. S. 2001, ApJ, 550, 212 [NASA ADS] [CrossRef] [Google Scholar]
- Binney, J., & Merrifield, M. 1998, Galactic astronomy, ed. J. Binney, & M. Merrifield, Princeton series in astrophysics (Princeton, NJ: Princeton University Press) [Google Scholar]
- Binney, J., & Tremaine, S. 2008, Galactic Dynamics, ed. J. Binney, & S. Tremaine, second edition (Princeton, NJ, USA: Princeton University Press) [Google Scholar]
- Bottema, R. 1993, A&A, 275, 16 [NASA ADS] [Google Scholar]
- Carlberg, R. G. 1986, ApJ, 310, 593 [NASA ADS] [CrossRef] [Google Scholar]
- de Lorenzi, F., Gerhard, O., Coccato, L., et al. 2009, MNRAS, 395, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Dehnen, W. 1993, MNRAS, 265, 250 [NASA ADS] [CrossRef] [Google Scholar]
- Dehnen, W. 2005, MNRAS, 360, 892 [NASA ADS] [CrossRef] [Google Scholar]
- Driver, S. P., Allen, P. D., Liske, J., & Graham, A. W. 2007, ApJ, 657, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Forbes, D. A., & Ponman, T. J. 1999, MNRAS, 309, 623 [NASA ADS] [CrossRef] [Google Scholar]
- Hernquist, L. 1993, ApJ, 409, 548 [NASA ADS] [CrossRef] [Google Scholar]
- Huertas-Company, M., Rouan, D., Soucail, G., et al. 2007, A&A, 468, 937 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krajnović, D., Cappellari, M., de Zeeuw, P. T., & Copin, Y. 2006, MNRAS, 366, 787 [NASA ADS] [CrossRef] [Google Scholar]
- Lake, G. 1989, AJ, 97, 1312 [NASA ADS] [CrossRef] [Google Scholar]
- Liske, J., Lemon, D. J., Driver, S. P., Cross, N. J. G., & Couch, W. J. 2003, MNRAS, 344, 307 [NASA ADS] [CrossRef] [Google Scholar]
- MacArthur, L. A., Ellis, R. S., Treu, T., et al. 2008, ApJ, 680, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Mao, S., & Mo, H. J. 1998, MNRAS, 296, 847 [NASA ADS] [CrossRef] [Google Scholar]
- Méndez-Abreu, J., Aguerri, J. A. L., Corsini, E. M., & Simonneau, E. 2008, A&A, 487, 555 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tremaine, S., Henon, M., & Lynden-Bell, D. 1986, MNRAS, 219, 285 [NASA ADS] [CrossRef] [Google Scholar]
- van der Kruit, P. C. 2001, in ASP Conf. Ser., Galaxy Disks and Disk Galaxies, ed. J. G. Funes & E. M. Corsini, 230, 119 [Google Scholar]
- Williams, R. J., Quadri, R. F., Franx, M., et al. 2010, ApJ, 713, 738 [NASA ADS] [CrossRef] [Google Scholar]
- Wyse, R. F. G. 1998, MNRAS, 293, 429 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 The distribution of stellar mass as a function of phase density, m(f), for model disk and spheroids with a mass of 5 × 1010 M⊙, and for a model of Milky Way-like disk galaxy with both a disk and a bulge component. |
| In the text | |
 |
Fig. 2 The cumulative mass in stars below any given phase density as a function of the volume of phase space occupied by those stars. The disk, spheroid and Milky Way-like models of Fig. 1 are shown. To evolve collisionlessly from one form to another, a stellar system can only move downward in this plot. |
| In the text | |
 |
Fig. 3 The phase density of stars in the local Universe as a function of the absolute magnitude of the galaxies that produce them, as derived from the Millennium Galaxy Catalogue. The panels show both the individual disk and spheroid components and the sum of the two. The projection of these plots by integrating over the distribution of galaxy luminosities shows the total stellar phase density of the local Universe. Here, f is expressed in M⊙pc-3(kms-1)-3 and m in pc3(kms-1)3Mpc-3. The dashed and dotted line show, respectively, the mean trend in effective and central phase density for components considered by Mao & Mo (1998). |
| In the text | |
 |
Fig. 4 The cumulative mass function derived from the Millennium Galaxy Catalogue for spheroids of mass ~ 5 × 1010 M⊙, and for a population of possible progenitor galaxies at masses between 1 × 108 M⊙ and 5 × 108 M⊙. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


