| Issue |
A&A
Volume 522, November 2010
|
|
|---|---|---|
| Article Number | A16 | |
| Number of page(s) | 7 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201015084 | |
| Published online | 27 October 2010 | |
Internal heating of old neutron stars: contrasting different mechanisms
Departamento de Astronomía y Astrofísica, Pontificia Universidad Católica de
Chile,
Casilla 306,
Santiago 22
Chile
e-mail: areisene@astro.puc.cl; areisene@astro.puc.cl
Received:
29
May
2010
Accepted:
26
July
2010
Context. The standard cooling models of neutron stars predict temperatures of T < 104 K for ages t > 107 yr. However, the likely thermal emission detected from the millisecond pulsar J0437-4715, of spin-down age ts ~ 7 × 109 yr, implies a temperature T ~ 105 K. Thus, a heating mechanism needs to be added to the cooling models in order to obtain agreement between theory and observation.
Aims. Several internal heating mechanisms could be operating in neutron stars, such as magnetic field decay, dark matter accretion, crust cracking, superfluid vortex creep, and non-equilibrium reactions (“rotochemical heating”). We study these mechanisms to establish which could be the dominant source of thermal emission from old pulsars.
Methods. We show by simple estimates that magnetic field decay, dark matter accretion, and crust cracking are unlikely to have a significant heating effect on old neutron stars. The thermal evolution for the other mechanisms is computed with the code of Fernández and Reisenegger. Given the dependence of the heating mechanisms on the spin-down parameters, we study the thermal evolution for two types of pulsars: young, slowly rotating “classical” pulsars and old, fast rotating millisecond pulsars.
Results. We find that magnetic field decay, dark matter accretion, and crust cracking do not produce any detectable heating of old pulsars. Rotochemical heating and vortex creep can be important both for classical pulsars and millisecond pulsars. More restrictive upper limits on the surface temperatures of classical pulsars could rule out vortex creep as the main source of thermal emission. Rotochemical heating in classical pulsars is driven by the chemical imbalance built up during their early spin-down, and is therefore strongly sensitive to their initial rotation period.
Key words: stars: neutron / dense matter / stars: rotation / pulsars: general / pulsars: individual: PSR J0437-4715 / pulsars: individual: PSR B0950+08
© ESO, 2010
1. Introduction
Neutron stars (NSs) are compact objects composed of a liquid core enveloped by a solid crust. The core is expected to contain superfluid neutrons and superconducting protons, while the crust contains heavy atomic nuclei arranged in a crystal lattice, coexisting with superfluid neutrons in its inner part. The high density of the NS core, up to ~ (3 − 9)ρ0, where ρ0 is the saturation nuclear matter density, cannot be reproduced in terrestrial laboratories. This turns the NSs into natural laboratories. The study of their thermal evolution, confronting theory and observation, provides a useful test for the understanding of the properties of matter at supernuclear density.
For all standard cooling models (Yakovlev & Pethick 2004), neutron stars cool down to surface temperatures Ts < 104 K within less than 107 yr. Nevertheless, the observation of ultraviolet thermal emission from millisecond pulsar J0437-4715 (Kargaltsev et al. 2004), whose spin-down age, corrected to the latest distance of 157 pc (Deller et al. 2008), is τsd ~ 7 × 109 yr (van Straten et al. 2001), shows a surface temperature of about ~ 105 K for this pulsar. Hence, a heating mechanism needs be to added to the standard cooling models to obtain agreement between theory and observation.
There are several heating mechanisms that can be present during the late stages of the thermal evolution. These include the frictional motion of superfluid neutron vortices (Alpar et al. 1984; Shibazaki & Lamb 1989; Larson & Link 1999), rotochemical heating (Reisenegger 1995, 1997; Fernández & Reisenegger 2005; Petrovich & Reisenegger 2010), magnetic field decay (Goldreich & Reisenegger 1992; Thompson & Duncan 1996; Pons et al. 2007), and crust cracking (Baym & Pines 1971; Cheng et al. 1992). Other mechanisms, based on more speculative hypotheses, such as a time variation of the gravitational constant (Jofré et al. 2006), the decay of exotic particles (Hannestad et al. 2002), or the accretion of dark matter particles (de Lavallaz & Fairbairn 2010; Kouvaris & Tinyakov 2010), could in principle also heat old neutron stars. In Schaab et al. (1999) and Larson & Link (1999), several of the internal heating mechanisms cited are studied and confronted with observational data of neutron stars (surface temperature upper limits). However, the oversimplified description of some heating mechanisms (rotochemical heating in Schaab et al. 1999) and the until then non-detection of thermal emission from neutron stars older than ~ 106 yr, made it impossible to obtain reliable conclusions.
The goal of this work is to provide a comparative analysis of the thermal evolution including different heating mechanisms. In order to do this, we discard some of them as not strong enough (magnetic field decay, dark matter accretion, and crust cracking), and we present a more detailed study of the most promising ones: vortex creep and rotochemical heating. We confront these mechanisms with the thermal emission detected in the millisecond pulsar J0437-4715 and the best available upper limits on the temperature of six other old pulsars. Owing to the dependence of heating mechanisms on spin-down parameters, which leads to different temperatures for different pulsars, we separately study the thermal evolution for two types of pulsars: young, strongly magnetized, and slowly rotating “classical” pulsars, and old, weakly magnetic, and fast rotating millisecond pulsars (MSPs).
The paper is organized as follows. In Sect. 2 we describe the different heating processes and assess their importance. In Sect. 3 we show the effects of vortex creep and rotochemical heating in classical and millisecond pulsars. In Sect. 4 the predictions are confronted with observed data. A summary of our main conclusions is given in Sect. 5.
2. Mechanisms
The cooling of a NS is caused by neutrino emission from the interior and by thermal photon emission from the surface of the star. The neutrino emission is determined by the state of matter in the core, which depends on the stellar mass and the properties of the matter at nuclear density. The evolution of the internal temperature of an NS is given by the thermal balance equation 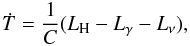 (1)where C is the total heat capacity of the star, Lγ is the photon luminosity, Lν is the neutrino luminosity, and LH is the power generated by internal heating mechanisms, of which we consider the following.
(1)where C is the total heat capacity of the star, Lγ is the photon luminosity, Lν is the neutrino luminosity, and LH is the power generated by internal heating mechanisms, of which we consider the following.
2.1. Magnetic field decay
Goldreich & Reisenegger (1992) studied the processes that promote the dissipation of magnetic energy in NSs. Later, Thompson & Duncan (1996) studied the resulting emission (X-rays, neutrinos, Alfvén waves) from very strongly magnetized NSs (“magnetars”), and Pons et al. (2007) showed observational evidence that suggests heating by this mechanism in different classes of relatively young, strongly magnetic NSs. Because the physical processes involved in the decay of NS magnetic fields are still uncertain, we only make an order-of-magnitude estimate of the magnetic field B required to produce a detectable surface temperature in old NSs.
At ages t > 106 yr, cooling is dominated by photon emission. The luminosity caused by the decay of the magnetic field in a NS with radius R and magnetic energy EB ~ (4πR3 / 3) ⟨ B2 ⟩ / 8π in a time scale t, is
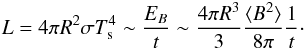 (2)In this way, the magnetic field required to account for an NS with a surface temperature Ts ~ 105 K (i.e. the detected temperature in J0437-4715) and radius R = 10 km is
(2)In this way, the magnetic field required to account for an NS with a surface temperature Ts ~ 105 K (i.e. the detected temperature in J0437-4715) and radius R = 10 km is 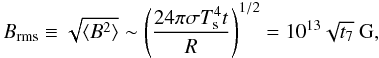 (3)where t7 is the age of the NS in units of 107 yr. An old classical pulsar of ~ 107 yr and an MSP of ~109 yr require, respectively, magnetic fields of ~ 1013 G and ~1014 G in order to obtain a detectable temperature1. Thus, the magnetic fields inferred from the spin-down in classical pulsars, ~1011 G, and MSPs, ~108 G, are much too low to produce detectable heating.
(3)where t7 is the age of the NS in units of 107 yr. An old classical pulsar of ~ 107 yr and an MSP of ~109 yr require, respectively, magnetic fields of ~ 1013 G and ~1014 G in order to obtain a detectable temperature1. Thus, the magnetic fields inferred from the spin-down in classical pulsars, ~1011 G, and MSPs, ~108 G, are much too low to produce detectable heating.
2.2. Dark matter accretion
Recently, Kouvaris & Tinyakov (2010) and de Lavallaz & Fairbairn (2010) studied the effects of dark matter (DM) accretion and annihilation in compact objects. One of these is the potential increase of the surface temperature of old NSs in sufficiently dense environments (e.g., the Galactic center and globular clusters). Because we are interested in the pulsars of the solar neighborhood, where the DM density is relatively low, we only make an order-of-magnitude estimate of the maximum possible thermal emission caused by this mechanism. The maximum possible accretion rate onto a NS is given by 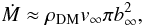 (4)where ρDM is the DM density, v∞ is the relative velocity between DM particles and the NS, and b∞ is the maximum impact parameter for a DM particle to hit NS. This is valid as long as the DM-baryon (or DM-lepton) cross section ⟨ σ ⟩ ≳ πR2 / Nbar ~ 10-45 cm2, so any DM particle entering the NS stays inside. If ⟨ σ ⟩ is smaller than this, Ṁ is reduced correspondingly. From the Milky Way (MW) rotation curve, the DM density in the solar neighborhood ρDM ~ 10-2 M⊙ pc-3. From Newtonian energy and angular momentum conservation, the maximum impact parameter is b∞ ≈ Rvesc / v∞, in the limit vesc ≫ v∞. Considering the escape velocity vesc ~ 2c / 3 and the typical velocities for NSs moving through the MW, v∞ ≳ 2 × 107 cm s-1, we can obtain an upper limit on the DM accretion rate, Ṁ ≲ 9 × 10-25 M⊙ yr-1. Hence, the maximum luminosity is ṀGM / R ≈ 1022 erg s-1 for stable DM , and Ṁc2 ≈ 5 × 1022 erg s-1 for decaying DM. Considering that the cooling is dominated by photon emission, these correspond to the surface temperatures ~ 2 × 103 K and ~ 3 × 103 K for stable and unstable matter, respectively. In order to get a detectable Ts ~ 105 K, a 106 times higher DM density is required (as perhaps found very near the Galactic center). Thus DM accretion does not have a significant effect in the solar neighborhood.
(4)where ρDM is the DM density, v∞ is the relative velocity between DM particles and the NS, and b∞ is the maximum impact parameter for a DM particle to hit NS. This is valid as long as the DM-baryon (or DM-lepton) cross section ⟨ σ ⟩ ≳ πR2 / Nbar ~ 10-45 cm2, so any DM particle entering the NS stays inside. If ⟨ σ ⟩ is smaller than this, Ṁ is reduced correspondingly. From the Milky Way (MW) rotation curve, the DM density in the solar neighborhood ρDM ~ 10-2 M⊙ pc-3. From Newtonian energy and angular momentum conservation, the maximum impact parameter is b∞ ≈ Rvesc / v∞, in the limit vesc ≫ v∞. Considering the escape velocity vesc ~ 2c / 3 and the typical velocities for NSs moving through the MW, v∞ ≳ 2 × 107 cm s-1, we can obtain an upper limit on the DM accretion rate, Ṁ ≲ 9 × 10-25 M⊙ yr-1. Hence, the maximum luminosity is ṀGM / R ≈ 1022 erg s-1 for stable DM , and Ṁc2 ≈ 5 × 1022 erg s-1 for decaying DM. Considering that the cooling is dominated by photon emission, these correspond to the surface temperatures ~ 2 × 103 K and ~ 3 × 103 K for stable and unstable matter, respectively. In order to get a detectable Ts ~ 105 K, a 106 times higher DM density is required (as perhaps found very near the Galactic center). Thus DM accretion does not have a significant effect in the solar neighborhood.
2.3. Crust cracking
This mechanism considers a rotating NS whose crust solidifies with an ellipsoidal form. The spin-down causes a gradual change to a more spherical shape. In this process, the stress in the crust of the NS is increased. However, the rigidity of the crust causes it to remain more oblate than it would be if it had no resistance to shear. When the crust reaches a critical deformation, it breaks, part of the accumulated strain energy is released, and the excess oblateness, due to the crust rigidity, is reduced. The mean stress σ in the crust caused by the spin-down is given by σ = μ(ϵ0 − ϵ) (Baym & Pines 1971), with ϵ = (I − I0) / I0, where μ is the mean shear modulus of the crust, I is the moment of inertia of the star, I0 is its non-rotating value, and ϵ0 is a value of ϵ at which the crust is stress-free. As the stellar rotation slows down, ϵ is correspondingly decreased, increasing the accumulated stress. Eventually, the crust cracks, ϵ0 is suddenly decreased, causing a discrete change Δ(ϵ0 − ϵ). The amount of strain energy released by this crack is (Baym & Pines 1971) 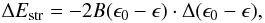 (5)and the time between successive quakes is
(5)and the time between successive quakes is 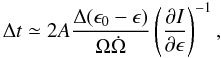 (6)where Ω is the angular velocity of the star, B ~ μVc / 42 (with Vc the crust volume), and A quantifies the increase in gravitational energy due to the deformation of the shape (for more detail, see Cutler et al. 2003; Zdunik et al. 2008). If ϵ0 − ϵ ≈ θc, the critical breaking strain angle, and the time between quakes is small compared to the timescale of thermal evolution, the time-averaged energy dissipation rate by this process is
(6)where Ω is the angular velocity of the star, B ~ μVc / 42 (with Vc the crust volume), and A quantifies the increase in gravitational energy due to the deformation of the shape (for more detail, see Cutler et al. 2003; Zdunik et al. 2008). If ϵ0 − ϵ ≈ θc, the critical breaking strain angle, and the time between quakes is small compared to the timescale of thermal evolution, the time-averaged energy dissipation rate by this process is 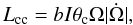 (7)where b = B / A. This expression, based on the formalism of Baym & Pines (1971), differs from that of Cheng et al. (1992), but agrees with the correction made by Schaab et al. (1999) for the particular case of a neutron star modeled as a Maclaurin spheroid.
(7)where b = B / A. This expression, based on the formalism of Baym & Pines (1971), differs from that of Cheng et al. (1992), but agrees with the correction made by Schaab et al. (1999) for the particular case of a neutron star modeled as a Maclaurin spheroid.
Cutler et al. (2003) calculated the “rigidity parameter” b for a realistic NS structure, with a solid crust afloat on a liquid core. They solved the strain field that develops as the NS spins down and found that b ~ 10-7, two orders of magnitude below the result found by Baym & Pines (1971) for a simplified model. On the other hand, Horowitz & Kadau (2009) recently found through N-body simulations that the Coulomb lattice of the NS crust can support a maximum strain angle θc ~ 10-1, three orders of magnitude higher than the value estimated by Smoluchowski & Welch (1970). Thus, for an NS of ~ 1.4 M⊙, the time-averaged crust-cracking luminosity is  , where Ṗ-20 is the period derivative measured in units of 10-20 and P5 ms is the period in units of 5 ms. For a representative classical pulsar (PSR B0950+08), P ~ 250 ms and Ṗ ~ 10-16 s s-1, so Lcc ~ 1025 erg s-1, while for the MSP J0437-4715, P = 5.76 ms and Ṗ = 5.73 × 10-20 s s-1, so Lcc ~ 4 × 1025 erg s-1. Comparing these results with the thermal emission from a pulsar with Ts ~ 105 K, L ~ 1029 erg s-1 (i.e., potentially detectable thermal emission from an NS in the solar neighborhood by the Hubble Space Telescope), we conclude that the crust-cracking mechanism does not produce detectable heating.
, where Ṗ-20 is the period derivative measured in units of 10-20 and P5 ms is the period in units of 5 ms. For a representative classical pulsar (PSR B0950+08), P ~ 250 ms and Ṗ ~ 10-16 s s-1, so Lcc ~ 1025 erg s-1, while for the MSP J0437-4715, P = 5.76 ms and Ṗ = 5.73 × 10-20 s s-1, so Lcc ~ 4 × 1025 erg s-1. Comparing these results with the thermal emission from a pulsar with Ts ~ 105 K, L ~ 1029 erg s-1 (i.e., potentially detectable thermal emission from an NS in the solar neighborhood by the Hubble Space Telescope), we conclude that the crust-cracking mechanism does not produce detectable heating.
Additionally, the high critical strain angle obtained by Horowitz & Kadau (2009) requires the star to have an initial deformation ϵ0 > θc ~ 10-1 in order to cause any cracking of the crust. However, for plausible initial rotation periods of classical pulsars (P0 > 15 ms), their initial deformation is only 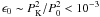 , where PK ~ 0.5 ms is the Keplerian period of the star. Hence, the crust-cracking mechanism is never activated in classical pulsars and probably operates only in MSPs with P0 < 2 ms. If the latter were the case, and now considering that all stresses in the crust are suddenly released, the internal thermal energy of the star is increased by ~
, where PK ~ 0.5 ms is the Keplerian period of the star. Hence, the crust-cracking mechanism is never activated in classical pulsars and probably operates only in MSPs with P0 < 2 ms. If the latter were the case, and now considering that all stresses in the crust are suddenly released, the internal thermal energy of the star is increased by ~ 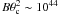 erg, corresponding to an internal temperature of 107 K and a surface temperature of ~ 5 × 105 K (Potekhin et al. 1997), which is dissipated within less than 107 yr. Hence, in MSPs of 108 − 9 yr, the increase in temperature due to catastrophic cracking is given by a narrow peak in the thermal evolution, which is unlikely to be detected because of the short timescale involved.
erg, corresponding to an internal temperature of 107 K and a surface temperature of ~ 5 × 105 K (Potekhin et al. 1997), which is dissipated within less than 107 yr. Hence, in MSPs of 108 − 9 yr, the increase in temperature due to catastrophic cracking is given by a narrow peak in the thermal evolution, which is unlikely to be detected because of the short timescale involved.
2.4. Vortex creep
The relatively low temperatures in the interior of NSs induce the formation of neutron Cooper pairs. These form a condensate with a macroscopic wave function. A consequence of this is that the vorticity in the superfluid must be concentrated in discrete vortex lines, whose microscopic distribution allows the superfluid to approximate a macroscopic rigid rotation.
As the star spins down, the vortex lines must move outward. As they move through the inner crust, they are pinned to the nuclear lattice until a critical velocity difference between the superfluid and the crust is reached. In this process, the pinning and unpinning of the vortex lines with respect to the nuclei of the crystal lattice release energy that heats the star. The energy-dissipation rate is given by (Alpar et al. 1984) 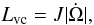 (8)where J ≃ ω̅Ip , with Ip the moment of inertia of the pinning layer and ω̅cr = (Ωs − Ωc)cr an average over the pinning zone of the critical lag between the angular velocity Ωc of the crust and the superfluid rotation rate Ωs.
(8)where J ≃ ω̅Ip , with Ip the moment of inertia of the pinning layer and ω̅cr = (Ωs − Ωc)cr an average over the pinning zone of the critical lag between the angular velocity Ωc of the crust and the superfluid rotation rate Ωs.
Vortex-nuclei interaction parameters in the semi-classical model (Donati & Pizzochero 2004), with the Argonne potential(a) and Gogny potential(b).
Vortex-nuclei interaction parameters in the quantum approach (Avogadro et al. 2008), with the SLy4 potential(a) and Skm* potential(b).
Donati & Pizzochero (2004) calculated the vortex-nucleus interaction in the inner crust of NSs with a semi-classical model. The density-dependent neutron pairing gaps used in the calculations are obtained from the Argonne potential and Gogny effective interaction. Table 1 shows the pinning energy calculated with this model for five zones of the inner crust. Similarly, Avogadro et al. (2008) calculated the vortex-nucleus interaction in the inner crust based on a Hartree-Fock-Bogoliubov quantum mean field theory. Table 2 shows the pinning energy for this approach. An important result of this, contrary to the prediction of the previous model, is that pinning of vortices on nuclei is favored at low density in the inner crust. We used both results to calculate the excess angular momentum J, which determines the luminosity for the vortex creep mechanism. In addition, we used Eq. (58) of Alpar et al. (1984) in the limit ENP ≫ kT, 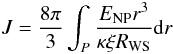 (9)where ENP is the pinning energy of a vortex on a nucleus, r is the radial coordinate, κ is the quantum of circulation of each vortex, ξ is the vortex coherence length, and RWS is the radius of the Wigner-Seitz cell. In order to calculate this integral, we generate NS structure models for specific masses and linearly interpolate the values of Tables 1 and 2 according to these models. For simplicity, we do not take relativistic effects into account because the corrections involved are minor, i.e. (1 − rg / R)1 / 2 ~ 0.8, with rg the Schwarzschild radius. In this way, for an NS of M ~ 1.4 M⊙ and a typical range of equations of state we find that the excess of angular momentum is J ~ (1043 − 1045) erg s. Thus, the vortex-creep luminosity Lvc ≃ (1029 − 1031) | Ω̇-14 | erg s-1, where Ω̇-14 is the angular velocity derivative in units of 10-14 s-2. This is similar to the luminosity inferred from the observation of the MSP J0437-4715.
(9)where ENP is the pinning energy of a vortex on a nucleus, r is the radial coordinate, κ is the quantum of circulation of each vortex, ξ is the vortex coherence length, and RWS is the radius of the Wigner-Seitz cell. In order to calculate this integral, we generate NS structure models for specific masses and linearly interpolate the values of Tables 1 and 2 according to these models. For simplicity, we do not take relativistic effects into account because the corrections involved are minor, i.e. (1 − rg / R)1 / 2 ~ 0.8, with rg the Schwarzschild radius. In this way, for an NS of M ~ 1.4 M⊙ and a typical range of equations of state we find that the excess of angular momentum is J ~ (1043 − 1045) erg s. Thus, the vortex-creep luminosity Lvc ≃ (1029 − 1031) | Ω̇-14 | erg s-1, where Ω̇-14 is the angular velocity derivative in units of 10-14 s-2. This is similar to the luminosity inferred from the observation of the MSP J0437-4715.
2.5. Rotochemical heating
In chemical equilibrium, in an NS composed of neutrons (n), protons (p), and leptons (l: electrons and muons), the chemical potentials satisfy ηnpl ≡ μn − μp − μl = 0. However, if the rotation of the star is slowing down, the centrifugal force is reduced, the central density of the star increases, and the chemical potentials are imbalanced, ηnpl ≠ 0. As the equilibrium composition is altered, the NS will relax to the new chemical equilibrium (via beta and inverse beta decays), releasing energy in the form of neutrinos, which leave the star, and heat, which is later radiated as photons. The evolution of the chemical imbalances is of the form (Fernández & Reisenegger 2005) 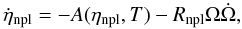 (10)where the function A quantifies the effect of reactions toward restoring chemical equilibrium, and the scalar Rnpl quantifies the departure from equilibrium due to the change in the angular velocity Ω of the star.
(10)where the function A quantifies the effect of reactions toward restoring chemical equilibrium, and the scalar Rnpl quantifies the departure from equilibrium due to the change in the angular velocity Ω of the star.
The luminosity generated by this mechanism is L = Γηnpl, where Γ = Γn → plν̅ − Γpl → nν. Here, Γn → plν̅ is the rate of reactions (integrated over the core) that transform the neutrons to protons and leptons through direct or modified Urca reactions, and Γpl → nν is the rate for the opposite process. In this way, the evolution of the internal temperature with rotochemical heating is given by the solution of the coupled differential Eqs. (1) and (9).
Reisenegger (1995) found that if the angular velocity Ω varies slowly over the time required to cool the star and achieve chemical equilibrium, the star reaches a quasi-steady state, where heating and cooling are balanced. Fernández & Reisenegger (2005) calculated the simultaneous solution of Ṫ = η̇npl = 0 for a typical range of equations of state and found that in an NS with a non-superfluid core and with modified Urca reactions, the photon luminosity in the quasi-steady state depends only on the period and its derivative, 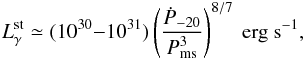 (11)which is close to matching the observation of MSP J0437-4715. Here, Ṗ-20 is the period derivative measured in units of 10-20 and Pms is the period in milliseconds. The characteristic timescale to reach this quasi-steady state is
(11)which is close to matching the observation of MSP J0437-4715. Here, Ṗ-20 is the period derivative measured in units of 10-20 and Pms is the period in milliseconds. The characteristic timescale to reach this quasi-steady state is 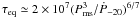 yr. On the other hand, Petrovich & Reisenegger (2010) considered the effects of nucleon superfluidity on rotochemical heating. They found that the chemical imbalances grow up to a value close to the energy gaps, which is higher than in the nonsuperfluid case. Therefore, the surface temperatures predicted with Cooper pairing are higher. For simplicity, we here only consider the non-superfluid case. However, we must not lose sight of the latter result.
yr. On the other hand, Petrovich & Reisenegger (2010) considered the effects of nucleon superfluidity on rotochemical heating. They found that the chemical imbalances grow up to a value close to the energy gaps, which is higher than in the nonsuperfluid case. Therefore, the surface temperatures predicted with Cooper pairing are higher. For simplicity, we here only consider the non-superfluid case. However, we must not lose sight of the latter result.
3. Effects
In order to solve the thermal balance equation, Eq. (1), and generate the evolutionary curves, we use the code of Fernández & Reisenegger (2005). This considers realistic equations state (EOSs), with a conventional NS divided into two regions: an isothermal interior and a thin envelope. In the interior, it considers a core composed of neutrons, protons, electrons, and muons, but ignores the potential Cooper pairing effect. The neutrino emissivity is generated by modified Urca reactions and direct Urca reactions, neglecting any other neutrino emission processes. In order to model the envelope, it uses the relation between internal and surface temperature from the fully accreted envelope model of Potekhin et al. (1997). The rotational evolution is assumed to be due to magnetic dipole radiation, without magnetic field decay.
 |
Fig. 1 Thermal evolution with the vortex creep mechanism. All curves show the interior temperature as a function of time, for stars with mass M = 1.4 M⊙, initial temperature T = 1011 K, and initial period P0 = 1 ms. The magnetic fields B = 108 G and B = 1011 G correspond to MSPs and classical pulsars, respectively. The excess angular momentum used is J = 1043 erg s. The solid lines show the evolution using the A18+ δυ + UIX* EOS, with only modified Urca reactions, and the dashed lines show the evolution using BPAL 22 EOS, with direct Urca reactions. The dotted lines show the evolution with passive cooling for direct and modified Urca reactions. |
3.1. Vortex creep
Figure 1 shows the resulting thermal evolution for the vortex creep mechanism for representative parameters of both classical pulsars and MSPs, with one EOS allowing only for modified Urca reactions (A18+δv+UIX* EOS, Akmal et al. 1998) and another one allowing for direct Urca reactions (BPAL 22, Prakash et al. 1988). As the residual spin-down at old ages is greater in pulsars with weaker magnetic fields, the predicted temperature is higher in the MSPs than in the classical pulsars. At very late times (t > 108 yr), the cooling is dominated by photon emission, which balances the heat generation by vortex friction. Therefore, the evolution of temperature becomes independent of the previous thermal history and the type of Urca reaction, and only depends on the current value of Ω̇, with the photon luminosity 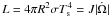 . The rotational evolution by magnetic dipole radiation yields Ω ∝ t − 1 / 2 in the limit Ω ≪ Ω0. Thus, the asymptotic decrease of the surface temperature with time in classical pulsars and MSPs is Ts ∝ t − 3 / 8.
. The rotational evolution by magnetic dipole radiation yields Ω ∝ t − 1 / 2 in the limit Ω ≪ Ω0. Thus, the asymptotic decrease of the surface temperature with time in classical pulsars and MSPs is Ts ∝ t − 3 / 8.
 |
Fig. 2 Thermal evolution with rotochemical heating. All curves correspond to stars with mass M = 1.4 M⊙, A18 + δυ + UIX* EOS (which allows only for modified Urca reactions), initial temperature T = 108 K, and magnetic field B = 108 G. The solid lines show the evolution of the internal temperature T and the chemical imbalance ηnpe, and the dotted line shows the passive cooling. |
 |
Fig. 3 Thermal evolution with rotochemical heating. All curves correspond to stars with mass M = 1.4 M⊙, A18 + δυ + UIX* EOS, initial temperature T = 1011 K, and magnetic field B = 1011 G. The solid and long-dashed lines show the evolution of the temperature and the chemical imbalance with initial periods P0 = 1 ms and P0 = 15 ms, respectively. The dotted line shows the passive cooling. |
3.2. Rotochemical heating
The thermal evolution for MSPs with rotochemical heating and modified Urca reactions is shown in Fig. 2. For this mechanism, the thermal evolution is coupled with the evolution of the chemical imbalances. Because the magnetic fields in MSPs are relatively weak, B ~ 108 G, the chemical imbalances induced by the spin-down grow slowly, causing chemical reactions at high ages, t ≳ 107 yr. An important prediction of this mechanism is that in the MSP regime, the star arrives at a quasi-steady state, where heating and cooling balanced, so the thermal evolution is independent of initial conditions and only depends on the current value of the product ΩΩ̇ (Fernández & Reisenegger 2005). When direct Urca reactions are present, the evolution is qualitatively similar, but the temperatures are strongly reduced, as shown in Sect. 4.
The evolution of classical pulsars is shown in Fig. 3 (see also Reisenegger et al. 2007). As in the previous figure, only modified Urca processes are active. Owing to the relatively strong magnetic fields present in this regime, B ≳ 1011 G, the rotational energy of the star is quickly consumed in the beginning of the thermal evolution by the magnetic dipole radiation. Because of this, high chemical imbalances are built up, proportional to the amount of rotational energy lost. Thus, for faster initial rotation, the chemical imbalance at later times will be higher. At ages above ~ 108 yr, the right-hand side of Eq. (9) is dominated by the reactions restoring the chemical equilibrium. When only modified Urca reactions are present and η ≫ kT, the chemical imbalance evolves according to η̇ ∝ − Γ ∝ − η7 (see Fernández & Reisenegger 2005), yielding η ∝ t − 1 / 6. Because in the last epoch of the thermal evolution the cooling of the star is caused mainly by photon emission, the luminosity is 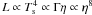 . Thus, the surface temperature decreases with age as Ts ∝ t − 1 / 3, only slightly more slowly than with vortex creep.
. Thus, the surface temperature decreases with age as Ts ∝ t − 1 / 3, only slightly more slowly than with vortex creep.
4. Comparison with observations
In order to identify the thermal emission at T ~ 105 K from the whole NS surface, it is necessary to obtain observations in the optical and specially in the ultraviolet range (Kargaltsev et al. 2004; Zavlin & Pavlov 2004). Thus, to confront the theoretical cooling models of old NSs with observations, we select the best and most restrictive observations in these bands, of seven very old pulsars: three MSPs and four classical pulsars. Among the MSPs, only J0437-4715 has detected thermal emission (Kargaltsev et al. 2004), and J2124-3358 (Mignani & Becker 2004) and J0030+0451 (Koptsevich et al. 2003) have good upper limits on their temperatures. The four selected classical pulsars, B1929+10 (Becker et al. 2006), B0950+08 (Zavlin & Pavlov 2004; Zharikov et al. 2004), B1133+16 (Zharikov et al. 2008), and J0108-1431 (Mignani et al. 2003) only have upper limits on the thermal emission from the whole NS surface.
The upper panel of Fig. 4 shows the thermal evolution of MSPs including vortex creep and rotochemical heating with modified Urca reactions. For the vortex creep mechanism the parameter J is highly uncertain, so we adjust it to the lowest value that is consistent with the thermal emission from MSP J0437-4715. This constrains it to J ≥ 5.5 × 1043 erg s if vortex creep is postulated as the main heating mechanism for this pulsar. For rotochemical heating, the surface temperature of this MSP can be quite precisely predicted, considering its mass M = 1.76 M⊙ (Verbiest et al. 2008) and an interior model given by the A18 + δυ + UIX* EOS. This prediction is 1.7σ below the observation of Kargaltsev et al. (2004).
 |
Fig. 4 Evolution of the surface temperature for a neutron star with vortex creep (long-dashed lines), rotochemical heating (solid lines), and passive cooling (dotted lines). All curves correspond to stars with the A18 + δυ + UIX* EOS and modified Urca reactions. The error bar shows the temperature measured for the MSP J0437-4715 and the arrows show the upper limits on the thermal emission for specific pulsars. Top panel: the curves correspond to MSPs with mass M = 1.76 M⊙, magnetic field B = 2.8 × 108 G, and initial temperature T = 108 K. Bottom panel: the curves correspond to classical pulsars with mass M = 1.4 M⊙, magnetic field B = 2.5 × 1011 G, and initial temperature T = 1011 K. The abscissa corresponds to the spin-down time (ts = Ω / 2 | Ω̇ | ). The initial periods for rotochemical heating are labeled on each curve. |
 |
Fig. 5 Evolution of the surface temperature for a neutron star with vortex creep (long-dashed lines), rotochemical heating (solid lines), and passive cooling (dotted lines). All curves correspond to stars with the BPAL 32 EOS and direct Urca reactions. The error bar shows the temperature measured for the MSP J0437-4715 and the arrows show the upper limits on the thermal emission for specific pulsars. Top panel: the curves correspond to MSPs with mass M = 1.76 M⊙, magnetic field B = 2.8 × 108 G, and initial temperature T = 108 K. Bottom panel: the evolutionary curves correspond to stars with mass M = 1.4 M⊙, magnetic field B = 2.5 × 1011 G, and initial temperature T = 1011 K. The abscissa corresponds to the spin-down time (ts = Ω / 2 | Ω̇ | ). The initial period for rotochemical heating is P0 = 1 ms. |
Similarly, the bottom panel shows the thermal evolution of the classical pulsars. For the vortex creep mechanism, we assumed that the parameter J is universal. Thus, to solve the thermal evolution in this regime, we used the previous value of J imposed by the MSP J0437-4715, resulting in a “phenomenological” temperature prediction slightly above the constraints for the pulsars B1929+10 and B0950+08. On the other hand, as we saw in Sect. 3.2, the evolution with rotochemical heating depends on the initial period of rotation, P0, for NSs with relatively high magnetic fields. Because of this, rotochemical heating can easily accommodate substantially lower temperatures if more restrictive observations of classical pulsars are available. The evolution at late times (t > 108 yr) is remarkably similar for both mechanisms. We showed that the relation between surface temperature and age is Ts ∝ t − 3 / 8 for vortex creep (Sect. 3.1), very slightly steeper than the relation Ts ∝ t − 1 / 3 for rotochemical heating with modified Urca reactions (Sect. 3.2) in the latter stage of the thermal evolution.
Figure 5 shows the thermal evolution considering the fast direct Urca processes. For the vortex creep mechanism, we used the same excess of angular momentum J as in the previous evolutionary curves, fixed to be consistent with the observed temperature of MSP J0437-4715. Because for ages ≳ 108 yr this mechanism does not depend on the Urca process type, the temperatures of the MSPs (upper panel) are the same as with modified Urca reactions. However, in classical pulsars (bottom panel) the thermal evolution is sensitive to the direct Urca processes and generates a predicted temperature slightly lower than the limit for PSR B0950+08. In this way, a more sensitive observation of this pulsar could discard vortex creep as the main source of the thermal emission detected from the MSP J0437-4715. On the contrary, the temperatures generated by rotochemical heating, both for classical pulsars and MSPs, are strongly reduced if direct Urca processes are considered. The temperature measured in J0437-4715 requires that the neutrino emission is produced only by modified Urca reactions (unless substantial Cooper pairing gaps are present, Petrovich & Reisenegger 2010) if rotochemical heating is the main source of heat.
Finally, we compare the excess angular momentum, J, that we estimated from the pinning energies of Tables 1 and 2 with the observations. In order to do this, we numerically integrated Eq. (8) over the inner crust of an NS with canonical mass M = 1.4 M⊙ and the A18+δv+UIX* EOS. In this way, with the pinning energy estimated by Donati & Pizzochero (2004), we obtain J = 3.8 × 1044 erg s for the Argonne interaction and J = 5.9 × 1044 erg s for the Gogny interaction. Similarly, but with the pinning energy estimated by Avogadro et al. (2008), J = 1.2 × 1043 erg s with the SLy4 interaction, and J = 6.8 × 1043 erg s with the Skm* interaction. Comparing these results with the value J = 5.5 × 1043 erg s, which is marginally compatible with both the observed temperatures of MSP J0437-4715 and the upper limits for the old classical pulsars, we find that the semi-classical model of Donati & Pizzochero (2004) overestimates the value of the excess angular mometum J, while the quantum approach of Avogadro et al. (2008), with the SLy4 interaction, roughly agrees with the value inferred from observations.
5. Conclusions
We studied five heating mechanisms that can be operating in old neutron stars: magnetic field decay, dark matter accretion, crust cracking, vortex creep, and rotochemical heating, and compared them with pulsar observations.
We found that magnetic field decay, dark matter accretion, and crust cracking cannot produce detectable heating in old pulsars. Owing to the high yield strain angle (Horowitz & Kadau 2009), the crust cracking mechanism does not operate in classical pulsars, and probably only operates in MSPs. The vortex creep and rotochemical heating can be important both for classical pulsars and MSPs.
In the evolutionary curves with vortex creep, and with the excess angular momentum, J, set to the lowest temperature compatible with the thermal emission detected from MSP J0437-4715, the predicted temperature turns out to be very near the observational upper limits for the classical pulsars B1929+10 and B1133+16. Likewise, rotochemical heating with modified Urca reactions and no Cooper pairing is only 1.7σ below the temperature measured in the MSP J0437-4715. However, the temperature prediction of rotochemical heating can be raised if a superfluid core is considered in the model.
The prediction of pinning energies in the inner crust of NSs via the semi-classical model for the vortex-nuclei interaction (Donati & Pizzochero 2004) overestimates the temperatures of B0950+08 and B1929+10. The recent estimations of pinning energies via a quantum approach (Avogadro et al. 2008) are consistent with the observations of classical pulsars and MSPs. Finally, more stringent constraints on the temperature of some classical pulsars such as B0950+08 could rule out the vortex creep mechanism as the main source of the thermal emission detected in the MSP J0437-4715.
These values might be reduced if a substantial fraction of the protons is the star are superconducting (Easson & Pethick 1977).
Acknowledgments
We thank Sebastián Reyes, Ricardo Ramírez, and Miguel Kiwi for discussions and comments that benefited this paper, and Rodrigo Fernández for letting us use his rotochemical heating code. This work was supported by Proyecto Regular FONDECYT 1060644, the FONDAP Center of Astrophysics (15010003), ALMA-CONICYT project 31070001, Proyecto Basal PFB-06/2007, Gemini-CONICYT project 32080004, and Proyecto Límite VRAID No 15/2010.
References
- Alpar, M. A., Anderson, P. W., Pines, D., & Shaham, J. 1984, ApJ, 276, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Akmal, A., Pandharipande, V. R., & Ravenhall, D. G. 1998, Phys. Rev. C, 58, 1804 [NASA ADS] [CrossRef] [Google Scholar]
- Avogadro, P., Barranco, F., Broglia, R. A., & Vigezzi, E. 2008, Nucl. Phys. A, 811, 378 [NASA ADS] [CrossRef] [Google Scholar]
- Baym, G., & Pines, D. 1971, Ann. Phys., 66, 816 [NASA ADS] [CrossRef] [Google Scholar]
- Becker, W., Kramer, M., Jessner, A., et al. 2006, ApJ, 645, 1421 [NASA ADS] [CrossRef] [Google Scholar]
- Cheng, K. S., Chau, W. Y., Zhang, J. L., & Chau, H. F. 1992, ApJ, 396, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Cutler, C., Ushomirsky, G., & Link, B. 2003, ApJ, 588, 975 [NASA ADS] [CrossRef] [Google Scholar]
- de Lavallaz, A., & Fairbairn, M. 2010, Phys. Rev. D, 81, 123521 [NASA ADS] [CrossRef] [Google Scholar]
- Deller, A., Verbiest, J., Tingay, S., & Bailes, M. 2008, ApJ, 685, L67 [NASA ADS] [CrossRef] [Google Scholar]
- Donati, P., & Pizzochero, P. 2004, Nucl. Phys. A, 742, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Easson I., & Pethick, C. 1977, Phys. Rev. D, 16, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Fernández, R., & Reisenegger, A. 2005, ApJ, 625, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P., & Reisenegger, A. 1992, ApJ, 395, 250 [NASA ADS] [CrossRef] [Google Scholar]
- Hannestad, S., Keränen, P., & Sannino, F. 2002, Phys. Rev. D, 66, 5002 [NASA ADS] [Google Scholar]
- Horowitz, C. J., & Kadau, K. 2009, Phys. Rev. Lett., 102, 1102 [Google Scholar]
- Jofré, P., Reisenegger, A., & Fernández, R. 2006, Phys. Rev. Lett., 97, 131102 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kargaltsev, O., Pavlov, G. G., & Romani, R. 2004, ApJ, 602, 327 [NASA ADS] [CrossRef] [Google Scholar]
- Koptsevich, A. B., Lundqvist, P., Serafimovich, N. I., Shibanov, Yu. A., & Sollerman, J. 2003, A&A, 400, 265 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kouvaris, C., & Tinyakov, P. 2010, Phys. Rev. D, 82, 063531 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, M. B., & Link, B. 1999, ApJ, 521, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Mignani, R. P., & Becker, W. 2004, AdSpR, 33, 616 [NASA ADS] [Google Scholar]
- Mignani, R. P., Manchester, R. N., & Pavlov, G. G. 2003, ApJ, 582, 978 [NASA ADS] [CrossRef] [Google Scholar]
- Prakash, M., Ainsworth, T. L., & Lattimer J. M. 1988, Phys. Rev. Lett., 61, 2518 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Petrovich, C., & Reisenegger, A. 2010, A&A, 521, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pons, J., Link B., Miralles, J., & Geppert U. 2007, Phys. Rev. Lett., 98, 071101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Potekhin, A. Y., Chabrier, G., & Yakovlev, D. G. 1997, A&A, 323, 415 [NASA ADS] [Google Scholar]
- Reisenegger, A. 1995, ApJ, 442, 749 [NASA ADS] [CrossRef] [Google Scholar]
- Reisenegger, A. 1997, ApJ, 485, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Reisenegger, A., Fernández, R., & Jofré, P. 2007, Ap&SS, 308, 413 [NASA ADS] [CrossRef] [Google Scholar]
- Schaab, Ch., Sedrakian, A., Weber, F., & Weigel, M. K. 1999, A&A, 346, 465 [NASA ADS] [Google Scholar]
- Shibazaki, N., & Lamb, F. K. 1989, ApJ, 346, 808 [NASA ADS] [CrossRef] [Google Scholar]
- Smoluchowski, R., & Welch, D. 1970, Phys. Rev. Lett., 24, 1191 [NASA ADS] [CrossRef] [Google Scholar]
- Thompson, C., & Duncan, R. C. 1996, ApJ, 473, 322 [NASA ADS] [CrossRef] [Google Scholar]
- van Straten, W., Bailes, M., Britton, M., et al. 2001, Nature, 412, 158 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Verbiest, J. P. W., Bailes, M., van Straten, W., et al. 2008, ApJ, 679, 675 [NASA ADS] [CrossRef] [Google Scholar]
- Yakovlev, D. G., & Pethick, C. J. 2004, ARA&A, 42, 169 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Zavlin, V. E., & Pavlov, G. G. 2004, ApJ, 616, 452 [NASA ADS] [CrossRef] [Google Scholar]
- Zdunik, J. L., Bejger, M., & Haensel, P. 2008, A&A, 491, 489 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zharikov, S. V., Shibanov, Yu. A., Mennickent, R. E., et al. 2004, A&A, 417, 1017 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zharikov, S. V., Shibanov, Yu. A., Mennickent, R. E., & Komarova, V. N. 2008, A&A, 479, 793 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Vortex-nuclei interaction parameters in the semi-classical model (Donati & Pizzochero 2004), with the Argonne potential(a) and Gogny potential(b).
Vortex-nuclei interaction parameters in the quantum approach (Avogadro et al. 2008), with the SLy4 potential(a) and Skm* potential(b).
All Figures
 |
Fig. 1 Thermal evolution with the vortex creep mechanism. All curves show the interior temperature as a function of time, for stars with mass M = 1.4 M⊙, initial temperature T = 1011 K, and initial period P0 = 1 ms. The magnetic fields B = 108 G and B = 1011 G correspond to MSPs and classical pulsars, respectively. The excess angular momentum used is J = 1043 erg s. The solid lines show the evolution using the A18+ δυ + UIX* EOS, with only modified Urca reactions, and the dashed lines show the evolution using BPAL 22 EOS, with direct Urca reactions. The dotted lines show the evolution with passive cooling for direct and modified Urca reactions. |
| In the text | |
 |
Fig. 2 Thermal evolution with rotochemical heating. All curves correspond to stars with mass M = 1.4 M⊙, A18 + δυ + UIX* EOS (which allows only for modified Urca reactions), initial temperature T = 108 K, and magnetic field B = 108 G. The solid lines show the evolution of the internal temperature T and the chemical imbalance ηnpe, and the dotted line shows the passive cooling. |
| In the text | |
 |
Fig. 3 Thermal evolution with rotochemical heating. All curves correspond to stars with mass M = 1.4 M⊙, A18 + δυ + UIX* EOS, initial temperature T = 1011 K, and magnetic field B = 1011 G. The solid and long-dashed lines show the evolution of the temperature and the chemical imbalance with initial periods P0 = 1 ms and P0 = 15 ms, respectively. The dotted line shows the passive cooling. |
| In the text | |
 |
Fig. 4 Evolution of the surface temperature for a neutron star with vortex creep (long-dashed lines), rotochemical heating (solid lines), and passive cooling (dotted lines). All curves correspond to stars with the A18 + δυ + UIX* EOS and modified Urca reactions. The error bar shows the temperature measured for the MSP J0437-4715 and the arrows show the upper limits on the thermal emission for specific pulsars. Top panel: the curves correspond to MSPs with mass M = 1.76 M⊙, magnetic field B = 2.8 × 108 G, and initial temperature T = 108 K. Bottom panel: the curves correspond to classical pulsars with mass M = 1.4 M⊙, magnetic field B = 2.5 × 1011 G, and initial temperature T = 1011 K. The abscissa corresponds to the spin-down time (ts = Ω / 2 | Ω̇ | ). The initial periods for rotochemical heating are labeled on each curve. |
| In the text | |
 |
Fig. 5 Evolution of the surface temperature for a neutron star with vortex creep (long-dashed lines), rotochemical heating (solid lines), and passive cooling (dotted lines). All curves correspond to stars with the BPAL 32 EOS and direct Urca reactions. The error bar shows the temperature measured for the MSP J0437-4715 and the arrows show the upper limits on the thermal emission for specific pulsars. Top panel: the curves correspond to MSPs with mass M = 1.76 M⊙, magnetic field B = 2.8 × 108 G, and initial temperature T = 108 K. Bottom panel: the evolutionary curves correspond to stars with mass M = 1.4 M⊙, magnetic field B = 2.5 × 1011 G, and initial temperature T = 1011 K. The abscissa corresponds to the spin-down time (ts = Ω / 2 | Ω̇ | ). The initial period for rotochemical heating is P0 = 1 ms. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


