EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 521 (October 2010) A&A, 521 (2010) A64 Full HTML
Free Access
Issue
A&A
Volume 521, October 2010
Article Number A64
Number of page(s) 14
Section Cosmology (including clusters of galaxies)
DOI https://doi.org/10.1051/0004-6361/201015208
Published online 21 October 2010
A&A 521, A64 (2010)

The evolution of cool-core clusters

J. S. Santos1 - P. Tozzi1 - P. Rosati2 - H. Böhringer3

1 - INAF, Osservatorio Astronomico di Trieste, via G.B. Tiepolo 11, 34131 Trieste, Italy
2 - European Southern Observatory, Karl-Schwarzchild Strasse 2, 85748 Garching, Germany
3 - Max-Planck-Institut für extraterrestrische Physik, Giessenbachstraße, 85748 Garching, Germany

Received 14 June 2010 / Accepted 4 August 2010

Abstract
Context. Cool-core clusters are characterized by strong surface brightness peaks in the X-ray emission from the Intra Cluster Medium (ICM). This phenomenon is associated with complex physics in the ICM and has been a subject of intense debate and investigation in recent years. The evolution of cool-cores is still poorly constrained because of the small sample statistics and the observational challenge of analysing high redshift clusters.
Aims. In order to quantify the evolution in the cool-core cluster population, we robustly measure the cool-core strength in a local, representative cluster sample, and in the largest sample of high-redshift clusters available to date.
Methods. We use high-resolution Chandra data of three representative cluster samples spanning different redshift ranges: (i) the low redshift sample from the 400 Square degree (SD) survey with median $\langle z \rangle = 0.08$; (ii) the high redshift sample from the 400 SD Survey with median $\langle z \rangle = 0.59$; and (iii) 15 clusters drawn from the Rosat Distant Cluster Survey and the Wide Angle Rosat Pointed Survey, with median $\langle z \rangle = 0.83$. Our analysis is based on the measurement of the surface brightness concentration, $c_{\rm SB}$ (Santos et al. 2008, A&A, 483, 35), which allows us to characterize the cool-core strength in low signal-to-noise data. We also obtain gas density profiles to derive cluster central cooling times and entropy. In addition to the X-ray analysis, we search for radio counterparts associated with the cluster cores.
Results. We find a statistically significant difference in the $c_{\rm SB}$ distributions of the two high-z samples, pointing towards a lack of concentrated clusters in the 400 SD high-z sample. Taking this into account, we confirm a negative evolution in the fraction of cool-core clusters with redshift, in particular for very strong cool-cores. This result is validated by the central entropy and central cooling time, which show strong anti-correlations with $c_{\rm SB}$. However, the amount of evolution is significantly smaller than previously claimed, leaving room for a large population of well formed cool-cores at $z\sim1$. Finally, we explore the potential of the proposed X-ray mission Wide Field X-ray Telescope to detect and quantify cool-cores up to z = 1.5.

Key words: X-rays: galaxies: clusters - galaxies: clusters: interacluster medium, galaxies: high-redshift

1 Introduction

X-ray observations show that the majority of local clusters have a prominent central surface brightness peak. In addition, the inferred cooling time of the intracluster medium in the core region is much shorter than the dynamical time of the cluster, implying the presence of a cooling flow (Fabian et al. 1994). However, the minimum temperature in the center is only a factor of $\sim$3 lower than the ambient temperature, therefore the gas does not appear to cool massively to low temperatures. The properties and the formation mechanism of these cool-cores (CC) are an open problem which forces one to consider complex non-gravitational physical processes in order to provide smoothly distributed heating on scales of about 100 kpc. A successful model is expected to include phenomena such as radiative cooling, heating by a central radio source, thermal conduction or other forms of feedback (see Peterson & Fabian 2006, and references therein).

The impact of cool-cores on the local cluster population has been extensively studied for over a decade (Peres et al. 1998). Occasionally, the cool-core phenomenon is described as a bimodal feature, with a clear separation between cool-cores and non cool-core clusters on the basis of the central value of the ICM entropy (e.g. Sanderson et al. 2009; Cavagnolo et al. 2009). Concurrently though, several works have distinguished between three regimes of cooling, with an intermediate category bridging the extremes (Leccardi et al. 2010; Bauer et al. 2005; Morandi & Ettori 2007). Contrary to the bimodal scenario, this approach suggests a gradual transition from the non cool-core to the cool-core status, with profound implications on the time scale and thus the nature of the heating mechanism.

A crucial aspect here is a proper definition of cool-core, since a variety of methods or cooling estimators have been proposed to classify and quantify cool cores in local clusters, producing results that occasionally lead to different interpretations. A comprehensive review and comparison of 16 different cooling estimators has been recently published by Hudson et al. (2010), using the local sample HIFLUCGS (Reiprich & Böhringer 2002). In this work, the central cooling time was selected as the most efficient probe to quantify cool-cores.

The quality of the cooling estimator is an important issue to consider because it depends significantly on the signal-to-noise ratio of the X-ray data, and therefore changes considerably for high-redshift clusters with respect to local ones. This aspect is particularly relevant since the evolution of cool-core clusters is a major piece of information in order to constrain the cool-core physics.

X-ray observations have established that cool-cores dominate the local cluster population, with an abundance of 50 to 70% (e.g. Chen et al. 2007; Dunn & Fabian 2008; Hudson et al. 2010). The evolution of cool-cores has been measured up to redshift 0.4. Using the high-z end of the BCS sample Bauer et al. (2005) concluded that the fraction of cool-cores does not significantly evolve up to $z \thicksim 0.4$. Their results, based on spatially resolved spectroscopy, showed that clusters in this redshift range have the same temperature decrement (about one-third), as the nearby CC's, and in addition, their central cooling times are similar.

Table 1:   400 SD low redshift sample.

At present, about twenty X-ray clusters with z>1 have been confirmed. While most of them were detected in ROSAT surveys, a significant fraction of serendipitous high-z clusters has been added in recent years thanks to the XMM-Newton archive. Nevertheless, the largest distant cluster samples with sufficiently deep follow-up observations are still the ones from ROSAT. Therefore, the study of the presence of cool-cores at redshift greater than 0.5 is plagued by low statistics, and currently is limited to two works. Using the 400 Square Degree Survey (hereafter 400 SD, Burenin et al. 2007) which reaches z=0.9, Vikhlinin et al. (2007) concluded, on the basis of a cuspiness parameter defined as the logarithmic derivative of the density profile, that there is a lack of cool-core clusters at 0.5 < z < 0.9, with respect to the local cluster population. They propose that such a strong negative evolution may be related to the higher cluster merging rate expected at these redshifts.

In Santos et al. (2008), we adopted a simple diagnostic based on the concentration of the surface brightness (which strongly anti-correlates with the central cooling time), and measured the fraction of cool-cores out to the current redshift limit ( $z \sim 1.4$) using mostly the RDCS sample. At variance with previous results, we found a significant fraction of what we term moderate cool-cores. To clarify these results we need a more detailed investigation as we propose in this Paper.

We present a comprehensive analysis of the characterization and abundance of cool-cores across the entire cluster population, out to the current highest redshift where clusters have been detected in the X-ray band. To this aim we analysed 3 representative samples corresponding to three different redshift ranges, using only Chandra data. The high-resolution and low background of Chandra are the key features that distinguish it as the only X-ray observatory capable of unveiling the small cores of distant clusters. Our analysis, based on the observed surface brightness and a simple concentration parameter (Santos et al. 2008), is uniform and robust over the entire explored range of redshifts. This investigation enables us to assess the impact of detection bias in the high-z cluster samples, and to measure on solid ground the evolution of cool-core cluster distribution. Furthermore, we investigate the presence of radio sources associated with the cluster cores by exploring the NVSS archive. Finally, we assess the potential of the next generation X-ray survey mission Wide Field X-ray Telescope (WFXT, Giacconi et al. 2009) in measuring the cool-core evolution.

The paper is organized as follows: in Sects. 2 and 3 we describe the low and high redshift samples, respectively. In Sect. 4 we describe the data reduction and analysis, devoting Sect. 5 to a careful investigation of the surface brightness concentration parameter. In Sect. 6 we perform surface brightness fits to the data using the well-known $\beta $-models. The entropy profiles and a histogram of K20 are discussed in Sect. 7, and the cooling time distribution follows in Sect. 8. In Sect. 9 we investigate the presence of radio sources in cool-core and non cool-core clusters. Section 10 is devoted to the future perspective with a next-generation X-ray survey mission. Our conclusions are summarized in Sect. 11. The cosmological parameters used throughout the paper are: H0 = 70 km s-1/Mpc, $\Omega_{\Lambda} = 0.7$ and $\Omega_{\rm m} = 0.3$.

2 The low redshift sample

The measured fraction of local cool-core clusters ranges from 70-90% (Peres et al. 1998, from the B55 sample), to 49% (Chen et al. 2007, from the HIFLUGCS sample), 45% (Sanderson et al. 2009, from a subsample of HIFLUGCS), and more recently 44-72% (Hudson et al. 2010, from the HIFLUGCS sample). The differences in these fractions are mostly due to different definitions of cool-core. To date, Hudson et al. (2010) is the only exhaustive work that explores the definition of cool-core and compares the currently used methods to quantify it. After examining 16 different cool-core diagnostics, they conclude that the central cooling time is the best parameter for low redshift clusters with high quality data, and the surface brightness concentration, $c_{\rm SB}$, presented in Santos et al. (2008), is chosen as the best parameter for distant clusters. These results reinforce our strategy to apply the same concentration diagnostics to local and distant cluster samples, and compare directly the measured distributions, avoiding the use of a sharp threshold in the definition of the cool-core strength.

The local cluster sample used in this work is drawn form the catalog of the 400 Square Degree (SD) Survey (Burenin et al. 2007), an X-ray survey which detected 266 confirmed galaxy clusters, groups or individual elliptical galaxies out to $z\sim1$ using archival ROSAT PSPC observations. The sample is complete down to a flux limit of $1.4 \times 10^{-13}$ erg s-1 cm-2. We extract a subsample of clusters observed with Chandra with z > 0.05, in order to be able to sample the surface brightness profiles out to a radius of 400 kpc within the field of view. Hence, our local sample spans the redshift range [0.05-0.217] (with a median redshift $\langle z \rangle = 0.08$) and includes 28 clusters (see Table 1 and Fig. 1). The well-known clusters Hydra-A and S1101, which show a very strong cool-core, are imaged only with ACIS-S and therefore we do not use them in our analysis.

3 The distant cluster samples

Beyond redshift 0.5 there are only three X-ray complete cluster samples, all selected from ROSAT PSPC pointed observations. They are: (i) the 400 SD (Burenin et al. 2007) high-z sample which include all clusters from the 400 SD catalog with $z\ge 0.5$; (ii) the Rosat Deep Cluster Survey (RDCS, Rosati et al. 1998); and (iii) the Wide Angle ROSAT Pointed Survey (WARPS, Jones et al. 1998).

These samples are still limited by small number statistics. Furthermore, observations of distant clusters undergo a strong surface brightness dimming $\propto $ (1+z)-4 and have a small angular size, thus the study of their central regions requires the high-resolution provided only by Chandra. Its excellent spatial resolution is mandatory to measure the central surface brightness of high redshift clusters, to the point that even the use of XMM-Newton, with a much larger collecting area but with a poorer resolution, would not be suitable for our study. While the distant 400 SD sample has been fully observed with Chandra, the RDCS and WARPS samples have been only partially observed with a Chandra follow up. For this reason, we merge them into the RDCS+WARPS sample. We point out that the RDCS+WARPS samples reach lower fluxes in comparison with the 400 SD sample, and therefore include the highest redshift clusters.

Current X-ray surveys from serendipitous pointings, such as the XMM-LSS (Pierre et al. 2006), the XMM-Newton Cluster Survey (Sahlén et al. 2009), the XMM-Newton Distant Cluster Project (XDCP[*], Böhringer et al. 2005), and the Swift X-ray Cluster Survey (Moretti et al. 2010, in prep.) will add new $z\sim1$ X-ray clusters in the next years. However, new detections will need an appropriate Chandra follow-up to have a better spatial resolution (in case of clusters detected with other instruments) or a better signal-to-noise ratio (in case of cluster discovered in shallow Chandra images). Another fundamental aspect is that in order to derive meaningful constraints on the evolution of high-z clusters, we must use samples with a well defined selection function. The three high redshift samples used in this work are consistent with each other in terms of number counts (see Burenin et al. 2007), hence they do not have evident bias in their selection function.

\begin{figure} \par\includegraphics[width=8cm,angle=0,clip]{15208fig1.ps} \vspace*{-2.5mm} \end{figure} Figure 1:

Low-z cluster sample drawn from the 400 SD survey. Images are normalized by the exposure maps and smoothed with a gaussian kernel of 3 pixel. The images have a size of $8 \times 8$ arcmin and are ordered with increasing redshift. Physical sizes of the individual images are shown in kpc at the bottom of the images.

Open with DEXTER

3.1 The 400 SD high-z sample: 0.5 < z < 0.9

This sample (see Table 2, Fig. 2) includes 20 clusters with 0.5 < z < 0.9. This is a subsample of the list of clusters used in Vikhlinin et al. (2009b) to constrain cosmological parameters. We opted not to use the same sample (starting at z = 0.35) to avoid evolutionary effects within the sample, and in order to have an average redshift comparable to that of the RDCS+WARPS sample. All clusters have been observed with Chandra with an exposure time long enough to gather at least 2000 net counts for each cluster. Therefore the quality of these images is suitable for our study.

Table 2:   400 SD high z sample.

3.2 The RDCS+WARPS sample: 0.6 < z < 1.3

\begin{figure} \par\includegraphics[width=9cm,angle=0,clip]{fig2.eps} \end{figure} Figure 2:

400 SD high-z sample. Images are normalized by the exposure maps and smoothed with a gaussian kernel of 3 pixel. The images have a size of $4 \times 4$ arcmin and are ordered with increasing redshift (from top left to bottom right).

Open with DEXTER

The RDCS has provided a deep, large area, X-ray selected cluster sample, with 115 spectroscopically-confirmed X-ray clusters of galaxies at $S > 3 \times 10^{-14}$ erg s-1 cm2 in the soft-band, selected from an area of 50 deg2, in a homogeneous and objective manner via a serendipitous search in ROSAT PSPC deep pointings. A deeper subsample with $S > 1 \times 10^{14}$ erg s-1 cm2 is defined over a more limited area of 5 deg2. To date, this subsample has the greatest number of spectroscopically identified distant clusters, with 11 at z > 0.6 for $S > 3 \times 10^{-14}$ erg s-1 cm2, and 17 for $S > 1 \times 10^{-14}$ erg s-1 cm2.

The WARPS is an X-ray selected survey for high redshift galaxy clusters based on serendipitous detections in targeted ROSAT PSPC observations. The survey covers an area of 71 deg2 and contains a complete sample of 129 clusters with a flux limit of $S \sim 6.5 \times 10^{-14}$ erg s-1 cm2.

The merged sample (see Table 3, Fig. 3) includes all clusters from the RDCS with redshift greater than 0.6 (10 out of 15 objects) observed with Chandra, in addition to 7 (out of 12) WARPS clusters with similar data. There is an overlap of 2 objects between the two samples (RDCS J0542-4100, WARP J0152.7-1357N), hence the combined sample has a total of 15 clusters. We note that four clusters are common to the RDCS+WARPS and the 400 SD high-z: WARP J1120.1+4318, RDCS J0542-4100, WARP J0152.7-1357N and WARP J1226.9+3332.

Table 3:   RDCS+WARPS sample.

4 Data reduction and spectral analysis

All data was taken from the public Chandra archive. We performed a standard data reduction starting from the level = 1 event files, using the CIAO 4.1 software package, with a recent version of the Calibration Database (CALDB 4.2). For observations taken in the VFAINT mode we ran the task acis_process_events to flag background events that are most likely associated with cosmic rays and distinguish them from real X-ray events. With this procedure, the ACIS particle background can be significantly reduced compared to the standard grade selection. We also apply the CTI correction to the observations taken when the temperature of the Focal Plane was 153 K. This procedure allows to recover the original spectral resolution partially lost because of the CTI. The correction applies only to ACIS-I chips, since the ACIS-S3 did not suffer from radiation damage. The data is filtered to include only the standard event grades 0, 2, 3, 4 and 6. We checked visually for hot columns left after the standard reduction. We identify the flickering pixels as the pixels with more than two events contiguous in time, where a single time interval was set to 3.3 s. For exposures taken in VFAINT mode, there are practically no flickering pixels left after filtering out bad events. We finally filter time intervals with high background by performing a 3$\sigma$ clipping of the background level using the script analyse_ltcrv. The removed time intervals always amount to less than 5% of the nominal exposure time for ACIS-I chips. We remark that our spectral analysis is not affected by any residual flare, since we are always able to compute the background from source-free regions around the clusters from the same observation (see below), thus taking into account any possible spectral distortion of the background itself induced by the flares.

\begin{figure} \par\includegraphics[width=9cm,angle=0]{15208fig3.ps} \end{figure} Figure 3:

RDCS+WARPS sample. Images are normalized by the exposure maps and smoothed with a gaussian kernel of 3 pixel. The individual images have a size of $4' \times 4'$ and are ordered with increasing redshift (from top left to bottom right).

Open with DEXTER

For the clusters in the distant samples, we perform a simple spectral analysis extracting the spectrum of each source from a circular region with radius $R_{\rm ext} = 40$ $^{\prime\prime}$ centered around the X-ray centroid. The background is always obtained from empty regions of the chip in which the source is located. This is possible since all the distant clusters have an extension of less than 3 arcmin (corresponding to a range in physical size of 1100-1500 kpc), as opposed to the 8 arcmin size of the ACIS-I/-S chips. The background file is scaled to the source file by the ratio of the geometrical area. In principle, the background regions may partially overlap with the outer virialized regions of the clusters. However, the cluster emission from these regions is negligible with respect to the instrumental background, and does not affect our results. Our background subtraction procedure, on the other hand, has the advantage of providing the best estimate of the background for that specific observation. The response matrices and the ancillary response matrices of each spectrum are computed respectively with mkacisrmf and mkwarf, for the same regions from which the spectra are extracted.

The spectra are analysed with XSPEC v12.5 (Arnaud et al. 1996) and fitted with a single-temperature mekal model (Kaastra 1992; Liedahl et al. 1995) using the solar abundance of Grevesse & Sauval (1998). The fits are performed over the energy range 0.5-8.0 keV. The free parameters in our spectral fits are temperature, metallicity and normalization. Local absorption is fixed to the Galactic neutral hydrogen column density ($N_{\rm H}$) taken from Wilms et al. (2000). We used Cash statistics applied to the source plus background, which is preferable for low S/N spectra (Nousek & Shue 1989). Redshifts are known from the literature for all the sources. The X-ray luminosity is computed in the rest-frame soft-band after extrapolating the surface brightness up to 1 Mpc (see Sect. 6). Best-fit temperatures and luminosities as shown in Tables 2 and 3. We also attempted to detect temperature gradients by dividing the cluster emission into an inner and an outer region, roughly with the same number of net counts. However, the difference between the two best fit values are generally much smaller than the one sigma error bars, hampering any meaningful conclusion on the presence of gradients in the high-redshift sample. We ascribe this result to the systematic bias towards higher temperatures when the signal-to-noise ratio is degraded in thermal spectra (see Leccardi & Molendi 2007). This effect tends to cancel the temperature gradients expected in cool-core clusters, making it impossible to characterize high redshift cool-cores on the basis of a spectral analysis.

For the local sample, a spatially resolved spectral analysis is in principle possible, given the much larger signal-to-noise. However, for simplicity we rely on the temperature and luminosity values measured by Cavagnolo et al. (2009) and Vikhlinin et al. (2009a) (see Table 1).

5 Surface brightness concentration, c$_{\sf SB}$

The simplest observational signature of the presence of a cool-core is a central spike in the surface brightness profile. This is also the only possible diagnostic we can apply to high redshift clusters given the difficulty in performing spectral analysis to detect the temperature decrease in the core region. There are two ways to evaluate the central spike: fitting a surface brightness profile and measuring the inner slope, or measuring the integrated emission within a given radius. The first method requires high signal-to-noise and suffers from systematics due to the choice of the fitting model. The second approach, which relies on integrated quantities, has the great advantage to be robust and minimizes the noise.

In Santos et al. (2008) we defined the phenomenological parameter $c_{\rm SB}$ that quantifies the excess emission in a cluster core by measuring the ratio of the surface brightness within a radius of 40 kpc with respect to the SB within a radius of 400 kpc: $c_{\rm SB} = {\rm SB} (r<40~{\rm kpc}) / {\rm SB} (r<400$ kpc). We note that using the slightly different definition $c_{\rm SB} = {\rm SB} (r<40~{\rm kpc}) / {\rm SB} (40<r<400~{\rm kpc})$, does not significantly improve the sensitivity of this estimator. This simple parameter has been shown to be robust and particularly useful when dealing with the low S/N data of distant clusters (e.g., Hudson et al. 2010). Instead, the cuspiness parameter (Vikhlinin et al. 2007) is based on the central density slope, which is more sensitive to the details in the SB profile. Given the range of signal-to-noise of our objects, the results based on the measured slope of the inner SB may be affected by large variance in the best fitting values. On the other hand, our parameter $c_{\rm SB}$ is based on simple photometry, and it provides an homogeneous characterization of our cluster sample which spans a wide range of S/N.

We validated the redshift independence of $c_{\rm SB}$(apart from possible K-corrections as described in the next subsection) by cloning low-z clusters to high redshift, therefore $c_{\rm SB}$ can be directly applied to the distant samples. In addition, we also showed that $c_{\rm SB}$ strongly anti-correlates with the central cooling time. Therefore we use this parameter to characterize the cluster population at high redshift, and, in order to have a fair comparison, we also apply the same diagnostics to the local clusters. We stress that working with a physical size instead of a scaled radius for the cooling region is crucial for this study. In Santos et al. (2008) we discussed at length this aspect and we concluded that the cooling radius does not evolve significantly with redshift, which is expected since the cool core phenomena is related with non-gravitational physics.

In this analysis we use the Chandra images in the soft-band (0.5-2.0 keV), after accounting for the vignetting effect computed at 1.5 keV. This is achieved by normalizing the exposure maps to the total exposure time and dividing the images by the normalized maps. This correction is particularly relevant for the measurement of $c_{\rm SB}$ in the local clusters, given their larger extension which implies a larger vignetting correction. With this procedure we also automatically correct for the gaps between the detector chips. In a few cases (A478, A2597, observed only with ACIS-S, and A85, whose observation lies close to the edge of one of the ACIS-I chips), the 400 kpc radius lies beyond the edge of the observed field. In these cases the measurement of $c_{\rm SB}$ requires an extrapolation of the surface brightness from about 300 kpc to 400 kpc according to the best fit $\beta $-model, as described in Sect. 6.

5.1 K-correction applied to the c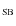$_{\rm SB}$ parameter: ``beheading''

A cluster with a single temperature ICM will be observed with the same value of $c_{\rm SB}$ at any redshift. However, in the presence of a cool-core, the spectral emission from the central region would have a softer spectrum with respect to the higher-temperature emission from the outer regions. This would introduce a different amount of K-correction between the inner 40 kpc emission and the total 400 kpc emission. For distant clusters it is impossible to derive the rest-frame $c_{\rm SB}$ value, since it would require the knowledge of the temperature profile of the ICM. However, in order to compare the $c_{\rm SB}$ distribution of local and distant clusters, we can follow the alternative approach of applying the K-correction to local clusters as if they were at the average redshift of the distance cluster sample. This is possible since we can exploit the knowledge of the temperature profiles in local clusters. We apply the K-correction in the assumption of no evolution of the temperature and metallicity profile, in order to test the null hypothesis of no evolution in the CC population.

We proceed as follows. We select a subsample of local clusters with a wide range of cool-core strength, with a signal-to-noise ratio large enough to allow us to perform spatially resolved spectroscopy. The clusters are listed in Table 4. All the clusters are observed with ACIS-I, and the radius corresponding to 400 kpc is always within the observed field. We divide the clusters into rings with equal number of net detected counts (about 3000 in the soft-band) and we measure the projected temperature and metallicity[*]. In Table 4 we also show the minimum and maximum temperatures measured in each cluster. After freezing the best fit parameters in each ring, we simulate the expected net counts for the same cluster at different redshifts, including therefore the most accurate K-correction. From the cloned surface brightness profile we measure the $c_{\rm SB}$ values at different redshifts. In this way we are able to quantify the apparent evolution of $c_{\rm SB}$ as a function of redshift for the same cluster. The effect of this apparent evolution, uniquely due to the X-ray K-correction, must be removed when comparing local and distant clusters.

Table 4:   Clusters used to compute the effect of K-correction on $c_{\rm SB}$.

We approximate the apparent evolution of the $c_{\rm SB}$ parameter as a function of redshift for this set of clusters. As shown in Fig. 4, the average behavior of $c_{\rm SB}(z)$ for cool-core clusters can be described with a simple power law. For strong cool-core clusters, we have roughly $\propto (1 + z)^{-\alpha}$, with $\alpha \sim 0.15$, which implies a decrease of about 13% at $z\sim1$. On the other hand, for weaker cool-cores (lower $c_{\rm SB}$) we expect a slower evolution. The K-correction is null for a flat temperature profile. We indeed find that $\alpha $ correlates with the minimum temperature, as shown in Fig. 5.

In order to predict an unbiased $c_{\rm SB}$ distribution at high-z we need to apply a correction of the order $\leq$$10\%$ as a function of redshift and cool-core strength (or minimum central temperature). A simple approximation, shown by the dashed line in Fig. 5 reads:

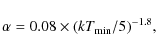
\begin{displaymath}\alpha = 0.08 \times (kT_{\min}/5)^{-1.8}, \end{displaymath} (1)

with a maximum value $\alpha = 0.2$. Therefore, we can modify the $c_{\rm SB}(0)$ values of the local sample by a factor $\propto $ $ (1+z)^{-\alpha(T_{\min})}$, considering the median redshift of the RDCS+WARPS sample, $\langle z \rangle = 0.83$. This correction corresponds to an average decrease in $c_{\rm SB}$by 4.3%, relative to the original values, and reaches at most 20% for the low temperature strong cool-cores A133 and A2597. The modified distribution can now be directly compared with that of distant clusters.

We also checked that the different values of the Galactic hydrogen column density, both in the local and in the high-z samples, do not significantly affect the measured $c_{\rm SB}$. The corrections are expected to be below 1-2%, and therefore we neglect this small effect.

\begin{figure} \par\includegraphics[width=8cm,angle=0,clip]{15208fig4.ps} \end{figure} Figure 4:

$c_{\rm SB}(z)$ for the clusters in Table 4. Continuous lines are approximate fits with a power law $\propto $ $(1+z)^{-\alpha }$.

Open with DEXTER

\begin{figure} \par\includegraphics[width=8cm,angle=0,clip]{15208fig5.ps} \end{figure} Figure 5:

Exponent $\alpha $ vs. minimum (central) temperature for clusters in Table 4. The dashed line represents Eq. (1).

Open with DEXTER

5.2 The c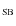$_{\rm SB}$ distributions

\begin{figure} \par\includegraphics[width=9cm,angle=0,clip]{15208f6.1.ps}\includegraphics[width=9cm,angle=0,clip]{15208f6.2.ps} \end{figure} Figure 6:

Left: distributions of $c_{\rm SB}$ for the two distant samples, RDCS+WARPS (solid, red) and 400 SD high-z (dash-dot, blue), and right: comparison between the K-corrected $c_{\rm SB}$ distribution of the local (dash, black) and the RDCS+WARPS samples.

Open with DEXTER

Before comparing the $c_{\rm SB}$ distribution of the local and distant samples, we compare the two distant samples separately. Their $c_{\rm SB}$ distributions are shown in Fig. 6, left panel. Quite unexpectedly, the shape and range of the two high-z $c_{\rm SB}$distributions are statistically different. We perform a K-S test and find a null hypothesis probability of 0.6%, implying that the two distant samples do have different distributions of cool-core strength. Taking into account that there are four clusters common to both samples, we repeated the test twice removing the common clusters from each sample and assigned them to the other one. This does not significantly affect the result of the K-S test, since we obtain null probabilities of 0.1% and 0.3%. The 400 SD high-z reaches $c_{\rm SB} = 0.10$, with median $c_{\rm SB} = 0.043$, whereas the RDCS+WARPS reaches $c_{\rm SB}=0.15$, with a median $c_{\rm SB}$ value equal to 0.082. The RDCS+WARPS clusters have thus a significantly higher surface brightness concentration with respect to the 400 SD clusters, as can be appreciated by a visual inspection of the cluster physical morphologies shown in Figs. 2 and 3. The difference in the surface brightness concentration between the two samples is confirmed by the $\beta $-model fitting performed in Sect. 6. These results point to a smaller dynamical range in surface brightness in the 400 SD high-z, relative to the RDCS+WARPS. We can exclude significant effects from K-correction or intrinsic evolution, given the large redshift overlap between the two samples, even though the RDCS+WARPS sample reaches a higher redshift (z = 1.27) with respect to the 400 SD high-z. Both the RDCS+WARPS and the 400 SD are samples based on ROSAT data, but are built with different selection criteria.

We argue that this difference is likely due to a bias of the detection algorithm used in the 400 SD survey against compact clusters with a relatively high mean surface brightness. This does not lead necessarily to sample incompleteness, as a different detection sensitivity for varying $\beta $ and core radii is taken into account when computing the selection function and the corresponding survey volume. This likely explains why number counts and luminosity functions of the three surveys are in very good agreement with each other. To check for these effects, we need to perform a detailed comparison of the selection criteria in the three surveys. This task goes beyond the scope of this work. In order to investigate the evolution of the cool-core cluster population, we decide to use the RDCS+WARPS only.

The K-corrected $c_{\rm SB}$ distribution of the local sample (shown on the right panel of Fig. 6) spans a broad range of values and reaches $c_{\rm SB} = 0.315$, with a significant peak at low $c_{\rm SB}$ ($\sim$0.04) and a median $c_{\rm SB}$equal to 0.079. We do not find any hint of a cool-core / non cool-core bimodality, as sometimes claimed in the literature (e.g., Sanderson et al. 2009), however we believe that higher statistics are needed to check for this effect.

We performed a K-S test comparing the local and distant RDCS+WARPS samples and found a null hypothesis probability of p = 16%, showing that the two $c_{\rm SB}$ distributions are comparable. Therefore, in our analysis we find that the bulk of the populations of distant and local clusters have comparable cool-core strength, despite the absence of strong cool-core clusters at high-z. Qualitatively, our findings are compatible with a significant population of cool-core clusters already at redshift $z \sim 1.2$ (5 Gyr after the Big Bang), while strong cool-cores must wait for a longer time span before they can develop (9 Gyr if they appear below $z \sim 0.5$). To reinforce these constraints, it is necessary to use larger samples of high-z clusters and to attempt a better characterization of distant cool-cores. The first occurrence is strongly limited by the lack of wide area cluster survey in the Chandra and XMM-Newton era, while the second strategy would require the use of a significant amount of Chandra time. It would be worth pursuing at best these two strategies, since the alternative is waiting for the next generation wide-area X-ray surveys with high spatial resolution.

For completeness we also report the results obtained using the local and distant 400 SD samples. The K-S test provides a probability of 0.5% that the two samples are drawn from the same distribution. This would be in agreement with the claim of strong cool-core evolution made by Vikhlinin et al. (2007). However we remark that such result, at odds with our findings, is unlikely to be a fair description of the cluster population at redshift greater than 0.5.

We assessed the impact of the 10 missing clusters from the RDCS+WARPS sample, i.e. clusters which have not been observed with Chandra, in our results. Assuming that all missing clusters are non-CC, the most conservative estimate of the fraction of CC in the RDCS+WARPS sample is 30%, which is significantly higher than the 10% fraction in the 400 SD high-z samples. Hence, we conclude that our results are not substantially affected by this incompleteness.

6 Surface brightness profile fitting

In this Section we derive a detailed description of the surface brightness profiles of the clusters in our sample, which will be later used to compute the gas density profiles, the entropy and the central cooling times. Unless one has very precise data, the isothermal $\beta $-model proposed by Cavaliere & Fusco-Femiano (1976) provides a fair description of the radial X-ray surface brightness profiles of galaxy clusters. We fit the azymuthally averaged profiles and use the fit parameters to characterize the morphology of the distant clusters.

Distant clusters have a small angular size and low photon statistics, therefore a single-$\beta $-model provides a good fit to the radial profiles. Our attempts to fit a double $\beta $-models to high-z clusters resulted in very small improvements, confirming that diagnostics based on surface brightness gradients rather than integral quantities, are more prone to statistical noise. Our fitting procedure, based on a Levenberg-Marquardt algorithm, constrain the parameter $\beta $ to the range $0.4 < \beta <1.0$. Our fitting function has the form

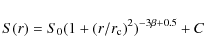
\begin{displaymath}S(r) = S_{0} (1+(r/r_{\rm c})^2) ^{-3 \beta + 0.5} + C \end{displaymath} (2)

where S0 is the central surface brightness, $r_{\rm c}$ is the core radius, and C is a constant background. The correlation between the best fit $r_{\rm c}$ and $\beta $ values is shown in Fig. 7 for the 400 SD high-z and RDCS+WARPS samples. The apparent correlation between $\beta $ and $r_{\rm c}$ is due to the tendency of the $\beta $-model to compensate for a larger core radius with a larger beta However, we notice that the two samples clearly populate a different $r_{\rm c}$-$\beta $ space. The RDCS+WARPS clusters prefer smaller core radii and larger $\beta $, in agreement with our analysis of the $c_{\rm SB}$ parameter distribution. We checked that the temperature distributions of both samples are statistically equivalent, so that the difference among the two samples in the $\beta $-$r_{\rm c}$ plane is not affected by any hidden correlation between the temperature and the fitting parameters.

Given the much larger signal-to-noise ratio, local clusters require a double $\beta $-model fit in order to properly describe the core. For the low-z sample our fitting function reads:

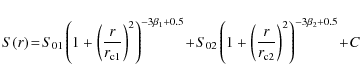
\begin{displaymath}S(r) \!=\! S_{01} \left(1+\left(\frac{r}{r_{\rm c1}}\right)^2... ...\frac{r}{r_{\rm c2}}\right)^2\right)^{-3\beta_{2}+0.5}\! +\! C \end{displaymath} (3)

\begin{figure} \par\includegraphics[width=8.5cm,angle=0,clip]{15208fig7.ps} \end{figure} Figure 7:

Correlation between the single $\beta $-model parameters, $r_{\rm c}$ and $\beta $ for the two samples of high-z clusters.

Open with DEXTER
The characterization of the surface brightness profile allows us to measure the total X-ray luminosity of the clusters in our sample. The contribution of the cool-core to the total cluster luminosity is known to be, at most, 30% in local clusters (see Peres et al. 1998). We investigate this effect in our local and distant samples by searching for a correlation between the total $L_{\rm X}$ and $c_{\rm SB}$. The luminosity excess would be best quantified by a double-$\beta $model, however, given the low significance of such a complex model to describe the low S/N data of the distant clusters, we resort to use only total cluster luminosities. Rest-frame X-ray luminosities in the 0.5-2.0 keV band are computed for the distant clusters by performing a spectral fit to the inner region with r = 40 $^{\prime\prime}$ (see Sect. 4), and extrapolating the flux to 1 Mpc according to the beta-model best-fit parameters. For the local sample we used the $L_{\rm X}$ values published in Vikhlinin et al. (2009a). In Fig. 8 we show our results. The three samples span approximately the same range of X-ray luminosities (with the distant samples reaching the faintest $L_{\rm X}$), however, no clear trend stands out from the $L_{\rm X}$- $c_{\rm SB}$. relation. One of the reasons for this result is that, a proper measure of an excess luminosity requires a robust characterization of the surface brightness profiles at radii smaller than 40 kpc, a condition that is hard to fulfill for the high-z cluster sample.

In the following, we will use the results of this Section to derive the entropy and cooling time of the clusters.

\begin{figure} \par\includegraphics[width=8.5cm,angle=0,clip]{15208fig8.ps} \end{figure} Figure 8:

X-ray soft-band luminosity $L_{\rm X}$ versus $c_{\rm SB}$. Black crosses refer to the 400 SD low-z sample, blue triangles represent the 400 SD high-z sample and the red circles correspond to the RDCS+WARPS sample. The black squares indicate the presence of a radio source in the cluster center.

Open with DEXTER

7 Entropy profiles and central entropy

Entropy is a fundamental property of the intracluster medium, more so than either temperature or density alone. The specific intracluster entropy, K, describes the thermodynamical history of the gas, and is defined as:

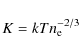
\begin{displaymath}K = kT n_{\rm e}^{-2/3} \end{displaymath} (4)

where T and $n_{\rm e}$ correspond to the cluster temperature and gas density respectively. It is well-known that the entropy profiles of local cool-cores are steeper in the inner region, relative to non-cool-cores, reaching values well below 100 keV/cm2(e.g., Donahue et al. 2006; Cavagnolo et al. 2009). We measured the cluster entropy profiles using the global cluster temperature to ensure a proper comparison between the local and distant samples. However, we did investigate the impact of using a single temperature instead of a more accurate temperature profile in the core entropy of the local clusters, by exploring the database of the ACCEPT[*] sample (Cavagnolo et al. 2009). The discussion on this comparison is presented in Sect. 7.1.

The gas density profiles were obtained by deprojecting the surface brightness profiles along the line of sight, $S(r) = \int \! n_{\rm e}^{2} ~ {\rm d}l$. We apply the simple and convenient $\beta $-model approximation to describe the surface brightness profiles, and use the best-fit model parameters derived in Sect. 6. The entropy profiles obtained in physical units are presented Fig. 9. Again we compare the two distant samples (see top panel of Fig. 9), but most importantly, we compare entropy of the local and the RDCS+WARPS clusters, presented in the bottom panel of Fig. 9. All profiles are very similar beyond r = 300 kpc. The turn over of the profiles takes place at a radius r = 100-150 kpc, which marks the transition from the core region to the cluster outer part. We have a good agreement with other works that present profiles of distant clusters, such as Morandi & Ettori (2007) that present entropy profiles of a sample of X-ray luminous clusters with 0.1 < z < 0.8, observed with Chandra. They find a high similarity between the entropy profiles of the low-z and distant clusters, outside the core region.

The central entropy of the local clusters shows a large spread at very small radii, below 20 kpc. This is in part caused by the very steep inner slopes of the profiles of cool-core clusters, that can be resolved down to very small scales (2 kpc).

\begin{figure} \par\includegraphics[width=8.5cm,angle=0,clip]{15208f9.1.ps}\par\includegraphics[width=8.5cm,angle=0,clip]{15208f9.2.ps} \end{figure} Figure 9:

Comparison between the entropy profiles of the two distant samples (top), and the 400 SD low-z relative to the RDCS+WARPS sample (bottom).

Open with DEXTER

7.1 Central entropy

In order to assess and compare the state of the ICM in the core of both the nearby and distant clusters, we measured the central entropy at a radius of 20 kpc (K20), a bound imposed by the resolution limit of the most distant objects. The distribution of K20 for the local and RDCS+WARPS samples is shown in Fig. 10. To quantify the agreement of these distributions and thus assess the evolution of core entropy, we performed a K-S test. The probability that the 400 SD low-z and the RDCS+WARPS are associated with the same parent distribution is 24%. In contrast, the probability that both 400 SD samples originate from the same distribution is a mere 5%. We note however that the local sample spans a much wider range of entropy, relative to the distant clusters: K20 (local) = [35-415] keV/cm2, whereas K20 (RDCS+WARPS) = [76-197] keV/cm2.

\begin{figure} \par\includegraphics[width=8.5cm,angle=0,clip]{15208fig10.ps} \vspace*{-0.3cm} \end{figure} Figure 10:

Distribution of the entropy measured at 20 kpc.

Open with DEXTER

In addition to comparing the central entropy of the local and distant clusters, we also investigated a correlation between K20 and $c_{\rm SB}$. The result is presented in Fig. 11 and shows a strong anti-correlation between these two quantities. A Spearman rank test confirms this relation with a coefficient $\rho = - 0.84$.

\begin{figure} \par\includegraphics[width=8.5cm,angle=0,clip]{15208fig11.ps} \vspace*{-0.3cm} \end{figure} Figure 11:

Correlation between central entropy K20 and the phenomenological parameter $c_{\rm SB}$. Error bars show typical measurement errors for the low and distant samples.

Open with DEXTER

As mentioned earlier, we used the global cluster temperature to compute K20, which may introduce a bias in the result, in particular for the local clusters that are well resolved down to a few kpc. Since all local clusters were independently analyzed by Cavagnolo et al., we used the cluster temperatures measured in the innermost bin (corresponding to about 10-20 kpc) and compared the histograms of K20 using both the central and global temperatures. The average difference between the two distributions is 15.3 keV/cm2 with a standard deviation of 32.0 keV/cm2. These distributions differ mainly for the nine clusters with K20 <100 keV/cm2, in which K20 ( $T_{\rm global}$) is on average two times higher than K20 ( $T_{\rm core}$). Above K20 = 100 keV/cm2 the difference between K20 ( $T_{\rm core}$) and K20 ( $T_{\rm global}$) scatters around the equality. Therefore, we expect the K20- $c_{\rm SB}$ relation to be even steeper for the local clusters, if one uses a resolved central temperature. We do not find any evidence for bimodality in the distributions of K20.

8 The central cooling time

The central cooling time is the measure most often used to quantify cool-cores, as it provides a time-frame for the evolutionary state of the gas. Adopting an isobaric cooling model for the central gas, $t_{\rm cool}$ can be computed as:

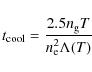
\begin{displaymath}t_{\rm cool} = \frac{2.5 n_{\rm g} T}{n_{\rm e}^{2} \Lambda(T)} \end{displaymath} (5)

where $\Lambda(T)$, $n_{\rm g}$, $n_{\rm e}$ and T are the cooling function, gas number density, electron number density and temperature respectively (Peterson & Fabian 2006), and with $n_{\rm g} =1.9 n_{\rm e}$. Using the global cluster temperature and thus considering our results as upper limits, we obtained the central cooling time measured within a 20 kpc radius (see Fig. 12). As expected, the $t_{\rm cool}$ distributions of the local and distant samples resemble the distributions of K20. The local clusters span the wide range of ages [0.7-32.6] Gyr, whereas the RDCS+WARPS sample is limited to [4.7-14.3] Gyr. For completeness, we report for each sample the fraction of clusters with a central cooling time lower than the age of the Universe at the cluster redshift: in the local sample, 15 out of 26 (58%); in the RDCS+WARPS, 4 out of 15 (27%), and in the 400 SD high-z, 2 out of 20 (10%). However, a more meaningful quantity would be the cooling time normalized to the age of the cluster, defined as the time elapsed since the last major merger event. Considering the age of the Universe at $z_{\rm obs}$ is misleading, as this is a loose upper bound on the age of the cluster.

A K-S test to the distributions of $t_{\rm cool}$ in the local and the RDCS+WARPS samples indicates a probability of 9% that these samples derived from the a common population. When comparing the local and distant samples from the 400 SD, the probability derived with the K-S test decreases to 4%.

Again we quantified the impact of using a core temperature in the cooling time measurements. A K-S test to the central cooling time distributions obtained with a core temperature and a global temperature indicates that it is likely that both samples originate from the same population, with a probability of 67%. The central cooling time measured with a resolved temperature is on average 0.3 Gyr shorter relative to the measurement with a global temperature. This effect is obviously stronger for cool-core clusters. We quantified this effect in clusters with central cooling time shorter than 5 Gyr, and we found that in this case, the ratio $t_{\rm cool}$( $T_{\rm global}$)/ $t_{\rm cool}$( $T_{\rm core}$) reaches a factor 1.4.

\begin{figure} \par\includegraphics[width=8.5cm,angle=0,clip]{15208fig12.ps} \vspace*{2.5mm}\end{figure} Figure 12:

Distribution of central cooling time for the local and distant samples. The dotted line marks the age of the Universe.

Open with DEXTER

We also find a strong anti-correlation between $t_{\rm cool}$ and $c_{\rm SB}$ (see Fig. 13), quantified with a Spearman rank test with coefficient $\rho = - 0.84$ and a probability of no correlation of <10-13. This anti-correlation was already shown in Santos et al. (2008), and more recently Hudson et al. (2010) confirmed it using the nearby HIFLUGCS sample.

\begin{figure} \par\includegraphics[width=8.5cm,angle=0,clip]{15208fig13.ps} \vspace*{2.5mm}\end{figure} Figure 13:

Correlation between central cooling time and the phenomenological parameter $c_{\rm SB}$. Error bars show typical measurement errors for the low and distant samples.

Open with DEXTER

9 Radio sources associated with cluster cores

In the current scenario, feedback from AGN in the radio mode plays a prominent role in the physics of cool-cores. Increasing evidence from radio and X-ray observations of local clusters show that the formation of bubbles due to radio jets associated to the central AGN may effectively satisfy the energy balance between cooling and heating in cool-core regions (see Blanton 2010). In this respect, the radio luminosity of the central galaxy can provide an important link between the black hole activity and the state of the intracluster medium.

While there are several works pointing out a correlation between the power associated to the radio activity of the central galaxy to the cool-core properties (see Sun et al. 2009), there are no similar studies at high redshift. Using data from the archive of the NRAO VLA Sky Survey (NVSS) at 1.4 GHz (Condon et al. 1998), which is sensitive down to $\sim$2.5 mJy, we investigated the presence of radio sources in the cores of our local and distant clusters. The two distant samples are entirely covered by the NVSS. To determine whether a radio source is related with the cluster core we adopted a conservative criterion of a maximum separation of about 20 $^{\prime\prime}$ between the X-ray centroid and the center of the radio galaxy. The 400 SD high-z has three radio sources (3/20), whereas the RDCS+WARPS sample has only 2 out of 15 clusters with a central radio source. This is expected since most of the radio sources associated with high-z clusters should be below the flux limit of the NVSS. Interestingly, the two clusters in the RDCS+WARPS with radio sources are also considered to be cool-cores with $c_{\rm SB}$ greater than 0.08.

The local sample is not fully covered by the NVSS (coverage of 73%, 19/26). However, we find a high fraction of clusters with a radio source (10/19) all associated with high $c_{\rm SB}$ values (i.e., greater than 0.08) It is worth noting that most local clusters without NVSS coverage are non-cool-cores, according to their $c_{\rm SB}$values. These results are reported in Tables 1-3.

We also obtained the 1.4 GHz luminosity, $L_{1.4~{\rm GHz}}$, of the radio sources associated with the cluster cores, using the fluxes provided by the NVSS catalog, and applying a K-correction with a power law with index 0.7. We placed upper limits on the non-detections using the NVSS flux detection threshold converted into luminosity. As shown in Fig. 14, the $L_{1.4~{\rm GHz}}$ corresponding to the local sample shows a trend with $c_{\rm SB}$, with the stronger cool-cores having correspondingly the most luminous radio sources (errors associated with the radio luminosities are smaller than 5%, therefore are not shown). To properly take into account the upper limits on the radio luminosity for the clusters with NVSS coverage and no detection for the central galaxy we used ASURV (Lavalley et al. 1992), the Survival Analysis package which employs the routines described in Feigelson & Nelson (1985) and Isobe et al. (1986). Survival analysis methods evaluate the probability of correlation and linear regression fits by dealing properly with non-detections (upper limits). We find a very strong (p > 99.0%) correlation between $c_{\rm SB}$ and $L_{1.4~{\rm GHz}}$ for the local sample, with a Spearman rank test coefficient $\rho = 0.82$.

\begin{figure} \par\includegraphics[width=8.5cm,angle=0,clip]{15208fig14.ps} \vspace*{2.5mm}\end{figure} Figure 14:

Relation between the radio luminosity of sources in close proximity to the cluster cores, $L_{1.4~{\rm GHz}}$, and the surface brightness concentration, $c_{\rm SB}$. Arrows refer to upper limits of non-detections. The dotted line at $1.1 \times 10^{25}$ WHz-1 marks the luminosity limit at z = 1 for NVSS sources, corresponding to the flux limit of 2.5 mJy.

Open with DEXTER

The type of radio source usually associated with local cool-cores is the FR-I, with an incidence rate of the order of 60%. Using the classification made by Fanaroff & Riley (1974) we identified the type of radio sources. We apply the FR-I/FR-II dividing line provided by Chiaberge et al. (2009), $L_{1.4~{\rm GHz}} \sim 4 \times 10^{25}$ W Hz-1, and conclude that, with the exception of the source likely associated with 400d J1221+4918, all radio sources belong to the low-luminosity type FR-I.

The radio sources in the cores of distant clusters populate the high $L_{1.4~{\rm GHz}}$ luminosity end, however the small number of detected sources does not allow us to draw any conclusion.

The study of radio sources in distant clusters is important to understand how the feedback mechanism shapes the evolution of cool-cores, and is particularly useful in searches of high-z clusters around FR-I sources (Chiaberge et al. 2009). However, the evolution of the radio luminosity function (RLF) remains a controversial issue requiring further studies. While Perlman et al. (2004) finds no evidence for evolution of the radio luminosity function up to z = 1, Branchesi et al. (2006) concludes that the RLF of distant X-ray clusters is very different from that of local rich Abell clusters, with a steeper slope at low radio powers ($\le$1024 WHz-1).

10 Looking into the future: perspectives with WFXT

With the present work we show that we can explore the population of cool-core clusters up to the highest redshift where X-ray clusters are selected ( $z \sim 1.4$) by fully exploiting the archive of Chandra. This study is possible thanks to the exquisite angular resolution of Chandra, which allows us to sample the cool-core region (corresponding to a radius of 40 kpc) at any redshift with a resolution factor (defined as the physical scale we want to resolve divided by the half energy width of the instrument PSF) of about 10. The only way to improve the present work is to add serendipitously discovered high redshift clusters followed-up with deep Chandra observations. Even though the number of z>1 X-ray clusters is slowly increasing thanks to ongoing surveys as the XMM-LSS; the XMM-Newton Cluster Survey; the XMM-Newton Distant Cluster Project; and the Swift X-ray Cluster Survey, sample statistics is not expected to increase significantly without a dedicated wide area, deep X-ray survey. Hence, it is instructive to look into the future X-ray missions to investigate the capability of characterizing the cool-core strength of high-z clusters.

Unfortunately, no proposed or planned X-ray facility foresees an angular resolution comparable to that of Chandra. Therefore, any future X-ray work on the evolution of cool-cores at high-redshift must deal with the blurring effect of the PSF on the cluster images. In order to have low systematics errors, we need to keep the HEW as low as possible. As shown in Santos et al. (2010), the capability to classify strong, moderate and non cool-core clusters up to $z \sim 1.5$ using $c_{\rm SB}$ is strongly dependent on the instrument HEW. Results obtained with $c_{\rm SB}$ are still reliable when the HEW is 5 arcsec, but beyond 10 $^{\prime\prime}$ it is no longer possible to confidently discriminate between a cool-core and a non cool-core cluster. Only two proposed X-ray missions expect to have a PSF with a 5 arcsec HEW at 1 keV: the International X-ray Observatory and the Wide Field X-ray Telescope.

The International X-ray Observatory (IXO) (see e.g., Bookbinder et al. 2010) is designed to have a great collecting power and high spectral resolution, therefore it will provide very detailed analysis of known or serendipitously discovered clusters, up to high-redshift. However, IXO will not be used in a survey mode for large area surveys, and thus it would not significantly increase the statistics of high-z cluster samples.

One of the most promising proposed X-ray missions is the Wide Field X-ray Telescope (WFXT), a medium-class mission designed to be two orders of magnitude more sensitive than any previous or planned X-ray mission for large area surveys, and to match in sensitivity the next generation of wide-area optical, IR and radio surveys. In five years of operation, WFXT will carry out three extragalactic surveys: the deep (400 ks, 100 deg2), medium (13 ks, 3000 deg2) and wide (2 ks, 20 000 deg2) surveys (see Giacconi et al. 2009). The combination of good angular resolution across the entire field of view ( $HEW \sim 5$ arcsec), large collecting area and large field of view (one square degree), makes WFXT the most efficient finding machine of X-ray clusters at z > 1. The expected number of high-z clusters detected in the WFXT surveys with signal-to-noise comparable to that of the cluster sample in this work (conservatively expressed as a lower bound of 1500 net counts), is shown in Table 5.

\begin{figure} \par\mbox{\includegraphics[width=4cm,height=4cm,angle=0,clip]{152... ...width=4cm,height=4cm,angle=0,clip]{15208f15.3.ps} }\vspace*{-3mm} \end{figure} Figure 15:

Simulated images of strong cool-core A1835 as seen by WFXT in medium exposure (13.2 ks), at redshifts 0.5 (left), 1.0 (middle) and 1.5 (right). The images have a size of $10 \times 10$ arcmin and are displayed in logarithmic scale.

Open with DEXTER

Table 5:   Expected number of clusters with temperature kT >3 keV and with more than 1500 net counts in the 0.5-7 keV band, in each one of the three planned WFXT surveys.

The image quality of WFXT allows one to robustly characterize the cool-core strength in clusters detected with more than 1500 net counts. Simulations of realistic WFXT fields have been produced in order to investigate this science case. Using the cloning technique (Santos et al. 2008), we simulated WFXT images of typical strong, moderate and non cool-core clusters at redshifts 0.5, 1.0 and 1.5. The templates chosen to perform the cloning simulations are A1835, A963 and A2163, which represent these three cluster types.

To obtain a quantitative assessment of the cool-core properties of the simulated clusters, we measured $c_{\rm SB}$. For the most interesting case of tracing the evolution of a strong cool-core (A1835, see Fig. 15), we measured $c_{\rm SB}= 0.184, 0.156$ and 0.152 at z = 0.5, 1.0 and 1.5, respectively, while the Chandra value in the original image is $c_{\rm SB}=0.246$. We, therefore, find an apparent evolution due to the angular resolution, which can be removed by applying a proper deconvolution of the PSF. However, and more importantly, we also confirm that the measure of $c_{\rm SB}$ at face-value allows us to assign each cluster to its own cool-core class (strong-, moderate- and non-CC) at any redshift. We conclude that, while the exact amount of evolution in the cool-core strength seen by WFXT is moderately affected by the angular resolution, we will be able to perform a similar study as presented here with Chandra data.

We note that z=1.5 is probably the redshift limit to perform this kind of analysis. The power of WFXT can be appreciated if we look at the number statistics below z = 1.5 in the medium survey, where we expect to detect 2190 (300) massive clusters (T > 3 keV) with a minimum of 1500 net counts (to allow for a robust $c_{\rm SB}$measurement and a spectral analysis), in the redshift range 0.5 <z< 1.0 ( 1.0 <z< 1.5).

11 Conclusions

In this paper we investigated the evolution of cool-core clusters across the entire redshift range currently available, i.e., out to z = 1.3. Our analysis is mostly based on the archival Chandra data of three cluster samples, and our results are derived mainly from the cluster X-ray surface brightness properties. In the following, we summarize our main results and conclusions:

  • The range of surface brightness spanned by the three samples (see Figs. 1-3) includes a wide variety of physical morphologies, illustrating that the samples are well representative of the X-ray luminous galaxy cluster population and therefore are suitable to investigate the evolution of the cool-cores.
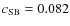  • The distributions of the surface brightness concentration, $c_{\rm SB}$, in the high-z cluster samples (Fig. 6, left panel) show that the two samples are statistically different: the 400 SD high-z sample lacks concentrated clusters, with median $c_{\rm SB}$ equal to 0.043, in contrast, the RDCS+WARPS spans a wider range of $c_{\rm SB}$, with median $c_{\rm SB}=0.082$. This finding suggests that the 400 SD high-z sample may be biased against concentrated morphologies.
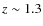  • The comparison between the local sample and the RDCS+WARPS clusters shows that the distributions of $c_{\rm SB}$ are not significantly different (see Fig. 6, right panel), exposing a well defined population of cool-cores already in place at $z \sim 1.3$; however, the high-z sample is deficient in very peaked (or strong cool-core, with 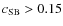$c_{\rm SB} > 0.15$) clusters.
  • The entropy profiles of the low and high-z samples agree well in the outskirts but show a large scatter in the inner regions; the comparison between the distributions of the entropy value at 20 kpc (K20) in the local and the RDCS+WARPS samples shows that, even though both distributions share the same median value (127 and 125 keV/cm2 in the local and distant samples, respectively) the distant sample covers a narrower range of central entropy, K20 = [76-197] keV/cm2, and does not reach values as low as the local sample.
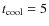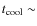  • We measured the cluster central cooling times at 20 kpc radius and found that the local sample spans a broad range of cooling time ([0.7-32.6] Gyr), with a median value of 9.3 Gyr, and a significant peak at $t_{\rm cool} = 5$ Gyr. The RDCS+WARPS sample shows a somewhat different behaviour, displaying a narrower range of cooling times, [4.7-14.3] Gyr, and a median $t_{\rm cool}\sim$ of 8.9 Gyr. We confirm the strong anti-correlation between $c_{\rm SB}$ and $t_{\rm cool}$, mirrored by the anticorrelation between $c_{\rm SB}$ and K20 (see Fig. 11).
  • our results on $c_{\rm SB}$, central entropy and central cooling time do not support recent claims of a cool-core/non cool-core bimodality.
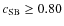  • Using the NVSS archive we identified radio sources in close vicinity with the cluster cores (<20 $^{\prime\prime}$). We find a significant correlation between $c_{\rm SB}$and the radio luminosity of sources in the local sample. All local clusters with a central radio source are cool-cores, since they have $c_{\rm SB} \ge 0.80$. The lack of radio data for the distant clusters does not allow us to draw any conclusion on the connection between the cool-core strength and the presence of a central radio galaxy (Fig. 14), which motivates us to explore this line of research in the future, using deep, high-resolution radio data, to investigate the interplay between the X-ray core, the brightest cluster galaxy and the central radio source, in high-redshift clusters.
Our findings can be used to significantly constrain the formation time-scale of cool-cores. We note that one of the most distant clusters discovered to date and not included in our high-z sample, XMMUJ2235 at z = 1.393 (Mullis et al. 2005) found within the framework of the XDCP (Böhringer et al. 2005), was also analysed in Santos et al. (2008) and Rosati et al. (2009). We measured $c_{\rm SB}$ equal to 0.103, confirming XMMUJ2235 as a cool-core cluster.

The results presented in this paper extend the current knowledge of the cool-core population to the most distant clusters known, and shows us that even at such large lookback times, we still find a large population of moderate cool-core clusters. A direct consequence is that a significant number of cool-cores develops on times scale comparable to the dynamical time scale of clusters ($\sim$1 Gyr).

With this work we are reaching the limit of what can be done with current X-ray missions to study the cores of the most distant galaxy clusters. The small number statistics of high-z clusters is the major limitation that prevents us from a more accurate understanding of the physics of the youngest clusters, although an equally important requirement for such a study is a high angular resolution, as the one reached by Chandra. A complementary strategy is to go as deep as possible with Chandra on high-z cool core clusters. In this way, we will exploit at best the presently limited sample of high-z clusters, in order to unveil the properties of their cool cores (temperature and metallicity profiles, presence of cavities associated to radio sources) and compare them to those in local clusters. This can be achieved only with very deep (several hundreds of ks) Chandra pointings.

A significant advancement in this research will be achieved when large samples are available, which will only be possible with the next generation X-ray survey missions. In particular, we showed that the next generation X-ray survey instruments with a large collecting area and good angular resolution will have the ability to resolve the central regions of strong cool-cores up to a redshift of 1.5.

Acknowledgements
We wish to thank S. Molendi, S. Borgani and S. Ettori for useful discussions in various stages of this study. We acknowledge support from ASI-INAF I/088/06/0. P.T. aknowledges support under the grant INFN PD51. P.R. acknowledges partial support by the DFG cluster of excellence Origin and Structure of the Universe (http://www.universe- cluster.de).

References

  1. Arnaud, K. A. 1996, Astronomical Data Analysis Software and Systems V, 5, ASP Conf. Ser., 101, 17 [Google Scholar]
  2. Bauer, F. E., Fabian, A. C., Sanders, J. S., Allen, S. W., & Johnstone, R. M. 2005, MNRAS, 359, 1481 [NASA ADS] [CrossRef] [Google Scholar]
  3. Blanton, E., Chandra's First Decade of Discovery Special Feature edition of the Proceedings of the National Academy of Sciences [arXiv:1004.0671] [Google Scholar]
  4. Böhringer, H., Mullis, C. R., Rosati, P., et al. 2005, ESO Messenger, 120, 33 [Google Scholar]
  5. Bookbinder, J. 2010, eprint [arXiv:1003.2847] [Google Scholar]
  6. Branchesi, M., Gioia, I. M., Fanti, C., Fanti, R., & Perley, R. 2006, A&A, 446, 97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Burenin, R. A., Vikhlinin, A., Hornstrup, A., et al. 2007, ApJS, 172, 561 [NASA ADS] [CrossRef] [Google Scholar]
  8. Cavagnolo, K. W., Donahue, M., Voit, G. M., & Sun, M. 2009, ApJS, 182, 12 [NASA ADS] [CrossRef] [Google Scholar]
  9. Cavaliere, A., & Fusco-Femiano, R. 1976, A&A, 49, 137 [NASA ADS] [Google Scholar]
  10. Chen, Y., Reiprich, T. H., Böhringer, H., Ikebe, Y., & Zhang, Y.-Y. 2007, A&A, 466, 805 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Chiaberge, M., Tremblay, G., Capetti, A., et al. 2009, ApJ, 696, 1103 [NASA ADS] [CrossRef] [Google Scholar]
  12. Condon, J. J., Cotton, W. D., Greisen, E. W., et al. 1998, AJ, 115, 1693 [NASA ADS] [CrossRef] [Google Scholar]
  13. Donahue, M., Horner, D. J., Cavagnolo, K. W., & Voit, G. M. 2006, ApJ, 643, 730 [NASA ADS] [CrossRef] [Google Scholar]
  14. Dunn, R. J. H., & Fabian, A. C. 2008, MNRAS, 385, 757 [NASA ADS] [CrossRef] [Google Scholar]
  15. Fabian, A. C., Crawford, C. S., & Mushotzky, R. F. 1994, MNRAS, 267, 779 [NASA ADS] [CrossRef] [Google Scholar]
  16. Fanaroff, B. L., & Riley, J. M. 1974, MNRAS, 167, 31P [Google Scholar]
  17. Feigelson, E. D., & Nelson, P. I. 1985, ApJ, 293, 192 [NASA ADS] [CrossRef] [Google Scholar]
  18. Giacconi, R., Borgani, S., Rosati, P., et al. 2009, astro2010: The Astronomy and Astrophysics Decadal Survey, 2010, 90 [arXiv:0902.4857] [Google Scholar]
  19. Grevesse, N., & Sauval, A. J. 1998, SSRv, 85, 161 [Google Scholar]
  20. Hudson, D. S., Mittal, R., Repirich, T. H., et al. 2010, A&A, 513, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Lavalley, M., Isobe, T., & Feigelson, E. 1992, Astronomical Data Analysis Software and Systems I, 25, 245 [Google Scholar]
  22. Leccardi, A., & Molendi, S. 2007, A&A, 427, 21 [CrossRef] [EDP Sciences] [Google Scholar]
  23. Leccardi, A., Rossetti, M., & Molendi, S. 2010, A&A, 510, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Liedahl, D. A., Osterheld, A. L., & Goldstein, W. H. 1995, ApJ, 438, L115 [NASA ADS] [CrossRef] [Google Scholar]
  25. Isobe, T., Feigelson, E. D., & Nelson, P. I. 1986, ApJ, 306, 490 [NASA ADS] [CrossRef] [Google Scholar]
  26. Jones, L. R., Scharf, C., Ebeling, H., et al. 1998, ApJ, 495, 100 [NASA ADS] [CrossRef] [Google Scholar]
  27. Kaastra, J. S. 1992 (Internal SRON-Leiden Report, updated version 2.0) [Google Scholar]
  28. Morandi, A., & Ettori, S. 2007, MNRAS, 380, 1521 [NASA ADS] [CrossRef] [Google Scholar]
  29. Mullis, C. R., Rosati, P., Lamer, G., et al. 2005, ApJ, 623, 85 [Google Scholar]
  30. Nousek, J. A., & Shue, D. R. 1989, ApJ, 342, 1207 [NASA ADS] [CrossRef] [Google Scholar]
  31. Peres, C. B., Fabian, A. C., Edge, A. C., et al. 1998, MNRAS, 298, 416 [NASA ADS] [CrossRef] [Google Scholar]
  32. Perlman, E. S., Frye, C., Ebeling, H., et al. 2004, Clusters of Galaxies: Probes of Cosmological Structure and Galaxy Evolution [Google Scholar]
  33. Peterson, J. R., & Fabian, A. C. 2006, Phys. Rep., 427, 1 [NASA ADS] [CrossRef] [Google Scholar]
  34. Pierre, M., Pacaud, F., Duc, P.-A., et al. 2006, MNRAS, 372, 591 [NASA ADS] [CrossRef] [Google Scholar]
  35. Reiprich, T. H., & Boheringer, H. 2002, ApJ, 567, 716 [NASA ADS] [CrossRef] [Google Scholar]
  36. Rosati, P., Della Ceca, R., Norman, C., & Giacconi, R. 1998, ApJ, 492, 21 [Google Scholar]
  37. Rosati, P., Tozzi, P., Gobat, R., et al. 2009, A&A, 508, 583 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Sanderson, A. J. R., O'Sullivan, E., & Ponman, T. J. 2009, MNARS, 395, 764 [Google Scholar]
  39. Sahlén, M., Viana, P. T. P., Liddle, A. R., et al. 2009, MNRAS, 397, 577 [NASA ADS] [CrossRef] [Google Scholar]
  40. Santos, J. S., Rosati, P., Tozzi, P., et al. 2008, A&A, 483, 35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Santos, J. S., Tozzi, P., & Rosati, P. 2010, to be published on the Mem. Soc. Astron. Ital. Suppl. [Google Scholar]
  42. Sun, M. 2009, ApJ, 704, 1586 [NASA ADS] [CrossRef] [Google Scholar]
  43. Vikhlinin, A., Burenin, R., Forman, W. R., et al. 2007, Heating versus Cooling in Galaxies and Clusters of Galaxies, 48 [CrossRef] [Google Scholar]
  44. Vikhlinin, A., Burenin, R. A., Ebeling, H., et al. 2009a, ApJ, 692, 1033 [NASA ADS] [CrossRef] [Google Scholar]
  45. Vikhlinin, A., Kravtsov, A. V., & Burenin, R. A. 2009b, ApJ, 692, 1060 [NASA ADS] [CrossRef] [Google Scholar]
  46. Wilms, J., Allen, A., & McCray, R. 2000, ApJ, 542, 914 [NASA ADS] [CrossRef] [Google Scholar]

Footnotes

... (XDCP[*]
http://www.xray.mpe.mpg.de/theorie/cluster/XDCP/xdcp_index.html
... metallicity[*]
We are not interested in deprojected quantities here, since we just want to estimate the K-correction effect on the surface brightness.
... ACCEPT[*]
http://www.pa.msu.edu/astro/MC2/accept/

All Tables

Table 1:   400 SD low redshift sample.

Table 2:   400 SD high z sample.

Table 3:   RDCS+WARPS sample.

Table 4:   Clusters used to compute the effect of K-correction on $c_{\rm SB}$.

Table 5:   Expected number of clusters with temperature kT >3 keV and with more than 1500 net counts in the 0.5-7 keV band, in each one of the three planned WFXT surveys.

All Figures

  \begin{figure} \par\includegraphics[width=8cm,angle=0,clip]{15208fig1.ps} \vspace*{-2.5mm} \end{figure} Figure 1:

Low-z cluster sample drawn from the 400 SD survey. Images are normalized by the exposure maps and smoothed with a gaussian kernel of 3 pixel. The images have a size of $8 \times 8$ arcmin and are ordered with increasing redshift. Physical sizes of the individual images are shown in kpc at the bottom of the images.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,angle=0,clip]{fig2.eps} \end{figure} Figure 2:

400 SD high-z sample. Images are normalized by the exposure maps and smoothed with a gaussian kernel of 3 pixel. The images have a size of $4 \times 4$ arcmin and are ordered with increasing redshift (from top left to bottom right).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,angle=0]{15208fig3.ps} \end{figure} Figure 3:

RDCS+WARPS sample. Images are normalized by the exposure maps and smoothed with a gaussian kernel of 3 pixel. The individual images have a size of $4' \times 4'$ and are ordered with increasing redshift (from top left to bottom right).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,angle=0,clip]{15208fig4.ps} \end{figure} Figure 4:

$c_{\rm SB}(z)$ for the clusters in Table 4. Continuous lines are approximate fits with a power law $\propto $ $(1+z)^{-\alpha }$.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,angle=0,clip]{15208fig5.ps} \end{figure} Figure 5:

Exponent $\alpha $ vs. minimum (central) temperature for clusters in Table 4. The dashed line represents Eq. (1).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,angle=0,clip]{15208f6.1.ps}\includegraphics[width=9cm,angle=0,clip]{15208f6.2.ps} \end{figure} Figure 6:

Left: distributions of $c_{\rm SB}$ for the two distant samples, RDCS+WARPS (solid, red) and 400 SD high-z (dash-dot, blue), and right: comparison between the K-corrected $c_{\rm SB}$ distribution of the local (dash, black) and the RDCS+WARPS samples.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,angle=0,clip]{15208fig7.ps} \end{figure} Figure 7:

Correlation between the single $\beta $-model parameters, $r_{\rm c}$ and $\beta $ for the two samples of high-z clusters.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,angle=0,clip]{15208fig8.ps} \end{figure} Figure 8:

X-ray soft-band luminosity $L_{\rm X}$ versus $c_{\rm SB}$. Black crosses refer to the 400 SD low-z sample, blue triangles represent the 400 SD high-z sample and the red circles correspond to the RDCS+WARPS sample. The black squares indicate the presence of a radio source in the cluster center.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,angle=0,clip]{15208f9.1.ps}\par\includegraphics[width=8.5cm,angle=0,clip]{15208f9.2.ps} \end{figure} Figure 9:

Comparison between the entropy profiles of the two distant samples (top), and the 400 SD low-z relative to the RDCS+WARPS sample (bottom).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,angle=0,clip]{15208fig10.ps} \vspace*{-0.3cm} \end{figure} Figure 10:

Distribution of the entropy measured at 20 kpc.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,angle=0,clip]{15208fig11.ps} \vspace*{-0.3cm} \end{figure} Figure 11:

Correlation between central entropy K20 and the phenomenological parameter $c_{\rm SB}$. Error bars show typical measurement errors for the low and distant samples.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,angle=0,clip]{15208fig12.ps} \vspace*{2.5mm}\end{figure} Figure 12:

Distribution of central cooling time for the local and distant samples. The dotted line marks the age of the Universe.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,angle=0,clip]{15208fig13.ps} \vspace*{2.5mm}\end{figure} Figure 13:

Correlation between central cooling time and the phenomenological parameter $c_{\rm SB}$. Error bars show typical measurement errors for the low and distant samples.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,angle=0,clip]{15208fig14.ps} \vspace*{2.5mm}\end{figure} Figure 14:

Relation between the radio luminosity of sources in close proximity to the cluster cores, $L_{1.4~{\rm GHz}}$, and the surface brightness concentration, $c_{\rm SB}$. Arrows refer to upper limits of non-detections. The dotted line at $1.1 \times 10^{25}$ WHz-1 marks the luminosity limit at z = 1 for NVSS sources, corresponding to the flux limit of 2.5 mJy.

Open with DEXTER
In the text

  \begin{figure} \par\mbox{\includegraphics[width=4cm,height=4cm,angle=0,clip]{152... ...width=4cm,height=4cm,angle=0,clip]{15208f15.3.ps} }\vspace*{-3mm} \end{figure} Figure 15:

Simulated images of strong cool-core A1835 as seen by WFXT in medium exposure (13.2 ks), at redshifts 0.5 (left), 1.0 (middle) and 1.5 (right). The images have a size of $10 \times 10$ arcmin and are displayed in logarithmic scale.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.