| Issue |
A&A
Volume 521, October 2010
|
|
|---|---|---|
| Article Number | A7 | |
| Number of page(s) | 12 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/200913650 | |
| Published online | 13 October 2010 | |
Spitzer spectral line mapping of the HH211 outflow
O. Dionatos1,2 - B. Nisini2 - S. Cabrit3 - L. Kristensen4 - G. Pineau des Forêts5,3
1 - Centre for Star and Planet Formation, Natural
History Museum of Denmark, University of Copenhagen, Øster Voldgade
5-7, 1350 Copenhagen, Denmark
2 -
INAF - Osservatorio Astronomico di Roma, via di Frascati, 33 00040 Monte Porzio Catone (RM), Italy
3 -
LERMA, Observatoire de Paris, UMR 8112 du CNRS, 61 avenue de l'Observatoire, 75014 Paris, France
4 -
Leiden Observatory, Leiden University, Niels Bohrweg 2, 2300 CA Leiden, The Netherlands
5 -
Institut Astrophysique Spatiale (IAS), UMR 8617, CNRS, Université Paris-Sud 11, Bâtiment 121, 91405 Orsay Cedex, France
Received 12 November 2010 / Accepted 3 June 2010
Abstract
Context. Jets from the youngest protostars are often
detected only at mm wavelengths, by means of line emission of CO and
SiO. However, it is not yet clear whether these jets are mostly
molecular or atomic, nor whether they trace ejected gas or an entrained
layer around an embedded atomic jet.
Aims. We investigate the warm gas content of the HH211 protostellar outflow to assess the jet mass-flux in the form of H2 and investigate the existence of an embedded atomic jet.
Methods. We employ archival Spitzer slit-scan observations of the HH211 outflow over 5.2-37 ![]() m
obtained with the low resolution IRS modules. Detected molecular and
atomic lines are interpreted by means of emission line diagnostics and
an existing grid of molecular shock models. The physical properties of
the warm gas are compared with those of other molecular jet tracers and
to the results of a similar study towards the L1448-C outflow.
m
obtained with the low resolution IRS modules. Detected molecular and
atomic lines are interpreted by means of emission line diagnostics and
an existing grid of molecular shock models. The physical properties of
the warm gas are compared with those of other molecular jet tracers and
to the results of a similar study towards the L1448-C outflow.
Results. We detected and mapped the v=0-0 S(0)-S(7) H2 lines as well as fine-structure lines of S, Fe+, and Si+. The H2 is detected to 5
![]() from the source and is characterized by a ``cool''
from the source and is characterized by a ``cool'' ![]() K and a ``warm''
K and a ``warm''
![]() K component, with an extinction
K component, with an extinction
![]() mag. The amount of cool H2
towards the jet agrees with that estimated from CO assuming fully
molecular gas. The warm component is well fitted by C-type shocks with
a low beam filling factor
mag. The amount of cool H2
towards the jet agrees with that estimated from CO assuming fully
molecular gas. The warm component is well fitted by C-type shocks with
a low beam filling factor ![]() 0.01-0.04 and a mass-flux similar to the cool H2. The fine-structure line emission arises from dense gas with ionization fraction
0.01-0.04 and a mass-flux similar to the cool H2. The fine-structure line emission arises from dense gas with ionization fraction
![]() ,
and is indicative of dissociative shocks. Line ratios with respect to
sulfur indicate that iron and silicon are depleted relative to solar
abundances by a factor
,
and is indicative of dissociative shocks. Line ratios with respect to
sulfur indicate that iron and silicon are depleted relative to solar
abundances by a factor ![]() 10-50.
10-50.
Conclusions. Spitzer spectral mapping observations reveal for the first time a cool H2 component towards the CO jet of HH211 consistent with the CO material being fully molecular and warm at ![]() 300 K.
These maps detect also for the first time an embedded atomic jet in the
HH211 outflow that can be traced close to the central source position.
Its significant iron and silicon depletion excludes an origin from
within the dust sublimation zone around the protostar. The
momentum-flux seems insufficient to entrain the CO jet, although
current uncertainties in jet speed and shock conditions are too large
to reach a definite conclusion.
300 K.
These maps detect also for the first time an embedded atomic jet in the
HH211 outflow that can be traced close to the central source position.
Its significant iron and silicon depletion excludes an origin from
within the dust sublimation zone around the protostar. The
momentum-flux seems insufficient to entrain the CO jet, although
current uncertainties in jet speed and shock conditions are too large
to reach a definite conclusion.
Key words: stars: formation - ISM: jets and outflows - ISM: individual objects: HH211-mm - infrared: ISM
1 Introduction
The process of mass accretion leading to the formation of low mass protostars is always associated with ejection of material in the form of well collimated high-velocity jets and/or wider slower bipolar outflows (Arce et al. 2007; Reipurth & Bachiller 1997). Accretion and ejection phenomena are believed to be intimately connected to the existence of a magnetized accretion disk around the forming protostar, but there has been no consensus so far about the exact ejection mechanism (Ferreira et al. 2006; Pudritz et al. 2007; Shang et al. 2007). The study of the physical properties of jets (e.g., temperature, density, abundances, mass flux) is therefore crucial to obtain indirect constraints on the mass accretion and ejection processes, especially in the case of protostars in the earliest evolutionary stages - the so-called Class 0 protostars - where the launching zone is heavily embedded in a dense cocoon of dust and gas.
Because of this high extinction, jets from the youngest Class 0 sources cannot be seen in the optical and are mostly traced in both near-IR H2 and mm CO and SiO lines (Davis & Smith 1996; McCaughrean et al. 1994; Guilloteau et al. 1992). However, it remains unclear whether the molecules trace a sheath of entrained ambient material around an unseen underlying atomic jet, or if they trace the primary jet material itself. In the latter case, the chemical composition of the jet (molecular versus atomic fraction, dust depletion) holds crucial information about the ejection zone, as the strong UV flux generated by the accretion shock should destroy dust grains and H2 molecules in the innermost regions of the disk. A wind from these inner zones would be mostly atomic even if CO and SiO are abundant - unless the mass flux is unusually large (Ruden et al. 1990).
Mid-infrared spectroscopic observations are essential to answer these questions. A Spitzer study of the innermost jet regions of the Class 0 L 1448 outflow (Dionatos et al. 2009) revealed an underlying deeply embedded atomic/ionic component, not seen in the near-IR range, as well as mid-IR H2 emission tracing the warm molecular content. Here we present a more extensive Spitzer mapping study of the HH211 outflow, a particularly interesting target that represents a ``text-book'' example of jet-driven flow.
HH211 is located in the IC 348 complex in Perseus at a distance estimated to be between 250 pc (Enoch et al. 2006), adopted in the current paper, and
![]() 320 pc (Herbig 1998; Lada et al. 2006). The driving source HH211-mm is detected in mm continuum emission (e.g. Gueth & Guilloteau 1999; Lee et al. 2007), and has been classified as a low-mass, low-luminosity Class 0 young stellar object (Froebrich 2005).
320 pc (Herbig 1998; Lada et al. 2006). The driving source HH211-mm is detected in mm continuum emission (e.g. Gueth & Guilloteau 1999; Lee et al. 2007), and has been classified as a low-mass, low-luminosity Class 0 young stellar object (Froebrich 2005).
The outflow was discovered by McCaughrean et al. (1994) in near-IR H2 emission tracing 2000 K hot, shocked gas in two
bright symmetric bowshocks separated by 0.13 pc with a faint chain of knots in between.
A few compact knots of atomic emission at optical and near-IR wavelengths (i.e.,
H![]() ,
[SII]6730 Å and [FeII]1.64
,
[SII]6730 Å and [FeII]1.64 ![]() m) are also seen
near the brightest H2 peaks (Caratti o Garatti et al. 2006; O'Connell et al. 2005; Walawender et al. 2005,2006).
The absence of any additional shock structures on larger scales makes
it the youngest outflow known so far, with a kinematical age of only
m) are also seen
near the brightest H2 peaks (Caratti o Garatti et al. 2006; O'Connell et al. 2005; Walawender et al. 2005,2006).
The absence of any additional shock structures on larger scales makes
it the youngest outflow known so far, with a kinematical age of only
![]() km s-1 (Gueth & Guilloteau 1999; Eislöffel et al. 2003a).
km s-1 (Gueth & Guilloteau 1999; Eislöffel et al. 2003a).
Low velocity CO J=2-1 (Gueth & Guilloteau 1999) and CO J=3-2 (Lee et al. 2007) observations delineate the shape of
a bipolar swept-up cavity with its ends tracing the H2
bow-shocks and its flanks connecting back to the driving source, while
the high-velocity components of the same transitions reveal an inner
well-collimated CO jet extending out to
![]() from the source.
The CO jet is also traced in SiO by means of interferometric observations of the J=1-0 (Chandler & Richer 2001), 5-4 (Hirano et al. 2006), and 8-7 (Lee et al. 2007) transitions, and single-dish multi-transition studies (Gibb et al. 2004; Nisini et al. 2002b). Excitation of these high J levels implies that the SiO jet is warmer and denser than the outflow cavity traced by low-velocity CO emission.
from the source.
The CO jet is also traced in SiO by means of interferometric observations of the J=1-0 (Chandler & Richer 2001), 5-4 (Hirano et al. 2006), and 8-7 (Lee et al. 2007) transitions, and single-dish multi-transition studies (Gibb et al. 2004; Nisini et al. 2002b). Excitation of these high J levels implies that the SiO jet is warmer and denser than the outflow cavity traced by low-velocity CO emission.
All observations reveal a highly bipolar structure, with blue- and
red-shifted lobes pointing southeast and northwest from the driving
source. The two lobes are well separated, and both this observed
morphology and the low observed radial velocities (![]() 20 km s-1, Gueth & Guilloteau 1999) imply that the inclination of the outflow is less than 10
20 km s-1, Gueth & Guilloteau 1999) imply that the inclination of the outflow is less than 10![]() from the plane of the sky (Gueth & Guilloteau 1999; Chandler & Richer 2001; Lee et al. 2007).
This simple geometry is favorable to modelling. Indeed, the CO cavity
shape is well fitted by a dynamical model of jet-driven bowshock
propagating into a medium of decreasing density (Gueth & Guilloteau 1999). This interpretation is supported by fitting
the near-IR line fluxes and morphologies at the apex of the redshifted lobe with a series of bowshocks (O'Connell et al. 2005). A Spitzer map obtained at the tip of the blue lobe indicates a higher excitation 40 km s-1 dissociative shock on that side, with a substantial UV flux (Tappe et al. 2008).
from the plane of the sky (Gueth & Guilloteau 1999; Chandler & Richer 2001; Lee et al. 2007).
This simple geometry is favorable to modelling. Indeed, the CO cavity
shape is well fitted by a dynamical model of jet-driven bowshock
propagating into a medium of decreasing density (Gueth & Guilloteau 1999). This interpretation is supported by fitting
the near-IR line fluxes and morphologies at the apex of the redshifted lobe with a series of bowshocks (O'Connell et al. 2005). A Spitzer map obtained at the tip of the blue lobe indicates a higher excitation 40 km s-1 dissociative shock on that side, with a substantial UV flux (Tappe et al. 2008).
In this paper, we present archival Spitzer-IRS slit-scan observations covering most of the HH211 flow with low spectral resolution (Sect. 3), which we analyze to address the physical conditions and the molecular and dust content. In Sect. 4, the detected rotational H2 transitions are employed as probes of the physical conditions in the jet close to the driving source and the shocked gas further out, and compared with an existing grid of C and J-type shock models. Atomic lines present in our spectra are treated separately as probes of a deeply embedded atomic jet, and used to measure dust depletion. Mass fluxes are inferred for the H2 and atomic components, and compared with those measured in CO and SiO, as well as to a similar study of the inner jet of L1448. Our conclusions are presented in Sect. 5.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13650fg1.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa13650-09/Timg25.png)
|
Figure 1:
Continuum-subtracted spectrum, integrated over a region of 612 square arcseconds covering the HH211 flow ( middle),
shown in comparison with a spectrum of the off-outflow region of the same area ( top). H2
emission from the 0-0 S(0)-S(7) lines is detected in the outflow,
together with atomic emission from the ground-state transitions of
[FeII],[SiII], and [SI]. The H2 S(0) and S(1) lines are also detected in the off-outflow spectrum,
which is indicative of a diffuse line emission component not related to the HH211 flow. Diffuse emission
from PAH features, such as the 11.3 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{13650fg2.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa13650-09/Timg26.png)
|
Figure 2:
H2 v=0-0 S(2)-S(7) line intensity maps of the HH211 flow observed with the Spitzer SL module, reconstructed with a pixel scale of 3.5
|
| Open with DEXTER | |
2 Observations and data reduction
Observations were obtained with the Spitzer satellite (Werner et al. 2004)
and retrieved from the Spitzer
Public Data Archive using the Leopard software. They
had been performed as part of the ``Shock dissipation in nearby star
forming regions'' program conducted by J. Bally (P.I.). In these, the
low resolution modules (
![]() )
of the Spitzer Infrared Spectrograph (IRS, Houck et al. 2004) were used in slit-scan mode to cover an area of
)
of the Spitzer Infrared Spectrograph (IRS, Houck et al. 2004) were used in slit-scan mode to cover an area of
![]() and 157
and 157
![]() for the short low (SL) and long low (LL) modules, respectively, centered on the Class 0 source HH211-mm (
for the short low (SL) and long low (LL) modules, respectively, centered on the Class 0 source HH211-mm (
![]() :03h43m56.5s,
:03h43m56.5s,
![]() :+32d00m51s).
A perpendicular scan step equal to the slit width of each module was
used, with a total integration time of 171 min. The combination of both
IRS low resolution modules gives a complete wavelength coverage of
5.2-37.0
:+32d00m51s).
A perpendicular scan step equal to the slit width of each module was
used, with a total integration time of 171 min. The combination of both
IRS low resolution modules gives a complete wavelength coverage of
5.2-37.0 ![]() m.
m.
Initial data processing was performed at the Spitzer Science Center using version 15 of the processing pipeline. Spectral data-cubes were compiled using the CUBISM software package (Smith et al. 2007) and bad/rogue pixels were masked by means of visual inspection.
Figure 1 presents the extracted continuum-subtracted spectrum, integrated over a region encompassing
the HH211 flow. The full series of H2
pure rotational lines (S(0)-S(7)) were detected, along with atomic and
ionic lines from the fundamental transitions of [SI], [FeII], and
[SiII] at 25 ![]() m, 26
m, 26 ![]() m, and 35
m, and 35 ![]() m, respectively. For comparison, Fig. 1 also shows a spectrum of a region encompassing the same
area but in a direction perpendicular to the outflow. The H2 S(0) and S(1) lines are also detected in this off-outflow spectrum,
which is indicative of a diffuse line emission component not related to the HH211 flow. Diffuse emission
from PAH features, such as the 11.3
m, respectively. For comparison, Fig. 1 also shows a spectrum of a region encompassing the same
area but in a direction perpendicular to the outflow. The H2 S(0) and S(1) lines are also detected in this off-outflow spectrum,
which is indicative of a diffuse line emission component not related to the HH211 flow. Diffuse emission
from PAH features, such as the 11.3 ![]() m feature, is also evident. In Fig. 1,
we also plot the on-source spectrum for an area equal to the LL pixel
size, after subtracting the contribution of an off-source,
free-of-line-emission position. This only removes zodiacal light and
reveals the
intrinsic mid-IR continuum from the central source, which is typical of
low-luminosity Class 0 sources.
m feature, is also evident. In Fig. 1,
we also plot the on-source spectrum for an area equal to the LL pixel
size, after subtracting the contribution of an off-source,
free-of-line-emission position. This only removes zodiacal light and
reveals the
intrinsic mid-IR continuum from the central source, which is typical of
low-luminosity Class 0 sources.
Subsequent analysis consisted of the construction of individual
line emission maps, using a customized pipeline;
in this, for each spatial pixel of the data-cube, the brightness of
each spectral line of interest was calculated by fitting a Gaussian
after subtracting a local second-order polynomial baseline. The
resulting line intensity maps have a square pixel of side equal to the
slit width of the IRS module, namely 3.5
![]() and 10.5
and 10.5
![]() for the SL and LL modules, respectively, while the diffraction limit of the telescope is 2.4
for the SL and LL modules, respectively, while the diffraction limit of the telescope is 2.4
![]() and 6.0
and 6.0
![]() at
at
![]() m and 25
m and 25 ![]() m,
respectively. The astrometric accuracy of the maps was found to be good
to within the limits imposed by the pixel size of each IRS module.
m,
respectively. The astrometric accuracy of the maps was found to be good
to within the limits imposed by the pixel size of each IRS module.
3 Spectral line maps
3.1 H 2 emission
Figure 2 presents the emission line maps of the S(2)-S(7) rotational H2 lines observed with the SL-IRS modules with a 3.5
![]() sampling. Contours shape a characteristic bipolar outflow pattern, where the H2 emission is detected down to a projected angular distance
sampling. Contours shape a characteristic bipolar outflow pattern, where the H2 emission is detected down to a projected angular distance ![]() 5
5
![]() from the driving source. Further downwind, peaks of emission that can be attributed to shocked gas are observed. In the H2 S(5) map of Fig. 2, we label these peaks as B1-B3 in the southeast, blue-shifted lobe and R1-R2 in the northwest, red-shifted lobe, respectively.
from the driving source. Further downwind, peaks of emission that can be attributed to shocked gas are observed. In the H2 S(5) map of Fig. 2, we label these peaks as B1-B3 in the southeast, blue-shifted lobe and R1-R2 in the northwest, red-shifted lobe, respectively.
Figure 3 shows the H2 S(5) emission map overlaid on the high-velocity CO J = 2
![]() 1 map of Gueth & Guilloteau (1999) (upper panel) and on the SiO J = 8
1 map of Gueth & Guilloteau (1999) (upper panel) and on the SiO J = 8
![]() 7 and CO
7 and CO
![]() maps of Lee et al. (2007) (lower panels). The grayscale background shows the near-IR H2 v=1-0 S(1) images from McCaughrean et al. (1994) or Hirano et al. (2006). Overall, the spatial correspondence between mid-IR and near-IR H2
lines is quite good except towards the broadest parts of the outflow
cavity, where the mid-IR emission appears to trail behind the near-IR
one.
maps of Lee et al. (2007) (lower panels). The grayscale background shows the near-IR H2 v=1-0 S(1) images from McCaughrean et al. (1994) or Hirano et al. (2006). Overall, the spatial correspondence between mid-IR and near-IR H2
lines is quite good except towards the broadest parts of the outflow
cavity, where the mid-IR emission appears to trail behind the near-IR
one.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{13650fg3.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa13650-09/Timg34.png)
|
Figure 3:
(Upper panel) H2 v=0-0 S(5) map (green contours) superimposed over the high velocity CO J = 2-1 map of Gueth & Guilloteau (1999); ( Lower panels) Inner part of the H2 v=0-0 S(5) map (green contours) superimposed on the SiO J = 8-7 and the CO J = 3-2 maps of Lee et al. (2007). The grayscale backgrounds show the H2 v=1-0 S(1) image from McCaughrean et al. (1994) ( top panel) or Hirano et al. (2006) (lower panels). The slight S-shape pattern of the S(5) emission map follows the brightness asymmetry of the cavity seen in the 2.12 |
| Open with DEXTER | |
In the southeastern - blue lobe, the peak of mid-IR H2 emission closest to the source (B1) coincides with the 2.12 ![]() m H2 knot G in the nomenclature of McCaughrean et al. (1994), the BII knot of the CO jet (Gueth & Guilloteau 1999) and knots BK4-6 in the SiO jet (Lee et al. 2007) (see lower panel of Fig. 3). Therefore, it appears to trace mostly the jet beam.
Further outwards, peak B2 is centered on a hole behind
the bowshock rim delineated in the near-IR image, while peak B3 appears
to lie on the bow rim (note however that the spatial extent of our SL
map does not fully cover the tip of this region).
m H2 knot G in the nomenclature of McCaughrean et al. (1994), the BII knot of the CO jet (Gueth & Guilloteau 1999) and knots BK4-6 in the SiO jet (Lee et al. 2007) (see lower panel of Fig. 3). Therefore, it appears to trace mostly the jet beam.
Further outwards, peak B2 is centered on a hole behind
the bowshock rim delineated in the near-IR image, while peak B3 appears
to lie on the bow rim (note however that the spatial extent of our SL
map does not fully cover the tip of this region).
![\begin{figure}
\par\includegraphics[width=13.2cm,clip]{13650fg4.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa13650-09/Timg35.png)
|
Figure 4:
Intensity maps of the HH211 flow in the H2S(1) and S(0) lines ( top row) and the atomic [SiII]35 |
| Open with DEXTER | |
Symmetrically on the redshifted side, the mid-IR H2 emission close to the source forms an extended curving ``finger'' tracing both the jet and the cavity wall north of it, as seen in the near-IR (see Fig. 3) and peak R1 coincides with the near-IR knot F of McCaughrean et al. (1994). However, peak R2 is again centered on the cavity behind the bright bow rim traced in the near-IR. The spatial offset between B2 and R2 with respect to the near-IR counterparts suggests that mid-IR emission in these broad regions may be tracing the outer bow-shock wings where gas is expected to be in lower excitation conditions.
![\begin{figure}
\par\includegraphics[width=15.3cm,clip]{13650fg5.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa13650-09/Timg36.png)
|
Figure 5:
Excitation diagrams of H2 in various pixel sizes. (Left) H2 columns in peak R1 from transitions in the SL module in 3.5
|
| Open with DEXTER | |
The top row of Fig. 4 presents the emission maps of the S(0)-S(1) rotational H2 lines observed with the LL-IRS modules with a 10.5
![]() sampling. Despite the lower angular resolution compared to the SL module, the H2S(1) line clearly delineates the same outflow pattern as in Fig. 3.
As discussed in Sect. 2, faint extended diffuse emission is also
present, and becomes mostly evident at the north end of the map;
diffuse emission is even more apparent in the H2 S(0) line map of Fig. 4.
sampling. Despite the lower angular resolution compared to the SL module, the H2S(1) line clearly delineates the same outflow pattern as in Fig. 3.
As discussed in Sect. 2, faint extended diffuse emission is also
present, and becomes mostly evident at the north end of the map;
diffuse emission is even more apparent in the H2 S(0) line map of Fig. 4.
This diffuse brightness may be caused by an extended
photo-dissociation region (PDR) created at the cloud surface by the illumination of FUV radiation
from nearby stars. The existence of a diffuse PDR is strongly supported
by the detection of diffuse PAH emission, which is indicative of UV
radiation in the field. The H2 diffuse emission has a brightness of the order of
10-5 erg/s/cm2 for both the S(0) and S(1) lines: according to the
Kaufman et al. (1999) model,
this intensity
is compatible with a PDR of density 104 cm-3 or higher and a FUV field of the
order of 102 times than the average interstellar field, measured in units of G0 (i.e.
in units of
![]() erg cm-2 s-1).
The most likely candidate to produce the diffuse PDR is the
erg cm-2 s-1).
The most likely candidate to produce the diffuse PDR is the ![]() Per B0.5 star,
located at a projected distance of about 15
Per B0.5 star,
located at a projected distance of about 15
![]() north of the HH211 system.
The FUV field of this star (assuming an effective temperature of 25 000 K, Hernández et al. 2005),
diluted for the distance, can account for a G
north of the HH211 system.
The FUV field of this star (assuming an effective temperature of 25 000 K, Hernández et al. 2005),
diluted for the distance, can account for a G
![]() ,
which is compatible with the estimation
given above, taking also into consideration projecting factors and partial field absorption
along the path.
We cannot exclude that part of the extended S(0) and S(1) H2 emission also originates in other outflows located
north and south of HH211-mm, seen in both optical and near-IR narrow band imaging of the region (Eislöffel et al. 2003b; Walawender et al. 2006).
However, no close spatial correspondence is evident at our spatial resolution.
,
which is compatible with the estimation
given above, taking also into consideration projecting factors and partial field absorption
along the path.
We cannot exclude that part of the extended S(0) and S(1) H2 emission also originates in other outflows located
north and south of HH211-mm, seen in both optical and near-IR narrow band imaging of the region (Eislöffel et al. 2003b; Walawender et al. 2006).
However, no close spatial correspondence is evident at our spatial resolution.
3.2 Atomic emission
The bottom row of Fig. 4 presents the emission line maps of
[SiII]35 ![]() m, [SI]25
m, [SI]25 ![]() m, and [FeII]26
m, and [FeII]26 ![]() m obtained from the LL-IRS modules with a 10.5
m obtained from the LL-IRS modules with a 10.5
![]() sampling.
The emission from the atomic and ionic lines is substantially weaker than that of the H2 lines.
However, unlike H2
lines that are not detected close to the driving source, all three fine
structure transition contours are continuous, indicative of emission
very close to the protostar HH211-mm. Morphologically, the [SI] and
[FeII] maps peak at the blue lobe bow-shock
sampling.
The emission from the atomic and ionic lines is substantially weaker than that of the H2 lines.
However, unlike H2
lines that are not detected close to the driving source, all three fine
structure transition contours are continuous, indicative of emission
very close to the protostar HH211-mm. Morphologically, the [SI] and
[FeII] maps peak at the blue lobe bow-shock![]() . Emission from [SiII] instead shows strong peaks on both the blue and red bow-shocks.
. Emission from [SiII] instead shows strong peaks on both the blue and red bow-shocks.
The enhanced atomic - ionic emission on the blue-lobe bowshock is
evidence of a highly energetic
interaction of the underlying jet with the ambient material. In the
same region, a wealth of other molecular and ionic lines such as OH, H2O, HD and [NeII] were mapped with Spitzer by Tappe et al. (2008), which collectively infer a strong UV flux typical of a 40 km s-1 dissociative shock. Such high velocity shocks in this region is also
consistent with the detection of optical H![]() and [SII] emission spots (Walawender et al. 2005,2006). In the following, we demonstrate that rotational H2 lines over the HH 211 outflow appear to trace slower shocks, either internal to the jet or in bowshock wings.
and [SII] emission spots (Walawender et al. 2005,2006). In the following, we demonstrate that rotational H2 lines over the HH 211 outflow appear to trace slower shocks, either internal to the jet or in bowshock wings.
Table 1:
Physical properties of the warm H2 component from H2 v=0-0 S(2)-S(7) lines extracted at the SL (3.5
![]() )
scale.
)
scale.
Table 2:
Physical properties of the cool H2 component from H2 v=0-0 S(0)-S(2) lines extracted at the LL (10.5
![]() )
scale.
)
scale.
4 Excitation conditions and mass fluxes
4.1 H 2 emission
4.1.1 Ortho to para ratio, extinction, and temperature components
The H2 pure rotational transitions are easily thermalized in protostellar outflow environments owing to their low critical densities (
![]() cm-3) and can be used to probe temperatures in the range between
cm-3) and can be used to probe temperatures in the range between ![]() 300
and 1500 K. The most direct way to estimate the temperature of the
emitting gas is by means of an excitation diagram (EXD); this involves
plotting the quantities
300
and 1500 K. The most direct way to estimate the temperature of the
emitting gas is by means of an excitation diagram (EXD); this involves
plotting the quantities
![]() against Eu,J, where Nu,J and Eu,J are the column density and the energy of the upper level, and gu the statistical weight including the spin degeneracy (2S+1). Considering LTE conditions, the values of these quantities for the observed H2 transitions
should fall on a straight line, from the inverse slope of which the
excitation temperature can be derived. Deviations from this linear
correlation can be used to constrain other physical properties, such as
the H2 ortho-to-para ratio (hereafter, OTP) and the optical extinction AV, as described below.
against Eu,J, where Nu,J and Eu,J are the column density and the energy of the upper level, and gu the statistical weight including the spin degeneracy (2S+1). Considering LTE conditions, the values of these quantities for the observed H2 transitions
should fall on a straight line, from the inverse slope of which the
excitation temperature can be derived. Deviations from this linear
correlation can be used to constrain other physical properties, such as
the H2 ortho-to-para ratio (hereafter, OTP) and the optical extinction AV, as described below.
Deviations of the OTP from its LTE value are reflected by vertical displacements between the ortho and para transitions in the EXD, forming a ``saw-tooth'' pattern between the two H2 species. The observed OTP was estimated by examining the alignment of the S(5) data point with the neighboring S(4) and S(6) transitions, following the method outlined in Wilgenbus et al. (2000); in all cases, the spatial OTP variations are small, and values lie very close, within the statistical error limits, to the high-temperature LTE value of 3.
The H2 S(3) transition at 9.7 ![]() m
is sensitive to the amount of dust along the line of sight, being
located within a wide-band silicate absorption feature at the same
wavelength; consequently, a visual extinction value can be estimated by
comparing the alignment of the S(3) point with those of S(2) and S(4),
having previously corrected for any deviations of the OTP ratio from
the equilibrium value. Visual extinction is then estimated by assuming
an
A9.7/AV ratio equal to 0.087 (Rieke & Lebofsky 1985). AV
is found to exhibit no regular pattern along the outflow and to range
between 7 and 9 mag, being consistent with previous estimates of 7-15
mag
by McCaughrean et al. (1994) and Caratti o Garatti et al. (2006)
m
is sensitive to the amount of dust along the line of sight, being
located within a wide-band silicate absorption feature at the same
wavelength; consequently, a visual extinction value can be estimated by
comparing the alignment of the S(3) point with those of S(2) and S(4),
having previously corrected for any deviations of the OTP ratio from
the equilibrium value. Visual extinction is then estimated by assuming
an
A9.7/AV ratio equal to 0.087 (Rieke & Lebofsky 1985). AV
is found to exhibit no regular pattern along the outflow and to range
between 7 and 9 mag, being consistent with previous estimates of 7-15
mag
by McCaughrean et al. (1994) and Caratti o Garatti et al. (2006)![]() .
.
Considering an average value of AV equal to 8 mag across the map, we dereddened all the detected H2 lines falling in the SL range (i.e. S(2) to S(7)) using the extinction law of Rieke & Lebofsky (1985). For all the points of the SL data cube where at least 3 H2 lines are detected above 3-![]() confidence level, we calculated the excitation temperature from the
slope of a least squares fit to the dereddened data points in the EXD.
An example of these operations is shown in the left panel of Fig. 5 in the case of the R1 peak.
confidence level, we calculated the excitation temperature from the
slope of a least squares fit to the dereddened data points in the EXD.
An example of these operations is shown in the left panel of Fig. 5 in the case of the R1 peak.
The results for the whole HH211 region are summarized in Fig. 6 in the form of an excitation temperature map. Common morphological characteristics between the excitation temperature map and the H2 S(2)-S(7) emissions are evident; peaks in excitation temperature tend to coincide with peaks of emission. At those peaks, temperature reaches values up to 1200 K, while in the more diffuse outflow regions the temperature is as low as 700 K. In Table 1, we report the derived excitation temperatures with this method for the peaks of the S(5) emission along the blue and the red lobes of the outflow.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{13650fg6.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa13650-09/Timg51.png)
|
Figure 6:
Excitation temperature map of the ``warm'' H2 component deduced from
the SL module map (3.5
|
| Open with DEXTER | |
In addition to the ``warm'' H2 component at ![]() 1100 K
indicated by the S(2)-S(7) lines, there is also evidence of a ``cool''
component from the S(0) and S(1) lines detected in the LL module. This
is illustrated in the central panel of Fig. 5, which shows an EXD of the R1+R2 region in the LL 10.5
1100 K
indicated by the S(2)-S(7) lines, there is also evidence of a ``cool''
component from the S(0) and S(1) lines detected in the LL module. This
is illustrated in the central panel of Fig. 5, which shows an EXD of the R1+R2 region in the LL 10.5
![]() pixel, including the S(0) and S(1) datapoints. For consistency, the
fluxes of S(2) to S(7) lines from the SL module were re-extracted at
the coarser LL module sampling. Because of the extended diffuse
emission, the S(0) line flux was obtained after subtracting the ambient
contribution estimated in adjacent off-outflow regions.
pixel, including the S(0) and S(1) datapoints. For consistency, the
fluxes of S(2) to S(7) lines from the SL module were re-extracted at
the coarser LL module sampling. Because of the extended diffuse
emission, the S(0) line flux was obtained after subtracting the ambient
contribution estimated in adjacent off-outflow regions.
While the resampled S(3)-S(7) emission retains the same ``warm''
temperature ![]() 1100 K, the data points for the S(0)-S(2) transitions show a steeper slope, which is evidence of a ``cool'' component at
1100 K, the data points for the S(0)-S(2) transitions show a steeper slope, which is evidence of a ``cool'' component at ![]() K not probed by the higher J
transitions. Another interesting result is that column densities
obtained from the S(2)-S(7) lines in the LL pixel are smaller than in
the SL pixel of 3.5
K not probed by the higher J
transitions. Another interesting result is that column densities
obtained from the S(2)-S(7) lines in the LL pixel are smaller than in
the SL pixel of 3.5
![]() ,
indicating that the warm component does not fill the LL pixel.
,
indicating that the warm component does not fill the LL pixel.
A similarly resampled EXD towards the LL1 peak also reveals a cool component at 300 K, in addition to the warm component traced by the J>2 lines. (see right-hand panel of Fig. 5). This resampling of the SL data was not possible at the LL peak B2+B3, as part of the corresponding LL pixel falls beyond the SL map coverage. This double temperature structure differs from a similar Spitzer analysis of the L1448 outflow where all v=0-0 lines from S(0) to S(7) are interpreted in terms of a dominant, single temperature component at 600-900 K.
4.1.2 Column densities and mass fluxes
The total H2 column density of the ``cool'' and ``warm''
components can be measured from the intersection of the linear fit to
the data points in the EXD with the N/g axis, multiplied by the partition function
![]() .
The later is estimated for the given temperatures, summing up for the first 35 energy levels of H2. Derived column densities for the two temperature components are reported in Tables 1 and 2 and range from
.
The later is estimated for the given temperatures, summing up for the first 35 energy levels of H2. Derived column densities for the two temperature components are reported in Tables 1 and 2 and range from
![]() for the warm component (averaged over the SL pixel size)
to
for the warm component (averaged over the SL pixel size)
to
![]() cm-2 for the cool component (averaged over the LL pixel size).
cm-2 for the cool component (averaged over the LL pixel size).
As already mentioned in the previous section, the inner peak of H2 emission at B1/LL1 coincides with peaks of the underlying CO and SiO jet; it is therefore instructive to compare the H2 column densities with those deduced from CO, taking into account the differing beam sizes, to investigate possible physical connections between the different tracers.
Lee et al. (2007) estimate an H2 column towards the inner CO jet of
![]() 1020 cm-2 in their 1
1020 cm-2 in their 1
![]() beam,
assuming an excitation temperature of 100 K and
a standard CO/H2 abundance ratio of
beam,
assuming an excitation temperature of 100 K and
a standard CO/H2 abundance ratio of
![]() (i.e. a fully molecular gas).
If the H2
mid-IR emission arises from the same narrow jet and is relatively
uniform along the jet axis, our derived column densities have to be
corrected for the different beam sizes across the jet
by a factor = pixel size / 1
(i.e. a fully molecular gas).
If the H2
mid-IR emission arises from the same narrow jet and is relatively
uniform along the jet axis, our derived column densities have to be
corrected for the different beam sizes across the jet
by a factor = pixel size / 1
![]() .
This increases the H2 columns
to
.
This increases the H2 columns
to
![]() cm-2 for the ``warm'' component, and to
cm-2 for the ``warm'' component, and to
![]() cm-2 for the ``cool'' component. This latter value is in excellent agreement with the CO-derived one. This coincidence
suggests that the ``cool'' H2 gas detected by Spitzer towards LL1 could be tracing the same material as its CO equivalent, which would then indeed be mostly molecular.
We also note that the temperature
of 300 K of the cool H2 matches that inferred from SiO line ratios in the jet (Hirano et al. 2006).
cm-2 for the ``cool'' component. This latter value is in excellent agreement with the CO-derived one. This coincidence
suggests that the ``cool'' H2 gas detected by Spitzer towards LL1 could be tracing the same material as its CO equivalent, which would then indeed be mostly molecular.
We also note that the temperature
of 300 K of the cool H2 matches that inferred from SiO line ratios in the jet (Hirano et al. 2006).
In contrast, the warm H2 component column density corrected for beam dilution across the jet
is 10 times lower than that of the CO jet. This may indicate that the warm H2 emission close to the source arises only from a lower-density outer envelope around the CO jet. Alternatively, the warm H2 component may trace thin shock-heated zones within the CO jet, thus filling only a fraction of the 3.5
![]() SL
pixel length along the jet and being affected by additional beam
dilution. We investigate the shock hypothesis in more detail in
Sect. 4.2).
SL
pixel length along the jet and being affected by additional beam
dilution. We investigate the shock hypothesis in more detail in
Sect. 4.2).
We may also determine a rough estimate of the one-sided mass flux of the cool and warm H2 components, assuming a uniform laminar flow across the corresponding pixel, using the relationship from Dionatos et al. (2009)
where
The value of ![]() is quite uncertain. Taking into account the radial velocities in the range 5-20 km s-1 measured for the near-IR H2 knots in the study of Salas et al. (2003), and assuming an inclination angle of between 5
is quite uncertain. Taking into account the radial velocities in the range 5-20 km s-1 measured for the near-IR H2 knots in the study of Salas et al. (2003), and assuming an inclination angle of between 5![]() and 10
and 10![]() (see Sect. 1),
tangential velocities may vary within the range 30-230 km s-1, introducing an absolute uncertainty of a factor 3 either way in the inferred
(see Sect. 1),
tangential velocities may vary within the range 30-230 km s-1, introducing an absolute uncertainty of a factor 3 either way in the inferred ![]() values.
In the following, we adopt
values.
In the following, we adopt
![]() km s-1 for ease of comparison with earlier work,
bearing in mind that
km s-1 for ease of comparison with earlier work,
bearing in mind that ![]() values scale proportionally to the assumed velocity.
In Col. 6 of Tables 1 and 2, we report the resulting
values scale proportionally to the assumed velocity.
In Col. 6 of Tables 1 and 2, we report the resulting ![]() for the peaks of emission along the outflow, for both temperature components.
for the peaks of emission along the outflow, for both temperature components.
For the cool H2 gas component, the laminar mass-flux is
![]() yr-1.
For comparison, the one-sided jet mass-loss rate based on CO J=3-2 emission obtained by Lee et al. (2007) is
yr-1.
For comparison, the one-sided jet mass-loss rate based on CO J=3-2 emission obtained by Lee et al. (2007) is
![]() yr-1, assuming the same velocity of 100 km s-1
and a compression factor of 3. Adjusting their estimate for helium, and
uncorrecting for compression, the laminar mass flux of the CO jet rises
to
yr-1, assuming the same velocity of 100 km s-1
and a compression factor of 3. Adjusting their estimate for helium, and
uncorrecting for compression, the laminar mass flux of the CO jet rises
to
![]() yr-1; this is in excellent agreement with the cool H2 laminar mass flux estimated here, and is again consistent with fluxes both tracing the same fully molecular gas.
yr-1; this is in excellent agreement with the cool H2 laminar mass flux estimated here, and is again consistent with fluxes both tracing the same fully molecular gas.
The warm H2 laminar mass-flux is 15-30 times lower at
![]() yr
yr
![]() .
Similar mass-flux estimates were inferred from the pure rotational H2 lines along the outflow of L1448 (Dionatos et al. 2009,
.
Similar mass-flux estimates were inferred from the pure rotational H2 lines along the outflow of L1448 (Dionatos et al. 2009,
![]() yr-1), where similar H2 columns were measured
yr-1), where similar H2 columns were measured![]() .
We note however that if the warm H2 does not trace a laminar flow as assumed, but arises in a single shock within the pixel, then the
relevant emitting length
.
We note however that if the warm H2 does not trace a laminar flow as assumed, but arises in a single shock within the pixel, then the
relevant emitting length ![]() along the flow will be generally narrower than the SL pixel size, and
the true mass flux will be higher than listed in Table 1. Mass-fluxes of the warm component in the case of shock hypothesis are presented in the next section.
along the flow will be generally narrower than the SL pixel size, and
the true mass flux will be higher than listed in Table 1. Mass-fluxes of the warm component in the case of shock hypothesis are presented in the next section.
4.2 Shock models for the warm H 2 component
As pointed out in Sect. 4.1, peaks of warm (![]() )
H2 emission coincide with peaks of temperature (Fig. 6)
and possibly correspond to regions of shocked gas. To constrain the
shock conditions in these regions, we employ the existing shock model
grid described in the work of Kristensen et al. (2007), which is based on the MHD-VODE multi-fluid steady shock code of Flower & Pineau des Forêts (2003). The grid includes both continuous (C) and jump (J) type shocks and predicts the H2 lines brightness for various values of pre-shock density (
)
H2 emission coincide with peaks of temperature (Fig. 6)
and possibly correspond to regions of shocked gas. To constrain the
shock conditions in these regions, we employ the existing shock model
grid described in the work of Kristensen et al. (2007), which is based on the MHD-VODE multi-fluid steady shock code of Flower & Pineau des Forêts (2003). The grid includes both continuous (C) and jump (J) type shocks and predicts the H2 lines brightness for various values of pre-shock density (
![]() ), shock velocity (
), shock velocity (![]() ), initial OTP ratio (
), initial OTP ratio (
![]() ), and transverse magnetic field density (
), and transverse magnetic field density (![]() ). The ranges of parameters investigated here are
). The ranges of parameters investigated here are
-
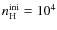 to 107 cm-3 by alternating factors of 5 and 2;
to 107 cm-3 by alternating factors of 5 and 2;
-
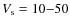 km s-1 with a step of 1 km s-1;
km s-1 with a step of 1 km s-1;
-
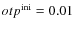 ,
1, 2, 3;
,
1, 2, 3;
-
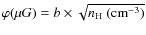 ,
where we fix b=1 for C and b=0 for J-type shocks.
,
where we fix b=1 for C and b=0 for J-type shocks.
We employed a ![]() fitting method to optimally reproduce the observed H2 emission selecting the most closely matching C or J-type steady shock models from the grid. The
fitting method to optimally reproduce the observed H2 emission selecting the most closely matching C or J-type steady shock models from the grid. The ![]() - fitting is performed with and without considering the S(2)
transition, since the latter may be dominated by the cool component
(see Fig. 5).
- fitting is performed with and without considering the S(2)
transition, since the latter may be dominated by the cool component
(see Fig. 5).
Table 3: Parameters of best-fit shock models of the S(3) to S(7) lines.
4.2.1 C-shocks
As a general trend, we found that steady C-shock models are able to
reproduce the observed S(2)-S(7) brightnesses only if we assume a small
beam-filling factor. For this reason we applied our ![]() fits to relative line brightnesses, scaled to the H2
S(5) line; to obtain the best-fitting models, we then calculated a
beam-filling factor as the average ratio of the observed to model line
brightness.
fits to relative line brightnesses, scaled to the H2
S(5) line; to obtain the best-fitting models, we then calculated a
beam-filling factor as the average ratio of the observed to model line
brightness.
In Fig. 7 we plot the EXDs of the best-fit ![]() models for each preshock density, scaled by the corresponding beam
filling factor, along with the observed data (filled circles) for the
peak of emission R1; we note that beam-filling factors decrease for
increasing values of density. There is a strong degeneracy among the
models, with a very small spread in column densities for
models for each preshock density, scaled by the corresponding beam
filling factor, along with the observed data (filled circles) for the
peak of emission R1; we note that beam-filling factors decrease for
increasing values of density. There is a strong degeneracy among the
models, with a very small spread in column densities for
![]() in the range between
in the range between
![]() and 107 cm-3 and velocities in the range 10-13 km s-1, although models for lower values of
and 107 cm-3 and velocities in the range 10-13 km s-1, although models for lower values of
![]() and velocities up to 30 km s-1 cannot be excluded; each one of these models can account fairly well for the observed emissions.
and velocities up to 30 km s-1 cannot be excluded; each one of these models can account fairly well for the observed emissions.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{13650fg7.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa13650-09/Timg92.png)
|
Figure 7:
Steady 1D C-shock model fits to the excitation diagram of the S(2)-S(7) lines at the peak of emission R1 in a 3.5
|
| Open with DEXTER | |
Figure 8 presents the EXD of most closely matching C-type shocks (red squares, always scaled by the corresponding beam filling factor) along with the observed data points (filled circles), for the peaks of emission observed along the outflow. The input parameters of the models are reported in Table 3. All C-shock models predict moderate shock velocities (10-15 km s-1) and an initial ortho-to-para ratio at the high temperature LTE value of 3.
Steady C-shock models reproduce the data only if we consider low beam-filling factors
![]() ,
or in other words a shock area
,
or in other words a shock area
![]() ,
corresponding to a typical size of
,
corresponding to a typical size of
![]() .
These dimensions are comparable to the reported jet width <1
.
These dimensions are comparable to the reported jet width <1
![]() in the interferometric CO and SiO maps of Lee et al. (2007). High post-shock densities in the same range as the best fit C-shock models (
in the interferometric CO and SiO maps of Lee et al. (2007). High post-shock densities in the same range as the best fit C-shock models (
![]() cm-3) were retrieved in the jet by SiO emission studies (Hirano et al. 2006; Nisini et al. 2002b; Lee et al. 2007), supporting our modeling results. The shock models predict thin H2 post-shock cooling zones of
cm-3) were retrieved in the jet by SiO emission studies (Hirano et al. 2006; Nisini et al. 2002b; Lee et al. 2007), supporting our modeling results. The shock models predict thin H2 post-shock cooling zones of
![]() ,
much smaller than the SL pixel size of 3.5
,
much smaller than the SL pixel size of 3.5
![]() ,
explaining the small warm column densities derived in the previous
section. The cooling zone is also smaller than the shock surface size
inferred from the filling factor, as required for the 1D planar
shock approximation to be locally valid.
,
explaining the small warm column densities derived in the previous
section. The cooling zone is also smaller than the shock surface size
inferred from the filling factor, as required for the 1D planar
shock approximation to be locally valid.
If the warm H2 emission indeed traces low-velocity
internal shocks within a fast jet beam, we may infer that the jet
mass-flux from the pre-shock density and the shock area is given by:
Considering a pre-shock density of
However, SiO is observed only within ![]() 15
15
![]() from the source, therefore pre-shock densities of
from the source, therefore pre-shock densities of
![]() cm-3 may apply only to the B1 region. In addition, the H2
emission in our maps remains unresolved only close to the driving
source. Further out at the bow-shocks, the emission appears slightly
resolved at the 3.5
cm-3 may apply only to the B1 region. In addition, the H2
emission in our maps remains unresolved only close to the driving
source. Further out at the bow-shocks, the emission appears slightly
resolved at the 3.5
![]() scale. A small
scale. A small
![]() would therefore imply that the bow-shock surface is highly patchy.
This is a reasonable possibility, since HST observations in several outflows have shown that what
appears to be an individual bow-shock at low resolution can be resolved into many
substructures of sub-arcsec scale (e.g. HH2 in Orion, Bally et al. 2002). In HH211, SMA observations, performed with a resolution of
would therefore imply that the bow-shock surface is highly patchy.
This is a reasonable possibility, since HST observations in several outflows have shown that what
appears to be an individual bow-shock at low resolution can be resolved into many
substructures of sub-arcsec scale (e.g. HH2 in Orion, Bally et al. 2002). In HH211, SMA observations, performed with a resolution of ![]() 1
1
![]() (Lee et al. 2007), show indeed
that the CO emission is highly clumped, in both the high velocity jet and
along the low velocity cavity ahead of the bow-shocks.
(Lee et al. 2007), show indeed
that the CO emission is highly clumped, in both the high velocity jet and
along the low velocity cavity ahead of the bow-shocks.
An alternative explanation of the small beam-filling factor in
the outer HH211 bow-shocks might be that the pre-shock density drops to
![]() 104 cm-3, so that the cooling length becomes comparable to the 3.5
104 cm-3, so that the cooling length becomes comparable to the 3.5
![]() pixel size; the hypothesis underlining our model comparison, that the
whole cooling zone fits inside the pixel, would then become invalid.
Indeed, O'Connell et al. (2005)
derived a low pre-shock density in the R1 and R2 regions by
fitting a 3D C-type bow-shocks to the near-IR ro-vibrational H2 lines. However, no predictions for the mid-IR H2 emissions were provided. Extension to the 3D bow-shock geometry of the model applied here (Gustafsson et al. 2010) will be needed to perform more reliable modeling of the outer bowshocks of HH211 than possible in the present analysis.
pixel size; the hypothesis underlining our model comparison, that the
whole cooling zone fits inside the pixel, would then become invalid.
Indeed, O'Connell et al. (2005)
derived a low pre-shock density in the R1 and R2 regions by
fitting a 3D C-type bow-shocks to the near-IR ro-vibrational H2 lines. However, no predictions for the mid-IR H2 emissions were provided. Extension to the 3D bow-shock geometry of the model applied here (Gustafsson et al. 2010) will be needed to perform more reliable modeling of the outer bowshocks of HH211 than possible in the present analysis.
![\begin{figure}
\par\includegraphics[width=16cm,clip]{13650fg8.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa13650-09/Timg104.png)
|
Figure 8:
Excitation diagrams for all emission peaks mapped with the SL module;
observed points (filled circles with error bars), are displayed along
with best |
| Open with DEXTER | |
4.2.2 J-shocks and non-steady C-shocks
In the case of J-shocks, absolute brightness can be fairly well matched
by models and beam-filling factors < 1 were not necessary to be
considered. The predicted pre-shock densities for J-shock models
![]() cm-3
are lower than those of the best fit C-shock ones. As a general trend
though, the best-fit J-shock models, represented by blue triangles in
Fig. 8 and listed in Table 4, cannot reproduce at the same time the slope of the observed data points, except for the red-shifted bowshock (R1 and R2).
cm-3
are lower than those of the best fit C-shock ones. As a general trend
though, the best-fit J-shock models, represented by blue triangles in
Fig. 8 and listed in Table 4, cannot reproduce at the same time the slope of the observed data points, except for the red-shifted bowshock (R1 and R2).
An analogous behavior was noted by Giannini et al. (2006), who used models produced by the same code of Flower & Pineau des Forêts (2003) to study the conditions of the HH54 outflow. Considering only the rotational H2 emission in reported excitation diagrams, Giannini et al. (2006) found that steady C-type shocks overpredict the observed v=0
column densities, whereas J-type shocks provide closer fits but cannot
at the same time reproduce the observed slope. In the case of HH54, it
is concluded that a non-steady, truncated C-shock with an embedded
J-type front (C+J shock) optimally reproduces the observed H2 emission. The same conclusion was also reached in the case of L1157 (Gusdorf et al. 2008a).
The overall effect as clearly evident in excitation diagrams is to
lower the column densities of low excitation energy levels (truncated
C-precursor) and increase the column densities of the rovibrational
energy levels of H2, excited in the J-type front (Flower et al. 2003).
In our case, such models may fit our mid-IR data in the outer bowshocks
without the need to consider a beam filling factor <1. A more
detailed comparison with unsteady C+J-shock models would be needed to
test this possibility, although such models were not included in our
adopted grid as the age of the shock would have, again, added an extra
free parameter to already degenerate fits. The shock ages would have to
be much shorter than the outflow dynamical age
of about 1000 yrs to reduce by a factor of 50 the warm H2 column (typically a shock age of 1/50 of the H2 cooling time, i.e. ![]() 2 (105 cm
2 (105 cm
![]() ) yrs).
) yrs).
Table 4: Physical properties of the atomic/ionic line component.
4.3 Atomic emission
As pointed out in section Sect. 3,
all atomic/ionic emission falls within the LL IRS module and
consequently these maps are of lower spatial resolution than the SL
ones. Since atomic emission is found to be enhanced at the bow shocks
but remains significant also close to the driving source, we focused
our analysis along the jet axis including the intermediate points LL1
and LL2 (see Fig. 4) between the bow shocks, where the [FeII] 26 ![]() m line is detected. To analyze the ionic emission, we followed the method employed by Dionatos et al. (2009), and the reader is referred to this article for a detailed description.
m line is detected. To analyze the ionic emission, we followed the method employed by Dionatos et al. (2009), and the reader is referred to this article for a detailed description.
4.3.1 Electron density
As a first step, the observed emissions of [SiII] and [FeII] were employed to constrain the electron density. In Fig. 9, the ratio of [SiII]34.8 ![]() m to [FeII]26.0
m to [FeII]26.0 ![]() m
as a function of the electron density is presented, for temperatures of
500 K, 1000 K, and 4000 K (solid and dashed lines). A
statistical equilibrium model was employed that uses the first 16
levels for [FeII] (Nisini et al. 2002a), and a two level system was considered for [SiII], for which radiative and collisional rates with electrons were taken from Dufton & Kingston (1991); a solar abundance ratio of Si+/Fe+
was considered, taking into account the similar ionization potential of
the two species and the similar sputtering efficiencies of Si and Fe
atoms from olivine grains in C-shocks, according to Fig. 2 of Gusdorf et al. (2008b).
In the diagram, we plot the observed ratio limits at the bow shocks for
clarity, but the results for the other points along the jet are similar
and are listed in Table 4. Lower limits to the electron density vary between 40 and 150 cm-3 for temperatures of 4000 K and 500 K, respectively, while upper limits converge for the considered temperatures to
m
as a function of the electron density is presented, for temperatures of
500 K, 1000 K, and 4000 K (solid and dashed lines). A
statistical equilibrium model was employed that uses the first 16
levels for [FeII] (Nisini et al. 2002a), and a two level system was considered for [SiII], for which radiative and collisional rates with electrons were taken from Dufton & Kingston (1991); a solar abundance ratio of Si+/Fe+
was considered, taking into account the similar ionization potential of
the two species and the similar sputtering efficiencies of Si and Fe
atoms from olivine grains in C-shocks, according to Fig. 2 of Gusdorf et al. (2008b).
In the diagram, we plot the observed ratio limits at the bow shocks for
clarity, but the results for the other points along the jet are similar
and are listed in Table 4. Lower limits to the electron density vary between 40 and 150 cm-3 for temperatures of 4000 K and 500 K, respectively, while upper limits converge for the considered temperatures to ![]() 400 cm-3. Temperature limits lower than a few thousand K are reported in the work of Tappe et al. (2008) for the blue-shifted bow shock considering a non-LTE analysis of the three [FeII] lines (18
400 cm-3. Temperature limits lower than a few thousand K are reported in the work of Tappe et al. (2008) for the blue-shifted bow shock considering a non-LTE analysis of the three [FeII] lines (18 ![]() m, 26
m, 26 ![]() m, and 35
m, and 35 ![]() m) that are detected with the high resolution IRS modules. Based on this, we
restricted the electron density lower limit to 100 cm-3 by assuming a maximum temperature of 3000 K.
m) that are detected with the high resolution IRS modules. Based on this, we
restricted the electron density lower limit to 100 cm-3 by assuming a maximum temperature of 3000 K.
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{13650fg9.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa13650-09/Timg109.png)
|
Figure 9:
Diagnostic diagram of the [SiII]35 |
| Open with DEXTER | |
4.3.2 Gas phase depletion
We investigate the depletion onto grains following the analysis of Dionatos et al. (2009).
We calculate the gas phase abundance of refractory elements such as
iron and silicon by comparing their emissions with the emission of a
non-refractory species, which in the present case is sulphur.
Theoretical emissivities of sulphur were calculated by considering a
five level statistical equilibrium code for an upper temperature limit
of 3000 K assumed from the work of Tappe et al. (2008) and a lower limit of 700 K imposed by the H2
analysis. For the excitation of sulphur, we also calculated the
emissivities due to collisions with atomic hydrogen, taking into
account that in environments of low ionization fraction and high total
density such excitation may prove to be significant, despite the
collisional de-excitation rates for atomic hydrogen being lower than
the electronic ones (Hollenbach & McKee 1989,
![]() )
for the [SI]25
)
for the [SI]25 ![]() m line. For these calculations,
we considered a medium in which
m line. For these calculations,
we considered a medium in which
![]() cm-3.
The excitation of [FeII] and [SiII] by H-collisions was not taken into
account because neutral hydrogen collisional rates are far less
important for ions (i.e.
cm-3.
The excitation of [FeII] and [SiII] by H-collisions was not taken into
account because neutral hydrogen collisional rates are far less
important for ions (i.e.
![]() weaker than electronic collisional rates), and are not available for all the levels considered in our model.
weaker than electronic collisional rates), and are not available for all the levels considered in our model.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{13650fg10.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa13650-09/Timg112.png)
|
Figure 10:
Diagnostic diagram of [FeII]26 |
| Open with DEXTER | |
The results of these calculations are illustrated in Fig. 10, where we plot the ratio of [FeII] 26 ![]() m to [SI]25
m to [SI]25 ![]() m against gas temperature for electron densities of 100 and 400 cm-3,
assuming that iron is fully ionised (which is the case in most
dissociative shocks) and has a solar abundance. The observed ratios for
the points R1+R2 and B1+B2 are way below the expected values, giving
rise to the hypothesis that iron is heavily depleted onto dust grains
in the considered regions, more so if the emitting gas is cooler. The
case including atomic hydrogen collisions with
m against gas temperature for electron densities of 100 and 400 cm-3,
assuming that iron is fully ionised (which is the case in most
dissociative shocks) and has a solar abundance. The observed ratios for
the points R1+R2 and B1+B2 are way below the expected values, giving
rise to the hypothesis that iron is heavily depleted onto dust grains
in the considered regions, more so if the emitting gas is cooler. The
case including atomic hydrogen collisions with
![]() cm-3 is plotted separately in Fig. 10. The iron depletion is less severe in this case but still substantial at about a factor 10.
cm-3 is plotted separately in Fig. 10. The iron depletion is less severe in this case but still substantial at about a factor 10.
In Table 5, we
provide the inferred gas phase depletion for temperatures of 700 and
3000 K, both without and with atomic hydrogen excitation of [SI].
The gas phase abundance of Fe+ is about 2-20% of the solar value for T=
3000 and 700 K, respectively, for all the points under
examination. Similarly low values were also found in the case of the
L1448 jet (5-20![]() ). Identical gas-phase depletions are obtained for Si+, but since we assumed a solar Fe+/Si+ ratio in the first place to derive our
). Identical gas-phase depletions are obtained for Si+, but since we assumed a solar Fe+/Si+ ratio in the first place to derive our ![]() values, this is just a self-consistency check. Interestingly, the
SiO abundance in the HH211 molecular jet, estimated to be
values, this is just a self-consistency check. Interestingly, the
SiO abundance in the HH211 molecular jet, estimated to be
![]() by Nisini et al. (2002b) and Chandler & Richer (2001),
corresponds to 3% of the solar abundance of silicon, therefore the
fraction of silicon released in the gas phase seems comparable in the
atomic and molecular components of HH211.
by Nisini et al. (2002b) and Chandler & Richer (2001),
corresponds to 3% of the solar abundance of silicon, therefore the
fraction of silicon released in the gas phase seems comparable in the
atomic and molecular components of HH211.
Table 5: Gas phase abundance of Fe+ and Si+ from line ratios to sulphur.
4.3.3 Density and mass flux of the atomic component
The total number of H nuclei in the emitting volume V can be derived from the line luminosity according to the relation
where Ai and fi are the spontaneous radiative decay rate and fractional population of the upper level, and [X/H] is the gas phase abundance of the atom/ion under consideration with respect to H nuclei. Line luminosities were integrated over the LL pixel size area, and the fraction of atoms at the upper level fi was calculated for
This relation was applied to [SI], the only non-refractory species detected, assuming that all Sulphur is in neutral form and employing its solar abundance (Asplund et al. 2005). These calculations for refractory species would be redundant, because their gas phase abundances from Table 5 were determined from their intensity ratio with respect to [SI].
Values of ![]() at individual positions are listed in Col. 7 of Table 4 assuming
an emitting volume in the LL pixel of
at individual positions are listed in Col. 7 of Table 4 assuming
an emitting volume in the LL pixel of
![]() (uniform narrow jet). The inferred
(uniform narrow jet). The inferred ![]() depends strongly on the adopted excitation conditions: it is about
depends strongly on the adopted excitation conditions: it is about
![]() cm-3 for T=3000 K,
cm-3 for T=3000 K,
![]() cm-3, and 8 times higher for T=700 K,
cm-3, and 8 times higher for T=700 K,
![]() cm-3. The ionisation fraction is then
cm-3. The ionisation fraction is then
![]() at 3000 K, or a factor of two lower at 700 K. This ionization
level appears to agree with the upper temperature, and therefore the
lower density range. If the fraction of H atoms is important for
at 3000 K, or a factor of two lower at 700 K. This ionization
level appears to agree with the upper temperature, and therefore the
lower density range. If the fraction of H atoms is important for
![]() cm-3, the
cm-3, the ![]() values would be reduced further by a factor 2, to a few 104 cm-3. In the case again, that the emission comes from a smaller volume, e.g. a small 1
values would be reduced further by a factor 2, to a few 104 cm-3. In the case again, that the emission comes from a smaller volume, e.g. a small 1
![]() knot as observed in the near-IR [FeII]1.64
knot as observed in the near-IR [FeII]1.64 ![]() m line, the density would increase to 105 cm-3.
m line, the density would increase to 105 cm-3.
The mass flux in the atomic/ionic component assuming a laminar flow can also be derived by applying the relationship given in Nisini et al. (2005) applied to the mid-IR lines in Dionatos et al. (2009)
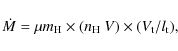
|
(4) |
where
Derived mass-flux values at the various emission peaks are listed in Col. 6 of Table 4 for a tangential speed of 100 km s-1 and
![]() (LL pixel size). As for
(LL pixel size). As for
![]() ,
they again depend strongly on the adopted excitation conditions. On the
basis of the ionization fraction considerations presented above, we
adopt the high-temperature, smaller
,
they again depend strongly on the adopted excitation conditions. On the
basis of the ionization fraction considerations presented above, we
adopt the high-temperature, smaller ![]() values of
values of
![]() yr-1. These are 20-50 times lower than the cool H2 jet mass-flux, assuming the same flow speed of 100 km s-1.
yr-1. These are 20-50 times lower than the cool H2 jet mass-flux, assuming the same flow speed of 100 km s-1.
However, we emphasize again that ![]() estimates assuming a laminar jet flow may be incorrect if the [SI]
emission arises from shocks, which is likely given the ionization
fraction inferred above. This is difficult to ascertain without the use
of appropriate shock models.
estimates assuming a laminar jet flow may be incorrect if the [SI]
emission arises from shocks, which is likely given the ionization
fraction inferred above. This is difficult to ascertain without the use
of appropriate shock models.
The atomic/ionic emission appears to require higher excitation shocks than those producing the mid-IR H2 lines. The low-velocity 10-15 km s-1 shock models that most accurately reproduce the warm H2 emission
are unable to reproduce also the observed [FeII] and [SiII] line
intensities unless the shocks are of J-type and these atoms are
essentially undepleted. As discussed in Sect. 4.3.2,
there is overwhelming evidence of the depletion of these refractory
species, so [FeII] and [SiII] probably originates from faster shocks
than those dominating the mid-IR H2 lines. It is indeed likely that the mid-IR atomic lines originates from the same dissociative shocks at
![]() km s-1 that produce the optical and NIR emission of H
km s-1 that produce the optical and NIR emission of H![]() ,
[SII], and [FeII] (Caratti o Garatti et al. 2006; O'Connell et al. 2005; Walawender et al. 2005,2006).
,
[SII], and [FeII] (Caratti o Garatti et al. 2006; O'Connell et al. 2005; Walawender et al. 2005,2006).
Unfortunately, our shock models do not yet include ionization and
dissociation by the shock UV flux, so we cannot explore the relevant
excitation range. However, we note that the J-shock models of Hollenbach & McKee (1989), which include UV flux, suggest that the [SI]25 ![]() m brightness is relatively independent of shock speed over the range 30-100 km s-1 and is roughly proportional to
m brightness is relatively independent of shock speed over the range 30-100 km s-1 and is roughly proportional to
![]() .
Our measured flux inside the LL 10.5
.
Our measured flux inside the LL 10.5
![]() pixel implies that
pixel implies that
![]() cm-3. From Eq. (2), we would infer a preshock mass-flux of
cm-3. From Eq. (2), we would infer a preshock mass-flux of
![]() yr-1, which is lower still by a factor 4-40 than the cool H2 jet mass-flux.
yr-1, which is lower still by a factor 4-40 than the cool H2 jet mass-flux.
These results suggest that the atomic component in the HH211 jet does not have enough momentum flux to entrain the CO/SiO/H2 jet, if their velocities are comparable and the shock compression in the cool H2/CO component does not exceed a factor of 3. The molecular jet would then have to trace material ejected from the accretion disk, while the atomic component would trace a separate ejection, e.g. from hotter more internal regions of the accretion disk. On the other hand, a higher compression factor in the cool H2/CO emitting zone, or a faster ionic jet would suffice to remove this discrepancy, therefore a definite conclusion on whether the molecular jet is ejected or entrained cannot be reached from the present data alone.
5 Conclusions
We have carried out Spitzer spectral mapping observations towards the jet driven by the Class 0 source HH211-mm. Molecular lines (pure rotational H2)
as well as fundamental atomic and ionic lines ([SI], [SiII], [FeII])
have been detected, and their maps follow the characteristic bipolar
outflow pattern traced by near-IR H2 and CO lines. The H2 emission becomes important only 5
![]() away from the driving source, while atomic and ionic lines are detected
very close to the protostar. In the inner part of the blue-shifted
lobe, the H2 emission was found to be spatially coincident with the high velocity jet observed in both CO and SiO.
away from the driving source, while atomic and ionic lines are detected
very close to the protostar. In the inner part of the blue-shifted
lobe, the H2 emission was found to be spatially coincident with the high velocity jet observed in both CO and SiO.
Our analysis of the observed H2 lines revealed two temperature components: ``cool'' gas at ![]() K dominating the mass, and ``warm'' gas at
K dominating the mass, and ``warm'' gas at
![]() K of 10 times lower
average column density. Once corrected for beam dilution, the column density of ``cool'' H2
towards the CO jet is compatible with hydrogen being mostly molecular.
The warmer component traced by the S(2) to S(7) lines is well fitted by
C-shock models of high density
K of 10 times lower
average column density. Once corrected for beam dilution, the column density of ``cool'' H2
towards the CO jet is compatible with hydrogen being mostly molecular.
The warmer component traced by the S(2) to S(7) lines is well fitted by
C-shock models of high density
![]() and a small shock-cross section of 0.5
and a small shock-cross section of 0.5
![]() ,
compatible with the density and width of the CO jet quoted by Lee et al. (2007). The warm H2 emission could then trace thin layers of warm post-shock gas within the CO jet.
,
compatible with the density and width of the CO jet quoted by Lee et al. (2007). The warm H2 emission could then trace thin layers of warm post-shock gas within the CO jet.
High-density C-shock models may also account for the brightness of the H2
mid-IR emission further downwind beyond the CO and SiO jet, but the
small shock surface filling factor of 0.01-0.04 is not easy to
reconcile with the spatial extension visible in Spitzer maps, unless the bow-shock wings are very clumpy. Lower density shocks of
![]() cm-3,
where the cooling zone spreads over several pixels and/or higher
preshock ionization may need to be considered in these regions, as
previously done when modeling near-IR H2 excitation in the red-shifted bow-shock of HH211 (O'Connell et al. 2005).
cm-3,
where the cooling zone spreads over several pixels and/or higher
preshock ionization may need to be considered in these regions, as
previously done when modeling near-IR H2 excitation in the red-shifted bow-shock of HH211 (O'Connell et al. 2005).
The detected fine structure lines mapped very close to the driving source are indicative of an embedded atomic jet. Line ratio diagnostics indicate a gas-phase depletion of iron and silicon of at least a factor of 10, and lower excitation conditions than in optically visible jets. An atomic jet of similar properties was also detected by Spitzer in the outflow of L1448-C (Dionatos et al. 2009). As suggested in that case, the detected atomic gas in the HH211-mm outflow may represent the equivalent of the forbidden emission line (FEL) region observed in more evolved ClassI/II sources. The gas depletion of iron and silicon indicates that dust grains have survived in the atomic flow, ruling out an origin from within the dust sublimation zone close to the protostar. The excitation conditions require faster shocks than those producing the H2 mid-IR lines.
Estimations of the molecular and atomic mass-flux rates have been
performed using both a laminar flow assumption and shock models. The
cool H2 mass-flux is comparable to that inferred from CO observations, with a value uncorrected for compression of
![]() yr-1 (V/100 km s-1); a similar value is found for the warm H2
if it arises from dense C-shocks as suggested by best-fit models. The
atomic component mass-flux is uncertain by a factor of 8 due to its
uncertain temperature, but considerations of the ionization fraction as
well as published dissociative shock models imply a lower mass-flux
than in the molecular jet. However, the momentum fluxes could become
comparable if the atomic jet is faster than the molecular jet, or if
the cool H2 and CO are affected by shock compression. Given
the uncertainties, it remains unclear whether the molecular CO jet
traces ambient gas entrained by the atomic jet, or if it has to be
ejected, for example in a molecular MHD disk wind as modeled by Panoglou et al. (2010).
yr-1 (V/100 km s-1); a similar value is found for the warm H2
if it arises from dense C-shocks as suggested by best-fit models. The
atomic component mass-flux is uncertain by a factor of 8 due to its
uncertain temperature, but considerations of the ionization fraction as
well as published dissociative shock models imply a lower mass-flux
than in the molecular jet. However, the momentum fluxes could become
comparable if the atomic jet is faster than the molecular jet, or if
the cool H2 and CO are affected by shock compression. Given
the uncertainties, it remains unclear whether the molecular CO jet
traces ambient gas entrained by the atomic jet, or if it has to be
ejected, for example in a molecular MHD disk wind as modeled by Panoglou et al. (2010).
This work is based on archival data obtained with the Spitzer Space Telescope, which is operated by the Jet Propulsion Laboratory, California Institute of Technology under a contract with NASA. It was supported in part by the European Community's Marie Curie Actions - Human Resource and Mobility within the JETSET (Jet Simulations, Experiments and Theory) network under contract MRTN-CT-2004 05592. Financial contribution from contract ASI I/016/07/0 is also acknowledged. The Centre for Star and Planet Formation is funded by the Danish National Research Foundation and the University of Copenhagen's programme of excellence.
References
- Arce, H. G., Shepherd, D., Gueth, F., et al. 2007, in Protostars and Planets V, ed. B. Reipurth, D. Jewitt, & K. Keil, 245 [Google Scholar]
- Asplund, M., Grevesse, N., & Sauval, A. J. 2005, in Cosmic Abundances as Records of Stellar Evolution and Nucleosynthesis, ed. T. G. Barnes, III & F. N. Bash, ASP Conf. Ser., 336, 25 [Google Scholar]
- Bally, J., Heathcote, S., Reipurth, B., et al. 2002, AJ, 123, 2627 [NASA ADS] [CrossRef] [Google Scholar]
- Caratti o Garatti, A., Giannini, T., Nisini, B., & Lorenzetti, D. 2006, A&A, 449, 1077 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chandler, C. J., & Richer, J. S. 2001, ApJ, 555, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, C. J., & Smith, M. D. 1996, A&A, 309, 929 [NASA ADS] [Google Scholar]
- Dionatos, O., Nisini, B., Garcia Lopez, R., et al. 2009, ApJ, 692, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Dufton, P. L., & Kingston, A. E. 1991, MNRAS, 248, 827 [NASA ADS] [Google Scholar]
- Eislöffel, J., Froebrich, D., Stanke, T., & McCaughrean, M. J. 2003a, ApJ, 595, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Eislöffel, J., Froebrich, D., Stanke, T., & McCaughrean, M. J. 2003b, ApJ, 595, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Enoch, M. L., Young, K. E., Glenn, J., et al. 2006, ApJ, 638, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Ferreira, J., Dougados, C., & Cabrit, S. 2006, A&A, 453, 785 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Flower, D. R., & Pineau des Forêts, G. 2003, MNRAS, 343, 390 [NASA ADS] [CrossRef] [Google Scholar]
- Flower, D. R., Le Bourlot, J., Pineau des Forêts, G., & Cabrit, S. 2003, MNRAS, 341, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Froebrich, D. 2005, ApJS, 156, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Giannini, T., McCoey, C., Nisini, B., et al. 2006, A&A, 459, 821 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gibb, A. G., Richer, J. S., Chandler, C. J., & Davis, C. J. 2004, ApJ, 603, 198 [NASA ADS] [CrossRef] [Google Scholar]
- Gueth, F., & Guilloteau, S. 1999, A&A, 343, 571 [NASA ADS] [Google Scholar]
- Guilloteau, S., Bachiller, R., Fuente, A., & Lucas, R. 1992, A&A, 265, L49 [NASA ADS] [Google Scholar]
- Gusdorf, A., Pineau Des Forêts, G., Cabrit, S., & Flower, D. R. 2008a, A&A, 490, 695 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gusdorf, A., Pineau Des Forêts, G., Cabrit, S., & Flower, D. R. 2008b, A&A, 490, 695 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gustafsson, M., Ravkilde, T., Kristensen, L. E., et al. 2010, A&A, 513, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hartigan, P., Morse, J. A., & Raymond, J. 1994, ApJ, 436, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Herbig, G. H. 1998, ApJ, 497, 736 [Google Scholar]
- Hernández, J., Calvet, N., Hartmann, L., et al. 2005, AJ, 129, 856 [NASA ADS] [CrossRef] [Google Scholar]
- Hirano, N., Liu, S.-Y., Shang, H., et al. 2006, ApJ, 636, L141 [NASA ADS] [CrossRef] [Google Scholar]
- Hollenbach, D., & McKee, C. F. 1989, ApJ, 342, 306 [NASA ADS] [CrossRef] [Google Scholar]
- Houck, J. R., Roellig, T. L., van Cleve, J., et al. 2004, ApJS, 154, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Kaufman, M. J., Wolfire, M. G., Hollenbach, D. J., & Luhman, M. L. 1999, ApJ, 527, 795 [NASA ADS] [CrossRef] [Google Scholar]
- Kristensen, L. E., Ravkilde, T. L., Field, D., Lemaire, J. L., & Pineau Des Forêts, G. 2007, A&A, 469, 561 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lada, C. J., Muench, A. A., Luhman, K. L., et al. 2006, AJ, 131, 1574 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, C.-F., Ho, P. T. P., Palau, A., et al. 2007, ApJ, 670, 1188 [NASA ADS] [CrossRef] [Google Scholar]
- McCaughrean, M. J., Rayner, J. T., & Zinnecker, H. 1994, ApJ, 436, L189 [NASA ADS] [CrossRef] [Google Scholar]
- Nisini, B., Caratti o Garatti, A., Giannini, T., & Lorenzetti, D. 2002a, A&A, 393, 1035 [Google Scholar]
- Nisini, B., Codella, C., Giannini, T., & Richer, J. S. 2002b, A&A, 395, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nisini, B., Bacciotti, F., Giannini, T., et al. 2005, A&A, 441, 159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- O'Connell, B., Smith, M. D., Froebrich, D., Davis, C. J., & Eislöffel, J. 2005, A&A, 431, 223 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Panoglou, D., et al. 2010, A&A, submitted [Google Scholar]
- Pudritz, R. E., Ouyed, R., Fendt, C., & Brandenburg, A. 2007, in Protostars and Planets V, ed. B. Reipurth, D. Jewitt, & K. Keil, 277 [Google Scholar]
- Reipurth, B., & Bachiller, R. 1997, in IAU Symposium, ed. W. B. Latter, S. J. E. Radford, P. R. Jewell, J. G. Mangum, & J. Bally, 170, 165 [Google Scholar]
- Rieke, G. H., & Lebofsky, M. J. 1985, ApJ, 288, 618 [NASA ADS] [CrossRef] [Google Scholar]
- Ruden, S. P., Glassgold, A. E., & Shu, F. H. 1990, ApJ, 361, 546 [NASA ADS] [CrossRef] [Google Scholar]
- Salas, L., Cruz-González, I., & Rosado, M. 2003, Rev. Mex. Astron. Astrofis., 39, 77 [NASA ADS] [Google Scholar]
- Shang, H., Li, Z., & Hirano, N. 2007, in Protostars and Planets V, ed. B. Reipurth, D. Jewitt, & K. Keil, 261 [Google Scholar]
- Smith, J. D. T., Armus, L., Dale, D. A., et al. 2007, PASP, 119, 1133 [NASA ADS] [CrossRef] [Google Scholar]
- Tappe, A., Lada, C. J., Black, J. H., & Muench, A. A. 2008, ApJ, 680, L117 [Google Scholar]
- Walawender, J., Bally, J., Kirk, H., et al. 2006, AJ, 132, 467 [NASA ADS] [CrossRef] [Google Scholar]
- Walawender, J., Bally, J., & Reipurth, B. 2005, AJ, 129, 2308 [NASA ADS] [CrossRef] [Google Scholar]
- Werner, M. W., Roellig, T. L., Low, F. J., et al. 2004, ApJS, 154, 1 [Google Scholar]
- Wilgenbus, D., Cabrit, S., Pineau des Forêts, G., & Flower, D. R. 2000, A&A, 356, 1010 [NASA ADS] [Google Scholar]
Footnotes
- ... bow-shock
![[*]](/icons/foot_motif.png)
- In the [FeII] 26
 m map, contours are interrupted just before the
actual blue-shifted bowshock peak; this is an artifact resulting from a
rogue pixel in the LL-IRS module that had to be masked out since it was
introducing unreliable brightness values forming a bright vertical
stripe across the map.
m map, contours are interrupted just before the
actual blue-shifted bowshock peak; this is an artifact resulting from a
rogue pixel in the LL-IRS module that had to be masked out since it was
introducing unreliable brightness values forming a bright vertical
stripe across the map.
- ...Caratti o Garatti
et al. (2006)
![[*]](/icons/foot_motif.png)
- O'Connell et al. (2005) reported a higher extinction of 25 mag in the redshifted lobe but considered their measurement as rather tentative given their observing conditions.
- ... measured
![[*]](/icons/foot_motif.png)
- Note that a typographical error was introduced in Table 2
of Dionatos et al. (2009);
the values of
 are
are  cm-2
at CS and
cm-2
at CS and  cm-2
for the other positions.
cm-2
for the other positions.
All Tables
Table 1:
Physical properties of the warm H2 component from H2 v=0-0 S(2)-S(7) lines extracted at the SL (3.5
![]() )
scale.
)
scale.
Table 2:
Physical properties of the cool H2 component from H2 v=0-0 S(0)-S(2) lines extracted at the LL (10.5
![]() )
scale.
)
scale.
Table 3: Parameters of best-fit shock models of the S(3) to S(7) lines.
Table 4: Physical properties of the atomic/ionic line component.
Table 5: Gas phase abundance of Fe+ and Si+ from line ratios to sulphur.
All Figures
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13650fg1.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa13650-09/Timg25.png)
|
Figure 1:
Continuum-subtracted spectrum, integrated over a region of 612 square arcseconds covering the HH211 flow ( middle),
shown in comparison with a spectrum of the off-outflow region of the same area ( top). H2
emission from the 0-0 S(0)-S(7) lines is detected in the outflow,
together with atomic emission from the ground-state transitions of
[FeII],[SiII], and [SI]. The H2 S(0) and S(1) lines are also detected in the off-outflow spectrum,
which is indicative of a diffuse line emission component not related to the HH211 flow. Diffuse emission
from PAH features, such as the 11.3 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{13650fg2.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa13650-09/Timg26.png)
|
Figure 2:
H2 v=0-0 S(2)-S(7) line intensity maps of the HH211 flow observed with the Spitzer SL module, reconstructed with a pixel scale of 3.5
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{13650fg3.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa13650-09/Timg34.png)
|
Figure 3:
(Upper panel) H2 v=0-0 S(5) map (green contours) superimposed over the high velocity CO J = 2-1 map of Gueth & Guilloteau (1999); ( Lower panels) Inner part of the H2 v=0-0 S(5) map (green contours) superimposed on the SiO J = 8-7 and the CO J = 3-2 maps of Lee et al. (2007). The grayscale backgrounds show the H2 v=1-0 S(1) image from McCaughrean et al. (1994) ( top panel) or Hirano et al. (2006) (lower panels). The slight S-shape pattern of the S(5) emission map follows the brightness asymmetry of the cavity seen in the 2.12 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=13.2cm,clip]{13650fg4.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa13650-09/Timg35.png)
|
Figure 4:
Intensity maps of the HH211 flow in the H2S(1) and S(0) lines ( top row) and the atomic [SiII]35 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15.3cm,clip]{13650fg5.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa13650-09/Timg36.png)
|
Figure 5:
Excitation diagrams of H2 in various pixel sizes. (Left) H2 columns in peak R1 from transitions in the SL module in 3.5
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{13650fg6.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa13650-09/Timg51.png)
|
Figure 6:
Excitation temperature map of the ``warm'' H2 component deduced from
the SL module map (3.5
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{13650fg7.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa13650-09/Timg92.png)
|
Figure 7:
Steady 1D C-shock model fits to the excitation diagram of the S(2)-S(7) lines at the peak of emission R1 in a 3.5
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16cm,clip]{13650fg8.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa13650-09/Timg104.png)
|
Figure 8:
Excitation diagrams for all emission peaks mapped with the SL module;
observed points (filled circles with error bars), are displayed along
with best |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{13650fg9.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa13650-09/Timg109.png)
|
Figure 9:
Diagnostic diagram of the [SiII]35 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{13650fg10.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa13650-09/Timg112.png)
|
Figure 10:
Diagnostic diagram of [FeII]26 |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



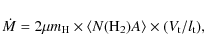
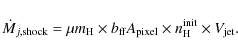
![\begin{displaymath}
n_{\rm H}~V=L(line) \left(h\nu A_i f_i \left[\frac{X}{H}\right] \right )^{-1},
\end{displaymath}](/articles/aa/full_html/2010/13/aa13650-09/img121.png)