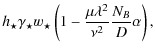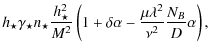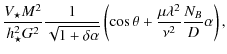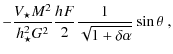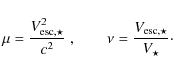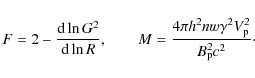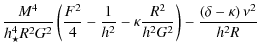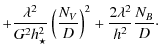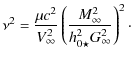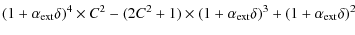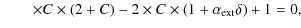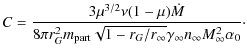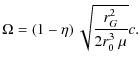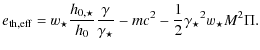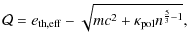EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 521 (October 2010) A&A, 521 (2010) A67 Full HTML
Free Access
Issue
A&A
Volume 521, October 2010
Article Number A67
Number of page(s) 11
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/200912920
Published online 21 October 2010
A&A 521, A67 (2010)

Relativistic spine jets from Schwarzschild black holes

Application to AGN radio-loud sources

Z. Meliani1,2 - C. Sauty2 - K. Tsinganos3 - E. Trussoni4 - V. Cayatte2

1 - Centrum voor Plasma Astrofysica, Celestijnenlaan 200B bus 2400, 3001 Leuven, Belgium
2 - Observatoire de Paris, LUTh., 92190 Meudon, France
3 - IASA and Section of Astrophysics, Astronomy & Mechanics Department of Physics, University of Athens, Panepistimiopolis 157 84, Zografos, Greece
4 - INAF - Osservatorio Astronomico di Torino, via Osservatorio 20, 10025 Pino Torinese (TO), Italy

Received 17 July 2009 / Accepted 9 June 2010

Abstract
Context. The two types of Fanaroff-Riley (FR) radio-loud galaxies, FR I and FR II, exhibit strong jets which have different properties. These differences may be associated to the central engine and/or the external medium.
Aims. The AGN classification FR I and FR II can be linked to the rate of electromagnetic Poynting flux extraction from the inner corona of the central engine by the jet. The collimation results from the distribution of the total electromagnetic energy across the jet, as compared to the corresponding distribution of the thermal and gravitational energies.
Methods. We use exact solutions of the fully relativistic magnetohydrodynamical (GRMHD) equations obtained by a nonlinear separation of the variables to study outflows from a Schwarzschild black hole corona.
Results. A strong correlation is found between the jet features and the energetic distribution of the plasma of the inner corona, which may be related to the efficiency of the magnetic rotator.
Conclusions. It is shown that observations of FR I and FR II jets may be partially constrained by our model for spine jets. The deceleration observed in FR I jets may be associated with a low magnetic efficiency of the central magnetic rotator and an important thermal confinement by the hot surrounding medium. Conversely, the strongly collimated and accelerated FR II outflows may be self-collimated by their own magnetic field because of the high efficiency of the central magnetic rotator.

Key words: magnetohydrodynamics (MHD) - relativity - galaxies: jets - galaxies: active - acceleration of particles - black hole physics

1 Introduction

According to the standard active galactic nuclei (AGN) paradigm, their radio luminosity is related to powerful relativistic jets (radio-loud AGN), or, to mildly sub-relativistic outflows (radio-quiet AGN). And, by assuming a supermassive black hole (BH) surrounded by an accretion disk/torus, the different AGN phenomenologies observed in both classes are related to the orientation of the axis of the BH/disk system with respect to the line of sight, and the thickness of the torus, which is responsible for the obscuration effects (Urry & Padovani 1995). Typical examples for radio-quiet AGN are the various types of Seyfert I-II galaxies, where uncollimated (or loosely collimated) winds are outflowing from the BH/disk system at a speed of a few thousand km s-1. However, besides their inclination to the line of sight the classification cannot be complete without invoking another key parameter to explain the outflow differences between the various AGN. These differences may be related to galaxy environment effects and/or intrinsic properties of the AGN, as shown in Fig. 1 (see e.g. Kaiser & Alexander 1997; Celotti 2003; Kaiser & Best 2007).

For radio loud objects a fundamental role is played by Doppler boosting, strongly affecting the luminosity and spectral properties of these AGN. Indeed, these radio sources are associated with powerful relativistic jets, which reach at the parsec scale high Lorentz factors $\gamma\sim 5{-}30$ (Kellermann et al. 2004; Urry & Padovani 1995; Piner et al. 2003). These jets are strongly collimated with opening angles on the order of $\sim $$3^{\circ}$ (Pushkarev et al. 2009). In nearby AGN recollimation is inferred from the inner radio jet structure (Horiuchi et al. 2006, for Cen A; Kovalev et al. 2007, for M 87). We recall that the main classes of radio loud AGN are Radio Quasars, Flat Spectrum and Broad Line Radio Galaxies, BL Lacs, Fanaroff Riley I (FR I) and Fanaroff Riley II (FR II) objects. According to the unified model, FR I objects are misaligned BL Lacs, while the parent population of FR II are Radio Quasars, Broad Line Radio Galaxies and the brightest BL Lacs, as sketched in Fig. 1. Regarding in particular the FR I and FR II dichotomy, we briefly outline below their main properties (Fanaroff & Riley 1974):

-
in FR II sources the extended radio morphology shows a clear, generally one-sided collimated (within a few degrees) thin jet, terminating into a hot spot and surrounded by diffuse blobs. Conversely, in FR I sources the collimated symmetric jets smoothly merge into the extended emitting regions;

-
FR II jets look highly relativistic and narrow along their whole length (tens of kpc). FR I jets are conversely relativistic only on pc scales (Bridle 1982), becoming subrelativistic and diffuse on kpc scales (Giovannini et al. 2005). However, in some FR I sources the structure of the jet in the kiloparsec scale appears more complicated, with an inner spine that remains relativistic and an outer shell that decelerates and becomes sub-relativistic (Canvin et al. 2005);

-
FR II sources are more powerful than the FR I ones, with a threshold power $\sim $1025 W Hz-1 sr-1 increasing with the radio galaxy luminosity (Ledlow & Owen 1996);

-
FR II are usually found in poor gas environments, with jets probably collimated by their helical magnetic fields (Hardcastle & Worrall 2000; Zavala & Taylor 2005; Asada et al. 2002) and slightly interacting with the external gas. Rich environments harbor mostly FR I sources and their jets, thermally confined (at least partially) and appearing to strongly interact with the intracluster medium (Kaiser & Alexander 1997; Gabuzda 2003; Laing et al. 1999). The measured transverse magnetic field suggests the presence of internal shocks where the tangled magnetic field is compressed (Gabuzda et al. 1994; Gómez et al. 2008). Those shocks could be the result of the thermal collimation of the jet. Below, we briefly discuss numerical versus analytical modeling of multicomponent jets.
There are two main theories to interpret the above observational characteristics. The first explains the morphological differences as mainly due to the different physical properties of the environment in which the relativistic jet propagates (Meliani et al. 2008; Bicknell 1995; De Young 1993; Gopal-Krishna & Wiita 2000; Laing et al. 1999). The second explains the dichotomy by involving a difference in the nature of the central engine, the spin of the central black hole, the accretion rate and the jet composition (Baum et al. 1995; Meier 1999; Meliani & Keppens 2009; Reynolds et al. 1996). Finally, there may be a combination of external and engine factors to explain the FR I/FR II dichotomy, as we have suggested in Meliani et al. (2006a) and studied in Wold et al. (2007).

\begin{figure} \par\includegraphics[height=7.4cm]{12920fg1.eps} \end{figure} Figure 1:

Standard classification of AGN sources following Urry & Padovani (1995). The horizontal axis represents the inclination of the source axis with the line of sight. The vertical axis we suggest that it may be linked to the efficiency of the underlying magnetic rotator to collimate the flow.

Open with DEXTER

Similarly to jets from young stellar objects, hereafter YSO (Ferreira et al. 2006), AGN jets probably have at least two components (Sol et al. 1989; Tsinganos & Bogovalov 2002), one originating in the surrounding Keplerian disk (Baum et al. 1995; Meier 2002; Begelman & Celotti 2004) and the other in the inner corona that surrounds the central black hole. This corona can be created by the ``CEntrifugal pressure supported Boundary Layer'' model (CENBOL) (Das & Chakrabarti 2002). The corona can also be created by the mechanism presented in Kazanas & Elison (1986). A third possibility to produce such a corona with pair plasma is the Blandford & Znajek (1977) model where the jet is powered by the spinning black hole. However, observations indicate that the jet should have both hadronic and leptonic components as explained in two-component models (Henry & Pelletier 1991; Fabian & Rees 1995).

The MHD equations can be solved through numerical simulations, which describe the evolution of the jet configuration. The availability of more and more powerful computing facilities and sophisticated numerical codes allows a quite complete description and understanding of the jet acceleration/collimation (Komissarov et al. 2007; Porth & Fendt 2010) and the accretion/ejection process (Gracia et al. 2009; McKinney & Blandford 2009; McKinney 2006; Koide et al. 1999,1998; Gracia et al. 2006). Recent numerical simulations have progressed to general relativistic magnetohydrodynamic (GRMHD) jet launching, as in McKinney (2006) and Hardee et al. (2007), also suggesting the formation of jets with two components. However, computational limits do not yet allow to follow simulations for very long times and reach exact stationary configurations. Simulations also fail at analyzing structures with very different scale lengths.

Nevertheless, tremendous progress in understanding the physics of relativistic jet acceleration/deceleration - and therefore the FR I/FR II dichotomy - has been made thanks to numerical simulations of jet propagation in the asymptotic regions. Some authors investigated the relativistic hydrodynamic jet propagation through the interstellar medium (Aloy et al. 1999; Rossi et al. 2008; Duncan & Hughes 1994; Martí et al. 1997; Komissarov & Falle 1998). They show that the different dynamics of FR I and FR II jets may be a consequence of the jet power. Many groups had also investigated the two-dimensional relativistic magnetized jet propagation in an external medium (Komissarov 1999; Leismann et al. 2005; Keppens et al. 2008; van Putten 1996) and 3D (e.g. Mizuno et al. 2007; Mignone et al. 2009). They showed that the interaction between the jet and the external medium depend on the magnetization of the jet and the density ratio between the jet and the external medium. The role of the environment may be crucial in HYbrid MOrphology Radio Sources (HYMORS), as shown by Gopal-Krishna & Wiita (2000, 2002). These radio sources appear to have a FR II type on one side and a FR I type diffuse radio lobe on the other side of the active nucleus. This last model for HYMORS has been recently confirmed by numerical simulations of two component jets (Meliani et al. 2008). Another alternative to the FR I/FR II dichotomy could come from the nature of the instabilities that develop in the jet, or at the jet interface with the external medium, or with another surrounding outflow component (Keppens et al. 2008). This is consistent with the fact that hydrodynamical jets with high Lorentz factors are more stable (Martí et al. 1997). Poloidal magnetic fields also help to stabilize the jet (Keppens et al. 2008). About the last possibility note that simulations by Meliani & Keppens (2009) confirm that the deceleration in FR I jets could be attributed to a strong Rayleigh-Taylor instability between the spine jet and the surrounding component, which supports a two component jet structure.

Parallel to the development of time-dependent simulations, steady jet solutions in GRMHD were first obtained numerically by solving the transfield equation in the force-free limit (Camenzind 1986). This study has been further developed in GRMHD by using first a Schwarzschild metric and then extending it to a Kerr metric (Fendt 1997). Yet this method cannot consistently incorporate the mass loading of the jet.

Exact models for disk winds can be constructed via a nonlinear separation of the governing MHD equations. This technique of radial self-similarity has been extensively explored in the context of stellar and relativistic jets by various authors (Ferreira 1997; Blandford & Payne 1982; Vlahakis & Königl 2004; Contopoulos 1994; Bardeen & Berger 1978; Li et al 1992).

Table 1:   The asymptotic jet speed in units of the escape speed from the base of the corona, for various values of the parameters $\kappa /2\lambda ^2$ and $\epsilon / 2\lambda ^2$.

Meridional self-similarity is another way to assume a variable separation, which is used to produce models of pressure-driven winds (Meliani et al. 2006a). It is also complementary to magnetically driven disk winds. These models may describe the inner spine jet from the central object necessary to sustain the outer disk wind, but where the radial self-similar models fail by construction. In this paper, we use these solutions and show that the collimation criterion developed in the frame of this model can help understand how the FR I/FR II dichotomy may influence the morphology of the inner spine jets. As a back reaction, the spine jet dynamics influences the outer jet, which was demonstrated in numerical simulations (Meliani et al. 2006b; Fendt 2009), even if the central jet is energetically very weak (Matsakos et al. 2009).

In Sect. 2 we briefly recall the main assumptions of the model. In Sect. 3 we summarize the details of the standard AGN jet classification and how it helps to constrain the parameters. In Sect. 4 we present an interesting solution for a FR I-type spine jet and in Sect. 5 another one for jets associated with FR II objects. In Sect. 6 we discuss and summarize the main implications of our model.

2 Model assumptions

2.1 The self-similar model

We use the ideal GRMHD equations in the background spacetime of a Schwarzschild black hole, and neglect the effects of self-gravity of matter outside the black hole. The spacetime curvature at a distance r from the black hole is given by the lapse function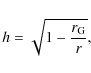

\begin{displaymath}h =\sqrt{1-\frac{r_{\rm G}}{r}}, \end{displaymath} (1)

where $r_{\rm G}$ is the Schwarzschild radius.

Following Meliani et al. (2006a), all physical quantities are normalized at the Alfvén radius $r_\star$ along the polar axis where the meridional angle is zero ($\theta=0$). We define a dimensionless spherical radius $R=r/r_\star$, cylindrical radius G, and magnetic flux function $\alpha$,

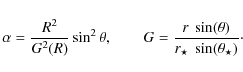
\begin{displaymath}\alpha=\frac{R^2}{G^2(R)}\sin^2 \theta , \qquad G=\frac{r~\sin(\theta)}{r_\star~\sin(\theta_\star)} \cdot \end{displaymath} (2)

To describe the GRMHD outflow of the coronal plasma, we use the relativistic meridionally self-similar solutions presented in Meliani et al. (2006a). The specific enthalpy, and density in the lab frame together with the pressure, velocity and magnetic field are given in terms of functions of the radial distance R
                               $\displaystyle h\gamma w$ = $\displaystyle h_{\star} \gamma_\star w_\star \left(1-\frac{\mu \lambda^2}{\nu^2} \frac{N_B}{D} \alpha \right) ,$ (3)
$\displaystyle h\gamma n$ = $\displaystyle h_{\star} \gamma_\star n_\star \frac{h_{\star}^2}{M^2}\left(1+\delta\alpha -\frac{\mu \lambda^2}{\nu^2} \frac{N_B}{D} \alpha \right) ,$ (4)
P = $\displaystyle P_0 + \frac{1}{2}{\gamma_{\star}}^2n_{\star}\frac{w_\star}{c^2} V_ {\star}^2\Pi(R)(1+\kappa\alpha),$ (5)
Vr = $\displaystyle \frac{V_\star M^2}{h_{\star}^2G^2} \frac{1}{\sqrt{1+\delta\alpha}} \left(\cos{\theta} +\frac{\mu \lambda^2}{\nu^2}\frac{N_B}{D} \alpha \right) ,$ (6)
$\displaystyle V_{\theta}$ = $\displaystyle -\frac{V_\star M^2}{h_{\star}^2G^2} \frac{h_{}F}{2}\frac{1}{\sqrt{1+\delta\alpha}} \sin{\theta} ~,$ (7)
$\displaystyle V_{\varphi}$ = $\displaystyle -\frac{h_{} }{{h_{\star}}} \frac{\lambda V_\star}{G^2} \frac{N_V}{D} \frac{R\sin{\theta}}{\sqrt{1+\delta\alpha}} ,$ (8)
Br = $\displaystyle \frac{B_\star}{G^2}\cos{\theta} ,$ (9)
$\displaystyle B_{\theta}$ = $\displaystyle - \frac{B_\star}{G^2}\frac{h_{}F}{2}\sin{\theta} ,$ (10)
$\displaystyle B_{\varphi}$ = $\displaystyle -\frac{\lambda B_\star}{G^2} \frac{h_{\star}}{h_{}} \frac{N_B}{D} R\sin{\theta} .$ (11)

where
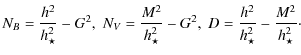
$\displaystyle N_B=\frac{h_{}^2 }{h_{\star}^2} - G^2 ,\;   (12)

The free parameters $\delta$ and $\kappa$ describe the deviation from spherical symmetry of the ratio of number density/enthalpy and pressure, respectively, while $\lambda$ is a constant controlling the angular momentum extracted by the jet. The constants $\nu$ and $\mu$ measure the escape speed in units of the light speed and the escape speed in units of Alfvén speed, at the Alfvén point along the polar axis, respectively,

\begin{displaymath} \mu=\frac{V_{{\rm esc,}\star}^2}{c^2}~, \qquad \nu=\frac{V_{{\rm esc,}\star}}{V_\star}\cdot \end{displaymath} (13)

Thus, all physical quantities are determined in terms of constant parameters, $\delta$, $\kappa$, $\lambda$, $\mu$, $\nu$ and the three unknown functions, $\Pi(R)$, F(R), and M2(R). Note that $\Pi(R)$ is the dimensionless pressure function, defined modulus a constant P0, F is the expansion factor, and M is the poloidal Alfvénic number,

\begin{displaymath} F=2-\frac{{\rm d}\ln{G^2}}{{\rm d}\ln{R}},\qquad M=\frac{4\pi h_{}^2 n w \gamma^2 V_{\rm p}^2} {B_{\rm p}^2 c^2}\cdot \end{displaymath} (14)

These three unknown functions $\Pi(R)$, F(R), and M2(R) are determined by three nonlinear equations. We start integrating these equations from the Alfvén critical surface, taking into account the corresponding regularity condition and then integrate downwind and upwind, crossing the other critical points, for details see Meliani et al. (2006a).

The light cylinder is defined by the function $x=\Omega~ L/ E$ becoming unity, where $\Omega$ is the angular speed, L the total angular momentum per unit mass and E the generalized Bernoulli integral. It is a measure of the energy flux of the magnetic rotator in units of the total energy flux. The s-s description is possible only if the jet is rotating at subrelativistic speeds. In such conditions x must remain small and therefore the light cylinder effects have to be negligible for our solution to be valid.

In this setup of the relativistic MHD problem an extra parameters exists $\epsilon$, which is constant everywhere (Meliani et al. 2006a)

                               $\displaystyle \epsilon$ = $\displaystyle \frac{M^{4}}{h_{\star}^4 R^2 G^2} \left(\frac{F^2}{4} - \frac{1}{... ...\kappa \frac{R^2}{h^2G^2}\right) -\frac{\left(\delta-\kappa\right)\nu^2}{h^2 R}$  
    $\displaystyle +\frac{\lambda^2}{G^2 h_{\star}^2} \left(\frac{N_V}{D}\right)^2 +\frac{2 \lambda^2}{h^2}\frac{N_B}{D}\cdot$ (15)

This is the relativistic generalization for a Schwarzschild black hole of the classical constant found in Sauty et al. (2004) which measures the magnetic energy excess or deficit on a nonpolar streamline, compared to the polar one. To first order, $\epsilon$ determines the fraction of Poynting flux carried by the jet in the asymptotic region, so that $(1-\epsilon/(2\lambda^2))$measures the fraction of the Poynting flux which is used in the jet acceleration. Thus, if $\epsilon>0$ we have an efficient magnetic rotator (EMR) where magnetic collimation may dominate, while if $\epsilon<0$ we have an inefficient magnetic rotator (IMR) where collimation cannot be of magnetic origin but should be thermal, if the flow is collimated.

3 New interpretation of the Fanaroff-Riley classification

We propose here to examine the vertical classification in Fig. 1 by means of our parameter $\epsilon$, or less ambitiously, to interpret how the various observations we have on FR I and FR II jets may influence the formation of the inner spine jet component. As in the non-relativistic case (Sauty et al. 1999), this parameter $\epsilon$ allows us to classify jets according to the efficiency of the central magnetic rotator. Jets emerging from efficient central magnetic rotators, $\epsilon>0$, collimate cylindrically without oscillations in the asymptotic region. In this type of jets, the velocity increases monotonically to reach its asymptotical maximum value. Conversely, jets associated with inefficient central magnetic rotators, $\epsilon<0$, are collimated mainly by the pressure of the external medium. Thus, this type of jets strongly interacts with the ambient medium, and this induces oscillations in their shape at the asymptotic region. The jet speed increases and oscillates. The plasma in those jets is accelerated until an intermediate region where the speed reaches its maximum value. Then, the acceleration of the jet stops in this region. Further away in the recollimation region the outflow slows down. Note that such jet oscillations could finally lead to a more turbulent outflow consistently with the numerical simulations of two-component jets we mentioned in introduction. After the recollimating region we cannot exclude the presence of shocks or instabilities. Thus it is difficult to know if the oscillations that appeared in the solutions would be observable or not.

In summary, we propose that a difference between these two types of spine jets associated with FR I and FR II radio galaxies may result from the competition between the magnetic and thermal confining mechanisms. Magnetic pinching and pressure gradient tend to compensate the transverse expansion of the jet because of the centrifugal force and the charge separation, which also induces an outward electric force. These two expanding forces are characterized by the free parameter $\lambda^2$, which measures the quantity of the angular momentum carried along the streamlines. The magnetic collimation is controlled by the parameter $\epsilon/\lambda^2$ (see Sauty et al. 1999). On the other hand, thermal collimation is controlled by the parameter $\kappa$, which defines the transverse variation of the pressure.

Hence, an appropriate way to classify the different jet solutions according to the nature of their collimation is based on the two free parameters $\kappa /2\lambda ^2$ and $\epsilon / 2\lambda ^2$(Sauty et al. 2004,2002,1999). The higher the value of those parameters, the stronger is the collimation and the lower is their terminal speed. This can be seen in Table 1 where we plot the asymptotic jet speed in units of the escape speed from the base of the corona for various solutions. As the efficiency of collimation increases, the efficiency of the acceleration decreases. In other words, tightly collimated jets (larger values of $\epsilon / 2\lambda ^2$, or, $\kappa /2\lambda ^2$) have lower terminal speeds. Thus the strong interaction with the external medium would naturally result into a decelerated flow even if it remains stable. Equally, a denser jet would radiate more on a large scale before the terminal shock with the ambient medium.

Table 1 also shows that jets from inefficient magnetic rotators are more powerful in transforming thermal energy into kinetic energy than those from efficient magnetic rotators. There are two reasons for this.

First, the centrifugal force at the base of the jet is important in EMR flows. Then, the last stable orbit of the plasma gets closer to the central black hole. Therefore, the corona extends closer to the black hole horizon. Thus, if the available total amount of thermal energy is the same in the corona, the plasma gravitational potential increases. Consequently, in EMR as $\epsilon/ (2\lambda^2)$ increases, more thermal energy is tapped in order to allow for the plasma to escape and less is left for accelerating it.

Second (see Fig. 2), an increase in the magnetic rotator efficiency limits the initial expansion of the outflow. The pinching magnetic force gets stronger after the Alfvén surface and the conversion of thermal energy into kinetic energy stops when the jet reaches its asymptotic cylindrical shape. This decrease of the jet asymptotic speed with the increase of the magnetic rotator efficiency may seem contradictory with the usual picture. However, in axial outflows the contribution of the Poynting flux to the total acceleration remains weak. This is of course different from relativistic disk wind models, where the acceleration is dominated by the conversion of the Poynting flux to the kinetic energy flux (Vlahakis & Königl 2004; Contopoulos 1994; Li et al 1992). Those jets are characterized by a strong inclination of the magnetic field lines and the rotation at the base of the outflow is almost Keplerian. Note also that, as expected, the efficiency of the acceleration increases as well with the degree of expansion, i.e., as $\kappa /2\lambda ^2$ decreases.

\begin{figure} \par {\rotatebox{0}{\resizebox{8.7cm}{5.5cm} {\includegraphics{12... ...ebox{0}{\resizebox{8.7cm}{5.5cm} {\includegraphics{12920fg2b.eps}}} \end{figure} Figure 2:

In a) we plot the Alfvén number M2 and in b) the cylindrical jet cross section G2 as functions of the distance for $\kappa /2\lambda ^2 = 0.05$ and four values of $\epsilon / 2\lambda ^2$ $(-0.5, -0.5\times 10^{-2}, 0.5\times 10^{-2},0.5)$, corresponding to Table 1.

Open with DEXTER

3.1 Estimation of the free parameters

In the sections below, we mainly explore two examples of typical solutions for relativistic jets. One is associated with an IMR so that the contribution of the external pressure is comparable to the magnetic one, while the second is associated to an EMR so that the jet is magnetically self-collimated. In order to find these solutions we first make an estimation of the free parameters of the model using our knowledge of the properties of FR I and FR II jets, in particular in the launching region on one hand and in the far asymptotic region on the other hand.

At the base of the outflow, we assume that the corona starts at the radial distance of the last stable orbit, that is around the radius of the Schwarzschild black hole, as discussed below. We consider that the last open streamlines, which emerge from the corona should be in sub-Keplerian rotation if they are anchored in the thick disk surrounding the central black hole. The last open streamline in the coronal jet is the one that crosses the equatorial plane at the edge of the magnetic dead zone, which we assume to have a dipolar configuration.

We also use some observational constraints in the asymptotic region of the jet. The opening angle of the jet has to be a few degrees. Six degrees is the value inferred for the well measured jet of M 87 (Biretta et al. 2002; Kovalev et al. 2007). We guess that the spine jet opening angle is even smaller and we took a value of $\simeq $$1^{\circ}$ at 1 pc. Then, from the expression of the dimensionless magnetic flux $\alpha$, by knowing the last streamline, we can deduce the asymptotic value of $G_{\infty}$:

$\displaystyle G_{\infty} = \frac{r_{\infty}}{r_{\star} \sqrt{\alpha_{\rm ext}}} \sin{\theta} ,$     (16)

where $\alpha_{\rm ext}$ is the last open streamline in the jet. As a reasonable estimate, we have taken $\alpha_{\rm ext} = 4$. Indeed, for lower values of $\alpha_{\rm ext}$, the value of $G_{\infty}$ becomes too high and therefore unrealistic for our model. We further assume that in the asymptotic region the Alfvén number is on the order of $M_{\infty}\simeq 5$: this is the order of magnitude found in the literature for relativistic magnetohydrodynamical jet propagation (Leismann et al. 2005; Keppens et al. 2008).

We know that the asymptotic Lorentz factors should be between $\sim $3 and 10 (see Piner et al. 2003). From the expression of the asymptotic velocity along the polar axis (Eq. (6)) we can deduce the value of the free parameter $\nu^2$ from Eq. (13),

$\displaystyle \nu^2 = \frac{\mu c^2}{V_{\infty}^2} \left(\frac{M^2_{\infty}}{h_{0\star}^2 G^2_{\infty}} \right)^2\cdot$     (17)

We used on purpose a rather lower limit for the Lorentz factor in order to avoid high effective temperatures in our model. Indeed, we can use the same solutions and upscale them to obtain higher Lorentz factors, but then the effective temperature would attain extremely high values above the mass temperature. However, the corresponding high pressure could receive a large contribution from a turbulent magnetic or ram pressure component in the jet (see Aibéo et al. 2007, for the solar wind). In that case the kinetic temperature would be lower. Nevertheless, as far as the collimation is concerned, this does not qualitatively affect our discussion about the dichotomy between FR I and FR II, and we kept this relatively low Lorentz factor.

We also used the observed mass-loss rate in the outflow to constrain the free parameter $\delta$. However, the spine jet probably carries only a small fraction of the observed energy flux in AGN jets, $L_{\rm jet,Kin} \sim 10^{43} ~{\rm ergs/s}$ (Allen et al. 2006) The energy flux of the coronal wind remains weak compared to the total mass carried by the disk-wind which is supposedly denser (Vlahakis & Konigl 2004), a situation similar to stellar jets associated with YSOs (Meliani et al. 2006b). Then $\delta$ is deduced from the assumed value for the mass-loss rate,

                                    $\displaystyle \dot{M}$ = $\displaystyle 2~\int_{\rm section} m_{\rm part}~h~\gamma~n~V_{p}~ {\rm d}S ,$  
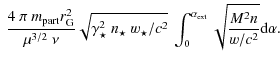
  = $\displaystyle ~\frac{4~\pi~ m_{\rm part }r_{\rm G}^2}{\mu^{3/2}~\nu}\sqrt{\gamm... ...}/c^2}}~ \int_{0}^{\alpha_{\rm ext}}\sqrt{\frac{M^{2} n}{w/c^2}}{\rm d}\alpha .$ (18)

We get an equation for $\delta$,

    $\displaystyle (1 + \alpha_{\rm ext} \delta)^4\times C^2 -(2 C^2+1 ) \times(1 + \alpha_{\rm ext} \delta)^3 +(1 + \alpha_{\rm ext} \delta)^2$  
    $\displaystyle \qquad \times C \times (2 + C) (19)

where C is another constant given by,
$\displaystyle C = \frac{3{\mu^{3/2}\nu (1 - \mu)}\dot{M}}{8 \pi r_{G}^2 m_{\rm ... ...qrt{1- r_G/r_{\infty}}} \gamma_{\infty} n_{\infty} M^2_{\infty}\alpha_{0}}\cdot$     (20)

The variable $n_{\infty}$ is the asymptotic density and $m_{\rm par}$the average mass of the particles. We consider a proton-electron fluid, $m_{\rm par} = m_{\rm proton}$.

For the mass-loss rate we choose $\dot{M} = n_{0} 10^{-6}\dot{M}_{\rm Edd}$, where $\dot{M}_{\rm Edd}$is the Eddington mass-loss rate. It corresponds to the value found for the relativistic Parker wind (Meliani et al. 2004). The asymptotic density is taken equal to $n_{\infty} = 10^{-8}\times n_{0}$ cm-3 (Meliani et al. 2004), with n0a dimensionless free parameter.

We suppose that the rotation is sub-Keplerian on the last open streamline of the jet at the equator. The parameter $\eta$measures the deviation of the rotation function $\Omega$ from its Keplerian value,

$\displaystyle \Omega = \left(1 - \eta\right) \sqrt{\frac{r_{G}^2}{2 r_{0}^3 ~\mu}} c.$   (21)

From the definition of $\Omega$(Eq. (21)) we can deduce the value of the free parameter $\lambda$, which is the constant controlling the angular momentum extracted by the jet,
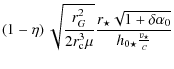
                            $\displaystyle \lambda$ = $\displaystyle \left(1 - \eta\right) \sqrt{\frac{r_{G}^2}{2 r_{\rm c}^3 \mu}} \frac{r_{\star} \sqrt{1 + \delta \alpha_{0}}}{h_{0 \star} \frac{v_{\star}}{c}}$  
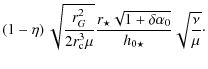
  = $\displaystyle \left(1 - \eta\right) \sqrt{\frac{r_{G}^2}{2 r_{\rm c}^3 \mu}} \f... ...{\star} \sqrt{1 + \delta \alpha_{0}}}{h_{0 \star} } \sqrt{\frac{\nu}{\mu}}\cdot$ (22)

As we mentioned earlier we assume that the corona forms above the last stable orbit at r0 = 3 rG. We choose a typical magnetic lever arm (i.e. Alfvén radius) of 10 times the Schwarzschild radius, $r_\star=10r_G$. It gives,
$\displaystyle R_{0} = \frac{r_{0}}{r_{\star}} = 0.3 .$   (23)

The parameter $\kappa$, which is the relative variation of the pressure with latitude, is calculated from an approximate expression of the coronal base, where $M_0 \rightarrow 0$ and d $M^2_0/{\rm d}R$ is finite in Eq. (A.2)-(A.5) (Meliani et al. 2006a) using,
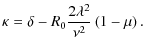
$\displaystyle \kappa = \delta - R_{0} \frac{2 \lambda^2}{\nu^2} \left(1 -\mu\right).$   (24)

To summarize, our free parameter estimates are:
1.
the Alfvén radius
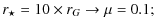
$\displaystyle r_{\star} = 10\times r_{G} \rightarrow \mu = 0.1 ;$   (25)

2.
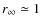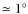the jet opening angle at $r_{\infty} \simeq 1$ pc is $\simeq 1^{\circ}$, which gives the asymptotic value of $G_{\infty}$ for the last streamline $\alpha_{\rm ext} = 4$;
3.
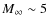for the asymptotic Alfvén number we chose $M_{\infty}\sim 5$;
4.
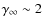the asymptotic Lorentz factor is taken to be $\gamma_{\infty} \sim 2$;
5.
the asymptotic density is taken equal to 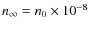$n_{\infty} = n_0 \times 10^{-8}$ cm-3;
6.
the new parameter $\eta$, which measures how sub-Keplerian the velocity is (the values differ from solution to solution);
7.
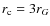the corona is supposed to be formed above the last stable orbit, $r_{\rm c} = 3 r_{G}$, which gives $\kappa$.
The parameter $\eta$ is not independent of the rest of the model. But it precisely measures the rotation of the footpoints and controls the efficiency of the magnetic rotator to collimate the jet. Thus we have an indirect way to determinate the properties of the disk from the asymptotic characteristics of the jet. If $\eta \rightarrow 0$, the open streamlines anchored in the accretion disk rotate with an almost Keplerian profile. On the other hand, if $\eta \rightarrow 1$, the open streamlines anchored in the accretion disk rotate very slowly, and the Poynting flux injected in the jet is low.

Before going further into our modeling of FR I and FR II jets, we need to introduce the notion of effective temperature.

3.2 Temperature

In polytropic relativistic winds (Meliani et al. 2004), the temperature is usually defined by the ideal gas equation of state P/n = kB T. Therefore, the knowledge of the specific pressure P/n, the specific thermal energy  $e_{\rm th}$ and the density completely describe the thermodynamics of the fluid (temperature T, enthalpy w and pressure P). However, as discussed in Meliani et al. (2004), flows cannot be adiabatic. The polytropic approximation is just a convenient way to mimic the heating that is ongoing in the flow. Therefore pressure, temperature and enthalpy are not the actual values but effective quantities that hide the necessary extra heating.

The temperature definition in meridional self-similar models is similarly delicate. Indeed, as indicated in STT99 and Meliani et al. (2006a) the total gas pressure is not necessarily limited to be the kinetic pressure. Moreover, the generalized specific thermal energy of the model, $e_{\rm th} = \left(w - m c^2 \right)- \displaystyle \frac{P}{n}$, is not restricted to the thermal energy. In self-similar model these two quantities are also effective quantities. They account for different physical processes of energy and momentum transport and dissipation. They can include the contribution of magnetohydrodynamic waves and viscous and/or radiative mechanisms. Actually, the complexity and variety of MHD processes that can contribute to the internal energy of a magnetized fluid makes the definition of the real thermal energy impossible.

Therefore the quantities $T_{\rm eff}=P/n$ and $e_{\rm th, eff}=e_{\rm th}$ are simply the specific effective temperature and thermal energy imposed by the dynamics of the outflow. They do not necessarily represent the kinetic temperature or the thermal energy. Instead they are simple tools to analyze the energetics of the flow. Below, we discuss the thermodynamical properties of the fluid with this effective temperature and not the kinetic temperature, which we cannot calculate.

$\displaystyle T_{\rm eff} = \frac{P}{k_{B} n} = \frac{1}{2 k_{B}}{\gamma_{\star}}^2 w_{\star} M^2 \Pi \frac{1 + \kappa\alpha}{1 + \delta \alpha} ,$   (26)

                           $\displaystyle e_{\rm th, eff}$ = $\displaystyle w - m c^2 -\frac{P}{ n}$  
  = $\displaystyle w - m c^2 - \frac{1}{2 k_{B}}{\gamma_{\star}}^2 \frac{w_{\star}}{c^2} M^2 \Pi \frac{1 + \kappa\alpha}{1 + \delta \alpha}\cdot$ (27)

Thus along the polar axis, the specific thermal energy is deduced from the Bernoulli equation as follows
$\displaystyle e_{\rm th, eff} = w_{\star} \frac{h_{0, \star}}{h_{0}} \frac{\gamma}{\gamma_{\star}} - m c^2 - \frac{1}{2}{\gamma_{\star}}^2 w_{\star} M^2 \Pi .$   (28)

We also define ${\cal Q}$ the heat content added to the fluid, which is the difference between the total effective internal energy of the fluid $e_{\rm th, eff}$ and the internal energy of the fluid obtained if it were adiabatic:
$\displaystyle {\cal Q} = e_{\rm th, eff} - \sqrt{ m c^2 + \kappa_{\rm pol} n^{\frac{5}{3} -1} } ,$   (29)

where $\kappa_{\rm pol}$ is a constant. It is determined from pressure and density at the flow boundary either in the asymptotic region or in the launching region (in adiabatic flows, we have $\kappa_{\rm pol}= P / n^{\frac{5}{3}}$).

4 Application I - Model of FR I spine jets

4.1 Parameters

The first solution we show here is adapted to model the spine jet of radio-loud galaxies of the FR I type. The environment of these jets, i.e. the host galaxy, is known to be rich and to contain dense gas. Moreover, the properties of the FR I jets on the pc scale are quite different from that on kpc scales. Indeed, in the region close to the nucleus (on the scale of a pc), FR I jets are accelerated to highly relativistic speeds.

Beyond this region, the jets interact with the external medium, which is denser. This interaction induces an observed deceleration of the jet. Thus, we assume that the outflow is likely confined by the pressure of the ambient medium, at least partially. In our model, these types of jets correspond to solutions associated with inefficient central magnetic rotators. In this solution $\eta = 0.90$, which gives an inefficient magnetic rotator.

The solution corresponds to parameters

            $\displaystyle \mu$ = 0.1 ,  
$\displaystyle \nu$ = 0.69 ,  
$\displaystyle \lambda$ = 0.85 ,  
$\displaystyle \delta$ = 1.45 ,  
$\displaystyle \kappa$ = 0.42 ,  
$\displaystyle \epsilon$ = -0.8475 . (30)

4.2 Morphology of the FR I-type jet

As seen in Fig. 3, the jet solution shows an initial expansion up to a distance of 100Schwarzschild radii, which then stops, after which the jet recollimates. The expansion of the jet is due to the strong initial inertia of the plasma carried along the external streamlines. The jet becomes collimated once it interacts with the ``external'' ambient medium that compresses it. What we call ``external'' medium refers to the gas surrounding the last valid streamline of the solution; this can be the actual external medium of the host galaxy, but considering the transverse expansion of the solution, it more likely corresponds to the over-pressured gas of the surrounding disk wind.

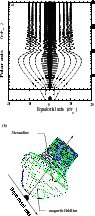
\begin{figure} \par {\rotatebox{0}{\resizebox{9.2cm}{10.0cm} {\includegraphics{1... ....8cm}{8.5cm} {\includegraphics{12920fg3b.eps}}} }\vspace*{-2.5mm} \end{figure} Figure 3:

Plot of the morphology of the solution corresponding to a FR I-type spine jet. In a) the projection of the streamlines on the poloidal plane is shown. The solid lines in the center correspond to lines where the conditions xA2 G2<10-2 and $({2 + \delta \alpha })/{\left (1 + \delta \alpha \right )^2} - 2<10^{-2}$are satisfied. The dashed lines correspond to xA2 G2<10-1 and $({2 + \delta \alpha })/{\left (1 + \delta \alpha \right )^2} - 2<10^{-1}$. The dashed-dotted lines correspond to xA2 G2>10-1 and $({2 + \delta \alpha })/{\left (1 + \delta \alpha \right )^2} - 2>10^{-1}$ (see Meliani et al. 2006a, for details).

Open with DEXTER

The jet compression for inefficient magnetic rotators generates strong oscillations in the asymptotic region of the jet even in the relativistic case (Meliani et al. 2006a). The light cylinder of this jet solution is at infinity. These oscillations result from a transfer of energy between the enthalpy and the Lorentz factor because $h\gamma w$ remains constant to first order with respect to $\alpha$.

\begin{figure} \par {\rotatebox{0}{\resizebox{9cm}{4.5cm}{\includegraphics{12920... ...ebox{9cm}{4.5cm} {\includegraphics{12920fg4b.eps}}} \vspace*{2.5mm} \end{figure} Figure 4:

In a) we plot the energetic fluxes normalized to the mass energy of the first solution for a ``FR I-type''' spine jet. In b) we plot for the same solution, the Lorentz factor $\gamma $ along four different streamlines. The solid line corresponds to the polar axis and the dotted line to the last streamline connected to the central corona. Other lines are intermediate ones.

Open with DEXTER

4.3 FR I-type jet kinematics

The jet acceleration occurs mainly in the intermediate region (Fig. 4b) where gravity becomes weak. Thus, all the enthalpy still remaining in the outflow is converted to kinetic energy.

The maximum Lorentz factor in this solution ( $\gamma = 2.8$) is obtained at the largest expansion of the jet radius, where the effective temperatures are already ultra relativistic ($\approx$1013 K). To explain this high effective temperature, part of the pressure must be of non-kinetic origin, with contribution from turbulent ram and magnetic pressure, as we discussed in Sect. 3.1. Thus this value of $\gamma $ is close to the lower observed ones, but already corresponds to a highly turbulent medium. The model can produce higher Lorentz factors provided the turbulent pressure level is sufficient. This is not the main topic of the qualitative discussion we address on the collimation of the jet itself.

In the region of re-collimation, the increase of the pressure induces a deceleration of the jet. The Lorentz factor decreases from $\gamma = 2.8$, its maximum value before the re-collimation, to $\gamma = 2$in the asymptotic region. As a matter of fact such a deceleration is a characteristic of FR I jets, as we mentioned. It is remarkable that this solution clearly shows that the main effect of the re-collimation by some external pressure is a global deceleration of the outflow, as observed in FR I jets. The distance of recollimation in this solution is smaller however than the usual parsec scale. This may be because we are dealing here only with the inner part of the jet, while observations may correspond to the surrounding disk-wind, or it can be because our Lorentz factor is too low. Moreover, we assume here that the external pressure of the host galaxy is somehow transmitted to the disk-wind, which in turn confines the spine jet. Keeping in mind these necessary precautions, this result by itself seems interesting, if we take into account the simplicity of our model.

4.4 FR I-type jet energetics

The temperature profile is characterized by four different regimes. The three first are the same as for the ``FR II'' jet solution, and we shall discuss it below. The fourth one corresponds to the asymptotic recollimated region of the ``FR I'' jet. There, the effective temperature reaches the high value of $T_{\rm eff} \sim 10^{13}~{\rm K}$, because of the strong compression of the outflow by the external medium (Fig. 5b). This effective temperature is high compared to the observed temperature in AGN jets that are usually on the order of $T\sim 10^{8}~{\rm K}$. This large difference can be explained however by some increase of the contribution of non-thermal mechanisms to the effective specific thermal energy $e_{\rm th, eff}$. As we mentioned before, we cannot directly compare this effective temperature with the kinetic temperature in the frame of this model.

5 Application II - model for FR II spine jets

5.1 Parameters

Conversely to the case of FR I, the environment of FR II radio-loud galaxies is relatively poor. Thus, jets from FR II galaxies should interact only slightly with the ambient medium. In these outflows, the velocity increases continuously until the asymptotic region. Indeed, unlike FR I outflows, the velocity in FR II jets is relativistic both on the parsec and kilo-parsec scales. Besides, FR II jets are so well collimated on large scales that they are very likely to have an asymptotic cylindrical shape. In our model these types of jets correspond to a solution associated with an efficient central magnetic rotator. Therefore, the value of the free parameter $\eta$ is probably lower, i.e. the rotation is closer to Keplerian velocity than for the solution for FR I. This increases the available Poynting flux at the base of the jet. Therefore, the jet will be collimated by the toroidal magnetic pinching without any oscillations.

The parameters for this specific solution are:

         $\displaystyle \mu$ = 0.1 ,  
$\displaystyle \nu$ = 0.65 ,  
$\displaystyle \lambda$ = 1.051 ,  
$\displaystyle \delta$ = 1.35 , (31)
$\displaystyle \kappa$ = 0.3 ,  
$\displaystyle \epsilon$ = 0.334 .  

This is an efficient magnetic rotator. It corresponds to a slightly lower value of $\eta = 0.86$. This shows that the efficiency is very sensitive to the variations of the rotation frequency.
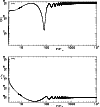
\begin{figure} \par {\rotatebox{0}{\resizebox{8.7cm}{4.5cm}{\includegraphics{129... ...tebox{0}{\resizebox{8.7cm}{4.5cm}{\includegraphics{12920fg5b.eps}}} \end{figure} Figure 5:

In a) we plot the temperature profile and in b) the density profile for the FR I-type jet solution. The density is normalized to n0 so that the mass-loss rate is $\dot{M} = n_{0} 10^{-6} ~\dot{M}_{\rm Edd}$.

Open with DEXTER

This FR II-type jet solution is characterized by a continuous expansion up to a distance of about 100 Alfvén radii again, but the outflow after this distance remains cylindrical, slightly expanding further out. This expansion is related to the high magnetic pressure at the base, together with the strong gravity, in addition to some non negligible contribution of the force of charge separation. However, the collimation of the jet in the asymptotic region is exclusively of magnetic origin. It is induced by the toroidal magnetic pinching force and the transverse magnetic pressure. These two forces balance the centrifugal and charge separation forces. Oscillations in the jet are very weak because to the relatively small contribution of the thermal confinement, as expected.

The opening angle of the last open streamline of the solution at a distance of one parsec is only $0.1^{\circ}$, which is rather narrow compared to our initial guess. This definitely rules out the possibility to describe the whole jet completely with this model. Instead, we prefer to see it as the spine or inner part of the jet that carries away the angular momentum of the central black hole. The situation is similar to what happens in YSOs where the stellar jet is responsible for the spinning down of the protostar, while the outer disk wind is responsible for the observed mass-loss.

5.2 FR II-type jet kinematics

The acceleration of this solution is continuous. First, there is a small but effective thermal acceleration in the lower region of the corona. In this region, the high thermal energy both accelerates the fluid up to 0.4c at a distance of 6 rG and enables it to escape from the deep gravitational potential. A second stronger thermal acceleration of the jet occurs beyond the Alfvén surface up to the collimation region. In this region, the pressure drops rapidly and asymptotically goes to negligible values. Therefore, the thermal energy is transformed into kinetic energy more effectively. In this intermediate regime the velocity in the flow increases from 0.4c to 0.92c on a scale on the order of 200 rG.

5.3 The light cylinder of the FR II-type solution

The light cylinder in the asymptotic region of the jet (Fig. 6) is roughly vertical and asymptotically parallel to the poloidal streamlines, which remain inside the light cylinder. However, in this solution conversely to the previous one, the light cylinder is not at infinity but at a distance of about 20 rG from the polar axis. This reduces the validity domain of the solution around its axis (cf. Meliani et al. 2006a) where the effects of the light cylinder can be neglected. Indeed self-similar disk-wind models can produce solutions crossing the light cylinder (Vlahakis & Königl 2003a,b). These solutions undergo a strong magnetic acceleration ideal to obtain high Lorentz factors in GRBs for instance. This is of course not necessarily the case for the spine jet, which can be accelerated by other means than the magnetocentrifugal process.

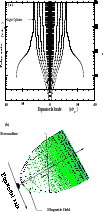
\begin{figure} \par {\rotatebox{0}{\resizebox{9.5cm}{10.0cm} {\includegraphics{1... ...x{0}{\resizebox{9.0cm}{8.5cm} {\includegraphics{12920fg6b.eps}}} }\end{figure} Figure 6:

The same as in Fig. 3 for the second solution corresponding to a FR II-type spine jet.

Open with DEXTER
\begin{figure} \par {\rotatebox{0}{\resizebox{8.8cm}{4.5cm}{\includegraphics{129... ...tebox{0}{\resizebox{8.8cm}{4.5cm}{\includegraphics{12920fg7b.eps}}} \end{figure} Figure 7:

In a) we plot the energetic fluxes normalized to the mass energy of the second solution for a ``FR II-type'' spine jet. In b) we plot for the same solution, the Lorentz factor $\gamma $ along four different streamlines. The solid line corresponds to the polar axis and the dotted line to the last streamline connected to the central corona. Other lines are intermediate ones.

Open with DEXTER
\begin{figure} \par {\rotatebox{0}{\resizebox{8.7cm}{4.5cm} {\includegraphics{12... ...box{0}{\resizebox{8.7cm}{4.5cm} {\includegraphics{12920fg8b.eps}}} \end{figure} Figure 8:

In a) we plot the temperature profile and in b) the density profile for the FR II-type jet solution. On the left the vertical lines delimitate the various domains of the temperature profile. On the right the density is normalized to n0 such that the mass-loss rate is $\dot{M} = n_{0} 10^{-6} ~\dot{M}_{\rm Edd}$.

Open with DEXTER

5.4 FR II-type jet energetics

The effective temperature profile of this second solution goes through four different regimes.

First, in the lower corona, the effective temperature increases extremely rapidly (Fig. 8a) from about $10^{12}~{\rm K}$ at the base to about $3\times10^{12}~{\rm K}$. This increase is due to some strong initial heating in the expanding corona. The large expansion induces a strong decrease of the density, but because of the heating, the pressure decreases less rapidly.

Second, in the intermediate region, the effective temperature still increases up to its maximum value of about $3\times10^{12}~{\rm K}$ after a relatively small decrease, because of the global expansion and drop of the density.

Third, we have a transition region after the maximum and the asymptotic part. The effective temperature decreases again to attain values around $10^{12}~{\rm K}$. This decrease is induced by the magnetic compression of the jet that brakes the density decreasing (Fig. 8b).

The effective temperature obtained in this solution is of course high compared to observed temperatures in AGN jets, which are typically on the order of $10^{8}~ {\rm K}$ in the asymptotic regions. As for FR I this indicates that the contribution of non-thermal energies to the acceleration and the heat of the jet are relevant.

6 Conclusions

We have applied exact GRMHD solutions from Meliani et al. (2006a) to the canonical classification of AGN jets (Urry & Padovani 1995) according to their morphology. Our model is constructed in the frame of general relativity using the metric of a central Schwarzschild black hole. It validates the classification of AGN proposed in Sauty et al. (2001) where the classical MHD solutions were used with some additional features due to relativistic effects. In this study it was proposed that the inner regions of jets (spines) are collimated by an external denser medium in FR I and by the force of magnetic pinching in FR II.

We first proposed a method to estimate the free parameters of the model from the known properties of AGN jets. In particular, the departure from Keplerian rotation at the footpoints of the fieldlines is measured by an extra parameter $\eta$. It turns out that we get very different classes of solutions by slightly changing this parameter.

First we obtained a recollimating solution for $\eta = 0.90$. On a small spatial scale the outflow expands and the Lorentz factor reaches a maximum of $\gamma = 2.8$ in the intermediate region. This Lorentz factor is obviously smaller by a factor of 2 to 3 than the observed values. We could rescale the whole solution to attain higher Lorentz factors, but at the prize of high temperature in the jet. Similarly to the Solar wind this would require extra sources to account for the heating. However, we were mostly interested in describing the general features of the solution and tried to explain the dichotomy between FR I and FR II jets rather than model specific observed jets.

Then the solution obtained for a typical FR I jet recollimates, undergoes several oscillations, and decelerates to a Lorentz factor of $\gamma = 2$in the asymptotic region. This decrease is related to thermal compression of the jet in the asymptotic region by the outer medium. We insist that this recollimation occurs on a scale smaller than one parsec and that the external pressure is certainly the pressure of the surrounding disk wind rather than the external gas from the host galaxy. However, if we assume that the extra pressure of the host galaxy can enhance the pressure in the disk wind, it is striking to note that our simple toy model for the spine jet shows a typical feature of FR I jets. Indeed FR I jets sometimes show a deceleration on the kiloparsec scale to non-relativistic speeds though they are usually highly relativistic on smaller scales. Besides this they are also known to have a rich ambient medium, and the external gas pressure is important, as seen in the X-ray (Capetti et al. 2002). Finally, that the FR I jet radius is larger on the kiloparsec scale can be due precisely to this recollimation effect, which enhances the density in a way that probably a larger part of the radio jet is emitted than suggested in the double component jet of Sol et al. (1989).

For the FR II jets, the optimal value found is $\eta = 0.86$, which also gives a maximum Lorentz factor of $\gamma \simeq 3$. That $\eta$ changes very little when we pass from the ``FR I''-type solution to the ``FR II''-type shows that the outflow properties are highly sensitive to the rotation velocity of the corona. The solution obtained is however very different because the gas expands monotonically and remains highly relativistic up to large distances, as observed in FR II jets. Moreover it is self-collimated by its own magnetic field throughout the length of the jet, something that is again characteristic of FR II jets, wherein there is evidence that the host galaxy gas is rather underdense.

On the other hand, that in these two cases $\eta$ is slightly smaller than 1 shows that the central launching region of the spine jet has to be slightly sub-Keplerian.

We did not discuss Seyfert galaxies, which are known to have outflows, though their winds are not very well collimated and are not relativistic with velocities of the order on 30 000 km s-1, as observed by the HST. Again, these flows can be understood in the frame of this simple self-similar model as non-collimated solutions, which are radial and exist only if the velocity does not reach relativistic values (Meliani et al. 2006a). These solutions are obtained if the magnetic rotator efficiency is very low, i.e. for $\epsilon$ very negative, in a way similar to the solar wind.

To summarize, we may conclude that using a simple toy model for spine jets, the usual classification of radio sources can be understood on one hand by projection effects and Doppler boosting and on the other by considering the efficiency of the central magnetic rotator. Of course this does not exclude any of the other explanations such as the role of the external confinement or shear instabilities. Indeed our FR I-type solution is at least partially confined by the disk wind, which may be a signature of external pressure confinement as well. This idea needs to be further explored with more sophisticated models or simulations combining the central coronal jet with an external disk wind, something worth to pursue in another study.

The next step we consider is the extension of the model to the Kerr metric. This is a unique chance to construct the first analytical models for a jet around a rotating black hole. One issue of this extension is to test the Blandford-Znajek mechanism (Blandford & Znajek 1977).

Acknowledgements
Z. Meliani acknowledges financial support from the FWO, grant G.027708. The authors thank Nektarios Vlahakis for helpful discussions and suggestions.

References

  1. Aibeo, A., Lima, J. J. G., & Sauty, C. 2007, A&A, 461, 685 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Allen, S. W., Dunn, R. J. H., Fabian, A. C., Taylor, G. B., & Reynolds, C. S. 2006, MNRAS, 372, 21 [NASA ADS] [CrossRef] [Google Scholar]
  3. Aloy, M. A., Ibáñez, J. M., Martí, J. M., & Müller, E. 1999, ApJS, 122, 151 [NASA ADS] [CrossRef] [Google Scholar]
  4. Asada, K., Inoue, M., Uchida, Y., et al. 2002, PASJ, 54, L39 [NASA ADS] [Google Scholar]
  5. Bardeen, J. M., & Berger, B. K. 1978, ApJ, 221, 105 [NASA ADS] [CrossRef] [Google Scholar]
  6. Baum, S. A., Zirbel, E. L., & O'Dea, C. P. 1995, ApJ, 451, 88 [NASA ADS] [CrossRef] [Google Scholar]
  7. Bicknell, G. V. 1995, ApJS, 101, 29 [NASA ADS] [CrossRef] [Google Scholar]
  8. Biretta, J., Junor, W., & Livio, M. 2002, New Astron. Rev., 46, 239 [NASA ADS] [CrossRef] [Google Scholar]
  9. Begelman, M. C., & Celotti, A. 2004, MNRAS, 352, L45 [NASA ADS] [CrossRef] [Google Scholar]
  10. Blandford, R. D., & Payne, D. G. 1982, MNRAS, 199, 883 [NASA ADS] [CrossRef] [Google Scholar]
  11. Blandford, R. D., & Znajek, R. L. 1977, MNRAS, 179, 433 [NASA ADS] [CrossRef] [Google Scholar]
  12. Bridle, A. H. 1992, Testing the AGN paradigm, AIP Conf. Proc., 254, 386 [Google Scholar]
  13. Camenzind, M. 1986, A&A, 156, 137 [NASA ADS] [Google Scholar]
  14. Canvin, J. R., Laing, R. A., Bridle, A. H., & Cotton, W. D. 2005, MNRAS, 363, 1223 [NASA ADS] [CrossRef] [Google Scholar]
  15. Capetti, A., Trussoni, E., Celotti, A., et al. 2002, New Astron. Rev., 46, 335 [NASA ADS] [CrossRef] [Google Scholar]
  16. Celotti, A. 2003, Ap&SS, 288, 175 [NASA ADS] [CrossRef] [Google Scholar]
  17. Contopoulos, J. 1994, ApJ, 432, 508 [NASA ADS] [CrossRef] [Google Scholar]
  18. Das, S., & Chakrabarti, K. 2002, JApA, 23, 143 [NASA ADS] [Google Scholar]
  19. De Young, D. S. 1993, ApJ, 405, L13 [NASA ADS] [CrossRef] [Google Scholar]
  20. Duncan, C., & Hughes, P. 1994, ApJ, 436, 119 [Google Scholar]
  21. Fabian, A. C., & Rees, M. J. 1995, MNRAS, 277, L55 [NASA ADS] [Google Scholar]
  22. Fanaroff, B. L., & Riley, J. M. 1974, MNRAS, 167, 31 [NASA ADS] [CrossRef] [Google Scholar]
  23. Fendt, C. 1997, A&A, 319, 1025 [NASA ADS] [Google Scholar]
  24. Fendt, C. 2009, ApJ, 692, 346 [NASA ADS] [CrossRef] [Google Scholar]
  25. Ferreira, J. 1997, A&A, 319, 340 [NASA ADS] [Google Scholar]
  26. Ferreira, J., Dougados, C., & Cabrit, S. 2006, A&A, 453, 785 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Gabuzda, D. C. 2003, Ap&SS, 288, 39 [NASA ADS] [CrossRef] [Google Scholar]
  28. Gabuzda, D. C., Mullan, C., Cawthorne, T. V., et al. 1994, ApJ, 435, 140 [NASA ADS] [CrossRef] [Google Scholar]
  29. Giovannini, G., Taylor, G. B., Feretti, L., et al. 2005, ApJ, 618, 635 [NASA ADS] [CrossRef] [Google Scholar]
  30. Gómez, J. L., Marscher, A. P., Jorstad, S. G., Agudo, I., & Roca-Sogorb, M. 2008, ApJ, 681, L69 [NASA ADS] [CrossRef] [Google Scholar]
  31. Gopal-Krishna, & Wiita, P. J. 2000, A&A, 363, 507 [NASA ADS] [Google Scholar]
  32. Gopal-Krishna, & Wiita, P. J. 2002, New Astr. Rev., 46, 357 [Google Scholar]
  33. Gracia, J., Vlahakis, N., Tsinganos, K. 2006, MNRAS, 367, 201 [NASA ADS] [CrossRef] [Google Scholar]
  34. Gracia, J., Vlahakis, N., Agudo, I., Tsinganos, K., & Bogovalov, S. V. 2009, ApJ, 695, 503 [NASA ADS] [CrossRef] [Google Scholar]
  35. Hardcastle, M. J., & Worrall, D. M. 2000, MNRAS, 319, 562 [NASA ADS] [CrossRef] [Google Scholar]
  36. Hardee, P., Mizuno, Y., & Nishikawa K.-I. 2007, Ap&SS, 311, 281 [NASA ADS] [CrossRef] [Google Scholar]
  37. Henri, G., & Pelletier, G. 1991, ApJ, 383, L7 [NASA ADS] [CrossRef] [Google Scholar]
  38. Horiuchi, S., Meier, D. L., Preston, R. A., & Tingay S. J. 2006, PASJ, 58, 211 [NASA ADS] [Google Scholar]
  39. Kaiser, C., & Alexander, P. 1997, MNRAS, 286, 215 [NASA ADS] [CrossRef] [Google Scholar]
  40. Kaiser, C., & Best, P. 2007, MNRAS, 381, 1548 [NASA ADS] [CrossRef] [Google Scholar]
  41. Kazanas, D., & Elison, D. C. 1986, ApJ, 304, 178 [NASA ADS] [CrossRef] [Google Scholar]
  42. Kellermann, K. I., Lister, M. L., Homan, D. C., et al. 2004, ApJ, 609, 539 [NASA ADS] [CrossRef] [Google Scholar]
  43. Keppens, R., Meliani, Z., van der Holst, B., Casse, F. 2008, A&A, 486, 663 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Koide, S., Shibata, K., & Kudoh, T. 1998, ApJ, 495L, 63 [Google Scholar]
  45. Koide, S., Shibata, K., & Kudoh, T. 1999, ApJ, 522, 727 [NASA ADS] [CrossRef] [Google Scholar]
  46. Komissarov, S. S. 1999, MNRAS, 308, 1069 [NASA ADS] [CrossRef] [Google Scholar]
  47. Komissarov, S. S., & Falle, S. A. 1998, MNRAS, 297, 1087 [NASA ADS] [CrossRef] [Google Scholar]
  48. Komissarov, S. S., Barkov, M. V., Vlahakis, N., & Königl, A. 2007, MNRAS, 380, 51 [NASA ADS] [CrossRef] [Google Scholar]
  49. Kovalev, Y. Y., Lister, M. L., Homan, D. C., & Kellermann, K. I. 2007, ApJ, 668, L27 [NASA ADS] [CrossRef] [Google Scholar]
  50. Laing, R. A., Parma, P., & de Ruiter, H. R. 1999, MNRAS, 306, 513 [NASA ADS] [CrossRef] [Google Scholar]
  51. Ledlow, M. J., & Owen, F. N. 1996, AJ, 112, 9 [NASA ADS] [CrossRef] [Google Scholar]
  52. Li, Z.-Y., Chiueh, T., & Begelman, M. C. 1992, ApJ, 394, 459 [NASA ADS] [CrossRef] [Google Scholar]
  53. Leismann, T., Antón, L., Aloy, M. A., et al. 2005, A&A, 436, 503 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Martí, J. M., Müller, E., Font, J. A., et al. 1997, ApJ, 479, 151 [NASA ADS] [CrossRef] [Google Scholar]
  55. Matsakos, T., Massaglia, S., Trussoni, E., et al. 2009, A&A, 502, 217 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  56. McKinney, J. C. 2006, MNRAS, 368, 1561 [NASA ADS] [CrossRef] [Google Scholar]
  57. McKinney, J. C., & Blandford, R. D., 2009, MNRAS, 394, L126 [NASA ADS] [CrossRef] [Google Scholar]
  58. Meier, D. L. 1999, ApJ, 522, 753 [NASA ADS] [CrossRef] [Google Scholar]
  59. Meier, D. L. 2002, New Astron. Rev., 46, 247 [Google Scholar]
  60. Meliani, Z., & Keppens, R. 2009, ApJ, 705, 1594 [NASA ADS] [CrossRef] [Google Scholar]
  61. Meliani, Z., Sauty, C., Tsinganos, K., & Vlahakis, N. 2004, A&A, 425, 773 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  62. Meliani, Z., Sauty, C., Vlahakis, N., Tsinganos, K., & Trussoni, E. 2006a, A&A, 447, 797 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  63. Meliani, Z., Casse, F., & Sauty, C. 2006b, A&A, 460, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  64. Meliani, Z., Giacomazzo, B., & Keppens, R. 2008, A&A, 491, 391 [Google Scholar]
  65. Mignone, A., Rossi, P., Bodo, G., Ferrari, A., & Massaglia, S. 2010, MNRAS, 402, 7 [NASA ADS] [CrossRef] [Google Scholar]
  66. Mizuno, Y., Hardee, P., & Nishikawa, K.-I. 2007, ApJ, 662, 835 [NASA ADS] [CrossRef] [Google Scholar]
  67. Piner, B. G., Unwin, S. C., Wehrle, A. E., et al. 2003, ApJ, 588, 716 [NASA ADS] [CrossRef] [Google Scholar]
  68. Porth, O., & Fendt, C. 2010, ApJ, 709, 1100 [NASA ADS] [CrossRef] [Google Scholar]
  69. Pushkarev, A. B., Kovalev, Y. Y., Lister, M. L., & Savolainen, T. 2009, A&A, 507, L33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  70. Rossi, P., Mignone, A., Bodo, G., et al. 2008, A&A, 488, 795 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  71. Reynolds, C. S., Di Matteo, T., Fabian, A. C., et al. 1996, MNRAS, 283, 111 [Google Scholar]
  72. Sauty, C., & Tsinganos, K. 1994, A&A, 287, 893 [NASA ADS] [Google Scholar]
  73. Sauty, C., Tsinganos, K., & Trussoni, E. 1999, A&A, 348, 327 [NASA ADS] [Google Scholar]
  74. Sauty, C., Tsinganos, K., & Trussoni, E. 2001, in Relativistic flows in astrophysics, ed. A. W. Guthmann, et al. (Heidelberg: Springer-Verlag), Lecture Notes in Physics, 589, 41 [Google Scholar]
  75. Sauty, C., Trussoni, E., & Tsinganos, K. 2002, A&A, 389, 1068 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  76. Sauty, C., Trussoni, E., & Tsinganos, K. 2004, A&A, 421, 797 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  77. Sol, H., Pelletier, G., & Asseo, E. 1989, MNRAS, 237, 411 [NASA ADS] [Google Scholar]
  78. Trussoni, E. 1998, Astrophysical Jets: Open Problems, ed. S. Massaglia, & G. Bodo (Amsterdam, The Netherlands: Gordon and Breach Science Publishers), 109 [Google Scholar]
  79. Tsinganos, K., & Bogovalov, S. 2002, MNRAS, 337, 553 [NASA ADS] [CrossRef] [Google Scholar]
  80. Urry, C. M., & Padovani, P. 1995, PASP, 107, 803 [NASA ADS] [CrossRef] [Google Scholar]
  81. van Putten, M. H. P. M. 1996, ApJ, 467, L57 [NASA ADS] [CrossRef] [Google Scholar]
  82. Vlahakis, N., & Königl, A. 2003a, ApJ, 596, 1104 [NASA ADS] [CrossRef] [Google Scholar]
  83. Vlahakis, N., & Königl, A. 2003b, ApJ, 596, 1080 [NASA ADS] [CrossRef] [Google Scholar]
  84. Vlahakis, N., & Königl, A. 2004, ApJ, 605, 656 [NASA ADS] [CrossRef] [Google Scholar]
  85. Wold, M., Lacy, M., & Armus, L. 2007, A&A, 470, 531 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  86. Zavala, R. T., & Taylor, G. B. 2005, ApJ, 626, L73 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1:   The asymptotic jet speed in units of the escape speed from the base of the corona, for various values of the parameters $\kappa /2\lambda ^2$ and $\epsilon / 2\lambda ^2$.

All Figures

  \begin{figure} \par\includegraphics[height=7.4cm]{12920fg1.eps} \end{figure} Figure 1:

Standard classification of AGN sources following Urry & Padovani (1995). The horizontal axis represents the inclination of the source axis with the line of sight. The vertical axis we suggest that it may be linked to the efficiency of the underlying magnetic rotator to collimate the flow.

Open with DEXTER
In the text

  \begin{figure} \par {\rotatebox{0}{\resizebox{8.7cm}{5.5cm} {\includegraphics{12... ...ebox{0}{\resizebox{8.7cm}{5.5cm} {\includegraphics{12920fg2b.eps}}} \end{figure} Figure 2:

In a) we plot the Alfvén number M2 and in b) the cylindrical jet cross section G2 as functions of the distance for $\kappa /2\lambda ^2 = 0.05$ and four values of $\epsilon / 2\lambda ^2$ $(-0.5, -0.5\times 10^{-2}, 0.5\times 10^{-2},0.5)$, corresponding to Table 1.

Open with DEXTER
In the text

  \begin{figure} \par {\rotatebox{0}{\resizebox{9.2cm}{10.0cm} {\includegraphics{1... ....8cm}{8.5cm} {\includegraphics{12920fg3b.eps}}} }\vspace*{-2.5mm} \end{figure} Figure 3:

Plot of the morphology of the solution corresponding to a FR I-type spine jet. In a) the projection of the streamlines on the poloidal plane is shown. The solid lines in the center correspond to lines where the conditions xA2 G2<10-2 and $({2 + \delta \alpha })/{\left (1 + \delta \alpha \right )^2} - 2<10^{-2}$are satisfied. The dashed lines correspond to xA2 G2<10-1 and $({2 + \delta \alpha })/{\left (1 + \delta \alpha \right )^2} - 2<10^{-1}$. The dashed-dotted lines correspond to xA2 G2>10-1 and $({2 + \delta \alpha })/{\left (1 + \delta \alpha \right )^2} - 2>10^{-1}$ (see Meliani et al. 2006a, for details).

Open with DEXTER
In the text

  \begin{figure} \par {\rotatebox{0}{\resizebox{9cm}{4.5cm}{\includegraphics{12920... ...ebox{9cm}{4.5cm} {\includegraphics{12920fg4b.eps}}} \vspace*{2.5mm} \end{figure} Figure 4:

In a) we plot the energetic fluxes normalized to the mass energy of the first solution for a ``FR I-type''' spine jet. In b) we plot for the same solution, the Lorentz factor $\gamma $ along four different streamlines. The solid line corresponds to the polar axis and the dotted line to the last streamline connected to the central corona. Other lines are intermediate ones.

Open with DEXTER
In the text

  \begin{figure} \par {\rotatebox{0}{\resizebox{8.7cm}{4.5cm}{\includegraphics{129... ...tebox{0}{\resizebox{8.7cm}{4.5cm}{\includegraphics{12920fg5b.eps}}} \end{figure} Figure 5:

In a) we plot the temperature profile and in b) the density profile for the FR I-type jet solution. The density is normalized to n0 so that the mass-loss rate is $\dot{M} = n_{0} 10^{-6} ~\dot{M}_{\rm Edd}$.

Open with DEXTER
In the text

  \begin{figure} \par {\rotatebox{0}{\resizebox{9.5cm}{10.0cm} {\includegraphics{1... ...x{0}{\resizebox{9.0cm}{8.5cm} {\includegraphics{12920fg6b.eps}}} }\end{figure} Figure 6:

The same as in Fig. 3 for the second solution corresponding to a FR II-type spine jet.

Open with DEXTER
In the text

  \begin{figure} \par {\rotatebox{0}{\resizebox{8.8cm}{4.5cm}{\includegraphics{129... ...tebox{0}{\resizebox{8.8cm}{4.5cm}{\includegraphics{12920fg7b.eps}}} \end{figure} Figure 7:

In a) we plot the energetic fluxes normalized to the mass energy of the second solution for a ``FR II-type'' spine jet. In b) we plot for the same solution, the Lorentz factor $\gamma $ along four different streamlines. The solid line corresponds to the polar axis and the dotted line to the last streamline connected to the central corona. Other lines are intermediate ones.

Open with DEXTER
In the text

  \begin{figure} \par {\rotatebox{0}{\resizebox{8.7cm}{4.5cm} {\includegraphics{12... ...box{0}{\resizebox{8.7cm}{4.5cm} {\includegraphics{12920fg8b.eps}}} \end{figure} Figure 8:

In a) we plot the temperature profile and in b) the density profile for the FR II-type jet solution. On the left the vertical lines delimitate the various domains of the temperature profile. On the right the density is normalized to n0 such that the mass-loss rate is $\dot{M} = n_{0} 10^{-6} ~\dot{M}_{\rm Edd}$.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.