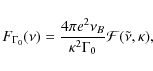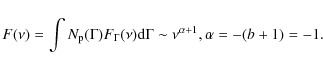| Issue |
A&A
Volume 520, September-October 2010
|
|
|---|---|---|
| Article Number | L1 | |
| Number of page(s) | 5 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201015212 | |
| Published online | 22 September 2010 | |
LETTER TO THE EDITOR
Gamma ray emission from magnetized relativistic GRB outflows
A. Neronov - V. Savchenko
ISDC Data Center for Astrophysics, Chemin d'Écogia 16, 1290 Versoix, Switzerland and Geneva Observatory, 51 Ch. des Maillettes, 1290 Sauverny, Switzerland
Received 15 June 2010 / Accepted 19 July 2010
Abstract
We argue that small pitch angle synchrotron emission provides an
important dissipation mechanism that has to be taken into account in
models of the formation of relativistic magnetized ![]() -ray
burst (GRB) outflows from newborn black holes and/or magnetars. We show
that if the GRB outflow is proton loaded, the spectral energy
distribution of this emission is expected to sharply peak in the
0.1-1 MeV energy band. If the small pitch-angle synchrotron
emission efficiently cools relativistic particles of the outflow,
the emission spectrum below the peak energy is a power law
with spectral index
-ray
burst (GRB) outflows from newborn black holes and/or magnetars. We show
that if the GRB outflow is proton loaded, the spectral energy
distribution of this emission is expected to sharply peak in the
0.1-1 MeV energy band. If the small pitch-angle synchrotron
emission efficiently cools relativistic particles of the outflow,
the emission spectrum below the peak energy is a power law
with spectral index
![]() ,
close to the typical spectral index of time-resolved GRB spectra.
Otherwise, the low energy spectral index can be as hard as
,
close to the typical spectral index of time-resolved GRB spectra.
Otherwise, the low energy spectral index can be as hard as
![]() ,
as observed at the beginning of the GRB pulses. We conjecture
that small pitch-angle synchrotron emission from proton-loaded
magnetized GRB outflow could significantly contribute to the Band
component of the prompt emission of GRBs, while electromagnetic cascade
initiated by the
protons may be responsible for the GeV component.
,
as observed at the beginning of the GRB pulses. We conjecture
that small pitch-angle synchrotron emission from proton-loaded
magnetized GRB outflow could significantly contribute to the Band
component of the prompt emission of GRBs, while electromagnetic cascade
initiated by the
protons may be responsible for the GeV component.
Key words: gamma-ray burst: general - radiation mechanisms: non-thermal
1 Introduction
A large amount of information about the time evolution of the spectral characteristics of prompt emission of ![]() -ray bursts (GRB) has been collected by CGRO/BATSE, Swift/BAT, INTEGRAL/ISGRI (see Mészáros 2006; and Piran 2004, for reviews) and, the Fermi/GBM (Band et al. 2009)
telescopes. It is firmly established that the majority of the
time-resolved GRB spectra could be well described by relatively
simple spectral models, such as
the Band model (Band et al. 1993),
or a cut-off or broken power-law model determined by three
main parameters: low and high energy photon indices
-ray bursts (GRB) has been collected by CGRO/BATSE, Swift/BAT, INTEGRAL/ISGRI (see Mészáros 2006; and Piran 2004, for reviews) and, the Fermi/GBM (Band et al. 2009)
telescopes. It is firmly established that the majority of the
time-resolved GRB spectra could be well described by relatively
simple spectral models, such as
the Band model (Band et al. 1993),
or a cut-off or broken power-law model determined by three
main parameters: low and high energy photon indices ![]() and
and ![]() ,
and peak (or break or cut-off) energy
,
and peak (or break or cut-off) energy ![]() (Piran 2004; Mészáros 2006).
(Piran 2004; Mészáros 2006).
The observed distribution of the low-energy power-law indices ![]() (of differential photon spectra given by
(of differential photon spectra given by
![]() )
of time-resolved GRB spectra is sharply peaked at the value
)
of time-resolved GRB spectra is sharply peaked at the value
![]() in the BATSE GRB (Band et al. 1993; Kaneko et al. 2006) and Swift/BAT (Savchenko & Neronov 2009) GRB samples. Deviations from this mean value toward
in the BATSE GRB (Band et al. 1993; Kaneko et al. 2006) and Swift/BAT (Savchenko & Neronov 2009) GRB samples. Deviations from this mean value toward ![]() (down to
(down to
![]() )
are preferentially observed at the initial moments of onset of GRB sub-pulses,
when the spectra could be as hard as
)
are preferentially observed at the initial moments of onset of GRB sub-pulses,
when the spectra could be as hard as
![]() (Preece et al. 2000; Savchenko & Neronov 2009; Kaneko et al. 2006). Evolution toward
(Preece et al. 2000; Savchenko & Neronov 2009; Kaneko et al. 2006). Evolution toward ![]() is commonly observed during the decay of individual sub-pulses and/or
at the end of the prompt GRB emission phase. The characteristic
value
is commonly observed during the decay of individual sub-pulses and/or
at the end of the prompt GRB emission phase. The characteristic
value
![]() is difficult to
reconcile with the conventionally assumed synchrotron and/or inverse
Compton mechanisms of prompt GRB emission. Alternative models,
which attempt to resolve this problem, include ``jitter'' radiation (Medvedev 2006; Medvedev & Loeb 1999) (see Kirk & Reville 2009, for a discussion of the potential problems of the jitter radiation model) and ``quasi thermal comptonization'' (Ghisellini & Celotti 1999) models.
is difficult to
reconcile with the conventionally assumed synchrotron and/or inverse
Compton mechanisms of prompt GRB emission. Alternative models,
which attempt to resolve this problem, include ``jitter'' radiation (Medvedev 2006; Medvedev & Loeb 1999) (see Kirk & Reville 2009, for a discussion of the potential problems of the jitter radiation model) and ``quasi thermal comptonization'' (Ghisellini & Celotti 1999) models.
Spectra of at least some GRBs contain a separate GeV-band component (e.g., Abdo et al. 2009a,b). The GeV emission has a different (relative to the Band component) temporal evolution (Ghisellini et al. 2010).
The absence of the high-energy cutoff in the spectrum of this
GeV component due to the pair-production imposes a lower bound on
the bulk Lorentz factors of the GRB outflows (about
![]() ,
e.g. Baring & Harding 1997; Abdo et al. 2009a).
Different models of the origin of the GeV emission have been
proposed, such as high-energy extention of the conventional afterglow (Kumar & Duran 2009; Ghirlanda et al. 2009), afterglow emission from a fireball in the
radiative regime (Ghisellini et al. 2010), and synchrotron (Razzaque et al. 2009) or cascade (Dermer & Atoyan 2006; Asano et al. 2009) emission from ultra high-energy (
,
e.g. Baring & Harding 1997; Abdo et al. 2009a).
Different models of the origin of the GeV emission have been
proposed, such as high-energy extention of the conventional afterglow (Kumar & Duran 2009; Ghirlanda et al. 2009), afterglow emission from a fireball in the
radiative regime (Ghisellini et al. 2010), and synchrotron (Razzaque et al. 2009) or cascade (Dermer & Atoyan 2006; Asano et al. 2009) emission from ultra high-energy (
![]() eV) protons.
eV) protons.
Several models of the formation of relativistic GRB outflows from
black holes or neutron stars, formed in result of core collapse of
massive stars, assume that the outflow is highly magnetized
(Komissarov & Barkov 2007; Bucciantini et al. 2009,2007; Komissarov et al 2007; Komissarov et al. 2009).
In these models,
the energy of the outflow is initially carried by the Poynting flux of
electromagnetic energy, so that the ratio of electromagnetic to
kinetic energy of the outflow, ![]() ,
is comparable to or much higher than unity. Numerical
MHD calculations show that the electromagnetic energy could be
converted in a dissipationless way to the kinetic energy of
relativistic particle outflow. Dissipation is absent because the
electromagnetic field forms a force-free configuration of
electromagnetic field,
,
is comparable to or much higher than unity. Numerical
MHD calculations show that the electromagnetic energy could be
converted in a dissipationless way to the kinetic energy of
relativistic particle outflow. Dissipation is absent because the
electromagnetic field forms a force-free configuration of
electromagnetic field,
![]() ,
where
,
where
![]() are the electric and magnetic fields and
are the electric and magnetic fields and ![]() is the flow velocity.
is the flow velocity.
In what follows we show that even if electromagnetic field is
force-free, the energy loss of relativistic particles in the
outflow is non-zero, because the directions of the velocities of
individual particles are scattered around the average direction of the
flow within a certain angle
![]() ,
where
,
where ![]() is the Lorentz factor of the outflow. This scatter in particle
velocities leads to radiative dissipation of the outflow energy,
the main dissipation mechanism being small pitch-angle synchrotron
emission. We demonstrate that a significant fraction of the power of
magnetized outflow could be dissipated by this mechanism even in the
outflow acceleration region.
is the Lorentz factor of the outflow. This scatter in particle
velocities leads to radiative dissipation of the outflow energy,
the main dissipation mechanism being small pitch-angle synchrotron
emission. We demonstrate that a significant fraction of the power of
magnetized outflow could be dissipated by this mechanism even in the
outflow acceleration region.
We derive the spectral characteristics of this emission and
show that they are consistent with those of the observed
GRB prompt emission spectra. The peak energy of the spectrum is
expected to be in the 0.1-1 MeV range for the outflows with
typical GRB parameters (bulk Lorentz factors, isotropic
luminosities). The low-energy spectral index is expected to evolve from
a very hard value
![]() toward a ``steady state'' value
toward a ``steady state'' value ![]() ,
which is expected to persist over the period of stable activity of
GRB central engine and/or up to the moment when interactions of
the high-energy protons with the synchrotron-cooled lower energy
protons begin to contribute significantly to the energy loss.
By comparing the spectral characteristics of proton synchrotron
emission with those observed in the prompt emission
,
which is expected to persist over the period of stable activity of
GRB central engine and/or up to the moment when interactions of
the high-energy protons with the synchrotron-cooled lower energy
protons begin to contribute significantly to the energy loss.
By comparing the spectral characteristics of proton synchrotron
emission with those observed in the prompt emission ![]() -ray spectra
of GRBs, we conjecture that emission from the pre-shock outflow
dominates during the prompt emission phase. We discuss possible
observational tests that would allow to test this conjecture.
-ray spectra
of GRBs, we conjecture that emission from the pre-shock outflow
dominates during the prompt emission phase. We discuss possible
observational tests that would allow to test this conjecture.
2 Generic properties of pre-shock relativistic GRB outflow
If the observed isotropic luminosity of GRB is
![]() ,
the energy flux carried by the GRB outflow ejected into a solid angle
,
the energy flux carried by the GRB outflow ejected into a solid angle ![]() is
is
![]()
![]()
![]() ,
where
,
where ![]() is the opening angle of the outflow. The energy density of the outflow at a distance D is
is the opening angle of the outflow. The energy density of the outflow at a distance D is
![]()
![]() .
It is convenient to parametrize the strength of the
electromagnetic field in the outflow in terms of magnetization
parameter
.
It is convenient to parametrize the strength of the
electromagnetic field in the outflow in terms of magnetization
parameter ![]() ,
,
![]() .
Using this a parametrization, the (electro)magnetic field strength at the distance D can be expressed as
.
Using this a parametrization, the (electro)magnetic field strength at the distance D can be expressed as
![]() G.
G.
The minimal possible angular scatter in the velocities of the particles is within a cone of opening angle
![]() (
(![]() is
a numerical factor of the order of 1). The non-zero angular
scatter in the particle velocities around the bulk velocity
is
a numerical factor of the order of 1). The non-zero angular
scatter in the particle velocities around the bulk velocity ![]() leads to the appearance of non-zero Lorentz force of the order of
leads to the appearance of non-zero Lorentz force of the order of
![]() ,
where e is particle charge and
,
where e is particle charge and
![]() G.
G.
Particle motions due to this uncompensated Lorentz force lead to
radiation. To calculate the properties of this radiation,
it is convenient to go into the reference frame moving with
velocity
![]() .
In this reference frame, the electric component of electromagnetic field is zero, the mean outflow velocity
.
In this reference frame, the electric component of electromagnetic field is zero, the mean outflow velocity ![]() is aligned with the magnetic field
is aligned with the magnetic field ![]() ,
and the radiation is synchrotron radiation of particles moving at small pitch angles in the magnetic field
,
and the radiation is synchrotron radiation of particles moving at small pitch angles in the magnetic field![]() . Unless
. Unless ![]() is orthogonal to
is orthogonal to ![]() ,
the velocity of the new frame
,
the velocity of the new frame
![]() .
Taking this into account, we do not distinguish the quantities
(such as photon energies) in different reference frames in the
order-of-magnitude estimates presented below.
.
Taking this into account, we do not distinguish the quantities
(such as photon energies) in different reference frames in the
order-of-magnitude estimates presented below.
Properties of synchrotron emission from particles moving at
small pitch angles with respect to the magnetic field significantly
differ from those of synchrotron emission from an isotropic particle
distribution (Epstein 1973; Lloyd & Petrosian 2000). The typical energy of the radiated photons,
![]()
where
To estimate the importance of small pitch angle synchrotron cooling as
a dissipation mechanism, one has to compare the synchrotron cooling
distance
![]() +
+
![]() with the typical distance scales of formation and propagation of the GRB outflow. Equating
with the typical distance scales of formation and propagation of the GRB outflow. Equating ![]() to D one can find that synchrotron emission can efficiently remove energy from relativistic protons out to the distance
to D one can find that synchrotron emission can efficiently remove energy from relativistic protons out to the distance
The typical distance scale of the GRB central engine
In the fireball model, it is commonly assumed that the bulk of the
power of the GRB outflow is transferred from the region of the
outflow formation to the internal shock region by relativistic protons,
while the fraction of the power carried by electrons is smaller by a
factor
![]() (Mészáros 2006).
The power of the proton-loaded outflow is transferred efficiently to
electrons only in the internal shock region, which is normally at large
distances
(Mészáros 2006).
The power of the proton-loaded outflow is transferred efficiently to
electrons only in the internal shock region, which is normally at large
distances
![]() .
In the unshocked outflow, electrons are affected,
in a similar way to protons, by the energy loss related to
the small pitch angle synchrotron emission. However, the energy losses
of electrons do not contribute significantly to the energy dissipation
in the distance range
.
In the unshocked outflow, electrons are affected,
in a similar way to protons, by the energy loss related to
the small pitch angle synchrotron emission. However, the energy losses
of electrons do not contribute significantly to the energy dissipation
in the distance range
![]() .
.
Synchrotron photons may freely escape from the GRB outflow if they are
produced at sufficiently large distances, where the GRB outflow is
optically thin with respect to Compton scattering. The mean free path
of photons with respect to the Compton scattering is
![]() ,
where
,
where
![]() is Thomson cross-section and
is Thomson cross-section and
![]() is the electron density of the outflow (we assume that the number
density of electrons is equal to the number density of protons). The
outflow becomes optically thin at the distance at which
is the electron density of the outflow (we assume that the number
density of electrons is equal to the number density of protons). The
outflow becomes optically thin at the distance at which
![]() given by
given by
![\begin{displaymath}%
{\cal D}_{\rm C}\simeq 5\times 10^{6}\left[\frac{L_{\rm iso...
...{-1}}}\right]\left[\frac{\Gamma_0}{10^4}\right]^{-3}~{\rm cm}.
\end{displaymath}](/articles/aa/full_html/2010/12/aa15212-10/img62.png)
|
(3) |
In GRBs with bulk Lorentz factors
3 Spectrum of emission from pre-shock proton loaded GRB outflow
This type of spectrum could be calculated by summing the spectra emitted from the outflow components moving at different angles ![]() with respect to the line of sight
with respect to the line of sight
where
The parameter
![]() in Eq. (4) could be expressed as (Epstein 1973; Ginzburg & Syrovatskii 1969)
in Eq. (4) could be expressed as (Epstein 1973; Ginzburg & Syrovatskii 1969)
| |
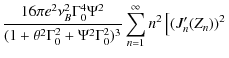
|
||
![$\displaystyle \left.+~\left\{\frac{1-\theta^2\Gamma_0^2+\Psi^2\Gamma_0^2}{2\theta\Psi\Gamma_0^2}J_n(Z_n)\right\}^2\right] \delta(\nu-\nu_n),$](/articles/aa/full_html/2010/12/aa15212-10/img77.png)
|
where
where
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{15212fg1}
\end{figure}](/articles/aa/full_html/2010/12/aa15212-10/Timg91.png)
|
Figure 1:
Spectra of small pitch-angle proton synchrotron emission from pre-shock GRB outflow for several values of |
| Open with DEXTER | |
4 High-energy emission from the ``tail'' of angular distribution
The spectrum marked ![]() in Fig. 1 is calculated based on the assumption that the angular distribution of particle velocities,
in Fig. 1 is calculated based on the assumption that the angular distribution of particle velocities,
![]() ,
is cut-off at the angle
,
is cut-off at the angle
![]() .
In general,
.
In general,
![]() may exhibit large angle ``tail'' extending beyond
may exhibit large angle ``tail'' extending beyond
![]() .
The spectrum of emission from protons moving at large pitch angles
.
The spectrum of emission from protons moving at large pitch angles
![]() extends up to the frequency
extends up to the frequency
![]() ,
while the frequency below which the spectrum is characterized by
,
while the frequency below which the spectrum is characterized by ![]() moves down to
moves down to
![]() (see Fig. 1). In the range
(see Fig. 1). In the range
![]() ,
the spectrum is characterized by a photon index
,
the spectrum is characterized by a photon index
![]() typical of synchrotron radiation from an isotropic particle distribution (Fig. 1). If the large pitch angle tail of
typical of synchrotron radiation from an isotropic particle distribution (Fig. 1). If the large pitch angle tail of
![]() has the form of a power-law,
has the form of a power-law,
![]() ,
the spectrum of emission above the characteristic (peak) frequency
,
the spectrum of emission above the characteristic (peak) frequency
![]() has the form of a power-law with photon index
has the form of a power-law with photon index ![]() .
In principle, the tail of the angular distribution could extend up
to
.
In principle, the tail of the angular distribution could extend up
to
![]() ,
such that the energy of synchrotron photons emitted by the large angle tail extends up to
,
such that the energy of synchrotron photons emitted by the large angle tail extends up to
![]() .
If the spectrum of proton synchrotron emission from particles moving at the angle
.
If the spectrum of proton synchrotron emission from particles moving at the angle
![]() peaks in the 100 keV-1 MeV energy band, the high-energy
(large pitch angle) tail of the synchrotron spectrum could extend up to
the 1-10 GeV band if
peaks in the 100 keV-1 MeV energy band, the high-energy
(large pitch angle) tail of the synchrotron spectrum could extend up to
the 1-10 GeV band if
![]() .
The presence of the large angle tails of proton angular distribution
could, therefore, be responsible for the appearance of high-energy
extensions of the prompt GRB spectra similar to that observed in
GRB 080916C (Abdo et al. 2009a).
Additional obvious possible sources of the GRB 080916C-like
high-energy tails in the GRB spectra are protons with energies
higher
than
.
The presence of the large angle tails of proton angular distribution
could, therefore, be responsible for the appearance of high-energy
extensions of the prompt GRB spectra similar to that observed in
GRB 080916C (Abdo et al. 2009a).
Additional obvious possible sources of the GRB 080916C-like
high-energy tails in the GRB spectra are protons with energies
higher
than
![]() in the outflow.
in the outflow.
5 Emission from a distribution of protons formed by the small pitch angle synchrotron cooling
The total proton energy-loss rate could be found by evaluating the integral of
![]() :
:
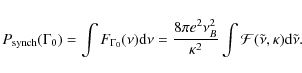
|
(6) |
As expected,
in the range of Lorentz factors
The overall spectral evolution of the pre-shock outflow emission is expected to be as follows. As soon as synchrotron cooling of the outflow particles becomes efficient, the spectrum of emission from the pre-shock outflow softens from
Small pitch-angle synchrotron emission leads not only to cooling but also to scattering in the proton beam across a wider angle ![]()
![]()
![]()
![]()
![]() .
The widening of the opening angle of particle distribution could lead
to the ``switching on'' of interactions between the particles of
the outflow. The mean free path of the highest energy protons with
respect to the pp interactions with low energy protons is given by
.
The widening of the opening angle of particle distribution could lead
to the ``switching on'' of interactions between the particles of
the outflow. The mean free path of the highest energy protons with
respect to the pp interactions with low energy protons is given by
![]()
![]()
![]() cm, where
cm, where
![]() cm2 is the cross-section of pp interactions and
cm2 is the cross-section of pp interactions and
![]() is the density of particles with gamma factor
is the density of particles with gamma factor ![]() .
The parameter
.
The parameter
![]() becomes comparable or shorter than
becomes comparable or shorter than
![]() as soon as synchrotron cooling leads to the appearance of protons with energies
as soon as synchrotron cooling leads to the appearance of protons with energies
![]() if
if
![]() .
.
Development of proton initiated cascade leads to injection of secondary electrons/positrons (as ![]() -rays
and well as neutrinos) which can largely outnumber the primary
electrons present in the unshocked GRB outflow. In constrast
to the primary electrons, synchrotron emission from these cascade
electrons could provide a significant energy dissipation mechanism of
the outflow. Although typical initial Lorentz factors of the secondary
electrons are
-rays
and well as neutrinos) which can largely outnumber the primary
electrons present in the unshocked GRB outflow. In constrast
to the primary electrons, synchrotron emission from these cascade
electrons could provide a significant energy dissipation mechanism of
the outflow. Although typical initial Lorentz factors of the secondary
electrons are
![]() ,
electrons are injected at the typical pitch angles
,
electrons are injected at the typical pitch angles
![]() ,
so that the synchrotron emission from the cascade electrons is not emitted in the small pitch angle regime.
,
so that the synchrotron emission from the cascade electrons is not emitted in the small pitch angle regime.
The ![]() -rays with energies above the pair production threshold
-rays with energies above the pair production threshold
![]() produce pairs in interactions among themselves and initiate the electromagnetic cascade. The highest energy
produce pairs in interactions among themselves and initiate the electromagnetic cascade. The highest energy ![]() -rays may also interact with protons via pion and pair production channels. The energy loss of protons due to the pp (and/or
-rays may also interact with protons via pion and pair production channels. The energy loss of protons due to the pp (and/or ![]() )
interactions is given by
)
interactions is given by
![]() ,
where
,
where
![]() is the typical inelasticity of pp collisions. As soon as the cooling of
the highest energy protons by means of pp and
is the typical inelasticity of pp collisions. As soon as the cooling of
the highest energy protons by means of pp and ![]() interactions becomes more efficient than the synchrotron cooling, the spectrum of protons is expected to soften to b>0 (see Eq. (7)). This should lead to the softening of the small pitch angle synchrotron emission spectrum to
interactions becomes more efficient than the synchrotron cooling, the spectrum of protons is expected to soften to b>0 (see Eq. (7)). This should lead to the softening of the small pitch angle synchrotron emission spectrum to ![]() and a decrease in its contribution to the overall GRB spectrum,
compared to the contribution from the cascade emission component. The
spectrum of emission from the proton-initiated cascade extends up to
the energy of the threshold of the pair production,
and a decrease in its contribution to the overall GRB spectrum,
compared to the contribution from the cascade emission component. The
spectrum of emission from the proton-initiated cascade extends up to
the energy of the threshold of the pair production,
![]() .
For the particular example of GRB 090902B,
the electromagnetic cascade component is then clearly identified
as the soft emission component extending up to the multi-GeV energies,
which becomes
dominant at the end of the prompt emission phase and persists for
.
For the particular example of GRB 090902B,
the electromagnetic cascade component is then clearly identified
as the soft emission component extending up to the multi-GeV energies,
which becomes
dominant at the end of the prompt emission phase and persists for
![]() s after the end of the prompt emission (Abdo et al. 2009b).
s after the end of the prompt emission (Abdo et al. 2009b).
Bursts that initiate with very hard spectra would be the most
interesting candidates for testing the hypothesis of small pitch-angle
proton synchrotron emission because they might possess the cyclotron
line at the frequency
![]() .
We search for this line at the energy close to the peak energy of very
hard GRB spectra to test the proposed model. The cyclotron line
feature may, however, have been ``washed out'' of the spectrum by a
non-negligible spread in the particle energies in the outflow and by
small angle Compton scattering if most of the small pitch-angle
synchrotron emission is generated at the distances
.
We search for this line at the energy close to the peak energy of very
hard GRB spectra to test the proposed model. The cyclotron line
feature may, however, have been ``washed out'' of the spectrum by a
non-negligible spread in the particle energies in the outflow and by
small angle Compton scattering if most of the small pitch-angle
synchrotron emission is generated at the distances
![]() .
In this case, the spectrum of emission from the pre-shock
outflow would be indistinguishable from the generic Band model spectra.
A complementary way of testing the small pitch angle proton
synchrotron model is to search for the appearance of neutrino signal
from pp interactions (Paczynski & Xu 1994) at the moment of softening of the spectrum of prompt emission to
.
In this case, the spectrum of emission from the pre-shock
outflow would be indistinguishable from the generic Band model spectra.
A complementary way of testing the small pitch angle proton
synchrotron model is to search for the appearance of neutrino signal
from pp interactions (Paczynski & Xu 1994) at the moment of softening of the spectrum of prompt emission to
![]() in GeV
in GeV ![]() -ray-loud GRBs. The neutrino signal is expected to be sharply peaked at energies
-ray-loud GRBs. The neutrino signal is expected to be sharply peaked at energies
![]() TeV
and its flux is expected to be comparable to the luminosity of the
cascade (GeV) component of the GRB spectrum. The peak energy
of neutrino signal can be predicted if the bulk Lorentz factor
TeV
and its flux is expected to be comparable to the luminosity of the
cascade (GeV) component of the GRB spectrum. The peak energy
of neutrino signal can be predicted if the bulk Lorentz factor ![]() is estimated from the measurement of the peak energy of the proton synchrotron component using Eq. (1). A search for the neutrino counterparts of the
GeV
is estimated from the measurement of the peak energy of the proton synchrotron component using Eq. (1). A search for the neutrino counterparts of the
GeV ![]() -ray loud GRBs becomes possible after a cross-correlation of the signal of Fermi/LAT-detected GRBs with the TeV neutrino signal detected bu the km3 scale neutrino telescope IceCube, which will become possible in the nearest future (Abbasi et al. 2009).
-ray loud GRBs becomes possible after a cross-correlation of the signal of Fermi/LAT-detected GRBs with the TeV neutrino signal detected bu the km3 scale neutrino telescope IceCube, which will become possible in the nearest future (Abbasi et al. 2009).
6 Summary
We have explored the possibility that small pitch-angle proton
synchrotron emission from the magnetized GRB outflow gives
significant contribution to the GRB spectrum. This emission
provides an important dissipation mechanism in the region of
acceleration of GRB outflows with high magnetization
parameter ![]() .
We have shown that the steady-state spectrum of this emission is expected to have photon index
.
We have shown that the steady-state spectrum of this emission is expected to have photon index ![]() ,
close to the characteristic photon index of the time-resolved
GRB spectra. A small pitch-angle proton synchrotron emission
component could also explain the extremely hard spectra
,
close to the characteristic photon index of the time-resolved
GRB spectra. A small pitch-angle proton synchrotron emission
component could also explain the extremely hard spectra
![]() observed at the beginning of some GRBs. The possibility that small
pitch angle proton synchrotron emission from the region of acceleration
of GRB outflow could be identified in the observed
GRB spectra implies that the models of formation of magnetized
relativistic outflow by newly born stellar mass black holes or
magnetars could be observationally tested. Whether a small pitch angle
synchrotron emission component exists in the GRB spectra could be
verified by searching for the cyclotron line features in spectra of
(some of the) hardest GRBs and/or searching for prompt
TeV neutrino emission from GeV
observed at the beginning of some GRBs. The possibility that small
pitch angle proton synchrotron emission from the region of acceleration
of GRB outflow could be identified in the observed
GRB spectra implies that the models of formation of magnetized
relativistic outflow by newly born stellar mass black holes or
magnetars could be observationally tested. Whether a small pitch angle
synchrotron emission component exists in the GRB spectra could be
verified by searching for the cyclotron line features in spectra of
(some of the) hardest GRBs and/or searching for prompt
TeV neutrino emission from GeV ![]() -ray-loud GRBs.
-ray-loud GRBs.
We would like to thank A.Taylor for discussions of the subject. The work of AN is supported by the Swiss National Science Foundation grant PP00P2_123426.
References
- Abdo, A. A., Ackermann, M., Arimoto, M., et al. (Fermi collaboration) 2009a, Science, 323, 1688 [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009b, ApJ, 706, L138 [NASA ADS] [CrossRef] [Google Scholar]
- Abbasi, R., Abdou, Y., Ackermann, M., et al. (IceCube collaboration) 2009, ApJ, 701, L47 [Google Scholar]
- Asano, K., Guiriec, S., & Meszaros, P. 2009, ApJ, 705, L191 [NASA ADS] [CrossRef] [Google Scholar]
- Baring, M. G., & Harding, A. K. 1997, ApJ, 491, L663 [NASA ADS] [CrossRef] [Google Scholar]
- Band, D., Matteson, J., Ford, L., et al. 1993, ApJ, 413, 281 [NASA ADS] [CrossRef] [Google Scholar]
- Band, D. L., Axelsson, M., Baldini, L., et al. 2009, ApJ, 701, 1673 [NASA ADS] [CrossRef] [Google Scholar]
- Bucciantini, N., Quataert, E., Arons, J., Metzger, B. D., & Thompson, T. A. 2007, MNRAS, 380, 1541 [NASA ADS] [CrossRef] [Google Scholar]
- Bucciantini, N., Quataert, E., Metzger, B. D., et al. 2009, MNRAS, 396, 2038 [NASA ADS] [CrossRef] [Google Scholar]
- Dermer, C. D., & Atoyan, A. 2006, N. J. Ph., 8, 122D [Google Scholar]
- Epstein, R. J. 1973, ApJ, 183, 593 [NASA ADS] [CrossRef] [Google Scholar]
- Ghisellini, G., & Celotti, A. 1999, ApJ, 511, L93 [NASA ADS] [CrossRef] [Google Scholar]
- Ghisellini, G., Ghirlanda, G., Nava, L., & Celotti., A. 2010, MNRAS, 403, 926 [NASA ADS] [CrossRef] [Google Scholar]
- Ghirlanda, G., Ghisellini, G., & Nava, L. 2010, A&A, 510, 7 [Google Scholar]
- Ginzburg, V. L., & Syrovatskii, S. I. 1969, ARA&A, 7, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Kaneko, Y., Preece, R. D., Briggs, M. S., et al. 2006, ApJS, 166, 298 [NASA ADS] [CrossRef] [Google Scholar]
- Komissarov, S. S., & Barkov, M. V. 2007, MNRAS, 320, 1029 [NASA ADS] [CrossRef] [Google Scholar]
- Komissarov, S. S., Barkov, M. V., Vlahakis, N., & Königl, A. 2007, MNRAS, 380, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Komissarov, S. S., Vlahakis, N., Königl, A., & Barkov, M. V. 2010, MNRAS, 394, 1182 [Google Scholar]
- Kumar, P., & Duran, R. B. 2009, MNRAS, 400, 75 [Google Scholar]
- Kirk, J. G., & Reville, B. 2010, ApJ, 710, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Lloyd, N. M., & Petrosian, V. 2000, ApJ, 543, 722 [NASA ADS] [CrossRef] [Google Scholar]
- Medvedev, M. 2006, ApJ, 637, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Medvedev, M., & Loeb, S. 1999, ApJ, 526, 697 [NASA ADS] [CrossRef] [Google Scholar]
- Mészáros, P. 2006, Rep. Prog. Phys., 69, 2259 [NASA ADS] [CrossRef] [Google Scholar]
- Paczynski, B., & Xu, G. 1994, ApJ, 427, 708 [NASA ADS] [CrossRef] [Google Scholar]
- Piran, T. 2004, Rev. Mod. Phys., 76, 1143 [Google Scholar]
- Preece, R. D., et al. 2000, ApJ, 506, L23 [Google Scholar]
- Razzaque, S., Dermer, C. D., & Finke, J. D. 2009 [arXiv:0908.0513] [Google Scholar]
- Savchenko, V., & Neronov, A. 2009, MNRAS, 396, 935 [NASA ADS] [CrossRef] [Google Scholar]
Footnotes
- ...
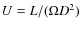
![[*]](/icons/foot_motif.png)
- We use natural system of units c=1.
- ... field
![[*]](/icons/foot_motif.png)
- In a special case
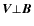 the reference frame moving with velocity
the reference frame moving with velocity 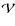 is comoving with the outflow and the radiation is cyclotron radiation.
is comoving with the outflow and the radiation is cyclotron radiation.
All Figures
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{15212fg1}
\end{figure}](/articles/aa/full_html/2010/12/aa15212-10/Timg91.png)
|
Figure 1:
Spectra of small pitch-angle proton synchrotron emission from pre-shock GRB outflow for several values of |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![\begin{displaymath}%
\epsilon_{\rm s} \!\simeq\! 6\times 10^{5}\kappa\left[\frac...
...}}\right]^{-1}\! \left[\frac{\Gamma_0}{10^4}\right]~\mbox{eV},
\end{displaymath}](/articles/aa/full_html/2010/12/aa15212-10/img42.png)
![\begin{displaymath}%
{\cal D}_{\rm s}\simeq 1.3\times 10^{9}\kappa^2\left[\frac{...
...1}}}\right]\left[\frac{\Gamma_0}{10^{4}}\right]^{-1}~{\rm cm}.
\end{displaymath}](/articles/aa/full_html/2010/12/aa15212-10/img49.png)