| Issue |
A&A
Volume 520, September-October 2010
Pre-launch status of the Planck mission
|
|
|---|---|---|
| Article Number | A2 | |
| Number of page(s) | 22 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/200912911 | |
| Published online | 15 September 2010 | |
Pre-launch status of the Planck mission
Planck pre-launch status: The optical system
J. A. Tauber1 - H. U. Norgaard-Nielsen2 - P. A. R. Ade22 - J. Amiri Parian3 - T. Banos4 - M. Bersanelli5 - C. Burigana6 - A. Chamballu7 - D. de Chambure24 - P. R. Christensen8 - O. Corre4 - A. Cozzani9 - B. Crill10 - G. Crone9 - O. D'Arcangelo11 - R. Daddato9 - D. Doyle9 - D. Dubruel4 - G. Forma4 - R. Hills12 - K. Huffenberger10 - A. H. Jaffe7 - N. Jessen2 - P. Kletzkine9 - J. M. Lamarre13 - J. P. Leahy14 - Y. Longval18 - P. de Maagt9 - B. Maffei14 - N. Mandolesi6 - J. Martí-Canales9 - A. Martín-Polegre9 - P. Martin4 - L. Mendes15 - J. A. Murphy16 - P. Nielsen17 - F. Noviello18 - M. Paquay9 - T. Peacocke16 - N. Ponthieu18 - K. Pontoppidan17 - I. Ristorcelli19 - J.-B. Riti4 - L. Rolo9 - C. Rosset20 - M. Sandri6 - G. Savini21 - R. Sudiwala22 - M. Tristram23 - L. Valenziano6 - M. van der Vorst9 - K. van 't Klooster9 - F. Villa6 - V. Yurchenko16
1 - European Space Agency (ESA), Research and
Scientific Support Dpt., Astrophysics Division, Keplerlaan 1, 2201AZ
Noordwijk, The Netherlands
2 -
Danish National Space Center, Juliane Mariesvej 28, 2100, Copenhagen, Denmark
3 -
PhotoCore GmbH, Affolternstrasse 115, 8050 Zürich, Switzerland
4 -
Thales Alenia Space, 100 Boulevard du Midi, BP 99, 06156 Cannes la Bocca, France
5 -
Università degli Studi di Milano, via Celoria 16, 20133 Milano, Italy
6 -
INAF-Istituto di Astrofisica Spaziale e Fisica Cosmica, Bologna, via Gobetti 101, 40129 Bologna, Italy
7 -
Blackett Laboratory, Imperial College, London SW7 2AZ, UK
8 -
Niels Bohr Institute, Blegdamsvej 17, 2100 Copenhagen, Denmark
9 -
European Space Agency, ESTEC, Keplerlaan 1, 2201 AZ Noordwijk, The Netherlands
10 -
Jet Propulsion Laboratory, California Institute of Technology, 4800 Oak Grove Drive, Pasadena, CA 91109, USA
11 -
IFP-CNR, Via Cozzi 53, Milano, Italy
12 -
Cavendish Laboratory, Dpt. of Physics, University of Cambridge, J. J. Thomson Avenue, Cambridge CB3 0HE, UK
13 -
LERMA, Observatoire de Paris, 61 Av. de l'Observatoire, 75014 Paris, France
14 -
Jodrell Bank Centre for Astrophysics, The University of Manchester, M13 9PL, UK
15 -
Planck
Science Office, European Space Agency, European Space Astronomy Centre,
PO Box - Apdo. de correos 78, 28691 Villanueva de la Cañada, Madrid,
Spain
16 -
NUI Maynooth, Dpt of Experimental Physics, Maynooth, Co. Kildare, Ireland
17 -
Ticra, Laederstraede 34, 21201 Copenhagen, Denmark
18 -
Institut d'Astrophysique Spatiale, CNRS (UMR8617), Université Paris-Sud 11, Batiment 121, 91405 Orsay, France
19
- CESR, Centre d'Étude Spatiale des Rayonnements, Université Paul
Sabatier and CNRS, 9 Av. du colonel Roche, BP44346, 31038 Toulouse
Cedex 4, France
20 - Laboratoire Astroparticule et Cosmologie (APC),
Université Paris Diderot - Paris 7 and CNRS, 10 rue A. Domon et L.
Duquet, 75205 Paris Cedex 13, France
21 -
Optical Science Laboratory, Dpt of Physics and Astronomy, UCL, London, WC1E 6BT, UK
22 -
Cardiff University, School of Physics and Astronomy, The Parade, Cardiff CF24 3AA, UK
23 -
Laboratoire de l'Accélerateur Linéaire, Université Paris 11, Bâtiment 200, 91898 Orsay, France
24 -
European Space Agency, Headquarters, 8-10 rue Mario Nikis, 75015 Paris, France
Received 17 July 2009 / Accepted 2 March 2010
Abstract
Planck is a scientific satellite that represents the next
milestone in space-based research related to the cosmic microwave
background, and in many other astrophysical fields. Planck was
launched on 14 May of 2009 and is now operational. The uncertainty
in the optical response of its detectors is a key factor allowing Planck
to achieve its scientific objectives. More than a decade of analysis
and measurements have gone into achieving the required performances. In
this paper, we describe the main aspects of the Planck optics
that are relevant to science, and the estimated in-flight performance,
based on the knowledge available at the time of launch. We also briefly
describe the impact of the major systematic effects of optical origin,
and the concept of in-flight optical calibration. Detailed discussions
of related areas are provided in accompanying papers.
Key words: cosmic microwave background - space vehicles: instruments - instrumentation: detectors - instrumentation: polarimeters - submillimeter: general - telescopes
1 Introduction
The ambitious goals of the Planck mission![]() (Tauber et al. 2010)
can only be met if its measurements can be calibrated to very high
accuracy. The accuracy of calibration on small angular scales depends
directly on the uncertainties in the angular radiation patterns of each
detector, to a level unprecedented in mm-wave astronomy. The Planck
goal to achieve photometric calibration of 1% in the key
CMB bands (70-217 GHz) implies that the beam characteristics
(solid angle, shape) must be known to sub-% levels. The impact of
beam uncertainties has been extensively analysed for WMAP (e.g., Hill
et al. 2009; Nolta et al. 2009) and analyses of the effect on the recovery by Planck of some cosmological parameters have also been performed (Huffenberger et al. 2010; Rocha et al. 2010), in both cases confirming the importance of optical uncertainties.
(Tauber et al. 2010)
can only be met if its measurements can be calibrated to very high
accuracy. The accuracy of calibration on small angular scales depends
directly on the uncertainties in the angular radiation patterns of each
detector, to a level unprecedented in mm-wave astronomy. The Planck
goal to achieve photometric calibration of 1% in the key
CMB bands (70-217 GHz) implies that the beam characteristics
(solid angle, shape) must be known to sub-% levels. The impact of
beam uncertainties has been extensively analysed for WMAP (e.g., Hill
et al. 2009; Nolta et al. 2009) and analyses of the effect on the recovery by Planck of some cosmological parameters have also been performed (Huffenberger et al. 2010; Rocha et al. 2010), in both cases confirming the importance of optical uncertainties.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{12911f1a.eps}\hspace*{1cm}
\includegraphics[width=7cm,clip]{12911f1b.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa12911-09/Timg26.png)
|
Figure 1:
(Left) The fully assembled Planck satellite and (right)
its telescope prior to integration. Three conical ``V-grooves''
(visible on the left as three horizontal lines) isolate thermally and
radiatively the warm Service Module (lower octagonal black box) from
the cold payload module. The topmost (or 3 |
| Open with DEXTER | |
For this reason, the optical system of Planck is a key element for the mission, and its design, manufacture, and verification programmes have been mission drivers in terms of cost and complexity. The success of the mission does not however depend entirely on the optical knowledge gathered on the ground. In-flight measurements of celestial sources are the principal source of information about the shapes of the main beams, and the ground knowledge allows us to tie the in-flight measurements to the beam shapes below the level at which they can be measured in flight. Confronting the ground predictions with the in-flight measurements allows us to build a reliable estimate of the optical response to very low amplitude levels, and therefore to predict or constrain the level of unwanted optical systematics such as straylight signals.
The objectives of the ground activities related to optics were to:
- build a mathematical model that allows us to predict and verify the in-flight performance with a combination of test and analysis;
- verify that the as-built optical system meets its major performance requirements, and evaluate the uncertainties in the performance predictions;
- verify that a number of systematic effects caused by the optics are either below a significant level, or can be dealt with in-flight.
- Section 5 describes the measurements of the geometry of the reflectors and telescope, and how they were combined with analysis to predict their geometry and alignment in-flight.
- Section 6 discusses the radio frequency (RF) measurements performed to verify the accuracy of the mathematical model (based on the GRASP software, GRASP Manual 2008) that converted the geometrical information into a prediction of the optical response in-flight.
- Section 7 describes how the GRASP model was used to determine uncertainties on the predicted optical response.
2 Background
The development of the Planck mission began with two proposals presented to ESA in May of 1993: COBRAS (Mandolesi et al. 1993) and SAMBA (Puget et al. 1993). Each of these proposed a payload formed by an offset Gregorian telescope focusing light onto an array of detectors (based on HEMT Low Noise Amplifiers for COBRAS and very low temperature bolometers for SAMBA) fed by corrugated horns. The two proposals were used to design a payload where a single COBRAS-like telescope fed two instruments (a COBRAS-like Low Frequency Instrument - LFI; and a SAMBA-like High Frequency Instrument - HFI) sharing a common focal plane. The telescope for this (COBRAS/SAMBA) satellite was essentially identical to the COBRAS design by Pagana (1993), namely a classical Gregorian paraboloid-ellipsoid combination obeying the so-called Dragone-Mizuguchi condition (which preserves polarisation purity on the optical axis). Subsequent studies culminating in the so-called Red Book of 1996 (Bersanelli et al. 1996) did not modify the initial design substantially, except for an increase in the reflector size to the maximum allowable by satellite constraints at the time, and for the detailed design of surrounding elements, e.g., supporting structure and baffle (see Fig. 1). In 1997, the design of the focal plane was substantially modified to improve the efficiency of use of its central area and the manufacturability of the HFI, yielding today's layout (see Fig. 2) in which the centre of the focal plane is occupied by the very-low-temperature, high-frequency HFI detectors (Lamarre et al. 2010), surrounded by the higher-temperature, lower-frequency LFI detectors (Bersanelli et al. 2010).
| Figure 2: The layout of the focal plane of Planck. The LFI horns surround the HFI focal plane (circular structure in the centre of the figure). See also Fig. 4. |
|
| Open with DEXTER | |
The new focal plane layout required a re-optimisation of the telescope, which was carried out in 1999 (Fargant et al. 2000). Because of the long wavelengths involved relative to the size of the optics, physical optics methods were required to correctly model the detector patterns in the far field. However, the computation times required with physical optics are too long to allow many iterations. Ray-tracing is a more efficient method but less accurate; however it is able to represent well enough the shape of the main beam for optimisation purposes. The optimisation was therefore carried out using the optical ray-tracing software CodeV, allowing variation of all the main parameters of the reflectors (conic constants and radius of curvature) and telescope (distances and angles between reflectors and focal plane). The merit function was the minimisation of the quadratic sum of the wavefront error (WFE) at 16 points in the focal plane field (8 for LFI and 8 for HFI). After each optimisation run, the radiation patterns were computed using physical optics with the GRASP software and the horn tapers were readjusted to keep spillover power within allowed straylight levels. Care was also taken to maintain minimum mechanical distances between horns, and to reduce obscuration and mutual electromagnetic effects. The resulting optimised telescope is an aplanatic one consisting of two ellipsoidal reflectors, and is described in Sect. 3 and Appendix A.
Once the intended optical prescription was established, high level requirements for hardware production were set mainly in terms of WFE, but also in terms of peak gain degradation, ellipticity, and straylight levels. The maximum WFE levels required for each detector were calculated (based on ideal feedhorns with specified taper levels and the optimised telescope design prescription), and we constrained the most accurate pre-launch estimate of the in-flight WFE to be lower than that level within a specified tolerance. The surface characteristics of the reflectors determine to a significant degree the total WFE of the system, and during their manufacture a specific set of mechanical requirements (Table 1) was imposed from a sub-allocation of the maximum WFEs. All the requirements, whether at system or reflector level, were required to be met at operational temperature.
Table 1: Design requirements of the Planck telescope reflectors.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12911f3a.eps}\vspace*{3mm}
\includegraphics[width=8cm,clip]{12911f3b.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa12911-09/Timg31.png)
|
Figure 3:
(Top) Two side
views of the payload module, showing mainly the three V-grooves, which
radiatively insulate the payload from the warm part of the satellite,
and the large baffle used for straylight control and radiative cooling.
(Bottom) A cross-sectional sketch of the optimised Planck
telescope design, showing the reflectors support structure and the
focal plane. The principal (right-handed) coordinate systems are
indicated. The rotation of the spin axis is about the
|
| Open with DEXTER | |
3 Mechanical configuration and manufacture
The major elements constituent of the optical system of Planck are considered to be the following (see Fig. 3):
- The detector feedhorns, designed, manufactured and tested by the LFI and HFI instrument teams (Villa et al. 2010, in prep.; Sandri et al. 2010; Maffei et al. 2010).
- The Planck telescope, consisting of:
- the primary and secondary reflectors (PR and SR), designed and manufactured by Astrium (Friedrichshafen, Germany);
- the support structure, designed and manufactured by Oerlikon Space (Zürich, Switzerland).
- The baffle
![[*]](/icons/foot_motif.png) surrounding the telescope, designed and manufactured by Contraves (Zürich, Switzerland).
surrounding the telescope, designed and manufactured by Contraves (Zürich, Switzerland).
- The third V-groove, which forms the floor of the cavity in which the telescope and focal plane are located, designed and manufactured by Thales Alenia Space (Cannes, France).
The detailed geometrical definition of the telescope (as designed and in flight) is described in Appendix A.
3.1 Thermal environment
Since Planck's objective is to detect extremely small
temperature variations in the CMB, we must ensure that all other
sources of radiation in the Planck frequency bands are reduced to a minimum.
Although the reflectivity of the Planck
reflectors is very high, they emit in this frequency range and will be
seen by the detectors. Therefore it is essential to minimize the
operational temperatures of the reflectors. The spacecraft's service
module has a temperature around 300 K, but the telescope supports
and the three so-called V-grooves (see Fig. 3) provide a very high thermal isolation. As a result, the top of the 3![]() V-groove
is expected to stabilise at a temperature around 47 K. The
baffle and the reflectors will have temperatures of between 40 and
43 K, low enough for the emission of the reflectors to dominate
the background noise of the detectors only at the highest frequencies.
V-groove
is expected to stabilise at a temperature around 47 K. The
baffle and the reflectors will have temperatures of between 40 and
43 K, low enough for the emission of the reflectors to dominate
the background noise of the detectors only at the highest frequencies.
3.2 Design and manufacture of the reflectors
The strong requirement imposed on the Planck reflectors to minimize deformations between room temperature and operational conditions (![]() 40 K)
led to the selection of carbon fiber reinforced plastic (CFRP)
honeycomb sandwich technology, in which a carefully controlled mixture
of carbon fibers and resin yields an effective thermal expansion
coefficient, which is close to zero in the
temperature range relevant to Planck.
40 K)
led to the selection of carbon fiber reinforced plastic (CFRP)
honeycomb sandwich technology, in which a carefully controlled mixture
of carbon fibers and resin yields an effective thermal expansion
coefficient, which is close to zero in the
temperature range relevant to Planck.
The main parameters driving the CFRP design are the size, mass, maximum reflector thickness and lowest eigenfrequency. Furthermore, because of the differences in mechanical properties of the CFRP and the adhesion between the front facesheet and the core, the CFRP membrane within each core cell has a tendency to become slightly concave (this effect is usually called ``dimpling''). Although the effect is small, it was expected based on a Finite Element Model to be systematically present in all core cells, and therefore to enhance the response of the telescope in specific narrow areas on the sky, away from the main beam (``grating lobes''). To decrease the dimpling effect, a thicker facesheet was required, which also increased the first eigenfrequency. The final design of the reflector sandwich structure was based on detailed simulations exploiting the full available volume and minimizing the dimpling effect and the mass. This resulted in the selection of hexagonal core cells with a pitch of 60 mm and a wall thickness of 0.8 mm; the final thickness of the facesheets in the center of the reflectors is 2.178 mm.
A more detailed discussion of the mechanical design and manufacturing of the Planck reflectors can be found in Stute (2005).
The Planck reflectors were produced by Astrium, Germany
(ASED), under contract to ESA and the Danish National Space Institute
(DTU-Space). The facesheets were made by laying carbon fibers on
high-precision, cast-steel, optically polished moulds. ASED developed a
numerically-controlled fiber placement technology, where the fibers are
impregnated during the lay-up process with a precise amount of resin.
To assure homogeneity, layers with the fiber direction at
different angles were combined to form a laminate. In the case of
the Planck
reflectors, the facesheets were doubly
curved. To assure a true-angle lay-up over the whole reflector,
ASED developed a special algorithm for their lay-up machine. The
facesheet fibers were laid up in 4 + 4 symmetrical layers (0![]() , 45
, 45![]() ,
-45
,
-45![]() , 90
, 90![]() ).
The fibers used for the top and bottom layers were selected especially
to prevent cracks on the surfaces of the facesheets. Once the fiber
material, the resin, and the details of the lay-up are selected, the
main parameter governing the mechanical properties of the laminate is
the fiber volume content. For Planck, the fiber volume content
was 60%, and a resin with low curing temperature was selected,
to minimize the build-up of internal stresses.
).
The fibers used for the top and bottom layers were selected especially
to prevent cracks on the surfaces of the facesheets. Once the fiber
material, the resin, and the details of the lay-up are selected, the
main parameter governing the mechanical properties of the laminate is
the fiber volume content. For Planck, the fiber volume content
was 60%, and a resin with low curing temperature was selected,
to minimize the build-up of internal stresses.
The cores for the inner honeycomb were produced by filament winding of hexagon-shaped mandrels, a fiber volume content being chosen so that the CTE matched the CTE of the facesheets. The honeycomb cells were glued together and the composite milled into the correct shape and size. Finally, the front facesheet, the core structure, and the back facesheet were glued together using the mould again as support.
The primary and secondary reflectors were manufactured in the same way, the only difference being their size and shape.
To fulfill the reflectivity requirement, the reflectors were coated with 0.5 ![]() m
vacuum-deposited aluminium. To assure good adhesion, first
a NiCr layer, then the aluminium layer, and on top a hard
protection layer of Plasil (Si
m
vacuum-deposited aluminium. To assure good adhesion, first
a NiCr layer, then the aluminium layer, and on top a hard
protection layer of Plasil (Si![]() )
were deposited. The coating was performed at the Balzer coating
facility in the Calar Alto Observatory in Spain. Measurements of the
emissivity are described in Appendix B.
)
were deposited. The coating was performed at the Balzer coating
facility in the Calar Alto Observatory in Spain. Measurements of the
emissivity are described in Appendix B.
3.3 The structure and baffle
The 2 Planck reflectors are supported by a CFRP structure of square tubes. The interface between the reflectors and the telescope structure consists of 3 so-called isostatic mounts (ISMs). The ISM's are weak in the radial but stiff in the tangential direction. This design assures that deformation of the telescope structure does not affect the reflectors. The ISMs are made of titanium.
The baffle surrounding the telescope is made from aluminium honeycomb, which is open on the outside to maximise the radiating surface. To minimize the background radiation inside the baffle cavity, the surfaces of the telescope structure are covered by aluminized kapton foil, while the inside of the baffle is coated with pure aluminium. Outside the cavity, the surfaces are coated with high emissivity paint to improve radiative cooling.
The baffle was assembled from simple shapes to simplify its implementation in the GRASP software model, and minimise the uncertainty in the predicted radiation pattern of the telescope. It is built from seven adjacent conical sections and one planar rear wall, joined to yield a smooth surface. The diffraction from these elementary surfaces is easily computable using geometrical theory of diffraction implemented in GRASP. The telescope cavity is closed at the bottom with the topmost conical V-groove. The front shape of the baffle (i.e., the wall behind the secondary mirror) was raised slightly to reduce the illumination of the top of the primary mirror by the Moon.
The edges of both reflectors and the rim of the baffle are covered with kapton foil. The effect of implementing curved edges was investigated and, although they produced a lower level of diffraction over a wider angular range, the uncertainty in the predicted results was higher because of the effect of creeping waves. The edges are therefore straight on both sides of the sandwich, a geometry that concentrates the edge-diffracted fields in a narrow region.
![\begin{figure}
\par\includegraphics[bb=1 1 1940 1500, width=0.45\textwidth]{1291...
...=300 1 1660 1410, width=0.35\textwidth]{12911f4b.eps}
\vspace*{5mm}
\end{figure}](/articles/aa/full_html/2010/12/aa12911-09/Timg39.png)
|
Figure 4:
The footprint of the focal plane as seen by an observer at infinity. The top panel shows predicted contours of each main beam (averaged across the band); the horizontal and vertical axis are in
|
| Open with DEXTER | |
4 In-flight optical characteristics
We summarise in this section the in-flight optical properties of Planck
inferred from the flight prediction exercise (see Sect. 7). The
properties of the focal plane are visually presented in Fig. 4, and the characteristics of the individual channels are listed in Table 2![]() .
.
Table 2: Predicted in-flight beam propertiesa.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12911f5a.eps}\vspace*{5mm}
\includegraphics[width=7.5cm,clip]{12911f5b.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa12911-09/Timg40.png)
|
Figure 5:
A typical far side lobe pattern for Planck
(in this case at 100 GHz), showing the main features of
interest. The horizontal axis corresponds to the angle around
|
| Open with DEXTER | |
The main features of the far sidelobes are summarised in Fig. 5, and some of the key figures are listed in Table 2. We draw attention to the grating lobes, which are expected to be produced by the reflector ``dimpling'' (Sect. 3.2). Interferometric measurements of the SR (Sect. 5.1) have shown that the dimples are not systematically present in all core cells (Fig. 6). GRASP simulations of the effect on the beam pattern of the derived SR deformation map show that the expected narrow and bright grating lobes are suppressed by the unsystematic behaviour of the small-scale structure: though power is scattered by the dimples, the resulting lobes are broadened and merge into the general sidelobe behaviour.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12911f6.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa12911-09/Timg41.png)
|
Figure 6:
The deformations of the SRFM on small scales at about 50 K as measured with |
| Open with DEXTER | |
While Planck was not originally designed to measure
polarisation, most of its detectors are linearly polarised, and its
capabilities in this respect have improved over the years in response
to the realisation that these measurements are extremely important
scientifically. Most horns contain two linearly polarised detectors
whose principal planes of polarisation are very close to 90![]() apart on the sky
apart on the sky![]() . Two of these horns, rotated by 45
. Two of these horns, rotated by 45![]() with respect to each other, are placed consecutively along the path swept by the FOV on the sky (see Fig. 4). This arrangement allows us to recover Stokes Q and U
by suitable addition and subtraction of the different detector outputs,
and reduces spurious polarisation due to beam mismatches (Leahy
et al. 2010; Rosset et al. 2010).
with respect to each other, are placed consecutively along the path swept by the FOV on the sky (see Fig. 4). This arrangement allows us to recover Stokes Q and U
by suitable addition and subtraction of the different detector outputs,
and reduces spurious polarisation due to beam mismatches (Leahy
et al. 2010; Rosset et al. 2010).
Each linearly polarised detector is mainly characterised by two
parameters: the orientation on the sky of the principal plane of
polarisation, and the cross-polar level (i.e. the sensitivity to
radiation polarised orthogonally to the principal plane). Estimates are
shown in Table 3.
We emphasize that both these parameters vary with angle within the
beam; their effective values therefore depend on the spatial
distribution of the source to which the beams couple. The
LFI detector assembly includes ortho-mode transducers (OMTs),
which feed orthogonal polarisations to the low-noise amplifiers. They
introduce an additional electrical rotation in the angle with rms
uncertainty
![]() ,
via their finite cross-polar response. Uncertainties in the
feed-horn cross-polar response at a level of <-30
(<-40) dB also contribute local errors of
,
via their finite cross-polar response. Uncertainties in the
feed-horn cross-polar response at a level of <-30
(<-40) dB also contribute local errors of
![]() (
(
![]() )
in the response pattern, but these
must be coherent over the beam to cause a net rotation. Differential
errors in the overall cross-polar leakage, reported in Table 3,
have a second-order effect on the angle: a -20 dB
(-40 dB) uncertainty corresponds to an angle uncertainty of 0
)
in the response pattern, but these
must be coherent over the beam to cause a net rotation. Differential
errors in the overall cross-polar leakage, reported in Table 3,
have a second-order effect on the angle: a -20 dB
(-40 dB) uncertainty corresponds to an angle uncertainty of 0
![]() 6 (0
6 (0
![]() 06).
Therefore, the total angle uncertainty for LFI detectors may be
dominated by cross-polar effects in the optical chain (telescope, horn,
and mainly OMT) rather than by mechanical uncertainties (see also
Leahy et al. 2010).
06).
Therefore, the total angle uncertainty for LFI detectors may be
dominated by cross-polar effects in the optical chain (telescope, horn,
and mainly OMT) rather than by mechanical uncertainties (see also
Leahy et al. 2010).
As for the angles, the cross-polar level measured depends on how the
source fills the beam. For the LFI, the only contribution is residual
Stokes V response and variation in the local polarisation
orientation within the beam; the values reported in Table 3
are based on GRASP flight prediction patterns integrated within the
-3 dB contours of the main beam. The calculations assume
perfect OMTs, and indeed these contribute negligibly to depolarisation
(Leahy et al. 2010). For HFI, the cross-polarisation is dominated not by the beam pattern, but by
direct coupling of the unwanted polarisation mode to the polarisation-sensitive bolometer in its cavity (Maffei et al. 2010).
This incoherent leakage differs fundamentally from that in the LFI,
though is functionally equivalent if the beam is filled by a
uniformly-polarised source. The values reported in Table 3 (see also Rosset et al. 2010)
are measured at pixel level (i.e., detector plus optical elements:
horns, filters, lens) using a source that fills the beam down to
20 dB; the uncertainty in the measured levels is in the range
![]() 0.1-0.2% for PSBs, and in the range
0.1-0.2% for PSBs, and in the range ![]() 0.2-1.5% for SWBs (which are also slightly
polarised).
0.2-1.5% for SWBs (which are also slightly
polarised).
Differences in the optical response of the orthogonally oriented detectors lead to a spurious detection of polarisation. A measure of this optical ``mismatch'' has been calculated using beams modelled on perfect reflectors and is reported in Table 3. This measure is useful to quantify the polarisation contamination of point sources in the beams. The spurious polarisation caused by diffuse emission is more accurately quantified by integrating the mismatch within the beam (as reported in Leahy et al. 2010), and is significantly lower than the values here reported.
The on-ground measurements of polarisation properties will be complemented in-flight with calibration observations of a bright and strongly polarised source, the Crab; this source, which is relatively compact at Planck resolution, has well-known polarisation characteristics whose knowledge is now being improved specifically for Planck (Aumont et al. 2010). The details of the polarisation calibration scheme are sketched in Sect. 7 and developed in detail in Leahy et al. (2010) for LFI and in a forthcoming publication for HFI.
The polarisation properties of the far side lobes are also of interest since the highly polarised Galactic emission could generate through them a spurious polarisation signal in the detectors. Fortunately, early studies (Hamaker & Leahy 2004) indicate that the rapid angular variability of both the polarised emission and the sidelobe polarised structure act to reduce the signal coupled into the detector.
5 Prediction of the in-flight geometry of the Planck telescope
The prediction of the in-flight geometry of the Planck optical system on the ground is one of the pillars of the pre-launch flight prediction. An overview of the test and verification programme is provided in Tauber et al. (2005). We now outline the programme of measurements of the geometry of both the reflectors and telescope, its main results, how they compared to predictions of the thermomechanical behaviour, and how they were used to establish the final on-ground alignment of the telescope. We emphasize here that the goal of the Planck optical measurement programme was not so much to ensure precise alignment at a given configuration, since the optical performance of the Planck telescope is rather insensitive to misalignment at the relevant wavelengths, and the science objectives do not depend on small variations in the optical performance. The goal was instead to be able to predict the alignment and the reflector surface deformations at operational conditions with as little uncertainty as possible, to improve the in-flight optical calibration.
Table 3: Predicted in-flight main beam polarisation propertiesa.
5.1 Measurement programme
The programme was based on interferometric and photogrammetric measurements of reflectors, telescope, and focal plane at as close to operational conditions as possible. Each measurement contributed some information to the final establishment of the telescope alignment. The main difficulty in designing this programme was related to the very low in-flight temperatures predicted (42 K for the PR and 45 K for the SR), which did not allow us to carry out a full end-to-end measurement in operational conditions.
The main elements of the measurement programme on the flight hardware were:
- 1.
- Photogrammetry of the PR and SR from ambient temperature down to
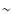 95 K (Amiri Parian et al. 2006a, 2007b). This technique, which was first tested on a qualification model of the SR (Amiri Parian et al. 2006b), allowed us to measure the figure of each reflector (radius of curvature R and conic constant k) and the
large-scale angular deformations at several temperatures between warmest and coldest. The measured trends of R and k were used to extrapolate these parameters to the operational temperature.
95 K (Amiri Parian et al. 2006a, 2007b). This technique, which was first tested on a qualification model of the SR (Amiri Parian et al. 2006b), allowed us to measure the figure of each reflector (radius of curvature R and conic constant k) and the
large-scale angular deformations at several temperatures between warmest and coldest. The measured trends of R and k were used to extrapolate these parameters to the operational temperature.
- 2.
- Interferometry at
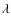 10
10 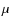 m of the SR at several temperatures between ambient temperature and
m of the SR at several temperatures between ambient temperature and 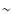 40 K (Roose et al. 2005, 2006).
These measurements traced the small-scale deformations of the SR down
to operational temperature. The deformation map of the SR at around
50 K is shown in Fig. 6.
The core walls and ``dimples'' are clearly visible for nearly all
cores. It is worth noting that the dimples do not behave as
expected, i.e. they do not all form a regular concave deformation.
Instead, the core deformations show multiple peaks whose amplitudes do
not vary systematically across the surface (see
also Sect. 5.2). Since interferometry does not preserve
large-scale information, it was combined with the photogrammetric
data to yield an accurate picture of the surface of the SR at 40 K
on all spatial scales of interest (Fig. 7).
Although interferometric measurements of the PR were also carried out,
its large size and long focal length required the acquisition of
interferograms in double-pass configuration. The noise due to
diffraction of light from the core walls increased considerably
relative to the SR, rendering the phase information contained in the
interferograms too noisy to be useful.
40 K (Roose et al. 2005, 2006).
These measurements traced the small-scale deformations of the SR down
to operational temperature. The deformation map of the SR at around
50 K is shown in Fig. 6.
The core walls and ``dimples'' are clearly visible for nearly all
cores. It is worth noting that the dimples do not behave as
expected, i.e. they do not all form a regular concave deformation.
Instead, the core deformations show multiple peaks whose amplitudes do
not vary systematically across the surface (see
also Sect. 5.2). Since interferometry does not preserve
large-scale information, it was combined with the photogrammetric
data to yield an accurate picture of the surface of the SR at 40 K
on all spatial scales of interest (Fig. 7).
Although interferometric measurements of the PR were also carried out,
its large size and long focal length required the acquisition of
interferograms in double-pass configuration. The noise due to
diffraction of light from the core walls increased considerably
relative to the SR, rendering the phase information contained in the
interferograms too noisy to be useful.
- 3.
- Photogrammetry of the whole telescope at several temperatures between ambient temperature and
 95 K (Amiri Parian et al. 2007a).
These measurements yielded the thermoelastic deformations of the
telescope structure, and the trend was used to extrapolate them to
operational temperature. To provide representative loads, the
object measured also included the two flight reflectors and a structure
representative of the focal plane. Measurements of the focal plane
deformations were correlated against thermoelastic predictions and used
to predict the deformations of the focal plane in-flight. The number of
targets on the reflectors was too low to achieve high accuracy on a
determination of their surface deformations, but adequate enough to
establish that their thermoelastic behaviour was consistent with the
photogrammetry at the reflector level.
95 K (Amiri Parian et al. 2007a).
These measurements yielded the thermoelastic deformations of the
telescope structure, and the trend was used to extrapolate them to
operational temperature. To provide representative loads, the
object measured also included the two flight reflectors and a structure
representative of the focal plane. Measurements of the focal plane
deformations were correlated against thermoelastic predictions and used
to predict the deformations of the focal plane in-flight. The number of
targets on the reflectors was too low to achieve high accuracy on a
determination of their surface deformations, but adequate enough to
establish that their thermoelastic behaviour was consistent with the
photogrammetry at the reflector level.
- 4.
- Theodolite measurements of targets placed on all the critical elements (reflectors, structure, focal plane) were used to tie together the coordinate frames of photogrammetry at reflector and telescope level to each other and to the spacecraft frame. These measurements were performed frequently, until integration of the satellite with the launcher, to verify the stability of the optical system throughout the satellite's assembly and integration programme.
Table 4: Planck reflector characteristics at ambient temperature and 40 K.
![\begin{figure}
\par\includegraphics[height=6.5cm,width=8.2cm,clip]{12911f7a.eps}...
...{5mm}
\includegraphics[height=6.5cm,width=7.5cm,clip]{12911f7b.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa12911-09/Timg58.png)
|
Figure 7: Most accurate (``best'') estimates (see Sect. 5.1) of the surface deformation of the Planck reflectors at operational temperature ( left: PR; right: SR) relative to the best-fit ellipsoids (Table 4). The horizontal and vertical axes are projected dimensions onto the reflector rim planes, and the colour scale corresponds to sagittal elevation. The SR image is of much higher spatial resolution than the PR, thanks to the availability of interferometric measurements; for the PR, only lower resolution photogrammetry was used. The right-hand side of the SR required patching of interpolated photogrammetry onto the trapezoidal-shaped feature (see Fig. 6) which was caused by vignetting of the interferometric data. |
| Open with DEXTER | |
5.2 Comparison to models
The measured deformation of the reflectors was compared to finite-element models (FEMs) of the behaviour on both large and medium scales, and on the scale of a single core cell. Unfortunately, the material properties that must be used in the models are affected by significant uncertainties. The conclusions that can be drawn are summarised below:
- 1.
- On the largest scales, the relevant parameters are the derivative of R and k (Table 4)
with respect to temperature. A stochastic analysis was performed
to search for a plausible combination of material parameters (mainly
CTEs) that would lead to a dR/dT and dk/dT
that match the results of photogrammetric data. A plausible
combination is found only for the PR; for the SR, the measured slopes
are more than a factor of 2 beyond the plausible range of
parameters. In addition, the photogrammetry data are only made
down to
 90 K,
whereas changes in the slope below this temperature are expected from
previous experience with similar materials. Therefore, the values
of R and K extrapolated to 40 K are affected
by significant uncertainty, being in practice constrained only to a
range between linear extrapolation and the value measured
at 90 K.
90 K,
whereas changes in the slope below this temperature are expected from
previous experience with similar materials. Therefore, the values
of R and K extrapolated to 40 K are affected
by significant uncertainty, being in practice constrained only to a
range between linear extrapolation and the value measured
at 90 K.
- 2.
- Medium-scale features are predicted by the FEMs, which are also found in the measured surfaces, namely local deformations around the isostatic mounts (ISMs), a large central ``shelf'' of diameter defined by the location of the ISMs, a depressed ring outside the circle of the ISMs, and a ``curling-up'' of the edge areas. However, the predicted amplitude of these features is smaller by an order of magnitude than what is measured.
- 3.
- On small scales, the behaviour is dominated by the dimpling,
i.e. the behaviour of the facesheet within each core cell as a
function of distance from the centre. The measured surface is much more
inhomogeneous than predicted by the FEMs, i.e. most cells do not
exhibit simple concave dimples but multiple-peak features with
amplitudes that are much higher than the FEM predicts
![[*]](/icons/foot_motif.png) .
The FEMs also predict that the dimpling depends on the distance from
the centre of the reflector, driven by the large-scale reflector
curvature. None of the FEM-predicted small-scale behaviour is clearly
reproduced in the measurements.
.
The FEMs also predict that the dimpling depends on the distance from
the centre of the reflector, driven by the large-scale reflector
curvature. None of the FEM-predicted small-scale behaviour is clearly
reproduced in the measurements.
5.3 In-flight alignment
The SR and focal plane were shimmed at ambient temperature such that when the telescope cools, the system will come into optimal alignment as determined by CodeV. The optimization took into account the predicted deformation of the mirrors and structure. The WFE for the nominal, best, and worst case deformations is shown in Fig. 8.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12911f8.eps}
\vspace{2mm}\end{figure}](/articles/aa/full_html/2010/12/aa12911-09/Timg59.png)
|
Figure 8: The rms WFE of the full set of horns for the three flight prediction scenarios (nominal or as-built, best and worst cases, defined in Sect. 7.1). The top panel shows the absolute WFE (in wavelengths), and the lower panel the WFE of the best and worst cases normalised by that of the nominal case. The frequency increases from right to left. The horn ID is labelled by instrument (HFI or LFI), frequency and increasing horn number (as in Fig. 4). The three cases were defined at 353 GHz (centre of the focal plane); at other frequencies, compensations mean that the ``worst-case'' WFE is not always larger than the ``best-case'' WFE. Nonetheless, the spread represents the uncertainty in the in-flight WFE at all frequencies. The best case is clearly very close to the nominal one in terms of the WFE, but the worst case is quite far, especially at the higher frequencies. |
| Open with DEXTER | |
The uncertainty in the in-flight alignment has the strongest influence on the uncertainty in the predicted beam shapes. The elements contributing the most to the alignment uncertainty are: (a) the rotation of the focal plane assembly; (b) displacement of the SR along the X direction (see Fig. 5).
A Monte Carlo analysis was performed of the full alignment budget,
taking into account all the expected thermo-elastic deformations in the
system. Code V was used to compute at 353 GHz the WFE of a
horn near the centre of the focal plane, for 3000 cases drawn from
the estimated error distributions of each misalignment type, including
displacements, rotations, and deformations of the reflector figures.
The set of 3000 cases covers the range of misalignment cases that
may be encountered in flight. For each case, the optimal location
of the telescope focal plane (i.e. the location that minimizes
WFE) was computed using sensitivity coefficients for each individual
misalignment, and compared to the design location of the feed horn
phase centre; the difference constitutes the true misalignment of
that case in an optical sense. The results of this analysis (see
Fig. 9) indicate that the misalignment uncertainty is of order ![]() mm (
mm (![]() )
in the defocus direction, which has a very significant impact on the
ability to predict the optical performance in-flight
(see Sect. 6.2).
)
in the defocus direction, which has a very significant impact on the
ability to predict the optical performance in-flight
(see Sect. 6.2).
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{12911f9a.eps}\par\includegraphics[width=8.5cm,clip]{12911f9b.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa12911-09/Timg62.png)
|
Figure 9: ( Top) The distribution of WFEs at 353 GHz for 3000 cases of thermo-elastic deformations drawn from the error distributions of all known cases leading to misalignment (see description in Sect. 5.2). ( Bottom) The distribution of defocus errors (i.e. the difference along the principal axis between the locations of the focal plane formed by the telescope and that of the feedhorn phase centre). The horizontal axis is defocus in millimetres. Note that the specific horn used in this analysis is displaced from its optimal location along the focal axis by about 0.35 mm; this is a result of the global optical design which necessarily required that some of the horn locations were not optimised. |
| Open with DEXTER | |
Early in the development, concerns were raised that the alignment
process relied on a complex accumulation of measurements and
extrapolations, which were not verified by an end-to-end measurement at
operating frequencies. It was noted that if a human error were
made in this process (and not caught by ``standard'' verification
practices), it would not be found until flight
(the ``Hubble'' problem). An end-to-end measurement of the
flight hardware is infeasible because of the need to operate the Planck
detectors at low temperatures, which cannot be achieved in an
RF measurement chamber. Therefore, an additional (coherent)
320 GHz detector/feedhorn assembly was placed in the focal plane,
whose purpose was to verify that no such human error had been made.
A special technique based on modulated reflectivity measurements
was developed (and validated on the qualification model of the Planck
telescope) that allowed us to measure the radiation pattern of this
detector in a compact antenna test range (CATR) with a dynamic range of
![]() 15 dB (Paquay et al. 2008).
The shape of the pattern varies rather sensitively with deviations from
the optimal location, in particular defocus. This measurement
therefore allowed us to
determine the location of the focal plane, at ambient conditions,
with an accuracy of
15 dB (Paquay et al. 2008).
The shape of the pattern varies rather sensitively with deviations from
the optimal location, in particular defocus. This measurement
therefore allowed us to
determine the location of the focal plane, at ambient conditions,
with an accuracy of ![]() mm (Paquay et al. 2008),
which was considered adequate to rule out human error. With this
(relatively low) accuracy, the predicted location was able to reproduce
the measured one
mm (Paquay et al. 2008),
which was considered adequate to rule out human error. With this
(relatively low) accuracy, the predicted location was able to reproduce
the measured one![]() .
.
6 Radio frequency verification
Although the design and verification of the Planck telescope
were based on specified WFE levels, ultimately it is the radio
frequency (RF) performance that matters. Measuring the
RF performance of the optical system at in-flight conditions (low
temperature, vacuum) is infeasible due to the dimensions involved in a
measurement setup. A Shack-Hartmann measurement of the entire
telescope at ![]() 10
10 ![]() m
was initially planned but eventually discarded as too complex and
costly. Instead, an RF measurement campaign based on the
qualification model of the Planck telescope (the ``RFQM'')
was implemented as a means of building confidence in the process of
estimating the flight predictions. The objectives of this campaign
(Forma et al. 2008)
were to: (a) measure the qualitative RF properties
of the optical system; and (b) validate the ability of GRASP to
predict the flight patterns based on geometrical information. The key
results of this campaign are: (a) a GRASP model that can be
applied to the geometry of the flight reflectors (referred to as FM for
``Flight Model''); and (b) the difference between predicted and
measured patterns, which provides a quantitative measure of the
uncertainty in the modelling based on
ground information.
m
was initially planned but eventually discarded as too complex and
costly. Instead, an RF measurement campaign based on the
qualification model of the Planck telescope (the ``RFQM'')
was implemented as a means of building confidence in the process of
estimating the flight predictions. The objectives of this campaign
(Forma et al. 2008)
were to: (a) measure the qualitative RF properties
of the optical system; and (b) validate the ability of GRASP to
predict the flight patterns based on geometrical information. The key
results of this campaign are: (a) a GRASP model that can be
applied to the geometry of the flight reflectors (referred to as FM for
``Flight Model''); and (b) the difference between predicted and
measured patterns, which provides a quantitative measure of the
uncertainty in the modelling based on
ground information.
The RFQM, including a representative focal plane structure and
all the important associated payload elements (e.g. baffle,
V-groove) was placed in a CATR and used to measure 4![]() radiation
patterns of flight-like horns at frequencies between 30 GHz and
320 GHz, including two orthogonal polarisation directions. The
surfaces of the reflectors were measured using photogrammetry, and the
alignment of the object tested was measured in-situ in great detail, in
both cases using techniques similar to those later used to align the
FM. The radiation patterns of the feedhorns used were separately
measured. The geometry of the GRASP model used for flight predictions
was based on all these measurements.
radiation
patterns of flight-like horns at frequencies between 30 GHz and
320 GHz, including two orthogonal polarisation directions. The
surfaces of the reflectors were measured using photogrammetry, and the
alignment of the object tested was measured in-situ in great detail, in
both cases using techniques similar to those later used to align the
FM. The radiation patterns of the feedhorns used were separately
measured. The geometry of the GRASP model used for flight predictions
was based on all these measurements.
6.1 Main beams
The RFQM main beams![]() were measured with a high sampling density. Examples are shown in Fig. 10.
The prediction model for the main beams is based on physical optics and
the only inputs to be adjusted are geometrical ones. The comparison of
predictions and measurements shows differences that increase
significantly from low to high frequencies. In terms of total
integrated power, the differences vary from a few tenths of one percent
(i.e. within measurement uncertainties) to 6-7 percent. These
differences can be partly attributed to measurement errors and other
CATR-induced systematics. However, even at low frequencies, where the
errors are very low and systematics well under control, differences
of
were measured with a high sampling density. Examples are shown in Fig. 10.
The prediction model for the main beams is based on physical optics and
the only inputs to be adjusted are geometrical ones. The comparison of
predictions and measurements shows differences that increase
significantly from low to high frequencies. In terms of total
integrated power, the differences vary from a few tenths of one percent
(i.e. within measurement uncertainties) to 6-7 percent. These
differences can be partly attributed to measurement errors and other
CATR-induced systematics. However, even at low frequencies, where the
errors are very low and systematics well under control, differences
of ![]() can be seen in some cases. Therefore the ability to predict the
in-flight patterns based on geometrical information acquired on the
ground has been validated to an accuracy of a few percent in total
power, increasing to levels of 5-6 percent at the higher
frequencies.
can be seen in some cases. Therefore the ability to predict the
in-flight patterns based on geometrical information acquired on the
ground has been validated to an accuracy of a few percent in total
power, increasing to levels of 5-6 percent at the higher
frequencies.
Cross-polar measurements were also performed for each detector (see Fig. 11), but were affected in some cases by significant systematic effects caused by (a) the weakness of the signals; (b) greater sensitivity to misalignments in the CATR; and (c) both poor cross-polar characteristics and poor knowledge of the CATR transmitter horns.
![\begin{figure}
\par\includegraphics[width=7.35cm,clip]{12911f10a.eps}
\includeg...
...2911f10b.eps}\par\includegraphics[width=7.55cm,clip]{12911f10c.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa12911-09/Timg66.png)
|
Figure 10:
Comparison of predicted (black lines) and measured (coloured lines) main beam copolar patterns at 30 GHz ( top), 70 GHz ( middle), and 320 GHz ( bottom).
The horizontal and vertical axis are in azimuth and elevation in the
RFQM coordinate system (degrees, arbitrary offsets). The double
coloured lines represent the
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{12911f11.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa12911-09/Timg67.png)
|
Figure 11:
Comparison of predicted (black lines) and measured (coloured lines)
main beam cross-polar patterns at 100 GHz. The horizontal and
vertical axis are in azimuth and elevation in the RFQM coordinate
system (degrees, offsets). The double coloured lines represent the
|
| Open with DEXTER | |
6.2 Far side lobes
When it comes to the computation of far side lobes, pure physical optics computations are too time consuming to be practical and it becomes necessary to use other techniques. The alternative provided by GRASP is ``Multi-GTD'' (Multi-ray Geometrical Theory of Diffraction, GRASP Manual 2008). In addition to the geometry of the system, it is also necessary to provide GRASP with the families of rays that it propagates to the far field. The number of families is theoretically infinite and needs to be restricted. The first iteration to this was blind, on the basis of experience and a first estimation of the amount of power carried by each ray family. The second iteration was based on the RFQM measurements, i.e., wherever there was a significant discrepancy between prediction and measurement, there was an attempt to improve the agreement by adding ray families or new geometrical elements. In this process, some additions to the initial model were implemented, yielding improvements in limited parts of the sphere (Nielsen 2008). Among the changes implemented were: improvement of the V-groove floor reflections, addition of side panels of the focal plane assembly as scatterers, and the addition of some new ray families whose contribution was more important than initially predicted. The most important improvement was possibly the correction by PO calculations in localised patches of the sphere of some unrealistically sharp features in the pattern produced by the multi-GTD technique. A typical result of the correlation exercise is shown in Fig. 12 at 100 and 320 GHz; similar analysis was carried out at all measured frequencies and over several regions of the sphere to yield the final GRASP models for the far sidelobes.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{12911f12a.eps}\hspace*{3mm}
\includegraphics[width=8.3cm,clip]{12911f12b.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa12911-09/Timg68.png)
|
Figure 12:
The figures show cuts in the radiation pattern at 100 GHz ( left) and 320 GHz ( right) in the elevation direction through the beam peak; the horizontal axis is in degrees, the peak of the main beam is at 85 |
| Open with DEXTER | |
The derived far sidelobe models can be compared to the measurements in Fig. 13. The qualitative correlation is generally quite good; all the major spillover features are reproduced with roughly the predicted peak levels, though many are not as sharp as in the predictions. The worst correlation is clearly seen at 320 GHz, where a number of bright spillover features are predicted but not detected. The measured level of the PR spillover at 30 GHz surprisingly also disagrees with models by about 3 dB (a large factor compared to the estimated measurement error).
One interesting feature is that the predicted deep nulls surrounding the main beam and bordered by the SR spillover, baffle spillover, and baffle edges, appear in general to be more filled with power in the measured case. A diffuse reflection field from the CATR could be responsible for this effect, or, as argued in Sect. 6.4, it could be attributed to dust deposited on the reflectors.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{12911f13a.eps}\includegrap...
....eps}\includegraphics[width=8.2cm,clip]{12911f13d.eps}
\vspace{-1mm}\end{figure}](/articles/aa/full_html/2010/12/aa12911-09/Timg69.png)
|
Figure 13: The RFQM radiation patterns, as measured ( left) and predicted ( right). Clockwise from top left: 30, 70, 320 and 100 GHz. The colour scales are in dB from peak. The coordinate system is as in Fig. 5. The measurements suffer from some systematic effects very close to the main beam. Residual artifacts are also visible in the far side lobes, e.g. horizontal features at 320 GHz. |
| Open with DEXTER | |
Table 5: Inputs used for flight predictions.
7 Flight performance predictions and associated uncertainties
7.1 Methodology
The knowledge gathered on the ground was distilled into a prediction of the optical performance in orbit. This prediction consists of GRASP calculations using the inputs (i.e. PO parameters and GTD ray families) correlated with the RFQM measurements (see Sect. 5), and the most accurate estimates of the geometry of the telescope in operational conditions. The most interesting aspect of this exercise is perhaps the estimation of the uncertainties associated with the prediction. To identify the uncertainty range in the estimation of radiation patterns in the far field, three different geometries were defined:
- a ``nominal case'', which corresponds to the most accurate (``best estimate'') of the as-built telescope and reflectors in operating conditions (as described in Sect. 5);
- a ``worst case'', which corresponds to a case where each
individual element of the geometrical configuration (feedhorn,
reflectors, alignment) has been deformed from its nominal value by an
amount corresponding to the
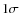 individual uncertainty in the direction of lower
directivity (the
individual uncertainty in the direction of lower
directivity (the 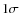 level was determined as described below);
level was determined as described below);
- a ``best case'', similar to the ``worst case'' but in the direction of higher directivity.
Table 5 contains a summary of the inputs used for each of the above cases.
The GRASP calculations are monochromatic, but the detectors are
rather wideband. This means that several monochromatic patterns must be
calculated for each detector, and then averaged![]() to simulate the pattern that the detector sees. In addition, since
most detectors are polarisation sensitive, each calculation should be
repeated for each orthogonal polarisation direction. The total number
of patterns to be calculated should ideally be several thousands, and
is therefore prohibitive in terms of computing resources.
As a compromise, for each main beam single polarisation
calculation, 5 frequencies were calculated across the band.
An indication of the effect of band-averaging is given in
Table 2.
to simulate the pattern that the detector sees. In addition, since
most detectors are polarisation sensitive, each calculation should be
repeated for each orthogonal polarisation direction. The total number
of patterns to be calculated should ideally be several thousands, and
is therefore prohibitive in terms of computing resources.
As a compromise, for each main beam single polarisation
calculation, 5 frequencies were calculated across the band.
An indication of the effect of band-averaging is given in
Table 2.
Table 6: Typical uncertainties in beam characteristics obtained from the ground.
7.2 Predicted uncertainties
The patterns resulting from the flight prediction are visually similar to those of Fig. 13; one example is given in Fig. 15. It is more interesting to review the predicted uncertainties, described for some representative cases in Table 6 and Figs. 14 and 15.
Table 6
shows that the range of possibilities allowed by the ground test is
quite significant, especially at high frequencies. The differences in
peak gain imply redistribution of power up to ![]() 10% at 353 GHz. However, Fig. 14 indicates that the vast majority of this power is concentrated within the -10 dB contour
10% at 353 GHz. However, Fig. 14 indicates that the vast majority of this power is concentrated within the -10 dB contour![]() .
These differences will be easily detectable when the beams are scanned
over planets, e.g. Jupiter, especially at the
higher frequencies (see Sect. 10). The uncertainties impacting the
measurement of polarisation should be quite minor, as can be seen
in the low X-Y mismatch differences indicated in Table 6.
.
These differences will be easily detectable when the beams are scanned
over planets, e.g. Jupiter, especially at the
higher frequencies (see Sect. 10). The uncertainties impacting the
measurement of polarisation should be quite minor, as can be seen
in the low X-Y mismatch differences indicated in Table 6.
In the far sidelobes, the main uncertainties in the predicted patterns are concentrated at the main spillover features, where differences of a few dB can be seen in Fig. 15. These differences imply factors of a few in the straylight signals.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12911f14.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa12911-09/Timg70.png)
|
Figure 14:
The ground uncertainty in the shape of three specific main beams at
centre frequency, represented as the azimuthally integrated power
(in percent of total) of the difference between the best- and
worst-case patterns, as a function of the integration radius
from peak. The horns included are 70 GHz (horn 23),
100 GHz (horn 1), and 353 GHz (horn 6). The
vertical lines indicate the location of the -3 dB radius at
each frequency. The peak differences occur near the -10 dB
contours from peak. For comparison, the contour level at which
a S/N |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{12911f15a.eps}\vspace*{3mm}
\includegraphics[width=8cm,clip]{12911f15b.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa12911-09/Timg71.png)
|
Figure 15: The top panel shows the predicted in-flight pattern at 353 GHz (horn 6). The colour scale is in dB from peak. The bottom panel shows the difference between best- and worst-case patterns for the same horn. The colour scale shows differences between -5 and +5 dB. The largest uncertainties are associated with the SR spillover lobes. |
| Open with DEXTER | |
8 Straylight
As shown in Fig. 5, light from the sky can enter the detectors not only through the main beam but from other angular directions, mainly confined to the three features marked, i.e. the PR, SR, and Baffle spillover lobes (De Maagt et al. 2000).
The PR spillover lobe contains the most power of the three.
Its location close to the spin axis means that this lobe moves
slowly across the sky in synchrony with the scanning strategy.
It couples most effectively to the Galactic plane when the spin
axis crosses it, once per full-sky survey. The signal at detector
level peaks at each crossing with an amplitude of order ![]() 1
1 ![]() K in antenna temperature at frequencies around 100 GHz (Burigana et al. 2004). At lower frequencies, the signal amplitude is increased by a few (to
K in antenna temperature at frequencies around 100 GHz (Burigana et al. 2004). At lower frequencies, the signal amplitude is increased by a few (to ![]() 5
5 ![]() K) as the spillover levels increase (see Table 2)
because of the geater importance of diffraction effects; at higher
frequencies, the amplitude decreases correspondingly. The PR spillover
lobe also couples to the CMB dipole, tracing a large-scale pattern
on the sky that depends closely on the details of the scanning
strategy, with peak-to-peak
amplitudes that can be as high as
K) as the spillover levels increase (see Table 2)
because of the geater importance of diffraction effects; at higher
frequencies, the amplitude decreases correspondingly. The PR spillover
lobe also couples to the CMB dipole, tracing a large-scale pattern
on the sky that depends closely on the details of the scanning
strategy, with peak-to-peak
amplitudes that can be as high as
![]() (scaled from Burigana et al. 2006)
at low multipoles; most of this signal remains constant in time with
only about 20% varying sinusoidally. The signals related to the PR
spillover are therefore of very
significant amplitude, and have to be detected in-flight and removed
(since as described in Sects. 5 and 6.2 the amplitude of the
spillover lobes is predicted from the ground at best with an
uncertainty of a factor of a few). This will be possible because
they are closely linked to the scanning strategy and to well known
sources in the sky, and redundancies in the observations can be used to
separate the two.
(scaled from Burigana et al. 2006)
at low multipoles; most of this signal remains constant in time with
only about 20% varying sinusoidally. The signals related to the PR
spillover are therefore of very
significant amplitude, and have to be detected in-flight and removed
(since as described in Sects. 5 and 6.2 the amplitude of the
spillover lobes is predicted from the ground at best with an
uncertainty of a factor of a few). This will be possible because
they are closely linked to the scanning strategy and to well known
sources in the sky, and redundancies in the observations can be used to
separate the two.
The SR spillover lobe typically contains less power than the PR spillover (2), and it is more closely linked to the main beam because it follows a similar path on the sky: the signal it produces will largely trace the Galactic plane. Because it is less closely linked to the scanning strategy than the PR spillover, it will be more difficult to directly measure its amplitude in-flight; however, it is more accurately known a-priori than that of the PR spillover, as it is mostly due to direct illumination of the feedhorns, whose individual responsivities have been measured on the ground.
Solar system objects may also produce a signal as they travel
through the far-sidelobes of the beam patterns. In the coordinate
system of Fig. 5 and with the current baseline orbit, the Sun traces a path within the region from ![]()
![]() 170
170![]() to 190
to 190![]() ,
the Earth from
,
the Earth from ![]()
![]() 165
165![]() to 195
to 195![]() ,
and the Moon from
,
and the Moon from ![]()
![]() 148
148![]() to 180
to 180![]() .
For the signal produced by the object to be weaker than 1
.
For the signal produced by the object to be weaker than 1 ![]() K,
the pattern directivity in this region should be less than
-46 dBi (Sun), -33 dBi (Earth) and -19 dBi (Moon)
K,
the pattern directivity in this region should be less than
-46 dBi (Sun), -33 dBi (Earth) and -19 dBi (Moon)![]() .
The flight prediction model meets this requirement with at least a
margin of 20 dB at 30 GHz, increasing to margin of more than
30 dB at 353 GHz (see Fig. 16),
but note that this margin may be eroded significantly at higher
frequencies because of the presence of dust (see Fig. 17).
.
The flight prediction model meets this requirement with at least a
margin of 20 dB at 30 GHz, increasing to margin of more than
30 dB at 353 GHz (see Fig. 16),
but note that this margin may be eroded significantly at higher
frequencies because of the presence of dust (see Fig. 17).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12911f16.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa12911-09/Timg73.png)
|
Figure 16:
Three cuts through the main beam in the telescope symmetry plane ( |
| Open with DEXTER | |
The level of polarised straylight was estimated in a simplified way (Hamaker & Leahy 2004). Typical peak values found for Stokes U and Q Galactic straylight at 30 GHz are 1-1.5 ![]() K, resulting from leakage of Stokes I. At frequencies near the minimum
of Galactic emission, the polarised straylight amplitude should be much lower (Hamaker & Leahy 2004, estimate by a factor of
K, resulting from leakage of Stokes I. At frequencies near the minimum
of Galactic emission, the polarised straylight amplitude should be much lower (Hamaker & Leahy 2004, estimate by a factor of ![]() 10).
In polarisation, the dipole straylight is relatively weak compared
to the Galactic contribution; this is because of the presence of both
positive and negative features in both sidelobe complexes, which tends
to cancel large-scale structures.
10).
In polarisation, the dipole straylight is relatively weak compared
to the Galactic contribution; this is because of the presence of both
positive and negative features in both sidelobe complexes, which tends
to cancel large-scale structures.
8.1 The effect of dust
Dust deposited on the telescope reflectors absorbs and scatters light and therefore modifies the radiation pattern produced by a clean reflecting surface. The effect on the pattern depends sensitively on the number, size, shape, and type (composition) of the dust particles. None of these quantities can be predicted with accuracy for the case of Planck in-flight. In particular, the deposition of particles from the rocket fairing could dominate the dust deposited on the reflectors in-flight, and yet this component of the dust distribution is very poorly known. Nonetheless, analyses have been performed to estimate the potential impact of dust on the beam patterns. This analysis was first described in De Maagt et al. (2000) and later reiterated to include the most accurate estimates of dust characteristics for Planck. It assumes that:
- The characteristics of the dust particles (shape, type, and size
distribution) are those found in clean rooms, which have been measured
and standardised (MIL-STD1246)
![[*]](/icons/foot_motif.png) , modified by deposition onto vertical surfaces and the integrated exposure time
, modified by deposition onto vertical surfaces and the integrated exposure time![[*]](/icons/foot_motif.png) .
.
- The multipole expansion (MPE) method is used to estimate the scattering of particles
![[*]](/icons/foot_motif.png) .
It allows us to calculate the bi-reflectance distribution function
(BRDF), which is the effective angular scattering function, for the
particles on the reflectors.
.
It allows us to calculate the bi-reflectance distribution function
(BRDF), which is the effective angular scattering function, for the
particles on the reflectors.
- The amount of dust on the reflectors in-flight is represented by an obscuration level of
 5000 ppm
5000 ppm![[*]](/icons/foot_motif.png) , which leads to a peak BRDF of order 0.08 sr-1 at 353 GHz (lower by an order of magnitude at 100 GHz, and higher by a factor of
, which leads to a peak BRDF of order 0.08 sr-1 at 353 GHz (lower by an order of magnitude at 100 GHz, and higher by a factor of  5 at 857 GHz).
5 at 857 GHz).
- The effect of dust on the surface of the baffle has been ignored.
| (1) | ||
|
(2) |
where K0 is the attenuation factor due to the obscuration by dust.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12911f17.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa12911-09/Timg76.png)
|
Figure 17: The estimated effect of
dust on a beam pattern at 353 GHz for an obscuration level
of 5000 ppm. The coloured lines reflect different assumptions
about the aggregation of dust over time on the reflectors; the most
robust estimate corresponds to
|
| Open with DEXTER | |
The resulting typical effect on a beam pattern is illustrated in Fig. 17.
We emphasize that the uncertainty in this estimate is large. One of the
features noted in the RFQM measurements is that at high
frequencies (i.e. at 100 and 320 GHz), the measured
patterns show gain levels in the mid-side lobe regions that are higher
than expected. Figure 12 shows a discrepancy (labelled ``3'') between the predicted and measured patterns, which could be caused by dust![]() ;
a corresponding feature is seen in the same angular region at
320 GHz at a level 10 dB higher, which is consistent with the
frequency dependence of dust scattering. A detailed 2D view
of the 100 GHz measured and predicted patterns (Fig. 18)
reinforces the indication. However, if these measured levels are
truly due to dust, then they are at a higher amplitude than even most
conservatively modelled. An alternative explanation is that they
are caused by diffuse reflection and scattering from the walls of
the CATR.
;
a corresponding feature is seen in the same angular region at
320 GHz at a level 10 dB higher, which is consistent with the
frequency dependence of dust scattering. A detailed 2D view
of the 100 GHz measured and predicted patterns (Fig. 18)
reinforces the indication. However, if these measured levels are
truly due to dust, then they are at a higher amplitude than even most
conservatively modelled. An alternative explanation is that they
are caused by diffuse reflection and scattering from the walls of
the CATR.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12911f18a.eps}\vspace*{2mm}
\includegraphics[width=7.5cm,clip]{12911f18b.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa12911-09/Timg77.png)
|
Figure 18: When viewed on the same
grid and at the same resolution, it becomes apparent that the
pattern measured on the RFQM at 100 GHz (above) does not have the
deep nulls seen in the most accurately predicted patterns (below).
It is possible that this filling-in of low-level power is due to
scattering by dust on the reflectors (see Sect. 8.1).
A similar effect is seen at 320 GHz (see Fig. 12) with a higher level of |
| Open with DEXTER | |
9 Self-emission
The payload and satellite radiate thermally within the detector bandwidths; if the radiating surface fluctuates in temperature or emissivity, a corresponding signal fluctuation at the detector will be generated. This is referred to as self-emission. The amplitude of the detected signal depends on:
- the amplitude of the temperature fluctuation;
- the emissivity of the surface;
- the RF coupling of the surface to the detector.
Both the baffle and the top of the primary reflector may be directly
illuminated by the Moon, when the angle of the spin axis to the Moon is
larger than 14.5![]() (respectively 25
(respectively 25![]() ),
in which case a spin-synchronous fluctuation is excited. These
situations will be avoided by mission planning but represent a useful
worst case to analyse.
),
in which case a spin-synchronous fluctuation is excited. These
situations will be avoided by mission planning but represent a useful
worst case to analyse.
The optical coupling levels from the payload elements to the detectors were estimated using GRASP and are shown in Table 7. The table shows that the worst-case spin-synchronous signals at the detector due to self-emission are of order nK. Signals that are present at other frequencies can be correlated to thermometer readings and are thus easy to remove.
Table 7: Optical coupling of payload elements to detectors
Farther from the payload, the Service Module contains a warm radiator
that dissipates into space the desorption heat used by the sorption
cooler. The amplitude of its temperature fluctuation is
large (![]() 1 K) but it is very weakly optically coupled to the detectors (with coupling below 10-17). The inner edge of the solar array may fluctuate with the spin but is also weakly coupled (10-13).
The strongest signal may be caused by the daily operation of the
telemetry transmitter, which is estimated to induce an increase in
temperature of several 100 mK at the top of the Service Module,
which is however very slow and very effectively decoupled from the top
V-groove.
1 K) but it is very weakly optically coupled to the detectors (with coupling below 10-17). The inner edge of the solar array may fluctuate with the spin but is also weakly coupled (10-13).
The strongest signal may be caused by the daily operation of the
telemetry transmitter, which is estimated to induce an increase in
temperature of several 100 mK at the top of the Service Module,
which is however very slow and very effectively decoupled from the top
V-groove.
10 In-flight characterisation plans
The in-flight optical characterisation is based on the observation of bright point sources. It has as its main objectives:
- 1.
- The measurement of the geometry of the focal plane, i.e., the relative direction and orientation of each of the Planck
beams with respect to the satellite reference frame (whose direction is
provided by the on-board star trackers). The basic method is to isolate
the region of each detector's time series data around known source
positions (especially planets), assuming a fiducial geometry for the
focal plane, using spacecraft attitude data from the star trackers. The
timestream data is then fit for the shape and location of the beam, and
used to measure individual detector locations. Assuming a rigid focal
plane, this can also be used to measure an overall rotation of the
focal plane. With simulated data, the nominal positions of the
HFI detectors are recovered with an rms of roughly 5 arcsec
using Saturn as a source, as shown in Fig. 19.
The locations of the LFI beams will be recovered at least
as well; and a rigid rotation of the focal plane is recovered with
an accuracy of
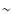 8 arcsec.
We note that this simulation is for one planet crossing only, but
several bright planets will be encountered every 6 months, which
will increase the accuracy of the recovery considerably, and allow us
to evaluate any slow drifts in the focal plane due to thermoelastic
effects.
8 arcsec.
We note that this simulation is for one planet crossing only, but
several bright planets will be encountered every 6 months, which
will increase the accuracy of the recovery considerably, and allow us
to evaluate any slow drifts in the focal plane due to thermoelastic
effects.
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{12911f19.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa12911-09/Timg89.png)
Figure 19: Reconstruction of HFI detector positions from Saturn. The upper left shows the reconstructed positions for each detector (the anomalous recovery of 545 GHz detectors is an artifact partly of the simulation and partly of the top-hat shaped beams), and the other panels show histograms in the in- and cross-scan directions and the total offset.
Open with DEXTER - 2.
- The measurement of the angular responsivity of each beam.
As described in Sects. 5 and 6, the flight prediction
does not achieve the sub-% accuracies required by Planck.
In-flight mapping of the beams therefore is the key that will allow us
to extend the photometric calibration from the very large angular
scales where the CMB dipole provides an excellent calibration
signal, to the beam-sized angular scales where the
CMB anisotropies still contain significant amounts of information.
The measurements will be performed principally on planets, which are
encountered during routine surveying of the sky at a frequency of once
every 6 months (or once each full sky survey). The technique
was analysed for the case of Planck (Burigana et al. 2001a,b; Naselsky et al. 2007; Huffenberger et al. 2010).
The last work is based on a realistic model of the detector response
including significant complicating factors such as the time response of
the HFI bolometers. It confirms that beam errors will be the
driving systematic in the estimation of some cosmological parameters.
In the worst case analysed, using no information about the optics
except the measurement of planets, Huffenberger et al.
(2010) find that a single
transit of Jupiter across the focal plane will measure the beam
transfer functions more accurately than 0.3% for the channels at
100-217 GHz which are the
most sensitive to the CMB. Constraining the beam with optical
modeling can lead to higher quality reconstruction, especially at the
larger angular scales.
The techniques studied so far are based on the mapping of individual beams and/or the recovery of a set of parameters that describe the beam in an optimal manner for a given scientific problem. It is also possible to combine beam maps at several frequencies to recover the most uncertain geometrical parameters of the telescope in-flight, namely the alignment and first-order reflector distortions; with an improved geometrical reconstruction, a more faithful GRASP model of each beam can then be constructed. Preliminary and simplistic analysis (Nielsen 2009) indicates this approach permits us to recover the beam shapes to sub-% accuracy in integrated power.
- 3.
- The determination of the angle of the principal plane of
polarisation for each detector.
Two aspects must be considered that lead to different classes of
systematic effects: relative and absolute calibration. Relative
calibration will be derived from Planck
data alone by fitting
cross-polarization and polarizer angles in the map making equation. Any
polarized region in the sky and in particular the high signal about the
Galactic plane will be used. Initial studies have shown we can expect a
precision around 1
 for the polarizer orientations, and superior to 1% for
cross-polarization leakage. More details about the method will be given
in a forthcoming paper.
for the polarizer orientations, and superior to 1% for
cross-polarization leakage. More details about the method will be given
in a forthcoming paper.
For absolute angle determination, the main calibrator is the Crab nebula (Tau A, NGC 1952), a supernova remnant of intense, stable, and known polarization. Dedicated observations at the IRAM 30 m telescope were conducted (Aumont et al. 2010) to map the Crab's polarization at 86 GHz with high precision (
 0.3
0.3 orientation uncertainty, and
orientation uncertainty, and  2% fractional polarisation uncertainty). Based on these maps and extrapolation of the synchrotron electromagnetic spectrum to Planck frequencies (Macías-Pérez et al. 2010), it is possible to construct an estimate of the signal measured by Planck
if the detectors have their nominal orientation and cross-polarization.
A maximum likelihood fit of the difference between this estimate
and the measured Planck signal provides the true polarization
properties of the detectors. Additional information may be provided by
other measurements of the Crab by SCUBA at 353 GHz and from
observations of a fraction of the Galactic plane by BICEP at 100
and 150 GHz. An analysis of the accuracy achievable by the
LFI channels is made in Leahy et al. (2010).
2% fractional polarisation uncertainty). Based on these maps and extrapolation of the synchrotron electromagnetic spectrum to Planck frequencies (Macías-Pérez et al. 2010), it is possible to construct an estimate of the signal measured by Planck
if the detectors have their nominal orientation and cross-polarization.
A maximum likelihood fit of the difference between this estimate
and the measured Planck signal provides the true polarization
properties of the detectors. Additional information may be provided by
other measurements of the Crab by SCUBA at 353 GHz and from
observations of a fraction of the Galactic plane by BICEP at 100
and 150 GHz. An analysis of the accuracy achievable by the
LFI channels is made in Leahy et al. (2010).
11 Conclusions
The complexity of the Planck payload, and the low temperatures achieved by the optical elements and detectors, have meant that no end-to-end measurement of the optical response could be made that fully represents the in-flight situation. The on-ground characterisation of the Planck optics was indeed based on multiple measurements of both qualification and flight models at feedhorn, reflector, and telescope level.
Using a variety of analytical techniques, all the subsystem-level measurements have been combined into a complete set of estimated in-flight performances and associated uncertainties. The ground-based analyses have allowed us to conclude that:
- The major characteristics of the main beams are within our requirements (Sect. 4).
- The predicted uncertainty of the alignment is too large to use the predicted beam shapes directly for calibration (Sect. 5). The shapes of the main beams will instead be measured in-flight using planets.
- The reliability of the GRASP models of the beam shapes has been verified to high accuracy (Sect. 6).
- The range of potential misalignments is such that the in-flight measurements can be used to correlate the GRASP beam models to high accuracy (Sect. 7). The optimised model can be used to extend the beam shape knowledge to levels far below those directly measurable in-flight. This knowledge will be used to measure effects such as Galactic straylight.
- A number of potential systematic effects have been shown to be below significance level (straylight produced by Solar System sources, grating lobes, self-emission). Others (Galactic straylight, dust) have been modelled to assess their potential effects.
The study, development, testing and data analysis of the combined Planck optical system has been carried out under the leadership of ESA in close collaboration with industry (Thales Alenia Space (Cannes, France) and Ticra (Copenhagen), and the optical experts of the LFI, HFI and DK-Planck Consortia. During the development, Thales Alenia Space was responsible for the overall payload system, and in particular for the design, manufacture and test of the telescope support structure, the baffle and the V-grooves. ESA, jointly with the Danish National Space Institute was responsible for the design and manufacture of the two reflectors. All of the cryogenic testing at reflector and telescope level was under the responsibility of ESA. J.T. wishes to emphasize especially the crucial, difficult, and very extensive modelling and data analysis of the system-level optics carried out by D. Dubruel, P. Nielsen, P. Martin, and R. Daddato, which have been crucial building blocks for our current understanding of the optical performance of Planck. Similarly important efforts have been carried out at instrument level and are described in Sandri et al. (2010) and Maffei et al. (2010).
Appendix A: Telescope definition
![\begin{figure}
\par\includegraphics[width=13.5cm,clip]{12911fA1.eps}
\vspace*{5mm}
\end{figure}](/articles/aa/full_html/2010/12/aa12911-09/Timg90.png)
|
Figure A.1:
Dimensioning and relative positioning of the two reflectors with respect to the telescope coordinate system (see Fig. 3).
|
| Open with DEXTER | |
Table A.1: Planck telescope parameters.
The Planck telescope is defined by the relative location of the best-fit ellipsoids defining the reflectors (see Table 4), and the relative location of the focal plane with respect to one of the reflectors (taken as the SR). Figure A.1 shows the relevant parameters for the design configuration, and Table A.1 shows the corresponding values for the nominal alignment in-flight.
Appendix B: Emissivity characterisation
![\begin{figure}
\par\includegraphics[height=6.6cm,width=8cm,clip]{12911fB1a.eps}\...
...aphics[height=6.6cm,width=6.1cm,clip]{12911fB1b.eps}
\vspace*{-2mm}
\end{figure}](/articles/aa/full_html/2010/12/aa12911-09/Timg95.png)
|
Figure B.1:
( Left) Measured dependence of the reflection loss (1-R) of a sample of Planck reflector material as a function of frequency, when the sample is at room temperature (296 K, upper curve), and at |
| Open with DEXTER | |
The emissivity of the reflectors contributes directly to the background
heat load on the detectors. However, at mm and submm wavelengths,
the emissivity of a metallic surface depends quite strongly on
wavelength, temperature, and the characteristics of the metal (purity,
thickness). Thin film effects may also set in: the thickness of
the coating of the Planck
reflectors corresponds to
only a few skin depths. Measurements of this characteristic at low
temperatures and short wavelengths are rare as they are quite difficult
and their accuracy is poor for low emissivity levels. Nonetheless, some
early measurements of samples of the Herschel telescope confirm strong dependence with temperature (Fischer et al. 2005). Although the coating of the Herschel telescope is almost identical to that of Planck,
the underlying material is different (CFRP vs. sintered silicon
carbide), and therefore specific measurements were needed. Reflection
loss measurements were carried out using a resonator at the Applied
Physics Institute in Nizhny-Novgorod (Parshin & Klooster 2008). Results are reproduced in Fig. B.1.
A conservative hypothesis that reflection loss is equivalent to
the emissivity of the clean reflectors would lead us to estimate the
latter as roughly 0.05%, 0.1%, 0.15%, and 0.2% at a
temperature of 120 K and frequencies of 50 GHz, 140 GHz,
340 GHz, and 500 GHz respectively. The emissivity must be
lower at the in-flight temperatures of the reflectors (![]() 40 K), by as much as a factor of
40 K), by as much as a factor of ![]() 2
at the highest frequencies. However, at high frequencies dust will
be a large, possibly dominant, element of the effective emissivity of
the reflectors; an in-flight contamination level of 5000 ppm (see
Sect. 6.3) leads in a worst case (large, black particles) to an
emissivity of order 0.5%.
2
at the highest frequencies. However, at high frequencies dust will
be a large, possibly dominant, element of the effective emissivity of
the reflectors; an in-flight contamination level of 5000 ppm (see
Sect. 6.3) leads in a worst case (large, black particles) to an
emissivity of order 0.5%.
Some reflectors made from CFRP have been shown to have a different reflectivity (![]() 10%) along and across the direction of the carbon fibres; the Planck samples however have been verified to have no orientation dependence (Parshin & Klooster 2008).
10%) along and across the direction of the carbon fibres; the Planck samples however have been verified to have no orientation dependence (Parshin & Klooster 2008).
References
- Amiri Parian, J., Gruen, A., & Cozzani, A. 2006a, in 6th International Conference on Space Optics, ESTEC, Noordwijk, 27-30 June [Google Scholar]
- Amiri Parian, J., Gruen, A., & Cozzani, A. 2006b, in 3rd IAG Symposium on Geodesy for Geothechnical and Structural Engineering, Baden, Austria, 22-24 May [Google Scholar]
- Amiri Parian, J., Riti, J. B., & Cozzani, A. 2007a, in 6th International Symposium on Environmental Testing for Space Programmes, ESTEC, Noordwijk, 12-14 June [Google Scholar]
- Amiri Parian, J., Gruen, A., & Cozzani, A. 2007b, J. Appl. Geodesy, 1, 137 [CrossRef] [Google Scholar]
- Aumont, J., Conversi, L., Thum, C., et al. 2010, A&A, 514, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bersanelli, M., Bouchet, F. R., Efstathiou, G., et al. 1996, Report on the Phase A Study of COBRAS/SAMBA, ESA Report D/SCI(96)3 [Google Scholar]
- Bersanelli, M., Mandolesi, N., Butler, C. R., et al. 2010, A&A, 520, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burigana, C., Natoli, P., Vittorio, N., Mandolesi, N, & Bersanelli, M. 2001a, Experim. Astron., 12, 87 [Google Scholar]
- Burigana, C., Maino, D., Górski, K. M., et al. 2001b, A&A, 373, 345 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burigana, C., Sandri, M., Villa, F., et al. 2004, A&A, 428, 311 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burigana, C., Gruppuso, A., & Finelli, F. 2006, MNRAS, 371, 1570 [NASA ADS] [CrossRef] [Google Scholar]
- De Maagt, P., Martín Polegre, A., & Crone, G. 2000, ESA doc. PT-TN-05967, Iss. 2, Dec. 2000 [Google Scholar]
- Dubruel, D., Cornut, M., Fargant, G., et al. 2000, ESA Conf. Proc., SP-444 [Google Scholar]
- Fargant, G., Dubruel, D., Cornut, M., et al. 2000, SPIE Proc., 4013, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Fischer, J., Klaassen, T., Hovenier, N., et al. 2005, Appl. Opt., 43, 3765 [Google Scholar]
- Forma, G., Dubruel, D., Martí-Canales, J., et al. 2008, Proc. of AMTA Annual Symposium, Boston MA, Nov. 16-21, 99 [Google Scholar]
- Franco, G., Fosalba, P., & Tauber, J. 2003, A&A, 405, 349 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- GRASP9 manual 2008, TICRA, http://www.ticra.com/ [Google Scholar]
- Hamaker, J. P., & Leahy, J. P. 2004, A study of CMB differencing polarimetry with particular reference to Planck, ESA Report SCI-A/2003.312/JT [Google Scholar]
- Hill, R. S., Weiland, J. L., Odegard, N., et al. 2009, ApJS, 180, 246 [NASA ADS] [CrossRef] [Google Scholar]
- Huffenberger, K. M., Crill, B. P., Lange, A. E., Górski, K. M., & Lawrence, C. R. 2010, A&A, 510, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lamarre, J.-M., Puget, J.-L., Ade, P. A. R., et al. 2010, A&A, 520, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leahy, J. P., Bersanelli, M., D'Arcangelo, O., et al. 2010, A&A, 520, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Macías-Pérez, J.-F., Mayet, F., Aumont, J., & Désert, F.-X. 2010, ApJ, 711, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Maffei, B., Noviello, F., Murphy, J. A., et al. 2010, A&A, 520, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mandolesi, N., & Smoot, G. F. 1993, Proposal for COBRAS - the Cosmic Background Radiation Anisotropy Satellite, submitted to ESA in 2003 in answer to the M3 call for mission ideas [Google Scholar]
- Naselsky, P. D., Verkhodanov, O. V., Christensen, P. R., & Chiang, L.-Y. 2007, Astr. Bull., 62, 285 [CrossRef] [Google Scholar]
- Nielsen, P. H. 1999, TICRA Report S-801-04 [Google Scholar]
- Nielsen, P. H. 2008, TICRA Report S-1287-01 [Google Scholar]
- Nielsen, P. H. 2009, Ticra report S-1487-05 [Google Scholar]
- Nolta, M. R., Dunkley, J., Hill, R. S., et al. 2009, ApJS, 180, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Pagana, E. 1993, COBRAS Antenna Subsystem Prelimnary Study, Technical Note F.P.M. Space srl Nr. 009/V93/PGM [Google Scholar]
- Paquay, M., Martí-Canales, J., Rolo, L., et al. 2008, Proc. of AMTA annual symposium, Boston MA, Nov. 16-21, 32 [Google Scholar]
- Parshin, V., & van der Klooster, C. 2008, 30th ESA Antenna Workshop [Google Scholar]
- Puget, J.-L. 1993, Proposal for SAMBA - the Satellite for Measurements of Background Anisotropies, submitted to ESA in 2003 in answer to the M3 call for mission ideas [Google Scholar]
- Rocha, G., Pagano, L., Górski, K. M., et al. 2010, A&A, 513, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roose, S., Houbrechts, Y., Mazzoli, A., et al. 2005, in Proceedings of the 2nd SPIE symposium on Advanced Optical Manufacturing and Testing Technologies, Xian, Proc. SPIE, 6150 [Google Scholar]
- Roose, S., Houbrechts, Y., Mazzoli, A., et al. 2006, in Proceedings of the International Conference SPECKLE06: Speckles, from grains to flowers, Nimes, France, Proc. SPIE, 6341 [Google Scholar]
- Rosset, C., Tristram, M., Ponthieu, N., et al. 2010, A&A, 520, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sandri, M., Villa, F., Bersanelli, M., et al. 2010, A&A, 520, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stute, T. 2005, paper 105516 in 28th ESA Antenna Workshop [Google Scholar]
- Tauber, J. A., De Chambure, D., Crone, G., et al. 2005, in Proceedings of the XXVIIIth General Assembly of URSI, New Delhi, India [Google Scholar]
- Tauber, J. A., Mandolesi, N., Puget, J.-L., et al. 2010, A&A, 520, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Villa, F., Bersanelli, M., Burigana, C., et al. 2001, AIP Proceedings of the Workshop on Experimental Cosmology at millimeter wavelengths, Cervinia, Italy, 9-13 July [Google Scholar]
- Yurchenko, V. B., & Lamarre, J.-M. 2005, JOSA A, 22, 2838 [NASA ADS] [CrossRef] [Google Scholar]
Footnotes
- ... mission
![[*]](/icons/foot_motif.png)
- Planck (http://www.esa.int/Planck) is a project of the European Space Agency - ESA - with instruments provided by two scientific Consortia funded by ESA member states (in particular the lead countries: France and Italy) with contributions from NASA (USA), and telescope reflectors provided in a collaboration between ESA and a scientific Consortium led and funded by Denmark.
- ... baffle
![[*]](/icons/foot_motif.png)
- The baffle is used for straylight control, but also has an important thermal function, increasing substantially the capacity to radiate passively to cold space.
- ...
![[*]](/icons/foot_motif.png)
- The two highest-frequency channels are based on multi-moded horns and spiderweb bolometers, which are sensitive to total power (Maffei et al. 2010). The angular response of these detectors on the sky is difficult to model and is addressed in a separate paper (Murphy et al. 2010, in prep.); only some basic characteristics are listed here. We note that the function of these detectors - to measure the foregrounds - implies that they do not need to be known as accurately as the channels near the peak of the CMB spectrum. Furthermore, the high signal-to-noise ratios on planets at these high frequencies and angular resolution imply that their response will be measured very accurately in-flight.
- ... sky
![[*]](/icons/foot_motif.png)
- A rotation of the angle is introduced by the telescope (see e.g. Franco et al. 2003), which has been compensated in the focal plane design.
- ... predicts
![[*]](/icons/foot_motif.png)
- This is fortunate because it significantly reduces the ordered dimples that would produce unwanted grating lobes.
- ... one
![[*]](/icons/foot_motif.png)
- The accuracy is probably far higher than that specified when taking into account all the information available in the pattern. A deviation of 0.5 mm between prediction and measurement was found along the defocus direction, which could not be related to any known systematic effect, and represents the limit of the uncertainty. This deviation was also seen on the RFQM, and is as yet unexplained. As a consequence, it is not safe to claim a superior accuracy in the measurement than the quoted one.
- ... beams
![[*]](/icons/foot_motif.png)
- Defined as the patterns within square windows around peak of 2.5, 1.0, 0.8, and 0.35 degrees at 30, 70, 100, and 320 GHz respectively. The windows are sized to include at least the -40 dB contours.
- ... averaged
![[*]](/icons/foot_motif.png)
- To compute the wideband pattern, the optical response within the band should be multiplied by the spectral transmission of each detector and the spectral emission law of the source in the sky. The latter varies from place to place on the sky.
- ... contour
![[*]](/icons/foot_motif.png)
- This is not too surprising since the worst case was selected to maximise defocus (considered more likely) at the expense of power in smaller scale aberrations.
- ... (Moon)
![[*]](/icons/foot_motif.png)
- To be compared to typical peak directivity levels of 51 dBi (30 GHz), 61.6 dBi (100 GHz) and 69.3 dBi (353 GHz).
- ... (MIL-STD1246)
![[*]](/icons/foot_motif.png)
- Particles gathered from clean rooms used for Planck have been analysed and their dielectric indices used in this analysis.
- ... time
![[*]](/icons/foot_motif.png)
- Particles deposited on surfaces tend to aggregate into ``fiber''-like shapes and therefore their size distribution changes with exposure time. This process is modelled via a so-called ``Hamberg'' relation; the related uncertainty is one of the largest in the whole analysis.
- ... particles
![[*]](/icons/foot_motif.png)
- Other methods are available, but MPE has been found to be the most conservative choice in the sense of producing the greatest disturbance.
- ...
 5000 ppm
5000 ppm![[*]](/icons/foot_motif.png)
- A very conservative in-flight prediction is in the range 3000-6000 ppm for each reflector, of which the launch component is estimated between 1000 and 4000 ppm. However, the latter is very likely to be at the low end of its range.
- ... dust
![[*]](/icons/foot_motif.png)
- The estimated obscuration by dust on the RFQM reflectors is larger than that
expected for Planck in-flight, i.e.
 10 000 ppm, which should increase the BRDF by a factor of
10 000 ppm, which should increase the BRDF by a factor of  2.
2.
All Tables
Table 1: Design requirements of the Planck telescope reflectors.
Table 2: Predicted in-flight beam propertiesa.
Table 3: Predicted in-flight main beam polarisation propertiesa.
Table 4: Planck reflector characteristics at ambient temperature and 40 K.
Table 5: Inputs used for flight predictions.
Table 6: Typical uncertainties in beam characteristics obtained from the ground.
Table 7: Optical coupling of payload elements to detectors
Table A.1: Planck telescope parameters.
All Figures
![\begin{figure}
\par\includegraphics[width=7cm,clip]{12911f1a.eps}\hspace*{1cm}
\includegraphics[width=7cm,clip]{12911f1b.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa12911-09/Timg26.png)
|
Figure 1:
(Left) The fully assembled Planck satellite and (right)
its telescope prior to integration. Three conical ``V-grooves''
(visible on the left as three horizontal lines) isolate thermally and
radiatively the warm Service Module (lower octagonal black box) from
the cold payload module. The topmost (or 3 |
| Open with DEXTER | |
| In the text | |
| |
Figure 2: The layout of the focal plane of Planck. The LFI horns surround the HFI focal plane (circular structure in the centre of the figure). See also Fig. 4. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12911f3a.eps}\vspace*{3mm}
\includegraphics[width=8cm,clip]{12911f3b.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa12911-09/Timg31.png)
|
Figure 3:
(Top) Two side
views of the payload module, showing mainly the three V-grooves, which
radiatively insulate the payload from the warm part of the satellite,
and the large baffle used for straylight control and radiative cooling.
(Bottom) A cross-sectional sketch of the optimised Planck
telescope design, showing the reflectors support structure and the
focal plane. The principal (right-handed) coordinate systems are
indicated. The rotation of the spin axis is about the
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[bb=1 1 1940 1500, width=0.45\textwidth]{1291...
...=300 1 1660 1410, width=0.35\textwidth]{12911f4b.eps}
\vspace*{5mm}
\end{figure}](/articles/aa/full_html/2010/12/aa12911-09/Timg39.png)
|
Figure 4:
The footprint of the focal plane as seen by an observer at infinity. The top panel shows predicted contours of each main beam (averaged across the band); the horizontal and vertical axis are in
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12911f5a.eps}\vspace*{5mm}
\includegraphics[width=7.5cm,clip]{12911f5b.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa12911-09/Timg40.png)
|
Figure 5:
A typical far side lobe pattern for Planck
(in this case at 100 GHz), showing the main features of
interest. The horizontal axis corresponds to the angle around
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12911f6.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa12911-09/Timg41.png)
|
Figure 6:
The deformations of the SRFM on small scales at about 50 K as measured with |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=6.5cm,width=8.2cm,clip]{12911f7a.eps}...
...{5mm}
\includegraphics[height=6.5cm,width=7.5cm,clip]{12911f7b.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa12911-09/Timg58.png)
|
Figure 7: Most accurate (``best'') estimates (see Sect. 5.1) of the surface deformation of the Planck reflectors at operational temperature ( left: PR; right: SR) relative to the best-fit ellipsoids (Table 4). The horizontal and vertical axes are projected dimensions onto the reflector rim planes, and the colour scale corresponds to sagittal elevation. The SR image is of much higher spatial resolution than the PR, thanks to the availability of interferometric measurements; for the PR, only lower resolution photogrammetry was used. The right-hand side of the SR required patching of interpolated photogrammetry onto the trapezoidal-shaped feature (see Fig. 6) which was caused by vignetting of the interferometric data. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12911f8.eps}
\vspace{2mm}\end{figure}](/articles/aa/full_html/2010/12/aa12911-09/Timg59.png)
|
Figure 8: The rms WFE of the full set of horns for the three flight prediction scenarios (nominal or as-built, best and worst cases, defined in Sect. 7.1). The top panel shows the absolute WFE (in wavelengths), and the lower panel the WFE of the best and worst cases normalised by that of the nominal case. The frequency increases from right to left. The horn ID is labelled by instrument (HFI or LFI), frequency and increasing horn number (as in Fig. 4). The three cases were defined at 353 GHz (centre of the focal plane); at other frequencies, compensations mean that the ``worst-case'' WFE is not always larger than the ``best-case'' WFE. Nonetheless, the spread represents the uncertainty in the in-flight WFE at all frequencies. The best case is clearly very close to the nominal one in terms of the WFE, but the worst case is quite far, especially at the higher frequencies. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{12911f9a.eps}\par\includegraphics[width=8.5cm,clip]{12911f9b.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa12911-09/Timg62.png)
|
Figure 9: ( Top) The distribution of WFEs at 353 GHz for 3000 cases of thermo-elastic deformations drawn from the error distributions of all known cases leading to misalignment (see description in Sect. 5.2). ( Bottom) The distribution of defocus errors (i.e. the difference along the principal axis between the locations of the focal plane formed by the telescope and that of the feedhorn phase centre). The horizontal axis is defocus in millimetres. Note that the specific horn used in this analysis is displaced from its optimal location along the focal axis by about 0.35 mm; this is a result of the global optical design which necessarily required that some of the horn locations were not optimised. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.35cm,clip]{12911f10a.eps}
\includeg...
...2911f10b.eps}\par\includegraphics[width=7.55cm,clip]{12911f10c.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa12911-09/Timg66.png)
|
Figure 10:
Comparison of predicted (black lines) and measured (coloured lines) main beam copolar patterns at 30 GHz ( top), 70 GHz ( middle), and 320 GHz ( bottom).
The horizontal and vertical axis are in azimuth and elevation in the
RFQM coordinate system (degrees, arbitrary offsets). The double
coloured lines represent the
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{12911f11.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa12911-09/Timg67.png)
|
Figure 11:
Comparison of predicted (black lines) and measured (coloured lines)
main beam cross-polar patterns at 100 GHz. The horizontal and
vertical axis are in azimuth and elevation in the RFQM coordinate
system (degrees, offsets). The double coloured lines represent the
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{12911f12a.eps}\hspace*{3mm}
\includegraphics[width=8.3cm,clip]{12911f12b.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa12911-09/Timg68.png)
|
Figure 12:
The figures show cuts in the radiation pattern at 100 GHz ( left) and 320 GHz ( right) in the elevation direction through the beam peak; the horizontal axis is in degrees, the peak of the main beam is at 85 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{12911f13a.eps}\includegrap...
....eps}\includegraphics[width=8.2cm,clip]{12911f13d.eps}
\vspace{-1mm}\end{figure}](/articles/aa/full_html/2010/12/aa12911-09/Timg69.png)
|
Figure 13: The RFQM radiation patterns, as measured ( left) and predicted ( right). Clockwise from top left: 30, 70, 320 and 100 GHz. The colour scales are in dB from peak. The coordinate system is as in Fig. 5. The measurements suffer from some systematic effects very close to the main beam. Residual artifacts are also visible in the far side lobes, e.g. horizontal features at 320 GHz. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12911f14.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa12911-09/Timg70.png)
|
Figure 14:
The ground uncertainty in the shape of three specific main beams at
centre frequency, represented as the azimuthally integrated power
(in percent of total) of the difference between the best- and
worst-case patterns, as a function of the integration radius
from peak. The horns included are 70 GHz (horn 23),
100 GHz (horn 1), and 353 GHz (horn 6). The
vertical lines indicate the location of the -3 dB radius at
each frequency. The peak differences occur near the -10 dB
contours from peak. For comparison, the contour level at which
a S/N |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{12911f15a.eps}\vspace*{3mm}
\includegraphics[width=8cm,clip]{12911f15b.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa12911-09/Timg71.png)
|
Figure 15: The top panel shows the predicted in-flight pattern at 353 GHz (horn 6). The colour scale is in dB from peak. The bottom panel shows the difference between best- and worst-case patterns for the same horn. The colour scale shows differences between -5 and +5 dB. The largest uncertainties are associated with the SR spillover lobes. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12911f16.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa12911-09/Timg73.png)
|
Figure 16:
Three cuts through the main beam in the telescope symmetry plane ( |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12911f17.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa12911-09/Timg76.png)
|
Figure 17: The estimated effect of
dust on a beam pattern at 353 GHz for an obscuration level
of 5000 ppm. The coloured lines reflect different assumptions
about the aggregation of dust over time on the reflectors; the most
robust estimate corresponds to
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12911f18a.eps}\vspace*{2mm}
\includegraphics[width=7.5cm,clip]{12911f18b.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa12911-09/Timg77.png)
|
Figure 18: When viewed on the same
grid and at the same resolution, it becomes apparent that the
pattern measured on the RFQM at 100 GHz (above) does not have the
deep nulls seen in the most accurately predicted patterns (below).
It is possible that this filling-in of low-level power is due to
scattering by dust on the reflectors (see Sect. 8.1).
A similar effect is seen at 320 GHz (see Fig. 12) with a higher level of |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{12911f19.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa12911-09/Timg89.png)
|
Figure 19: Reconstruction of HFI detector positions from Saturn. The upper left shows the reconstructed positions for each detector (the anomalous recovery of 545 GHz detectors is an artifact partly of the simulation and partly of the top-hat shaped beams), and the other panels show histograms in the in- and cross-scan directions and the total offset. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=13.5cm,clip]{12911fA1.eps}
\vspace*{5mm}
\end{figure}](/articles/aa/full_html/2010/12/aa12911-09/Timg90.png)
|
Figure A.1:
Dimensioning and relative positioning of the two reflectors with respect to the telescope coordinate system (see Fig. 3).
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=6.6cm,width=8cm,clip]{12911fB1a.eps}\...
...aphics[height=6.6cm,width=6.1cm,clip]{12911fB1b.eps}
\vspace*{-2mm}
\end{figure}](/articles/aa/full_html/2010/12/aa12911-09/Timg95.png)
|
Figure B.1:
( Left) Measured dependence of the reflection loss (1-R) of a sample of Planck reflector material as a function of frequency, when the sample is at room temperature (296 K, upper curve), and at |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


