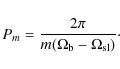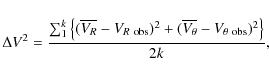EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 519 (September 2010) A&A, 519 (2010) A70 Full HTML
Free Access
Issue
A&A
Volume 519, September 2010
Article Number A70
Number of page(s) 13
Section Galactic structure, stellar clusters, and populations
DOI https://doi.org/10.1051/0004-6361/201014646
Published online 15 September 2010
A&A 519, A70 (2010)

N-body simulations in reconstruction of the kinematics of young stars in the Galaxy

P. Rautiainen1 - A. M. Mel'nik2

1 - Department of Physics/Astronomy Division, University of Oulu, PO Box 3000, 90014 Oulun yliopisto, Finland
2 - Sternberg Astronomical Institute, 13, Universitetskii pr., Moscow 119992, Russia

Received 31 March 2010 / Accepted 21 May 2010

Abstract
Aims. We try to determine the Galactic structure by comparing the observed and modeled velocities of OB-associations in the 3 kpc solar neighborhood.
Methods. We made N-body simulations with a rotating stellar bar. The galactic disk in our model includes gas and stellar subsystems. The velocities of gas particles averaged over large time intervals (${\sim}8$ bar rotation periods) are compared with the observed velocities of the OB-associations.
Results. Our models reproduce the directions of the radial and azimuthal components of the observed residual velocities in the Perseus and Sagittarius regions and in the Local system. The mean difference between the model and observed velocities is $\Delta V=3.3$ km s-1. The optimal value of the solar position angle  $\theta _{\rm b}$ providing the best agreement between the model and observed velocities is $\theta_{\rm b}=45$ $\pm$ $5^\circ$, in good accordance with several recent estimates. The self-gravitating stellar subsystem forms a bar, an outer ring of subclass R1, and slower spiral modes. Their combined gravitational perturbation leads to time-dependent morphology in the gas subsystem, which forms outer rings with elements of the R1- and R2-morphology. The success of N-body simulations in the Local System is likely due to the gravity of the stellar R1-ring, which is omitted in models with analytical bars.

Key words: Galaxy: structure - Galaxy: kinematics and dynamics

1 Introduction

The consensus since the 1990s has been that the Milky Way is a barred galaxy (see, e.g. Blitz et al. 1993; Blitz & Spergel 1991). The estimate for the size of the large-scale bar has grown from initial $R_{\rm bar} \approx 2{-}3$ kpc to current estimates $R_{\rm bar}=3{-}5$ kpc (Cabrera-Lavers et al. 2008; Habing et al. 2006; Cabrera-Lavers et al. 2007). The position angle of the bar is thought to be in the range $15^\circ{-}45^\circ$ (Englmaier & Gerhard 2006; Blitz et al. 1993; Weiner & Sellwood 1999; Kuijken 1996; Benjamin et al. 2005; Cabrera-Lavers et al. 2007; Minchev et al. 2010). The differences in the position angle estimates may indicate that the innermost structure is actually a triaxial bulge (Cabrera-Lavers et al. 2008). On the other hand, this ambiguity may be partly caused by our unfavorable viewing angle near the disk plane, which also hinders study of other aspects of Galactic morphology.

The suggested configurations for the spiral morphology of the Galaxy include models or sketches containing from two to six spiral arms (see e.g. Vallée 2005,2008, and references therein). A case has also been suggested where a two-armed structure dominates in the old stellar population, whereas the gas and young stellar population exhibits a four-armed structure (Churchwell et al. 2009; Lépine et al. 2001). In addition to spiral arms, there may be an inner ring or pseudoring surrounding the bar, which manifests itself as the so-called 3-kpc arm(s) (Churchwell et al. 2009; Dame & Thaddeus 2008). Also, speculations about a nuclear ring with a major axis of about 1.5 kpc have been made (Rodriguez-Fernandez & Combes 2008). Different kinds of rings - nuclear rings, inner rings and outer rings - are often seen in the disks of spiral galaxies, especially if there is also a large-scale bar (Buta & Combes 1996). Thus, the presence of an outer ring in the Galaxy may also be considered plausible (Kalnajs 1991).

Since the outer rings have an elliptic form, the broken outer rings (pseudorings) resemble two tightly wound spiral arms. Nevertheless their connection with the density-wave spiral arms is not very obvious because their formation does not need the spiral-shaped perturbation in the stellar disk. The main ingredient for their formation is a rotating bar. Both test particle simulations (Bagley et al. 2009; Schwarz 1981; Byrd et al. 1994) with an analytical bar and N-body simulations (Rautiainen & Salo 2000,1999), where the bar forms in the disk by instability, show that the outer rings and pseudorings are typically located in the region of the outer Lindblad resonance (OLR). Two main classes of the outer rings and pseudorings have been identified: the R1-rings and R'1-pseudorings elongated perpendicular to the bar and the R2-rings and R'2-pseudorings elongated parallel to the bar. In addition, there is a combined morphological type R1R2' that shows elements of both classes (Buta 1995,1986; Buta & Crocker 1991; Buta & Combes 1996; Buta et al. 2007).

Schwarz (1981) connected two main types of the outer rings with two main families of periodic orbits existing near the OLR of the bar (Contopoulos & Grosbol 1989; Contopoulos & Papayannopoulos 1980). The stability of orbits enables gas clouds to follow them for a long time period. The R1-rings are supported by x1(2)-orbits (using the nomenclature of Contopoulos & Grosbol 1989) lying inside the OLR and elongated perpendicular to the bar, while the R2-rings are supported by x1(1)-orbits situated a bit outside the OLR and elongated along the bar. There is also another conception of the ring formation. Romero-Gómez et al. (2007) show that Lyapunov periodic orbits around L1 and L2 equilibrium points can lead to the formation of the spiral arms and the outer rings. They associate the spiral arms emanating from the bar's tips with the unstable manifolds of Lyapunov orbits. This approach can be useful for explaining of the motion of gas particles as well (Athanassoula et al. 2009).

Besides the bar the galactic disks often contain spiral arms, which modify the shape of the gravitational perturbation. In the simplest case, the pattern speeds of the bar and spiral arms are the same. In many studies this assumption has been used for constructing the gravitational potential from near-IR observations (which represent the old stellar population better than the visual wavelengths). Several galaxies with outer rings have been modeled by this method, and findings are in good accordance with studies made by using analytical bars: the outer rings tend to be located near the OLR (Salo et al. 1999), although in some cases they can be completely confined within the outer 4/1-resonance, (Treuthardt et al. 2008).

A real galactic disk provides further complications, which can be studied by N-body models, where the bars and spiral arms are made of self-gravitating particles. In particular, there can often be one or more modes rotating more slowly than the bar (Masset & Tagger 1997; Sellwood & Sparke 1988; Rautiainen & Salo 1999). Even if there is an apparent connection between the ends of the bar and the spiral arms, it is no guarantee that the pattern speeds are equal - the break between the components may be seen only for a short time before the connection reappears (see Fig. 2 in Sellwood & Sparke 1988). Sometimes the bar mode can contain a considerable spiral part that forms the observed spiral, together with the slower modes (Rautiainen & Salo 1999). The multiple modes can also introduce cyclic or semi-cyclic variations in the outer spiral morphology: outer rings of different types can appear and disappear temporarily (Rautiainen & Salo 2000).

In Mel'nik & Rautiainen (2009, hereafter Paper I), we considered models with analytical bars. In this case the motion of gas particles is determined only by the bar. We found that the resonance between the epicyclic motion and the orbital motion creates systematical noncircular motions that depend on the position angle of a point with respect to the bar elongation and on the class of the outer ring. The resonance kinematics typical of the outer ring of subclass R1R2' reproduces the observed velocities in the Perseus and Sagittarius regions well.

In Paper I we also suggested that the two-component outer ring could be misinterpreted as a four-armed spiral. In some galaxies with the combined R1R2'-morphology, the R1-component can also be seen in the near infrared, but the R2-component is usually prominent only in blue (Byrd et al. 1994). This could explain the ambiguity of the number of spiral arms in the Galaxy. N-body simulations confirm that the R'1-rings can be forming in the self-gravitating stellar subsystem, while the R2'-rings usually exist only in the gas component (Rautiainen & Salo 2000).

In the present paper we study the effect of multiple modes and their influence on the kinematics and distribution of gas particles. We construct N-body models to study the influence of self-gravity in the stellar component on the kinematics of gas particles. We compare the model velocities of gas particles with the observed velocities of OB-associations in the neighborhood 3 kpc from the Sun.

This paper has the following structure. Observational data are considered in Sect. 2. Section 3 is devoted to models and describes the essential model parameters, the evolution of the stellar and gas components: formation of the bar and the interplay between the bar and slower spiral modes. In Sect. 3 we also analyze the general features of the gas morphology. Section 4 is devoted to the comparison between the observed and modeled kinematics. Both momentary and average velocities of gas particles are considered. The influence of the bar position angle  $\theta _{\rm b}$ on the model velocities is also investigated in Sect. 4, as are the evolutionary aspects of kinematics. Section 5 consists of conclusions and discussion.

2 Observational data

\begin{figure} \par\includegraphics[width=17.5cm,clip]{14646fg1.eps} \vspace*{5mm} \end{figure} Figure 1:

a) The residual velocities of OB-associations projected on to the galactic plane. It also shows the grouping of OB-associations into regions of intense star formation. b) The mean VR- and $V_\theta $-velocities of OB-associations in the stellar-gas complexes. The X-axis is directed away from the galactic center, and the Y-axis is in the direction of the galactic rotation. The Sun is at the origin.

Open with DEXTER

We have compared the mean residual velocities of OB-associations in the regions of intense star formation with those of gas particles in our models. These regions practically coincide with the stellar-gas complexes identified by Efremov & Sitnik (1988). The residual velocities characterize the non-circular motions in the galactic disks. They are calculated as differences between the observed heliocentric velocities (corrected for the motion to the apex) and the velocities due to the circular rotation law. We used the list of OB-associations by Blaha & Humphreys (1989), the line-of-sight velocities (Barbier-Brossat & Figon 2000), and proper motions (Hipparcos 1997; van Leeuwen 2007) to calculate their median velocities along the galactic radius-vector, VR, and in the azimuthal direction, $V_\theta $. Figure 1 shows the residual velocities of OB-associations in the regions of intense star formation. It also indicates the grouping of OB-associations into stellar-gas complexes. For each complex we calculated the mean residual velocities of OB-associations, which are listed in Table 1. Positive radial residual velocities VR are directed away from the Galactic center, and the positive azimuthal residual velocities $V_\theta $ are in the sense of Galactic rotation. Table 1 also contains the rms errors of the mean velocities, the mean Galactocentric distances R of OB-associations in the complexes, the corresponding intervals of galactic longitudes l and heliocentric distances r, and names of OB-associations the region includes (see also Mel'nik & Dambis 2009).

The Galactic rotation curve derived from an analysis of the kinematics of OB-associations is nearly flat in the 3-kpc solar neighborhood and corresponds to the linear velocity at the solar distance of $\Theta_0=220$ km s-1 (Mel'nik et al. 2001; Mel'nik & Dambis 2009). The nearly flat form of the Galactic rotation curve was found in many other studies (Bobylev et al. 2007; Pont 1994; Dambis et al. 1995; Clemems 1985; Burton & Gordon 1978; Russeil 2003; Brand & Blitz 1993).

We adopted the Galactocentric distance of the Sun to be R0=7.5 kpc (Rastorguev et al. 1994; Dambis et al. 1995; Glushkova et al. 1998, and other papers), which is consistent with the so-called short distance scale for classical Cepheids (Berdnikov et al. 2000).

3 Models

3.1 The model parameters

We made several N-body models, which satisfy ``broad observational constraints'': the rotation curve is essentially flat and the size of the bar is acceptable. From these models we have chosen our best-fitting case, which we describe here in more detail.

The rotation curve of our best-fitting model is illustrated in Fig. 2. In the beginning, the rotation curve is slightly falling in the solar neighborhood, but the mass rearrangement in the disk during the bar formation makes it rise slightly. We scaled the simulation units to correspond to our preferred values of the solar distance from the Galactic center and the local circular velocity. This also gives the scales for masses and time units. However, in the following discussion we will use simulation time units, one corresponding to approximately 100 million years, and the full length of the simulation is 6 Gyr.

\begin{figure} \par\includegraphics[width=14.5cm,clip]{14646fg2.eps} \end{figure} Figure 2:

The rotation curve (solid line) of the N-body model at T=0 ( left) and at T=55 ( right). The contributions from the bulge (dash-dotted line), disk (dashed line) and halo (dotted line) are also indicated.

Open with DEXTER

The bulge and halo components are analytical, whereas the stellar disk is self-gravitating. The bulge is represented by a Plummer sphere, mass $M_{\rm bulge}=1.17$ $\times$ $10^{10}~M_\odot$, and scale length $R_{\rm bulge}=0.61$ kpc. The dark halo was included as a component giving a halo rotation curve of form

\begin{displaymath}% V(R)={V_{\rm max}R \over \sqrt{R^2+R_{\rm c}^2}}, \end{displaymath} (1)

where $V_{\rm max} = 210~{\rm km~s}^{-1}$ is the asymptotic maximum on the halo contribution to the rotation curve and $R_{\rm c} = 7.6~{\rm kpc}$ the core radius.

The N-body models are two-dimensional, and the gravitational potential due to self-gravitating particles is calculated by using a logarithmic polar grid (108 radial and 144 azimuthal cells). The N-body code we used has been written by Salo (for more details on the code, see Salo & Laurikainen 2000; Salo 1991). The value of the gravitation softening is about 0.2 kpc on the adopted length scale. The mass of the disk $M_{\rm disk}=3.51$ $\times$  $10^{10}~M_\odot$.

The disk is composed of 8 million gravitating stellar particles, whose initial distribution is an exponential disk reaching about 10 scale lengths. The disk and halo have nearly equal contribution to the rotation curve at the solar distance. The initial scale length of the disk was about 2 kpc, but after the bar formation, it forms a twin profile disk: the inner profile becomes steeper and the outer profile shallower, and the exponential scale length corresponds to about 3 kpc outside the bar region. The initial value of the Toomre-parameter $Q_{\rm T}$ was 1.75.

The gas disk was modeled by inelastically colliding test particles as was done in Paper I. The initial velocity dispersion of the gas disk was low, about $2~{\rm km~ s}^{-1}$, but it reached typical values in the range $5{-}15~{\rm km~s}^{-1}$ during the simulation. If collisions are omitted, the velocity dispersion of the test particles rises much higher into the range $25{-}50~{\rm km~s}^{-1}$. The model used in the kinematical analysis contains 40 000 gas particles initially distributed as a uniform disk with an outer radius of 9.2 kpc.

3.2 Evolution of the stellar component

The inner regions quickly develop a small spiral (at $T \sim 2.5$), which then evolves to a clear bar ($T \sim 5$). Its original pattern speed  $\Omega_{\rm b}$ is about $80~{\rm km~s}^{-1}~{\rm kpc}^{-1}$, meaning that when it forms it does not have an Inner Lindblad Resonance (ILR). In its early phase the bar slows down quite quickly ( $\Omega_{\rm b} \approx 60~{\rm km~s}^{-1}~{\rm kpc}^{-1}$ at T=10), but the deceleration rate soon settles down: $\Omega_{\rm b} \approx 54~{\rm km~s}^{-1}~{\rm kpc}^{-1} $ at T=20 and $\Omega_{\rm b} \approx 47~{\rm km~s}^{-1}~{\rm kpc}^{-1}$ at T=55. In this model the bar's slowing down is accompanied by its growth, and the bar can always be considered dynamically fast (see e.g. Debattista & Sellwood 2000). Using the same method to determine the bar length as Rautiainen et al. (2008) (a modification of one used by Erwin 2005), we get $R_{\rm bar}= 4.0$ $\pm$ 0.6 kpc at T=55 and $R_{\rm CR}/R_{\rm bar} = 1.2$ $\pm$ 0.2. There is no secondary bar in this model.

\begin{figure} \par\includegraphics[width=12.5cm,clip]{14646fg3.eps} \end{figure} Figure 3:

The amplitude spectra of the relative density perturbations in the model disk. The frames show the amplitude spectra of the stellar or gas component at various times (indicated on the frame titles). The contour levels are 0.025, 0.05, 0.1, 0.2, 0.4, and 0.8, calculated with respect to the azimuthal average surface density at each radius. The continuous lines show the frequencies $\Omega $ and $\Omega \pm \kappa /m$, and the dashed curves indicate the frequencies  $\Omega \pm \kappa /4$ in the m=2 amplitude spectrum.

Open with DEXTER

\begin{figure} \par\includegraphics[width=13cm,clip]{14646fg4.eps} \vspace*{2mm} \end{figure} Figure 4:

The reconstructed modes in the stellar component (see text) for T=50-60 time interval. The enhanced density compared to the azimuthally averaged profile at each radius is shown. The shades of gray (darker corresponds to higher surface density) have been chosen to emphasize the features. The circles in the bar mode indicate ILR (1.4 kpc), CR (4.6 kpc), and OLR (8.1 kpc), whereas the inner 4/1 (4.6 kpc) and CR (7.1 kpc) are shown for the mode S1.

Open with DEXTER

The amplitude spectra of the relative density perturbations (see e.g. Masset & Tagger 1997; Rautiainen & Salo 1999) (Fig. 3) show that the bar mode is not the only one in the disk, but there are also slower modes. The strongest of these modes, hereafter the S1 mode, has an overlap of resonance radii with the bar: the corotation radius of the bar is approximately the same as the inner 4/1-resonance radius of the slower mode (at T=55 the  $R_{\rm CR}$ of the bar and the inner 4/1 resonance radius of the S1 mode are both about 4.6 kpc). This resonance overlap does not seem to be a coincidence: when the amplitude spectra from different time intervals are compared, one can see that both the bar and the S1 modes slow down so that the resonance overlap remains (see Fig. 3). Furthermore, this resonance overlap was the most common case in the simulations of Rautiainen & Salo (1999). Also, the S1 mode has a strong m=1signal and a maximum near its corotation at 7.1 kpc. The bar mode is also seen as a strong signal in the m=4 spectrum, but only inside CR - the spiral part seems to be almost pure m=2 mode. Altogether, the signals with m>2 tend to be much weaker than features seen in m=1 and m=2 amplitude spectra.

We have also tried to reconstruct the shapes of the modes seen in the amplitude spectra. This was done by averaging the surface density in coordinate frames rotating with the same angular velocities as the modes. No assumptions were made about the shapes of the modes. On the other hand, one should take these reconstructions with some caution, because the evolution of the two modes, the effect of slower (but weaker) modes, and short-lived waves may affect them. The results for the bar and the S1 mode at the time interval T=50-60 are shown in Fig. 4. The mode $\Omega_{\rm p}=47~{\rm km~s}^{-1}~{\rm kpc}^{-1}$ clearly shows the bar and symmetrical spiral structure that forms an R1 outer ring or pseudoring. By the T=50-60 interval, the density amplitude of the bar mode is about 15-20 per cent in the outer ring region, where the maxima and minima have roughly the same strength. On the other hand, by T=50-60, the mode $\Omega_{\rm p}=31~{\rm km~s}^{-1}~{\rm kpc}^{-1}$ is clearly lopsided, which is not surprising considering the signal seen in the m=1 amplitude spectrum. There is a minimum with an amplitude of about 30% and a maximum of about 15% at $R \approx 7$ kpc, which corresponds to the CR of the S1 mode. Earlier, at  $T \approx 20$, the S1 mode does not have the m=1 characteristic but exhibits a multiple-armed structure beyond its CR, accompanied by a clear signal in the m=3 amplitude spectrum.

3.3 The morphological changes in the gas component

The amplitude spectra for the gas component at the interval T=50-60 are also shown in Fig. 3. Due to fewer particles, they include more noise, but otherwise they are quite similar. In addition to the bar mode, the S1 mode is also seen, but now it is more conspicuous in the m=1 spectrum.

\begin{figure} \par\includegraphics[width=16cm,clip]{14646fg5.eps} \vspace*{4mm} \end{figure} Figure 5:

The gas morphology at selected times. The bar is vertical in all frames, whose width is 20 kpc.

Open with DEXTER

The result of having several modes is the quite complicated evolution of the model (see Fig. 5): at different times, the morphology of the outer gaseous disk can be described as R1R2', R2', R1' or just as open spiral arms, which can sometimes be followed over 400 degrees. There is no evolutionary trend between the morphological stages, since they all appear several times during the model time span. The shape of the inner ring also changes by being sometimes more elongated or even consisting of tightly wound pair of spiral arms. On the broader sense, the overall Hubble stage of the model stays the same for several Gyr.

Although the slow modes in the stellar component can be clearly seen outside the bar radius (about 4 kpc), they become pronounced in the gas from $R \approx 6$ kpc. To study their effect on the gas morphology, we selected gas particles located at the annulus 7<R<10 kpc and calculated their number within every 5$^\circ$-sector along $\theta $. Such density profiles were built for 301 moments from the interval T = 30-60 (T $\approx$ 3-6 Gyr) with a step $\Delta T=0.1$ (${\sim}10$ Myr). Earlier stages were not considered, because then the pattern speed of the bar was changing so fast that it complicated the analysis. At every moment the distribution of gas density along $\theta $ was approximated by one-fold (m=1), two-fold (m=2), and four-fold (m=4) sinusoidal wave:

\begin{displaymath}% \sigma=\sigma_0+A_m\cos(m \theta +\phi_m), \end{displaymath} (2)

where $\sigma$ is the gas density in a segment, $\sigma_0$ is the average density in the annulus, $\phi_m$ and Am are the phase and amplitude of the corresponding sinusoidal approximation, respectively.

\begin{figure} \par\includegraphics[width=17cm,clip]{14646fg6.eps} \end{figure} Figure 6:

The perturbation in the density of gas particles, $\sigma '=\sigma -\sigma _0$, located at the annulus 7<R<10 kpc along azimuthal angle $\theta $ built for different moments. It also shows its approximation by two-fold ( left panel) and one-fold ( right panel) sinusoids.

Open with DEXTER

\begin{figure} \par\includegraphics[width=17cm,clip]{14646fg7.eps} \end{figure} Figure 7:

Variations in the phase $\phi $ (black curve) and amplitude A (gray curve) of the sinusoids that approximate the distribution of gas particles located at the distances 7<R<10 kpc along $\theta $. Subscripts 1 and 2 are related to the one- and two-fold sinusoids, respectively.

Open with DEXTER

Figure 6 demonstrates the motion of maxima in the distribution of gas particles along $\theta $. We made the density profiles in the reference frame co-rotating with the bar, whose major axis is always oriented in the direction $\theta=0^\circ$. Azimuthal angle $\theta $ is increasing in the sense of the galactic rotation, so the supposed position of the Sun is about $\theta=315^\circ$. To illustrate the motion of density crests, we selected two intervals T = 35.5-37.5 and T = 52.5-54.5 with a high amplitude of density perturbation. These density profiles indicate the motion of density maxima in the opposite direction to that of galactic rotation (i.e. they actually rotate more slowly than the bar), which means an increase in the phase $\phi_m$ of the sinusoidal wave (Eq. (2)).

\begin{figure} \par\includegraphics[width=16.5cm,clip]{14646fg8.eps} \vspace*{2.5mm} \end{figure} Figure 8:

Variations in the mean velocities of gas particles located within the boundaries of the stellar-gas complexes. The left panel is related to the radial component VR and the right one to the azimuthal one $V_\theta $.

Open with DEXTER

Figure 7 exhibits the variations in the phase $\phi_m$ and amplitude Am of the sinusoidal wave at the time intervals T = 30-40, 40-50, and 50-60. The subscripts 1 and 2 are related to the one- and two-fold sinusoids. Rotation of the density maxima causes the sharp changes in the phase when it achieves the value of $\phi=360^\circ$, and at the new turn its value must fall to zero. These changes enable us to accurately calculate the mean values of the periods for the propagation of the sinusoidal waves, which appear to be P1=3.3 $\pm$ 0.4 and P2=1.5 $\pm$ 0.4. Remember that we study the density oscillations in the reference frame co-rotating with the bar, so the period P of beating oscillations between the bar and slow modes is determined by the relation:

\begin{displaymath}% P_m=\frac{2\pi}{m(\Omega_{\rm b}-\Omega_{\rm sl})}\cdot \end{displaymath} (3)

The periods, P1 and P2, appear to correspond to slow modes rotating with the pattern speeds $\Omega=28$ $\pm$ 2 km s-1 kpc-1 and $\Omega=26$ $\pm$ 6 km s-1 kpc-1, respectively. It is more convenient to use simulation units here. The transformation coefficient between them and (km s-1 kpc-1) is k=9.77, and the value of  $\Omega_{\rm b}$ is $\Omega_{\rm b}=4.8$ s.u. The m=4 wave manifested itself in two density maxima separated by the angle $\Delta \theta\approx90^\circ$ (Fig. 6, right panel). The analysis of phase motion of four-fold sinusoid reveals the period P4=0.81 $\pm$ 0.15, which corresponds to slow mode rotating with the speed $\Omega_{\rm sl}=28$ $\pm$ 4 km s-1 kpc-1 (Eq. (3)). Probably, it is mode $\Omega=28$ $\pm$ 4 km s-1 kpc-1 that causes the strong variations in gas density with the periods P1=3.3, P2=1.5, and P4=0.8 when it works as m=1, m=2, and m=4 density perturbations, respectively. This mode is well-defined in the gas and star power spectra made for the interval T = 50-60 (Fig. 3).

Let us have a look at the amplitude variations (Fig. 7). The highest value of A2 equal A2=200 (particles per 5$^\circ$-sector) is observed at the time T=36.0 (left panel). On the other hand, A1 achieves its highest value of A1=220 at the time T=56.5 (right panel). Amplitude A4 reaches its maximum value of A4=180 at the time interval T=53-55. Thus, the highest values of the amplitudes A1, A2, and A4 are nearly the same.

Figure 6 (left panel) indicates the growth of the amplitude of m=2 perturbation under a specific orientation of the density clumps. The amplitude of the sinusoidal wave is at its maximum at the moments T=36.0 and 37.5 when the density clumps are located near the bar's minor axis, $\theta=90^\circ$ and 270$^\circ$. This growth is also seen in Fig. 7 (left panel) for the interval T = 30-40: the amplitude A2 is at its maximum at the moments when $\phi_2\approx 180^\circ$. This phase corresponds to the location of maxima of m=2 sinusoid at $\theta=90^\circ$ and $\theta=270^\circ$ (Eq. (2)).

Our analysis revealed slight variations in the speed of the strongest slow mode, and they depend on its orientation with respect to the bar: Fig. 7 (left panel) shows that the tilt of the phase curve, $\phi_2(t)$, is variable. We can see that the slow mode rotates a bit faster when $\phi_2\approx 180^\circ$ (density clumps are near the bar's minor axis) and more slowly when $\phi_2=0$ or 360$^\circ$ (the clumps are near the bar's major axis). Probably, the variations in the speed of the slow mode are connected with the change in the form of the density crests due to tidal interaction between the bar mode (bar+R1-ring) and the slow mode.

\begin{figure} \par\includegraphics[width=15cm,clip]{14646fg9.eps} \vspace*{5mm} \end{figure} Figure 9:

Distribution of the negative and positive average residual velocities calculated in squares. The squares with positive velocities are shown in black, while those with negative ones are given in gray. Only squares that satisfy the condition $n>\overline {m}/2$ are depicted. The left panel represents the radial velocities, while the right one shows the azimuthal ones. It also demonstrates the boundaries of the stellar-gas complexes. The position angle of the Sun is supposed to be $\theta _{\rm b}=45^\circ $. The bar is oriented along the Y-axis, the galaxy rotates clockwise, and a division on the X- and Y-axis corresponds to 1 kpc.

Open with DEXTER

4 Kinematics of gas particles. Comparison with observations

4.1 Momentary and average velocities

We start our kinematical study with the interval T = 50-60 (5-6 Gyr in physical time). At this period the bar rotates with a nearly constant pattern speed of $\Omega_{\rm b}=47$ km s-1 kpc-1 which simplifies the analysis. The interval T = 50-60 also provides the best agreement between the model and observed velocities.

We determined the positions and velocities of gas particles at 101 moments separated by the step $\Delta T=0.1$. For each moment we selected gas particles located within the boundaries of the stellar gas complexes and calculated their mean velocities and velocity dispersions. To determine the positions of the complexes, we need to choose the position angle of the Sun with respect to the bar elongation,  $\theta _{\rm b}$. In this section we adopted the value of $\theta _{\rm b}=45^\circ $, which gives the best fit between the model and observed velocities.

Figure 8 shows the variations in the mean residual velocities, VR and $V_\theta $, calculated for five complexes at different moments. The residual velocities were computed as differences between the model velocities and the velocities due to the rotation curve. It is clearly seen that the momentary velocities oscillate near the average values within the limits of ${\sim}\pm20$ km s-1. Two processes are probably responsible for these oscillations. The first is the slow modes that cause a quasi-periodic low in the velocity variations. The second process is likely connected with the short-lived perturbations, e.g. from transient spiral waves in the stellar component. The averaging of velocities over long time interval reduces the influence of slow modes and occasional perturbations.

Table 2 represents the average values of the momentary residual velocities, $\overline {V_R}$ and  $\overline {V_\theta }$, calculated over 101 moments. It also gives the average values of velocity dispersions,  $\overline{\sigma_R}$ and  $\overline{\sigma_\theta}$, and the average number of particles  $\overline{n}$ in the complexes. Since the bar has two tips, we calculated velocities for two opposite positional angles, $\theta _{\rm b}=45^\circ $ and $\theta_{\rm b}=225^\circ$, and used their mean values. The averaged residual velocities are determined with the errors of 0.4-1.4 km s-1. The relatively low level of the errors is due to the large number of moments considered (N=101).

When comparing Tables 2 and 1, one can see that our model reproduces the directions of the radial and azimuthal components of the residual velocities in the Perseus and Sagittarius regions and in the Local System. We succeed in the Sagittarius region where our model reproduces the observed velocities with the accuracy 1.4 km s-1. Unfortunately, in the Perseus region the model residual velocity  $\vert\overline{V_R}\vert$ is too high, and the difference between the model and observed velocities achieves 5.8 km s-1 there. Our model can also reproduce the positive $\overline {V_R}$ velocity in the Local System, which deviates only 1.5 km s-1 from the observed one.

We now consider the mean difference between the model and observed velocities $\Delta V$ calculated for the radial and azimuthal components:

\begin{displaymath}% \Delta V^2=\frac{\sum^k_1 \left\{ (\overline{V_R}-V_{R~{\rm... ...+ (\overline{V_\theta}-V_{\theta~{\rm obs}})^2 \right\} }{2k}, \end{displaymath} (4)

where k is a number of complexes. The value of $\Delta V$ computed for three complexes (the Sagittarius and Perseus regions and the Local System) equals $\Delta V=3.3$ km s-1. Another situation is observed in the Carina and Cygnus regions where we cannot even reproduce the direction of the observed residual velocities. The mean value of the velocity deviations achieves $\Delta V=13.3$ km s-1 there.

To demonstrate the distribution of the average velocities on the galactic plane, we divided the area (-10<x<+10, -10<y<+10 kpc) into small squares of a size 0.250 $\times$ 0.250 kpc. For each square we calculated the average values of the residual velocities of gas particles. Then we averaged residual velocities over 101 moments for the interval T = 50-60. The average residual velocities in squares are shown in Fig. 9. We depicted only squares that contain high enough number of particles, $n>\overline {m}/2$, where n is the number of particles accumulated in a square over 101 moments but  $\overline{m}$ is their number averaged over all squares, $\overline{m}=463$.

In Paper I we have built similar figures for models with analytical bars. Two different moments were considered: when the broken rings (pseudorings) were observed and when they transformed into pure rings. The pseudorings and pure rings created different kinematical pictures. We connected the main kinematical features of the pseudorings with the gas outflow and those of the pure rings with the resonance. The distribution of the negative and positive velocities obtained for N-body simulations (Fig. 9) strongly resembles that of the pseudorings in models with analytical bars, giving support to the ``averaging process'' adopted here. This similarity suggests there is gas outflow in the present model (see also Sect. 4.4).

4.2 Velocities in the complexes under different values of the solar position angle ${\theta _b}$

We studied the dependence of the average residual velocities  $\overline {V_R}$ and  $\overline {V_\theta }$ on the solar position angle  $\theta _{\rm b}$. Figures 10a,b shows 5 curves that demonstrate the velocity changes in 5 complexes. The sharpest changes in the radial velocity  $\overline {V_R}$are observed in the Local System and in the Cygnus region, and the radial velocities in the other complexes depend only weakly on the choice of  $\theta _{\rm b}$. As for the azimuthal component, the strongest changes can be seen in the Sagittarius, Carina, and Perseus regions, but the velocity changes are modest in other complexes. Practically speaking, the optimal value of  $\theta _{\rm b}$provided the best agreement between the model and observed velocities is determined by the radial velocity in the Local System and by the azimuthal velocity in the Sagittarius region. These velocities achieve their observed values of VR=5.3 and $V_\theta=-1$ km s-1 under $\theta_{\rm b}=43^\circ$ and $\theta_{\rm b}=48^\circ$, respectively.

We now consider the sum of square differences between the model and observed velocities, $\chi ^2$, obtained for the radial and azimuthal components under different values of  $\theta _{\rm b}$. Figure 10c shows the $\chi ^2$-function computed for three complexes: the Perseus and Sagittarius regions and the Local System. It is clearly seen that $\chi ^2$ achieves its minimum values at the interval $\theta_{\rm b} >40^\circ$. We chose $\theta _{\rm b}=45^\circ $ as the optimal value because it reproduces the observational velocity $V_\theta=-1$ km s-1 well in the Sagittarius region. Models with analytical bars in Paper I gave the same result.

\begin{figure} \par\includegraphics[width=8.8cm,clip]{14646fg10.eps} \vspace*{5mm} \end{figure} Figure 10:

Dependence of the average residual velocities,  $\overline {V_R}$ a) and $\overline {V_\theta }$  b), and the $\chi ^2$-function  c) on the solar position angle  $\theta _{\rm b}$. The curves calculated for different complexes are shown by different lines. The $\chi ^2$-function was computed for three complexes: the Perseus and Sagittarius regions and the Local System.

Open with DEXTER

4.3 Analysis of periodicity in oscillations of the momentary velocities

Now we approximate the oscillations in the radial and azimuthal components of the momentary velocities, VR and $V_\theta $ (Fig. 8), by the sinusoidal law:

\begin{displaymath}% V_R (\textrm{or }V_\theta)=A_1\sin(2\pi T/P)+A_2\cos(2\pi T/P), \end{displaymath} (5)

where P is a period of oscillations, $A_0=\sqrt{A_1^2+A_2^2}$ is an amplitude of oscillations, and T is time counted from T0=50.

We use the standard least square method to solve the system of 101 equations, which are linear in the parameters A1 and A2 for each value of nonlinear parameter P. We then determine the value of P that minimizes the sum of squared normalized residual velocities $\chi ^2$. Figure 11 presents the $\chi ^2$-curves built for the oscillations of the radial velocity in 5 complexes, but the curves made for the azimuthal velocities have no conspicuous minima. It is clearly seen that $\chi ^2$-curves demonstrate deep minima in the Cygnus and Perseus regions and in the Local System. These minima correspond to the best periods in approximating the velocity oscillations that have the following values: P=2.7 $\pm$ 0.4 in the Cygnus region, P=2.9 $\pm$ 1.0 in the the Local System, and P=1.6 $\pm$ 0.2 in the Perseus region. We have already obtained period P=1.5 when studying density oscillations on the galactic periphery (Sect. 3.3). Probably, the strongest slow mode $\Omega=28$ km s-1 kpc-1 is also responsible for the velocity oscillations: the beating oscillations between the bar mode and a two-armed pattern rotating with the speed $\Omega=28$ km s-1 kpc-1 must have the period of P=1.6 and those calculated for one-armed perturbation have a period of P=3.2 (Eq. (3)). Some of the small differences between the pattern speeds derived from the amplitude spectra and those obtained from kinematical analysis may be due to tidal interaction in the stellar component between the bar and slow modes.

\begin{figure} \par\includegraphics[width=8.8cm,clip]{14646fg11.eps} \end{figure} Figure 11:

$\chi ^2$-functions built for studying periodicity in the oscillations of the radial velocities, VR, in 5 complexes. The minima on the curves must correspond to the best periods in approximation of the velocity oscillations.

Open with DEXTER

Table 1:   Observed residual velocities of OB-associations in the stellar-gas complexes.

4.4 Evolutional aspects of kinematics at the time interval T = 30-60

Let us compare the average residual velocities calculated for different time intervals T = 30-40, 40-50, and 50-60 (Tables 2-4). Generally, most changes in the residual velocities do not exceed 4.0 km s-1 and are likely caused by occasional perturbations. On the other hand, radial velocities  $\overline {V_R}$ in the Local System and in the Cygnus region demonstrate the ongoing growth, which can be connected with the evolution of the outer rings.

Figure 12 shows the surface density of gas particles averaged in squares at different time intervals. The average density was calculated in the reference frame that rotates with the speed of the bar. The light-gray, dark-gray, and black colors represent squares containing the increasing number of particles, $n>\overline {m}/2$, $n>\overline {m}$, and $n>2\overline {m}$, respectively, where n is the number of particles accumulated in a square over 101 moments and $\overline{m}$ is their number averaged over all squares, $\overline{m}=463$. It is clearly seen that the major axis of the outer ring R2 changes its orientation: it goes $\alpha\sim20^\circ$ahead of the bar at the interval T = 30-40, but this angle increases to $\alpha\sim45^\circ$ at the intervals T = 40-50 and T = 50-60. Moreover, the outer ring changes its morphology: we can identify two outer rings of classes R1 and R2 at the interval T = 30-40, while there is only one outer ring with an intermediate orientation of $\alpha\approx45^\circ$ at the intervals T = 40-50 and 50-60. Its shape becomes rounder at the interval T = 50-60.

Let us consider more thoroughly the distribution of gas particles at the interval T = 50-60 (Fig. 12). It is clearly seen that the surface density of gas particles at the distance range of R=6-9 kpc is nearly twice the average density all over the disk  $\overline{m}$. The density perturbation inside the outer ring can be approximated by two spiral arms with a pitch angle of i=6 $\pm$ $1^\circ$. The density perturbation inside them reaches to 100 per cent with respect to the average gas density in the disk. This is considerably larger than the density perturbation seen in the stellar component (15-20 per cent).

Table 2:   Model residual velocities averaged on interval T = 50-60.

Figure 13 shows the profiles of the surface density of gas particles averaged at the different time intervals. We can see the growth of the density hump at the distance of $R \approx 7$ kpc, which indicates the growth of the outer ring. In contrast, the hump at $R\approx 3$ kpc is decreasing, which reflects the weakening of the inner ring. At the interval T = 50-60, the maximum in the gas density distribution is located at the distance R=7.3 kpc, which is just in the middle between the outer 4/1 resonance (6.4 kpc) and the OLR (8.1 kpc) of the bar.

Tables 2-4 also represent the velocity dispersions of gas particles in the stellar gas complexes. We can see that their average values stay at nearly the same level of $\overline{\sigma_R}=9.7$ $\pm$ 0.1 and $\overline{\sigma_\theta}=6.3$ $\pm$ 0.2 km s-1 during the period T = 30-60. The maximum growth, which does not exceed ${\sim}20$ per cent, is observed in the Perseus region. The model velocity dispersions somewhat exceed the observed values derived for OB-associations in the stellar-gas complexes, $\sigma_{R~{\rm obs}}=7.7$ and $\sigma_{\theta~{\rm obs}}=5.2$ km s-1, but this difference is below 30 per cent.

\begin{figure} \par\includegraphics[width=17.5cm,clip]{14646fg12.eps} \vspace*{5mm} \end{figure} Figure 12:

The surface density of gas particles averaged in squares at the time intervals T = 30-40, 40-50, and 50-60. The light-gray, dark-gray, and black colors represent squares containing the increasing number of particles: $n>\overline {m}/2$, $n>\overline {m}$, and $n>2\overline {m}$, respectively. The position of the Sun is shown by the specific symbol. The bar is oriented along the Y-axis, the galaxy rotates clockwise, and a division on the X- and Y-axis corresponds to 1 kpc.

Open with DEXTER

Table 3:   Model residual velocities averaged on interval T = 30-40.

Table 4:   Model residual velocities averaged on interval T = 40-50.

5 Conclusions

We have presented N-body simulations that reproduce the kinematics of OB-associations in the Perseus and Sagittarius regions and in the Local System. The velocities of gas particles averaged over large time intervals (1 Gyr or 8 bar rotation periods) reproduce the directions of the observed velocities in these regions. The mean difference between the model and observed velocities calculated for the radial and azimuthal components is $\Delta V=3.3$ km s-1 there.

The galactic disk in our model includes two subsystems. The behavior of the stellar subsystem is modeled by 8 million gravitating collisionless particles. The stellar disk quickly forms a bar. Its original pattern speed is quite high, but it first quickly decreases and then moves to a slow decrease with $\Omega \approx 50~{\rm km~s}^{-1}~{\rm kpc}^{-1}$ for several Gyr. With our favored value of the solar distance, $R_0=7.5~{\rm kpc}$, this sets us close to the OLR ( $R_{\rm OLR}=8.1~{\rm kpc}$). This agrees with studies of local stellar velocity distribution (Dehnen 2000; Minchev et al. 2010; Fux 2001), although they tend to set the OLR slightly inside R0. The optimal value of the solar position angle  $\theta _{\rm b}$ providing the best agreement between the model and observed velocities is $\theta_{\rm b}=45$ $\pm$ $5^\circ$. The bar is quite long ( $R_{\rm bar} \approx 4.0$ kpc), but both its size and orientation are consistent with the parameters derived from infrared observations (Cabrera-Lavers et al. 2007; Benjamin et al. 2005).

\begin{figure} \par\includegraphics[width=8.8cm,clip]{14646fg13.eps} \end{figure} Figure 13:

Profiles of the surface density of gas particles averaged at the intervals T = 30-40, 40-50, and 50-60.

Open with DEXTER

The stellar disk also creates an outer ring of class R1 rotating with the pattern speed of the bar, and the corresponding density perturbation amounts to 15-20 per cent of the average density at the same distance. Besides the bar, the stellar disk includes several slow modes. The strongest of these rotates with the pattern speed of $\Omega \approx 30~{\rm km~s}^{-1}~{\rm kpc}^{-1}$ and is often clearly lopsided.

The gas subsystem is modeled by 40 000 massless particles that move in the potential created by the stellar particles (and analytical bulge and halo) and can collide with each other inelastically. The gas disk forms an outer ring that exhibits quasi-periodic changes in its morphology because it has several modes. One can identify elements of R1- and R2-morphology, and the outer ring can often be classified as R1R2'. The gas density perturbation inside the ring can be approximated by two spiral arms with the pitch angle of i=6 $\pm$ $1^\circ$.

The models with analytical bars (Paper I) reproduced the residual velocities well in the Perseus and Sagittarius regions. We explained this success by the resonance between the relative orbital rotation of the bar and the epicyclic motion. The Sagittarius region must be located slightly inside the OLR where resonance orbits are elongated perpendicular to the bar, whereas the Perseus region must lie outside the OLR where periodic orbits are oriented along the bar. However, models with the analytical bar failed dramatically with the Local System where they yielded only negative radial velocities $-24<V_R<-16~{\rm km~s}^{-1}$, whereas the observed value is $+5.3~{\rm km~s}^{-1}$. The success of N-body simulations with the Local System is likely due to the gravity of the stellar R1-ring, which is omitted in models with analytical bars.

To study the effects of the gravity of the R1-ring we construct more simple models with a ``time averaged bar potential''. This was done by calculating the average density distribution in the frame rotating with the bar. This process should average out most of the effect of slower modes and leave bar and the R1-ring that corotates with the bar. The preliminary study shows that momentary velocities in these models are in a good agreement with the average velocities in the present N-body simulation. The detailed description of these models will be done in our next paper.

To simplify the analysis at this point we are forced to ignore a lot of processes which are important at such long time interval as 6 Gyr. We do not consider the accumulation of gas at the galactic center, the transitions between the gas and stellar subsystems, resonant interaction between the bar and halo, or the minor mergers and satellite accretion. Considering the effects of these processes may be done in a later phase.

Acknowledgements
We want to thank H. Salo who wrote the simulation code we have used in this study. This work was partly supported by the Russian Foundation for Basic Research (project Nos. 10-02-00489).

References

  1. Athanassoula, E., Romero-Gómez, M., & Masdemont, J. J. 2009, MNRAS, 394, 67 [NASA ADS] [CrossRef] [Google Scholar]
  2. Bagley, M., Minchev, I., & Quillen, A. C. 2009, MNRAS, 395, 537 [NASA ADS] [CrossRef] [Google Scholar]
  3. Barbier-Brossat, M., & Figon, P. 2000, A&AS, 142, 217 [Google Scholar]
  4. Benjamin, R. A., Churchwell, E., Babler, B. L. et al. 2005, ApJ, 630, L149 [NASA ADS] [CrossRef] [Google Scholar]
  5. Berdnikov, L. N., Dambis, A. K., & Vozyakova, O. V. 2000, A&AS, 143, 211 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Bissantz, N., & Gerhard, O. 2002, MNRAS, 330, 591 [NASA ADS] [CrossRef] [Google Scholar]
  7. Blaha, C., & Humphreys, R. M. 1989, AJ, 98, 1598 [NASA ADS] [CrossRef] [Google Scholar]
  8. Blitz, L., & Spergel, D. N. 1991, ApJ, 379, 631 [NASA ADS] [CrossRef] [Google Scholar]
  9. Blitz, L., Binney, J., Lo, K. J., Bally, J., & Ho, P. T. P. 1993, Nature, 361, 417 [NASA ADS] [CrossRef] [Google Scholar]
  10. Bobylev, V. V., Bajkova, A. T., & Lebedeva, S. V. 2007, Astron. Lett., 33, 720 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  11. Burton, W. B., & Gordon, M. A. 1978, A&A, 63, 7 [NASA ADS] [Google Scholar]
  12. Buta, R. 1986, ApJS, 61, 609 [NASA ADS] [CrossRef] [Google Scholar]
  13. Buta, R. 1995, ApJS, 96, 39 [NASA ADS] [CrossRef] [Google Scholar]
  14. Buta, R., & Crocker, D. A. 1991, AJ, 102, 1715 [NASA ADS] [CrossRef] [Google Scholar]
  15. Buta, R., & Combes, F. 1996, Fund. Cosmic Phys., 17, 95 [Google Scholar]
  16. Buta, R., Corwin, H. G., & Odewahn, S. C. 2007, The de Vaucouleurs Atlas of Galaxies (Cambridge Univ. Press) [Google Scholar]
  17. Byrd, G., Rautiainen, P., Salo, H., Buta, R., & Crocker, D. A. 1994, AJ, 108, 476 [NASA ADS] [CrossRef] [Google Scholar]
  18. Brand, J., & Blitz, L. 1993, A&A, 275, 67 [NASA ADS] [Google Scholar]
  19. Cabrera-Lavers, A., Hammersley, P. L., Gonzalez-Fernandez, C., et al. 2007, A&A, 465, 825 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Cabrera-Lavers, A., González-Fernández, C., Garzón, F., Hammersley, P. L., & López-Corredoira, M. 2008, A&A, 491, 781 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Churchwell, E., Babler, B. L., Meade, M. R., et al. 2009, PASP, 121, 213 [NASA ADS] [CrossRef] [Google Scholar]
  22. Clemens, D. P. 1985, ApJ, 295, 422 [NASA ADS] [CrossRef] [Google Scholar]
  23. Contopoulos, G., & Papayannopoulos, Th. 1980, A&A, 92, 33 [NASA ADS] [Google Scholar]
  24. Contopoulos, G., & Grosbol, P. 1989, A&ARv, 1, 261 [NASA ADS] [CrossRef] [Google Scholar]
  25. Dambis, A. K., Mel'nik, A. M., & Rastorguev, A. S. 1995, Astron. Lett., 21, 291 [Google Scholar]
  26. Dame, T. M., & Thaddeus, P. 2008, ApJ, 683, L143 [NASA ADS] [CrossRef] [Google Scholar]
  27. Debattista, V. P., & Sellwood, J. A. 2000, ApJ, 543, 704 [NASA ADS] [CrossRef] [Google Scholar]
  28. Dehnen, W. 2000, AJ, 119, 800 [NASA ADS] [CrossRef] [Google Scholar]
  29. Efremov, Y. N., & Sitnik, T. G. 1988, Sov. Astron. Lett., 14, 347 [Google Scholar]
  30. Englmaier, P., & Gerhard, O. 2006, CeMDA, 94, 369 [Google Scholar]
  31. Erwin, P. 2005, MNRAS, 364, 283 [NASA ADS] [CrossRef] [Google Scholar]
  32. Fux, R. 2001, A&A, 373, 511 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. ESA 1997, The Hipparcos and Tycho Catalogs, ESA SP-1200 [Google Scholar]
  34. Glushkova, E. V., Dambis, A. K., Mel'nik, A. M., & Rastorguev, A. S. 1998, A&A, 329, 514 [NASA ADS] [Google Scholar]
  35. Habing, H. J., Sevenster, M. N., Messineo, M., van de Ven, G., & Kuijken, K. 2006, A&A, 458, 151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Kalnajs, A. J. 1991, in Dynamics of Disc Galaxies, ed. B. Sundelius, Göteborgs Univ., Göteborg, 323 [Google Scholar]
  37. Kuijken, K. 1996, in Unsolved problems of the Milky Way, ed. L. Blitz, & P. Teuben (Dordrecht: Kluwer), ASP Conf. Ser., 91, 504 [Google Scholar]
  38. van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Lépine, J. R. D., Mishurov, Y. N., & Dedikov, S. Y. 2001, ApJ, 546, 234 [NASA ADS] [CrossRef] [Google Scholar]
  40. Masset, F., & Tagger, M. 1997, A&A, 322, 442 [NASA ADS] [Google Scholar]
  41. Mel'nik, A. M., & Dambis, A. K. 2009, MNRAS, 400, 518 [NASA ADS] [CrossRef] [Google Scholar]
  42. Mel'nik, A. M., & Rautiainen, P. 2009, Astron. Lett., 35, 609 (Paper I) [NASA ADS] [CrossRef] [Google Scholar]
  43. Mel'nik, A. M., Dambis, A. K., & Rastorguev, A. S. 2001, Astron. Lett., 27, 521 [Google Scholar]
  44. Minchev, I., Boily, C., Siebert, A., & Bienayme, O. 2010, MNRAS, in press [arXiv:0909.3516] [Google Scholar]
  45. Pont, F., Mayor, M., & Burki, G. 1994, A&A, 285, 415 [NASA ADS] [Google Scholar]
  46. Rastorguev, A. S., Pavlovskaya, E. D., Durlevich, O. V., & Filippova, A. A. 1994, Astron. Lett., 20, 591 [Google Scholar]
  47. Rautiainen, P., & Salo, H. 1999, A&A, 348, 737 [NASA ADS] [Google Scholar]
  48. Rautiainen, P., & Salo, H. 2000, A&A, 362, 465 [NASA ADS] [Google Scholar]
  49. Rautiainen, P., Salo, H., & Laurikainen, E. 2008, MNRAS, 388, 1803 [NASA ADS] [CrossRef] [Google Scholar]
  50. Rodriguez-Fernandez, N. J., & Combes, F. 2008, A&A, 489, 115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Romero-Gómez, M., Athanassoula, E., Masdemont, J. J., & García-Gómez, C. 2007, A&A, 472, 63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Russeil, D. 2003, A&A, 397, 133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Salo, H. 1991, A&A, 243, 118 [NASA ADS] [Google Scholar]
  54. Salo, H., & Laurikainen, E. 2000, MNRAS, 319, 377 [NASA ADS] [CrossRef] [Google Scholar]
  55. Salo, H., Rautiainen, P., Buta, R., et al. 1999, AJ, 117, 792 [NASA ADS] [CrossRef] [Google Scholar]
  56. Schwarz, M. P. 1981, ApJ, 247, 77 [NASA ADS] [CrossRef] [Google Scholar]
  57. Sellwood, J. A., & Sparke, L. S. 1988, MNRAS, 231, 25P [NASA ADS] [CrossRef] [Google Scholar]
  58. Treuthardt, P., Salo, H., Rautiainen, P., & Buta, R. 2008, AJ, 136, 300 [NASA ADS] [CrossRef] [Google Scholar]
  59. Vallée, J. P. 2005, AJ, 130, 569 [NASA ADS] [CrossRef] [Google Scholar]
  60. Vallée, J. P. 2008, AJ, 135, 1301 [NASA ADS] [CrossRef] [Google Scholar]
  61. Weiner, B. J., & Sellwood, J. A. 1999, ApJ, 524, 112 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1:   Observed residual velocities of OB-associations in the stellar-gas complexes.

Table 2:   Model residual velocities averaged on interval T = 50-60.

Table 3:   Model residual velocities averaged on interval T = 30-40.

Table 4:   Model residual velocities averaged on interval T = 40-50.

All Figures

  \begin{figure} \par\includegraphics[width=17.5cm,clip]{14646fg1.eps} \vspace*{5mm} \end{figure} Figure 1:

a) The residual velocities of OB-associations projected on to the galactic plane. It also shows the grouping of OB-associations into regions of intense star formation. b) The mean VR- and $V_\theta $-velocities of OB-associations in the stellar-gas complexes. The X-axis is directed away from the galactic center, and the Y-axis is in the direction of the galactic rotation. The Sun is at the origin.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=14.5cm,clip]{14646fg2.eps} \end{figure} Figure 2:

The rotation curve (solid line) of the N-body model at T=0 ( left) and at T=55 ( right). The contributions from the bulge (dash-dotted line), disk (dashed line) and halo (dotted line) are also indicated.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=12.5cm,clip]{14646fg3.eps} \end{figure} Figure 3:

The amplitude spectra of the relative density perturbations in the model disk. The frames show the amplitude spectra of the stellar or gas component at various times (indicated on the frame titles). The contour levels are 0.025, 0.05, 0.1, 0.2, 0.4, and 0.8, calculated with respect to the azimuthal average surface density at each radius. The continuous lines show the frequencies $\Omega $ and $\Omega \pm \kappa /m$, and the dashed curves indicate the frequencies  $\Omega \pm \kappa /4$ in the m=2 amplitude spectrum.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=13cm,clip]{14646fg4.eps} \vspace*{2mm} \end{figure} Figure 4:

The reconstructed modes in the stellar component (see text) for T=50-60 time interval. The enhanced density compared to the azimuthally averaged profile at each radius is shown. The shades of gray (darker corresponds to higher surface density) have been chosen to emphasize the features. The circles in the bar mode indicate ILR (1.4 kpc), CR (4.6 kpc), and OLR (8.1 kpc), whereas the inner 4/1 (4.6 kpc) and CR (7.1 kpc) are shown for the mode S1.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=16cm,clip]{14646fg5.eps} \vspace*{4mm} \end{figure} Figure 5:

The gas morphology at selected times. The bar is vertical in all frames, whose width is 20 kpc.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=17cm,clip]{14646fg6.eps} \end{figure} Figure 6:

The perturbation in the density of gas particles, $\sigma '=\sigma -\sigma _0$, located at the annulus 7<R<10 kpc along azimuthal angle $\theta $ built for different moments. It also shows its approximation by two-fold ( left panel) and one-fold ( right panel) sinusoids.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=17cm,clip]{14646fg7.eps} \end{figure} Figure 7:

Variations in the phase $\phi $ (black curve) and amplitude A (gray curve) of the sinusoids that approximate the distribution of gas particles located at the distances 7<R<10 kpc along $\theta $. Subscripts 1 and 2 are related to the one- and two-fold sinusoids, respectively.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=16.5cm,clip]{14646fg8.eps} \vspace*{2.5mm} \end{figure} Figure 8:

Variations in the mean velocities of gas particles located within the boundaries of the stellar-gas complexes. The left panel is related to the radial component VR and the right one to the azimuthal one $V_\theta $.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=15cm,clip]{14646fg9.eps} \vspace*{5mm} \end{figure} Figure 9:

Distribution of the negative and positive average residual velocities calculated in squares. The squares with positive velocities are shown in black, while those with negative ones are given in gray. Only squares that satisfy the condition $n>\overline {m}/2$ are depicted. The left panel represents the radial velocities, while the right one shows the azimuthal ones. It also demonstrates the boundaries of the stellar-gas complexes. The position angle of the Sun is supposed to be $\theta _{\rm b}=45^\circ $. The bar is oriented along the Y-axis, the galaxy rotates clockwise, and a division on the X- and Y-axis corresponds to 1 kpc.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{14646fg10.eps} \vspace*{5mm} \end{figure} Figure 10:

Dependence of the average residual velocities,  $\overline {V_R}$ a) and $\overline {V_\theta }$  b), and the $\chi ^2$-function  c) on the solar position angle  $\theta _{\rm b}$. The curves calculated for different complexes are shown by different lines. The $\chi ^2$-function was computed for three complexes: the Perseus and Sagittarius regions and the Local System.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{14646fg11.eps} \end{figure} Figure 11:

$\chi ^2$-functions built for studying periodicity in the oscillations of the radial velocities, VR, in 5 complexes. The minima on the curves must correspond to the best periods in approximation of the velocity oscillations.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=17.5cm,clip]{14646fg12.eps} \vspace*{5mm} \end{figure} Figure 12:

The surface density of gas particles averaged in squares at the time intervals T = 30-40, 40-50, and 50-60. The light-gray, dark-gray, and black colors represent squares containing the increasing number of particles: $n>\overline {m}/2$, $n>\overline {m}$, and $n>2\overline {m}$, respectively. The position of the Sun is shown by the specific symbol. The bar is oriented along the Y-axis, the galaxy rotates clockwise, and a division on the X- and Y-axis corresponds to 1 kpc.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{14646fg13.eps} \end{figure} Figure 13:

Profiles of the surface density of gas particles averaged at the intervals T = 30-40, 40-50, and 50-60.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.