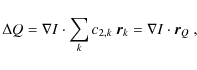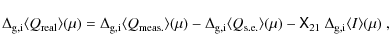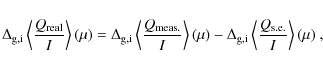| Issue |
A&A
Volume 519, September 2010
|
|
|---|---|---|
| Article Number | A18 | |
| Number of page(s) | 9 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201014500 | |
| Published online | 07 September 2010 | |
Observations of solar scattering polarization at high spatial resolution
F. Snik1 - A. G. de Wijn2 - K. Ichimoto3 - C. E. Fischer1 - C. U. Keller1 - B. W. Lites2
1 - Sterrekundig Instituut Utrecht, Princetonplein 5, 3584 CC, Utrecht, The Netherlands
2 - High Altitude Observatory, National Center for Atmospheric Research, PO Box 3000, CO, 80307-3000 Boulder, USA
3 - Kwasan and Hida Observatories, Kyoto University, Kurabashira Kamitakara-cho, Takayama-city, 506-1314 Gifu, Japan
Received 25 March 2010 / Accepted 10 May 2010
Abstract
Context. The weak, turbulent magnetic fields that supposedly
permeate most of the solar photosphere are difficult to observe,
because the Zeeman effect is virtually blind to them. The Hanle effect,
acting on the scattering polarization in suitable lines, can in
principle be used as a diagnostic for these fields. However, the
prediction that the majority of the weak, turbulent field resides in
intergranular lanes also poses significant challenges to scattering
polarization observations because high spatial resolution is usually
difficult to attain.
Aims. We aim to measure the difference in scattering
polarization between granules and intergranules. We present the
respective center-to-limb variations, which may serve as input for
future models.
Methods. We perform full Stokes filter polarimetry at different solar limb positions with the CN band filter of the Hinode-SOT
Broadband Filter Imager, which represents the first scattering
polarization observations with sufficient spatial resolution to discern
the granulation. Hinode-SOT offers unprecedented spatial
resolution in combination with high polarimetric sensitivity. The CN
band is known to have a significant scattering polarization signal, and
is sensitive to the Hanle effect. We extend the instrumental
polarization calibration routine to the observing wavelength, and
correct for various systematic effects.
Results. The scattering polarization for granules
(i.e., regions brighter than the median intensity of non-magnetic
pixels) is significantly larger than for intergranules. We derive that
the intergranules (i.e., the remaining non-magnetic pixels)
exhibit
![]() less scattering polarization for
less scattering polarization for
![]() ,
although systematic effects cannot be completely excluded.
,
although systematic effects cannot be completely excluded.
Conclusions. These observations constrain MHD models in
combination with (polarized) radiative transfer in terms of CN band
line formation, radiation anisotropy, and magnetic fields.
Key words: Sun: magnetic topology - techniques: polarimetric
1 Introduction
![\begin{figure}
\par\includegraphics[width=9cm,clip]{14500f1.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa14500-10/Timg10.png)
|
Figure 1:
The intensity and scattering polarization spectrum at |
| Open with DEXTER | |
With the increasing sensitivity of solar spectropolarimeters, a
substantial amount of knowledge about quiet Sun magnetic fields is
obtained using the Zeeman effect in suitable spectral lines (for a
recent overview, see De Wijn et al. 2009).
However, the Zeeman effect is virtually blind to turbulent (i.e.,
mixed-polarity) magnetic fields because the polarization signals in
such observations cancel out for opposite polarities within a
resolution element.
A different line polarization effect can be used to probe these weak,
turbulent magnetic fields: the Hanle effect, which acts on lines with
scattering polarization (see, e.g., Trujillo Bueno 2009).
This scattering polarization is observed near the solar limb, where the scattering angle is close to 90![]() .
However, the degree of polarization (Stokes Q/I, with +Q parallel to the local limb) is low:
.
However, the degree of polarization (Stokes Q/I, with +Q parallel to the local limb) is low: ![]() 0.01 down to 10-5 (Stenflo & Keller 1997).
In general, the Hanle effect constitutes a depolarization of the line by weak magnetic fields of
0.01 down to 10-5 (Stenflo & Keller 1997).
In general, the Hanle effect constitutes a depolarization of the line by weak magnetic fields of ![]() 0-
0-
![]() .
.
With an analysis based on the Hanle effect, Trujillo Bueno et al. (2004) were able to infer a ubiquitous turbulent magnetic field in the quiet Sun with an average strength of ![]()
![]() .
With an indirect method, the authors conjecture a difference in
turbulent magnetic field strengths between granules and intergranules,
with averages of
.
With an indirect method, the authors conjecture a difference in
turbulent magnetic field strengths between granules and intergranules,
with averages of ![]()
![]() and 300-
and 300-
![]() ,
respectively.
This dichotomy between granules and intergranules is also observed in the MHD simulations of Vögler & Schüssler (2007),
which exhibited local dynamo action by the convection.
A direct observational constraint is required to confirm these
hypotheses and models, and to investigate the presence of a local
dynamo in the solar photosphere.
To this end, we perform filter observations of solar scattering
polarization at high spatial resolution, to resolve the granulation
pattern near the limb.
High spatial resolution is very difficult to attain in current
ground-based observations of scattering polarization, because adaptive
optics systems do not perform well in quiet regions near the solar
limb.
At the long effective exposure times of several minutes that are
required to reach sufficient polarimetric sensitivity, the atmospheric
seeing and solar evolution usually smear out the granulation pattern.
We present the first observations of solar scattering polarization at
high spatial resolution, obtained with the Solar Optical Telescope
(SOT) of the Hinode satellite.
The only filter position of SOT that enables these observations is the broad-band filter at the CN band head (
,
respectively.
This dichotomy between granules and intergranules is also observed in the MHD simulations of Vögler & Schüssler (2007),
which exhibited local dynamo action by the convection.
A direct observational constraint is required to confirm these
hypotheses and models, and to investigate the presence of a local
dynamo in the solar photosphere.
To this end, we perform filter observations of solar scattering
polarization at high spatial resolution, to resolve the granulation
pattern near the limb.
High spatial resolution is very difficult to attain in current
ground-based observations of scattering polarization, because adaptive
optics systems do not perform well in quiet regions near the solar
limb.
At the long effective exposure times of several minutes that are
required to reach sufficient polarimetric sensitivity, the atmospheric
seeing and solar evolution usually smear out the granulation pattern.
We present the first observations of solar scattering polarization at
high spatial resolution, obtained with the Solar Optical Telescope
(SOT) of the Hinode satellite.
The only filter position of SOT that enables these observations is the broad-band filter at the CN band head (
![]() ,
see Fig. 1).
The CN band is usually employed to study photospheric magnetic fields through proxy-magnetometry (see, e.g., Uitenbroek & Tritschler 2007).
It is known that the continuum polarization at this blue wavelength is relatively large (
,
see Fig. 1).
The CN band is usually employed to study photospheric magnetic fields through proxy-magnetometry (see, e.g., Uitenbroek & Tritschler 2007).
It is known that the continuum polarization at this blue wavelength is relatively large (![]()
![]() at
at
![]() ,
where
,
where ![]() is the heliocentric angle; see Trujillo Bueno & Shchukina 2009), and that the molecular lines are sensitive to the Hanle effect (Shapiro et al. 2007).
Indeed, Shapiro et al. (2007)
show that the CN band lines depolarize the continuum near the band head
(their Fig. 8). This depolarization is visible as the dips with an
absolute range of
is the heliocentric angle; see Trujillo Bueno & Shchukina 2009), and that the molecular lines are sensitive to the Hanle effect (Shapiro et al. 2007).
Indeed, Shapiro et al. (2007)
show that the CN band lines depolarize the continuum near the band head
(their Fig. 8). This depolarization is visible as the dips with an
absolute range of
![]() in the continuum of Q/I of
in the continuum of Q/I of ![]()
![]() in Fig. 1.
in Fig. 1.
Our aim is to measure the center-to-limb variation (CLV) of the scattering polarization in Hinode CN band filtergrams and to characterize the differences therein between granules and intergranules. There are many effects that contribute to a possible difference in scattering polarization between granules and intergranular lanes:
- 1.
- the chemistry of the CN molecule formation (see Asensio Ramos & Trujillo Bueno 2003) that cause formation differences of the molecular lines (see Trujillo Bueno et al. 2004);
- 2.
- the scattering anisotropy variations (see, e.g., Trujillo Bueno & Shchukina 2009);
- 3.
- the different degrees of Hanle depolarization due to differences in (turbulent) magnetic field strength.
- 1.
- spurious signals due to solar evolution and (residual) image motion during the polarization modulation cycle;
- 2.
- coupling of the instrumental polarization to the detector non-linearity or dark bias (cf. Keller 1996), which results in a print-through of the intensity signal (i.e. the granulation) in Q/I.
where
The Hinode observations are presented in Sect. 2. The data reduction and the methods to eliminate spurious polarization signals are detailed in Sect. 3. The results are presented and discussed in Sect. 4, and final conclusions are drawn in Sect. 5.
2 Observations
2.1 CN band observations
Full-Stokes observations in the CN band were obtained on 2007 October 21-22 with the Hinode-Solar Optical Telescope (SOT) (Suematsu et al. 2008; Kosugi et al. 2007; Tsuneta et al. 2008).
These are the first scattering polarization observations with sufficient spatial resolution (![]()
![]() )
to discern the granulation pattern near the limb.
Polarimetric observations with the Hinode
Broadband Filter Imager (BFI) are not offered as a standard mode, but
they are possible because all the light entering the SOT instruments is
polarimetrically modulated by a continuously rotating wave plate, and
the light between the Narrowband Filter Imager (NFI) and the BFI is
split by a polarizing beam-splitter, which therefore acts as a
polarization analyzer for both instruments (only with a
)
to discern the granulation pattern near the limb.
Polarimetric observations with the Hinode
Broadband Filter Imager (BFI) are not offered as a standard mode, but
they are possible because all the light entering the SOT instruments is
polarimetrically modulated by a continuously rotating wave plate, and
the light between the Narrowband Filter Imager (NFI) and the BFI is
split by a polarizing beam-splitter, which therefore acts as a
polarization analyzer for both instruments (only with a ![]() rotation between them).
By extending the observing software, the BFI data were polarimetrically demodulated in the same way as NFI data.
rotation between them).
By extending the observing software, the BFI data were polarimetrically demodulated in the same way as NFI data.
Because high spatial resolution is crucial for our analysis, we choose
to observe in the CN band with small effective exposure times in order
not to be very susceptible to solar evolution, and repeat the
observations many times.
The modulation/demodulation mode was necessarily ``shuttered'', because
the BFI does not have the option of masking parts of the CCD for
shutterless operation.
Each set of observations consists of 15 frames, each of which was
acquired using eight sub-exposures of
![]() ,
leading to a total effective exposure time of
,
leading to a total effective exposure time of
![]() per frame.
Because of a delay incurred by the CCD readout, it takes approximately
per frame.
Because of a delay incurred by the CCD readout, it takes approximately
![]() to complete the acquisition of the Stokes vector.
The observations are binned
to complete the acquisition of the Stokes vector.
The observations are binned ![]() on-chip to increase S/N per pixel.
We performed simultaneous scans of the same field of view (FOV) with
the spectropolarimeter (SP) in ``fast map'' mode (with limited spatial
resolution, but slightly increased sensitivity), to measure the strong,
signed magnetic fields, using the Zeeman effect in the Fe I line pair at
on-chip to increase S/N per pixel.
We performed simultaneous scans of the same field of view (FOV) with
the spectropolarimeter (SP) in ``fast map'' mode (with limited spatial
resolution, but slightly increased sensitivity), to measure the strong,
signed magnetic fields, using the Zeeman effect in the Fe I line pair at
![]() .
.
Data were obtained for various positions along the solar limb: the north (N) limb, the north-west (NW) limb, and the east (E) limb. These complementary data sets are used to verify the measurement of a solar scattering polarization signal (and not an instrumental effect), and to assess systematic effects in the linear Stokes parameters (U/I, Q/I) that should not contain scattering polarization. Henceforth we employ the global Stokes coordinate system of Hinode that has +Q oriented parallel to the N limb.
All raw frames are run through the standard Hinode pipeline![]() that performs dark subtraction, flat fielding, cosmic ray hit removal, and polarimetric demodulation.
that performs dark subtraction, flat fielding, cosmic ray hit removal, and polarimetric demodulation.
2.2 Na I D
 observations
observations
During the same observing sequence, full Stokes line scans of the Na I D
![]() line were also performed with the NFI instrument.
Na I D
line were also performed with the NFI instrument.
Na I D
![]() is known to have a scattering polarization of
is known to have a scattering polarization of ![]()
![]() (Stenflo & Keller 1997) with an antisymmetric signature in the line wings (due to interaction with the D2 line), and often with a peaked line core polarization of yet unknown origin (Trujillo Bueno et al. 2002; Stenflo et al. 2001; Casini & Manso Sainz 2005).
Filter observations in the D1 and D2 lines with limited spatial resolution were performed by Stenflo et al. (2002), without measuring significant scattering polarization signatures in the D1 line.
(Stenflo & Keller 1997) with an antisymmetric signature in the line wings (due to interaction with the D2 line), and often with a peaked line core polarization of yet unknown origin (Trujillo Bueno et al. 2002; Stenflo et al. 2001; Casini & Manso Sainz 2005).
Filter observations in the D1 and D2 lines with limited spatial resolution were performed by Stenflo et al. (2002), without measuring significant scattering polarization signatures in the D1 line.
Unfortunately, the Hinode line scan observations in the D1 line exhibit instrumental effects at the 10-3 level, which prevents us from detecting real scattering polarization signals.
A polarization that varies with ![]() is detected in Q/I
at the N limb, but it does not rotate in polarization direction at the
other limb positions, indicating that it is an instrumental effect that
causes a print-through of the intensity limb darkening.
In all Stokes U/I observations, a blotchy, varying instrumental polarization pattern is measured.
The origin of these two effects is currently unknown.
is detected in Q/I
at the N limb, but it does not rotate in polarization direction at the
other limb positions, indicating that it is an instrumental effect that
causes a print-through of the intensity limb darkening.
In all Stokes U/I observations, a blotchy, varying instrumental polarization pattern is measured.
The origin of these two effects is currently unknown.
![\begin{figure}
\par\mbox{\includegraphics[width=8.2cm,clip]{14500f2a.eps} \hskip...
...s} \hskip10mm
\includegraphics[width=8.2cm,clip]{14500f2d.eps} }
\end{figure}](/articles/aa/full_html/2010/11/aa14500-10/Timg35.png)
|
Figure 2:
Stokes I and Q/I observations in the CN band at 388 nm at the north limb of the Sun. The bin limits of |
| Open with DEXTER | |
3 Data reduction
3.1 Instrumental polarization
As the BFI instrument has never been polarimetrically calibrated, we extrapolated the polarimetric measurement model of Ichimoto et al. (2008) to the observing wavelength of
![]() .
The retardance of the rotating wave plate is known at this wavelength
to be 9.338 waves.
All measured Stokes parameters have an opposite sign in the BFI data
compared to the NFI, because the polarizing beam-splitter analyzes
linear polarization with a direction at
.
The retardance of the rotating wave plate is known at this wavelength
to be 9.338 waves.
All measured Stokes parameters have an opposite sign in the BFI data
compared to the NFI, because the polarizing beam-splitter analyzes
linear polarization with a direction at ![]() with respect to the NFI.
with respect to the NFI.
The theoretical ![]() matrix (see Ichimoto et al. 2008)
for the shuttered CN band observations, which describes the
polarimetric efficiencies with its diagonal elements and cross-talk
with its non-diagonal elements and takes into account the exposure
intervals during the continuous modulation, is calculated to be
matrix (see Ichimoto et al. 2008)
for the shuttered CN band observations, which describes the
polarimetric efficiencies with its diagonal elements and cross-talk
with its non-diagonal elements and takes into account the exposure
intervals during the continuous modulation, is calculated to be
The
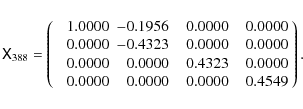
The CN band data at the N limb after correction of instrumental polarization (cf. Eq. (2)) are presented in Fig. 2. A clear scattering polarization signal is detected parallel to the limb, which increases towards the limb. Similar signals are also detected at the NW and E limb, with the correct direction of linear polarization (i.e., -U and -Q, respectively), confirming the solar origin of the signal. The pointing stability at the E limb proved to be poor, so we discarded that data set.
We chose not to rotate the local Stokes coordinate system so that Q/I would always be oriented parallel to the limb to prevent the introduction or mixing of systematic effects. All measurements are therefore presented in the global [Q,U] coordinate system of Hinode (see Ichimoto et al. 2008, which incidentally has the opposite sign of Stokes U as compared with the current Hinode pipeline).
3.2 Masking
Various data masks were created to enable a statistical analysis of the N and NW data sets.
First, the pixels at the edges of the two CCD halves were flagged and discarded, as were dead pixels.
The obtained SP scans were converted to line-of-sight and plane-of-sky total line polarization maps with the stksimages routine included in the Hinode-SP pipeline.
Then these maps were warped to the BFI coordinate system and sampling with the equations of Centeno et al. (2009).
The SP results for the N limb are presented in the lower panels of Fig. 2.
Because we are primarily interested in the polarization signals in the internetwork quiet Sun, all pixels exceeding ![]() of the noise in the transverse magnetograms were excluded.
The spatial resolution of the fast map SP data is course enough to
accommodate co-registration errors between the SP data and the BFI
data.
Furthermore, it is expected that formation height differences between
the CN band and in Fe I 630.15 and
of the noise in the transverse magnetograms were excluded.
The spatial resolution of the fast map SP data is course enough to
accommodate co-registration errors between the SP data and the BFI
data.
Furthermore, it is expected that formation height differences between
the CN band and in Fe I 630.15 and
![]() make features appear at slightly different locations (shifted in the
limbward direction) when observing close to the limb, where the
atmospheric stratification is observed almost perpendicularly.
The spatial resolution of the SP data (
make features appear at slightly different locations (shifted in the
limbward direction) when observing close to the limb, where the
atmospheric stratification is observed almost perpendicularly.
The spatial resolution of the SP data (
![]() )
is courser than these expected shifts (
)
is courser than these expected shifts (![]()
![]() ).
To a large extent these magnetic masks only take out the polar faculae
that are also apparent in the CN band intensity data of Fig. 2.
Because the intensity of these faculae is much higher than the
surroundings, the magnetic masks also serve to decrease systematic
cross-talk effects from Stokes I to Q/I or U/I.
The remaining pixels are now assumed to represent the quiet Sun.
Polarization signals are observed practically everywhere in the longitudinal SP maps (see also Tsuneta et al. 2008).
Because of the limited spatial resolution of the fast map SP data,
magnetic structure at granular scales cannot be distinguished very
close to the limb.
).
To a large extent these magnetic masks only take out the polar faculae
that are also apparent in the CN band intensity data of Fig. 2.
Because the intensity of these faculae is much higher than the
surroundings, the magnetic masks also serve to decrease systematic
cross-talk effects from Stokes I to Q/I or U/I.
The remaining pixels are now assumed to represent the quiet Sun.
Polarization signals are observed practically everywhere in the longitudinal SP maps (see also Tsuneta et al. 2008).
Because of the limited spatial resolution of the fast map SP data,
magnetic structure at granular scales cannot be distinguished very
close to the limb.
We assigned a value for
![]() to each pixel.
These
to each pixel.
These ![]() masks are used to sort the data in bins of
masks are used to sort the data in bins of ![]() intervals to produce plots of the CLV of the CN band scattering polarization as a function of
intervals to produce plots of the CLV of the CN band scattering polarization as a function of ![]() .
We chose a bin size for
.
We chose a bin size for ![]() of
0.04, which is a compromise between sufficient sampling of the CLV and
obtaining sufficient statistics on granules and pixel noise within each
bin.
The bin limits are overplotted as contours on the N limb data of
Fig. 2.
Because the scattering polarization decreases rapidly with increasing
limb distance, but the bins grow in size, the relative noise of the
measured scattering polarization does not vary rapidly.
After binning, we integrated over all pixels in a
of
0.04, which is a compromise between sufficient sampling of the CLV and
obtaining sufficient statistics on granules and pixel noise within each
bin.
The bin limits are overplotted as contours on the N limb data of
Fig. 2.
Because the scattering polarization decreases rapidly with increasing
limb distance, but the bins grow in size, the relative noise of the
measured scattering polarization does not vary rapidly.
After binning, we integrated over all pixels in a ![]() bin to increase the S/N of the measured scattering polarization.
In this way, specific spatial information is lost, except for a
dedicated averaging over ``granules'' and ``intergranules'', as
explained below.
bin to increase the S/N of the measured scattering polarization.
In this way, specific spatial information is lost, except for a
dedicated averaging over ``granules'' and ``intergranules'', as
explained below.
We fit the limb darkening in the quiet sun data as a function of ![]() (without binning) with a 5th-degree polynomial
(without binning) with a 5th-degree polynomial
![]() (cf. Neckel 1996).
The ``granules'' and ``intergranules'' are subsequently selected to
have a higher and lower intensity than the median value of the
limb-darkening corrected intensity data, respectively. Any definition
of ``granules'' and ``intergranules'' is necessarily somewhat
arbitrary.
The median value is chosen to balance the number statistics between
``granules'' and ``intergranules'', and also to deal with spurious
polarization signals, as elaborated in the next subsection.
(cf. Neckel 1996).
The ``granules'' and ``intergranules'' are subsequently selected to
have a higher and lower intensity than the median value of the
limb-darkening corrected intensity data, respectively. Any definition
of ``granules'' and ``intergranules'' is necessarily somewhat
arbitrary.
The median value is chosen to balance the number statistics between
``granules'' and ``intergranules'', and also to deal with spurious
polarization signals, as elaborated in the next subsection.
The granular pattern is clearly resolved down to ![]() as shown in Fig. 2.
The granulation close to the limb appears foreshortened.
The bright parts are in fact the hot granular walls (see Keller et al. 2004).
This means that the identification of ``granules'' and
``intergranules'' does not necessarily coincide with a similar
identification at disk center.
The terms ``granules'' and ``intergranules'' used throughout this paper
should therefore be interpreted with this caveat in mind.
as shown in Fig. 2.
The granulation close to the limb appears foreshortened.
The bright parts are in fact the hot granular walls (see Keller et al. 2004).
This means that the identification of ``granules'' and
``intergranules'' does not necessarily coincide with a similar
identification at disk center.
The terms ``granules'' and ``intergranules'' used throughout this paper
should therefore be interpreted with this caveat in mind.
3.3 Spurious polarization signals
Spatially varying, spurious polarization signals are clearly observed in the Q/I, U/I and also the V/I data, similar to the structure in the top right panel of Fig. 2. A large fraction of these signals is caused by cross-talk between the Stokes parameters introduced through image motion during the modulation, which is not completely corrected by the image stabilization system of the Hinode-SOT. Note that at the high polarimetric sensitivity levels of these observations, a minute displacement of 1 milliarcsecond already creates a detectable signature in the polarization data.
We assume that the displacements are indeed small and constant over the
FOV, and modeled this spurious signal due to residual image motion
similar to Lites (1987).
Let ![]() and
and ![]() denote the modulation matrix and the demodulation matrix.
In a single-beam instrument, cross-talk from I will dominate.
For Q, we then have
denote the modulation matrix and the demodulation matrix.
In a single-beam instrument, cross-talk from I will dominate.
For Q, we then have
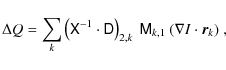
|
(3) |
where
where
We remove effects of image motion during the modulation cycle using an ![]() found for each frame by minimizing
found for each frame by minimizing
![]() in an area away from the limb, where the angled brackets denote averaging over that area.
Note that with Eq. (1)
in an area away from the limb, where the angled brackets denote averaging over that area.
Note that with Eq. (1)
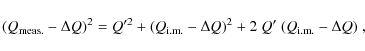
|
(5) |
where
In the absence of limb darkening, the average value of Q in the ``granules'' and the
``intergranules'' is not affected by a correction according to Eq. (4),
but the spread of the distribution around this average is decreased.
This is because the definition of ``granules'' and ``intergranules'' as
pixels exhibiting more and less intensity than the median is such that
after adding up all selected pixels, the residual value of
![]() is zero: for both the ``granules'' and the ``intergranules'' mask it
constitutes an integration of the derivative (gradient) of the
intensity image over an interval with identical intensity values at the
boundaries.
is zero: for both the ``granules'' and the ``intergranules'' mask it
constitutes an integration of the derivative (gradient) of the
intensity image over an interval with identical intensity values at the
boundaries.
The influence of the limb darkening is calculated as
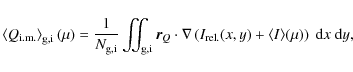
|
(6) |
which is a normalized integration over all ``granules'' (g) or ``intergranules'' (i) over the bin with average value
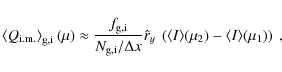
|
(7) |
where
The remaining spurious signals are due to solar evolution and are difficult to model.
They are, however, very relevant for our investigation: during the polarimetric modulation (![]() 10 s) all pixels change intensity because of the dynamic granulation.
Therefore this effect may create an artificial difference in Q/I and U/I for ``granules'' and ``intergranules''.
This difference is expected to be very similar in magnitude for Stokes Q and Stokes U, because they are (de-)modulated with identical amplitude.
However, after correction for the modulation phase delay the demodulation sequence is slightly different for Q and U.
The center-to-limb behavior of these spurious signals for ``granules'' and ``intergranules'' is investigated for U/I in the N limb data set, where ideally only scattering polarization signals are present in Q/I and vice versa with the data at the NW limb.
With the slow variation of the appearance of the granulation away from disk center, the difference between
10 s) all pixels change intensity because of the dynamic granulation.
Therefore this effect may create an artificial difference in Q/I and U/I for ``granules'' and ``intergranules''.
This difference is expected to be very similar in magnitude for Stokes Q and Stokes U, because they are (de-)modulated with identical amplitude.
However, after correction for the modulation phase delay the demodulation sequence is slightly different for Q and U.
The center-to-limb behavior of these spurious signals for ``granules'' and ``intergranules'' is investigated for U/I in the N limb data set, where ideally only scattering polarization signals are present in Q/I and vice versa with the data at the NW limb.
With the slow variation of the appearance of the granulation away from disk center, the difference between
![]() and
and
![]() is expected to be a smooth function.
is expected to be a smooth function.
The real solar data can now be referenced to the instrumental
polarization and spurious signals due to solar evolution (and other
unknown effects). With the assumptions and procedures described in this
subsection, Eq. (1) is converted to
where
assuming that
![\begin{figure}
\par\mbox{\includegraphics[width=8cm,clip]{14500f3a.eps} \hskip10...
...ncludegraphics[width=8cm,clip]{14500f3d.eps} }\\
\vspace*{-0.5mm}
\end{figure}](/articles/aa/full_html/2010/11/aa14500-10/Timg77.png)
|
Figure 3: Results for the center-to-limb variation of the CN band scattering polarization data at the N and NW limb. The upper panels present the measured scattering polarization after splitting the binned data according to ``granules'' and ``intergranules'' and subtracting the obtained difference between ``granules'' and ``intergranules'' in the reference data (shown in the lower panels) and the polarization offset c. The CLV fit of the combined data of the scattering polarization is represented by the dotted curve. The results for ``granules'' and ``intergranules'' are represented separately by the solid and dashed curves, respectively. |
| Open with DEXTER | |
4 Results and discussion
The Q/I and U/I data as a function of ![]() for the N and NW limb are presented in Fig. 3.
The observed CLV of the scattering polarization is plotted in the upper
panels, after splitting the data according to ``granules'' and
``intergranules'', and referencing it to the observed difference in the
U/I data at the N limb.
The reference signals for the scattering polarization signals are plotted in the lower panels of Fig. 3
and are defined as the linear polarization measurements for the
(normalized) Stokes parameter that should not contain scattering
polarization, so U/I for the N limb data and Q/I for the NW limb data.
The absolute values for the reference signals are irrelevant, because the polarization offset
for the N and NW limb are presented in Fig. 3.
The observed CLV of the scattering polarization is plotted in the upper
panels, after splitting the data according to ``granules'' and
``intergranules'', and referencing it to the observed difference in the
U/I data at the N limb.
The reference signals for the scattering polarization signals are plotted in the lower panels of Fig. 3
and are defined as the linear polarization measurements for the
(normalized) Stokes parameter that should not contain scattering
polarization, so U/I for the N limb data and Q/I for the NW limb data.
The absolute values for the reference signals are irrelevant, because the polarization offset
![]() is poorly known at this level for both Q/I and U/I.
The reference signals exhibit a difference of similar magnitude for the N and NW data.
Yet, the systematic difference is flat with
is poorly known at this level for both Q/I and U/I.
The reference signals exhibit a difference of similar magnitude for the N and NW data.
Yet, the systematic difference is flat with ![]() at the N limb, whereas it slightly varies with
at the N limb, whereas it slightly varies with ![]() at the NW limb.
The reason for this may be somehow related to the fact that the
rectangular FOV is not aligned with the NW limb direction, whereas at
the N limb the FOV is oriented much more symmetrically with respect to
the scattering polarization signals.
Because the magnitude of the reference signals is the same, and because
Q and U
are modulated with identical amplitude, we assumed that the difference
in the reference signals (e.g., due to solar evolution) is the
same for both data sets.
The reference signals at the N limb (in the lower left panel of
Fig. 3) are obviously the cleanest, and we adopted the average difference measured in U/I as a reference for the scattering polarization data for ``granules'' and ``intergranules''.
at the NW limb.
The reason for this may be somehow related to the fact that the
rectangular FOV is not aligned with the NW limb direction, whereas at
the N limb the FOV is oriented much more symmetrically with respect to
the scattering polarization signals.
Because the magnitude of the reference signals is the same, and because
Q and U
are modulated with identical amplitude, we assumed that the difference
in the reference signals (e.g., due to solar evolution) is the
same for both data sets.
The reference signals at the N limb (in the lower left panel of
Fig. 3) are obviously the cleanest, and we adopted the average difference measured in U/I as a reference for the scattering polarization data for ``granules'' and ``intergranules''.
The error bars in the plots of Fig. 3 are the ![]() ``standard errors'' of the data within each bin.
The standard error is defined as
``standard errors'' of the data within each bin.
The standard error is defined as
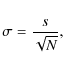
|
(10) |
where s is the sample standard deviation and N is the number of samples, and represents the accuracy with which the average value in each bin is known, provided the noise is Gaussian. Because systematic effects are still present in the bins (e.g., variation of polarization within the bins, residual spurious signals), these error bars merely serve as an indication of the uncertainty in the averaged data points. Therefore the error bars could not be used to quantify the significance of the differences between scattering polarization in ``granules'' and ``intergranules'', and we needed to resort to combining data at different
After subtracting the found average polarization difference found for the reference signals, the CLV of the scattering polarization in both data sets appears to be smooth (upper panels of Fig. 3). Moreover, apparent differences between the CLV of ``granules'' and ``intergranules'' are readily observed in both cases. In general, the difference between the scattering polarization signals appear to scale with the total scattering polarization, with the signals in the ``granules'' being larger. This indicates that the origin of this difference is likely to be solar, because many instrumental effects and solar evolution introduce an absolute difference, whereas physical effects on the Sun, such as differences in scattering anisotropy and Hanle depolarization, introduce mostly relative effects.
Note that the absolute value of the measured scattering polarization is about 40% higher at the NW compared to the N limb.
The cause for this is either a reduced value of the
![]() in the
in the ![]() matrix, or a real solar effect such as overall depolarization due to stronger turbulent magnetic fields at the N pole.
The only remarkable difference in the corresponding SP maps is the presence of polar faculae at the N limb (see also Tsuneta et al. 2008).
Incidentally, such a systematic variation along the limb was not found in observations of scattering polarization in C2 lines by Kleint et al. (2010).
In any case, this difference in absolute value once more makes it
necessary to characterize the difference in scattering polarization
between ``granules'' and ``intergranules'' as a relative difference,
i.e.,
matrix, or a real solar effect such as overall depolarization due to stronger turbulent magnetic fields at the N pole.
The only remarkable difference in the corresponding SP maps is the presence of polar faculae at the N limb (see also Tsuneta et al. 2008).
Incidentally, such a systematic variation along the limb was not found in observations of scattering polarization in C2 lines by Kleint et al. (2010).
In any case, this difference in absolute value once more makes it
necessary to characterize the difference in scattering polarization
between ``granules'' and ``intergranules'' as a relative difference,
i.e.,
To obtain a first quantitative measure of the differences in scattering polarization between ``granules'' and ``intergranules'', and, more importantly, establish the zero point of the polarization scale, we performed curve fits of the CLV of the measured scattering polarization according to Stenflo et al. (1997),
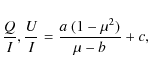
|
(12) |
in which a represents the amplitude of the scattering polarization, and c fits the unknown offset of the polarization scale, which is the main goal of this fitting procedure. The fit parameter b was introduced by Stenflo et al. (1997) to improve the fits of the CLV of many lines exhibiting scattering polarization. First, the combined data was fitted. The results of these fits are shown in the top panels of Fig. 3 with dotted curves. Note that inclusion of the limb darkening function in the fit, as suggested by Stenflo et al. (1997) and references therein, did not improve the fit quality and in fact slightly increased the 1
![\begin{figure}
\par\includegraphics[width=9cm,clip]{14500f4}
\end{figure}](/articles/aa/full_html/2010/11/aa14500-10/Timg89.png)
|
Figure 4:
Relative differences between ``granules'' and ``intergranules'' for the data from Fig. 3. The data were shifted by
|
| Open with DEXTER | |
The relative differences between ``granules'' and ``intergranules'' as a function of ![]() for both data sets is plotted in Fig. 4.
The error bars are the propagated ``standard errors'', which are
treated as Gaussians.
So again, these error bars do not properly incorporate systematic
effects, but give a rough indication of the total error of the data
points.
It is clear from this plot that the average of most (if not all)
measured relative differences are
for both data sets is plotted in Fig. 4.
The error bars are the propagated ``standard errors'', which are
treated as Gaussians.
So again, these error bars do not properly incorporate systematic
effects, but give a rough indication of the total error of the data
points.
It is clear from this plot that the average of most (if not all)
measured relative differences are ![]() 0, indicating a significant decrease of scattering polarization in the ``intergranules''.
It is however also obvious that these average values exhibit systematic effects as a function of
0, indicating a significant decrease of scattering polarization in the ``intergranules''.
It is however also obvious that these average values exhibit systematic effects as a function of ![]() .
To analyze granulation that is clearly resolved by the observations, we now discarded the data for
.
To analyze granulation that is clearly resolved by the observations, we now discarded the data for ![]() .
Furthermore, the N limb data above
.
Furthermore, the N limb data above ![]() is conspicuously different from the rest of the data as the difference
in scattering polarization between ``granules'' and ``intergranules''
between
is conspicuously different from the rest of the data as the difference
in scattering polarization between ``granules'' and ``intergranules''
between ![]() and
and ![]() is fully consistent with zero, whereas all other data points (including those between
is fully consistent with zero, whereas all other data points (including those between ![]() and
and ![]() at the NW limb) are distributed fairly smoothly around a value below zero.
We therefore computed the average value for both data sets between
at the NW limb) are distributed fairly smoothly around a value below zero.
We therefore computed the average value for both data sets between ![]() and
and ![]() ,
where the data in Fig. 4 appears to behave in a relatively random fashion, and, moreover, is consistent between the N and NW data sets.
Also, the reference signals in the lower panels of Fig. 3 are most consistent in this region.
The obtained average plus/minus the standard deviation thereof are overplotted as a dashed and dotted lines, respectively.
The obtained value for the relative difference of scattering polarization between ``intergranules'' and
``granules'' for
,
where the data in Fig. 4 appears to behave in a relatively random fashion, and, moreover, is consistent between the N and NW data sets.
Also, the reference signals in the lower panels of Fig. 3 are most consistent in this region.
The obtained average plus/minus the standard deviation thereof are overplotted as a dashed and dotted lines, respectively.
The obtained value for the relative difference of scattering polarization between ``intergranules'' and
``granules'' for
![]() is
is
![]() .
Of course, systematic effects cannot be completely excluded either for
this result which used a limited amount of data, but we adopted it as
our main result that is least affected by systematic effects.
.
Of course, systematic effects cannot be completely excluded either for
this result which used a limited amount of data, but we adopted it as
our main result that is least affected by systematic effects.
Note that also most data outside the chosen ![]() range
match the adopted relative difference, except for the four data-points
that correspond to zero difference.
Interestingly, the two ``zero'' data points at the N limb correspond to
a region of enhanced facular activity, which also harbors strong
magnetic fields outside the apparent faculae according to the
longitudinal (Stokes V) SP map of Fig. 2.
The observations at the NW limb at those values of
range
match the adopted relative difference, except for the four data-points
that correspond to zero difference.
Interestingly, the two ``zero'' data points at the N limb correspond to
a region of enhanced facular activity, which also harbors strong
magnetic fields outside the apparent faculae according to the
longitudinal (Stokes V) SP map of Fig. 2.
The observations at the NW limb at those values of ![]() harbor much weaker magnetic fields.
If the Hanle effect is the dominating factor for the absolute line
polarization, then this implies that at this region close to polar
faculae, both the granules and the intergranules are permeated by
strong magnetic fields.
Because of its proximity to the limb, it is difficult to assess from
the SP data whether there is increased magnetic activity at the values
of
harbor much weaker magnetic fields.
If the Hanle effect is the dominating factor for the absolute line
polarization, then this implies that at this region close to polar
faculae, both the granules and the intergranules are permeated by
strong magnetic fields.
Because of its proximity to the limb, it is difficult to assess from
the SP data whether there is increased magnetic activity at the values
of ![]() at the NW limb that exhibit zero difference in scattering polarization.
But it is obvious from the data in Fig. 3 that the absolute values of the scattering polarization are also consistently lower there.
at the NW limb that exhibit zero difference in scattering polarization.
But it is obvious from the data in Fig. 3 that the absolute values of the scattering polarization are also consistently lower there.
It is worth remarking that the observed absolute difference between ``granules'' and ``intergranules'' of ![]()
![]() in Fig. 3 corresponds well with a Hanle depolarization difference from
in Fig. 3 corresponds well with a Hanle depolarization difference from
![]() to
to
![]() in Fig. 8 of Shapiro et al. (2007), which matches the prediction by Trujillo Bueno et al. (2004).
It is, however, required to compare the data presented herein to an MHD
model with realistic line synthesis of the CN band before any final
statements about the nature of the weak, turbulent magnetic fields can
be made.
The results presented in Figs. 3 and 4 are therefore most useful as constraints to future models.
in Fig. 8 of Shapiro et al. (2007), which matches the prediction by Trujillo Bueno et al. (2004).
It is, however, required to compare the data presented herein to an MHD
model with realistic line synthesis of the CN band before any final
statements about the nature of the weak, turbulent magnetic fields can
be made.
The results presented in Figs. 3 and 4 are therefore most useful as constraints to future models.
5 Conclusions
We conclude that there is a significant difference in the scattering polarization signals between ``granules''
and ``intergranules'' (as defined in Sect. 3) in the CN band as shown in Fig. 4.
It is determined that the ``intergranules'' exhibit
![]() less scattering polarization for
less scattering polarization for
![]() .
The physical cause for this difference (formation effects, scattering
anisotropy variations, different turbulent magnetic field strengths)
cannot be established from these observations, but could be obtained by
confronting the obtained data with a realistic MHD model combined with
detailed polarized line synthesis of the CN band.
.
The physical cause for this difference (formation effects, scattering
anisotropy variations, different turbulent magnetic field strengths)
cannot be established from these observations, but could be obtained by
confronting the obtained data with a realistic MHD model combined with
detailed polarized line synthesis of the CN band.
Two polarization effects are observed in the data that correlate with the presence of polar faculae: the overall scattering polarization at the N limb is lower than at the NW limb, and the difference in scattering polarization between ``granules'' and ``intergranules'' at a region of strong facular activity is zero. Both these observations could be understood in terms of the Hanle effect, indicating the presence of stronger (turbulent) magnetic fields near the polar faculae. Unfortunately, the CN band and spectropolarimeter observations are dominated by noise and are moreover not strictly cotemporal. This seriously complicates the interpretation of correlation analyses between both data sets. Therefore no conclusion can be drawn as to whether or not the magnetic fields measured by the SP have any significant effect on the CN band scattering polarization.
It is impossible to completely exclude systematic effects and assess their influence on the obtained results. One way of addressing the systematic effects is to construct a complete physical model for the reference signals in the lower panels of Fig. 3. But more trust in the data can also be obtained by showing that the possible physical effects on the Sun indeed have a similar scaling effect on the scattering polarization, as observed in the data after correcting with the (additive) reference signals.
On the one hand, the CN band is well suited for scattering
polarization observations because its absolute scattering polarization
signals are relatively large, mostly due to the rapid increase of the
continuum polarization towards the blue (see Trujillo Bueno & Shchukina 2009).
On the other hand, the radiative transfer in the (molecular) CN band is
relatively difficult to model compared to some other atomic lines.
More suitable for observations of scattering polarization at high
spatial resolution are therefore lines like
Ba II at
![]() ,
Sr I at
,
Sr I at
![]() ,
and Na I D2,
all of which have a sizable scattering polarization (
,
and Na I D2,
all of which have a sizable scattering polarization (![]()
![]() )
and are relatively well understood.
A narrow-band tunable filter needs to be employed for these narrow
lines. This introduces the possibility to distinguish line and
continuum polarization, which is not possible for the CN band
observations.
Because no such capabilities are planned in space in the foreseeable
future, observations of scattering polarization at high spatial
resolution need to be attempted from the ground to further constrain
models of weak, turbulent magnetic fields in the solar photosphere.
)
and are relatively well understood.
A narrow-band tunable filter needs to be employed for these narrow
lines. This introduces the possibility to distinguish line and
continuum polarization, which is not possible for the CN band
observations.
Because no such capabilities are planned in space in the foreseeable
future, observations of scattering polarization at high spatial
resolution need to be attempted from the ground to further constrain
models of weak, turbulent magnetic fields in the solar photosphere.
We thank Roberto Casini for useful discussions. Hinode is a Japanese mission developed and launched by ISAS/JAXA, collaborating with NAOJ as a domestic partner, NASA and STFC (UK) as international partners. Scientific operation of the Hinode mission is conducted by the Hinode science team organized at ISAS/JAXA. This team mainly consists of scientists from institutes in the partner countries. Support for the post-launch operation is provided by JAXA and NAOJ (Japan), STFC (UK), NASA, ESA, and NSC (Norway).
References
- Asensio Ramos, A., & Trujillo Bueno, J. 2003, in: Solar Polarization, Proceedings of the Conference held 30 September-4 October, 2002 at Tenerife, Canary Islands, Spain. ed. J. Trujillo-Bueno, & J. S. Almeida (San Francisco: ASP), ASP Conf. Proc., 307, 195 [Google Scholar]
- Casini, R., & Manso Sainz, R. 2005, ApJ, 624, 1025 [NASA ADS] [CrossRef] [Google Scholar]
- Centeno, R., Lites, B. W., de Wijn, A. G., & Elmore, D. 2009, in: proceedings of the Second Hinode Science Meeting, held in Boulder, CO, Sept 30-Oct 3, 2008, ASP Conf. Ser., 415, 323 [NASA ADS] [Google Scholar]
- de Wijn, A. G., Stenflo, J. O., Solanki, S. K., & Tsuneta, S. 2009, Space Sci. Rev., 144, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Gandorfer, A. 2005, The Second Solar Spectrum: A high spectral resolution polarimetric survey of scattering polarization at the solar limb in graphical representation (Zürich: vdf Hochschulverlag), 3, 3160 [NASA ADS] [Google Scholar]
- Ichimoto, K., Lites, B., Elmore, D., et al. 2008, Sol. Phys., 249, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Keller, C. U. 1996, Sol. Phys., 164, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Keller, C. U., Schüssler, M., Vögler, A., & Zakharov, V. 2004, ApJ, 607, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Kleint, L., Berdyugina, S. V., Shapiro, A. I., & Bianda, M. 2010, Proceedings of SOHO-23: Understanding a Peculiar Solar Minimum, ASP Conf. Ser., 428, 103 [Google Scholar]
- Kosugi, T., Matsuzaki, K., Sakao, T., et al. 2007, Sol. Phys., 243, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Lites, B. W. 1987, Appl. Opt., 26, 3838 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Neckel, H. 1996, Sol. Phys., 167, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Shapiro, A. I., Berdyugina, S. V., Fluri, D. M., & Stenflo, J. O. 2007, A&A, 475, 349 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stenflo, J. O. 2004, Rev. Mod. Astron., 17, 269 [NASA ADS] [Google Scholar]
- Stenflo, J. O., & Keller, C. U. 1997, A&A, 321, 927 [NASA ADS] [Google Scholar]
- Stenflo, J. O., Bianda, M., Keller, C. U., & Solanki, S. K. 1997, A&A, 322, 985 [NASA ADS] [Google Scholar]
- Stenflo, J. O., Gandorfer, A., Wenzler, T., & Keller, C. U. 2001, A&A, 367, 1033 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stenflo, J. O., Gandorfer, A., Holzreuter, R., et al. 2002, A&A, 389, 314 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Suematsu, Y., Tsuneta, S., Ichimoto, K., et al. 2008, Solar Phys., 249, 197 [Google Scholar]
- Trujillo Bueno, J. 2009, in Solar Polarization 5: In Honor of Jan Stenflo ASP Conference Series, proceedings of the conference held 17-21 September, 2007 at Centro Stefano Franscini-Monte Verit, Ascona, Switzerland. ed. S. V. Berdyugina, K. N. Nagendra, & R. Ramelli (San Francisco: Astronomical Society of the Pacific), 405, 65 [Google Scholar]
- Trujillo Bueno, J., Casini, R., Landolfi, M., & Landi Degl'Innocenti, E. 2002, ApJ, 566, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Trujillo Bueno, J., Shchukina, N., & Asensio Ramos, A. 2004, Nature, 430, 326 [Google Scholar]
- Trujillo Bueno, J., & Shchukina, N. 2009, ApJ, 694, 1364 [NASA ADS] [CrossRef] [Google Scholar]
- Tsuneta, S., Ichimoto, K., Katsukawa, Y., et al. 2008, ApJ, 688, 1374 [Google Scholar]
- Tsuneta, S., Suematsu, Y., Ichimoto, K., et al. 2008, Sol. Phys., 249, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Uitenbroek, H., & Tritschler, A. 2007, A&A, 462, 1157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vögler, A., & Schüssler, M. 2007, A&A, 465, L43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Footnotes
- ... pipeline
![[*]](/icons/foot_motif.png)
- The Hinode pipeline is implemented in the IDL SSW, see http://www.lmsal.com/solarsoft/.
All Figures
![\begin{figure}
\par\includegraphics[width=9cm,clip]{14500f1.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa14500-10/Timg10.png)
|
Figure 1:
The intensity and scattering polarization spectrum at |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[width=8.2cm,clip]{14500f2a.eps} \hskip...
...s} \hskip10mm
\includegraphics[width=8.2cm,clip]{14500f2d.eps} }
\end{figure}](/articles/aa/full_html/2010/11/aa14500-10/Timg35.png)
|
Figure 2:
Stokes I and Q/I observations in the CN band at 388 nm at the north limb of the Sun. The bin limits of |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[width=8cm,clip]{14500f3a.eps} \hskip10...
...ncludegraphics[width=8cm,clip]{14500f3d.eps} }\\
\vspace*{-0.5mm}
\end{figure}](/articles/aa/full_html/2010/11/aa14500-10/Timg77.png)
|
Figure 3: Results for the center-to-limb variation of the CN band scattering polarization data at the N and NW limb. The upper panels present the measured scattering polarization after splitting the binned data according to ``granules'' and ``intergranules'' and subtracting the obtained difference between ``granules'' and ``intergranules'' in the reference data (shown in the lower panels) and the polarization offset c. The CLV fit of the combined data of the scattering polarization is represented by the dotted curve. The results for ``granules'' and ``intergranules'' are represented separately by the solid and dashed curves, respectively. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{14500f4}
\end{figure}](/articles/aa/full_html/2010/11/aa14500-10/Timg89.png)
|
Figure 4:
Relative differences between ``granules'' and ``intergranules'' for the data from Fig. 3. The data were shifted by
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.