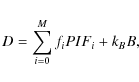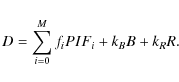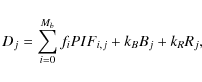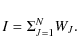EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 519 (September 2010) A&A, 519 (2010) A107 Full HTML
Free Access
Issue
A&A
Volume 519, September 2010
Article Number A107
Number of page(s) 11
Section Astronomical instrumentation
DOI https://doi.org/10.1051/0004-6361/200913814
Published online 20 September 2010
A&A 519, A107 (2010)

INTEGRAL/IBIS 7-year All-Sky Hard X-ray Survey

I. Image reconstruction[*]

R. Krivonos1,2 - M. Revnivtsev2,3 - S. Tsygankov1,2 - S. Sazonov2 - A. Vikhlinin2,4 - M. Pavlinsky2 - E. Churazov1,2 - R. Sunyaev1,2

1 - Max-Planck-Institute für Astrophysik, Karl-Schwarzschild-Str. 1, 85740 Garching bei München, Germany
2 - Space Research Institute, Russian Academy of Sciences, Profsoyuznaya 84/32, 117997 Moscow, Russia
3 - Excellence Universe Cluster, Munich Technical University, Boltzman-Str. 2, 85748 Garching bei München, Germany
4 - Harvard-Smithsonian Center for Astrophysics, 60 Garden Street, Cambridge, MA 02138, USA

Received 7 December 2009 / Accepted 20 May 2010

Abstract
This paper is the first in a series devoted to the hard X-ray whole sky survey performed by the INTEGRAL observatory over seven years. Here we present an improved method for image reconstruction with the IBIS coded mask telescope. The main improvements are related to the suppression of systematic effects that strongly limit sensitivity in the region of the Galactic plane (GP), especially in the crowded field of the Galactic center (GC). We extended the IBIS/ISGRI background model to take into account the Galactic ridge X-ray emission (GRXE). To suppress residual systematic artifacts on a reconstructed sky image, we applied nonparametric sky image filtering based on wavelet decomposition. The implemented modifications of the sky reconstruction method decrease the systematic noise in the ${\sim}20$ Ms deep field of GC by  ${\sim}44\%$, and practically remove it from the high-latitude sky images. New observational data sets, along with an improved reconstruction algorithm, allow us to conduct the hard X-ray survey with the best currently available minimal sensitivity 3.7 $\times $ 10-12 erg s-1 cm-2 $\sim$ 0.26 mCrab in the 17-60 keV band at a $5\sigma $ detection level. The survey covers $90\%$ of the sky down to the flux limit of 6.2 $\times $ 10-11 erg s-1 cm-2 ( ${\sim}4.32$ mCrab) and $10\%$ of the sky area down to the flux limit of 8.6 $\times $ 10-12 erg s-1 cm-2 ( ${\sim}0.60$ mCrab).

Key words: methods: data analysis - methods: observational - techniques: image processing - surveys - X-rays: general -
Galaxy: general

1 Introduction

Since its launch in October 2002, the INTEGRAL observatory (Winkler et al. 2003) has gathered a huge observational data set that allows us to perform the most sensitive hard X-ray survey to date. The main scientific results and source catalogs have been reported in many relevant papers concerning partial sky coverage (e.g. Bird et al. 2007; Revnivtsev et al. 2006a; Bird et al. 2006; Bazzano et al. 2006; Bassani et al. 2006; Revnivtsev et al. 2003; Krivonos et al. 2005; Bird et al. 2004; Molkov et al. 2004) and full sky studies (Bird et al. 2010; Sazonov et al. 2007; Krivonos et al. 2007b; Beckmann et al. 2009).

Recently, great progress in surveying the hard X-ray sky was achieved with the Burst Alert Telescope (BAT; Barthelmy et al. 2005) at the Swift observatory (Gehrels et al. 2004). The Swift/BAT survey provides very homogeneous sky coverage in the 15-195 keV energy band with a current maximum sensitivity of 2.2 $\times $ 10-11 erg s-1 cm-2. The distribution of survey sensitivity peaks in the extragalactic sky. The survey results and source catalogs have been reported in papers by Tueller et al. (2010) and Cusumano et al. (2010). As seen from the large sample of detected active galactic nuclei (AGNs), the results of the Swift/BAT survey are very valuable for extragalactic studies. However, due to the relatively poor angular resolution of the instrument, its imaging capabilities in the regions of Galactic plane (GP) and especially the Galactic center (GC) are limited. On the other hand, the sky coverage by the Swift/BAT survey is nearly uniform, therefore only a small fraction of its total operational time was devoted to observations of the Galaxy.

In contrast to Swift, the INTEGRAL observatory provides an all-sky survey with exposure more concentrated in the GP, having a typical limiting flux of less than 1.43 $\times $ 10-11 erg s-1 cm-2 (1 mCrab) in the working energy range 17-60 keV. With an angular resolution almost twice as good for Swift/BAT, one can effectively disentangle sources in such crowded regions as the GC. This makes the Swift/BAT and INTEGRAL surveys complementary.

INTEGRAL has already accumulated a lot of exposure time in the direction of the GP with a maximum of $\sim$20 Ms of nominal time in the direction of the GC. However, the growing exposure time devoted to the GP and GC is not reflected by a corresponding increase in survey sensitivity. Observations in these regions are strongly affected by the systematics related to the crowded field of the GC and strong Galactic X-ray background radiation.

In this work we address the question of improving the sensitivity of the ongoing INTEGRAL hard X-ray survey. In Sect. 2 we discuss several aspects of the sky reconstruction method of the IBIS coded-mask telescope (Ubertini et al. 2003). In Sect. 3 we implement Galactic background corrections to the sky reconstruction method. Section 4 introduces a modified sky reconstruction method with sky image filtering procedure based on à trous wavelet decomposition. The properties of the resulting all-sky survey are presented in Sect. 5.

Throughout the article the exposure will be expressed taking instrumental dead time into account, i.e. showing the effective exposure time, rather than the total exposure.

2 General sky reconstruction method

IBIS is a coded aperture imaging telescope. The sky is projected onto the detector plane through the transparent and opaque elements of the mask mounted above the detector plane. Generally, the sky reconstruction is based on the deconvolution of the detector image with a known mask pattern. We (EC) developed IBIS/ISGRI sky reconstruction method and have partially described it in our previous publications (Krivonos et al. 2007a; Revnivtsev et al. 2004; Krivonos et al. 2007b,2005). The basic idea we used is presented in Fenimore & Cannon (1981) and Skinner et al. (1987). For the standard IBIS/ISGRI analysis we refer the reader to the paper by Goldwurm et al. (2003). Here we outline only those steps that are essential for this study.

2.1 IBIS telescope coding aperture

The quality of the reconstructed sky image directly depends on our understanding of the coding procedure. For example, the mask's supporting structure can significantly reduce the number of low - energy photons passed though the open mask elements. Other assembly elements like screws, plates, and glue strips attaching the IBIS mask to the supporting structure also block the incoming photons, modifying the shadow cast by a point source on the detector.

In our package we implemented the best known configuration of all the known elements of the telescope, which contribute to the shadowgram. We could not find the exact size of the assembly screws that attach the mask, plates and glue strips. The approximate parameters of these elements were found by comparing real and model detector shadowgrams illuminated by a strong source at different azimuthal angles.

2.2 Detector exposure

In general the detector image, produced when observing M point sources with an underlying flat sky background, can be represented by the superposition of shadow patterns of sources (``pixel illumination fraction'', PIF) and the detector background map B:

\begin{displaymath}% D = \sum_{i=0}^{M} f_iPIF_i + k_{B}B, \end{displaymath} (1)

where fi is the source flux, $B=B_{\rm CXB}+B_{\rm det}$ represents a detector background map, containing photon counts from cosmic X-ray background (CXB), and detector instrumental noise. We assume that the detector illumination by CXB and intrinsic ISGRI background have a similar pattern, and can be merged into the background map B. The last is estimated by an accumulation detector image over a large number of observations without strong sources in the field of view. Obviously, background map B should contain the current detector background pattern due to the long-term variation in background environment related to the Sun and cosmic rays (Lebrun 2005). For a given observation, we use a background map accumulated during the nearest set of extragalactic observations. Typically, we construct a new background map for every ${\sim}50{-}70$ spacecraft orbits (150-200 days).

\begin{figure} \par\includegraphics[width=8.8cm,clip]{13814fg1.ps} \end{figure} Figure 1:

Sky image of a 2.7 ks observation of the bright source Crab Nebula. The source is in the center of the field of view. The periodic mask pattern leads to many false sources on the reconstructed sky. The most significant false peaks are located in vertexes of a  ${\sim }10.5^{\circ }$square around the source, oriented in detector coordinates as illustrated by the yellow square. The image is shown in significance with a squared root color map ranging from 0 to 25. Such color schemes are used for all the sky images in this paper in order to emphasize sky background variations. The black and blue colors correspond to pixel values from 0 to 2. The red pixels have values of around 5. The yellow to white color transition corresponds to 15 and more. Figure 2 demonstrates an image profile extracted from the $1^{\circ }$ $\times $ $29^{\circ }$ green region.

Open with DEXTER

When two sources are located close to each other (at separation comparable with IBIS/ISGRI angular resolution), the direct solution of Eq. (1) for flux fi can be unstable giving results with infinite errors. In other words, the detector count rate in a given sky direction can be explained by two (or more) sources having any absolute flux.

2.3 Replicated mask pattern

IBIS mask has replicated patterns (see Reglero et al. 2001; Ubertini et al. 2003; Goldwurm et al. 2003). This pattern of the mask has an advantage because, ideally, it has a much narrower point spread function and flat side lobes in the central part of the reconstructed image (Fenimore & Cannon 1978). But at the same time it causes serious complications because of the very significant side peaks of the point spread function. This means that a simple deconvolution algorithm sees ``ghost'' sources at certain sky positions (see Figs. 1 and 2), related to the position of the real source and the size of the replicated mask pattern.

The sources in a variety of sky positions within a field of view create shadows with similar patterns, which causes uncertainty in the source flux determination (the direct solution of Eq. (1) is impossible). Unfortunately, this situation is not rare in the crowded field of the GC, as shown in Fig. 3. Due to observational constraints, IBIS FOV was mainly co-aligned with axes of the equatorial coordinate system (``N-E'' notation). As a result, there are a number of bright sources which permanently appeared in mutual ``ghost'' positions. This leads to an additional uncertainty of the source flux determination. The following source pairs can be affected by mutual flux interplay: GX 340+0 and XTE J1743-363, XTE J1701-462 and GX 349+2, GX 9+9 and GX 13+1, and the triplet GX 1+4, XTE J1818-245 and GX 17+2.

\begin{figure} \par\includegraphics[width=8.5cm,clip]{13814fg2.ps} \end{figure} Figure 2:

Image profile extracted from the green region in Fig. 1. The profile demonstrates the response of the IBIS/ISGRI imaging system to the point source.

Open with DEXTER

2.4 Iterative removal of cataloged sources

For a good quality all-sky map, suitable for searching for new weak sources, the ghosts of known bright sources have to be removed. This is done during the reconstruction of images of individual observations (ScWs) with an effective exposure of 1-3 ks. Instead of a blind search for bright sources in each individual observation we use a catalog of known sources to control the removal of ghosts. Indeed, for many regions of sky, the final map is the result of stacking hundreds and thousands of individual observations. Therefore, a relatively weak object, far too faint to be detected in an individual observation, may appear as a very significant source in the final map. Since the amplitude of the ghosts scales with the intensity of the true source, it is clear that ghost removal should be applied even to objects that are too faint to be detected in individual science windows. For crowded fields (like the GC region), this implies that ghosts of some 100 sources should be removed in individual observations.

The whole procedure requires not only the list of sources to be removed from the detector image, but also a sequence of Iterative Removal Of Sources (IROS, see Goldwurm et al. 2003; Krivonos et al. 2005). It is expected (and confirmed by direct tests) that the brightest (most significant) objects have to be removed first, since the source flux f is evaluated by assuming that there is only one source in the field of view. The significance of the source detection is evaluated by reconstructing an image prior to iterative source removal and checking the fluxes at the positions of cataloged sources. The list of objects ranked according to their significance is then used as input for iterative source removal procedure. This poses the problem of ranking weak sources, since their flux (and ranking) is determined with a large uncertainty in the individual science window (e.g. the flux from the source can be negative). We made several tests with various ranking schemes for weak (less than $3\sigma$ detection) sources, checking the rms of the final maps and fluxes of cataloged sources. The final scheme implemented in our analysis uses the absolute value of the source detection significance to rank the order of source removal.

\begin{figure} \par\includegraphics[width=17.5cm,clip]{13814fg3.ps} \end{figure} Figure 3:

INTEGRAL/IBIS hard X-ray (17-60 keV) map of the sky region around the GC. The green squares demonstrate the relative sky positions of false side peaks (``ghosts'', see Fig. 1) of selected bright sources.

Open with DEXTER

2.5 ISGRI pixel filtering

As described in Krivonos et al. (2007b) the hot and dead ISGRI detector pixels were screened from the analysis. This was done using quite crude filtering criteria and some noisy pixels may still be present on the detector shadowgram. They may not be visible on an individual detector image, but can be revealed by those accumulated over several observations.

To estimate the effect induced by ``noisy'' pixels, we simulated a detector image for a typical ScW exposure of 2 ks, and inserted one pixel in an arbitrary position exceeding the mean detector count rate (40 cnts/pix/ScW) by a factor of ${\sim}2.5$ (${\sim}9.5$ standard deviations). For a typical ScW such a weak pecular pixel introduced negligible systematic noise and the reconstructed sky was dominated by Poisson statistics. However, with increasing exposure, the effect became more significant. We accumulated the mosaic image of a 280 ks staring[*] observation of NGC 4151 with a simulated detector and one hot pixel. When the position of a noisy pixel was randomly distributed on a detector in every observation, the total mosaic did not contain any significant systematic residuals. When a noisy pixel was fixed on the detector, the standard deviation of reconstructed sky was ${\sim}20\%$ higher, than without a hot pixel on the detector.

To perform additional ISGRI pixel cleaning, we followed the general approach also employed by Eckert et al. (2008). We stacked detector images obtained during the spacecraft orbit after removing flux from known X-ray sources (Sect. 2.4), detector background map B (Sect. 2.2), and Galactic X-ray background (Sect. 3). The distribution of pixels on a stacked detector image was described well by Gaussian with zero mean. Thus we expected that $99.7\%$ of the pixels have a value in the range $[-3\sigma,+3\sigma]$. The ISGRI detector contains 128 $\times $ 128 pixels, which gives us ${\sim}50$ of them with an expected value greater than $3\sigma$. However, we typically detected 200-300 deviations from zero to over $3\sigma$. We removed these pixels from further analysis. Filtering done in this way reduces the detector area by ${\sim}2\%$, and has a minor effect on flux from serendipitous, faint sources.

3 Galactic background

During observations of the GC region, the IBIS field of view contains many discrete sources (Fig. 4). But in contrast to high galactic latitude observations, the underlying sky background is not flat. From early X-ray observations we know that the Galaxy reveals itself as a strong diffuse emitter (e.g. Worrall et al. 1982). The morphology of the Galactic X-ray background at energies above 20 keV is now relatively well known. As shown in recent RXTE and INTEGRAL investigations (Krivonos et al. 2007a; Revnivtsev et al. 2006b), the X-ray background is traced by the near-infrared brightness of the Galaxy (blue contours in Fig. 4). We refer to the Galactic X-ray background later as ``Ridge'' emission or GRXE (Galactic ridge X-ray emission).

The measured 17-60 keV GRXE intensity per IBIS FOV reaches 200 mCrab in the region of the Galactic bulge. Such strong emission will not appear on a deconvolved IBIS/ISGRI sky, because the coded mask technique is not suitable for building an image of sources with angular sizes larger than the telescope's angular resolution (12$^\prime$). However, the presence of Galactic X-ray background in the IBIS FOV strongly affects the overall shape of the ISGRI detector shadowgram, which leads to the appearence of systematic noise on the reconstructed sky images.

\begin{figure} \par\includegraphics[width=4.4cm,clip]{13814fg4a.eps}\hspace*{1mm} \includegraphics[width=4.4cm,clip]{13814fg4b.eps} \end{figure} Figure 4:

Two relative alignments of the GP in the IBIS FOV, left centered and the right shifted along the galactic latitude. The blue contours are isophotes of the $4.9~\mu{\rm m}$surface brightness of the Galaxy (COBE/DIRBE) revealing the bulge/disk structure of the inner Galaxy. The NIR brightness of the galaxy traces the hard X-ray ridge emission. The small and large rounded squares on each plot demonstrate the full and partial coded areas, respectively. The points show sky positions of the hard X-ray sources detected on the 20 Ms time-averaged map (Figs. 11 and 3). A signal-to-noise ratio of the sources is shown by black (5-10), blue (10-30), and red (>30). The difference in detector illumination by the Ridge is shown in Fig. 5.

Open with DEXTER

The detector exposure by the point source and GRXE is different. The point source forms a shadow on the detector. Each exposed pixel contains an approximately constant source count rate, therefore the source shadowgram is flat (in illuminated pixels). This is explicitly assumed in Eq. (1). When IBIS FOV contains the Galactic ridge emission, one detector pixel ``sees'' different parts of the Ridge through the mask's open elements. The resulting detector image is convolution of the Ridge sky brightness distribution with the IBIS mask and the collimator response.

To model the contribution of the Ridge component to the detector, we have to assume some predefined sky surface brightness distribution. The Ridge emission at energies 17-60 keV is traced well by the near-infrared brightness of the Galaxy. The volume density distribution has been intensively investigated by COBE/DIRBE (see e.g. Dwek et al. 1995). We used the Galactic disk and bulge model from Revnivtsev et al. (2006b), which describes the COBE/DIRBE data in the simplest way. The model was taken from the near-infrared data and renormalized to fit X-ray intensity measured by INTEGRAL. We produced sky brightness maps by integrating the model volume density through the line of sight.

\begin{figure} \par\includegraphics[width=4.4cm,clip]{13814fg5a.ps}\hspace*{1mm} \includegraphics[width=4.4cm,clip]{13814fg5b.ps} \end{figure} Figure 5:

The contribution of Galactic X-ray background to the ISGRI detector count rate for different alignments of the GP in the IBIS FOV (see also Fig. 4). The detector count rate normalization is estimated from actual observation of the GC in the energy range 17-60 keV. The corresponding images in Figs. 4 and 5 are co-aligned in detector coordinates. The ridge, appearing in the given FOV corner, illuminates the opposite corner in the detector image.

Open with DEXTER

The contribution of the Ridge emission to the ISGRI detector can be implemented with the so-called ``gray mask'' approach: the given detector pixel sees the Ridge emission through the open mask elements in a solid angle limited by the telescope collimator.

To demonstrate Ridge detector exposure, we projected GRXE sky brightness onto the detector using two positions relative to the IBIS FOV. In position ``A'' the central part of the Ridge emission is placed in FOV on-axis (spacecraft pointing $l=0^{\circ}$, b=0, Fig. 4, left), and position ``B'' when the Ridge is $7^{\circ}$ away from the FOV center ( $l=0^{\circ}$, $b=7^{\circ}$, Fig. 4, right). The Ridge detector illumination implemented with the ``gray mask'' is shown in Fig. 5.

As clearly seen from the modeled detector images, the Ridge emission introduces large-scale variations on the ISGRI detector. When IBIS is centered on the GP (position ``A''), the Ridge contribution to the detector image has a relatively flat shape with some curvature. In contrast, detector variations have a significant gradient when the GP intersects FOV several degrees away from its center (position ``B''). That configuration strongly warps the detector image, which will obviously affect the source flux estimates and, consequently, the accuracy of the source shadowgrams removal.

The impact of this Ridge emission in the IBIS FOV to the reconstructed sky image is significant. The comprehensive demonstration of this effect directly on the GC data is not possible due to more serious effects related to the very complicated detector exposure to many bright sources. That is why, in order to show the Ridge contribution in the reconstructed sky, we used the relatively simple and clean 280 ks observation of NGC 4151 for reference (Fig. 8, left). The artificial detector Ridge component with actual normalization measured in the GC (position ``B'') was added to the detector image of every spacecraft observation. Since we used staring observations, this operation was equivalent to placing Ridge on the sky $7^{\circ}$ away from the NGC 4151. The quality of the final mosaic (Fig. 6, left) was very poor and the signal-to-noise ratio (hereafter S/N) distribution of pixels had strong non-Gaussian wings (Fig. 6). The standard deviation of image was 1.7, in contrast to 1.3 of the referenced sky. Thus, we can conclude that the Ridge emission can introduce significant systematic noise to the reconstructed sky. However the degree of image worsening depends on the exposure and pattern of the observations.

\begin{figure} \par\includegraphics[width=4.25cm,clip]{13814fg6a.eps}\includegraphics[width=4.4cm,clip]{13814fg6b.eps} \end{figure} Figure 6:

Left: the sky mosaic of 280 ks observation of NGC 4151 in staring mode. The Ridge contribution (Fig. 5, right) was artificially added to the detector plane for each individual observation. For reference see the left image in Fig. 8. Right: S/N distribution of a number of pixels in a reference and current sky images shown by red and blue histograms, respectively. The long dashed line represents the normal distribution with unit variance and zero mean.

Open with DEXTER

We next consider the typical IBIS/ISGRI observation of the GC region (position ``A''), as the most representative observation containing many bright sources and strong Ridge emission in the FOV. The detector image is shown in the left frame of Fig. 7. For comparison we show on the right the detector image containing only one bright source in FOV. The observations were separated by a 10-h time interval when the background count rate had not changed significantly, i.e., the background map for both images is the same. In the right image the background and source counts are clearly distinguished. This leads to straightforward application of the standard coded mask reconstruction algorithm (Sect. 2). The left image contains many overlapping shadowgrams of bright sources. The assumed background model is not accurate and the general method is confused.

The catalog of predefined source positions in the GC provides about a hundred objects in the FOV. Among them, 6-8 bright sources are usually detected with S/N>5 in the typical $\sim$2.5 ks observation. By summing up all $PIF {\rm s}$ of these sources, one can show that practically all detector pixels are illuminated by at least one source, which is seen in the left image of Fig. 7. This means that any measurements of source fluxes in the GC will be affected by the correlations of source shadowgrams, especially for those having replicated patterns due to the periodic mask elements. Furthemore, there are no source-free pixels to estimate the background count rate. Flux measurement, based on the balance matrix (Goldwurm et al. 2003; Krivonos et al. 2005) is inaccurate, because the background map for a given source is strongly affected by other sources. The general reconstruction algorithm works ``as is'', trying to estimate the fluxes of the brightest source and leaving many systematic artifacts on the detector and consequently, on the resulting sky image.

The situation is further complicated by the fact that practically all ISGRI pixels are illuminated at the same time by the Ridge emission (see Fig. 5). This leads to a high correlation between shadowgrams of a manifold of sources and the Ridge.

\begin{figure} \par\includegraphics[width=8.8cm,clip]{13814fg7.ps} \end{figure} Figure 7:

Left: the ISGRI detector image of the GC region ( $l=3.9^{\circ }$, $b=2.1^{\circ }$). Right: the shadowgram of a sky region containing only one bright source Sco X-1 ( $l=4.5^{\circ }$, $b=30.0^{\circ }$).

Open with DEXTER

Summing up all mentioned effects, we conclude, that Eq. (1) based on simple background map B is unsuitable for Galactic observations, and the iterative source removal is not valid when the detector map is warped by the Ridge. Generally, sky reconstruction is highly complicated in the case of the GC observations. To a large extent, the INTEGRAL/IBIS/ISGRI survey sensitivity is limited by systematic uncertainties, and new exposures in the GC have only minor effects on the total sensitivity.

4 Modified sky reconstruction method

The sky reconstruction method for IBIS/ISGRI should be able to split a detector image into the following layers:

  • source 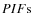$PIF {\rm s}$: characterized by a flat count rate and the pattern of the projected mask;

  • illumination by the Ridge: has certain low-(spatial)-frequency variations. The characteristic variations depend on the telescope orientation relative to the GP and GC;

  • ISGRI background layer: contains the CXB flux and instrumental background, and has a smooth count rate.
All these layers correlate to different degrees with each other owing to the shared detector area. We modify Eq. (1) to accommodate the Ridge component R:

\begin{displaymath}% D = \sum_{i=0}^{M} f_iPIF_i + k_{B}B + k_{R}R. \end{displaymath} (2)

The direct simultaneous solution of Eq. (2) is practically impossible before the components are orthogonalized. At first, we tried to reduce the mutual correlation between layers using different spatial features of the layers and the short list of sources. To do this, we selected Mb bright sources with S/N>7 which appeared in the FOV. We fit the relation (2) with the modeled Ridge contribution R, source PIFs, and background map B. The fitting procedure was unstable, producing inadequate estimates of the layer normalizations. We noticed high uncertainty in determination of Ridge and Background map components, respectively, kR and kB, due to its high mutual correlation.

One possible way of further disentangling the Ridge layer from others is to use different spacecraft orientations relative to the GP. To do this, we attempted to simultaneously fit the nearest Q observations (ScWs) before and after the current one:

\begin{displaymath}% D_j = \sum_{i=0}^{M_b} f_iPIF_{i,j} + k_{B}B_j + k_{R}R_j, \end{displaymath} (3)

where index j is running in the range [-Q,+Q] relative to the current observation j=0, and Mb denotes the number of bright sources that appeared in the FOV of every $j\in[-Q,+Q]$ observation with S/N>7. The on-axis direction of all selected observations is requested to be inside $15^{\circ}$ radius around the position of current observation.

We fitted large data sets using Eq. (3) for different Q>0 and found the Ridge component kR much better constrained with respect to the other layers. Guided by the stability of the fitting procedure, we chose Q=6 as an reasonable selection criteria. Generally, the procedure is more stable for more spatially scattered observations in the direction perpendicular to the GP. Among the available INTEGRAL observational patterns we have found that the best pattern for this approach is the Galactic Center Deep Exposure (GCDE, Core Program, see e.g. Winkler et al. 1999) and the Galactic Latitude Scans (PI Sunyaev). The fitting procedure running on large data sets of the usual 5 $\times $ 5 pattern (see ISOC Newsletter #12, September 2004), and the Galactic Plane Scans (GPS, Core Program, see e.g. Rodriguez et al. 2003; Del Santo et al. 2003) is not as stable, but still provides valuable results.

We should note that the contribution of the $i{\rm th}$ source ( fiPIFi,j) in Eq. (3) is estimated under the assumption of the constant flux fi during the considered time interval. In a similar way, the detector background count rate kB is also considered constant. For the chosen value of Q=6, the maximum number of observations is 13, which is in total ${\sim}25$ ks. Generally, for such a time interval, the majority of galactic X-ray sources do not vary by a factor of more than $\sim$2, except during the outburst activity.

Actually, the modified sky reconstruction algorithm described here is used only for constraining the Ridge component and its subsequent subtraction. After this step, the IROS procedure (Sect. 2.4) is applied in the usual manner on the detector plane of the given observation (ScW).

The employed procedure still does not allow us to completely resolve the problem of highly correlated shadowgrams on the detector in the case of the GC observations, but it at least reduces the systematic residuals on mosaic images introduced by Ridge emission.

4.1 Removing systematic residuals from sky images

After removing the source shadowgrams and the background from the detector, we still see the systematic effects on sky images. These residuals can be clearly seen on deep extragalactic observations performed in staring mode when sky images are stacked (pixel-to-pixel) in detector coordinates. All systematic residuals, not visible on images of individual observations (with an exposure of $\sim$2 ks) are amplified on the stacked image. The sky region around NGC 4151, was reconstructed with the help of the general deconvolution algorithm from the data collected in the staring mode, as shown in the left image of Fig. 8. The characteristic chessboard-like squares and ripples are clearly seen in the fully coded (central $10^\circ$ $\times $ $10^\circ$ square) and partically coded (outer parts) field of view.

The absence of bright sources in the field of view during these staring observations makes it clear that the presence of the patterns seen in Fig. 8 does not depend on the accuracy of our model of source shadowgram. We also cannot attribute visible systematic artifacts to the detector noisy pixels, because they were filtered out (Sect. 2.5).

The major origin of these patterns on the sky is the limited knowledge of the background pattern on the detector. It may consist of several unaccounted for parts, like the unexpected variations in pixel gains, the effective lifetimes, and lifetimes of the detector modules (the ISGRI detector has 8 modules of pixels, which in many cases change, see e.g. Fig. 5). Judging from a particular pattern of residuals on the sky, the major effect is due to the inaccurate estimate of efficiency and the energy band-passes of the detector pixels.

In the context of the general sky reconstruction method, it becomes extremely difficult to correct this problem because of the continuous degradation of detector pixels and the variation in the background environment. Despite our understanding of the origin of the residual structures on the sky, we decided to implement an alternate solution to this problem. Because the spatial scale of systematic artifacts on the sky is significantly different from the scale of the point sources, we implemented the wavelet-based image filtering procedure.

The key point of all wavelet methods is that the wavelet transform (WT) is able to distinguish structures as a function of the spatial scale, and thus is well suited to detecting small scale structures on an image embedded within larger scale features. That is why WT has been widely used for structure analysis of galaxy clusters (Slezak et al. 1994; Grebenev et al. 1995a; Rosati et al. 1995; Vikhlinin et al. 1997; Biviano et al. 1996).

In the context of an individual IBIS/ISGRI observation, we are interested in removing all large-scale structures from non-uniform sky background rather than in detecting of point sources. The task is greatly simplified by the coded-mask aperture technique not being able to reconstruct an image of objects with a spatial size greater than the angular resolution of the telescope. For point source detection, all structures that are more extended than a point source can be safely removed. In other words, we do not need any thresholds to distinguish noise and signal, so we can remove systematic residuals with a given angular scale ``as is''. In this way, the WT works as a non-parametric sky background approximation. In the similar way, the wavelet transform was used for subtracting nonuniform background and for filtering images obtained with the coded-mask X-ray telescope ART-P aboard the GRANAT mission (Grebenev et al. 1995b).

4.2 Wavelet decomposition method

To decompose a sky image, we use the à trous digital wavelet transform (DWT) algorithm because it allows easy reconstruction (Slezak et al. 1994; Starck & Murtagh 1994; Vikhlinin et al. 1997). The method uses a kernel KJ = FJ - FJ+1, where integer J is the so-called spatial scale index. Each FJ is constructed by five weighting coefficients  [1,4,6,4,1]/16 spaced by a 2J-1 interval. Each FJ can be roughly approximated by a Gaussian of width 2J-1 (F1 is a $\delta$-function). The convolution of an image with FJ preserves flux ( $\Sigma F_J=1,\forall _J$), and convolution with KJ emphasizes the structures with the characteristic size ${\approx}2^{J-1}$ pixels, or 2J+1 arcmin in the case of the IBIS/ISGRI image ( $1~{\rm pix}\approx4\hbox{$^\prime$ }$). Thus, low J values correspond to small spatial variations or high frequency, and high J reflects large spatial variations or low frequency.

\begin{figure} \par\includegraphics[width=4.3cm,clip]{13814fg8a.ps}\includegraphics[width=4.3cm,clip]{13814fg8b.ps} \end{figure} Figure 8:

Sky region around NGC 4151 accumulated with a sequence of 95 staring observations (spacecraft orbits 74-76). The total dead-time corrected exposure is 280 ks. The angular size of each image is $30^{\circ }$ $\times $  $30^{\circ }$. The left mosaic image is obtained by the general method (Sect. 2). The image on the right was produced by summing up images of individual observations corrected with à trous wavelet decomposition algorithm (Sect. 4.1). The standard deviation of source-free pixels in the left and right images relates as 1.3 and 1.0, respectively. The new hard X-ray source IGR J11203+4531, detected during this observation is labeled in green. To illustrate how the algorithm works, we extracted the vertical profile from the green rectangular region in the left image (Fig. 10).

Open with DEXTER

On the largest scale, N the kernel KN=FN. The original image I can be easily decomposed to its convolutions, WJ (``wavelet planes of scale J''), with kernels KJ:

\begin{displaymath}% I=\Sigma_{J=1}^N W_J. \end{displaymath} (4)

Therefore, we can consider WJ an image containing ``flux'' on scale J, and the sum of all fluxes yields the original image. This is the basis of the wavelet decomposition algorithm. The original image is convolved with the wavelet of the first scale. The wavelet plane on the first scale is removed from the image. We then go to the next scale J+1. In other words, we remove all small-scale features from the image before working on larger scales. That is why the small-scale features (high spatial frequency) do not affect the convolution on larger scales (at low spatial frequency). Obviously, this algorithm greatly reduces the interference of the point source with large-scale kernels.

To remove the large-scale systematic structures seen in the left image of Fig. 8, we start with a deconvolved source-free sky image of individual observation: 1) flux image is decomposed to the wavelet planes. The systematic residuals are clearly seen on scales J=5,6,7. After that; we 2) restore the original image by Eq. (4) omitting these scales; and 3) return the source fluxes to the sky as described in the general reconstruction method (Goldwurm et al. 2003; Krivonos et al. 2005).

We should stress that DWT filtering is used on sky flux images, where systematic residuals are emphasized. The sky variance map was not filtered, because it only contains formal uncertainties related to the exposure time for a given sky direction.

4.3 Impact on point sources

Table 1:   Reconstruction of the point source flux with different sets of wavelet planes.

According to the above section, the cleaning procedure operates on the source-free images, i.e. images free of cataloged sources. Therefore, DWT filtering does not directly affect the flux of known sources. However, if position of the source is unknown, its flux will not be removed from the detector before sky deconvolution, which means that source will appear on the sky. In this case, the DWT filtering will clean sky background with an embedded point source. The important question is how the implemented DWT filtering affects the flux of such a point source. The main idea is that the DWT procedure must not significantly change the point source flux.

To investigate this issue, we used standard on-axis observation of the bright source, Crab Nebula, with a total exposure of 2.7 ks. We performed DWT decomposition of the reconstructed sky image of Crab, for the range of scales 1-8. The image was then reconstructed by summing up selected wavelet scales. Crab flux was estimated on the final sky image, convolved with the effective point spread function (Krivonos et al. 2007b). Table 1 contains the measured Crab flux for the different sets of wavelet scales. The flux is expressed as a fraction relative to the flux in the original sky image. As seen from the table, ${\sim}94\%$ of the point source flux resides in the high-frequency wavelet scales 1-4, and the rest contributes to the low-frequency scales 5-8.

If we assume that the point source is significantly affected when ${\sim}5\%$ of its flux is greater than the $1\sigma$ survey detection threshold, then wavelet filtering distorts only the point sources at a detection level of  ${>}20\sigma$. Obviously, such strong known sources are removed from the detector shadowgram before sky deconvolution, and returned to the sky image after the DWT filtering in steps 1-2. New sources detected in the survey generally have a detection significance of less than $10\sigma$. We conclude that the implemented wavelet filtering method does not affect the flux of point sources, and does not introduce significant distortion to the survey sensitivity.

4.4 Extragalactic sky

\begin{figure} \par\includegraphics[width=8.8cm,clip]{13814fg9.eps} \end{figure} Figure 9:

Signal-to-noise ratio distribution of a number of pixels in a 280 ks staring-mode observation of NGC 4151. The SNR distribution of the image obtained with the general method (Fig. 8, left) is shown in red. The blue histogram shows pixel variance distribution of the sky mosaic accumulated with WT cleaned images (Sect. 4.1). The dashed line represents the normal distribution with unit variance and zero mean.

Open with DEXTER

We performed DWT cleaning procedure (Sect. 4.2) for each observation of the already mentioned NGC 4151 staring mode campaign. The resulting image is presented in Fig. 8, to the right. It is clearly seen that all large-scale artifacts are totally removed, leaving a clean sky image. To demonstrate this improvement, we built S/N distribution for pixels in the source-free sky image. The S/N distribution of the original image (Fig. 8, left) is represented in Fig. 9 by the red histogram. It can be approximated by a Gaussian with $\sigma\approx1.3$, which is consistent with the measured standard deviation of image pixels. The SNR histogram of the wavelet filtered sky image is plotted in blue. The last is well approximated by a normal distribution with a unit variance and zero mean, which means that the systematic noise has been completely removed. Assuming a normal distribution of N=183 606 pixels on a cleaned image, we expect 5 occurrences at a significance level $\sigma=\pm4.2$. However, we detect 12 and 2 excesses at negative and positive values, respectively. We conclude that, for the simplified case of extragalactic observation, the DWT filtering significantly supresses (practically removes) systematic noise.

Until now, about 3 Ms of INTEGRAL exposure time has been performed in staring mode. Usually, these observations are excluded from sky mosaics owing to high systematics. By cleaning these observations with DWT we can add them to the survey.

It is interesting to note that, by averaging the archival staring observation of NGC 4151, we detected a new transient source IGR J11203+4531 at sky position RA = $\rm 11^h20^m21.60^s$, Dec = $\rm 45^d31^m48.0^s$ (equinox 2000.0, uncertainty 4 arcmin). The source was found at the FOV edge where strong systematics prevented its detection before (see Figs. 8 and 10). The source is seen at S/N=5.3 on the original mosaic with $\rm rms=1.3$, which gives $4\sigma$ excess. The systematics is gone on the cleaned sky, and the source has S/N=5.7 on the image with $\rm rms=1.0$; i.e., the source is revealed at $5.7\sigma$. This is demonstrated by the average image profiles shown in Fig. 10. The follow-up Swift/XRT observation of IGR J11203+4531 revealed two nearby sources with coordinates RA = $\rm 11^h20^m26.92^s$, Dec = +45:34:53.77 and RA = $\rm 11^h20^m33.76^s$, Dec = +45:28:17.92 (error radii according to the ``xrtcentroid'' program are 5.96 and 5.31 arcsec, respectively).

\begin{figure} \par\mbox{\includegraphics[width=8.5cm]{13814fg10a.ps}\includegra... ...0b.ps}\includegraphics[width=8.5cm]{13814fg10d.ps} }\vspace*{5mm} \end{figure} Figure 10:

Illustration of a non-parametric approximation of sky background  a) and  b) and source detection  c) and  d) with an à trous DWT algorithm. The black histogram in the panel  a) is a vertically averaged profile of the sky image in Fig. 8, extracted from the denoted green region. Blue, green, and magenta curves are vertical profiles of corresponding wavelet components on the spatial scales J=5,6,7 ( ${\sim }1,2,4$ degrees). The sum of these components (red curve) represents a sky-image background approximation that need to be subtructed. The corresponding residual profile is shown in the bottom panel  b). The abscissa axis is measured in the offset from the position of newly detected hard X-ray source IGR J11203+4531 (red arrow). The right panels  c and  d) have been made in the same way. The black histogram in the top panel  c) demonstrates an actual S/N pixel values extracted along the line perpendicular to the green rectangular region in Fig. 8, and crossing the source IGR J11203+4531. The long dashed lines represent the actual detection thresholds in standard deviations scaled from the rms value measured on all the image pixels.

Open with DEXTER

4.5 GC region

However, we are mainly interested in improving sensitivity in the region of the GP where most of the exposures were collected. The sky image of the GP with the maximum available exposure (${\sim}20$ Ms in the GC) produced by the general reconstruction method is shown in the upper image in Fig. 11. The sky background behind the bright sources is contaminated by strong systematics, which significantly limits sensitivity for source detection. In the same data set, by taking the Galactic X-ray background into account and using DWT sky filtering, we obtain a new deep image of the GP demonstrated in the lower panel. As seen from the sky image, most of the systematic artifacts are removed, leaving a more or less uniform sky background. Obviously, the quality of the reconstructed sky is improved.

To demonstrate the efficiency of the improved reconstruction method, we built the S/N distribution of the source-free $30^{\circ }$ $\times $ $30^{\circ }$ region around the GC for general and DWT-corrected sky (Fig. 13). The S/N distribution for the general sky has wide non-Gaussian sidelobes. The histogram representing the cleaned sky is narrow, but still far from normal distribution. This means that systematic artifacts are reduced, but still present on the sky. We measured the standard deviation of image pixels masking out bright sources. For the cleaned and general sky, standard deviation relates as 1.33/1.84, which gives us the total sensitivity improvement of  ${\sim}28\%$. After taking out the irreducible Poisson statistics with unit standard deviation, the suppression of systematic noise in the ${\sim}20$ Ms deep field of the GC region is  ${\sim}44\%$.

\begin{figure} \par\includegraphics[width=17cm,clip]{13814fg11a.ps}\vspace*{-1mm} \includegraphics[width=17cm,clip]{13814fg11b.ps} \end{figure} Figure 11:

Map of the sky region near the GP obtained with IBIS/ISGRI in the 17-60 keV energy band. The total exposure is about 20 Ms in the GC region. Upper panel: sky mosaic acquired by the general sky reconstruction method (see Sect. 2). Lower panel: sky mosaic produced by an improved reconstruction algorithm (Sect. 4). The corresponding S/N distributions of pixels in a $30^{\circ }$ $\times $ $30^{\circ }$ region around the GC are shown in Fig. 13.

Open with DEXTER

5 Survey

For our analysis we used all data publicly available in July 2009 and observations performed as a part of the GRXE study program (PI Sunyaev). The latter is mainly based on the Russian quota of INTEGRAL observing time. The sky image of any individual observation was produced by the modified sky reconstruction method described in this work. The obtained sky images were added to the all-sky mosaics covering the whole sky.

Table 2:   Survey limiting flux in mCrabs for source detection at the $5\sigma $ significance level (17-60 keV, $1~{\rm mCrab}=1.43$ $\times $ 10-11 erg s-1 cm-2).

The survey coverage area is shown in Fig. 12. We calculated a fraction of the sky area covered by the survey at nominal and effective sensitivity. In the first case, the sensitivity is essentially the detection threshold, estimated from actual exposure. The effective sensitivity was estimated by multiplying the nominal error map by variances of local background. The limiting flux and sensitivity for $10\%$ and $90\%$ of the sky coverage are summarized in Table 2.

General sky reconstruction method: the survey's limiting flux for the longest exposure is ${\sim}35\%$ higher than nominal. For a large coverage area at high limiting flux, which is typical of high-latitude observations, the effective sensitivity is ${\sim}15\%$ lower than expected.

Modified sky reconstruction method: the survey effective coverage is apparently closer to the nominal. In the region of low limiting flux, the effective sensitivity is ${\sim}27\%$ worse than nominal. The sky coverage at high flux is consistent with what is expected from an actual exposure, i.e. Poisson statistics.

In Fig. 14 we show survey sensitivity as a function of exposure time. Generally, the survey sensitivity grows with exposure by T-1/2 as expected. The region of high exposure in the GC is noticeable by its reduced sensitivity in contrast to extragalactic observations where the limiting flux is expected to follow pure statistics. Again, the survey sensitivity of the modified method is closer to a nominal sensitivity.

6 Conclusion

We presented the improved sky reconstruction method for the IBIS telescope, which suppresses the systematic effects. First, the method considers extended Galactic X-ray ridge emission that strongly affects the background illumination of the ISGRI detector. Second, we applied a non-parametric (model-free) background approximation based on an à trous wavelet decomposition. The wavelet cleaning was naturally integrated into the sky reconstruction process with the main advantage that we knew exactly what we were filtering out without distorting the original sky flux. The overall systematic noise in the ${\sim}20$ Ms deep field of the GC was reduced by  ${\sim}44\%$, thereby improving the the total sensitivity of observations by  ${\sim}28\%$. The reconstructed sky images of high galactic latitude fields were practically free of systematic residuals, and the sensitivity was consistent with what is expected from Poisson statistics.

\begin{figure} \par\includegraphics[width=8.9cm,clip]{13814fg12.ps} \end{figure} Figure 12:

Fraction of the sky surveyed as a function of the limiting flux for source detection with $5\sigma $ significance. The black curve demonstrates sky coverage for nominal sensitivity. The effective sensitivity estimated for general and modified sky reconstruction methods are shown by the red and blue curves, respectively (see Sect. 5).

Open with DEXTER

\begin{figure} \vspace*{-3mm} \includegraphics[width=8.1cm,clip]{13814fg13.eps} \end{figure} Figure 13:

Distribution of formal pixel significance in a $30^{\circ }$ $\times $ $30^{\circ }$ region around the GC (Fig. 11). For plot description see Fig. 9.

Open with DEXTER

\begin{figure} \par\includegraphics[width=8.8cm,clip]{13814fg14a.ps}\vspace*{1mm} \includegraphics[width=8.8cm,clip]{13814fg14b.ps} \end{figure} Figure 14:

Measured $5\sigma $ limiting flux for cataloged source positions on the final total average all-sky map, as a function of effective dead-time corrected exposure time. The top and bottom panels demonstrate the sensitivity of general and modified sky reconstruction methods, respectively. The blue points reflect nominal sensitivity changing with exposure by T-1/2 as expected. The solid line represents the fit to the nominal sensitivity versus exposure: $f^{5\sigma }_{\rm lim}=0.77$ $\times $ $(T/{\rm Ms})^{-1/2}$ mCrab. The green and red points are $5\sigma $ actual sensitivity taking into account background variations in the field of each $20^{\circ }$ $\times $ $20^{\circ }$ sky projection (Sect. 5). The sensitivity measured in (and out of) sky region $\vert l\vert<20^{\circ }$ and $\vert b\vert<15^{\circ }$ is shown in red (green).

Open with DEXTER

Most of the INTEGRAL observing time was spent in the GP and GC, giving us the possibility of conducting the most sensitive survey ever made of the Milky Way above 20 keV. The minimal detectable flux with a $5\sigma $ detection level reached the level of 3.7 $\times $ 10-12 erg s-1 cm-2, which is ${\sim}0.26$ mCrab in the 17-60 keV energy band. The survey covered $90\%$ of the sky down to the flux limit of 6.2 $\times $ 10-11 erg s-1 cm-2 ( ${\sim}4.32$ mCrab) and $10\%$ of the sky area down to the flux limit of 8.6 $\times $ 10-12 erg s-1 cm-2 ( ${\sim}0.60$ mCrab). A catalog of sources detected in the survey is presented in the paper by Krivonos et al. (2010).

Acknowledgements
We are grateful to the anonymous referee for the critical remarks that helped us improve the paper. The data used were from the European and Russian INTEGRAL Science Data Centers[*]'[*]. The work was supported by the President of the Russian Federation (through the program supporting leading scientific schools, project NSH-5069.2010.2), by the Presidium of the Russian Academy of Sciences/RAS (the program ``Origin, Structure, and Evolution of Objects of the Universe''), by the Division of Physical Sciences of the RAS (the program ``Extended objects in the Universe'', OFN-17), and by the Russian Basic Research Foundation (project 09-02-00867). S.S. acknowledges the support of the Dynasty Foundation. R.K. would like to express his sincere gratitude to Kate O'Shea for her support in the preparation of the paper.

References

  1. Barthelmy, S. D., Barbier, L. M., Cummings, J. R., et al. 2005, Space Sci. Rev., 120, 143 [NASA ADS] [CrossRef] [Google Scholar]
  2. Bassani, L., Molina, M., Malizia, A., et al. 2006, ApJ, 636, L65 [NASA ADS] [CrossRef] [Google Scholar]
  3. Bazzano, A., Stephen, J. B., Fiocchi, M., et al. 2006, ApJ, 649, L9 [NASA ADS] [CrossRef] [Google Scholar]
  4. Beckmann, V., Soldi, S., Ricci, C., et al. 2009, A&A, 505, 417 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Bird, A. J., Barlow, E. J., Bassani, L., et al. 2004, ApJ, 607, L33 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bird, A. J., Barlow, E. J., Bassani, L., et al. 2006, ApJ, 636, 765 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Bird, A. J., Malizia, A., Bazzano, A., et al. 2007, ApJS, 170, 175 [NASA ADS] [CrossRef] [Google Scholar]
  8. Bird, A. J., Bazzano, A., Bassani, L., et al. 2010, ApJS, 186, 1 [NASA ADS] [CrossRef] [Google Scholar]
  9. Biviano, A., Durret, F., Gerbal, D., et al. 1996, A&A, 311, 95 [NASA ADS] [Google Scholar]
  10. Cusumano, G., La Parola, V., Segreto, A., et al. 2010, A&A, 510, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Del Santo, M., Rodriguez, J., Ubertini, P., et al. 2003, A&A, 411, L369 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Dwek, E., Arendt, R. G., Hauser, M. G., et al. 1995, ApJ, 445, 716 [CrossRef] [Google Scholar]
  13. Eckert, D., Produit, N., Paltani, S., Neronov, A., & Courvoisier, T. J.-L. 2008, A&A, 479, 27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Fenimore, E. E., & Cannon, T. M. 1978, APO, 17, 337 [Google Scholar]
  15. Fenimore, E. E., & Cannon, T. M. 1981, Appl. Opt., 20, 1858 [Google Scholar]
  16. Gehrels, N., Chincarini, G., Giommi, P., et al. 2004, ApJ, 611, 1005 [NASA ADS] [CrossRef] [Google Scholar]
  17. Goldwurm, A., David, P., Foschini, L., et al. 2003, A&A, 411, L223 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Grebenev, S. A., Forman, W., Jones, C., & Murray, S. 1995a, ApJ, 445, 607 [NASA ADS] [CrossRef] [Google Scholar]
  19. Grebenev, S. A., Pavlinsky, M. N., & Sunyaev, R. A. 1995, Proc. of the Workshop, Imaging in High Energy Astronomy, held in Anacapri, Sept. 26-30, 1994, ed. L. Bassani, & G. di Cocco (Dordrecht: Kluwer Academic Publishers), 155 [Google Scholar]
  20. Krivonos, R., Vikhlinin, A., Churazov, E., et al. 2005, ApJ, 625, 89 [NASA ADS] [CrossRef] [Google Scholar]
  21. Krivonos, R., Revnivtsev, M., Churazov, E., et al. 2007a, A&A, 463, 957 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Krivonos, R., Revnivtsev, M., Lutovinov, A., et al. 2007b, A&A, 475, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Krivonos, R., Tsygankov, S., Revnivtsev, M., et al. 2010, A&A, in press [Google Scholar]
  24. Lebrun, F. 2005, IEEE Transactions on Nuclear Science, 52, 3119 [NASA ADS] [CrossRef] [Google Scholar]
  25. Molkov, S. V., Cherepashchuk, A. M., Lutovinov, A. A., et al. 2004, AstL, 30, 534 [Google Scholar]
  26. Reglero, V., Sánchez, F., Rodrigo, J., et al. 2001, ESASP, 459, 619 [NASA ADS] [Google Scholar]
  27. Revnivtsev, M. G., Sazonov, S. Y., Gilfanov, M. R., & Sunyaev, R. A. 2003, Astron. Lett., 29, 587 [NASA ADS] [CrossRef] [Google Scholar]
  28. Revnivtsev, M., Sunyaev, R., Varshalovich, D., et al. 2004, Astron. Lett., 30, 382 [NASA ADS] [CrossRef] [Google Scholar]
  29. Revnivtsev, M. G., Sazonov, S. Y., Molkov, S. V., et al. 2006a, Astron. Lett., 32, 145 [NASA ADS] [CrossRef] [Google Scholar]
  30. Revnivtsev, M., Sazonov, S., Gilfanov, M., Churazov, E., & Sunyaev, R. 2006b, A&A, 452, 169 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Rodriguez, J., Del Santo, M., Lebrun, F., et al. 2003, A&A, 411, L373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Rosati, P., della Ceca, R., Burg, R., Norman, C., & Giacconi, R. 1995, ApJ, 445, L11 [NASA ADS] [CrossRef] [Google Scholar]
  33. Sazonov, S., Revnivtsev, M., Krivonos, R., Churazov, E., & Sunyaev, R. 2007, A&A, 462, 57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Skinner, G. K., Ponman, T. J., Hammersley, A. P., & Eyles, C. J. 1987, Ap&SS, 136, 337 [NASA ADS] [CrossRef] [Google Scholar]
  35. Slezak, E., Durret, F., & Gerbal, D. 1994, AJ, 108, 1996 [NASA ADS] [CrossRef] [Google Scholar]
  36. Starck, J.-L., & Murtagh, F. 1994, A&A, 288, 342 [NASA ADS] [Google Scholar]
  37. Tueller, J., Baumgartner, W. H., Markwardt, C. B., et al. 2010, ApJS, 186, 378 [NASA ADS] [CrossRef] [Google Scholar]
  38. Ubertini, P., Lebrun, F., Di Cocco, G., et al. 2003, A&A, 411, L131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Vikhlinin, A., Forman, W., & Jones, C. 1997, ApJ, 474, L7 [NASA ADS] [CrossRef] [Google Scholar]
  40. Winkler, C., Gehrels, N., Lund, N., Schönfelder, V., & Ubertini, P. 1999, Astrophys. Lett. Commun., 39, 361 [Google Scholar]
  41. Winkler, C., Courvoisier, T. J.-L., Di Cocco, G., et al. 2003, A&A, 411, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Worrall, D. M., Marshall, F. E., Boldt, E. A., & Swank, J. H. 1982, ApJ, 255, 111 [NASA ADS] [CrossRef] [Google Scholar]

Footnotes

... reconstruction[*]
Based on observations with INTEGRAL, an ESA project with the instruments and science data center funded by ESA member states (especially the PI countries: Denmark, France, Germany, Italy, Switzerland, Spain), Czech Republic, and Poland, and with the participation of Russia and the USA.
... staring[*]
All observations performed in ``staring'' mode have fixed orientation and the roll angle of the telescope.
... Centers[*]
http://isdc.unige.ch
...'[*]
http://hea.iki.rssi.ru/rsdc

All Tables

Table 1:   Reconstruction of the point source flux with different sets of wavelet planes.

Table 2:   Survey limiting flux in mCrabs for source detection at the $5\sigma $ significance level (17-60 keV, $1~{\rm mCrab}=1.43$ $\times $ 10-11 erg s-1 cm-2).

All Figures

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{13814fg1.ps} \end{figure} Figure 1:

Sky image of a 2.7 ks observation of the bright source Crab Nebula. The source is in the center of the field of view. The periodic mask pattern leads to many false sources on the reconstructed sky. The most significant false peaks are located in vertexes of a  ${\sim }10.5^{\circ }$square around the source, oriented in detector coordinates as illustrated by the yellow square. The image is shown in significance with a squared root color map ranging from 0 to 25. Such color schemes are used for all the sky images in this paper in order to emphasize sky background variations. The black and blue colors correspond to pixel values from 0 to 2. The red pixels have values of around 5. The yellow to white color transition corresponds to 15 and more. Figure 2 demonstrates an image profile extracted from the $1^{\circ }$ $\times $ $29^{\circ }$ green region.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{13814fg2.ps} \end{figure} Figure 2:

Image profile extracted from the green region in Fig. 1. The profile demonstrates the response of the IBIS/ISGRI imaging system to the point source.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=17.5cm,clip]{13814fg3.ps} \end{figure} Figure 3:

INTEGRAL/IBIS hard X-ray (17-60 keV) map of the sky region around the GC. The green squares demonstrate the relative sky positions of false side peaks (``ghosts'', see Fig. 1) of selected bright sources.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=4.4cm,clip]{13814fg4a.eps}\hspace*{1mm} \includegraphics[width=4.4cm,clip]{13814fg4b.eps} \end{figure} Figure 4:

Two relative alignments of the GP in the IBIS FOV, left centered and the right shifted along the galactic latitude. The blue contours are isophotes of the $4.9~\mu{\rm m}$surface brightness of the Galaxy (COBE/DIRBE) revealing the bulge/disk structure of the inner Galaxy. The NIR brightness of the galaxy traces the hard X-ray ridge emission. The small and large rounded squares on each plot demonstrate the full and partial coded areas, respectively. The points show sky positions of the hard X-ray sources detected on the 20 Ms time-averaged map (Figs. 11 and 3). A signal-to-noise ratio of the sources is shown by black (5-10), blue (10-30), and red (>30). The difference in detector illumination by the Ridge is shown in Fig. 5.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=4.4cm,clip]{13814fg5a.ps}\hspace*{1mm} \includegraphics[width=4.4cm,clip]{13814fg5b.ps} \end{figure} Figure 5:

The contribution of Galactic X-ray background to the ISGRI detector count rate for different alignments of the GP in the IBIS FOV (see also Fig. 4). The detector count rate normalization is estimated from actual observation of the GC in the energy range 17-60 keV. The corresponding images in Figs. 4 and 5 are co-aligned in detector coordinates. The ridge, appearing in the given FOV corner, illuminates the opposite corner in the detector image.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=4.25cm,clip]{13814fg6a.eps}\includegraphics[width=4.4cm,clip]{13814fg6b.eps} \end{figure} Figure 6:

Left: the sky mosaic of 280 ks observation of NGC 4151 in staring mode. The Ridge contribution (Fig. 5, right) was artificially added to the detector plane for each individual observation. For reference see the left image in Fig. 8. Right: S/N distribution of a number of pixels in a reference and current sky images shown by red and blue histograms, respectively. The long dashed line represents the normal distribution with unit variance and zero mean.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{13814fg7.ps} \end{figure} Figure 7:

Left: the ISGRI detector image of the GC region ( $l=3.9^{\circ }$, $b=2.1^{\circ }$). Right: the shadowgram of a sky region containing only one bright source Sco X-1 ( $l=4.5^{\circ }$, $b=30.0^{\circ }$).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=4.3cm,clip]{13814fg8a.ps}\includegraphics[width=4.3cm,clip]{13814fg8b.ps} \end{figure} Figure 8:

Sky region around NGC 4151 accumulated with a sequence of 95 staring observations (spacecraft orbits 74-76). The total dead-time corrected exposure is 280 ks. The angular size of each image is $30^{\circ }$ $\times $  $30^{\circ }$. The left mosaic image is obtained by the general method (Sect. 2). The image on the right was produced by summing up images of individual observations corrected with à trous wavelet decomposition algorithm (Sect. 4.1). The standard deviation of source-free pixels in the left and right images relates as 1.3 and 1.0, respectively. The new hard X-ray source IGR J11203+4531, detected during this observation is labeled in green. To illustrate how the algorithm works, we extracted the vertical profile from the green rectangular region in the left image (Fig. 10).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{13814fg9.eps} \end{figure} Figure 9:

Signal-to-noise ratio distribution of a number of pixels in a 280 ks staring-mode observation of NGC 4151. The SNR distribution of the image obtained with the general method (Fig. 8, left) is shown in red. The blue histogram shows pixel variance distribution of the sky mosaic accumulated with WT cleaned images (Sect. 4.1). The dashed line represents the normal distribution with unit variance and zero mean.

Open with DEXTER
In the text

  \begin{figure} \par\mbox{\includegraphics[width=8.5cm]{13814fg10a.ps}\includegra... ...0b.ps}\includegraphics[width=8.5cm]{13814fg10d.ps} }\vspace*{5mm} \end{figure} Figure 10:

Illustration of a non-parametric approximation of sky background  a) and  b) and source detection  c) and  d) with an à trous DWT algorithm. The black histogram in the panel  a) is a vertically averaged profile of the sky image in Fig. 8, extracted from the denoted green region. Blue, green, and magenta curves are vertical profiles of corresponding wavelet components on the spatial scales J=5,6,7 ( ${\sim }1,2,4$ degrees). The sum of these components (red curve) represents a sky-image background approximation that need to be subtructed. The corresponding residual profile is shown in the bottom panel  b). The abscissa axis is measured in the offset from the position of newly detected hard X-ray source IGR J11203+4531 (red arrow). The right panels  c and  d) have been made in the same way. The black histogram in the top panel  c) demonstrates an actual S/N pixel values extracted along the line perpendicular to the green rectangular region in Fig. 8, and crossing the source IGR J11203+4531. The long dashed lines represent the actual detection thresholds in standard deviations scaled from the rms value measured on all the image pixels.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=17cm,clip]{13814fg11a.ps}\vspace*{-1mm} \includegraphics[width=17cm,clip]{13814fg11b.ps} \end{figure} Figure 11:

Map of the sky region near the GP obtained with IBIS/ISGRI in the 17-60 keV energy band. The total exposure is about 20 Ms in the GC region. Upper panel: sky mosaic acquired by the general sky reconstruction method (see Sect. 2). Lower panel: sky mosaic produced by an improved reconstruction algorithm (Sect. 4). The corresponding S/N distributions of pixels in a $30^{\circ }$ $\times $ $30^{\circ }$ region around the GC are shown in Fig. 13.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.9cm,clip]{13814fg12.ps} \end{figure} Figure 12:

Fraction of the sky surveyed as a function of the limiting flux for source detection with $5\sigma $ significance. The black curve demonstrates sky coverage for nominal sensitivity. The effective sensitivity estimated for general and modified sky reconstruction methods are shown by the red and blue curves, respectively (see Sect. 5).

Open with DEXTER
In the text

  \begin{figure} \vspace*{-3mm} \includegraphics[width=8.1cm,clip]{13814fg13.eps} \end{figure} Figure 13:

Distribution of formal pixel significance in a $30^{\circ }$ $\times $ $30^{\circ }$ region around the GC (Fig. 11). For plot description see Fig. 9.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{13814fg14a.ps}\vspace*{1mm} \includegraphics[width=8.8cm,clip]{13814fg14b.ps} \end{figure} Figure 14:

Measured $5\sigma $ limiting flux for cataloged source positions on the final total average all-sky map, as a function of effective dead-time corrected exposure time. The top and bottom panels demonstrate the sensitivity of general and modified sky reconstruction methods, respectively. The blue points reflect nominal sensitivity changing with exposure by T-1/2 as expected. The solid line represents the fit to the nominal sensitivity versus exposure: $f^{5\sigma }_{\rm lim}=0.77$ $\times $ $(T/{\rm Ms})^{-1/2}$ mCrab. The green and red points are $5\sigma $ actual sensitivity taking into account background variations in the field of each $20^{\circ }$ $\times $ $20^{\circ }$ sky projection (Sect. 5). The sensitivity measured in (and out of) sky region $\vert l\vert<20^{\circ }$ and $\vert b\vert<15^{\circ }$ is shown in red (green).

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.